Cycle Existence for All Edges in Folded Hypercubes under Scope Faults
Abstract
1. Introduction
2. Preliminaries
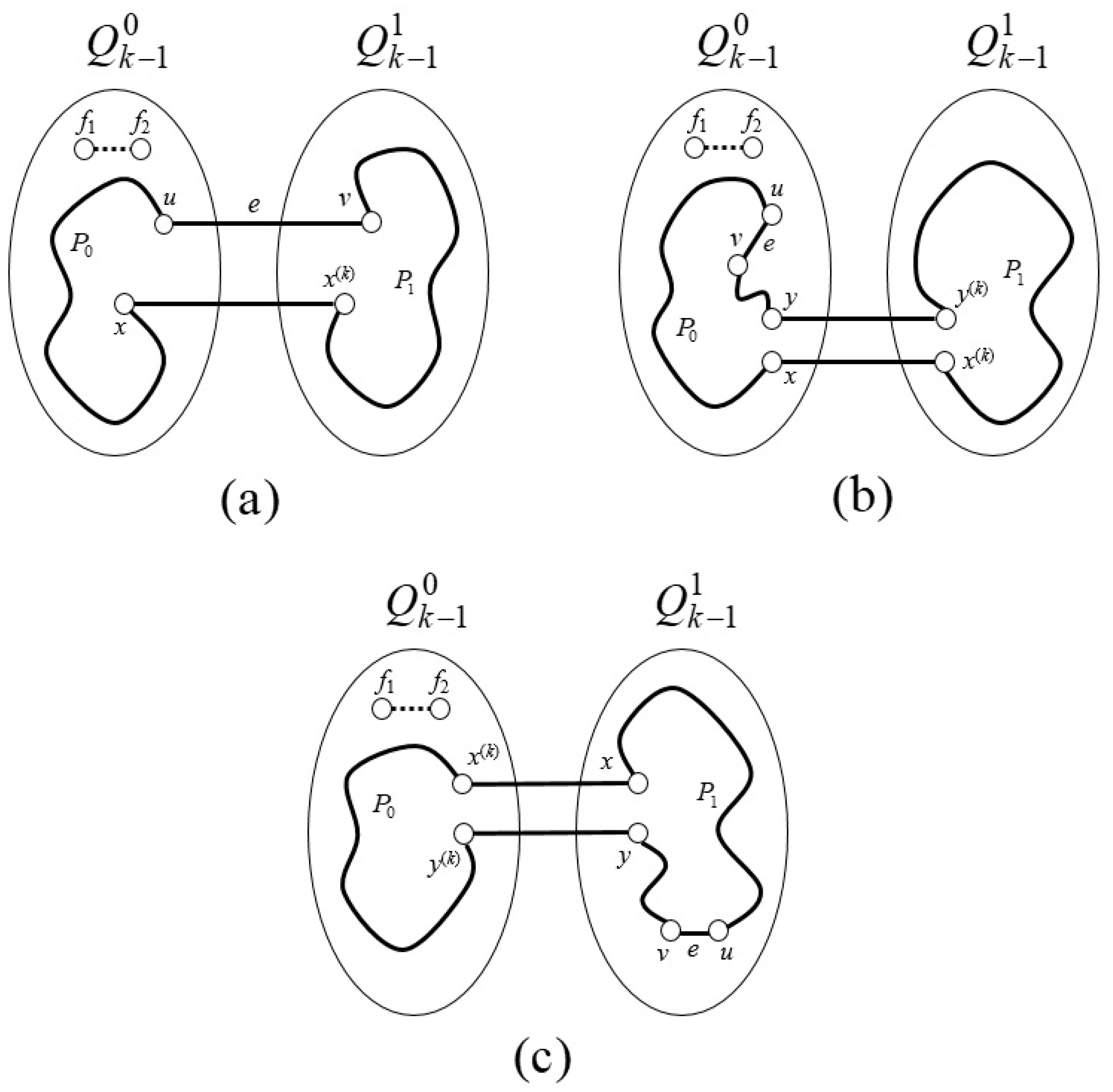
- Case 1. and are in different subcubes. Assuming and , we can make the following argument without losing generality. Let be a neighbor of in that is free of faults and is not one of or . (Note that since , must have more than four neighbors in .) By the induction hypothesis, can lie on a fault-free cycle of length in , which can be represented as . Observe that is the neighbor of in , and . As per Lemma 4, there is a path of length in . Consequently, the cycle comprising of the sequence has a length of , and it contains the edge in (Figure 2a).
- Case 2. and both are in . Using the induction hypothesis, we assume that edge belongs to a fault-free cycle in with length . We consider another edge in and express as . Since and belong to and their Hamming distance is 1, Lemma 4 implies there exists a path with length in . Therefore, the cycle has length and includes edge in (Figure 2b).
- Case 3. and both are in . Given in , by Lemma 4, we know that there exists a path of length in . Since , the length of is more than 15 in , so there must exist an edge in such that in . Since in , by induction hypothesis, can lie on a fault-free cycle of length in . We can express as . Now, we can express as . Therefore, the cycle has length and includes edge in (Figure 2c).
3. Every Cycle of Contains Any Edge
- Case 1. For . Since the structure of is symmetric. Without loss of generality, the scope faulty four-cycle F4 can be categorized into two types: those that do not contain complement edges and those that contain complement edges . With this assumption, we can observe that every fault-free edge in Table 2 and Table 3 can be found in at least one even cycle with a length between 4 to 12 in and , respectively. Hence, the case satisfies the lemma.
- Case 2. For . Assuming the symmetry of the structure of , we can, without loss of generality, consider as either or . By using Definition 1, we can apply the 2-partition on to generate two 4-dimensional subcubes, and , such that and . For any fault-free edge in , we can investigate its distribution using the following scenarios.
- Case 2.1. or . Assuming no loss of generality, we can consider . In this case, we need to account for the fact that can be found in every even cycle of length l with in . Consequently, the following subcases emerge.
- Case 2.1.1. Even length l with . By Lemma 3, since and , there exists a fault-free path of every odd length 3, 5, 7, 9, and 11 in , respectively. Thus, can form the cycle of every even length l with which obtains the edge in . Without loss of generality, we may select a cycle with length 12 and let be any edge in such that in . Then, can be expressed as . Since is fault-free in , forms a cycle of even leng which obtains the edge in . Note that , and in . By Lemma 3, there exists a fault-free path of every odd length 3, 5, 7, 9, and 11 in , respectively. Then, forms a cycle of every even length l with which obtains the edge in .
- Case 2.1.2. Even length l with . Given that and are adjacent faulty vertices and is a fault-free edge in , by Lemma 5, can be on a cycle of length 14 in . We select an edge from such that in . Then, can be expressed as . This gives rise to the following subcases.
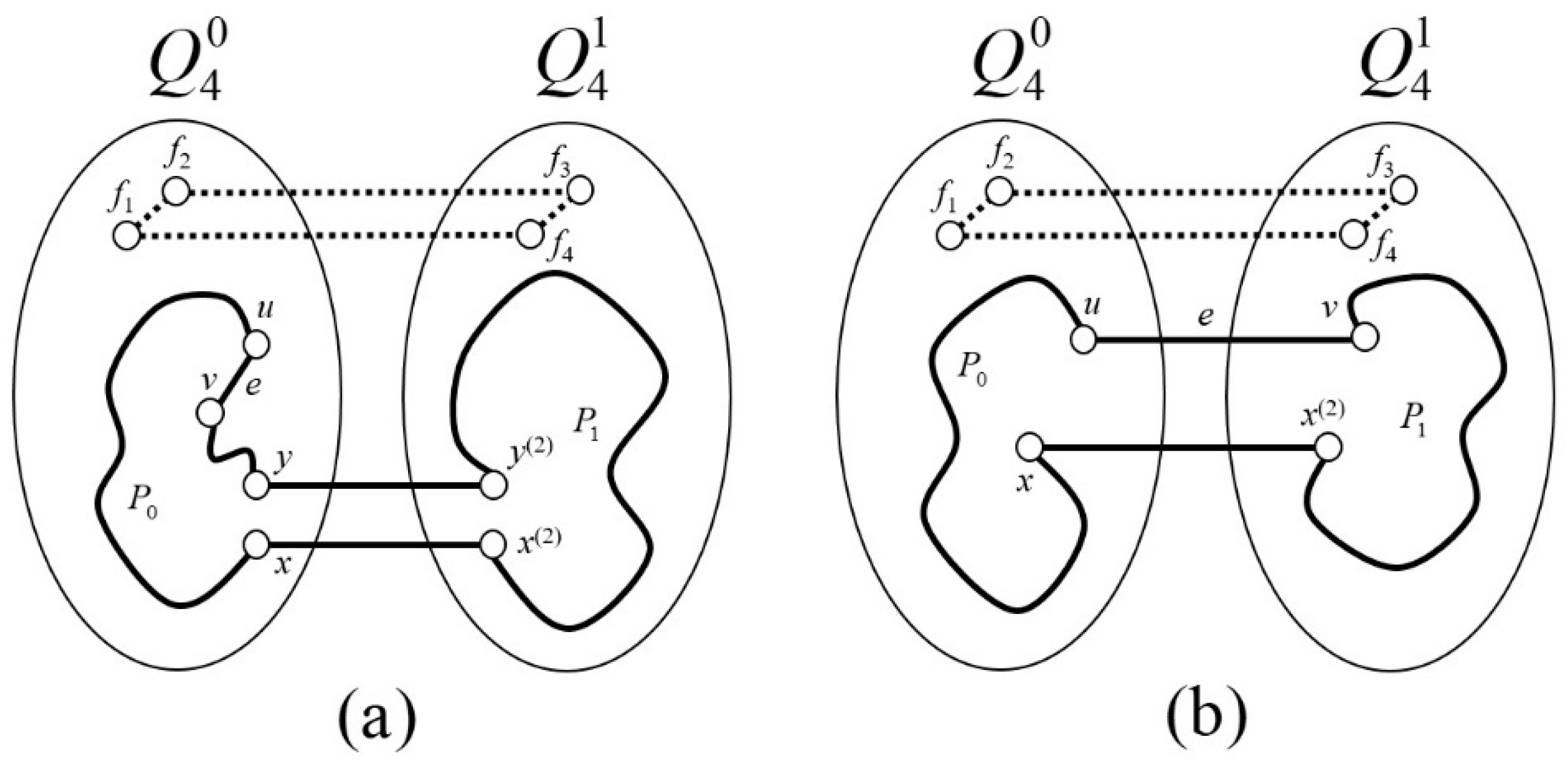
- Case 2.1.2.1. . Lemma 3 guarantees that a fault-free path of odd length 11 exists in , where . Therefore, the cycle can be expressed as , which has even length , and includes the edge in (Figure 3a).
- Case 2.1.2.2. . Given that and are two adjacent faulty vertices and is a fault-free edge in , by Lemma 5, can be on a cycle of even length 14 in . We note that can be represented as . Hence, forms a cycle of even length , which obtains the edge in .
- Case 2.2. . Assuming without loss of generality, and . We must then consider that can be obtained in any even cycle of length l with in . This gives rise to the following subcases.
- Case 2.2.1. Even length l with . Let be a fault-free neighbor of in such that in . This is possible as the neighbor of in are 4 vertices and at most one of them belongs to or , by the hypercube structure. Therefore, there exists at least one vertex that meets this condition. Without loss of generality, assume and . Note that and in and , respectively. Thus, forms a cycle of even length that contains the edge in . Moreover, since and , by Lemma 3, there exists a fault-free path of every odd length 3, 5, 7, 9, and 11 in , respectively. Therefore, can form the cycle of every even length l with that contains the edge in . To construct every cycle of even length l with , we select a path with length 11 in . Then, in , since and , by Lemma 3, there exists a fault-free path of every odd length 3, 5, 7, 9, and 11 in , respectively. Therefore, forms a cycle of every even length l with that contains the edge in .
- Case 2.2.2. Even length l with . Given that and are two adjacent faulty vertices and is an edge without faults in , according to Lemma 5, can exist on a cycle that has a length of 14 in after removing vertices and . The cycle can be expressed as . Based on this, the following subcases arise.
- Case 2.2.2.1. . Given that and , we can use Lemma 3 to conclude that there exists a fault-free path of odd length 11 in . Using this information, we can construct a cycle of even length by considering the path This cycle obtains the edge in (Figure 3b).
- Case 2.2.2.2. . According to Lemma 5, since and are two adjacent faulty vertices and is a fault-free edge in , the edge can lie on a cycle of even length 14 in . This cycle can be expressed as . Therefore, forms a cycle of even length that includes the edge in .
- Case 2.3. . Assuming without loss of generality, is in and is in . Next, we select a fault-free neighbor of in such that is not equal to either or in . It should be noted that the Hamming distance between and is one in , and the Hamming distance between and is one in . Using this approach, an edge can lie on a cycle of every even length l with in can be constructed similar to that in Case 2.2 of Lemma 6.
- Case 3. For . Suppose we have a fault-free edge in . Our goal is to show that can lie on a cycle of every even length l with in . Since and , by using Corollary 1, we can conclude that can lie on a cycle of every even length l with in . However, we also need to show that can lie on a cycle of every even length l with in . Here, be the set of faulty extreme vertices, taken from any four cycles in . As per Definition 1, since , the edges of the cycle are contained within two dimensions i and j, where and . As a result, a k-partition of exists such that one pair of adjacent vertices of the quadrilateral belongs to and the other pair belongs to . Here, we can select , and , without any loss of generality. After partition, we can explore the distribution of the edge and show that it can lie on a cycle of every even length l with in .
- Case 3.1. or . Let us assume without loss of generality that . Since and are two adjacent faulty vertices and is a fault-free edge in , we can use Lemma 5 to show that edge can lie on a cycle of length in that does not contain . We can then select any edge in such that in . Then, can be expressed as . We can then consider the following subcases.
- Case 3.1.1. . Given that and , we can use Lemma 3 to conclude that a fault-free path of odd length exists in . This path, combined with the paths and between vertices and , and vertices and respectively, can be used to form a cycle of even length . This cycle obtains the edge in . The cycle is given by .
- Case 3.1.2. . Assuming and are two adjacent faulty vertices and is a fault-free edge in , then by Lemma 5, we know that can lie on a cycle of even length in after removing faulty vertices and . The cycle can be expressed as . Therefore, we can conclude that is a cycle with even length . This cycle includes the edge and can be found in .
- Case 3.2. . Assuming without loss of generality, and , we can choose a fault-free neighbor of in such that in . Since and are two adjacent faulty vertices and be a fault-free edge in , by applying Lemma 5, we know that can lie on a cycle of length in after removing faulty vertices and . The cycle can be expressed as , which leads to the following subcases.
- Case 3.2.1. . Using Lemma 3, we can show that there exists a fault-free path of odd length in since and . Therefore, the cycle has an even length of and it contains the edge in .
- Case 3.2.2. . Using Lemma 5, we know that since and are adjacent faulty vertices and is a fault-free edge in , edge can lie on a cycle of even length in . We can express as . As a result, forms a cycle of even length , which obtains the edge in .
- Case 3.3. . Assuming and without loss of generality, we can choose a fault-free neighbor of in such that . In and , we have and , respectively. The process of constructing the edge lying on a cycle of every even length and in is similar to that described in Case 3.2 of Lemma 6.
- Case 1. For . Since the structure of is symmetric. Without loss of generality, the scope faulty four-cycle F4 can be categorized into two types: those that do not contain complement edges and those that contain complement edges . Then, using Table 4 and Table 5, we can observe that every fault-free edge can be found in at least one cycle of odd length ranging from 5 to 11 in and , respectively. Hence, the lemma holds for the case .
- Case 2. For every even . Suppose that is an edge in that is free of faults. Our goal is to show that can lie on a cycle of every odd length l such that in . Here, , , , } be the set of faulty extreme vertices, taken from any four cycles in . Note that for every even . Therefore, by Corollary 1, we know that can lie on a cycle of every odd length l with in . We also need to consider the case where can lie on a cycle of every odd length l such that in . For every even , the edges of the cycle , , , } are contained within two dimensions i and j, where and . According to Definition 1, a k-partition of exists such that one pair of adjacent vertices of the quadrilateral belongs to and the other pair belongs to . Here, we can select and . After partition, we can explore the distribution of the edge and show that it can lie on a cycle of every even length l with in .
- Case 2.1. or . It is permissible to assume that . This assumption results in the following subcases.
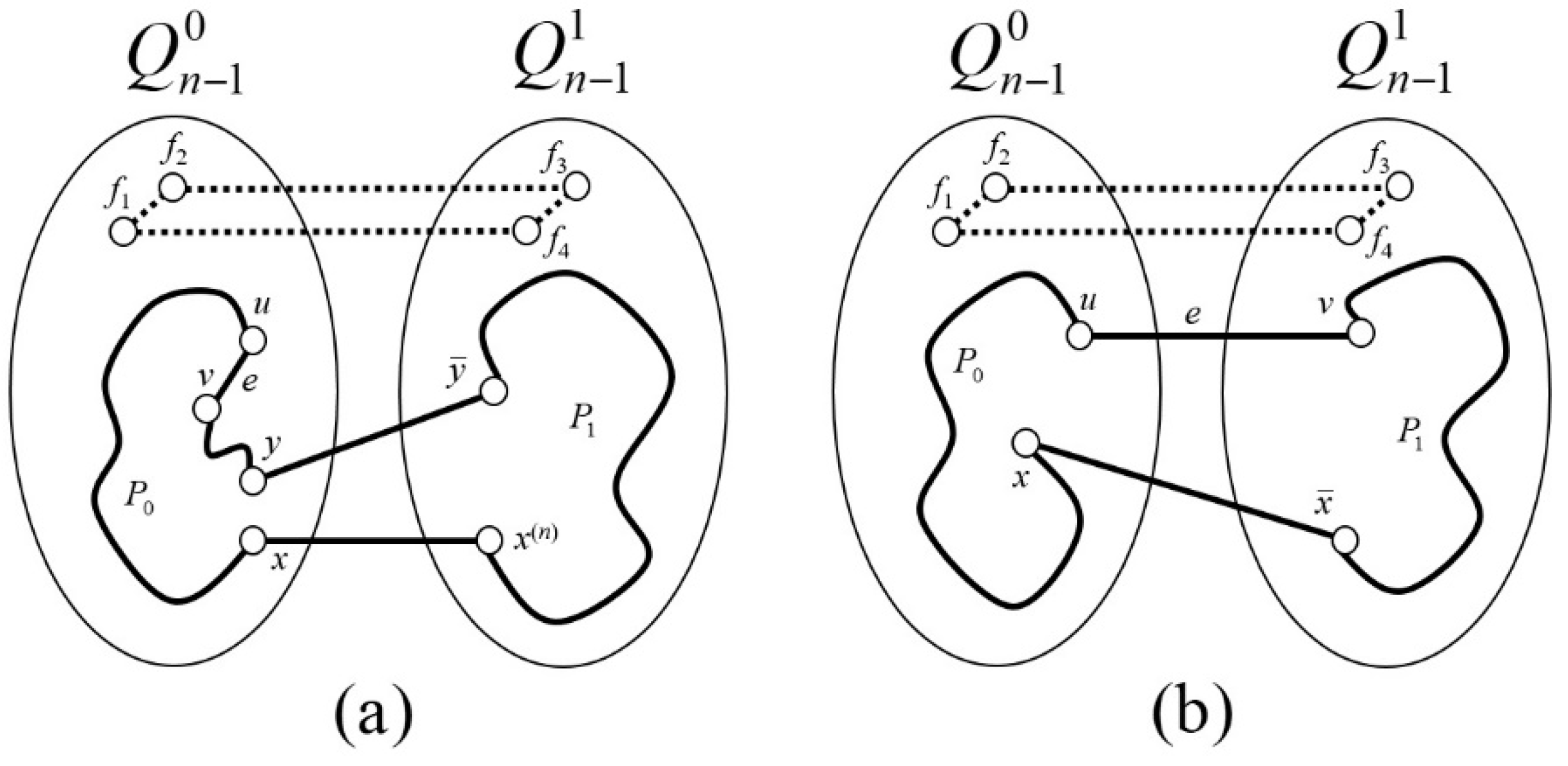
- Case 2.1.1. . According to Lemma 3, in , there exists a fault-free path of odd length in , since and . Let be an edge in such that in . Since for every even , it is not difficult to find such an edge . By Lemma 2, there exists a fault-free path of even length in , since and are two adjacent faulty vertices and in . Note that is even for every even , which means that vertices and are in the same partite set. Then, the cycle forms a cycle of odd length , which obtains the edge in (Figure 4a).
- Case 2.1.2. . Since is a fault-free edge in and and are two adjacent faulty vertices, Lemma 5 implies that can lie on a cycle with even length in . Let be any edge in such that in . We can express as . Since and are two adjacent faulty vertices and in , Lemma 2 implies that there exists a fault-free path of even length in . Then, the cycle has an odd length of , which contains the edge in .
- Case 2.2. . Assuming without loss of generality, we can take to be an element of and to be an element of . We can then find a neighbor of in that is free from faults and satisfies the condition in . This gives rise to the following subcases.
- Case 2.2.1. . By utilizing Lemma 3, it can be observed that a fault-free path of odd length exists in since and in . Moreover, as per Lemma 2, a fault-free path of even length exists in because and are two adjacent faulty vertices and in . Therefore, the cycle of odd length obtains the edge in (Figure 4b).
- Case 2.2.2. . Given that and are two adjacent faulty vertices, and is a fault-free edge in , we can apply Lemma 5 to conclude that can lie on a cycle of even length in . We can represent this cycle as . Note that and are two adjacent faulty vertices and in . By applying Lemma 2, we can find a fault-free path of even length in . We can then construct a cycle of odd length obtains the edge in .
- Case 2.3. . We can assume, without loss of generality, that is a vertex in and is a vertex in . Let be a fault-free neighbor of in such that in . Note that and in and , respectively. The construction of the edge lying on a cycle of odd length or in is similar to that described in Case 2.2 of Lemma 7.
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tien, S.; Raghavendra, C.; Sridhar, M. Generalized Hypercubes and Hyperbus structure for a computer network. In Hawaii International Conference on System Science; IEEE: New York, NY, USA, 1990; pp. 91–100. [Google Scholar]
- El-Amawy, A.; Latifi, S. Properties and performance of folded hypercubes. IEEE Trans. Parallel Distrib. Syst. 1991, 2, 31–42. [Google Scholar] [CrossRef]
- Ma, M.; Xu, J.; Du, Z. Edge-fault-tolerant hamiltonicity of folded hypercubes. J. Univ. Sci. Technol. China 2006, 36, 244–248. [Google Scholar]
- Xu, J.-M.; Ma, M.; Du, Z. Edge-fault-tolerant properties of hypercubes and folded hypercubes and folded hypercubes. Australas. J. Comb. 2006, 35, 7–16. [Google Scholar]
- Fu, J.-S. Fault-free cycles in folded hypercubes with more faulty elements. Inf. Process. Lett. 2008, 108, 261–263. [Google Scholar] [CrossRef]
- Hsieh, S.-Y. Some edge-fault-tolerant properties of the folded hypercube. Networks 2007, 51, 92–101. [Google Scholar] [CrossRef]
- Cheng, D.; Hao, R.-X.; Feng, Y.-Q. Cycles embedding on folded hypercubes with faulty nodes. Discret. Appl. Math. 2013, 161, 2894–2900. [Google Scholar] [CrossRef]
- Cheng, D.; Hao, R.-X.; Feng, Y.-Q. Embedding even cycles on folded hypercubes with conditional faulty edges. Inf. Process. Lett. 2015, 115, 945–949. [Google Scholar] [CrossRef]
- Kuo, C.-N.; Cheng, Y.-H. Fault-free cycles embedding in folded hypercubes with F4. Theor. Comput. Sci. 2020, 820, 85–90. [Google Scholar] [CrossRef]
- Kuo, C.-N.; Cheng, Y.-H. Every edge lies on cycles of folded hypercubes with a pair of faulty adjacent vertices. Discret. Appl. Math. 2021, 294, 1–9. [Google Scholar] [CrossRef]
- Hsu, L.-H.; Lin, C.-K. Graph Theory and Interconnection Networks; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Hsieh, S.-Y.; Kuo, C.-N. Hamiltonian-connectivity and strongly Hamiltonian-laceability of folded hypercubes. Comput. Math. Appl. 2007, 53, 1040–1044. [Google Scholar] [CrossRef]
- Ma, M.; Liu, G.; Pan, X. Path embedding in faulty hypercubes. Appl. Math. Comput. 2007, 192, 233–238. [Google Scholar] [CrossRef]
- Li, T.-K.; Tsai, C.-H.; Tan, J.J.; Hsu, L.-H. Bipanconnectivity and edge-fault-tolerant bipancyclicity of hypercubes. Inf. Process. Lett. 2003, 87, 107–110. [Google Scholar] [CrossRef]
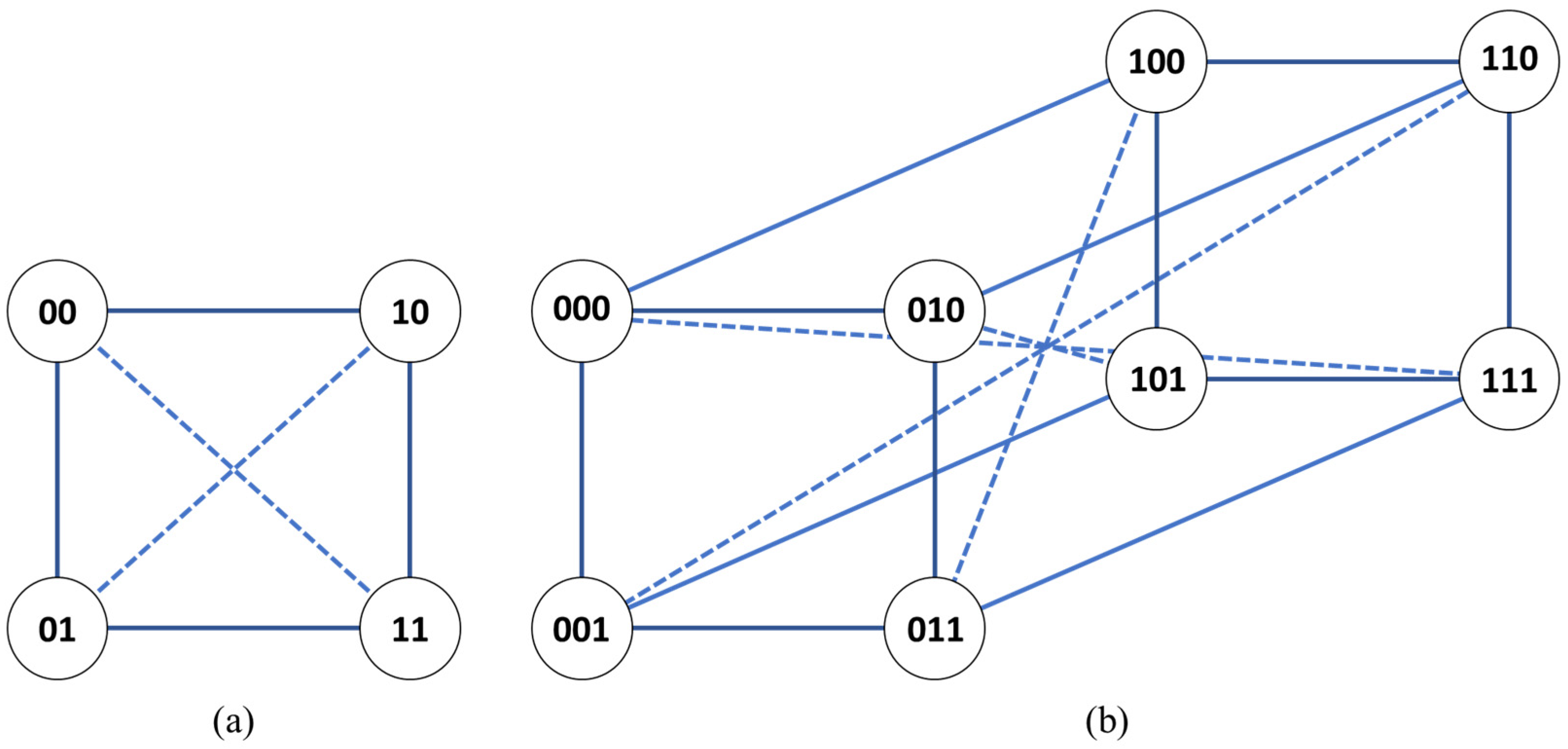
| Each Edge e is a Part of a Minimum of One Cycle with a Length of 14. |
|---|
| <0010; 0011; 1011; 1111; 0111; 0110; 0100; 0101; 1101; 1001; 1000; 1100; 1110; 1010; 0010> |
| <0101; 0111; 0011; 0010; 0110; 0100; 1100; 1000; 1010; 1110; 1111; 1011; 1001; 1101; 0101> |
| <0100; 0101; 0111; 0011; 0010; 0110; 1110; 1111; 1011; 1010; 1000; 1001; 1101; 1100; 0100> |
| <0100; 0101; 0111; 0011; 0010; 0110; 1110; 1111; 1101; 1001; 1011; 1010; 1000; 1100; 0100> |
| Cycle Length l | Edge e is Present in at Least One of the l Cycles Listed |
|---|---|
| l = 4 | <0101; 0111; 0110; 0100; 0101> |
| <1001; 1011; 1010; 1000; 1001> | |
| <1101; 1111; 1110; 1100; 1101> | |
| <1001; 1101; 1100; 1000; 1001> | |
| <1011; 1111; 1110; 1010; 1011> | |
| <0101; 1010; 1000; 0111; 0101> | |
| <0100; 0110; 1001; 1011; 0100> | |
| <0100; 1100; 1101; 0101; 0100> | |
| <0111; 0110; 1110; 1111; 0111> | |
| l = 6 | <0101; 1101; 1111; 1110; 1100; 0100; 0101> |
| <0111; 1111; 1011; 1010; 1110; 0110; 0111> | |
| <0111; 0101; 0100; 0110; 1001; 1000; 0111> | |
| <1011; 1001; 1000; 1010; 0101; 0100; 1011> | |
| <1001; 1101; 1100; 1000; 1010; 1011; 1001> | |
| l = 8 | <0101; 0100; 1100; 1000; 1001; 1011; 1111; 1101; 0101> |
| <0101; 0111; 0110; 0100; 1011; 1001; 1000; 1010; 0101> | |
| <0110; 1001; 1101; 1100; 1110; 1010; 1000; 0111; 0110> | |
| <0110; 1110; 1010; 1011; 1001; 1101; 1111; 0111; 0110> | |
| <1111; 1110; 1100; 1101; 1001; 1000; 1010; 1011; 1111> | |
| l = 10 | <0101; 0111; 0110; 0100; 1100; 1110; 1010; 1011; 1111; 1101; 0101> |
| <0101; 0100; 1011; 1001; 0110; 0111; 1000; 1100; 1110; 1010; 0101> | |
| <1001; 1000; 1010; 1110; 0110; 0111; 1111; 1011; 0100; 0110; 1001> | |
| <1001; 1101; 1100; 1110; 1111; 1011; 1010; 0101; 0100; 0110; 1001> | |
| l = 12 | <0111; 0101; 0100; 0110; 1110; 1100; 1000; 1010; 1011; 1001; 1101; 1111; 0111> |
| <0101; 1010; 1011; 0100; 0110; 1001; 1000; 0111; 1111; 1110; 1100; 1101; 0101> | |
| <0111; 0110; 0100; 1100; 1110; 1010; 1000; 1001; 1011; 1111; 1101; 0101; 0111> |
| Cycle Length l | Edge e is Present in at Least One of the l Cycles Listed |
|---|---|
| l = 4 | <0011; 0111; 0110; 0010; 0011> |
| <0111; 0101; 0100; 0110; 0111> | |
| <0101; 0100; 1100; 1101; 0101> | |
| <1000; 1100; 1101; 1001; 1000> | |
| <1001; 1011; 1010; 1000; 1001> | |
| <0011; 1011; 1010; 0010; 0011> | |
| <0101; 1010; 1011; 0100; 0101> | |
| <0111; 1000; 1001; 0110; 0111> | |
| <0011; 1100; 1101; 0010; 0011> | |
| l = 6 | <0011; 1100; 1000; 1001; 1101; 0010; 0011> |
| <0010; 0110; 0111; 0011; 1011; 1010; 0010> | |
| <0111; 0101; 0100; 0110; 1001; 1000; 0111> | |
| <0101; 1010; 1000; 1001; 1011; 0100; 0101> | |
| <0101; 1101; 1100; 0100; 0110; 0111; 0101> | |
| l = 8 | <0011; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0011> |
| <0110; 0111; 0101; 0100; 1011; 1010; 1000; 1001; 0110> | |
| <1100; 0100; 0110; 0010; 0011; 0111; 0101; 1101; 1100> | |
| <1000; 0111; 0011; 1011; 1010; 0010; 0110; 1001; 1000> | |
| <1010; 0101; 0111; 0110; 0100; 1011; 1001; 1000; 1010> | |
| l = 10 | <0011; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0110; 0111; 0011> |
| <0100; 1011; 1001; 0110; 0010; 0011; 0111; 0101; 1101; 1100; 0100> | |
| <0101; 1010; 1011; 1001; 1000; 0111; 0011; 0010; 0110; 0100; 0101> | |
| <0111; 0110; 0010; 1010; 1000; 1100; 1101; 1001; 1011; 0011; 0111> | |
| l = 12 | <0011; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0110; 0100; 0101; 0111; 0011> |
| <0100; 1100; 1101; 0101; 1010; 1011; 1001; 1000; 0111; 0011; 0010; 0110; 0100> | |
| <0011; 0010; 0110; 1001; 1101; 1100; 1000; 1010; 1011; 0100; 0101; 0111; 0011> | |
| <0011; 0111; 0101; 0100; 0110; 0010; 1010; 1000; 1100; 1101; 1001; 1011; 0011> | |
| <0101; 0100; 0110; 0111; 0011; 0010; 1010; 1011; 1001; 1000; 1100; 1101; 0101> |
| Cycle Length l | Edge e is Present in at Least One of the l Cycles Listed |
|---|---|
| l = 5 | <0111; 1000; 1001; 1101; 1111; 0111> |
| <0101; 1010; 1011; 1111; 1101; 0101> | |
| <0100; 1011; 1001; 1101; 1100; 0100> | |
| <0110; 1001; 1000; 1100; 1110; 0110> | |
| <1000; 1010; 1110; 1111; 0111; 1000> | |
| <0110; 0111; 0101; 1101; 1001; 0110> | |
| <0101; 0100; 0110; 1001; 1101; 0101> | |
| l = 7 | <0101; 1010; 1011; 0100; 0110; 1001; 1101; 0101> |
| <0111; 1000; 1001; 1011; 1010; 1110; 1111; 0111> | |
| <0100; 0101; 0111; 0110; 1110; 1111; 1011; 0100> | |
| <0100; 1100; 1000; 1010; 1110; 1111; 1011; 0100> | |
| <1111; 1101; 1100; 1110; 1010; 0101; 0111; 1111> | |
| l = 9 | <0101; 1101; 1111; 0111; 1000; 1010; 1110; 1100; 0100; 0101> |
| <0101; 0111; 0110; 0100; 1011; 1001; 1000; 1100; 1101; 0101> | |
| <0101; 1010; 1011; 1001; 1101; 1111; 1110; 0110; 0111; 0101> | |
| <0110; 1001; 1101; 1111; 1011; 1010; 1000; 1100; 1110; 0110> | |
| l = 11 | <0101; 1010; 1011; 0100; 0110; 1001; 1000; 1100; 1110; 1111; 1101; 0101> |
| <0100; 0101; 0111; 1000; 1001; 1101; 1111; 1011; 1010; 1110; 1100; 0100> | |
| <0111; 0110; 0100; 0101; 1010; 1011; 1001; 1000; 1100; 1110; 1111; 0111> | |
| <0110; 0111; 0101; 0100; 1011; 1010; 1000; 1001; 1101; 1100; 1110; 0110> |
| Cycle Length l | Edge e is Present in at Least One of the l Cycles Listed |
|---|---|
| l = 5 | <0011; 1100; 1000; 1001; 1011; 0011> |
| <0011; 0010; 1010; 1000; 0111; 0011> | |
| <0010; 1101; 0101; 0100; 0110; 0010> | |
| <0010; 1101; 0101; 0111; 0110; 0010> | |
| <1100; 1101; 1001; 0110; 0100; 1100> | |
| <1010; 1011; 0100; 0110; 0010; 1010> | |
| <1010; 1011; 1001; 1101; 0101; 1010> | |
| l = 7 | <0011; 1100; 1000; 1001; 1011; 1010; 0010; 0011> |
| <0100; 1011; 1001; 0110; 0111; 1000; 1100; 0100> | |
| <0101; 1010; 1000; 1001; 1101; 1100; 0100; 0101> | |
| <0010; 1101; 0101; 0100; 0110; 0111; 0011; 0010> | |
| <1011; 0011; 0010; 0110; 0111; 0101; 1010; 1011> | |
| l = 9 | <0011; 1100; 1101; 1001; 1011; 1010; 0010; 0110; 0111; 0011> |
| <0010; 1101; 1100; 1000; 1010; 0101; 0100; 1011; 0011; 0010> | |
| <0100; 1001; 1000; 0111; 0101; 1101; 1100; 0011; 0010; 0110> | |
| <0110; 0100; 1100; 1000; 1010; 0101; 0111; 0011; 0010; 0110> | |
| l = 11 | <0011; 1100; 1101; 1001; 1000; 1010; 0010; 0110; 0100; 0101; 0111; 0011> |
| <0010; 1101; 1001; 0110; 0111; 1000; 1010; 0101; 0100; 1011; 0011; 0010> | |
| <0101; 1101; 1001; 1011; 1010; 1000; 1100; 0011; 0010; 0110; 0100; 0101> | |
| <0100; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0011; 0111; 0110; 0100> |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, C.-N.; Cheng, Y.-H. Cycle Existence for All Edges in Folded Hypercubes under Scope Faults. Mathematics 2023, 11, 3391. https://doi.org/10.3390/math11153391
Kuo C-N, Cheng Y-H. Cycle Existence for All Edges in Folded Hypercubes under Scope Faults. Mathematics. 2023; 11(15):3391. https://doi.org/10.3390/math11153391
Chicago/Turabian StyleKuo, Che-Nan, and Yu-Huei Cheng. 2023. "Cycle Existence for All Edges in Folded Hypercubes under Scope Faults" Mathematics 11, no. 15: 3391. https://doi.org/10.3390/math11153391
APA StyleKuo, C.-N., & Cheng, Y.-H. (2023). Cycle Existence for All Edges in Folded Hypercubes under Scope Faults. Mathematics, 11(15), 3391. https://doi.org/10.3390/math11153391







