Differential Evolution with Group-Based Competitive Control Parameter Setting for Numerical Optimization

Abstract

Differential evolution (DE) is one of the most popular and widely used optimizers among the community of evolutionary computation. Despite numerous works having been conducted on the improvement of DE performance, there are still some defects, such as premature convergence and stagnation. In order to alleviate them, this paper presents a novel DE variant by designing a new mutation operator (named “DE/current-to-pbest_id/1”) and a new control parameter setting. In the new operator, the fitness value of the individual is adopted to determine the chosen scope of its guider among the population. Meanwhile, a group-based competitive control parameter setting is presented to ensure the various search potentials of the population and the adaptivity of the algorithm. In this setting, the whole population is randomly divided into multiple equivalent groups, the control parameters for each group are independently generated based on its location information, and the worst location information among all groups is competitively updated with the current successful parameters. Moreover, a piecewise population size reduction mechanism is further devised to enhance the exploration and exploitation of the algorithm at the early and later evolution stages, respectively. Differing from the previous DE versions, the proposed method adaptively adjusts the search capability of each individual, simultaneously utilizes multiple pieces of successful parameter information to generate the control parameters, and has different speeds to reduce the population size at different search stages. Then it could achieve the well trade-off of exploration and exploitation. Finally, the performance of the proposed algorithm is measured by comparing with five well-known DE variants and five typical non-DE algorithms on the IEEE CEC 2017 test suite. Numerical results show that the proposed method is a more promising optimizer.

1. Introduction

Differential Evolution (DE), proposed by Storn and Price [1] in 1995, is a population-based stochastic search algorithm. Like other evolutionary algorithms, the DE algorithm contains mutation, crossover, and selection operations. Due to its simple structure and excellent performance, the DE algorithm has been widely studied and used in many scientific and engineering fields, such as engineering scheduling problems [2,3,4], resource allocation problems in mobile communication [5], UAV path planning problems [6], biomedical problems [7], and so on. However, the performance of the DE algorithm is still challenged when facing increasingly complex optimization problems, where a large number of local optima usually exist, and then premature convergence and stagnation easily occur.

As pointed out in Ref. [8], the performance of DE is mainly dependent on its mutation strategy and control parameter setting. In fact, the mutation strategy plays an important role in the search ability of DE on the search space during the evolution process, and the control parameter setting can adjust its search characteristic. Consequently, a series of works have been conducted on the improvement of DE performance in the past decades by enhancing the mutation operation [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41] and control parameter setting [9,28,30,42,43,44,45,46,47,48,49]. Particularly, the previous mutation approaches are always achieved through designing a new mutation operator [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] and integrating multiple mutation strategies [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. With respect to generating a new mutation operator, one important and popular way is to exploit the underlying information of the population to construct the search direction, thus enhancing the search effectiveness and efficiency of the algorithm. On the other hand, the combined mutation strategy often employs multiple operators with various search characteristics to balance the exploration and exploitation of the algorithm. It should be mentioned that compared to the combined mutation approaches, the development of a new operator does not require the determination of the candidate mutation operator pool in advance, and does not need to consider the selection rule of candidate operators, which are often very difficult to decide. Thus, it is desirable to develop a more promising new mutation operator.

Up to now, through fully exploiting the underlying information of the population, many mutation operators have been presented [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. For example, to balance well the exploration and exploitation of the algorithm, based on the scheme of “DE/current-to-best/1”, which makes the algorithm easily fall into the local optimum, Zhang et al. [9] proposed a new mutation operator, named “DE/current-to-pbest/1”, where the top p% individuals of the population are randomly used to guide the search and an external archive is used to store historical inferiority solutions to enhance the diversity of the population. To fully exploit the advantage of individuals, Gong and Cai [10] proportionally selected the parents for the mutation process based on the fitness values of individuals (rank-DE), and Wang et al. [11] simultaneously employed the fitness value and diversity of individuals to determine their probability of participating into the mutation. By employing the comprehensive ranking of individuals based on both fitness and diversity, Cheng et al. [24] proposed a mutation operator (FDDE). In order to promote the optimization ability of DE in solving complicated optimization problems, Liu et al. [25] devised a simple yet effective mutation scheme by using a non-linear selection probability for each individual, while by utilizing the population’s holistic information and the direction of differential vector, an enhanced mutation operator was designed to avoid the issue of local optimal trapping [26]. Although the above methods can effectively improve the performance of DE, the special characteristic of the individual is rarely considered to determine its guider under the framework of DE/current-to-guiding/1, which might be helpful to effectively adjust the search requirements of different individuals. Thus, it is desirable to devise a more adaptive and promising mutation operator for DE.

Moreover, for the existing control parameter settings, one of the most successful and attractive approaches is to design an adaptive control mechanism, which can adaptively adjust the search capability of the algorithm. To do this, numerous adaptive methods have been developed over recent decades [9,28,30,42,43,44,45,46,47,48,49]. For example, to ensure the robustness of the algorithm, Liu et al. [42] used a fuzzy logic controller to tune the control parameters of mutation and crossover operations, and then proposed a fuzzy adaptive differential evolution algorithm. By integrating the scale factor with individuals, Brest et al. [43] proposed another self-adapting parameter control strategy (jDE), where the successful parameter shall be continuously entered into the next generation and the failure one will be randomly recreated. Meanwhile, by making full use of the search information of the population, Zhang et al. [9] presented an adaptive parameter setting, and Tanabe et al. [44] further introduced the historical success information of the population to create the scale factor and crossover rate for each individual, and put forward a history-based adaptive approach (SHADE). On the other hand, for the population size, Tanabe et al. [45] presented a linear reduction mechanism to dynamically adjust the population during the whole evolutionary process. Further, by using the performance of the best individual, Xia et al. [48] developed an adaptive control mechanism to increase or decrease the population. Moreover, to adaptively adjust the population diversity and balance the exploration and exploitation of the algorithm, Zeng et al. [49] further proposed a sawtooth-linear population size adaptive method to maintain the search ability of the algorithm. Even though these methods above could effectively strengthen the adaptivity and robustness of the algorithm for different search states and problems, the ones with the historical search information are usually adopted to set the control parameters for the whole population, the result of which may be that when there are some biases that obtain the successful offspring, they lead to a serious degradation on the performance of the algorithm. Meanwhile, despite many adaptive mechanisms having been designed for the population size and having promoted the performance of DE, they often adopt one single rule to adjust the population size, and even require additionally measuring the search state of the population, which may be not able to fully satisfy the varying search needs of the algorithm at different evolutionary stages and may seriously increase the computational burden. Therefore, it is necessary to make further efforts in developing a more effective parameter control setting.

Based on the considerations above, in this paper, we propose a new DE algorithm, named differential evolution with group-based competitive control parameter setting (GCIDE). Specifically, the main contributions of this paper are as follows.

(1)

In order to make full use of the fitness value of individuals to adjust their search capability, under the framework of “DE/current-to-guiding/1”, a new mutation operator named “DE/current-to-pbest_id/1” is first proposed. In the new operator, each individual’s fitness value is employed to determine the chosen range of its associated guider among the whole population, i.e., decide the parameter p in the “DE/current-to-pbest/1” for each target individual. Compared to the existing related methods [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], the proposed operator adaptively assigns a suitable guider for each individual to adjust its search capability based on its special characteristic. Thus, this new operator can effectively satisfy the search requirements of different individuals, thus enhancing the search effectiveness of the algorithm.

(2)

To alleviate the degradation of DE performance caused by the successful biases, a grouping-based competitive parameter control method is also proposed to create the scale factors and crossover rates for the population. In this proposed method, the population is first randomly and equally divided into k groups, the control parameters for the individuals in each group are independently generated with an adaptive manner, and the location parameters with the worst performance are competitively updated by using the successful parameters of the current population. Differing from the related adaptive methods [42,43,44,45], the proposed setting can simultaneously use multiple historical pieces of successful information to independently generate the control parameters for the population, and the worst one is dynamically replaced by the current successful information during the whole evolutionary process. Then, the developed setting is capable of not only avoiding being mislead by biases, but also maintaining the adaptive ability of the algorithm.

(3)

In order to further meet the different search needs of the algorithm at different search stages, by designing and integrating two different non-linear schemes, a piecewise population reduction mechanism is presented to dynamically adjust the population size during the evolutionary process. Unlike the previous approaches [46,47,48,49], this new method, respectively, adopts a non-linear formula with slower or quicker reduction speed to set the population size, and when a smaller population size is generated, the corresponding worst individuals will be removed from the current population. Thereby, this mechanism could more effectively enhance the exploration and exploitation of the algorithm at the early and later search stages, respectively.

Finally, to verify the performance of the GCIDE, numerical experiments are conducted by comparing with five well-known DE variants and five other non-DE heuristic algorithms on the 30 benchmark functions from IEEE CEC 2017 [50] and three real applications. Numerical results show that the GCIDE has a more competitive performance.

The rest of this paper is organized as follows. In Section 2, the related work is simply described. In Section 3, we present the proposed GCIDE algorithm in detail. In Section 4, experimental results of the proposed algorithm are given. Finally, Section 5 concludes this paper.

2. Related Work

In this section, we shall introduce the classical differential evolution algorithm and the typical previous works, respectively.

2.1. Classical Differential Evolution

Herein, the four basic operations of the classical differential evolution algorithm are described in detail, including initialization, mutation, crossover, and selection [1].

First, a population with NP solutions, $S^G=\left\{X_i^G:\hspace{1em}i=1,2,\cdots ,NP\right\}$, is randomly generated in the search space. $X_i^G=\left(x_{i,1}^G,x_{i,2}^G,\cdots ,x_{i,D}^G\right)$ denotes the i-th individual in S^G, and G is the current number of iterations. In detail, the j-th dimension $X_{i,j}^G$ of $X_i^G$ can be generated by

$$X_{i,j}^G=L_j+\left(U_j-L_j\right)·rand\hspace{0.17em}.$$

(1)

Here, $L_j$ and $U_j$ denote the j-th dimension lower and upper boundaries of the decision space, respectively, and rand is a random number between 0 and 1 within uniform distribution.

After the initialization, for each target individual $X_i^G$, its corresponding mutant vector $V_i^G$ is generated by special mutation operation. Herein, four commonly used mutation operations are described as follows:

DE/rand/1:

$$V_i^G=X_{r1}^G+F\cdot \left(X_{r2}^G-X_{r3}^G\right)\hspace{0.17em},$$

(2)

DE/best/1:

$$V_i^G=X_{best}^G+F\cdot \left(X_{r1}^G-X_{r2}^G\right)\hspace{0.17em},$$

(3)

DE/rand-to-best/1:

$$V_i^G=X_{r1}^G+F\cdot \left(X_{best}^G-X_{r1}^G\right)+F\cdot \left(X_{r2}^G-X_{r3}^G\right)\hspace{0.17em},$$

(4)

DE/current-to-best/1:

$$V_i^G=X_i^G+F\cdot \left(X_{best}^G-X_i^G\right)+F\cdot \left(X_{r1}^G-X_{r2}^G\right)\hspace{0.17em}.$$

(5)

Herein, F is a scaling factor ranging from [0, 1], $r1,r2,r3\in \left\{1,2,\cdots ,NP\right\}$ are three randomly selected and exclusive indexes having $r_1\ne r_2\ne r_3\ne i$, and $X_{best}^G$ denotes the best individual in the population at the generation G evaluated by its fitness value.

In order to avoid the mutant individuals exceeding the search space and suitably dealing with each variable according to its search characteristic, the following constraint handling technique in [9] is adopted here. Specifically, if $v_{i,j}^G$ is beyond the feasible domain region $\left[L_j,U_j\right]$, it will be readjusted in the feasible domain region by

$$v_{i,j}^G=\{\begin{array}{l}\min \left\{U_j,2L_j-v_{i,j}^G\right\},\hspace{1em}if\hspace{0.17em}{v}_{i,j}^G<L_j\hspace{0.17em},\\ \max \left\{L_j,2U_j-v_{i,j}^G\right\},\hspace{1em}if\hspace{0.17em}{v}_{i,j}^G>U_j\hspace{0.17em}.\end{array}$$

(6)

Subsequently, the trial vector $U_i^G=\left(u_{i,1}^G,u_{i,2}^G,\cdots ,u_{i,D}^G\right)$ is generated by crossover operation between the target vector $X_i^G=\left(x_{i,1}^G,x_{i,2}^G,\cdots ,x_{i,D}^G\right)$ and the mutation vector $V_i^G=\left(v_{i,1}^G,v_{i,2}^G,\cdots ,v_{i,D}^G\right)$. The specific operation is as follow:

$$u_{i,j}^G=\{\begin{array}{l}{v}_{i,j}^G,\hspace{1em}if\hspace{0.17em}rand\le Cr\hspace{0.17em}or\hspace{0.17em}j=j_{rand}\hspace{0.17em},\\ x_{i,j}^G,\hspace{1em}otherwise\hspace{0.17em}.\end{array}$$

(7)

Here, $Cr\in \left[0,1\right]$ is the crossover probability, and $j_{rand}$ is a randomly generated index in $\left[1,\hspace{0.17em}D\right]$.

Finally, the target vector is compared with the trial vector according to their fitness values, and the one with a better fitness value survives to the next generation. The binomial crossover operation is as follow:

$$X_i^{G+1}=\{\begin{array}{l}{U}_i^G,\hspace{1em}if\hspace{0.17em}f\left(U_i^G\right)\le f\left(X_i^G\right)\hspace{0.17em},\\ X_i^G,\hspace{1em}otherwise\hspace{0.17em}.\end{array}$$

(8)

Here, $f\left(U_i^G\right)$ and $f\left(X_i^G\right)$ are the fitness values of $U_i^G$ and $X_i^G$, respectively.

Noticeably, once the DE algorithm is called, the initialization will be first executed, and then the mutation, crossover, and selection operations are repeated until the pre-given termination criterion is satisfied.

2.2. Related Researches

As is well-known, the performance of DE is heavily related to its mutation operation and control parameter setting. As a result, various mutation strategies and control parameter settings have been presented to enhance the search ability of DE [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. Particularly, with respect to the mutation scheme, the information of individual or population have been fully exploited to design an improved mutation operator [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Concretely, by randomly choosing a guider for each individual from the top p% individuals, Zhang et al. [9] proposed mutation operator “DE/current-to-pbest/1”. Through employing the fitness values of individuals to decide the parents in the mutation process, Gong and Cai [10] presented a rank-based mutation operator. Meanwhile, by simultaneously considering the fitness value and diversity of individuals, Wang et al. [11] put forward an enhanced mutation operation. Similarly, to alleviate all individuals in the population having an equal chance to be selected as the parents, Cai et al. [13] combined the fitness and position information of the population simultaneously to choose the parents in the mutation. By utilizing both the fitness value and decision space information of the population, Sharifi-Noghabi et al. [15] also designed a union-based mutation operator. By randomly selecting three individuals from the population and using the best one as the base vector and the difference vectors as the disturb item, Mohamed and Suganthan [16] devised a triangular mutation operator. By utilizing both the fitness value and novelty of individuals, Xia et al. [18] also proposed a new parent selection method for the mutation of DE. To get a better perception of the landscape of objectives, Meng et al. [21] introduced a depth information-based external archive and used it to create the difference vector in the mutation process. By using the best individual and a randomly selected individual to generate the base vector, Ma and Bai [22] presented a novel mutation scheme. Moreover, via employing the comprehensive ranking of individuals based on both fitness and diversity, Cheng et al. [24] proposed a new mutation operator (FDDE). Liu et al. [25] devised a simple yet effective mutation scheme by using a non-linear selection probability for each individual, while Li et al. [26] developed an enhanced mutation operator to avoid the issue of local optimal trapping by utilizing the population’s holistic information and the direction of differential vector.

On the other hand, for integrating the benefits of multiple mutation operators, many combined strategies were also designed [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. For example, by using four different mutation operators as the mutation pool, and dynamically choosing one among them for each individual based on their historical successful ratio, Qin et al. [27] presented a self-adaptive selection mechanism. By simultaneously employing three mutation operators for every individual to generate offspring, Wang et al. [28] developed a composite mutation strategy. Gui et al. [30] randomly divided the whole population into multiple groups and assigned different mutation operators for each individual within one group based on its role. Li et al. [31] introduced reinforcement learning to dynamically provide the selection chance of each candidate mutation operator. By introducing the idea of a cultural algorithm and different mutation strategies into belief space, Deng et al. [35] proposed a new combined mutation strategy to balance the global exploration ability and local optimization ability. Moreover, for constraint optimization problems, Qiao et al. [38] presented a self-adaptive resources allocation-based mutation strategy by assigning a suitable operator to each individual based on its performance feedback. Besides, by hybridizing with an estimation of distribution algorithm, Li et al. [40] designed a hybrid DE variant, and by dividing the whole population into leader-adjoint populations and separately assigning one operator for each subpopulation, Li et al. [41] further proposed a combined way to integrate the advantages of several different operators.

Moreover, with respect to the control parameters involved in the DE algorithm, many adaptive approaches have also been presented over recent decades [9,28,30,42,43,44,45,46,47,48,49]. In particular, for the scale factor and crossover rate, by making full use of the successful parameters, Zhang et al. [9] presented an adaptive parameter setting, and Tanabe et al. [44] further introduced the historical success information of the population and put forward a history-based adaptive approach (SHADE). By introducing a fuzzy logic controller, Liu et al. [42] proposed a fuzzy adaptive parameter control method, and by integrating the scale factor with individuals and adaptively updating it according to the performance of its corresponding offspring, Brest et al. [42] proposed another self-adapting parameter control strategy (jDE). Moreover, for the population size, by linearly reducing the size of the population during the evolution process, Tanabe et al. [45] presented a linear reduction mechanism. Meanwhile, by fully using the diversity of the population to evaluate its search state, Poláková et al. [47] dynamically increased or decreased the population, and by fully using the performance of the best individual to evaluate the search state of the population, Xia et al. [48] designed an adaptive control mechanism to dynamically adjust the size of the population. Moreover, by introducing a sawtooth-linear function to calculate the size of the population, Zeng et al. [49] further proposed a sawtooth-linear population size adaptive method to maintain the search ability of the algorithm.

Notably, as described above, one can find that the special characteristic of the individual is rarely considered to determine its guider under the framework of DE/current-to-guiding/1, the adaptive parameter settings with the historical search information are usually adopted to set the control parameters for the whole population, and the existing population size control approaches often adopt one single rule to adjust the population size, and even require additionally measuring the search state of the population. Thus, the biases that obtain the successful offspring could not be effectively handled and would lead to a serious degradation of the performance of the algorithm, while the varying search needs of the algorithm may not be fully satisfied at different evolutionary stages, and the computational cost of the algorithm might be seriously increased. Therefore, it is necessary to develop a more promising DE variant.

3. Proposed Algorithm

In this section, we provide a detailed description of the proposed algorithm (GCIDE), including a new mutation strategy, named DE/current-to-pbest_id/1, a group-based competitive control parameter setting, and a piecewise population size reduction mechanism.

3.1. New Mutation Strategy

As can be seen from the Introduction, the settings of p in the existing versions of DE/current-to-pbest/1 are usually fixed or controlled by a formula related to the number of iterations. These may result in inefficient searches for the algorithm and the risk of falling into local optimum. For this, a new mutation strategy named DE/current-to-pbest_id/1 is proposed in this paper as follows:

$$V_i^G=X_i^G+F\cdot \left(X_{pbest\_id}^G-X_i^G\right)+F\cdot \left(X_{r1}^G-X_{r2}^G\right)\hspace{0.17em},$$

(9)

where $X_{pbest\_id}^G$ is the associated guiding individual for the target individual by randomly selecting from the top p of individuals in the current population.

From Equation (9), we can see that the selection of $X_{pbest\_id}^G$ depends on the value of p for every target individual. A smaller p makes the population converge to the better individuals quickly. This can ensure the convergence speed of the algorithm to some extent, but increases the risk of falling into the local optimum. A larger p can ensure the diversity of the population during the evolutionary process to a certain extent, but has the limitation of slow convergence. Thus, by using the fitness information of individuals, the following equation is designed to set its corresponding p by

$$p_i=0.2\times \frac{f_i-f_{\min }}{\left(f_{\max }-f_{\min }\right)+\sigma }+0.11\hspace{0.17em},$$

(10)

where $f_i$ is the fitness value of $X_i^G$. $f_{\min }$ and $f_{\max }$ are the minimum fitness value and maximum fitness value in the population, respectively, $\sigma$ is a very small positive number to prevent p from generating invalid values in the later iteration, and is set to 0.01 here. From Equation (10), individuals with smaller fitness values are more inclined to exploitation and their corresponding p are smaller, while individuals with larger fitness values are more inclined to exploration, and their corresponding p are larger. Thus, this setting can make full use of the characteristics of different individuals, and thus balance well the exploration and exploitation of the algorithm.

3.2. Group-Based Competitive Control Parameter Setting

The widely used methods for adjusting the control parameters are the adaptive ones using the historical successful parameters. For example, in references [9,44], all the successful parameters of individuals are employed to update their generation distributions for the next population. However, when there are some biases which obtain the successful offspring in the last iteration, they may result in misleading the creation of the next parameters, and are used for every individual. This could cause a serious degradation of the performance of the algorithm. For this, a group-based competitive control parameter setting shall be proposed in this subsection.

In this new method, the population is first randomly divided into k groups with equal sizes, and the parameters including crossover rate Cr and scaling factor F of individuals in each group are independently generated. Specifically, for the i-th individual $X_{i,k}^G$ in the k-th group, its corresponding crossover rate Cr_i and scaling factor F_i are generated by

$$\{\begin{array}{l}C{r}_i=rand{n}_i\left({\mu }_{C{r}_k},0.1\right)\hspace{0.17em},\\ F_i=rand{c}_i\left({\mu }_{F_k},0.1\right)\hspace{0.17em},\end{array}$$

(11)

where $rand{n}_i\left({\mu }_{C{r}_k},0.1\right)$ is a normal distribution with mean ${\mu }_{C{r}_k}$ and standard deviation 0.1, $rand{c}_i\left({\mu }_{F_k},0.1\right)$ is a Cauchy distribution with mean ${\mu }_{F_k}$ and standard deviation 0.1. At the beginning of the algorithm, we let ${\mu }_{C{r}_i}={\mu }_{F_i}=0.5$ for $i=1,2,\cdots ,k$. Notably, in order to avoid being mislead by the bias occurring in the last iteration, and also effectively ensure the adaptivity of the algorithm, the historical successful parameters are still adopted here, but they are only used to update the values of ${\mu }_{Cr}$ and ${\mu }_F$ for the group with the worst performance. Specifically, the detailed update procedures of ${\mu }_{Cr}$ and ${\mu }_F$ can be, respectively, described as

$$\{\begin{array}{l}{\mu }_{C{r}_{idx},G+1}=\{\begin{array}{l}mea{n}_{WL}\left(S_{Cr}\right),\hspace{1em}if\hspace{0.17em}{S}_{Cr}\ne \varnothing \hspace{0.17em}and\hspace{0.17em}\max \left\{S_{Cr}\right\}>0\hspace{0.17em},\\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}if\hspace{0.17em}{S}_{Cr}\ne \varnothing \hspace{0.17em}and\hspace{0.17em}{\mu }_{C{r}_{idx},G}=0\hspace{0.17em},\\ {\mu }_{C{r}_{idx},G},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}otherwise\hspace{0.17em}.\end{array}\\ mea{n}_{WL}=\frac{{\displaystyle \sum _{s=1}^{\left|S_{Cr}\right|}{w}_s\cdot S_{Cr}^2\left(s\right)}}{{\displaystyle \sum _{s=1}^{\left|S_{Cr}\right|}{w}_s\cdot S_{Cr}\left(s\right)}}\hspace{0.17em},\\ w_s=\frac{△f_s}{{\displaystyle \sum _{s=1}^{\left|S_{Cr}\right|}△f_s}},\hspace{0.17em}\end{array}$$

(12)

$$\{\begin{array}{l}{\mu }_{F_{idx},G+1}=\{\begin{array}{l}mea{n}_{WL}\left(S_F\right),\hspace{1em}if\hspace{0.17em}{S}_F\ne \varnothing \hspace{0.17em},\hspace{0.17em}\\ {\mu }_{F_{idx},G},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}otherwise\hspace{0.17em},\end{array}\\ mea{n}_{WL}=\frac{{\displaystyle \sum _{s=1}^{\left|S_F\right|}{w}_s\cdot S_F^2\left(s\right)}}{{\displaystyle \sum _{s=1}^{\left|S_F\right|}{w}_s\cdot S_F\left(s\right)}}\hspace{0.17em},\\ w_s=\frac{△f_s}{{\displaystyle \sum _{s=1}^{\left|S_F\right|}△f_s}}\hspace{0.17em}.\end{array}$$

(13)

Herein, $S_{Cr}$ and $S_F$ are the sets of successful Cr and F, respectively, $\Delta f_s$ is the fitness deviation between the target individual $X_s$ and its offspring $U_s$, and idx denotes the index of the group with the worst performance, which is characterized by the success rate $r_j$ (j = 1, 2, …, k) of the individuals in the group here as

$$\{\begin{array}{l}{r}_j=\{\begin{array}{l}\frac{n{s}_j^2}{ns\cdot \left(n{s}_j+n{f}_j\right)},\hspace{1em}if\hspace{0.17em}n{s}_j>0\hspace{0.17em},\\ \epsilon ,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hspace{0.17em}.\end{array}\\ ns={\displaystyle \sum _{j=1}^{k}n{s}_j}\hspace{0.17em}.\end{array}$$

(14)

Here, $\epsilon$ is a very small positive number and is set to 0.01, $n{s}_j$ is the number of successful individuals in the j-th group, and $n{f}_j$ is the number of unsuccessful individuals in the j-th group. Note that if there are multiple groups who have the same minimal success rate, the updated ${\mu }_{Cr}$ and ${\mu }_F$ will be employed for the group randomly selected among them. Obviously, from Equations (11)–(14), one can see that the number of groups k might importantly affect the performance of the proposed setting. In fact, a larger k may lead to the defect that the overly outdated successful parameters are stored for a long time and employed to generate the control parameters, which have not been suitable for the search requirements of the current population, thus degrading the search effectiveness of the algorithm. Thereby, the value of k should not be too large, and we set k to 4 in this paper by a series of tuning experiments, which can be further found in Section 4.1.

As can be seen from the above, this proposed setting not only makes full use of the successful parameters to maintain the adaptivity of the algorithm for varying search states, but also avoids being mislead by the successful biases. Thus, it is capable of enhancing the optimization of the algorithm further.

3.3. A Piecewise Population Reduction Mechanism

In most DE variants, although their parameters are automatically adjusted, the population size often remains constant throughout the search process. In fact, smaller population sizes tend to lead to faster convergence, but increase the risk of convergence to a local optimum. On the other hand, a larger population size encourages a wide search, but tends to converge more slowly.

Based on this consideration, we further propose a deterministic rule-based population reduction mechanism herein, which prefers to fully explore the solution space at the early stage of evolution, while converging quickly to find the best solution at the later stage of evolution. In detail, the specific formula for computing the population size is as follows:

$$\{\begin{array}{l}NP=\frac{\left(\frac{1}{3}N{P}_{init}-N{P}_{init}\right)}{{\left(\frac{2}{3}FE{S}_{\max }-N{P}_{init}\right)}^2}\times {\left(FES-N{P}_{init}\right)}^2+N{P}_{init},\hspace{1em}if\hspace{0.17em}FES\le \frac{2}{3}FE{S}_{\max }\hspace{0.17em},\\ NP=\frac{\left(\frac{1}{3}N{P}_{init}-N{P}_{\min }\right)}{{\left(\frac{2}{3}FE{S}_{\max }-N{P}_{\min }\right)}^2}\times {\left(FES-FE{S}_{\max }\right)}^2+N{P}_{\min },\hspace{0.17em}\mathrm{otherwise}\hspace{0.17em}.\end{array}$$

(15)

Herein, $N{P}_{ini}$ and $N{P}_{\min }$ denote the initial and minimum population sizes, respectively, and $FE{S}_{\max }$ and $FES$ denote the maximum and current number of function evaluations, respectively. From Equation (15), it can be seen that at the early and later stages of evolution, the population size is monotonously reduced and has a slower and faster speed, separately. When the new population size is smaller than the current one, the next population will just consist of the best NP individuals in the current population based on their fitness values. Thus, this mechanism is able to effectively promote the balance between exploration and exploitation.

Specifically, by integrating the proposed mutation strategy, a group-based competitive control parameter setting and a piecewise population reduction mechanism, the overall procedure of the proposed algorithm GCIDE is also shown in Algorithm 1.

Algorithm 1 The detailed procedure of GCIDE

1: Input the initial parameters, including population size NP, the number of groups k, the prime values of ${\mu }_{Cr}$ and ${\mu }_F$ for each group, and the number of generation G = 0.

2: Randomly initialize population $S^G=\left\{X_i^G:\hspace{1em}i=1,2,\cdots ,NP\right\}$ by Equation (1);

3: Evaluate the fitness value of each individual;

4: while Termination condition is not satisfied

5:   Randomly divide the population with equal k groups;

6:   For each group, create the control parameters for its individuals by Equation (11);

7:   for i = 1:NP

8:      Calculate the p value for each individual by Equation (10);

9:      Perform mutation using Equation (9);

10:    Perform crossover using Equation (7);

11:    Perform selection using Equation (8);

12:  end for

13:  Calculate the success rate $r_j$ for each group by Equation (14);

14:  Update the control parameters by Equations (12)–(14);

15:  Calculate the new population size using Equation (15), and create the next population;

16:  G = G + 1

17: end while

From Algorithm 1, one can see that in each generation, the population is first randomly divided into k groups, and the control parameters for individuals in each group are independently created by the corresponding location parameters. After this, the proposed mutation strategy is employed to create the mutant individual for each target individual, and the binomial crossover operation is used to generate its offspring. Subsequently, the greedy selection strategy is adopted to update the current population according to the fitness value, and the presented piecewise population reduction mechanism is further utilized to remove the unpromising individuals from the current population. In particular, the proposed mutation strategy makes full use of the fitness value of individuals to properly choose a guider from the population to create its search direction, which can adaptively adjust the search ability of each individual. Meanwhile, the proposed group-based competitive control parameter setting can simultaneously utilize multiple successful parameter information to generate the control parameters for the current population, and competitively update the worst historical location information with the current search records during the whole evolution process. This setting can not only maintain the adaptivity of the algorithm for varying search environments, but also alleviate being mislead by the successful biases. Moreover, the presented piecewise population reduction mechanism reduces the size of the population slowly and quickly at the early and later stages of evolution separately, which can effectively ensure the exploration of the algorithm at the beginning of the search process, and speed up the convergence of the algorithm at the final evolution stage. Therefore, the proposed GCIDE can properly adjust the search ability of each individual, and effectively satisfy the trade-off between exploration and exploitation of the algorithm.

3.4. Complexity Analysis

Compared with classic DE, whose complexity is $O\left(G_{\max }\times NP\times D\right)$, GCIDE has additional computational burdens caused by three parts, including the mutation operation, the parameter control setting, and the population reduction mechanism. Herein, $G_{\max }$ is the maximal number of generations. During one generation, the computation complexity of the mutation operation just includes that of calculating the value of p_i, which needs to find the maximum and minimum fitness values among the current population. Thus, its extra complexity is $O\left(3\times G_{\max }\times NP\right)$. Meanwhile, for the parameter control setting, its only extra part is to calculate the success rate of every group based on their fitness values. Thereby, its extra complexity is $O\left(G_{\max }\times NP\right)$. Moreover, the extra complexity of the population reduction mechanism is $O\left(G_{\max }\times NP\right)$. As a result, the total complexity of GCIDE is $O\left(G_{\max }\times NP\times (D+5)\right)$, simplified as $O\left(G_{\max }\times NP\times D\right)$. Therefore, the new algorithm will not cause extra serious computational burden.

4. Numerical Experimental Results and Analysis

In this section, a series of experiments are performed to verify the advantage of our proposed GCIDE. Firstly, the optimal choice of the newly introduced parameters was determined experimentally. Then, comparative experiments with five typical DE variants and five typical non-DE heuristic algorithms are conducted on the IEEE CEC 2017 test suite [50]. In this test suite, four different types of functions are included, namely unimodal functions, simple multimodal functions, hybrid functions, and composition functions. To obtain statistical results, each algorithm carries out 30 independent runs on each benchmark function. Moreover, a validity experiment is conducted on the newly proposed strategy of GCIDE. Finally, the performance of GCIDE is verified on three practical problems.

4.1. Sensitivity Analyses of k and NP_ini

From Section 3, we can find that there are two parameters in the proposed algorithm, the number of groups k and the initial population size NP_ini. To analyze the effects of k and NP_ini on the performance of GCIDE, numerous experiments are conducted on eight typical functions by setting k and NP_ini to different values. These eight chosen functions are unimodal functions F01 and F02, simple multimodal functions F05 and F07, hybrid functions F10 and F16, and composition functions F21 and F26; and k and NP_ini are, respectively, set to 4, 6, 8, and 10, and 12D, 18D, 23D, and 25D. Table 1 lists the numerical results of GCIDE with different k and NP_ini, while the best results of each function are marked in bold (the same below).

Table 1. Numerical results of GCIDE with various k and NP_ini.

-	Function	F1		F2		F5		F7
NPini	Group Number	Mean	Std	Mean	Std	Mean	Std	Mean	Std
12D	k = 4	1.47 × 10−14	2.59 × 10−15	2.33 × 10−1	6.26 × 10−1	8.43 × 100	1.52 × 100	3.68 × 101	1.40 × 100
	k = 6	1.23 × 10−14	4.91 × 10−15	1.80 × 100	9.86 × 100	9.43 × 100	1.60 × 100	3.70 × 101	7.77 × 10−1
	k = 8	1.23 × 10−14	4.91 × 10−15	0.00 × 100	0.00 × 100	9.80 × 100	1.51 × 100	3.73 × 101	1.18 × 100
	k = 10	1.33 × 10−14	3.61 × 10−15	6.67 × 10−2	2.54 × 10−1	9.94 × 100	1.90 × 100	3.77 × 101	1.37 × 100
18D	k = 4	1.47 × 10−14	4.55 × 10−15	1.93 × 100	1.00 × 101	8.22 × 100	1.70 × 100	3.68 × 101	1.13 × 100
	k = 6	1.47 × 10−14	2.59 × 10−15	1.90 × 100	9.84 × 100	8.44 × 100	1.35 × 100	3.64 × 101	1.26 × 100
	k = 8	1.37 × 10−14	2.59 × 10−15	3.33 × 10−2	1.83 × 10−1	9.79 × 100	1.38 × 100	3.68 × 101	1.40 × 100
	k = 10	1.42 × 10−14	0.00 × 10+00	1.38 × 10+2	7.48 × 102	8.74 × 100	1.10 × 100	3.63 × 101	1.20 × 100
23D	k = 4	1.47 × 10−14	4.55 × 10−15	1.87 × 100	1.00 × 101	7.35 × 100	1.27 × 100	3.63 × 101	1.14 × 100
	k = 6	1.75 × 10−14	6.11 × 10−15	6.67 × 10−2	2.54 × 10−1	8.65 × 100	1.45 × 100	3.59 × 101	1.17 × 100
	k = 8	1.71 × 10−14	5.78 × 10−15	0.00 × 100	0.00 × 100	9.42 × 100	1.49 × 100	3.65 × 101	1.32 × 100
	k = 10	1.61 × 10−14	4.91 × 10−15	3.33 × 10−2	1.83 × 10−1	9.46 × 100	1.65 × 100	3.73 × 101	1.51 × 100
25D	k = 4	1.99 × 10−14	1.03 × 10−14	1.87 × 100	1.00 × 101	7.81 × 100	1.65 × 100	3.57 × 101	1.05 × 100
	k = 6	1.75 × 10−14	7.16 × 10−15	6.67 × 10−2	2.54 × 10−1	8.56 × 100	1.78 × 100	3.67 × 101	1.27 × 100
	k = 8	2.04 × 10−14	9.65 × 10−15	1.33 × 10−1	3.46 × 10−1	8.96 × 100	1.89 × 100	3.70 × 101	1.45 × 100
	k = 10	1.89 × 10−14	7.77 × 10−15	0.00 × 100	0.00 × 100	9.65 × 100	1.96 × 100	3.67 × 101	1.33 × 100
-	Function	F10		F16		F21		F26
NPini	Group Number	Mean	Std	Mean	Std	Mean	Std	Mean	Std
12D	k = 4	1.54 × 103	1.91 × 102	1.83 × 102	1.14 × 102	2.08 × 102	1.94 × 100	9.24 × 102	5.52 × 101
	k = 6	1.58 × 103	1.98 × 102	2.07 × 102	8.23 × 101	2.09 × 102	1.99 × 100	9.33 × 102	5.99 × 101
	k = 8	1.48 × 103	2.01 × 102	1.93 × 102	8.66 × 101	2.10 × 102	1.95 × 100	9.23 × 102	5.60 × 101
	k = 10	1.51 × 103	2.10 × 102	2.02 × 102	1.17 × 102	2.11 × 102	1.85 × 100	9.38 × 102	5.13 × 101
18D	k = 4	1.50 × 103	2.75 × 102	1.56 × 102	8.94 × 101	2.09 × 102	1.72 × 100	9.13 × 102	5.34 × 101
	k = 6	1.60 × 103	1.96 × 102	1.33 × 102	8.11 × 101	2.08 × 102	1.81 × 100	9.12 × 102	4.63 × 101
	k = 8	1.52 × 103	2.63 × 102	1.48 × 102	9.84 × 101	2.09 × 102	1.67 × 100	9.27 × 102	5.15 × 101
	k = 10	1.59 × 103	2.13 × 102	1.31 × 102	9.24 × 101	2.09 × 102	1.77 × 100	9.22 × 102	4.51 × 101
23D	k = 4	1.55 × 103	1.91 × 102	1.58 × 102	9.59 × 101	2.08 × 102	1.52 × 100	9.09 × 102	4.62 × 101
	k = 6	1.59 × 103	2.74 × 102	1.53 × 102	7.50 × 101	2.08 × 102	1.66 × 100	9.15 × 102	5.04 × 101
	k = 8	1.58 × 103	1.97 × 102	1.79 × 102	9.45 × 101	2.09 × 102	1.85 × 100	9.23 × 102	4.77 × 101
	k = 10	1.54 × 103	2.35 × 102	1.97 × 102	8.83 × 101	2.10 × 102	1.83 × 100	9.24 × 102	4.46 × 101
25D	k = 4	1.53 × 103	2.36 × 102	1.53 × 102	9.54 × 101	2.07 × 102	1.76 × 100	9.27 × 102	6.42 × 101
	k = 6	1.57 × 103	2.05 × 102	1.32 × 102	9.59 × 101	2.09 × 102	1.68 × 100	9.12 × 102	6.40 × 101
	k = 8	1.57 × 103	2.19 × 102	1.55 × 102	1.07 × 102	2.09 × 102	1.64 × 100	9.12 × 102	4.69 × 101
	k = 10	1.58 × 103	2.25 × 102	1.64 × 102	9.59 × 101	2.10 × 102	1.43 × 100	9.12 × 102	4.10 × 101

According to the results shown in Table 1, on unimodal functions F1 and F2, GCIDE gets the superior results when the initial population size is 12D and 23D and the group number is six and eight. Meanwhile, on simple multimodal functions F5 and F7, GCIDE has excellent performance when the initial population size is 23D and 25D and the group number is four. Besides, on the hybrid functions F10 and F16, one can see that a smaller initial population size and a larger group number have the better results. Finally, on the composition functions F21 and F26, a larger initial population size and a smaller group number are more advantageous for GCIDE. Moreover, Table 2 further reports the rankings of GCIDE with various parameter values, which are based on the Friedman test [51]. From Table 2, it can be seen that GCIDE has the best ranking when the initial population size is 23D and the group number is four. Therefore, these two parameter values will be used in this paper.

Table 2. Ranking of GCIDE with various parameter values.

NPini	12D				18D				23D				25D
k	4	6	8	10	4	6	8	10	4	6	8	10	4	6	8	10
Ranking	7.56	7.19	7.88	8.13	8.13	11.00	8.81	11.50	5.75	7.38	8.81	10.88	6.94	7.13	9.44	9.50

4.2. Comparison and Discussion

In this subsection, we shall evaluate the performance of GCIDE by comparing it with five well-known DE variants (JADE [9], jDE [43], FDDE [24], rank-DE [10], and SHADE [44]) and five other typical heuristic algorithms (EPSO [52], MKE [53], HGSA [54], HLWCA [55], AOA [56]), respectively.

Particularly, among the chosen five other heuristic algorithms above, EPSO is a recent and well-known variant of PSO, which properly integrates five different top PSO variants. MKE is a new memetic evolutionary algorithm by randomly selecting some Monkey King particles, and then separately transforming them to a small group of monkeys for exploitation. Meanwhile, HGSA and HLWCA are both heuristic optimizers inspired by physics. HGSA is an enhanced gravitational search algorithm by designing hierarchical structures to interact with the population to enhance the exploration of the algorithm, while HLWCA is a recent variant of the water cycle algorithm by introducing the idea of hierarchical learning. Moreover, AOA is a new meta-heuristic method, which simulates the distributional behavior of the main arithmetic operators in mathematics. Obviously, these methods above have a certain representativeness. Thus, it is meaningful and reasonable to compare GCIDE with them here.

In these experiments, the parameters involved in the above ten compared algorithms are set to the same settings as in their original papers, and those of our method are set to the mentioned settings in Section 3. For clarity, their detailed parameter settings are further given in Table 3.

Table 3. Parameter settings.

Algorithm	Parameter Settings
JADE [9]	${\mu }_F=0.5,\hspace{0.17em}F\sim C\left({\mu }_F,0.1\right),\hspace{0.17em}Cr\sim N\left({\mu }_{Cr},0.1\right),\hspace{0.17em}p=0.05,\hspace{0.17em}c=0.1$
jDE [43]	$F=0.5,\hspace{0.17em}Cr=0.9,\hspace{0.17em}{\tau }_F={\tau }_{Cr}=0.1,\hspace{0.17em}{F}_l=0.1,\hspace{0.17em}{F}_u=0.9$
FDDE [24]	$F=0.5,\hspace{0.17em}Cr=0.9,\hspace{0.17em}{\tau }_F={\tau }_{Cr}=0.1,\hspace{0.17em}{F}_l=0.1,\hspace{0.17em}{F}_u=0.9,\hspace{0.17em}w\in \left(0.2,\hspace{0.17em}0.8\right)$
rank-DE [10]	$F=0.5,\hspace{0.17em}Cr=0.9,\hspace{0.17em}{\tau }_F={\tau }_{Cr}=0.1,\hspace{0.17em}{F}_l=0.1,\hspace{0.17em}{F}_u=0.9$
SHADE [44]	${\mu }_F=0.5,\hspace{0.17em}F\sim C\left({\mu }_F,0.1\right),\hspace{0.17em}{\mu }_{Cr}=0.5,\hspace{0.17em}Cr\sim N\left({\mu }_{Cr},0.1\right),\hspace{0.17em}p=0.2,\hspace{0.17em}H=100$
EPSO [52]	$N_{pop}=30,\hspace{0.17em}{g}_1=15,\hspace{0.17em}{g}_2=25$
MKE [53]	$FC=0.7$
HGSA [54]	$G_0=100,\hspace{0.17em}L=100,\hspace{0.17em}{w}_1\left(t\right)=1-t^6/T^6,\hspace{0.17em}{w}_2\left(t\right)=t^6/T^6,\hspace{0.17em}K\in \left[n,2\right]$
HLWCA [55]	$N_{pop}=200,\hspace{0.17em}{N}_{sr}=30,\hspace{0.17em}{d}_{\max }={10}^{-8},\hspace{0.17em}c=2$
AOA [56]	$N_{pop}=30,\hspace{0.17em}\alpha =5,\hspace{0.17em}\mu =0.5$
GCIDE	$N{P}_{init}=23\cdot D,\hspace{0.17em}k=4,\hspace{0.17em}{\mu }_{F_i}={\mu }_{C{r}_i}=0.5,\hspace{0.17em}i=1,2,\cdots ,k,\hspace{0.17em}N{P}_{\min }=k$

4.2.1. Comparison with Five DE Variants

First, five DE variants are selected as the comparison algorithms to verify the performance of GCIDE, including JADE [9], jDE [43], FDDE [24], rank-DE [10], and SHADE [44]. Table 4 and Table 5 provide the comparison results of GCIDE and five compared algorithms on the IEEE CEC2017 benchmark test suite with D = 30 and D = 50, respectively. Herein, “+”, “−” and “=” indicate that GCIDE has better, worse, and similar performance than the compared algorithms, respectively, “Ranking” is the average rank based on the Friedman test [51] (the same below).

Table 4. Numerical results of GCIDE, JADE, jDE, FDDE, rank-DE, and SHADE on IEEE CEC 2017 test suite when D = 30.

Algorithms	JADE	jDE	FDDE	Rank-DE	SHADE	GCIDE
Functions	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std
F01	1.42 × 10−14 3.73 × 10−15 (−)	1.14 × 10−14 5.78 × 10−15 (−)	7.11 × 10−15 7.23 × 10−15 (−)	1.23 × 10−14 4.91 × 10−15 (−)	1.18 × 10−14 5.39 × 10−15 (−)	1.52 × 10−14 3.61 × 10−15
F02	1.04 × 101 2.16 × 101 (+)	6.70 × 102 3.37 × 103 (+)	0.00 × 100 0.00 × 100 (−)	1.84 × 104 9.70 × 104 (+)	3.85 × 102 1.49 × 103 (+)	1.00 × 10−1 4.03 × 10−1
F03	1.03 × 104 1.65 × 104 (+)	8.43 × 104 1.58 × 103 (+)	9.54 × 10−8 2.68 × 10−7 (+)	2.08 × 10−9 2.89 × 10−9 (+)	9.66 × 10−14 3.70 × 10−14 (−)	2.01 × 10−13 1.08 × 10−13
F04	4.60 × 101 2.50 × 101 (+)	5.83 × 101 1.11 × 101 (+)	5.36 × 101 1.83 × 101 (+)	4.62 × 101 2.63 × 101 (+)	5.08 × 101 2.02 × 101 (+)	2.94 × 101 3.10 × 101
F05	2.53 × 101 3.93 × 100 (+)	4.03 × 101 6.78 × 100 (+)	1.68 × 102 1.31 × 101 (+)	3.42 × 101 7.77 × 100 (+)	1.46 × 101 2.81 × 100 (+)	7.96 × 100 1.58 × 100
F06	1.67 × 10−13 6.50 × 10−14 (−)	1.14 × 10−13 0.00 × 100 (−)	2.79 × 10−7 8.94 × 10−7 (−)	4.14 × 10−5 1.64 × 10−4 (+)	2.66 × 10−5 2.89 × 10−5 (+)	8.48 × 10−6 7.50 × 10−6
F07	5.41 × 101 4.73 × 100 (+)	7.53 × 101 7.25 × 100 (+)	2.04 × 102 9.66 × 100 (+)	8.95 × 101 3.33 × 101 (+)	4.46 × 101 2.92 × 100 (+)	3.58 × 101 1.06 × 100
F08	2.52 × 101 4.18 × 100 (+)	4.40 × 101 6.69 × 100 (+)	1.60 × 102 3.64 × 101 (+)	3.71 × 101 7.12 × 100 (+)	1.55 × 101 2.43 × 100 (+)	8.41 × 100 1.40 × 100
F09	2.98 × 10−3 1.63 × 10−2 (+)	0.00 × 100 0.00 × 100 (−)	1.51 × 10−2 8.29 × 10−2 (+)	1.33 × 100 1.27 × 100 (+)	2.98 × 10−3 1.63 × 10−2 (+)	5.31 × 10−14 5.77 × 10−14
F10	1.86 × 103 2.54 × 102 (+)	2.63 × 103 3.31 × 102 (+)	6.51 × 103 4.19 × 102 (+)	4.38 × 103 5.05 × 102 (+)	1.74 × 103 2.25 × 102 (+)	1.53 × 103 3.10 × 102
F11	3.64 × 101 2.88 × 101 (+)	2.33 × 101 2.42 × 101 (+)	2.12 × 101 3.07 × 101 (+)	5.69 × 101 3.96 × 101 (+)	2.97 × 101 2.36 × 101 (+)	1.84 × 101 2.35 × 101
F12	1.04 × 103 3.47 × 102 (+)	8.55 × 103 6.79 × 103 (+)	1.53 × 104 1.85 × 104 (+)	7.14 × 103 7.39 × 103 (+)	1.21 × 103 4.28 × 102 (+)	9.93 × 102 3.87 × 102
F13	4.56 × 101 2.71 × 101 (+)	3.92 × 101 2.55 × 101 (+)	8.16 × 101 2.09 × 101 (+)	7.92 × 101 1.48 × 102 (+)	3.98 × 101 2.99 × 101 (+)	1.48 × 101 6.60 × 100
F14	6.03 × 103 7.93 × 103 (+)	2.77 × 101 1.23 × 101 (+)	4.94 × 101 1.72 × 101 (+)	4.42 × 101 1.74 × 101 (+)	3.14 × 101 5.12 × 100 (+)	2.24 × 101 1.22 × 100
F15	6.34 × 102 1.35 × 103 (+)	1.34 × 101 3.92 × 100 (+)	8.77 × 100 6.65 × 100 (+)	4.27 × 101 4.71 × 101 (+)	2.43 × 101 1.56 × 101 (+)	3.48 × 100 1.31 × 100
F16	3.76 × 102 1.65 × 102 (+)	4.36 × 102 1.46 × 102 (+)	2.49 × 102 2.57 × 102 (+)	3.77 × 102 2.37 × 102 (+)	2.72 × 102 1.43 × 102 (+)	1.40 × 102 9.45 × 101
F17	7.78 × 101 2.26 × 101 (+)	9.33 × 101 2.37 × 101 (+)	6.74 × 101 2.80 × 101 (+)	8.32 × 101 7.23 × 101 (+)	4.87 × 101 1.09 × 101 (+)	3.14 × 101 7.54 × 100
F18	1.68 × 104 3.89 × 104 (+)	5.38 × 101 6.29 × 101 (+)	2.14 × 101 9.55 × 100 (−)	1.99 × 102 3.29 × 102 (+)	7.97 × 101 5.60 × 101 (+)	2.19 × 101 1.28 × 100
F19	2.02 × 103 3.30 × 103 (+)	1.12 × 101 2.82 × 100 (+)	7.54 × 100 1.64 × 100 (+)	2.37 × 101 2.34 × 101 (+)	1.53 × 101 1.49 × 101 (+)	7.03 × 100 1.59 × 100
F20	1.08 × 102 5.61 × 101 (+)	8.25 × 101 4.18 × 101 (+)	2.66 × 101 3.36 × 101 (−)	9.47 × 101 7.52 × 101 (+)	5.89 × 101 3.77 × 101 (+)	4.07 × 101 9.98 × 100
F21	2.26 × 102 3.67 × 100 (+)	2.44 × 102 5.25 × 100 (+)	3.61 × 102 1.13 × 101 (+)	2.39 × 102 9.26 × 100 (+)	2.16 × 102 3.02 × 100 (+)	2.08 × 102 1.43 × 100
F22	1.00 × 102 0.00 × 100 (=)	1.00 × 102 8.30 × 10−14 (=)	5.55 × 102 1.73 × 103 (+)	8.17 × 102 1.67 × 103 (+)	1.00 × 102 8.30 × 10−14 (=)	1.00 × 102 2.27 × 10−13
F23	3.72 × 102 5.52 × 100 (+)	3.91 × 102 6.99 × 100 (+)	4.94 × 102 5.22 × 101 (+)	3.89 × 102 1.07 × 101 (+)	3.64 × 102 4.17 × 100 (+)	3.45 × 102 3.29 × 100
F24	4.41 × 102 6.29 × 100 (+)	4.61 × 102 6.39 × 100 (+)	5.63 × 102 4.79 × 101 (+)	4.63 × 102 1.34 × 101 (+)	4.38 × 102 4.69 × 100 (+)	4.22 × 102 2.62 × 100
F25	3.87 × 102 1.56 × 10−1 (=)	3.87 × 102 1.38 × 101 (=)	3.87 × 102 4.51 × 10−2 (=)	3.87 × 102 1.36 × 100 (=)	3.87 × 102 8.66 × 10−2 (=)	3.87 × 102 5.06 × 10−2
F26	1.15 × 103 1.71 × 102 (+)	1.36 × 103 9.09 × 101 (+)	1.35 × 103 5.28 × 102 (+)	1.42 × 103 2.50 × 102 (+)	1.09 × 103 5.47 × 101 (+)	9.06 × 102 3.35 × 101
F27	5.05 × 102 7.78 × 100 (−)	5.01 × 102 6.19 × 100 (−)	4.96 × 102 8.53 × 100 (−)	5.12 × 102 9.69 × 100 (+)	5.07 × 102 7.34 × 100 (+)	5.05 × 102 4.19 × 100
F28	3.17 × 102 3.92 × 101 (+)	3.45 × 102 5.66 × 101 (+)	3.36 × 102 5.17 × 101 (+)	3.43 × 102 5.88 × 101 (+)	3.16 × 102 4.15 × 101 (+)	3.14 × 102 3.67 × 101
F29	4.88 × 102 3.48 × 101 (+)	5.07 × 102 4.09 × 101 (+)	4.06 × 102 5.10 × 101 (−)	5.26 × 102 8.43 × 101 (+)	4.71 × 102 3.80 × 101 (+)	4.37 × 102 6.35 × 100
F30	2.33 × 103 9.02 × 102 (+)	2.15 × 103 1.47 × 102 (+)	2.04 × 103 9.40 × 101 (−)	2.20 × 103 3.34 × 102 (+)	2.10 × 103 1.61 × 102 (+)	2.06 × 103 7.02 × 101
+/−/=	25/3/2	23/5/2	20/9/1	27/2/1	25/3/2
Ranking	3.97	3.95	3.63	4.77	2.97	1.72

Table 5. Numerical results of GCIDE, JADE, jDE, FDDE, rank-DE, and SHADE on IEEE CEC 2017 test suite when D = 50.

Algorithms	JADE	jDE	FDDE	Rank-DE	SHADE	GCIDE
Functions	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std
F01	4.69 × 10−14 1.94 × 10−14 (−)	1.04 × 10−7 2.73 × 10−7 (−)	2.61 × 10−2 3.95 × 10−2 (+)	1.91 × 10−7 3.97 × 10−7 (−)	4.88 × 10−14 2.13 × 10−14 (−)	4.61 × 10−7 1.20 × 10−6
F02	7.32 × 1011 3.27 × 1012 (+)	7.56 × 108 2.59 × 109 (+)	9.99 × 1011 3.63 × 1012 (+)	9.07 × 10+14 4.90 × 10+15 (+)	8.27 × 1012 3.23 × 1013 (+)	2.15 × 106 9.52 × 106
F03	3.60 × 104 4.89 × 104 (+)	5.82 × 102 1.03 × 103 (+)	4.68 × 103 1.84 × 103 (+)	9.18 × 100 1.23 × 101 (+)	3.39 × 10−13 1.01 × 10−13 (−)	4.99 × 10−9 2.13 × 10−8
F04	3.33 × 101 3.80 × 101 (−)	6.71 × 101 5.03 × 101 (−)	8.32 × 101 5.31 × 101 (+)	5.07 × 101 4.03 × 101 (−)	5.72 × 101 4.79 × 101 (−)	7.98 × 101 4.07 × 101
F05	5.27 × 101 8.71 × 100 (+)	9.42 × 101 1.05 × 101 (+)	2.28 × 102 1.58 × 101 (+)	7.53 × 101 1.60 × 101 (+)	3.23 × 101 6.26 × 100 (+)	1.80 × 101 2.04 × 100
F06	1.36 × 10−13 4.63 × 10−14 (−)	1.14 × 10−13 0.00 × 100 (−)	4.73 × 10−8 1.42 × 10−7 (−)	1.34 × 10−2 4.16 × 10−2 (+)	8.99 × 10−4 1.27 × 10−3 (+)	1.03 × 10−4 8.19 × 10−5
F07	1.03 × 102 6.48 × 100 (+)	1.48 × 102 1.29 × 101 (+)	2.93 × 102 1.14 × 101 (+)	1.69 × 102 7.23 × 101 (+)	8.20 × 101 6.31 × 100 (+)	6.11 × 101 1.26 × 100
F08	5.38 × 101 9.40 × 100 (+)	9.24 × 101 9.22 × 100 (+)	2.28 × 102 1.75 × 101 (+)	8.41 × 101 1.48 × 101 (+)	3.32 × 101 5.25 × 100 (+)	1.86 × 101 1.85 × 100
F09	1.18 × 100 8.46 × 10−1 (+)	3.01 × 10−2 8.70 × 10−2 (+)	2.75 × 10−1 6.71 × 10−1 (+)	1.76 × 101 1.88 × 101 (+)	8.50 × 10−1 9.37 × 10−1 (+)	2.98 × 10−3 1.63 × 10−2
F10	3.75 × 103 2.99 × 102 (+)	4.99 × 103 3.26 × 102 (+)	9.19 × 103 3.92 × 102 (+)	8.93 × 103 1.13 × 103 (+)	3.40 × 103 3.07 × 102 (+)	3.05 × 103 4.18 × 102
F11	1.17 × 102 2.93 × 101 (+)	5.14 × 101 1.26 × 101 (−)	5.28 × 101 2.09 × 101 (−)	1.32 × 102 4.77 × 101 (+)	1.23 × 102 3.57 × 101 (+)	6.53 × 101 1.29 × 101
F12	4.43 × 103 2.35 × 103 (+)	5.38 × 104 3.78 × 104 (+)	1.18 × 105 5.25 × 104 (+)	4.42 × 104 3.01 × 104 (+)	5.75 × 103 3.40 × 103 (+)	2.94 × 103 1.01 × 103
F13	3.29 × 102 2.35 × 102 (+)	2.61 × 103 3.06 × 103 (+)	6.25 × 103 7.19 × 103 (+)	3.33 × 102 4.26 × 102 (+)	3.10 × 102 1.97 × 102 (+)	6.43 × 101 3.31 × 101
F14	3.10 × 104 7.14 × 104 (+)	6.32 × 101 1.81 × 101 (+)	6.47 × 101 5.17 × 101 (+)	4.22 × 102 3.84 × 102 (+)	1.96 × 102 6.75 × 101 (+)	3.13 × 101 3.12 × 100
F15	3.45 × 102 1.62 × 102 (+)	7.45 × 101 8.25 × 101 (+)	5.70 × 101 3.47 × 101 (+)	2.36 × 102 3.67 × 102 (+)	3.60 × 102 1.28 × 102 (+)	4.16 × 101 1.26 × 101
F16	8.46 × 102 2.16 × 102 (+)	9.81 × 102 1.90 × 102 (+)	9.05 × 102 4.87 × 102 (+)	9.64 × 102 2.98 × 102 (+)	7.98 × 102 1.83 × 102 (+)	4.05 × 102 8.51 × 101
F17	5.75 × 102 1.31 × 102 (+)	6.89 × 102 1.14 × 102 (+)	6.28 × 102 3.01 × 102 (+)	5.65 × 102 2.17 × 102 (+)	5.05 × 102 1.52 × 102 (+)	3.38 × 102 9.46 × 101
F18	2.18 × 104 8.69 × 104 (+)	2.23 × 103 2.16 × 103 (+)	6.79 × 103 5.09 × 103 (+)	9.66 × 103 6.45 × 103 (+)	2.04 × 102 1.40 × 102 (+)	4.20 × 101 1.18 × 101
F19	1.31 × 102 4.25 × 101 (+)	2.76 × 101 8.63 × 100 (+)	1.02 × 102 4.07 × 102 (+)	1.00 × 102 4.04 × 101 (+)	1.54 × 102 5.24 × 101 (+)	2.51 × 101 4.08 × 100
F20	4.56 × 102 9.56 × 101 (+)	4.99 × 102 1.25 × 102 (+)	5.13 × 102 2.46 × 102 (+)	4.09 × 102 2.37 × 102 (+)	3.25 × 102 1.14 × 102 (+)	1.38 × 102 5.32 × 101
F21	2.53 × 102 8.19 × 100 (+)	2.95 × 102 1.04 × 101 (+)	4.34 × 102 1.06 × 101 (+)	2.85 × 102 1.49 × 101 (+)	2.34 × 102 4.61 × 100 (+)	2.18 × 102 2.49 × 100
F22	2.97 × 103 2.05 × 103 (+)	5.23 × 103 1.44 × 103 (+)	9.79 × 103 3.32 × 102 (+)	8.97 × 103 1.57 × 103 (+)	3.43 × 103 1.39 × 103 (+)	1.01 × 102 4.45 × 100
F23	4.77 × 102 9.49 × 100 (+)	5.15 × 102 1.28 × 101 (+)	6.36 × 102 3.42 × 101 (+)	5.16 × 102 1.88 × 101 (+)	4.57 × 102 9.96 × 100 (+)	4.31 × 102 9.23 × 100
F24	5.42 × 102 9.53 × 100 (+)	5.79 × 102 8.05 × 100 (+)	5.65 × 102 1.32 × 101 (+)	5.84 × 102 1.86 × 101 (+)	5.32 × 102 6.70 × 100 (+)	5.09 × 102 5.85 × 100
F25	5.17 × 102 3.61 × 101 (−)	5.09 × 102 3.99 × 101 (−)	4.89 × 102 2.15 × 101 (−)	5.19 × 102 3.90 × 101 (−)	5.22 × 102 3.77 × 101 (−)	5.39 × 102 2.39 × 101
F26	1.60 × 103 9.58 × 101 (+)	1.99 × 103 9.92 × 101 (+)	2.47 × 103 6.61 × 102 (+)	2.14 × 103 1.80 × 102 (+)	1.39 × 103 7.11 × 101 (+)	1.23 × 103 6.37 × 101
F27	5.61 × 102 3.56 × 101 (+)	5.51 × 102 2.72 × 101 (+)	5.42 × 102 2.22 × 101 (+)	6.15 × 102 6.31 × 101 (+)	5.48 × 102 2.15 × 101 (+)	5.39 × 102 1.01 × 101
F28	4.83 × 102 2.27 × 101 (−)	4.81 × 102 2.32 × 101 (−)	4.72 × 102 2.18 × 101 (−)	4.93 × 102 2.57 × 101 (−)	4.81 × 102 2.45 × 101 (−)	5.00 × 102 1.85 × 101
F29	4.84 × 102 7.34 × 101 (+)	5.28 × 102 6.15 × 101 (+)	3.85 × 102 1.02 × 102 (+)	7.53 × 102 2.40 × 102 (+)	4.63 × 102 8.44 × 101 (+)	3.79 × 102 2.08 × 101
F30	6.83 × 105 7.15 × 104 (+)	6.11 × 105 3.54 × 104 (−)	6.24 × 105 4.12 × 104 (−)	7.31 × 105 1.40 × 105 (+)	6.60 × 105 9.10 × 104 (+)	6.29 × 105 3.63 × 104
+/−/=	25/5/0	23/7/0	25/5/0	26/4/0	25/5/0
Ranking	3.57	3.62	4.30	4.63	3.02	1.87

As can be seen from Table 4, when D = 30, the proposed GCIDE obtains better results in most test functions, except for nine, including F1–F3, F6, F18, F20, F27, and F29–F30. Specifically, compared to JADE, GCIDE wins 25, loses 3, and holds 2. Against jDE, GCIDE wins 23, loses 5, and holds 2. Compared with FDDE, GCIDE wins 20, loses 9, and holds 1. Compared with rank-DE, GCIDE wins 27, loses 2, and holds 1. Compared with SHADE, GCIDE wins 25, loses 3, and holds 2. Meanwhile, when D = 50, from Table 5, the proposed GCIDE has a clear advantage in both unimodal functions, simple multimodal functions, hybrid functions, and composition functions, and just loses the advantage in eight functions, including F1, F3–F4, F6, F11, F25, F28, and F30. Specifically, compared to JADE, GCIDE wins 25, loses 5, and holds 0. Against jDE, GCIDE wins 23, loses 7, and holds 0. Compared with FDDE, GCIDE wins 25, loses 5, and holds 0. Compared with rank-DE, GCIDE wins 26, loses 4, and holds 0. Compared with SHADE, GCIDE wins 25, loses 5, and holds 0.

To verify the significance of GCIDE, Table 6 and Table 7 list the statistical results of GCIDE and its competitors based on Wilcoxon signed-rank tests [51] when D = 30 and D = 50, respectively. From Table 6 and Table 7, it can be seen that GCIDE has more R+ values compared to the other five algorithms in the cases of both D = 30 and D = 50, and the obtained p-values are all much less than 0.05. Thus, there is a significant difference between GCIDE and its comparison algorithms.

Table 6. Comparison results of GCIDE with JADE, jDE, FDDE, rank-DE, and SHADE based on Wilcoxon signed-rank tests when D = 30.

Algorithm	R+	R−	p	Significance
GCIDE vs. JADE	394	41	0.000	+
GCIDE vs. jDE	418	17	0.000	+
GCIDE vs. FDDE	354	111	0.012	+
GCIDE vs. rank-DE	453	12	0.000	+
GCIDE vs. SHADE	376	59	0.001	+

Table 7. Comparison results of GCIDE with JADE, jDE, FDDE, rank-DE, and SHADE based on Wilcoxon signed-rank tests when D = 50.

Algorithm	R+	R−	p	Significance
GCIDE vs. JADE	439.5	25.5	0.000	+
GCIDE vs. jDE	404	61	0.000	+
GCIDE vs. FDDE	413	52	0.000	+
GCIDE vs. rank-DE	448	17	0.000	+
GCIDE vs. SHADE	431	34	0.000	+

Moreover, to clearly show the convergence performance of GCIDE, the evolution curves of GCIDE and five compared algorithms are also depicted on eight typical functions, including F1, F2, F5, F7, F16, F17, F21, and F26. Figure 1 and Figure 2 draw their evolution curves when both D = 30 and D = 50, respectively. As shown in Figure 1, when D = 30, the convergence trend of GCIDE is slower in the early evolutionary stage and rapid when entering the late evolutionary stage. In particular, for simple multimodal functions F5 and F7, GCIDE converges quickly to find better solutions when other algorithms fall into local optima. For other hybrid and composition functions, GCIDE has a similar performance to its compared algorithms, but has a higher accuracy. Meanwhile, when D = 50, as shown in Figure 2, GCIDE still shows higher convergence accuracy. Therefore, GCIDE has a better convergence performance.

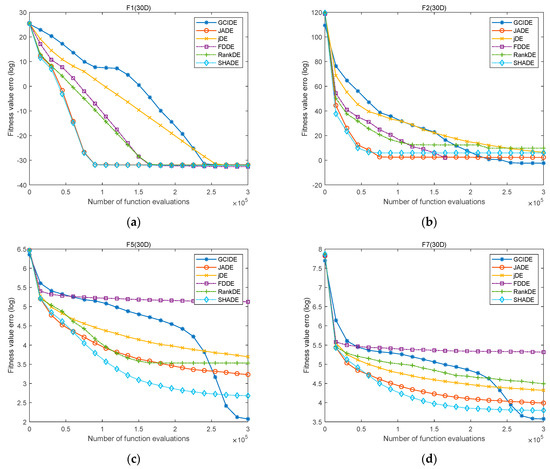
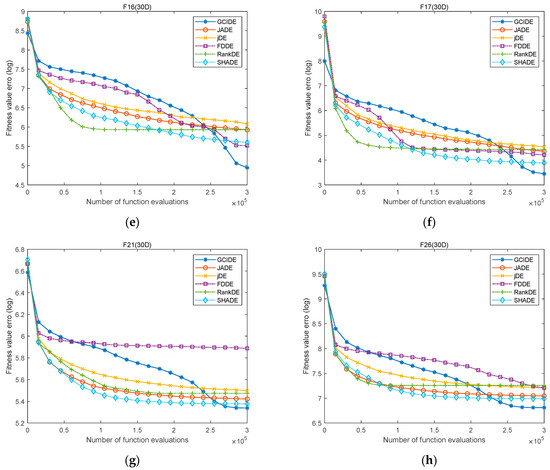
Figure 1. The evolution curves of GCIDE, JADE, jDE, FDDE, rank−DE, and SHADE on F1 (a), F2 (b), F5 (c), F7 (d), F16 (e), F17 (f), F21 (g), F26 (h) with D = 30.

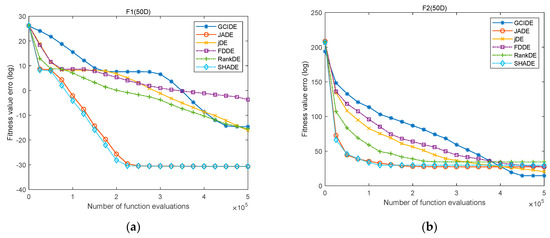
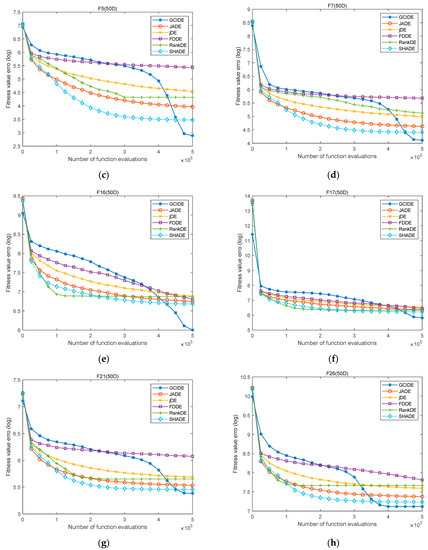
Figure 2. The evolution curves of GCIDE, JADE, jDE, FDDE, rank−DE, and SHADE on F1 (a), F2 (b), F5 (c), F7 (d), F16 (e), F17 (f), F21 (g), F26 (h) with D = 50.

4.2.2. Comparison with Five Other Heuristic Algorithms

Five non-DE heuristic algorithms are further selected as comparison algorithms to show the performance of GCIDE, including EPSO [52], MKE [53], HGSA [54], HLWCA [55], and AOA [56]. Table 8 and Table 9 provide the comparison results of GCIDE and these five compared algorithms on the IEEE CEC2017 test suite with D = 30 and D = 50, respectively.

Table 8. Numerical results of GCIDE, EPSO, MKE, HGSA, HLWCA, and AOA on IEEE CEC 2017 test suite when D = 30.

Algorithms	EPSO	MKE	HGSA	HLWCA	AOA	GCIDC
Functions	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std
F01	2.82 × 100 3.33 × 100 (+)	1.18 × 10−14 5.39 × 10−15 (−)	3.52 × 102 3.57 × 102 (+)	7.77 × 102 1.22 × 103 (+)	4.23 × 1010 6.20 × 109 (+)	1.52 × 10−14 3.61 × 10−15
F02	2.67 × 10−1 5.21 × 10−1 (+)	7.33 × 10−1 3.66 × 100 (+)	7.11 × 101 4.89 × 101 (+)	2.48 × 1020 1.34 × 1021 (+)	5.73 × 1051 3.14 × 1052 (+)	1.00 × 10−1 4.03 × 10−1
F03	2.02 × 10−5 1.33 × 10−5 (+)	9.08 × 10−4 1.32 × 10−3 (+)	3.19 × 104 3.19 × 103 (+)	2.14 × 103 1.60 × 103 (+)	7.42 × 104 6.92 × 103 (+)	2.01 × 10−13 1.08 × 10−13
F04	7.52 × 10−1 4.39 × 10−1 (−)	2.48 × 101 2.99 × 101 (−)	1.32 × 102 4.03 × 100 (+)	7.31 × 101 3.21 × 101 (+)	9.20 × 103 2.19 × 103 (+)	2.94 × 101 3.10 × 101
F05	6.25 × 101 5.41 × 100 (+)	6.19 × 101 1.85 × 101 (+)	1.12 × 102 6.99 × 100 (+)	8.25 × 101 3.01 × 101 (+)	3.22 × 102 3.43 × 101 (+)	7.96 × 100 1.58 × 100
F06	1.37 × 10−12 3.86 × 10−13 (−)	8.14 × 10−6 1.83 × 10−5 (−)	2.92 × 100 1.84 × 100 (+)	1.54 × 10−3 2.77 × 10−3 (+)	6.91 × 101 5.76 × 100 (+)	8.48 × 10−6 7.50 × 10−6
F07	1.17 × 102 7.47 × 100 (+)	1.06 × 102 1.56 × 101 (+)	3.85 × 101 1.32 × 100 (+)	1.42 × 102 2.19 × 101 (+)	6.00 × 102 5.54 × 101 (+)	3.58 × 101 1.06 × 100
F08	4.12 × 101 6.93 × 100 (+)	7.32 × 101 1.94 × 101 (+)	1.24 × 102 6.70 × 100 (+)	8.00 × 101 2.70 × 101 (+)	2.48 × 102 2.73 × 101 (+)	8.41 × 100 1.40 × 100
F09	1.48 × 101 6.30 × 100 (+)	3.30 × 10−1 4.20 × 10−1 (+)	3.41 × 10−14 5.30 × 10−14 (−)	9.00 × 101 1.41 × 102 (+)	4.95 × 103 9.29 × 102 (+)	5.31 × 10−14 5.77 × 10−14
F10	1.65 × 103 2.50 × 102 (+)	3.31 × 103 7.32 × 102 (+)	3.18 × 103 2.65 × 102 (+)	3.37 × 103 6.61 × 102 (+)	5.27 × 103 5.50 × 102 (+)	1.53 × 103 3.10 × 102
F11	4.85 × 101 1.25 × 101 (+)	4.14 × 101 2.72 × 101 (+)	8.90 × 101 1.12 × 101 (+)	6.69 × 101 3.31 × 101 (+)	2.63 × 103 1.01 × 103 (+)	1.84 × 101 2.35 × 101
F12	2.18 × 103 3.99 × 102 (+)	9.88 × 103 1.19 × 104 (+)	1.93 × 104 7.47 × 103 (+)	2.76 × 105 7.12 × 105 (+)	8.03 × 109 2.02 × 109 (+)	9.93 × 102 3.87 × 102
F13	8.49 × 101 2.33 × 101 (+)	1.15 × 102 3.55 × 102 (+)	1.78 × 102 1.22 × 102 (+)	7.12 × 102 4.21 × 102 (+)	4.05 × 104 1.34 × 104 (+)	1.48 × 101 6.60 × 100
F14	8.89 × 101 2.03 × 101 (+)	5.53 × 101 1.51 × 101 (+)	1.96 × 102 2.44 × 101 (+)	5.55 × 102 4.25 × 102 (+)	5.17 × 104 4.80 × 104 (+)	2.24 × 101 1.22 × 100
F15	6.77 × 101 1.92 × 101 (+)	2.60 × 101 1.38 × 101 (+)	1.56 × 102 6.48 × 101 (+)	6.60 × 102 4.54 × 102 (+)	1.82 × 104 6.10 × 103 (+)	3.48 × 100 1.31 × 100
F16	4.14 × 102 1.46 × 102 (+)	7.95 × 102 2.32 × 102 (+)	1.34 × 103 1.57 × 102 (+)	4.13 × 102 1.50 × 102 (+)	2.84 × 103 1.33 × 103 (+)	1.40 × 102 9.45 × 101
F17	1.27 × 102 2.54 × 101 (+)	2.31 × 102 1.33 × 102 (+)	7.12 × 102 1.09 × 102 (+)	1.88 × 102 7.29 × 101 (+)	1.10 × 103 3.54 × 102 (+)	3.14 × 101 7.54 × 100
F18	2.50 × 104 1.26 × 104 (+)	5.34 × 101 2.24 × 101 (+)	1.72 × 104 4.37 × 103 (+)	9.90 × 104 8.30 × 104 (+)	6.59 × 105 5.18 × 105 (+)	2.19 × 101 1.28 × 100
F19	6.74 × 101 2.47 × 101 (+)	1.45 × 101 6.56 × 100 (+)	1.13 × 102 4.60 × 101 (+)	7.38 × 102 9.86 × 102 (+)	1.07 × 106 1.08 × 105 (+)	7.03 × 100 1.59 × 100
F20	2.56 × 102 4.56 × 101 (+)	2.52 × 102 1.21 × 102 (+)	8.43 × 102 1.33 × 102 (+)	2.71 × 102 1.18 × 102 (+)	7.26 × 102 1.81 × 102 (+)	4.07 × 101 9.98 × 100
F21	4.18 × 101 3.06 × 101 (−)	2.69 × 102 1.70 × 101 (+)	1.55 × 102 1.07 × 101 (−)	1.50 × 102 0.00 × 100 (−)	5.09 × 102 4.82 × 101 (+)	2.08 × 102 1.43 × 100
F22	4.20 × 101 6.06 × 100 (−)	9.52 × 102 1.48 × 103 (+)	1.47 × 102 7.87 × 100 (+)	1.50 × 102 0.00 × 100 (+)	6.02 × 103 5.71 × 102 (+)	1.00 × 102 2.27 × 10−13
F23	5.39 × 102 7.77 × 100 (+)	4.14 × 102 1.42 × 101 (+)	4.02 × 102 1.13 × 102 (+)	5.67 × 102 1.41 × 101 (+)	1.19 × 103 1.80 × 102 (+)	3.45 × 102 3.29 × 100
F24	2.00 × 102 1.10 × 10−12 (−)	4.81 × 102 1.45 × 101 (+)	2.00 × 102 1.41 × 10−9 (−)	6.62 × 102 4.03 × 102 (+)	1.50 × 103 2.31 × 102 (+)	4.22 × 102 2.62 × 100
F25	4.01 × 102 1.23 × 100 (+)	3.87 × 102 1.23 × 10−1 (+)	2.00 × 102 2.67 × 10−8 (−)	3.71 × 102 1.27 × 102 (−)	1.85 × 103 4.54 × 102 (+)	3.87 × 102 5.06 × 10−2
F26	2.00 × 102 9.62 × 10−11 (−)	1.60 × 103 3.18 × 102 (+)	2.00 × 102 2.40 × 10−8 (−)	1.64 × 103 1.21 × 103 (+)	8.02 × 103 1.18 × 103 (+)	9.06 × 102 3.35 × 101
F27	8.59 × 102 3.96 × 101 (+)	5.10 × 102 9.15 × 100 (+)	1.16 × 103 2.05 × 102 (+)	7.79 × 102 4.60 × 101 (+)	1.80 × 103 3.48 × 102 (+)	5.05 × 102 4.19 × 100
F28	4.42 × 102 3.24 × 101 (+)	3.55 × 102 6.15 × 101 (+)	2.00 × 102 4.00 × 10−8 (−)	5.23 × 102 3.49 × 102 (+)	3.40 × 103 6.67 × 102 (+)	3.14 × 102 3.67 × 101
F29	4.34 × 102 5.15 × 101 (−)	6.18 × 102 1.72 × 102 (+)	4.72 × 102 1.89 × 101 (+)	5.02 × 102 9.81 × 101 (+)	3.26 × 103 1.12 × 103 (+)	4.37 × 102 6.35 × 100
F30	2.22 × 103 5.64 × 102 (+)	2.54 × 103 7.90 × 102 (+)	2.60 × 104 6.35 × 103 (+)	7.73 × 103 1.23 × 104 (+)	2.70 × 108 7.74 × 108 (+)	2.06 × 103 7.02 × 101
+/−/=	23/7/0	27/3/0	24/6/0	28/2/0	30/0/0
Ranking	2.59	2.98	3.62	4.21	5.97	1.64

Table 9. Numerical results of GCIDE, EPSO, MKE, HGSA, HLWCA, and AOA on IEEE CEC 2017 test suite when D = 50.

Algorithms	EPSO	MKE	HGSA	HLWCA	AOA	GC-IDC
Functions	Mean/ Std	Mean/ Std	Mean/ Std	Mean/ Std	Mean/ Std	Mean/ Std
F01	3.92 × 103 9.21 × 101 (+)	2.80 × 10−4 8.09 × 10−4 (+)	1.16 × 103 1.05 × 103 (+)	5.89 × 103 6.69 × 103 (+)	1.05 × 1011 5.21 × 109 (+)	4.61 × 10−7 1.20 × 10−6
F02	3.35 × 101 2.14 × 101 (−)	1.45 × 108 3.43 × 108 (+)	4.62 × 10+13 6.49 × 10+13 (+)	1.07 × 1035 3.92 × 1035 (+)	3.46 × 1084 1.28 × 1085 (+)	2.15 × 106 9.52 × 106
F03	1.33 × 101 9.63 × 100 (+)	8.54 × 101 7.81 × 101 (+)	9.37 × 104 5.95 × 103 (+)	1.58 × 104 5.78 × 103 (+)	1.68 × 105 1.56 × 104 (+)	4.99 × 10−9 2.13 × 10−8
F04	6.26 × 101 2.90 × 101 (−)	4.10 × 101 4.89 × 101 (−)	7.14 × 101 3.07 × 101 (−)	8.34 × 101 2.23 × 101 (+)	2.70 × 104 4.55 × 103 (+)	7.98 × 101 4.07 × 101
F05	1.45 × 102 1.60 × 101 (+)	1.53 × 102 3.25 × 101 (+)	2.58 × 102 1.24 × 101 (+)	1.72 × 102 4.40 × 101 (+)	5.85 × 102 3.43 × 101 (+)	1.80 × 101 2.04 × 100
F06	7.74 × 10−11 1.06 × 10−10 (−)	1.03 × 10−2 4.78 × 10−2 (+)	5.93 × 100 1.30 × 100 (+)	2.32 × 100 2.52 × 100 (+)	8.66 × 101 4.67 × 100 (+)	1.03 × 10−4 8.19 × 10−5
F07	2.56 × 102 1.55 × 101 (+)	2.38 × 102 4.86 × 101 (+)	6.72 × 101 1.81 × 100 (+)	3.28 × 102 8.08 × 101 (+)	1.13 × 103 7.15 × 101 (+)	6.11 × 101 1.26 × 100
F08	9.33 × 101 1.17 × 101 (+)	1.51 × 102 3.18 × 101 (+)	2.99 × 102 1.55 × 101 (+)	1.85 × 102 4.19 × 101 (+)	6.21 × 102 3.68 × 101 (+)	1.86 × 101 1.85 × 100
F09	1.67 × 102 5.47 × 101 (+)	2.71 × 101 5.98 × 101 (+)	6.82 × 10−14 5.66 × 10−14 (−)	1.16 × 103 6.98 × 102 (+)	2.21 × 104 3.02 × 103 (+)	2.98 × 10−3 1.63 × 10−2
F10	3.90 × 103 2.82 × 102 (+)	6.99 × 103 1.12 × 103 (+)	5.06 × 103 3.36 × 102 (+)	7.14 × 103 1.04 × 103 (+)	1.13 × 104 5.33 × 102 (+)	3.05 × 103 4.18 × 102
F11	2.29 × 102 3.15 × 101 (+)	8.82 × 101 2.57 × 101 (+)	1.56 × 102 1.71 × 101 (+)	1.82 × 102 5.69 × 101 (+)	1.52 × 104 2.46 × 103 (+)	6.53 × 101 1.29 × 101
F12	3.50 × 103 4.96 × 102 (+)	6.88 × 104 4.40 × 104 (+)	4.23 × 104 8.61 × 103 (+)	4.86 × 105 2.13 × 106 (+)	6.55 × 1010 1.22 × 1010 (+)	2.94 × 103 1.01 × 103
F13	3.01 × 103 1.89 × 103 (+)	9.50 × 102 2.15 × 103 (+)	1.66 × 104 2.47 × 103 (+)	2.68 × 104 1.76 × 104 (+)	4.52 × 109 4.07 × 109 (+)	6.43 × 101 3.31 × 101
F14	9.63 × 101 1.95 × 101 (+)	1.58 × 102 8.80 × 101 (+)	1.75 × 102 1.34 × 101 (+)	7.87 × 102 8.89 × 102 (+)	6.91 × 105 7.37 × 105 (+)	3.13 × 101 3.12 × 100
F15	2.89 × 103 7.75 × 101 (+)	8.63 × 101 5.12 × 101 (+)	2.32 × 103 6.67 × 102 (+)	3.90 × 103 2.98 × 103 (+)	3.03 × 104 7.94 × 103 (+)	4.16 × 101 1.26 × 101
F16	8.81 × 102 1.84 × 102 (+)	1.43 × 103 3.41 × 102 (+)	1.76 × 103 2.89 × 102 (+)	1.23 × 103 3.61 × 102 (+)	5.40 × 103 1.36 × 103 (+)	4.05 × 102 8.51 × 101
F17	5.70 × 102 1.31 × 102 (+)	9.54 × 102 2.91 × 102 (+)	1.24 × 103 1.23 × 102 (+)	7.75 × 102 2.78 × 102 (+)	2.42 × 103 3.33 × 102 (+)	3.38 × 102 9.46 × 101
F18	6.85 × 104 3.04 × 104 (+)	4.99 × 103 3.45 × 103 (+)	8.91 × 104 2.11 × 104 (+)	3.42 × 105 2.49 × 105 (+)	1.67 × 107 1.23 × 107 (+)	4.20 × 101 1.18 × 101
F19	1.34 × 102 4.23 × 101 (+)	5.70 × 101 4.20 × 101 (+)	3.97 × 103 1.10 × 103 (+)	7.42 × 103 8.31 × 103 (+)	4.66 × 105 1.33 × 104 (+)	2.51 × 101 4.08 × 100
F20	7.22 × 102 1.17 × 102 (+)	8.72 × 102 3.12 × 102 (+)	1.67 × 103 1.87 × 102 (+)	8.32 × 102 2.92 × 102 (+)	1.51 × 103 2.71 × 102 (+)	1.38 × 102 5.32 × 101
F21	7.15 × 101 2.55 × 101 (−)	3.52 × 102 3.20 × 101 (+)	1.03 × 102 3.32 × 101 (−)	9.83 × 101 3.96 × 101 (−)	9.86 × 102 7.80 × 101 (+)	2.18 × 102 2.49 × 100
F22	1.10 × 102 1.83 × 101 (+)	7.60 × 103 1.18 × 103 (+)	3.19 × 102 1.03 × 101 (+)	1.94 × 102 4.93 × 101 (+)	1.29 × 104 7.10 × 102 (+)	1.01 × 102 4.45 × 100
F23	8.42 × 102 2.58 × 101 (+)	5.83 × 102 4.95 × 101 (+)	7.27 × 102 1.83 × 102 (+)	9.33 × 102 5.04 × 101 (+)	2.23 × 103 3.01 × 102 (+)	4.31 × 102 9.23 × 100
F24	2.00 × 102 8.64 × 10−11 (−)	6.41 × 102 3.63 × 101 (+)	2.00 × 102 5.32 × 10−13 (−)	5.33 × 102 5.62 × 102 (+)	2.46 × 103 3.87 × 102 (+)	5.09 × 102 5.85 × 100
F25	4.84 × 102 2.33 × 101 (−)	5.05 × 102 3.93 × 101 (−)	2.00 × 102 5.09 × 10−12 (−)	5.14 × 102 4.20 × 101 (−)	1.13 × 104 1.61 × 103 (+)	5.39 × 102 2.39 × 101
F26	2.00 × 102 1.15 × 10−9 (−)	2.57 × 103 3.87 × 102 (+)	2.00 × 102 2.29 × 10−12 (−)	2.00 × 102 0.00 × 100 (−)	1.35 × 104 1.08 × 103 (+)	1.23 × 103 6.37 × 101
F27	1.37 × 103 9.08 × 101 (+)	5.95 × 102 6.29 × 101 (+)	2.44 × 103 4.49 × 102 (+)	1.00 × 103 8.10 × 101 (+)	4.30 × 103 6.60 × 102 (+)	5.39 × 102 1.01 × 101
F28	4.39 × 102 2.43 × 101 (−)	4.89 × 102 2.29 × 101 (−)	2.00 × 102 4.15 × 10−12 (−)	4.99 × 102 3.60 × 101 (−)	8.56 × 103 8.79 × 102 (+)	5.00 × 102 1.85 × 101
F29	1.02 × 103 1.47 × 102 (+)	8.77 × 102 2.53 × 102 (+)	6.40 × 102 3.26 × 101 (+)	1.13 × 103 2.82 × 102 (+)	1.71 × 104 7.45 × 103 (+)	3.79 × 102 2.08 × 101
F30	1.78 × 104 4.01 × 103 (−)	6.54 × 105 5.71 × 104 (+)	8.74 × 104 7.57 × 103 (−)	2.30 × 104 6.34 × 103 (−)	3.11 × 108 5.75 × 107 (+)	6.29 × 105 3.63 × 104
+/−/=	21/9/0	27/3/0	22/8/0	25/5/0	30/0/0
Ranking	2.57	3.17	3.40	4.07	5.97	1.83

From Table 8, it can be seen that the proposed GCIDE obtains better results in most of the functions except for eleven test functions when D = 30, including F1, F4, F6, F9, F21, F22, F24–F26, F28, and F29. Specifically, compared to EPSO, GCIDE wins 23, loses 7, and holds 0. Against MKE, GCIDE wins 27, loses 3, and holds 0. Compared with HGSA, GCIDE wins 24, loses 6, and holds 0. Compared with HLWCA, GCIDE wins 28, loses 2, and holds 0. Compared with AOA, GCIDE is better on all test functions. Meanwhile, when D = 50, from Table 9, the proposed GCIDE is also absolutely superior on the nineteen functions, including F1, F3, F5, F7, F8, F10–F20, F22, F23, F27, and F29. Specifically, compared to EPSO, GCIDE wins 23, loses 7, and holds 0. Against MKE, GCIDE wins 27, loses 3, and holds 0. Compared with HGSA, GCIDE wins 22, loses 8, and holds 0. Compared with HLWCA, GCIDE wins 25, loses 5, and holds 0. Compared with AOA, GCIDE is better on all test functions.

To verify the significance of GCIDE, Table 10 and Table 11 list the statistical results of GCIDE and its competitors based on Wilcoxon signed-rank tests [51] when D = 30 and D = 50, respectively. From Table 10 and Table 11, it can be seen that GCIDE has more R+ values compared to the other five algorithms in the cases of both D = 30 and D = 50, and the obtained p-values are all much less than 0.05. Thus, there is a significant difference between GCIDE and its comparison algorithms.

Table 10. Comparison results of GCIDE with EPSO, MKE, HGSA, HLWCA, and AOA based on Wilcoxon signed-rank tests when D = 30.

Algorithm	R+	R−	p	Significance
GCIDE vs. EPSO	339	126	0.028	+
GCIDE vs. MKE	447	18	0.000	+
GCIDE vs. HGSA	366	99	0.006	+
GCIDE vs. HLWCA	403	62	0.000	+
GCIDE vs. AOA	435	0	0.000	+

Table 11. Comparison results of GCIDE with EPSO, MKE, HGSA, HLWCA, and AOA based on Wilcoxon signed-rank tests when D = 50.

Algorithm	R+	R−	p	Significance
GCIDE vs. EPSO	439.5	25.5	0.000	+
GCIDE vs. MKE	404	61	0.000	+
GCIDE vs. HGSA	413	52	0.000	+
GCIDE vs. HLWCA	448	17	0.000	+
GCIDE vs. AOA	435	0	0.000	+

4.3. Effectiveness of the Proposed Strategies

In this section, we conduct comparative experiments on the effectiveness of the strategies. For simplicity, we denote the variant of GCIDE using a fixed population size by GCIDE-1 and the variant of GCIDE without grouping the parameter control by GCIDE-2. Also, to investigate the effect of different mutation strategies on the performance of GCIDE, we further choose two additional mutation operators DE/rand/1 and DE/best/1, and denote the GCIDE with them by GCIDE (rand) and GCIDE (best), separately. Table 12 provides the numerical results of GCIDE and its four variants above on the IEEE CEC 2017 test suite with D = 30.

Table 12. Numerical results of GCIDE and its four variants above on IEEE CEC 2017 test suite with D = 30.

Algorithm	GCIDE-1	GCIDE-2	GCIDE (Rand)	GCIDE (Best)	GCIDE
Function	Mean Std	Mean Std	Mean Std	Mean Std	Mean Std
F01	1.42 × 10−14 0.00 × 100 (−)	1.56 × 10−14 4.34 × 10−15 (+)	7.87 × 100 2.88 × 101 (+)	9.76 × 10−14 1.81 × 10−13 (+)	1.52 × 10−14 3.61 × 10−15
F02	1.77 × 104 9.70 × 104 (+)	3.33 × 10−2 1.83 × 10−1 (−)	3.33 × 1010 9.78 × 1010 (+)	2.90 × 1021 1.59 × 1022 (+)	1.00 × 10−1 4.03 × 10−1
F03	3.06 × 10−5 1.68 × 10−4 (+)	1.31 × 10−13 4.76 × 10−14 (−)	5.21 × 103 2.00 × 104 (+)	6.76 × 10−13 3.92 × 10−13 (+)	2.01 × 10−13 1.08 × 10−13
F04	2.03 × 101 2.82 × 101 (−)	3.80 × 101 2.92 × 101 (+)	6.88 × 101 3.26 × 101 (+)	2.31 × 101 2.83 × 101 (−)	2.94 × 101 3.10 × 101
F05	1.53 × 101 2.78 × 100 (+)	1.00 × 101 1.79 × 100 (+)	3.50 × 101 8.77 × 100 (+)	5.55 × 101 1.67 × 101 (+)	7.96 × 100 1.58 × 100
F06	5.92 × 10−4 1.02 × 10−3 (+)	4.41 × 10−6 3.79 × 10−6 (−)	2.15 × 10−6 2.51 × 10−6 (−)	6.25 × 10−1 5.60 × 10−1 (+)	8.48 × 10−6 7.50 × 10−6
F07	4.35 × 101 2.08 × 100 (+)	4.09 × 101 2.48 × 100 (+)	6.15 × 101 9.47 × 100 (+)	9.58 × 101 1.76 × 101 (+)	3.58 × 101 1.06 × 100
F08	1.73 × 101 3.94 × 100 (+)	1.01 × 101 2.01 × 100 (+)	3.33 × 101 8.69 × 100 (+)	5.59 × 101 1.48 × 101 (+)	8.41 × 100 1.40 × 100
F09	1.78 × 10−1 3.52 × 10−1 (+)	3.79 × 10−14 5.45 × 10−14 (−)	1.74 × 10−13 1.54 × 10−13 (+)	5.06 × 101 4.89 × 101 (+)	5.31 × 10−14 5.77 × 10−14
F10	1.75 × 103 2.15 × 102 (+)	1.57 × 103 2.39 × 102 (+)	1.99 × 103 4.13 × 102 (+)	2.89 × 103 8.90 × 102 (+)	1.53 × 103 3.10 × 102
F11	5.41 × 101 3.22 × 101 (+)	9.89 × 100 1.22 × 101 (−)	1.26 × 101 4.63 × 100 (−)	9.22 × 101 3.92 × 101 (+)	1.84 × 101 2.35 × 101
F12	1.32 × 103 6.92 × 102 (+)	1.09 × 103 3.06 × 102 (+)	1.01 × 103 8.68 × 102 (+)	1.14 × 104 8.07 × 103 (+)	9.93 × 102 3.87 × 102
F13	4.34 × 101 3.67 × 101 (+)	1.49 × 101 6.82 × 100 (+)	2.45 × 101 8.06 × 100 (+)	2.45 × 102 2.01 × 102 (+)	1.48 × 101 6.60 × 100
F14	3.06 × 101 8.66 × 100 (+)	2.31 × 101 1.49 × 100 (+)	1.14 × 101 7.53 × 100 (−)	1.17 × 102 3.53 × 101 (+)	2.24 × 101 1.22 × 100
F15	2.38 × 101 1.57 × 101 (+)	3.80 × 100 1.37 × 100 (+)	1.05 × 101 3.46 × 100 (+)	9.90 × 101 7.76 × 101 (+)	3.48 × 100 1.31 × 100
F16	3.71 × 102 1.22 × 102 (+)	1.43 × 102 8.37 × 101 (+)	2.08 × 102 1.19 × 102 (+)	6.72 × 102 2.95 × 102 (+)	1.40 × 102 9.45 × 101
F17	5.63 × 101 3.25 × 101 (+)	2.75 × 101 6.92 × 100 (−)	3.53 × 101 1.16 × 101 (+)	1.98 × 102 1.21 × 102 (+)	3.14 × 101 7.54 × 100
F18	4.24 × 101 2.20 × 101 (+)	2.17 × 101 1.18 × 100 (−)	2.40 × 101 4.46 × 100 (+)	5.77 × 101 2.33 × 101 (+)	2.19 × 101 1.28 × 100
F19	1.45 × 101 8.76 × 100 (+)	7.24 × 100 1.62 × 100 (+)	6.53 × 100 1.66 × 100 (−)	6.40 × 101 3.18 × 101 (+)	7.03 × 100 1.59 × 100
F20	9.36 × 101 5.40 × 101 (+)	4.19 × 101 7.19 × 100 (+)	2.98 × 101 1.52 × 101 (−)	1.86 × 102 1.25 × 102 (+)	4.07 × 101 9.98 × 100
F21	2.15 × 102 2.83 × 100 (+)	2.08 × 102 2.19 × 100 (+)	2.33 × 102 7.95 × 100 (+)	2.60 × 102 1.59 × 101 (+)	2.08 × 102 1.43 × 100
F22	1.00 × 102 1.85 × 10−13 (=)	1.00 × 102 2.27 × 10−13 (=)	1.00 × 102 2.63 × 10−10 (=)	1.00 × 102 5.68 × 102 (=)	1.00 × 102 2.27 × 10−13
F23	3.59 × 102 5.76 × 100 (+)	3.54 × 102 3.65 × 100 (+)	3.77 × 102 9.51 × 100 (+)	4.08 × 102 1.86 × 101 (+)	3.45 × 102 3.29 × 100
F24	4.29 × 102 3.30 × 100 (+)	4.20 × 102 2.91 × 100 (−)	4.49 × 102 1.02 × 101 (+)	4.74 × 102 1.57 × 101 (+)	4.22 × 102 2.62 × 100
F25	3.87 × 102 3.67 × 10−1 (=)	3.87 × 102 4.04 × 10−2 (=)	3.87 × 102 7.57 × 10−2 (=)	3.87 × 102 1.59 × 100 (=)	3.87 × 102 5.06 × 10−2
F26	1.09 × 103 6.72 × 101 (+)	9.83 × 102 3.78 × 101 (+)	1.22 × 103 1.47 × 102 (+)	1.70 × 103 3.78 × 102 (+)	9.06 × 102 3.35 × 101
F27	5.11 × 102 6.30 × 100 (+)	5.05 × 102 5.63 × 100 (+)	4.98 × 102 1.02 × 101 (−)	5.29 × 102 1.08 × 101 (+)	5.05 × 102 4.19 × 100
F28	3.48 × 102 5.63 × 101 (+)	3.16 × 102 3.26 × 101 (+)	3.25 × 102 4.20 × 101 (+)	3.53 × 102 6.26 × 101 (+)	3.14 × 102 3.67 × 101
F29	4.61 × 102 1.45 × 101 (+)	4.30 × 102 1.13 × 101 (−)	4.35 × 102 1.43 × 101 (−)	6.97 × 102 1.23 × 102 (+)	4.37 × 102 6.35 × 100
F30	2.22 × 103 1.90 × 102 (+)	2.07 × 103 4.48 × 101 (+)	2.18 × 103 7.99 × 101 (+)	3.36 × 103 1.45 × 103 (+)	2.06 × 103 7.02 × 101
+/−/=	26/2/2	18/10/2	21/7/2	27/1/2
Ranking	3.42	2.02	3.05	4.73	1.78

As can be seen from Table 12, the mutation strategy has a large effect on the performance of GCIDE, and both DE/rand/1 and DE/best/1 fail to achieve good optimization performance. Besides, we can see that GCIDE-2 performs worse than GCIDE on the simple multi-peaked functions and combinatorial functions. Meanwhile, the overall performance of GCIDE-1 is poorer than GCIDE on all test functions. The reason for this is that the group-based parameter control method effectively reduces the mutual misleading of parameters, and the piecewise population size reduction mechanism can effectively enhance the performance of the algorithm by making the algorithm inclined to exploration in the early stage and exploitation in the later stage. Thereby, the proposed strategies can effectively promote the optimization performance of GCIDE.

4.4. Real Applications

In this subsection, three practical problems are further adopted and tested to show the practicality of GCIDE, including the Design of Tension/Compression Spring [57], the side collision problem of automobiles [58], and the Spread Spectrum Radar Polyphase Code Design [59].

4.4.1. Design of Tension/Compression Spring

First, the tension/compression spring design problem [57] is used to show the performance of GCIDE. This problem is subject to constraints on minimum deflection, shear stress, surge frequency, limits on the outside diameter, and design variables. The design variables are the mean coil diameter D(=x₁), the wire diameter d(=x₂), and the number of active coils N(=x₃). The problem can be stated as:

$$\min f\left(X\right)=\left(x_3+2\right)x_2{x}_1^2,$$

(16)

and it is subject to the following constraints:

$$\{\begin{array}{l}{g}_1\left(X\right)=1-\frac{x_2^3{x}_3}{71785x_1^4}\le 0,\\ g_2\left(X\right)=\frac{4x_2^2-x_1{x}_2}{12566\left(x_2{x}_1^3-x_1^4\right)}+\frac{1}{5108x_1^2}-1\le 0,\\ g_3\left(X\right)=1-\frac{140.45x_1}{x_2^2{x}_3}\le 0,\\ g_4\left(X\right)=\frac{x_1+x_2}{1.5},\end{array}$$

(17)

while the ranges of these variables are

$$\{\begin{array}{l}0.05\le x_1\le 2,\\ 0.25\le x_2\le 1.3,\\ 2\le x_3\le 1.5.\end{array}$$

(18)

The numerical results of GCIDE and five DE variants used in the last subsection on this problem are shown in Table 13, where each algorithm is run 30 times to obtain the mean, standard deviation, the best and worst values. From Table 13, it can be seen that GCIDE, FDDE, rank-DE, and SHADE have the same performance on mean, best and worst values, and GCIDE has the best result on standard deviation. This shows that GCIDE has strong solving ability and better stability than other compared algorithms on this real problem.

Table 13. Numerical results of GCIDE, JADE, jDE, FDDE, rank-DE, and SHADE on the tension/compression spring design problem.

Algorithms	Mean	Std	Best	Worst
GCIDE	2.11 × 10−1	6.91 × 10−17	2.11 × 10−1	2.11 × 10−1
JADE	2.25 × 10−1	9.69 × 10−1	2.20 × 10−1	2.43 × 10−1
jDE	2.69 × 10−1	5.19 × 10−1	2.28 × 10−1	2.91 × 10−1
FDDE	2.11 × 10−1	8.15 × 10−17	2.11 × 10−1	2.11 × 10−1
rank-DE	2.11 × 10−1	7.73 × 10−17	2.11 × 10−1	2.11 × 10−1
SHADE	2.11 × 10−1	8.93 × 10−17	2.11 × 10−1	2.11 × 10−1

4.4.2. Side Collision Problem of Automobile

Moreover, there are common forms of collisions, such as frontal collisions, side collisions, and rear-end collisions. Among them, side collisions are less frequent than the other two forms of collisions, yet side collisions are the most harmful to drivers and passengers. Moreover, with the increasing influence of C-NCAP management rules on consumers, automakers are also paying more attention to the passive safety of cars. In detail, more descriptions and discussions on this problem can be found in reference [58].

For clarity, this practical problem can be modelled by the following optimization problem with 11 decision variables:

$$\min :\hspace{1em}F\left(X\right)=f\left(X\right)+M\cdot \left({\displaystyle \sum _{i=1}^{10}{g}_i^2\left(X\right)}\right)\hspace{0.17em}.$$

(19)

Here, $f\left(X\right)$ is a function on the weight of the door, M denotes the penalty term here and is set to 1000, and $g_i\left(X\right)$ denotes the constraint function, which can be shown below:

$$\begin{gathered} f\left(X\right)=1.98+4.90x_1+6.67x_2+6.98x_3+4.01x_4+1.78x_5+2.73x_7, \\ {g}_1\left(X\right)=1.16-0.3717x_2{x}_4-0.00931x_2{x}_{10}-0.484x_3{x}_9+0.01343x_6{x}_{10}-1\le 0, \\ {g}_2\left(X\right)=46.36-9.9x_2-12.9x_1{x}_2-0.484x_3{x}_9+0.1107x_3{x}_{10}-32\le 0, \\ \begin{array}{l}{g}_3\left(X\right)=33.86+2.95x_3+0.1792x_3-5.057x_1{x}_2-11.0x_2{x}_8-0.0215x_5{x}_{10}-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}9.98x_7{x}_8+22.0x_8{x}_9-32\le 0,\end{array} \\ \begin{array}{l}{g}_4\left(X\right)=28.98+3.818x_3-4.2x_1{x}_2+0.0207x_5{x}_{10}+6.63x_6{x}_9-7.7x_7{x}_8+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.32x_9{x}_{10}-32\le 0,\end{array} \\ \begin{array}{l}{g}_5\left(X\right)=0.261-0.0159x_1{x}_2-0.188x_1{x}_8-0.019x_2{x}_7+0.0144x_3{x}_5+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.0008757x_5{x}_{10}+0.08045x_6{x}_9+0.00139x_8{x}_{11}+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.00001575x_{10}{x}_{11}-0.32\le 0,\end{array} \\ \begin{array}{l}{g}_6\left(X\right)=0.214+0.00817x_5-0.131x_1{x}_8-0.0704x_1{x}_9+0.03099x_2{x}_6-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.018x_2{x}_7+0.0208x_3{x}_8+0.121x_3{x}_9-0.00364x_5{x}_6+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.0007715x_5{x}_{10}-0.0005354x_6{x}_{10}+0.00121x_8{x}_{11}+0.00184x_9{x}_{10}-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.02x_2^2-0.32\le 0,\end{array} \\ \begin{array}{l}{g}_7\left(X\right)=0.74-0.62x_2-0.163x_3{x}_8+0.001232x_3{x}_{10}-0.166x_7{x}_9+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.227x_2^2-0.32\le 0,\end{array} \\ \begin{array}{l}{g}_8\left(X\right)=4.72-0.5x_4-0.19x_2{x}_3-0.0122x_4{x}_{10}+0.009325x_6{x}_{10}+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.000191x_{11}^2-4\le 0,\end{array} \\ \begin{array}{l}{g}_9\left(X\right)=10.58-0.674x_1{x}_2-1.95x_2{x}_8+0.02054x_3{x}_{10}-0.0198x_4{x}_{10}+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.028x_6{x}_{10}-9.9\le 0,\end{array} \\ \begin{array}{l}{g}_{10}\left(X\right)=16.45-0.489x_3{x}_7-0.843x_5{x}_6+0.0432x_9{x}_{10}-0.0556x_9{x}_{11}-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0.000786x_{11}^2-15.7\le 0.\end{array} \end{gathered}$$

(20)

Here, $x_1$ is the B-pillar inner, $x_2$ is the B-pillar reinforcement, $x_3$ is the floor side inner, $x_4$ is the cross member, $x_5$ is the door beam, $x_6$ is the door beltline reinforcement, $x_7$ is the roof rail, $x_8$ is the materials of B-pillar inner, $x_9$ is the floor side inner, $x_{10}$ is the barrier height, and $x_{11}$ is the hitting position. The ranges of these variables are

$$\{\begin{array}{l}0.5\le x_1,\hspace{0.17em}{x}_2,\hspace{0.17em}{x}_3,\hspace{0.17em}{x}_4,\hspace{0.17em}{x}_5,\hspace{0.17em}{x}_6,\hspace{0.17em}{x}_7\le 1.5,\\ x_8,\hspace{0.17em}{x}_9\in \left\{0.192,\hspace{0.17em}0.345\right\},\\ -30\le x_{10},\\ x_{11}\le +30.\end{array}$$

(21)

As described above, we have D = 11 in this experiment. Table 14 lists the experimental results of GCDE, JADE, jDE, FDDE, rank-DE, and SHADE with 30 independent runs on this problem, and their mean, standard deviation, best and worst values of the 30 running results are given. From Table 14, we can see that GCIDE gets the best results in all terms of indicators. Thus, GCIDE is a more promising optimizer for this real problem.

Table 14. Numerical results of GCIDE, JADE, jDE, FDDE, rank-DE, and SHADE on the side collision problem of automobile.

Algorithms	Mean	Std	Best	Worst
GCIDE	1.58 × 101	1.09 × 10−1	1.56 × 101	1.62 × 101
JADE	2.09 × 101	1.81 × 10−1	2.07 × 101	2.11 × 101
jDE	2.82 × 101	1.39 × 100	2.55 × 101	3.12 × 101
FDDE	2.09 × 101	1.86 × 10−1	2.07 × 101	2.11 × 101
rank-DE	2.74 × 101	1.36 × 100	2.49 × 101	3.08 × 101
SHADE	2.77 × 101	1.61 × 100	2.38 × 101	3.06 × 101

4.4.3. Spread Spectrum Radar Polyphase Code Design

Finally, the other real engineering problem, namely Spread Spectrum Radar Polyphase Code Design (SSRPPCD) [59], is also used to demonstrate the effectiveness of GCIDE. In detail, this problem can be mathematically described as:

$$\underset{X\in \Omega }{\min }f\left(X\right)=\max \left\{{\varphi }_1\left(X\right),\hspace{0.17em}\cdots ,\hspace{0.17em}{\varphi }_{2m}\left(X\right)\right\}.$$

(22)

Herein, $\mathsf{\Omega }=\left\{X=\left(x_1,\hspace{0.17em}\cdots ,\hspace{0.17em}{x}_D\right)\in R^D|0\le x_j\le 2\pi \hspace{0.17em}for\hspace{0.17em}j=1,\cdots ,\hspace{0.17em}D\right\}$, $m=2D-1$, ${\varphi }_{m+i}\left(X\right)=-{\varphi }_i\left(X\right)$ for $i=1,\hspace{0.17em}\cdots ,\hspace{0.17em}m$ and

$$\{\begin{array}{l}{\varphi }_{2i-1}\left(X\right)={\displaystyle \sum _{j=1}^D\cos \left({\displaystyle \sum _{k=\left|2i-j-1\right|+1}^j{x}_k}\right)},\hspace{1em}i=1,\hspace{0.17em}\cdots ,\hspace{0.17em}D,\\ {\varphi }_{2i}\left(X\right)=0.5+{\displaystyle \sum _{j=1+1}^D\cos \left({\displaystyle \sum _{k=\left|2i-j\right|+1}^j{x}_k}\right)},\hspace{0.17em}i=1,\hspace{0.17em}\cdots ,\hspace{0.17em}D-1.\end{array}$$

(23)

From the description of the problem, it is clear that the problem has a complex structure, which is a great challenge for the performance of the algorithm.

Table 15 lists the numerical results of GCDE and JADE, jDE, FDDE, rank-DE, and SHADE when D = 30, and their mean, standard deviation, best and worst values of the 30 running results are given. From Table 15, one can see that GCIDE has better performance than its all counterparts in terms of mean value, standard deviation, best value and worst value. Thus, GCIDE is better optimizer on this problem.

Table 15. Numerical results of GCIDE, JADE, jDE, FDDE, rank-DE, and SHADE on the Spread Spectrum Radar Polyphase Code Design when D = 30.

Algorithms	Mean	Std	Best	Worst
GCIDE	2.48 × 100	9.64 × 10−2	2.10 × 100	2.64 × 100
JADE	2.52 × 100	1.27 × 10−1	2.20 × 100	2.74 × 100
jDE	2.79 × 100	1.60 × 10−1	2.33 × 100	3.02 × 100
FDDE	2.96 × 100	1.02 × 10−1	2.74 × 100	3.16 × 100
rank-DE	2.70 × 100	3.95 × 10−1	2.33 × 100	2.93 × 100
SHADE	2.63 × 100	1.27 × 10−1	2.27 × 100	2.85 × 100

5. Conclusions

In this paper, an enhanced DE (GCIDE) algorithm was presented for solving global optimization problems. In GCIDE, a new mutation operator named “DE/current-to-pbest_id/1” was first developed to properly adjust the search ability of each individual by using its fitness value to determine the chosen range of its guider. Meanwhile, a group-based competitive parameter control setting was proposed to maintain the various search requirements of the population by randomly and equally dividing the whole population into multiple groups, independently creating the control parameters for each group, and competitively updating the worst location parameter information with the current successful parameters. Moreover, a piecewise population size reduction mechanism was further put forward to enhance the exploration and convergence of the population at the early and later search stages, respectively. Compared to the existing DE variants, GCIDE adaptively adjusts the chosen range of the guider for each individual, independently generates the control parameters for each group, and competitively replaces the worst location parameter information among all groups with the current successful parameters, while reducing the population size with different speeds at different search periods. Thus, GCIDE is capable of effectively enhancing the adaptivity of the algorithm and balancing well its exploration and exploitation. At last, the performance of GCIDE was evaluated and discussed by conducting a series of experiments on the benchmark functions from the IEEE CEC 2017 test suite and three real applications. Experimental results indicated the superiority of GCIDE compared to ten typical or well-known compared methods.

It should be also mentioned that the fitness value of the individual is just used to measure its characteristic and then adjust its search performance in this paper, which might be not able to precisely evaluate its search potential. Besides, the special requirement of individuals is not fully taken into consideration during the generation of control parameters, and only a few real applications are introduced in the current paper. Thereby, we will further design a new evaluation approach on the search characteristic of individuals, a more effective and efficient adaptive parameter control method, and apply GCIDE to more practical optimization problems in the future.