Modeling the Cigarette Consumption of Poor Households Using Penalized Zero-Inflated Negative Binomial Regression with Minimax Concave Penalty

Abstract

The cigarette commodity is the second largest contributor to the food poverty line. Several aspects imply that poor people consume cigarettes despite having a minimal income. In this study, we are interested in investigating factors influencing poor people to be active smokers. Since the consumption number is a set of count data with zero excess, we have an overdispersion problem. This implies that a standard Poisson regression technique cannot be implemented. On the other hand, the factors involved in the model need to be selected simultaneously. Therefore, we propose to use a zero-inflated negative binomial (ZINB) regression with a minimax concave penalty (MCP) to determine the dominant factors influencing cigarette consumption in poor households. The data used in this study were microdata from the National Socioeconomic Survey (SUSENAS) conducted in March 2019 in East Java Province, Indonesia. The result shows that poor households with a male head of household, having no education, working in the informal sector, having many adult household members, and receiving social assistance tend to consume more cigarettes than others. Additionally, cigarette consumption decreases with the increasing age of the head of household.

1. Introduction

Indonesia has committed to poverty alleviation in the agenda for Sustainable Development Goals (SDGs) and the National Medium-Term Development Plan 2020–2024. It is expected to be able to reduce the national and regional poverty rates. However, from 2010 to 2020, the poverty rate in one of the provinces in Indonesia, East Java Province, was consistently higher than the national poverty rate. The poverty rate in East Java is still at the double-digit level compared to the national poverty rate, which has reached a single-digit level since 2018. This indicates a need for targeted poverty alleviation programs in East Java.

The Indonesia National Socioeconomic Survey conducted in 2019 indicated that the cigarette commodity is the second largest contributor to poverty after rice. The contribution is around 11.82 percent in urban areas and 10.74 percent in rural areas. It indicates that cigarettes are one of the basic needs of poor households in East Java. Cigarette consumption in low-income families is related to their smoking behavior. It is measured by the smoking intensity, represented by the number of cigarettes consumed.

The number of cigarettes consumed is a type of count data (the non-negative integer values). Poisson and negative binomial regressions are commonly used to build predictive models on count data [1]. However, the high frequency of data with zero values can make the regression model less precise in explaining the data. The count data with excess zeros may have significant variations that cause overdispersion.

The zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB) models can be applied to accommodate the excess zero observation. However, the ZIP model assumes that the variance and mean must be equal, which is called equidispersion. As a result, it is not easy to qualify the actual data. Meanwhile, the ZINB model has no such assumption [2]. The ZINB model is more suitable for accommodating the overdispersion that the ZIP model cannot overcome [1].

The various factors of demographic and socioeconomic conditions may determine cigarette consumption in poor households [3]. The inclusion of many predictor variables in the regression model may lead to multicollinearity conditions. Therefore, a parsimonious model is required for better interpretation and more accurate prediction [4]. On the other hand, stepwise or subset selection methods have weaknesses, including inconsistency between the model selection algorithm and many hypothesis testing problems [5]. Therefore, we implement a method that can select variables and estimate coefficients simultaneously, as proposed by [6]. Hence, this study aims to estimate the model parameters and select the variables to determine the dominant factors influencing cigarette consumption of poor households in East Java, Indonesia, by applying the penalized zero-inflated negative binomial (ZINB) regression model.

Binomial models are extensively used, and numerous techniques have been suggested for estimation, prediction, and various other applications. In the case of estimation and variable selection within the normal linear model, the field of sparse estimation encompasses various methods such as the least absolute shrinkage and selection operator (LASSO) [7], smoothly clipped absolute deviation (SCAD) [8], and minimax concave penalty (MCP) [9].

2. Materials and Methods

2.1. Data

The data were taken from the microdata of the National Socioeconomic Survey (SUSENAS) conducted in March 2019 in East Java Province, Indonesia. The response variable is the weekly average cigarette consumption of poor households during the past month. The predictors are related to household characteristics. For example, a discussion on the poverty data was delivered by [10]. The detailed predictors are presented in Table 1.

Table 1. Predictor Variables.

Variable	Description
Residence	0: rural, 1: urban
Gender	0: female, 1: male
Marital status	0: married, 1: single, 2: divorce
Age
Education	0: college, 1: secondary, 2: primary, 3: no education
Working status	0: not working, 1: formal, 2: informal
Adult household members
Household members who use the Internet
Household members who do not work
Social assistance	0: no receive, 1: receive
Toddler existence	0: no, 1: yes
Housing tenure	0: owner, 1: rent, 2: free rent, 3: other
Health expenditure
Education expenditure

2.2. Zero-Inflated Negative Binomial (ZINB)

The zero-inflated negative binomial (ZINB) regression is a model to accommodate the overdispersion problem caused by excess zeros in the response variable. The ZINB regression model in which the response variable $Y_i$ has a probability density function as follows [1,11]:

$$P\left(Y_i=y_i\right)=\left\{\begin{array}{ll}{\pi }_i+\left(1-{\pi }_i\right)\left(\frac{\theta }{{\mu }_i+\theta }\right)& ,if y_i=0\\ \left(1-{\pi }_i\right)\frac{\Gamma \left(\theta +y_i\right)}{\Gamma \left(y_i+1\right)\Gamma \left(\theta \right)}{\left(\frac{{\mu }_i}{{\mu }_i+\theta }\right)}^{y_i}{\left(\frac{\theta }{{\mu }_i+\theta }\right)}^{\theta }& ,if y_i>0\end{array}\right.$$

(1)

where $0\le {\pi }_i\le 1$ is the success probability, ${\mu }_i\ge 0$ is the conditional expectation of the response, $i=1,\dots ,n$, and $\frac{1}{\theta }$ is the dispersion parameter with $\theta >0$. Assume ${\mu }_i$ and ${\pi }_i$ are parameters that depend on the predictor vectors ${\overrightarrow{x}}_i$ and ${\overrightarrow{v}}_i$, respectively. The length of the predictor vector ${\overrightarrow{x}}_i$ is $q_1$, while the length of the predictor vector ${\overrightarrow{v}}_i$ is $q_2$. Therefore, the equation of the link function is as follows:

$$\log \left({\mu }_i\right)={\overrightarrow{x}}_i^T\overrightarrow{\beta } \mathrm{and} \log \left(\frac{{\pi }_i}{1-{\pi }_i}\right)={\overrightarrow{v}}_i^t\overrightarrow{\zeta }$$

(2)

where $\overrightarrow{\beta }$ and $\overrightarrow{\zeta }$ are the regression coefficients. For $n$ independent random samples, let $\overrightarrow{\phi }=\left({\overrightarrow{\beta }}^t,\theta ,{\overrightarrow{\zeta }}^t\right)$ be the log-likelihood function given by:

$$\mathcal{l}\left(\overrightarrow{\varphi }\right)={\displaystyle \sum _{y_i=0}\log \left[{\pi }_i+\left(1-{\pi }_i\right){\left(\frac{\theta }{{\mu }_i+\theta }\right)}^{\theta }\right]}+{\displaystyle \sum _{y_i>0}\log \left[\left(1-{\pi }_i\right)\frac{\Gamma \left(\theta +y_i\right)}{\Gamma \left(y_i+1\right)\Gamma \left(\theta \right)}{\left(\frac{{\mu }_i}{{\mu }_i+\theta }\right)}^{\theta }\right]}$$

(3)

2.3. Penalized Zero-Inflated Negative Binomial (ZINB) Regression

Variable selection is the key to producing a parsimonious model to facilitate model interpretation [12]. The modern variable selection methods were developed to overcome the weaknesses of the traditional methods by adding the penalized likelihood or penalty function. The selection of variables using the penalized ZINB regression model is as follows [4]:

$$p\mathcal{l}\left(\phi \right)=\mathcal{l}\left(\phi \right)-p\left(\overrightarrow{\beta },\overrightarrow{\zeta }\right)$$

(4)

where $\mathcal{l}\left(\phi \right)$ is the log-likelihood of the ZINB function and $p\left(\overrightarrow{\beta },\underrightarrow{\zeta }\right)$ is the non-negative penalty function given by:

$$p\left(\overrightarrow{\beta },\underrightarrow{\zeta }\right)=n{\displaystyle \sum _{j=1}^{q_1}p\left({\lambda }_{NB};\left|{\beta }_j\right|\right)+n{\displaystyle \sum _{k=1}^{q_2}p}}\left({\lambda }_{BI};\left|{\zeta }_k\right|\right)$$

(5)

where $q_1$ and $q_2$ are the number of parameters for the NB and zero components, respectively. ${\beta }_j$ represents the NB component parameter coefficients and ${\zeta }_k$ represents the zero component parameter coefficients. Tuning parameters ${\lambda }_{NB}$ and ${\lambda }_{BI}$ are determined by data-driven methods. Intercept and parameter $\theta$ are always included in the model; hence, they are not penalized.

This study used three penalty functions, as follows:

• Least absolute shrinkage and selection operator (LASSO). The penalty function is given by [3]:

  $$p\left({\lambda }^L;\left|\xi \right|\right)={\lambda }^L\left|\xi \right|$$

  (6)

  where $\xi$ is the penalty coefficients.
• Smoothly clipped absolute shrinkage (SCAD). The first derivative of the SCAD penalty function on [0, ∞) is given by [8]:

  $$p_{{\lambda }^S}^{\prime }\left(\xi \right)={\lambda }^S\left\{I\left(\xi \le {\lambda }^S\right)\right.+\frac{\left({\gamma }^S{\lambda }^S-\xi \right)}{\left({\gamma }^S-1\right){\lambda }^S}+I\left(\xi >{\lambda }^S\right)$$

  (7)
  For ${\gamma }^S>2,{\lambda }^S\ge 0,\xi >0$ where $I\left(.\right)$ is the indicator function.
• Minimax concave penalty (MCP). The first derivative of the MCP penalty function on [0, ∞) is given by [13]:

  $$p^{\prime }{}_{{\lambda }^M,{\gamma }^M}\left(\xi \right)=\left\{\begin{array}{l}{\lambda }^M-\frac{\xi }{{\gamma }^M}, \mathrm{if} \xi \le {\gamma }^M{\lambda }^M\\ 0, \mathrm{if} \xi >{\gamma }^M{\lambda }^M\end{array}\right.$$

  (8)

2.4. The EM Algorithm

The expectation maximization (EM) algorithm is generally applied to mixture models [12]. It is often used in missing data problems. The EM algorithm has two main steps: the expectation step (E-step) and the maximization step (M-step).

Let $Z_i=1$ if $Y_i$ is a zero value observation and $Z_i=0$ if $Y_i$ is from a negative binomial (NB) distribution. Since $\overrightarrow{z}={\left(z_1,\dots ,z_n\right)}^t$ is not observable, it is often treated as missing data. If complete data $\left(Y_i,z_i\right)$ are available, the penalized log-likelihood function is given by [4]:

$$p{\mathcal{l}}_c\left(\varphi \right)={\displaystyle \sum _{i=1}^n\left\{z_i{\overrightarrow{v}}_i\overrightarrow{\zeta }-\log \left(1+\exp \left({\overrightarrow{v}}_i\overrightarrow{\zeta }\right)\right)+\left(1-z_i\right)\log \left(f\left(y_i;\overrightarrow{\beta },\theta \right)\right)\right\}}-p\left(\overrightarrow{\beta },\overrightarrow{\zeta }\right)$$

(9)

where $f\left(y_i;\beta ,\theta \right)=\frac{\Gamma \left(\theta +y_i\right)}{\Gamma \left(y_i+1\right)\Gamma \left(\theta \right)}{\left(\frac{{\mu }_i}{{\mu }_i+\theta }\right)}^Y{\left(\frac{\theta }{{\mu }_i+\theta }\right)}^{\theta }$ and $p\left(\overrightarrow{\beta },\overrightarrow{\zeta }\right)$ is a non negative penalty function.

The EM algorithm computes the expectation of the complete data log-likelihood, which is linear in z. The log-likelihood of Equation (4) is maximized iteratively by alternating between estimating $z_i$ by its conditional expectation under the current estimates $\widehat{\varphi }$ (E-step) and maximizing Equation (11) (M-step) by $z_i$ from the E-step. The iteration stops when the estimated $\widehat{\phi }$ converges.

The E-step estimates $z_i$ by its conditional mean $z_i{}^{\left(m\right)}$, given the data and assuming that the current estimates ${\widehat{\phi }}^{\left(m\right)}$ are provided by the right model parameters. The conditional expectation of $z$ at iteration $m$ is given by:

$${\widehat{z}}_i^{\left(m\right)}={\left\{\begin{array}{l}\left(1+\exp \left(-v_i{\widehat{\zeta }}^{\left(m\right)}\right){\left[\frac{{\widehat{\theta }}^{\left(m\right)}}{\exp \left(x_i{\widehat{\beta }}^{\left(m\right)}\right)+{\widehat{\theta }}^{\left(m\right)}}\right]}^{\widehat{\theta }}\right)\\ 0, \mathrm{if} y_i>0\end{array}\right.}^{-1},\mathrm{if} y_i=0$$

(10)

Therefore, the expectation of the complete data loglikelihood can be expressed as follows:

$$\begin{array}{ll}Q\left(\varphi {\left|\widehat{\varphi }\right.}^{\left(m\right)}\right)& =E\left(p{\mathcal{l}}_c\left(\varphi \left|y,z\right.\right)\left|y,{\widehat{\varphi }}^{\left(m\right)}\right.\right)\hfill \\ & =Q_1\left(\overrightarrow{\beta },\theta {\left|\widehat{\varphi }\right.}^{\left(m\right)}\right)+Q_2\left(\overrightarrow{\zeta }{\left|\widehat{\varphi }\right.}^{\left(m\right)}\right)\hfill \end{array}$$

(11)

where $Q_1\left(\overrightarrow{\beta },\theta {\left|\widehat{\varphi }\right.}^{\left(m\right)}\right)={\displaystyle \sum _{i=1}^n\left(1-{\widehat{z}}_i^{\left(m\right)}\right)}\log \left(f\left(y_i,\overrightarrow{\beta },\theta \right)\right)-n{\displaystyle \sum _{j=1}^{q_1}p\left({\lambda }_{NB},\left|{\beta }_j\right|\right)}$ and $Q_2\left(\overrightarrow{\zeta }\left|{\widehat{\phi }}^{\left(m\right)}\right.\right)={\displaystyle \sum _{i=1}^n{\widehat{z}}_i^{\left(m\right)}{v}_i\overrightarrow{\zeta }}-\log \left(1+\exp \left(v_i\overrightarrow{\zeta }\right)\right)-n{\displaystyle \sum _{k=1}^{q_2}p\left({\lambda }_{BI},\left|{\zeta }_k\right|\right)}$.

The EM algorithm updates the estimates by maximizing Equation (11), which can easily be achieved because $\left(\overrightarrow{\beta },\theta \right)$ and $\zeta$ are two disjoint terms. The first term, $Q_1\left(\overrightarrow{\beta },\theta \left|{\widehat{\phi }}^{\left(m\right)}\right.\right)$, is the weighted penalized NB log-likelihood function, whereas the second term, $Q_2\left(\overrightarrow{\zeta }\left|{\widehat{\phi }}^{\left(m\right)}\right.\right)$, is the penalized logistic log-likelihood function. The EM performs an iterative procedure for the E-step and M-step until the optimum parameter $\widehat{\varphi }$ is obtained.

The EM algorithm requires parameter estimation of the two terms, which are the components of the penalized ZINB model. Meanwhile, the NB and logistic regression models are generalized linear models (GLMs). The parameter estimation of regularized GLMs used the modified iteratively reweighted least squares (IRLS) algorithm. It uses a coordinate descent algorithm to optimize the penalized weighted least squares [12].

2.5. Tuning Parameter Selection

The tuning parameter can be determined using the Bayesian information criterion (BIC) as follows [4]:

$$BIC=-2\mathcal{l}\left(\widehat{\varphi };{\lambda }_{NB},{\lambda }_{BI}\right)+\log \left(n\right)df$$

(12)

where $\widehat{\varphi }$ is the estimated parameter, ${\mathit{\lambda }}_{\mathit{N}\mathit{B}}>0$ is the tuning parameter of the NB component, ${\mathit{\lambda }}_{\mathit{B}\mathit{I}}>0$ is the tuning parameter of the zero component, and $\mathcal{l}\left(.\right)$ is the log-likelihood function. The degrees of freedom are given by $df={\displaystyle \sum _{j=0,\dots ,q_1}1\left\{{\beta }_j\ne 0\right\}}+{\displaystyle \sum _{k=0,\dots ,q_2}1\left\{{\zeta }_k\ne 0\right\}}+1$, including the degree of freedom for the scale parameter θ. The first step is to construct a solution path based on the paired shrinkage parameters. The algorithm generates two decreasing sequenced parameters, ${\lambda }_{NB}^{\left(1\right)}>{\lambda }_{NB}^{\left(2\right)}>\dots >{\lambda }_{NB}^{\left(M\right)}$ and ${\lambda }_{BI}^{\left(1\right)}>{\lambda }_{BI}^{\left(2\right)}>\dots >{\lambda }_{BI}^{\left(M\right)}$. Subsequently, sequences $\left({\lambda }_{NB}^{\left(1\right)},{\lambda }_{BI}^{\left(1\right)}\right),\dots ,\left({\lambda }_{NB}^{\left(M\right)},{\lambda }_{BI}^{\left(M\right)}\right)$ are paired. In principle, the large value can be chosen in such a way that all the coefficients are zero, except the intercepts. The tuning parameter can be chosen based on the smallest BIC value [12].

3. Results

This study observed 3010 poor household samples from the National Socioeconomic Survey (SUSENAS) in March 2019 in East Java. All computations in this section are presented in Appendix A. Based on the data, the highest number of cigarette consumption in poor households was 720 cigarettes per week during the past month. In contrast, the smallest consumption was 0 cigarettes (no smoking). In other words, 41.4 percent of no-smoking poor households is indicated by the histogram decreasing to the right (Figure 1). Meanwhile, the mean is around 45 cigarettes per week during the past month, with a relatively large standard deviation of 62.49. It indicated that the range of data variation was so extensive that cigarette consumption among poor households varied considerably. The standard deviation value is greater than the mean value, which causes overdispersion.

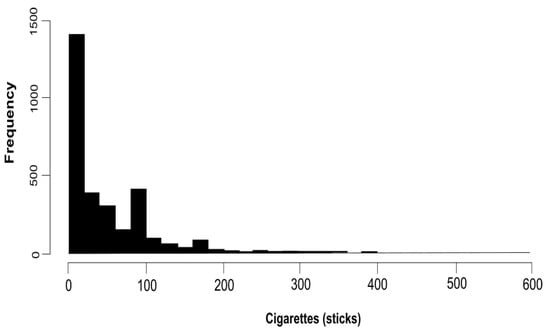
Figure 1. Histogram of Cigarette Consumption of Poor Households in East Java 2019.

Figure 2 demonstrates that most poor households who smoked lived in rural areas. It is in line with a related study that cigarette consumption is higher among low-income families living in rural areas than in urban areas [14]. The poor households who smoked had a male head of household and were married. The head of the poor household who smoked generally had low education. Based on the previous study, families with a head of household who did not attend school tended to consume cigarettes more than those who attended school [15]. Smoking also appeared to be more prevalent in those employed than those unemployed. Cigarette consumption of poor households who worked in informal sectors is higher than those who worked in formal sectors. The previous study showed that families with a head of household who worked in the informal sector tended to smoke more than those who did not [16].

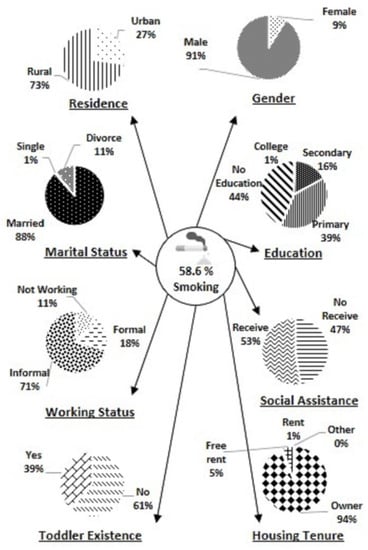
Figure 2. The Characteristics of Poor Households who Smoking in East Java 2019.

Based on Figure 2, most poor households who smoked received social assistance. Moreover, poor households with children under five had a lower smoking percentage. In addition, more than 50% of poor households who smoked lived in their own house.

Overdispersion checking was done by comparing the variance and mean. If the variance is greater than the mean, an overdispersion occurs. Overdispersion checking can also be seen from the statistical dispersion, namely the division between the Pearson chi-square statistical value and the degrees of freedom [5]. Based on the processing, the Pearson chi-square statistical value is 170,923 with a degree of freedom of 2989. Hence, the statistical dispersion is 57.1841, which indicates an overdispersion on the response variable.

The excess zero testing in the count data was done using the score test [17]. The result indicated that the p-value of $2.22\times {10}^{-16}$ is smaller than the 5 percent significance level. It also indicated that the response variables have excess zeros, so the zero inflation regression model is more appropriate. ZINB regression with Backward Elimination (BE) regression for 14 predictor variables was employed to model the cigarette consumption of poor households in East Java. The likelihood ratio test was done to test parameter estimation simultaneously, whereas the Wald test was employed to test the parameters partially [18]. The result indicated that the likelihood ratio is 877.1114, greater than ${\chi }_{\left(40,0.05\right)}^2$, which is 55.76. In other words, at least one predictor variable influenced the response variable.

In the early steps of modeling the ZINB penalized regression, the tuning parameter was selected based on the smallest BIC value. In each penalty function, two tuning parameters were to be determined: the tuning parameter for the negative binomial component ${\lambda }_{NB}$ and the tuning parameter for the zero component ${\lambda }_{BI}$. In addition, there was an additional tuning parameter in the SCAD and MCP penalty functions [19,20,21].

Based on Table 2, the ZINB-LASSO model selected predictor variables more minor than other penalized ZINB models. Because of the characteristics of the LASSO penalty function, only one variable could be chosen among the predictor variables with a high correlation [22]. The predictor variables selected in the zero component of the ZINB-SCAD and ZINB-MCP models were generally the same. Meanwhile, the selected predictors of the ZINB-MCP in the NB component were the least.

Table 2. ZINB Model on Poor Household Cigarette Consumption.

Variable	Category	Negative Binomial (NB) Component				Zero Component
		BE	LASSO	SCAD	MCP	BE	LASSO	SCAD	MCP
Intercept		3.6657 (0.1021)	3.7446 (0.0838)	3.8485 (0.082)	3.7802 (0.078)	1.7833 (0.2522)	1.4862 (0.1060)	1.7264 (0.2086)	1.8367 (0.2159)
Residence	Rural
Gender	Male	0.1262 (0.0585)				−1.3886 (0.1142)	−0.9839 (0.0937)	−1.4053 (0.1091)	−1.3676 (0.1096)
Marital status	Single					0.7911 (0.3892)
	Divorce
Age		−0.0062 (0.0014)	−0.0019 (0.0015)	−0.0072 (0.0015)	−0.0052 (0.0015)	0.0177 (0.0035)		0.0175 (0.0032)	0.0173 (0.0033)
Education	Secondary			−0.0033 (0.0527)		0.3112 (0.1204)
	Primary
	No Educ	0.2160 (0.0364)	0.0887 (0.0399)	0.2088 (0.0418)	0.1598 (0.0394)	−0.3659 (0.0988)		−0.4156 (0.0950)	−0.4035 (0.0956)
Working status	Formal			0.0105 (0.0473)
	Informal					−0.2369 (0.0881)			−0.2186 (0.0867)
Adult members		0.2436 (0.0157)	0.1976 (0.0186)	0.2444 (0.0175)	0.2368 (0.0172)	−0.4990 (0.0468)	−0.3687 (0.0395)	−0.5628 (0.0410)	−0.5599 (0.0410)
Household members who use the internet
Household members who do not work			0.0035 (0.0132)			−0.0848 (0.0347)	−0.0078 (0.0290)
Social assistance	Receive			0.0005 (0.0354)		−0.2975 (0.0826)		−0.3306 (0.0820)	−0.324 (0.0821)
Toddler existence	Yes	0.0807 (0.0380)
Housing tenure	Rent
	Free rent	0.1522 (0.0737)		0.0395 (0.0159)
	Other
Health expenditure		−0.0099 (0.0033)		−0.003 (0.0031)
Education expenditure
Theta		2.1949 (1.0339)	2.1476 (0.0814)	2.181 (0.0812)	2.17 (0.0813)

The estimated coefficients with standard errors in parentheses.

As seen in Table 3, the ZINB-MCP model has the smallest BIC value than the other four regression models. Moreover, the number of parameter coefficients of the penalized ZINB-MCP model is relatively smaller than the other models, indicating that the ZINB-MCP model is parsimonious. Thus, the ZINB-MCP model could better model the cigarette consumption data of poor households in East Java in 2019. Based on the results of parameter estimation in Table 2, the ZINB-MCP model equation is as follows:

Table 3. Bayesian Information Criterion (BIC) on ZINB Model.

Model	BIC
ZINB-BE	21,917.3
ZINB-LASSO	21,992.9
ZINB-SCAD	21,928.3
ZINB-MCP	21,899.4

• ZINB-MCP model in the negative binomial (NB) component

  $$\widehat{\mu }=\exp \left(3.7802-0.0052X_4+0.1598X_{5d_1}+0.2368X_7\right)$$
• ZINB-MCP model in the zero component

  $$\ln \left(\frac{\widehat{\pi }}{1-\widehat{\pi }}\right)=1.8367-1.3676X_2+0.0173X_4-0.4035X_{5d_3}-0.2186X_{6d_2}-0.5599X_7-0.3240X_{10}$$

The zero component model shows that the gender of the head of the household had a significant effect on cigarette consumption in poor households. Poor households with a male head of household tended to consume more cigarettes than those with a female house of household. The Indonesian Demographic and Health Survey (IDHS) in 2012 showed that most of the heads of households in Indonesia were male smokers [16]. Meanwhile, NB and zero component models showed that the age variable significantly influenced cigarette consumption in poor households. Based on a previous study, cigarette consumption will decrease as the age of the head of household increases [6]. It indicates that most of the young heads of households smoked cigarettes. Therefore, controlling tobacco or cigarette consumption should be targeted at all ages.

The education variable of the head of household significantly influenced cigarette consumption in poor households according to the NB and zero component models. The low-income families whose head of household did not attend school tended to consume more cigarettes than poor households whose head of household had higher education. This result aligns with studies in 48 low- and middle-income countries. Those who do not attend school generally smoke three times more than those who are educated [6]. An educated person will have great awareness of the health risks of smoking [23]. Therefore, education is the primary key to reducing cigarette consumption in poor households.

The zero component model found that the working status variable of the head of household significantly influenced cigarette consumption in poor households. Poor households with a head of household who worked in the informal sector tended to consume more cigarettes than those who did not, which is in line with the previous study [16]. Therefore, it is necessary to put various efforts into increasing awareness of the dangers of smoking by disseminating numerous media that are easily accessible to households. Provincial and regency/city governments need to impose the regulation of non-smoking areas.

The NB and zero component models showed that the number of adult members variable significantly influenced cigarette consumption in poor households. In line with the previous study, adding one adult member would increase cigarette consumption in poor households. It is reasonable that the household member who smokes is an adult.

Furthermore, the zero component model found that the social assistance variable significantly influenced cigarette consumption in poor households. Poor households that received social assistance were more likely to consume cigarettes than those that did not. In line with the previous study, the average number of cigarettes consumed by the head of a household of poor households will increase along with the amount of social assistance received [24]. This phenomenon relates to the household’s behavior (moral hazard) in allocating excess income. They will likely not spend the additional income from social assistance benefits on basic needs. Another study showed that middle- or low-income households often allocate food expenditure for cigarette consumption [25]. Therefore, the government should encourage low-income families to use the social assistance benefits for food consumption, support education, health, and basic needs other than cigarette consumption, to improve their standard of living to get out of poverty.

4. Discussion

Modeling the behavior of cigarette consumption is carried out using a technique called Zero-Inflated Negative Binomial (ZINB) with Backward Elimination (BE) regression. Due to some potential covariates, we then need to combine its classical technique with a variable selection procedure. Hence, we penalized the ZINB regression using three penalty functions (LASSO, SCAD, and MCP). Based on the smallest BIC and RMSE values, the penalized ZINB-MCP regression performs better than the others. We also investigate that out of 14 predictor variables (10 dummy), six predictors (two dummy) are selected, those are; gender of the head of household, age of head of household, education of the head of household in the non-school category, working status of head of household in informal sector category, number of adult household members, and social assistance. We found that some variables have a negative effect, for example, the cigarettes consumptions are decreasing as the age of the consumers increases.

5. Conclusions

According to the results, it can be concluded that modeling and selection variables of cigarette consumption of poor households used classical (ZINB-BE) and modern methods, namely penalized ZINB regression using three penalty functions (LASSO, SCAD, and MCP). The best model was obtained based on the smallest BIC value, namely the ZINB-MCP model. This study indicated that poor households with a male head of household who was young, had no education, worked in the informal sector, had many adult household members, and received social assistance tended to consume more cigarettes. Therefore, the awareness of poor households for reducing cigarette consumption should be supported by improving their education and knowledge.