Improving Newton–Schulz Method for Approximating Matrix Generalized Inverse by Using Schemes with Memory

Abstract

Some iterative schemes with memory were designed for approximating the inverse of a nonsingular square complex matrix and the Moore–Penrose inverse of a singular square matrix or an arbitrary $m\times n$ complex matrix. A Kurchatov-type scheme and Steffensen’s method with memory were developed for estimating these types of inverses, improving, in the second case, the order of convergence of the Newton–Schulz scheme. The convergence and its order were studied in the four cases, and their stability was checked as discrete dynamical systems. With large matrices, some numerical examples are presented to confirm the theoretical results and to compare the results obtained with the proposed methods with those provided by other known ones.

1. Introduction

Calculating the inverse of a matrix, especially of a large size, is a very difficult task with a high computational cost. The alternative is the use of iterative algorithms to estimate it. In a vast range of fields, such as image and signal processing [1,2,3,4], encryption [5,6], control system analysis [7,8], etc., it is necessary to calculate the inverse or different generalized inverses in order to solve the problems posed.

In recent years, many iterative schemes of different orders of convergence have been designed to estimate the inverse of a complex matrix A or some generalized inverse (Moore–Penrose inverse, Drazin inverse, etc.). In 2013, Weiguo et al. in [9] constructed a sequence of third-order iterations converging to the Moore–Penrose matrix. In the same year as well, Toutounian and Soleymani in [10] presented a high-order method for approximating inverses and pseudo-inverses of complex matrices based on Homeier’s scheme, with a derivative-free composition. More recently, Stanimirovic et al. in [11] designed efficient transformations of the hyperpower iterative method for computing the generalized inverses $A_{T,S}^{\left(2\right)}$ with the aim of minimizing the number of required matrices by matrix products per cycle. In 2020, Kaur et al. established in [12] new formulations of the fifth-order hyperpower method to compute the weighted Moore–Penrose inverse, improving the efficiency indices. Such approximations were found to be robust and effective when implemented as a preconditioned matrix to solve the linear systems. All these schemes were designed with the starting point of iterative procedures without memory, that is where each new iteration is calculated using only the information provided by the previous iterate.

Iterative procedures that use more than one previous iterate to calculate the next one are called methods with memory. In the context of matrix inverse approximations, the secant scheme was proposed by the authors in [13]. For a nonsingular matrix, the secant method gives an estimation of the inverse and, when the matrix is singular, an approximation of the pseudo-inverse and Drazin inverse. Furthermore, the superlinear convergence was demonstrated in all cases.

In this manuscript, we focused on constructing several iterative methods with memory, free of inverse operators and with different orders of convergence, for finding the inverse of a nonsingular complex matrix. We also analyzed the proposed schemes for computing the Moore–Penrose inverse of complex rectangular matrices. On the other hand, these procedures allow approximating other generalized inverses such as the Drazin inverse, the group inverse, etc., although this is beyond the scope of this work.

Let A be a complex $n\times n$ nonsingular matrix. The design of iterative algorithms without memory for estimating the inverse matrix, which we call Newton–Schulz-type methods, is mostly based on iterative solvers for the scalar equation $f\left(x\right)=0$ applied to the nonlinear matrix equation:

$$F\left(X\right)=X^{-1}-A=0,$$

(1)

where $F:{\mathbb{C}}^{n\times n}\to {\mathbb{C}}^{n\times n}$ is a nonlinear matrix function.

The most-used iterative scheme to approximate $A^{-1}$ is the Newton–Schulz scheme [14]:

$$X_{k+1}=X_k(2I-A{X}_k),k=0,1,\dots ,$$

(2)

where I is an identity matrix of size $n\times n$.

On the other hand, in the context of iterative procedures with memory, the authors presented in [13] a secant-type method (SM), whose iterative expression is:

$$X_{k+1}=X_{k-1}+X_k-X_{k-1}A{X}_k,k=0,1,2,\dots ,$$

(3)

where $X_0$, $X_{-1}$ are the starting guesses. With a particular choice of the initial approximations, the authors proved that sequence $\left\{X_k\right\}$, obtained by (3), converges to $A^{-1}$ with order of convergence $1.618$.

To analyze the convergence order of the iterative methods with memory for solving nonlinear equations $f\left(x\right)=0$, the R-order is used (see [15]), which we summarize below.

Theorem 1.

Let ψ be an iterative method with memory that generates a sequence $\left\{x_k\right\}$ of approximations to the root α of $f\left(x\right)=0$, and let this sequence converge to α. If there exists a nonzero constant η and nonnegative numbers $t_i$, $i=0,1,\dots ,m$, such that the inequality:

$${\displaystyle |e_{k+1}|\le \eta \prod _{i=0}^m{\left|e_{k-i}\right|}^{t_i}}$$

holds, then the R-order of convergence of the iterative method ψ satisfies the inequality:

$$O_R(\psi ,\alpha )\ge s^{*},$$

where $s^{*}$ is the unique positive root of the equation:

$${\displaystyle s^{m+1}-\sum _{i=0}^m{t}_i{s}^{m-i}=0.}$$

Here, $e_k=x_k-\alpha$ denotes the error of the approximation in the kth iterative step.

Continuing with the idea of designing iterative procedures with memory, in this work, we used the scalar iterative methods of Kurchatov and Steffensen with memory, which we adapted to the context of matrix equations. In the scalar case, this kind of procedure can reach a higher order of convergence than schemes without memory with the same number of functional evaluations and usually has better stability properties. However, as far as we know, only the secant scheme has been extended to matrix equations with good results, in [13].

Kurchatov’s scheme is an iterative algorithm with memory with quadratic convergence to solve scalar equations $f\left(x\right)=0$ (see [16]), which is deduced from Newton’s method by substituting $f^{\prime }\left(x\right)$ by Kurchatov’s divided difference, that is:

$$x_{k+1}=x_k-\frac{f\left(x_k\right)}{f{[x_k,x_{k-1}]}_K}=x_k-\frac{2(x_k-x_{k-1})f\left(x_k\right)}{f(2x_k-x_{k-1})-f\left(x_{k-1}\right)},k=1,2,\dots$$

(4)

Regarding Steffensen’s scheme, it was initially developed in [17], where the derivative $f^{\prime }\left(x\right)$ was replaced by the divided difference $f[x_k,x_k+f\left(x_k\right)]$. It still holds the original quadratic convergence, but in practice, the set of converging initial estimations is quite smaller than that of Newton’s scheme. It was Traub who, in [18], introduced an accelerating parameter $\gamma$ in the divided difference such that $f^{\prime }\left(x_k\right)\approx f[x_k,x_k+\gamma f\left(x_k\right)]$ derived an iterative method whose error equation was:

$$e_{k+1}=(1+\gamma f^{\prime }\left(\alpha \right))c_2{e}_k^2+O\left(e_k^3\right),$$

with $c_2=\frac{1}{2}\frac{f^{″}\left(\alpha \right)}{f^{\prime }\left(\alpha \right)}$. With the aim of increasing the order of convergence of the scheme, Traub defined an approximation of $\gamma =-\frac{1}{f^{\prime }\left(\alpha \right)}$ by ${\gamma }_k=-\frac{1}{f[x_k,x_{k-1}]}$, obtaining the procedure:

$$x_{k+1}=x_k-\frac{f\left(x_k\right)}{f[x_k+{\gamma }_{k}f\left(x_k\right),x_k]},k=0,1,2,\dots ,$$

which, given initial values $x_0$ and ${\gamma }_0$, has order of convergence $1+\sqrt{2}$.

The stability of these schemes with memory for scalar problems was analyzed firstly in [19,20], showing very stable performance in both cases. In what follows, some definitions and properties about vectorial discrete dynamical systems are introduced. These tools are shown to be useful in the following sections.

Basic Concepts of Qualitative Studies of Schemes with Memory

Let us start with an iterative scheme with memory, which is used to solve the scalar problem $f\left(x\right)=0$, using two previous iterates to calculate the next one:

$$x_{k+1}=\psi (x_{k-1},x_k),k\ge 1,$$

with $x_0$ and $x_1$ being its seeds. Therefore, a solution $\alpha$ is estimated whether $x_{k+1}=x_k$ or, equivalently, $x_k=\psi (x_{k-1},x_k)$. This estimation can be obtained as a fixed point of $\mathsf{\Psi }:{\mathbb{R}}^2⟶{\mathbb{R}}^2$ by means of:

$$\begin{array}{c}\hfill \mathsf{\Psi }\left(x_{k-1},x_k\right)=(x_k,\psi (x_{k-1},x_k)),k=1,2,\dots ,\end{array}$$

with again $x_0$ and $x_1$ being the seeds.

To study the qualitative behavior of a fixed point iterative scheme with memory, it is applied on a low-degree polynomial $p\left(x\right)$, generating a vectorial rational operator, $G\left(x\right)$. Then, the orbit of $(z,x)\in {\mathbb{R}}^2$ is the set:

$$\left\{(z,x),G\left((z,x)\right),\dots ,G^m\left((z,x)\right),\dots \right\}.$$

Therefore, a point $(z,x)$ is fixed if it is the only point belonging to its orbit, and it is a T-periodic point if is orbit is only defined by $\left\{(z,x),G\left((z,x)\right),\dots ,G^{T-1}\left((z,x)\right)\right\}$ and $G^T\left((z,x)\right)=(z,x)$.

On the other hand, the orbit of a point can be classified depending on its asymptotic behavior, according to the next result.

Theorem 2

([21], p. 558). Let $G:{\mathbb{R}}^n\to {\mathbb{R}}^n$ be ${\mathcal{C}}^2$. Let us also assume that $x^{*}$ is a period-k point. Let ${\lambda }_i$, $i=1,2,\dots ,n$ be the eigenvalues of the Jacobian $G^{\prime }\left(x^{*}\right)$:

(a) 

If $|{\lambda }_j|<1$, $j=1,2,\dots ,n$, then $x^{*}$ is an attractor. It is said to be a superattractor if $|{\lambda }_j|=0$.

(b) 

If ${\lambda }_{j_0}$ exists such that $|{\lambda }_{j_0}|>1$, then the periodic point is unstable (repelling or saddle).

(c) 

If $|{\lambda }_j|>1$, $j=1,2,\dots ,n$, then $x^{*}$ is a repulsor.

Moreover, we define a point $x_c\in {\mathbb{R}}^2$ as a critical point of G if $det\left(G^{\prime }\left(x_c\right)\right)=0$. Indeed, if $x_c$ is not a zero of $p\left(x\right)$, it is named a free critical point. In a similar way, if a fixed point is not a zero of $p\left(x\right)$, it is named a strange fixed point.

Denoting by $x^F\in {\mathbb{R}}^2$ an attracting fixed point of: G, its basin of attraction $\mathcal{B}\left(x^F\right)$ is defined as:

$$\mathcal{B}\left(x^F\right)=\left\{(z,x)\in {\mathbb{R}}^n:G^m\left((z,x)\right)\to x^F,m\to \infty \right\}.$$

The union of all the basins of attraction of G is defined as the Fatou set, $\mathcal{F}\left(G\right)$, and its complementary set in ${\mathbb{R}}^2$ is the Julia set $\mathcal{J}\left(G\right)$. It holds all the repelling fixed points and sets the boundary among the basins of attraction.

In Section 2 and Section 3, we build a Kurchatov-type and a Steffensen-type iterative method with memory, respectively, to estimate the inverse of a nonsingular complex matrix. Both schemes are free of inverse operators, and we prove their order of convergence and stability. In Section 4, we extend these schemes to calculate the Moore–Penrose inverse of a complex rectangular matrix. Section 5 is devoted to the numerical tests to analyze their performance and confirm the theoretical results. We end the work with some conclusions.

2. Kurchatov-Type Method

The Kurchatov divided difference was defined by [16] as:

$$f{[x_{k-1},2x_k-x_{k-1};f]}_K={\displaystyle \frac{f(2x_k-x_{k-1})-f\left(x_{k-1}\right)}{2(x_k-x_{k-1})}}.$$

For an equation $f\left(x\right)=0$, Kurchatov’s method has order or convergence two and iterative expression:

$$x_{k+1}=x_k-{\displaystyle \frac{f\left(x_k\right)}{f{[x_k,x_{k-1}]}_K}}=x_k-{\displaystyle \frac{2f\left(x_k\right)(x_k-x_{k-1})}{f(2x_k-x_{k-1})-f\left(x_{k-1}\right)}}.$$

If we apply this method to $F\left(X\right)=X^{-1}-A$, where $F:{\mathbb{C}}^{n\times n}\to {\mathbb{C}}^{n\times n}$ and $A\in {\mathbb{C}}^{n\times n}$ is an $n\times n$ nonsingular matrix, not necessarily diagonalizable, we obtain:

$$\begin{array}{ccc}\hfill X_{k+1}& =& X_k-2{[F(2X_k-X_{k-1})-F\left(X_{k-1}\right)]}^{-1}F\left(X_k\right)(X_k-X_{k-1})\hfill \\ & =& X_k-2{[{(2X_k-X_{k-1})}^{-1}-X_{k-1}^{-1}]}^{-1}(X_k^{-1}-A)(X_k-X_{k-1}).\hfill \end{array}$$

(5)

Next, we show a technical lemma whose result we use later.

Lemma 1.

Let $A,B\in {\mathbb{C}}^{n\times n}$ be invertible and commutative, $AB=BA$, then:

$${\left(2A-B\right)}^{-1}-B^{-1}=2{\left(2A-B\right)}^{-1}{B}^{-1}(B-A).$$

Proof. 

Using algebraic manipulations,

$$\begin{array}{ccc}\hfill 2{\left(2A-B\right)}^{-1}{B}^{-1}(B-A)& =& {\left(2A-B\right)}^{-1}{B}^{-1}(2B-2A)\hfill \\ & =& {\left(2A-B\right)}^{-1}{B}^{-1}\left[B-(2A-B)\right]\hfill \\ & =& {\left(2A-B\right)}^{-1}\left[I-B^{-1}(2A-B)\right]\hfill \\ & =& {\left(2A-B\right)}^{-1}-{\left(2A-B\right)}^{-1}{B}^{-1}(2A-B)\hfill \\ & =& {\left(2A-B\right)}^{-1}-B^{-1}{\left(2A-B\right)}^{-1}(2A-B)\hfill \\ & =& {\left(2A-B\right)}^{-1}-B^{-1},\hfill \end{array}$$

and the lemma is proven. □

It is known that, for any nonsingular $n\times n$ complex matrix A, there exist $n\times n$ unitary matrices U and V, such that $U^{*}AV=\mathsf{\Sigma }$, $\mathsf{\Sigma }$ being the diagonal matrix of the singular values of A, $\mathsf{\Sigma }=\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$ with ${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_n>0$ and $A=U\mathsf{\Sigma }{V}^{*}$. Moreover, $U^{*}$ is the conjugate transpose of U. Then, $X_k=V{D}_k{U}^{*}$, that is $D_k=V^{*}{X}_{k}U$, $D_k^{-1}=U^{*}{X}_k^{-1}V$, and $X_k^{-1}=U{D}_k^{-1}{V}^{*}$, and we apply them in Equation (5).

$$\begin{array}{cc}\hfill V{D}_{k+1}{U}^{*}& =V{D}_k{U}^{*}-2{[{(2V{D}_k{U}^{*}-V{D}_{k-1}{U}^{*})}^{-1}-U{D}_{k-1}^{-1}{V}^{*}]}^{-1}{W}_1{W}_2,\hfill \end{array}$$

where $W_1=U{D}_k^{-1}{V}^{*}-U\mathsf{\Sigma }{V}^{*}$ and $W_2=V{D}_k{U}^{*}-V{D}_{k-1}{U}^{*}$. If the initial approximations $X_{-1}$, $X_0$ satisfy $D_0=V^{*}{X}_{0}U$ and $D_{-1}=V^{*}{X}_{-1}U$ are diagonal matrices, then all the matrices $D_k$ are diagonal and $D_i{D}_j=D_j{D}_i$, for all $i,j$. Applying several algebraic manipulations on the last equation, we can ensure:

$$\begin{array}{cc}\hfill V{D}_{k+1}{U}^{*}& =V{D}_k{U}^{*}-2{[U{(2D_k-D_{k-1})}^{-1}{V}^{*}-U{D}_{k-1}^{-1}{V}^{*}]}^{-1}U(D_k^{-1}-\mathsf{\Sigma })V^{*}V(D_k-D_{k-1})U^{*}\hfill \\ \hfill & =V{D}_k{U}^{*}-2V{[{(2D_k-D_{k-1})}^{-1}-D_{k-1}^{-1}]}^{-1}{U}^{*}U(D_k^{-1}-\mathsf{\Sigma })V^{*}V(D_k-D_{k-1})U^{*}.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill D_{k+1}& =D_k-2{[{(2D_{k-1}-D_k)}^{-1}-D_{k-1}^{-1}]}^{-1}(D_k^{-1}-\mathsf{\Sigma })(D_k-D_{k-1})\hfill \\ \hfill & =D_k-2{[{(2D_{k-1}-D_k)}^{-1}-D_{k-1}^{-1}]}^{-1}(D_k-D_{k-1})(D_k^{-1}-\mathsf{\Sigma }).\hfill \end{array}$$

Using Lemma 1, we obtain:

$$\begin{array}{cc}\hfill {[{(2D_{k-1}-D_k)}^{-1}-D_{k-1}^{-1}]}^{-1}& ={\left[2{(2D_k-D_{k-1})}^{-1}{D}_{k-1}^{-1}(D_{k-1}-D_k)\right]}^{-1}\hfill \\ \hfill & =\frac{1}{2}(2D_k-D_{k-1})D_{k-1}{(D_{k-1}-D_k)}^{-1}.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill D_{k+1}& =D_k-(2D_k-D_{k-1}){(D_{k-1}-D_k)}^{-1}(D_k^{-1}-\mathsf{\Sigma })(D_k-D_{k-1})D_{k-1}\hfill \\ \hfill & =D_k+(2D_k-D_{k-1})D_k^{-1}(I-D_k\mathsf{\Sigma })D_{k-1}.\hfill \end{array}$$

Finally,

$$X_{k+1}=X_k+(2X_k-X_{k-1})X_k^{-1}(I-X_{k}A)X_{k-1}.$$

(6)

In this iterative expression, still, an inverse matrix appears. Therefore, Kurchatov’s scheme is not directly transferable for the calculation of the matrix inverses.

Therefore, we propose a slight change in the Kurchatov divided difference scheme:

$$f{[x_k,2x_{k-1}-x_k]}_{KT}={\displaystyle \frac{f(2x_{k-1}-x_k)-f\left(x_k\right)}{2(x_{k-1}-x_k)}},$$

obtaining a new iterative scheme,

$$x_{k+1}=x_k-{\displaystyle \frac{f\left(x_k\right)}{f{[x_k,2x_{k-1}-x_k]}_{KT}}}=x_k-{\displaystyle \frac{2(x_{k-1}-x_k)f\left(x_k\right)}{f(2x_{k-1}-x_k)-f\left(x_k\right)}}.$$

Now, we apply this iterative procedure to the matrix equation $F\left(X\right)=X^{-1}-A$:

$$\begin{array}{ccc}\hfill X_{k+1}& =& X_k-2{\left(F(2X_{k-1}-X_k)-F\left(X_k\right)\right)}^{-1}F\left(X_k\right)(X_{k-1}-X_k)\hfill \\ & =& X_k-2{\left[{\left(2X_{k-1}-X_k\right)}^{-1}-X_k^{-1}\right]}^{-1}\left(X_k^{-1}-A\right)(X_{k-1}-X_k).\hfill \end{array}$$

Using the transformations defined above and Lemma 1, we obtain:

$$\begin{array}{cc}\hfill V{D}_{k+1}{U}^{*}& =V{D}_k{U}^{*}+2{[{(2V{D}_{k-1}{U}^{*}-V{D}_k{U}^{*})}^{-1}-U{D}_k^{-1}{V}^{*}]}^{-1}{W}_1{W}_2\hfill \\ \hfill & =V\left\{D_k-2{[{(2D_{k-1}-D_k)}^{-1}-D_k^{-1}]}^{-1}(D_k^{-1}-\mathsf{\Sigma })(D_{k-1}-D_k)\right\}{U}^{*},\hfill \end{array}$$

and then,

$$\begin{array}{cc}\hfill D_{k+1}& =D_k-2{[{(2D_{k-1}-D_k)}^{-1}-D_k^{-1}]}^{-1}(D_k^{-1}-\mathsf{\Sigma })(D_{k-1}-D_k)\hfill \\ \hfill & =2D_{k-1}-(D_k-2D_{k-1})\mathsf{\Sigma }{D}_k.\hfill \end{array}$$

Finally,

$$\begin{array}{cc}\hfill D_{k+1}& =2D_{k-1}-(D_k-2D_{k-1})\mathsf{\Sigma }{D}_k\hfill \end{array}$$

(7)

From this expression, by using again the transformations defined above, we have

$$\begin{array}{cc}\hfill V^{*}{X}_{k+1}U& =2V^{*}{X}_{k-1}U-(V^{*}{X}_{k}U-2V^{*}{X}_{k-1}U)U^{*}AV{V}^{*}{X}_{k}U\hfill \\ \hfill & =V^{*}\left[2X_{k-1}-(X_k-2X_{k-1})A{X}_k\right]U,\hfill \end{array}$$

and

$$X_{k+1}=2X_{k-1}-(2X_{k-1}-X_k)A{X}_k,$$

(8)

where three matrix products appear, but there are no inverse operators. Equation (8) corresponds to the iterative scheme of the modified Kurchatov-type method for matrix inversion, which we call $MKTM$.

2.1. Convergence Analysis

Let us consider now two $n\times n$ unitary matrices U and V, satisfying $\mathsf{\Sigma }=U^{*}AV=\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$, where the singular values ${\sigma }_i$, $i=1,2,\dots ,n$ of A fulfill ${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_n>0$. We define again $D_k=V^{*}{X}_{k}U$, $X_k=V{D}_k{U}^{*}$. By using Equation (7), we obtain:

$$D_{k+1}=2D_{k-1}-(2D_{k-1}-D_k)D_k\mathsf{\Sigma }.$$

Next, we demonstrate the order of convergence of the iterative procedure $MKTM$.

Theorem 3.

Let $A\in {\mathbb{C}}^{n\times n}$ be a nonsingular matrix and $X_{-1}$ and $X_0$ be the initial approximation such that matrices $V^{*}{X}_{-1}U$ and $V^{*}{X}_{0}U$ are diagonal. Then, sequence $\left\{X_k\right\}$ obtained by means of the iterative expression (8), where $\mathsf{\Sigma }=U^{*}AV$ is the singular-value decomposition of A, converges to the inverse $A^{-1}$, with convergence order 1.6180.

Proof. 

Let us denote $d_k=diag(d_k^1,d_k^2,\dots ,d_k^n)$. By means of component-by-component calculations, we obtain:

$$d_{k+1}^j=2d_{k-1}^j-(2d_{k-1}^j-d_k^j)d_k^j{\sigma }_j,j=1,2,\dots ,n.$$

(9)

Let us also denote $e_k^j=d_k^j-1/{\sigma }_j$; by subtracting $\frac{1}{{\sigma }_j}$ from the both sides of the last equation, we obtain:

$$\begin{array}{ccc}\hfill e_{k+1}^j& =& 2d_{k-1}^j-(2d_{k-1}^j-d_k^j)d_k^j{\sigma }_j-\frac{1}{{\sigma }_j}\hfill \\ & =& {\sigma }_j\left({\displaystyle \frac{2d_{k-1}^j}{{\sigma }_j}}-2d_{k-1}^j{d}_k^j+{\left(d_{k-1}^j\right)}^2-{\displaystyle \frac{1}{{\sigma }_j^2}}\right)\hfill \\ & =& {\sigma }_j\left[-2d_{k-1}^j\left(d_k^j-{\displaystyle \frac{1}{{\sigma }_j}}\right)+\left(d_k^j-{\displaystyle \frac{1}{{\sigma }_j}}\right)\left(d_k^j+{\displaystyle \frac{1}{{\sigma }_j}}\right)\right]\hfill \\ & =& -2{\sigma }_j{e}_{k-1}^j{e}_k^j+{\left(e_k^j\right)}^2{\sigma }_j.\hfill \end{array}$$

This result shows that, for each $j=1,2,\dots ,n$, $d_{k+1}$ in Equation (9) converges to ${\displaystyle \frac{1}{{\sigma }_j}}$ with order of convergence $(1+\sqrt{5})/2\approx 1.6180$, which is the only positive root of ${\lambda }^2-\lambda -1=0$ (see Theorem 1). In this way, for each $j=1,2,\dots ,n$, there exists ${\left\{C_k^j\right\}}_k$ satisfying $C_k^j>0$, $\forall k$. Moreover, $C_k^j$ tends to zero when $k\to \infty$. Indeed, $\left|e_{k+1}^j\right|\le C_k^j\left|{\left(e_k^j\right)}^2\right|$, $j=1,2,\dots ,n$. Furthermore,

$${∥D_{k+1}-{\mathsf{\Sigma }}^{-1}∥}_2^2=\sum _{j=1}^n{\left(e_k^j\right)}^2\le \sum _{j=1}^n{\left(C_k^j\right)}^2{\left(e_k^j\right)}^2\le n{M}_k^2{∥D_k-{\mathsf{\Sigma }}^{-1}∥}_2^2,$$

with ${\displaystyle M_k=\underset{1\le j\le n}{max}\left\{C_k^j\right\}}$. Using this result, we obtain:

$$\begin{array}{cc}\hfill {∥X_{k+1}-A^{-1}∥}_2& ={∥V{D}_{k+1}{U}^{*}-V{\mathsf{\Sigma }}^{-1}{U}^{*}∥}_2={∥V(D_{k+1}-{\mathsf{\Sigma }}^{-1})U^{*}∥}_2\hfill \\ \hfill & \le M_k\sqrt{n}{∥D_k-{\mathsf{\Sigma }}^{-1}∥}_2\hfill \\ \hfill & \le M_k\sqrt{n}{∥X_k-A^{-1}∥}_2.\hfill \end{array}$$

Therefore, we can affirm that $\left\{X_k\right\}$ converges to $A^{-1}$. □

To demonstrate the stability of the modified Kurchatov-type iterative scheme, we used the definition introduced by Higham in [14] for the stability of the iterative scheme $Z_{k+1}=H\left(Z_k\right)$, with a fixed point $Z_{*}$. Assuming that H is Frechét differentiable in fixed point $Z_{*}$, then the process is stable in a neighborhood of $Z_{*}$ if there exists a positive constant C such that $\parallel H^{\prime }{\left(Z_{*}\right)}^k\parallel \le C,\forall k>0$.

Theorem 4.

The modified Kurchatov-type iterative scheme to estimate the inverse of a nonsingular complex matrix defined by expression (8) is stable.

Proof. 

The modified Kurchatov-type method can be written as follows:

$$KT\left(Z_k\right)=KT\left(\begin{array}{c}{X}_k\\ X_{k-1}\end{array}\right)=\left[\begin{array}{c}2X_{k-1}+(2X_{k-1}-X_k)A{X}_k\\ X_k\end{array}\right].$$

So, denoting by $P={(P_1,P_2)}^T$, we conclude

$$K{T}^{\prime }\left(\begin{array}{c}{X}_k\\ X_{k-1}\end{array}\right)P=\left[\begin{array}{c}2X_{k-1}A{P}_1-A{X}_k{P}_1-X_{k}A{P}_1+2P_2-2A{X}_k{P}_2\\ P_1\end{array}\right].$$

Now, as $Z=Z^{*}={(A^{-1},A^{-1})}^T$, we get

$$K{T}^{\prime }\left(Z^{*}\right)P=\left[\begin{array}{cc}0& 0\\ I& 0\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\end{array}\right]=\left[\begin{array}{c}0\\ P_1\end{array}\right]$$

Therefore, matrix $K{T}^{\prime }\left(Z^{*}\right)$ is idempotent, and (8) is a stable iterative process. □

2.2. Qualitative Analysis of Kurchatov-Type Scheme

Now, we considered the Kurchatov-type scheme as a scalar iterative procedure for solving nonlinear equations, analyzed its convergence, and studied its stability. In this analysis, the stability is understood as the dependence on the initial estimations. It is made by applying the vectorial real dynamical concepts to the Kurchatov-type scheme, whose expression is:

$$x_{k+1}=x_k-\frac{f\left(x_k\right)}{f[x_k,2x_{k-1}-x_k]},k=0,1,2,\dots$$

In the following result, we show that this scheme for solving nonlinear scalar equations $f\left(x\right)=0$ has superlinear convergence.

Theorem 5.

Let us consider a sufficiently differentiable function $f:I\subseteq \mathbb{R}\to \mathbb{R}$ in an open neighborhood I of the simple root α of nonlinear equation $f\left(x\right)=0$. Furthermore, let us assume that $f^{\prime }\left(x\right)$ is continuous at α and that $x_0$ and α are near enough between them. Then, sequence $x_k$, $k=0,1,2,\dots$, generated by the Kurchatov-type scheme, converges to α with order of convergence $\frac{1+\sqrt{5}}{2}$, its error equation being:

$$e_{k+1}=2c_2{e}_{k-1}{e}_k+{\mathcal{O}}_2(e_{k-1},e_k),$$

where ${\mathcal{O}}_2(e_{k-1},e_k)$ means that the following terms in the error equation depend on the powers of errors $e_{k-1}$ and $e_k$ such that the sum of the exponents is at least two; moreover, $e_k=x_k-\alpha$ and $c_q=\frac{1}{q!}\frac{f^{\left(q\right)}\left(\alpha \right)}{f^{\prime }\left(\alpha \right)}$, $q\ge 2$.

Proof. 

It is known that the Taylor expansion of $f\left(x_k\right)$ around $\alpha$ is:

$$f\left(x_k\right)=f^{\prime }\left(\alpha \right)\left[e_k+c_2{e}_k^2+c_3{e}_k^3\right]+\mathcal{O}\left(e_k^3\right).$$

By using the Genocchi–Hermite formula (see [15]) and the expansion of $f^{\prime }(x+th)$ in the Taylor series around x,

$$f[x,x+h]={\int }_0^1{f}^{\prime }(x+th)dt=f^{\prime }\left(x\right)+{\displaystyle \frac{1}{2!}}{f}^{″}\left(x\right)h+{\displaystyle \frac{1}{3!}}{f}^{‴}\left(x\right)h^2+\mathcal{O}\left(h^3\right),$$

(10)

with $h=2x_{k-1}-2x_k=2(e_{k-1}-e_k)$, the expansion of the divided difference is:

$$f[x_k,2x_{k-1}-x_k]=f^{\prime }\left(\alpha \right)\left[1+2c_2{e}_k+3c_3{e}_k^2+(c_2+3c_3{e}_k)h+4c_{3}h\right]+\mathcal{O}\left(h^3\right).$$

Then, the expression of the difference divided as a function of the errors $e_{k-1}$ and $e_k$ is:

$$f[x_k,2x_{k-1}-x_k]=f^{\prime }\left(\alpha \right)\left[1+2c_2{e}_{k-1}-2c_3{e}_{k-1}{e}_k+4c_3{e}_{k-1}^2+c_3{e}_k^2\right]+{\mathcal{O}}_3\left(e_{k-1},e_k\right).$$

Therefore,

$$\frac{f\left(x_k\right)}{f[x_k,2x_{k-1}-x_k]}=e_k-2c_2{e}_{k-1}{e}_k+{\mathcal{O}}_2\left(e_{k-1},e_k\right).$$

By applying Theorem 1, the only positive real root of ${\lambda }^2-\lambda -1=0$ (where the coefficients correspond to the exponents of $e_{k-1}$ and $e_k$ in the error equation) is the convergence order of the method, that is $\frac{1+\sqrt{5}}{2}$. □

From now on, we denote by $KT$ the fixed point operator associated with the Kurchatov-type method applied on $p\left(z\right)=z^2-1$. As it does not use derivatives, it is not possible to establish a scaling theorem. Therefore, we cannot make the analysis on generic second-degree polynomials.

The fixed point operator depends on two variables: $x_k$ (denoted by x) and $x_{k-1}$ (denoted by z). Therefore,

$$KT\left(z,x\right)=\left(x,-\frac{x^2-2xz-1}{2z}\right).$$

Let us analyze now the qualitative performance of the rational operator by means of the asymptotic behavior of the fixed points and the existence of free critical points.

Theorem 6.

The only fixed points of rational operator KT are the roots $x=z=\pm 1$, both being superattracting. Moreover, KT has no free critical points.

Proof. 

We solve equation:

$$KT\left(z,x\right)=\left(x,x\right)\iff x=z \mathrm{and} x=-\frac{x^2-2xz-1}{2z}\iff x=\pm 1,$$

finding that the only fixed points are $(-1,-1)$ and $(1,1)$. To study their stability, we considered:

$$K{T}^{\prime }(z,x)=\left(\begin{array}{cc}0& 1\\ \frac{(-1+x)(1+x)}{2z^2}& -\frac{x-z}{z}\end{array}\right)$$

and therefore, its eigenvalues are:

$${\lambda }_1(z,x)={\displaystyle \frac{z-x-\sqrt{-2+3x^2-2xz+z^2}}{2z}}$$

and:

$${\lambda }_2(z,x)={\displaystyle \frac{z-x+\sqrt{-2+3x^2-2xz+z^2}}{2z}}.$$

As ${\lambda }_1(-1,-1)={\lambda }_2(1,1)=(0,0)$, we concluded that fixed points $(1,1)$ and $(-1,-1)$ are superattracting.

As an immediate consequence of this analysis of $K{T}^{\prime }(z,x)$ and its eigenvalues ${\lambda }_i(z,x)$, $i=1,2$, the only $(z,x)\in {\mathbb{R}}^2$ satisfying ${\lambda }_1(z,x)={\lambda }_2(z,x)=(0,0)$ are those $(z,x)=(\pm 1,\pm 1)$, where $z=x$. Then, they are the only critical points, and there do not exist free critical points. □

From this results, we concluded that no other performance than convergence to the roots is possible, when the Kurchatov-type is applied on $p\left(x\right)$, as any other basin of attraction would need a free critical point inside.

In Figure 1, we show the dynamical plane of the KT operator, x and z being real, corresponding to the abscissa and ordinate axis, respectively (see [22] for the routines). The mesh used has $1000\times 1000$ points, and the maximum amount of iterations is 40. The distance to the root lower than ${10}^{-3}$ is the stopping criterion.

Figure 1. Dynamical plane of the Kurchatov-type scheme on $p\left(z\right)=z^2-1$.

Then, if each point of the mesh is considered as a seed of the method, when it converges to one of the roots of $p\left(z\right)$ (located in $x=z$), it is represented in orange or green color, depending on the root it has converged to. The color is brighter the lower the amount of iterations is. When the initial estimation, after the iterative process, reaches 40 iterations with no convergence, it is colored in black.

In Figure 1, we observe that the basins of attraction of both roots of $p\left(z\right)$ have symmetric shapes. In spite of the only basins of attraction being those of the roots (Theorem 6), there are black areas in the dynamical planes. They correspond to areas of slow convergence, whose initial estimations converge with a higher number of iterations.

In [19,20], the stability analysis of the secant and Steffensen with memory schemes was performed, among other iterative schemes with memory. In both cases, the dynamical planes plotted showed full convergence to the roots, without black areas of slow convergence or divergence. Later on, we checked how the the differences among the Kurchatov-type and secant or Steffensen with memory stability affected their numerical performance.

3. Steffensen with Memory

Now, we considered the Traub–Steffensen family [18], whose iterative expression is:

$$x_{k+1}=x_k-\frac{f\left(x_k\right)}{f[x_k+\gamma f\left(x_k\right),x_k]},$$

(11)

where $\gamma$ is an arbitrary constant different from zero. Furthermore, if $\gamma =1$ in this iterative scheme, we obtain the well-known Steffensen method [17]. It is easy to show that this iterative procedure has order of convergence two for any value of $\gamma$, its error equation being:

$$e_{k+1}=c_2(1+\gamma f^{\prime }\left(\alpha \right))e_k^2+\mathcal{O}\left[e_k^3\right],$$

(12)

where $e_k=x_k-\alpha$ represents the error in each iteration and $c_j=\frac{1}{j!}{f}^{\left(j\right)}\left(\alpha \right)/f^{\prime }\left(\alpha \right)$, $j\ge 2$. Let us also remark that this is a derivative-free scheme without memory, because it uses only the information of the current iteration. Studying the equation of the error (12) of family (11), we notice that, if $\gamma =-1/f\left(\alpha \right)$, the iterative scheme (11) achieves the third order of convergence. This value of the parameter cannot be used, as $\alpha$ is unknown. Therefore, the approximation of $f^{\prime }\left(\alpha \right)$ as the first-order divided differences $\gamma =-1/f[x_k,x_{k-1}]$ is employed, obtaining $x_k+\gamma f\left(x_k\right)=x_k-f\left(x_k\right)/f[x_k,x_{k-1}]$, which is the secant scheme, and (11) is an iterative procedure with memory.

3.1. Iterative Scheme Design for the Matrix Inverse

Our aim now was to adapt Steffensen’s scheme with memory to solve the matrix Equation (1). In [23] Monsalve et al. adapted the secant method to estimate the solution of Equation (1) for A diagonalizable, and in [13], the authors extended this result to any nonsingular matrix by means of the expression:

$$W_{k+1}=W_{k-1}+W_k-W_{k-1}A{W}_k,k\ge 0,$$

(13)

where $W_0$ and $W_{-1}$ are the seeds.

In a similar way, Expression (11) for matrix equations takes the form:

$$\begin{array}{cc}\hfill X_{k+1}& =X_k-{[F\left(X_k\right)-F\left(W_k\right)]}^{-1}F\left(X_k\right)(X_k-W_k)\hfill \\ \hfill & =X_k-{\left[X_k^{-1}-W_k^{-1}\right]}^{-1}(X_k^{-1}-A)(X_k-X_{k-1}),\hfill \end{array}$$

(14)

which includes the inverse calculations for the estimation of $A^{-1}$. This circumstance must be avoided.

As A is a nonsingular $n\times n$ complex matrix, there exist $n\times n$ unitary matrices U and V, such that $\mathsf{\Sigma }=U^{*}AV=\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$, where ${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_n>0$ are the singular values of A. We define $X_k=V{D}_k{U}^{*}$ and $X_k^{-1}=U{D}_k^{-1}{V}^{*}$. Then, Equation (14) takes the form:

$$V{D}_{k+1}{U}^{*}=V{D}_k{U}^{*}-{\left[U{D}_k^{-1}{V}^{*}-UD{w}_k^{-1}{V}^{*}\right]}^{-1}(U{D}_k^{-1}{V}^{*}-U\mathsf{\Sigma }{V}^{*})(V{D}_k{U}^{*}-V{D}_{k-1}{U}^{*})$$

(15)

If the initial approximations $X_{-1}$ and $X_0$ satisfy $D^{-1}=V^{*}{X}^{-1}U$ and $D_0=V^{*}{X}_{0}U$, then $D_k$ are diagonal matrices and $D_i{D}_j=D_j{D}_i$ for all $i,j$. By applying several algebraic manipulations on Equation (15), we can ensure:

$$\begin{array}{cc}\hfill V{D}_{k+1}{U}^{*}=& V{D}_k{U}^{*}-{\left[U{D}_k^{-1}{V}^{*}-{(V{D}_{k-1}{U}^{*}+V{D}_k{U}^{*}-V{D}_{k-1}{U}^{*}U\mathsf{\Sigma }{V}^{*}V{D}_k{U}^{*})}^{-1}\right]}^{-1}\hfill \\ \hfill & (U{D}_k^{-1}{V}^{*}-U\mathsf{\Sigma }{V}^{*})(V{D}_{k-1}U\ast U\mathsf{\Sigma }{V}^{*}V{D}_k{U}^{*}-V{D}_{k-1}{U}^{*})\hfill \\ \hfill =& V\left\{D_k-{[D_k^{-1}-{(D_{k-1}+D_k-D_{k-1}\mathsf{\Sigma }{D}_k)}^{-1}]}^{-1}(D_k^{-1}-\mathsf{\Sigma })D_{k-1}(\mathsf{\Sigma }{D}_k-I)\right\}{U}^{*},\hfill \end{array}$$

(16)

and therefore,

$$\begin{array}{cc}\hfill D_{k+1}=& D_k-{[D_k^{-1}-{(D_{k-1}+D_k-D_{k-1}\mathsf{\Sigma }{D}_k)}^{-1}]}^{-1}(D_k^{-1}-\mathsf{\Sigma })D_{k-1}(\mathsf{\Sigma }{D}_k-I)\hfill \\ \hfill =& D_{k-1}+(I-D_{k-1}\mathsf{\Sigma })(2I-D_k\mathsf{\Sigma })D_k,\hfill \end{array}$$

(17)

where I denotes the identity matrix of size n. Now, taking $D_k=V^{*}{X}_{k}U$ and $D_k^{-1}=U^{*}{X}_k^{-1}V$ and after more algebraic manipulations, we obtain:

$$\begin{array}{cc}\hfill X_{k+1}& =X_{k-1}+(I-X_{k-1}A)(2I-X_{k}A)X_k,k=1,2,\dots ,\hfill \end{array}$$

(18)

given the initial approximations $X_0$ and $X_{-1}$. We denote this iterative scheme with memory as $SMM$. Let us remark that Expression (18) does not include inverse operators, as intended.

3.2. Convergence Analysis and Stability

We present in the next result the convergence analysis of the iterative method given by Expression (18).

Theorem 7.

Let $U^{*}AV=\mathsf{\Sigma }$ be the singular-value decomposition of the a nonsingular matrix $A\in {\mathbb{C}}^{n\times n}$. Furthermore, let $X_0$ and $X_{-1}$ be the initial approximations to $A^{-1}$, such that $V^{*}{X}_{-1}U$ and $V^{*}{X}_{0}U$ are diagonal matrices. Then, sequence $\left\{X_k\right\}$, generated by (18), converges to $A^{-1}$ with order of convergence $1+\sqrt{2}\approx 2.4142$.

Proof. 

Let U and V be unitary matrices such that $U^{*}AV=\mathsf{\Sigma }$, $\mathsf{\Sigma }$ being the diagonal matrix of the singular values ${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_n>0$ of A. Furthermore, by denoting $D_k=V^{*}{X}_{k}U$ and $X_k=V{D}_k{U}^{*}$ for $k=-1,0,1,\dots$, from Equation (18), we obtain:

$$\begin{array}{cc}\hfill V{D}_{k+1}{U}^{*}& =V{D}_{k-1}{U}^{*}+(VI{V}^{*}-V{D}_{k-1}{U}^{*}U\mathsf{\Sigma }{V}^{*})(2VI{V}^{*}-V{D}_{k}U\ast U\mathsf{\Sigma }{V}^{*})V{D}_k{U}^{*}\hfill \\ \hfill & =V\left[D_{k-1}+(I-D_{k-1}\mathsf{\Sigma })(2I-D_k\mathsf{\Sigma })D_k\right]U^{*}.\hfill \end{array}$$

Let us remark that $D_k=diag(d_k^1,d_k^2,\dots ,d_k^n)$, for $k=-1,0,1,\dots$. Therefore,

$$D_{k+1}=D_{k-1}+(I-D_{k-1}\mathsf{\Sigma })(2I-D_k\mathsf{\Sigma })D_k.$$

(19)

Therefore, in Equation (19), using component-by-component calculations, we obtain:

$$d_{k+1}^j=d_{k-1}^j+(1-d_{k-1}^j{\sigma }_j)(2-d_k^j{\sigma }_j)d_k^j,\dots j=1,2,\dots ,n.$$

(20)

We denote $e_k^j=d_k^j-1/{\sigma }_j$. We subtract ${\displaystyle \frac{1}{{\sigma }_j}}$ from both sides of Equation (20), and we obtain:

$$\begin{array}{ccc}\hfill e_{k+1}^j& =& e_{k-1}^j+{\sigma }_j\left(\frac{1}{{\sigma }_j}-d_{k-1}^j\right){\sigma }_j\left(\frac{2}{{\sigma }_j}-d_k^j\right)d_k^j\hfill \\ & =& {\sigma }_j^2{\left(e_k^j\right)}^2{e}_{k-1}.\hfill \end{array}$$

(21)

Theorem 1 allows us to conclude that, for each j from 1 to n, $d_{k+1}$ converges to ${\displaystyle \frac{1}{{\sigma }_j}}$ with the convergence order the only positive root of ${\lambda }^2-2\lambda -1=0$, $\lambda =1+\sqrt{2}\approx 2.4142$ (see [15]). In this way, for each $j=1,2,\dots ,n$, there exist a sequence ${\left\{C_k^j\right\}}_k$ satisfying $C_k^j>0$, $\forall k$, and ${\left\{C_k^j\right\}}_k\to 0$ when $k\to \infty$. Indeed, $|e_{k+1}^j|\le C_k^j\left|{\left(e_k^j\right)}^2\right|$, $1\le j\le n$. On the other hand,

$${∥D_{k+1}-{\mathsf{\Sigma }}^{-1}∥}_2^2=\sum _{j=1}^n{\left(e_k^j\right)}^2\le \sum _{j=1}^n{\left(C_k^j\right)}^2{\left[{\left(e_k^j\right)}^2\right]}^2\le n{M}_k^2{∥D_k-{\mathsf{\Sigma }}^{-1}∥}_2^2,$$

where ${\displaystyle M_k=\underset{1\le j\le n}{max}\left\{C_k^j\right\}}$. Using this result, we obtain:

$$\begin{array}{cc}\hfill {∥X_{k+1}-A^{-1}∥}_2& ={∥V(D_{k+1}-{\mathsf{\Sigma }}^{-1})U^{*}∥}_2\hfill \\ \hfill & \le {∥V∥}_2{∥D_{k+1}-{\mathsf{\Sigma }}^{-1}∥}_2{∥U^{*}∥}_2={∥D_{k+1}-{\mathsf{\Sigma }}^{-1}∥}_2\hfill \\ \hfill & \le M_k\sqrt{n}{∥D_k-{\mathsf{\Sigma }}^{-1}∥}_2\hfill \\ \hfill & \le M_k\sqrt{n}{∥X_k-A^{-1}∥}_2.\hfill \end{array}$$

Then, $\left\{X_k\right\}$ converges to $A^{-1}$, and the proof is finished. □

In the following result, we prove the stability of this scheme.

Theorem 8.

Steffensen’s method with memory to estimate the inverse of a given matrix with the expression (18) is a stable iterative scheme.

Proof. 

Steffensen’s scheme with memory can be written as a fixed point scheme as follows:

$$S\left(Z_k\right)=S\left(\begin{array}{c}{X}_k\\ X_{k-1}\end{array}\right)=\left[\begin{array}{c}{X}_{k-1}+(I-X_{k-1}A)(2I-X_{k}A)X_k\\ X_k\end{array}\right].$$

Then, given $P={(P_1,P_2)}^T$, we deduce that:

$$S^{\prime }\left(\begin{array}{c}{X}_k\\ X_{k-1}\end{array}\right)P=\left[\begin{array}{c}{P}_1-A(2I-X_{k}A)X_k{P}_1-(I-X_{k-1}A)A{X}_k{P}_2+(I-X_{k-1}A)(2I-X_{k}A)P_2\\ P_1\end{array}\right].$$

Next, for $Z=Z^{*}={(A^{-1},A^{-1})}^T$, we have:

$$S^{\prime }\left(Z^{*}\right)P=\left[\begin{array}{cc}0& 0\\ I& 0\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\end{array}\right]=\left[\begin{array}{c}0\\ P_1\end{array}\right];$$

therefore, $S^{\prime }\left(Z^{*}\right)$ is an idempotent matrix, and the iterative process (18) is stable. □

4. Approximating the Moore–Penrose Inverse

For a complex matrix that is not necessarily square, the pseudo-inverse can be defined as an object similar to an inverse matrix. Given a complex matrix, it is possible to define many possible pseudo-inverses, but the most-frequent one is the Moore–Penrose inverse.

In cases when a system of equations has no solution, there is no inverse of the matrix of the coefficients that defines the system. In these cases, it may be useful to find a value that is an approximate solution in terms of error minimization, such as being able to find the best fit of a dataset using the pseudo-inverse (Moore–Penrose inverse) of the coefficient matrix. See, for example, the classical texts of Ben-Israel [24] and Higham [14].

We now extend the proposed iterative methods of this manuscript for calculating the Moore–Penrose inverse $A^{†}$ of an $m\times n$ complex matrix A. This is the unique $n\times m$ matrix X that satisfies the following conditions:

$$AXA=A,XAX=X,{\left(AX\right)}^{*}=AX,{\left(XA\right)}^{*}=XA.$$

A computationally simple and accurate way to compute the Moore–Penrose inverse is through the use of the singular-value decomposition of A. Then, if the rank of A is $r\le min(m,n)$, we obtain:

$$A=U\left[\begin{array}{cc}\mathsf{\Sigma }& 0\\ 0& 0\end{array}\right]V^{*}$$

(22)

where $\mathsf{\Sigma }=\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_r)$, ${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_r>0$, with $U\in {\mathbb{C}}^{m\times m}$ and $V\in {\mathbb{C}}^{n\times n}$ a unitary matrix. Furthermore, it is known that:

$$A^{†}=V^{*}\left[\begin{array}{cc}{\mathsf{\Sigma }}^{-1}& 0\\ 0& 0\end{array}\right]U,$$

(23)

where ${\mathsf{\Sigma }}^{-1}=\mathrm{diag}(1/{\sigma }_1,1/{\sigma }_2,\dots ,1/{\sigma }_r)$.

Theorem 9.

Let $A\in {\mathbb{C}}^{m\times n}$ be a matrix with singular-value decomposition satisfying (22) whose $rank\left(A\right)=r$. If $X_{-1}$ and $X_0$ are the initial estimations such that:

$$V^{*}{X}_{-1}U=\left[\begin{array}{cc}{\mathsf{\Sigma }}_{-1}& 0\\ 0& 0\end{array}\right]and{V}^{*}{X}_{0}U=\left[\begin{array}{cc}{\mathsf{\Sigma }}_0& 0\\ 0& 0\end{array}\right],$$

given that ${\mathsf{\Sigma }}_{-1}$ and ${\mathsf{\Sigma }}_0$ are diagonal matrices of size $r\times r$, then the sequences $\left\{X_k\right\}$, generated by Equation (18) using SSM and (8) using MKTM, converge to $A^{†}$ with order of convergence $1+\sqrt{2}$ and $(1+\sqrt{5})/2$, respectively.

Proof. 

Given the singular-value decomposition of A (see (22)), we define the matrix $D_k$:

$$D_k=V^{*}{X}_{k}U=\left[\begin{array}{cc}{\mathsf{\Sigma }}_k& 0\\ 0& 0\end{array}\right],$$

for any fixed arbitrary value of k, with ${\mathsf{\Sigma }}_k\in {\mathbb{C}}^{r\times r}$. Now, by using the iterative expression in Equation (18) and (8), we obtain:

$$\left[\begin{array}{cc}{\mathsf{\Sigma }}_{k+1}& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}{\mathsf{\Sigma }}_{k-1}+(I-{\mathsf{\Sigma }}_{k-1}\mathsf{\Sigma })(2I-{\mathsf{\Sigma }}_k\mathsf{\Sigma }){\mathsf{\Sigma }}_k& 0\\ 0& 0\end{array}\right],$$

and

$$\left[\begin{array}{cc}{\mathsf{\Sigma }}_{k+1}& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}2{\mathsf{\Sigma }}_{k-1}-(2{\mathsf{\Sigma }}_{k-1}-{\mathsf{\Sigma }}_k){\mathsf{\Sigma }}_k\mathsf{\Sigma }& 0\\ 0& 0\end{array}\right],$$

respectively. Because ${\mathsf{\Sigma }}_{-1}$ and ${\mathsf{\Sigma }}_0$ are diagonal matrices, then all matrices ${\mathsf{\Sigma }}_k$ are diagonal as well. Then, the expression ${\mathsf{\Sigma }}_{k+1}={\mathsf{\Sigma }}_{k-1}+(I-{\mathsf{\Sigma }}_{k-1}\mathsf{\Sigma })(2I-{\mathsf{\Sigma }}_k\mathsf{\Sigma }){\mathsf{\Sigma }}_k$ and ${\mathsf{\Sigma }}_{k+1}=2{\mathsf{\Sigma }}_{k-1}-(2{\mathsf{\Sigma }}_{k-1}-{\mathsf{\Sigma }}_k){\mathsf{\Sigma }}_k\mathsf{\Sigma }$ represents r scalar uncoupled iterations converging to $\frac{1}{{\sigma }_i}$, $1\le i\le r$, with order of convergence $1+\sqrt{2}$ using $SSM$ and $(1+\sqrt{5})/2$ using $MKTM$, i.e.,

$$\left|\right|{\mathsf{\Sigma }}_{k+1}-{\mathsf{\Sigma }}^{-1}{\left|\right|}_2^2\le r{M}_k^2\left|\right|{\mathsf{\Sigma }}_k-{\mathsf{\Sigma }}^{-1}{\left|\right|}_2^2,$$

with $M_k=\underset{1\le i<r}{max}\left\{C_k^2\right\}$, $C_k^{-1}>0$, such that $\left\{e_k^i\right\}$ tends to zero if k tends to infinity. Just as was argued in (8), we have that:

$$\left|\right|X_{k+1}-A^{†}{\left|\right|}_2\le \sqrt{r}{M}_k\left|\right|X_k-A^{†}{\left|\right|}_2.$$

Therefore, we can say that $\left\{X_k\right\}$ converges to $A^{†}$, with the desired order of convergence. □

5. Numerical Experiments

In this section, we present the numerical tests of the behavior of the Steffensen method with memory (SMM) and Kurchatov type’s (MKTM) designed to calculate the inverse and the Moore–Penrose inverse applied to different matrices. For comparison, we used the Newton–Schulz method (NS) [14], and the secant method (SM) [13]. The numerical calculations were made with MATLAB 2022a (MathWorks, USA) using a 3 GHz 10-Core Intel Xeon W processor, 64 GB 2666 MHz DDR4 (iMac Pro). As stopping criteria for all numerical tests, we used $\left|\right|X_{k+1}-X_k{\left|\right|}_2<{10}^{-6}$ or $\left|\right|F\left(X_{k+1}\right){\left|\right|}_2<{10}^{-6}$, $F\left(X\right)=0$ being the nonlinear matrix equation to be solved for estimating the inverse or pseudo-inverse of a complex matrix A.

In addition, when verifying the theoretical results numerically, we used the order of approximate computational convergence (COC) introduced by Jay [25], defined as:

$$\mathrm{order}\approx COC=\frac{ln\left(\right|\left|F\left(X_{k+1}\right)\right|{|}_2/\left|\right|F\left(X_k\right)|{|}_2}{ln\left(\right|\left|F\left(X_k\right)\right|{|}_2/\left|\right|F\left(X_{k-1}\right)|{|}_2}.$$

Another form of the numerical approximation of the order of theoretical convergence presented by the authors in [26], denoted as ACOC, is defined as:

$$\mathrm{order}\approx ACOC=\frac{ln\left(\right||X_{k+1}-X_k|{|}_2/\left|\right|X_k-X_{k-1}\left|{|}_2\right)}{ln\left(\right||X_k-X_{k-1}|{|}_2/\left|\right|X_{k-1}-X_{k-2}\left|{|}_2\right)}.$$

To show the order of convergence of the methods in the numerical tests, we used any of these estimates of computational order. In the tables, we write “-” when the COC (or ACOC) vector is unstable. Furthermore, the mean of elapsed time after 50 executions of the codes appears in the tables, calculated by using the CPU-time command.

Example 1.

As a first example, we looked for the inverse random matrices of size $n\times n$, where $n=10,100,200,300,400$, and 500. Since Newton–Schulz’s method needs one initial point, we took it as $X_0=A^T/{\left|\right|A\left|\right|}^2$. The rest of the methods need two initial points, which we took as $X_{-1}=A^T/{\left|\right|A\left|\right|}^2$ and $X_0=0.5X_{-1}$.

Table 1 shows the results obtained by approximating the inverses of nonsingular random matrices of sizes $n=10,100,200,300,400$, and 500 using the Newton–Schulz, secant, Steffensen with memory, and Kurchatov-type methods. The number of iterations, residuals, and the COC value are shown. The results confirmed the theoretical order of convergence obtained from each method. Using all methods, the approximation of the inverse of A was obtained. In all cases, the Steffensen method with memory showed better results in terms of the number of iterations and the computational time. The graphs shown in Figure 2 represent the results presented in Table 1 for the cases of matrices of $n=10,300$, and 500.

Table 1. Results obtained by approximating the inverse of random matrices of different sizes.

Method	n	Iter	$\left|\right|{\mathit{X}}_{\mathit{k}+1}-{\mathit{X}}_{\mathit{k}}{\left|\right|}_2$	$\left|\right|\mathit{F}\left({\mathit{X}}_{\mathit{k}+1}\right){\left|\right|}_2$	COC	E-Time
NS	10	25	$7.5\times {10}^{-3}$	$1.9\times {10}^{-9}$	2.0000	0.0151
SM	10	35	$7.4\times {10}^{-4}$	$2.0\times {10}^{-9}$	1.6180	0.0141
SMM	10	15	$1.2\times {10}^{-1}$	$2.4\times {10}^{-8}$	2.4142	0.0136
MKTM	10	45	$1.8\times {10}^{-3}$	$1.3\times {10}^{-8}$	1.6119	0.0147
NS	100	29	$2.5\times {10}^{-4}$	$1.4\times {10}^{-11}$	2.0000	0.0660
SM	100	40	$1.6\times {10}^{-3}$	$3.8\times {10}^{-8}$	1.6181	0.1043
SMM	100	22	$2.4\times {10}^{-2}$	$5.0\times {10}^{-9}$	2.4142	0.0501
KT	100	53	$5.7\times {10}^{-4}$	$9.2\times {10}^{-9}$	1.6687	0.1293
NS	200	28	$1.6\times {10}^{-4}$	$4.4\times {10}^{-11}$	2.0000	0.2656
SM	200	39	$8.3\times {10}^{-5}$	$1.5\times {10}^{-9}$	1.6180	0.3803
SMM	200	24	$4.5\times {10}^{-2}$	$2.6\times {10}^{-7}$	2.4142	0.1676
MKTM	200	50	$2.6\times {10}^{-3}$	$5.8\times {10}^{-7}$	1.6172	0.5134
NS	300	32	$2.9\times {10}^{-2}$	$1.4\times {10}^{-7}$	2.0000	0.6303
SM	300	45	$7.0\times {10}^{-3}$	$2.9\times {10}^{-7}$	1.6180	0.8967
SMM	300	25	$1.2\times {10}^{-2}$	$5.9\times {10}^{-10}$	2.4142	0.4222
MKTM	300	60	$1.6\times {10}^{-4}$	$9.2\times {10}^{-10}$	1.6193	1.3173
NS	400	33	$8.8\times {10}^{-4}$	$1.6\times {10}^{-10}$	2.0000	0.9306
SM	400	46	$1.5\times {10}^{-3}$	$2.7\times {10}^{-8}$	1.6181	1.6293
SMM	400	25	$1.3\times {10}^{-4}$	$2.5\times {10}^{-7}$	2.4142	0.6986
MKTM	400	61	$2.6\times {10}^{-3}$	$9.5\times {10}^{-8}$	1.6841	2.4109
NS	500	36	$2.5\times {10}^{-2}$	$2.1\times {10}^{-8}$	2.0000	1.8538
SM	500	51	$1.4\times {10}^{-3}$	$5.8\times {10}^{-9}$	1.6180	2.8333
SMM	500	28	$3.0\times {10}^{-2}$	$8.0\times {10}^{-10}$	2.4076	1.1715
MKTM	500	67	$1.1\times {10}^{-2}$	$3.4\times {10}^{-7}$	1.6336	4.1268

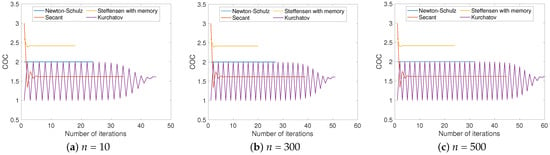
Figure 2. Graphs of the number of iterations vs. COC for three of the cases in Table 1.

Example 2.

Now, we built square matrices of size $n\times n$ using different MATLAB functions, such as:

(a) 

$A=gallery{(}^{\prime }lehme{r}^{\prime },n)$. Symmetric and positive definite matrix of size $n\times n$, $a_{i,j}=i/j,\forall i,j$.

(b) 

$A=gallery{(}^{\prime }rieman{n}^{\prime },n)$. Riemann matrix of size $n\times n$.

(c) 

$A=gallery{(}^{\prime }ri{s}^{\prime },n)$. Hankel matrix of size $n\times n$.

(d) 

$A=gallery{(}^{\prime }grca{r}^{\prime },n)$. Toeplitz matrix of size $n\times n$.

(e) 

$A=gallery{(}^{\prime }lesli{e}^{\prime },n)$. Leslie matrix of size $n\times n$ with application in problems of population models.

(f) 

$A=gallery{(}^{\prime }parte{r}^{\prime },n)$. Parter matrix of size $n\times n$.

Here, we used as stopping criteria $\left|\right|X_{k+1}-X_k{\left|\right|}_2<{10}^{-10}$ or $\left|\right|F\left(X_{k+1}\right){\left|\right|}_2<{10}^{-10}$ and the same initial approximations as in Example 1. The numerical results obtained are shown in Table 2 and Figure 3. As in the previous example, the proposed methods showed a good performance in terms of stability, precision, and number of iterations required.

Table 2. Results obtained by approximating the inverse of classical square matrices of different sizes.

Method	Matrix	n	Iter	$\left|\right|{\mathit{X}}_{\mathit{k}+1}-{\mathit{X}}_{\mathit{k}}{\left|\right|}_2$	$\left|\right|\mathit{F}\left({\mathit{X}}_{\mathit{k}+1}\right){\left|\right|}_2$	COC	E-Time
NS	Lehmer	10	19	$3.5\times {10}^{-7}$	$5.7\times {10}^{-15}$	-	0.0162
SM	Lehmer	10	26	$1.9\times {10}^{-7}$	$1.7\times {10}^{-13}$	1.6177	0.0157
SMM	Lehmer	10	14	$7.6\times {10}^{-4}$	$4.2\times {10}^{-11}$	2.4142	0.0149
MKTM	Lehmer	10	33	$1.6\times {10}^{-7}$	$1.8\times {10}^{-13}$	1.6384	0.0168
NS	Riemann	100	24	$5.0\times {10}^{-8}$	$9.2\times {10}^{-14}$	1.5057	0.0638
SM	Riemann	100	33	$1.5\times {10}^{-7}$	$2.1\times {10}^{-12}$	1.5057	0.0800
SMM	Riemann	100	18	$7.5\times {10}^{-5}$	$4.6\times {10}^{-12}$	2.3949	0.0482
MKTM	Riemann	100	43	$1.8\times {10}^{-8}$	$1.8\times {10}^{-12}$	2.3949	0.1013
NS	Henkel	200	10	$3.7\times {10}^{-9}$	$1.9\times {10}^{-15}$	-	0.0850
SM	Henkel	200	13	$2.0\times {10}^{-9}$	$2.5\times {10}^{-15}$	1.6070	0.1093
SMM	Henkel	200	7	$1.0\times {10}^{-6}$	$9.5\times {10}^{-16}$	2.3550	0.0360
MKTM	Henkel	200	14	$3.4\times {10}^{-8}$	$4.1\times {10}^{-13}$	1.5931	0.0418
NS	Toeplitz	300	10	$2.5\times {10}^{-9}$	$1.1\times {10}^{-15}$	-	0.1672
SM	Toeplitz	300	13	$1.5\times {10}^{-9}$	$4.3\times {10}^{-15}$	1.6165	0.2077
SMM	Toeplitz	300	7	$6.2\times {10}^{-6}$	$2.0\times {10}^{-13}$	2.4143	0.1272
MKTM	Toeplitz	300	15	$2.5\times {10}^{-10}$	$9.7\times {10}^{-16}$	1.5111	0.2319
NS	Leslie	400	23	$4.3\times {10}^{-5}$	$4.7\times {10}^{-12}$	2.0000	0.5788
SM	Leslie	400	32	$5.3\times {10}^{-6}$	$2.3\times {10}^{-11}$	1.6180	0.8384
SMM	Leslie	400	18	$3.4\times {10}^{-6}$	$3.1\times {10}^{-16}$	2.1993	0.4909
MKTM	Leslie	400	42	$5.8\times {10}^{-8}$	$1.1\times {10}^{-13}$	-	1.1811
NS	Parter	500	10	$7.5\times {10}^{-8}$	$3.7\times {10}^{-15}$	1.9969	1.3828
SM	Parter	500	13	$4.8\times {10}^{-8}$	$9.8\times {10}^{-13}$	1.6181	0.4933
SMM	Parter	500	7	$5.1\times {10}^{-5}$	$2.5\times {10}^{-11}$	2.4144	0.2832
MKTM	Parter	500	15	$3.4\times {10}^{-8}$	$8.3\times {10}^{-13}$	1.6433	0.5984

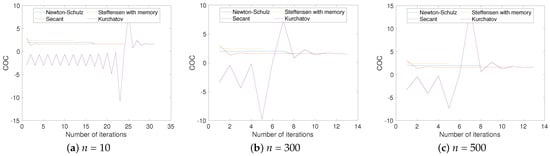
Figure 3. Graphs of the number of iterations vs. COC for three of the sizes in Table 2.

Example 3.

Finally, we tested the methods for computing the Moore–Penrose inverse of $m\times n$ random matrices for different values of m and n. The matrices of the initial approximations were calculated in the same way as in the previous examples, and the stopping criterion was the one used in Example 1.

The results obtained for the number of iterations, the residuals, and the ACOC value of Example 3 are shown in Table 3 and Figure 4. The methods gave us an approximation of the inverse Moore–Penrose and showed the same behavior as in the previous examples.

Table 3. Results obtained to approximate the Moore–Penrose inverse of a rectangular random matrix.

Method	m	n	Iter	$\left|\right|{\mathit{X}}_{\mathit{k}+1}-{\mathit{X}}_{\mathit{k}}{\left|\right|}_2$	ACOC	E-Time
NS	20	10	11	$1.2\times {10}^{-7}$	2.0086	0.0162
SM	20	10	17	$9.5\times {10}^{-9}$	1.6220	0.0152
SMM	20	10	10	$1.6\times {10}^{-10}$	2.4159	0.0158
MKTM	20	10	20	$3.2\times {10}^{-7}$	1.7104	0.0221
NS	200	100	16	$1.1\times {10}^{-8}$	2.0049	0.0916
SM	200	100	24	$4.2\times {10}^{-9}$	1.6217	0.1406
SMM	200	100	14	$1.3\times {10}^{-12}$	2.4147	0.0766
MKTM	200	100	30	$1.7\times {10}^{-8}$	1.7264	0.1773
NS	300	400	19	$3.1\times {10}^{-4}$	2.1197	0.3610
SM	300	400	29	$8.6\times {10}^{-6}$	1.6446	0.5411
SMM	300	400	16	$1.7\times {10}^{-4}$	2.5496	0.3397
MKTM	300	400	37	$7.6\times {10}^{-5}$	1.4546	0.7319
NS	500	600	21	$3.8\times {10}^{-4}$	2.1114	1.0525
SM	500	600	32	$3.9\times {10}^{-6}$	1.6380	1.7327
SMM	500	600	18	$2.7\times {10}^{-6}$	2.4445	0.8430
MKTM	500	600	41	$7.0\times {10}^{-5}$	1.4333	2.3384
NS	1000	900	25	$7.2\times {10}^{-13}$	2.0001	4.6221
SM	1000	900	36	$1.1\times {10}^{-8}$	1.6217	6.8167
SMM	1000	900	20	$1.2\times {10}^{-7}$	2.4249	3.2718
MKTM	1000	900	47	$3.6\times {10}^{-7}$	-	9.5099

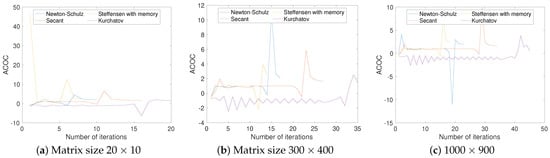
Figure 4. Graphs of the number of iterations vs. ACOC for three of the sizes in Table 3.

6. Conclusions

In this manuscript, we widened the set of iterative methods able to be applied for estimating generalized inverses of complex matrices, by using schemes with memory able to improve the Newton–Schulz scheme. Two procedures with memory were designed for approximating the inverses of nonsingular complex matrices or pseudo-inverses, in the case that the matrices are singular. The order of convergence and stability were proven, and in the case of the Steffensen with memory scheme, its order of convergence improved that of the Newton–Schulz method.

The method using Kurchatov’s divided differences cannot be directly adapted to estimate generalized inverses of complex matrices. To overcome this difficulty, Kurchatov-type divided differences were used. In this process, there was a decrease in the order of convergence of the starting method and a change in its behavior.

The technique used to adapt the iterative methods can be applied to the resolution of other types of matrix equations with an especially significant role in various areas such as control theory, dynamic programming, ladder networks, statistics, etc.

This research opens new ways in the design of iterative procedures for solving this kind of nonlinear matrix equation, with promising numerical performance, which showed agreement with theoretical results and stable results.