Bifurcation of an SIRS Model with a Modified Nonlinear Incidence Rate

Abstract

An SIRS epidemic model with a modified nonlinear incidence rate is studied, which describes that the infectivity is strong at first as the emergence of a new disease or the reemergence of an old disease, but then the psychological effect will weaken the infectivity. Lastly, the infectivity goes to a saturation state as a result of a crowding effect. The nonlinearity of the functional form of the incidence of infection is modified, which is more reasonable biologically. We analyze the stability of the associated equilibria, and the basic reproduction number and the critical value which determine the dynamics of the model are derived. The bifurcation analysis is presented, including backward bifurcation, saddle-node bifurcation, Bogdanov–Takens bifurcation of codimension two and Hopf bifurcation. To study Hopf bifurcation of codimension three of the model when some assumptions hold, the focus values are calculated. Numerical simulations are shown to verify our results.

1. Introduction

In epidemiology modeling, there are several factors that substantially affect the dynamical behavior of the models. Therein, the incidence rate is very crucial for describing the spreading of disease; in general, some nonlinear incidence rates play key roles in producing the rich dynamics, including bistability (backward bifurcation) and periodicity [1,2,3,4,5]. The general incidence rate $k{I}^{p}S/(1+\alpha I^q)$$(q=p-1)$ was investigated by Liu et al. [6,7]. Hethcote and van den Driessche [8] considered the case $p\ge q$. Tang et al. [9] and Hu et al. [10] proposed that the incidence function $k{I}^p/(1+\alpha I^q)$ with respect to I, which measures the infection force of a disease, includes three cases: (I) if $p<q$, it is unbounded; (II) if $p=q$, it is saturated; (III) if $p<q$, it is nonmonotone. the first case may be true in the early process of the disease or the number of the infective individuals $I\left(t\right)$ is small, but will become unrealistic when $I\left(t\right)$ is getting larger.

In the second scenario, considering the inhibitory effect from the behavioral change of the susceptible individuals when the number of infective individuals increases, Ruan and Wang [4] studied a model with a saturated nonlinear incidence rate $k{I}^{2}S/(1+\alpha I^2)$, where $k{I}^2$ measures the infection force of the disease and $1/(1+\alpha I^2)$ describes the inhibitory effect, and they investigated the global dynamics of the model. The incidence function $k{I}^2/(1+\alpha I^2)$ monotonously and eventually goes to a saturation level $\frac{k}{\alpha }$ as I becomes larger. However, when a new infectious disease emerges which people know little about and to which they are caught off guard, the infection force of the disease increases rapidly until the disease attracts people’s attention, and they will change their behaviors, such as giving up risky behavior or taking precautionary measures to reduce the transmission, and then, the infection force will decrease. This is the psychological effect. The outbreak of 2019 novel coronavirus diseases (COVID-19) in Wuhan, Hubei Province, China, showed such psychological effects on the general public, including aggressive measures and policies, such as rapid isolation of suspected cases, confirmed cases, and contacts; restrictions on mobility; travel restrictions; keeping distance from others; mask-wearing; etc., was clearly successful in mitigating spread and reducing the local transmission of COVID-19 in China [11,12,13]. Similarly, in the epidemic outbreak of severe acute respiratory syndrome (SARS) in 2003 [14], these measures, including border screening, mask-wearing [15], quarantine [16], isolation, etc., proved to be effective in reducing the spread of SARS. Obviously, the monotone incidence rates may not be used to describe the psychological effect perfectly. Xiao and Ruan [17] proposed an epidemic model with incidence $kIS/(1+\alpha I^2)$ to model the effect and carried out a global analysis of the model and showed that either the number of infective individuals tends to zero as time evolves or the disease persists. The dynamics of this model was relatively simple.

Xiao and Zhou [18] and Zhou et al. [19] studied an epidemic model with the nonmonotonic incidence rate of saturated mass action $kIS/(1+\beta I+\alpha I^2)$, and Xiao and Zhou carried out a global analysis and showed the existence of bistability and periodicity. Zhou et al. presented the bifurcation analysis of the model, such as Hopf bifurcation and Bogdanov–Takens bifurcation. Both nonmonotonic and saturated incidence functions $kI/(1+\alpha I^2)$ and $kI/(1+\beta I+\alpha I^2)$ approach zero when I tends to infinite, which implies that the psychological or inhibitory effect is so strong that the disease incidence becomes zero, which may be unreasonable for some diseases, such as influenza. Considering a more reasonable incidence function which goes up at first at the onset of a disease, then goes down because of the psychological effect, and goes to a saturation level at length due to the crowding effect, Lu et al. [20] proposed a generalized nonmonotone and saturated incidence rate $k{I}^{2}S/(1+\beta I+\alpha I^2)$, where parameter $\beta >-2\sqrt{\alpha }$ to make $1+\beta I+\alpha I^2>0$ hold for all $I\ge 0$, and when $\beta \ge 0$, the incidence function $k{I}^2/(1+\beta I+\alpha I^2)$ increases monotonously to a saturated level $\frac{k}{\alpha }$ as I goes to infinite. When $-2\sqrt{\alpha }<\beta <0$, $k{I}^2/(1+\beta I+\alpha I^2)$ is nonmonntonic, which grows at first and then descends to a saturated level $\frac{k}{\alpha }$ as $I\to \infty$. They studied the following model with this incidence rate and found that the model showed rich dynamical behaviors, including saddle-node bifurcation, Bogdanov–Takens bifurcation of codimension two, and degenerate Hopf bifurcation of codimension two.

$$\left\{\begin{array}{c}\frac{dS}{dt}=b-dS-\frac{k{I}^2}{1+\beta I+\alpha I^2}S+\nu R,\hfill \\ \frac{dI}{dt}=\frac{k{I}^2}{1+\beta I+\alpha I^2}S-(d+\gamma )I,\hfill \\ \frac{dR}{dt}=\gamma I-(d+\nu )R.\hfill \end{array}\right.$$

(1)

where S represents susceptible compartment, I represents infective compartment, and R represents recovered compartment. All parameters except $\beta$ are positive in the model. Here, b is the natural birth rate, d is the natural death rate, $\mu$ is the recovery rate, k is the infection rate, and $\alpha$ describes the psychological effect. Recovered individuals lose immunity and move into susceptible compartment S at rate $\nu$.

The basic reproduction number $R_0$ is the single most important parameter in epidemic modeling, which measures the average number of secondary infections caused by a single infectious individual in an entirely susceptible population during the mean infectious period [21]. The incidence rate $k{I}^{2}S/(1+\beta I+\alpha I^2)$, with combination of monotonicity, nonmonotonicity, and saturation properties, seems reasonable to describe the transmission process of some specific infectious diseases. In fact, the basic reproduction number of model (1) with the incidence rate is zero, but they proved that the disease still persisted for some parameters and initial conditions, which seems unreasonable. Moreover, the parameter $\beta$ can take a negative value and does not have a realistic biological meaning, and it may seem be farfetched to endow the incidence rate with the combination of monotonicity, nonmonotonicity, and saturation properties. Hence, by the above analysis, we propose a more reasonable incidence rate:

$$f\left(I\right)S=\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}S,$$

where the incidence function $f\left(I\right)=\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}$ reserves the combination of monotonicity, nonmonotonicity, and saturation properties, i.e., when $k_1=0$, $f\left(I\right)$ increases monotonously to a saturated level $\frac{k_2}{\alpha }$ as I goes to infinite; when $k_1>0$, $f\left(I\right)$ is nonmonntonic, which increases at first and then decreases to a saturated level $\frac{k_2}{\alpha }$ as I tends to infinite (see Figure 1). Moreover, the basic reproduction number and all parameters have biological meaning with reasonable explanation. Moreover, this incidence rate enriches the model with more rich dynamical behaviors. In fact, in 2000, an epidemic model with the incidence rate $(k_{1}I+k_2{I}^2)S$ was proposed by P. van den Driessche et al. [2], considering the contact rate may depend on the fraction of infective individuals or on the severity of infection in the infected individual, and Li et al., 2007 [22] and Li et al., 2014 [23] presented that the model showed very rich dynamical behaviors, including backward bifurcation, the Hopf bifurcation and Bogdanov–Takens bifurcation, and canard phenomenon, respectively.

Figure 1. The incidence function $f\left(I\right)=\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}$ for $k_1=0$, $k_1=1$ and $k_1=2$.

This paper focuses on the detailed dynamics analysis of the following SIRS (Susceptible-Infected-Recovered-Susceptible) epidemic model:

$$\left\{\begin{array}{c}\frac{dS}{dt}=b-dS-\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}S+\nu R,\hfill \\ \frac{dI}{dt}=\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}S-(d+\gamma )I,\hfill \\ \frac{dR}{dt}=\gamma I-(d+\nu )R.\hfill \end{array}\right.$$

(2)

where the biological meaning of the parameters are the same as model (1), $(k_{1}I+k_2{I}^2)S$ measures linear and nonlinear hazards of infection, and $\frac{1}{1+\alpha I^2}$ describes the psychological effect. The basic reproduction number $R_0$ of the model is $\frac{b{k}_1}{d(d+\gamma )}$, and we will perform a qualitative dynamics analysis for model (2); it is shown that there may be two endemic equilibria, which gives rise to the phenomenon of bistability (backward bifurcation) when parameters are lying in some region. We will investigate the local stability of these equilibria, classify the types of the equilibria, and discuss different kinds of bifurcation phenomena. A saddle-node bifurcation will be investigated for different perturbation parameters. Next, we will prove that the model can undergo Bogdanov–Takens bifurcation of, at most, codimension two, and the model with some specific parameters values can bifurcate at least three limit cycles through Hopf bifurcation of codimension three. Numerical simulations for these bifurcation phenomena will be presented to illustrate our theoretical results.

The organization of this paper is as follows. Existence and types of equilibria are presented in Section 2 by reducing the model to a two-dimensional system. In Section 3, we study the backward bifurcation, saddle-node bifurcation, and Bogdanov–Takens bifurcation of codimension two; Hopf bifurcation of codimension two; and Hopf bifurcation of codimension three. This paper ends with a brief conclusion and discussion of the results in Section 4.

2. Existence and Types of Equilibria

Note that the equation for the total population N is given by $\frac{dN}{dt}=b-dN,$ where $N=S+I+R$. Since $N\to N_0=\frac{b}{d}$ as $t\to \infty$, it is clear that:

$$\Omega =\left\{(S,I,R):S,I,R\ge 0,S+I+R=N_0\right\}$$

is a positively invariant region for model (2). Hence, our study on the dynamics of model (2) is focused on the region $\Omega$. Substituting $N_0-I-R$ for S in model (2), we can obtain the following reduced model by eliminating S from the equations:

$$\left\{\begin{array}{c}\frac{dI}{dt}=\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}(N_0-I-R)-(d+\gamma )I,\hfill \\ \frac{dR}{dt}=\gamma I-(d+\nu )R.\hfill \end{array}\right.$$

(3)

Rescale model (3) by using $x=\sqrt{\frac{k_2}{d+\nu }}I, y=\sqrt{\frac{k_2}{d+\nu }}R, \theta =(d+\nu )t,$ and let $\beta =\frac{k_1}{\sqrt{k_2(d+\nu )}},$ $p=\frac{d+\nu }{k_2}\alpha ,$ $m=\frac{d+\gamma }{d+\nu }, \Lambda =\sqrt{\frac{k_2}{d+\nu }}{N}_0, q=\frac{\gamma }{d+\nu }.$ For simplicity, we still denote $\theta$ by t and obtain:

$$\left\{\begin{array}{c}\frac{dx}{dt}=\frac{x^2+\beta x}{1+p{x}^2}(\Lambda -x-y)-mx,\hfill \\ \frac{dy}{dt}=qx-y.\hfill \end{array}\right.$$

(4)

It is evident that:

$$\beta \ge 0,\Lambda ,m,p,q>0,m>q,$$

(5)

and the positively invariant region of model (4) is:

$$D=\left\{\right(x,y\left)\right|x\ge 0,y\ge 0,x+y\le \Lambda \}.$$

By using the next generation matrix [24], we derive the basic reproduction number $R_0=\frac{\beta \Lambda }{m}.$ Model (3) always has a equilibrium $E_0(0,0)$. To find other equilibria of the model, we set:

$$\frac{x^2+\beta x}{1+p{x}^2}(\Lambda -x-y)-mx=0,qx-y=0,$$

(6)

and obtain:

$$(mp+q+1)x^2+(\beta q+\beta -\Lambda )x+m-\beta \Lambda =0,$$

(7)

The discriminant of (7) is:

$$\Delta ={(\Lambda -\beta -\beta q)}^2-4(m-\beta \Lambda )(mp+q+1).$$

From (6) and (7), there are at the utmost two endemic equilibria $E_1(x_1,y_1)$ and $E_2(x_2,y_2)$ in model (4), and they can merge into a unique endemic equilibrium $E_{*}(x_{*},y_{*})$, where:

$$\begin{array}{cc}\hfill & x_1=\frac{\Lambda -\beta (1+q)-\sqrt{\Delta }}{2(1+q+mp)},y_1=q{x}_1,\hfill \\ & x_2=\frac{\Lambda -\beta (1+q)+\sqrt{\Delta }}{2(1+q+mp)},y_2=q{x}_2,\hfill \\ \hfill & x_{*}=\frac{\Lambda -\beta (1+q)}{2(1+q+mp)},y_{*}=q{x}_{*}.\hfill \end{array}$$

and:

$$x_1+x_2=\frac{\Lambda -\beta (1+q)}{1+q+mp},x_1{x}_2=\frac{m-\beta \Lambda }{1+q+mp}.$$

From $\Delta =0$, we derive $p=\frac{{(\Lambda -\beta -\beta q)}^2-4(1+q)(m-\beta \Lambda )}{4m(m-\beta \Lambda )}$. Let:

$$p_{*}=\frac{{(\Lambda -\beta -\beta q)}^2-4(1+q)(m-\beta \Lambda )}{4m(m-\beta \Lambda )}$$

(8)

and $p_{*}>0$, i.e.,

$$\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda .$$

(9)

Therefore, the following theorem is derived.

Lemma 1. 

Under the condition of (5), for model (4), the equilibrium $E_0(0,0)$ always exists. Moreover,

(I) Model (4) has no endemic equilibria if and only if one of the following conditions holds:

(I.1) $m\ge \beta \Lambda$ and $\Lambda \le \beta +\beta q$,

(I.2) $\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q$ and $p>p_{*}$,

(I.3) $m\ge \frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$ and $\Lambda >\beta +\beta q$.

(II) There exists a unique endemic equilibrium $E_{*}(x_{*},y_{*})$ if and only if $\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q$ and $p=p_{*}$.

(III) There exists a unique endemic equilibrium $E_2(x_2,y_2)$ if and only if one of the following conditions holds:

(III.1) $m=\beta \Lambda$ and $\Lambda >\beta +\beta q$,

(III.2) $m<\beta \Lambda$.

(IV) There exist two endemic equilibria $E_1(x_1,y_1)$ and $E_2(x_2,y_2)$ if and only if:

$\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q$ and $p<p_{*}$, where $0<x_1<x_{*}<x_2$.

We denote a critical value $1-\frac{{(\Lambda -\beta -\beta q)}^2}{4m(mp+q+1)}$ by $R_c$, and $0<R_c<1$. Moreover, $R_c>0$ is equivalent to $p>p_0$, where $p_0=\frac{{(\Lambda -\beta -\beta q)}^2-4m(q+1)}{4m^2}.$ Note that $p>p_0$, i.e., $k_1>k_1^{*}$, where

$$k_1^{*}=\frac{k_{2}b\left(d+v\right)}{d\left(\gamma +d+v\right)}-2\frac{\sqrt{\left(d+\nu \right)\left(d+\gamma \right)\left(\gamma +d+\nu \right)k_2+\alpha {\left(d+\nu \right)}^2{\left(d+\gamma \right)}^2}}{\gamma +d+\nu }.$$

Then, $\Delta =0$ (i.e., $p=p_{*}$) is equivalent to $R_0=R_c$. Hence, Lemma 1 can be written as the following result,

Theorem 1. 

For model (4), there always exists a disease-free equilibrium $E_0$ with the conditions in (5) hold. Moreover,

(1) If $R_0<1$ and

(1.1) $\Lambda \le \beta q+\beta$, there are no endemic equilibria;

(1.2) $\Lambda >\beta q+\beta$, there exist two endemic equilibria $E_1$ and $E_2$ for $R_0>R_c$ and when $p>p_0$ these two equilibria coalesce into $E_{*}$ for $R_0=R_c$.

(2) If $R_0=1$,

(2.1) $\Lambda \le \beta q+\beta$, there are no endemic equilibria;

(2.2) $\Lambda >\beta q+\beta$, there exists a unique endemic equilibrium $E_2$;

(3) If $R_0>1$, there exists a unique endemic equilibrium $E_2$.

Now, let us study the types of these equilibria of model (4),

Theorem 2. 

For model (4), the equilibrium $E_0(0,0)$ is:

$R_0<1$: an attracting node;

$R_0>1$: a hyperbolic saddle;

$R_0=1$ and

•$\Lambda >\beta +\beta q$: a saddle-node of codimension 1;

•$\Lambda <\beta +\beta q$: a saddle-node of codimension 1;

•$\Lambda =\beta +\beta q$: a repelling semi-hyperbolic node of codimension 2.

Proof. 

For model (4), $-1$, and $m(R_0-1)$ are two eigenvalues of Jacobian at $E_0$. If $R_0<1$, $E_0$ is an attracting node. If $R_0>1$, $E_0$ is a hyperbolic saddle. If $R_0=1$, the second eigenvalue is zero. To determine the type of $E_0$, we linearize model (4) at $E_0$ and diagonalize the linear part, and on the center manifold, we have:

$$\begin{array}{cc}\frac{dX}{dt}=\hfill & \left(\Lambda -\beta q-\beta \right)X^2+\left(\Lambda \beta p+1+q-\beta \left(\beta q-\Lambda +\beta \right)q\right)X^3\hfill \\ & +\left(\beta q-\Lambda +\beta \right)q{X}^4+O\left(X^5\right).\hfill \end{array}$$

(10)

Hence, $E_0$ is a saddle-node of codimension one when $\Lambda \ne \beta +\beta q$ [25].

If $R_0=1$ and $\Lambda =\beta +\beta q$, model (10) becomes:

$$\frac{dX}{dt}=\left(1+\left(\beta q+\beta \right)\beta p+q\right)X^3+O\left(X^5\right).$$

(11)

Therefore, $E_0$ is a semi-hyperbolic repelling node. □

Theorem 3. 

For model (4), the disease-free equilibrium $E_0$ is globally asymptotical stable if (I.1), or (I.2), or (I.3) of Lemma 1 (i.e., (1.1) or (2.1) of Theorem 1) holds.

Proof. 

Note that $x=0$ is an invariant line and D is positively invariant; by index theory [26], we can conclude that there are no nontrivial periodic orbits in ${\mathbb{R}}_{+}^2$ when model (4) has no endemic equilibria. □

Remark 1. 

According to Theorem 1 and model (3), note that $\Lambda \le \beta q+\beta$ is equivalent to $k_1\ge k_{10}$, where $k_{10}=\frac{k_{2}b\left(d+v\right)}{d\left(\gamma +d+v\right)},$ which implies that when $\frac{k_1}{k_2}$, which measures the proportion of the linear over nonlinear hazards of infection, is larger than or equal to $\frac{b\left(d+v\right)}{d\left(\gamma +d+v\right)}$, and $R_0\le 1$, i.e., on average, an infected individual produces less than or equal to one new infected individual over the course of its infectious period, the infection cannot grow, that is, the disease cannot invade the population.

3. Bifurcation Analysis

3.1. Backward Bifurcation and Saddle-Node Bifurcation

From Theorem 3, we know that $E_0$ is globally asymptotically stable when model (4) has no endemic equilibria. Next, we will discuss the bifurcation of model (4) with endemic equilibria.

Theorem 4. 

For model (4), we choose $R_0$ as the bifurcation parameter.

(1) When $R_0=1$, model (4) undergoes forward bifurcation if $\Lambda <\beta q+\beta$; model (4) undergoes backward bifurcation if $\Lambda >\beta q+\beta$; model (4) undergoes pitchfork bifurcation if $\Lambda =\beta q+\beta$.

(2) When $p>p_0$, model (4) undergoes saddle-node bifurcation when $R_0$ passes through $R_c$ if $q\ne q_{*}$. When $R_0=R_c$, $E_0$ is a saddle-node if $q\ne q_{*}$, and $E_{*}$ is a cusp if $q=q_{*}$.

Proof. 

For the first statement (1), since $R_0$ can be seen as the function of the parameters $\beta$, $\Lambda$, and m, without loss of generality, we can choose m as the bifurcation parameter. Let $m=\beta \Lambda +\epsilon$, and plug m into model (4), where $\epsilon =0$ corresponds to $R_0=1$. We linearize model (4) at $E_0$ and diagonalize the linear part. One can obtain the following reduced model on the center manifold by applying the center manifold theorem with the parameter $\epsilon$.

$$\frac{dX}{dt}=-\epsilon X-\left(\frac{\left(\Lambda -\beta \right)\epsilon }{q}+\frac{\beta q-\Lambda +\beta }{q}\right)X^2+O\left(X^3\right).$$

(12)

Denoting the right side of model (12) as $F(X,\epsilon )$, we can derive:

$$\begin{array}{cc}\hfill & F(0,0)=0,\frac{\partial F}{\partial X}(0,0)=0,\frac{\partial F}{\partial \epsilon }(0,0)=0,\hfill \\ \hfill & \frac{{\partial }^{2}F}{\partial X\partial \epsilon }(0,0)=-1,\frac{{\partial }^{2}F}{{\partial }^{2}X}(0,0)=2\frac{\Lambda -\beta q-\beta }{q}.\hfill \end{array}$$

Therefore, model (12) undergoes a transcritical bifurcation if $\Lambda \ne \beta q+\beta$ [27].

Since $\frac{\partial R_0}{\partial \epsilon }{|}_{\epsilon =0}=-\frac{1}{\beta \Lambda }<0$, when $R_0$ crosses $R_0=1$, model (4) undergoes forward and backward bifurcation if $\Lambda <\beta q+\beta$ and $\Lambda >\beta q+\beta$, respectively.

If $\Lambda =\beta q+\beta$, model (12) on the center manifold becomes:

$$\begin{array}{cc}\hfill \frac{dX}{dt}& =-\epsilon X-\beta \epsilon X^2-\frac{1}{q^2}\left[\left({\beta }^{2}pq+{\beta }^{2}p+1\right){\epsilon }^2-\left(2{\beta }^{2}pq+2{\beta }^{2}p+q+2\right)\epsilon \right.\hfill \\ \hfill & \left.+{\beta }^{2}pq+{\beta }^{2}p+q+1\right]X^3+O\left(X^4\right).\hfill \end{array}$$

(13)

For simplicity, we still denote the right side of model (13) as $F(X,\epsilon )$, and derive:

$$\begin{array}{cc}\hfill & F(0,0)=0,\frac{\partial F}{\partial X}(0,0)=0,\frac{\partial F}{\partial \epsilon }(0,0)=0,\frac{{\partial }^{2}F}{\partial X\partial \epsilon }(0,0)=-1,\hfill \\ \hfill & \frac{{\partial }^{2}F}{{\partial }^{2}X}(0,0)=0,\frac{{\partial }^{3}F}{{\partial }^{3}X}(0,0)=-\frac{\left(q+1\right)\left({\beta }^{2}p+1\right)}{q^2}<0.\hfill \end{array}$$

Therefore, model (13) undergoes pitchfork bifurcation if $\Lambda =\beta q+\beta$ [27].

For $\epsilon =0$, model (12) and model (13) become model (10) and model (11), respectively.

The second statement (2) will be discussed in detail in the following part. □

Now, we study the dynamics of model (4) near the positive equilibria. The positive equilibria with coordinates $(x,y)$ satisfy:

$$(x+\beta )(\Lambda -x-y)-m(1+p{x}^2)=0,y=qx,$$

and the Jacobian matrix of model (4) at the equilibrium $E(x,y)$ is:

$$J\left(E\right)=\left[\begin{array}{cc}\frac{\left(\beta +2x\right)\left(-qx+\Lambda -x\right)}{p{x}^2+1}-\frac{\beta x+x^2}{p{x}^2+1}-\frac{2mp{x}^2}{p{x}^2+1}-m& -\frac{\beta x+x^2}{p{x}^2+1}\\ q& -1\end{array}\right].$$

Then, the determinant of $J\left(E\right)$ is:

$$det\left(J\left(E\right)\right)=\frac{\left(3mp+3q+3\right)x^2+\left(2\beta q-2\Lambda +2\beta \right)x-\beta \Lambda +m}{p{x}^2+1},$$

and its sign is determined by:

$$S_D=\left(3mp+3q+3\right)x^2+\left(2\beta q-2\Lambda +2\beta \right)x-\beta \Lambda +m.$$

(14)

Similarly, we obtain the trace of $J\left(E\right)$:

$$tr\left(J\left(E\right)\right)=\frac{\left(-3mp-p-2q-3\right)x^2+\left(2\Lambda -\beta q-2\beta \right)x+\beta \Lambda -m-1}{p{x}^2+1},$$

and its sign is determined by:

$$S_T=\left(-3mp-p-2q-3\right)x^2+\left(-\beta q+2\Lambda -2\beta \right)x+\beta \Lambda -m-1.$$

(15)

Set:

$$\begin{array}{cc}\hfill & A_1=\Lambda -\beta q-\beta ,A_2=(q+1)(\Lambda \beta -2m)+{\Lambda }^2,A_3={\beta }^{2}q+\Lambda \beta +{\beta }^2-2m,\hfill \\ & C_1={\Lambda }^2+\Lambda \beta -2m,C_2=\Lambda \beta +{\beta }^2-2m-2,\hfill \\ \hfill & C_3=(\Lambda -\beta )(2\Lambda \beta m+\Lambda \beta -2m^2)+2\Lambda ,C_4=\Lambda m-\beta m+\Lambda ,\hfill \\ \hfill & C_5=2m^2+2m-2\Lambda \beta m-\Lambda \beta ,q_{*}=\frac{C_1}{C_5},q_{**}=\frac{C_1}{2m-\Lambda \beta }.\hfill \end{array}$$

Note that $C_1>0$ if $m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$; $C_2<0$ if $m>\beta \Lambda$ and $\Lambda >\beta +\beta q$; $C_4>0$ if $\Lambda >\beta +\beta q$; $C_5>0$ if $m>\beta \Lambda$. Then, there is the following theorem.

Theorem 5. 

For model (4), when $\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q$, $p=p_{*}$ and conditions in (5) hold, there is a unique positive equilibrium $E_{*}(x_{*},y_{*})$. Moreover,

(I) if $q\ne q_{*}$, then $E_{*}(x_{*},y_{*})$ is a saddle-node, which is attracting (or repelling) if $q<q_{*}$ or $q>q_{**}$ (or $q_{*}<q<q_{**}$);

(II) if $q=q_{*}$, then $E_{*}(x_{*},y_{*})$ is a cusp of codimension two.

Proof. 

We plug $x=x_{*}$ and $p=p_{*}$ into $S_D$ and $S_T$, and then obtain $S_D\left(x_{*}\right)=0$ and:

$$S_T\left(x_{*}\right)=\frac{\left(2m^2+2m-2\Lambda \beta m-\Lambda \beta \right)q-{\Lambda }^2-\Lambda \beta +2m}{\left(\Lambda \beta -2m\right)q+{\Lambda }^2+\Lambda \beta -2m}.$$

Since $m>\beta \Lambda$, $C_5>0$ and $q_{*}<q_{**}$. Hence, $S_T\left(x_{*}\right)>0$ if and only if $q_{*}<q<q_{**}$. Conversely, if $q<q_{*}$ or $q>q_{**}$, $S_T\left(x_{*}\right)<0$.

Letting $X=x-x_{*}$, $Y=y-y_{*}$, $p=p_{*}$ and expanding the right-hand sides of model (4) as a Taylor series gives (X, Y are rewritten as x, y, respectively):

$$\left\{\begin{array}{cc}\hfill \frac{dx}{dt}& =-a_{11}qx+a_{11}y+a_{12}{x}^2+a_{13}xy,\hfill \\ \hfill \frac{dy}{dt}& =qx-y,\hfill \end{array}\right.$$

(16)

where:

$$\begin{array}{cc}\hfill & a_{11}=\frac{2m\left(\Lambda \beta -m\right)}{\left(q+1\right)\left(\Lambda \beta -2m\right)+{\Lambda }^2},a_{13}=-\frac{m\Lambda A_1^2}{A_2^2},\hfill \\ \hfill & a_{12}=\frac{m{A}_1^2\left(2\left({\left(q+1\right)}^2\beta -\left(3q+1\right)\Lambda \right)m+\left(q^2-1\right)\Lambda {\beta }^2+2{\Lambda }^2\beta q+{\Lambda }^3\right)}{2A_2^2{A}_3}.\hfill \end{array}$$

Letting $X=\frac{qx+a_{11}qy}{a_{11}q+1}$, $Y=\frac{-qx+y}{a_{11}q+1}$, we convert model (16) to (X, Y are rewritten as x, y, respectively):

$$\left\{\begin{array}{cc}\hfill \frac{dx}{dt}=& b_{11}{x}^2+b_{12}xy+b_{13}{y}^2,\hfill \\ \hfill \frac{dy}{dt}=& -b_{20}y+b_{21}{x}^2+b_{22}xy+b_{23}{y}^2,\hfill \end{array}\right.$$

(17)

where:

$$\begin{array}{cc}\hfill b_{11}=& \frac{A_1^{3}m}{2q{A}_3{A}_2{b}_{20}},b_{12}=-\frac{m{A}_1^2{b}_{01}}{A_2^2{A}_3{b}_{20}},b_{13}=\frac{qm{A}_1^2{a}_{11}{b}_{02}}{2A_2^2{A}_3{b}_{20}},\hfill \\ \hfill b_{20}=& a_{11}q+1,b_{21}=-\frac{A_1^{3}m}{2q{A}_3{A}_2{b}_{20}},b_{22}=\frac{m{A}_1^2{b}_{01}}{A_2^2{A}_3{b}_{20}},b_{23}=-\frac{qm{A}_1^2{a}_{11}{b}_{02}}{2A_2^2{A}_3{b}_{20}},\hfill \\ \hfill b_{01}=& \left(q+1\right)\left(1-a_{11}\right)\Lambda {\beta }^2+\left(\left({\Lambda }^{2}q+2m{\left(q+1\right)}^2\right)a_{11}+{\Lambda }^2\right)\beta \hfill \\ & +\left({\Lambda }^3-2m\left(2q+1\right)\Lambda \right)a_{11}-2\Lambda m,\hfill \\ \hfill b_{02}=& \left(2{\Lambda }^2\beta q+{\Lambda }^3+\left({\beta }^2{q}^2-{\beta }^2-6mq-2m\right)\Lambda +2\beta m{\left(q+1\right)}^2\right)a_{11}\hfill \\ & +2{\Lambda }^2\beta +\left(2{\beta }^{2}q+2{\beta }^2-4m\right)\Lambda .\hfill \end{array}$$

On the center manifold, we have:

$$\frac{dx}{dt}=c_{11}{x}^2+O\left(x^3\right),$$

where:

$$c_{11}=-\frac{m{A}_1^3}{2q{C}_5\left(q-q_{*}\right)A_3}.$$

Note that $A_3<0$ when $m>\beta \Lambda$, and then, $c_{11}\ne 0.$ Hence, according to Theorems 7.1–7.3 in Zhang et al. [28], $E_{*}$ is a saddle-node of codimension one. Then, we obtain the conclusion in (I).

For the second conclusion in (II), substituting $q=q_{*}$ into (16), we obtain:

$$\left\{\begin{array}{cc}\hfill \frac{dx}{dt}=& x-\frac{1}{d_{10}}y-d_{11}xy+d_{12}{x}^2,\hfill \\ \hfill \frac{dy}{dt}=& d_{10}x-y,\hfill \end{array}\right.$$

(18)

where:

$$\begin{array}{cc}\hfill d_{11}=& \frac{\Lambda C_4^2}{m{C}_1^2},d_{12}=\frac{\left(m(\beta -\Lambda )(\Lambda \beta -m)+\Lambda ({\beta }^2-m-2)\right)C_4^2}{m{C}_2{C}_1{C}_5},d_{10}=\frac{C_1}{C_5}.\hfill \end{array}$$

Next, let $X=d_{10}(1-d_{10})x+d_{10}y$, $Y=d_{10}x-y$. We transform model (18) into (X, Y are rewritten as x, y, respectively):

$$\left\{\begin{array}{cc}\hfill \frac{dx}{dt}& =y+a_1{x}^2+{o\left(\right|(x,y)|}^2),\hfill \\ \hfill \frac{dy}{dt}& =d_1{x}^2+e_{1}xy++{o\left(\right|(x,y)|}^2),\hfill \end{array}\right.$$

(19)

where:

$$\begin{array}{cc}\hfill a_1=& \frac{C_4^3\left(\Lambda \beta -m\right)\left(C_1-C_5\right)}{C_2{C}_1^{2}m{C}_5},d_1=-\frac{C_4^3\left(\Lambda \beta -m\right)}{C_{2}m{C}_1^2},e_1=-\frac{C_4^2{e}_0}{C_2{C}_1^{2}m{C}_5},\hfill \\ \hfill e_0=& \left(2m+2\right)\beta {\Lambda }^4+\left(\left(4m^2-2m\right){\beta }^2+8m^3+12m^2+4m\right)\Lambda -4\beta m^3\hfill \\ \hfill & +\left(\left(2m+3\right){\beta }^2-2m^2-2m\right){\Lambda }^3+\left({\beta }^3-\left(10m^2+14m+2\right)\beta \right){\Lambda }^2.\hfill \end{array}$$

Based on Remark 1 of section 2.13 in [26], we obtain the following equivalent model of (19) in a small neighborhood of $(0,0)$:

$$\left\{\begin{array}{cc}\hfill \frac{dx}{dt}& =y,\hfill \\ \hfill \frac{dy}{dt}& =d_1{x}^2+(e_1+2a_1)xy+o\left(\right|(x,y){|}^3),\hfill \end{array}\right.$$

(20)

where:

$$e_1+2a_1=-\frac{C_4^2{C}_3}{C_{2}m{C}_1^2}$$

Note that $d_1<0$ because of $C_2<0$.

By contradiction, we will prove $e_1+2a_1\ne 0$( i.e., $C_3\ne 0$). Setting $C_3=0$, then:

$$\begin{array}{c}\hfill C_3=\left(2\beta -2\Lambda \right)m^2+\left(2{\Lambda }^2\beta -2\Lambda {\beta }^2\right)m+{\Lambda }^2\beta -\Lambda {\beta }^2+2\Lambda =0.\end{array}$$

We regard $C_3$ as a function of variable m and assume the real solutions of the function exist, that is, $m=m_{1,2}$ and it is evident that $m_1,m_2<\beta \Lambda$. However $m>\beta \Lambda$ leads to a contradiction. In fact, $C_3<0$; hence, $e_1+2a_1<0.$ Utilizing the results on page 167 of [26], $E_{*}(x_{*},y_{*})$ is a cusp of codimension two. □

Remark 2. 

When $\beta =0(i.e.,k_1=0)$, model (4) becomes model (1.3) of Tang et al. [9]. From Theorem 5, we prove that model (4) undergoes Bogdanov–Takens bifurcation of codimension at most two near $E\ast$, and it revises the corresponding results in [9].

Remark 3. 

From Theorem 4 and Theorem 5, when $k_1^{*}<k_1<k_{10}$ ( i.e., $\Lambda >\beta +\beta q$) for model (4), the disease will be eliminated if $R_0<R_c$ (i.e., $p>p_{*}$ and $k_1>k_1^{*}$), and if $R_0=R_c$ (i.e., $p=p_{*}$ and $k_1>k_1^{*}$), model (4) will present complex dynamics and these conditions are not enough to determine the dynamical behaviors, and the disease will persist or die out, which depends on the values of $k_1$ and $k_2$ (or q).

Finally, we give the following the phase portraits via Matlab software (Figure 2).

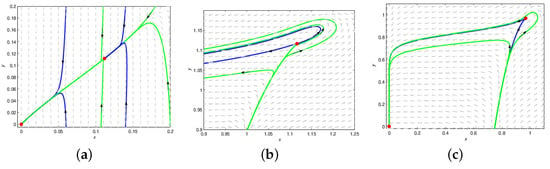
Figure 2. The phase diagram for model (4) with a unique endemic equilibrium: (a) an attracting saddle-node for $\beta =\frac{1}{5}, q=1, m=1, \Lambda =4, p=\frac{71}{5}$; (b) a repelling saddle-node for $\beta =1.7228,$ $q=1,$ $m=94.7654, \Lambda =42.3881, p=0.1629$; (c) a cusp of codimension two for $\beta =0.5, q=1.0019,$ $m=32$, $\Lambda =33, p=0.4535$.

Theorem 6. 

If $\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q$, $p<p_{*}$ and conditions in (5) hold, there are two endemic equilibria $E_1(x_1,y_1)$ and $E_2(x_2,y_2)$ for model (4). Furthermore, $E_1$ must be a hyperbolic saddle, and then, $E_2$ will be:

(i) a stable hyperbolic focus (or node) if $S_T\left(x_2\right)<0$; or

(ii) a weak focus (or a center) if $S_T\left(x_2\right)=0$; or

(iii) an unstable hyperbolic focus (or node) if $S_T\left(x_2\right)>0$.

Proof. 

For $E_1$ and $E_2$, the signs of $S_D\left(x_1\right)$, $S_D\left(x_2\right)$ and $S_T\left(x_2\right)$ are determined by $S_D$ and $S_T$. By some simple calculations, we obtain:

$$S_D\left(x_1\right)=\left(3mp+3q+3\right){x_1}^2+\left(2\beta q-2\Lambda +2\beta \right)x_1+m-\beta \Lambda ,$$

$$S_D\left(x_2\right)=\left(3mp+3q+3\right){x_2}^2+\left(2\beta q-2\Lambda +2\beta \right)x_2+m-\beta \Lambda .$$

Moreover, since $x_1$ and $x_2$ are two different positive roots of (7), we obtain:

$$\begin{array}{cc}\hfill & (mp+q+1)x_1^3+(\beta q+\beta -\Lambda )x_1^2+(m-\beta \Lambda )x_1=0,\hfill \\ \hfill & 3\left(mp+q+1\right){x_1}^2+2\left(\beta q-\Lambda +\beta \right)x_1+m-\beta \Lambda <0,\hfill \\ \hfill & (mp+q+1)x_2^3+(\beta q+\beta -\Lambda )x_2^2+(m-\beta \Lambda )x_2=0,\hfill \\ \hfill & 3\left(mp+q+1\right){x_2}^2+2\left(\beta q-\Lambda +\beta \right)x_2+m-\beta \Lambda >0,\hfill \end{array}$$

which yield $S_D\left(x_1\right)<0$ and $S_D\left(x_2\right)>0$. Then, these conclusions hold. □

Remark 4. 

When $m=\beta \Lambda ,\Lambda >\beta +\beta q$, or $m<\beta \Lambda$, model (4) has a unique positive equilibrium $E_2(x_2,y_2)$ and a disease-free equilibrium $E_0$. $E_0$ is a hyperbolic saddle or saddle-node, and the types and stability of $E_2$ are the same as Theorem 6. Moreover, from Theorem 6, when $R_0>1$ (i.e., $m<\beta \Lambda$), that is, each infected individual produces, on average, more than one new infection, or when $R_0=1$ and $\frac{k_1}{k_2}<\frac{b\left(d+v\right)}{d\left(\gamma +d+v\right)}$, which imply that when the proportion of the linear over nonlinear hazards of infection is less than $\frac{b\left(d+v\right)}{d\left(\gamma +d+v\right)}$, on average, each infected individual produces one new infection, and the disease will persist in the form of multiple periodic coexistent oscillations bifurcated from the equilibrium $E_2$.

Remark 5. 

$\Lambda >\beta +\beta q$ and $p<p_{*}$ are equivalent to $k_1<k_{10}$ and $R_0>R_c$, respectively. Hence, when $k_1^{*}<k_1<k_{10}$, model (4) presents complex dynamics, and the disease will persist in the form of multiple periodic cycles if $R_0>R_c$.

3.2. Bogdanov–Takens Bifurcation

In this subsection, we will choose $\Lambda$ and q as bifurcation parameters, and study Bogdanov–Takens bifurcation of codimension two for model (4). In fact, we have the following theorem:

Theorem 7. 

When $\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q$, $p=p_{*}$, $q=q_{*}$ and conditions in (5) hold, model (4) has a cusp $E_{*}(x_{*},y_{*})$ of codimension two (i.e., Bogdanov–Takens singularity). If we choose Λ and q as bifurcation parameters, Bogdanov–Takens bifurcation of codimension two in a small neighborhood of the unique positive equilibrium $E_{*}(x_{*},y_{*})$ occurs. Hence, there exists some parameter values such for which model (4) produces an unstable limit cycle, and model (4) produces an unstable homoclinic loop for some other parameter values.

Proof. 

We choose $\Lambda$ and q as bifurcation parameters and consider:

$$\left\{\begin{array}{c}\frac{dx}{dt}=\frac{x^2+\beta x}{1+p_{*}{x}^2}(\Lambda +{\lambda }_1-x-y)-mx,\hfill \\ \frac{dy}{dt}=(q_{*}+{\lambda }_2)x-y,\hfill \end{array}\right.$$

(21)

where $({\lambda }_1,{\lambda }_2)$ is a parameter vector in near $(0,0)$. We focus on the phase portraits of model (21) with x and y lying near $E_{*}(x_{*},y_{*})$. Let $X=x-x_{*}$, $Y=y-y_{*}$. Then, we rewrite model (21) as (X, Y are rewritten as x, y, respectively):

$$\left\{\begin{array}{c}\frac{dx}{dt}=b_1+b_{2}x-\frac{1}{q_{*}}y+b_3{x}^2+b_{4}xy+P_1(x,y,{\lambda }_1,{\lambda }_2),\hfill \\ \frac{dy}{dt}=b_5+b_{6}x-y,\hfill \end{array}\right.$$

(22)

where $P_1(x,y,{\lambda }_1,{\lambda }_2)$ is a $C^{\infty }$ function at least of third order with respect to $(x,y)$, and:

$$\begin{array}{c}{b}_1=\frac{{\lambda }_1}{q_{*}},b_2=\frac{\Lambda C_4^2{\lambda }_1}{m{C}_1^2}+1,b_3=\frac{C_4^2{b}_{31}}{m^2{C}_1^3{C}_2{C}_5},\hfill \\ b_{32}={\Lambda }^4\beta m+\left(2{\beta }^{2}m-m^2+m+2\right){\Lambda }^3+\beta m\left({\beta }^2-8m-7\right){\Lambda }^2\hfill \\ +m^2\left({\beta }^2+6m+6\right)\Lambda -2\beta m^3,\hfill \\ b_{31}=C_4{b}_{32}{\lambda }_1-m\left(m(\beta -\Lambda )(\Lambda \beta -m)+\Lambda ({\beta }^2-m-2)\right)C_1^2,\hfill \\ b_4=-\frac{C_4^2\Lambda }{m{C}_1^2},b_5=-\frac{{\lambda }_2{C}_5}{C_4},b_6={\lambda }_2+q_{*}.\hfill \end{array}$$

Let $X=x$ and $Y=b_1+b_{2}x-\frac{1}{q_{*}}y+b_3{x}^2+b_{4}xy+P_1(x,y,{\lambda }_1,{\lambda }_2)$ (we rewrite X, Y as x, y, respectively). Then, we obtain the following model:

$$\left\{\begin{array}{c}\frac{dx}{dt}=y,\hfill \\ \frac{dy}{dt}=c_1+c_{2}x+c_{3}y+c_4{x}^2+c_{5}xy+c_6{y}^2+Q_1(x,y,{\lambda }_1,{\lambda }_2),\hfill \end{array}\right.$$

(23)

where $Q_1(x,y,{\lambda }_1,{\lambda }_2)$ is a $C^{\infty }$ function at least of third order with respect to $(x,y)$ and:

$$\begin{array}{cc}\hfill & c_1=\frac{b_1{q}_{*}-b_5}{q_{*}},c_2=\frac{b_4{b}_5{q}_{*}+b_2{q}_{*}-b_6}{q_{*}},c_3=0,\hfill \\ \hfill & c_4=-b_1{b}_4^2{q}_{*}^2+b_4{b}_6+b_3,c_5=b_1{b}_4^2{q}_{*}^2+b_4{b}_2{q}_{*}+2b_3,c_6=-b_4{q}_{*}.\hfill \end{array}$$

Next, let $dt=(1-c_{6}x)d\tau$; then, model (23) becomes (we still denote $\tau$ by t):

$$\left\{\begin{array}{c}\frac{dx}{dt}=y(1-c_{6}x),\hfill \\ \frac{dy}{dt}=(1-c_{6}x)\left(c_1+c_{2}x+c_{3}y+c_4{x}^2+c_{5}xy+c_6{y}^2+Q_1(x,y,{\lambda }_1,{\lambda }_2)\right).\hfill \end{array}\right.$$

(24)

Letting $X=x$, $Y=y(1-c_{6}x)$, and rewriting X, Y as x, y, respectively, we obtain:

$$\left\{\begin{array}{c}\frac{dx}{dt}=y,\hfill \\ \frac{dy}{dt}=d_1+d_{2}x+d_3{x}^2+d_{4}xy+Q_2(x,y,{\lambda }_1,{\lambda }_2),\hfill \end{array}\right.$$

(25)

where $Q_2(x,y,{\lambda }_1,{\lambda }_2)$ is a $o\left(\right|(x,y){|}^2)$ and:

$$d_1=c_1,d_2=c_2-2c_1{c}_6,d_3=c_4-2c_2{c}_6+c_1{c}_6^2,d_4=c_5.$$

Note that when ${\lambda }_1={\lambda }_2=0$, it is easy to derive that:

$$\begin{array}{cc}\hfill & d_1=0,d_2=0,d_3=\frac{C_4^3\left(\Lambda \beta -m\right)}{m{C}_1{C}_2{C}_5}<0,d_4=\frac{C_4^2{C}_3}{m{C}_1{C}_2{C}_5}<0.\hfill \end{array}$$

Introducing a new time $t=\frac{d_4}{d_3}\tau$, we denote $\tau$ by t again. Moreover, performing a scaling by introducing the new variables:

$$X=\frac{d_4^2}{d_3}x,Y=\frac{d_4^3}{d_3^2}y,$$

and rewriting X, Y as x, y, respectively, we obtain:

$$\left\{\begin{array}{c}\frac{dx}{dt}=y,\hfill \\ \frac{dy}{dt}={\beta }_1+{\beta }_{2}x+x^2+xy+{O\left(\right|\left|(x,y)\right||}^3),\hfill \end{array}\right.$$

(26)

where ${\beta }_1=\frac{d_4^4}{d_3^3}{d}_1,{\beta }_2=\frac{d_4^2}{d_3^2}{d}_2.$ Since:

$$\begin{array}{cc}\hfill & {\left|\frac{\partial ({\beta }_1,{\beta }_2)}{\partial ({\lambda }_1,{\lambda }_2)}\right|}_{({\lambda }_1,{\lambda }_2)=0}=\frac{C_3^6}{q_{*}m{\left(\Lambda \beta -m\right)}^5{C}_4^3{C}_2{C}_1^2}\ne 0,\hfill \end{array}$$

for $\beta \Lambda <m<\frac{{(\Lambda -\beta -\beta q)}^2}{4(1+q)}+\beta \Lambda$, $\Lambda >\beta +\beta q_{*}$ and $q_{*}>0.$ The transformation is an invertible smooth change of parameters near the origin. Hence, model (26) undergoes Bogdanov–Takens bifurcation of codimension two when $({\lambda }_1,{\lambda }_2)$ changes in a small neighborhood of $(0,0)$. □

Based on the study of [26], we get the bifurcation curves with second-order approximations (please refer to Supplementary Information at the end of the paper for more details or the link: http://dx.doi.org/10.13140/RG.2.2.14757.17121 (accessed on 1 May 2023)).

(i)

The saddle-node bifurcation curve is:

$$\begin{array}{cc}\hfill SN& =\left\{({\beta }_1,{\beta }_2)\right|{\beta }_1=0,{\beta }_2\ne 0\}\hfill \\ \hfill & =\left\{({\lambda }_1,{\lambda }_2)|-\frac{C_3^2\Lambda {\lambda }_1}{m{\left(\Lambda \beta -m\right)}^2{C}_1^2}+\frac{C_3^2\left(-2\Lambda \beta m+{\Lambda }^2+2m^2\right){\lambda }_2}{m{C}_4^2{\left(\Lambda \beta -m\right)}^2{C}_1{q}_{*}}\right.\hfill \\ \hfill & +\frac{2{\lambda }_1^2{C}_2{\Lambda }^2{C}_3}{{\left(\Lambda \beta -m\right)}^3{C}_1^4{m}^2}\left\{4{\Lambda }^4\beta m^2-\dots -6\Lambda m^2\right\}\hfill \\ \hfill & -2\frac{{\lambda }_2{\lambda }_1{C}_2\Lambda C_3}{{\left(\Lambda \beta -m\right)}^3{C_4}^2{C_1}^3{q}_{*}{m}^2}\left\{4{\Lambda }^6\beta m^3-\dots -6{\Lambda }^3{m}^2\right\}\hfill \\ \hfill & +\left.\frac{2C_3^2\left({\Lambda }^2-2\Lambda \beta m+2m^2\right)\Lambda \left(2{\Lambda }^{2}m+{\Lambda }^2-2m^2\right)C_2{\lambda }_2^2}{m^2{C}_1^2{C}_4^3{\left(\Lambda \beta -m\right)}^3{q}_{*}^2}=0,{\beta }_2\ne 0\right\}.\hfill \end{array}$$

(ii)

The Hopf bifurcation curve is:

$$\begin{array}{cc}\hfill H& =\left\{({\beta }_1,{\beta }_2)\right|{\beta }_2=\sqrt{-{\beta }_1},{\beta }_1<0\}\hfill \\ \hfill & =\left\{({\lambda }_1,{\lambda }_2)|-\frac{C_3^4{\lambda }_1}{C_{4}m{C_1}^2{\left(\Lambda \beta -m\right)}^3{C}_2}+\frac{C_3^4{\lambda }_2}{q_{*}{C}_4^{2}m{C}_1{\left(\Lambda \beta -m\right)}^3{C}_2}\right.\hfill \\ \hfill & +\frac{C_3^3{\lambda }_1^2}{C_2{C}_1^4{(\Lambda \beta -m)}^4{m}^2{C}_4}\left(12{\Lambda }^6{\beta }^2{m}^2-\dots +36{\Lambda }^2{m}^2\right)\hfill \\ \hfill & -\frac{C_3^3{\lambda }_1{\lambda }_2}{C_2{m}^2{C}_4^2{(\Lambda \beta -m)}^4{C}_1^3{q}_{*}}\left(22{\Lambda }^6{\beta }^2{m}^2-\dots +44{\Lambda }^2{m}^2\right)\hfill \\ \hfill & +\frac{C_3^4{\lambda }_2^2}{m^2{C}_4^4{(\Lambda \beta -m)}^4{C}_1^2{q}_{*}^2}6{\Lambda }^4{m}^2-\dots +4m^4),{\beta }_1<0\}.\hfill \end{array}$$

(iii)

The homoclinic bifurcation curve is:

$$\begin{array}{cc}\hfill HL& =\left\{({\beta }_1,{\beta }_2)\right|{\beta }_2=\frac{5}{7}\sqrt{-{\beta }_1},{\beta }_1<0\}\hfill \\ \hfill & =\left\{({\lambda }_1,{\lambda }_2)|-\frac{25{C_3}^4{\lambda }_1}{49C_{4}m{C_1}^2{\left(\Lambda \beta -m\right)}^3{C}_2}+\frac{25{C_3}^4{\lambda }_2}{49q_{*}{C_4}^{2}m{C}_1{\left(\Lambda \beta -m\right)}^3{C}_2}\right.\hfill \\ \hfill & +\frac{{\lambda }_1^2{C}_3^3}{49C_2{C}_1^4{(\Lambda \beta -m)}^4{m}^2{C}_4}(348{\Lambda }^6{\beta }^2{m}^2-\dots +900{\Lambda }^2{m}^2)\hfill \\ \hfill & -\frac{C_3^3{\lambda }_1{\lambda }_2}{49C_2{C}_4^2{m}^2{(\Lambda \beta -m)}^4{C}_1^3{q}_{*}}(-992{\Lambda }^4+\dots +716{\Lambda }^2{m}^2)\hfill \\ & \left.+\frac{C_3^4{\lambda }_2^2}{49m^2{C}_4^4{(\Lambda \beta -m)}^4{C}_1^2{q}_{*}^2}(150{\Lambda }^4{m}^2-\dots +196m^4),{\beta }_1<0\right\}.\hfill \end{array}$$

Next, the following bifurcation draft and phase graphs are shown via Matlab software.

From Figure 3, we show corresponding bifurcation draft and phase graphs for model (4) with $\beta =0.5,m=32$ and $\Lambda =33$.

Figure 3. The bifurcation draft and phase graphs for model (4) with $\beta =0.5,m=32,\Lambda =33$. (a) Bifurcation draft. (b) No endemic equilibria exist for model (4) with $({\lambda }_1,{\lambda }_2)=(0.05,0.0517)$, which are valued from region I. (c) An unstable focus $E_2$ and a saddle $E_1$ for model (4) with $({\lambda }_1,{\lambda }_2)=(0.05,0.5165)$, which are valued from region II. (d) An unstable limit cycle encloses a stable focus $E_2$ for model (4) with $({\lambda }_1,{\lambda }_2)=(0.05,0.516)$, which are valued from region III. (e) An unstable homoclinic loop for model (4) with $({\lambda }_1,{\lambda }_2)=(0.05,0.5155)$, which are valued on HL. (f) A stable focus $E_2$ and a saddle $E_1$ for model (4) with $({\lambda }_1,{\lambda }_2)=(0.05,0.515)$, which are valued from region IV.

(a) From Figure 3a, it can be seen that the small neighborhood of the origin in the parameter $({\lambda }_1,{\lambda }_2)$-plane is divided by bifurcation curves SN, H, and HL into four regions.

(b) When $({\lambda }_1,{\lambda }_2)=(0,0)$, the unique positive equilibrium is a cusp of codimension 2 (shown in Figure 2c).

(c) No equilibria exist (shown in Figure 3b) if the parameters are valued in region I.

(d) Entering from region I into region II, the parameters are valued on the saddle-node curve $SN$, the endemic equilibrium $E_{*}$ emerges and it is a saddle-node.

(e) When the parameters cross SN into region II, the saddle-node turns into two positive equilibria through saddle-node bifurcation; one is an unstable node $E_2$ and the other is a saddle $E_2$ (shown in Figure 3c).

(f) Then, the node turns into a stable focus and loses stability when the parameters cross the Hopf bifurcation boundary H and an unstable limit cycle bifurcates from the subcritical Hopf bifurcation (shown in Figure 3d).

(g) When the parameters cross region III and lie on the curve HL, an unstable homoclinic cycle bifurcates from the homoclinic bifurcation (shown in Figure 3e).

(h) When the parameters cross III into region IV, the homoclinic cycle breaks up and the corresponding manifold eventually tends to the stable focus $E_2$ (shown in Figure 3f).

3.3. Hopf Bifurcation of Codimension Two

From Theorem 6, Hopf bifurcation near $E_2(x_2,y_2)$ may occur. We obtain a reduced model (4) by the variable substitution:

$$\overline{x}=\frac{x}{x_2},\overline{y}=\frac{y}{y_2},\tau =x_2^{2}t,$$

(27)

then, we transform model (4) into (we rewrite $\tau$ as t):

$$\left\{\begin{array}{c}\frac{d\overline{x}}{dt}=\frac{{\overline{x}}^2+\frac{\beta }{x_2}\overline{x}}{1+p{x}_2^2{\overline{x}}^2}(\frac{\Lambda }{x_2}-\overline{x}-q\overline{y})-\frac{m}{x_2^2}\overline{x},\hfill \\ \frac{d\overline{y}}{dt}=\frac{1}{x_2^2}(\overline{x}-\overline{y}),\hfill \end{array}\right.$$

(28)

Substituting the following scaling for the parameters:

$$\overline{\beta }=\frac{\beta }{x_2},\overline{\Lambda }=\frac{\Lambda }{x_2},\overline{m}=\frac{m}{x_2^2},a=\frac{1}{x_2^2},\overline{p}=p{x}_2^2,\overline{q}=q,$$

in model (28), and removing the bars, we have:

$$\left\{\begin{array}{c}\frac{dx}{dt}=\frac{x^2+\beta x}{1+p{x}^2}(\Lambda -x-qy)-mx,\hfill \\ \frac{dy}{dt}=a(x-y).\hfill \end{array}\right.$$

(29)

There is an equilibrium $\overline{E_2}(1,1)$( i.e., $E_2(x_2,y_2)$ of model (4)), which makes the following equation true:

$$\Lambda =\frac{m(1+p)}{1+\beta }+q+1.$$

Since $x_1{x}_2=\frac{m-\beta \Lambda }{mp+q+1}$ for model (4), then $\frac{x_1}{x_2}=\frac{\overline{m}-\overline{\beta }\overline{\Lambda }}{\overline{m}\overline{p}+\overline{q}+1}$ by (27), we remove the bars and obtain $m\ge \beta \Lambda$ and $q>m-mp-\beta \Lambda -1$ due to $0\le \frac{x_1}{x_2}<1$. Note that if $\Lambda =\frac{m(1+p)}{1+\beta }+q+1,$ then the conditions in (5) under above parameter scaling become:

$$\beta \ge 0,p,q,m,a>0,\frac{m-pm(1+2\beta )}{{(\beta +1)}^2}-1<q<\frac{m}{a},m\ge \frac{\beta (\beta +1)(q+1)}{1-\beta p}.$$

(30)

Then, performing the change of time $dt=(1+p{x}^2)(1+\beta )d\tau$ and plugging $\Lambda =\frac{m(1+p)}{1+\beta }+q+1$ into (29), we have (rewrite $\tau$ as t):

$$\left\{\begin{array}{c}\frac{dx}{dt}=(1+\beta )x\left(x\left(m+mp+(1+q-x-qy)(1+\beta )\right)-(1+p{x}^2)m\right),\hfill \\ \frac{dy}{dt}=(1+p{x}^2)(1+\beta )a(x-y),\hfill \end{array}\right.$$

(31)

where $m,p,q,\beta ,a$ meet with (30). Actually, model (31) is topologically equivalent to model (29) in ${\mathbb{R}}^2=\{(x,y):x\ge 0,y\ge 0\}$; moreover, $1+p{x}^2>0$ holds for all $x\ge 0$. Next, we analyze the Hopf bifurcation near ${\overline{E}}_2(1,1)$ in model (31), which is equivalent to the Hopf bifurcation near $E_2(x_2,y_2)$ in model (4).

Theorem 8. 

Under the conditions in (30), there is an equilibrium ${\overline{E}}_2(1,1)$ for model (31). Furthermore,

(I) when $a<a_{*}$, ${\overline{E}}_2(1,1)$ is an unstable hyperbolic node or focus;

(II) when $a>a_{*}$, ${\overline{E}}_2(1,1)$ is a locally asymptotically stable hyperbolic node or focus;

(III) when $a=a_{*}$, ${\overline{E}}_2(1,1)$ is a fine focus or center,

where

$$a_{*}=\frac{m-{(1+\beta )}^2-pm(1+2\beta )}{(\beta +1)(p+1)}.$$

Proof. 

The Jacobian matrix of model (31) at ${\overline{E}}_2(1,1)$ is:

$$J\left({\overline{E}}_2(1,1)\right)=\left[\begin{array}{cc}m-{(1+\beta )}^2-pm(1+2\beta )& -{\left(1+\beta \right)}^{2}q\\ a\left(1+p\right)\left(1+\beta \right)& -a\left(1+p\right)\left(1+\beta \right)\end{array}\right].$$

(32)

We obtain the determinant of $J\left({\overline{E}}_2(1,1)\right)$, which is:

$$det\left(J\left({\overline{E}}_2\right)\right)=a(p+1)(1+\beta )[(q+1){(\beta +1)}^2+m(2\beta p+p-1)].$$

Moreover, the trace is:

$$tr\left(J\left({\overline{E}}_2\right)\right)=-(\beta +1)(p+1)a+m-{(1+\beta )}^2-pm(1+2\beta ).$$

Under the conditions in (30), we obtain that $det\left(J\left({\overline{E}}_2\right)\right)>0$ and $tr\left(J\left({\overline{E}}_2\right)\right)$$=0(>0$ or $<0)$ if $a=a_{*}(a<a_{*}$ or $a>a_{*})$; hence, the conclusions hold. □

Note that Theorem 8 is true for $a_{*}>0$, i.e.,

$${(\beta +1)}^2+m(2\beta p+p-1)<0,\mathit{or}m>{(1+\beta )}^2,p<\frac{m-{(1+\beta )}^2}{m(1+2\beta )}.$$

Next, the case (III) of Theorem 8 is discussed, where Hopf bifurcation near ${\overline{E}}_2(1,1)$ of model (31) may occur when the following conditions are satisfied:

$$\begin{array}{cc}\hfill & a=a_{*},m>{(1+\beta )}^2,p<\frac{m-{(1+\beta )}^2}{m(1+2\beta )},\hfill \\ \hfill & \frac{m-pm(1+2\beta )}{{(\beta +1)}^2}-1<q<\frac{m}{a_{*}},m\ge \frac{\beta (\beta +1)(q+1)}{1-\beta p}.\hfill \end{array}$$

(33)

Firstly, the following transversality condition holds:

$$\frac{d}{da}\left(tr\left(J\left({\overline{E}}_2\right)\right)\right){|}_{a=a_{*}}=-(\beta +1)(p+1)<0.$$

Next, we evaluate the first Lyapunov coefficient $l_1$.

Let $X=x-1,Y=y-1,$ and $a=a_{*}$. Then, model (31) becomes:

$$\left\{\begin{array}{cc}\hfill \frac{dX}{dt}=& KX-q{(1+\beta )}^{2}Y-q(1+\beta )(2+\beta )XY\hfill \\ & +(K-(1+\beta )(1+mp))X^2-(1+\beta )\left(q{X}^{2}Y-(1+mp)X^3\right),\hfill \\ \hfill \frac{dY}{dt}=& KX-KY-\frac{2pK}{p+1}XY+\frac{2pK}{p+1}{X}^2-\frac{pK}{p+1}{X}^{2}Y+\frac{pK}{p+1}{X}^3.\hfill \end{array}\right.$$

(34)

where $K=-2\beta mp-{\beta }^2-mp-2\beta +m-1$. Let $\omega =\sqrt{K{(1+\beta )}^{2}q-K^2}$ and $X=2\Phi -\frac{2\omega }{K}\Psi ,Y=2\Phi$; then, we obtain the following model:

$$\left\{\begin{array}{cc}\hfill \frac{d\Phi }{dt}=& e_{11}\Psi +e_{12}\Phi \Psi +e_{13}{\Psi }^2+e_{14}{\Phi }^2\Psi +e_{15}\Phi {\Psi }^2+e_{16}{\Psi }^3,\hfill \\ \hfill \frac{d\Psi }{dt}=& e_{21}\Phi +e_{22}{\Phi }^2+e_{23}\Phi \Psi +e_{24}{\Psi }^2+e_{25}{\Phi }^2\Psi +e_{26}\Phi {\Psi }^2+e_{27}{\Phi }^3+e_{28}{\Psi }^3.\hfill \end{array}\right.$$

(35)

where:

$$\begin{array}{cc}\hfill e_{11}=& -\omega ,e_{12}=-\frac{4p\omega }{p+1},e_{13}=\frac{4p{\omega }^2}{K(p+1)},e_{14}=-\frac{4p\omega }{p+1},e_{15}=\frac{8p{\omega }^2}{K(p+1)},\hfill \\ \hfill e_{16}=& -\frac{4p{\omega }^3}{K^2(p+1)},e_{21}=\omega ,e_{22}=\frac{2K}{\omega }\left((1+\beta )(\beta q+mp+2q+1)-K\right),\hfill \\ \hfill e_{23}=& \left(\frac{4K}{(p+1)}-2(1+\beta )(\beta q+2mp+2q+2)\right),\hfill \\ \hfill e_{24}=& \left(\frac{4p}{p+1}-2+\frac{2}{K}(\beta +1)(mp+1)\right)\omega ,\hfill \\ \hfill e_{25}=& -4\left(\frac{pK}{p+1}+(\beta +1)(3mp+2q+3)\right),\hfill \\ \hfill e_{26}=& \left(\frac{4}{K}(\beta +1)(3mp+q+3)+\frac{8p}{p+1}\right)\omega ,\hfill \\ \hfill e_{27}=& \frac{4K}{\omega }(\beta +1)(mp+q+1),e_{28}=-\left(\frac{4p{\omega }^2}{K(p+1)}+\frac{4{\omega }^2}{K^2}(\beta +1)(mp+1)\right).\hfill \end{array}$$

According to Theorem 3.3 of [25] or formula (3.4.11) on Page 152 of [29], we obtain the first Lyapunov coefficient $l_1$ by Maple:

$$l_1=-\frac{q{\left(\beta +1\right)}^2\left(q\left(c_{1}m+c_0\right)+d_2{m}^2+d_{1}m+c_0\right)}{2{\omega }^3{\left(p+1\right)}^2}$$

(36)

where:

$$\begin{array}{cc}\hfill c_1=& \beta p^3-3\left(\beta +2\right)\left(2{\beta }^2+2\beta +1\right)p^2+\left(2{\beta }^3+6{\beta }^2+9\beta +2\right)p+\beta ,\hfill \\ \hfill c_0=& {\left(\beta +1\right)}^3\left(\beta p^2-3\beta p-3p+1\right),\hfill \\ \hfill d_2=& \beta p^4-\left(16{\beta }^2+15\beta +6\right)p^3+\left(15\beta +4\right)p^2-\left(\beta +6\right)p,\hfill \\ \hfill d_1=& \left(3{\beta }^3+3{\beta }^2+2\beta \right)p^3-\left(12{\beta }^3+36{\beta }^2+27\beta +9\right)p^2\hfill \\ & +\left({\beta }^3+9{\beta }^2+18\beta +4\right)p-\beta -3.\hfill \end{array}$$

Let $q=q_0=-\frac{d_2{m}^2+d_{1}m+c_0}{c_{1}m+c_0}>0$, we obtain $l_1{|}_{q=q_0}=0$. Therefore, based on the above caculations, we obtain the following result easily.

Theorem 9. 

When $(\beta ,m,p)\in \left\{(\beta ,m,p)\right|(d_2{m}^2+d_1+c_0)(c_{1}m+c_0)<0\}$, and the conditions in (33) hold, the following statements hold.

(I) If $q>q_0$ (i.e., $l_1<0$), then model (31) generates supercritical Hopf bifurcation and a stable limit cycle bifurcates from ${\overline{E}}_2(1,1)$.

(II) If $q<q_0$ (i.e., $l_1>0$), then model (31) generates subcritical Hopf bifurcation and an unstable limit cycle bifurcates from ${\overline{E}}_2(1,1)$.

(III) If $q=q_0$ (i.e., $l_1=0$), then model (31) may generate degenerate Hopf bifurcation and multiple limit cycles may bifurcate from ${\overline{E}}_2(1,1)$.

When $c_1,c_0\ne 0$ and $m=-\frac{c_0}{c_1}$, and the conditions in (33) hold, we have:

(I) If $c_0>0$ (i.e., $l_1<0$), then model (31) generates supercritical Hopf bifurcation and a stable limit cycle bifurcates from ${\overline{E}}_2(1,1)$;

(II) If $c_0<0$ (i.e., $l_1>0$), then model (31) generates subcritical Hopf bifurcation and an unstable limit cycle bifurcates from ${\overline{E}}_2(1,1)$.

Proof. 

Through simple calculations, we obtain the following results.

Case 1, when $c_1=0$ for $\beta >0$ and $p>0$, it is evident that $c_0\ne 0$, then $l_1=0$ if and only if $q=q_0$.

Case 2, when $c_1\ne 0$ and $c_0=0$, then $l_1=0$ if and only if $q=q_0$.

Case 3, when $c_1,c_0\ne 0$ and $c_{1}m+c_0=0$, we obtain $m=-\frac{c_0}{c_1}$, then:

$$d_2{m}^2+d_{1}m+c_0=\frac{\beta {\left(p+1\right)}^3\left(2\beta +p+3\right)c_0{\left({\beta }^{2}p+1\right)}^2}{{c_1}^2}\ne 0.$$

Therefore, $l_1\ne 0$ and $Sign\left(l_1\right)=Sign(-c_0)$.

Case 4, when $c_1\ne 0$, $c_0\ne 0$ and $c_{1}m+c_0\ne 0$, then $l_1=0$ if and only if $q=q_0$. □

To numerically illustrate the results of the bifurcation analysis, with the help of Matlab software, we simulate an subcritical Hopf bifurcation with parameter values: $\beta =0.4,$ $m=9$, $q=6,p=0.4,a=0.2857$, one unstable limit cycle, bifurcated from the equilibrium $E_2(1,1)$ of model (29) with parameter $\alpha$ perturbed to $0.2857+0.03$, which is shown in Figure 4a. When the parameters become $\beta =0.8,m=9,q=4,p=0.1,a=1.7273$, a stable limit cycle will arise from ${\overline{E}}_2(1,1)$ of model (29) with small perturbation $-0.03$ on $\alpha$ occurring (see Figure 4b). The coexistence of two limit cycles with the parameter values $\beta =0.4,m=3,q=2.4269+0.1,p=0.1,a=0.3247-0.0002$ is shown in Figure 4c. The limit cycle with large amplitude is unstable, and the one with small amplitude is stable; both surround the stable endemic equilibrium ${\overline{E}}_2(1,1)$.

Figure 4. (a) An unstable limit cycle for model (31) with $\beta =0.4, m=9, q=6, p=0.4, a=0.2857+0.03$. (b) A stable limit cycle for model (31) with $\beta =0.8, m=9, q=4, p=0.1, a=1.7273-0.03$. (c) Two limit cycles for model (31) with $\beta =0.4, m=3, q=2.4269+0.1, p=0.1, a=0.3247-0.0002$.

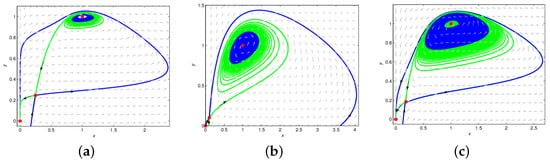
Remark 6. 

From Figure 4a, there are three equilibria, a disease-free equilibrium, which is a stable node, and two endemic equilibria, where one is a saddle and the other is a stable focus. An unstable limit cycle encloses the focus. Therefore, the long-term disease dynamics may depend on the initial values of the populations, similar to Figure 4b,c.

3.4. Hopf Bifurcation of Codimension Three

From Theorem 9, Hopf bifurcation of codimension three may occur for model (31) with $q=q_0$. In this section, we will study the phenomenon. To obtain the normal form of model (31), we make another transformation of $X=2\Phi +\frac{2\omega }{K}\Psi , Y=2\Phi$, and $\tau =\omega t$; then, system (34) becomes:

$$\left\{\begin{array}{cc}\hfill \frac{d\Phi }{dt}=& \Psi +h_{11}\Phi \Psi +h_{12}{\Psi }^2+h_{13}{\Phi }^2\Psi +h_{14}\Phi {\Psi }^2+h_{15}{\Psi }^3,\hfill \\ \hfill \frac{d\Psi }{dt}=& -\Phi +h_{21}{\Phi }^2+h_{22}\Phi \Psi +h_{23}{\Psi }^2+h_{24}{\Phi }^2\Psi +h_{25}\Phi {\Psi }^2+h_{26}{\Phi }^3+h_{27}{\Psi }^3,\hfill \end{array}\right.$$

(37)

where:

$$\begin{array}{cc}\hfill h_{11}=& \frac{4p}{p+1},h_{12}=\frac{4p\omega }{K(p+1)},h_{13}=\frac{4p}{p+1},h_{14}=\frac{8p\omega }{K(p+1)},\hfill \\ \hfill h_{15}=& \frac{4p{\omega }^2}{K^2(p+1)},h_{21}=\frac{2K}{{\omega }^2}\left(K-(1+\beta )(\beta q+mp+2q+1)\right),\hfill \\ \hfill h_{22}=& \frac{2}{\omega }\left(\frac{2K}{(p+1)}-(1+\beta )(\beta q+2mp+2q+2)\right),\hfill \\ \hfill h_{23}=& 2-\frac{4p}{p+1}-\frac{2}{K}(\beta +1)(mp+1),\hfill \end{array}$$

$$\begin{array}{cc}\hfill h_{24}=& -\frac{4}{\omega }\left(\frac{pK}{p+1}+(\beta +1)(3mp+2q+3)\right),\hfill \\ \hfill h_{25}=& -\frac{4}{K}(\beta +1)(3mp+q+3)-\frac{8p}{p+1},\hfill \\ \hfill h_{26}=& -\frac{4K}{{\omega }^2}(\beta +1)(mp+q+1),h_{27}=-\frac{4p\omega }{K(p+1)}-\frac{4\omega }{K^2}(\beta +1)(mp+1).\hfill \end{array}$$

Next, applying the Maple program [28], we obtain the following focus values:

$$\begin{array}{cc}\hfill f_1=& \frac{1}{4{P_2}^3{P_1}^3}\left({P_1}^4{P_2}^2{P_3}^2+{P_1}^2{P_2}^4{P_3}^2+5{P_1}^4{P_2}^2{P}_3+7{P_1}^2{P_2}^4{P}_3\right.\hfill \\ \hfill & +{P_1}^2{P_2}^2{P}_3{P}_5\beta +2{P_2}^6{P}_3+{P_2}^4{P}_3{P}_5\beta +2{P_1}^4{P}_3{P}_4+8{P_1}^2{P_2}^4\hfill \\ \hfill & +3{P_1}^2{P_2}^2{P}_3{P}_4+2{P_1}^2{P_2}^2{P}_3{P}_5+2{P_1}^2{P_2}^2{P}_5\beta +8{P_2}^6+{P_2}^4{P}_3{P}_4\hfill \\ \hfill & +2{P_2}^4{P}_3{P}_5+6{P_2}^4{P}_5\beta +{P_2}^2{P_5}^2{\beta }^2+6{P_1}^4{P}_4+14{P_1}^2{P_2}^2{P}_4\hfill \\ & +8{P_1}^2{P_2}^2{P}_5+{P_1}^2{P}_4{P}_5\beta +8{P_2}^4{P}_4+12{P_2}^4{P}_5+3{P_2}^2{P}_4{P}_5\beta \hfill \\ \hfill & \left.+4{P_2}^2{P_5}^2\beta +2{P_1}^2{P_4}^2+2{P_1}^2{P}_4{P}_5+2{P_2}^2{P_4}^2+6{P_2}^2{P}_4{P}_5+4{P_2}^2{P_5}^2\right),\hfill \\ \hfill f_2=& -\frac{1}{96P_2^7{P}_1^7}\left(10{P_1}^{10}{P_2}^4{P_3}^4+55{P_1}^8{P_2}^6{P_3}^4+44{P_1}^6{P_2}^8{P_3}^4+\dots \right),\hfill \\ \hfill f_3=& -\frac{1}{9216P_2^{11}{P}_1^{11}}\left(1850{P_1}^{16}{P_2}^6{P_3}^6+3197{P_1}^{14}{P_2}^8{P_3}^6+\dots \right),\hfill \end{array}$$

where $P_1=\frac{\omega }{\sqrt{K}},P_2=\sqrt{K},P_3=-\frac{4p}{p+1},P_4=-2\left(1+\beta \right)\left(mp+1\right),P_5=-2q(1+\beta ),$ $f_i,i=1,2,3,$ are lengthy polynomials in $\beta ,p,m,$ and $q.$

It is extremely difficult or impossible to solve $f_1=f_2=f_3=0$ for four parameters. We consider a specific case $p=\frac{1}{2(2\beta +1)}$ and $m=n_1{(1+\beta )}^2$ by introducing a new parameter $n_1>0$, which implies that p which describes the psychological effect is inversely proportional to $\beta$, which measures the infection force of the disease, and m, which represents the infection remove rate is proportional to $\beta$. Biologically, it means that the infection force of the disease is positively related to the psychological or inhibitory effect and the infection remove rate (including recovery rate and disease-related death rate). Under the assumptions, model (29) with parameters $\beta$ and $n_1$ will exhibit Hopf bifurcation of codimension three. Let:

$$\begin{array}{cc}\hfill z_1=& -\left(64{\beta }^6+432{\beta }^5+1084{\beta }^4+1353{\beta }^3+906{\beta }^2+313\beta +44\right)n_1^3\hfill \\ \hfill & +\left(256{\beta }^7+1984{\beta }^6+5712{\beta }^5+8060{\beta }^4+6044{\beta }^3+2348{\beta }^2+396\beta \right.\hfill \\ \hfill & \left.+12\right){n_1}^2+\left(384{\beta }^4+1008{\beta }^3+1000{\beta }^2+440\beta +72\right)n_1\hfill \\ \hfill & -8\left(\beta +1\right)\left(4{\beta }^2-\beta -2\right){\left(1+2\beta \right)}^2,\hfill \\ \hfill z_2=& \left(32{\beta }^5+104{\beta }^4+120{\beta }^3+51{\beta }^2-\beta -4\right)n_1-2\left(4{\beta }^2+7\beta +2\right){\left(1+2\beta \right)}^3,\hfill \\ \hfill Q_3=& \left(576{\beta }^7+3272{\beta }^6+7122{\beta }^5+7500{\beta }^4+3736{\beta }^3+484{\beta }^2-250\beta -72\right)n_1^2\hfill \\ \hfill & +\left(256{\beta }^8+576{\beta }^7-1152{\beta }^6-5628{\beta }^5-9095{\beta }^4-8059{\beta }^3-4178{\beta }^2\right.\hfill \\ \hfill & \left.-1190\beta -144\right)n_1-512{\beta }^8-3456{\beta }^7-11072{\beta }^6-19968{\beta }^5-21188{\beta }^4\hfill \\ \hfill & -13370{\beta }^3-4884{\beta }^2-940\beta -72.\hfill \end{array}$$

In fact, we have the following theorem.

Theorem 10. 

If $q=q_0$, $z_1>0$, $z_2\ge 0$, $n_1>2$, and $Q_3=0$, model (29) (i.e., model (4)) undergoes a Hopf bifurcation of codimension three around the equilibrium $\overline{E_2}(1,1)$ (i.e., $E_2(x_2,y_2)$ in model (4)), three limit cycles bifurcate from $\overline{E_2}(1,1)$, and the outermost limit cycle is stable.

Proof. 

From the assumptions $p=\frac{1}{2(2\beta +1)}$ and $m=n_1{(1+\beta )}^2$, we get:

$$a_{*}=\frac{(2\beta +1)(n_1-2)(1+\beta )}{3+4\beta },$$

where $n_1>2$ and $q>\frac{n_1}{2}-1$; then:

$$\begin{array}{cc}\hfill & P_1=\frac{(1+\beta )}{2}\sqrt{4q-2n_1+4},P_2=\frac{(1+\beta )}{2}\sqrt{2n_1-4},P_3=-\frac{4}{3+4\beta },\hfill \\ \hfill & P_4=-(1+\beta )\left(\frac{n_1{(1+\beta )}^2}{2\beta +1}+2\right),P_5=-2q(1+\beta ).\hfill \end{array}$$

Then, the first focus value $f_1$ becomes:

$$\begin{array}{cc}\hfill & f_1=\frac{2q\left(Q_0-2\left(2\beta +1\right)Q_{1}q\right)}{{(2q+2-n_1)}^{3/2}{(n_1-2)}^{3/2}{(1+\beta )}^2{(2\beta +1)}^2{(3+4\beta )}^2},\hfill \end{array}$$

when $f_1=0$, we obtain $q=q_0=\frac{Q_0}{2\left(2\beta +1\right)Q_1}$, where:

$$\begin{array}{cc}\hfill Q_0=& \left(64{\beta }^4+304{\beta }^3+412{\beta }^2+225\beta +44\right){\left(\beta +1\right)}^2{n}_1^2\hfill \\ \hfill & -2\left(2\beta +1\right)\left(16{\beta }^5+48{\beta }^4-17{\beta }^3-125{\beta }^2-104\beta -26\right)n_1\hfill \\ \hfill & -4\left(\beta +1\right)\left(4{\beta }^2-\beta -2\right){\left(2\beta +1\right)}^2,\hfill \\ \hfill Q_1=& \left(32{\beta }^5+168{\beta }^4+260{\beta }^3+152{\beta }^2+23\beta -4\right)n_1\hfill \\ \hfill & +16{\beta }^4+20{\beta }^3-6{\beta }^2-14\beta -4,\hfill \end{array}$$

the conditions of Hopf bifurcation in (33) become:

$$\begin{array}{cc}\hfill & q_0>0,\frac{z_1}{2(1+2\beta )Q_1(n_1-2)}>0,\hfill \\ \hfill & \frac{n_1(4\beta +3)}{2(1+2\beta )Q_1}\left({\beta }^2+4\beta +2\right)Q_2>0,\frac{n_1(\beta +1)}{(3\beta +2)Q_1}({\beta }^2+4\beta +2)z_2\ge 0,\hfill \end{array}$$

that is:

$$\begin{array}{cc}\hfill & Q_0>0,Q_1>0,z_1>0,z_2\ge 0,n_1>2,\hfill \end{array}$$

(38)

where:

$$\begin{array}{cc}\hfill Q_2=& 16{\beta }^3+16{\beta }^2{n}_1+44{\beta }^2+23\beta n_1+34\beta +8n_1+8.\hfill \end{array}$$

When $f_1=0$, the second focus value $f_2$ becomes:

$$\begin{array}{cc}\hfill & f_2=-\frac{4Q_0^2{n_1}^3{\left({\beta }^2+4\beta +2\right)}^3{Q}_3{Q}_2^2}{3{\left(2q_0+2-n_1\right)}^{\frac{7}{2}}{\left(n_1-2\right)}^{\frac{5}{2}}{\left(1+\beta \right)}^3{\left(2\beta +1\right)}^5{Q_1}^5}.\hfill \end{array}$$

Hence, $f_2=0$ if and only if $Q_3=0$.

When $f_1=0$ (i.e., $q=q_0=\frac{Q_0}{2\left(2\beta +1\right)Q_1}$), we obtain the third focus value $f_3$:

$$\begin{array}{cc}\hfill f_3& =\frac{1}{9}\frac{f_{33}{Q_0}^2}{{\left(n_1-2\right)}^{\frac{9}{2}}{\left({\beta }^2+4\beta +2\right)}^{\frac{3}{2}}{\left(2\beta +1\right)}^{\frac{7}{2}}{\left(1+\beta \right)}^5{\left(3+4\beta \right)}^{\frac{13}{2}}{Q_1}^{\frac{5}{2}}{Q_2}^{\frac{7}{2}}{n_1}^{\frac{3}{2}}}.\hfill \end{array}$$

where $f_{33}$ is a redundant polynomial in variables $\beta$ and $n_1$, which is given in the end of the paper (please refer to the link http://dx.doi.org/10.13140/RG.2.2.14757.17121 for more details) (accessed on 1 May 2023).

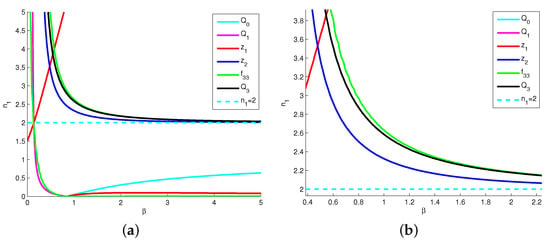
Evidently, the two polynomial equations $f_2=f_3=0$ are equivalent to $Q_3=f_{33}=0$. Under the conditions in (38), $Q_3=f_{33}=0$ has no solutions for $\beta$ and $n_1$ by simple calculation via Maple, and $f_{33}$ is above $Q_3$ on the $\beta$-$n_1$ plane (see Figure 5). Hence, when $f_2=0$ (i.e., $Q_3=0$), it is easy to derive that the third focus value $f_3<0$ under the conditions in (38).

Figure 5. (a) Graphs of the regions on the $\beta$-$n_1$ plane. Under the conditions in (38), the black line under the red line on the right is the value range of parameters $\beta$ and $n_1$, where Hopf bifurcation of codimension three will occur. (b) The value range is zoomed near $n_1=2$.

In conclusion, when the conditions in (38) hold, $Q_3=0$ should be the critical part of the black line which is under the red line on the right (see Figure 5), which makes $f_1=f_2=0$ and $f_3<0$ true. Moreover, a simple calculation via Maple shows that on the black critical line:

$$\begin{array}{c}\hfill det\left[\frac{\partial (f_1,f_2)}{\partial (\beta ,n_1)}\right]=Q_4\ne 0,\end{array}$$

where $Q_4$ is given in the end of the paper (please refer to the link http://dx.doi.org/10.13140/RG.2.2.14757.17121 for more details) (accessed on 1 May 2023), which implies that if the values of parameters $\beta$ and $n_1$ are on the black critical line, model (29) will exhibit Hopf bifurcation of codimension three and the outermost limit cycle is stable, since $f_3<0$. □

4. Conclusions and Discussions

In this paper, we focus on the bifurcation analysis of an SIRS epidemic model with a nonmonotone and saturated incidence rate. The incidence rate plays a key role in describing the spreading of infectious diseases and in producing the rich dynamics, including bistability (backward bifurcation) and periodicity. Based on research work conducted by pioneers, in 2019, a generalized nonmonotone and saturated incidence function $k{I}^2/(1+\beta I+\alpha I^2)$ in model (1) was proposed by Lu et al. [20]; they considered that the incidence function, which described the infection force, should not be just monotonic, nonmonotonic, or saturated, but the combination of monotonicity, nonmonotonicity, and saturation properties. Considering the psychological and crowding effect, the incidence function seemed reasonable to describe the infection force of some specific infectious diseases. However, we have found that the basic reproduction number of model (1) with the incidence rate $k{I}^{2}S/(1+\beta I+\alpha I^2)$ is zero, but the disease can still be persistent. Recently, Wang et al. [30] proved that model (1) can display bistable behaviors (backward bifurcation) with the threshold ${\mathbb{R}}_0=\frac{bk}{\beta d(d+\gamma )}$, which is not the basic reproduction number of the model, and how to calculate the basic reproduction number of this model is still an open question. Hence, the incidence rate is difficult to understand. Moreover, the biological meaning of parameter $\beta$ is undefined, and the condition $\beta >-2\sqrt{\alpha }$ is mandatory.

Hence, we propose a more reasonable incidence rate $\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}S$ with the combination of monotonicity, nonmonotonicity, and saturation properties. When $k_1=0$, the incidence function $f\left(I\right)=\frac{k_{1}I+k_2{I}^2}{1+\alpha I^2}$ becomes the saturated incidence function in [4], which increases monotonously and then goes to $\frac{k_2}{\alpha }$ as $I\to \infty$ (see Figure 1). When $k_1>0$, $f\left(I\right)$ increases firstly and then decreases to $\frac{k_2}{\alpha }$ as $I\to \infty$ (see Figure 1), which describes the fact that the infection force of some infectious diseases grows rapidly to the maximum as a new disease emerges or an old disease reemerges, and then trends to a value. We have carried out a qualitative analysis in this paper. The basic reproduction $R_0$ of model (2) is $\frac{b{k}_1}{d(d+\gamma )}$; we present that model (2) can undergo backward bifurcation with $R_0$ as the perturbation parameter if $\Lambda >\beta q+\beta$; backward bifurcation was proposed by Castillo-Chavez and Song [31] to illustrate that even if the basic reproduction number $R_0<1$, disease outbreaks are still possible. The backward bifurcation has further epidemiological implications by providing a threshold $R_c$; when $\Lambda >\beta q+\beta$, model (2) shows bistable behavior (endemic equilibrium $E_2$ and disease-free equilibrium are stable) if $R_c<R_0<1$, and the model has an unique endemic equilibrium $E_2$ and the disease-free equilibrium becomes unstable if $R_0>1$. Moreover, a saddle-node bifurcation at the threshold $R_c$ has been studied. In our paper, there are the basic reproduction number $R_0$, threshold $R_c$, and critical values $k_1^{*}$ and $k_{10}$ of $k_1$, which measure the linear hazard of infection to determine the dynamic of model (4). Briefly, when $R_0\le 1$ and $\frac{k_1}{k_2}$, which measures the proportion of the linear over nonlinear hazards of infection, is larger than or equal to $\frac{b\left(d+v\right)}{d\left(\gamma +d+v\right)}$, the disease can be eliminated for all initial populations. When $R_0>1$ or $R_0=1$ and $\frac{k_1}{k_2}<\frac{b\left(d+v\right)}{d\left(\gamma +d+v\right)}$, the disease will persist in the form of multiple periodic coexistent oscillations bifurcated from the equilibrium $E_2$, or coexistent steady states for some initial populations. When $\frac{k_1}{k_2}<\frac{b\left(d+v\right)}{d\left(\gamma +d+v\right)}$, model (4) will present complex dynamics, including backward, saddle-node, and Hopf bifurcation, etc. In fact, when $k_1^{*}<k_1<k_{10}$, the disease will disappear $R_0<R_c$, but the disease will persist if $R_0>R_c$, and for $R_0=R_c$, these conditions are not enough to determine the dynamical behaviors, which implies the disease will persist or die out, which depends on the values of independent parameters $k_1$ and $k_2$ (or q), and it requires further assessment.

Moreover, we have proved that the model undergoes Bogdanov–Takens bifurcation of, at most, codimension two, which revises the results in [9] for $k_1=0$. Our studies on Hopf bifurcation of codimension two and three enrich the dynamics of SIRS epidemic models. In fact, it is difficult to take a complete analysis of Hopf bifurcation of codimension three. Assuming that the infection force of the disease measured by $\beta$ is positively related to the psychological effect and the infection remove rate (including recovery rate and disease-related death rate), we obtain a complete qualitative analysis on Hopf bifurcation of codimension three for model (2). Next, we consider applying the model to practical problems, using the model for parameter estimation, and combining the actual data for numerical simulation and prediction analysis, so as to provide referable suggestions for the actual work department.