Stability and Bifurcations in a Nutrient–Phytoplankton–Zooplankton Model with Delayed Nutrient Recycling with Gamma Distribution

Abstract

Two nutrient–phytoplankton–zooplankton (NZP) models for a closed ecosystem that incorporates a delay in nutrient recycling, obtained using the gamma distribution function with one or two degrees of freedom, are analysed. The models are described by systems of ordinary differential equations of four and five dimensions. The purpose of this study is to investigate how the mean delay of the distribution and the total nutrients affect the stability of the equilibrium solutions. Local stability theory and bifurcation theory are used to determine the long-time dynamics of the models. It is found that both models exhibit comparable qualitative dynamics. There are a maximum of three equilibrium points in each of the two models, and at most one of them is locally asymptotically stable. The change of stability from one equilibrium to another takes place through a transcritical bifurcation. In some hypotheses on the functional response, the nutrient–phytoplankton–zooplankton equilibrium loses stability via a supercritical Hopf bifurcation, causing the apparition of a stable limit cycle. The way in which the results are consistent with prior research and how they extend them is discussed. Finally, various application-related consequences of the results of the theoretical study are deduced.

1. Introduction

Plankton are floating organisms that provide a food source for other organisms ranging from shellfish to whales. As such, they play a crucial role in aquatic foodwebs [1]. Phytoplankton are organisms, such as algae, which carry out photosynthesis and are an important means of carbon storage in the ocean [2]. Zooplankton feed on phytoplankton or other zooplankton and include insect larvae and jellyfish. Due to their fundamental role in aquatic ecosystems and their influence on the global carbon cycle, it is important to understand the temporal dynamics of plankton ecosystems.

A variety of different models have been proposed for plankton ecosystems, emphasizing different aspects of these complex systems [3,4,5,6,7,8,9,10,11]. Here, we study a model due to Kloosterman et al. [12], which focussed on two aspects. The chemical nutrients in the system are recycled, thus the system is closed—the total amount of nutrient remains constant. This recycling takes time (e.g., due to decomposition of dead organisms) and thus the model should include a time delay. Both are important features of plankton ecosystems that lead to interesting mathematics.

The model of Kloosterman et al. [12] is called an NPZ model as it is a system with three compartments, representing the dissolved nutrient (N ), the amount of phytoplankton (P), and the amount of zooplankton (Z). It is described by the following equations:

$$\left\{\begin{array}{ccc}\frac{dN}{dt}\left(t\right)\hfill & =\hfill & \lambda {\int }_0^{\infty }P\left(t-u\right)\eta \left(u\right)du+\delta {\int }_0^{\infty }Z\left(t-u\right)\eta \left(u\right)du\hfill \\ \hfill & \hfill & +\left(1-\gamma \right)g{\int }_0^{\infty }Z\left(t-u\right)h\left(P\left(t-u\right)\right)\eta \left(u\right)du-\mu P\left(t\right)f\left(N\left(t\right)\right)\hfill \\ \frac{dP\left(t\right)}{dt}\hfill & =\hfill & \mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\lambda P\left(t\right)\hfill \\ \frac{dZ\left(t\right)}{dt}\hfill & =\hfill & \gamma gZ\left(t\right)h\left(P\left(t\right)\right)-\delta Z\left(t\right)\hfill \end{array}\right..$$

(1)

Here, $\lambda ,\mu ,\gamma ,\delta$ and g are positive parameters representing biological properties while $\eta$ is an appropriate distribution representing the time delay in nutrient recycling.

The function f stands for the phytoplankton nutrient uptake as a function of the available nutrient and it has the following properties [4]:

$$f\left(0\right)=0,f^{\prime }\left(N\right)>0,f^{″}\left(N\right)<0,\underset{N\to \infty }{lim}f\left(N\right)=1.$$

(2)

Similarly, the function h stands for the available phytoplankton and it must satisfy conditions [13,14]:

$$h\left(0\right)=0,h^{\prime }\left(P\right)>0,\underset{P\to \infty }{lim}h\left(P\right)=1.$$

(3)

Kloosterman et al. [12] investigated how this model for a planktonic ecosystem is affected by the quantity of biomass it contains and by the delay distribution. They described the existence of the equilibrium points and gave some stability results for a general distribution function, using methods as in [15]. Other stability results considered particular cases of the distribution function and relied primarily on numerical work.

In this study, we assume that the delay follows a gamma distribution function, with either one or two degrees of freedom, as these numbers of freedom degrees correspond to the biological data. We derive two models, described by systems of ordinary differential equations (ODEs), and analyse how the local stability and local bifurcation of the equilibrium points depend on the amount of total nutrients and on the mean delay of the distribution.

For the numerical simulations we have used a Holling type II functional response for f,

$$f\left(N\right)=\frac{N}{N+k_N},$$

with $k_N>0.$ For function h, we used either a Holling Type II functional response

$$h\left(P\right)=\frac{P}{P+k_P},$$

or a Holling Type III response

$$h\left(P\right)=\frac{P^2}{P^2+k_P^2},$$

with $k_P>0.$

Using this delay, we have extended the results obtained in [12].

2. The Models

Consider $\eta$ the gamma distribution of mean $\tau$, with k degrees of freedom:

$$\eta \left(u\right)=\left\{\begin{array}{c}\frac{k^k}{{\tau }^k\left(k-1\right)!}{u}^{k-1}{e}^{-\frac{k}{\tau }u},u\ge 0\\ 0,u<0\end{array}\right.$$

(4)

Starting from system (1) and using the gamma distribution function for the cases $k=1$ and $k=2$, and some appropriate new variables, we derive two models, described by systems of ordinary differential equations (ODEs), without explicit delay. This reduction is often called the linear chain trick [16,17,18].

For the case $k=1$, we obtain a 4-dimensional system of ODEs, which is then reduced to a three-dimensional one. This will be called the weak model.

For $k=2$, we obtain a five-dimensional system of ODEs that can be reduced to a four-dimensional system, which will be called the strong model.

2.1. The Weak Model

If $k=1,$ we have $\eta \left(u\right)=\frac{1}{\tau }{e}^{-\frac{u}{\tau }},$ for $u\ge 0.$ Denoting

$$Q\left(t\right)=\underset{0}{\stackrel{\infty }{\int }}[\lambda P\left(t-u\right)+\delta Z\left(t-u\right)+\left(1-\gamma \right)gZ\left(t-u\right)h\left(P\left(t-u\right)\right)]e^{-\frac{u}{\tau }}du,$$

(5)

the equation describing the evolution of the dissolved nutrient N can be written as:

$$\frac{dN}{dt}\left(t\right)=\frac{1}{\tau }Q\left(t\right)-\mu P\left(t\right)f\left(N\left(t\right)\right).$$

In addition, using the change of variable $t-u=\theta ,$ we have:

$$\begin{array}{ccc}\hfill Q\left(t\right)& =& -\underset{t}{\stackrel{-\infty }{\int }}[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]e^{-\frac{t-\theta }{\tau }}d\theta \hfill \\ & =& \underset{-\infty }{\stackrel{t}{\int }}[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]e^{-\frac{t-\theta }{\tau }}d\theta .\hfill \end{array}$$

It follows:

$$\begin{array}{cc}\hfill \frac{dQ}{dt}\left(t\right)& =\lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)\hfill \\ \hfill & +\underset{-\infty }{\stackrel{t}{\int }}[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]e^{-\frac{t-\theta }{\tau }}\left(-\frac{1}{\tau }\right)d\theta .\hfill \end{array}$$

With the change of variable $t-u=\theta ,$ we have

$$\frac{dQ}{dt}\left(t\right)=\lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)-\frac{1}{\tau }Q\left(t\right)$$

Thus, we obtain a 4D model ($NPZQ$), called “the weak model” in the following, described by

$$\left\{\begin{array}{c}\frac{dN\left(t\right)}{dt}=\frac{1}{\tau }Q\left(t\right)-\mu P\left(t\right)f\left(N\left(t\right)\right),\hfill \\ \frac{dP\left(t\right)}{dt}=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\lambda P\left(t\right),\hfill \\ \frac{dZ\left(t\right)}{dt}=\gamma gZ\left(t\right)h\left(P\left(t\right)\right)-\delta Z\left(t\right),\hfill \\ \frac{dQ\left(t\right)}{dt}=\lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)-\frac{1}{\tau }Q\left(t\right).\hfill \end{array}\right.$$

(6)

Since the conservation law $\frac{d}{dt}(N+P+Z+Q)=0$ is fulfilled, we obtain $N\left(t\right)+P\left(t\right)+Z\left(t\right)+Q\left(t\right)=N_T^1=constant.$ The substitution $Q\left(t\right)=N_T^1-N\left(t\right)-P\left(t\right)-Z\left(t\right),$ leads to the following reduced 3D system:

$$\left\{\begin{array}{c}\frac{dN\left(t\right)}{dt}=\frac{1}{\tau }\left(N_T^1-N\left(t\right)-P\left(t\right)-Z\left(t\right)\right)-\mu P\left(t\right)f\left(N\left(t\right)\right)\hfill \\ \frac{dP\left(t\right)}{dt}=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\lambda P\left(t\right),\hfill \\ \frac{dZ\left(t\right)}{dt}=\gamma gZ\left(t\right)h\left(P\left(t\right)\right)-\delta Z\left(t\right).\hfill \end{array}\right.$$

(7)

with the phase space

$$D_1=\left\{\left(N,P,Z\right),N\ge 0,P\ge 0,Z\ge 0,N+P+Z\le N_T^1\right\}.$$

(8)

2.2. The Strong Model

If the number of freedom degrees is $k=2,$ we have $\eta \left(u\right)=\frac{4}{{\tau }^2}u{e}^{-\frac{2}{\tau }u},$ for $u\ge 0.$ Denoting

$$Q_1\left(t\right)={\int }_0^{\infty }[\lambda P\left(t-u\right)+\delta Z\left(t-u\right)+\left(1-\gamma \right)gZ\left(t-u\right)h\left(P\left(t-u\right)\right)]\frac{2}{\tau }u{e}^{-\frac{2}{\tau }u}du,$$

(9)

the equation describing the evolution of the dissolved phytoplankton nutrient from (1) reads:

$$\frac{dN}{dt}\left(t\right)=\frac{2}{\tau }{Q}_1\left(t\right)-\mu P\left(t\right)f\left(N\left(t\right)\right).$$

(10)

In addition, using the change of variable $t-u=\theta ,$ we have

$$\begin{array}{ccc}\hfill Q_1\left(t\right)& =& -\frac{2}{\tau }{\int }_t^{\infty }[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]\left(t-\theta \right)e^{-\frac{2}{\tau }\left(t-\theta \right)}d\theta \hfill \\ & =& \frac{2}{\tau }{\int }_{-\infty }^t[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]\left(t-\theta \right)e^{-\frac{2}{\tau }\left(t-\theta \right)}d\theta .\hfill \end{array}$$

Denoting by

$$Q_2\left(t\right)={\int }_{-\infty }^t[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]e^{-\frac{2}{\tau }\left(t-\theta \right)}d\theta ,$$

(11)

it follows:

$$\frac{d{Q}_1}{dt}\left(t\right)=\frac{2}{\tau }\left(Q_2\left(t\right)-Q_1\left(t\right)\right),$$

(12)

$$\begin{array}{ccc}\hfill \frac{d{Q}_2}{dt}\left(t\right)& =& \lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)\hfill \\ & & +{\int }_{-\infty }^t[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)]e^{-\frac{2}{\tau }\left(t-\theta \right)}\left(-\frac{2}{\tau }\right)d\theta \hfill \\ & =& \lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)-\frac{2}{\tau }{Q}_2\left(t\right).\hfill \end{array}$$

Thus, we obtain the following 5D model $\left(NPZ{Q}_1{Q}_2\right)$, also called “the strong model”:

$$\left\{\begin{array}{c}\frac{dN\left(t\right)}{dt}=\frac{2}{\tau }{Q}_1\left(t\right)-\mu P\left(t\right)f\left(N\left(t\right)\right),\hfill \\ \frac{dP\left(t\right)}{dt}=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\lambda P\left(t\right),\hfill \\ \frac{dZ\left(t\right)}{dt}=\gamma gZ\left(t\right)h\left(P\left(t\right)\right)-\delta Z\left(t\right),\hfill \\ \frac{d{Q}_1\left(t\right)}{dt}=\frac{2}{\tau }\left(Q_2\left(t\right)-Q_1\left(t\right)\right),\hfill \\ \frac{d{Q}_2}{dt}\left(t\right)=\lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)-\frac{2}{\tau }{Q}_2\left(t\right).\hfill \end{array}\right.$$

(13)

Obviously, the conservation law

$$\frac{d}{dt}(N+P+Z+Q_1+Q_2)=0$$

(14)

is fulfilled, so we can substitute $Q_2\left(t\right)=N_T^2-N\left(t\right)-P\left(t\right)-Z\left(t\right)-Q_1\left(t\right),$ leading to the following reduced 4D system of ordinary differential equations (ODE):

$$\left\{\begin{array}{c}\frac{dN\left(t\right)}{dt}=\frac{2}{\tau }{Q}_1\left(t\right)-\mu P\left(t\right)f\left(N\left(t\right)\right),\hfill \\ \frac{dP\left(t\right)}{dt}=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\lambda P\left(t\right),\hfill \\ \frac{dZ\left(t\right)}{dt}=\gamma gZ\left(t\right)h\left(P\left(t\right)\right)-\delta Z\left(t\right),\hfill \\ \frac{d{Q}_1\left(t\right)}{dt}=\frac{2}{\tau }\left(N_T^2-N\left(t\right)-P\left(t\right)-Z\left(t\right)-2Q_1\left(t\right)\right),\hfill \end{array}\right.$$

(15)

with the phase space

$$D_2=\left\{\left(N,P,Z,Q_1\right)\in R^4,N\ge 0,P\ge 0,Z\ge 0,Q_1>0,N+P+Z+Q_1\le N_T^2\right\}.$$

(16)

Also, for consistency, the initial conditions of the ODE model must satisfy

$$\begin{array}{ccc}\hfill Q_1\left(0\right)& =-& \frac{2}{\tau }{\int }_{-\infty }^0\left[\lambda P\left(\theta \right)+\delta Z\left(\theta \right)+\left(1-\gamma \right)gZ\left(\theta \right)h\left(P\left(\theta \right)\right)\right]\theta e^{\frac{2}{\tau }\theta }d\theta \hfill \end{array}$$

2.3. The Model without Delay

In the absence of delay, the model (1) is described by the following equations:

$$\left\{\begin{array}{c}\frac{dN\left(t\right)}{dt}=\lambda P\left(t\right)+\delta Z\left(t\right)+\left(1-\gamma \right)gZ\left(t\right)h\left(P\left(t\right)\right)-\mu P\left(t\right)f\left(N\left(t\right)\right)\hfill \\ \frac{dP\left(t\right)}{dt}=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\lambda P\left(t\right)\hfill \\ \frac{dZ\left(t\right)}{dt}=\gamma gZ\left(t\right)h\left(P\left(t\right)\right)-\delta Z\left(t\right)\hfill \end{array}\right..$$

(17)

Using conservation law $N_T^0=N\left(t\right)+P\left(t\right)+Z\left(t\right),$ this system can be reduced to the following 2D system:

$$\left\{\begin{array}{c}\frac{dP}{dt}=\mu Pf\left(N_T^0-P-Z\right)-gZh\left(P\right)-\lambda P\hfill \\ \frac{dZ}{dt}=\gamma gZh\left(P\right)-\delta Z\hfill \end{array}\right.,$$

(18)

with the phase space

$$D_0=\left\{\left(P,Z\right)\in {\mathbb{R}}^2,P\ge 0,Z\ge 0,P+Z\le N_T^0\right\}.$$

(19)

In the following, $N_T$ shall denote the biomass of the model. Thus, when referring to the model without delay $N_T=N_T^0$, for the weak model $N_T=N_T^1$, while for the strong model $N_T=N_T^2$.

3. Equilibrium Solutions

In this section, we determine the stationary solutions of the two reduced systems (7) and (15), for the NPZ model with delayed gamma distribution, with one or two degrees of freedom. These solutions correspond to the equilibrium points of the corresponding dynamical systems.

Each of the three systems has at most three equilibrium points în the region of interest, namely:

-

A trivial equilibrium $E_1$, with no phytoplankton and no zooplankton;

-

An equilibrium with phytoplankton and no zooplankton, denoted $E_2$;

-

An equilibrium with both phytoplankton and zooplankton, denoted $E_3$.

These equilibria may coexist for certain values of the total nutrients. The same property is valid for the reduced 2D system (18) for the NPZ model without delay.

3.1. Equilibrium Points for the System without Delay

In [12], it is shown that under the assumptions

$$\lambda <\mu ,\delta <g\gamma$$

(20)

system (18) has at most three equilibrium points in $D_0,$ depending on the value of the total nutrient $N_T.$ Denoting as

$$N_{T_1}=f^{-1}\left(\frac{\lambda }{\mu }\right),N_{T_2}=f^{-1}\left(\frac{\lambda }{\mu }\right)+h^{-1}\left(\frac{\delta }{g\gamma }\right),$$

(21)

the equilibrium points of system (18) are $E_1=\left(0,0\right),$ for all $N_T,$ $E_2=\left(\widehat{P},0\right),$ with $\widehat{P}=N_T-N_{T_1},$ for all $N_T\ge N_{T_1},$ and $E_3=\left(P^{*},Z^{*}\right),$ with $P^{*}=h^{-1}\left(\frac{\delta }{g\gamma }\right),$ and $Z^{*}$ unique solution of the equation

$$Z^{*}=\frac{\mu \gamma }{\delta }{P}^{*}\left(f\left(N_T-P^{*}-Z^{*}\right)-\frac{\lambda }{\mu }\right),$$

(22)

for all $N_T,$ with $N_T\ge N_{T_2}.$

3.2. Equilibrium Points for the Reduced Weak System (7)

The system (7) possesses at most three equilibria with the first three coordinates non-negative, solutions of the system

$$\left\{\begin{array}{c}\frac{1}{\tau }\left(N_T-N-P-Z\right)-\mu Pf\left(N\right)=0\hfill \\ \mu Pf\left(N\right)-gZh\left(P\right)-\lambda P=0\hfill \\ \gamma gZh\left(P\right)-\delta Z=0\hfill \end{array}\right.$$

(23)

It follows that the trivial equilibrium is $E_1=\left(N_T,0,0\right).$

The equilibrium with only phytoplankton is $E_2=\left(\widehat{N},\widehat{P},0\right),$ with $f\left(\widehat{N}\right)=\frac{\lambda }{{}^{\mu }}.$ Taking into account the properties of $f,$ if the condition

$$\lambda <\mu$$

(24)

is satisfied (that is the growth rate of the plankton must be greater than the death rate), then there exists an unique $\widehat{N},$ namely $\widehat{N}=f^{-1}\left(\frac{\lambda }{\mu }\right),$ satisfying this condition. From the first equation we obtain

$$\widehat{P}=\frac{1}{1+\lambda \tau }\left(N_T-\widehat{N}\right).$$

(25)

while from the conservation law we obtain

$$\widehat{Q}=\lambda \tau \widehat{P}.$$

(26)

This equilibrium is in the domain of interest $D_1$ if and only if $N_T\ge \widehat{N}.$ Note that if $N_T=f^{-1}\left(\frac{\lambda }{\mu }\right),$ then $E_1=E_2.$

The equilibrium with both phyto- and zooplankton is $E_3=\left(N^{*},P^{*},Z^{*}\right),$ with $h\left(P^{*}\right)=\frac{\delta }{\gamma g}$ from the third equation in (23). If condition

$$\delta <\gamma g$$

(27)

is satisfied, then there exists an unique $P^{*}>0$ such that $h\left(P^{*}\right)=\frac{\delta }{\gamma g},$ namely

$$P^{*}=h^{-1}\left(\frac{\delta }{\gamma g}\right).$$

(28)

and

$$Z^{*}=\frac{\gamma \mu }{\delta }\left(f\left(N^{*}\right)-\frac{\lambda }{\mu }\right)h^{-1}\left(\frac{\delta }{\gamma g}\right).$$

(29)

The condition $f\left(N^{*}\right)\ge \frac{\lambda }{\mu }$ must be satisfied in order to have $Z^{*}\ge 0.$ As f is an increasing function, it follows that $N^{*}\ge f^{-1}\left(\frac{\lambda }{\mu }\right)$ and using the first equation of system (23) we have

$$\begin{array}{ccc}\hfill N_T& =& N^{*}+P^{*}+Z^{*}+\tau \mu P^{*}f\left(N^{*}\right)\hfill \\ & \ge & f^{-1}\left(\frac{\lambda }{\mu }\right)+\left(1+\lambda \tau \right)h^{-1}\left(\frac{\delta }{\gamma g}\right).\hfill \end{array}$$

To show that there exists an $N^{*}$ such that

$$N_T=N^{*}+P^{*}\left(1-\frac{\gamma \lambda }{\delta }+\mu \left(\tau +\frac{\gamma }{\delta }\right)f\left(N^{*}\right)\right)$$

(30)

is satisfied, consider the function

$$F\left(N\right)=N+\left(1-\frac{\gamma \lambda }{\delta }+\mu \left(\tau +\frac{\gamma }{\delta }\right)f\left(N\right)\right)h^{-1}\left(\frac{\delta }{\gamma g}\right)-N_T.$$

It follows that $F\left(f^{-1}\left(\frac{\lambda }{\mu }\right)\right)<0$ and $\underset{N\to \infty }{lim}F\left(N\right)=\infty .$ As F is an increasing function, there exists an unique value $N^{*}$ such that $F\left(N^{*}\right)=0.$

Denote, as in [12], $N_{T_2}\left(\tau \right)=f^{-1}\left(\frac{\lambda }{\mu }\right)+\left(1+\lambda \tau \right)h^{-1}\left(\frac{\delta }{\gamma g}\right).$ Remark that $N_{T_2}\left(0\right)=N_{T_2}$. As a consequence, the third equilibrium point $\left(N^{*},P^{*},Z^{*}\right)$ exists in $D_1$ and is uniquely determined by (30) if the conditions $N_T\ge N_{T_2}\left(\tau \right)$ and (20) are satisfied. Note that if $N_T=N_{T_2}\left(\tau \right),$ then $E_3=E_2.$ The transitions between the equilibrium points will be discussed further in Section 5.

Finally, we note that if $\left(N_0,P_0,Z_0\right)$ is an equilibrium of system (7), then $\left(N_0,P_0,Z_0,Q_0\right),$ with $Q_0=\tau \mu P_{0}f\left(N_0\right)$ is an equilibrium point for system solution of system (6) and conversely.

In Figure 1, the coordinates $N,P,Z,Q$ of the three equilibrium points are represented as functions of the total nutrient $N_T$, for a fixed $\tau =5$. As function h, a type II functional response was considered. The values of the parameters used for simulations are $\mu =5.9$, $g=7$, $\lambda =0.017$, $\gamma =0.7$, $\delta =0.17$, $k_N=1$, $k_P=1$, as in [12]. For these values of the parameters, the following values where obtained for thresholds: $N_{T_1}=0.0028$, $N_{T_2}\left(\tau \right)=0.0418$.

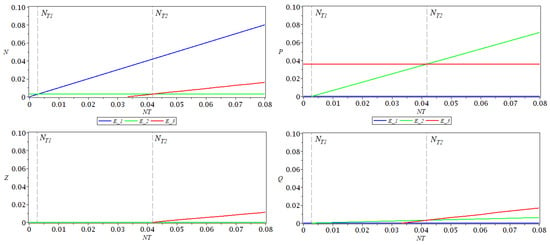
Figure 1. $N,P,Z,Q$ as functions of $N_T$, for fixed $\tau =5$, for the equilibrium points $E_1$ (blue line), $E_2$ (green line), $E_3$ (red line), using a type II response.

3.3. Equilibria for the Reduced Strong Model (15)

The equilibria of system (15) correspond to the solutions of the system

$$\left\{\begin{array}{c}\frac{2}{\tau }{Q}_1-\mu Pf\left(N\right)=0\hfill \\ \mu Pf\left(N\right)-gZh\left(P\right)-\lambda P=0\hfill \\ \gamma gZh\left(P\right)-\delta Z=0\hfill \\ \frac{2}{\tau }\left(N_T-N-P-Z-2Q_1\right)=0\hfill \end{array}\right.$$

(31)

Substituting

$$Q_1=\frac{\tau }{2}\mu Pf\left(N\right),$$

(32)

from the first equation into the last equation in (31), the remaining three equations coincide with system (23). Consequently, we obtain the same expressions for $N,P,$ and Z as for system (23). Taking into account (32), we obtain the following equilibrium points for system (15):

(1)

The trivial equilibrium $E_1=\left(N_T,0,0,0\right),$ for all $N_T\ge 0;$

(2)

The equilibrium with no zooplankton $E_2=\left(\widehat{N},\widehat{P},0,{\widehat{Q}}_1\right),$ with $Q_1=\frac{\tau \lambda }{2}\widehat{P},$

for all $N_T$, with $N_T\ge N_{T_1},$ if $\lambda <\mu$;

(3)

The equilibrium $E_3=\left(N^{*},P^{*},Z^{*},Q_1^{*}\right)$, with $Q_1^{*}=\frac{\mu \tau }{2}f\left(N^{*}\right)h^{-1}\left(\frac{\delta }{\gamma g}\right),$

for all $N_T,$ with $N_T\ge N_{T_2}\left(\tau \right),$ if $\lambda <\mu$ and $\delta <\gamma g$.

Note that if $\left(N_0,P_0,Z_0,Q_0\right)$ is an equilibrium of system (15), then $\left(N_0,P_0,Z_0,Q_0,Q_0\right)$ is an equilibrium point for system solution of system (13) and conversely.

In Figure 2, there are represented the coordinates $N,P,Z,Q_1$ of the three equilibrium points as functions of the total nutrient $N_T$, for a fixed $\tau =5$. As function h, a type III functional response was considered. The values of the parameters used for simulations are $\mu =5.9$, $g=7$, $\lambda =0.017$, $\gamma =0.7$, $\delta =0.17$, $k_N=1$, $k_P=1$, as in [12]. For these values of the parameters, the following values were obtained for stability thresholds: $N_{T_1}=0.0028$, $N_{T_2\left(\tau \right)}=0.2085$, $N_{T_3\left(\tau \right)}=1.0967$. Remark that $E_1=E_2$ at $N_T=N_{T_1}$ and $E_2=E_3$ at $N_T=N_{T_2}\left(\tau \right)$.

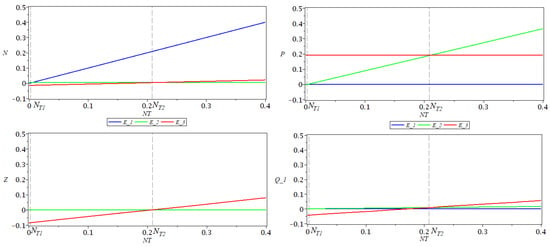
Figure 2. $N,P,Z,Q_1$ as functions of $N_T$, for fixed $\tau =5$, for the equilibrium points $E_1$ (blue line), $E_2$ (green line), $E_3$ (red line), using a type III response.

Comparing the systems with and without delay, we see the following.

• The equilibrium point $E_1$ is unaffected by the delay.
• For the equilibrium point $E_2$, the value of P is reduced by the delay.
• For the equilibrium point $E_3$, the values of N and Z are reduced by the delay.
• The first transition point is unaffected by the delay, $N_{T_1}=N_{T_1}\left(\tau \right),$ while the second transition point is increased by the delay, $N_{T_2}<N_{T_2}\left(\tau \right),$ if $\tau >0.$

4. Local Stability

For all three systems (7), (15) and (18), we find that at each value of the total nutrient at most one of the equilibrium points is locally asymptotically stable. More precisely,

• for $N_T<N_{T_1},$ the only equilibrium point is $E_1,$ and it is asymptotically stable,
• for $N_{T_1}<N_T<N_{T_2}\left(\tau \right)$ the equilibrium $E_2$ is asymptotically stable, while $E_1$ is unstable,
• and, finally, as $N_T>N_{T_2}\left(\tau \right),$ the equilibrium $E_3$ is asymptotically stable either for all $N_T>N_{T_2}\left(\tau \right)$ or there exists an $N_{T_3}\left(\tau \right)$ such that $E_3$ is asymptotically stable for $N_{T_2}\left(\tau \right)<N_T<N_{T_3}\left(\tau \right)$, and unstable for $N_T>N_{T_3}\left(\tau \right),$ depending on the response function $h,$ while the other two equilibria are unstable.

Note that for the system without delay (18), $N_{T_2}$ is equal to $N_{T_2}\left(0\right)$. Our results for $E_1$ and $E_2$ reproduce the results of [12] for the system with general delay (1), while our results for $E_3$ improve those of [12].

Note that, for the two-dimensional reduced system without delay (18), the local stability of the equilibria on the boundary of the domain can be extended to global stability [12]. Those arguments cannot apply for systems (7) and (15). Results on the global stability could be obtained using Lyapunov functions, if they can be constructed.

4.1. The System without Delay

In [12], it is shown that the equilibrium $E_1$ is globally asymptotically stable on $D_0$ if $N_T<N_{T_1},$ the equilibrium $E_2$ is globally asymptotically stable on $D_0,$ except for the z axis, if $N_{T_1}<N_T<N_{T_2},$ while the stability of the equilibrium point $E_3$ depends on the sign of the quantity $T,$ denoting the trace of the Jacobi matrix $J_0$ at $\left(P^{*},Z^{*}\right),$

$$J_0\left(N_T\right)=\left(\begin{array}{cc}\frac{\delta Z^{*}}{\gamma P^{*}}-\mu P^{*}a-g{Z}^{*}b& -\mu P^{*}a-\frac{\delta }{\gamma }\\ \gamma gb{Z}^{*}& 0\end{array}\right).$$

Here, to simplify the expression, we denoted $a=f^{\prime }\left(N_T-P^{*}-Z^{*}\right)$, $b=h^{\prime }\left(P^{*}\right).$

They proved that if $h^{\prime }\left(P^{*}\right)\ge h\left(P^{*}\right)/P^{*},$ then the equilibrium point $E_3$ is stable for all $N_T>N_{T_2}.$ This is valid for a type III zooplankton grazing response function $h.$ While if $h^{\prime }\left(P^{*}\right)<h\left(P^{*}\right)/P^{*},$ then there exists a unique value $N_{T_3}$ of the total nutrient, such that the equilibrium point $E_3$ is asymptotically stable for all $N_{T_2}<N_T<N_{T_3}$ and unstable if $N_T>N_{T_3}.$ The value $N_{T_3}$ is found as the unique solution of the equation $T\left(N_T\right)=0,$ with

$$T\left(N_T\right)=g{Z}^{*}\left(\frac{h\left(P^{*}\right)}{P^{*}}-h^{\prime }\left(P^{*}\right)\right)-\mu P^{*}{f}^{\prime }\left(N_T-P^{*}-Z^{*}\right).$$

(33)

For $N_T=N_{T_3},$ the Jacobi matrix $J_0$ has the purely imaginary eigenvalues ${\lambda }_{1,2}\left(N_T\right)=\pm i{\omega }_0,$ with ${\omega }_0>0,$ ${\omega }_0^2=\gamma gb{Z}^{*}\left(\mu P^{*}a+\frac{\delta }{\gamma }\right).$ Close to $N_{T_3},$ we have $\mathrm{Re}{\lambda }_{1,2}\left(N_T\right)=\frac{1}{2}T\left(N_T\right).$ Consequently,

$$\frac{d}{d{N}_T}\mathrm{Re}{\lambda }_{1,2}\left(N_T\right)=\frac{1}{2}\frac{d}{d{N}_T}T\left(N_T\right)>0,$$

(34)

and thus the transversality condition in the Hopf bifurcation theorem is satisfied. A Hopf bifurcation takes place for $N_T=N_{T_3}$ if the Lyapunov coefficient $L_1\left(N_{T_3}\right)$ is non-zero.

4.2. The Weak Model Case

We analyse here the stability of the equilibrium points for the system (7) corresponding to the gamma distribution delay, with one degree of freedom.

Proposition 1.

For the equilibrium point $E_1$ of system (7), the following statements hold:

(i) 

If $N_T<N_{T_1}$, then $E_1$ is locally asymptotically stable in $D_1$;

(ii) 

If $N_T>N_{T_1}$, then $E_1$ is a (2,1) type saddle point;

(iii) 

If $N_T=N_{T_1}$, then $E_1$ is a fold singularity.

Proof. 

The Jacobian matrix $J_1$ associated to system (7) at $E_1=\left(N_T,0,0\right),$

$$J_1=\left(\begin{array}{ccc}-\frac{1}{\tau }& -\frac{1}{\tau }-\mu f\left(N_T\right)& -\frac{1}{\tau }\\ 0& \mu f\left(N_T\right)-\lambda & 0\\ 0& 0& -\delta \end{array}\right)$$

has the eigenvalues

$${\lambda }_1^1=-\frac{1}{\tau }<0,{\lambda }_2^1=\mu \left(f\left(N_T\right)-\frac{\lambda }{\mu }\right),{\lambda }_3^1=-\delta <0.$$

As two eigenvalues are negative, the topological type of $E_1$ is determined by the sign of ${\lambda }_2^1.$ Thus, the equilibrium point $E_1$ is an attractor if ${\lambda }_2^1<0$, i.e., $f\left(N_T\right)<\frac{\lambda }{\mu }.$ As f is an increasing function, we have ${\lambda }_2^1<0$ if $N_T<f^{-1}\left(\frac{\lambda }{\mu }\right)=N_{T_1}.$ □

Proposition 2.

The equilibrium point $E_2=\left(\widehat{N},\widehat{P},0\right)$ of system (7) is locally asymptotically stable in $D_1$ if and only if

$$N_{T_1}<N_T<N_{T_2}\left(\tau \right).$$

In addition,

(i) 

if $N_T$ $=N_{T_1}$ or $N_T=N_{T_2}\left(\tau \right)$ then $E_2$ is a fold singularity;

(ii) 

if $N_T>N_{T_2}\left(\tau \right)$ then $E_2$ is a saddle point of type (2,1);

(iii) 

if $N_T$ $<N_{T_1}$ then $E_2$ is not in $D_1.$

Proof. 

For the equilibrium $E_2=\left(\widehat{N},\widehat{P},0\right),$ we obtain the Jacobi matrix

$$J_2=\left(\begin{array}{ccc}-\frac{1}{\tau }-\mu \widehat{P}{f}^{\prime }\left(\widehat{N}\right)& -\frac{1}{\tau }-\lambda & -\frac{1}{\tau }\\ \mu \widehat{P}{f}^{\prime }\left(\widehat{N}\right)& 0& -gh\left(\widehat{P}\right)\\ 0& 0& \gamma gh\left(\widehat{P}\right)-\delta \end{array}\right)$$

and the characteristic equation

$$\left(X^2+p_{1}X+p_2\right)\left(X-\gamma gh\left(\widehat{P}\right)+\delta \right)=0$$

with

$$\begin{array}{ccc}\hfill p_1& =& \frac{1}{\tau }+\mu \widehat{P}{f}^{\prime }\left(\widehat{N}\right),\hfill \\ \hfill p_2& =& \frac{\mu \left(1+\lambda \tau \right)}{\tau }\widehat{P}{f}^{\prime }\left(\widehat{N}\right).\hfill \end{array}$$

Thus, one eigenvalue is ${\lambda }_3^2=\gamma g\left(h\left(\widehat{P}\right)-\frac{\delta }{\gamma g}\right)$ and we have ${\lambda }_3^2<0$ if $h\left(\widehat{P}\right)<\frac{\delta }{\gamma g}$(that is $\widehat{P}<P^{*},$ as h is an increasing function). Consequently, ${\lambda }_3^2<0$ iff

$$N_T<f^{-1}\left(\frac{\lambda }{\mu }\right)+\left(1+\lambda \tau \right)h^{-1}\left(\frac{\delta }{\gamma g}\right)=N_{T_2}\left(\tau \right)$$

and ${\lambda }_3^2=0$ if $N_T=N_{T_2}\left(\tau \right)$.

The other two eigenvalues ${\lambda }_1^2,{\lambda }_2^2,$ are solutions of the equation $X^2+p_{1}X+p_2=0.$ Further, if $N_T>N_{T_1},$ it follows that $p_1>0,p_2>0,$ both solutions of this equation have negative real parts. As a consequence, if $N_{T_1}<N_T<N_{T_2}\left(\tau \right)$, all eigenvalues have negative real parts, hence the equilibrium point $E_2$ is an attractor.

Note that if $N_T=N_{T_1},$ then $p_2=0,$ $p_1>0,$ thus ${\lambda }_2^2=0$ and $\mathrm{Re}\left({\lambda }_1^2\right)<0.$ The equilibrium point $E_2$ is a fold singularity both at $N_T=N_{T_1}$ and $N_T=N_{T_2}\left(\tau \right)$. □

For the equilibrium point $E_3=\left(N^{*},P^{*},Z^{*}\right)$ of system (7), the Jacobi matrix reads

$$J_3=\left(\begin{array}{ccc}-\frac{1}{\tau }-\mu Pa& -\frac{1}{\tau }-\mu c& -\frac{1}{\tau }\\ \mu Pa& \mu c-g{Z}^{*}b-\lambda & -\frac{\delta }{\gamma }\\ 0& \gamma g{Z}^{*}b& 0\end{array}\right),$$

where, to simplify computation, we denoted:

$$a=f^{\prime }\left(N^{*}\right)>0,b=h^{\prime }\left(P^{*}\right)>0,c=f\left(N^{*}\right)>0,d=h\left(P^{*}\right)>0,$$

(35)

Thus, the characteristic polynomial of $J_3$ reads

$$X^3+a_1{X}^2+a_{2}X+a_3,$$

(36)

with

$$\begin{array}{ccc}\hfill a_1& =& \frac{1}{\tau }+\lambda -c\mu +\mu P^{*}a+Z^{*}bg\hfill \\ \hfill a_2& =& \frac{1}{\tau }\left(\lambda -c\mu +\mu P^{*}a+Z^{*}bg\right)+g\delta Z^{*}b+\lambda \mu P^{*}a+g\mu P^{*}{Z}^{*}ab\hfill \\ \hfill a_3& =& \frac{g}{\tau }{Z}^{*}b\left(\delta +P^{*}a\gamma \mu +\tau \mu \delta P^{*}a\right)\hfill \end{array}$$

(37)

Using the Routh–Hurwitz criterion [19], all the roots of the characteristic polynomial have negative real parts if and only if the following conditions are satisfied:

$$\left(i\right)a_1>0,\left(ii\right)a_3>0,\left(iii\right)a_1{a}_2-a_3>0.$$

(38)

Thus, the equilibrium point $E_3$ is asymptotically stable if all these conditions are fulfilled. In [12], one result on the stability of $E_3$ with the weak gamma distributed delay was obtained. For completeness and for comparison with the strong gamma distribution case, we repeat that result here with proof.

Proposition 3.

If

$$P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\ge 0,$$

(39)

then the equilibrium $E_3$ of system (7) is locally asymptotically stable for all $N_T>N_{T_2}\left(\tau \right).$

Proof. 

The equilibrium point $E_3$ is stable if all conditions in (38) are fulfilled. To simplify computation, denote

$$A=\mu P^{*}a>0,B=\mu c-\lambda >0,C=\frac{\gamma gb{P}^{*}}{\delta }>0,D=\frac{\delta }{\gamma }>0,T=A+B\left(C-1\right)$$

Note that, $C-1=\frac{\gamma g}{\delta }\left(P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\right)>0$. With these notations, we can write

$$\begin{array}{ccc}\hfill a_1& =& T+\frac{1}{\tau },\hfill \\ \hfill a_2& =& BCD\gamma +ABC+A\lambda +\frac{1}{\tau }T,\hfill \end{array}$$

As all parameters are positive, it follow that $a_3>0.$ As $T>0,$ conditions $a_1>0$ and $a_2>0$ are satisfied. As

$$a_1{a}_2-a_3=AT\left(BC+\lambda \right)+B^{2}CD\gamma \left(C-1\right)+\frac{1-\gamma }{\tau }ABC+\frac{\lambda }{\tau }A+\frac{1}{{\tau }^2}T\left(T\tau +1\right)>0,$$

(40)

condition (iii) in (38) is satisfied. Consequently, all eigenvalues have negative real parts, and $E_3$ is an attractor for all $N_T>N_{T_2}\left(\tau \right).$ □

Proposition 4.

If

$$P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)<0,$$

(41)

the following assertions hold for the equilibrium point $E_3$ of system (7).

(i) 

For $N_T>N_{T_2}\left(\tau \right),$ close to $N_{T_2}\left(\tau \right),$ the equilibrium point $E_3$ is an attractor.

(ii) 

If $a_1{a}_2-a_3>0$, then $E_3$ is locally asymptotically stable.

(iii) 

If $a_1{a}_2-a_3=0$ then $E_3$ is a Hopf singularity.

(iv) 

If $a_1{a}_2-a_3<0$ then $E_3$ is a (1,2) saddle point. In addition, for each τ there exists a value $N_{T_3}\left(\tau \right),$ given by

$$N_{T_3}\left(\tau \right)=min\left\{N_T,N_T>N_{T_2}\left(\tau \right),a_1{a}_2-a_3=0\right\},$$

such that $E_3\left(N_T\right)$ is locally asymptotically stable for all $N_{T_2}\left(\tau \right)<N_T<N_{T_3}\left(\tau \right)$ and unstable for $N_T>N_{T_3}\left(\tau \right),$ close to $N_{T_3}\left(\tau \right).$

Proof. 

(i) The coefficient $a_3$ is equal to 0 if and only $Z^{*}=0$, which occurs when $f\left(N^{*}\right)=\frac{\lambda }{\mu }.$ The discussion following (29) then shows that $a_3=0$ at $N_T=N_{T_2}\left(\tau \right),$ and $a_3>0$ for $N_T>N_{T_2}\left(\tau \right).$

For $N_T=N_{T_2}\left(\tau \right),$ the other two coefficients of the characteristic equation associated to $E_3$,

$$\begin{array}{ccc}\hfill a_1& =& \frac{1}{\tau }+\mu P^{*}a>0,\hfill \\ \hfill a_2& =& \frac{1}{\tau }\mu P^{*}a+\lambda \mu P^{*}a>0,\hfill \end{array}$$

have positive values, and also $a_1{a}_2-a_3=a_1{a}_3>0.$ As the expressions $a_1,a_2,a_1{a}_2-a_3$ are continuous functions of $N_T,$ they remain positive for $N_T>N_{T_2}\left(\tau \right),$ in a neighbourhood of $N_{T_2}\left(\tau \right).$ Hence (i).

(ii) Considering $a_1$ as a function of $N_T,$ we obtain

$$\underset{N_T\to \infty }{lim}{a}_1\left(N_T\right)=\frac{1}{\tau }+\lambda +\frac{\gamma }{\delta }\left(\mu -\lambda \right)P^{*}>\frac{1}{\tau }+\lambda >0.$$

Also,

$$\frac{d{a}_1}{d{N}_T}=\mu \left(P^{*}{f}^{\prime \prime }\left(N^{*}\right)+f^{\prime }\left(N^{*}\right)\left(\frac{P^{*}{h}^{\prime }\left(P^{*}\right)}{h\left(P^{*}\right)}-1\right)\right)\frac{d{N}^{*}}{d{N}_T}$$

Differentiating with respect to $N_T$ in (30), we obtain

$$1=\frac{d{N}^{*}}{d{N}_T}\left(1+\frac{\mu (\gamma +\tau \delta }{\delta }{P}^{*}{f}^{\prime }\left(N^{*}\right)\right),$$

hence $\frac{d{N}^{*}}{d{N}_T}>0.$ As $f^{\prime \prime }<0$ and $\frac{P^{*}{h}^{\prime }\left(P^{*}\right)}{h\left(P^{*}\right)}-1<0$, it follows that $\frac{d{a}_1}{d{N}_T}<0,$ thus $a_1$ is a decreasing function of $N_T.$ Consequently, $a_1>\frac{1}{\tau }+\lambda >0.$ The result follows by applying the Routh–Hurwitz criterion [19].

(iii) The characteristic polynomial (36) has a pair of purely imaginary roots ${\lambda }_{1,2}=\pm \omega i$ if conditions

$$a_2={\omega }^2>0,a_1{a}_2-a_3=0.$$

As $a_1>0,a_3>0$ for all $N_T>N_{T_2}\left(\tau \right),$ if $a_1{a}_2-a_3=0$ then $a_2>0$. Thus, $E_3$ is a Hopf singularity.

(iv) As $a_1>0,a_3>0$ for all $N_T>N_{T_2}\left(\tau \right),$ and $(a_1{a}_2-a_3)\left(N_{T_2}\left(\tau \right)\right)>0,$ it follows that $N_{T_3}\left(\tau \right)$ is the minimum value of $N_T>N_{T_2}\left(\tau \right)$ for which condition $a_1{a}_2-a_3>0$ is not satisfied. □

For the type II response function h, we have

$$P{h}^{\prime }\left(P\right)-h\left(P\right)=-\frac{P^2}{{\left(P+k_P\right)}^2}<0,\forall P\ge 0.$$

In this case, Proposition 4 applies for the stability of the equilibrium point $E_3.$ See Figure 3.

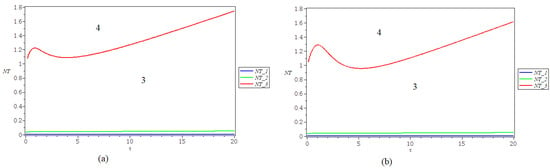
Figure 3. Regions in the $(\tau ,N_T)$ plane that exhibit different behaviours for the equilibrium $E_3$, using the Type II response for: (a) the weak model; (b) the strong model. Region 3 is where the $E_3$ and is stable, but where $E_1$, $E_2$ are unstable. For parameters on the curve separating regions 3 and 4, $E_3$ is a Hopf singularity, while in region 4, $E_3$ is unstable. A Hopf bifurcation may take place when parameters cross from region 3 to region 4.

For the type III response function h, we obtain

$$P{h}^{\prime }\left(P\right)-h\left(P\right)=\frac{\left(k_P^2-P^2\right)P^2}{{\left(P^2+k_P^2\right)}^2}.$$

In this case, if $P^{*}\le k_P$ (i.e., $\frac{\delta }{g\gamma }\le h\left(k_P\right)),$ then $P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\ge 0$ and the equilibrium point $E_3$ is stable for all $N_T>N_{T_2}\left(\tau \right).$ If $h\left(k_P\right)<\frac{\delta }{g\gamma }<1,$ then Proposition 4 applies for the stability of the equilibrium point $E_3.$

4.3. The Strong Model Case

Proposition 5.

The following assertions hold for the equilibrium point $E_1$ of system (15).

(i) 

If $N_T<N_{T_1}$, then $E_1$ is locally asymptotically stable in $D_2.$

(ii) 

If $N_T>N_{T_1}$, then $E_1$ is a (3,1) type saddle point.

(iii) 

If $N_T=N_{T_1}$, then $E_1$ is a fold singularity.

Proof. 

For the equilibrium $E_1=\left(N_T,0,0,0\right)$, we obtain the Jacobi matrix

$$J_1=\left(\begin{array}{cccc}0& -\mu f\left(N_T\right)& 0& \frac{2}{\tau }\\ 0& \mu f\left(N_T\right)-\lambda & 0& 0\\ 0& 0& -\delta & 0\\ -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{4}{\tau }\end{array}\right),$$

and the characteristic polynomial ${\left(X+\frac{2}{\tau }\right)}^2\left(X+\delta \right)\left(X+\lambda -\mu f\left(N_T\right)\right).$ Thus, $J_1$ has the eigenvalues

$${\lambda }_1^1={\lambda }_2^1=-\frac{2}{\tau }<0,{\lambda }_3^1=-\delta <0,{\lambda }_4^1=\mu \left(f\left(N_T\right)-\frac{\lambda }{\mu }\right).$$

As three eigenvalues are negative, the topological type of $E_1$ is determined by the sign of ${\lambda }_4^1.$ Thus, the equilibrium point $E_1$ is an attractor if ${\lambda }_4^1<0$, i.e., $f\left(N_T\right)<\frac{\lambda }{\mu }.$ As f is an increasing function, we obtain ${\lambda }_4^1<0$ if $N_T<f^{-1}\left(\frac{\lambda }{\mu }\right)=N_{T_1}.$ □

Proposition 6.

The equilibrium $E_2=\left(\widehat{N},\widehat{P},0,{\widehat{Q}}_1\right)$ of system (15) is locally asymptotically stable in $D_2$ if and only if

$$N_{T_1}<N_T<N_{T_2}\left(\tau \right).$$

In addition,

(i) 

If $N_T$ $=N_{T_1}$ or $N_T=N_{T_2}\left(\tau \right)$, then the equilibrium $E_2$ is a fold singularity;

(ii) 

If $N_T>N_{T_2}\left(\tau \right)$, then the equilibrium $E_2$ is a saddle point of type (3,1);

(iii) 

If $N_T$ $<N_{T_1}$, then the equilibrium $E_2$ is not in $D_2.$

Proof. 

For the equilibrium $E_2=\left(\widehat{N},\widehat{P},0,{\widehat{Q}}_1\right),$ we obtain the Jacobi matrix

$$J_2=\left(\begin{array}{cccc}-\mu \widehat{P}{f}^{\prime }\left(\widehat{N}\right)& -\lambda & 0& \frac{2}{\tau }\\ \mu \widehat{P}{f}^{\prime }\left(\widehat{N}\right)& 0& -gh\left(\widehat{P}\right)& 0\\ 0& 0& \gamma gh\left(\widehat{P}\right)-\delta & 0\\ -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{4}{\tau }\end{array}\right)$$

and the characteristic equation

$$\left(X^3+p_1{X}^2+p_{2}X+p_3\right)\left(X-\gamma gh\left(\widehat{P}\right)+\delta \right)=0$$

with

$$\begin{array}{ccc}\hfill p_1& =& \frac{4}{\tau }+\mu \widehat{P}{f}^{\prime }\left(\widehat{N}\right),\hfill \\ \hfill p_2& =& \frac{4}{{\tau }^2}+\frac{\mu \left(4+\lambda \tau \right)}{\tau }\widehat{P}{f}^{\prime }\left(\widehat{N}\right),\hfill \\ \hfill p_3& =& \frac{4\mu \left(1+\tau \lambda \right)}{{\tau }^2}\widehat{P}{f}^{\prime }\left(\widehat{N}\right).\hfill \end{array}$$

Thus, one eigenvalue is ${\lambda }_4^2=\gamma g\left(h\left(\widehat{P}\right)-\frac{\delta }{\gamma g}\right)$ and we have ${\lambda }_4^2<0$ if $h\left(\widehat{P}\right)<\frac{\delta }{\gamma g}$(that is $\widehat{P}<P^{*},$ as h is an increasing function). Consequently, ${\lambda }_4^2<0$ if

$$N_T<f^{-1}\left(\frac{\lambda }{\mu }\right)+\left(1+\lambda \tau \right)h^{-1}\left(\frac{\delta }{\gamma g}\right)=N_{T_2}\left(\tau \right)$$

and ${\lambda }_4^2=0$ as $N_T=N_{T_2}\left(\tau \right).$ The other three eigenvalues ${\lambda }_1^2,{\lambda }_2^2,{\lambda }_3^2$ are solutions of the equation $X^3+p_1{X}^2+p_{2}X+p_3=0.$ According to the Routh–Hurwitz criterion, all solutions of this equation have negative real parts if conditions

$$p_1>0,p_3>0,p_1{p}_2>p_3$$

are fulfilled. As all parameters $\mu ,\lambda ,\tau$ are positive, if $N_T>N_{T_1}$ the first two conditions $p_1>0,p_3>0$ are satisfied. A simple computation shows that the third condition is also satisfied if $N_T>N_{T_1}.$ As a consequence, if $N_{T_1}<N_T<N_{T_2}\left(\tau \right)$ all eigenvalues have negative real part, hence the equilibrium point $E_2$ is an attractor.

Note that if $N_T=N_{T_1},$ then $p_3=0,$ $p_1>0,$ $p_2>0,$ thus ${\lambda }_3^2=0$ and $\mathrm{Re}\left({\lambda }_{1,2}^2\right)<0.$ The equilibrium point $E_2$ is a fold singularity both at $N_T=N_{T_1}$ and $N_T=N_{T_2}\left(\tau \right)$. □

For the equilibrium $E_3=\left(N^{*},P^{*},Z^{*},Q_1^{*}\right)$ of system (15), the Jacobi matrix reads

$$J_3=\left(\begin{array}{cccc}-\mu P^{*}{f}^{\prime }\left(N^{*}\right)& -\mu f\left(N^{*}\right)& 0& \frac{2}{\tau }\\ \mu P^{*}{f}^{\prime }\left(N^{*}\right)& \mu f\left(N^{*}\right)-g{Z}^{*}{h}^{\prime }\left(P^{*}\right)-\lambda & -gh\left(P^{*}\right)& 0\\ 0& \gamma g{Z}^{*}{h}^{\prime }\left(P^{*}\right)& \gamma gh\left(P^{*}\right)-\delta & 0\\ -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{4}{\tau }\end{array}\right)$$

and the characteristic polynomial is

$$X^4+b_1{X}^3+b_2{X}^2+b_{3}X+b_4,$$

(42)

with

$$\begin{array}{cc}\hfill b_1& =\frac{4}{\tau }+\mu P^{*}{f}^{\prime }\left(N^{*}\right)+\frac{\gamma g}{\delta }\left(\mu f\left(N^{*}\right)-\lambda \right)\left(P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\right),\hfill \\ \hfill b_2& =\frac{4}{{\tau }^2}+\frac{4}{\tau }\left(\lambda -f\left(N^{*}\right)\mu +\mu P^{*}{f}^{\prime }\left(N^{*}\right)+g{Z}^{*}{h}^{\prime }\left(P^{*}\right)\right)+g\delta Z^{*}{h}^{\prime }\left(P^{*}\right)+\lambda \mu P^{*}{f}^{\prime }\left(N^{*}\right)+g\mu P^{*}{Z}^{*}{f}^{\prime }\left(N^{*}\right)h^{\prime }\left(P^{*}\right)\hfill \\ \hfill b_3& =\frac{4}{\tau }\left(g\delta Z^{*}{h}^{\prime }\left(P^{*}\right)+c{\mu }^2{P}^{*}{f}^{\prime }\left(N^{*}\right)+\mu P^{*}{f}^{\prime }\left(N^{*}\right)\left(\lambda -c\mu +g{Z}^{*}{h}^{\prime }\left(P^{*}\right)\right)\right)+\frac{4}{{\tau }^2}\left(\lambda -c\mu +\mu P^{*}{f}^{\prime }\left(N^{*}\right)+g{Z}^{*}{h}^{\prime }\left(P^{*}\right)\right)\hfill \\ \hfill & +g\delta Z^{*}{h}^{\prime }\left(P^{*}\right)\left(\lambda -c\mu +\mu P{f}^{\prime }\left(N^{*}\right)+gZ{h}^{\prime }\left(P^{*}\right)\right)-g\delta Z{h}^{\prime }\left(P^{*}\right)\left(\lambda -c\mu +gZ{h}^{\prime }\left(P^{*}\right)\right),\hfill \\ \hfill b_4& =\frac{4g}{{\tau }^2}\left(\delta +\mu \left(\gamma +\delta \tau \right)P^{*}{f}^{\prime }\left(N^{*}\right)\right)\frac{\mu \gamma }{\delta }\left(f\left(N^{*}\right)-\frac{\lambda }{\mu }\right)P^{*}{h}^{\prime }\left(P^{*}\right).\hfill \end{array}$$

(43)

Using the Routh–Hurwitz criterion [19], all the roots of the characteristic polynomial have negative real parts if and only if the following conditions are satisfied:

$$\left(i\right)b_1>0,b_2>0,b_3>0,b_4>0,\left(ii\right)b_5=b_1{b}_2-b_3>0,\left(iii\right)b_6=\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4>0.$$

(44)

Thus, the equilibrium point $E_3$ is stable if all these conditions are fulfilled.

Proposition 7.

For the equilibrium point $E_3$ of system (15), the following assertions hold.

(i) 

For $N_T>N_{T_2}\left(\tau \right),$ close to $N_{T_2}\left(\tau \right),$ the equilibrium point $E_3$ is an attractor.

(ii) 

If one of the conditions $b_j>0,$ $j=\overline{1,6}$, in (44) is not satisfied, then $E_3$ is unstable. In addition, for each τ there exists a value $N_{T_3}\left(\tau \right),$ given by

$$N_{T_3}\left(\tau \right)=min\left\{N_T\left|N_T>N_{T_2}\left(\tau \right),\right.{\prod }_{j=1}^6{b}_j=0\right\},$$

such that $E_3$ is locally asymptotically stable for all $N_{T_2}\left(\tau \right)<N_T<N_{T_3}\left(\tau \right).$

Proof. 

The coefficient $b_4$ is equal to 0 if and only $f\left(N^{*}\right)=\frac{\lambda }{\mu }.$ Thus, we have $b_4=0$ at $N_T=N_{T_2}\left(\tau \right),$ and $b_4>0$ for $N_T>N_{T_2}\left(\tau \right).$

At $N_T=N_{T_2}\left(\tau \right),$ the other three coefficients of the characteristic equation associated with $E_3$ have the following values:

$$\begin{array}{cc}\hfill b_1& =\frac{4}{\tau }+\mu P^{*}a>0,\hfill \\ \hfill b_2& =\frac{4}{{\tau }^2}+\frac{4}{\tau }\mu P^{*}a+{\mu }^2{P}^{*}ac>0,\hfill \\ \hfill b_3& =\frac{4}{\tau }{\mu }^2{P}^{*}ac+\frac{4}{{\tau }^2}\mu P^{*}a>0.\hfill \end{array}$$

In addition, we have

$$\begin{array}{cc}\hfill b_5& =\left({\mu }^2{P}^{*}ac+\frac{4}{\tau }\mu P^{*}a\tau +\frac{16}{{\tau }^2}\right)\mu P^{*}a+\frac{16}{{\tau }^3}>0,\hfill \\ \hfill b_6& =b_3{b}_5>0.\hfill \end{array}$$

As the expressions $b_j,j=\overline{1,6},$ are continuous functions of $N_T,$ they remain positive for $N_T>N_{T_2}\left(\tau \right),$ in a neighbourhood of $N_{T_2}\left(\tau \right).$ Hence (i). Obviously, $N_{T_3}\left(\tau \right)$ is the minimum value of $N_T>N_{T_2}\left(\tau \right)$ for which one of the conditions (44) is not satisfied. □

Remark 1.

As for $N_T>N_{T_2}\left(\tau \right),$ we have $b_4>0,$ none of the eigenvalues ${\lambda }_i^3,i=\overline{1,4},$ can be 0. Thus, the topological type of $E_3$ could change only with the appearance of a pair of purely imaginary eigenvalues. Using the Viète relations, if conditions

$$b_1{b}_3>0,\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4=0,$$

(45)

are satisfied, then the equilibrium point $E_3$ is a Hopf singularity. If

$$b_1=0,b_2>0,b_3=0,b_4>0,b_2^2-4b_4>0,$$

(46)

then the equilibrium point $E_3$ has two pairs of purely imaginary eigenvalues and it is a double-Hopf singularity.

Proposition 8.

Assume

$$P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\ge 0,$$

(47)

(i) 

If $\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4>0,$ then the equilibrium $E_3$ of system (15) is locally asymptotically stable for all $N_T>N_{T_2}\left(\tau \right).$

(ii) 

If $\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4=0,$ then $E_3$ is a Hopf singularity.

(iii) 

If $\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4<0,$ then $E_3$ is unstable. In addition, for each τ, there exists a value $N_{T_3}\left(\tau \right),$ given by

$$N_{T_3}\left(\tau \right)=min\left\{N_T\left|N_T>N_{T_2}\left(\tau \right)\right.,\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4=0\right\},$$

such that $E_3$ is locally asymptotically stable for all $N_{T_2}\left(\tau \right)<N_T<N_{T_3}\left(\tau \right).$

Proof. 

The equilibrium point $E_3$ is stable if all conditions in (38) are fulfilled. To simplify computation, denote:

$$\begin{array}{ccc}\hfill a& =& f^{\prime }\left(N^{*}\right)>0,b=h^{\prime }\left(P^{*}\right)>0,c=f\left(N^{*}\right)>0,d=h\left(P^{*}\right)>0,\hfill \\ \hfill A& =& \mu P^{*}a>0,B=\mu c-\lambda >0,C=\frac{\gamma gb{P}^{*}}{\delta }>0,D=\frac{\delta }{\gamma }>0,T=A+B\left(C-1\right)\hfill \end{array}$$

Note that, $C-1=\frac{\gamma g}{\delta }\left(P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\right)>0$. With these notations, we can write:

$$\begin{array}{cc}\hfill b_1& =T+\frac{4}{\tau },\hfill \\ \hfill b_2& =BCD\gamma +ABC+A\lambda +\frac{4}{\tau }T+\frac{4}{{\tau }^2},\hfill \\ \hfill b_3& =ABCD\gamma +\frac{4}{\tau }\left(BCD\gamma +ABC+A\lambda \right)+\frac{4}{{\tau }^2}T,\hfill \\ \hfill b_4& =\frac{1}{{\tau }^2}ABC\gamma \left(AD\tau +A+D\right)\hfill \end{array}$$

As all parameters are positive, it follow that $b_4>0.$ As $T>0,$ conditions $b_1>0,$ $b_2>0,$ $b_3>0$ are satisfied if the hypothesis (47) is true. As

$$b_1{b}_2-b_3=AT\left(BC+\lambda \right)+B^{2}CD\gamma \left(C-1\right)+\frac{4}{{\tau }^3}{\left(T\tau +2\right)}^2,$$

condition $b_1{b}_2-b_3>0$ is satisfied if (47).

Consequently, if $\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4>0,$ then all eigenvalues have negative real parts, thus $E_3$ is an attractor.

If $\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4<0,$ at least two eigenvalues have negative real parts, thus $E_3$ is unstable. As for $N_T=N_{T_2}\left(\tau \right)$ we have

$$\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4=\left({\mu }^2{P}^{*}ac+\frac{4}{\tau }\mu P^{*}a+\frac{24}{{\tau }^2}\right)\mu P^{*}a+\frac{16}{{\tau }^3}>0,$$

the expression continue to be positive for $N_T>N_{T_2}\left(\tau \right),$ close to $N_{T_2}\left(\tau \right).$ Obviously, $N_{T_3}\left(\tau \right)$ is the minimum value of $N_T>N_{T_2}\left(\tau \right)$ for which $\left(b_1{b}_2-b_3\right)b_3-b_1^2{b}_4=0.$ □

In Figure 3, there are represented the strata in the $(\tau ,N_T)$ plane that exhibit different behaviours for the three equilibrium points, obtained in the case of a type II response $h\left(P\right)=\frac{P}{P+k_P}$. The curve denoted NT_1 (blue line) separates the strata where $E_1$ changes stability with $E_2$. The equilibrium $E_2$ is stable for parameters in the stratum limited by the curves NT_1 (blue line) and NT_2 (green line). The equilibrium $E_3$ is stable for parameters in region 3, in the stratum limited by the curves NT_2 (green line) and NT_3 (red line), and loses stability in region 4. The other two equilibria are unstable in regions 3 and 4.

The values of the parameters used for simulations are $\mu =5.9$, $g=7$, $\lambda =0.017$, $\gamma =0.7$, $\delta =0.17$, $k_N=1$, $k_P=1$. The results are consistent with the ones obtained in [12].

5. Local Bifurcations

In the previous section, we proved that at each value of the total nutrients at most one of the equilibrium points is locally asymptotically stable. In this section, we show that the change of stability is realized either through a transcritical bifurcation or a Hopf bifurcation that may occur at a fold singular point or at a Hopf singularity, respectively.

5.1. Transcritical Bifurcations

Two transcritical bifurcations undergo for both the weak and the strong models, namely:

(i)

at $N_T=N_{T_1},$ the equilibrium points $E_1$ and $E_2$ collide and interchange stability;

(ii)

at $N_T=N_{T_2}\left(\tau \right),$ the equilibrium points $E_2$ and $E_3$ collide and interchange stability.

We prove these results by using the Sotomayor theorem [20], ([21], p. 338).

5.1.1. Transcritical Bifurcations for the Weak Model

Proposition 9.

A transcritical bifurcation takes place at the equilibrium $E_1$ of system (7) as $N_T=N_{T_1}$.

Proof. 

As $N_T=N_{T_1}$ we have $E_2=E_1$ and the equilibrium $E_1$ is a fold singularity. We consider $\epsilon =\mu f\left(N_T\right)-\lambda$ as the bifurcation parameter, and the bifurcation value is ${\epsilon }_0=0.$ It follows $\lambda =\mu f\left(N_T\right)-\epsilon ,$ and at $\epsilon =0$ we have $\lambda =\mu f\left(N_{T_1}\right).$ The normal form on the centre manifold is determined using Sotomayor theorem [20,21]. In order to carry this out, consider first two eigenvectors $v,$ $w\in {\mathbb{R}}^4,$ such that $J_{1}v=0$ and $w^T{J}_1=0.$ As for $J_2=J_1=\left(\begin{array}{ccc}-\frac{1}{\tau }& -\frac{1}{\tau }-\lambda & -\frac{1}{\tau }\\ 0& 0& 0\\ 0& 0& -\delta \end{array}\right),$ we obtain that $w^T=\left(0,1,0\right)$ and $v^T=\left(-\left(\lambda \tau +1\right),1,0\right).$ Then, we compute the quantities $A,$ $B,$ C in Sotomayor theorem, where

$$\begin{array}{ccc}\hfill A& =& \frac{1}{⟨v,w⟩}⟨w,\frac{\mathit{\partial }\Phi }{\mathit{\partial }\epsilon }(E_2,{\epsilon }_0)⟩,B=\frac{1}{⟨v,w⟩}\sum _{i,j,k=1}^3{w}_i{v}_j{v}_k\frac{{\mathit{\partial }}^2{\Phi }_i}{\mathit{\partial }{x}_j\mathit{\partial }{x}_k}(E_2,{\epsilon }_0),\hfill \\ \hfill C& =& \frac{2}{⟨v,w⟩}\sum _{i,j=1}^3{w}_i{v}_j\frac{{\mathit{\partial }}^2{\Phi }_i}{\mathit{\partial }{x}_j\mathit{\partial }\epsilon }\left(E_2,{\epsilon }_0\right),\hfill \end{array}$$

with ${\epsilon }_0=0$ and $\left(x_1,x_2,x_3\right)=\left(N,P,Z\right),$ and $\Phi$ is the vector field associated with system (7). As $⟨v,w⟩=1$ and vector w has only one non-zero component, we need only the second component of the vector field $\Phi ,$ which can be written as

$${\Phi }_2\left(N,P,Z\right)=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\left(\mu f\left(N_T\right)-\epsilon \right)P\left(t\right).$$

We obtain

$$\begin{array}{ccc}\hfill A& =& \frac{\mathit{\partial }{\Phi }_2}{\mathit{\partial }\epsilon }(E_2,0)=0,\hfill \\ \hfill B& =& \sum _{j,k=1}^4{v}_j{v}_k\frac{{\mathit{\partial }}^2{\Phi }_2}{\mathit{\partial }{x}_j\mathit{\partial }{x}_k}(E_2,0)=-2\left(\lambda \tau +1\right)\mu f^{\prime }\left(N_{T_1}\right)\ne 0,\hfill \end{array}$$

and

$$C=2\sum _{j=1}^4{v}_j\frac{{\mathit{\partial }}^2{\Phi }_2}{\mathit{\partial }{x}_j\mathit{\partial }\epsilon }\left(E_2,0\right)=2v_2\frac{{\mathit{\partial }}^2{\Phi }_2}{\mathit{\partial }P\mathit{\partial }\epsilon }\left(E_2,0\right)=-2\ne 0.$$

Consequently, a transcritical bifurcation takes place as $\epsilon =0,$ i.e., $f\left(N_T\right)=\frac{\lambda }{\mu }$. □

In a similar way we prove that a transcritical bifurcation takes place when the equilibria $E_2$ and $E_3$ coincides, as $N_T=N_{T_2}\left(\tau \right).$

Proposition 10.

A transcritical bifurcation takes place at the equilibrium $E_2$ of system (7) as $N_T=N_{T_2}\left(\tau \right)$.

Proof. 

As $N_T=N_{T_2}\left(\tau \right)$ we have $E_2=E_3=\left(N_0,P_0,Z_0\right)$, with $N_0=N_{T_1},$ $P_0=\frac{1}{1+\lambda \tau }(N_{T_2}\left(\tau \right)$

$-N_{T_1})$, $Z_0=0,$ and the equilibrium is a fold singularity. We consider $\epsilon =\delta -\gamma gh\left(\widehat{P}\right)$ as the bifurcation parameter, and the bifurcation value is $\epsilon =0.$ Apply the Sotomayor theorem [21] as above. Consider two eigenvectors $v,$ $w\in {\mathbb{R}}^4,$ such that $J_{2}v=0$ and $w^T{J}_2=0.$ As $J_2=\left(\begin{array}{ccc}-\frac{1}{\tau }-\mu P_0{f}^{\prime }\left(N_0\right)& -\frac{1}{\tau }-\lambda & -\frac{1}{\tau }\\ \mu P_0{f}^{\prime }\left(N_0\right)& 0& -\frac{\delta }{\gamma }\\ 0& 0& 0\end{array}\right),$ we obtain that $w^T=\left(0,0,1\right)$ and $v^T=\left(v_1,v_2,v_3\right),$ with $v_1=\frac{\delta }{\gamma \mu P_0{f}^{\prime }\left(N_{T_1}\right)},v_2=-\frac{1}{\lambda \tau +1}\left(\frac{\tau \delta }{\gamma }+1+\frac{\delta }{\gamma \mu P_0{f}^{\prime }\left(N_{T_1}\right)}\right)\ne 0,v_3=1.$ As $⟨v,w⟩=1$ and vector w has only one non-zero component, we need only the third component of the vector field $\Phi ,$ which can be written as

$${\Phi }_3\left(N,P,Z\right)=\gamma gZh\left(P\left(t\right)\right)-\left(\epsilon +\gamma gh\left(\widehat{P}\right)\right)Z.$$

We obtain

$$\begin{array}{ccc}\hfill A& =& \frac{\mathit{\partial }{\Phi }_2}{\mathit{\partial }\epsilon }(E_2,{\epsilon }_0)=0,\hfill \\ \hfill B& =& \sum _{j,k=1}^4{v}_j{v}_k\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }{x}_j\mathit{\partial }{x}_k}(E_2,{\epsilon }_0)=2v_2{v}_3\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }Z\mathit{\partial }P}(E_2,{\epsilon }_0)=2v_2\gamma g{h}^{\prime }\left(P_0\right)\ne 0,\hfill \end{array}$$

and

$$C=2\sum _{j=1}^4{v}_j\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }{x}_j\mathit{\partial }\epsilon }\left(E_2,{\epsilon }_0\right)=2v_3\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }Z\mathit{\partial }\epsilon }\left(E_2,{\epsilon }_0\right)=-2\ne 0.$$

Consequently, a transcritical bifurcation takes place as $\epsilon =0,$ i.e., $N_T=N_{T_2}\left(\tau \right)$. □

Remark 2.

At the bifurcation, point the two equilibria $E_2$ and $E_3$ have the same eigenvalues, ${\lambda }_j^2={\lambda }_j^3,j=\overline{1,3},$ with $\mathrm{Re}{\lambda }_j^2<0,$ for $j=1,2,$ and ${\lambda }_3^2={\lambda }_3^3=0.$ As a consequence of the transcritical bifurcation, the eigenvalues these two eigenvalues change signs when passing through the bifurcation values, while the real parts of the other three pairs of eigenvalues remain negative close to the bifurcation value, due to continuity. Thus, the two equilibria exchange stability. Consequently, close to $N_T=N_{T_2}\left(\tau \right)$, if $N_T<N_{T_2}\left(\tau \right)$ the equilibrium point $E_2$ is an attractor and $E_3$ is a saddle of type (2,1), while if $N_T>N_{T_2}\left(\tau \right)$ the equilibrium point $E_2$ is a saddle of type (2,1) and $E_3$ is an attractor.

5.1.2. Transcritical Bifurcations for the Strong Model

Proposition 11.

A transcritical bifurcation takes place at the equilibrium $E_1$ of system (15) as $N_T=N_{T_1}$.

Proof. 

As $N_T=N_{T_1}$, we have $E_2=E_1$ and the equilibrium is a fold singularity. We consider $\epsilon =\mu f\left(N_T\right)-\lambda$ as the bifurcation parameter, and the bifurcation value is $\epsilon =0.$ It follows $\lambda =\mu f\left(N_T\right)-\epsilon ,$ and at $\epsilon =0$ we have $\lambda =\mu f\left(N_{T_1}\right).$ Consider two eigenvectors $v,$ $w\in {\mathbb{R}}^4,$ such that $J_{2}v=0$ and $w^T{J}_2=0.$ As $J_2=\left(\begin{array}{cccc}0& -\lambda & 0& \frac{2}{\tau }\\ 0& 0& 0& 0\\ 0& 0& -\delta & 0\\ -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{4}{\tau }\end{array}\right),$ we obtain that $w^T=\left(0,1,0,0\right)$ and $v^T=\left(-\left(\lambda \tau +1\right),1,0,\frac{\lambda \tau }{2}\right).$ Then compute the quantities $A,$ $B,$ C in Sotomayor theorem. As $⟨v,w⟩=1$ and vector w has only one non-zero component, we need only the second component of the vector field $\Phi ,$ associated with system (15), which can be written as

$${\Phi }_2\left(N,P,Z,Q_1\right)=\mu P\left(t\right)f\left(N\left(t\right)\right)-gZh\left(P\left(t\right)\right)-\left(\mu f\left(N_T\right)-\epsilon \right)P\left(t\right).$$

We obtain

$$\begin{array}{ccc}\hfill A& =& \frac{\mathit{\partial }{\Phi }_2}{\mathit{\partial }\epsilon }(E_2,0)=0,\hfill \\ \hfill B& =& \sum _{j,k=1}^4{v}_j{v}_k\frac{{\mathit{\partial }}^2{\Phi }_2}{\mathit{\partial }{x}_j\mathit{\partial }{x}_k}(E_2,0)=-2\left(\mu f\left(N_{T_1}\right)\tau +1\right)\mu f^{\prime }\left(N_{T_1}\right)\ne 0,\hfill \end{array}$$

and

$$C=2\sum _{j=1}^4{v}_j\frac{{\mathit{\partial }}^2{\Phi }_2}{\mathit{\partial }{x}_j\mathit{\partial }\epsilon }\left(E_2,0\right)=2v_2\frac{{\mathit{\partial }}^2{\Phi }_2}{\mathit{\partial }P\mathit{\partial }\epsilon }\left(E_2,0\right)=-2\ne 0.$$

Consequently, a transcritical bifurcation takes place as $\epsilon =0,$ i.e., $f\left(N_T\right)=\frac{\lambda }{\mu }$. □

In a similar way, we prove that a transcritical bifurcation takes place when the equilibria $E_2$ and $E_3$ of system (15) coincides, as $N_T=N_{T_2}\left(\tau \right).$

Proposition 12.

A transcritical bifurcation takes place at the equilibrium $E_2$ of system (15) as $N_T=N_{T_2}\left(\tau \right)$.

Proof. 

As $N_T=N_{T_2}\left(\tau \right)$, we have $E_2=E_3=\left(N_0,P_0,Z_0,Q_{10}\right)$, with $N_0=N_{T_1},$ $P_0=\frac{1}{1+\lambda \tau }\left(N_{T_2}\left(\tau \right)-N_{T_1}\right),$ $Z_0=0,$ $Q_{10}=\frac{\lambda \tau }{2}{P}_0,$ and the equilibrium is a fold singularity. We consider $\epsilon =\delta -\gamma gh\left(\widehat{P}\right)$ as the bifurcation parameter, and the bifurcation value is $\epsilon =0.$ Apply the Sotomayor theorem [21] as above. Consider two eigenvectors $v,$ $w\in {\mathbb{R}}^4,$ such that $J_{2}v=0$ and $w^T{J}_2=0.$ As $J_2=\left(\begin{array}{cccc}-\mu Pa& -\lambda & 0& \frac{2}{\tau }\\ \mu Pa& 0& -\frac{\delta }{\gamma }& 0\\ 0& 0& 0& 0\\ -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{2}{\tau }& -\frac{4}{\tau }\end{array}\right),$ we obtain that $w^T=\left(0,0,1,0\right)$ and $v^T=\left(v_1,v_2,v_3,v_4\right),$ with $v_1=\frac{\delta }{\gamma \mu P_0{f}^{\prime }\left(N_{T_1}\right)},v_2=-\frac{1}{\lambda \tau +1}\left(\frac{\tau \delta }{\gamma }+1+\frac{\delta }{\gamma \mu P_0{f}^{\prime }\left(N_{T_1}\right)}\right)\ne 0,v_3=1,$ $v_4=\frac{\tau }{2(\lambda \tau +1)}\left(\frac{\delta }{\gamma }-\left(1+\frac{\delta }{\gamma \mu P_0{f}^{\prime }\left(N_{T_1}\right)}\right)\right).$ As $⟨v,w⟩=1$ and vector w has only one non-zero component, we need only the third component of the vector field $\Phi ,$ which can be written as

$${\Phi }_3\left(N,P,Z,Q_1\right)=\gamma gZh\left(P\left(t\right)\right)-\left(\epsilon +\gamma gh\left(\widehat{P}\right)\right)Z.$$

We obtain

$$\begin{array}{ccc}\hfill A& =& \frac{\mathit{\partial }{\Phi }_3}{\mathit{\partial }\epsilon }(E_2,{\epsilon }_0)=0,\hfill \\ \hfill B& =& \sum _{j,k=1}^4{v}_j{v}_k\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }{x}_j\mathit{\partial }{x}_k}(E_2,{\epsilon }_0)=2v_2{v}_3\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }Z\mathit{\partial }P}(E_2,{\epsilon }_0)=2v_2\gamma g{h}^{\prime }\left(P_0\right)\ne 0,\hfill \end{array}$$

and

$$C=2\sum _{j=1}^4{v}_j\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }{x}_j\mathit{\partial }\epsilon }\left(E_2,{\epsilon }_0\right)=2v_3\frac{{\mathit{\partial }}^2{\Phi }_3}{\mathit{\partial }Z\mathit{\partial }\delta }\left(E_2,{\epsilon }_0\right)=-2\ne 0.$$

Consequently, a transcritical bifurcation takes place as ${\epsilon }_0=0,$ i.e., $N_T=N_{T_2}\left(\tau \right)$. □

Remark 3.

At the bifurcation point the two equilibria $E_2$ and $E_3$ have the same eigenvalues, ${\lambda }_j^2={\lambda }_j^3,j=\overline{1,4},$ with $\mathrm{Re}{\lambda }_j^2<0,$ for $j=1,2,3,$ and ${\lambda }_4^2={\lambda }_4^3=0.$ As a consequence of the transcritical bifurcation, the eigenvalues these two eigenvalues change signs when passing through the bifurcation values, while the real parts of the other three pairs of eigenvalues remain negative close to the bifurcation value, due to continuity. Thus, the two equilibria exchange stability. Consequently, close to $N_T=N_{T_2}\left(\tau \right)$, if $N_T<N_{T_2}\left(\tau \right)$ the equilibrium point $E_2$ is an attractor and $E_3$ is a saddle of type (3,1), while if $N_T>N_{T_2}\left(\tau \right)$ the equilibrium point $E_2$ is a saddle of type (3,1) and $E_3$ is an attractor.

5.2. Hopf Bifurcations

A Hopf bifurcation may occur at a Hopf singularity. As we proved in Section 4, only the equilibrium point $E_3$ is a Hopf non-hyperbolic point, in certain conditions (see Propositions 4, 7 and 8). At such a singular point, a Hopf bifurcation takes place if the conditions of the Hopf bifurcation theorem [22] are fulfilled.

5.2.1. Hopf Bifurcations for the Weak Model

As a consequence of Proposition 3, if $P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\ge 0,$ then the equilibrium point $E_3=\left(N^{*},P^{*},Z^{*}\right)$ of system (7) is locally asymptotically stable for all $N_T>N_{T_2}\left(\tau \right)$, so there can be no Hopf bifurcation in this case.

If $P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)<0,$ then equilibrium point $E_3$ is a Hopf sigularity for parameters in the bifurcation stratum defined by the equation

$$a_1{a}_2-a_3=0,$$

(48)

with $a_1,a_2,a_3$ given by (37). Consequently, for each $N_T>N_{T_2}\left(\tau \right)$ such that (48), a Hopf bifurcation may occur, and a branch of periodic solutions may emerge around $E_3.$

Note that the eigenvalues of the Jacobi matrix associated with $E_3$ are ${\lambda }_{1,2}^1=\pm i\omega ,$ ${\lambda }_3^1=-a_1,$ with ${\omega }^2=a_2.$ Thus, as $a_1>0$, the centre manifold of $E_3$ is attractive. As a consequence, if the conditions of the Andronov–Hopf bifurcation theorem [22] are satisfied and a supercritical Hopf bifurcation takes place (i.e., the first Lyapunov coefficient is negative), then the stable limit cycle born through this bifurcation on the extended centre manifold is locally asymptotically stable.

For the type II response function h, in the hypotheses of Proposition 4, a Hopf bifurcation may take place for each $\tau ,$ at the bifurcation value $N_T=N_{T_3}\left(\tau \right).$

The numerical simulations in Figure 4 show the existence of a stable limit cycle for values of $N_T>N_{T_3}\left(\tau \right).$ The values of the parameters used for simulations are $\mu =5.9$, $g=7$, $\lambda =0.017$, $\gamma =0.7$, $\delta =0.17$, $k_N=1$, $k_P=1$. The results are consistent with the ones obtained in [12]. For $\tau =5$, the approximate value of $N_T$ for the Hopf bifurcation is $N_{T_3}\left(\tau \right)=1.096.$ The simulations show time series for an initial point closed to the equilibrium $E_3$, proving an evolution towards the steady state $E_3$ for $N_T=1.05<N_{T_3}\left(5\right)$ and to a limit cycle for $N_T=1.2>N_{T_3}\left(5\right)$.

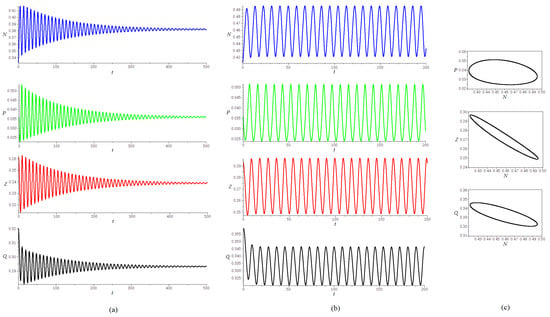
Figure 4. Simulations for the weak model, using a type II response $h\left(P\right)=\frac{P}{P+k_P}$: (a) $\tau =5$, $N_T=1.05$, showing an evolution towards $E_3$; (b) $\tau =5$, $N_T=1.2$, showing a periodic behavior; (c) projections of the attractor, for $\tau =5$, $N_T=1.2$, $t\in [400,500]$. The stable limit cycle may appear through a supercritical Hopf bifurcation at $N_{T_3}\left(\tau \right)=1.096$.

For the type III response function h, for the values of the parameters considered for simulations we have $\frac{\delta }{g\gamma }\le h\left(k_P\right),$ so there are no Hopf bifurcations at $E_3,$ as $N_T>N{T}_2\left(\tau \right).$

5.2.2. Hopf Bifurcation for the Strong Model

According to Proposition 8, if $P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)\ge 0$ the equilibrium point $E_3=\left(N^{*},P^{*},Z^{*},Q_1^{*}\right)$ of system (15) is a Hopf singularity if condition

$$(b_1{b}_2-b_3)b_3-b_1^2{b}_4=0,$$

(49)

with $b_j,j=\overline{1,4}$ given by (43), is satisfied.

If $P^{*}{h}^{\prime }\left(P^{*}\right)-h\left(P^{*}\right)<0,$ the equilibrium point $E_3$ is a Hopf singularity for parameters in the bifurcation stratum defined by the conditions (45). Consequently, for each $N_T>N_{T_2}\left(\tau \right)$ such that (45), a Hopf bifurcation may occur.

For the type II response function h, Proposition 8 does not apply. For the considered values of the parameters, $\mu =5.9$, $g=7$, $\lambda =0.017$, $\gamma =0.7$, $\delta =0.17$, $k_N=1$, $k_P=1$, we have found that, for $(\tau ,N_T)$ on the curve defined by (49) in the $(\tau ,N_T)$ parameter plane, the equilibrium $P^{*}$ is a Hopf singularity. This curve separates regions 3 and 4 in Figure 3b, and a Hopf bifurcation may take place when the parameters cross this curve.

For $\tau =5$, the approximate value of $N_T$ for the Hopf bifurcation is $N_{T_3}\left(\tau \right)=0.955$. The simulations in Figure 5, show the projections of parts of the trajectories for an initial point near the equilibrium $E_3$, proving an evolution towards a stable limit cycle, for (a) $N_T=1.05>N_{T_3}\left(5\right)$, (b) $N_T=1.096>N_{T_3}\left(5\right)$ and (c) $N_T=1.2>N_{T_3}\left(5\right)$.

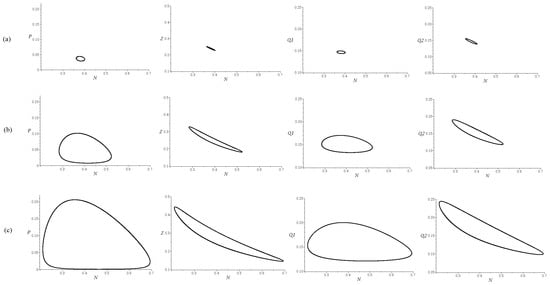
Figure 5. Simulations for the strong model, using a type II response $h\left(P\right)=\frac{P}{P+k_P}$. Projections of the attractor for $\tau =5$ and (a) $N_T=1.05$; (b) $N_T=1.096$; (c) $N_T=1.2$; $t\in [700,800]$. The stable limit cycle may appear through a supercritical Hopf bifurcation at $N_{T_3}\left(\tau \right)=0.955$.

The trajectories in Figure 4 and Figure 5 were obtained using the DEtools package in MAPLE 18, applying the fourth-order Runge–Kutta method, with a stepsize 0.01.

Remark 4.

As the parameters vary away from the Hopf bifurcation curve, the limit cycle born through the Hopf bifurcation may disappear, may double the period, etc. Since the dimensions of both the weak and the strong models are greater than three, strange attractors may also exist. Nevertheless, as the domains for each of the two models are bounded, the ω-limit set for each model is also bounded, and so are their attractors.

6. Discussion

In this study, we have analysed two NPZ models for a closed ecosystem with three compartments, dissolved nutrient, phytoplankton and zooplankton, incorporating a delay in nutrient recycling. The models were obtained starting from a NPZ model introduced in [12], by using the gamma distribution function with one or two degrees of freedom. The aim of the paper was to study how the stability and bifurcation of the equilibrium solutions depend on the total amount of nutrient and the delay.

We have shown that each of the two models have at most three equilibrium points in the region of interest, and that at most one of the equilibrium points is locally asymptotically stable at each value of the total nutrients. More precisely,

(1)

For $N_T<N_{T_1},$ there is only one equilibrium point with no phytoplankton and no zooplankton ($E_1)$, which is asymptotically stable;

(2)

For $N_{T_1}<N_T<N_{T_2}\left(\tau \right)$ the equilibrium $E_2$ with phytoplankton and no zooplankton is asymptotically stable, while $E_1$ is unstable;

(3)

As $N_T>N_{T_2}\left(\tau \right),$ the first two equilibria are unstable, while the equilibrium $E_3$ with both phytoplankton and zooplankton is asymptotically stable either for all $N_T>N_{T_2}\left(\tau \right)$ or there exists an $N_{T_3}\left(\tau \right)$ such that $E_3$ is stable for $N_{T_2}\left(\tau \right)<N_T<N_{T_3}\left(\tau \right)$, and unstable for $N_T>N_{T_3}\left(\tau \right),$ close to $N_{T_3}\left(\tau \right),$ depending on the response function $h.$

Further, we have proven that the changes of stability at $N_{T_1}$ and $N_{T_2}\left(\tau \right)$ occur through transcritical bifurcations. Finally, we have shown that the change of stability at $N_{T_3}$ is a Hopf singularity and the associated bifurcation will lead to stable limit cycles if it is supercritical. Numerical simulations show the existence of stable limit cycles for each delay $\tau ,$ close to the bifurcation value $N_T=N_{T_3}\left(\tau \right).$

Thus, for each of the two considered models, the $\omega$-limit sets contains at most one equilibrium point. In specific hypotheses on the response function h, the $\omega$-limit sets may contain a limit cycle for certain values of the parameters $N_T$ and $\tau$. However, as the dimension of both models is greater than 2, the $\omega$-limit sets may also contain strange attractors.

Our results on the existence of equilibria are consistent with those of [12] for the system with a general distribution (1), who showed the equilibrium values of $N,P,Z$ are only affected by the mean delay and not the form of the distribution. The stability result (1) above reproduces that of [12] for the general distribution case. The stability result (2) is stronger than that of [12] for a general distribution, and thus is likely a consequence of our choice of distributions. In fact, [12] showed that if the system has a discrete delay (Dirac distribution), then the equilibrium $E_2$ may undergo a Hopf bifurcation; however, we show that it is not possible for the distributions we consider. Our results extend those of [12] by proving the stability result (3) for the two systems studied and by proving the types of bifurcations that occur as the stability of the equilibrium points changes. Further, we showed the possibility of a codimension-two double Hopf bifurcation in the system with the two-degrees of freedom gamma distribution.

To conclude, we discuss the implications of our work for application. The general trend of bifurcations of the equilibrium points as the total amount of nutrients is increased is as follows: first, the phytoplankton only equilibrium point, $E_2$, appears and then the coexistence equilibrium point, $E_3$. This is is biologically plausible: as more nutrients are available, the system can support more organisms. Our work highlights the fact that a delay in the recycling can be stabilizing: the amount of nutrients needed for the transcritical bifurcation leading to the emergence of $E_3$ to occur increases with the size of the mean delay. We also showed, for a given amount of total nutrients, the delay decreases the equilibrium size of at least one of $N,P,Z$. This is because some of the nutrients are stored in the other compartments of the system, which represent the nutrients that are being recycled. Both these results were identical for the weak and strong models. Where these models differ was in the effect of the delay on the Hopf bifurcation of the $E_3$ equilibrium point. For both models, as the delay is increased we observe the same qualitative effect: the Hopf bifurcation value $N_{T3}$ increases, then decreases, then increases. However, the variation is larger for the strong model than for the weak model. Thus, the $N_{T3}$ for the weak model is less than that for the strong model for small enough delay, with the reverse for large enough delay.