A Proposed Analytical and Numerical Treatment for the Nonlinear SIR Model via a Hybrid Approach

Abstract

This paper re-analyzes the nonlinear Susceptible–Infected–Recovered (SIR) model using a hybrid approach based on the Laplace–Padé technique. The proposed approach is successfully applied to extract several analytic approximations for the infected and recovered individuals. The domains of applicability of such analytic approximations are addressed. In addition, the present results are validated through various comparisons with the Runge–Kutta numerical method. The obtained analytical results agree with the numerical ones for a wide range of numbers of contacts featured in the studied model. The efficiency of the present analysis reveals that it can be implemented to deal with other systems describing real-life phenomena.

1. Introduction

Mathematical models of real-life phenomena are often governed by ordinary differential equations (ODEs) or partial differential equations (PDEs). Searching for analytical or numerical solutions for such models requires accurate methods, whether analytical or numerical, for the better interpretation of the involved phenomena. In this context, mathematicians have invented and developed many ways to solve mathematical and physical models. For example, the Adomian decomposition method (ADM) [1,2,3,4,5,6,7,8,9,10,11] is one of the most popular methods which has been widely used during recent decades; the same applies to the homotopy perturbation method (HPM) [12,13,14,15], the homotopy analysis method (HAM) [16,17], and the differential transform method (DTM) [18,19,20,21]. However, each of these methods has its own advantages, but at the same time has some defects that must be faced and overcome. Although the above-mentioned methods were found effective in solving a considerable number of mathematical/physical models, a massive amount of computational work is sometimes needed to reach the desired accuracy. The major step when applying the ADM is to calculate the Adomian polynomials of the involved nonlinear terms, while the HPM requires an effective canonical form for the equation/system being solved in addition to imposing an auxiliary parameter. Moreover, one of the main difficulties of the HAM lies in the necessity of choosing an effective/accurate initial guess function, according to which the solution is constructed. Therefore, any unfavorable choice of such an initial guess function will give either an inaccurate or divergent solution.

In order to avoid all the aforementioned difficulties, we will present in this study an alternative approach that may be appropriate and direct to solve ODEs. The first step of the suggested approach is mainly based on obtaining a series solution of the governing equation and then deriving the Laplace transform (LT) of this series. The second step is to construct the Padé approximants of the transformed series and then apply the inverse LT as a final step to construct the approximate analytic solution. For this purpose, it is possible to construct different forms of Padé approximants, including diagonal and non-diagonal. Accordingly, different approximations can be constructed for the required analytic solution. The accuracy of our approach can be validated via performing comparisons with other trusted methods, whether analytical or numerical. In addition, the accuracy of the current method can be evaluated, independently, through calculating the residual errors resulting from the substitution of the obtained approximate analytic solution into the governing equation/system.

The nonlinear Susceptible–Infected–Recovered (SIR) model is considered in this paper as a test example. The SIR model has been employed in Refs. [22,23] to study the COVID-19 pandemic, which is still of interest to many researchers worldwide. The SIR model was first established in Ref. [22] by means of the following system of ODEs:

$$\begin{array}{ccc}& & \frac{dR}{d\tau }=I\left(\tau \right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & \frac{dI}{d\tau }=\sigma \left[1-R\left(\tau \right)-I\left(\tau \right)\right]I\left(\tau \right)-I\left(\tau \right),\hfill \end{array}$$

(2)

where $I\left(t\right)$ and $R\left(t\right)$ are the infected and the recovered individuals, respectively. $S\left(t\right)$ represents the susceptible individuals, $S\left(t\right)=1-R\left(t\right)-I\left(t\right)$. The parameter $\sigma$ describes the transmission rate, which is used to estimate the number of contacts between susceptible and infected individuals. The initial conditions (ICs) are

$$R\left(0\right)=A,I\left(0\right)=B.$$

(3)

A summary of the paper is as follows. In Section 2, a power series solution (PSS) for the system (1)–(3) is derived. Section 3 focuses on applying the proposed approach through combining the LT and the Padé approximants. Furthermore, different analytical approximations for $R\left(\tau \right)$ and $I\left(\tau \right)$ are established in Section 3. Section 4 is devoted to validating the obtained results, where several comparisons with the Runge–Kutta method are conducted. Moreover, the domains of applicability of the current analysis are demonstrated and addressed in Section 4. In addition, the accuracy of our approach is explored and confirmed via residual errors. The paper is concluded in Section 5.

2. The Series Solution

The system of Equations (1) and (2) can be easily reduced to the following second-order nonlinear ODE:

$$\frac{d^{2}R}{d{\tau }^2}=(\sigma -1)\frac{dR}{d\tau }-\sigma \left(R+\frac{dR}{d\tau }\right)\frac{dR}{d\tau },$$

(4)

under the ICs

$$R\left(0\right)=A,\frac{dR\left(0\right)}{d\tau }=B.$$

(5)

Let us search for a power series solution (PSS) of Equations (4) and (5) in the form:

$$R\left(\tau \right)=\sum _{n=0}^{\infty }{a}_n{\tau }^n.$$

(6)

In view of (5) and (6), the terms $a_0$ and $a_1$ are A and B, respectively. Furthermore, we have

$$\left(R+\frac{dR}{d\tau }\right)\frac{dR}{d\tau }=\sum _{n=0}^{\infty }\sum _{k=0}^n(n-k+1)\left(a_k+(k+1)a_{k+1}\right)a_{n-k+1}{\tau }^n.$$

(7)

Substituting (6) and (7) into (4) implies

$$a_{n+2}=\frac{(\sigma -1)a_{n+1}}{n+2}-\frac{\sigma }{(n+1)(n+2)}\sum _{k=0}^n(n-k+1)\left(a_k+(k+1)a_{k+1}\right)a_{n-k+1},n\ge 0.$$

(8)

Using the initial terms $a_0=A$ and $a_1=B$, the coefficients of the series can be generated and are given as

$$\begin{array}{c}{a}_2=-\frac{1}{2}B\left(1+\sigma (B+A-1)\right),\hfill \end{array}$$

(9)

$$\begin{array}{c}{a}_3=\frac{1}{6}B{\left(1+\sigma (B+A-1)\right)}^2+\frac{1}{6}{\sigma }^2{B}^2\left(B+A-1\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}{a}_4=\hfill & -\frac{1}{24}B{\left(1+\sigma (B+A-1)\right)}^3-\frac{1}{6}{\sigma }^2{B}^2\left(1+\sigma (B+A-1)\right)\left(B+A-1\right)-\hfill \\ & \frac{1}{24}{\sigma }^3{B}^3\left(B+A-1\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}{a}_5=\hfill & \frac{1}{120}B{\left(1+\sigma (B+A-1)\right)}^4+\frac{11}{120}{\sigma }^2{B}^2\left(B+A-1\right)+\frac{1}{120}{\sigma }^3{B}^3\left(B+A-1\right)\times \hfill \\ & \left[7+11\sigma \left(B+A-1\right)\right]+\frac{1}{120}{\sigma }^4{B}^4\left(B+A-1\right),\hfill \end{array}$$

(12)

and so on. Employing the above coefficients in Equation (6), we obtain the following PSS for $R\left(\tau \right)$:

$$\begin{array}{cc}R\left(\tau \right)=\hfill & A+B\tau -B\left(1+\sigma (B+A-1)\right)\frac{{\tau }^2}{2!}+\left[B{\left(1+\sigma (B+A-1)\right)}^2+{\sigma }^2{B}^2\left(B+A-1\right)\right]\frac{{\tau }^3}{3!}+\hfill \\ & \left[-B{\left(1+\sigma (B+A-1)\right)}^3-4{\sigma }^2{B}^2\left(1+\sigma (B+A-1)\right)\left(B+A-1\right)-{\sigma }^3{B}^3\left(B+A-1\right)\right]\frac{{\tau }^4}{4!}+\hfill \\ & [B{\left(1+\sigma (B+A-1)\right)}^4+11{\sigma }^2{B}^2\left(B+A-1\right)+{\sigma }^3{B}^3\left(B+A-1\right)\left[7+11\sigma \left(B+A-1\right)\right]+\hfill \\ & {\sigma }^4{B}^4\left(B+A-1\right)]\frac{{\tau }^5}{5!}+\dots ,\hfill \end{array}$$

(13)

while the PSS for $I\left(\tau \right)$ can be obtained through differentiating (6) once with respect to $\tau$, which gives

$$I\left(\tau \right)=\sum _{n=0}^{\infty }(n+1)a_{n+1}{\tau }^n.$$

(14)

i.e.,

$$\begin{array}{cc}I\left(\tau \right)=\hfill & B-B\left(1+\sigma (B+A-1)\right)\tau +\left[B{\left(1+\sigma (B+A-1)\right)}^2+{\sigma }^2{B}^2\left(B+A-1\right)\right]\frac{{\tau }^2}{2!}+\hfill \\ & \left[-B{\left(1+\sigma (B+A-1)\right)}^3-4{\sigma }^2{B}^2\left(1+\sigma (B+A-1)\right)\left(B+A-1\right)-{\sigma }^3{B}^3\left(B+A-1\right)\right]\frac{{\tau }^3}{3!}+\hfill \\ & [B{\left(1+\sigma (B+A-1)\right)}^4+11{\sigma }^2{B}^2\left(B+A-1\right)+{\sigma }^3{B}^3\left(B+A-1\right)\left[7+11\sigma \left(B+A-1\right)\right]+\hfill \\ & {\sigma }^4{B}^4\left(B+A-1\right)]\frac{{\tau }^4}{4!}+\dots ,\hfill \end{array}$$

(15)

where the terms of the preceding PSS may be increased as needed to ensure the desired accuracy. However, it will be shown later that the PSS has limitations regarding the domain of convergence. Such drawbacks can be overcome by the current approach which is the subject of the next section.

3. The Laplace–Padé Technique

3.1. Approximation for $R\left(\tau \right)$

Applying the Laplace transform (LT) to series (6) yields

$$\overline{R}\left(s\right)=\frac{a_0}{s}+\frac{a_1}{s^2}+\frac{2a_2}{s^3}+\frac{6a_3}{s^4}+\frac{24a_4}{s^5}+\frac{120a_5}{s^6}+\dots .$$

(16)

Suppose that $s_1=1/s$; then,

$$\overline{R}\left(s_1\right)=a_0{s}_1+a_1{s}_1^2+2a_2{s}_1^3+6a_3{s}_1^4+24a_4{s}_1^5+120a_5{s}_1^6+\dots$$

(17)

Constructing Padé [1/1] for the last series gives

$${\overline{R}}_{[1/1]}\left(s_1\right)=\frac{a_0{s}_1}{1-\frac{a_1}{a_0}{s}_1}.$$

(18)

Reversing the last expression with respect to s, we obtain

$${\overline{R}}_{[1/1]}\left(s\right)=\frac{a_0}{s-\frac{a_1}{a_0}}.$$

(19)

The inversion of ${\overline{R}}_{[1/1]}\left(s\right)$ gives the approximation $R_{[1/1]}\left(\tau \right)$ as

$$R_{[1/1]}\left(\tau \right)=a_0{e}^{\frac{a_1}{a_0}\tau }.$$

(20)

The Padé [1/2] for series (17) is

$${\overline{R}}_{[1/2]}\left(s_1\right)=\frac{a_0{s}_1}{1-q_1{s}_1+q_2{s}_1^2},$$

(21)

where

$$q_1=\frac{a_1}{a_0},q_2={\left(\frac{a_1}{a_0}\right)}^2-\frac{2a_2}{a_0}.$$

(22)

Equation (21) implies

$${\overline{R}}_{[1/2]}\left(s\right)=\frac{a_{0}s}{s^2-q_{1}s+q_2},$$

(23)

and hence,

$$R_{[1/2]}\left(\tau \right)=a_0{e}^{\frac{1}{2}{q}_1\tau }\left[cosh\left(\frac{1}{2}\sqrt{q_1^2-4q_2}\tau \right)+\frac{q_1}{\sqrt{q_1^2-4q_2}}sinh\left(\frac{1}{2}\sqrt{q_1^2-4q_2}\tau \right)\right],$$

(24)

provided that

$$q_1^2-4q_2>0.$$

(25)

This expression transforms to the trigonometric form

$$R_{[1/2]}\left(\tau \right)=a_0{e}^{\frac{1}{2}{q}_1\tau }\left[cos\left(\frac{1}{2}\sqrt{4q_2-q_1^2}\tau \right)+\frac{q_1}{\sqrt{4q_2-q_1^2}}sin\left(\frac{1}{2}\sqrt{4q_2-q_1^2}\tau \right)\right],$$

(26)

when

$$4q_2-q_1^2>0.$$

(27)

From (17), we have the following expression for Padé [2/2] $\left(s_1\right)$:

$${\overline{R}}_{[2/2]}\left(s_1\right)=\frac{a_0{s}_1+p_1{s}_1^2}{1-r_1{s}_1+r_2{s}_1^2},$$

(28)

where

$$p_1=\frac{a_1^3-4a_0{a}_1{a}_2+6a_0^2{a}_3}{a_1^2-2a_0{a}_2},r_1=\frac{2(a_1{a}_2-3a_0{a}_3)}{a_1^2-2a_0{a}_2},r_2=\frac{2(2a_2^2-3a_1{a}_3)}{a_1^2-2a_0{a}_2}.$$

(29)

Based on (28), we have

$${\overline{R}}_{[2/2]}\left(s\right)=\frac{a_{0}s+p_1}{s^2-r_{1}s+r_2},$$

(30)

which leads to

$$R_{[2/2]}\left(\tau \right)=e^{\frac{1}{2}{r}_1\tau }\left[a_{0}cosh\left(\frac{1}{2}\sqrt{r_1^2-4r_2}\tau \right)+\frac{2p_1+a_0{r}_1}{\sqrt{r_1^2-4r_2}}sinh\left(\frac{1}{2}\sqrt{r_1^2-4r_2}\tau \right)\right],r_1^2-4r_2>0,$$

(31)

or equivalently,

$$R_{[2/2]}\left(\tau \right)=e^{\frac{1}{2}{r}_1\tau }\left[a_{0}cos\left(\frac{1}{2}\sqrt{4r_2-r_1^2}\tau \right)+\frac{2p_1+a_0{r}_1}{\sqrt{4r_2-r_1^2}}sin\left(\frac{1}{2}\sqrt{4r_2-r_1^2}\tau \right)\right],4r_2-r_1^2>0.$$

(32)

Similarly, one can obtain

$${\overline{R}}_{[2/3]}\left(s\right)=\frac{a_0{s}^2+u_{1}s}{s^3-v_1{s}^2+v_{2}s+v_3},$$

(33)

which can be inverted to give

$$R_{[2/3]}\left(\tau \right)=h_1{e}^{z_1\tau }+h_2{e}^{z_2\tau }+h_3{e}^{z_3\tau },$$

(34)

where the quantities $u_1$, $v_i$ and $h_i$ ($i=1,2,3$) are given by

$$\begin{array}{ccc}& & u_1=\frac{a_1^4-6a_0{a}_1^2{a}_2+4a_0^2{a}_2^2+12a_0^2{a}_1{a}_3-24a_0^3{a}_4}{a_1^3-4a_0{a}_1{a}_2+6a_0^2{a}_3},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}& & v_1=\frac{2\left(a_1^2{a}_2-2a_0{a}_2^2-3a_0{a}_1{a}_3+12a_0^2{a}_4\right)}{a_1^3-4a_0{a}_1{a}_2+6a_0^2{a}_3},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}& & v_2=\frac{2\left(2a_1{a}_2^2-3a_1^2{a}_3-6a_0{a}_2{a}_3+12a_0{a}_1{a}_4\right)}{a_1^3-4a_0{a}_1{a}_2+6a_0^2{a}_3},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}& & v_3=\frac{4\left(-2a_2^3+6a_1{a}_2{a}_3-9a_0{a}_3^2-6a_1^2{a}_4+12a_0{a}_2{a}_4\right)}{a_1^3-4a_0{a}_1{a}_2+6a_0^2{a}_3},\hfill \end{array}$$

(38)

and

$$h_1=\frac{a_0{z}_1^2+u_1{z}_1}{(z_1-z_2)(z_1-z_3)},h_2=\frac{a_0{z}_2^2+u_1{z}_2}{(z_2-z_1)(z_2-z_3)},h_3=\frac{a_0{z}_3^2+u_1{z}_3}{(z_3-z_1)(z_3-z_2)}.$$

(39)

Furthermore, $z_1$, $z_2$, and $z_3$ are three distinct roots of the cubic algebraic equation

$$z^3-v_1{z}^2+v_{2}z+v_3=0.$$

(40)

Furthermore, we can calculate the diagonal Padé approximant ${\overline{R}}_{[3/3]}\left(s\right)$ as

$${\overline{R}}_{[3/3]}\left(s\right)=\frac{a_0{s}^2+w_{1}s+w_2}{s^3-d_1{s}^2+d_{2}s+d_3},$$

(41)

which has the following inversion:

$$R_{[3/3]}\left(\tau \right)=l_1{e}^{m_1\tau }+l_2{e}^{m_2\tau }+l_3{e}^{m_3\tau },$$

(42)

where the quantities $w_1$, $w_2$, $d_i$ and $l_i$ ($i=1,2,3$) are

$$\begin{array}{c}{w}_1=\frac{2\left(a_1{a}_2^3-3a_1^2{a}_2{a}_3-3a_0{a}_2^2{a}_3+9a_0{a}_1{a}_3^2+3a_1^3{a}_4-18a_0^2{a}_3{a}_4-15a_0{a}_1^2{a}_5+30a_0^2{a}_2{a}_5\right)}{2a_2^3-6a_1{a}_2{a}_3+9a_0{a}_3^2+6a_1^2{a}_4-12a_0{a}_2{a}_4},\hfill \end{array}$$

(43)

$$\begin{array}{cc}{w}_2=\hfill & (4a_2^4-18a_1{a}_2^2{a}_3+9a_1^2{a}_3^2+36a_0{a}_2{a}_3^2+24a_1^2{a}_2{a}_4-48a_0{a}_2^2{a}_4-72a_0{a}_1{a}_3{a}_4+144a_0^2{a}_4^2-\hfill \\ & 30a_1^3{a}_5+120a_0{a}_1{a}_2{a}_5-180a_0^2{a}_3{a}_5)/(2a_2^3-6a_1{a}_2{a}_3+9a_0{a}_3^2+6a_1^2{a}_4-12a_0{a}_2{a}_4),\hfill \end{array}$$

(44)

$$\begin{array}{ccc}& & d_1=\frac{3\left(2a_2^2{a}_3-3a_1{a}_3^2-4a_1{a}_2{a}_4+12a_0{a}_3{a}_4+10a_1^2{a}_5-20a_0{a}_2{a}_5\right)}{2a_2^3-6a_1{a}_2{a}_3+9a_0{a}_3^2+6a_1^2{a}_4-12a_0{a}_2{a}_4},\hfill \end{array}$$

(45)

$$\begin{array}{ccc}& & d_2=\frac{6\left(3a_2{a}_3^2-4a_2^2{a}_4-6a_1{a}_3{a}_4+24a_0{a}_4^2+10a_1{a}_2{a}_5-30a_0{a}_3{a}_5\right)}{2a_2^3-6a_1{a}_2{a}_3+9a_0{a}_3^2+6a_1^2{a}_4-12a_0{a}_2{a}_4},\hfill \end{array}$$

(46)

$$\begin{array}{ccc}& & d_3=\frac{6\left(-9a_3^3+24a_2{a}_3{a}_4-24a_1{a}_4^2-20a_2^2{a}_5+30a_1{a}_3{a}_5\right)}{2a_2^3-6a_1{a}_2{a}_3+9a_0{a}_3^2+6a_1^2{a}_4-12a_0{a}_2{a}_4},\hfill \end{array}$$

(47)

and

$$l_1=\frac{a_0{m}_1^2+w_1{m}_1+w_2}{(m_1-m_2)(m_1-m_3)},l_2=\frac{a_0{m}_2^2+w_1{m}_2+w_2}{(m_2-m_1)(m_2-m_3)},l_3=\frac{a_0{m}_3^2+w_1{m}_3+w_2}{(m_3-m_1)(m_3-m_2)}.$$

(48)

while $m_i$, $i=1,2,3$ are three distinct roots of the cubic equation

$$m^3-d_1{m}^2+d_{2}m+d_3=0.$$

(49)

Remark 1.

It should be noted that the inversion of Equation (41) depends on the three roots of the denominator. To clarify this point, assume that $m_i$, $i=1,2,3$ are three distinct roots of the denominator in (41), i.e., $s^3-d_1{s}^2+d_{2}s+d_3=(s-m_1)(s-m_2)(s-m_3)$; then, one can rewrite Equation (41) as

$${\overline{R}}_{[3/3]}\left(s\right)=\frac{a_0{s}^2+w_{1}s+w_2}{s^3-d_1{s}^2+d_{2}s+d_3}=\frac{a_0{s}^2+w_{1}s+w_2}{(s-m_1)(s-m_2)(s-m_3)}.$$

Using partial fractions, we can express ${\overline{R}}_{[3/3]}\left(s\right)$ as

$${\overline{R}}_{[3/3]}\left(s\right)=\frac{l_1}{s-m_1}+\frac{l_2}{s-m_2}+\frac{l_3}{s-m_3},$$

where $l_i$, $i=1,2,3$ are given by Equation (48). It is now clear that the inversion of ${\overline{R}}_{[3/3]}\left(s\right)$ in the last equation gives Formula (42).

3.2. Approximation for $I\left(\tau \right)$

Proceeding as above, one can obtain

$${\overline{I}}_{[1/1]}\left(s\right)=\frac{a_1}{s-\frac{2a_2}{a_1}},$$

(50)

and

$${\overline{I}}_{[2/2]}\left(s\right)=\frac{a_{1}s+b_1}{s^2-c_{1}s+c_2}.$$

(51)

The inversions of the above expressions give

$$I_{[1/1]}\left(\tau \right)=a_1{e}^{\frac{2a_2}{a_1}\tau },$$

(52)

and

$$I_{[2/2]}\left(\tau \right)=e^{\frac{1}{2}{c}_1\tau }\left[a_{1}cosh\left(\frac{1}{2}\sqrt{c_1^2-4c_2}\tau \right)+\frac{2b_1+a_1{c}_1}{\sqrt{c_1^2-4c_2}}sinh\left(\frac{1}{2}\sqrt{c_1^2-4c_2}\tau \right)\right],c_1^2-4c_2>0,$$

(53)

where

$$b_1=\frac{4(a_2^3-3a_1{a}_2{a}_3+3a_1^2{a}_4)}{2a_2^2-3a_1{a}_3},c_1=\frac{6(a_2{a}_3-2a_1{a}_4)}{2a_2^2-3a_1{a}_3},c_2=\frac{6(3a_3^2-4a_2{a}_4)}{2a_2^2-3a_1{a}_3}.$$

(54)

The approximation $I_{[3/3]}\left(\tau \right)$ can also be established using the same procedure. However, it will be shown later that $I_{[2/2]}\left(\tau \right)$ is sufficient to achieve the desired accuracy.

4. Results and Validation

In this section, we focus on validating the accuracy of the current analysis. Various comparisons are performed to reveal the validity of the present PSS and the Padé approximants for the recovered and infected individuals $R\left(\tau \right)$ and $I\left(\tau \right)$, respectively. The explicit Runge–Kutta method (ERKM) is chosen as a reference numerical method to explore the effectiveness and efficiency of our accuracy.

To achieve this task, we may express the j-term of the PSS for $R\left(\tau \right)$ and $I\left(\tau \right)$, respectively, as

$${\Phi }_j\left(\tau \right)=\sum _{n=0}^{j-1}{a}_n{\tau }^n,{\Psi }_j\left(\tau \right)=\sum _{n=0}^{j-1}(n+1)a_{n+1}{\tau }^n.$$

(55)

Before launching into the main target of this section, we may shed some light on the domains of applicability/inapplicability for the expressions of $R_{[2/2]}\left(\tau \right)$ and $I_{[2/2]}\left(\tau \right)$ in Equations (31) and (53), respectively. It can be noted from Figure 1 that the approximation $R_{[2/2]}\left(\tau \right)$ is applicable in certain domains for A and B when $\sigma =0.7$. However, Figure 2 shows that the corresponding approximation $I_{[2/2]}\left(\tau \right)$, at $\sigma =0.7$, is applicable in all possible domains of A and B provided that $A+B=1$ is not satisfied, i.e., $A+B\ne 1$. Actually, it can be declared that the restriction $A+B=1$ leads to exact expressions of $R\left(\tau \right)$ and $I\left(\tau \right)$. In such cases, the PSS (13) reduces to

$$R\left(\tau \right)=A+B\left(\tau -\frac{{\tau }^2}{2!}+\frac{{\tau }^3}{3!}-\frac{{\tau }^4}{4!}+\frac{{\tau }^5}{5!}+\dots \right)=1-B{e}^{-\tau },$$

(56)

while the PSS (15) becomes

$$I\left(\tau \right)=B\left(\tau -\frac{{\tau }^2}{2!}+\frac{{\tau }^3}{3!}-\frac{{\tau }^4}{4!}+\frac{{\tau }^5}{5!}+\dots \right)=B{e}^{-\tau }.$$

(57)

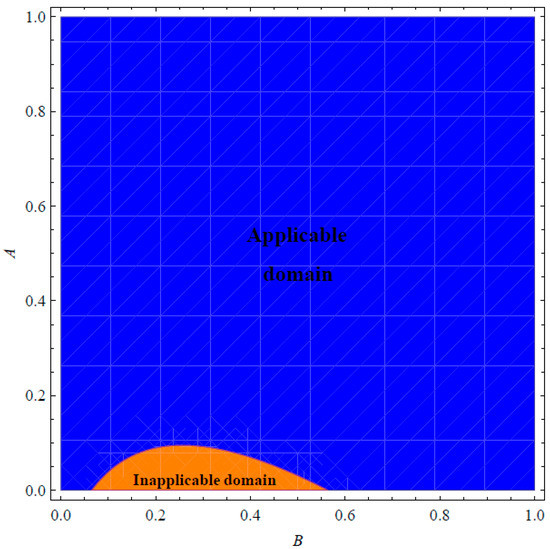
Figure 1. Applicability/inapplicability domains of the $R_{[2/2]}\left(\tau \right)$ at $\sigma =0.7$.

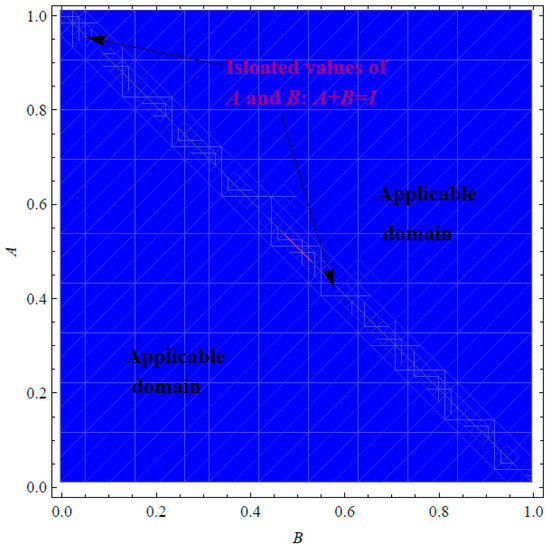
Figure 2. Applicability/inapplicability domains of the $I_{[2/2]}\left(\tau \right)$ at $\sigma =0.7$.

In addition, Figure 3 and Figure 4 show the applicability/inapplicability domains of $R_{[2/2]}\left(\tau \right)$ and $I_{[2/2]}\left(\tau \right)$ at $\sigma =0.9$. In Figure 5, the curves of the PSS ${\Phi }_{10}\left(\tau \right)$ and the Padé approximant $R_{[2/2]}\left(\tau \right)$ are compared with the numerical solution at $A=0$, $B={10}^{-3}$, and $\sigma =0.5$. This figure indicates that the domain of agreement with the numerical solution is increased through $R_{[2/2]}\left(\tau \right)$, while the PSS ${\Phi }_{10}\left(\tau \right)$ coincides with the numerical solution in a short domain. Furthermore, Figure 6 confirms this conclusion regarding the Padé approximant $I_{[2/2]}\left(\tau \right)$ and the PSS ${\Psi }_{10}\left(\tau \right)$. Similar results can be seen in Figure 7, Figure 8, Figure 9 and Figure 10. It can be observed from Figure 7 ($\sigma =0.7$) and Figure 9 ($\sigma =0.9$) that the difference between the $R_{[2/2]}\left(\tau \right)$ and the numerical solution slightly increases at large values of $\tau$ but the $R_{[2/2]}\left(\tau \right)$ is still better than the PSS ${\Phi }_{10}\left(\tau \right)$.

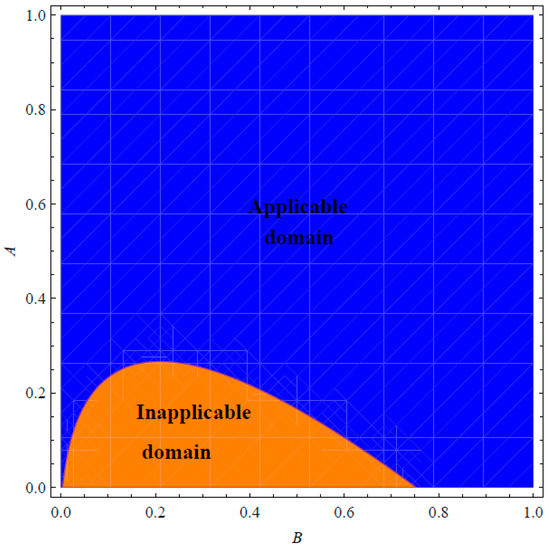
Figure 3. Applicability/inapplicability domains of the $R_{[2/2]}\left(\tau \right)$ at $\sigma =0.9$.

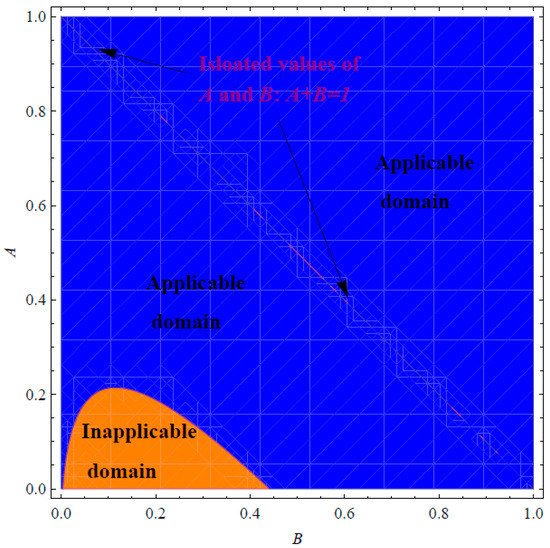
Figure 4. Applicability/inapplicability domains of the $I_{[2/2]}\left(\tau \right)$ at $\sigma =0.9$.

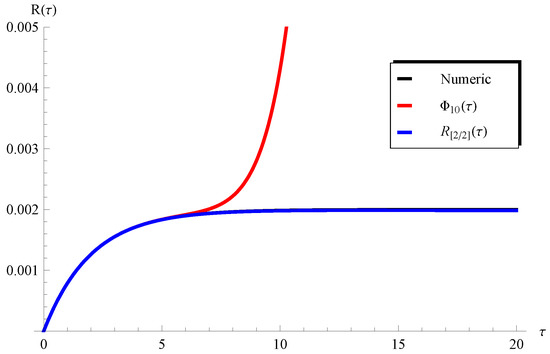
Figure 5. Plots of the PSS ${\Phi }_{10}\left(\tau \right)$, the $R_{[2/2]}\left(\tau \right)$, and the numerical solution at $A=0$, $B={10}^{-3}$, and $\sigma =0.5$.

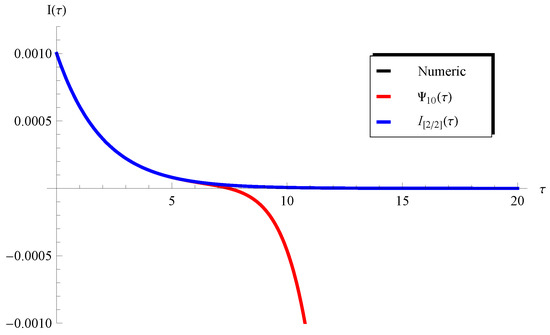
Figure 6. Plots of the PSS ${\Psi }_{10}\left(\tau \right)$, the $I_{[2/2]}\left(\tau \right)$, and the numerical solution at $A=0$, $B={10}^{-3}$, and $\sigma =0.5$.

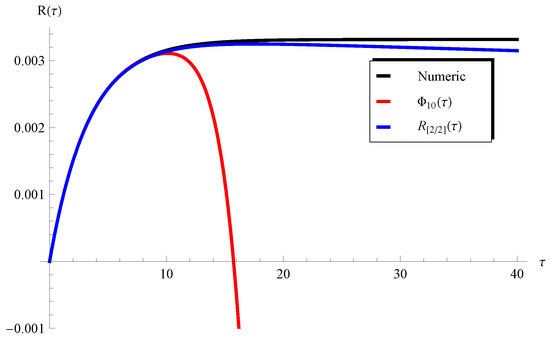
Figure 7. Plots of the PSS ${\Phi }_{10}\left(\tau \right)$, the $R_{[2/2]}\left(\tau \right)$, and the numerical solution at $A=0$, $B={10}^{-3}$, and $\sigma =0.7$.

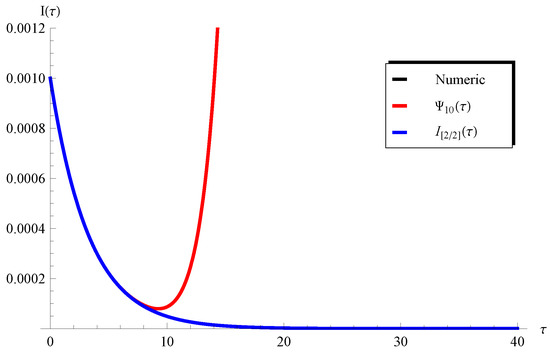
Figure 8. Plots of the PSS ${\Psi }_{10}\left(\tau \right)$, the $I_{[2/2]}\left(\tau \right)$, and the numerical solution at $A=0$, $B={10}^{-3}$, and $\sigma =0.7$.

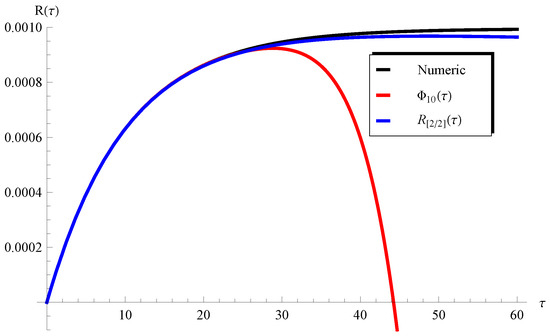
Figure 9. Plots of the PSS ${\Phi }_{10}\left(\tau \right)$, the $R_{[2/2]}\left(\tau \right)$, and the numerical solution at $A=0$, $B={10}^{-4}$, and $\sigma =0.9$.

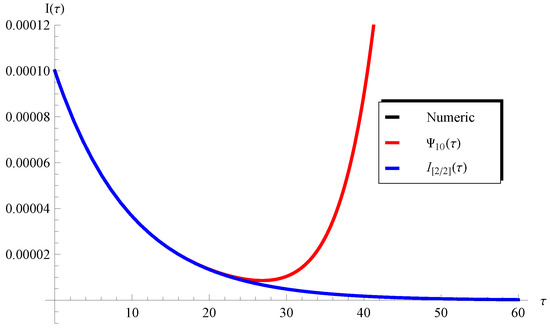
Figure 10. Plots of the PSS ${\Psi }_{10}\left(\tau \right)$, the $I_{[2/2]}\left(\tau \right)$, and the numerical solution at $A=0$, $B={10}^{-4}$, and $\sigma =0.9$.

Such a limitation can be easily overcome through considering a higher-order Padé approximant, as will be demonstrated later. On the other hand, one can see from Figure 8 ($\sigma =0.7$) and Figure 10 ($\sigma =0.9$) that the curves of the $I_{[2/2]}\left(\tau \right)$ are in full agreement with the numerical ones in the whole domain of $\tau$. In order overcome the limitations mentioned above, the higher-order Padé approximant $R_{[3/3]}\left(\tau \right)$ is depicted in Figure 11 and Figure 12 at $\sigma =0.9$ and $\sigma =0.95$, respectively. It is clear from these figures that the approximation $R_{[3/3]}\left(\tau \right)$ agrees with the numerical solution in the whole domain. Moreover, the residual error $RE\left(\tau \right)$ for Equations (1) and (2) is depicted in Figure 13 and Figure 14 using the current Padé approximants $R_{[2/2]}$ and $I_{[2/2]}$. Furthermore, numerical comparisons are performed between the present PSS ${\Phi }_{10}\left(\tau \right)$, ${\Psi }_{10}\left(\tau \right)$, $R_{[2/2]}\left(\tau \right)$, and the $I_{[2/2]}\left(\tau \right)$ with the ERKM in Table 1 and Table 2.

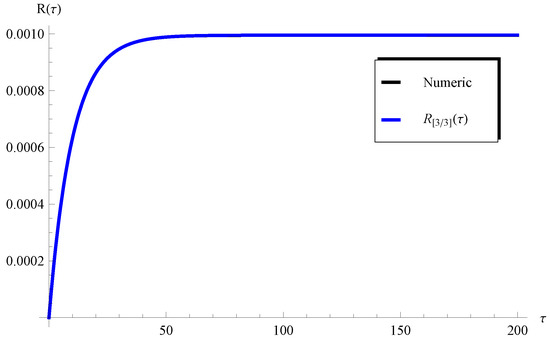
Figure 11. Plots of the $R_{[3/3]}\left(\tau \right)$ and the numerical solution at $A=0$, $B={10}^{-4}$, and $\sigma =0.9$.

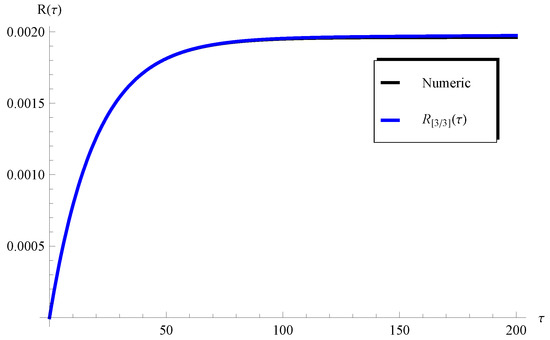
Figure 12. Plots of the $R_{[3/3]}\left(\tau \right)$ and the numerical solution at $A=0$, $B={10}^{-4}$, and $\sigma =0.95$.

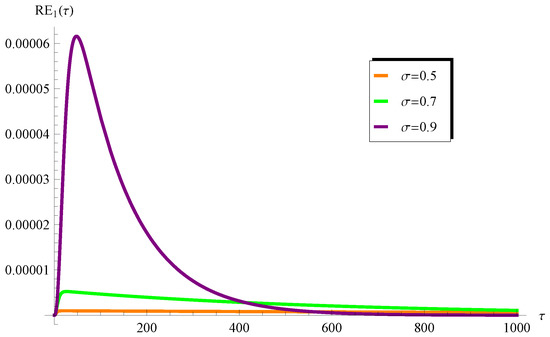
Figure 13. Variation in the residual $R{E}_1\left(\tau \right)$ at various values of $\sigma$ when $A=0$ and $B={10}^{-3}$.

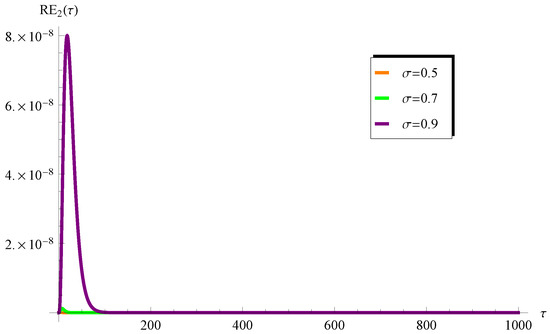
Figure 14. Variation of the residual $R{E}_2\left(\tau \right)$ at various values of $\sigma$ when $A=0$ and $B={10}^{-3}$.

Table 1. Comparisons of the present PSS ${\Phi }_{10}\left(\tau \right)$ and the LT-Padé approximant $R_{[2/2]}\left(\tau \right)$ with the ERKM at $\sigma =0.5$, $A=0$ and $B=0.001$.

$\mathit{\tau }$	${\mathsf{\Phi }}_{10}\left(\mathit{\tau }\right)$ (Present)	${\mathit{R}}_{[2/2]}\left(\mathit{\tau }\right)$ (Present)	ERKM (Numerical)
5	0.0018364	0.0018327	0.0018338
10	0.0043093	0.0019785	0.0019837
15	0.1220652	0.0019860	0.0019959
20	1.9188949	0.0019820	0.0019969
25	16.160833	0.0019772	0.0019970
30	91.203779	0.0019722	0.0019970
35	390.97111	0.0019673	0.0019970
40	1372.0035	0.0019624	0.0019970
45	4135.3979	0.0019575	0.0019970
50	11061.598	0.0019526	0.0019970

Table 2. Comparisons of the present PSS ${\Psi }_{10}\left(\tau \right)$ and the LT-Padé approximant $I_{[2/2]}\left(\tau \right)$ with the ERKM at $\sigma =0.5$, $A=0$ and $B=0.001$.

$\mathit{\tau }$	${\mathsf{\Psi }}_{10}\left(\mathit{\tau }\right)$ (Present)	${\mathit{I}}_{[2/2]}\left(\mathit{\tau }\right)$ (Present)	ERKM (Numerical)
5	$+8.1388\times {10}^{-5}$	$8.1751\times {10}^{-5}$	$8.1749\times {10}^{-5}$
10	$-4.6305\times {10}^{-4}$	$6.6776\times {10}^{-6}$	$6.6762\times {10}^{-6}$
15	$-2.8065\times {10}^{-2}$	$5.4540\times {10}^{-7}$	$5.4521\times {10}^{-7}$
20	$-4.8604\times {10}^{-1}$	$4.4546\times {10}^{-8}$	$4.4400\times {10}^{-8}$
25	$-0.4315\times {10}^{+1}$	$3.6384\times {10}^{-9}$	$3.6015\times {10}^{-9}$
30	$-0.2524\times {10}^{+2}$	$2.9717\times {10}^{-10}$	$2.9778\times {10}^{-10}$
35	$-0.1110\times {10}^{+3}$	$2.4274\times {10}^{-11}$	$2.4386\times {10}^{-11}$
40	$-0.3975\times {10}^{+3}$	$1.9824\times {10}^{-12}$	$2.5862\times {10}^{-12}$
45	$-0.1217\times {10}^{+4}$	$1.6491\times {10}^{-13}$	$1.7257\times {10}^{-13}$
50	$-0.3296\times {10}^{+4}$	$1.3225\times {10}^{-14}$	$1.7449\times {10}^{-13}$

In order to reveal the effectiveness of the our approach over the homotopy perturbation method (HPM) in the literature [23], we present a comparison between the $R_{[3/3]}\left(\tau \right)$ (present), the numerical solution, and the HPM (Ref. [23]) at $\sigma =0.9$ and $\sigma =0.95$ in Figure 15 and Figure 16, respectively, when $A=0$ and $B={10}^{-4}$. These figures show that our solution is closer to the numerical one (nearly identical) when compared with the HPM in Ref. [23].

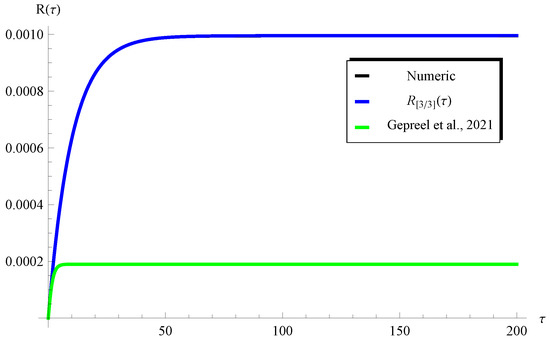
Figure 15. Comparison between the $R_{[3/3]}\left(\tau \right)$ (present), the numerical solution, and the HPM (Ref. [23]) at $A=0$, $B={10}^{-4}$, and $\sigma =0.9$.

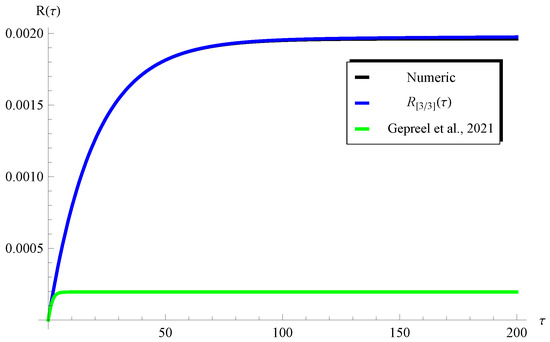
Figure 16. Comparison between the $R_{[3/3]}\left(\tau \right)$ (present), the numerical solution, and the HPM (Ref. [23]) at $A=0$, $B={10}^{-4}$, and $\sigma =0.95$.

The above results reveal that the accuracy can be enhanced by applying the current hybrid approach. This is of course one of the main advantages of the proposed method.

5. Conclusions

In this paper, the nonlinear SIR model was solved using a hybrid approach. The proposed technique was based on combining the LT and the Padé approximants. Various analytic approximations were successfully conducted for the infected and the recovered individuals. Moreover, such analytic approximations were found to be applicable in specific domains, which were described analytically and graphically. The performed comparisons with the explicit Runge–Kutta numerical method reveal the accuracy of the obtained results. Furthermore, the calculated residuals confirm this conclusion. The effectiveness of our approach reveals its ability to treat other mathematical and physical models in the applied sciences.