Property (h) of Banach Lattice and Order-to-Norm Continuous Operators

Abstract

In this paper, we introduce the property $(h)$ on Banach lattices and present its characterization in terms of disjoint sequences. Then, an example is given to show that an order-to-norm continuous operator may not be $\sigma$-order continuous. Suppose $T:E\to F$ is an order-bounded operator from Dedekind $\sigma$-complete Banach lattice E into Dedekind complete Banach lattice F. We prove that T is $\sigma$-order-to-norm continuous if and only if T is both order weakly compact and $\sigma$-order continuous. In addition, if E can be represented as an ideal of $L_0(\mu )$, where $(\Omega ,\Sigma ,\mu )$ is a $\sigma$-finite measure space, then T is $\sigma$-order-to-norm continuous if and only if T is order-to-norm continuous. As applications, we extend Wickstead’s results on the order continuity of norms on E and $E^{\prime }$.

1. Introduction

Throughout this paper, E and F will denote Banach lattices, whereas X and Y will denote Archimedean Riesz spaces. The set of all positive vectors of X is called the positive cone of X, and is denoted by $X^{+}$. Similarly, $E^{+}:=\{x\in E:x\ge 0\}$. A net $\{x_{\alpha }\}$ in X is said to be order convergent to x, written as $x_{\alpha }\stackrel{o}{\to }0$, if there exists another net $\{p_{\alpha }\}$ in X satisfying $p_{\alpha }\downarrow 0$, such that $|x_{\alpha }-x|\le p_{\alpha }$ for all $\alpha$. Put $e\in X^{+}$. The net $\{x_{\alpha }\}$ in X converges e-uniformly to x if there exists a positive real number net $\{{\epsilon }_{\alpha }\}$ with ${\epsilon }_{\alpha }\downarrow 0$, such that $|x_{\alpha }-x|\le {\epsilon }_{\alpha }e$ for all $\alpha$. In this case, we write $x_{\alpha }\to x$(e-ru). And the net $\{x_{\alpha }\}$ in X converges relatively uniformly to x, denoted by $x_{\alpha }\stackrel{ru}{\to }x$, if there exists e in $X^{+}$ such that $\{x_{\alpha }\}$ converges e-uniformly to x. Every relatively uniformly convergent sequence is also order convergent.

Recall that E is said to

• Have an order-continuous norm if $x_{\alpha }\stackrel{\Vert ·\Vert }{\to }0$ whenever $x_{\alpha }\stackrel{o}{\to }0$ in E.
• Have a $\sigma$-order continuous norm if $x_n\stackrel{\Vert ·\Vert }{\to }0$ whenever $x_n\stackrel{o}{\to }0$ in E.
• Be a $KB$ space if every increasing norm-bounded sequence in $E^{+}$ has a norm limit.

The concepts of order convergence and relative uniform convergence are identical on E if and only if E has an order-continuous norm; see [1] (Proposition 3). If H is a closed sublattice of E and $\{x_n\}\subset H$, then $x_n\stackrel{ru}{\to }0$ in H if and only if $x_n\stackrel{ru}{\to }0$ in E; see [2] (Proposition 2.12).

Niculescu [3] extended Lozanovskii’s results on Banach lattices with $\sigma$-order continuous norms to type A operators defined on Banach lattices. In 2021, Jalili et al. continued the study of operator versions of order-continuous norm and introduced order-to-norm continuous operators (see [4]). An operator $T:E\to F$ is said to be

• Type A if $\{T{x}_n\}$ is norm convergent whenever $0\le x_n\downarrow$ in E.
• Order weakly compact if for every $x\in E^{+}$, $T[0,x]$ is weakly compact in F.
• M weakly compact if $T{x}_n\stackrel{\Vert ·\Vert }{\to }0$ for every norm-bounded disjoint sequence $\{x_n\}$ in E.
• Order-to-norm continuous if $T{x}_{\alpha }\stackrel{\Vert ·\Vert }{\to }0$ whenever $x_{\alpha }\stackrel{o}{\to }0$ in E.
• $\sigma$-order-to-norm continuous if $T{x}_n\stackrel{\Vert ·\Vert }{\to }0$ whenever $x_n\stackrel{o}{\to }0$ in E.
• order continuous if $T{x}_{\alpha }\stackrel{o}{\to }0$ whenever $x_{\alpha }\stackrel{o}{\to }0$ in E.
• $\sigma$-order continuous if $T{x}_n\stackrel{o}{\to }0$ whenever $x_n\stackrel{o}{\to }0$ in E.

In Theorem 2, we also present that every order-bounded $\sigma$-order-to-norm continuous operator into a Banach lattice with property $(h)$ (see Definition 1) can be defined in order relation. It is proved in [3] (Lemma 3.1) that type A operators and order weakly compact operators are equivalent. Moreover, $T:E\to F$ is order weakly compact if and only if $T{x}_n\stackrel{\Vert ·\Vert }{\to }0$ for every order bounded disjoint sequence $\{x_n\}$ in E. Meyer-Nieberg shows that every order weakly compact operator $T:E\to F$ admits a factorization through a Banach lattice $G_T$ with an order continuous norm. These details can be found in [5] (Theorem 3.4.6) and [6] (Theorem 5.58). Now, we are in position to list some necessary notes. The natural factorization of $T:E\to F$ occurs through a quotient space. We define lattice seminorm $q_T$ on E as $q_T(x)=sup\{\Vert Ty\Vert :\mid y\mid \le \mid x\mid \}$ for every $x\in E$. Let $N(T)$ be the null ideal $\{x\in E:q_T(x)=0\}$ of $q_T$. And let $Q_T:E\to E/N(T)$ denote the canonical projection. Suppose that $G_T$ is the norm completion of normed Riesz space $E/N(T)$ under the quotient norm $\Vert Q_{T}x\Vert =q_T(x)$. The formula $S_T(Q_{T}x)=Tx$ gives rise to a well-defined continuous operator $S_T:E/N(T)\to F$ with $\Vert S_T\Vert \le 1$. Hence, S extends to all of $G_T$, satisfying $\Vert S_T\Vert \le 1$. We have the factorization of T,

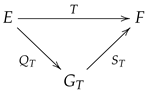
Moreover, if $T:E\to F$ is order bounded and F is Dedekind complete, then the modulus $|T|:E\to F$ of T exists. Given any $0<x\in E$, $\Vert |T|x\Vert \ge q_T(x)$, hence

$$\{x\in E:|T|(|x|)=0\}\subset N(T).$$

To see $N(T)\subset \{x\in E:|T|(|x|)=0\}$, put $0<x\in N(T)$. Since $\Vert Ty\Vert \le q_T(x)=0$ for every $|y|\le x$, by [6] (Theorem 1.18), we have $|T|x=sup\{|Ty|:|y|\le x\}=0$. It follows that

$$\{x\in E:|T|(|x|)=0\}=N(T).$$

In this paper, we mainly study the relative uniform order convergence of sequence on Banach lattices. At the same time, the main results of the article relate to the properties of $\sigma$-order-to-norm continuous and order-to-norm continuous operators. We refer the reader to [5,6,7,8] for unexplained terminology on Banach lattices.

2. Banach Lattices with Property ($\mathbf{h}$)

Every relatively uniformly convergent sequence converges in norm. However, the opposite may be not true. $e_n$ denotes the sequence of real numbers whose $nth$ term is one and the rest are zero. $\frac{1}{n}{e}_n\stackrel{\Vert ·\Vert }{\to }0$ in $l_1$ but not relatively uniformly convergent. Recall that E is said to be an $AM$-space if $\Vert x\vee y\Vert =max\{\Vert x\Vert ,\Vert y\Vert \}$ for $x,y\in E^{+}$. In [9] (Proposition 2), Wirth proved that E is isomorphic to an $AM$-space if and only if every norm convergent sequence in E is relatively uniformly convergent and if and only if every norm convergent sequence in E is order convergent. If E is a $AM$-space or $\sigma$-order continuous Banach lattice, then for every sequence $\{x_n\}$ in E, $x_n\stackrel{ru}{\to }0$ if and only if $x_n\stackrel{o}{\to }0$ and $x_n\stackrel{\Vert ·\Vert }{\to }0$.

Definition 1.

The Banach lattice E has property (h), provided that $x_n\stackrel{ru}{\to }0$ if and only if $x_n\stackrel{o}{\to }0$ and $x_n\stackrel{\Vert ·\Vert }{\to }0$ in E.

Example 1.

Let E be the $L_{\infty }$-sum of the space sequence $\{E_n:E_n=l_1,n\in \mathbb{N}\}$ i.e.,

$$E=l_{\infty }(l_1):=\{a=(a_1,a_2,\dots ,a_n,\dots ):a_n\in l_1\mathrm{and}\Vert a\Vert :=\underset{n}{sup}\Vert a_n{\Vert }_1<+\infty \}.$$

E is a Dedekind complete Banach lattice without order continuous norm under the pointwise ordering. In fact, E lacks property $(h)$.

Proof. 

Define a sequence $\{z_m\}$ in E by

$$\begin{array}{cc}\hfill & (e_1,0,0,\dots ,0,\dots ),\hfill \\ \hfill & (0,\frac{1}{2}{e}_1,0,\dots ,0,\dots ),(0,\frac{1}{2}{e}_2,0,\dots ,0,\dots ),\hfill \\ \hfill & \dots \hfill \\ \hfill & \underset{kthterm}{\underbrace{(0,0,0,\dots ,\frac{1}{k}{e}_1,\dots )}},\underset{kthterm}{\underbrace{(0,0,0,\dots ,\frac{1}{k}{e}_2,\dots )}},\dots ,\underset{kthterm}{\underbrace{(0,0,0,\dots ,\frac{1}{k}{e}_k,\dots )}},\hfill \\ \hfill & \dots \hfill \end{array}$$

Evidently, $\{z_m\}$ is an order-bounded disjoint norm null sequence and $\Vert {\sum }_{j=\frac{m(m+1)}{2}+1}^{\frac{m(m+1)}{2}+m+2}{z}_j\Vert =1$ for all m. We claim that $z_m\stackrel{ru}{\to }0$ is not true. Otherwise, there exists $e\in E^{+}$ and a real number sequence $\{{\epsilon }_m\}$ satisfying ${\epsilon }_m\downarrow 0$, such that $0\le z_m\le {\epsilon }_{m}e$ for all $m\in \mathbb{N}$. It follows that for every $m\in \mathbb{N}$,

$$\sum _{j=\frac{m(m+1)}{2}+1}^{\frac{m(m+1)}{2}+m+2}{z}_j=\underset{j=\frac{m(m+1)}{2}+1}{\overset{\frac{m(m+1)}{2}+m+2}{\bigvee }}{z}_j\le {\epsilon }_{\frac{m(m+1)}{2}+1}e.$$

This implies that

$$1=\Vert \sum _{j=\frac{m(m+1)}{2}+1}^{\frac{m(m+1)}{2}+m+2}{z}_j\Vert \le {\epsilon }_{\frac{m(m+1)}{2}+1}\Vert e\Vert$$

for every m. We obtain a contradiction. □

Recall that in a discrete Banach lattice E, $x_n\stackrel{o}{\to }0$ for every order bounded norm null sequence $\{x_n\}$ in E.

Proposition 1.

Let E be a discrete Dedekind σ-complete Banach lattice. The following assertions are equivalent.

(1) 

E has property (h).

(2) 

$x_n\stackrel{ru}{\to }0$ if and only if $\{x_n\}$ is order bounded and $x_n\stackrel{\Vert ·\Vert }{\to }0$.

Recall that Riesz space X has principal projection property if and only if every principal band is a projection band i.e., for every $u\in X$, ${\bigvee }_{n=1}^{\infty }y\wedge n|u|$ exists for each $y\in X^{+}$. In this case, for $u\in E^{+}$, the band projection from E onto $\left[u\right]$ by $P_u:E\to \left[u\right]$ is defined by $P_{u}x={\bigvee }_{n=1}^{\infty }y\wedge n|u|$ for every $x\in X^{+}$, where $\left[u\right]$ is the principal band generated by u in E. By [6] (Theorem 1.47), every Dedekind $\sigma$-complete Riesz space has principal projection property. The following lemmas will be useful in the sequel discussions of property $(h)$.

Lemma 1

([5], Proposition 2.8.2). If Riesz space X has principal projection property, then the following statements are hold.

(1) 

For any $x,y$ in $X^{+}$, there exist disjoint elements $e_1,e_2$ in X, such that $x\vee y=e_1+e_2$ and $e_1\le x,e_2\le y$.

(2) 

For any $x,y,z$ in $X^{+}$ with $x\le y\vee z$, there exist disjoint elements $x_1,x_2$ in X, such that $x=x_1+x_2$ and $x_1\le y,x_2\le z$.

Lemma 2

([6], Theorem 4.12). Let X be a Riesz space and $0\le x_n\uparrow \le x$ in X. For every $k\in \mathbb{N}$, there exist disjoint sequences $\{y_n^1\},\{y_n^2\},\dots ,\{y_n^k\}$ of $[0,x]$, such that for each n,

$$y_n^1+y_n^2+\dots +y_n^k\le x_{n+1}-x_n\le y_n^1+y_n^2+\dots +y_n^k+\frac{2}{k+3}x.$$

Lemma 3

([10], Theorem 105.15). If $x_n\downarrow$ and $x_n\stackrel{\Vert ·\Vert }{\to }0$ in E, then $x_n\stackrel{ru}{\to }0$ in E.

Next, we characterize Banach lattices with property $(h)$ in terms of disjoint sequences.

Theorem 1.

Let E be a Dedekind σ-complete Banach lattice. The following assertions are equivalent.

(1) 

E has property (h).

(2) 

$x_n\stackrel{ru}{\to }0$ for every order-bounded disjoint norm null sequence $\{x_n\}$ in E.

Proof. 

$(1)\Rightarrow (2)$ is evident. $(2)\Rightarrow (1)$ Let $0\le x_n\stackrel{o}{\to }0$ and $x_n\stackrel{\Vert ·\Vert }{\to }0$. Since E is a Dedekind $\sigma$-complete Banach lattice, according to [5] (Proposition 1.1.10), $x_n\stackrel{o}{\to }0$ implies ${\bigvee }_{i=n}^{\infty }{x}_i\downarrow 0$. We assert that ${\bigvee }_{i=n}^{\infty }{x}_i\stackrel{\Vert ·\Vert }{\to }0$. Next, we prove the assertion by contradiction. Assume that ${\bigvee }_{i=n}^{\infty }{x}_i\stackrel{\Vert ·\Vert }{\to }0$ is not true. According to [11] (Theorem 15.4), $\{{\bigvee }_{i=n}^{\infty }{x}_i\}$ is not a Cauchy sequence since ${\bigvee }_{i=n}^{\infty }{x}_i\downarrow 0$. Thus, we can find ${\epsilon }_0>0$ and a subsequence $\{{\bigvee }_{i=n_m}^{\infty }{x}_i\}$ of $\{{\bigvee }_{i=n}^{\infty }{x}_i\}$, such that

$$\Vert \underset{i=n_m}{\overset{\infty }{\bigvee }}{x}_i-\underset{i=n_{m+1}}{\overset{\infty }{\bigvee }}{x}_i\Vert \ge {\epsilon }_0$$

for every $m\in \mathbb{N}$. Note that $0\le {\bigvee }_{i=1}^{\infty }{x}_i-{\bigvee }_{i=n_m}^{\infty }{x}_i\uparrow {\bigvee }_{i=1}^{\infty }{x}_i$. According to Lemma 2, there are disjoint sequences $\{z_m^1\},\{z_m^2\},\dots ,\{z_m^k\}$, such that for every n,

$$z_m^1+z_m^2+\dots +z_m^k\le \underset{i=n_m}{\overset{\infty }{\bigvee }}{x}_i-\underset{i=n_{m+1}}{\overset{\infty }{\bigvee }}{x}_i\le z_m^1+z_m^2+\dots +z_m^k+\frac{2}{k+3}\underset{i=1}{\overset{\infty }{\bigvee }}{x}_i.$$

It follows from ${\bigvee }_{i=n_m}^{\infty }{x}_i-{\bigvee }_{i=n_{m+1}}^{\infty }{x}_i={({\bigvee }_{i=n_m}^{n_{m+1}-1}{x}_i-{\bigvee }_{i=n_{m+1}}^{\infty }{x}_i)}^{+}$ that $0\le z_m^j\le {\bigvee }_{i=n_m}^{n_{m+1}-1}{x}_i$ for every $j=1,2,\dots ,k$ and $m\in \mathbb{N}$. By Lemma 1, for every $j=1,2,\dots ,k$ and $m\in \mathbb{N}$ there exist pairwise disjoint elements $w_{n_m}^j,w_{n_m+1}^j,\dots ,w_{n_{m+1}-1}^j$, such that $z_m^j={\sum }_{i=n_m}^{n_{m+1}-1}{w}_i^j$ and $w_i^j\le x_i$ for each $i=n_m,n_m+1,\dots ,n_{m+1}-1$. It follows that the order-bounded disjoint sequence is $w_i^j\stackrel{\Vert ·\Vert }{\to }0$ for every $j=1,2,\dots ,k$. Therefore, according to the assumption of $(2)$, $w_i^j{\stackrel{ru}{\to }}_{i}0$. We can find $e^1,e^2,\dots ,e^k\in E^{+}$ and $\{{\epsilon }_i^1\},\{{\epsilon }_i^2\},\dots ,\{{\epsilon }_i^k\}\subset \mathbb{R}$, such that ${\epsilon }_i^j\downarrow 0$ for every j and $0\le w_i^j\le {\epsilon }_i^j{e}^j$ for every i and j. Therefore,

$$\begin{array}{cc}\hfill {\epsilon }_0& \le \Vert \underset{i=n_m}{\overset{\infty }{\bigvee }}{x}_i-\underset{i=n_{m+1}}{\overset{\infty }{\bigvee }}{x}_i\Vert \le \Vert z_m^1\Vert +\Vert z_m^2\Vert +\dots +\Vert z_m^k\Vert +\frac{2}{k+3}\Vert \underset{i=1}{\overset{\infty }{\bigvee }}{x}_i\Vert \hfill \\ \hfill & =\Vert \sum _{i=n_m}^{n_{m+1}-1}{w}_i^1\Vert +\Vert \sum _{i=n_m}^{n_{m+1}-1}{w}_i^2\Vert +\dots +\Vert \sum _{i=n_m}^{n_{m+1}-1}{w}_i^k\Vert +\frac{2}{k+3}\Vert \underset{i=1}{\overset{\infty }{\bigvee }}{x}_i\Vert \hfill \\ \hfill & \le {\epsilon }_{n_m}^1\Vert e^1\Vert +{\epsilon }_{n_m}^2\Vert e^2\Vert +\dots +{\epsilon }_{n_m}^k\Vert e^k\Vert +\frac{2}{k+3}\Vert \underset{i=1}{\overset{\infty }{\bigvee }}{x}_i\Vert .\hfill \end{array}$$

Letting $m\to \infty$, we determine that ${\epsilon }_0\le \frac{2}{k+3}\Vert {\bigvee }_{i=1}^{\infty }{x}_i\Vert$ for every k. This is a contradiction. Hence, ${\bigvee }_{i=n}^{\infty }{x}_i\stackrel{\Vert ·\Vert }{\to }0$. According to Lemma 3, ${\bigvee }_{i=n}^{\infty }{x}_i\stackrel{ru}{\to }0$. This implies $x_n\stackrel{ru}{\to }0$. □

Remark 1.

Let $\{y_n\}$ and $\{z_n\}$ be two sequences in Riesz space X. $\{y_n\}$ is said to be dominated by $\{z_n\}$, written as $\{y_n\}\preccurlyeq \{z_n\}$, if $|y_n|\le |z_n|$ for every $n\in \mathbb{N}$. According to the proof of Theorem 1, for every sequence $\{x_n\}$ in Dedekind σ-complete Banach lattice, $x_n\stackrel{ru}{\to }0$ if and only if the following statements hold:

(1) 

$x_n\stackrel{o}{\to }0$.

(2) 

If $\{w_n\}\preccurlyeq \{x_n\}$, then $w_n\stackrel{ru}{\to }0$.

In general, the property $(h)$ cannot imply $AM$ or order-continuous property.

Example 2.

Let E be the $L_1$-sum of the space sequence $\{E_n:E_n=l_{\infty },n\in \mathbb{N}\}$ i.e.,

$$E=l_1(l_{\infty }):=\{a=(a_1,a_2,\dots ,a_n,\dots ):a_n\in l_1\mathrm{and}\Vert a\Vert :=\sum _{n=1}^{\infty }\Vert a_n{\Vert }_1<+\infty \}.$$

E is a Dedekind complete Banach lattice. Evidently, E is neither $AM$-space nor an order-continuous Banach lattice. However, E has property $(h)$.

Proof. 

Suppose that $x\in E^{+}$ and $\{x^n\}$ is a disjoint norm null sequence in $[0,x]$, where $x=(x_1,x_2,\dots ,x_m,\dots )$. For every $m\in \mathbb{N}$, define the projection $P_m:E\to E$ by $P_{m}a=a_m$ for every $a=(a_1,a_2,\dots ,a_m,\dots )\in E$. Now, fixed m, $\{P_m{x}^n\}$ is a disjoint norm null sequence in $[0,P_{m}x]\subset P_{m}E=l_{\infty }$. Note that $l_{\infty }$ is an $AM$-space. It follows that $P_m{x}^n\stackrel{ru}{\to }0$ in $P_{m}E$ for every m. For fixed $\epsilon >0$, there exists $2\le N\in \mathbb{N}$, such that ${\sum }_{m=N}^{\infty }\Vert x_m\Vert \le \epsilon$. Therefore,

$$\Vert \underset{m=N}{\overset{\infty }{\bigvee }}\underset{n=1}{\overset{\infty }{\bigvee }}{P}_m{x}^n\Vert \le \Vert \underset{m=N}{\overset{\infty }{\bigvee }}{P}_{m}x\Vert =\Vert \underset{m=N}{\overset{\infty }{\bigvee }}{x}_m\Vert \le \epsilon .$$

For every $n\in \mathbb{N}$, ${\bigvee }_{k=n}^{\infty }{x}^k={\bigvee }_{k=n}^{\infty }{\bigvee }_{m=1}^{\infty }{P}_m{x}^k={\bigvee }_{m=1}^{\infty }{\bigvee }_{k=n}^{\infty }{P}_m{x}^k={\sum }_{m=1}^{N-1}{\bigvee }_{k=n}^{\infty }{P}_m{x}^k+{\bigvee }_{m=N}^{\infty }{\bigvee }_{k=n}^{\infty }{P}_m{x}^k$. Given any $m\in \mathbb{N}$, ${lim}_{n\to \infty }\Vert {\bigvee }_{k=n}^{\infty }{P}_m{x}^k\Vert =0$ since $P_m{x}^n\stackrel{ru}{\to }0$. It follows that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}\Vert \underset{k=n}{\overset{\infty }{\bigvee }}{x}^k\Vert & =\underset{n\to \infty }{lim\; sup}\Vert \sum _{m=1}^{N-1}\underset{k=n}{\overset{\infty }{\bigvee }}{P}_m{x}^k+\underset{m=N}{\overset{\infty }{\bigvee }}\underset{k=n}{\overset{\infty }{\bigvee }}{P}_m{x}^k\Vert \hfill \\ \hfill & \le \underset{n\to \infty }{lim\; sup}\Vert \sum _{m=1}^{N-1}\underset{k=n}{\overset{\infty }{\bigvee }}{P}_m{x}^k\Vert +\underset{n\to \infty }{lim\; sup}\Vert \underset{m=N}{\overset{\infty }{\bigvee }}\underset{k=n}{\overset{\infty }{\bigvee }}{P}_m{x}^k\Vert \hfill \\ \hfill & \le \underset{n\to \infty }{lim\; sup}\Vert \sum _{m=1}^{N-1}\underset{k=n}{\overset{\infty }{\bigvee }}{P}_m{x}^k\Vert +\Vert \underset{m=N}{\overset{\infty }{\bigvee }}{x}_m\Vert \hfill \\ \hfill & \le \underset{n\to \infty }{lim\; sup}\sum _{m=1}^{N-1}\Vert \underset{k=n}{\overset{\infty }{\bigvee }}{P}_m{x}^k\Vert +\epsilon =\epsilon \hfill \end{array}$$

Therefore, ${lim}_{n\to \infty }\Vert {\bigvee }_{k=n}^{\infty }{x}^k\Vert =0$. According to Lemma 3, we obtain $x^n\stackrel{ru}{\to }0$. □

In general, every Dedekind $\sigma$-complete Banach lattice contains a norm closed ideal which has property (h).

Definition 2.

Let E be a Banach lattice. An element $x\in E$ is said to have property (h) if every disjoint sequence $\{x_n\}\subset [0,|x|]$ with $x_n\stackrel{\Vert ·\Vert }{\to }0$ is uniformly convergent. The collection of all elements that have property (h) is denoted by $E^h$.

In Example 1, it is easy to verify that $E^h=c_0(l_1)$.

Theorem 2.

Let E be a Dedekind σ-complete Banach lattice. $E^h$ is a norm-closed ideal of E.

Proof. 

(1)

$E^h$ is an ideal of E. Given any $x,y\in E^h$ and $\alpha ,\beta \in \mathbb{R}$, if $\{z_n\}$ is a disjoint sequence such that $0\le z_n\le |\alpha x+\beta y|$ and $z_n\stackrel{\Vert ·\Vert }{\to }0$, then due to the Riesz decomposition property of [6] (Theorem 1.13), there exist two positive disjoint sequences, $\{z_{n,1}\}$ and $\{z_{n,2}\}$, such that $z_n=z_{n,1}+z_{n,2}$ and $z_{n,1}\le |\alpha ||x|,z_{n,2}\le |\beta ||y|$ for every n. Then, $z_{n,i}\stackrel{ru}{\to }0$ for $i=1,2$. This implies that $z_n=z_{n,1}+z_{n,2}\stackrel{ru}{\to }0$. We obtain that $|\alpha x+\beta y|\in E^h$ for every $x,y\in E^h$ and $\alpha ,\beta \in \mathbb{R}$. It is easy to see that $x\in E^h$ if and only $|x|\in E^h$. And the condition $0\le z\le x\in E^h$ and $z\in E$ can imply that $y\in E^h$. We have proved that $E^h$ is an ideal of E.

(2)

Assume that $x_n\stackrel{\Vert ·\Vert }{\to }x$ in E with $\{x_n\}\subset E^h$. Let $\{z_n\}$ be a disjoint sequence in $[0,|x|]$. For every $\epsilon >0$, there exists $N\in \mathbb{N}$, such that $\Vert |x|-|x_N|\Vert \le \epsilon$. It follows from $x_N\in E^h$ that $z_n\wedge |x_N|\stackrel{ru}{\to }0$. Thus, we can find $e\in E^{+}$ and a real number sequence $\{{\epsilon }_n\}$ with ${\epsilon }_n\downarrow 0$, such that $0\le z_n\wedge |x_N|\le {\epsilon }_{n}e$ for every n. For every $m>n$, we have

$$|z_m\wedge |x|-z_m\wedge |x_N||\wedge |z_n\wedge |x|-z_n\wedge |x_N||\le (2z_m)\wedge (2z_n)=2(z_m\wedge z_n)=0.$$

It follows that $\{|z_n\wedge |x|-z_n\wedge |x_N||\}$ is a disjoint sequence. According to Birkhoff’s inequalities (see [6], Theorem 1.9), for every $n,k\in \mathbb{N}$,

$$\begin{array}{cc}\hfill & \Vert \sum _{i=n}^{n+k}{z}_i\Vert =\Vert \sum _{i=n}^{n+k}(z_i\wedge |x|-z_i\wedge |x_N|+z_i\wedge |x_N|)\Vert \hfill \\ \hfill & \le \Vert \sum _{i=n}^{n+k}|z_i\wedge |x|-z_i\wedge |x_N||+\sum _{i=n}^{n+k}(z_i\wedge |x_N|)\Vert \hfill \\ \hfill & \le \Vert \sum _{i=n}^{n+k}|z_i\wedge |x|-z_i\wedge |x_N||\Vert +\Vert \sum _{i=n}^{n+k}(z_i\wedge |x_N|)\Vert \hfill \\ \hfill & =\Vert \underset{i=n}{\overset{n+k}{\bigvee }}|z_i\wedge |x|-z_i\wedge |x_N||\Vert +\Vert \underset{i=n}{\overset{n+k}{\bigvee }}(z_i\wedge |x_N|)\Vert \hfill \\ \hfill & \le \Vert ||x|-|x_N||\Vert +{\epsilon }_n\Vert e\Vert \le \epsilon +{\epsilon }_n\Vert e\Vert .\hfill \end{array}$$

This implies that the series ${\sum }_{n=1}^{\infty }|z_n|$ converges in its norm. Therefore, ${\sum }_{i=n}^{\infty }|z_i|\stackrel{\Vert ·\Vert }{\to }0$. According to Lemma 3, $|z_n|\le {\sum }_{i=n}^{\infty }|z_i|\stackrel{ru}{\to }0$. This implies that $x_n\stackrel{ru}{\to }0$. Based on the proceeding deduction, we conclude that $x\in E^h$. Hence, $E^h$ is a closed subspace of E. □

3. Order-to-Norm Continuous Operators on Banach Lattices

Evidently, every $\sigma$-order-to-norm continuous operator from a Dedekind $\sigma$-complete Banach lattice to another Banach lattice is order weakly compact. The identity operator on Banach lattice without $\sigma$-order continuous norm is neither order-to-norm continuous nor order weakly compact.

Example 3.

Let $E=c_0$ and $F=l_1$. Then, there is an operator $T:E\to F$ which is order-to-norm continuous and order weakly compact but not σ-order continuous.

Proof. 

According to Dvoretzky–Rogers’ theorem (see [12], Theorem 2), there is an unconditionally convergent series ${\sum }_{n=1}^{\infty }{x}_n$ in $l_1$, such that $\Vert x_n\Vert =\frac{1}{n^{\frac{3}{4}}}$ for every n. Define $T:E\to F$ by

$$Tw=\sum _{n=1}^{\infty }w(n)x_n$$

for all $w\in E$. When using [13] (Corollary 2.5), T is not order bounded. Therefore, there exists $x\in E^{+}$, such that $T[0,x]$ is not order bounded, i.e., $\{{\bigvee }_{i=1}^n|T{x}_i|:x_i\in [0,x],n\in \mathbb{N}\}$ is not order bounded. Note that $F=l_1$ is a $KB$ space. $\{{\bigvee }_{i=1}^n|T{x}_i|:x_i\in [0,x],n\in \mathbb{N}\}$ is not norm bounded. Therefore, there exists an increasing sequence $\{n_k\}\subset \mathbb{N}$ and a subsequence ${\{x_i\}}_{i=n_1}^{\infty }$ of $[0,x]$, such that $\Vert {\bigvee }_{i=n_k}^{n_{k+1}-1}|T{x}_i|\Vert \ge k^2$ for every k. Define a sequence ${\{z_i\}}_{i=n_1}^{\infty }$ in $[0,x]$ by $z_i=\frac{1}{k}{x}_i$ for every $n_k\le i\le n_{k+1}-1$ and $k\in \mathbb{N}$. Clearly, $z_i\stackrel{ru}{\to }0$. We claim that T is not $\sigma$-order continuous. Otherwise, T is $\sigma$-order continuous. This implies that $T{z}_i\stackrel{o}{\to }0$. It follows that there is $y\in F$, such that $|T{z}_i|\le y$ for every i. Hence,

$$k\le \Vert \underset{i=n_k}{\overset{n_{k+1}-1}{\bigvee }}|T{z}_i|\Vert \le \Vert y\Vert .$$

This is a contradiction. □

Every order-bounded $\sigma$-order-to-norm continuous operator in a Banach lattice with property $(h)$ can be defined in order.

Proposition 2.

Let $E,F$ be Banach lattices with F Dedekind complete. $T:E\to F$ is an order-bounded operator. The following statements hold.

(1) 

If T is σ-order-to-norm continuous, then T is σ-order continuous.

(2) 

If F has property $(h)$, then the following assertions are equivalent.

($2a$)

$T{x}_n\stackrel{ru}{\to }0$ for every $x_n\stackrel{o}{\to }0$ in E.

($2b$)

T is σ-order-to-norm continuous.

Proof. 

(1)

Let $x_n\stackrel{o}{\to }0$ in E. We have $\Vert {\bigwedge }_{k=1}^{\infty }|T{x}_k|\Vert \le \Vert T{x}_n\Vert \to 0$. It follows that ${\bigwedge }_{k=1}^{\infty }|T{x}_k|=0$. According to [6] (Theorem 1.56), T is $\sigma$-order continuous.

(2)

$(2a)\Rightarrow (2b)$ is evident. $(2b)\Rightarrow (2a)$ Note that $T{x}_n\stackrel{\Vert ·\Vert }{\to }0$ and $T{x}_n\stackrel{o}{\to }0$ for every $x_n\stackrel{o}{\to }0$ in E. Since F has property $(h)$, we have $T{x}_n\stackrel{ru}{\to }0$.

□

Recall that a net $\{x_{\alpha }\}$ in E is said to be laterally decreasing if $(x_{\alpha }-x_{\beta })\wedge x_{\beta }=0$ for all $\alpha ⪯\beta$. If E is Dedekind $\sigma$-complete, then $\{x_n\}\subset E^{+}$ is laterally decreasing to zero if and only if there is a disjoint sequence $\{e_n\}$ in $E^{+}$, such that $x_n={\bigvee }_{i=n}^{\infty }{e}_i$ for every n.

Lemma 4

([14], Proposition 0.3.5). Let E be a Dedekind σ-complete Banach lattice. The following statements hold.

(1) 

If $x_{\alpha }\downarrow 0$ in E, then for every $\epsilon >0$ and index ${\alpha }_0$, there exists a net $\{y_{\alpha }\}$ satisfying $y_{\alpha }\downarrow 0$, such that $P_{y_{\alpha }}{x}_{{\alpha }_0}\le \frac{1}{\epsilon }{x}_{\alpha }$ for all α and $x_{\alpha }\le P_{y_{\alpha }}{x}_{{\alpha }_0}+\epsilon x_{{\alpha }_0}$ for $\alpha \ge {\alpha }_0$. Therefore, there exists a laterally decreasing net $\{z_{\alpha }\}\subset E^{+}$ such that $z_{\alpha }\le \frac{1}{\epsilon }{x}_{\alpha }$ for all α and $x_{\alpha }\le z_{\alpha }+\epsilon x_{{\alpha }_0}$ for $\alpha \ge {\alpha }_0$.

(2) 

If $x_n\downarrow 0$ in E, then for every $\epsilon >0$, there exists an order-bounded disjoint sequence $\{w_n\}\subset E^{+}$, such that ${\bigvee }_{i=n}^{\infty }{w}_i\le \frac{1}{\epsilon }{x}_n$ and $x_n\le {\bigvee }_{i=n}^{\infty }{w}_i+\epsilon x_1$ for all n.

Lemma 5

([5], Lemma 3.4.3). Let $T:E\to F$ be a norm-bounded operator between two Banach lattices. Then, $q_T(x)=sup\{|y^{\prime }T|(|x|):\Vert y^{\prime }\Vert \le 1\}$ for every $x\in E$.

The $\sigma$-order-to-norm continuous operators have a number of nice characterizations.

Theorem 3.

Let E be a Dedekind σ-complete Banach lattice and F Dedekind complete. If $T:E\to F$ is an order-bounded operator, then the following statements are equivalent.

(1) 

T is σ-order-to-norm continuous.

(2) 

$T:E\to F$ admits a factorization through an order-continuous Banach lattice $G_T$,

where the factor $Q_T$ is a σ-order-to-norm continuous lattice homomorphism and $S_T$ is a norm-bounded operator.

(3) 

$T({\bigvee }_{n=1}^{\infty }{w}_n)={\sum }_{n=1}^{\infty }T{w}_n$ for every order-bounded disjoint sequence $\{w_n\}$ in $E^{+}$.

(4) 

$T{x}_n\stackrel{w}{\to }0$ for every $x_n\stackrel{o}{\to }0$ in E i.e., $y^{\prime }T:E\to R$ is a σ-order continuous functional for every $y^{\prime }\in F^{\prime }$.

(5) 

$T{x}_n\stackrel{w}{\to }0$ for every $x_n\downarrow 0$ in E.

(6) 

$T{x}_n\stackrel{\Vert ·\Vert }{\to }0$ for every $x_n\downarrow 0$ in E.

(7) 

T is order weakly compact and T is σ-order continuous.

Proof. 

The derivation of the proof of this theorem is shown as follows

$$(1)\Rightarrow (6)\Rightarrow (5)\iff (4)\Rightarrow (1)\Rightarrow (2)\Rightarrow (3)\Rightarrow (1)\Rightarrow (7)\Rightarrow (6).$$

$(5)\iff (4)$ is obtained by [6] (Theorem 1.56). $(1)\Rightarrow (6)$ and $(6)\Rightarrow (5)$ are evident.

$(1)\Rightarrow (7)$ follows directly from Proposition 2.

$(1)\Rightarrow (2)$ Let $x_n\stackrel{o}{\to }0$ in E. If $q_T(x_n)\nrightarrow 0$, then passing to a subsequence, we assume that there exists ${\epsilon }_0>0$, such that $q_T(x_n)\ge {\epsilon }_0$ for every n. According to Lemma 5,

$$q_T(x_n)=sup\{|y^{\prime }T|(|x_n|):\Vert y^{\prime }\Vert \le 1\}.$$

Therefore, for all n, we can find some $y_n^{\prime }\in B_{F^{\prime }}$ satisfying $|y_n^{\prime }T|(|x_n|)\ge \frac{{\epsilon }_0}{2}$. According to [6] (Theorem 1.18), $|y_n^{\prime }T|(x_n)=sup\{|y_n^{\prime }Tz|:|z|\le |x_n|\}$. It follows that there exists $z_n\in [-|x_n|,|x_n|]$, such that $|y_n^{\prime }T{z}_n|\ge \frac{{\epsilon }_0}{4}$. Hence, $z_n\stackrel{o}{\to }0$ and $\frac{{\epsilon }_0}{4}\le |y_n^{\prime }T{z}_n|\le \Vert T{z}_n\Vert$ for every $n\in \mathbb{N}$. This is a contradiction. We find that $\Vert Q_T{x}_n\Vert =q_T(x_n)\to 0$ for every $x_n\stackrel{o}{\to }0$ in E.

$(2)\Rightarrow (3)$ Suppose that $\{w_n\}$ is an order-bounded disjoint sequence in E. Since E is Dedekind $\sigma$-complete, ${\bigvee }_{n=1}^{\infty }{w}_n$ exists in E. Therefore,

$$\sum _{i=1}^n{Q}_T{e}_i=\underset{i=1}{\overset{n}{\bigvee }}{Q}_T{e}_i\uparrow Q_T(\underset{n=1}{\overset{\infty }{\bigvee }}{w}_n).$$

Note that $G_T$ has an order-continuous norm. $Q_T({\bigvee }_{n=1}^{\infty }{w}_n)={\sum }_{n=1}^{\infty }{Q}_T{w}_n$. This implies that

$$T(\underset{n=1}{\overset{\infty }{\bigvee }}{w}_n)=S_T{Q}_T(\underset{n=1}{\overset{\infty }{\bigvee }}{w}_n)=S_T(\sum _{n=1}^{\infty }{Q}_T{w}_n)=\sum _{n=1}^{\infty }T{w}_n.$$

$(3)\Rightarrow (1)$ Let $\{z_n\}$ be an order-bounded disjoint sequence in E. Evidently,

$$\sum _{n=1}^{\infty }{(y^{\prime }T)}^{+}{z}_n=\underset{n\to \infty }{lim}\sum _{i=1}^n{(y^{\prime }T)}^{+}{z}_i=\underset{n\to \infty }{lim}{(y^{\prime }T)}^{+}\underset{i=1}{\overset{n}{\bigvee }}{z}_i\le {(y^{\prime }T)}^{+}(\underset{n=1}{\overset{\infty }{\bigvee }}{z}_n)$$

for any $y^{\prime }\in F^{\prime }$. To see ${(y^{\prime }T)}^{+}({\bigvee }_{n=1}^{\infty }{z}_n)\le {\sum }_{n=1}^{\infty }{(y^{\prime }T)}^{+}{z}_n$, put $\epsilon >0$. In view of [6] (Theorem 1.18), ${(y^{\prime }T)}^{+}x=sup\{|y^{\prime }Tz|:0\le z\le x\}$, there exists $0\le z\le {\bigvee }_{n=1}^{\infty }{z}_n$, such that ${(y^{\prime }T)}^{+}({\bigvee }_{n=1}^{\infty }{z}_n)\le |y^{\prime }Tz|+\epsilon$. By our assumption in $(3)$,

$$Tz=T(\underset{n=1}{\overset{\infty }{\bigvee }}z\wedge z_n)=\sum _{n=1}^{\infty }Tz\wedge z_n.$$

It follows that

$$\begin{array}{cc}\hfill {(y^{\prime }T)}^{+}(\underset{n=1}{\overset{\infty }{\bigvee }}{z}_n)& \le |y^{\prime }Tz|+\epsilon =|y^{\prime }T(\underset{n=1}{\overset{\infty }{\bigvee }}z\wedge z_n)|+\epsilon \hfill \\ \hfill & =|\sum _{n=1}^{\infty }{y}^{\prime }Tz\wedge z_n|+\epsilon \le \sum _{n=1}^{\infty }|y^{\prime }Tz\wedge z_n|+\epsilon \hfill \\ \hfill & \le \sum _{n=1}^{\infty }{(y^{\prime }T)}^{+}z\wedge z_n+\epsilon \le \sum _{n=1}^{\infty }{(y^{\prime }T)}^{+}{z}_n+\epsilon .\hfill \end{array}$$

This implies that ${(y^{\prime }T)}^{+}({\bigvee }_{n=1}^{\infty }{z}_n)={\sum }_{n=1}^{\infty }{(y^{\prime }T)}^{+}{z}_n$. Similarly,

$${(y^{\prime }T)}^{-}(\underset{n=1}{\overset{\infty }{\bigvee }}{z}_n)=\sum _{n=1}^{\infty }{(y^{\prime }T)}^{-}{z}_n.$$

So $|y^{\prime }T|({\bigvee }_{n=1}^{\infty }{z}_n)={\sum }_{n=1}^{\infty }|y^{\prime }T|z_n$. The order continuity of norm on $G_T$ implies the series ${\sum }_{n=1}^{\infty }{Q}_T{z}_n$ converges in norm. Therefore, in view of Lemma 5,

$$\begin{array}{cc}\hfill \Vert Q_T\underset{k=n}{\overset{\infty }{\bigvee }}{z}_k\Vert & =\underset{\Vert y^{\prime }\Vert \le 1}{sup}|y^{\prime }T|\underset{k=n}{\overset{\infty }{\bigvee }}{z}_k=\underset{\Vert y^{\prime }\Vert \le 1}{sup}\sum _{k=n}^{\infty }|y^{\prime }T|z_k\hfill \\ \hfill & =\underset{\Vert y^{\prime }\Vert \le 1}{sup}\underset{m}{sup}\sum _{k=n}^m|y^{\prime }T|z_k=\underset{m}{sup}\underset{\Vert y^{\prime }\Vert \le 1}{sup}\sum _{k=n}^m|y^{\prime }T|z_k\hfill \\ \hfill & =\underset{m}{sup}\Vert \sum _{k=n}^m{Q}_T{z}_k\Vert \le \Vert \sum _{k=n}^{\infty }{Q}_T{z}_k\Vert .\hfill \end{array}$$

Let $x_n\stackrel{o}{\to }0$ in E. Suppose that $|x_n|\le p_n\downarrow 0$. According to Lemma 4, for every $\epsilon >0$, there exists a positive disjoint sequence $\{w_n\}$, such that $0\le p_n\le {\bigvee }_{i=n}^{\infty }{w}_i+\epsilon p_1$ and ${\bigvee }_{i=n}^{\infty }{w}_i\le \frac{1}{\epsilon }{p}_n$ for every n. Therefore,

$$\Vert Q_T{p}_n\Vert \le \Vert Q_T\underset{i=n}{\overset{\infty }{\bigvee }}{w}_i\Vert +\epsilon \Vert Q_T{p}_1\Vert \le \Vert \sum _{i=n}^{\infty }{Q}_T{w}_i\Vert +\epsilon \Vert Q_T{p}_1\Vert .$$

This implies that ${lim\; sup}_{n\to \infty }\Vert Q_T{x}_n\Vert \le {lim\; sup}_{n\to \infty }\Vert Q_T{p}_n\Vert \le \epsilon \Vert Q_T{p}_1\Vert$ for every $\epsilon >0$. Therefore, ${lim}_{n\to \infty }\Vert Q_T{x}_n\Vert =0$, hence ${lim}_{n\to \infty }T{x}_n={lim}_{n\to \infty }{S}_T{Q}_T{x}_n=0$.

$(4)\Rightarrow (1)$ By this assumption, T is an order weakly compact operator and $y^{\prime }T$ is a $\sigma$-order continuous operator for every $y^{\prime }\in F^{\prime }$. Therefore, according to [5] (Theorem 3.4.4), $Q_T$ is order weakly compact and $|y^{\prime }T|$ is a $\sigma$-order continuous operator for every $y^{\prime }\in F^{\prime }$. We obtain that the series ${\sum }_{n=1}^{\infty }{Q}_T{z}_n$ converges in norm for every order-bounded disjoint sequence $\{z_n\}$ in E. Given any an order-bounded disjoint sequence $\{z_n\}$ in $E^{+}$, we also have $|y^{\prime }T|({\sum }_{i=1}^n{z}_i)\uparrow |y^{\prime }T|({\bigvee }_{n=1}^{\infty }{z}_n)$. This implies that

$$\sum _{n=1}^{\infty }|y^{\prime }T|z_n=\underset{n\to \infty }{lim}|y^{\prime }T|(\sum _{i=1}^n{z}_i)=|y^{\prime }T|(\underset{n=1}{\overset{\infty }{\bigvee }}{z}_n).$$

The rest of the verification is contained in $(3)\Rightarrow (1)$.

$(7)\Rightarrow (6)$ Suppose that T is order weakly compact and $\sigma$-order continuous. Let $x_n\downarrow 0$ in E. Then, $x_1-x_n\uparrow x_1$, according to [5] (Theorem 3.4.4), there exists $y\in F$, such that $T(x_1-x_n)\stackrel{\Vert ·\Vert }{\to }y$. Then, the $\sigma$-order continuity of T implies $T(x_1-x_n)\stackrel{o}{\to }T{x}_1$. Therefore, $y=T{x}_1$. We obtain that $T{x}_n\stackrel{\Vert ·\Vert }{\to }0$. □

Remark 2.

In the above theorem, since $G_T$ has an order continuous norm, T is σ-order-to-norm continuous. It is also equivalent to $Q_T$ is σ-order continuous.

Let $L_{\sigma on}(E,F)$ be the collection of all order-bounded $\sigma$-order-to-norm continuous operators from E to F. We are interested in when $L_{\sigma on}(E,F)$ is an ideal in $L_b(E,F)$. Evidently, if F has an order-continuous norm, then, as demonstrated by Proposition 2 and [1] (Proposition 3), $L_{\sigma on}(E,F)=L_b(E,F)$. Recall that a Banach lattice E is said to be order-bounded $AM$ if the series ${\sum }_{n=1}^{\infty }|x_n|$ converges in E for every unconditional convergent series ${\sum }_{n=1}^{\infty }{x}_n$ in E with $\{{\sum }_{i=1}^n{x}_i\}$ order bounded. And E has a weakly Fatou property if there exists $r>0$ such that for every net $x_{\alpha }\uparrow x$ in E, it follows that $\Vert x_{\alpha }\Vert \le r{sup}_{\alpha }\Vert x_{\alpha }\Vert$.

Corollary 1.

Let Banach lattice $E,F$ be Dedekind complete and $T:E\to F$ be an order-bounded operator. If one of the following statements holds

(1) 

F is an $AM$-space with an order unit.

(2) 

F is order bounded $AM$ and F has a weakly Fatou property.

Thus, T is σ-order-to-norm continuous if and only if $|T|$ is σ-order-to-norm continuous.

In this case, $L_{\sigma on}(E,F)$ is an ideal in $L_b(E,F)$.

Proof. 

(1)

Suppose that F is an $AM$-space with an order unit and $T:E\to F$ is a $\sigma$-order-to-norm continuous operator. According to Theorem 3, $T:E\to F$ admits a factorization through an order-continuous Banach lattice $G_T$,

where the factor $Q_T$ is a $\sigma$-order continuous lattice homomorphism and $S_T$ is a norm-bounded operator. Since F has an order unit, $S_T$ is order bounded. Let $x_n\stackrel{o}{\to }0$ in $E^{+}$. We have $Q_T{x}_n\stackrel{ru}{\to }0$. Therefore,

$$|T|x_n=|S_T{Q}_T|x_n\le |S_T|Q_T{x}_n\stackrel{ru}{\to }0.$$

(2)

For every $x\in E^{+}$, we write the restriction of T to $I_x$ as $T_x$, where $I_x$ is the ideal generated by x in E. Evidently, T is order weakly compact if and only if $T_x$ is weakly compact for every $x\in E^{+}$. According to S. Kakutani’ theorem (see [6], Theorem 4.29), for every $x\in E^{+}$, there is Hausdorff compact topological space K, such that $I_e$ is isomorphic to $C(K)$. In view of [15] (Theorem 3.3), $|T_x|$ is weakly compact for every $x\in E^{+}$. Therefore, $|T|$ is order weakly compact. It follows from the order continuity of T that $|T|$ is order continuous; see [6] (Theorem 1.56). By Theorem 3, $|T|$ is $\sigma$-order-to-norm continuous.

□

In general, $L_{\sigma on}(E,F)$ may not be a band in $L_b(E,F)$. For example, let $P_n$ be the band projection from $l_{\infty }$ onto $span\{e_n\}$. Then, ${\sum }_{k=1}^n{P}_k\uparrow$ and is contained in $L_{\sigma on}(l_{\infty },l_{\infty })$. However, ${sup}_n{\sum }_{k=1}^n{P}_k\uparrow i{d}_{\infty }$, the identity operator on $l_{\infty }$, is not $\sigma$-order-to-norm continuous.

Theorem 4.

Let Banach lattice E be Dedekind complete. The followings are equivalent.

(1) 

E has order continuous norm.

(2) 

Every order-bounded operator from E to $l_{\infty }$ is σ-order-to-norm continuous.

(3) 

Every order-bounded σ-order continuous operator from E to $l_{\infty }$ is σ-order-to-norm continuous.

Proof. 

$(1)\Rightarrow (2)$ and $(2)\Rightarrow (3)$ are trivial.

$(3)\Rightarrow (1)$ If E is not order continuous, then there exists an order bounded sequence $\{x_n\}$ of disjoint elements such that $\lambda =\underset{n}{inf}\Vert x_n\Vert >0$. As shown by [14] (Proposition 0.5.5), the sublattice

$$F=\{(o)\sum _{n=1}^{\infty }{t}_n{x}_n:(t_n)\in l_{\infty }\}$$

is norm closed regular and order isomorphic to $l_{\infty }$, where $(o){\sum }_{n=1}^{\infty }{t}_n{x}_n$ is the order limit of sequence $\{{\sum }_{k=1}^n{t}_k{x}_k\}$. There exists an interval preserving projection P from E onto F; see [14] (Proposition 0.5.5). We can find $0<y_n^{\prime }\in E^{\prime }$ satisfying $y_n^{\prime }(x_n)=\Vert x_n\Vert$ and $\Vert y_n^{\prime }\Vert =1$. Let $P_n$ be the band projection onto the band $\left[\{x_n\}\right]$ generated by $\{x_n\}$ in E. Set $x_n^{\prime }=\frac{1}{\Vert x_n\Vert }{y}_n^{\prime }{P}_n$, then $x_n^{\prime }\wedge x_m^{\prime }=0$ for $n\ne m$, $\underset{n}{sup}\Vert x_n^{\prime }\Vert \le \frac{1}{\lambda }$ and $x_n^{\prime }(x_m)={\delta }_{nm}$, where ${\delta }_{nm}=1,n=m$ and ${\delta }_{nm}=0,n\ne m$. The operator $P:E\to F$ is defined by

$$Pz=(o)\sum _{n=1}^{\infty }{x}_n^{\prime }(z)x_n$$

for every $z\in E$. Clearly, P is a projection from E onto F. Now, define the lattice isomorphism $S:F\to l_{\infty }$ by $Su=(t_n)$ for every $u=(o){\sum }_{n=1}^{\infty }{t}_n{x}_n\in F$. Suppose that $T=SP$. Clearly, T is $\sigma$-order continuous. Note that

$$T{x}_n=SP{x}_n=S(\frac{x_n}{\Vert x_n\Vert })=\frac{e_n}{\Vert x_n\Vert };$$

hence, $\{T{x}_n\}$ does not converge to 0 in norm. This proves that the operator T is $\sigma$-order continuous but $\sigma$-order-to-norm continuous. □

Suppose that $(\Omega ,\Sigma ,\mu )$ is a measure space and $L_0(\mu )$ is the Riesz space of all real valued $\mu$-measurable functions f on $\Omega$. Now, our aim comes down to studying the relationship between $\sigma$-order-to-norm continuous operators and order-to-norm continuous operators on the subspaces of $L_0(\mu )$. Recall that a Riesz subspace Z of X is called a regular sublattice of X if $x_{\alpha }\stackrel{o}{\to }0$ in Z implies $x_{\alpha }\stackrel{o}{\to }0$ in X.

Lemma 6.

Let E be a Dedekind σ-complete Banach lattice which is lattice isomorphic to a regular sublattice of $L_0(\mu )$. If $(\Omega ,\Sigma ,\mu )$ is a finite measure space i.e., $\mu (\Omega )<+\infty$, then for every $x_0\in E^{+}$ and every $\{y_{\alpha }\}\subset E^{+}$ satisfying $y_{\alpha }\downarrow$ and $P_{y_{\alpha }}{x}_0\downarrow 0$, there exists a subsequence $\{P_{y_{{\alpha }_n}}{x}_0\}$ of $\{P_{y_{\alpha }}{x}_0\}$, such that $P_{y_{{\alpha }_n}}{x}_0\downarrow 0$.

Proof. 

Let $x_0\in E^{+}$. Suppose $\{y_{\alpha }\}$ is a net in $E^{+}$ satisfying $y_{\alpha }\downarrow$ and $P_{y_{\alpha }}{x}_0\downarrow 0$. Identifying E with its copy in $L_0(\mu )$, put $A=\{\omega \in \Omega :x_0(\omega )>0\}$. Evidently, $x_0=x_0{\chi }_A$, where ${\chi }_A$ is the characteristic function of A. Fixed $\alpha$, it follows that $x_0\wedge n{y}_{\alpha }\uparrow P_{y_{\alpha }}{x}_0$ in E and $x_0{\chi }_A\wedge n{y}_{\alpha }=x_0\wedge n{y}_{\alpha }\uparrow x_0{\chi }_{A_{\alpha }\cap A}$ in $L_0(\mu )$, where $A_{\alpha }=\{\omega \in \Omega :y_{\alpha }(\omega )>0\}$. Since E is a regular sublattice of $L_0(\mu )$, for every $\alpha$, we have $P_{y_{\alpha }}{x}_0=x_0{\chi }_{A_{\alpha }}=x_0{\chi }_{A_{\alpha }\cap A}$. Therefore, $x_0{\chi }_{A_{\alpha }\cap A}=P_{y_{\alpha }}{x}_0\downarrow 0$ in E. Then, ${\chi }_{A_{\alpha }\cap A}\downarrow 0$ in $L_0(\mu )$; hence, ${\chi }_{A_{\alpha }\cap A}\downarrow 0$ in $L_1(\mu )$, where $L_1(\mu )$ represents real absolutely integrable functions on a measure space $\Omega$. By the continuity of norm on $L_1(\mu )$, ${lim}_{\alpha }{\Vert {\chi }_{A_{\alpha }\cap A}\Vert }_1={lim}_{\alpha }{\int }_{\Omega }{\chi }_{A_{\alpha }\cap A}d\mu =0$. Therefore, there exists an increasing subsequence $\{{\alpha }_n\}$ of $\{\alpha \}$, such that $\Vert {\chi }_{A_{{\alpha }_n}}{\Vert }_1\downarrow 0$. It follows that ${\chi }_{A_{{\alpha }_n}\cap A}\downarrow 0$ in $L_1(\mu )$. This implies that $x_0{\chi }_{A_{{\alpha }_n}\cap A}\downarrow 0$ in $L_0(\mu )$. We obtain that $P_{y_{{\alpha }_n}}{x}_0=x_0{\chi }_{A_{{\alpha }_n}\cap A}\downarrow 0$ in E. □

Theorem 5.

Let E be a Dedekind σ-complete Banach lattice and F a Dedekind complete Banach lattice. $T:E\to F$ is an order-bounded operator. If one of the following conditions holds:

($H1$)

$(\Omega ,\Sigma ,\mu )$ is a finite measure space and E is lattice isomorphic to a regular sublattice of $L_0(\mu )$;

($H2$)

$(\Omega ,\Sigma ,\mu )$ is a σ-finite measure space and E is lattice isomorphic to an ideal of $L_0(\mu )$;

then the following statements hold.

(1) 

If T is a σ-order-to-norm continuous operator, then the following assertions hold.

($1a$)

$E/N(T)$ is an ideal in $G_T$.

($1b$)

$Q_T$ is order continuous and $N(T)$ is a band in E.

($1c$)

T is order continuous.

(2) 

T is σ-order-to-norm continuous if and only if T is order weakly compact and order continuous.

(3) 

T is σ-order-to-norm continuous if and only if T is order-to-norm continuous.

(4) 

Every σ-order continuous functional on E is order continuous.

Proof. 

(1a) If $v=Q_{T}x\in E/N(T)$, then $|v|=Q_T|x|\in E/N(T)$. Put $v\in G_T$ and $0\le v\le Q_{T}x$ (where $x\ge 0$). Note that $Q_T{x}_n\stackrel{\Vert ·\Vert }{\to }v$ for some sequence $\{x_n\}$ in $E^{+}$. Passing to a subsequence, we can assume that $Q_T{x}_n\stackrel{ru}{\to }v$ in $G_T$. It follows that ${\bigvee }_{k=n}^{\infty }{Q}_T{x}_k\downarrow v$ in $G_T$. According to Remark 2, $Q_T$ is $\sigma$-order continuous. We have

$$\underset{k=n}{\overset{\infty }{\bigvee }}(Q_{T}x\wedge Q_T{x}_k)=\underset{k=n}{\overset{\infty }{\bigvee }}{Q}_T(x\wedge x_k)=Q_T(\underset{k=n}{\overset{\infty }{\bigvee }}(x\wedge x_k))\downarrow Q_T(\underset{n=1}{\overset{\infty }{\bigwedge }}\underset{k=n}{\overset{\infty }{\bigvee }}(x\wedge x_k)).$$

At the same time,

$$\underset{k=n}{\overset{\infty }{\bigvee }}(Q_{T}x\wedge Q_T{x}_k)=Q_{T}x\wedge \underset{k=n}{\overset{\infty }{\bigvee }}{Q}_T{x}_k\downarrow Q_{T}x\wedge v=v.$$

This implies that $v=Q_T({\bigwedge }_{n=1}^{\infty }{\bigvee }_{k=n}^{\infty }(x\wedge x_k))\in E/N(T)$.

(1b) Firstly, in two cases, we will prove that $Q_T$ is order continuous. To see this, it is sufficient to prove that ${\bigwedge }_{\alpha }|Q_T{x}_{\alpha }|=0$ for every $x_{\alpha }\downarrow 0$ in E. Let $x_{\alpha }\downarrow 0$ in E. For a fixed ${\alpha }_0$ and given any $\epsilon >0$, by Lemma 4, there exists a decreasing net $\overline{x_{\alpha }}$, such that $P_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}\le \frac{1}{\epsilon }{x}_{\alpha }$ and $0\le x_{\alpha }\le P_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}+\epsilon x_{{\alpha }_0}$ for every $\alpha \ge {\alpha }_0$.

Case 1.

The assertion $(H2)$ is true.

According to Lemma 6, there exists a subsequence $\{{\alpha }_n\}$ of $\{\alpha \}$, such that $P_{\overline{x_{{\alpha }_n}}}{x}_{{\alpha }_0}\downarrow 0$. Therefore, based on the statements $(2)$ and $(3)$ of Theorem 3, $Q_T{P}_{\overline{x_{{\alpha }_n}}}{x}_{{\alpha }_0}\stackrel{\Vert ·\Vert }{\to }0$. For every $\epsilon >0$,

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim\; sup}\Vert Q_T{x}_{{\alpha }_n}\Vert \le \underset{n\to \infty }{lim\; sup}\Vert Q_T{P}_{\overline{x_{{\alpha }_n}}}{x}_{{\alpha }_0}+\epsilon Q_T{x}_{{\alpha }_0}\Vert \le \epsilon \Vert Q_T{x}_{{\alpha }_0}\Vert \hfill \end{array}$$

It follows that ${lim}_{n\to \infty }\Vert Q_T{x}_{{\alpha }_n}\Vert =0$. Hence,

$$\Vert \underset{\alpha }{\bigwedge }|Q_T{x}_{\alpha }|\Vert \le \Vert \underset{n=1}{\overset{\infty }{\bigwedge }}|Q_T{x}_{{\alpha }_n}|\Vert \le \Vert Q_T{x}_{{\alpha }_n}\Vert \to 0.$$

We have ${\bigwedge }_{\alpha }|Q_T{x}_{\alpha }|=0$. This implies that ${\bigwedge }_{\alpha }|Q_T{x}_{\alpha }|=0$ for every $x_{\alpha }\downarrow 0$ in E. According to [6] (Theorem 1.56), $Q_T$ is order continuous.

Case 2.

The assertion $(H1)$ is true.

Since $(\Omega ,\Sigma ,\mu )$ is a $\sigma$-finite measure space, there is a disjoint sequence $\{B_m\}$ of subsets of $\Omega$, such that ${\bigcup }_{m=1}^{\infty }{B}_m=\Omega$ and $\mu (B_m)<+\infty$ for all m. Identifying E with its copy in $L_0(\mu )$, since E is an ideal in $L_0(\mu )$, we have $x_{{\alpha }_0}{\chi }_{B_m}\in E$ for every m. Then, $x_{{\alpha }_0}={\bigvee }_{m=1}^{\infty }{x}_{{\alpha }_0}{\chi }_{B_m}$. For every $\alpha$, put $A_{\alpha }=\{\omega \in \Omega :\overline{x_{\alpha }}(\omega )>0\}$. Hence,

$$P_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}=x_{{\alpha }_0}{\chi }_{A_{\alpha }}=\underset{m=1}{\overset{\infty }{\bigvee }}{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}$$

for every $\alpha$. Fixed $m\in \mathbb{N}$, $x_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\downarrow 0$ in $L_0(B_m,\mu )$ since $x_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\le P_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}\downarrow 0$ in $L_0(\mu )$ for every m. Note that the band generated $\left[x_{{\alpha }_0}{\chi }_{B_m}\right]$ by $x_{{\alpha }_0}{\chi }_{B_m}$ in E is contained in $L_0(B_m,\mu )$. Then, $x_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\downarrow 0$ in $\left[x_{{\alpha }_0}{\chi }_{B_m}\right]$. In the view of Case 1, $Q_T{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\downarrow 0$. Let $v={\bigwedge }_{\alpha }{\bigvee }_{m=1}^{\infty }{Q}_T{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}$. Without loss of generality, assume that $\alpha \ge {\alpha }_0$ for every $\alpha$.

$$v\wedge Q_T{x}_{{\alpha }_0}{\chi }_{A_{{\alpha }_0}\cap B_m}\le Q_T{x}_{{\alpha }_0}{\chi }_{A_{{\alpha }_0}\cap B_m}\wedge \underset{m=1}{\overset{\infty }{\bigvee }}{Q}_T{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}=Q_T{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\downarrow 0.$$

We have $v\wedge Q_T{x}_{{\alpha }_0}{\chi }_{A_{{\alpha }_0}\cap B_m}=0$ for all m hence $v={\bigvee }_{m=1}^{\infty }v\wedge Q_T{x}_{{\alpha }_0}{\chi }_{A_{{\alpha }_0}\cap B_m}=0$ i.e., ${\bigvee }_{m=1}^{\infty }{Q}_T{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\downarrow 0$. Note that $Q_T$ is $\sigma$-order continuous. We obtain

$$Q_T{P}_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}=Q_T\underset{m=1}{\overset{\infty }{\bigvee }}{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}=\underset{m=1}{\overset{\infty }{\bigvee }}{Q}_T{x}_{{\alpha }_0}{\chi }_{A_{\alpha }\cap B_m}\downarrow 0.$$

By the order continuity of norm on $G_T$, ${lim}_{\alpha }\Vert Q_T{P}_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}\Vert =0$. For every $\epsilon >0$,

$$\begin{array}{cc}\hfill & \underset{\alpha }{lim\; sup}\Vert Q_T{x}_{\alpha }\Vert \le \underset{\alpha }{lim\; sup}\Vert Q_T{P}_{\overline{x_{\alpha }}}{x}_{{\alpha }_0}+\epsilon Q_T{x}_{{\alpha }_0}\Vert \le \epsilon \Vert Q_T{x}_{{\alpha }_0}\Vert .\hfill \end{array}$$

Hence, ${lim}_{\alpha }\Vert Q_T{x}_{\alpha }\Vert =0$. And $\Vert {\bigwedge }_{\alpha }|Q_T{x}_{\alpha }|\Vert \le \Vert Q_T{x}_{\alpha }\Vert$ implies that ${\bigwedge }_{\alpha }|Q_T{x}_{\alpha }|=0$. We also obtain ${\bigwedge }_{\alpha }|Q_T{x}_{\alpha }|=0$ for every $x_{\alpha }\downarrow 0$ in E. According to [6] (Theorem 1.56), $Q_T$ is order continuous.

Next, we prove that $N(T)$ is a band in E. Since $q_T(·)$ is a Riesz seminorm on E, $N(T)$ is an ideal in E. If $0\le z_{\alpha }\uparrow z$ in E with $z_{\alpha }\in N(T)$, then $Q_T{z}_{\alpha }\uparrow Q_{T}z$. Note that $G_T$ has an order continuous norm. $0=q_T(x_{\alpha })=\Vert Q_T{z}_{\alpha }\Vert \to \Vert Q_{T}z\Vert =q_T(z)$. We have $q_T(z)=0$ hence $z\in N_T$. This implies taht $N(T)$ is a band in E.

(1c) According to the proof of (1b), $Q_T$ is order continuous; hence, it is also order-to-norm continuous. If $x_{\alpha }\downarrow 0$ in E, then $Q_T{x}_{\alpha }\stackrel{\Vert ·\Vert }{\to }0$ in $G_T$. We have $\Vert {\bigwedge }_{\alpha }|T{x}_{\alpha }|\Vert \le \Vert T{x}_{\alpha }\Vert =\Vert S_T{Q}_T{x}_{\alpha }\Vert \to 0$. Hence, ${\bigwedge }_{\alpha }|T{x}_{\alpha }|=0.$ According to [6] (Theorem 1.56), T is order continuous.

$(2)$ and $(3)$ are obtained by $(1)$ and Theorem 3. $(4)$ is a simple indirect argument of $(3)$. □

Recall that a net $\{x_{\alpha }\}$ in E is said to be unbounded order convergent to 0 (or $uo$-converges to 0), written as $x_{\alpha }\stackrel{uo}{\to }0$, if $|x_{\alpha }|\wedge u\stackrel{o}{\to }0$ for every $u\in E^{+}$. The details on unbounded order convergence can be found in [16,17]. As an application of $\sigma$-order-to-norm continuous operators, we give a characterization of $\sigma$-order continuous M-weakly compact operators.

Theorem 6.

Let E be Dedekind σ-complete Banach lattice and F Dedekind complete. If $T:E\to F$ is an order-bounded operator, then the following statements are equivalent.

(1) $T{x}_n\stackrel{\Vert ·\Vert }{\to }0$ for every norm-bounded $x_n\stackrel{uo}{\to }0$ in E.

(2) T is M-weakly compact and T is σ-order continuous.

Proof. 

$(1)\Rightarrow (2)$ is obvious in Proposition 2.

$(2)\Rightarrow (1)$ This is similar to the proof of $(1)\Rightarrow (2)$ in Theorem 3 (replace “$0\le x_n\stackrel{o}{\to }0$ in E” with “disjoint $\{x_n\}$ in $B_E$”) in which $Q_T$ is M-weakly compact. Note that every M-weakly compact operator is order weakly compact. In view of Theorem 3 and Theorem 5, $Q_T$ is order-to-norm continuous. According to [6] (Theorem 5.60), for every $\epsilon >0$, there exists $z\in E^{+}$ such that $\Vert Q_T{(|x|-z)}^{+}\Vert <\epsilon$ for every $x\in B_E$. Given any $\{x_n\}\subset B_E$ with $x_n\stackrel{uo}{\to }0$, we have $|x_n|\wedge z\stackrel{o}{\to }0$; hence,

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}\Vert Q_T{x}_n\Vert & =\underset{n\to \infty }{lim\; sup}\Vert Q_T((|x_n{|-z)}^{+}+|x_n|\wedge z)\Vert \hfill \\ \hfill & \le \epsilon +\underset{n\to \infty }{lim\; sup}\Vert Q_T(|x_n|\wedge z)\Vert =\epsilon \hfill \end{array}$$

for every $\epsilon >0$. This implies that $Q_T{x}_n\stackrel{\Vert ·\Vert }{\to }0$. We obtain that $T{x}_n=S_T{Q}_T{x}_n\stackrel{\Vert ·\Vert }{\to }0$. The proof is complete. □

Recall that $T:E\to F$ is said to be L-weakly compact if every disjoint sequence in the solid hull $sol(T{B}_E)$ of $T{B}_E$ converges to zero. Meyer-Nieberg prove in [6] (Theorem 5.64) that the notions of L- and M-weakly compact operators are in duality to each other. By [6] (Theorem 1.73), every order-bounded operator has an order-continuous adjoint. Note that the norm dual of a Banach lattice is a Dedekind complete Banach lattice. We are now in the position to give a new characterization of L-weakly compact operators.

Corollary 2.

Let $E,F$ be Banach lattices and $T:E\to F$ be an order-bounded operator. The following statements are equivalent.

$(1)$ $T^{\prime }{x}_n^{\prime }\stackrel{\Vert ·\Vert }{\to }0$for every norm-bounded $x_n^{\prime }\stackrel{uo}{\to }0$ in $E^{\prime }$.

$(2)$ T is L-weakly compact.

In [17] (Theorem 5), A.W. Wickstead gave a characterization of the order continuity of norms on E and $E^{\prime }$ in terms of unbounded order convergent nets. To be precise, E and $E^{\prime }$ have order continuous norms if and only if every norm-bounded net in E which $uo$-converges to zero must converge weakly to zero. It does not suffice to consider only sequences in this equivalence, as is shown by the space of all continuous real-valued functions on the one point compactification of an uncountable discrete space. A norm-bounded $uo$-convergent sequence there must converge in norm, so certainly weakly ([18], Example 33.1).

Theorem 7.

Let E be a Banach lattice. The following statements are equivalent.

$(1)$ E is Dedekind σ-complete and $x_n\stackrel{w}{\to }0$ for every norm-bounded $x_n\stackrel{uo}{\to }0$ in E.

$(2)$ E and $E^{\prime }$ have order-continuous norms.

Proof. 

$(2)\Rightarrow (1)$ is by [17] (Theorem 5). $(1)\Rightarrow (2)$ Based on the assumption of $(2)$, for every $x^{\prime }\in E^{\prime }$, $x^{\prime }(x_n)\to 0$ for every norm-bounded $x_n\stackrel{uo}{\to }0$. According to Theorem 6, for every $x^{\prime }\in E^{\prime }$, $x^{\prime }$ is M-weakly compact and $\sigma$-order continuous. In the view of [11] (Theorem 39.5), E has a $\sigma$-order continuous norm if and only if for each $x^{\prime }\in {(E^{\prime })}^{+}$, $x^{\prime }(x_n)\downarrow 0$ whenever $x_n\downarrow 0$ in E. We find that E has a $\sigma$-order continuous norm. Note that E is Dedekind $\sigma$-complete. According to [14] (Theorem 1.1), E has an order-continuous norm. It is proved in [10] (Theorem 116.1) that $E^{\prime }$ has an order-continuous norm if and only if $x_n\stackrel{w}{\to }0$ for every norm-bounded disjoint sequence $\{x_n\}$ in E. Note that every disjoint sequence must $uo$-converge to zero. Again, based on the assumption of $(2)$, $E^{\prime }$ has an order-continuous norm. □

4. Conclusions and Recommendation

This paper under review aims to further explore $\sigma$-order-to-norm continuous and order-to-norm continuous operators. To prove that the $\sigma$-order-to-norm continuous operator can be defined using the order relation, we introduce a basic property of Banach lattices, namely the property (h). Theorem 3 plays an important role in this paper, in which we present a number of nice characterizations for a $\sigma$-order-to-norm continuous operator. This result is also the basis for our extension on Wickstead’s results on the order continuity of norms on E and $E^{\prime }$.

This research can be categorized under the topic “Operators Acting on Banach Lattices and Related Applications”. Our future work is to extend these results to more general spaces (e.g., topological Riesz spaces) as well as applying them to the field of non-linear analysis. In [19], Çevik and Altun introduce and investigate a class of spaces equipped with vetor metrics, mainly vector metric spaces. One of the research components could be the application of relative uniform convergence to the fixed point theory on vector metric spaces. Based on [20,21,22], we could consider replacing order convergence, in the definition of vectorial convergence (see [19], Definition 2.4), with relative uniform convergence to obtain more of the properties of vectorially continuous functions (see [20], Definition 3).