Parameter Estimation for Nonlinear Diffusion Problems by the Constrained Homotopy Method

Abstract

This paper studies a parameter estimation problem for the non-linear diffusion equation within multiphase porous media flow, which has important applications in the field of oil reservoir simulation. First, the given problem is transformed into an optimization problem by using optimal control framework and the constraints such as well logs, which can restrain noise and improve the quality of inversion, are introduced. Then we propose the widely convergent homotopy method, which makes natural use of constraints and incorporates Tikhonov regularization. The effectiveness of the proposed approach is demonstrated on illustrative examples.

1. Introduction

The non-linear diffusion equation, which can approximatively describe the multiphase porous media flow processes, has received considerable attention in recent years due to increasing applications in science and engineering. An oil reservoir simulation based on the inverse problem for this equation has many important applications in fields, such as oil and gas exploration and management of petroleum reservoirs. For example, it can help reservoir engineers make important decisions about the type of the recovery method, fluid production and injection rates, and well locations. From then on, a variety of effective numerical methods have appeared in the literatures of the inverse problem for non-linear diffusion problems [1,2,3,4,5,6]. This inverse problem can be viewed as a parametric data-fitting problem. It is possible to formalize such a problem in the optimal control framework where a control functional defined in terms of discrepancy between measurement and computed data is minimized over a model space. Generally speaking, this inverse problem is very difficult to solve, because of its own ill-posedness and non-linearity. The ill-posed property makes the parameter field susceptible to the noise in the measurement data, while the non-linear dependence of the measurement data with respect to the parameter field causes the presence of numerous local minima. For the non-linear ill-posed problem, conventional linearized methods, such as the Gauss–Newton method [7], Landweber method [8], Levenberg–Marquardt method [9], are locally convergent. The recent popular methods (e.g., trust region algorithm [10], neural networks algorithm [11], genetic algorithm [12], simulated annealing algorithm [13]) have global convergence properties, but the efficiency is much worse than before, along with the searching space decreasing. When the level of the noise in the measurement data is high, all these methods fail to converge. Consequently, the shortcomings of the above methods motivate us to construct a globally convergent, efficient, and stable algorithm.

The novel and effective homotopy method has been successfully used to solve non-linear problems, such as time- or space-fractional heat equations [14], fractional-order convection–reaction–diffusion equations [15], fractional-order Kolmogorov and Rosenau–Hyman equations [16], second kind integral equations [17], and so on. A remarkable advantage of this method is that it exhibits global convergence under certain weak assumptions [18]. Lately, the homotopy method has also been extended for dealing with inverse problems. Many authors studied the homotopy solution of geophysical inverse problems [19,20,21]. Słota et al. [22,23] and Hetmaniok et al. [24] presented the applications of the homotopy method for solving inverse Stefan problems. Hu et al. [25] considered the homotopy algorithm to improve PEM identification of ARMAX models. Zhang et al. [26] proposed the non-linear and non-convex image reconstruction algorithm based on the homotopy method. Biswal et al. [27], Hetmaniok et al. [28,29], and Shakeri and Dehghan [30], respectively, considered the Jeffery–Hamel flow inverse problem, the inverse heat conduction problem and the diffusion equation inverse problem by the homotopy perturbation method. Liu [31,32] formulated the multigrid-homotopy approach directly in a framework of non-linear inverse problems, and formulated the wavelet multiscale-homotopy algorithm for the solution of partial differential equation parameter identification problems.

Generally speaking, a parameter inversion for non-linear diffusion problems estimates parameters only using the measurement data, which usually have a low signal-to-noise ratio. In order to restrain the noise and improve the quality of inversion, the constraint condition has a wide application in the inversion fields, such as atmospheric research [33], petrophysics [34], remote sensing of environment [35], and geological exploration [36]. This is because the constraint condition, recorded from the interior of the object to be measured, has a high signal-to-noise ratio.

In this article, a well-log constraint is introduced for the parameter estimation for non-linear diffusion problems, and an optimization problem is formed by the finite difference discretization. This problem is a typical ill-posed problem, so the Tikhonov regularization needs to be imposed. In order to overcome the weakness of the local convergence of conventional methods, the homotopy method is applied to the normal equation of the regularized control functional, and then the constrained homotopy method is constructed. Numerical simulations conducted with two synthetic examples illustrate the effectiveness of this method.

2. Mathematical Model

The non-linear diffusion equation, describing, approximatively, the multiphase porous media flow processes, has one of the following two forms

$$u_t-\nabla ·(\upsilon (x,y)N(\nabla u)\nabla u)=\phi (x,y,t),t\in (0,T),$$

(1)

or

$$u_t-\nabla ·(\upsilon (x,y)N\left(u\right)\nabla u)=\phi (x,y,t),t\in (0,T),$$

(2)

where $u(x,y,t)$ is the concentration at $(x,y)$ and at time t, $\upsilon (x,y)$ is the permeability at $(x,y)$ in the medium, $\phi (x,y,t)$ is a piecewise smooth source function, N is the positive non-linear function of $\nabla u$ or u, which is used to model the main characteristics of the non-linearity associated with the permeability parameter in the multiphase porous media flow. For simplicity, the problem is studied in the unit square domain $\Omega =[0,1]\times [0,1]$ under the initial-boundary conditions

$$\begin{array}{cc}\hfill & u(x,y,0)=\psi (x,y),(x,y)\in \Omega ,\hfill \\ \hfill & u(x,y,t)=\eta (x,y,t),(x,y)\in \partial \Omega ,t\in (0,T).\hfill \end{array}$$

(3)

Equation (1) or Equation (2) with (3) form the direct problem of the non-linear diffusion equation, however, permeability $\upsilon$ is not known in engineering practice. What we know is only some measurement data, for example,

$$u(x^m,y^m,t)={\varphi }^m\left(t\right),m=1,2,\dots ,M,t\in (0,T).$$

(4)

Then, the unknown permeability $\upsilon$ can be estimated from Equation (1) or Equation (2) with (3) and (4). The permeability $\upsilon (x^{\ast },y)$ at all depths of constraint point $x^{\ast }$ can be obtained from the measurement data of well logs, which is necessary for the constrained inversion.

3. Parameter Estimation Framework

By the finite difference scheme, Equations (1)–(4) can be discretized as follows

$$\left\{\begin{array}{c}\frac{u_{i,j}^k-u_{i,j}^{k-1}}{\Delta t}-\nabla ·({\upsilon }_{i,j}{N}_{i,j}^k\nabla u_{i,j}^k)=\phi (i\Delta x,j\Delta y,k\Delta t),\hfill \\ i=1,2,\dots ,I-1;j=1,2,\dots ,J-1;k=1,2,\dots ,K,\hfill \\ u_{i,j}^0=\psi (i\Delta x,j\Delta y),i=0,1,\dots ,I;j=0,1,\dots ,J,\hfill \\ u_{0,j}^k=\eta (0,j\Delta y,k\Delta t),j=0,1,\dots ,J;k=1,2,\dots ,K,\hfill \\ u_{1,j}^k=\eta (1,j\Delta y,k\Delta t),j=0,1,\dots ,J;k=1,2,\dots ,K,\hfill \\ u_{i,0}^k=\eta (i\Delta x,0,k\Delta t),i=0,1,\dots ,I;k=1,2,\dots ,K,\hfill \\ u_{i,1}^k=\eta (i\Delta x,1,k\Delta t),i=0,1,\dots ,I;k=1,2,\dots ,K,\hfill \\ u_{x^m,y^m}^k={\varphi }^m(k\Delta t),m=1,2,\dots ,M;k=1,2,\dots ,K,\hfill \end{array}\right.$$

(5)

where

$$\begin{array}{cc}& u_{i,j}^k=u(i\Delta x,j\Delta y,k\Delta t),{\upsilon }_{i,j}=\upsilon (i\Delta x,j\Delta y),\hfill \\ & N_{i,j}^k=N(\nabla u_{i,j}^k)/N\left(u_{i,j}^k\right),I=1/\Delta x,J=1/\Delta y,K=T/\Delta t.\hfill \end{array}$$

$\Delta x$, $\Delta y$ are the spatial step sizes, and $\Delta t$ is the time step size. The concrete expression for $\nabla ·({\upsilon }_{i,j}{N}_{i,j}^k\nabla u_{i,j}^k)$ is not the focus of this article, so we do not describe it here. For interested readers, see [37].

Equation (5) can define a non-linear operator equation

$$A({\rm Y})=\Phi ,$$

(6)

where

$$\begin{array}{cc}& {{\rm Y}}^{\top }=({\upsilon }_{1,1},{\upsilon }_{1,2},\dots ,{\upsilon }_{1,J},{\upsilon }_{2,1},{\upsilon }_{2,2},\dots ,{\upsilon }_{2,J},\dots ,{\upsilon }_{I,1},{\upsilon }_{I,2},\dots ,{\upsilon }_{I,J}),\hfill \\ & {\Phi }^{\top }=({\varphi }^1(\Delta t),{\varphi }^1(2\Delta t),\dots ,{\varphi }^1(K\Delta t),{\varphi }^2(\Delta t),{\varphi }^2(2\Delta t),\dots ,{\varphi }^2(K\Delta t),\hfill \\ & \dots ,{\varphi }^M(\Delta t),{\varphi }^M(2\Delta t),\dots ,{\varphi }^M(K\Delta t)).\hfill \end{array}$$

Let ${\widehat{\varphi }}^m\left(t\right)$ denote the measurement data and form the vector $\widehat{\Phi }$ in the same sequence as $\Phi$, and let

$$\begin{array}{cc}& {{\rm Y}}_i^{\top }=({\upsilon }_{i,1},{\upsilon }_{i,2},\dots ,{\upsilon }_{i,J}),\hfill \\ & {\widehat{{\rm Y}}}_{i^{\ast }}^{\top }=({\upsilon }_{i^{\ast },1},{\upsilon }_{i^{\ast },2},\dots ,{\upsilon }_{i^{\ast },J}),\hfill \end{array}$$

where ${\widehat{{\rm Y}}}_{i^{\ast }}^{\top }$ is the permeability from the well logs of a well located at point $i^{\ast }$ in the $x-$direction. Now we define the admissible set

$$\Pi =({\rm Y},{{\rm Y}}_{i^{\ast }}={\widehat{{\rm Y}}}_{i^{\ast }})$$

and the optimal control problem as follows. Find ${{\rm Y}}^{\ast }\in \Pi$ satisfying

$${{\rm Y}}^{\ast }=arg\underset{{\rm Y}\in \Pi }{min}\{\parallel A({\rm Y})-\widehat{\Phi }{\parallel }^2\}.$$

It is difficult to solve this problem directly so usually one transforms it into another easier-to-solve form.

Let us assume

$${\widehat{{\rm Y}}}^{\top }=(\underset{(i^{\ast }-1)\times J}{\underbrace{0,0,\dots ,0}},{\upsilon }_{i^{\ast },1},{\upsilon }_{i^{\ast },2},\dots ,{\upsilon }_{i^{\ast },J},0,0,\dots ,0),$$

$$G={\left(\begin{array}{cccccccccccc}0& & & & & & & & & & & \\ & 0& & & & & & & & & & \\ & & \ddots & & & & & & & & & \\ & & & 0& & & & & & & & \\ & & & & 1& & & & & & & \\ & & & & & 1& & & & & & \\ & & & & & & \ddots & & & & & \\ & & & & & & & 1& & & & \\ & & & & & & & & 0& & & \\ & & & & & & & & & 0& & \\ & & & & & & & & & & \ddots & \\ & & & & & & & & & & & 0\end{array}\right)}_{(I\times J)\times (I\times J)}.$$

Obviously

$$\parallel G{\rm Y}-\widehat{{\rm Y}}{\parallel }^2=0,\forall {\rm Y}\in \Pi .$$

Therefore, the above optimal control problem can be rewritten, without constraint, as

$$min\{\parallel A({\rm Y})-\widehat{\Phi }{\parallel }^2+\beta \parallel G{\rm Y}-\widehat{{\rm Y}}{\parallel }^2\},$$

(7)

where $\beta$ is a constraint parameter to determine the strength of the constraint. This unconstrained optimal control problem (7) will be used to approximate the solution of the original constrained optimal control problem. The minimum of Equation (7) and ${{\rm Y}}^{\ast }$ are close to each other when $\beta$ is large enough, and consequently in the specific inversion process, $\beta$ must be specified large enough, such that the solution of Equation (7) can well approximate ${{\rm Y}}^{\ast }$.

4. Inversion Method

4.1. Basic Iterative Method

Due to the ill-posed property of Equation (7), Tikhonov regularization needs to be imposed

$$min\{\parallel A({\rm Y})-\widehat{\Phi }{\parallel }^2+\beta \parallel G{\rm Y}-\widehat{{\rm Y}}{\parallel }^2+{\alpha }_1\parallel B_1({\rm Y}-{{\rm Y}}^0){\parallel }^2+{\alpha }_2\parallel B_2({\rm Y}-{{\rm Y}}^0){\parallel }^2\},$$

(8)

where ${\alpha }_1$, ${\alpha }_2$ are the regularization parameters, $B_1$, $B_2$ are, respectively, the second-order smooth matrices in the $x-$ and $y-$direction (see [37]), and ${{\rm Y}}^0$ is an initial estimate.

It is obvious that Equation (8) is equivalent to the corresponding normal equation

$$A^{\prime }{({\rm Y})}^{\top }(A({\rm Y})-\widehat{\Phi })+\beta G^{\top }(G{\rm Y}-\widehat{{\rm Y}})+({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)({\rm Y}-{{\rm Y}}^0)=0,$$

(9)

where ${}^{\prime }$ represents derivative of A with respect to ${\rm Y}$. The second derivative appears in the Newton iterative method, so we use a successive linearization method to solve Equation (9).

If we make the hypothesis that the kth approximation ${{\rm Y}}^k$ of ${{\rm Y}}^{\ast }$ has been obtained, then in order to avoid the impact of the second derivative, the linear function $L_k({\rm Y})=A^{\prime }\left({{\rm Y}}^k\right)({\rm Y}-{{\rm Y}}^k)+A\left({{\rm Y}}^k\right)$ is used to replace $A({\rm Y})$, where $L_k({\rm Y})$ is the linear approximation of $A({\rm Y})$ at point ${{\rm Y}}^k$. The regularized control functional in Equation (8) is transformed into

$$\parallel L_k({\rm Y})-\widehat{\Phi }{\parallel }^2+\beta \parallel G{\rm Y}-\widehat{{\rm Y}}{\parallel }^2+{\alpha }_1\parallel B_1({\rm Y}-{{\rm Y}}^0){\parallel }^2+{\alpha }_2{\parallel B_2({\rm Y}-{{\rm Y}}^0)\parallel }^2,$$

(10)

and its normal equation is

$$\begin{array}{cc}\hfill & A^{\prime }{\left({{\rm Y}}^k\right)}^{\top }(A^{\prime }\left({{\rm Y}}^k\right)({\rm Y}-{{\rm Y}}^k)+A\left({{\rm Y}}^k\right)-\widehat{\Phi })+\beta G^{\top }(G{\rm Y}-\widehat{{\rm Y}})\hfill \\ \hfill & +({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)({\rm Y}-{{\rm Y}}^0)=0,\hfill \end{array}$$

(11)

the solution of which is exactly the next approximation ${{\rm Y}}^{k+1}$ to ${{\rm Y}}^{\ast }$:

$$\begin{array}{cc}\hfill & {{\rm Y}}^{k+1}={{\rm Y}}^k-{[A^{\prime }{\left({{\rm Y}}^k\right)}^{\top }{A}^{\prime }\left({{\rm Y}}^k\right)+\beta G^{\top }G+{\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2]}^{-1}\hfill \\ \hfill & \times [A^{\prime }{\left({{\rm Y}}^k\right)}^{\top }(A\left({{\rm Y}}^k\right)-\widehat{\Phi })+\beta G^{\top }(G{{\rm Y}}^k-\widehat{{\rm Y}})\hfill \\ \hfill & +({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)({{\rm Y}}^k-{{\rm Y}}^0)],k=0,1,2,\dots \hfill \end{array}$$

(12)

This iterative method is actually a variant of the iteratively regularized Gauss–Newton method [38], and has the same fast convergence speed and good stability as the latter, however it is a locally convergent method.

4.2. Homotopy Method

To improve the local convergence of Equation (12), the homotopy method is introduced to solve Equation (9). We take into account the following fixed-point homotopy equation

$$\begin{array}{cc}\hfill & P({\rm Y},\chi )=\chi [A^{\prime }{({\rm Y})}^{\top }(A({\rm Y})-\widehat{\Phi })+\beta G^{\top }(G{\rm Y}-\widehat{{\rm Y}})\hfill \\ \hfill & +({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)({\rm Y}-{{\rm Y}}^0)]+(1-\chi )[{\rm Y}-{{\rm Y}}^0]=0,\hfill \end{array}$$

(13)

where $\chi \in [0,1]$ is the homotopy parameter.

To obtain ${{\rm Y}}^{\ast }$, we first rearrange Equation (13) as

$$\begin{array}{cc}\hfill & \chi [A^{\prime }{({\rm Y})}^{\top }(A({\rm Y})-\widehat{\Phi })+\beta G^{\top }(G{\rm Y}-\widehat{{\rm Y}})]\hfill \\ \hfill & +[(1-\chi )I+\chi ({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)]({\rm Y}-{{\rm Y}}^0)=0,\hfill \end{array}$$

(14)

and then divide the interval $[0,1]$ into $0={\chi }_0<{\chi }_1<\cdots <{\chi }_D=1$. For $\chi ={\chi }_d$, the iterative method similar to Equation (12) is applied to Equation (14) in sequence from $d=1$ to $d=D$. For $P({\rm Y},{\chi }_1)$, the initial estimate can be chosen as ${{\rm Y}}^0$, which is already known. The initial estimate of $P({\rm Y},{\chi }_{d+1})$ is chosen as ${{\rm Y}}^d$, which is obtained by solving $P({\rm Y},{\chi }_d)$. Therefore, we can have the iterative formula

$$\begin{array}{cc}\hfill & {{\rm Y}}_{h+1}^d={{\rm Y}}_h^d-[{\chi }_d{A}^{\prime }{\left({{\rm Y}}_h^d\right)}^{\top }{A}^{\prime }\left({{\rm Y}}_h^d\right)+{\chi }_d\beta G^{\top }G+(1-{\chi }_d)I\hfill \\ \hfill & +{\chi }_d({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2){]}^{-1}\times \{{\chi }_d{A}^{\prime }{\left({{\rm Y}}_h^d\right)}^{\top }(A\left({{\rm Y}}_h^d\right)-\widehat{\Phi })\hfill \\ \hfill & +{\chi }_d\beta G^{\top }(G{{\rm Y}}_h^d-\widehat{{\rm Y}})+[(1-{\chi }_d)I+{\chi }_d({\alpha }_1{B}_1^{\top }{B}_1\hfill \\ \hfill & +{\alpha }_2{B}_2^{\top }{B}_2\left)\right]({{\rm Y}}_h^d-{{\rm Y}}^0)\},h=0,1,\dots ,d_T,\hfill \\ \hfill & {{\rm Y}}_0^d={{\rm Y}}^{d-1},{{\rm Y}}^d={{\rm Y}}_{d_T+1}^d,d=1,2,\dots ,D.\hfill \end{array}$$

(15)

The stopping point $d_T$ is defined here as the point at which the modification is equal to or less than a threshold value.

Equation (15) has a fast convergence rate similar to the variant of the regularized Gauss–Newton method (12), so a good approximation to ${{\rm Y}}^d$ can be obtained by only one iteration when ${\chi }_d-{\chi }_{d-1}$ is small enough. In order to save unnecessary computational cost, we can let

$$d_T=0,{\chi }_d=\frac{d}{D},d=1,2,\dots ,D,$$

where $d_T=0$ means that we use Equation (15) to iterate one step to obtain ${{\rm Y}}_1^d$, and then have ${{\rm Y}}^d={{\rm Y}}_1^d$. In this way, Equation (15) is simplified as follows:

$$\begin{array}{cc}\hfill & {{\rm Y}}^{d+1}={{\rm Y}}^d-[\frac{d}{D}{A}^{\prime }{\left({{\rm Y}}^d\right)}^{\top }{A}^{\prime }\left({{\rm Y}}^d\right)+\frac{d}{D}\beta G^{\top }G+(1-\frac{d}{D})I\hfill \\ \hfill & +\frac{d}{D}({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2){]}^{-1}\times \{\frac{d}{D}{A}^{\prime }{\left({{\rm Y}}^d\right)}^{\top }(A\left({{\rm Y}}^d\right)-\widehat{\Phi })\hfill \\ \hfill & +\frac{d}{D}\beta G^{\top }(G{{\rm Y}}^d-\widehat{{\rm Y}})+[(1-\frac{d}{D})I+\frac{d}{D}({\alpha }_1{B}_1^{\top }{B}_1\hfill \\ \hfill & +{\alpha }_2{B}_2^{\top }{B}_2\left)\right]({{\rm Y}}^d-{{\rm Y}}^0)\},d=0,1,\dots ,D-1.\hfill \end{array}$$

(16)

Then, consider the iterative result ${{\rm Y}}^D$ of Equation (16) as the initial estimate for Equation (12), and compute the solution ${{\rm Y}}^{\ast }$ of Equation (9) by iterating Equation (12). That is, Equations (16) and (12) are combined into the constrained homotopy method, which has not only fast convergence speed and good stability, but also a global region of convergence.

When $\beta =0$, Equation (8) is the habitual parameter inversion for non-linear diffusion problems, and Equations (16) and (12) can, respectively, be re-expressed as

$$\begin{array}{cc}\hfill & {{\rm Y}}^{d+1}={{\rm Y}}^d-[\frac{d}{D}{A}^{\prime }{\left({{\rm Y}}^d\right)}^{\top }{A}^{\prime }\left({{\rm Y}}^d\right)+(1-\frac{d}{D})I\hfill \\ \hfill & +\frac{d}{D}({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2){]}^{-1}\times \{\frac{d}{D}{A}^{\prime }{\left({{\rm Y}}^d\right)}^{\top }(A\left({{\rm Y}}^d\right)-\widehat{\Phi })\hfill \\ \hfill & +[(1-\frac{d}{D})I+\frac{d}{D}({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)]({{\rm Y}}^d-{{\rm Y}}^0)\},\hfill \\ \hfill & d=0,1,\dots ,D-1.\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill & {{\rm Y}}^{k+1}={{\rm Y}}^k-{[A^{\prime }{\left({{\rm Y}}^k\right)}^{\top }{A}^{\prime }\left({{\rm Y}}^k\right)+{\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2]}^{-1}\hfill \\ \hfill & \times [A^{\prime }{\left({{\rm Y}}^k\right)}^{\top }(A\left({{\rm Y}}^k\right)-\widehat{\Phi })+({\alpha }_1{B}_1^{\top }{B}_1+{\alpha }_2{B}_2^{\top }{B}_2)({{\rm Y}}^k-{{\rm Y}}^0)],\hfill \\ \hfill & k=0,1,2,\dots \hfill \end{array}$$

(18)

From the expressions of Equations (17) and (18) (Equation (18) is just the iteratively regularized Gauss–Newton method), we can see that Equation (17) has the same calculation amount and storage requirement as Equation (18) at each step. What is important is the application of the first-order derivative, the evaluation of the adjoint operator, and the forward-modeling run. However, the most important is that Equation (17) has a wider convergence region than Equation (18).

4.3. Global Convergence of Homotopy Method

Equation (13) can actually be seen as the normal equation of the following optimal control problem:

$$\begin{array}{cc}\hfill & min{J}_{\chi }({\rm Y})=\left\{\chi \right[\parallel A({\rm Y})-\widehat{\Phi }{\parallel }^2+\beta \parallel G{\rm Y}-\widehat{{\rm Y}}{\parallel }^2+{\alpha }_1{\parallel B_1({\rm Y}-{{\rm Y}}^0)\parallel }^2\hfill \\ \hfill & +{\alpha }_2\parallel B_2({\rm Y}-{{\rm Y}}^0){\parallel }^2]+(1-\chi )\parallel {\rm Y}-{{\rm Y}}^0{\parallel }^2\}.\hfill \end{array}$$

(19)

Let

$$\begin{array}{cc}\hfill & J_{{\chi }_d}({\rm Y})={\chi }_d[\parallel A({\rm Y})-\widehat{\Phi }{\parallel }^2+\beta \parallel G{\rm Y}-\widehat{{\rm Y}}{\parallel }^2+{\alpha }_1{\parallel B_1({\rm Y}-{{\rm Y}}^0)\parallel }^2\hfill \\ \hfill & +{\alpha }_2\parallel B_2({\rm Y}-{{\rm Y}}^0){\parallel }^2]+(1-{\chi }_d){\parallel {\rm Y}-{{\rm Y}}^0\parallel }^2,\hfill \end{array}$$

(20)

then our next result, similar to the Theorem 3.1 of [39], gives certain conditions that validate the global convergence of homotopy method.

Theorem 1.

For any $d\in \{0,1,\dots ,D\}$, assume that ${{\rm Y}}_{\ast }^d$ is the global minimum of $J_{{\chi }_d}({\rm Y})$ and $J_{\chi }({\rm Y})$ is differentiable with respect to χ. Assume, also, that there exist a $\delta >0$ such that $J_{{\chi }_d}({\rm Y})$ has no local minimum in the region $J_{{\chi }_d}({\rm Y})<\delta +J_{{\chi }_d}\left({{\rm Y}}_{\ast }^d\right)$. Then, all the global minima ${{\rm Y}}_{\ast }^d$ of $J_{{\chi }_d}({\rm Y})$$(d=0,1,\dots ,D)$ can be computed by sequentially minimizing $J_{{\chi }_d}({\rm Y})$, with a sufficiently small $\Delta \chi ={\chi }_{d+1}-{\chi }_d$.

Proof of Theorem 1.

Since $J_{\chi }({\rm Y})$ is differentiable with respect to $\chi$, denote $\parallel \frac{\partial }{\partial \chi }{J}_{\chi }({\rm Y})\parallel \le L$, where L is a positive constant.

Then

$$\begin{array}{cc}& J_{{\chi }_{d+1}}\left({{\rm Y}}_{\ast }^d\right)\le J_{{\chi }_d}\left({{\rm Y}}_{\ast }^d\right)+L\Delta \chi \le J_{{\chi }_d}\left({{\rm Y}}_{\ast }^{d+1}\right)+L\Delta \chi \hfill \\ & \le J_{{\chi }_{d+1}}\left({{\rm Y}}_{\ast }^{d+1}\right)+2L\Delta \chi \le J_{{\chi }_{d+1}}\left({{\rm Y}}_{\ast }^{d+1}\right)+\delta ,\hfill \end{array}$$

with $\Delta \chi =\frac{\delta }{2L}$.

It follows from the assumption that the initial estimate ${{\rm Y}}_{\ast }^d$ is in a region where there is no additional local minimum. □

5. Numerical Experiments and Results

We have performed two numerical experiments to test the merits of our method. In all experiments, some basic parameters are

$$\begin{array}{cc}& \phi (x,y,t)=0,\psi (x,y)=sin\left(\pi x\right)sin\left(\pi y\right),\eta (x,y,t)=0,\hfill \\ & T=0.06,\Delta t=0.002,\Delta x=\Delta y=1/24,{{\rm Y}}^0\equiv 5,\hfill \\ & \beta ={10}^4,{\alpha }_1={\alpha }_2={10}^{-6},x^{\ast }=12/24,D=5,\hfill \end{array}$$

where the values of the regularization parameters ${\alpha }_1$, ${\alpha }_2$ are chosen by trial and error.

In the first numerical experiment, we consider a horizontal stratified medium containing two interfaces, as shown in Figure 1, and take $N\left(u\right)=u^2-u+1$. To illustrate the noise sensitivity, 40, 30, 20, and 10 dB Gaussian noises are, respectively, added to the measurement data, and then, the parameter is estimated from noisy data. The inversion results of the homotopy method with 40 and 30 dB Gaussian noises added are shown in Figure 2, and the inversion results of the constrained homotopy method with 40, 30, 20, and 10 dB Gaussian noises added are shown in Figure 3. To compare differences among the three methods, the constrained homotopy method (Equations (12) and (16)), the homotopy method (Equations (17) and (18)), and the constrained method (Equation (12)), Table 1 tabulates the relative errors and CPU times of the inversion results by these methods.

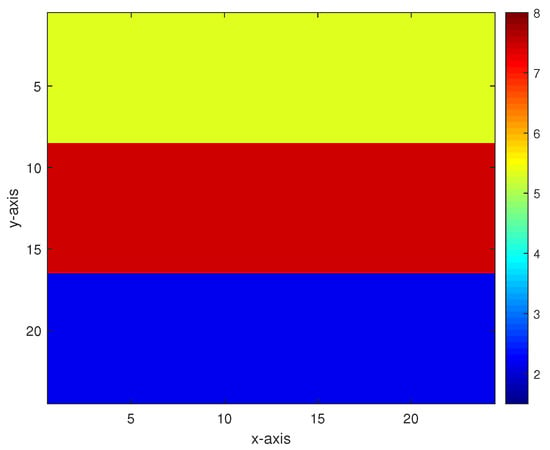
Figure 1. True model in the first experiment.

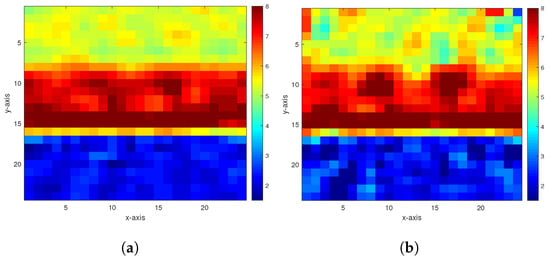
Figure 2. The inversion results of the homotopy method in the first experiment. (a,b) are the inversion results with 40 and 30 dB Gaussian noises, respectively.

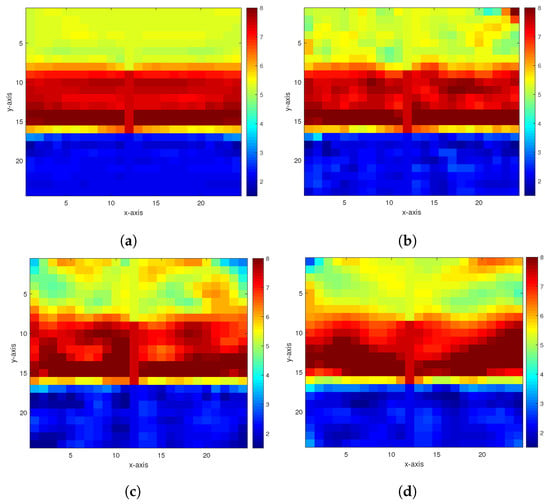
Figure 3. The inversion results of the constrained homotopy method in the first experiment. (a–d) are the inversion results with 40, 30, 20, and 10 dB Gaussian noises, respectively.

Table 1. Comparison of the three methods in the first experiment.

Noise Level	Inversion Method	Relative Error	CPU Run Time (s)
40 dB	Constrained homotopy method	0.0835	228.9241
	Homotopy method	0.0890	256.4925
	Constrained method	No convergence	No convergence
30 dB	Constrained homotopy method	0.0849	230.9774
	Homotopy method	0.1062	257.6150
	Constrained method	No convergence	No convergence
20 dB	Constrained homotopy method	0.0921	259.9313
	Homotopy method	No convergence	No convergence
	Constrained method	No convergence	No convergence
10 dB	Constrained homotopy method	0.1018	284.2159
	Homotopy method	No convergence	No convergence
	Constrained method	No convergence	No convergence

In the second numerical experiment, we take $N(\nabla u)=\frac{1}{1-{0.1|\nabla u|}^2}$, and consider the model of two anomalous bodies in a homogeneous medium with a permeability of 5.82. The anomalous bodies have the permeability of 1.88 and 8.13, respectively. Figure 4 and Figure 5, respectively, show this model and inversion results of the homotopy method with 40 and 30 dB Gaussian noises added. Figure 6 shows the inversion results of the constrained homotopy method with 40, 30, 20, and 10 dB Gaussian noises added. For comparison, Table 2 tabulates the relative errors and CPU times of the inversion results by the constrained homotopy method, the homotopy method, and the constrained method.

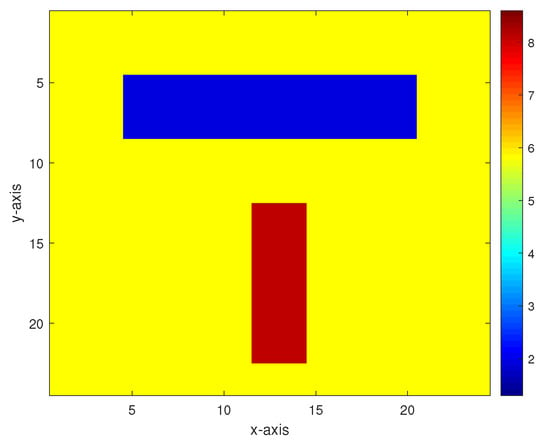
Figure 4. True model in the second experiment.

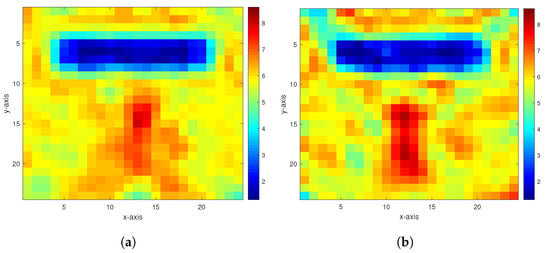
Figure 5. The inversion results of the homotopy method in the second experiment. (a,b) are the inversion results with 40 and 30 dB Gaussian noises, respectively.

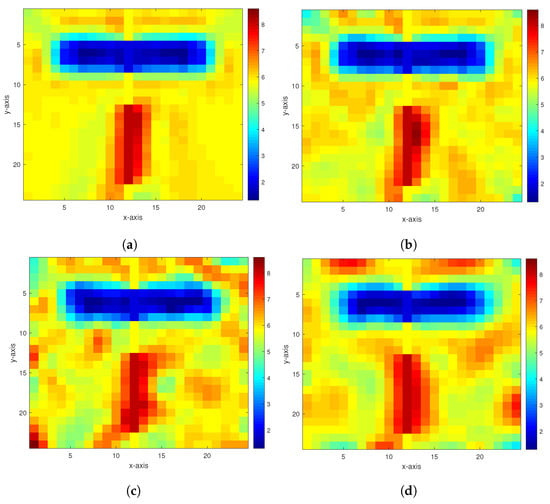
Figure 6. The inversion results of the constrained homotopy method in the second experiment. (a–d) are the inversion results with 40, 30, 20, and 10 dB Gaussian noises, respectively.

Table 2. Comparison of the three methods in the second experiment.

Noise Level	Inversion Method	Relative Error	CPU Run Time (s)
40 dB	Constrained homotopy method	0.0633	223.1658
	Homotopy method	0.0799	224.1277
	Constrained method	No convergence	No convergence
30 dB	Constrained homotopy method	0.0674	224.3204
	Homotopy method	0.0805	249.1969
	Constrained method	No convergence	No convergence
20 dB	Constrained homotopy method	0.0827	225.0038
	Homotopy method	No convergence	No convergence
	Constrained method	No convergence	No convergence
10 dB	Constrained homotopy method	0.0871	251.2146
	Homotopy method	No convergence	No convergence
	Constrained method	No convergence	No convergence

Table 1 and Table 2 show that:

(1)

The constrained homotopy method has global convergence, fast convergence speed, and good stability;

(2)

Both the constrained homotopy method and the homotopy method have wider region of convergence than the constrained method;

(3)

The constrained homotopy method has a stronger noise suppression ability than the homotopy method.

6. Conclusions

This paper presents an application of constrained homotopy method to the parameter estimation for non-linear diffusion problems. Numerical results shows the feasibility and effectiveness of this method. Compared with the constrained method and the homotopy method, our approach has wider region of convergence and stronger noise suppression ability.