Abstract
The application of solid mechanics theory for material behavior faces the discrete nature of modern or biological material. Despite the developed methods of homogenization, there are deviations between simulated and experiments results. The reason is homogenization, which mathematically involves a type of interpolation. The situation gets worse for complex structured materials. On the other hand, a topological approach can help in such analysis, but such an approach has computational costs. At the same time, increasing modern computational capabilities remove this barrier. This study is focused on building a method to analyze material structure in a topological sense. The orientation distribution function was used to describe the structure of the material. The plane case was investigated. Quadratic and biquadratic forms of interpolant were investigated. The persistent homology approach was used for topology analysis. For this purpose, a persistence diagram for quadratic and biquadratic forms was found and analyzed. In this study, it is shown how scaling the origin point cloud influences H1 points in the persistence diagram. It was assumed that the topology of the biquadratic form can be understood as a superposition of quadratic forms. Quantitative estimates are given for ellipticity and H1 points. A dataset of micro photos was processed using the proposed method. Furthermore, the supply criteria for the interpolation choice in quadratic or biquadratic forms was formulated.
Keywords:
orientation distribution function; mean intercept length; fabric tensor; topology analyses; persistent homology MSC:
55N31
1. Introduction
Solid mechanics assume continuum space. Of course, most materials differ from this state. For these purposes, different types of materials’ symmetry are considered (e.g., tetragonal, orthorhombic, etc.). So, quantifying the material structure has become an important task, because the concrete type of symmetry should be found for the current material. Moreover, even if the type of symmetry is known, the corresponding mechanical properties should be found. This task has become crucial for composite and biological materials. So, one of the popular approaches is mathematical modelling [1,2,3]. In these cases, the microstructure’s mechanics are simulated directly, and then some general relation is investigated. Then, for real models, this relation is usually used [4]. In other words, the homogenization approach is widespread. The weak points of such methods are computational labor and the idealization of the microstructure. Of course, in models, some idealized geometry is used, and real objects deviate from the ideal, which causes difficulty. For example, bone structure has a complicated architecture, and in different points of the bone different structures appear. The most common measurements have a histological origin, and, in fact, they have mean or relative characteristic [5,6]. So, some clusterization by tissue type of the object is performed. Then, isotropic [7,8] or orthotropic properties [9] and continuum mechanics are used. It is obvious that such an approach suffers from large spread. However, the received values of mechanical properties vary a lot, and modern approaches are focused on personalization of the tissue models, such as computed tomography [10] and digital volume correlation [11]. Computed tomography allows not only the simulation of the object behavior but also analyses of the structure. So, the alternative is the orientation distribution function [12,13,14]. Such an approach compares the structure with some distribution and then the distribution can be interpolated. Then, the interpolation is used for measuring the structure. Furthermore, the weak point of the approach is the type of interpolation. Thus, quadratic form interpolation is well known, but it does not suit all distributions. The background of the quadratic interpolation is a three (two in R2) orthogonal materials symmetry planes hypothesis. Or, in other words, there is a hypothesis of orthotropic materials. The objectivity of the hypothesis is in question. Contrariwise, the topological approach for data analysis has become widespread [15,16,17]. Furthermore, such an approach allows for quantifying the shape of the structure and, consequently, for understanding the material symmetry. Despite this, there is a lack of research dedicated to material structure analyses via the topological approach. So, this study is focused on topological analyses of the material structure. The R2 case was investigated, and the orientation’s distribution function was used for the material structure description. Quadratic and biquadratic interpolations were considered.
2. Materials and Methods
2.1. Orientation Distribution Function
Let us consider the macroscopic scalar property of the material φ (Figure 1). Usually, the φ depends on the material distribution in the sample. The distribution depends on position x and orientation vector n. So, φ can be defined by mapping from unit sphere to reals:
The scalar-valued function f should satisfy the condition:
The invariance of f leads to existing function h:
So, h can be expanded in the following Fourier series [18,19,20]:
where
where F is the first two tensor spherical harmonics and they form the orthogonal basis of the functions.
The three coefficients in the basis can be determined from f(n) via the integrals [21]:
In mechanics, it is widespread that the second order tensor is used to describe the microstructural anisotropy in orthotropic materials.
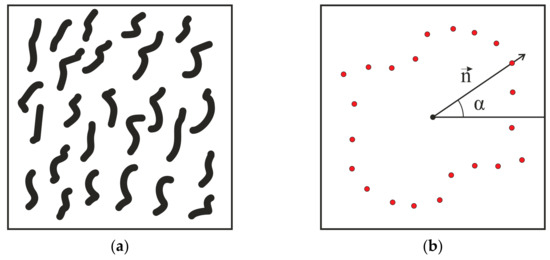

Figure 1.
Example of the scalar property of the material: (a)—material distribution, (b)—mean intercept length data.
There is also the so-called mean intercept length (MIL) tensor [22] or fabric tensor [23,24] (Figure 2). The MIL tensor is defined as:
Furthermore, the fabric tensor is defined as:
Such an approximation can be useful to determine the elastic tensor:
where ϕ—porosity, H—fabric tensor, and ρ—scale factor depending on the materials.
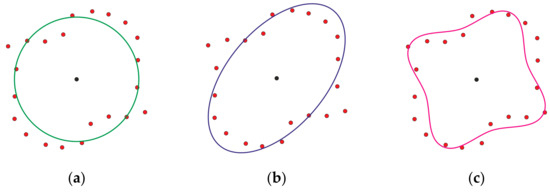

Figure 2.
Example of Fourier series of the mean intercept length distribution: (a)—0 order interpolation, (b)—2 order interpolation, (c)—4 order interpolation.
2.2. Application of Orientation Distribution Function
Obviously, the interpolant of the orientation distribution function can be applied for fabric distribution, e.g., for micro photos. Previously, the authors developed a method for the analysis of the quality of the derma’s recovery. For this purpose, collagen distribution in the area was analyzed from the orthotropic media point of view [25,26].
The method’s idea is to compare the micro photo and the vector field. The vector field consists of fabric tensor eigenvectors normalized by the degree of anisotropy, where the degree of anisotropy is an eigenvalues ratio:
In this case, the quality of the derma’s recovery can be estimated by the following equation:
In other words, the relative content of the fabric tensor with a low degree of anisotropy is measured. Such an approach assumes that the equality of all eigenvalues leads to isotropic distribution. This was shown by Cowin [27], who developed a general representation of an elastic tensor as a function of the solid volume fraction and of the invariants of the fabric tensor. Furthermore, it was shown that eigenvectors of the fabric tensor are orthotropic axes.
So, the question regards the quality of MIL interpolation by the fabric tensor. Furthermore, as the distribution is badly interpolated by the constant, there are distributions that are badly interpolated by the fabric tensor. On the other hand, four order interpolation is harder to analyze. This is why it was decided to develop a method for distribution analyses.
2.3. Topological Approach
Let us define a function
where T—topological space.
In this case, Ta can be defined as:
With the obvious property:
Such inclusions produce a map of homologous groups
Considering the sequence:
We receive:
This leads to homeomorphism:
This homeomorphism can endure topological classes from Tai to Taj. Topological classes can appear (birth), disappear (death), or unite. The image of homeomorphism keeps this information; denote it:
The Betti number can be calculated as rank:
The simplicial complex is used, so let us consider the simplicial complex K and denote ζ as:
We receive:
and
In these cases, the birth of class [c] of homology Hp in Ki can be defined as
The death of class [c] of homology Hp in Ki can be defined as
The birth and death of class [c] are illustrated in Figure 3.
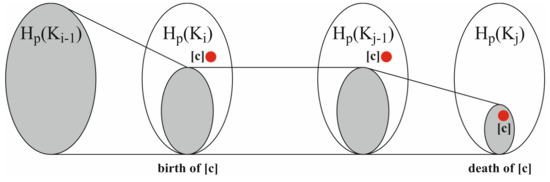
Figure 3.
Homology map illustration of the birth and death of class [c].
So, let us describe some technical notes. We consider a point cloud:
In the first step, a distance matrix should be built:
where d is a Euclidean distance between points:
The received distance matrix can be understood as an adjacency matrix for a constant value of dij. So, each unique value of dij generates a finite graph. Let us collect unique values in ascending order in a vector d. In this case, the adjacency matrix for dK-balls can be built as:
where θ—Heaviside step function.
A point cloud and graphs for unique distances are shown in Figure 4. An adjacency matrix for the shown point cloud is:
where the vector of unique distances is:
The incidence matrix can be built using the adjacency matrix and the unique distances vector. Each unique distance produces a set of lines ordered by the minimal point index. An incidence matrix for the example is:
Let us consider the birth and death of class [c] for the point cloud in the example from [28]. Initially, there are 5 classes (each point in Figure 4); d1 produces the death of two classes (list of classes: point 1, point 5, and the complex of points 2, 3, and 4 in Figure 4). Only one class is left for d2 (the complex of all connected points in Figure 4).
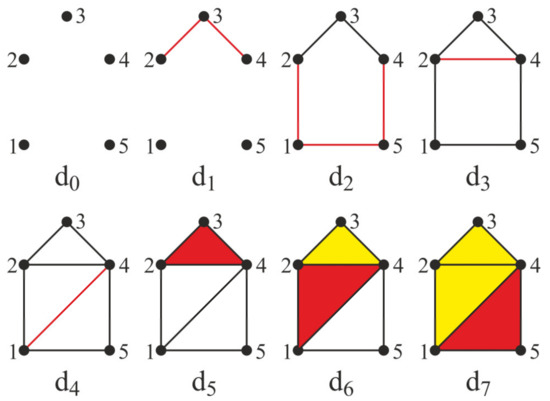

Figure 4.
Example of a simplex construction for a point cloud, red color for objects are just appeared, black colors for H0 object, yellow color for H1 objects.
Then, there appears for d3 new classes, and the list of classes is: the complex of connected points 1, 2, 4, and 5 and the complex of connected points 2, 3, and 4. In the next step (diameter d4), the complex of connected points 1, 2, 4, and 5 breaks into two complexes: the connected points 1, 2, and 4 and the complex of connected points 1, 4, and 5. Each complex of connected points is a 1-dimensional complex. Starting with a d5 diameter, 1-dimensional complexes disappear. In the 6th step, complex 2, 3, and 4 became closed, which means that the simplex is covered with d5 spheres. So, the 1-dimensional complex is dead. Complexes 1, 2, and 4 and 1, 4, and 5 are dead on d6 and d7, respectively.
The incidence matrix can be built for 1-dimensional complexes:
So, the rows in (33) are lines: 2-3, 3-4, 2-1, 1-5, 5-4, 2-4, and 1-4. Furthermore, the columns are area objects: (2-3)-(3-4)-(2-4), (1-2)-(2-4)-(1-4), and (1-4)-(5-4)-(1-5). The 1-dimensional complex’s death is described by the corresponding diameter value. So, knowing the incidence matrices, B0 and B1 information about the birth and death of 0-dimensional and 1-dimensional complexes can be obtained.
To find a birth of a 1-dimensional complex, a cycle should be found in the B0 graph. To find a death of a 1-dimensional complex, a diameter overlapping the whole cycle should be found. This problem can be decomposed by overlapping the simplex. For this purpose, the following equation was used:
where xi is a vector of the simplex vertices, D is the diameter of the overlapping, and x is a point of the circles’ intersection.
The common way to represent a complex’s birth and death is through a persistence barcode and a persistence diagram. So, the persistence barcode for 0-dimension complexes of the example are shown in Figure 5a. Each interval starts from the birth of the complex and ends in a point corresponding to the death diameter [29,30]. In Figure 5b, the persistence barcode for 1-dimension complexes of the example is shown. Understanding the diameters of the birth and death as points in R2 leads us to a persistence diagram (Figure 5c). It is obvious that points have a sense if they are higher than the bisector; otherwise, they immediately were born and died (if a point is on the bisector) or they died before birth (if a point is under the bisector) [31,32]. Scaling the point cloud leads to scaling the 0-dimension persistence barcode and shifting the 1-dimension persistence barcode. In Figure 5c, the scaled points are shown by circles with black contours.
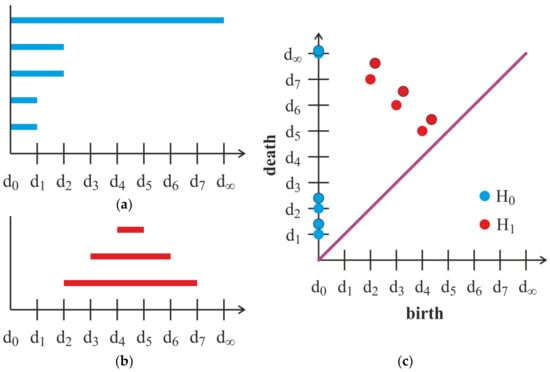
Figure 5.
Persistence barcodes for 0-dimension complexes (a) and 1-dimension complexes (b); persistence diagram (c): circles with black contours correspond to scaled point cloud.
So, the general algorithm of the construction of B0 and B1 matrixes is presented in pseudocode below Algorithm 1.
| Algorithm 1: B0 and B1 matrixes construction |
| Input: x, vector of dimension N Output: B0 and B1 matrixes for each xi for j in range [i, N] d(i,j) = distance(x(i), x(j)) by Equation (28) end for end for dUnique ← unique(d(i,j)) V, E ← null B0, B1 ← null k = 0 for i in range of dUnique j = findRows(d == dUnique(i)) V += number(j) E += findNumber(d == dUnique(i)) B0(j,i) ← dUnique(i) F = 2 − V − E if F > 0 k += 1 cycle = findCycle(B0 == dUnique(i)) D = findOverLap(cycle) by Equation (34) B1(k,:) ← D end if end for |
Where B0 and B1 are arrays to store the incidence matrixes for H0 and H1, respectively; d is the distance matrix; dUnice is the vector with unique distance values; V, E, and F are temporary variables to store the number of vertices, edges, and faces for a certain distance; and for the cycle store graphs cycles, D stores the overlapping distances for the cycles.
In the case of numerical calculations, some noisy results appear. In Figure 5c, a bisector is highlighted. If a point appears on a bisector, it means that the birth and death of the complex was immediate. If a point appears under a bisector, it means that the complex died before birth. Such points should be filtered. To filter the persistence diagram, bottleneck distance was used:
2.4. Research Design
Consider the 2nd order interpolation (quadratic form) of MIL in the following form:
The biquadratic form for the 4th order interpolation [33] was used in the following equation:
Assuming M2 in diagonal form (space is oriented by the eigenvectors of M2), two parameters of M2 and three parameters of M3 were varied. According to (2) and (6), only antisymmetric and closed curves were inspected [34,35].
The point clouds of curves were obtained by varying the parameters in (36) and (37). Schematically, the received curves are shown in Figure 6. All curves were scaled in a square [−0.5, 0.5] × [−0.5, 0.5]. A persistence diagram was built for each curve. Persistence diagrams were filtered near the bisector using bottleneck distance (35) with relative value 1%.

Figure 6.
Distinctive types of curves.
Let us focus on the quadratic form interpolation of MIL. The scale factor of the point cloud will shift H1 points in a persistence diagram in a radial line direction (see Lemma 1 below). Ellipticity will decrease the death value of H1 (see Lemma 2 below).
Lemma 1.
Scaling both axes for R2 point cloud data leads to shifting the H0 points in a persistence diagram in the death direction and shifting the H1 points in a persistence diagram with a constant aspect ratio of birth and death values.
Proof of Lemma 1.
Let us consider the scale transform as:
where s—scale factor, I—identity matrix, and y—new coordinates.
The Euclidean distance (28) will be changed as follows:
So, all unique distances (31) will be multiplied by s; this means that all H0 points will be shifted in a persistence diagram in the death direction.
The birth of graph cycles depends only on unique distances. So, all birth points will be multiplied by scale s. Consider the overlapping Equation (34) in scaled axes:
This leads to multiplying by scale s the overlapping diameter. Because the multipliers of the birth and death dimeters are equal, the aspect ratio will be constant. □
Lemma 2.
Birth and death values when scaled by λ (0 < λ < 1) in one direction point cloud in R2 cannot be higher than the origin values.
Proof of Lemma 2.
Let us consider changes in distances in scaled dimension. Define the origin distance as d0:
Then, estimate the distance in scaled dimension dλ:
By considering the dλ as a function of λ, monotony can be shown for 0 < λ ≤ 1:
This leads to
The decline of the distance values in the scaled space means that the distance values in the adjacency matrix (29) cannot be higher than in the origin space. That means that the death values of H0 and the birth values of H1 cannot increase. Moreover, overlapping distance values (34) cannot be higher than in origin space, too. Furthermore, that means that death values of H1 cannot increase. □
2.5. Numerical Example
Then, 10 μm tissue sections were cut with a microtome (Thermo Scientific, Waltham, MA, USA, HM325) to obtain 5 μm thick cuts. These were dehydrated and stained either according to the Mallory protocol or with hematoxylin/eosin.
The histological samples were documented on a Carl Zeiss Axio Imager 2 microscope with magnification of 100×. The image size was about 4164 × 3120 with 150 dpi. The images were taken from a dataset [26]. On the micro photos, the skin biopsy was presented. The biopsy data include the epidermis, the dermis, and the subcutaneous panniculus carnosus muscle. The Cartesian grid was built for images. The cell size was 400 × 400 pixels with 150 dpi. The binarization threshold was calculated by Otsu’s method for a blue channel.
To estimate the direction of the collagen orientation, the histological images were aligned with a 2-D Cartesian grid, and the MIL was calculated for each element [36]. Previously, the analysis was obtained through the aspect ratio of fitting ellipse eigenvalues. In this study, the persistence diagram was built for received MILs. MIL distribution was calculated by the following equation:
where L—is an intercept length in n direction, ω is a binary function, 1 is for material, and 0 is for no material.
3. Results and Discussion
Numerical investigation of a quadratic form’s persistent diagram shows linear dependence between the death–birth aspect ratio and ellipticity (see the blue line in Figure 7). Let us define the slope value as a death–birth aspect ratio. Linear regression was used for interpolation (see the orange line in Figure 7):
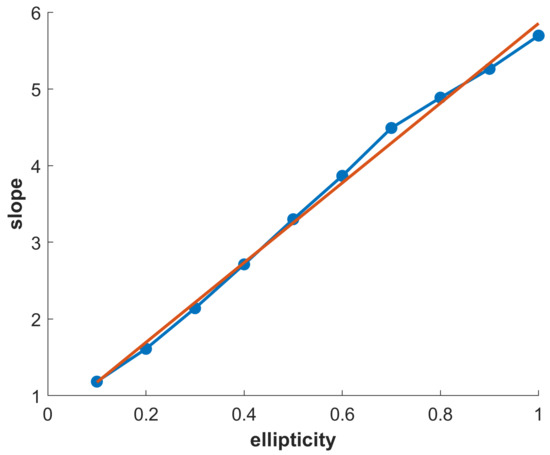
Figure 7.
Numerical results (blue points) and linear interpolation (orange line) for slope and ellipticity values.
The received parameters of linear regression are shown in Table 1.

Table 1.
Results of linear regression.
According to Lemma 1, the slope values are constant for scaling the whole data. This fact allows for the use of the linear regression results for quantifying the ellipticity by points in a persistent diagram.
Numerical investigation of a biquadratic form’s persistent diagram shows a significant difference in the case of cross-like curves (e.g., the green curve in Figure 6). In this case, the second H1 point appears in the persistent diagram. Meanwhile, all quadratic forms follow by one H1 point.
Some typical point clouds can be highlighted (see Figure 8c) for the received MIL distribution (47) of derma micro photos. Original (see Figure 8a) and binarized (see Figure 8b) cells from micro photos are shown, too. Quadratic interpolation was performed (36), and in Figure 8c, corresponding eigenvectors are shown. It should be noted that received point clouds are not all well-interpolated by quadratic form (e.g., the cyan point cloud in Figure 8). This points to the fact that for analysis, eigenvalues and eigenvectors are used, and some received interpolants are crucially mistaken. However, on the other hand, the persistence diagram for the cyan point cloud in Figure 8 shows two H1 points (see cyan points in Figure 9). The same is true for cross-like biquadratic curves.

Figure 8.
Example of elements of origin image (a), element of binarized image (b), MIL point cloud (c).
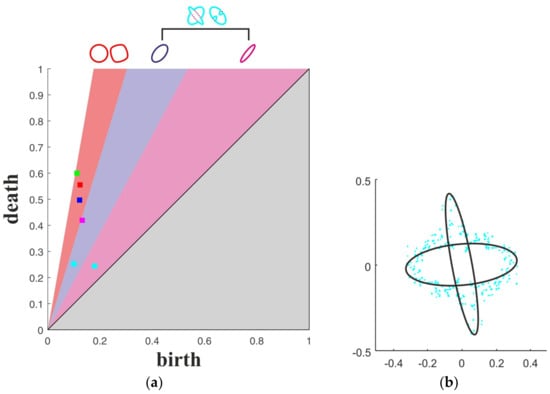
Figure 9.
Persistent diagram (a) for typical point clouds (colors of H1 points correspond to colors of MILs in Figure 8) and (b) interpolation by two quadratic forms of a cross-like point cloud.
On the other hand, persistence diagrams for biquadratic forms allowed for identifying the areas of curve shape persistence. Numerical results show that flattering shifts the point on the persistent diagram to the right. Moreover, a second H1 point appears when a new direction of flattering appears (see Figure 9). The area under the bisector is highlighted by a grey color. For example, MIL distribution (the cyan point cloud in Figure 8c) can be implied as a superposition of two ellipses with different aspect ratios of semi axes. In a persistent diagram, these are expressed by two cyan points in Figure 9a.
In contrast, the green point cloud from Figure 8c is the closest to the circle, and the corresponding point on the persistent diagram (the green point in Figure 9) is the closest to the ideal (the left side of the red area). Next, the MILs (the red and blue point clouds in Figure 8c) are flattered in one direction, and these lead to shifting to the right of points in the persistent diagram (the red and blue points in Figure 9a). The values of the slope for lines separating the area by flattering degree are presented in Table 1. Slope values for the H1 point of the cyan point cloud were 2.5266 and 1.4194, respectively. Using inverse regression, the calculated ellipticity was 0.3609 and 0.1490, respectively. The interpolations by the two ellipses with the following flattering are shown in Figure 9b.
So, the persistent diagram of the concrete MIL point cloud can be understood as decomposition by the number of ellipses. In this case, the number of H1 points describes the number of composite ellipses, and slope values allow for quantifying the flattering of composite ellipses. The distance from origin quantifies the scale of the composite ellipses. On the one hand, according to this information, MIL distribution can be classified; on the other hand, the required interpolant can be used. Additionally, the number of H1 points can provide information about the materials’ symmetry. So, one H1 point (or elliptic interpolation) indicates orthotropic material; in contrast, more than one H1 point raises questions about the orthotropic hypothesis.
Focusing on micro photos analysis from a topological point of view, some items should be highlighted. The number of H1 points in the persistent diagram indicates the suitable interpolation order. This indicates the symmetry of the MIL distribution; consequently, this also indicates the material symmetry and the orthotropic aspect ratio. With regard to the derma analysis, this information allows for the estimation of the quality of healing (by Equation (11)). Cells with two H1 points can be analyzed by elliptic decomposition or in terms of biquadratic interpolant. Numerical results showed that two H1 points appear in cells where collagen distribution deviates from normal. Of course, these facts need to be additionally investigated in proper ways.
4. Conclusions
In this article, a persistent diagram was built for a quadratic form set and for an antisymmetric biquadratic form set. It was found that the number of H1 points determines the shape of the curve. Meanwhile, each H1 point can be understood as an ellipse. The ratio of coordinates is a slope coefficient, which determines the flattering ratio of the ellipse. Linear regression was found for ellipticity and slope values. It was shown that the points shift with the constant slope value describes the scale factor of the origin point cloud. More than one H1 point determines the biquadratic origin of the data. Furthermore, slope values can be used for interpolation by the number of ellipses. The proposed method was applied on a micro photo dataset. The material was analyzed in terms of the mean intercept length distribution. Distinctive point clouds were presented and discussed in terms of the topology structure. Slope values for applying the proposed method were presented.
Of course, most presented results are numerical, but they are a background for more certain analytical research. More detailed analyses of the topological structure of the antisymmetric biquadratic form can improve our understanding of corresponding persistent diagrams and our understanding of the symmetry of materials (in terms of distribution function), as a consequence. So, the aforementioned topics define research development. A separate issue is the generalization of the R3 case.
Author Contributions
Conceptualization, O.S.; methodology, O.S., V.S. and R.Z.; software, V.S. and V.P.; validation, V.S., V.P. and E.S.; writing—original draft preparation, E.S. and O.S.; supervision, O.S. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the subsidy allocated to Kazan Federal University for the state assignment in the sphere of scientific activities, project No. FZSM-2023-0009.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, O.S., upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alizadeh, E.; Omairey, S.; Zysset, P. Investigating the post-yield behavior of mineralized bone fibril arrays using a 3D non-linear finite element unit-cell model. J. Mech. Behav. Biomed. Mater. 2023, 139, 105660. [Google Scholar] [CrossRef] [PubMed]
- Schenk, D.; Zysset, P. Personalized loading conditions for homogenized finite element analysis of the distal sections of the radius. Biomech. Model Mechanobiol. 2023, 22, 453–466. [Google Scholar] [CrossRef] [PubMed]
- Dalbosco, M.; Carniel, T.A.; Fancello, E.A.; Holzapfel, G.A. Multiscale numerical analyses of arterial tissue with embedded elements in the finite strain regime. Comput. Methods Appl. Mech. Eng. 2021, 381, 113844. [Google Scholar] [CrossRef]
- Bachmann, S.; Pahr, D.H.; Synek, A. A density-dependent target stimulus for inverse bone (re)modeling with homogenized finite element models. Ann. Biomed. Eng. 2023, 51, 925–937. [Google Scholar] [CrossRef] [PubMed]
- Nagl, K.; Reisinger, A.; Pahr, D.H. The biomechanical behavior of 3D printed human femoral bones based on generic and patient-specific geometries. 3D Print. Med. 2022, 8, 35. [Google Scholar] [CrossRef]
- Silva-Henao, J.D.; Synek, A.; Pahr, D.H.; Reisinger, A.G. Selection of animal bone surrogate samples for orthopaedic screw testing based on human radius CT-derived bone morphology. Med. Eng. Phys. 2022, 103, 103786. [Google Scholar] [CrossRef]
- Sadyrin, E.V. Modeling the mechanism of reducing enamel mineral density in the vicinity of the fisure tip. Russ. J. Biomech. 2023, 27, 31–39. [Google Scholar]
- Maslov, L.B.; Dmitryuk, A.Y.; Zhmaylo, M.A.; Kovalenko, A.N. Study of the strength of a hip endoprosthesis made of polymeric material. Russ. J. Biomech. 2022, 26, 19–33. [Google Scholar]
- Casari, D.; Michler, J.; Zysset, P.; Schwiedrzik, J. Microtensile properties and failure mechanisms of cortical bone at the lamellar level. Acta Biomater. 2021, 120, 135–145. [Google Scholar] [CrossRef]
- Keaveny, T.M.; Clarke, B.L.; Cosman, F.; Orwoll, E.S.; Siris, E.S.; Khosla, S.; Bouxsein, M.L. Biomechanical Computed Tomography analysis (BCT) for clinical assessment of osteoporosis. Osteoporos. Int. 2020, 31, 1025–1048. [Google Scholar] [CrossRef]
- Dall’Ara, E.; Tozzi, G. Digital volume correlation for the characterization of musculoskeletal tissues: Current challenges and future developments. Front. Bioeng. Biotechnol. 2022, 10, 1010056. [Google Scholar] [CrossRef] [PubMed]
- Fleps, I.; Bahaloo, H.; Zysset, P.K.; Ferguson, S.J.; Palsson, H.; Helgason, B. Empirical relationships between bone density and ultimate strength: A literature review. J. Mech. Behav. Biomed. Mater. 2020, 110, 103866. [Google Scholar] [CrossRef] [PubMed]
- Varga, P.; Willie, B.M.; Stephan, C.; Kozloff, K.M.; Zysset, P.K. Finite element analysis of bone strength in osteogenesis imperfect. Bone 2020, 133, 115250. [Google Scholar] [CrossRef]
- Kichenko, A.A. Cancellous bone tissue remodelling: Mathematical modeling. Russ. J. Biomech. 2019, 23, 284–304. [Google Scholar]
- Nie, C.-X. Topological similarity of time-dependent objects. Nonlinear Dyn. Vol. 2023, 111, 481–492. [Google Scholar] [CrossRef]
- Offroy, M.; Duponchel, L. Topological data analysis: A promising big data exploration tool in biology, analytical chemistry and physical chemistry. Anal. Chim. Acta 2016, 910, 1–11. [Google Scholar] [CrossRef]
- Skaf, Y.; Laubenbacher, R. Topological data analysis in biomedicine: A review. J. Biomed. Inform. 2022, 130, 104082. [Google Scholar] [CrossRef]
- Vilenkin, N.J. Special functions and the theory of group representations. Transl. Math. Monogr. 1968, 22, 613. [Google Scholar]
- Bunge, G. Texture Analysis in Material Science: Mathematical Methods, 1st ed.; Butterworth & Co: London, UK, 1986; p. 595. [Google Scholar]
- Jones, M.N. Spherical Harmonics and Tensors for Classical Field Theory, 1st ed.; Research Studies Press: New York, NY, USA, 1985; p. 244. [Google Scholar]
- Kanatani, K. Distribution of directional data and fabric tensors. Int. J. Eng. Sci. 1984, 2, 149–164. [Google Scholar]
- Harrigan, T.P.; Mann, R.W. Characterization of microstructural anisotropy in orthotropic materials using a second rank tensor. J. Mater. Sci. 1984, 19, 761–767. [Google Scholar] [CrossRef]
- Tozeren, A.; Skalak, R. Does fabric tensor exist for a fabric? J. Mater. Sci. 1989, 24, 1700–1706. [Google Scholar] [CrossRef]
- Cowin, S.C. The relationship between the elasticity tensor and the fabric tensor. Mech. Mater. 1985, 4, 137–147. [Google Scholar] [CrossRef]
- Semenova, E.; Gerasimov, O.; Koroleva, E.; Ahmetov, N.; Baltina, T.; Sachenkov, O. Automatic processing and analysis of the quality healing of derma injury. Adv. Intell. Syst. Comput. 2019, 831, 107–113. [Google Scholar]
- Baidamshina, D.R.; Koroleva, V.A.; Trizna, E.Y.; Pankova, S.M.; Agafonova, M.N.; Chirkova, M.N.; Vasileva, O.S.; Akhmetov, N.; Shubina, V.V.; Porfiryev, A.G.; et al. Anti-biofilm and wound-healing activity of chitosan-immobilized Ficin. Int. J. Biol. Macromol. 2020, 164, 4205–4217. [Google Scholar] [CrossRef] [PubMed]
- Cowin, S.C.; Mehrabadi, M.M. Anisotropic symmetries in linear elasticity. Appl. Mech. Rev. 1995, 48, 247–285. [Google Scholar] [CrossRef]
- Aktas, M.E.; Akbas, E.; Fatmaoui, A.E. Persistence homology of networks: Methods and applications. Appl. Netw. Sci. 2019, 4, 61. [Google Scholar] [CrossRef]
- Amezquita, E.J.; Quigley, M.Y.; Ophelders, T.; Munch, E.; Chitwood, D.H. The shape of things to come: Topological data analysis and biology, from molecules to organisms. Dev. Dyn. 2020, 249, 816–833. [Google Scholar] [CrossRef]
- Hylton, A.; Henselman-Petrusek, G.; Sang, J.; Short, R. Tuning the performance of a computational persistent homology package. Softw. Pract. Exp. 2019, 49, 885–905. [Google Scholar] [CrossRef]
- Attali, D.; Lieutier, A.; Salinas, D. Efficient data structure for representing and simplifying simplicial complexes in high dimensions. In Proceedings of the Twenty-Seventh Annual Symposium on Computational Geometry, SoCG ’11, Paris, France, 13–15 June 2011; pp. 501–509. [Google Scholar]
- Preti, G.; De Francisci Morales, G.; Bonchi, F. STruD: Truss decomposition of simplicial complexes. In Proceedings of the Web Conference 2021 (WWW ’21), Ljubljana, Slovenia, 19–23 April 2021; pp. 3408–3418. [Google Scholar]
- Basset, A.B. Classification of quartic curves. Nature 1902, 67, 80. [Google Scholar] [CrossRef]
- Bastien, G.; Rogalski, M. The periodic orbits of a dynamical system associated with a family of QRT-maps. Qual. Theory Dyn. Syst. 2020, 19, 57. [Google Scholar] [CrossRef]
- Pettigrew, J.; Roberts, J.A.G. Characterizing singular curves in parametrized families of biquadratics. J. Phys. A Math. Theor. 2008, 41, 115203. [Google Scholar] [CrossRef]
- Yaikova, V.V.; Gerasimov, O.V.; Fedyanin, A.O.; Zaytsev, M.A.; Baltin, M.E.; Baltina, T.V. and Sachenkov, O.A. Automation of Bone Tissue Histology. Front. Phys. 2019, 7, 91. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).