Tangled Cord of FTTM₄

Abstract

Fuzzy Topological Topographic Mapping (FTTM) is a mathematical model that consists of a set of homeomorphic topological spaces designed to solve the neuro magnetic inverse problem. A sequence of FTTM, denoted as $FTT{M}_n$, is an extension of FTTM that is arranged in a symmetrical form. The special characteristic of FTTM, namely the homeomorphisms between its components, allows the generation of new FTTM. Later, the $FTT{M}_n$ can also be viewed as a graph. Previously, a group of researchers defined an assembly graph and utilized it to model a DNA recombination process. Some researchers then used this to introduce the concept of tangled cords for assembly graphs. In this paper, the tangled cord for $FTT{M}_4$ is used to calculate the Eulerian paths. Furthermore, it is utilized to determine the least upper bound of the Hamiltonian paths of its assembly graph. Hence, this study verifies the conjecture made by Burns et al.

1. Introduction and Motivation

Fuzzy Topographic Topological Mapping (FTTM) was introduced to solve the neuro magnetic inverse problem, in particular, sources of electroencephalography (EEG) signals recorded from an epileptic patient [1]. Originally, the model was a 4-tuple of topological spaces of its respective homeomorphic mappings [1]. Unlike the works of Abbas et al. [2] and Shukala et al. [3] on graphical metric spaces, our mappings are purely ordinary topological mappings. The topological spaces are Magnetic Plane (MC), Base Magnetic Plane (BM), Fuzzy Magnetic Field (FM), and Topographic Magnetic Field (TM). The FTTM is defined formally as follows (see Figure 1).

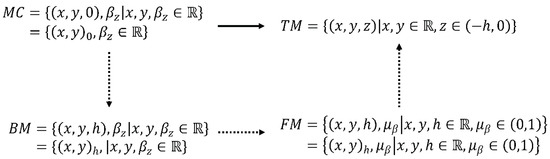
Figure 1. The FTTM [4].

Definition 1

([1]). Let $FTTM=\left(MC,BM,FM,TM\right)$ such that $MC,BM,FM,TM$ are topological spaces that are homeomorphics, namely, $MC\cong BM\cong FM\cong TM$. The set of ${FTTM}_i$ is denoted by $FTTM=\left\{{FTTM}_i:i=1,2,3,\dots ,n\right\}$. The sequence of ${nFTTM}_i$ of FTTM is ${FTTM}_1,{FTTM}_2,{FTTM}_3,$${FTTM}_4,\dots ,{FTTM}_n$, such that ${MC}_i\cong {MC}_{i+1},{BM}_i\cong {BM}_{i+1}$, ${FM}_i\cong {FM}_{i+1}$ and ${TM}_i\cong {TM}_{i+1}$.

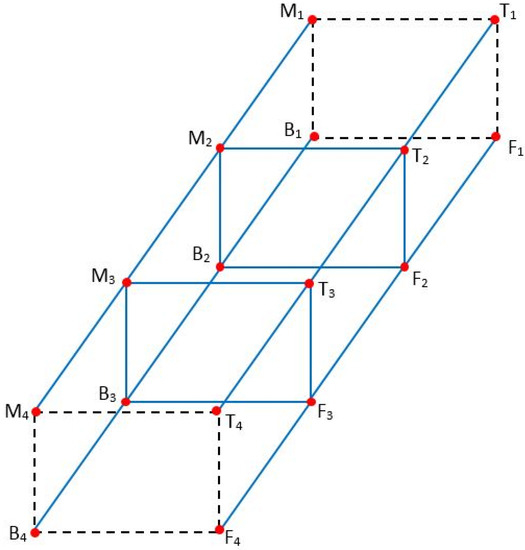
Basically $FTT{M}_n$ (see Figure 2) is an extension of FTTM and is illustrated in the following Figure 2. It is arranged in a symmetrical form and can accommodate magnetoencephalography (MEG) or electroencephalography (EEG) signals, as well as grey scale image data [1,5]. This accommodative feature of FTTM is due to its homeomorphic structures.

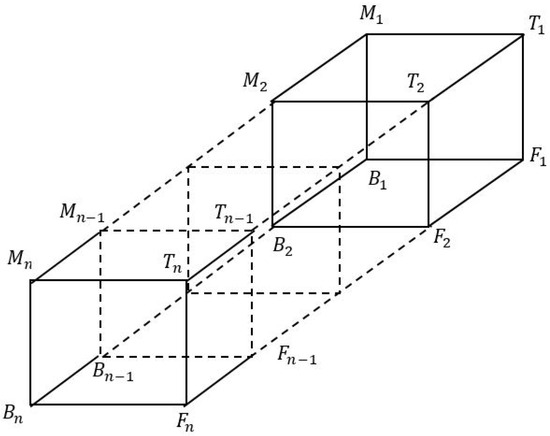
Figure 2. The sequence of $FTT{M}_n$.

In 2009, a notion of an assembly graph was first introduced by Angeleska, Jonoska, and Saito [6]. Meanwhile, Burns et al. [7] conducted a study on polynomial invariant for the assembly graph and its properties. The authors also suggested the possibility that only a tangled cord can achieve the upper bound in the assembly graph for every positive integer [7]. Later, an assembly graph of $FTT{M}_n$ was developed by Shukor et al. [4]. The authors established the relations and determined the lower and upper bounds for the assembly graph of $FTT{M}_n$ [1].

The aim of this paper is to establish an assembly graph as a tangled cord as well as to discover the least upper bound of the assembly graph $FTT{M}_4$. In Section 2, a brief review of the concept of the assembly graph and the tangled cord is presented, while Section 3 covers the previous related works on the assembly graph of $FTT{M}_n$. Next, a transverse eulerian paths for the assembly graph of $FTT{M}_4$ is shown in Section 4. The results are discussed in Section 5, where the tangled cord of $FTT{M}_4$ is presented, in which the whole processes involves enumerating all the Hamiltonian polygonal paths and non-consecutive vertices Hamiltonian polygonal paths. Consequently, the proposed conjecture by Burns et al. [7] is proven. The conclusion is drawn in Section 6.

2. Concepts of Assembly Graph and Tangled Cord

As mention in Section 1, the assembly graph was created by researchers in [6], and then Burns et al. broadened the structure of the assembly graph as the tangled cord [7]. Some formal definitions and theorems related to the assembly graph and its properties are as follows.

Definition 2

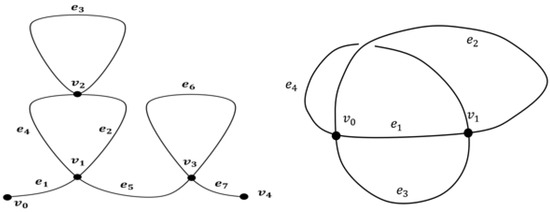
([6]). An assembly graph is a finite connected graph where all vertices are rigid vertices of valency 1 or 4. A vertex of valency 1 is called an end point. Let $\mathsf{\Gamma }=(V,E)$ be a finite graph with a set of vertices, V, and a set of edges, E. The number of 4-valent vertices in Γ is denoted with $\left|\mathsf{\Gamma }\right|$. The assembly graph is called trivial if $\left|\mathsf{\Gamma }\right|=0$ (see Figure 3).

Figure 3. Examples of Assembly Graphs.

Definition 3

([6]). A transverse path in Γ is a sequence $\gamma =\left(v_0,e_1,v_1,e_2,\dots ,e_n,v_n\right)$ if $v_0,v_n$ are endpoints, or $\left(v_0,e_1,v_1,e_2,\dots ,e_n\right),$ if $v_0$ is a 4-valent vertex and $e_n\in E\left(v_0\right),satisfying$ the following conditions: (1) $v_0,\dots ,v_n$ is a sequence of a subset of vertices Γ, with possible repetition of the same vertex at most twice, (2) $\left\{e_1,\dots ,e_n\right\}$ is a set of distinct edges, and (3) each $e_i$ is not a neighbor of $e_{i-1}$ with respect to the rigid vertex $v_{i-1},i=2,\dots ,n$ and in the case where $v_0$ is a 4-valent vertex, $e_1$ is not a neighbor of $e_n$ with respect to the rigid vertex $v_0$.

Definition 4

([6]). An assembly graph Γ is called simple if there is a transverse Eulerian path in γ, meaning there is a transverse path, γ, that contains every edge from Γ exactly once.

Theorem 1

([6]). In a simple assembly graph, there is a unique equivalence class of transverse Eulerian paths.

Theorem 2

([7]). If Γ is a simple assembly graph with $\left|\mathsf{\Gamma }\right|=k$ and C is the collection of all Hamiltonian polygonal paths of Γ, then

$$\left|C\right|\le F_{2k+1}-1$$

(1)

where $F_k$ is the kth Fibonacci number.

Angeleska et al. also develop a convention of using words to represent simple assembly graphs [6]. A word is an element in the free monoid, ${\mathsf{\Sigma }}^{*}$, and an alphabet is a finite set, $\mathsf{\Sigma }$. Let $\mathsf{\Gamma }$ be a simple directed assembly graph with the initial vertex i and the terminal vertex t as its two end points. Subsequently, Burns et al. referred to the double-occurrence word as an assembly word in which every symbol appears exactly twice [7]. The definition of assembly word is given in [8] as follows.

Definition 5

([8]). An assembly word or a double occurrence word is a word in a certain alphabet, $S=\{a_1,a_2,\dots \}$, such that every symbol, $a_i$, either occurs in the word exactly twice or does not occur at all.

Moreover, Burns et al. [7] introduced the concept of a tangled cord, and the structure of the tangled cord (see Figure 4) is from the assembly word pattern [9]. Recall that the assembly word is a word in which every symbol appears exactly twice, and these words are also referred to as double occurrence words. Then, the researchers developed some properties of tangled cord as follows.

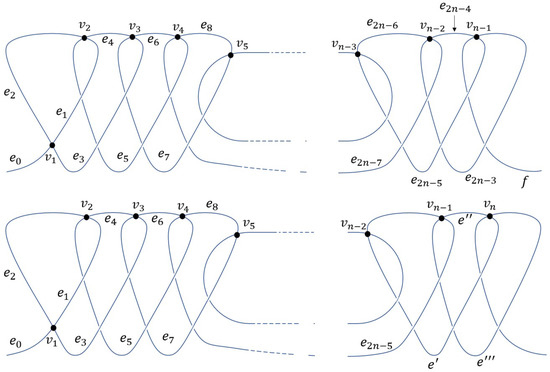
Figure 4. The structure of the tangled cord.

Definition 6

([7]). The tangled cord, ${\mathcal{T}}_n$, of size n, for a positive integer, n, is an assembly graph with assembly word:

$$1213243\dots (n-1)(n-2)n(n-1)n$$

(2)

Specifically, ${\mathcal{T}}_1=11,{\mathcal{T}}_2=1212,{\mathcal{T}}_3=121323$, and ${\mathcal{T}}_n$ is obtained from ${\mathcal{T}}_{n-1}$ by replacing the last letter, $n(n-1)$, by the subword $n(n-1)n$.

Theorem 3

([7]). The tangled cord, ${\mathcal{T}}_n$, has $\left(\frac{n+1}{2}\right)$ distinct Hamiltonian polygonal paths.

Due to Theorem 2, Definition 6, and Theorem 3, Burns et al. [7] then proposed their conjecture as follows;

Conjecture 1

([7]). The upper bound in Theorem 2 is achieved for every positive integer, n, only by the tangled cord ${\mathcal{T}}_n$.

3. Assembly Graph of ${\mathbf{FTTM}}_{\mathbf{4}}$

A graph of $FTT{M}_n$ contains many subgraphs, including assembly graphs. A new concept called maximal assembly graph for assembly subgraphs of $FTT{M}_n$ is introduced.

Definition 7

([1]). Let $G_1,G_2,G_3,\dots ,G_n$ be subgraphs of $G(V,E)$ whereby each $G_i$ is an assembly graph. A maximal assembly subgraph of $G_i$ is defined as $\left|{\mathsf{\Gamma }}_{G_i}\right|=max\left\{\left|{\mathsf{\Gamma }}_{G_1}\right|,\left|{\mathsf{\Gamma }}_{G_2}\right|,\dots ,\left|{\mathsf{\Gamma }}_{G_n}\right|\right\}$.

Now, the assembly graph for $FTT{M}_n$ is given as follows.

Definition 8

([1]). The maximal assembly graph of $FTT{M}_n$ is

$${\mathsf{\Gamma }}_{FTT{M}_n}=FTT{M}_n-\left[E\left(FTT{M}_1\right)\cup E\left(FTT{M}_n\right)\right]forn\ge 3$$

(3)

and $\left|{\mathsf{\Gamma }}_{FTT{M}_n}\right|$ is the number of its 4-valent vertices.

Theorem 4

([1]). The ${FTTM}_4$ consists of an assembly subgraph.

Consider ${FTTM}_4=\left(V\left({FTTM}_4\right),E\left({FTTM}_4\right),{\psi }_{{FTTM}_4}\right)$ such that ${\psi }_{{FTTM}_4}:E\to V\times V$.

The eight vertices of ${\mathit{FTTM}}_4$ (see Figure 5) that have a valency of four are $M_2,B_2,F_2,T_2,M_3,$ $B_3,F_3,and{T}_3$ such that

$$\begin{array}{c}valency\left(M_2\right)=\left|\left\{e_5,e_8,e_9,e_{17}\right\}\right|=valency\left(B_2\right)=\left|\left\{e_5,e_6,e_{10},e_{18}\right\}\right|=\\ valency\left(F_2\right)=\left|\left\{e_6,e_7,e_{11},e_{19}\right\}\right|=valency\left(T_2\right)=\left|\left\{e_7,e_8,e_{12},e_{20}\right\}\right|=\\ valency\left(M_3\right)=\left|\left\{e_{13},e_{16},e_{17},e_{25}\right\}\right|=valency\left(B_3\right)=\left|\left\{e_{13},e_{14},e_{18},e_{26}\right\}\right|=\\ \begin{array}{c}valency\left(F_3\right)=\left|\left\{e_{14},e_{15},e_{19},e_{27}\right\}\right|=valency\left(T_3\right)=\left|\left\{e_{15},e_{16},e_{20},e_{28}\right\}\right|=4\end{array}\end{array}$$

(4)

and $M_1,B_1,F_1,T_1,M_4,B_4,F_4,and{T}_4$ have a valency of one such that

$$\begin{array}{c}\begin{array}{c}valency\left(M_1\right)=\left|\left\{e_9\right\}\right|=valency\left(B_1\right)=\left|\left\{e_{12}\right\}\right|=valency\left(F_1\right)=\left|\left\{e_{11}\right\}\right|\\ =valency\left(T_1\right)=\left|\left\{e_{10}\right\}\right|=valency\left(T_1\right)=\left|\left\{e_{10}\right\}\right|=valency\left(M_4\right)=\left|\left\{e_{25}\right\}\right|\\ =valency\left(B_4\right)=\left|\left\{e_{26}\right\}\right|=valency\left(F_4\right)=\left|\left\{e_{27}\right\}\right|=valency\left(T_4\right)=\left|\left\{e_{28}\right\}\right|\end{array}\\ =1.\end{array}$$

(5)

$\therefore {FTTM}_4$ consists of an assembly subgraph with $\left|{\mathsf{\Gamma }}_{{FTTM}_4}\right|=8$.

Figure 5. Assembly Graph of $FTT{M}_4$.

Furthermore, Shukor et al. [1] guaranteed that $FTT{M}_4$ has a set of Hamiltonian paths.

Theorem 5

([1]). The ${\mathsf{\Gamma }}_{{FTTM}_4}$ consists of a set of Hamiltonian polygonal paths.

Earlier, Burns et al. [7] proved Theorem 2. Later, Shukor et al. proved the version of Theorem 2 for $FTT{M}_n$ successfully as follows [1].

Theorem 6

([1]). Let $FTT{M}_n$ be a sequence of n-FTTM for $n\ge 3$ and C is the set of all Hamiltonian polygonal paths of $FTT{M}_n$, then

$$\left|C\right|\le F_{8n+1}-1.$$

(6)

4. Transverse Eulerian Paths for Assembly Graph of ${\mathbf{FTTM}}_{\mathbf{4}}$

Angeleska et al. developed a convention of using words to represent simple assembly graphs, including transverse paths [6]. The theorems for transverse paths for the assembly graph of $FTT{M}_n$ are necessary as follows.

Theorem 7.

The maximal assembly graph of ${FTTM}_n$, ${\mathsf{\Gamma }}_{{FTTM}_n}$, is a simple graph.

Proof. 

Let ${\mathsf{\Gamma }}_{{FTTM}_n}$ be the maximal assembly graph. Therefore, ${\mathsf{\Gamma }}_{{FTTM}_n}={FTTM}_n-\left[E\left({FTTM}_1\right)\cup E\left({FTTM}_n\right)\right]forn\ge 3$ by Definition 8. It is a simple graph because it does not have any loops or parallel edges. □

Theorem 8.

The maximal assembly graph of ${FTTM}_n$, ${\mathsf{\Gamma }}_{{FTTM}_n}$, must contains a transverse path.

Proof. 

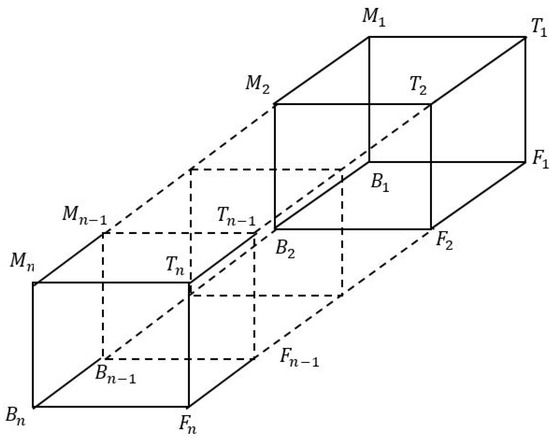
Let ${\mathsf{\Gamma }}_{{FTTM}_n}$ be the maximal assembly graph. Therefore, ${\mathsf{\Gamma }}_{{FTTM}_n}={FTTM}_n-\left[E\left({FTTM}_1\right)\cup E\left({FTTM}_n\right)\right]forn\ge 3$ by Definition 8. Thus, ∃ 4 open vertices in the front $\left(M_1,B_1,F_1,T_1\right)$ and at the back $\left(M_n,B_n,F_n,T_n\right)$ in which all of them are end points whereby each of them has valency of 1 (see Figure 6).

Figure 6. Sequence of ${FTTM}_n$.

By Definition 3, ∃ the path in ${\mathsf{\Gamma }}_{{FTTM}_n}$ that is a transverse path because it must be in the form of $\left(v_1,e_1,\dots ,e_{n-1},v_n\right)$, such that $v_1\in V\left({FTTM}_2\right)$, $v_n\in V\left({FTTM}_{n-1}\right)$, and $e_i\in \left\{{FTTM}_n-\left[E\left({FTTM}_1\right)\cup E\left({FTTM}_n\right)\right]\right\}$ for $i\in 1,2,\dots ,n-1.$ □

Theorem 9.

The maximal assembly graph of ${FTTM}_n$, ${\mathsf{\Gamma }}_{{FTTM}_n}$, contains unique equivalence tranverse Eulerian paths.

Proof. 

Theorem 7 guarantees the maximal assembly graph of ${FTTM}_n$, ${\mathsf{\Gamma }}_{{FTTM}_n}$, which is a simple graph. Theorem 6 assures that, in a simple assembly graph, there is a unique equivalence class of transverse Eulerian paths. Therefore, the maximal assembly graph of ${FTTM}_n$, ${\mathsf{\Gamma }}_{{FTTM}_n}$, contains unique equivalence tranverse Eulerian paths. □

Example 1.

Eulerian paths with consecutive vertices for ${\mathsf{\Gamma }}_{{FTTM}_4}$ (see Figure 7).

$$E_1=\left(M_2,e_5,B_2,e_6,F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3\right);$$

$$S_{E_1}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_1^R=\left(M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_6,B_2,e_5,M_2\right);$$

$$S_{E_1^R}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_2=\left(B_2,e_6,F_2,e_7,T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3\right);$$

$$S_{E_2}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_2^R=\left(B_3,e_{13},M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_7,F_2,e_6,B_2\right);$$

$$\begin{array}{c}{S}_{E_2^R}\end{array}=1,2,3,4,1,1,2,3,4,1$$

$$E_3=\left(F_2,e_7,T_2,e_8,M_2,e_5,B_2,e_6{,F_2,e}_{11},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3\right);$$

$$S_{E_3}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_3^R=\left(F_3,e_{14},B_3,e_{13},M_3,e_{16},T_3,e_{15}{,F_3,e}_{11},F_2,e_6,B_2,e_5,M_2,e_8,T_2,e_7,F_2\right);$$

$$S_{E_3^R}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_4=\left(T_2,e_8,M_2,e_5,B_2,e_6,F_2,e_7,T_2{,e}_{12},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3\right);$$

$$S_{E_4}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_4^R=\left(T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_{16},T_3{,e}_{12},T_2,e_7,F_2,e_6,B_2,e_5,M_2,e_8,T_2\right);$$

$$S_{E_4^R}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_5=\left(M_2,e_8,T_2,e_7,F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{14},B_{3^{{}^{\prime }}}{e}_{13},M_3\right);$$

$$S_{E_5}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_5^R=\left(M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_6,F_2,e_7,T_{2^{{}^{\prime }}}{e}_8,M_2\right);$$

$$S_{E_5^R}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_6=\left(T_2,e_7,F_2,e_6,B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_{3^{{}^{\prime }}}{e}_{13},M_3,e_{16},T_3\right);$$

$$S_{E_6}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_6^R=\left(T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_5,B_{2^{{}^{\prime }}}{e}_6,F_2,e_7,T_2\right);$$

$$S_{E_6^R}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_7=\left(F_2,e_6,B_2,e_5,M_2,e_8,T_2,e_7{,F_{2}e}_{11},F_3,e_{14},B_{3^{{}^{\prime }}}{e}_{13},M_3,e_{16},T_3,e_{15},F_3\right);$$

$$S_{E_7}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_7^R=\left(F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{14}{,F_3,e}_{11},F_2,e_7,{T_2}_{{}^{\prime }}{e}_8,M_2,e_5,B_2,e_6,F_2\right);$$

$$S_{E_7^R}=(1,2,3,4,1,1,2,3,4,1)$$

$$E_8=\left(B_2,e_5,M_2,e_8,T_2,e_7{,F_2,e}_6,B_2,e_{10},B_{3^{{}^{\prime }}}{e}_{13},M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3\right);$$

$$S_{E_8}=(1,2,3,4,1,1,2,3,4,1)$$

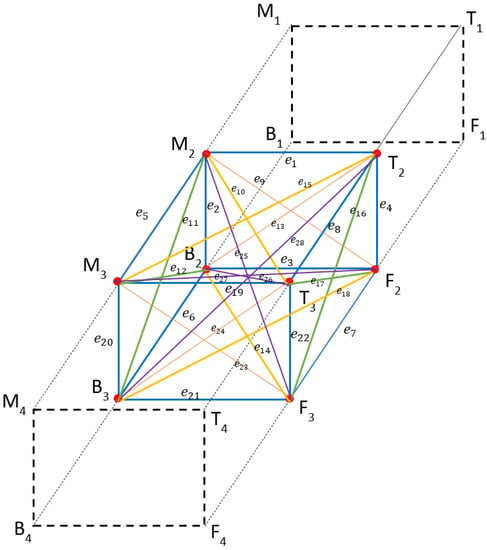
$$S_{E_8^R}=(1,2,3,4,1,1,2,3,4,1)$$

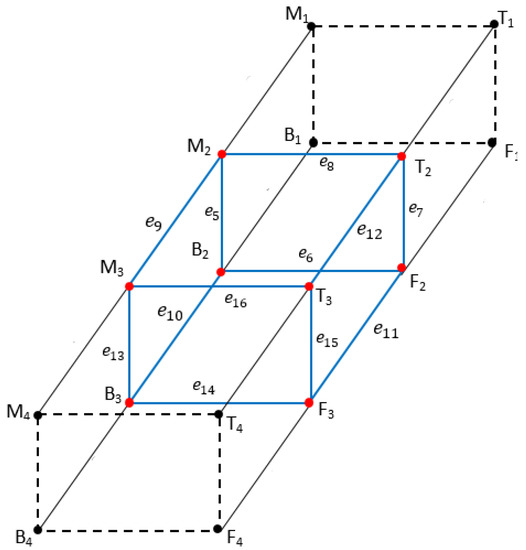
Figure 7. Eulerian paths with consecutive vertices for ${\mathsf{\Gamma }}_{{FTTM}_4}$.

$E_1...E_8$ represent the edges and $S_{E_1}...S_{E_8}$ represent the corresponding assembly words.

Clearly, $(1,2,3,4,1,1,2,3,4,1)=S_{E_1}\cong S_{E_1^R}\cong S_{E_2}\cong S_{E_2^R}\cong S_{E_3}\cong S_{E_3^R}\cong S_{E_4}\cong S_{E_4^R}\cong S_{E_5}\cong S_{E_5^R}\cong S_{E_6}\cong S_{E_6^R}\cong S_{E_7}\cong S_{E_7^R}\cong S_{E_8}\cong S_{E_8^R}$.

5. Tangled Cord of ${\mathbf{FTTM}}_{\mathbf{4}}$

The upper bound is achieved in Conjecture 1 of Burns et al. [7] and refers to the sharp upper bound (least upper bound) (https://math.stackexchange.com/questions/1985794/what-does-it-mean-when-a-bound-is-sharp, (accessed on 22 October 2022)). In other words, the term sharp upper bound means when the greatest lower bound is equal to the least upper bound.

We are now ready to introduce the sharp upper bound (least upper bound) for ${FTTM}_4$, i.e., the version of proven Conjecture 1 for $FTT{M}_4.$

Theorem 10.

When ${\mathsf{\Gamma }}_{{FTTM}_4}$ is the assembly graph of $FTT{M}_4$ and C is the set of all its distinct Hamiltonian polygonal paths, then $\left|C\right|={\mathcal{T}}_4$, whereby ${\mathcal{T}}_4$ is its tangled cord.

Proof. 

(by construction) Let ${\mathsf{\Gamma }}_{{FTTM}_4}$ be the assembly graph of $FTT{M}_4$ and $\left|{\mathsf{\Gamma }}_{{FTTM}_4}\right|=8$ (see Section 2). The ${\mathsf{\Gamma }}_{{FTTM}_4}$ is a simple graph guaranteed by Theorem 7. Therefore, ${\mathsf{\Gamma }}_{{FTTM}_4}$ is a simple assembly graph. Angeleska et al. developed a convention of using words to represent simple assembly graphs [1]. Thus, ${\mathsf{\Gamma }}_{{FTTM}_4}$ can be presented using words because it is a simple assembly graph.

The ${\mathsf{\Gamma }}_{{FTTM}_4}$ consists of a set of Hamiltonian polygonal paths represented by ${\gamma }_1...{\gamma }_{144}$ that are in [10]. These are now listed as assembly words represented by $S_1...S_{144}$ and presented as follows.

$$\begin{array}{c}{\gamma }_1=\left\{\begin{array}{c}{M}_2,e_8,T_2,e_7,F_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{15},F_3\end{array}\right\};S_1=\left(12344123\right)\end{array}$$

$$\begin{array}{c}{\gamma }_2=\left\{\begin{array}{c}{M}_2,e_8,T_2,e_7,F_2,e_6,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3\end{array}\right\};S_2=\left(12344321\right)\end{array}$$

$$\begin{array}{c}{\gamma }_3=\left\{\begin{array}{c}{M}_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2\end{array}\right\};S_3=\left(12332144\right)\end{array}$$

$$\begin{array}{c}{\gamma }_4=\left\{\begin{array}{c}{M}_2,e_8,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_6,F_2,e_{11},F_3\end{array}\right\};S_4=\left(12213344\right)\end{array}$$

$$\begin{array}{c}{\gamma }_5=\left\{\begin{array}{c}{M}_2,e_8,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_6,B_2\end{array}\right\};S_5=\left(12213443\right)\end{array}$$

$$\begin{array}{c}{\gamma }_6=\left\{\begin{array}{c}{M}_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{11},F_2,e_6,B_2,e_{10},B_3,e_{13},M_3\end{array}\right\};S_6=\left(12233441\right)\end{array}$$

$$\begin{array}{c}{\gamma }_7=\left\{\begin{array}{c}{M}_2,e_5,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_7,T_2\end{array}\right\};S_7=\left(12213443\right)\end{array}$$

$$\begin{array}{c}{\gamma }_8=\left\{\begin{array}{c}{M}_2,e_5,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_{11},F_3\end{array}\right\};S_8=\left(12213344\right)\end{array}$$

$$\begin{array}{c}{\gamma }_9=\left\{\begin{array}{c}{M}_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{11},F_2,e_7,T_2,e_{12},T_3,e_{16},M_3\end{array}\right\};S_9=\left(12233441\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{10}=\left\{\begin{array}{c}{M}_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{14},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2\end{array}\right\};S_{10}=\left(12332144\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{11}=\left\{\begin{array}{c}{M}_2,e_5,B_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3\end{array}\right\};S_{11}=\left(12344123\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{12}=\left\{\begin{array}{c}{M}_2,e_5,B_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3\end{array}\right\};S_{12}=\left(12344321\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{13}=\left\{\begin{array}{c}{M}_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_7,F_2,e_6,B_2\end{array}\right\};S_{13}=\left(11234432\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{14}=\left\{\begin{array}{c}{M}_2,e_9,M_3,e_{13},B_3,e_{18},B_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{15},F_3\end{array}\right\};S_{14}=\left(11223443\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{15}=\left\{\begin{array}{c}{M}_2,e_9,M_3,e_{13},B_3{e}_{10},B_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{12},T_2\end{array}\right\};S_{15}=\left(11223344\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{16}=\left\{\begin{array}{c}{M}_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{110},B_2,e_6,F_2,e_7,T_2\end{array}\right\};S_{16}=\left(11234432\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{17}=\left\{\begin{array}{c}{M}_2,e_9,M_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_{10},B_3,e_{14},F_3\end{array}\right\};S_{17}=\left(11223443\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{18}=\left\{\begin{array}{c}{M}_2,e_9,M_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{10},B_2\end{array}\right\};S_{18}=\left(11223344\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{19}=\left\{\begin{array}{c}{B}_2,e_5,M_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{13},M_3,e_{16},T_3\end{array}\right\};S_{19}=\left(12344123\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{20}=\left\{\begin{array}{c}{B}_2,e_5,M_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3\end{array}\right\};S_{20}=\left(12344321\right)\end{array}$$

$$\begin{array}{c}{\gamma }_{21}=\left\{\begin{array}{c}{B}_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2\end{array}\right\};S_{21}=\left(12332144\right)\end{array}$$

$${\gamma }_{22}=\left\{\begin{array}{c}{B}_2,e_5,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_7,F_2\end{array}\right\};S_{22}=\left(12213443\right)$$

$${\gamma }_{23}=\left\{\begin{array}{c}{B}_2,e_5,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_7,T_2,e_{12},T_3\end{array}\right\};S_{23}=\left(12213344\right)$$

$${\gamma }_{24}=\left\{\begin{array}{c}{B}_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_{11},F_3,e_{14},B_3\end{array}\right\};S_{24}=\left(12233441\right)$$

$${\gamma }_{25}=\left\{\begin{array}{c}{B}_2,e_6,F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3\end{array}\right\};S_{25}=\left(12344123\right)$$

$${\gamma }_{26}=\left\{\begin{array}{c}{B}_2,e_6,F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3\end{array}\right\};S_{26}=\left(12344321\right)$$

$${\gamma }_{27}=\left\{\begin{array}{c}{B}_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2\end{array}\right\};S_{27}=\left(12332144\right)$$

$${\gamma }_{28}=\left\{\begin{array}{c}{B}_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_9,M_3,e_{13},B_3\end{array}\right\};S_{28}=\left(12233441\right)$$

$${\gamma }_{29}=\left\{\begin{array}{c}{B}_2,e_6,F_2,e_{11},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_{12},T_3\end{array}\right\};S_{29}=\left(12213344\right)$$

$${\gamma }_{30}=\left\{\begin{array}{c}{B}_2,e_6,F_2,e_{11},F_3,e_{14},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_8,M_2\end{array}\right\};S_{30}=\left(12213443\right)$$

$${\gamma }_{31}=\left\{\begin{array}{c}{B}_2,e_{10},B_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{11},F_2\end{array}\right\};S_{31}=\left(11223344\right)$$

$${\gamma }_{32}=\left\{\begin{array}{c}{B}_2,e_{10},B_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{15},T_3\end{array}\right\};S_{32}=\left(11223443\right)$$

$${\gamma }_{33}=\left\{\begin{array}{c}{B}_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_7,T_2,e_8,M_2\end{array}\right\};S_{33}=\left(11234432\right)$$

$${\gamma }_{34}=\left\{\begin{array}{c}{B}_2,e_{10},B_3,e_{13},F_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{16},T_3\end{array}\right\};S_{34}=\left(11223443\right)$$

$${\gamma }_{35}=\left\{\begin{array}{c}{B}_2,e_{10},B_3,e_{13},F_3,e_{11},F_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_9,M_2\end{array}\right\};S_{35}=\left(11223344\right)$$

$${\gamma }_{36}=\left\{\begin{array}{c}{B}_2,e_{10},B_3,e_{13},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_8,T_2,e_7,F_2\end{array}\right\};S_{36}=\left(11234432\right)$$

$${\gamma }_{37}=\left\{\begin{array}{c}{F}_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2\end{array}\right\};S_{37}=\left(12332144\right)$$

$${\gamma }_{38}=\left\{\begin{array}{c}{F}_2,e_7,T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{15},F_3\end{array}\right\};S_{38}=\left(12344321\right)$$

$${\gamma }_{39}=\left\{\begin{array}{c}{F}_2,e_7,T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3\end{array}\right\};S_{39}=\left(12344123\right)$$

$${\gamma }_{40}=\left\{\begin{array}{c}{F}_2,e_7,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_5,B_2\end{array}\right\};S_{40}=\left(12213443\right)$$

$${\gamma }_{41}=\left\{\begin{array}{c}{F}_2,e_7,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_9,M_3\end{array}\right\};S_{41}=\left(12213344\right)$$

$${\gamma }_{42}=\left\{\begin{array}{c}{F}_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3\end{array}\right\};S_{42}=\left(12233441\right)$$

$${\gamma }_{43}=\left\{\begin{array}{c}{F}_2,e_6,B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3\end{array}\right\};S_{43}=\left(12344321\right)$$

$${\gamma }_{44}=\left\{\begin{array}{c}{F}_2,e_6,B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3\end{array}\right\};S_{44}=\left(12344123\right)$$

$${\gamma }_{45}=\left\{\begin{array}{c}{F}_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2\end{array}\right\};S_{45}=\left(12332144\right)$$

$${\gamma }_{46}=\left\{\begin{array}{c}{F}_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3\end{array}\right\};S_{46}=\left(12233441\right)$$

$${\gamma }_{47}=\left\{\begin{array}{c}{F}_2,e_6,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_8,T_2\end{array}\right\};S_{47}=\left(12213443\right)$$

$${\gamma }_{48}=\left\{\begin{array}{c}{F}_2,e_6,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_9,M_3\end{array}\right\};S_{48}=\left(12213344\right)$$

$${\gamma }_{49}=\left\{\begin{array}{c}{F}_2,e_{11},F_3,e_{14},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_8,M_2,e_5,B_2\end{array}\right\};S_{49}=\left(11234432\right)$$

$${\gamma }_{50}=\left\{\begin{array}{c}{F}_2,e_{11},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{12},T_2\end{array}\right\};S_{50}=\left(11223344\right)$$

$${\gamma }_{51}=\left\{\begin{array}{c}{F}_2,e_{11},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{16},M_3\end{array}\right\};S_{51}=\left(11223443\right)$$

$${\gamma }_{52}=\left\{\begin{array}{c}{F}_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_5,M_2,e_8,T_2\end{array}\right\};S_{52}=\left(11234432\right)$$

$${\gamma }_{53}=\left\{\begin{array}{c}{F}_2,e_{11},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{10},B_2\end{array}\right\};S_{53}=\left(11223344\right)$$

$${\gamma }_{54}=\left\{\begin{array}{c}{F}_2,e_{11},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{13},M_3\end{array}\right\};S_{54}=\left(11223443\right)$$

$${\gamma }_{55}=\left\{\begin{array}{c}{T}_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{10},B_2,e_6,F_2,e_{11},F_3,e_{15},T_3\end{array}\right\};S_{55}=\left(12233441\right)$$

$${\gamma }_{56}=\left\{\begin{array}{c}{T}_2,e_8,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_6,F_2\end{array}\right\};S_{56}=\left(12213443\right)$$

$${\gamma }_{57}=\left\{\begin{array}{c}{T}_2,e_8,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_6,B_2,e_{10},B_3\end{array}\right\};S_{57}=\left(12213344\right)$$

$${\gamma }_{58}=\left\{\begin{array}{c}{T}_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2\end{array}\right\};S_{58}=\left(12332144\right)$$

$${\gamma }_{59}=\left\{\begin{array}{c}{T}_2,e_8,M_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{15},B_3,e_{13},M_3,e_{16},T_3\end{array}\right\};S_{59}=\left(12344321\right)$$

$${\gamma }_{60}=\left\{\begin{array}{c}{T}_2,e_8,M_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3\end{array}\right\};S_{60}=\left(12344123\right)$$

$${\gamma }_{61}=\left\{\begin{array}{c}{T}_2,e_7,F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{15},T_3\end{array}\right\};S_{61}=\left(12344321\right)$$

$$\begin{array}{c}{\gamma }_{62}=\left\{\begin{array}{c}{T}_2,e_7,F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{14},B_3\end{array}\right\}\end{array};S_{62}=\left(12344123\right)$$

$${\gamma }_{63}=\left\{\begin{array}{c}{T}_2,e_7,F_2,e_6,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2\end{array}\right\};S_{63}=\left(12332144\right)$$

$${\gamma }_{64}=\left\{T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_9,M_3,e_{16},T_3\right\};S_{64}=\left(12233441\right)$$

$${\gamma }_{65}=\left\{\begin{array}{c}{T}_2,e_7,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_5,M_2\end{array}\right\};S_{65}=\left(12213443\right)$$

$${\gamma }_{66}=\left\{\begin{array}{c}{T}_2,e_7,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_{10},B_3\end{array}\right\};S_{66}=\left(12213344\right)$$

$${\gamma }_{67}=\left\{\begin{array}{c}{T}_2,e_{12},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{14},B_3\end{array}\right\};S_{67}=\left(11223443\right)$$

$${\gamma }_{68}=\left\{\begin{array}{c}{T}_2,e_{12},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{11},F_2\end{array}\right\};S_{68}=\left(11223344\right)$$

$${\gamma }_{69}=\left\{\begin{array}{c}{T}_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_6,B_2,e_5,M_2\end{array}\right\};S_{69}=\left(11234432\right)$$

$${\gamma }_{70}=\left\{\begin{array}{c}{T}_2,e_{12},T_3,e_{15},F_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{13},B_3\end{array}\right\};S_{70}=\left(11223443\right)$$

$${\gamma }_{71}=\left\{\begin{array}{c}{T}_2,e_{12},T_3,e_{15},F_3,e_{11},F_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_9,M_2\end{array}\right\};S_{71}=\left(11223344\right)$$

$${\gamma }_{72}=\left\{\begin{array}{c}{T}_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_5,B_2,e_6,F_2\end{array}\right\};S_{72}=\left(11234432\right)$$

$${\gamma }_{73}=\left\{\begin{array}{c}{M}_3,e_9,M_2,e_5,B_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3\end{array}\right\};S_{73}=\left(11234432\right)$$

$${\gamma }_{74}=\left\{\begin{array}{c}{M}_3,e_9,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_7,F_2\end{array}\right\};S_{74}=\left(11223443\right)$$

$${\gamma }_{75}=\left\{\begin{array}{c}{M}_3,e_9,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{11},F_2,e_7,T_2,e_{12},T_3\end{array}\right\};S_{75}=\left(11223344\right)$$

$${\gamma }_{76}=\left\{\begin{array}{c}{M}_3,e_9,M_2,e_8,T_2,e_7,F_2,e_{18},B_2,e_{10},B_3,e_{14},F_3,e_{15},T_3\end{array}\right\};S_{76}=\left(11234432\right)$$

$${\gamma }_{77}=\left\{\begin{array}{c}{M}_3,e_9,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_6,F_2\end{array}\right\};S_{77}=\left(11223443\right)$$

$${\gamma }_{78}=\left\{\begin{array}{c}{M}_3,e_9,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{19},F_2,e_6,B_2,e_{10},B_3\end{array}\right\};S_{78}=\left(11223344\right)$$

$${\gamma }_{79}=\left\{\begin{array}{c}{M}_3,e_{13},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{15},T_3\end{array}\right\};S_{79}=\left(12213443\right)$$

$${\gamma }_{80}=\left\{\begin{array}{c}{M}_3,e_{13},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{11},F_2\end{array}\right\};S_{80}=\left(12213344\right)$$

$${\gamma }_{81}=\left\{\begin{array}{c}{M}_3,e_{13},B_3,e_{10},B_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2\end{array}\right\};S_{81}=\left(12233441\right)$$

$${\gamma }_{82}=\left\{\begin{array}{c}{M}_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_8,T_2,e_{12},T_3\end{array}\right\};S_{82}=\left(12332144\right)$$

$${\gamma }_{83}=\left\{\begin{array}{c}{M}_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_6,F_2\end{array}\right\};S_{83}=\left(12344123\right)$$

$${\gamma }_{84}=\left\{\begin{array}{c}{M}_3,e_{13},B_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_5,M_2\end{array}\right\};S_{84}=\left(12344321\right)$$

$${\gamma }_{85}=\left\{\begin{array}{c}{M}_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2\end{array}\right\};S_{85}=\left(12233441\right)$$

$${\gamma }_{86}=\left\{\begin{array}{c}{M}_3,e_{16},T_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{14},B_3\end{array}\right\};S_{86}=\left(12213443\right)$$

$${\gamma }_{87}=\left\{\begin{array}{c}{M}_3,e_{16},T_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{11},F_2\end{array}\right\};S_{87}=\left(12213344\right)$$

$${\gamma }_{88}=\left\{\begin{array}{c}{M}_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_7,F_2\end{array}\right\};S_{88}=\left(12344123\right)$$

$${\gamma }_{89}=\left\{\begin{array}{c}{M}_3,e_{16},T_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_6,F_2,e_7,T_2,e_8,M_2\end{array}\right\};S_{89}=\left(12344321\right)$$

$${\gamma }_{90}=\left\{\begin{array}{c}{M}_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_5,B_2,e_{10},B_3\end{array}\right\};S_{90}=\left(12332144\right)$$

$${\gamma }_{91}=\left\{\begin{array}{c}{B}_3,e_{10},B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_7,T_2\end{array}\right\};S_{91}=\left(11223443\right)$$

$${\gamma }_{92}=\left\{\begin{array}{c}{B}_3,e_{10},B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_{11},F_3\end{array}\right\};S_{92}=\left(11223344\right)$$

$${\gamma }_{93}=\left\{\begin{array}{c}{B}_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3\end{array}\right\};S_{93}=\left(11234432\right)$$

$${\gamma }_{94}=\left\{\begin{array}{c}{B}_3,e_{10},B_2,e_6,F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{16},T_3,e_{15},F_3\end{array}\right\};S_{94}=\left(11234432\right)$$

$${\gamma }_{95}=\left\{\begin{array}{c}{B}_3,e_{10},B_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_8,T_2\end{array}\right\};S_{95}=\left(11223443\right)$$

$${\gamma }_{96}=\left\{\begin{array}{c}{B}_3,e_{10},B_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_9,M_3\end{array}\right\};S_{96}=\left(11223344\right)$$

$${\gamma }_{97}=\left\{\begin{array}{c}{B}_3,e_{13},M_3,e_9,M_2,e_5,B_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{15},F_3\end{array}\right\};S_{97}=\left(12213443\right)$$

$${\gamma }_{98}=\left\{\begin{array}{c}{B}_3,e_{13},M_3,e_9,M_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{15},T_3,e_{12},T_2\end{array}\right\};S_{98}=\left(12213344\right)$$

$${\gamma }_{99}=\left\{\begin{array}{c}{B}_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_{12},T_3,e_{15},F_3,e_{11},F_2,e_6,B_2\end{array}\right\};S_{99}=\left(12233441\right)$$

$${\gamma }_{100}=\left\{\begin{array}{c}{B}_3,e_{13},M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_8,T_2\end{array}\right\};S_{100}=\left(12344123\right)$$

$${\gamma }_{101}=\left\{\begin{array}{c}{B}_3,e_{13},M_3,e_{16},T_3,e_{15},F_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_5,B_2\end{array}\right\};S_{101}=\left(12344321\right)$$

$${\gamma }_{102}=\left\{\begin{array}{c}{B}_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_6,F_2,e_{11},F_3\end{array}\right\};S_{102}=\left(12332144\right)$$

$${\gamma }_{103}=\left\{\begin{array}{c}{B}_3,e_{14},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_6,F_2,e_7,T_2\end{array}\right\};S_{103}=\left(12344123\right)$$

$${\gamma }_{104}=\left\{\begin{array}{c}{B}_3,e_{14},F_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_6,B_2\end{array}\right\};S_{104}=\left(12344321\right)$$

$${\gamma }_{105}=\left\{\begin{array}{c}{B}_3,e_{14},F_3,e_{15},T_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_5,M_2,e_9,M_3\end{array}\right\};S_{105}=\left(12332144\right)$$

$${\gamma }_{106}=\left\{\begin{array}{c}{B}_3,e_{14},F_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{16},M_3\end{array}\right\};S_{106}=\left(12213443\right)$$

$${\gamma }_{107}=\left\{\begin{array}{c}{B}_3,e_{14},F_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{12},T_2\end{array}\right\};S_{107}=\left(12213344\right)$$

$${\gamma }_{108}=\left\{\begin{array}{c}{B}_3,e_{14},F_3,e_{11},F_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_9,M_2,e_5,B_2\end{array}\right\};S_{108}=\left(12233441\right)$$

$${\gamma }_{109}=\left\{\begin{array}{c}{F}_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_8,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3\end{array}\right\};S_{109}=\left(11234432\right)$$

$${\gamma }_{110}=\left\{\begin{array}{c}{F}_3,e_{11},F_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_8,M_2\end{array}\right\};S_{110}=\left(11223443\right)$$

$${\gamma }_{111}=\left\{\begin{array}{c}{F}_3,e_{11},F_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_{17},M_2,e_8,T_2,e_{12},T_3\end{array}\right\};S_{111}=\left(11223344\right)$$

$${\gamma }_{112}=\left\{\begin{array}{c}{F}_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{13},M_3,e_{16},T_3\end{array}\right\};S_{112}=\left(11234432\right)$$

$${\gamma }_{113}=\left\{\begin{array}{c}{F}_3,e_{11},F_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_{10},B_3\end{array}\right\};S_{113}=\left(11223344\right)$$

$${\gamma }_{114}=\left\{\begin{array}{c}{F}_3,e_{11},F_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_5,M_2\end{array}\right\};S_{114}=\left(11223443\right)$$

$$\begin{array}{c}{\gamma }_{115}=\left\{\begin{array}{c}{F}_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_5,B_2{e}_6,F_2,e_7,T_2,e_{12},T_3\end{array}\right\}\end{array};S_{115}=\left(12332144\right)$$

$${\gamma }_{116}=\left\{\begin{array}{c}{F}_3,e_{14},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_6,F_2\end{array}\right\};S_{116}=\left(12344321\right)$$

$${\gamma }_{117}=\left\{\begin{array}{c}{F}_3,e_{14},B_3,e_{13},M_3,e_{16},T_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_5,M_2\end{array}\right\};S_{117}=\left(12344123\right)$$

$${\gamma }_{118}=\left\{\begin{array}{c}{F}_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_9,M_3,e_{16},T_3,e_{12},T_2,e_7,F_2\end{array}\right\};S_{118}=\left(12233441\right)$$

$${\gamma }_{119}=\left\{\begin{array}{c}{F}_3,e_{14},B_3,e_{10},B_2,e_6,F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{16},T_3\end{array}\right\};S_{119}=\left(12213443\right)$$

$${\gamma }_{120}=\left\{\begin{array}{c}{F}_3,e_{14},B_3,e_{10},B_2,e_6,F_2,e_7,T_2,e_{12},T_3,e_{16},M_3,e_9,M_2\end{array}\right\};S_{120}=\left(12213344\right)$$

$${\gamma }_{121}=\left\{\begin{array}{c}{F}_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_7,F_2\end{array}\right\};S_{121}=\left(12344321\right)$$

$${\gamma }_{122}=\left\{\begin{array}{c}{F}_3,e_{15},T_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_6,F_2,e_7,T_2,e_8,M_2\end{array}\right\};S_{122}=\left(12344123\right)$$

$${\gamma }_{123}=\left\{\begin{array}{c}{F}_3,e_{15},T_3,e_{16},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_6,B_2,e_{10},B_3\end{array}\right\};S_{123}=\left(12332144\right)$$

$${\gamma }_{124}=\left\{\begin{array}{c}{F}_3,e_{15},T_3,e_{12},T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{10},B_2,e_6,F_2\end{array}\right\};S_{124}=\left(12233441\right)$$

$${\gamma }_{125}=\left\{\begin{array}{c}{F}_3,e_{15},T_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{13},B_3\end{array}\right\};S_{125}=\left(12213443\right)$$

$${\gamma }_{126}=\left\{\begin{array}{c}{F}_3,e_{15},T_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_9,M_2\end{array}\right\};S_{126}=\left(12213344\right)$$

$${\gamma }_{127}=\left\{\begin{array}{c}{T}_3,e_{12},T_2,e_8,M_2,e_5,B_2,e_6,F_2,e_{11},F_3,e_{14},B_3,e_{13},M_3\end{array}\right\};S_{127}=\left(11234432\right)$$

$${\gamma }_{128}=\left\{\begin{array}{c}{T}_3,e_{12},T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{10},B_2,e_6,F_2,e_{11},F_3\end{array}\right\};S_{128}=\left(11223344\right)$$

$${\gamma }_{129}=\left\{\begin{array}{c}{T}_3,e_{12},T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_6,B_2\end{array}\right\};S_{129}=\left(11223443\right)$$

$${\gamma }_{130}=\left\{\begin{array}{c}{T}_3,e_{12},T_2,e_7,F_2,e_6,B_2,e_5,M_2,e_9,M_3,e_{13},B_3,e_{14},F_3\end{array}\right\};S_{130}=\left(11234432\right)$$

$${\gamma }_{131}=\left\{\begin{array}{c}{T}_3,e_{12},T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_5,B_2\end{array}\right\};S_{131}=\left(11223443\right)$$

$${\gamma }_{132}=\left\{\begin{array}{c}{T}_3,e_{12},T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{10},B_2,e_5,M_2,e_9,M_3\end{array}\right\};S_{132}=\left(11223344\right)$$

$${\gamma }_{133}=\left\{\begin{array}{c}{T}_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_6,B_2,e_5,M_2,e_8,T_2\end{array}\right\};S_{133}=\left(12344321\right)$$

$${\gamma }_{134}=\left\{\begin{array}{c}{T}_3,e_{16},M_3,e_{13},B_3,e_{14},F_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_5,B_2\end{array}\right\};S_{134}=\left(12344123\right)$$

$${\gamma }_{135}=\left\{\begin{array}{c}{T}_3,e_{16},M_3,e_{13},B_3,e_{10},B_2,e_5,M_2,e_8,T_2,e_7,F_2,e_{11},F_3\end{array}\right\};S_{135}=\left(12332144\right)$$

$${\gamma }_{136}=\left\{\begin{array}{c}{T}_3,e_{16},M_3,e_9,M_2,e_5,B_2,e_{10},B_3,e_{14},F_3,e_{11},F_2,e_7,T_2\end{array}\right\};S_{136}=\left(12233441\right)$$

$${\gamma }_{137}=\left\{\begin{array}{c}{T}_3,e_{16},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_6,B_2,e_{10},B_3,e_{14},F_3\end{array}\right\};S_{137}=\left(12213443\right)$$

$${\gamma }_{138}=\left\{\begin{array}{c}{T}_3,e_{16},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_{11},F_3,e_{14},B_3,e_{10},B_2\end{array}\right\};S_{138}=\left(12213344\right)$$

$${\gamma }_{139}=\left\{\begin{array}{c}{T}_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_5,B_2,e_6,F_2,e_7,T_2\end{array}\right\};S_{139}=\left(12344321\right)$$

$${\gamma }_{140}=\left\{\begin{array}{c}{T}_3,e_{15},F_3,e_{14},B_3,e_{13},M_3,e_9,M_2,e_8,T_2,e_7,F_2,e_6,B_2\end{array}\right\};S_{140}=\left(12344123\right)$$

$${\gamma }_{141}=\left\{\begin{array}{c}{T}_3,e_{15},F_3,e_{14},B_3,e_{10},B_2,e_6,F_2,e_7,T_2,e_8,M_2,e_9,M_3\end{array}\right\};S_{141}=\left(12332144\right)$$

$${\gamma }_{142}=\left\{\begin{array}{c}{T}_3,e_{15},F_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_9,M_3,e_{13},B_3,e_{10},B_2\end{array}\right\};S_{142}=\left(12213344\right)$$

$${\gamma }_{143}=\left\{\begin{array}{c}{T}_3,e_{15},F_3,e_{11},F_2,e_7,T_2,e_8,M_2,e_5,B_2,e_{10},B_3,e_{13},M_3\end{array}\right\};S_{143}=\left(12213443\right)$$

$${\gamma }_{144}=\left\{\begin{array}{c}{T}_3,e_{15},F_3,e_{11},F_2,e_6,B_2,e_{10},B_3,e_{13},M_3,e_9,M_2,e_8,T_2\end{array}\right\};S_{144}=\left(12233441\right)$$

$$\left(12344123\right)=S_1\cong S_{11}\cong S_{19}\cong S_{25}\cong S_{39}\cong S_{44}\cong S_{60}\cong S_{62}\cong S_{83}\cong S_{88}\cong S_{100}\cong S_{103}\cong S_{117}\cong S_{122}\cong S_{134}\cong S_{140}$$

$$\left|S_1\right|=16$$

$${\left(12344321\right)=S}_2\cong S_{12}\cong S_{20}\cong S_{26}{\cong S}_{38}\cong S_{43}\cong S_{59}\cong S_{61}\cong S_{84}\cong S_{89}\cong S_{101}\cong S_{104}\cong S_{116}\cong S_{121}\cong S_{133}\cong S_{139}$$

$$\left|S_2\right|=16$$

$${\left(12332144\right)=S}_3\cong S_{10}\cong S_{21}\cong S_{27}{\cong S}_{37}\cong S_{45}\cong S_{58}\cong S_{63}\cong S_{82}\cong S_{90}\cong S_{102}\cong S_{105}\cong S_{115}\cong S_{123}\cong S_{135}\cong S_{141}$$

$$\left|S_3\right|=16$$

$${\left(12213344\right)=S}_4\cong S_8\cong S_{23}\cong S_{29}{\cong S}_{41}\cong S_{48}\cong S_{57}\cong S_{66}\cong S_{80}\cong S_{87}\cong S_{98}\cong S_{107}\cong S_{120}\cong S_{126}\cong S_{138}\cong S_{142}$$

$$\left|S_4\right|=16$$

$${\left(12213443\right)=S}_5\cong S_7\cong S_{23}\cong S_{30}{\cong S}_{40}\cong S_{47}\cong S_{56}\cong S_{65}\cong S_{79}\cong S_{86}\cong S_{97}\cong S_{106}\cong S_{119}\cong S_{125}\cong S_{137}\cong S_{143}$$

$$\left|S_5\right|=16$$

$${\left(12233441\right)\cong S}_6\cong S_9\cong S_{24}\cong S_{28}\cong S_{42}\cong S_{46}\cong S_{55}\cong S_{64}\cong S_{81}\cong S_{85}\cong S_{99}\cong S_{108}\cong S_{118}\cong S_{124}\cong S_{136}\cong S_{144}$$

$$\left|S_6\right|=16$$

$$\left(11234432\right)=S_{13}\cong S_{33}\cong S_{36}\cong S_{49}\cong S_{52}\cong S_{69}\cong S_{72}\cong S_{73}\cong S_{76}\cong S_{93}\cong S_{94}\cong S_{109}\cong S_{112}\cong S_{127}\cong S_{130}$$

$$\left|S_7\right|=16$$

$$\left(11223443\right)=S_{14}\cong S_{17}\cong S_{32}\cong S_{34}\cong S_{51}\cong S_{54}\cong S_{67}\cong S_{70}\cong S_{74}\cong S_{77}\cong S_{91}\cong S_{95}\cong S_{110}\cong S_{114}\cong S_{129}\cong S_{131}$$

$$\left|S_8\right|=16$$

$$\left(11223344\right)=S_{15}\cong S_{18}\cong S_{31}\cong S_{35}\cong S_{50}\cong S_{53}\cong S_{68}\cong S_{71}\cong S_{75}\cong S_{78}\cong S_{92}\cong S_{96}\cong S_{111}\cong S_{113}\cong S_{128}\cong S_{132}$$

$$\left|S_9\right|=16$$

and there is a missing equivalence class of assembly words, $S_m$, that is

$\left(12132434\right)=S_m\cong (M,B,M,F,B,T,F,T)\cong (M,B,M,T,B,F,T,F)\cong (M,F,M,B,F,T,B,T)\cong (M,F,M,T,F,B,T,B)$$\cong (M,T,M,B,T,F,B,F)\cong (M,T,M,F,T,B,F,B)\cong (B,M,B,F,M,T,F,T)\cong (B,M,B,T,M,F,T,F)$$\cong (B,F,B,M,F,T,M,T)\cong (B,F,B,T,F,M,T,M)\cong (B,T,B,M,T,F,M,F)$$\cong (B,T,B,F,T,M,F,M)\cong (F,M,F,B,M,T,B,T)\cong (F,M,F,T,M,B,T,B)\cong (F,B,F,M,B,T,M,T)$$\cong (F,B,F,T,B,M,T,M)\cong (F,T,F,M,T,B,M,B)\cong (F,T,F,B,T,M,B,M)$$\cong (T,M,T,B,M,F,B,F)\cong (T,M,T,F,M,B,F,B)\cong (T,B,T,M,B,F,M,F)\cong (T,B,T,F,B,M,F,M)$$\cong (T,F,T,M,F,B,M,B)\cong (T,F,T,B,F,M,B,M)$ ∣ $S_m$ $\mid =16$

The list of the non-consecutive vertices Hamiltonian polygonal paths (see Figure 8) are presented in Appendix A. However, $S_m$ was not considered in the calculated Hamiltonian paths earlier because the vertices were non-consecutives due to the non-existence of edges between farther vertices (not adjacent to one another), as depicted in the following figure, ${FTTM}_4$.

Figure 8. Non-consecutive vertices Hamiltonian polygonal paths.

In that case, ${\mathsf{\Gamma }}_{{FTTM}_4}$ exhibits nine sets of consecutive vertices Hamiltonian polygonal paths, namely, $S_1,S_2,S_3,S_4,S_5,S_6,S_{13},S_{14},\mathrm{and}{S}_{15}$, and a set with non-consecutive vertices Hamiltonian polygonal paths, that is $S_m$. Hence, ${\mathsf{\Gamma }}_{{FTTM}_4}$ has 10 distinct Hamiltonian polygonal paths, as shown earlier. But then, $10=\frac{120}{12}=\frac{5.4.3.2.1}{2.1(3.2.1)}=\frac{5!}{2!(5-2)!}=\left(\begin{array}{c}5\\ 2\end{array}\right)=\left(\begin{array}{c}4+1\\ 2\end{array}\right)={\mathcal{T}}_4$ as stated by Theorem 3. This concurs with the proposed Conjecture 1 by Burns et al. [7].

Therefore, if C is the set of all its distinct Hamiltonian polygonal paths of the assembly graph of $FTT{M}_4$, namely ${\mathsf{\Gamma }}_{{FTTM}_4}$, then $\left|C\right|={\mathcal{T}}_4$, whereby ${\mathcal{T}}_4$ is its tangled cord as required. □

Example 2.

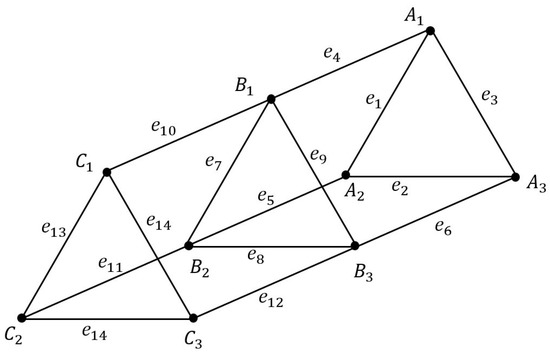
A set of $A_3^3=\left\{A,B,C\right\}$ such that $A=\left\{\left(A_1,A_2,A_3\right):A_1\cong A_2\cong A_3\right\}$, $B=\left\{\left(B_1,B_2,B_3\right):B_1\cong B_2\cong B_3\right\}$ and $C=\left\{\left(C_1,C_2,C_3\right):C_1\cong C_2\cong C_3\right\}$ as depicted in Figure 9 below.

Figure 9. A graph of $A_3^3=\left\{A,B,C\right\}$.

The identified assembly graph of $A_3^3$ is ${{\mathsf{\Gamma }}_{A_3^3}=A}_3^3-\left(E\left(A\right)-E\left(B\right)\right)=B$ and the set of its Hamiltonian paths is

$\gamma =\left\{{\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4,{\gamma }_5,{\gamma }_6\right\}$

such that

${\gamma }_1=\left\{B_1,e_7,B_2,E_8{,B}_3\right\};S_1=\left(123\right)$; ${\gamma }_2=\left\{B_1,e_9,B_3,E_8{,B}_2\right\};S_2=\left(123\right)$; ${\gamma }_3=\left\{B_2,e_8,B_3,E_9{,B}_1\right\};S_3=\left(123\right)$; ${\gamma }_4=\left\{B_2,e_7,B_1,E_9{,B}_3\right\};S_4=\left(123\right)$; ${\gamma }_5=\left\{B_3,e_9,B_1,E_7{,B}_2\right\};S_6=\left(123\right)$; ${\gamma }_6=\left\{B_3,e_8,B_2,E_7{,B}_1\right\};S_7=\left(123\right)$.

As a matter of fact, ${\gamma }_1$,${\gamma }_2$,${\gamma }_3$, ${\gamma }_4$,${\gamma }_5$, and ${\gamma }_6$ are also Eulerian paths of ${\mathsf{\Gamma }}_{A_3^3}$. Because the Hamiltonian and Eulerian paths are the same for ${\mathsf{\Gamma }}_{A_3^3}$, each of them is just a cyclic (see Figure 10).

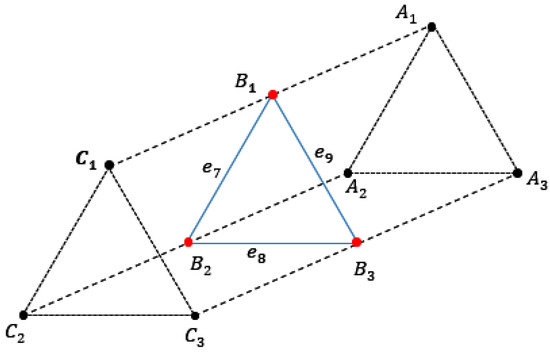
Figure 10. Hamiltonian paths in $A_3^3$ graph.

The $A_3^3$ is a ${\mathcal{T}}_0$, therefore it does not have distinct Hamiltonian paths because $\left(\begin{array}{c}0+1\\ 2\end{array}\right)=\left(\begin{array}{c}1\\ 2\end{array}\right)=\frac{1!}{2!(0-2)!}=\frac{1}{2(-2)!}$ is undefined, i.e., $-2!$ is undefined.

Therefore, all the Hamiltonian paths in $A_3^3$ are similar.

Furthermore, Ahmad et al. [9] and Shukor et al. [1] simulated and listed all Hamiltonian paths with consecutive vertices in the assembly graph of ${FTTM}_n$ for $n=3,4,\dots ,10$ as follows (see Table 1).

Table 1. Hamiltonian polygonal paths (with consecutive vertices) in the assembly graph of ${FTTM}_n$.

${\mathit{FTTM}}_{\mathit{n}}$	Vertices	4-Valent Vertices	% Hamiltonian Polygonal Paths
3	12	4	8
4	16	8	144
5	20	12	1168
6	24	16	8032
7	28	20	49,312
8	32	24	281,248
9	36	28	1,523,920
10	40	32	7,953,408

However, a similar form of a sequence of Hamiltonian polygonal paths for ${FTTM}_n$ in Table 1 has not been previously reported in the Online Encyclopedia of Integer Sequences (OEIS) (http://oeis.org, (accessed on 22 October 2022)). The non-existence of such a sequence in OEIS was anticipated by Burns et al. earlier [7].

6. Conclusions

Fuzzy Topological Topographic Mapping (FTTM) is a mathematical model that consists of a set of homeomorphic topological spaces designed to solve the neuro magnetic inverse problem. A sequence of FTTM, ${FTTM}_n$, is an extension of FTTM that is arranged in a symmetrical form. The special characteristic of FTTM, namely the homeomorphisms between its components, allows the generation of new FTTM. Later, the ${FTTM}_n$ can also be viewed as a graph. Angeleska et al. defined an assembly graph for modeling their DNA recombination [6]. Then, the concept of a tangled cord for assembly graphs was introduced by Burns et al. for the same purpose [7]. This paper has demonstrated a concept to calculate the Eulerian paths and to determine the least upper bound of the Hamiltonian paths of the assembly graph of ${FTTM}_4$.