Abstract
Let G be a connected graph; the edge Mostar index of G is defined as where and denote the number of edges in G that are closer to vertex u than to vertex v and the number of edges that are closer to vertex v than to vertex u, respectively. In this paper, we determine the upper bound of the edge Mostar index for all bicyclic graphs and identify the extremal graphs that achieve this bound.
MSC:
05C09; 05C35; 05C92
1. Introduction
The scope of the analysis carried out in the article concerns finite, undirected, and simple graphs. For terms and symbols, please refer to []. Let and denote cycles and stars with m edges, respectively. For a connected graph G, the set of vertices is denoted by and the set of edges is denoted by . For a vertex , the degree of u, denoted by (or simply ), is the number of edges which are incident to u. If , then the vertex u is called a pendant vertex of G. Furthermore, if either or , then the edge is called a pendant edge of G. For denote the distance between u and v in G, namely the length of the shortest path connecting vertex u and vertex v.
Chemical graph theory is one of the research directions of graph theory, and topological indices are the main research content of chemical graph theory. Topological indices are the invariants of the graph, which usually reflect the chemical and pharmacological properties of the molecule. Among all the topological indices, the most well known is the Wiener index. The definition is as follows:
This topological index is widely studied in the field of chemical graph theory, see [,,]. For , define the following set:
Therefore, the sets , and form a partition of the vertices in G. Let , and denote the number of vertices in the three sets above, respectively. Evidently, if the graph G has n vertices, then .
A well-established property of the Wiener index is its formula []:
which is applicable for a tree T. In order to generalize the above formula to the general graph G, Gutman [] introduced a new topological index and subsequently called it the Szeged index:
For any , we define the distance from the edge e to the vertex x as:
Similarly, based on the above definition, we define another three sets , , and as follows:
Let , and denote the number of edges in the three sets above, respectively. Evidently, if the graph G has m edges, then .
Then, the edge Szeged index [] of a graph G is defined by:
where and denote the number of edges in G that are closer to vertex u than to vertex v and the number of edges that are closer to vertex v than to vertex u, respectively.
Recently, Došlić et al. proposed a new topological index called the Mostar index, which was introduced in []. It can be written as:
For results on the Mostar index, one can refer to [,,,,].
Similarly, the edge Mostar index of a graph G is described as follows:
Example, for a path of length 3, denote its four vertices as , , , . For , we have , , then . Then, for , we have , , then . Finally, for , we have , , then . So, according to the definition of the edge Mostar index, we obtain
With respect to the edge Mostar index, the extremal graphs among polymers [], trees and unicyclic graphs [], cacti graphs with fixed cycles [], cycle-related graphs [], and the minimum values of bicyclic graphs [], have been studied.
In this paper, we provide an upper bound for the edge Mostar index of connected bicyclic graphs and characterize the graphs that achieve this upper bound.
Theorem 1.
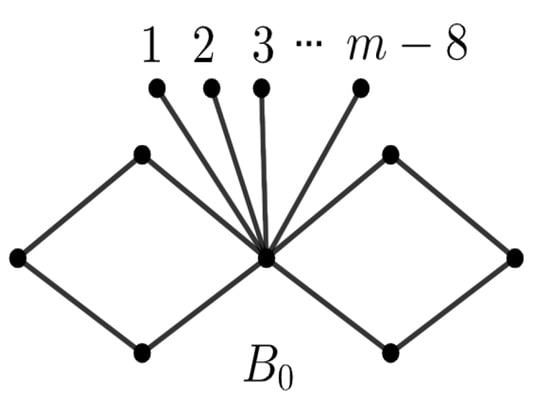
Let G be a connected bicyclic graph with edges. Then
the equality holds if and only if (see Figure 1).

Figure 1.
The graph for Theorem 1.
2. Preparation
For the sake of convenience, let ; then, the definition of the edge Mostar index of a graph G can be further written as
A subgraph H of a graph G is isometric if the distance between any pair of vertices in H is the same as the distance between the same pair of vertices in G.
Lemma 1
([]). Let . Then,
the equality holds if and only if is a pendent edge.
Lemma 2.
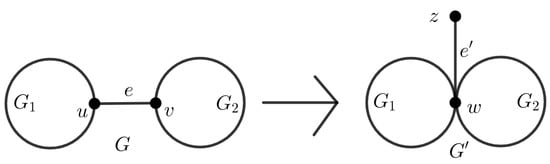
Let be a cut edge, but not a pendent edge, in the connected graph G. is obtained by contracting the edge e into a vertex w and adding a pendent edge to this vertex, (see Figure 2). Then, .

Figure 2.
Transformation of cut edge.
Proof.
Let , and . Then, based on the definition of the edge Mostar index, we know that , . The of other edges stays unchanged. Then,
So, . □
We now consider the graph , where is the graph obtained from the and by identifying one vertex. Assume that w is common vertex of and . Obviously, w is a cut vertex of the graph G. For each edge , the vertex w belongs to one of the three sets . Because every path connecting u(or v) and any vertex in is must pass through w. So, all vertices of must be contained in one of the three sets . Then, we have that all the edges in belong to one of the three sets: . Thus, the contribution of to depends entirely on the size of , namely, changing the structure of does not change the value of . Furthermore, because the pendent edge contributes the most to , we have the following lemma:
Lemma 3.
Let be a connected graph with m edges. Then,
where the common vertex of is the center vertex of .
Let , where the common vertex w of is the center vertex of , and we call w is the center vertex of .
Lemma 4
([]). Let G be an m-edge connected unicyclic graph. Then,
the equality holds if and only if , for ; or , for ; , for .
Lemma 5.
Let be a connected graph and be an unicyclic graph, where and . Then, , for ; , for ; , for , where the common vertex of () is the center vertex of ().
Proof.
If . Then, by Lemma 4, we get:
Similarly, if , then ; and if , then . □
3. Proof of Theorem 1
A theta graph consists of two vertices, and , which are connected by three internally disjoint paths , and , each with lengths , and c, respectively. By symmetry, we can assume that .
Let G be a bicyclic graph; then, .
Based on the definition of bicyclic graphs and theta graphs, bicyclic graphs can be divided into two types []:
Let be the set of connected bicyclic graphs with m-edge and exactly two cycles.
Let be the set of connected bicyclic graphs with m-edge and three cycles; namely, if , then it must have a subgraph isomorphic to .
Theorem 2.
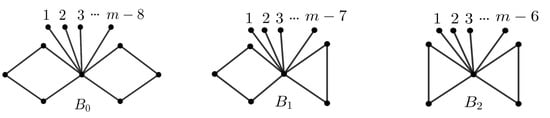
Let . If , then , and the equality holds if and only if . If , then , and the equality holds if and only if ; If , then , and the equality holds if and only if (see Figure 3).

Figure 3.
The graph for Theorem 2.
Proof.
Because , then the graph G contains exactly two cycles. Furthermore, by Lemma 2, there are two unicyclic graphs and such that . Suppose that , , then . By repeated using Lemma 5, we get
for ;
for ;
for .
Clearly, and . Therefore, the proof is complete. □
Now, we consider the bicyclic graphs referred to . For any edge of a graph G, based on Lemma 1, we have
The equality holds if and only if is a pendent edge. To determine the maximum value of the edge Mostar index, it is more convenient to consider the expression , which we call the deficit of e. This deficit is denoted by .
For a graph G, the symbol represents the sum of the deficits of all edges in the graph G. By summing over all edges one obtains, .
Lemma 6.
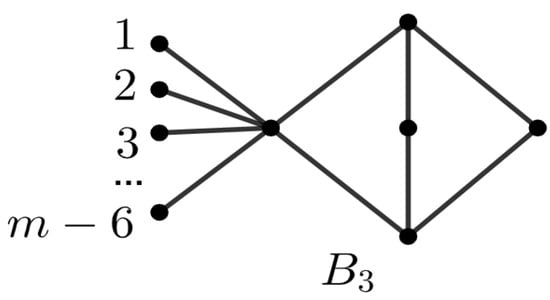
Let . Then, (see Figure 4).

Figure 4.
The graph for Lemma 6.
Proof.
In graph , both non-pendent edges on the left have a deficit of 6, whereas the remaining non-pendent edges both have a deficit of 4. Therefore, the deficit of is 28. Thus, we obtain . □
Corollary 1.
Let . If G is a graph with the maximum edge Mostar index, then .
Lemma 7.
For any two edges and f in a connected graph G, we have .
Proof.
Without loss of generality, assume that , then .
Furthermore, if , then , a contradiction. Thus, . Hence, . □
Lemma 8.
Let G be a connected bicyclic graph with m edges and an odd cycle. Then, we have .
Proof.
Let C be an odd cycle in G, and an arbitrary edge. we claim that there are two adjacent vertices and in C, such that .
Suppose that this is not the case. Let a denote the minimum value of the distance between a vertex in the cycle C and the edge f, and let b denote the maximum value of the distance between a vertex in the cycle C and the edge f. Then, for any vertex in the cycle C whose distance from the edge f is k, we have .
Let
By assumption, there are no two adjacent vertices in the cycle C with the same distance from the edge f; therefore, from Lemma 7, we can obtain . So, every edge in C has one vertex in set X and the other vertex in set Y. This means that cycle C is a bipartite graph, which implies that it is an even-length cycle. This contradicts our assumption. Thus, there are two adjacent vertices and in C such that .
Because and , we obtain
This means that the deficit contribution of edge f to edge is 1. Because edge f can be any edge of G, the sum of the deficits of edges in C is at least m. Because G is a bicyclic graph, it includes an edge e that is neither a pendent edge nor in C. According to Lemma 1, we have . Thus, the deficit of edge e is at least 1.
In conclusion, the deficit of a bicyclic graph G with an odd cycle is at least . □
Theorem 3.
Let . If , then , and the equality holds if and only if .
Proof.
Let G be a bicyclic graph containing as a subgraph and with the maximum edge Mostar index. First, it follows from Lemma 2 that all edges in the graph G are pendent edges except for the edges contained in . Second, if graph G contains an odd cycle, then according to Lemma 8, , which contradicts Corollary 1. Therefore, graph G does not contain odd cycles. This implies that have the same parity.
By the definition of a theta graph, we have . Let C be the shortest cycle in G. Now, take any edge of C. Assume that path has edges closer to vertex u than to vertex v, and edges closer to vertex v than to vertex u, such that . In addition, let us assume that the graph G has p pendent edges that are closer to vertex u than to vertex v, and q pendent edges that are closer to vertex v than to vertex u. Furthermore, we have . Because C is isometric, for , we have
Furthermore, because the cycle C is even, is even and . If , then , which is a contradiction by Corollary 1. Thus, . There are two cases.
Case 1: and . Because G contains an isometric cycle of length , we can conclude that . Therefore, the graph G contains as a subgraph. Let and be vertices of degree three in of graph G, whereas are vertices of degree two. Because , , we have
Similarly, , , , , . Then, for the graph G, , a contradiction with Corollary 1.
Case 2: and . Because G contains an isometric cycle of length , we can conclude that . Therefore, the graph G contains as a subgraph. Suppose that and are vertices of degree three in of graph G, and are vertices of degree two. Let be the number of pendent edges of and .
If , we have , , , , , . Then, for the graph G, , a contradiction with Corollary 1. So, . Similarly, there are also .
If and , we have , , , , , . Then, for the graph G, , a contradiction with Corollary 1. Therefore, all pendent edges in G must be associated with the same fixed vertex of degree two in .
Clearly, and . Therefore, the proof is complete. □
Finally, Theorem 1 can be proved by Theorems 2 and 3.
Author Contributions
Writing—original draft, H.W.; Writing—review & editing, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (Grant No. 11961040).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin, Germany, 2008. [Google Scholar]
- Gutman, I.; Klavzar, S.; Mohar, B. (Eds.) Fifty Years of the Wiener Index. In MATCH Communications in Mathematical and in Computer Chemistry; Faculty of Science, University of Kragujevac: Kragujevac, Serbia, 1997; Volume 35, pp. 1–259. [Google Scholar]
- Gutman, I.; Yeh, Y.N.; Lee, S.L.; Luo, Y.L. Some recent results in the theory of the Wiener number. Indian J. Chem. 1993, 32A, 651–661. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Gutman, I. A formula for the Wiener number of trees and its extension to graphs containing cycles. Graph Theory Notes N. Y. 1994, 27, 9–15. [Google Scholar]
- Gutman, I.; Ashrafi, A.R. The edge version of the Szeged index. Croat. Chem. Acta 2008, 81, 263–266. [Google Scholar]
- Došlić, T.; Martinjak, I.; Škrekovski, R.; Spuzevic, S.T.; Zubac, I. Mostar index. J. Math. Chem. 2018, 56, 2995–3013. [Google Scholar] [CrossRef]
- Ali, A.; Došlić, T. Mostar index: Results and perspectives. Appl. Math. Comput. 2021, 404, 226–245. [Google Scholar] [CrossRef]
- Dehgardi, N.; Azari, M. More on Mostar index. Appl. Math. E-Notes. 2020, 20, 316–322. [Google Scholar]
- Hayat, F.; Zhou, B. On cacti with large Mostar index. Filomat 2019, 33, 4865–4873. [Google Scholar] [CrossRef]
- Tepeh, A. Extremal bicyclic graphs with respect to Mostar index. Appl. Math Ematics Comput. 2019, 355, 319–324. [Google Scholar] [CrossRef]
- Tratnik, N. Computing the Mostar index in networks with applications to molecular graphs. Iran. J. Math. Chem. 2021, 12, 1–18. [Google Scholar]
- Ghanbari, N.; Alikhani, S. Mostar index and edge Mostar index of polymers. Comput. Appl. Math. 2021, 40, 1–21. [Google Scholar] [CrossRef]
- Liu, H.; Song, L.; Xiao, Q.; Tang, Z. On edge Mostar index of graphs. Iran. J. Math. Chem. 2020, 11, 95–106. [Google Scholar]
- Yasmeen, F.; Akhter, S.; Ali, K.; Rizvi, S.T.R. Edge Mostar indices of cacti graph with fixed cycles. Front. Chem. 2021, 9, 440–452. [Google Scholar] [CrossRef] [PubMed]
- Havare, O.C. Mostar Index (Mo) and edge Mo index for some cycle related graphs. Rom. J. Math. Comput. Sci. 2020, 10, 53–66. [Google Scholar]
- Ghalavand, A.; Ashrafi, A.R.; Hakimi-Nezhaad, M. On Mostar and Edge Mostar Indices of Graphs. J. Math. 2021, 2021, 6651220. [Google Scholar] [CrossRef]
- Liu, M.; Ji, S. On minimum revised edge Szeged index of bicyclic graphs. AKCE Int. J. Graphs Comb. 2022, 19, 249–254. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).