On the Degree Distribution of Haros Graphs

Abstract

Haros graphs are a graph-theoretical representation of real numbers in the unit interval. The degree distribution of the Haros graphs provides information regarding the topological structure and the associated real number. This article provides a comprehensive demonstration of a conjecture concerning the analytical formulation of the degree distribution. Specifically, a theorem outlines the relationship between Haros graphs, the corresponding continued fraction of its associated real number, and the subsequent symbolic paths in the Farey binary tree. Moreover, an expression that is continuous and piecewise linear in subintervals defined by Farey fractions can be derived from an additional conclusion for the degree distribution of Haros graphs.

1. Introduction

The study of the structure of real numbers has been approached from a variety of perspectives [1,2,3,4]. The representation by continued fractions and the representation through the Farey tree are examples of canonical representations [5,6,7]. Recent graph-theoretical research has provided a new representation of real numbers using Haros graphs [8]. These graphs are swayed by the approach of Horizontal Visibility Graphs to the quasiperiodic route [9,10,11,12]. Furthermore, Haros graphs are similar to other structures, such as Farey graphs [13,14,15]. Haros graphs provide a graph description of the unit interval $[0,1]$ establishing a one-to-one correspondence with the well-known Farey sequences ${\mathcal{F}}_n$, where

$${\mathcal{F}}_n=\left\{\frac{p}{q}\in [0,1]:0\le p\le q\le n,(p,q)=1\right\}.$$

The Haros graph set $\mathcal{G}$ is recursively generated from an initial graph (defined as two nodes joined by an edge) and the concatenation graph-operator ⊕ shown in Figure 1. Hence, the set $\mathcal{G}$ may be represented as a binary tree (see Figure 1). Since ${lim}_n{\mathcal{F}}_n=[0,1]$, the bijection can be extended to the unit interval, where rational numbers are associated with finite Haros graphs, and irrational numbers correspond to infinite Haros graphs.

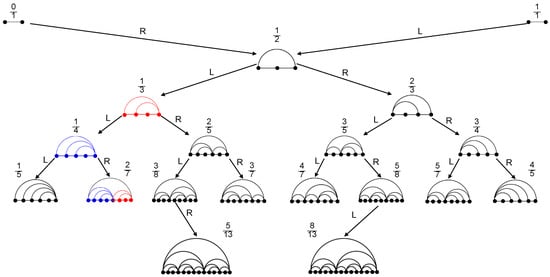
Figure 1. Six levels of the Haros graph tree with Haros graphs $G_{p/q}$ associated with the corresponding rational fractions $p/q$ (due to space constraints, only two of these are shown at the sixth level). The first level is formed by two copies of the initial graph $G_0$. The graph operator merges the two nearby extreme nodes, adding a connection to the resulting graph that connects the new extreme nodes. On the left, the Haros graph $G_{2/7}$ is generated by concatenating $G_{1/4}$ (blue) and $G_{1/3}$ (red), i.e., $G_{2/7}=G_{1/4}\oplus G_{1/3}$.

Consequently, a one-to-one correspondence $\tau$ exists between real numbers $x\in [0,1]$ and Haros graphs $\tau \left(x\right)=G_x\in \mathcal{G}$. One of the main features investigated in [8] is the degree distribution $P(k,x)$ of Haros graphs $G_x$, which is the probability that a randomly selected node in $G_x$ has degree k. The degree distribution was deemed a fruitful tool because Haros graphs are uniquely determined by the degree sequence [16], whereas the degree distribution is a marginal distribution of the degree sequence. Indeed, the degree distribution for the three initial values of k confirms:

$$P(k,x<1/2)=\left\{\begin{array}{cc}x,\hfill & k=2\hfill \\ 1-2x,\hfill & k=3\hfill \\ 0,\hfill & k=4;\hfill \end{array}\right.P(k,x>1/2)=\left\{\begin{array}{cc}1-x,\hfill & k=2\hfill \\ 2x-1,\hfill & k=3\hfill \\ 0,\hfill & k=4.\hfill \end{array}\right.$$

(1)

In contrast to the initial values, which are related to the real number x associated with $G_x$, the closed form of the degree distribution $P(k,x)$ has only been drawn for degrees $k\ge 5$. Taking the above fact into account, this paper outlines two theorems to complete the degree distribution expression, based on two distinct approaches. Initially, a complete description of $P(k,x)$ is provided only in terms of the continued fraction of x or, alternatively, in terms of the Haros graph creation process codified along the symbolic binary path. The second result demonstrates the properties of $P(k,x)$ as a continuous real-valued piecewise linear function.

This paper is separated into four sections. Section 2 gives a brief overview of Haros graphs and their connections to Farey sequences, continued fractions, and the Farey binary tree. Section 3 provides the two main results: the first theorem states the closed form of $P(k,p/q)$ with respect to truncations of the continued fraction of $p/q$, whereas a second theorem rewrites the preceding result using the position of $p/q$ in the Farey binary tree. Section 4 concludes the work. In addition, Appendix A includes detailed proofs for the assertions in Section 3.

2. Preliminaries

The Farey binary tree is a canonical way of representing the set of rational numbers in $[0,1]$ as a binary tree starting with the fractions $0/1,1/1$—the elements of the Farey sequence ${\mathcal{F}}_1$—and creating new irreducible fractions by the mediant sum of two consecutive fractions in ${\mathcal{F}}_n$:

$$\frac{p}{q}\oplus \frac{r}{s}=\frac{p+r}{q+s}.$$

(2)

The binary tree representation allocates each rational number to a level k of the tree, denoted ${\ell }_k$. For instance, the three first levels consist of:

$${\ell }_1=\left\{\frac{0}{1},\frac{1}{1}\right\};{\ell }_2=\left\{\frac{1}{2}\right\};{\ell }_3=\left\{\frac{1}{3},\frac{2}{3}\right\}.$$

This representation is closely related to the continued fraction, a powerful technique for representing a real number in the interval $[0,1]$ as

$$x=\frac{1}{a_1+\frac{1}{a_2+\frac{1}{a_3+\dots }}}=[a_1,a_2,a_3,\dots ].$$

The relationship was presented in [7], and it has been established that a number with a continued fraction expression $[a_1,a_2,a_3,\dots ]$ is associated with a symbolic binary path in the Farey binary tree $L^{a_1}{R}^{a_2}{L}^{a_3}\dots$, where $L^q$ is interpreted as a sequence of q symbols L (if the symbolic path is finite, the last symbol has an index $a_n-1$). Therefore, since every irrational number has an infinite continued fraction, the irrational numbers are reachable through an infinite path in the Farey binary tree. Moreover, the continued fraction allows a sequence of rational so-called convergents [6] defined as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{p}_k=\hfill & a_k·p_{k-1}+p_{k-2}\hfill \\ q_k=\hfill & a_k·q_{k-1}+q_{k-2},\hfill \end{array}\right.\end{array}$$

(3)

with initial values $p_{-2}=0,q_{-2}=1,p_{-1}=1,$ and $q_{-1}=0$, where

$$\underset{k\to \infty }{lim}\frac{p_k}{q_k}=\underset{k\to \infty }{lim}[a_1,\dots ,a_k]=[a_1,a_2,\cdots ]=x.$$

As stated in the preceding section, the Haros graphs set $\mathcal{G}$ provides a graph-based representation of the unit interval $[0,1]$. The primary objective is to reproduce, in a graph scenario, the mediant sum—described in Equation (2)—that was utilized to construct ${\mathcal{F}}_n$ [1]. The concatenation graph is depicted in Figure 1, and Flanagan et al. [17] provide a comprehensive definition. Every Haros graph G (except for the initial graph) is therefore described as $G=G_L\oplus G_R$, where $G_L,G_R$ are also Haros graphs. However, just as the mediant sum only takes to two nearby fractions in Farey sequences, Haros graphs only can be concatenated if $G_L$ and $G_R$ are also adjacent.

In order to analyze the topological structure of a Haros graph, the probability distribution degree $P(k,x)$ proves to be a useful instrument. Equation (1) identifies the three first values of k, although by construction $P(k,0)=P(k,1)=0$. In addition, for degrees $k\ge 5$, Theorem 2, in [8], determines that the degree values for which $P(k,x)=0$ rely on the symbol repetition—$RR$ or $LL$—in the symbolic path of the Haros graph tree to reach $G_x$. Moreover, the same research conjectures follow for the closed form of $P(k,x)$. The aim is to provide a formal proof of this claim.

Prior to this, a brief explanation of the emergence of degrees $k\ge 5$ is provided: the emergence of degrees $k\ge 5$ occurs if there is a change in symbol $L\to R$ or $R\to L$ in the path of the Haros graph tree. Consequently, the degree it emerges, or not, is related to the level at which this symbolic change occurs. Suppose that we have covered the path $L^{a_1}{R}^{a_2}\dots L^{a_{k-1}}$. Next, the downstream of $R^{a_k}$ generates a new degree, which had previously appeared as a boundary node before the shift in direction (the node resulting from the identification of the extreme nodes). Specifically, in the first downstream R, the degree appears in the merging node, and the number of nodes with this degree increases by one with each descent. Therefore, when we reach $R^{a_k-1}$, there will be $0+(a_k-1)=a_k-1$ nodes of that degree. In addition, the Haros graph achieved is associated with $p_k/q_k=[a_1,\dots ,a_k]$.

Now, in order to reach the Haros graph associated with $[a_1,\dots ,a_k,a_{k+1}]$, we must descend to R and then $a_{k+1}-1$ times to L. If there were $a_k-1$ nodes of that degree previously, a new descent will result in $a_k$ nodes. Then, performing a descent $L^{a_{k+1}-1}$ requires concatenating the Haros graph reached by $R^{a_k}$ with $a_{k+1}-1$ copies of the Haros graph reached by $R^{a_k-1}$, so that the resultant Haros graph has $(a_k-1)·(a_{k+1}-1)+a_k=(a_k-1)·\left(a_{k+1}\right)+1$ nodes of that degree.

In other words, the emergence of the degree occurs, according to the recursive equation $q_n=q_{n-2}+a_n·q_{n-1}$, where the terms $a_i$ correspond to the continued fraction $[a_k-1,a_{k+1},\dots ,a_m]$, with initial conditions $q_{-1}=0,q_0=1$. Hence, this recursive equation converges to the denominator of the continued fraction $[a_k-1,a_{k+1},\dots ,a_m]$.

3. Main Results

The first presented result provides an explicit description of the degree distribution related to the truncations of the continued fraction of $p/q$, the rational number associated with Haros graph $G_{p/q}$:

Theorem 1. 

Let $p/q\in [0,1/2]$, with $p/q=[a_1,\dots ,a_m]$. Then, the degree distribution $P(k,p/q)$ of the Haros graph $G_{p/q}$ is:

$$P\left(k,\frac{p}{q}\right)=\left\{\begin{array}{cc}p/q,\hfill & k=2\hfill \\ (q-2p)/q,\hfill & k=3\hfill \\ 0,\hfill & k=4\hfill \\ s^{\left(l\right)}/q,\hfill & for values k=\sum _{i=1}^l{a}_i+3, with \forall l=1,\dots ,m-1,\hfill \\ \hfill & where r^{\left(l\right)}/s^{\left(l\right)}=[a_{l+1}-1,\dots ,a_m]\hfill \\ 1/q,\hfill & if k=\sum _{i=1}^m{a}_i+2\hfill \\ 0,\hfill & otherwhise.\hfill \end{array}\right.$$

(4)

Proof. 

See Appendix A.1 for a complete proof. □

The theorem has several consequences: first, it unveils the whole expression for $P(k,x)$ providing a large amount of topological information. Moreover, as stated in the previous section, the values $k\ge 5$ are related to the continued fraction and, consequently, with the symbolic path reached in the Haros graph tree. In addition, the result reduces the computational cost for obtaining the degree distribution $P(k,p/q)$ of the Haros graph $G_{p/q}$. Initially, we observe that the denominator of the n-th convergent $q_n$ of $p/q$ verifies $q_n\ge {\varphi }^{n-1}$, where $\varphi$ is the Golden number [18]. Hence, as the Haros graph $G_{p_n/q_n}$ has $q_n+1$ nodes, its growth is exponential, but Theorem 1 uses only continued fractions [3,19].

Let us illustrate an example: consider the Haros graph $G_{10/23}$, where $10/23=[a_1,a_2,a_3]=[2,3,3]$. Hence, the symbolic path in the Haros graph tree is $L^2{R}^3{L}^2$ (see Figure 2 for an illustration). Numerically, its degree distribution is as follows:

$$P\left(k,\frac{10}{23}\right)=\{\begin{array}{ll}\frac{10}{23},& k=2,\\ \frac{3}{23},& k=3,\\ 0,& k=4,\\ \frac{7}{23},& k=5,\\ \frac{2}{23},& k=8,\\ \frac{1}{23},& k=10,\\ 0,& \mathrm{otherwise}.\end{array}$$

(5)

Figure 2. Haros graph $G_{10/23}$. As $10/23=[2,3,3]$, it is clear that the binary symbolic path to reach this Haros graph is $LLRRRLL=L^2{R}^3{L}^{3-1}$. According to the boundary node convention, the extreme nodes are identified as a single boundary node, while the total number of degrees is maintained. Then, the degree sequence is $[3,2,5,2,5,2,8,3,2,5,2,5,2,8,3,2,5,2,5,2,5,2,5+5=10]$.

Then, we can verify that there are $m_{5,10/23}=7$ nodes of degree $k=5$ and that this number corresponds with the denominator of the continued fraction

$$[a_2-1,a_3]=[2,3]=\frac{3}{7};$$

moreover, there are $m_{8,10/23}=2$ nodes of degree $k=8$, which is the denominator of the continued fraction

$$[a_3-1]=\left[2\right]=\frac{1}{2}.$$

Lastly, $k=10$ corresponds with the degree of the boundary node; therefore, it only appears once.

With Theorem 1, we are able to provide a proof for the conjecture presented in [8]. Contrary to the previous finding, the subsequent theorem results in a formulation of the degree distribution relating to the number x, but the computation of $P(k,x)$ for every k depends on the location of x in the subintervals given by the levels in the Farey binary tree ${\ell }_k$.

Theorem 2. 

Let $p/q\in [0,1/2]$ and the associated Haros graph $G_{p/q}$. Let us consider ${\ell }_{k-3}={\left\{\frac{a_i}{b_i}\right\}}_{i=1}^{2^{k-5}}$, and ${\ell }_{k-2}={\left\{\frac{p_j}{q_j}\right\}}_{j=1}^{2^{k-4}}$; clearly, we have $\forall i=1,\dots ,2^{k-5}$:

$$\frac{p_{2i-1}}{q_{2i-1}}<\frac{a_i}{b_i}<\frac{p_{2i}}{q_{2i}}.$$

(6)

Therefore, the degree distribution of the Haros graph $G_{p/q}$ for degrees $k\ge 5$ is:

$$P\left(k,\frac{p}{q}\right)=\{\begin{array}{l}{q}_{2i-1}·(p/q)-p_{2i-1},\mathrm{if}p/q\in \left(\frac{p_{2i-1}}{q_{2i-1}},\frac{a_i}{b_i}\right),\forall i=1,\dots ,2^{k-5},\\ -q_{2i}·(p/q)+p_{2i},\mathrm{if}p/q\in \left(\frac{a_i}{b_i},\frac{p_{2i}}{q_{2i}}\right),\forall i=1,\dots ,2^{k-5},\\ 1/q_j,\mathrm{if}\frac{p}{q}=\frac{p_j}{q_j}\in {\ell }_{k-2},\\ 0,\mathrm{otherwise}.\end{array}$$

(7)

Proof. 

See Appendix A.2 for a complete proof. □

The theorem can be extended from rational numbers to all real numbers. Figure 3 depicts a numerical computation of $P(k,x)$ for the first values of $k\ge 5$ verifying the statement of Theorem 2. Moreover, this new formulation allows the following statement to emphasize some aspects of the degree distribution $P(k,x)$ as a real function over the variable x:

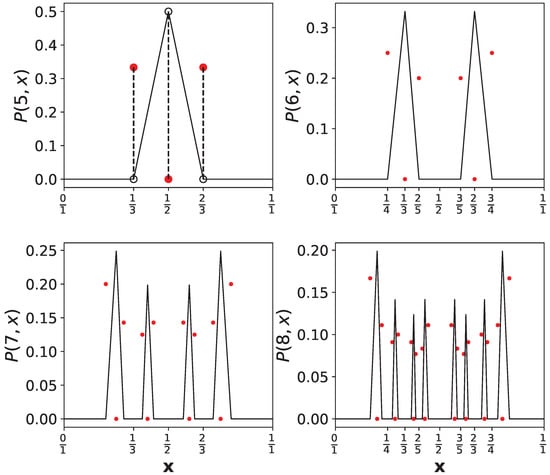
Figure 3. The numerical computation of the degree distribution $P(k,x)$ as a function of x for $k=5,6,7,8$, and for all Haros graphs $G_x$ with $x\in {\mathcal{F}}_{1000}$. The red points represent removable discontinuities, whereas the solid black lines shows the piecewise linear behavior. Due to the lack of space, only the left upper panel of $P(5,x)$ accurately shows that the red points represent the Haros graph located in levels ${\ell }_{\kappa }$, for $\kappa =5-3=2$, i.e., the Haros graph $G_{1/2}$ (without nodes of degree $k=5$), and for $\kappa =5-2=3$, i.e., the Haros graphs $G_{1/3},G_{2/3}$, where the degree $k=5$ is located at the boundary node.

Corollary 1. 

The degree distribution $P(k,x)$ over the variable x is a piecewise linear and continuous function, with the exception of the measure null set.

Now, let us illustrate the theorem by applying the result to the case when $k=5$. Then, it is a simple matter to confirm that if $p/q\in (1/3,1/2)$, then

$$P\left(k=5,\frac{p}{q}\right)=3·\frac{p}{q}-1=\frac{3p-q}{q}.$$

In comparison, the continued fractions of rational numbers $p/q\in (1/3,1/2)$ start with the term $a_1=2$. In virtue of Theorem 1, the degree $k=a_1+3=5$ would have a frequency of $s^{\left(1\right)}/q$, where $s^{\left(1\right)}$ is the denominator of $[a_2-1,a_3,\dots ,a_m]$. Let us examine how the two expressions coincide:

$$\begin{array}{c}\hfill \frac{p}{q}=\frac{1}{2+\frac{1}{a_2+\ddots }}\Rightarrow \frac{q}{p}-2=\frac{q-2p}{p}=\frac{1}{a_2+\frac{1}{a_3+\ddots }}\Rightarrow \\ \hfill \frac{p}{q-2p}-1=\frac{3p-q}{q-2p}=(a_2-1)+\frac{1}{a_3+\frac{1}{a_4+\ddots }}\Rightarrow \\ \hfill \frac{q-2p}{3p-q}=\frac{1}{(a_2-1)+\frac{1}{a_3+\frac{1}{a_4+\ddots }}}.\end{array}$$

Hence, $3p-q$ is the denominator of the continued fraction $[a_2-1,a_3,\dots ,a_m]$ according to Theorem 1. This finding may be generalizable to all degree values k, requiring the partition of $[0,1]$ by the levels ${\ell }_{k-3}$ and ${\ell }_{k-2}$.

4. Conclusions

The topological properties of rational Haros graphs were investigated in detail. The full formulation of the degree distribution $P(k,x)$ of a Haros graph $G_x$ was demonstrated. Different methods were used to prove two theorems. The first theorem unveiled the closed form of $P(k,x)$ obtained by truncations of the continued fraction of x. With this result, not only did we obtain the complete expression of the degree distribution, but we also computed it more efficiently. The second theorem provided a piecewise linear and continuous expression of $P(k,x)$, except for a measure null set. This result confirmed a conjecture presented in [8] revealing that the degree distribution exhibited a self-similar behavior related to the subintervals defined by Farey fractions.

Appendix A.1. Proof of Theorem 1

Proof. 

The values $k=2,3,4$ are calculated in (1), while the value $k={\sum }_{i=1}^m{a}_i+2$ corresponds to the degree of the boundary node, which has a frequency of 1 according to the the results of Appendix B in [8].

Let us consider the Haros graph $G_{p/q}$, with $p/q=[a_1,\dots ,a_m]$. Thus, the symbolic path in the Haros graph tree is $L^{a_1}{R}^{a_2}\dots X^{a_m-1}$, with $X=L$ or $X=R$ depending on whether m is odd or even, respectively. In virtue of Theorem 2 presented in [8], it can be determined that nonzero values of the degree distribution $P(k,p/q)$ correspond to the degrees $k={\sum }_{i=1}^l{a}_i+3$ for the values $l=1,2,\dots ,m-1$. It remains, however, to determine its precise value. To accomplish this, we conduct an induction exercise on the levels of the Haros graph tree ${\ell }_n$:

At level ${\ell }_4$, the first Haros graph with degree $k\ge 5$ is associated to $2/5=[a_1,a_2]=[2,2]$ proving that

$$P\left(a_1+3,\frac{2}{5}\right)=P\left(5,\frac{2}{5}\right)=\frac{1}{5},$$

the value of the denominator of the continued fraction $[a_2-1]=[2-1]=\left[1\right]=1/1$. This level also includes the Haros graph $G_{1/4}$, which fulfils the theorem because it contains only the boundary node with degree $k\ge 5$.

We assume the result holds for all levels of the Haros graph tree ${\ell }_{\kappa }$, with $\kappa \le n$. Let us verify that it is satisfied at level $\kappa =n+1$. To accomplish this, we consider an arbitrary Haros graph $G_{p/q}$ at level n, where $p/q=[a_1,\dots ,a_m]$. Henceforth, we demonstrate that both its left and right descendants satisfy Equation (4).

Let us suppose, without loss of generality, that the last descents that result until we reach $G_{p/q}$ are left descents L, as seen in Figure A1. Moreover, Cvitanovic et al. [20] showed that if $p/q=[a_1,\dots ,a_m]$, then its left descendant is expressed in a continued fraction as $[a_1,\dots ,a_m+1]$, whereas the right descendant has a continued fraction expression $[a_1,\dots ,a_m-1,2]$.

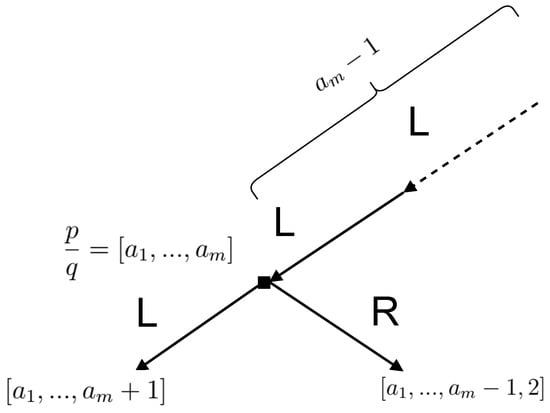
Figure A1. Diagram of the descendants of the Haros graph $G_{p/q}$, with $p/q=[a_1,\dots ,a_m]$. Let us suppose that the Haros graph $G_{p/q}$ contains a symbolic path that terminates in $a_m-1$ descents to the left L (the result is analogous for descents to right R). The continued fraction for the left descendant of the Haros graph is $[a_1,\dots ,a_m+1]$, whereas the right descendant has a continued fraction $[a_1,\dots ,a_m-1,2]$.

Let us start by dealing with the left descendant. This case is depicted in Figure A2, which illustrates how this descendant is formed by concatenating the convergent of order $m-1$ of $p/q$ with $p/q$ itself. By setting a value $l\in \left\{1,2\dots ,m-2\right\}$, we will be in the degree $k_l={\sum }_{i=1}^l{a}_i+3$. Now, it is clear that the number of nodes with degree $k_l$ in the left descendant is equal to the total of the number of nodes with that degree in its two ascendants $G_{p_{m-1}/q_{m-1}}$ and $G_{p/q}$.

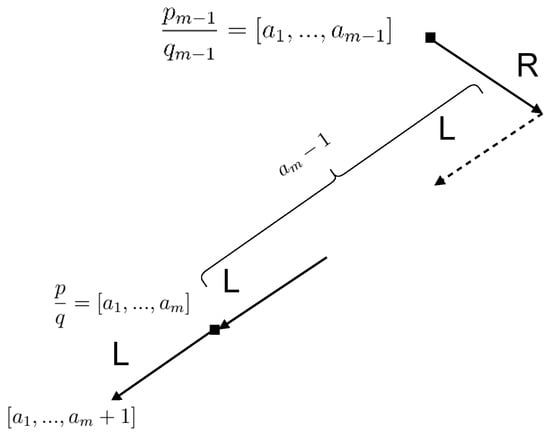
Figure A2. Diagram of the construction for the left descendant of $G_{p/q}$, where $p/q=[a_1,\dots ,a_m]$. The left descendant is expressed as $[a_1,\dots ,a_m+1]$ and is obtained by concatenating $G_{p_{m-1}/q_{m-1}}$ and $G_{p/q}$, where $p_{m-1}/q_{m-1}$ is the convergent of order $m-1$ of $p/q$.

By induction hypothesis, the denominators of the continued fractions are the number of nodes of degree $k_l$ of its ascendants, denoted by $s_{p/q}^{(l,m)}$ and $s_{p/q}^{(l,m-1)}$, respectively. Hence, we have:

$$\frac{r_{p/q}^{(l,m)}}{s_{p/q}^{(l,m)}}:=[a_{l+1}-1,\dots ,a_m],$$

(A1)

and

$$\frac{r_{p/q}^{(l,m-1)}}{s_{p/q}^{(l,m-1)}}:=[a_{l+1}-1,\dots ,a_{m-1}].$$

(A2)

This notation also reflects that the term of Equation (A2) is the previous convergent of Equation (A1). The recursivity of the continued fractions (shown in Equation (3)) entails:

$$s_{p/q}^{(l,m)}=s_{p/q}^{(l,m-2)}+a_m·s_{p/q}^{(l,m-1)}.$$

(A3)

Denoting by $s_L^{\left(l\right)}$ the number of nodes with degree $k_l$ in the left descendant, we obtain the conclusion that:

$$\begin{array}{ccc}\hfill s_L^{\left(l\right)}& =\hfill & \hfill s_{p/q}^{(l,m)}+s_{p/q}^{(l,m-1)}=\left(s_{p/q}^{(l,m-2)}+a_m·s_{p/q}^{(l,m-1)}\right)+s_{p/q}^{(l,m-1)}\\ \hfill & =\hfill & \hfill s_{p/q}^{(l,m-2)}+(a_m+1)·s_{p/q}^{(l,m-1)},\end{array}$$

(A4)

where the right-hand side of Equation (A4) is the denominator of the continued fraction $[a_{l+1}-1,\dots ,a_m+1]$, as we aimed to demonstrate.

The value $l=m-1$ is required to complete the study of the left descendant; therefore, it is necessary to check the result for the degree $k_{m-1}={\sum }_{i=1}^{m-1}{a}_i+3$. The reason for separate consideration is that $G_{p_{m-1}/q_{m-1}}$ does not contain the degree $k_{m-1}$. Nonetheless, this degree first appears at the level ${\sum }_{i=1}^{m-1}{a}_i+1$ of the Haros graph tree, i.e., as the boundary node of the right descendant of $G_{p_{m-1}/q_{m-1}}$. The number of nodes with that degree will increase by one with each successive left descent until the Haros graph $G_{p/q}$ is reached. Moreover, the induction hypothesis applied to $p/q$ determines that there are $s_{p/q}^{(m-1,m)}$ nodes of this degree, i.e., the denominator of

$$[a_m-1]=\frac{1}{a_m-1}.$$

Therefore, there will be $s_{p/q}^{(m-1,m)}+1$ nodes, or equivalently, there will be $a_m$ nodes of this degree. This number is the denominator of the truncated continued fraction $[(a_m+1)-1]=\left[a_m\right]$, thus finishing the study of the left descent.

Let us now turn our attention to the right descendant, depicted in Figure A3. In this instance, the concatenation occurs between the Haros graph $G_{p/q}$ and its right ancestor, i.e., the Haros graph associated with the continued fraction $[a_1,\dots ,a_m-1]$.

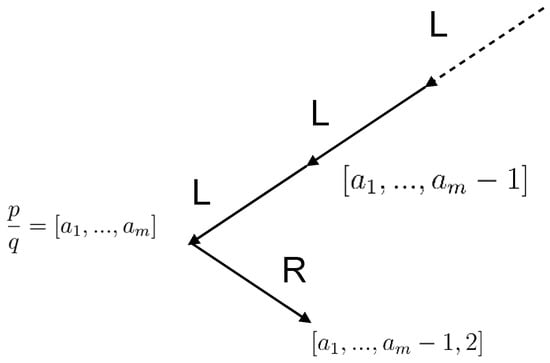
Figure A3. Diagram of the construction for the right descendant of $G_{p/q}$, where $p/q=[a_1,\dots ,a_m]$. The right descendant is expressed as $[a_1,\dots ,a_m+1]$ and is obtained by concatenating the Haros graphs $G_{p_{m-1}/q_{m-1}}$ and $G_{p/q}$, where $p_{m-1}/q_{m-1}$ is the $m-1$-th convergent of $p/q$.

Let us consider the degrees $k_l={\sum }_{i=1}^l{a}_i+3$, with $l\in \left\{1,2,\dots ,m-1\right\}$. The right descendant is obtained by concatenating $G_{p/q}\oplus G_{a/b}$, where $\frac{a}{b}=[a_1,\dots ,a_m-1]$. Therefore, we must represent the truncations of $p/q$ and $a/b$, as well as their convergents, which are indicated as follows:

$$\frac{r_{p/q}^{(l,m)}}{s_{p/q}^{(l,m)}}=[a_{l+1}-1,\dots ,a_{m-1},a_m],$$

(A5)

and

$$\frac{r_{a/b}^{(l,m)}}{s_{a/b}^{(l,m)}}=[a_{l+1}-1,\dots ,a_{m-1},a_m-1].$$

(A6)

It is easy to show that the continued fractions in Equations (A5) and (A6) match in all the terms with the exception of the last one; hence, all the denominators of the convergent with $t\le m-1$, we verify that $s_{p/q}^{(l,t)}=s_{a/b}^{(l,t)}$. Using the induction hypothesis, the recursive Equation (3) for the convergent, and denoting by $s_R^{\left(l\right)}$ the number of nodes of degree $k_l$ in the right descendant, we have:

$$\begin{array}{ccc}\hfill s_R^{\left(l\right)}& =& s_{p/q}^{(l,m)}+s_{a/b}^{(l,m)}\hfill \\ & =& (s_{p/q}^{(l,m-2)}+\left(a_m\right)·s_{p/q}^{(l,m-1)})+(s_{a/b}^{(l,m-2)}+(a_m-1)·s_{a/b}^{(l,m-1)})\hfill \\ & =& (s_{a/b}^{(l,m-2)}+\left(a_m\right)·s_{a/b}^{(l,m-1)})+(s_{a/b}^{(l,m-2)}+(a_m-1)·s_{a/b}^{(l,m-1)})\hfill \\ & =& 2·s_{a/b}^{(l,m-2)}+2·(a_m-1)·s_{a/b}^{(l,m-1)}+s_{p/q}^{(l,m-1)}\hfill \\ & =& 2(s_{a/b}^{(l,m-2)}+·(a_m-1)·s_{a/b}^{(l,m-1)})+s_{a/b}^{(l,m-1)}\hfill \\ & =& 2·s_{a/b}^{(l,m)}+s_{a/b}^{(l,m-1)},\hfill \end{array}$$

(A7)

where the right-hand side of Equation (A7) is the denominator of the truncated continued fraction $[a_{l+1}-1,\dots ,a_{m-1},a_m-1,2]$. Finally, the right descent has a single node with degree

$$k=\sum _{i=1}^{m-1}{a}_i+(a_m-1)+3=\sum _{i=1}^m{a}_i+2.$$

This is the merging node obtained by the concatenating the extreme nodes of $p/q$ and $a/b$, in agreement with the denominator of the last truncated right descendant, which is $[2-1]=\left[1\right]=1/1$, thereby ending the proof. □

Appendix A.2. Proof of Theorem 2

In order to demonstrate the result, we must introduce the continuants, recursively defined polynomials stated by Euler, where:

$$\begin{array}{ccc}\hfill K_0& =& 1;\hfill \\ \hfill K_1\left(x_1\right)& =& x_1;\hfill \\ \hfill K_n(x_1,\dots ,x_n)& =& x_n·K_{n-1}(x_1,\dots ,x_{n-1})+K_{n-2}(x_1,\dots ,x_{n-2}),\mathrm{for}n\ge 2.\hfill \end{array}$$

(A8)

The continuants allow us to express the continued fractions as

$$\frac{p}{q}=[a_1,\dots ,a_n]=\frac{K_{n-1}(a_2,\dots ,a_n)}{K_n(a_1,\dots ,a_n)}.$$

(A9)

In addition, two properties of the continuants must be introduced. The first generalizes the definition (A8) $\forall m$, with $1\le m<n$ as follows:

$$\begin{array}{ccc}\hfill K_n(x_1,\dots ,x_n)& =\hfill & \hfill K_m(x_1,\dots ,x_m)·K_{n-m}(x_{m+1},\dots ,x_n)\\ \hfill & +\hfill & \hfill K_{m-1}(x_1,\dots ,x_{m-1})·K_{n-m-1}(x_{m+2},\dots ,x_n).\end{array}$$

(A10)

The second equality was established by Muir and Metzler in [21]:

$$K_n(x_1,\dots ,x_n)·K_{n-2}(x_2,\dots ,x_{n-1})-K_{n-1}(x_1,\dots ,x_{n-1})·K_{n-1}(x_2,\dots ,x_n)={(-1)}^n.$$

(A11)

Proof. 

The intervals, where the degree distribution $P(k,p/q)>0$, are determined by the elements $a_i/b_i\in {\ell }_{k-3}$, i.e., the Farey fractions of a certain level in the Farey tree, and their descendants located at a lower level $p_{2i-1}/q_{2i-1}\in {\ell }_{k-2}$. Let us first establish that

$$\frac{a_i}{b_i}=[{\alpha }_1,\dots ,{\alpha }_r];$$

then, if r is even, we obtain

$$\frac{p_{2i-1}}{q_{2i-1}}=[{\alpha }_1,\dots ,{\alpha }_r+1];\frac{p_{2i}}{q_{2i}}=[{\alpha }_1,\dots ,{\alpha }_r-1,2],$$

(A12)

whereas for r odd we have:

$$\frac{p_{2i}}{q_{2i}}=[{\alpha }_1,\dots ,{\alpha }_r+1];\frac{p_{2i-1}}{q_{2i-1}}=[{\alpha }_1,\dots ,{\alpha }_r-1,2].$$

(A13)

Let us suppose, without loss of generality, the case r odd, and consider a rational number

$$\frac{p}{q}\in \left(\frac{p_{2i-1}}{q_{2i-1}}=[{\alpha }_1,\dots ,{\alpha }_r+1],\frac{a_i}{b_i}=[{\alpha }_1,\dots ,{\alpha }_r]\right).$$

Then, the first r terms of the continued fraction are determined as follows:

$$\frac{p}{q}=[{\alpha }_1,\dots ,{\alpha }_r,b_{r+1},\dots ,b_m].$$

Furthermore, if $a_i/b_i=[{\alpha }_1,\dots ,{\alpha }_r]\in {\ell }_{k-3}$, then $k={\sum }_{i=1}^r{\alpha }_i+3$. Let us verify that the numerator of the expression $q_{2i-1}·(p/q)-p_{2i-1}$ stated in Theorem 2 and the term $s^{\left(r\right)}$ stated in Theorem 1 have the same value for the degree $k={\sum }_{i=1}^r{\alpha }_i+3$. Hence, applying the continuant expression in Equation (A9) to $p/q$ and $p_{2i-1}/q_{2i-1}$ (described in Equation (A12)), and the property presented in Equation (A10), we obtain:

$$\begin{array}{ccc}\hfill q_{2i-1}·p-q·p_{2i-1}& =& K({\alpha }_1,\dots ,{\alpha }_r+1)·K({\alpha }_2,\dots ,{\alpha }_r,b_{r+1},\dots ,b_m)\hfill \\ & & -K({\alpha }_1,\dots ,{\alpha }_r,b_{r+1},\dots ,b_m)·K({\alpha }_2,\dots ,{\alpha }_r+1)\hfill \\ & =& K({\alpha }_1,\dots ,{\alpha }_r+1)·\left[K({\alpha }_2,\dots ,{\alpha }_r)·K(b_{r+1},\dots ,b_m)\right.\hfill \\ & & +\left.K({\alpha }_2,\dots ,{\alpha }_{r-1})·K(b_{r+2},\dots ,b_m)\right]\hfill \\ & & -K({\alpha }_2,\dots ,{\alpha }_r+1)·\left[K({\alpha }_1,\dots ,{\alpha }_r)·K(b_{r+1},\dots ,b_m)\right.\hfill \\ & & +\left.K({\alpha }_1,\dots ,{\alpha }_{r-1})·K(b_{r+2},\dots ,b_m)\right]\hfill \\ & =& K(b_{r+1},\dots ,b_m)·\left[K({\alpha }_1,\dots ,{\alpha }_r+1)·K({\alpha }_2,\dots ,{\alpha }_r)\right.\hfill \\ & & \left.-K({\alpha }_2,\dots ,{\alpha }_r+1)·K({\alpha }_1,\dots ,{\alpha }_r)\right]\hfill \\ & & +K(b_{r+2},\dots ,b_m)·\left[K({\alpha }_1,\dots ,{\alpha }_r+1)·K({\alpha }_2,\dots ,{\alpha }_{r-1})\right.\hfill \\ & & \left.-K({\alpha }_2,\dots ,{\alpha }_r+1)·K({\alpha }_1,\dots ,{\alpha }_{r-1})\right].\hfill \end{array}$$

(A14)

Using the definition (A8) for $K({\alpha }_1,\dots ,{\alpha }_r+1)$, we obtain:

$$K({\alpha }_1,\dots ,{\alpha }_r+1)=K({\alpha }_1,\dots ,{\alpha }_r)+K({\alpha }_1,\dots ,{\alpha }_{r-1}),$$

(A15)

and applying the Equation (A11), we obtain the following value for the first bracket in Equation (A14):

$$\begin{array}{c}\hfill K({\alpha }_1,\dots ,{\alpha }_r+1)·K({\alpha }_2,\dots ,{\alpha }_r)-K({\alpha }_2,\dots ,{\alpha }_r+1)·K({\alpha }_1,\dots ,{\alpha }_r)\\ \hfill =K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_r)+K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r)\\ \hfill -K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_r)-K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_r)\\ \hfill =K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r)-K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_r)\\ \hfill ={(-1)}^{r+1}=1.\end{array}$$

In addition, for the second bracket in Equation (A14), we have:

$$\begin{array}{c}\hfill K({\alpha }_1,\dots ,{\alpha }_r+1)·K({\alpha }_2,\dots ,{\alpha }_{r-1})-K({\alpha }_2,\dots ,{\alpha }_r+1)·K({\alpha }_1,\dots ,{\alpha }_{r-1})\\ \hfill =K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_{r-1})+K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_{r-1})\\ \hfill -K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_{r-1})-K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_{r-1})\\ \hfill =K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_{r-1})-K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_{r-1})\\ \hfill ={(-1)}^r=-1.\end{array}$$

Therefore, Equation (A14) is simplified as follows:

$$\begin{array}{c}\hfill q_{2i-1}·p-q·p_{2i-1}=K(b_{r+1},\dots ,b_m)-K(b_{r+2},\dots ,b_m),\end{array}$$

(A16)

where the right-hand side is:

$$\begin{array}{c}\hfill K(b_{r+1},\dots ,b_m)-K(b_{r+2},\dots ,b_m)\\ \hfill =b_{r+1}·K(b_{r+2},\dots ,b_m)+K(b_{r+3},\dots ,b_m)-K(b_{r+2},\dots ,b_m)\\ \hfill =(b_{r+1}-1)·K(b_{r+2},\dots ,b_m)+K(b_{r+3},\dots ,b_m)\\ \hfill =K(b_{r+1}-1,b_{r+2},\dots ,b_m),\end{array}$$

(A17)

i.e., it is the denominator of the truncated continued fraction $[b_{r+1}-1,\dots ,b_m]$, as we aimed to demonstrate. Observe that if r is even, $p_{2i}/q_{2i}$ has a continued fraction expression $[{\alpha }_1,\dots ,{\alpha }_r+1]$, and the argumentation would be valid with the opposite sign $-q_{2i}·p+q·p_{2i}$.

It remains to verify the result for rational numbers:

$$\frac{p}{q}\in \left(\frac{a_i}{b_i}=[{\alpha }_1,\dots ,{\alpha }_r],\frac{p_{2i}}{q_{2i}}=[{\alpha }_1,\dots ,{\alpha }_r-1,2],\right).$$

In that case, the first r terms of the continued fraction of $p/q$ are determined as:

$$\frac{p}{q}=[{\alpha }_1,\dots ,{\alpha }_r-1,1,b_{r+2},\dots ,b_m].$$

Reproducing the scheme of the demonstration in the last case, we obtain

$$\begin{array}{ccc}\hfill -q_{2i}·p+q·p_{2i}& =& -K({\alpha }_1,\dots ,{\alpha }_r-1,2)·K({\alpha }_2,\dots ,{\alpha }_r-1,1,b_{r+2},\dots ,b_m)\hfill \\ & & +K({\alpha }_1,\dots ,{\alpha }_r-1,1,b_{r+2},\dots ,b_m)·K({\alpha }_2,\dots ,{\alpha }_r-1,2)\hfill \\ & =& -K({\alpha }_1,\dots ,{\alpha }_r-1,2)·\left[K({\alpha }_2,\dots ,{\alpha }_r-1,1)·K(b_{r+2},\dots ,b_m)\right.\hfill \\ & & +\left.K({\alpha }_2,\dots ,{\alpha }_r-1)·K(b_{r+3},\dots ,b_m)\right]\hfill \\ & & +K({\alpha }_2,\dots ,{\alpha }_r-1,2)·\left[K({\alpha }_1,\dots ,{\alpha }_r-1,1)·K(b_{r+2},\dots ,b_m)\right.\hfill \\ & & +\left.K({\alpha }_1,\dots ,{\alpha }_r-1)·K(b_{r+3},\dots ,b_m)\right]\hfill \\ & =& -K(b_{r+2},\dots ,b_m)·\left[K({\alpha }_1,\dots ,{\alpha }_r-1,2)·K({\alpha }_2,\dots ,{\alpha }_r)\right.\hfill \\ & & \left.-K({\alpha }_2,\dots ,{\alpha }_r-1,2)·K({\alpha }_1,\dots ,{\alpha }_r)\right]\hfill \\ & & +K(b_{r+3},\dots ,b_m)·\left[K({\alpha }_2,\dots ,{\alpha }_r-1,2)·K({\alpha }_1,\dots ,{\alpha }_r-1)\right.\hfill \\ & & \left.-K({\alpha }_1,\dots ,{\alpha }_{r-1},2)·K({\alpha }_2,\dots ,{\alpha }_r-1)\right].\hfill \end{array}$$

(A18)

Using the definition (A8) for $K({\alpha }_1,\dots ,{\alpha }_r-1,2)$, we have:

$$\begin{array}{ccc}\hfill K({\alpha }_1,\dots ,{\alpha }_r-1,2)& =& 2·K({\alpha }_1,\dots ,{\alpha }_r-1)+K({\alpha }_1,\dots ,{\alpha }_{r-1})\hfill \\ & =& 2·\left[({\alpha }_r-1)·K({\alpha }_1,\dots ,{\alpha }_{r-1})+K({\alpha }_1,\dots ,{\alpha }_{r-2})\right]+K({\alpha }_1,\dots ,{\alpha }_{r-1})\hfill \\ & =& 2·\left({\alpha }_r\right)·K({\alpha }_1,\dots ,{\alpha }_{r-1})-2·K({\alpha }_1,\dots ,{\alpha }_{r-1})\hfill \\ & & +2·K({\alpha }_1,\dots ,{\alpha }_{r-2})+K({\alpha }_1,\dots ,{\alpha }_{r-1})\hfill \\ & =& 2·\left({\alpha }_r\right)·K({\alpha }_1,\dots ,{\alpha }_{r-1})-K({\alpha }_1,\dots ,{\alpha }_{r-1})+2·K({\alpha }_1,\dots ,{\alpha }_{r-2})\hfill \\ & =& 2·K({\alpha }_1,\dots ,{\alpha }_r)-K({\alpha }_1,\dots ,{\alpha }_{r-1}).\hfill \end{array}$$

(A19)

The first bracket in Equation (A18) is now:

$$\begin{array}{c}\hfill K({\alpha }_1,\dots ,{\alpha }_r-1,2)·K({\alpha }_2,\dots ,{\alpha }_r)-K({\alpha }_2,\dots ,{\alpha }_r-1,2)·K({\alpha }_1,\dots ,{\alpha }_r)\\ \hfill =2·K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_r)-K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r)\\ \hfill -2·K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_r)+K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_r)\\ \hfill =K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_r)-K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r)\\ \hfill ={(-1)}^r=-1.\end{array}$$

In addition, the second bracket requires the following equality:

$$K({\alpha }_1,\dots ,{\alpha }_r-1)=K({\alpha }_1,\dots ,{\alpha }_r)-K({\alpha }_1,\dots ,{\alpha }_{r-1}),$$

resulting in:

$$\begin{array}{c}\hfill K({\alpha }_2,\dots ,{\alpha }_r-1,2)·K({\alpha }_1,\dots ,{\alpha }_r-1)-K({\alpha }_1,\dots ,{\alpha }_r-1,2)·K({\alpha }_2,\dots ,{\alpha }_r-1)\\ \hfill =2·K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_r-1)-K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_r-1)\\ \hfill -2·K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_r-1)+K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r-1)\\ \hfill =2·K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_r)-2·K({\alpha }_2,\dots ,{\alpha }_r)·K({\alpha }_1,\dots ,{\alpha }_{r-1})\\ \hfill -K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_r)+K({\alpha }_2,\dots ,{\alpha }_{r-1})·K({\alpha }_1,\dots ,{\alpha }_{r-1})\\ \hfill -2·K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_r)+2·K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_{r-1})\\ \hfill +K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r)-K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_{r-1})\\ \hfill =K({\alpha }_1,\dots ,{\alpha }_r)·K({\alpha }_2,\dots ,{\alpha }_{r-1})-K({\alpha }_1,\dots ,{\alpha }_{r-1})·K({\alpha }_2,\dots ,{\alpha }_r)\\ \hfill ={(-1)}^r=-1.\end{array}$$

Thus, Equation (A18) is simplified as:

$$\begin{array}{c}\hfill -q_{2i}·p+q·p_{2i}=K(b_{r+2},\dots ,b_m)-K(b_{r+3},\dots ,b_m)=K(b_{r+2}-1,b_{r+3},\dots ,b_m),\end{array}$$

i.e., it is the denominator of the continued fraction $[b_{r+2}-1,\dots ,b_m]$, or equivalently, $s^{(r+1)}$ for $k={\sum }_{i=1}^{r-1}{\alpha }_i+({\alpha }_r-1)+1+3={\sum }_{i=1}^r{\alpha }_i+3$, as we want to demonstrate. To conclude, if r is even, then $p_{2i-1}/q_{2i-1}=[{\alpha }_1,\dots ,{\alpha }_r-1,2]$, and changing the sign to equality $q_{2i-1}·p-q·p_{2i-1}$ results in equivalent reasoning. □