Performance Analysis of Regularized Convex Relaxation for Complex-Valued Data Detection

Abstract

In this work, we study complex-valued data detection performance in massive multiple-input multiple-output (MIMO) systems. We focus on the problem of recovering an n-dimensional signal whose entries are drawn from an arbitrary constellation $\mathcal{K}\subset \mathbb{C}$ from m noisy linear measurements, with an independent and identically distributed (i.i.d.) complex Gaussian channel. Since the optimal maximum likelihood (ML) detector is computationally prohibitive for large dimensions, many convex relaxation heuristic methods have been proposed to solve the detection problem. In this paper, we consider a regularized version of this convex relaxation that we call the regularized convex relaxation (RCR) detector and sharply derive asymptotic expressions for its mean square error and symbol error probability. Monte-Carlo simulations are provided to validate the derived analytical results.

1. Introduction

Detection of complex-valued data from noisy linear measurements appears often in many communication applications, such as massive multiple-input multiple-output (MIMO) signal detection [1], multiuser detection [2], decoding of space-time codes [3], etc. In this work, we consider the problem of recovering an n-dimensional complex-valued signal whose entries are drawn from an arbitrary constellation $\mathcal{K}\subset \mathbb{C}$ from m noisy linear measurements in a massive MIMO application. Although the maximum likelihood (ML) detector can achieve excellent performance, its computational complexity becomes prohibitive as the problem size increases [2]. To achieve an acceptable performance with a low computing complexity, various convex optimization-based heuristics have been developed. One popular convex relaxation approach of the ML is the box-relaxation used in [4,5]. Regularization-based techniques have been employed in [6,7] to further improve the performance of the box-relaxation in massive MIMO applications. Sparsity-aware regularization methods based on ideas from compressed sensing were used in [8,9,10]. Sum of absolute values (SOAV) optimization [11] uses a similar sparsity-based approach, and has been applied in many wireless communication problems [12,13,14].

There are a few theoretical analysis approaches for the convex optimization-based signal reconstruction problems. One of the main technical tool used in the sharp asymptotic analysis of such problems is the convex Gaussian min-max theorem (CGMT) framework [15,16]. The CGMT has been used to analyze the performance of various optimization problems [4,6,7,8,12,15,17]. However, prior performance analysis using the CGMT was only established for real-valued constellations such as binary phase-shift keying (BPSK) and pulse amplitude modulation (PAM) using the box-relaxation method [4]. For the complex-valued constellations, to the best of our knowledge, the CGMT was only applied in one work [5], which considers the performance of convex-relaxation, but without regularization.

The heuristic method proposed in this work is to relax the discrete set $\mathcal{K}$ to a convex and continuous set $\mathcal{V}$, and then solve the detection problem using a regularized convex optimization program followed by hard-thresholding. We call this method the regularized convex relaxation (RCR) detector, and we sharply analyze its asymptotic performance in terms of its mean square error (MSE) and symbol error probability (SEP) in the limit of $m\to \infty \mathrm{and}n\to \infty$ with a fixed rate. Furthermore, we will show the additional performance gains attained by adding the convex relaxation constraint. We assume an independent and identically distributed (i.i.d.) complex Gaussian channel matrix and additive white Gaussian noise. Our results also enable us to select the optimal regularization factor to further improve the detection performance. As a concrete example, we focus our attention on studying the performance of the RCR detector for phase-shift keying (PSK) and quadrature amplitude modulation (QAM) constellations. Monte-Carlo simulations are provided to validate our analytical expressions.

2. Problem Formulation

2.1. Notation

The basic notations used throughout this article are gathered here. We use $\mathbb{R}$ and $\mathbb{C}$ to represent the sets of real and complex numbers, respectively. In addition, ${\mathbb{Z}}_{+}$ is used to indicate the set of positive integers. For a complex scalar $z\in \mathbb{C}$, $z_R$, and $z_I$ represent the real and imaginary parts of z, respectively, and $\left|z\right|=\sqrt{z_R^2+z_I^2}$. We use the letter j to denote the complex unit, i.e., $j^2=-1$. A real Gaussian distribution with mean $\mu$ and variance ${\sigma }^2$ is indicated by $\mathcal{N}(\mu ,{\sigma }^2)$. Similarly, $\mathcal{CN}(\mu ,{\sigma }^2)$ indicates a complex Gaussian distribution with real and imaginary parts drawn independently from $\mathcal{N}({\mu }_R,\frac{{\sigma }^2}{2})$ and $\mathcal{N}({\mu }_I,\frac{{\sigma }^2}{2})$, respectively. $X\sim p_X$ implies that the random variable X has a density $p_X$. Bold lower-case letters are reserved for vectors, e.g., $\mathit{x}$, with $x_i$ denoting its i-th entry. The Euclidean norm of a vector is denoted by $\parallel ·\parallel$. Matrices are represented by bold upper-case letters, e.g., $\mathit{A}$, while ${(·)}^{\top }$ represents the transpose operator. We reserve the letters G and Z to denote independent real standard Gaussian random variables. Similarly, $G_c$ is reserved to denote a complex $\mathcal{CN}(0,2)$ Gaussian random variable. Notations $\mathbb{E}[·]$ and $\mathbb{P}(·)$ indicate the expectation and probability operators, respectively. Symbols “$\stackrel{d}{=}$” and “$\stackrel{P}{⟶}$” are used to designate equivalence in distribution, and convergence in probability, respectively. Finally, for a closed and nonempty convex set $\mathcal{V}\subset \mathbb{C}$, and for any vector $\mathit{x}\in {\mathbb{C}}^n$, we define its distance and projection functions, respectively, as follows

$$\begin{array}{c}\hfill \mathcal{D}(\mathit{x};\mathcal{V})=\underset{\mathit{a}\in {\mathcal{V}}^n}{min}\parallel \mathit{x}-\mathit{a}\parallel ,\end{array}$$

(1)

$$\begin{array}{c}\hfill \mathsf{\Pi }(\mathit{x};\mathcal{V})=\arg \underset{\mathit{a}\in {\mathcal{V}}^n}{min}\parallel \mathit{x}-\mathit{a}\parallel .\end{array}$$

(2)

2.2. Problem Setup

We need to recover an n-dimensional complex-valued transmit vector ${\mathit{s}}_0\in {\mathcal{K}}^n\subset {\mathbb{C}}^n$, where $\mathcal{K}$ is the discrete transmit modulation constellation (e.g., PSK, QAM, etc.). The received signal vector $\mathit{r}\in {\mathbb{C}}^m$ is given by

$$\begin{array}{c}\hfill \mathit{r}=\mathit{H}{\mathit{s}}_0+\mathit{v},\end{array}$$

(3)

where $\mathit{H}\in {\mathbb{C}}^{m\times n}$ is the MIMO channel matrix that has $\mathcal{CN}(0,\frac{1}{n})$ i.i.d. entries and $\mathit{v}\in {\mathbb{C}}^m$ is the noise vector with $\mathcal{CN}(0,{\sigma }^2)$ i.i.d. entries. Under the current setup, the signal-to-noise ratio (SNR) is $\mathrm{SNR}$$=1/{\sigma }^2$.

Detector: The optimum detector that minimizes the error rate is proven to be the maximum likelihood (ML) detector [2], which solves the following optimization problem

$$\begin{array}{c}\hfill {\widehat{\mathit{s}}}_{\mathrm{ML}}:=\arg \underset{\mathit{s}\in {\mathcal{K}}^n}{min}\frac{1}{2}{\parallel \mathit{H}\mathit{s}-\mathit{r}\parallel }^2.\end{array}$$

(4)

This is computationally prohibitive in the considered massive MIMO setup; due to the discreteness nature of the constraints set $\mathcal{K}$. Instead, in this paper, we consider the regularized convex relaxation (RCR) detector. The RCR recovers $\mathit{s}$ following the next two steps:

$$\begin{array}{cc}\hfill & \widehat{\mathit{s}}:=\arg \underset{\mathit{s}\in {\mathcal{V}}^n}{min}\frac{1}{2}{\parallel \mathit{H}\mathit{s}-\mathit{r}\parallel }^2+\frac{\zeta }{2}{\parallel \mathit{s}\parallel }^2,\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill & s_i^{★}:=\arg \underset{c\in \mathcal{K}}{min}|c-{\widehat{s}}_i|,i=1,2,\cdots ,n,\hfill \end{array}$$

(5b)

where in the first step (5a), the discrete set $\mathcal{K}$ is relaxed to a convex set $\mathcal{V}$, and then we solve a regularized version of this relaxed problem with $\zeta >0$ being the regularization factor. In the second step (5b), each entry of $\widehat{\mathit{s}}$ is mapped to its closest point in $\mathcal{K}$ to produce the final estimate ${\mathit{s}}^{★}$.

2.3. Performance Measures

In this paper, we provide sharp performance analysis of the RCR detector in terms of the problem parameters such as $\mathrm{SNR}$, $\zeta ,m,n$, $\mathcal{K}$ and $\mathcal{V}$. We will consider two different performance measures, namely the MSE and the SEP discussed next.

Mean Square Error (MSE): this metric is used to quantify the performance of the estimation step in (5a). It is defined as follows:

$$\begin{array}{c}\hfill \mathrm{MSE}:=\frac{1}{n}{\parallel {\mathit{s}}_0-\widehat{\mathit{s}}\parallel }^2.\end{array}$$

(6)

Another important performance metric is the symbol error probability.

Symbol Error Probability (SEP): the symbol error rate (SER) analyzes the performance of the second (detection) step in (5b), and it is defined as:

$$\mathrm{SER}:=\frac{1}{n}\sum _{i=1}^n{\mathrm{𝟙}}_{\{s_i^{★}\ne s_{0,i}\}},$$

(7)

where ${\mathrm{𝟙}}_{\{·\}}$ represents the indicator function.

Another interesting related measure is the symbol error probability (SEP) that is given as

$$\mathrm{SEP}:=\mathbb{E}\left[\mathrm{SER}\right]=\frac{1}{n}\sum _{i=1}^n\mathbb{P}\left(s_i^{★}\ne s_{0,i}\right),$$

(8)

where the expectation is taken over the channel, the noise and the signal constellation.

Next, we introduce the notation ${\mathcal{V}}_x$ for $x\in \mathcal{K}$, as the set of all points in $\mathcal{V}$ that will be mapped to x in (5b). Equivalently

$${\mathcal{V}}_x:=\left\{b\in \mathcal{V}:\forall a\in \mathcal{K},|b-x|<|b-a|\right\}.$$

(9)

With this notation at hand, we can rewrite the $\mathrm{SEP}$ in (8) as

$$\mathrm{SEP}=\frac{1}{n}\sum _{i=1}^n\mathbb{P}\left({\widehat{s}}_i\notin {\mathcal{V}}_{s_{0,i}}\right),$$

(10)

where ${\widehat{s}}_i$ is a minimizer of (5a).

2.4. Technical Assumptions

We assume that the entries of ${\mathit{s}}_0$ are sampled i.i.d. from a probability density function $p_{s_0}$, with $\mathbb{P}(b_1+j{b}_2)=\mathbb{P}(b_2+j{b}_1),\forall b_1,b_2\in \mathbb{R}$. Furthermore, we assume that ${\mathit{s}}_0$ is normalized to have zero-mean and unit-variance, i.e., $\mathbb{E}\left[S_0\right]=0$, and $\mathbb{E}\left[S_0^2\right]=1$. The convex set $\mathcal{V}$ is assumed to be symmetric, i.e., if $(b_1+j{b}_2)\in \mathcal{V}$, then $(b_2+j{b}_1)\in \mathcal{V}$ as well. Finally, we assume a high-dimensional regime in which $m\to \infty ,\mathrm{and}n\to \infty$ with a proportional rate $\kappa :=\frac{m}{n}\in (0,\infty )$.

3. Asymptotic Performance Analysis

3.1. Main Asymptotic Results

This section provides our main results on the performance evaluation of the RCR detector in the considered high dimensional setting.

Theorem 1

(Asymptotics of the RCR). Let $\mathrm{MSE}$, and $\mathrm{SEP}$ be the mean square error and symbol error probability of the RCR detector in (5), respectively, for an unknown signal ${\mathit{s}}_0\in {\mathcal{K}}^n$ with entries sampled i.i.d. from a distribution $p_{s_0}$. Let $\mathcal{V}$ be a convex relaxation of $\mathcal{K}$ that satisfies the assumption of Section 2.4. For fixed $\zeta \ge 0$, and $\kappa >0$, if following optimization problem

$$\begin{array}{cc}\hfill \underset{\alpha >0}{min}\underset{\beta >0}{max}& \kappa \alpha \beta -\frac{{\beta }^2}{2}-\frac{\alpha {\beta }^2}{\beta +2\zeta \alpha }+\frac{\beta }{2\alpha }\left({\sigma }^2+1\right)-\frac{{\beta }^2}{2\alpha \beta +4\zeta {\alpha }^2}\hfill \\ \hfill & +\left(\frac{\beta }{2\alpha }+\zeta \right)\mathbb{E}\left[{\mathcal{D}}^2\left(\frac{\beta }{\beta +2\zeta \alpha }\left(S_0-\alpha G_c\right);\mathcal{V}\right)\right]\hfill \end{array}$$

(11)

has a unique solution $({\alpha }_{*},{\beta }_{*})$, then it holds in probability that

$$\underset{n\to \infty }{lim}\mathrm{MSE}=2\kappa {\alpha }_{*}^2-{\sigma }^2,$$

(12)

and

$$\underset{n\to \infty }{lim}\mathrm{SEP}=\mathbb{P}\left(\mathsf{\Pi }\left(\frac{{\beta }_{*}}{{\beta }_{*}+2\zeta {\alpha }_{*}}\left(S_0-{\alpha }_{*}{G}_c\right);\mathcal{V}\right)\notin {\mathcal{V}}_{S_0}\right),$$

(13)

where the expectation and probability in the above expressions are taken over $S_0$∼$p_{s_0}$ and $G_c$∼$\mathcal{CN}(0,2)$. Here, $\mathcal{D}(·)$ and $\mathsf{\Pi }(·)$ are the distance and projection functions defined in (1) and (2), respectively. In addition, the set ${\mathcal{V}}_{S_0}$ is as defined in (9).

Proof. 

See Section 5. □

Theorem 1 provides high dimensional asymptotic expressions to calculate the MSE and SEP of the RCR detector under an arbitrary complex-valued constellation.

Remark 1.

The objective function in (11) is convex-concave and only includes scalar variables. Thus, first-order optimality conditions may be used to efficiently calculate ${\alpha }_{*}$ and ${\beta }_{*}$ numerically.

3.2. Modulation Schemes

Using Theorem 1, we can sharply characterize the performance of the RCR detector for a general complex-valued constellation $\mathcal{K}$, which can be relaxed to an arbitrary convex set $\mathcal{V}$. To better comprehend our result and demonstrate how to adapt it to different schemes, we will concentrate on two conventional schemes, PSK and QAM constellations, which will be addressed next.

3.2.1. M-PSK Constellation

In an M-PSK constellation, where $M=2^k$, for some $k\in {\mathbb{Z}}_{+}$, each entry of ${\mathit{s}}_0$ is randomly drawn from the set

$$\mathcal{K}=\left\{exp\left(\frac{2\pi i}{M}\right),i=0,1,\cdots ,M-1\right\},M\ge 4.$$

Note that this work focuses on complex-constellations, but the “$M=2$”-case corresponds to the real-valued BPSK constellation, which has already been studied in [6]. The elements of $\mathcal{K}$ are uniformly distributed over the unit circle in the complex plane, and therefore we suggest the use of the so-called circular-relaxation (CR), where we choose the set

$$\begin{array}{c}\hfill {\mathcal{V}}^{\mathrm{CR}}=\{x\in \mathbb{C}:|x|\le 1\}\end{array}$$

(14)

as the convex relaxation set in (5a). The projection function on this set has the following form:

$$\begin{array}{c}\hfill \mathsf{\Pi }(\mathit{x};{\mathcal{V}}^{\mathrm{CR}})=\left\{\begin{array}{c}\mathit{x},\mathrm{if}\left|\mathit{x}\right|\le 1\hfill \\ \frac{\mathit{x}}{\left|\mathit{x}\right|},\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(15)

Due to the symmetric nature of the M-PSK constellation, the asymptotic $\mathrm{SEP}$ can be derived in the following closed-form:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\mathrm{SEP}=\mathbb{P}\left(\left|\frac{Z}{G-\frac{1}{{\alpha }_{*}}}\right|\ge tan\left(\frac{\pi }{M}\right)\right),\end{array}$$

(16)

where Z and G are i.i.d. $\mathcal{N}(0,1)$ random variables.

3.2.2. M-QAM Constellation

In this paper, we will only consider square QAM constellations, where $M=2^{2k}$, such as 4-QAM, 16-QAM, 64-QAM, etc. Then, the constellation set is given by

$$\begin{array}{c}\hfill \mathcal{K}=\left\{(a+jb)\in \mathbb{C}:a,b\in \left\{\frac{-(\sqrt{M}-1)}{\sqrt{E_{\mathrm{avg}}}},\frac{-(\sqrt{M}-3)}{\sqrt{E_{\mathrm{avg}}}},\cdots ,\frac{\sqrt{M}-1}{\sqrt{E_{\mathrm{avg}}}}\right\}\right\},\end{array}$$

(17)

where we normalize the constellation points by $E_{\mathrm{avg}}:=\frac{2(M-1)}{3}$; to have unit average power. ($E_{\mathrm{avg}}$ represents the average power of the non-normalized M-QAM symbols.) The convex relaxation that is often used for this modulation is known as the box-relaxation (BR) [4] which is given as

$$\begin{array}{c}\hfill {\mathcal{V}}^{\mathrm{BR}}=\left\{(a+jb)\in \mathbb{C}:\left|a\right|\le \frac{\sqrt{M}-1}{\sqrt{E_{\mathrm{avg}}}},\left|b\right|\le \frac{\sqrt{M}-1}{\sqrt{E_{\mathrm{avg}}}}\right\}.\end{array}$$

(18)

Similar to the preceding subsection, to apply Theorem 1, we must first construct the projection and distance functions of ${\mathcal{V}}^{\mathrm{BR}}$, which is straightforward for a box set. Then, the $\mathrm{SEP}$ can be calculated using (13). In this scenario, unlike in the M-PSK case, the SEP of the detector is not the same for various symbols in $\mathcal{K}$; this is due to the fact that an M-QAM constellation includes distinct types of points, namely inner, edge, and corner points.

4. Numerical Simulation Results

In Figure 1, we plotted the MSE and SEP performances as functions of the regularizer $\zeta$ for a 16-QAM constellation with BR. These figures verify the accuracy of the prediction of Theorem 1 when compared to Monte-Carlo (MC) empirical simulations. In addition, from those figures we can see a clear minimum value of $\zeta$ that gives the best MSE and SEP performance. Thus, Theorem 1 can be used to select the optimum value of the regularizer.

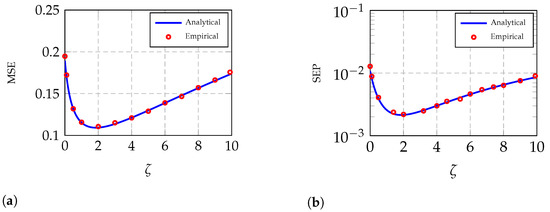
Figure 1. MSE and SEP versus the regularizer for 16-QAM with Box-Relaxation (BR), with $\kappa =1.5,n=128,\mathrm{SNR}=15\mathrm{dB}$. The analytical curve is based on Theorem 1. The data are averaged over 50 independent MC trials. (a) MSE performance vs. the regularizer. (b) SEP performance vs. the regularizer.

Furthermore, Figure 2 verifies the accuracy of the MSE and SEP predictions of Theorem 1 as functions of the SNR, for a 16-PSK modulation scheme with circular relaxation. It is worth noting that, while the theorem requires $m\to \infty \mathrm{and}n\to \infty$, the theoretical predictions already are precise for moderate size of the problem, in this simulation $n=128$. In this figure, we also plotted the unconstrained regularized least-squares (RLS) (without convex relaxation, i.e., $\mathcal{V}=\mathbb{R}$). Besides, it can be seen that the RCR detector outperforms the RLS.

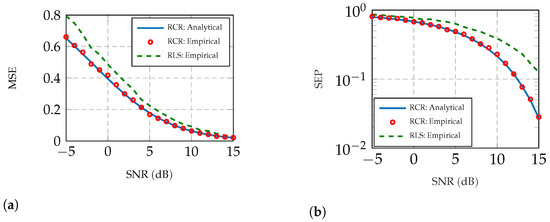
Figure 2. Performance of the Circular-Relaxation (CR) for a 16-PSK signal vector as a function of the SNR. The analytical curve is based on Theorem 1. For the empirical simulations, we used $\kappa =2,n=128$, and data are averaged over 50 independent MC iterations. (a) MSE performance. (b) SEP performance.

Furthermore, under a box-relaxation, we apply Theorem 1 to sharply characterize the MSE and SEP of a 16-QAM modulated system as functions of the SNR. The result is shown in Figure 3, which again illustrates the high accuracy of our results, as well as that RCR detector outperforms the RLS.

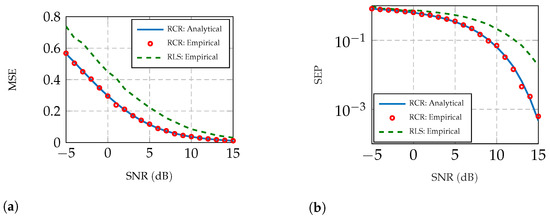
Figure 3. Box-Relaxation (BR) performance for 16-QAM. The analytical prediction is based on Theorem 1. We used $\kappa =2,n=128$ and data are averaged over 50 independent MC trials. (a) MSE performance vs. SNR. (b) SEP performance vs. SNR.

Finally, we should point out that in all of the numerical simulations illustrated above, we considered overdetermined systems, i.e., $\kappa >1$. We conclude this section by presenting another simulation example for an underdetermined system, with $\kappa =0.8$, while all other parameters are the same as in the previous example. The MSE performance is summarized in Table 1. This table confirms the sharpness of our predictions for underdetermined systems as well.

Table 1. MSE performance of RCR and RLS detectors. We used a 16-QAM signal vector with BR. We set $\kappa =0.8,n=128$, and the data are averaged over 50 independent MC iterations.

SNR (dB)	MSE (RCR): Analytical	MSE (RCR): Empirical	MSE (RLS): Empirical
0	$0.4932$	$0.4894$	$0.6446$
5	$0.3323$	$0.3411$	$0.3801$
10	$0.2104$	$0.2085$	$0.2993$
15	$0.1212$	$0.1295$	$0.2395$
20	$0.0492$	$0.0513$	$0.2227$

5. Sketch of the Proof

In this section, we provide a sketch of the proof of Theorem 1. For the reader’s convenient, we summarize the main tool used in our analysis, namely the CGMT, in the next subsection.

5.1. CGMT: An Analysis Tool

We must first identify the analysis’s key component, which is the CGMT. We only summarize the theorem’s formulation here, and we recommend the reader to [4,15] for the full technical prerequisites. In particular, let us consider the following (stochastic) optimization problems, which are called the primal optimization (PO) problem and the auxiliary optimization (AO) problem, respectively.

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\mathit{X}\right):=\underset{\mathit{a}\in {\mathcal{S}}_{\mathit{a}}}{min}\underset{\mathit{b}\in {\mathcal{S}}_{\mathit{b}}}{max}{\mathit{b}}^{\top }\mathit{X}\mathit{a}+\mathcal{T}(\mathit{a},\mathit{b}),\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill & \psi ({\mathit{g}}_1,{\mathit{g}}_2):=\underset{\mathit{a}\in {\mathcal{S}}_{\mathit{a}}}{min}\underset{\mathit{b}\in {\mathcal{S}}_{\mathit{b}}}{max}\parallel \mathit{a}\parallel {\mathit{g}}_1^{\top }\mathit{b}+\parallel \mathit{b}\parallel {\mathit{g}}_2^{\top }\mathit{a}+\mathcal{T}(\mathit{a},\mathit{b}),\hfill \end{array}$$

(19b)

where $\mathit{X}\in {\mathbb{R}}^{\tilde{m}\times \tilde{n}},{\mathit{g}}_1\in {\mathbb{R}}^{\tilde{m}}$, and ${\mathit{g}}_2\in {\mathbb{R}}^{\tilde{n}}$ all have i.i.d. standard Gaussian elements. The sets ${\mathcal{S}}_{\mathit{a}}\subset {\mathbb{R}}^{\tilde{n}},{\mathcal{S}}_{\mathit{b}}\subset {\mathbb{R}}^{\tilde{m}}$ are assumed to be be convex and compact sets, and $\mathcal{T}:{\mathbb{R}}^{\tilde{n}}\times {\mathbb{R}}^{\tilde{m}}\mapsto \mathbb{R}$. Moreover, we assume that the function $\mathcal{T}$ is independent $\mathit{X}$. Let ${\mathit{a}}_{\mathsf{\Psi }}:={\mathit{a}}_{\mathsf{\Psi }}\left(\mathit{X}\right)$, and ${\mathit{a}}_{\psi }:={\mathit{a}}_{\psi }({\mathit{g}}_1,{\mathit{g}}_2)$ be any optimizers of (19a) and (19b), respectively. In addition, let $\mathcal{T}(\mathit{a},\mathit{b})$ be convex-concave continuous on ${\mathcal{S}}_{\mathit{a}}\times {\mathcal{S}}_{\mathit{b}}$.

Based on the assumptions stated above, the CGMT shows an asymptotic equivalence between the PO and AO problems, which is explicitly expressed in the following theorem. This theorem’s proof may be found in [15].

Theorem 2

(CGMT [4]). Suppose $\mathcal{S}$ is an arbitrary open subset of ${\mathcal{S}}_{\mathit{a}}$, and ${\mathcal{S}}^c={\mathcal{S}}_{\mathit{a}}\backslash \mathcal{S}$. Let ${\psi }_{{\mathcal{S}}^c}({\mathit{g}}_1,{\mathit{g}}_2)$ be the optimal objective of the optimization in (19b), when the minimization over $\mathit{a}$ is constrained over $\mathit{a}\in {\mathcal{S}}^c$. Suppose that there exist positive constants $\eta <\delta$, such that in the limit of $\tilde{n}\to \infty$: $\psi ({\mathit{g}}_1,{\mathit{g}}_2)\stackrel{P}{⟶}\eta$, and ${\psi }_{{\mathcal{S}}^c}({\mathit{g}}_1,{\mathit{g}}_2)\stackrel{P}{⟶}\delta$. Then, it holds

$$\underset{\tilde{n}\to \infty }{lim}\mathbb{P}({\mathit{a}}_{\mathsf{\Psi }}\in \mathcal{S})=1.$$

(20)

It also holds that ${lim}_{\tilde{n}\to \infty }\mathbb{P}({\mathit{a}}_{\psi }\in \mathcal{S})=1.$

5.2. Asymptotic Analysis

In this part, we provide an outline of the ideas used to prove our main results based on the CGMT framework. We start by rewriting (5a) by a simple change of variables from $\mathit{s}$ to the error vector $\mathit{w}:=\mathit{s}-{\mathit{s}}_0$, to get:

$$\begin{array}{c}\hfill \widehat{\mathit{w}}:=\arg \underset{\mathit{w}\in {\mathcal{V}}^n-{\mathit{s}}_0}{min}\frac{1}{2}{\parallel \mathit{H}\mathit{w}-\mathit{v}\parallel }^2+\frac{\zeta }{2}{\parallel \mathit{w}+{\mathit{s}}_0\parallel }^2.\end{array}$$

(21)

Next, let $\tilde{\mathit{H}}:=\left[\begin{array}{cc}{\mathit{H}}_R& -{\mathit{H}}_I\\ {\mathit{H}}_I& {\mathit{H}}_R\end{array}\right]\in {\mathbb{R}}^{2m\times 2n}$, and $\tilde{\mathit{v}}:=\left[\begin{array}{c}{\mathit{v}}_R\\ {\mathit{v}}_I\end{array}\right]\in {\mathbb{R}}^{2m}$, where ${\mathit{H}}_R,{\mathit{v}}_R$ (${\mathit{H}}_I,{\mathit{v}}_I$) are the real (imaginary) parts of $\mathit{H}$ and $\mathit{v}$, respectively. With this, and normalizing (21) by $\frac{1}{n}$, we have

$$\begin{array}{c}\hfill \widehat{\mathit{w}}:=\underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-{\mathit{s}}_{0,i}\end{array}}{arg\; min}\frac{1}{2n}\parallel \frac{1}{\sqrt{2n}}\tilde{\mathit{H}}\tilde{\mathit{w}}-\tilde{\mathit{v}}{\parallel }^2+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2,\end{array}$$

(22)

where ${\tilde{\mathit{s}}}_0:=\left[\begin{array}{c}{\mathit{s}}_{0,R}\\ {\mathit{s}}_{0,I}\end{array}\right]\in {\mathbb{R}}^{2n}$. Because of the dependence between the entries of $\tilde{\mathit{H}}$, the above optimization is difficult to analyze and the CGMT framework cannot be used directly here. However, as discussed in [5], one can use Lindeberg methods as in [18] to replace $\tilde{\mathit{H}}$ with a Gaussian matrix that has i.i.d. entries without affecting the asymptotic performance, then we obtain

$$\begin{array}{c}\hfill \widehat{\mathit{w}}=\underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{arg\; min}\frac{1}{2n}\parallel \frac{1}{\sqrt{2n}}\mathit{A}\tilde{\mathit{w}}-\tilde{\mathit{v}}{\parallel }^2+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2,\end{array}$$

(23)

where $\mathit{A}\in {\mathbb{R}}^{2m\times 2n}$ has i.i.d. $\mathcal{N}(0,1)$ components, and $\tilde{\mathit{v}}$ has i.i.d. $\mathcal{N}(0,\frac{{\sigma }^2}{2})$ elements. Next, we proceed to apply the CGMT by rewriting (23) as the following min-max optimization:

$$\begin{array}{c}\hfill \underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}\underset{\mathit{u}\in {\mathbb{R}}^{2m}}{max}\frac{{\mathit{u}}^{\top }\mathit{A}\tilde{\mathit{w}}}{2n\sqrt{2n}}-\frac{{\mathit{u}}^{\top }\tilde{\mathit{v}}}{2n}-\frac{{\parallel \mathit{u}\parallel }^2}{8n}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2.\end{array}$$

(24)

A remaining technical caveat is that the maximization over $\mathit{u}$ appears unconstrained, i.e., the feasibility set over $\mathit{u}$ is not compact. For this, we can follow the approach in [15] (Appendix A), by assuming that the maximizer of (24) satisfies $\parallel \widehat{\mathit{u}}\parallel \le B_{\mathit{u}}$, for a sufficiently large constant $B_{\mathit{u}}>0$, that is independent of n. This will not affect the optimization problem with high probability. Thus, we get the following problem

$$\begin{array}{c}\hfill \underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}\underset{\parallel \mathit{u}\parallel \le B_{\mathit{u}}}{max}\frac{{\mathit{u}}^{\top }\mathit{A}\tilde{\mathit{w}}}{2n\sqrt{2n}}-\frac{{\mathit{u}}^{\top }\tilde{\mathit{v}}}{2n}-\frac{{\parallel \mathit{u}\parallel }^2}{8n}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2.\end{array}$$

(25)

The above problem is in the form of a PO of the CGMT. Thus, the associated simplified AO problem is given as:

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}& \underset{\parallel \mathit{u}\parallel \le B_{\mathit{u}}}{max}\frac{\parallel \tilde{\mathit{w}}\parallel {\mathit{g}}_1^{\top }\mathit{u}}{2n\sqrt{2n}}+\frac{\parallel \mathit{u}\parallel {\mathit{g}}_2^{\top }\tilde{\mathit{w}}}{2n\sqrt{2n}}-\frac{{\mathit{u}}^{\top }\tilde{\mathit{v}}}{2n}-\frac{{\parallel \mathit{u}\parallel }^2}{8n}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2,\hfill \end{array}$$

(26)

where ${\mathit{g}}_1\in {\mathbb{R}}^{2m}$ and ${\mathit{g}}_2\in {\mathbb{R}}^{2n}$ have i.i.d. $\mathcal{N}(0,1)$ entries. With some abuse of notation on ${\mathit{g}}_1$, we can see that

$$\begin{array}{c}\hfill {\left(\frac{\parallel \tilde{\mathit{w}}\parallel }{\sqrt{2n}}{\mathit{g}}_1-\tilde{\mathit{v}}\right)}^{\top }\mathit{u}\stackrel{d}{=}{\mathit{g}}_1^{\top }\mathit{u}\sqrt{\frac{\parallel \tilde{\mathit{w}}{\parallel }^2}{2n}+\frac{{\sigma }^2}{2}}.\end{array}$$

(27)

Hence, (26) becomes

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}& \underset{\parallel \mathit{u}\parallel \le B_{\mathit{u}}}{max}{\mathit{g}}_1^{\top }\mathit{u}\sqrt{\frac{\parallel \tilde{\mathit{w}}{\parallel }^2}{2n}+\frac{{\sigma }^2}{2}}+\frac{\parallel \mathit{u}\parallel {\mathit{g}}_2^{\top }\tilde{\mathit{w}}}{2n\sqrt{2n}}-\frac{{\parallel \mathit{u}\parallel }^2}{8n}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2.\hfill \end{array}$$

(28)

Fixing $\beta :=\frac{\parallel \mathit{u}\parallel }{\sqrt{2n}}$, the optimization over $\mathit{u}$ simplifies to

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}& \underset{\beta >0}{max}\frac{\beta \parallel {\mathit{g}}_1\parallel }{\sqrt{2n}}\sqrt{\frac{\parallel \tilde{\mathit{w}}{\parallel }^2}{2n}+\frac{{\sigma }^2}{2}}+\frac{\beta {\mathit{g}}_2^{\top }\tilde{\mathit{w}}}{2n}-\frac{{\beta }^2}{4}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2.\hfill \end{array}$$

(29)

The square root in the above problem can be expressed using the following identity (Note that at optimality, ${\tau }_{*}=\chi$.)

$$\begin{array}{c}\hfill \chi =\underset{\tau >0}{min}\frac{1}{2}\left(\frac{{\chi }^2}{\tau }+\tau \right),\mathrm{for}\chi >0,\end{array}$$

(30)

which yields the following optimization problem

$$\begin{array}{cc}\hfill \underset{\tau >0}{min}\underset{\beta >0}{max}& \frac{\tau \beta \parallel {\mathit{g}}_1\parallel }{2\sqrt{2n}}+\frac{{\sigma }^2\parallel {\mathit{g}}_1\parallel \beta }{4\tau \sqrt{2n}}-\frac{{\beta }^2}{4}\hfill \\ \hfill & +\underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}\left\{\frac{\beta \parallel {\mathit{g}}_1\parallel }{2\tau \sqrt{2n}}\frac{\parallel \tilde{\mathit{w}}{\parallel }^2}{2n}+\frac{\beta {\mathit{g}}_2^{\top }\tilde{\mathit{w}}}{2n}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2\right\}.\hfill \end{array}$$

(31)

Using the weak law of large numbers (WLLN): $\frac{\parallel {\mathit{g}}_1\parallel }{\sqrt{2n}}\stackrel{P}{⟶}\sqrt{\kappa }$, then the previous problem reduces to

$$\begin{array}{cc}\hfill \underset{\tau >0}{min}\underset{\beta >0}{max}& \frac{\tau \beta \sqrt{\kappa }}{2}+\frac{{\sigma }^2\beta \sqrt{\kappa }}{4\tau }-\frac{{\beta }^2}{4}\hfill \\ \hfill & +\underset{\begin{array}{c}\tilde{\mathit{w}}\in {\mathbb{R}}^{2n}\\ {\tilde{w}}_i+j{\tilde{w}}_{i+n}\in \mathcal{V}-s_{0,i}\end{array}}{min}\left\{\frac{\beta \sqrt{\kappa }}{2\tau }\frac{\parallel \tilde{\mathit{w}}{\parallel }^2}{2n}+\frac{\beta {\mathit{g}}_2^{\top }\tilde{\mathit{w}}}{2n}+\frac{\zeta }{2n}{\parallel \tilde{\mathit{w}}+{\tilde{\mathit{s}}}_0\parallel }^2\right\}.\hfill \end{array}$$

(32)

Defining $\alpha :=\frac{\tau }{\sqrt{\kappa }}$, and by a completion of squares in the minimization over $\tilde{\mathit{w}}$, and using the WLLN, we obtain the following scalar (deterministic) optimization problem

$$\begin{array}{cc}\hfill \underset{\alpha >0}{min}\underset{\beta >0}{max}& \frac{\alpha \beta \kappa }{2}+\frac{{\sigma }^2\beta }{4\alpha }-\frac{{\beta }^2}{4}-\frac{{\beta }^2}{\frac{2\beta }{\alpha }+4\zeta }+\frac{1}{2}\left(\frac{\beta }{2\alpha }-\frac{\frac{{\beta }^2}{4{\alpha }^2}}{\frac{\beta }{2\alpha }+\zeta }\right)\hfill \\ \hfill & +\frac{1}{2}\left(\frac{\beta }{2\alpha }+\zeta \right)\mathbb{E}\left[{\mathcal{D}}^2\left(\frac{\frac{\beta }{2\alpha }}{\frac{\beta }{2\alpha }+\zeta }{S}_0-\frac{\beta }{\frac{\beta }{\alpha }+2\zeta }{G}_c;\mathcal{V}\right)\right],\hfill \end{array}$$

(33)

where the expectation in the above expression is taken over $S_0\sim p_{s_0}$ and $G_c\sim \mathcal{CN}(0,2)$.The $\mathrm{SEP}$ of $\widehat{\mathit{w}}$ in (23) can be derived in a similar way to the proof of [5] to get

$$\mathrm{SEP}\stackrel{P}{⟶}\mathbb{P}\left(\mathsf{\Pi }\left(\frac{\frac{{\beta }_{*}}{2{\alpha }_{*}}}{\frac{{\beta }_{*}}{2{\alpha }_{*}}+\zeta }{S}_0-\frac{{\beta }_{*}}{\frac{{\beta }_{*}}{{\alpha }_{*}}+2\zeta }{G}_c;\mathcal{V}\right)\notin {\mathcal{V}}_{S_0}\right),$$

(34)

where ${\alpha }_{*}$ and ${\beta }_{*}$ are optimizers of (33). Simplifying (33) and (34) concludes the proof of the SEP part of Theorem 1.

The MSE expression can be proven in a similar way by noting that

$$\begin{array}{c}\hfill \frac{\parallel \tilde{\mathit{w}}{\parallel }^2}{2n}+\frac{{\sigma }^2}{2}={\widehat{\tau }}_n^2,\end{array}$$

(35)

where ${\widehat{\tau }}_n$ is the solution of (32). Hence, using ${\widehat{\alpha }}_n=\frac{{\widehat{\tau }}_n}{\sqrt{\kappa }}$, and ${\widehat{\alpha }}_n\stackrel{P}{⟶}{\alpha }_{*}$, where ${\alpha }_{*}$ is the solution of (33), we conclude, by applying the CGMT, that

$$\begin{array}{c}\hfill \frac{\parallel \widehat{\mathit{w}}{\parallel }^2}{n}\stackrel{P}{⟶}2\kappa {\alpha }_{*}^2-{\sigma }^2,\end{array}$$

(36)

which completes the proof of the MSE part of Theorem 1.

6. Discussion and Conclusions

In this article, we provided sharp performance analysis of the regularized convex relaxation detector when used in complex-valued data detection. In particular, we studied its MSE and SEP performance in a massive MIMO application with arbitrary constellation schemes such as QAM and PSK. Numerical simulations show a close match to the obtained asymptotic results. In addition, the derived results can be used to optimally select the detector’s parameters such as the regularization factor. Furthermore, note that the asymptotic results of Theorem 1 depend only on the parameters of the problem such as the regularization factor $\zeta$, the SNR, the ratio of receive to transmit antennas $\kappa$, etc. Thus, given the derived asymptotic MSE or SEP expressions, one may predict the error performance of a wireless communication system as a function of these hyper-parameters in advance. This may lead to the design of efficient communication systems in an optimal manner. Furthermore, we showed that this convex relaxation outperforms the unconstrained regularized least-squares detector.