Curves on Non-Orientable Surfaces and Crosscap Transpositions

Abstract

Let $N_{g,n}$ be a non-orientable surface of genus g with n punctures and one boundary component. In this paper, we describe multicurves in $N_{g,n}$ making use of generalized Dynnikov coordinates, and give explicit formulae for the action of crosscap transpositions and their inverses on the set of multicurves in $N_{g,n}$ in terms of generalized Dynnikov coordinates. This provides a way to solve on non-orientable surfaces various dynamical and combinatorial problems that arise in the study of mapping class groups and Thurston’s theory of surface homeomorphisms, which were solved only on orientable surfaces before.

1. Introduction

Mapping class groups have been one of the most extensively studied topics in low-dimensional topology for over a century since the work of Dehn. Given a surface S, the mapping class group $MCG\left(S\right)$ is the group of isotopy classes of all homeomorphisms (orientation preserving if S is orientable) of S and is generated by Dehn twists in the case where S is orientable [1]. However, Lickorish [2] showed that when S is non-orientable, $MCG\left(S\right)$ is not generated by Dehn twists alone but Dehn twists about two-sided simple closed curves and crosscap slides [2]; see, for instance [1,3], for the descriptions of generators of $MCG\left(S\right)$. An element of $MCG\left(S\right)$ is called a mapping class. A crosscap transposition is a mapping class of a non-orientable surface represented by a homeomorphism supported on a Klein bottle minus a disk interchanging two crosscaps [3]. Because a crosscap transposition is the product of a crosscap slide and a Dehn twist, crosscap transpositions can be used instead of crosscap slides as a generator of the mapping class group [3]. When S is orientable, the natural action of $MCG\left(S\right)$ on the boundary of Teichmüller space [4,5] of S (and hence on the set of multicurves on S) has been given in [4] making use of Dehn–Thurston coordinates, and in [6] making use of triangulation coordinates. However, for the case where S is non-orientable, no description of $MCG\left(S\right)$ in terms of a coordinate system has been introduced so far. In this paper, we give explicit formulae (Theorem 2) for the action of crosscap transpositions and their inverses on the set of multicurves in $N_{g,n}$ in terms of generalized Dynnikov coordinates, providing the first results in the literature regarding the action of a mapping class of a non-orientable surface in terms of global coordinates (by global coordinates we mean a coordinate system that describes multicurves in a unique way such as Dehn–Thurston coordinates [4,5]). The formulae can be considered as the analogue of the update rules that describe the action of the n-braid group on the set of multicurves on the n-punctured disk in terms of Dynnikov coordinates [7], which works much faster and is more direct than the usual train-track approach [4], and hence has several useful combinatorial and dynamical applications [7,8,9,10]. The analogy between the formulae in Theorem 2 and the update rules provides a way for studying such problems regarding the action of crosscap transpositions also on non-orientable surfaces in an efficient way.

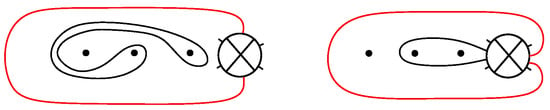
Let $N_{g,n}$ ($g\ge 2$) be a non-orientable surface of genus g with n punctures and one boundary component. In all figures of this paper, each disk labelled with a cross on $N_{g,n}$ represents a crosscap, a model for a Möbius band [3,11], which is constructed by removing an open disk from the surface and identifying the antipodal points on the boundary component of the resulting disk. Throughout we shall use a standard model of $N_{g,n}$ as depicted in Figure 1, where the punctures and the crosscaps lie on the horizontal diameter of the surface.

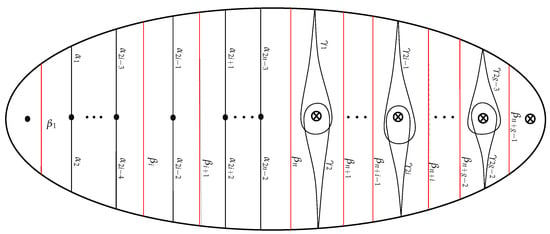
Figure 1. The arcs ${\alpha }_i$, ${\beta }_i$, ${\gamma }_i$ and the core curves $c_i$ of the crosscaps on $N_{g,n}$.

We say that a simple closed curve in $N_{g,n}$ is essential if it does not bound an unpunctured disk, once punctured disk, or an unpunctured annulus. If a regular neighborhood of an essential simple closed curve in $N_{g,n}$ is an annulus, it is called 2-sided, and if it is a Möbius band it is called 1-sided. We say that a curve is a Möbius curve if it is the core curve (the 1-sided center curve of a crosscap) or a double cover of the core curve of a crosscap. A multicurve in $N_{g,n}$ is a disjoint union of finitely many essential simple closed curves in $N_{g,n}$ modulo isotopy. We write ${\mathfrak{L}}_{g,n}$ to denote the set of multicurves in $N_{g,n}$.

Multicurves on orientable surfaces are usually described by techniques such as the Dehn–Thurston coordinate system or train tracks [4,5,12]. An alternative way to describe multicurves on finitely punctured disks is to use the Dynnikov coordinate system [5]. In 2016, Papadopoulos and Penner [11] provided analogues for non-orientable surfaces of several results from the Thurston theory of surfaces [5,12], including the Dehn–Thurston coordinate function. Following their work, the generalized Dynnikov coordinate system was introduced in [13] for multicurves in $N_{g,n}$, which provides an explicit bijection between ${\mathfrak{L}}_{g,n}$ and a certain subset of $({\mathbb{Z}}^{2(n+g-2)}\times {\mathbb{Z}}^g)\backslash \left\{0\right\}$. Here, we give a modified version of the generalized Dynnikov coordinate system together with the formulae in Theorem 1 (a corrected version of Theorem 2.14 in [13]) for the inverse of the Dynnikov coordinate function. Furthermore, with a slight modification, we also describe generalized Dynnikov coordinates for multicurves in $N_{g,0}$, which was not covered in [13]. Let $n>1$. The generalized Dynnikov coordinates can be described as follows:

Let ${\mathcal{A}}_{g,n}$ be the set of arcs ${\alpha }_i$ ($1\le i\le 2n-2$), ${\gamma }_i$ ($1\le i\le 2g-2$), and ${\beta }_i$ ($1\le i\le n+g-1$) as depicted in Figure 1: the arcs ${\alpha }_{2i-3}$ and ${\alpha }_{2i-2}$ ($2\le i\le n$) join the i-th puncture to the boundary, the teardrops${\gamma }_{2i-1}$ and ${\gamma }_{2i}$ encircle the i-th crosscap and have endpoints on the boundary, and the arc ${\beta }_i$$(1\le i\le n-1)$ has endpoints on the boundary and passes between the i-th and $(i+1)$-th punctures, ${\beta }_n$ passes between the n-th puncture and the first crosscap, and ${\beta }_{n+i}$$(2\le i\le g-1)$ passes between the i-th crosscap and the $(i+1)$-th crosscap. Finally, $c_i$ ($1\le i\le g$) denotes the core curve of the i-th crosscap, which we denote ${\otimes }_i$ throughout.

Given $\mathcal{L}\in {\mathfrak{L}}_{g,n}$, let L be a minimal representative of $\mathcal{L}$ (that is, L intersects each of the arcs and curves minimally). For the sake of brevity, let ${\alpha }_i,{\beta }_i$, ${\gamma }_i$ also denote the number of intersections of L with the corresponding arcs. We write $c_i=-1$ if $\mathcal{L}$ contains the i-th core curve, $c_i=-2m$ if $\mathcal{L}$ contains m disjoint copies of the double cover of the i-th core curve, and $c_i=-2m-1$ if $\mathcal{L}$ contains m disjoint copies of the double cover of the i-th core curve plus the core curve itself. Otherwise, $c_i$ denotes the number of intersections of L with the core curve of the i-th crosscap ${\otimes }_i$. It will always be clear from the context whether the symbols ${\alpha }_i,{\beta }_i$, ${\gamma }_i$ and $c_i$ refer to arcs and curves rather than to integers. We write $(\alpha ;\beta ;\gamma ,c)\in {\mathbb{Z}}^{3n+4g-5}\backslash \left\{0\right\}$ for the collection of these integers associated with $\mathcal{L}$. Let $x^{+}=max(x,0)$ throughout the text.

Let the function $\rho :{\mathfrak{L}}_{g,n}\to ({\mathbb{Z}}^{2(n+g-2)}\times {\mathbb{Z}}^g)\backslash \left\{0\right\}$ be defined by

$$\rho \left(\mathcal{L}\right)=(a;b;t;c):=(a_1,\dots ,a_{n-1};b_1,\dots ,b_{n+g-2};t_1,\dots ,t_{g-1};c_1,\dots ,c_g)$$

where

$$\begin{array}{cc}\hfill {\displaystyle a_i}& =\frac{{\alpha }_{2i}-{\alpha }_{2i-1}}{2};1\le i\le n-1,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\displaystyle t_i}& =\frac{{\gamma }_{2i}-{\gamma }_{2i-1}}{2};1\le i\le g-1,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill b_i& =\frac{{\beta }_i-{\beta }_{i+1}}{2};1\le i\le n+g-2\hfill \end{array}$$

(3)

We say that $(a;b;t;c)$ are the generalized Dynnikov coordinates of $\mathcal{L}\in {\mathfrak{L}}_{g,n}$.

Notation 1.

Let ${\psi }_i=max(c_i^{+}-|b_{n+i-1}|,0)$ (the use of this parameter will be explained later) and ${\mathcal{S}}_{g,n}=\{(a;b;t;c)\in ({\mathbb{Z}}^{2(n+g-2)}\times {\mathbb{Z}}^g)\backslash \left\{0\right\}:|t_i|+{\psi }_{i}isevenfor1\le i\le g-1\}$.

Remark 1.

Note the special case $n=1$ where there is no $a_i$ coordinate, and the special case $g=1$ where there is no $t_i$ coordinate.

The intersection numbers $(\alpha ;\beta ;\gamma ;c)$ (and hence the multicurve $\mathcal{L}$) can be recovered from the generalized Dynnikov coordinates $(a;b;t;c)\in {\mathcal{S}}_{g,n}$. Theorem 1 gives the inverse of the generalized Dynnikov coordinate function by presenting a formula that describes multicurves from given generalized Dynnikov coordinates.

Theorem 1.

Let $(a;b;t;c)\in {\mathcal{S}}_{g,n}$. Then $(a;b;t;c)$ corresponds to a unique multicurve in $\mathcal{L}\in {\mathfrak{L}}_{g,n}$, which has

$$\begin{array}{cc}\hfill {\displaystyle {\alpha }_i}& =\left\{\begin{array}{cc}{(-1)}^i{a}_{\lceil i/2\rceil }+\frac{{\beta }_{\lceil i/2\rceil }}{2}\hfill & \hfill if b_{\lceil i/2\rceil }\ge 0,\\ {(-1)}^i{a}_{\lceil i/2\rceil }+\frac{{\beta }_{1+\lceil i/2\rceil }}{2}\hfill & \hfill if b_{\lceil i/2\rceil }\le 0,\end{array}\right.\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\displaystyle {\gamma }_i}& =\left\{\begin{array}{cc}{(-1)}^i{t}_{\lceil i/2\rceil }+{\beta }_{n+\lceil i/2\rceil -1}+{\psi }_{\lceil i/2\rceil }\hfill & \hfill if b_{n+\lceil i/2\rceil }-1\ge 0,\\ {(-1)}^i{t}_{\lceil i/2\rceil }+{\beta }_{n+\lceil i/2\rceil }+{\psi }_{\lceil i/2\rceil }\hfill & \hfill if b_{n+\lceil i/2\rceil }-1\le 0,\end{array}\right.\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\beta }_i& =Z_i+2max(0,c_g^{+}-\frac{Z_{n+g-1}}{2})\hfill \end{array}$$

(6)

where

$$\begin{array}{cc}\hfill X_i& =2\left[{\displaystyle \left|a_i\right|+max(b_i,0)+\sum _{k=1}^{i-1}{b}_k}\right]\hfill \\ \hfill Y_i& =2\left[{\displaystyle max(b_{n+i-1},0)+\sum _{k=1}^{n+i-2}{b}_k}\right]+\left|t_i\right|+{\psi }_i\hfill \\ \hfill Z_i& =\underset{\begin{array}{c}1\le s\le n-1\\ 1\le t\le g-1\end{array}}{max}\left\{X_s,Y_t\right\}-2\sum _{k=1}^{i-1}{b}_k\hfill \end{array}$$

Here $\lceil x\rceil$ denotes the smallest integer that is not less than x.

The main goals of this paper are first to prove Theorem 1 (correcting the proof of Theorem 2.14 in [13]) and then give the derivation of the formulae in Theorem 2 that describes how generalized Dynnikov coordinates change under the action of crosscap transpositions $u_i$ and $u_i^{-1}$ ($1\le i\le g-1$). Here the i-th crosscap transposition $u_i$ exchanges crosscaps ${\otimes }_i$ and ${\otimes }_{i+1}$ in the counterclockwise direction. Therefore, Theorem 2 computes for each mapping class $\beta$ written as a word of crosscap transpositions, $\beta :{\mathcal{S}}_{g,n}\to {\mathcal{S}}_{g,n}$ given by $\beta (a;t;b;c)=\rho \circ \beta \circ {\rho }^{-1}(a;t;b;c).$ We note that, although the formulae in Theorem 1 and Theorem 2 seem to have a complicated form, the method we use to obtain them is transparent as it purely relies on algebraic calculations and the properties of multicurves in terms of their associated intersection numbers $(\alpha ;\beta ;\gamma ;c)$. In addition, the formulae are ideally suited for computer implementation. For computational and notational convenience, we use the notations in Notation 2 and Notation 3 in Theorem 2.

Notation 2.

For computational and notational convenience, we will work in the max-plus semiring $(\mathbb{R},max,+)$ and write $\left[x+y\right]:=max(x,y),\left[xy\right]:=x+y,\left[x/y\right]:=x-y,\left[1\right]:=0$.

To prove Theorem 2, we shall make use of particular arc systems called clovers and scales, each of which is associated with an exceptional parameter, certain linear combinations of generalized Dynnikov coordinates, denoted $d_i,e_i,{\overline{e}}_i,f_i,{\overline{f}}_i,g_i$ and ${\overline{g}}_i$ described in Section 3.

Notation 3.

For notational convenience, we write $B_j=2b_j$ (i.e., $\left[B_j\right]:=\left[b_j^2\right]$) in Theorem 2.

Theorem 2.

Let $(a;b;t;c)\in {\mathcal{S}}_{g,n}$ where ${\mathcal{S}}_{g,n}$ is as described in Notation 1, and write $u_i(a,b)=(a^{\prime };b^{\prime };t^{\prime };c^{\prime })$ and $u_i^{-1}(a,b)=(a^{″};b^{″};t^{″};c^{″})$. Then $a_j^{\prime }=a_j^{″}=a_j$, $b_j^{\prime }=b_j^{″}=b_j$ for all $1\le j\le n$; $(c_i^{\prime },c_{i+1}^{\prime })=(c_{i+1},c_i)$ and $(c_i^{″},c_{i+1}^{″})=(c_{i+1},c_i)$ for $1\le i\le g-1$; and for $1\le i\le g-3$ we have

$$\begin{array}{ccc}\hfill \begin{array}{cc}\hfill t_i^{\prime }& =\left[g_i\left(t_i(1+d_i{B}_{n+i-1})+d_i{B}_{n+i-1}{t}_{i+1}\right)\right]\hfill \\ \hfill t_{i+1}^{\prime }& =\left[\frac{t_i{t}_{i+1}{B}_{n+i}}{f_i(t_i(d_i+B_{n+i})+d_i{t}_{i+1})}\right]\hfill \\ \hfill t_i^{″}& =\left[\frac{t_i{t}_{i+1}}{\overline{g_i}\left(t_i{d}_i{B}_{n+i-1}+t_{i+1}(d_i{B}_{n+i-1}+1)\right)}\right]\hfill \\ \hfill t_{i+1}^{″}& =\left[\frac{\overline{f_i}\left(t_{i+1}(B_{n+i}+d_i)+d_i{t}_i\right)}{B_{n+i}}\right]\hfill \end{array}& \hfill & \hfill \begin{array}{cc}\hfill B_{n+i}^{\prime }& =\left[\frac{e_i}{d_i}{B}_{n+i}\left(\frac{t_i^{\prime }+t_{i+1}^{\prime }}{t_{i+1}^{\prime }}\right)\frac{t_i}{t_i+t_{i+1}}\right]\hfill \\ \hfill B_{n+i-1}^{\prime }& =\left[\frac{B_{n+i}{B}_{n+i-1}}{B_{n+i}^{\prime }}\right]\hfill \\ \hfill B_{n+i-1}^{″}& =\left[\frac{B_{n+i}{B}_{n+i-1}}{B_{n+i}^{″}}\right],\hfill \\ \hfill B_{n+i}^{″}& =\left[\frac{\overline{e_i}}{d_i}{B}_{n+i}\left(\frac{t_i^{″}+t_{i+1}^{″}}{t_i^{″}}\right)\frac{t_{i+1}}{t_i+t_{i+1}}\right]\hfill \end{array}\end{array}$$

(7)

In the special case the formulae above is interpreted as

$$\begin{array}{ccc}\hfill \begin{array}{cc}\hfill t_{g-1}^{\prime }& =\left[g_{g-1}\left(t_{g-1}+d_{g-1}{B}_{n+g-2}(1+t_{g-1})\right)\right]\hfill \\ \hfill t_{g-1}^{″}& =\left[\frac{t_{g-1}}{{\overline{g}}_{g-1}\left(d_{g-1}{B}_{n+g-2}(1+t_{g-1})\right)}\right]\hfill \end{array}& \hfill & \hfill \begin{array}{cc}\hfill B_{n+g-2}^{\prime }& =\left[\frac{d_{g-1}}{e_{g-1}}{B}_{n+g-2}\frac{1+t_{g-1}}{t_{g-1}(1+t_{g-1}^{\prime })}\right]\hfill \\ \hfill B_{n+g-2}^{″}& =\left[\frac{d_{g-2}}{{\overline{e}}_{g-2}}{B}_{n+g-2}\frac{t_{g-1}^{″}(1+t_{g-1})}{1+t_{g-1}^{″}}\right].\hfill \end{array}\end{array}$$

(8)

In all other cases $t_j^{\prime }=t_j$, $t_j^{″}=t_j$ and $b_j^{\prime }=b_j^{″}=b_j$.

The paper is organized as follows. Section 2 gives background material and contains a detailed study of generalized Dynnikov coordinates, giving proofs of Theorem 1 and Theorem 3. In Section 3, we introduce the notions of clovers and scales, certain collections of adjacent arcs in ${\mathcal{A}}_{g,n}$ and their images under $u_i$ and $u_i^{-1}$, from which we obtain clover and scale equalities given in Lemmas 5, 9, 12 and 13, which play key roles in the derivation of the formulae in Theorem 2.

2. Constructing Multicurves from Generalized Dynnikov Coordinates

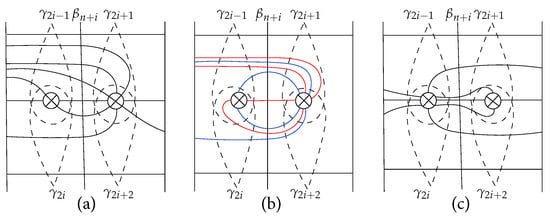
Let L be a minimal representative of $\mathcal{L}\in {\mathfrak{L}}_{g,n}$. In this section we prove Theorem 1, recalling basic properties of L in terms of the intersection numbers $(\alpha ;\beta ;\gamma ;c)$. Let $1\le i\le n-1$ and $S_i$ denote the region bounded by the arcs ${\beta }_i$ and ${\beta }_{i+1}$ containing puncture $i+1$. We denote by $S_0$ the left most region bounded by ${\beta }_1$ and the boundary containing the first puncture. Now, let $1\le i\le g$, and $S_i^{\prime }$ denote the region bounded by the arcs ${\beta }_{n+i-1}$ and ${\beta }_{n+i}$ containing ${\otimes }_i$; $S_g^{\prime }$ denotes the right most region bounded by ${\beta }_{n+g-1}$ and the boundary containing ${\otimes }_g$. Because L is minimal, there are finitely many connected components of $L\cap S_i$ [10] and $L\cap S_i^{\prime }$ [13], as depicted in Figure 2 and Figure 3. Above, below, left loop, and right loop components of $L\cap S_i$ are depicted red, green, blue, and orange, respectively, in Figure 2. In $S_i^{\prime }$, above, below, and straight components are depicted in red, green, and purple respectively; left core and non-core loop components are depicted in blue, and right core and non-core loop components are depicted in orange, where a loop component of $L\cap S_i^{\prime }$ is called a core loop if it intersects ${\otimes }_i$, and a non-core loop if it doesn’t. Finally, Möbius curves are depicted in black. Observe that there can only be left loop components in $S_0$, and only right loop components in $S_g^{\prime }$. The following lemma gives two important equalities, which are obvious from Figure 2 and Figure 3.

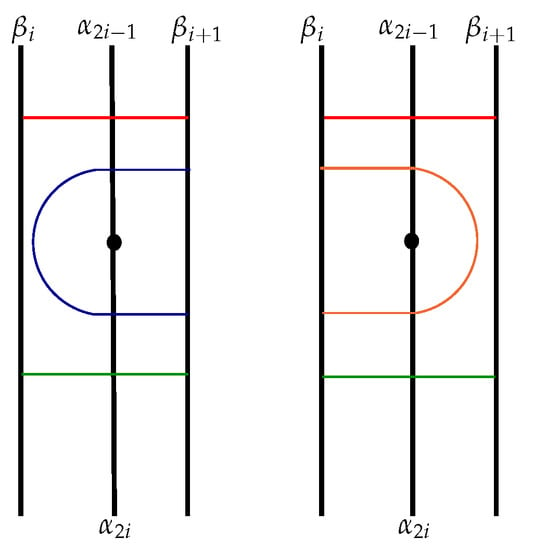
Figure 2. Connected components of $L\cap S_i$.

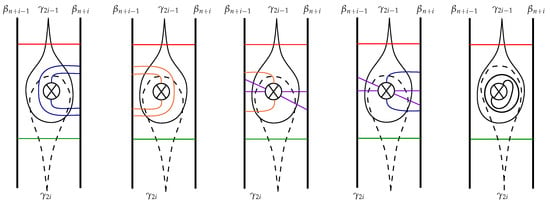
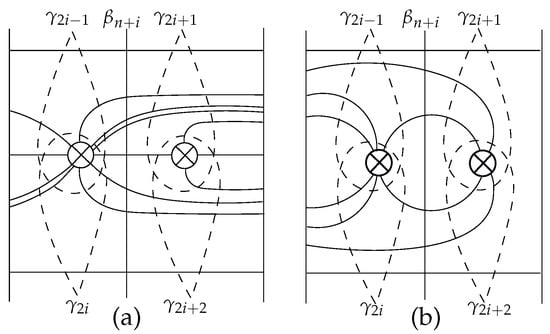
Figure 3. Connected components of $L\cap S_i^{\prime }$.

Lemma 1.

Let L be a minimal representative of a multicurve $\mathcal{L}\in {\mathfrak{L}}_{g,n}$ with intersection numbers $(\alpha ;\beta ;\gamma ;c)$. Let ${\psi }_i$ denote the number of straight components of $L\cap S_i^{\prime }$. Then,

$$\begin{array}{cc}\hfill max({\beta }_i,{\beta }_{i+1})& ={\alpha }_{2i-1}+{\alpha }_{2i}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill max({\beta }_{n+i-1},{\beta }_{n+i})& =\frac{{\gamma }_{2i-1}+{\gamma }_{2i}}{2}-{\psi }_i\hfill \end{array}$$

(10)

Remark 2.

Given a minimal representative L of $\mathcal{L}\in {\mathfrak{L}}_{g,n}$, we can initially observe that every component of L intersects each ${\beta }_i$ and hence each ${\alpha }_{2i-1}\cup {\alpha }_{2i}$ and ${\gamma }_{2i-1}\cup {\gamma }_{2i}$ an even number of times. Therefore $a_i,t_i$, and $b_i$ are integers.

Lemma 2.

For each $1\le i\le n+g-2$ let $b_i=\frac{{\beta }_i-{\beta }_{i+1}}{2}$. Then there are $|b_i|$ loop components in $S_i$ ( $1\le i\le n-1$) and $|b_{n+i-1}|$ loop components in $S_i^{\prime }$ ($1\le i\le g-1)$. If $b_j>0$, the loop components are right, and if $b_j<0$ ($j=i,n+i-1$), the loop components are left.

Proof. 

We prove the statement for $S_i$ (the argument for $S_i^{\prime }$ is identical). Let $1\le i\le n-1$. We first note that there cannot be both left loop and right loop components in $S_i$, as the curves are mutually disjoint. Assume without loss of generality that ${\beta }_{i+1}\ge {\beta }_i$. Observe from Figure 2 that the additional intersections on ${\beta }_{i+1}$ come from left loop components in $S_i$, as above and below components intersect both ${\beta }_i$ and ${\beta }_{i+1}$ the same number of times. Because each left loop intersects ${\beta }_{i+1}$ twice, it follows that there are $-b_i=\frac{{\beta }_{i+1}-{\beta }_i}{2}$ left loop components in $S_i$. Same argument holds for right loop components in $S_i$. □

Remark 3.

There are only left loop components of $L\cap S_0^{\prime }$ and only right loop components of $L\cap S_g^{\prime }$, number of which are respectively given by $\frac{{\beta }_1}{2}$ and $\frac{{\beta }_{n+g-1}}{2}$. It immediately follows that there are $c_g^{+}$ core loops and hence ${\lambda }_g=\frac{{\beta }_{n+g-1}}{2}-c_g^{+}$ non-core loops of $L\cap S_g^{\prime }$.

Lemma 3.

Let $1\le i<n+g-2$, and ${\lambda }_i$, ${\lambda }_{c_i}$, and ${\psi }_i$ denote the number of non-core loop, core loop and straight components of $L\cap S_i^{\prime }$ respectively. Then,

$$\begin{array}{cc}\hfill {\psi }_i& =max(c_i^{+}-|b_{n+i-1}|,0)\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\lambda }_i& =max\left(\right|b_{n+i-1}|-c_i^{+},0),{\lambda }_{c_i}=\left|b_{n+i-1}\right|-{\lambda }_i\hfill \end{array}$$

(12)

Proof. 

If $c_i^{+}=0$ there can be no straight or core loop components of $L\cap S_i^{\prime }$. Assume that $c_i^{+}\ne 0$ i.e. $c_i>0$. Observe from Figure 3 that we have

$$\begin{array}{cc}\hfill c_i& ={\psi }_i+{\lambda }_{c_i}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill |b_{n+i-1}|& ={\lambda }_i+{\lambda }_{c_i}.\hfill \end{array}$$

(14)

If $c_i-\left|b_{n+i-1}\right|\ge 0$, there exist components of $L\cap S_i^{\prime }$ other than core loop components that intersect the crosscap. Such components can only be straight components and hence ${\psi }_i>0$ and ${\lambda }_i=0$, as non-core loops and straight components cannot exist at the same time. Then, $|b_{n+i-1}|={\lambda }_{c_i}$ and hence ${\psi }_i=c_i-\left|b_{n+i-1}\right|$ by (13) and (14). If $c_i-\left|b_{n+i-1}\right|<0$, then there exist non-core loop components as well as core loop components. That is, ${\lambda }_i>0$ and hence ${\psi }_i=0$. Therefore, $c_i={\lambda }_{c_i}$ and so ${\lambda }_i=\left|b_{n+i-1}\right|-c_i$ by (13) and (14). Therefore, we get ${\psi }_i=max(c_i^{+}-|b_{n+i-1}|,0)$ and ${\lambda }_i=max\left(\right|b_{n+i-1}|-c_i^{+},0)$ as required. We immediately get from (14) that ${\lambda }_{c_i}=\left|b_{n+i-1}\right|-{\lambda }_i$. □

Remark 4.

There are $b_i^{+}=max(b_i,0)$ right loops and ${(-b_i)}^{+}=max(-b_i,0)$ left loops in $S_i$. Similarly, there are $b_{n+i-1}^{+}$ right loops and ${(-b_{n+i-1})}^{+}$ left loops in $S_i^{\prime }$.

The following Lemma is obvious because each above and below component in $S_i$ intersects ${\alpha }_{2i-1}$ and ${\alpha }_{2i}$, and each above and below component in $S_i^{\prime }$ intersects ${\gamma }_{2i-1}$ and ${\gamma }_{2i}$, respectively (see Figure 2 and Figure 3).

Lemma 4.

Let there be $A_i$ and $B_i$$(1\le i\le n-1)$ above and below components of $L\cap S_i$; and $A_i^{\prime }$ and $B_i^{\prime }$$(1\le i\le g-1)$ above and below components of $L\cap S_i^{\prime }$, respectively. Then,

$$\begin{array}{cc}\hfill A_i& ={\alpha }_{2i-1}-\left|b_i\right|\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill B_i& ={\alpha }_{2i}-\left|b_i\right|\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill A_i^{\prime }& =\frac{{\gamma }_{2i-1}}{2}-{\psi }_i-\left|b_{n+i-1}\right|\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill B_i^{\prime }& =\frac{{\gamma }_{2i}}{2}-{\psi }_i-\left|b_{n+i-1}\right|\hfill \end{array}$$

(18)

The curve $\mathcal{L}$ in Figure 4 has generalized Dynnikov coordinates $\rho \left(\mathcal{L}\right)=(-1,-1;0,2;1,1,1)$ and satisfies $A_1^{\prime }=A_2^{\prime }=0;B_1^{\prime }=0;B_2^{\prime }=2;{\lambda }_1={\lambda }_2=0,{\lambda }_3=1;{\lambda }_{c_1}={\lambda }_{c_2}=1={\lambda }_{c_3}=1$; ${\psi }_1={\psi }_2=0$. These parameters will frequently be referred to throughout the paper.

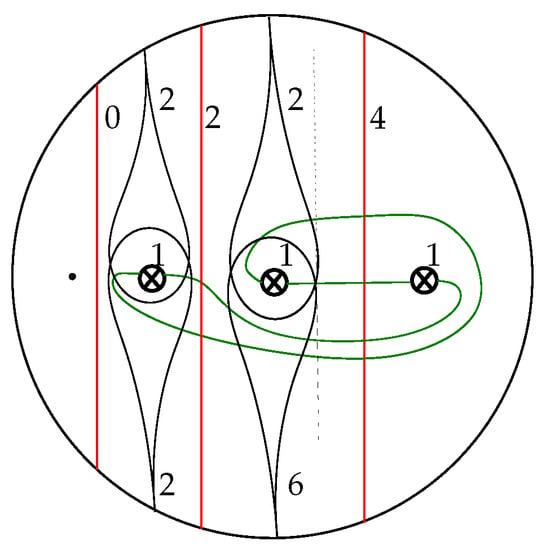
Figure 4. A curve $\mathcal{L}$ in $N_{3,1}$ with generalized Dynnikov coordinates $\rho \left(\mathcal{L}\right)=(-1,-1;0,2;1,1,1)$.

The generalized Dynnikov coordinate function $\rho :{\mathfrak{L}}_{g,n}\to {\mathcal{S}}_{g,n}$ is a bijection: to describe its inverse, it is sufficient to describe a function from ${\mathcal{S}}_{g,n}$ to ${\mathbb{Z}}^{3n+4g-5}\backslash \left\{0\right\}$, which sends each $(a;b;t;c)\in {\mathcal{S}}_{g,n}$ to the intersection numbers $(\alpha ;\beta ;\gamma ;c)$ associated with a multicurve $\mathcal{L}$ with $\rho \left(\mathcal{L}\right)=(a;b;t;c)$. This is established in the proof of Theorem 1.

Proof of Theorem 1.

Let L be a minimal representative of $\mathcal{L}\in {\mathfrak{L}}_{g,n}$ with generalized Dynnikov coordinates $\rho \left(\mathcal{L}\right)=(a;b;t;c)$. We first note that $2|a_i|=|{\alpha }_{2i-1}-{\alpha }_{2i}|$ and $2|t_i|=|{\gamma }_{2i-1}-{\gamma }_{2i}|$ give the difference between below and above components in $S_i$ and $S_i^{\prime }$, respectively, by Lemma 4. In addition, $|b_i|$ and $|b_{n+i-1}|$ give the number of loop components in $S_i$ and $S_i^{\prime }$ respectively by Lemma 2. Let $m_i$ and $n_i$ be the smaller of above and below components of $L\cap S_i$ and $L\cap S_i^{\prime }$, respectively. From Figure 2 and Figure 3, it is straightforward to compute ${\beta }_i$ and ${\beta }_{n+i-1}$:

For $1\le i\le n-1$,

$$\begin{array}{cc}\hfill {\beta }_i& =\left\{\begin{array}{cc}2m_i+2\left|a_i\right|\hfill & if b_i\le 0;\hfill \\ 2m_i+2\left|a_i\right|+2b_i\hfill & if b_i\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

For $1\le i\le g-1$

$$\begin{array}{cc}\hfill {\beta }_{n+i-1}& =\left\{\begin{array}{cc}2n_i+\left|t_i\right|+{\psi }_i\hfill & if b_{n+i-1}\le 0;\hfill \\ 2n_i+\left|t_i\right|+{\psi }_i+2b_{n+i-1}\hfill & if b_{n+i-1}\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

from which we get

$$\begin{array}{cc}\hfill {\beta }_i& =2\left[\left|a_i\right|+max(b_i,0)+m_i\right]\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\beta }_{n+i-1}& =|t_i|+{\psi }_i+2\left[max(b_{n+i-1},0)+n_i\right]\hfill \end{array}$$

(20)

As ${\beta }_{n+i-1}$ is even from Remark 2, equality (20) implies that $|t_i|+{\psi }_i$ should be even. That is, $|t_i|+max(c_i-|b_{n+i-1}|,0)$ is even by Lemma 3.

Now, consider a subarc of L that intersects the last crosscap exactly once, has zero intersection with the other crosscaps, and intersects the horizontal diameter of the surface only between the first puncture and the boundary exactly once, as shown in Figure 5. Each such arc intersects each ${\beta }_i$ and ${\gamma }_i$ twice, and each ${\alpha }_i$ exactly once. We say that such arcs are almost boundary parallel, and write R for the number of almost boundary parallel arcs.

Figure 5. Two multicurves oin $N_{1,3}$ with $R=1$.

Using ${\displaystyle {\beta }_i={\beta }_1-2\sum _{j=1}^{i-1}{b}_j}$ ($1\le i\le n+g-1$) and subtracting $2R$ from both sides of Equations (19) and (20) we get

$$\begin{array}{cc}\hfill {\beta }_1-2R& =2\left[{\displaystyle \left|a_i\right|+max(b_i,0)+m_i-R+\sum _{j=1}^{i-1}{b}_j}\right]\mathrm{for}1\le i\le n-1\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\beta }_1-2R& =2\left[{\displaystyle max(b_{n+i-1},0)+n_i-R+\sum _{j=1}^{n+i-2}{b}_j}\right]+\left|t_i\right|+{\psi }_i\mathrm{for}1\le i\le g-1.\hfill \end{array}$$

(22)

One crucial fact is that $m_i-R=0$ for some $1\le i\le n-1$ or $n_i-R=0$ for some $1\le i\le g-1$ as otherwise there would be both above and below components in each of the $S_i$ and $S_i^{\prime }$ except for those that arise from almost boundary arcs, but this would mean L contains boundary parallel curves, which is impossible. Then,

When $m_i-R=0$;

$$\begin{array}{c}\hfill {\beta }_1-2R=2\left[{\displaystyle \left|a_i\right|+max(b_i,0)+\sum _{j=1}^{i-1}{b}_j}\right].\end{array}$$

When $m_i-R>0$;

$$\begin{array}{c}\hfill {\beta }_1-2R>2\left[{\displaystyle \left|a_i\right|+max(b_i,0)+\sum _{j=1}^{i-1}{b}_j}\right].\end{array}$$

When $n_i-R=0$;

$$\begin{array}{c}\hfill {\beta }_1-2R=2\left[{\displaystyle max(b_{n+i-1},0)+\sum _{j=1}^{n+i-2}{b}_j}\right]+\left|t_i\right|+{\psi }_i.\end{array}$$

When $n_i-R>0$;

$$\begin{array}{c}\hfill {\beta }_1-2R>2\left[{\displaystyle max(b_{n+i-1},0)+\sum _{j=1}^{n+i-2}{b}_j}\right]+\left|t_i\right|+{\psi }_i.\end{array}$$

Therefore, setting

$$\begin{array}{cc}\hfill X_i& =2\left[{\displaystyle \left|a_i\right|+max(b_i,0)+\sum _{j=1}^{i-1}{b}_j}\right]\hfill \\ \hfill Y_i& =2\left[{\displaystyle max(b_{n+i-1},0)+\sum _{j=1}^{n+i-2}{b}_j}\right]+\left|t_i\right|+{\psi }_i\hfill \end{array}$$

we get

$${\beta }_1-2R=\underset{\begin{array}{c}1\le s\le n-1\\ 1\le k\le g-1\end{array}}{max}\left\{X_s,Y_k\right\}$$

(23)

and hence

$${\beta }_i-2R=\underset{\begin{array}{c}1\le s\le n-1\\ 1\le t\le g-1\end{array}}{max}\left\{X_s,Y_k\right\}-2\sum _{j=1}^{i-1}{b}_j$$

(24)

as required. Next, we compute R. Let

$$Z_i=\underset{\begin{array}{c}1\le s\le n-1\\ 1\le k\le g-1\end{array}}{max}\left\{X_s,Y_k\right\}-2\sum _{j=1}^{i-1}{b}_j$$

By (24), ${\beta }_{n+g-1}=Z_{n+g-1}+2R$. By Remark 4, ${\beta }_{n+g-1}=2c_g+2{\lambda }_g$. It follows that when $Z_{n+g-1}>2c_g$, we have ${\beta }_{n+g-1}>2c_g$ and hence ${\lambda }_g\ne 0$. Therefore, $R=0$ since almost boundary parallel arcs and non-core loop components of $L\cap S_g^{\prime }$ cannot exist at the same time, and when $Z_{n+g-1}<2c_g$ we have $Z_{n+g-1}<{\beta }_{n+g-1}$ and hence $R>0$ and ${\lambda }_g=0$, which implies ${\beta }_{n+g-1}=Z_{n+g-1}+2R=2c_g$ that is $R=c_g-\frac{Z_{n+g-1}}{2}$. Therefore, $R=max(0,c_g-\frac{Z_{n+g-1}}{2})$.

To compute ${\alpha }_i$ and ${\gamma }_i$, we make use of the equalities in Lemma 1:

$$\begin{array}{cc}\hfill max({\beta }_i,{\beta }_{i+1})& ={\alpha }_{2i-1}+{\alpha }_{2i}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill max({\beta }_{n+i-1},{\beta }_{n+i})& =\frac{{\gamma }_{2i-1}+{\gamma }_{2i}}{2}-{\psi }_i\hfill \end{array}$$

(26)

As $2a_i={\alpha }_{2i}-{\alpha }_{2i-1}$ ($1\le i\le n-1$), we get from (25) that

If ${\beta }_i\ge {\beta }_{i+1}$ (i.e., $b_i\ge 0$)

$$\begin{array}{c}\hfill {\alpha }_{2i}=a_i+\frac{{\beta }_i}{2};\mathrm{and}{\alpha }_{2i-1}=-a_i+\frac{{\beta }_i}{2}.\end{array}$$

If ${\beta }_{i+1}\ge {\beta }_i$ (i.e., $b_i\le 0$)

$$\begin{array}{c}\hfill {\alpha }_{2i}=a_i+\frac{{\beta }_{i+1}}{2};\mathrm{and}{\alpha }_{2i-1}=-a_i+\frac{{\beta }_{i+1}}{2}.\end{array}$$

That is to say:

$$\begin{array}{cc}\hfill {\alpha }_i& =\left\{\begin{array}{cc}{(-1)}^i{a}_{\lceil i/2\rceil }+\frac{{\beta }_{\lceil i/2\rceil }}{2}\hfill & \mathrm{if} b_{\lceil i/2\rceil }\ge 0;\hfill \\ {(-1)}^i{a}_{\lceil i/2\rceil }+\frac{{\beta }_{1+\lceil i/2\rceil }}{2}\hfill & \mathrm{if} b_{\lceil i/2\rceil }\le 0\hfill \end{array}\right.\end{array}$$

Similarly, as $2t_i={\gamma }_{2i}-{\gamma }_{2i-1}$ for each $1\le i\le g-1$, we get from (26) that

If ${\beta }_{n+i-1}\ge {\beta }_{n+i}$ (i.e., $b_{n+i-1}\ge 0$)

$$\begin{array}{c}\hfill {\gamma }_{2i}=t_i+{\beta }_{n+i-1}+{\psi }_i;\mathrm{and}{\gamma }_{2i-1}=-t_i+{\beta }_{n+i-1}+{\psi }_i,\end{array}$$

If ${\beta }_{n+i-1}\le {\beta }_{n+i}$ (i.e., $b_{n+i-1}\le 0$)

$$\begin{array}{c}\hfill {\gamma }_{2i}=t_i+{\beta }_{n+i}+{\psi }_i;\mathrm{and}{\gamma }_{2i-1}=-t_i+{\beta }_{n+i}+{\psi }_i.\end{array}$$

That is to say:

$$\begin{array}{cc}\hfill {\displaystyle {\gamma }_i}& =\left\{\begin{array}{cc}{(-1)}^i{t}_{\lceil i/2\rceil }+{\beta }_{n+\lceil i/2\rceil -1}+{\psi }_{\lceil i/2\rceil }\hfill & \hfill \mathrm{if} b_{n+\lceil i/2\rceil -1}\ge 0,\\ {(-1)}^i{t}_{\lceil i/2\rceil }+{\beta }_{n+\lceil i/2\rceil }+{\psi }_{\lceil i/2\rceil }\hfill & \hfill \mathrm{if} b_{n+\lceil i/2\rceil -1}\le 0,\end{array}\right.\hfill \end{array}$$

(27)

as required. □

Remark 5.

We note that the generalized Dynnikov coordinates for multicurves can be extended in a natural way to generalized Dynnikov coordinates of measured foliations. The construction is similar to the case of Dynnikov coordinates of measured foliations on finitely punctured disks [9].

Generalized Dynnikov Coordinates on $N_{g,0}$

Let $N_{g,0}$ be the standard model of a non-orientable surface of genus g with one boundary component as shown in Figure 6, and denote by ${\mathfrak{L}}_{g,0}$ the set of multicurves on $N_{g,0}$. Let ${\mathcal{S}}_{g,n}=\{t;b;c)\in ({\mathbb{Z}}^{2(g-2)}\times {\mathbb{Z}}^g)\backslash \left\{0\right\}:|t_i|+{\psi }_i\mathrm{is}\mathrm{even}1\le i\le g-2\}$. Let the function $\rho :{\mathfrak{L}}_{g,0}\to {\mathcal{S}}_{g,0}$ be defined by

$$\rho \left(\mathcal{L}\right)=(t;b;c):=(t_1,\dots ,t_{g-2};b_1,\dots ,b_{g-2};c_1,\dots ,c_g)$$

where

$$\begin{array}{cc}\hfill {\displaystyle t_i}& =\frac{{\gamma }_{2i}-{\gamma }_{2i-1}}{2};1\le i\le g-2,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill b_i& =\frac{{\beta }_i-{\beta }_{i+1}}{2};1\le i\le g-2\hfill \end{array}$$

(29)

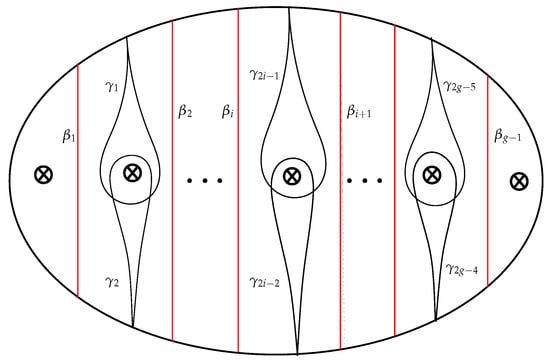
Figure 6. The arcs ${\gamma }_i$, ${\beta }_i$ and the core curves $c_i$ on $N_{g,0}$.

Remark 6.

For $1\le i\le g-1$, ${\psi }_i$, ${\lambda }_i$ and ${\lambda }_{c_i}$ are as given in Lemma 3. For $i=1$ we have ${\psi }_1=0$, ${\lambda }_1=\frac{{\beta }_1}{2}-c_1^{+}$, and ${\lambda }_{c_1}=c_1^{+}$. Similarly, for $i=g$ we have ${\psi }_g=0$, ${\lambda }_g=\frac{{\beta }_{g-1}}{2}-c_g^{+}$, and ${\lambda }_{c_g}=c_g^{+}$ as each component of $L\cap S_0^{\prime }$ and $L\cap S_g^{\prime }$ intersecting the core curves should be core loop components.

The inverse of the coordinate function $\rho$ is described similarly. However, we need to extend the definition of almost boundary parallel arcs, as they could also arise from the first crosscap as shown in Figure 7. That is, an almost boundary parallel arc associated with crosscap g is a subarc of L that intersects crosscap g exactly once, has zero intersection with crosscaps 2 through $g-1$; and intersects either crosscap 1 or the diameter between crosscap 1 and the boundary exactly once, as shown in Figure 7a,b. An almost boundary parallel arc associated with crosscap 1 is described similarly.

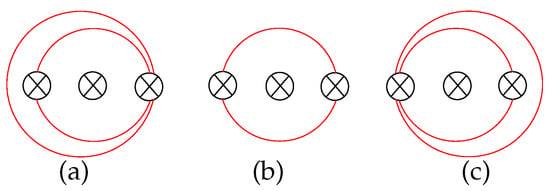
Figure 7. Almost boundary arcs on $N_{3,0}$: (a) $R_1=1,R_3=2$; (b) $R_1=R_3=1$; (c) $R_1=2,R_3=1$.

We write $R_1$ and $R_g$ for the number of almost boundary parallel arcs associated with crosscap 1 and crosscap g, respectively. Observe from Figure 7 that there are $R=max(R_1,R_g)$ almost boundary components in total. By the same argument as in the proof of Theorem 1, we have ${\beta }_i=Z_i+2R$ where

$${\displaystyle Z_i=\underset{1\le s\le g-1}{max}\left\{{\displaystyle 2max(b_s,0)+{\psi }_s+\left|t_s\right|+2\sum _{j=1}^{s-1}{b}_j}\right\}-\sum _{j=1}^{i-1}{b}_j}$$

(30)

as there are no $a_i$ coordinates. Then, ${\beta }_1-2R=Z_1$ and ${\beta }_{g-1}-2R=Z_{g-1}$. We have $R_1=max(0,c_1^{+}-\frac{Z_1}{2})$ and $R_g=max(0,c_g^{+}-\frac{Z_{g-1}}{2})$ yielding $R=max(0,c_1^{+}-\frac{Z_1}{2},c_g^{+}-\frac{Z_{g-1}}{2})$. The computation of intersection numbers on the arcs ${\gamma }_i$ is as in the proof of Theorem 1. Therefore, we get Theorem 3 where $\lceil x\rceil$ again denotes the smallest integer that is not less than x.

Remark 7.

Note the special case $g=2$ where there are only $c_1$ and $c_2$ coordinates.

Theorem 3.

Let $(t;b;c)\in {\mathcal{S}}_{g,0}$. Then $(t;b;c)$ corresponds to a unique multicurve in $\mathcal{L}\in {\mathcal{L}}_{g,0}$ that has

$$\begin{array}{cc}\hfill {\displaystyle {\gamma }_i}& =\left\{\begin{array}{cc}{(-1)}^i{t}_{\lceil i/2\rceil }+{\beta }_{n+\lceil i/2\rceil -1}+{\psi }_{\lceil i/2\rceil }\hfill & \hfill if b_{n+\lceil i/2\rceil }-1\ge 0,\\ {(-1)}^i{t}_{\lceil i/2\rceil }+{\beta }_{n+\lceil i/2\rceil }+{\psi }_{\lceil i/2\rceil }\hfill & \hfill if b_{n+\lceil i/2\rceil }-1\le 0,\end{array}\right.\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\beta }_i& =Z_i+2max(0,c_g-\frac{Z_{g-1}}{2},c_1-\frac{Z_1}{2})\hfill \end{array}$$

(32)

where

$${\displaystyle Z_i=\underset{1\le s\le g-1}{max}\left\{{\displaystyle 2max(b_s,0)+{\psi }_s+\left|t_s\right|+2\sum _{j=1}^{s-1}{b}_j}\right\}-\sum _{j=1}^{i-1}{b}_j}$$

Theorem 4.

Let $\mathcal{L}\in {\mathfrak{L}}_{g,0}$ have generalized Dynnikov coordinates $(t;b;c)$. Let $(t^{\prime };b^{\prime };c^{\prime })$ and $(t^{″};b^{″};c^{″})$ be the generalized Dynnikov coordinates of $u_i\left(\mathcal{L}\right)$ and $u_i^{-1}\left(\mathcal{L}\right)$, respectively. Then $(c_{i-1}^{\prime },c_i^{\prime })=(c_i,c_{i-1})$ and $(c_{i-1}^{″},c_i^{″})=(c_i,c_{i-1})$ for $1\le i\le g$; and for $1<i\le g-2$$(b^{\prime };t^{\prime })$ and $(b^{″};t^{‴})$ are as given in Equation (7), replacing the subscript i with $i-1$; for $i=g-1$$t_{g-2}^{\prime },b_{g-2}^{\prime },t_{g-2}^{″},b_{g-2}^{″}$ are as given in Equation (8) replacing the subscripts $g-1$ and $n+g-2$ with $g-2$; and for $i=1$ we have

$$\begin{array}{ccc}\hfill \begin{array}{cc}\hfill t_1^{\prime }& =\left[\frac{t_1{B}_1}{f_0(1+B_1)+t_1}\right]\hfill \\ \hfill t_1^{″}& =\left[\frac{\overline{f_0}(t_1(B_1+1)+t_1)}{B_1}\right]\hfill \end{array}& \hfill & \hfill \begin{array}{cc}\hfill B_1^{\prime }& =\left[B_1{e}_0\frac{(1+t_1^{\prime })}{t_1^{\prime }}\frac{1}{(1+t_1)}\right]\hfill \\ \hfill B_1^{″}& =\left[{\overline{e}}_0{B}_1\frac{(1+t_1^{″})}{t_1^{″}}\frac{t_1}{(1+t_1)}\right]\hfill \end{array}\end{array}$$

In all other cases $t_j^{\prime }=t_j$, $t_j^{″}=t_j$ and $b_j^{\prime }=b_j^{″}=b_j$.

3. Action of Crosscap Transpositions

The goal of this section is to prove Theorem 2, which describes how generalized Dynnikov coordinates change under the action of $u_i$ and $u_i^{-1}$ ($1\le i\le g-1$). The key ingredient for the derivation of the formulae in Theorem 2 is a set of equalities associated with particular arc systems that we call clovers and scales. These equalities are given in Lemmas 5, 9, 12, and 13.

3.1. Clovers and Scales

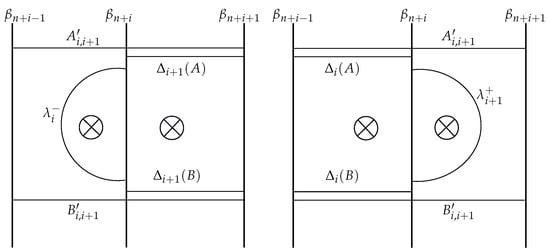
A clover and a scale about crosscaps ${\otimes }_i$ and ${\otimes }_{i+1}$ are two different configurations consisting of two vertices $v_1,v_2$ at $\partial N_{g,n}$ (identified to the puncture at ∞), five arcs $T_1,T_2,T_3,T_4,T_5$ with end points $v_1,v_2$, and a curve ${\mathcal{C}}_i$ such that the teardrops $T_1$ and $T_2$ encircle ${\otimes }_i$, the teardrops $T_3$ and $T_4$ encircle ${\otimes }_{i+1}$, $T_5$ joins $v_1$ and $v_2$; and ${\mathcal{C}}_i$ is the essential simple closed curve bounding crosscaps i and $i+1$, as shown in Figure 8. We say that the clover has leaves$T_1,T_2,T_3$, and $T_4$; diagonal arc $T_5$, and diagonal curve $C_i$. The scale has leaves $T_1,T_4,T_5$, and $C_i$, and diagonal teardrops$T_2$ and $T_3$.

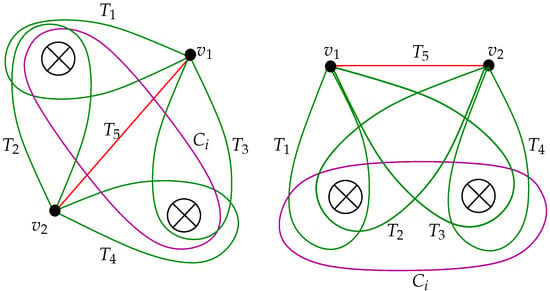
Figure 8. A clover and a scale.

To compute the action of $u_i$ and its inverse $u_i^{-1}$ ($1\le i\le g-1$) in terms of generalized Dynnikov coordinates, we will make use of certain equalities associated with clovers and scales in $S_i^{\prime }\cup S_{i+1}^{\prime }$, which we shall call clover and scale equalities throughout. We shall consider three types of clovers and four types of scales to obtain clover and scale equalities. These clovers and scales are depicted in Section 3.1.2 and Section 3.1.3 respectively.

Clover and scale equalities can be considered as a generalization of a well known equation commonly known as the flip move, which lets us change coordinates from one triangulation to another on punctured orientable surfaces [14]. Namely, if Q is a rectangle in a surface S and $X_1,X_2,X_3,X_4,X_5$, and $X_6$ are the number of intersections on the four edges and the diagonals of Q with all of its corners at the punctures and containing no punctures in its interior, and $X_{ij}$ denotes the number of arcs joining edge $X_i$ to $X_j$ then there are two possibilities: either $X_{12}$ or $X_{34}$ is zero, as the curves are non intersecting. This yields the well-known equation

$$max(X_1+X_2,X_3+X_4)=X_5+X_6.$$

The method here will be similar and use case by case analysis for components of $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$ intersecting the clovers and the scales. In what follows, we will again denote by L a minimal representative of a multicurve $\mathcal{L}\in {\mathfrak{L}}_{g,n}$ with $\rho \left(\mathcal{L}\right)=(a,b;t,c)$ and intersection numbers $(\alpha ;\beta ;\gamma ;c)$ where $c\ge 0$ (i.e. we omit Möbius curves).

3.1.1. Components of $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$

We can list all topological possibilities for connected components of $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$ ($1\le i\le g-1$), up to isotopy, making use of their intersections with the core curves $c_i$ and $c_{i+1}$, and the arcs ${\gamma }_l$ ($2i-1\le l\le 2i+1$) and ${\beta }_l$ ($n+l-1\le l\le n+l+1$) (and hence from their generalized Dynnikov coordinates). Let ${\otimes }_i$ and ${\otimes }_{i+1}$ denote crosscap i and crosscap $i+1$, respectively. Given a connected component X of $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$ we associate with it a signature vector $\widehat{v_i}=(\widehat{c_i},{\widehat{c}}_{i+1};{\widehat{b}}_{n+i-1},{\widehat{b}}_{n+i})\in {\mathbb{Z}}_{\ge 0}^2\times {\mathbb{Z}}^2$ such that $\widehat{c_i}$ and ${\widehat{c}}_{i+1}$ give the number of intersections between X and the core curves of ${\otimes }_i$ and ${\otimes }_{i+1}$, respectively, and for $j=i,i+1$

$$\begin{array}{c}\hfill {\widehat{b}}_j=\frac{{\widehat{\beta }}_{n+j-1}-{\widehat{\beta }}_{n+j}}{2}\end{array}$$

(33)

where $\widehat{{\beta }_k}$ denote the number of intersections of X with ${\beta }_k$$(k=n+j-1,n+j)$.

Remark 8.

Note that each signature vector $\widehat{v_i}$ must satisfy Equation (10) of Lemma 1, and the inequality $sgn\left({\widehat{b}}_{n+i-1}\right)sgn\left({\widehat{b}}_{n+i}\right)\le 0$ as X is a connected component of $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$.

Then each connected component of $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$ is either a simple closed curve supported in $S_i^{\prime }\cup S_{i+1}^{\prime }$ or one of the following arcs described in Notation 4.

Notation 4.

Let $2i-1\le l\le m\le 2i+2$ and $k=i,i+1$.

• $X_{lm}^{v_i}$:

  (a)

  If $(l,m)\ne (2i-1,2i),(2i+1,2i+2)$ it passes above (resp. below) ${\otimes }_i$ if $l=2i-1$ (resp. $l=2i$), and it passes above (resp. below) ${\otimes }_{i+1}$ if $m=2i+1$ (resp. $m=2i+2$). It has one end point on ${\beta }_{n+i-1}$ and the other on ${\beta }_{n+i+1}$.

  (b)

  If $(l,m)=(2i-1,2i)$ it passes both above and below ${\otimes }_i$, and it has both end points on ${\beta }_{n+i-1}$. The case $(l,m)=(2i+1,2i+2)$ is described similarly.

  (c)

  If $l=m$ it passes above (resp. below) ${\otimes }_i$ if $l=2i-1$ (resp. $l=2i$) and has both end points on ${\beta }_{n+i-1}$. The case $l=m=2i+1$ is described similarly.

• $X_{l;k}^{v_i}$: it passes above (resp. below) ${\otimes }_i$ if $l=2i-1$ (resp. $l=2i$). It has ${\psi }_i=1$ and both end points on ${\beta }_{n+i-1}$. The cases $l=2i+1$ and $l=2i+2$ are described similarly.
• $X_i$, $X_i^{v_i}$, $X_{i+1}$, $X_{i+1}^{v_i}$, and $X_{ii+1}$: none of these components pass above or below ${\otimes }_i$ and ${\otimes }_{i+1}$; $X_i$ and $X_i^{v_i}$ have both end points on ${\beta }_{n+i-1}$ with ${\psi }_i=0$ and ${\psi }_i\ne 0$, respectively; $X_{i+1}$ and $X_{i+1}^{v_i}$ are described similarly; $X_{ii+1}$ has one end point on ${\beta }_{n+i-1}$ and the other on ${\beta }_{n+i+1}$.

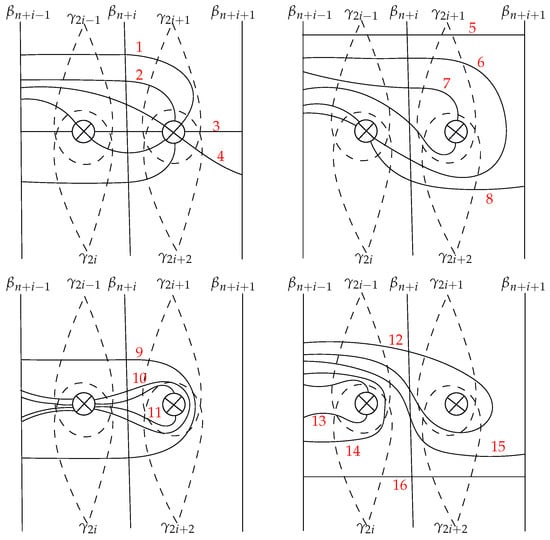
See, for example, the arcs 5, 15, 16 for item 1(a); 2, 9, 14 for item 1(b); 7, 12 for item 1(c); 1,4, 6, 8 for item 2; and 3, 10, 11, 13 for item 3 in Figure 9.

Figure 9. $1:X_{2i-1;i}^{(1,1;0,1)}$, $2:X_{2i-12i}^{(0,1;0,1)}$, $3:X_{ii+1}$, $4:X_{2i-1;i+1}$, $5:X_{2i-12i+1}$, $6:X_{2i-1;i}^{(1,0;0,1)}$, $7:X_{2i-12i-1}^{(0,1;0,1)}$, $8:X_{2i+2;i}$, $9:X_{2i-12i}^{(0,0;0,1)}$, $10:X_i^{(2,0;0,1)}$, $11:X_i^{(2,1;0,1)}$, $12:X_{2i-12i-1}^{(0,0;0,1)}$, $13:X_i$, $14:X_{2i-12i}^{(0,0;1,0)}$, $15:X_{2i-12i+2}$, $16:X_{2i2i+2}$.

Notation 5.

We shall omit the superscript ${\widehat{v}}_i$ for when ${\widehat{b}}_{n+i-1}={\widehat{b}}_{n+i}=0$. See, for example, the arcs 3, 4, 5, 8, 15, and 16 in Figure 9. We write $\left[P_i\right]$ for the set of simple closed curves in $S_i^{\prime }\cup S_{i+1}^{\prime }$, and $\left[X_{lm}^{v_i}\right]$, $\left[X_{l;k}^{v_i}\right]$, and $\left[X_i\right]$ for the set of arcs described in item 1, item 2, and item 3, respectively.

Notation 6.

Here and in what follows, we write $L_i$ to denote the arc system $L\cap (S_i^{\prime }\cup S_{i+1}^{\prime })$ for convenience.

Definition 1.

Let X be a component of $L_i$ with signature vector $\widehat{v_i}=(\widehat{c_i},{\widehat{c}}_{i+1};{\widehat{b}}_{n+i-1},{\widehat{b}}_{n+i})$. We say that X is a standard arc if at least one of ${\widehat{b}}_{n+i-1}$ and ${\widehat{b}}_{n+i}$ equals zero (Figure 9). We say that X is twisted if ${\widehat{b}}_{n+i-1}<0$ and ${\widehat{b}}_{n+i}>0$.

Definition 2.

We say that a component of $L_i$ is a positive arc if it satisfies $t_i-t_{i+1}>0$, it is negative if $t_i-t_{i+1}<0$, and it is neutral if $t_{i+1}-t_i=0$.

Figure 9 depicts examples of negative and neutral standard components of $L_i$. Other standard components can be obtained by symmetry, reflecting them in the arc ${\beta }_{n+i}$ or the diameter of the surface.

Remark 9.

As ${\widehat{b}}_{n+i-1}<0$ and ${\widehat{b}}_{n+i}>0$, and $t_i-t_{i+1}=0$ for a simple closed curve in $S_i^{\prime }\cup S_{i+1}^{\prime }$, we regard each such curve neutral and twisted.

Definition 3.

A twisted component of $L_i$ is called a negatively (resp. positively) half twisted arc if it is the $u_i^{-1}$ (resp. $u_i$) image of a standard arc. A negative (resp. positive) twisted component of $L_i$ that is not half twisted is called negatively (resp. positively) highly twisted. Each simple closed curve and twisted neutral component of $L_i$ is called neutrally twisted.

Notation 7.

Let ${\lambda }_k$ denote the number of non-core loop components of $L\cap S_k^{\prime }$ ($k=i,i+1$). We denote

$${\lambda }_{i+1}^{+}=\left\{\begin{array}{cc}{\lambda }_{i+1}\hfill & if{b}_{n+i}>0\hfill \\ 0\hfill & if{b}_{n+i}<0\hfill \end{array}\right.\mathrm{and}{\lambda }_i^{-}=\left\{\begin{array}{cc}{\lambda }_i\hfill & if{b}_{n+i-1}<0\hfill \\ 0\hfill & if{b}_{n+i-1}>0\hfill \end{array}\right.$$

We describe ${\lambda }_{c_{i+1}}^{+}$ and ${\lambda }_{c_i}^{-}$ similarly. Elsewhere $x^{+}$ denotes $max(x,0)$.

Let $A_i^{\prime }$ and $B_i^{\prime }$ be the number of above and below components of $L_i$ given in Lemma 4.

Notation 8.

Let $A_{i,i+1}^{\prime }=min(A_i^{\prime },A_{i+1}^{\prime })$ and $B_{i,i+1}^{\prime }=min(B_i^{\prime },B_{i+1}^{\prime })$. We write

$$\begin{array}{c}\hfill {\Delta }_i\left(A\right)=A_i^{\prime }-A_{i,i+1}^{\prime }and{\Delta }_{i+1}\left(A\right)=A_{i+1}^{\prime }-A_{i,i+1}^{\prime }\end{array}$$

(34)

$$\begin{array}{c}\hfill {\Delta }_i\left(B\right)=B_i^{\prime }-B_{i,i+1}^{\prime }and{\Delta }_{i+1}\left(B\right)=B_{i+1}^{\prime }-B_{i,i+1}^{\prime }\end{array}$$

(35)

Remark 10.

Geometrically, $A_{i,i+1}^{\prime }$ and $B_{i,i+1}^{\prime }$ give the number of components of $L_i$ that lie entirely above and below the diameter of the surface, respectively. Therefore, $A_{i,i+1}^{\prime }=X_{2i-12i+1}$ and $B_{i,i+1}^{\prime }=X_{2i2i+2}$. Then, ${\Delta }_i\left(A\right)$ (resp. ${\Delta }_i\left(B\right)$) is the number of above (resp. below) components of $L\cap S_i^{\prime }$ that are not contained in the arcs $X_{2i-1,2i+1}$ (resp. $X_{2i,2i+2}$); ${\Delta }_{i+1}\left(A\right)$ and ${\Delta }_{i+1}\left(B\right)$ are interpreted similarly.

Figure 10 illustrates these parameters, which we will refer to later to describe other parameters.

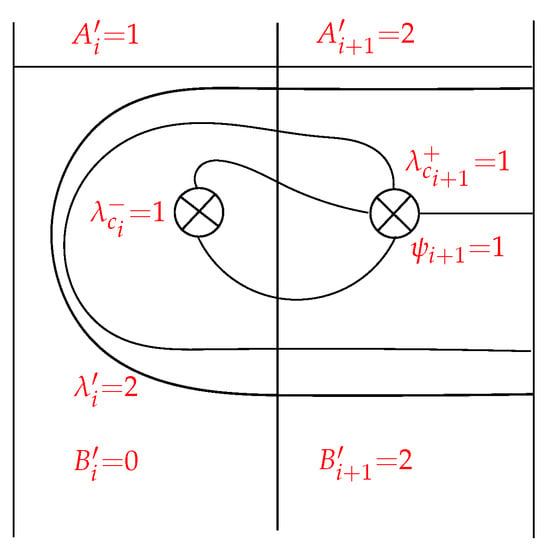
Figure 10. $A_{i,i+1}^{\prime }=1,B_{i,i+1}^{\prime }=0,{\Delta }_i\left(A\right)={\Delta }_i\left(B\right)=0,{\Delta }_{i+1}\left(A\right)=1,{\Delta }_{i+1}\left(B\right)=2$.

Remark 11.

The condition $t_i-t_{i+1}>0$ in Definition 2 implies that either ${\Delta }_i\left(B\right)\ne 0$ or ${\Delta }_{i+1}\left(A\right)\ne 0$ holds for a positive component. Then, $X_{lm}^{v_i}$ is positive if $l=2i+1$ or $m=2i$. Similarly, $X_{l;k}^{v_i}$ ($k=i,i+1$) is positive if $l=2i+1$ or $l=2i$. Similar arguments hold for negative components. Similarly, the condition $t_{i+1}-t_i=0$ implies that a neutral component in item 1(a) (i.e. $X_{2i-12i+1}$ and $X_{2i2i+2}$) and item 2 has ${\Delta }_k\left(A\right)={\Delta }_k\left(B\right)=0$ ($k=i,i+1$). A neutral component in item 1(b) has either ${\Delta }_i\left(A\right)\ne 0$ and ${\Delta }_i\left(B\right)\ne 0$ (i.e. $X_{2i-12i}^{v_i}$) or ${\Delta }_{i+1}\left(A\right)\ne 0$ and ${\Delta }_{i+1}\left(B\right)\ne 0$ (i.e. $X_{2i+12i+2}^{v_i}$).

Definition 4.

We say that two arcs in $S_i^{\prime }\cup S_{i+1}^{\prime }$ are compatible if they can be embedded disjointly in $S_i^{\prime }\cup S_{i+1}^{\prime }$.

A positive and a negative arc are compatible only when they form the arc systems scissors, anchors, or ribbons.

Definition 5.

Scissors at ${\otimes }_i$ consist of the arcs $X_{2i+2;i}$ and $X_{2i+1;i}$ (Figure 11a), and scissors at ${\otimes }_{i+1}$ consist of the arcs $X_{2i;i+1}$ and $X_{2i-1;i+1}$.

Figure 11. (a) Scissors at ${\otimes }_i$ with $X_{2i+2;i}=2$ and $X_{2i+1;i}=1$, (b) a left anchor with $X_{2i+2,i+1}^{(1,1;-1,0)}=1$ and $X_{2i+1,i+1}^{(1,1;-1,0)}=1$; (c) a left ribbon with $X_{2i+2;i}^{(2,1;-1,1)}=1$ and $X_{2i+1;i}^{(2,1;-1,1)}=1$.

A left anchor consists of $X_{2i+2,i+1}^{(1,1;-1,0)}$ and $X_{2i+1,i+1}^{(1,1;-1,0)}$ (see Figure 11b), and a right anchor consists of $X_{2i;i}^{(1,1;0,1)}$ and $X_{2i-1;i}^{(1,1;0,1)}$.

A left ribbon consists of arcs from the sets $\left[X_{2i+2;i}\right]$ and $\left[X_{2i+1;i}\right]$ (arcs of a ribbon are twisted and can have different signature vectors)(Figure 11c). A right ribbon consists of elements from the sets $\left[X_{2i;i+1}\right]$ and $\left[X_{2i-1;i+1}\right]$. Note that scissors, ribbons, and anchors may contain multiple copies of the same arc.

The positive and negative arcs of given scissors are respectively called positive and negative arms for the scissors. For example, $X_{2i+2;i}$ and $X_{2i+1;i}$ are negative and positive arms of the scissors, respectively. Positive and negative arms of anchors and ribbons are described similarly.

Remark 12.

Note that scissors, anchors, and ribbons are not compatible with each other. If a component of $L_i$ is compatible with any scissors, anchors, or ribbons, it must be a neutral arc.

Definition 6.

If $L_i$ comprises standard arcs it is called standard, and if it contains at least one twisted arc it is called twisted. If it contains positive arcs possibly with neutral arcs it is called positive. The case when $L_i$ is negative is described similarly. If $L_i$ contains only neutral arcs it is called neutral, and if it contains both positive and negative arcs it is called mixed.

Therefore, $L_i$ is mixed if and only if it contains either scissors or an anchor or a ribbon, and that the only case where $L_i$ is both twisted and mixed is when it contains ribbons.

3.1.2. Clover Equalities

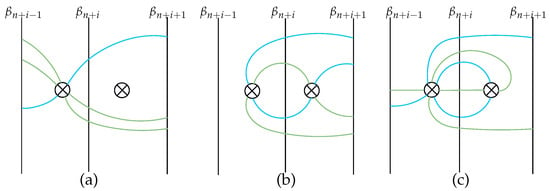
Let $u_i^{-1}(\gamma ;\beta )=({\gamma }^{\prime };{\beta }^{\prime })$ and $u_i(\gamma ;\beta )=({\gamma }^{″};{\beta }^{″})$. A clover of type I has leaves ${\gamma }_{2i-1},{\gamma }_{2i},{\gamma }_{2i+1}$, ${\gamma }_{2i+2}$, the diagonal arc ${\beta }_{n+i}$, and the diagonal curve $C_i$ (Figure 12a). A clover of type II and a clover of type III are the images of a clover of type I under the mapping classes $u_i^{-1}$ and $u_i$, respectively, and hence are as depicted in Figure 12b and Figure 12c, respectively.

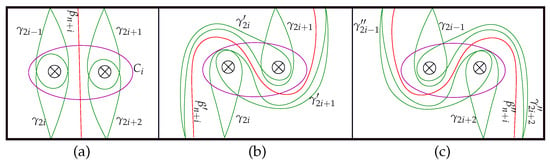
Figure 12. (a) A clover of type I, (b) a clover of type II, and (c) a clover of type III.

We present equalities associated with a clover of type I, type II, and type III given in Lemma 5, Lemma 9, and Lemma 12, respectively. Here and in what follows we abuse notation again using the symbols in Notation 4 to denote the number of corresponding components of $L_i$, and the symbols $\gamma ;\beta ,{\gamma }^{\prime };{\beta }^{\prime },{\gamma }^{″};{\beta }^{″}$ to denote the number of intersections. First, we fix some notation that will be necessary in the proof of Lemma 5.

Notation 9.

Given scissors at ${\otimes }_i$ and scissors at ${\otimes }_{i+1}$ let $s_i=min(X_{2i+1;i},X_{2i+2;i})$ and $s_{i+1}=min(X_{2i-1;i+1},X_{2i;i+1})$, respectively. Given a right and a left anchor in $S_i^{\prime }\cup S_{i+1}^{\prime }$ let $z_i=min(X_{2i-1,i}^{(1,1;0,1)},X_{2i,i}^{(1,1;0,1)})$ and $z_{i+1}=min(X_{2i+1,i+1}^{(1,1;-1,0)},X_{2i+2,i+1}^{(1,1;-1,0)})$, respectively. Given a left and a right ribbon in $S_i^{\prime }\cup S_{i+1}^{\prime }$ let $r_i=min(X_{2i+1;i}^{v_i},X_{2i+2;i}^{v_i^{\prime }})$ and $r_{i+1}=min(X_{2i-1;i+1}^{v_i},X_{2i;i+1}^{v_i^{\prime }})$, respectively. Finally, let $N_i$ and $N_{i+1}$ denote the sum of all neutral arcs from the sets $\left[X_{2i+12i+2}\right]$ and $\left[X_{2i-12i}\right]$, respectively, described in 1(b) in Notation 4 except for the standard components $X_{2i-12i}^{(0,0;0,1)}$ and $X_{2i+12i}^{(0,0;-1,0)}$ (i.e., those with zero intersection with the crosscaps). For each $1\le i\le g-1$ we set $d_i={ϵ}_i+{ϵ}_{i+1}$ where ${ϵ}_i=s_i+z_{i+1}+w_i+N_i$ and ${ϵ}_{i+1}=s_{i+1}+z_i+w_{i+1}+N_{i+1}$.

Remark 13.

If ${ϵ}_i\ne 0$ then ${ϵ}_{i+1}=0$, and that only one of $s_i,z_{i+1}$ and $w_i$ can be different than zero by Remark 12. Similarly, if ${ϵ}_{i+1}\ne 0$ then ${ϵ}_i=0$ and only one of $s_{i+1},z_i$ and $w_{i+1}$ is nonzero.

Lemma 5

(Equality for a clover of type I). Given a clover of type I in $S_i^{\prime }\cup S_{i+1}^{\prime }$ we have

$$\begin{array}{c}\hfill 2{\beta }_{n+i}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2d_i.\end{array}$$

(36)

where $d_i$ is as given in Notation 9.

Proof. 

Let $\left[X_{2i-12i}\right]=\left\{X_{2i-12i}^{v_i}\right\}$, $\left[X_{2i+12i+2}\right]=\left\{X_{2i+12i+2}^{v_i}\right\}$, and $\left[X_i\right]$ be the sets of neutral components of $L_i$ described in item 1(b) and item 3. of Notation 4, respectively. For $2i-1\le l\le m\le 2i+2$ with $(l,m)\ne (2i-1,2i),(2i+1,2i+2)$ and $k\in \{i,i+1\}$, write $\left[X_l\right]=\{X_{l,m}^{v_i},X_{l;k}^{v_i}\}$ for the set of components described in item 1(a), item 1(c), and item 2 of Notation 4, and $\left[P_i\right]$ for the set of simple closed curves supported in $S_i^{\prime }\cup S_{i+1}^{\prime }$. By Remark 12 we have the following cases:

Case 1:

$L_i$ is either positive or negative or neutral:

(i)

$\left[X_{2i-1}\right]\cup \left[X_{2i+2}\right]\ne \varnothing$ and $\left[X_{2i}\right]\cup \left[X_{2i+1}\right]=\varnothing$;

(ii)

$\left[X_{2i-1}\right]\cup \left[X_{2i+2}\right]=\varnothing$ and $\left[X_{2i}\right]\cup \left[X_{2i+1}\right]\ne \varnothing$;

(iii)

$\left[X_{2i-1}\right]\cup \left[X_{2i+2}\right]=\varnothing$ and $\left[X_{2i}\right]\cup \left[X_{2i+1}\right]=\varnothing$;

Case 2:

$L_i$ is mixed, that is, either scissors or an anchor or a ribbon exists. There are two subcases:

(i)

$\left[X_{2i+1}\right]\cup \left[X_{2i+2}\right]\ne \varnothing$ and $\left[X_{2i-1}\right]\cup \left[X_{2i}\right]=\varnothing$;

(ii)

$\left[X_{2i-1}\right]\cup \left[X_{2i+2}\right]=\varnothing$ and $\left[X_{2i}\right]\cup \left[X_{2i+1}\right]\ne \varnothing$;

For Case 1 we have $s_k=z_k=r_k=0$ ($k=i,i+1$) because $L_i$ is not mixed. Suppose first that Case 1(i) holds. Then, $L_i$ is negative by Remark 11 and Definition 4 (see, for example, Figure 13a), and we have ${\gamma }_{2i-1}+{\gamma }_{2i+2}>{\gamma }_{2i}+{\gamma }_{2i+1}$. First assume that $L_i$ is standard. It is easy to check that each negative standard component in $\left[X_{2i-1}\right]\cup \left[X_{2i+2}\right]$, each curve in $\left[P_i\right]$ and each neutral component except for $X_{2i-12i}^{(0,1;0,1)}$ and $X_{2i+12i+2}^{(0,1;0,1)}$ satisfies

$$\begin{array}{c}\hfill 2{\beta }_{n+i}+C_i={\gamma }_{2i-1}+{\gamma }_{2i+2}=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1}).\end{array}$$

(37)

Figure 13. (a) Case 1(i) where $L_i$ is standard; (b) Case 1(i) where $L_i$ is twisted, and (c) Case 1(iii).

Suppose that $X_{2i-12i}^{(0,1;0,1)}\ne 0$ and hence $X_{2i+12i+2}^{(0,1;0,1)}=0$ (note that elements of $\left[X_{2i-12i}\right]$ and $\left[X_{2i+12i+2}\right]$ are not compatible). We check that $X_{2i-12i}^{(0,1;0,1)}$ satisfies ${\gamma }_{2i-1}+{\gamma }_{2i+2}={\gamma }_{2i}+{\gamma }_{2i+1}$, and

$$2{\beta }_{n+i}+C_i-({\gamma }_{2i-1}+{\gamma }_{2i+2})=2X_{2i-12i}^{(0,1;0,1)}.$$

That is,

$$\begin{array}{c}\hfill 2{\beta }_{n+i}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2X_{2i-12i}^{(0,1;0,1)}.\end{array}$$

(38)

A similar argument holds for the case $X_{2i-12i}^{(0,1;0,1)}=0$ and $X_{2i+12i+2}^{(1,0;-1,0)}\ne 0$, and we get

$$\begin{array}{c}\hfill 2{\beta }_{n+i}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2X_{2i+12i+2}^{(1,0;-1,0)}.\end{array}$$

(39)

Equalities (37)–(39) are also satisfied for corresponding twisted components; given a standard component $X_{l,m}$ of $L_i$ with intersection numbers ${\gamma }_j(2i-1\le j\le 2i+2)$, ${\beta }_{n+i}$, and $C_i$, the twisted component $X_{l,m}^{v_i}$ has the same number of intersections on $C_i$ and increases the number of intersections on each ${\gamma }_j(2i-1\le j\le 2i+2)$ and $2{\beta }_{n+i}$ (and hence $2{\beta }_{n+i}+C_i$) by the same amount determined by its signature vector (Figure 13b). Therefore, equality (37) is also satisfied for each $X_{l,m}^{v_i}$. A similar argument holds for other twisted components. Then we have $d_i={ϵ}_i=N_i$, and

$$2{\beta }_{n+i}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2d_i$$

as required. Case 1(ii) follows by symmetry. For Case 1(iii), we note that as $L_i$ consists of only neutral components and each neutral component satisfies ${\gamma }_{2i-1}+{\gamma }_{2i+2}={\gamma }_{2i}+{\gamma }_{2i+1}$ except for $X_{2i-12i}^{(0,1;0,1)}$ and $X_{2i+12i+2}^{(0,1;0,1)}$ as shown above, we get either ${ϵ}_i=N_i\ne 0$ or ${ϵ}_{i+1}=N_{i+1}\ne 0$ as $X_{2i-12i}^{(0,1;0,1)}$ and $X_{2i+12i+2}^{(0,1;0,1)}$ are not compatible. Therefore, $d_i={ϵ}_i+{ϵ}_{i+1}$, and

$$\begin{array}{c}\hfill 2{\beta }_{n+i}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2d_i.\end{array}$$

(40)

as required.

Case 2(i) is divided into three subcases. Either $L_i$ contains scissors at ${\otimes }_i$ or a left anchor or a left ribbon by Definition 5 and Remark 12. Assume that $L_i$ contains scissors at ${\otimes }_i$. Then we have $X_{2i+1;i}\ne 0$, $X_{2i+2;i}\ne 0$ and hence $d_i={ϵ}_i=s_i=min(X_{2i+1;i},X_{2i+2;i})+N_i$ where $N_i=X_{2i+12i+2}^{(1,0;-1,0)}$ (twisted neutral components are not compatible with scissors). We obtain

$$\begin{array}{cc}\hfill 2{\beta }_{n+i}+C_i-2X_{2i+1;i}-2X_{2i+12i+2}^{(1,0;-1,0)}& ={\gamma }_{2i-1}+{\gamma }_{2i+2}\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill 2{\beta }_{n+i}+C_i-2X_{2i+2;i}-2X_{2i+12i+2}^{(1,0;-1,0)}& ={\gamma }_{2i}+{\gamma }_{2i+1}\hfill \end{array}$$

(42)

as shown in Figure 14a. Observe that ${\gamma }_{2i-1}+{\gamma }_{2i+2}\ge {\gamma }_{2i}+{\gamma }_{2i+1}$ if and only if $X_{2i+2;i}\ge X_{2i+1;i}$. Then from Equations (41) and (42) we get

$$\begin{array}{cc}\hfill 2{\beta }_{n+i}+C_i& =max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2min(X_{2i+2;i},X_{2i+1;i})+2X_{2i+12i+2}^{(1,0;-1,0)}\hfill \\ \hfill & =max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1})+2s_i+2X_{2i+12i+2}^{(1,0;-1,0)}.\hfill \end{array}$$

as required. Similarly, if $L_i$ contains a left anchor, it contains no scissors, no ribbons, and no right anchor. We have $d_i=z_{i+1}+N_i$ and Equation (36) is verified analogously. The case when there is a left ribbon is proved similarly. Case 2(ii) is also divided into three subcases: Either $L_i$ contains scissors at ${\otimes }_{i+1}$ or a right anchor or a right ribbon by Definition 5 and Remark 12 (see for instance Figure 14b). Then Case 2(ii) follows immediately from Case 2(i) by symmetry. □

Figure 14. (a) Example for Case 2(i) and (b) example for Case 2(ii).

The proof of Lemma 5 shows that each component of $L_i$ except for certain arcs and arc systems satisfies

$$2{\beta }_{n+i}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i}+{\gamma }_{2i+1}).$$

We shall call these arcs and arc systems exceptional arcs and arc systems with respect to a clover type I; and $d_i$ the exceptional parameter for a clover of type I.

Definition 7.

Each neutral arc in $\left[X_{2i+12i+2}\right]\backslash \left\{X_{2i+12i+2}^{(0,0;-1,0)}\right\}$ and $\left[X_{2i-12i}\right]\backslash \left\{X_{2i-12i}^{(0,0;0,1)}\right\}$ is called an exceptional arc with respect to a clover type I at ${\otimes }_i$ and ${\otimes }_{i+1}$, respectively (for example, in Figure 9, the arc labeled 2 is an exceptional arc at ${\otimes }_i$, whereas the arc labeled 9 is not); scissors, ribbons, and anchors in $S_i^{\prime }\cup S_{i+1}^{\prime }$ are called exceptional arc systems with respect to a clover of type I.

Let ${\Delta }_k\left(A\right)$ and ${\Delta }_k\left(B\right)$ $(k=i,i+1)$ be as described in Notation 8. The proof of Lemma 6 follows immediately from the definition of exceptional arcs and arc systems.

Lemma 6.

${\Delta }_{i+1}\left(A\right)\ne 0$ and ${\Delta }_{i+1}\left(B\right)\ne 0$ if and only if there exists at least one of the following arc or arc systems in $S_i^{\prime }\cup S_{i+1}^{\prime }$: an arc from the set $\left[X_{2i+12i+2}\right]$, scissors at ${\otimes }_i$, a left anchor, or a left ribbon. Similarly, ${\Delta }_i\left(A\right)\ne 0$ and ${\Delta }_i\left(B\right)\ne 0$ if and only if at least one of the following exists in $S_i^{\prime }\cup S_{i+1}^{\prime }$: an arc from the set $\left[X_{2i-12i}\right]$, scissors at ${\otimes }_{i+1}$, a right anchor, or a right ribbon.

Then, we can compute the exceptional parameter $d_i={ϵ}_i+{ϵ}_{i+1}$ in terms of generalized Dynnikov coordinates. We first give the following preliminary lemma.

Lemma 7.

Let $X_{2i+12i+2}^{(0,0;-1,0)}$ and $X_{2i-12i}^{(0,0;0,1)}$ be as given in Notation 4. Then,

$$\begin{array}{cc}\hfill X_{2i+12i+2}^{(0,0;-1,0)}& =min({\Delta }_{i+1}\left(A\right),{\Delta }_{i+1}\left(B\right),{\lambda }_i^{-})\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill X_{2i-12i}^{(0,0;0,1)}& =min({\Delta }_i\left(A\right),{\Delta }_i\left(B\right),{\lambda }_{i+1}^{+})\hfill \end{array}$$

(44)

Proof. 

The proof follows from Remark 10 and Figure 15 (also see [10]). □

Figure 15. Computation for $X_{2i+12i+2}^{(0,0;-1,0)}$ and $X_{2i-12i}^{(0,0;0,1)}$.

Lemma 8.

Let ${ϵ}_k$ $(k=i,i+1$) be as described in Notation 9. Then $d_i={ϵ}_i+{ϵ}_{i+1}$ where

$$\begin{array}{cc}\hfill {ϵ}_i& =min({\Delta }_{i+1}\left(A\right),{\Delta }_{i+1}\left(B\right))-X_{2i+12i+2}^{(0,0;-1,0)}\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {ϵ}_{i+1}& =min({\Delta }_i\left(A\right),{\Delta }_i\left(B\right))-X_{2i-12i}^{(0,0;0,1)}\hfill \end{array}$$

(46)

and $X_{2i-12i}^{(0,0;0,1)}$ and $X_{2i+12i+2}^{(0,0;-1,0)}$ are as given in Lemma 7.

Proof. 

We compute ${ϵ}_i$; ${ϵ}_{i+1}$ is computed analogously reflecting in the arc ${\beta }_{n+i}$. If at least one of ${\Delta }_{i+1}\left(A\right)$ and ${\Delta }_{i+1}\left(B\right)$ is equal to zero then ${ϵ}_i=0$ by Lemma 6. Suppose that ${\Delta }_{i+1}\left(A\right)\ne 0$ and ${\Delta }_{i+1}\left(B\right)\ne 0$.

Case 1:

There exists no exceptional arc system with respect to a clover type I in which case there must be exceptional arcs from the set $\left[X_{2i+12i+2}\right]$.

Case 2:

There exists an exceptional arc system with respect to a clover type I, which can be either scissors at ${\otimes }_i$ or a left anchor or a left ribbon possibly with compatible exceptional arcs from the set $\left[X_{2i+12i+2}\right]$.

We have two subcases in Case 1: (a) ${\Delta }_{i+1}\left(A\right)\le {\Delta }_{i+1}\left(B\right)$ and (b) ${\Delta }_{i+1}\left(A\right)\ge {\Delta }_{i+1}\left(B\right)$. Assume that we are in Case 1(a). Then there exist negative but no positive arcs in $S_i^{\prime }\cup S_{i+1}^{\prime }$ as only negative components increase the difference ${\Delta }_{i+1}\left(B\right)-{\Delta }_{i+1}\left(A\right)$ by Remark 11 and that there is no exceptional arc system with respect to a clover type I in $S_i^{\prime }\cup S_{i+1}^{\prime }$ by assumption. As each element of $\left[X_{2i+12i+2}\right]$ increases ${\Delta }_{i+1}\left(A\right)$ and ${\Delta }_{i+1}\left(B\right)$ by 1, and $N_i$ of those are exceptional we have

$$\begin{array}{cc}\hfill {\Delta }_{i+1}\left(A\right)& =N_i+X_{2i+12i+2}^{(0,0;-1,0)}\le {\Delta }_{i+1}\left(B\right)\hfill \end{array}$$

(recall that $X_{2i+12i+2}^{(0,0;-1,0)}$ is the only element of $\left[X_{2i+12i+2}\right]$ that is not exceptional). Because $d_i={ϵ}_i=N_i$ we get $d_i=min({\Delta }_{i+1}\left(A\right),{\Delta }_{i+1}\left(B\right))-X_{2i+12i+2}^{(0,0;-1,0)}$ as required. Case 1(b) is proved similarly. Now assume that we are in Case 2. Assume that there exists scissors at ${\otimes }_i$. As the only element of $\left[X_{2i+12i+2}\right]$ that is compatible with the scissors is the standard exceptional arc $X_{2i+12i+2}^{(1,0;-1,0)}$, we have $N_i=X_{2i+12i+2}^{(1,0;-1,0)}$, and hence $d_i={ϵ}_i=s_i+N_i$. By Remark 12, every other arc compatible with the scissors is neutral and has no affect on ${\Delta }_{i+1}\left(A\right)$ and ${\Delta }_{i+1}\left(B\right)$. Therefore,

$$\begin{array}{cc}\hfill {\Delta }_{i+1}\left(A\right)& =X_{2i+1;i}+X_{2i+12i+2}^{(1,0;-1,0)}\hfill \\ \hfill {\Delta }_{i+1}\left(B\right)& =X_{2i+2;i}+X_{2i+12i+2}^{(1,0;-1,0)}\hfill \end{array}$$

As $s_i=min(X_{2i+1;i},X_{2i+2;i})$, $N_i=X_{2i+12i+2}^{(1,0;-1,0)}$ and $X_{2i+12i+2}^{(0,0;-1,0)}=0$ we obtain

$$d_i=min({\Delta }_{i+1}\left(A\right),{\Delta }_{i+1}\left(B\right))=min({\Delta }_{i+1}\left(A\right),{\Delta }_{i+1}\left(B\right))+X_{2i+12i+2}^{(0,0;-1,0)}$$

as required. In the cases when there is a left anchor and a left ribbon, we note that there may exist both twisted and standard exceptional arcs in $\left[X_{2i+12i+2}\right]$. In addition, $X_{2i+12i+2}^{(0,0;-1,0)}=0$ if there exists a left ribbon and $X_{2i+12i+2}^{(0,0;-1,0)}\ge 0$ if there exists a left anchor. Again, as each positive (resp. negative) arm of a left anchor or a left ribbon increases ${\Delta }_{i+1}\left(A\right)$ (resp. ${\Delta }_{i+1}\left(B\right)$) by 1, and only neutral arcs are compatible with exceptional arc and arc systems, the proof follows similarly. □

Taking the $u_i^{-1}$ images of exceptional arcs with respect to a clover type I in $S_i^{\prime }\cup S_{i+1}^{\prime }$, we obtain elements of $\left[X_{2i+2;i+1}\right]$ and $\left[X_{2i-1;i}\right]$, which are called exceptional arcs with respect to a clover of type II in $S_i^{\prime }\cup S_{i+1}^{\prime }$ (Figure 16). Similarly, taking the $u_i^{-1}$ images of scissors, anchors, and ribbons in $S_i^{\prime }\cup S_{i+1}^{\prime }$ we get negatively half twisted scissors, anchors, and ribbons, which are called exceptional arc systems with respect to a clover type II in $S_i^{\prime }\cup S_{i+1}^{\prime }$ (see Figure 17). This leads us to the equality in Lemma 9. First we introduce some notation for the parameters associated with exceptional arc and arc systems with respect to a clover type II.

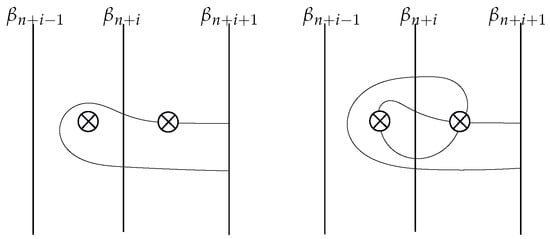
Figure 16. $u_i^{-1}$ images of exceptional arcs of type I give exceptional arcs of type II.

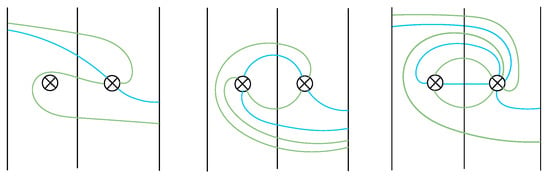
Figure 17. $u_i^{-1}$ images of scissors, anchors, and ribbons, ordered from left to right, are exceptional arc systems with respect to a clover of type II.

Notation 10.

Let $e_i={ϵ}_i^{\prime }+{ϵ}_{i+1}^{\prime }$ where ${ϵ}_i^{\prime }=s_i^{\prime }+z_i^{\prime }+r_i^{\prime }+N_i^{\prime }$ where $N_i^{\prime }$ and $N_{i+1}^{\prime }$ denote the number of exceptional arcs of type II that are from the sets $\left[X_{2i-1;i}\right]$ and $\left[X_{2i+2;i}\right]$, respectively, and

$$\begin{array}{cc}\hfill s_i^{\prime }& =min\left(u_i^{-1}\left(X_{2i+1;i}\right),u_i^{-1}\left(X_{2i+2;i}\right)\right),s_{i+1}^{\prime }=min\left(u_i^{-1}\left(X_{2i-1;i+1}\right),u_i^{-1}\left(X_{2i;i+1}\right)\right),\hfill \\ \hfill z_i^{\prime }& =min\left(u_i^{-1}\left(X_{2i+1,i+1}^{(1,1;-1,0)}\right),u_i^{-1}\left(X_{2i+2,i+1}^{(1,1;-1,0)}\right)\right),z_{i+1}^{\prime }=min\left(u_i^{-1}\left(X_{2i-1,i}^{(1,1;0,1)}\right),u_i^{-1}\left(X_{2i,i}^{(1,1;0,1)}\right)\right),\hfill \\ \hfill r_i^{\prime }& =min\left(u_i^{-1}\left(X_{2i+1,i}^{v_i}\right),u_i^{-1}\left(X_{2i+2,i}^{v_i^{\prime }}\right)\right),r_{i+1}^{\prime }=min\left(u_i^{-1}\left(X_{2i-1,i+1}^{v_i}\right),u_i^{-1}\left(X_{2i,i+1}^{v_i^{\prime }}\right)\right).\hfill \end{array}$$

The value $e_i$ is called the exceptional parameter for a clover of type II.

Lemma 9

(Equality for a clover of type II). Given a clover of type II we have

$$\begin{array}{c}\hfill 2{\beta }_{n+i}^{\prime }+C_i=max({\gamma }_{2i+1}+{\gamma }_{2i},{\gamma }_{2i+1}^{\prime }+{\gamma }_{2i}^{\prime })+2e_i.\end{array}$$

(47)

where the exceptional parameter $e_i$ is as given in Notation 10.

We require the following parameters to compute $e_i$ and the other exceptional parameters in terms of generalized Dynnikov coordinates.

Notation 11.

Let X be a component of $L_i$ with $\widehat{v_i}=(\widehat{c_i},{\widehat{c}}_{i+1};{\widehat{b}}_{n+i-1},{\widehat{b}}_{n+i})$. Write

$$\begin{array}{cc}\hfill {\widehat{\chi }}_i\left(A\right)& ={\left({\widehat{b}}_{n+i}\right)}^{+}-{\widehat{\Delta }}_i\left(A\right),{\widehat{\chi }}_{i+1}\left(A\right)={(-{\widehat{b}}_{n+i-1})}^{+}-{\widehat{\Delta }}_{i+1}\left(A\right)\hfill \\ \hfill {\widehat{\chi }}_i\left(B\right)& ={\left({\widehat{b}}_{n+i}\right)}^{+}-{\widehat{\Delta }}_i\left(B\right),{\widehat{\chi }}_{i+1}\left(B\right)={(-{\widehat{b}}_{n+i-1})}^{+}-{\widehat{\Delta }}_{i+1}\left(B\right)\hfill \end{array}$$

Definition 8.

We define $\chi \left(X\right)$ as follows:

$$\chi \left(X\right)=\left\{\begin{array}{cc}min({\widehat{\chi }}_i\left(B\right),{\widehat{\chi }}_{i+1}\left(A\right))\hfill & ifXispositive\hfill \\ min({\widehat{\chi }}_i\left(A\right),{\widehat{\chi }}_{i+1}\left(B\right)),\hfill & ifXisnegative\hfill \\ min({\widehat{\chi }}_k\left(A\right),{\widehat{\chi }}_k\left(B\right)),\hfill & ifXisneutral\hfill \end{array}\right.$$

We note that if X is neutral, ${\widehat{\chi }}_k\left(A\right)={\widehat{\chi }}_k\left(B\right)$ for each $k=i,i+1$.

Geometrically, $\chi \left(X\right)$ gives information about the amount of twist of X and reveals whether X is positive, negative, or neutral by Remark 11. Observe that a standard component X of $L_i$ either has $\chi \left(X\right)=0$ or $\chi \left(X\right)=-1$. The possibilities for the latter case are given in Remark 14.

Remark 14.

Let X be standard. When X is negative, $\chi \left(X\right)=-1$ if and only if

$$X\in \{X_{2i-12i-1}^{(0,0;0,1)},X_{2i-12i-1}^{(0,1;0,1)},X_{2i+22i+2}^{(0,0;-1,0)},X_{2i+22i+2}^{(1,0;-1,0)},X_{2i-12i+2}\}$$

See, for instance, $l_2=X_{2i+22i+2}^{(0,0;-1,0)},l_3=X_{2i+22i+2}^{(1,0;-1,0)},l_3^{☆}=X_{2i-12i+2}$ in Figure 18. Similarly, when X is positive, $\chi \left(X\right)=-1$ if and only if

$$X\in \{X_{2i+12i+1}^{(0,0;-1,0)},X_{2i+12i+1}^{(1,0;-1,0)},X_{2i2i}^{(0,0;0,1)},X_{2i2i}^{(0,1;0,1)},X_{2i2i+1}\}.$$

Figure 18. The set $S_0$.

Remark 15.

Note that a standard arc cannot be compatible with a highly twisted arc X with $\chi \left(X\right)>1$. Furthermore, if an arc X has ${\psi }_{i+1}\ne 0$, it is either a standard arc or a highly twisted arc from the sets $\left[X_{2i+2;i+1}\right]$ or $\left[X_{2i+1;i+1}\right]$. A similar argument holds for an arc X with ${\psi }_i\ne 0$.

Definition 9.

Suppose that $L_i$ is not mixed. We define $\chi \left(i\right)$ for $L_i$ by replacing X with $L_i$ and removing all hats from the symbols given in Notation 11.

Notation 12.

Let $X_{2i-12i}=X_{2i-12i}^{(0,0;0,1)}$ and $X_{2i+12i+2}=X_{2i+12i+2}^{(0,0;-1,0)}$ be as given in Lemma 7. For notational simplicity we shall denote ${\mathrm{\Lambda }}_i={\lambda }_i^{-}-X_{2i+12i+2},{\mathrm{\Lambda }}_{i+1}={\lambda }_{i+1}^{+}-X_{2i-12i}$ and

$$\begin{array}{cc}\hfill {\overline{\Delta }}_i\left(B\right)& ={\Delta }_i\left(B\right)-X_{2i-12i},{\overline{\Delta }}_i\left(A\right)={\Delta }_i\left(A\right)-X_{2i-12i}\hfill \\ \hfill {\overline{\Delta }}_{i+1}\left(B\right)& ={\Delta }_{i+1}\left(B\right)-X_{2i+12i+2},{\overline{\Delta }}_{i+1}\left(A\right)={\Delta }_{i+1}\left(A\right)-X_{2i+12i+2}\hfill \end{array}$$

We also introduce the following components for twisted components of $L_i$:

$$\begin{array}{c}\hfill p_1=2{(-b_{n+i-1})}^{+}-{\Delta }_{i+1}\left(B\right),p_2=2{\left(b_{n+i}\right)}^{+}-{\Delta }_i\left(A\right)\\ \hfill p_3=2{(-b_{n+i-1})}^{+}-{\Delta }_{i+1}\left(A\right),p_4=2{\left(b_{n+i}\right)}^{+}-{\Delta }_i\left(B\right)\end{array}$$

Geometrically, $p_1$ denotes the number of loop components of $L\cap S_i^{\prime }$ that are not contained in below components of $L\cap S_{i+1}^{\prime }$ for a twisted component of $L_i$. The interpretation of the other parameters $p_k$ is similar.

To understand these parameters better, let us consider Figure 10 again where $L_i$ consists of three components: $l_1=X_{2i+12i+2},l_2=X_{2i+1,2i+2}$, and $l_3=X_{2i+2;i+1}^{(1,2;-1,1)}$. Because $l_1$ and $l_2$ are neutral $\chi \left(l_1\right)=\chi \left(l_2\right)=0$. Additionally, $l_3$ is a negative twisted component with $\chi \left(l_3\right)=min(1,1)=1$ and $p_1=3$.

Lemma 10.

Let $L_i$ be negative. Then, $e_i={ϵ}_i^{\prime }+{ϵ}_{i+1}^{\prime }$ where

$${ϵ}_i^{\prime }=min({\mathrm{\Lambda }}_i,{\psi }_{i+1},{\overline{\Delta }}_{i+1}\left(B\right),p_1)and{ϵ}_{i+1}^{\prime }=min({\mathrm{\Lambda }}_{i+1},{\psi }_i,{\overline{\Delta }}_i\left(A\right),p_2)$$

(48)

Proof. 

Here we only prove ${ϵ}_i^{\prime }$. The formula for ${ϵ}_{i+1}^{\prime }$ is obtained similarly. We first note that each exceptional arc in $\left[X_{2i+2;i+1}\right]$ and negatively half twisted scissors at ${\otimes }_i$, left anchor and left ribbon increases each ${\lambda }_i^{-},{\psi }_{i+1},{\Delta }_{i+1}\left(B\right)$ by 1 (see Figure 16 and Figure 17). Therefore if at least one of ${\lambda }_i^{-},{\psi }_{i+1},{\Delta }_{i+1}\left(B\right)$ equals zero for $L_i$ we get ${ϵ}_i^{\prime }=0$. For convenience, let us say that a subset of $L_i$ has property P if it satisfies ${\lambda }_i^{-}\ne 0$, ${\psi }_{i+1}\ne 0$ and ${\Delta }_{i+1}\left(B\right)\ne 0$. The proof is based on constructing all possible configurations of arcs (i.e., compatible sets) satisfying property P, and verifying that Equation (48) holds for each such collection of arcs. Let $L_i$ have property P. The constraint provided by property P and Remark 11 imply that each element of $L_i$ belongs to one of the two sets described as follows: The first set I is the subset of $L_i$ whose elements affect none of the values ${\lambda }_i^{-}$, ${\psi }_{i+1}$ and ${\Delta }_{i+1}\left(B\right)$ yet are compatible with those satisfying property P. The second set S contains negative components affecting at least one of ${\lambda }_i^{-}$, ${\psi }_{i+1}$, ${\Delta }_{i+1}\left(B\right)$. Furthermore, S is partitioned into two subsets $S_0$ and $S_1$ such that if $X\in S_0$ then $\chi \left(X\right)\le 0$ and X is one of the following arcs depicted in Figure 18; and if $X\in S_1$ then $\chi \left(X\right)\ge 1$ and X is compatible with an arc with ${\psi }_{i+1}\ne 0$. In particular, if $X\in S_1$ with ${\psi }_{i+1}=0$ it has $\chi \left(X\right)=1$ and it is one of the arcs $l_{15},l_{16},l_{17},l_{18}$ depicted in Figure 19; and if ${\psi }_{i+1}\ne 0$, it is a highly twisted exceptional arc from the set $\left[X_{2i+2;i+1}\right]$ such as $l_{18}$ and $l_{19}$, as depicted in Figure 19. Let ${\mathcal{C}}_k$ be the family of k-element subsets of $L_i$ (i.e., possible configurations of exactly k arcs from the sets $S_0$ and $S_1$) satisfying property P. Again, by abuse of notation the symbols $l_i$ we use to indicate these arcs will also denote the number of corresponding arcs.

Figure 19. The case where each arc X in $S_1$ has $\chi \left(X\right)=1$.

First, observe from Figure 16 and Figure 17 that $l_0$ is a standard exceptional arc with respect to a clover type II. In addition, $l_{18},l_{19}$ are examples for twisted exceptional arcs and $\{l_1,l_9\}$, $\{l_4,l_8\}$, and $\{l_{12},l_{15}\}$ form exceptional arc systems with respect to a clover type II.

• $\chi \left(i\right)\le 0$: Each component of $L_i\backslash I$ belongs to $S_0$ where $\chi \left(l_2\right)=\chi \left(l_3\right)=\chi \left(l_{☆}\right)=-1$; and $\chi \left(l_k\right)=0$ for every other $l_k$ in $S_0$. As to be explained later in Remark 16, we need another parameter $p_1=2{(-b_{n+i-1})}^{+}-{\Delta }_{i+1}\left(B\right)$. For simplicity, we list the 4–tuples $({\lambda }_i,{\psi }_{i+1},{\Delta }_{i+1}\left(B\right),p_1)$ in Table 1 corresponding to the arcs $l_k$ in $S_0$. Observe from Table 1 that $l_0$ is the only element satisfying property P alone hence ${\mathcal{C}}_1=\left\{\left\{l_0\right\}\right\}$. Furthermore, it increases each ${\lambda }_i,{\psi }_{i+1}$, ${\Delta }_{i+1}\left(B\right)$ and $p_1$ by 1, yielding ${ϵ}_i^{\prime }=N_i=l_0=min\left(M_1,p_1\right)$ as required. In order to construct ${\mathcal{C}}_k$ $(k>1$), we make use of another set $I_k$, which is the set of k-tuples $(i_1,i_2,\cdots ,i_k)$ for the compatible components $l_{i_1},l_{i_2},\cdots ,l_{i_k}$ where $i_j\in \{☆,k:0\le k\le 14\}$. We chose to use the star symbol here to indicate that $l_{☆}$ is the only arc that is not compatible with any exceptional arc or arc system (in fact it is compatible with only $l_1,l_2$, and $l_3$). We get, $I_2=I_2^{\left(1\right)}\cup I_2^{\left(2\right)}\cup I_2^{\left(3\right)}$, where

  $$I_2^{\left(1\right)}=\{(0,j):1\le j\le 14\},I_2^{\left(2\right)}=\{(1,☆),(1,j):1<j<14,j\ne 7,8\}\mathrm{and}$$

  $$\begin{array}{cc}\hfill I_2^{\left(3\right)}=& \left\{\right(2,3),(2,☆),(2,7),(2,9),(2,14),(3,☆),(3,4),(3,7),(3,8),(3,9),(3,10),(3,14),(4,6)\hfill \\ & ,(4,8),(4,10),(4,12),(4,14),(5,6),(5,13),(5,14),(6,12),(6,13),(6,14),(7,8),(7,9),\hfill \\ & (7,10),(7,14),(8,9),(8,10),(8,14),(9,10),(9,11),(10,12),(11,13),(12,13)\}.\hfill \end{array}$$

  and obtain that ${\mathcal{C}}_2={\mathcal{C}}_2^{\left(1\right)}\cup {\mathcal{C}}_2^{\left(2\right)}$ where

  $${\mathcal{C}}_2^{\left(1\right)}=\left\{\{l_0,l_j\}:1\le j\le 14\right\}\mathrm{and}{\mathcal{C}}_2^{\left(2\right)}=\left\{\{l_1,l_2\},\{l_1,l_9\},\{l_4,l_8\},\{l_4,l_{14}\},\{l_5,l_{14}\},\{l_6,l_{14}\}\right\}.$$
  Table 1. $({\lambda }_i,{\psi }_{i+1},{\Delta }_{i+1}\left(B\right),p_1)$ for the arcs of $S_0$.

  ${\mathit{l}}_0$ $(1,1,1,1)$	${\mathit{l}}_1$ $(0,1,0,0)$	${\mathit{l}}_2$ $(1,0,2,0)$	${\mathit{l}}_3$ $(0,0,2,0)$	${\mathit{l}}_{☆}$ $(0,0,1,-1)$	${\mathit{l}}_4$ $(0,1,1,1)$	${\mathit{l}}_5$ $(1,2,0,2)$	${\mathit{l}}_6$ $(0,2,0,2)$
  $l_7$ $(2,0,2,2)$	$l_8$ $(1,0,2,2)$	$l_9$ $(1,0,1,1)$	$l_{10}$ $(0,0,1,1)$	$l_{11}$ $(1,0,0,2)$	$l_{12}$ $(0,1,0,2)$	$l_{13}$ $(1,1,0,2)$	$l_{14}$ $(1,0,1,1)$

First consider ${\mathcal{C}}_2^{\left(1\right)}$. Recall that to compute the parameters associated with a compatible set, we simply add the corresponding components of arcs. For example, from Table 1 we compute that $(M_1,p_1)=(1,1)$ for $(l_0,l_1)$. We immediately check that for each $\{l_0,l_j\}\in {\mathcal{C}}_2^{\left(1\right)}$ we have $l_0=N_i^{\prime }=M_1\le p_1$, and and therefore ${ϵ}_i^{\prime }=N_i^{\prime }=l_0=min\left(M_1,p_1\right)$ (note that taking multiple copies of arcs does not change the formula). We continue with ${\mathcal{C}}_2^{\left(2\right)}$. The set $\{l_1,l_2\}$ contains no exceptional arc or arc systems with respect to a clover type II, and observe from Table 1 as above that $p_1=0$. Therefore, ${ϵ}_i^{\prime }=0=min(M_1,p_1)$ as required. Similarly, we check $\{l_1,l_9\}$. This set contains negatively half twisted scissors (Figure 17) but no exceptional arcs hence we have ${ϵ}_i^{\prime }=s_i^{\prime }$. We check that $l_1={\psi }_{i+1}$ and $l_9={\lambda }_i={\Delta }_{i+1}$. Therefore, $s_i^{\prime }=M_1=min(l_1,l_9)$. Furthermore, $p_1$ is increased by 1 by both $l_1$ and $l_9$. This implies $M_1\le p_1$ yielding ${ϵ}_i^{\prime }=s_i^{\prime }=min\left(M_1,p_1\right)$ as required. Similarly, $\{l_4,l_8\}$ is a negatively half twisted left anchor (Figure 17) and hence ${ϵ}_i^{\prime }=z_i^{\prime }$. We check that $z_i^{\prime }=min(l_4,l_8)=M_1\le p_1$ yielding ${ϵ}_i^{\prime }=z_i^{\prime }=min\left(M_1,p_1\right)$ as required. Finally, none of $(l_j,l_{14})\in {\mathcal{C}}_2^{\left(2\right)}$ contains an exceptional arc or arc system. Since $l_{14}=X_{2i+12i+2}^{(0,0;-1,0)}$ we get $M_1=0$ yielding ${ϵ}_i^{\prime }=0$ as expected. The formula can be verified similarly for elements of ${\mathcal{C}}_3$ as follows.

We have $I_3=I_3^{\left(1\right)}\cup I_3^{\left(2\right)}\cup I_3^{\left(3\right)}$ where $I_3^{\left(1\right)}=\{(0,j,k):(j,k)\in I_2,j,k\ne ☆\}$ and $I_3^{\left(2\right)}=\{(1,j,k):(j,k)\in I_2,j,k\notin \{7,8,14\}\}$ and

$$\begin{array}{cc}\hfill I_3^{\left(3\right)}=\{& (2,3,7),(2,3,9),(2,3,☆),(2,3,14),(2,7,9),(3,4,8),(3,4,10),(3,4,14),(3,7,8),(3,7,9),\hfill \\ & (3,7,10),(3,7,14),(3,8,9),(3,8,10),(3,8,14),(3,9,10),(4,6,12),(4,6,14),(4,8,10),\hfill \\ & (4,8,14),(4,10,12),(5,6,13),(5,6,14),(6,12,13),(7,8,9),(7,8,10),(7,8,14),\hfill \\ & (7,9,10),(8,9,10)\}.\hfill \end{array}$$

Hence, ${\mathcal{C}}_3={\mathcal{C}}_3^{\left(1\right)}\cup {\mathcal{C}}_3^{\left(2\right)}$ where ${\mathcal{C}}_3^{\left(1\right)}=\left\{\{l_0,l_j,l_k\}:(j,k)\in I_2,j,k\ne ☆\right\}$ and

$$\begin{array}{cc}\hfill {\mathcal{C}}_3^{\left(2\right)}=\{& \{l_1,l_2,l_3\},\{l_1,l_2,l_{☆}\},\{l_1,l_2,l_9\},\{l_1,l_3,l_9\},\{l_1,l_9,l_{10}\},\{l_1,l_9,l_{11}\},\{l_3,l_4,l_8\},\{l_3,l_4,l_{14}\},\hfill \\ \hfill & \{l_4,l_6,l_{14}\},\{l_4,l_8,l_{10}\},\{l_4,l_8,l_{14}\},\{l_5,l_6,l_{14}\}\}.\hfill \end{array}$$

First consider ${\mathcal{C}}_3^{\left(1\right)}$. If $(j,k)\in I_1^{\left(2\right)}$ we get $\{l_0,l_0,l_k\}(1\le k\le 14)$, and the proof is similar to that of ${\mathcal{C}}_2^{\left(1\right)}$. If $(j,k)\in I_2^{\left(2\right)}$ we get $\{l_0,l_1,l_k\}$ ($1\le k\le 13$, $k\ne 7,8$). We compute from Table 1 that for each k with $k\ne 2,9$ we have that ${ϵ}_i^{\prime }=l_0=N_i^{\prime }=M_1=min(M_1,p_1)$. For $k=2$ we get that ${ϵ}_i^{\prime }=N_i=l_0=p_1=min(M_1,p_1)$. Similarly for $k=9$ we compute that ${ϵ}_i^{\prime }=s_i^{\prime }+N_i^{\prime }=min(l_1,l_9)+l_0=min(M_1,p_1)$ ($L_i$ contains half twisted scissors $\{l_1,l_9\}$). If $(j,k)\in I_2^{\left(3\right)}$ we have ${ϵ}_i^{\prime }=l_0=M_1=min(M_1,p_1)$ since $M_1=0$ for each corresponding $(l_j,l_k)$; and for $\{l_0,l_4,l_8\}$ we have ${ϵ}_i^{\prime }=z_i^{\prime }+N_i^{\prime }=min(l_4,l_8)+l_0=M_1=min(M_1,p_1)$ ($L_i$ contains half twisted anchor $\{l_4,l_8\}$).

Finally, for $\{l_j,l_k,l_m\}\in {\mathcal{C}}_3^{\left(2\right)}$ we similarly verify from Table 1 that for $(i,j,k)\in \left\{\right(1,2,3),(1,2,☆\left)\right\}$${ϵ}_i^{\prime }=p_1=0$; for $(i,j,k)\in \left\{\right(1,2,9),(1,3,9),(1,9,10),(1,9,11\left)\right\}$${ϵ}_i^{\prime }=s_i^{\prime }=min(M_1,p_1)$; for $\{l_3,l_4,l_8\},\{l_4,l_8,l_{10}\},\{l_4,l_8,l_{14}\}$${ϵ}_i^{\prime }=M_1=min(M_1,p_1)$, and for $\{l_3,l_4,l_{14}\},\{l_4,l_6,l_{14}\},\{l_5,l_6,l_{14}\}$${ϵ}_i^{\prime }=M_1=0=min(M_1,p_1)$. Similarly, we have $I_4=I_4^{\left(1\right)}\cup I_4^{\left(2\right)}\cup I_4^{\left(3\right)}$ where

$$I_4^{\left(1\right)}=\{(0,j,k,m):(j,k,m)\in I_3,j,k,m\ne ☆\},I_4^{\left(2\right)}=\{(1,j,k,m):(j,k,m)\in I_3,j,k,m\notin \{7,8\}\}$$

and $I_4^{\left(3\right)}=\left\{(2,3,7,9),(3,4,8,10),(3,7,8,9),(3,7,8,10),(3,8,9,10),(7,8,9,10)\right\}$.

We get ${\mathcal{C}}_4={\mathcal{C}}_4^{\left(1\right)}\cup {\mathcal{C}}_4^{\left(2\right)}$ where ${\mathcal{C}}_4^{\left(1\right)}=\left\{\{l_0,l_j,l_k,l_m\}:(j,k,m)\in I_3,j,k,m\ne ☆\right\}$

$$\begin{array}{cc}\hfill {\mathcal{C}}_4^{\left(2\right)}=\left\{\right\{& l_1,l_2,l_3,l_9\},\{l_1,l_2,l_3,l_{☆}\},\{l_1,l_3,l_9,l_{10}\},\{l_3,l_4,l_8,l_{10}\},\{l_3,l_4,l_8,l_{14}\}\}.\hfill \end{array}$$

In addition, ${\mathcal{C}}_5={\mathcal{C}}_5^{\left(1\right)}\cup {\mathcal{C}}_5^{\left(2\right)}$ where ${\mathcal{C}}_5^{\left(1\right)}=\left\{\{l_0,l_j,l_k,l_m,l_n\}:(j,k,m,n)\in I_4,j,k,m,n\ne ☆\right\}$ and ${\mathcal{C}}_5^{\left(2\right)}=\varnothing$ as there is no 5 element compatible set that does not contain $l_0$ but satisfies property P. And finally, ${\mathcal{C}}_6=\{l_0,l_3,l_7,l_8,l_9,l_{10}\}$. We note that there is no ${\mathcal{C}}_k$ with $k\ge 6$. The verification of the formula for $k=4,5,6$ is analogous.

2.

${\chi }_i>0$: At least a component of $L_i\backslash I$ belongs to the set $S_1$. There are two subcases depending on whether or not $L_i$ contains a highly twisted arc X with $\chi \left(X\right)>1$.

(a)

No component X of $L_i$ has $\chi \left(X\right)>1$: Then $L_i$ contains a highly twisted arc X that has $\chi \left(X\right)=1$ (Figure 19). Let ${\mathcal{A}}_k$ denote the set of arcs that are compatible with the arc $l_k\in S_1$. Then,

$$\begin{array}{cc}\hfill {\mathcal{A}}_{15}& =\{l_0,l_8,l_9,l_{10},l_{12},l_{16},l_{19},l_{20}\},{\mathcal{A}}_{16}=\{l_0,l_9,l_{11},l_{10},l_{15},l_{20}\},{\mathcal{A}}_{17}=\{l_0,l_8,l_9,l_{18},l_{19}\},\hfill \\ \hfill {\mathcal{A}}_{18}& =\{l_0,l_7,l_9,l_{17},l_{20}\},{\mathcal{A}}_{19}=\{l_0,l_4,l_6,l_8,l_{10},l_{17},l_{15}\},{\mathcal{A}}_{20}=\{l_0,l_5,l_6,l_{11},l_{15},l_{18}\}\hfill \end{array}$$

Any compatible set containing $l_k\in S_1$ is constructed from elements of ${\mathcal{A}}_k$ such that property P is satisfied. Therefore, a compatible set $\mathcal{C}$ can contain the standard exceptional arc $l_0$ (which is compatible with each element of $S_1$) and the twisted exceptional arcs $l_{19}$ and $l_{20}$. The only exceptional arc system $\mathcal{C}$ can contain is the negatively half twisted ribbon, which is the arc system $\{l_{12},l_{15}\}$. Consider, for example, the compatible sets containing $l_{15}$. Each such set is constructed from ${\mathcal{A}}_{15}$ in such a way that it contains at least one of $l_0,l_{12},l_{19}$, and $l_{20}$ so that ${\psi }_{i+1}\ne 0$ (the other two assumptions ${\lambda }_i\ne 0$ and ${\Delta }_{i+1}\left(B\right)\ne 0$ are satisfied by each element in $S_1$). We immediately check that for each such compatible set we have $p_1\ge M_1$ and $M_1=N_i^{\prime }+r_i^{\prime }$ where $r_i^{\prime }=min(l_{12},l_{15})$. Therefore, ${ϵ}_i^{\prime }=N_i^{\prime }+r_i^{\prime }=min(M_1,p_1)$ as required.

(b)

Some component X of $L_i$ has $\chi \left(X\right)>1$: Then $l_0=0$, $s_i^{\prime }=z_i^{\prime }=r_i^{\prime }=0$ by Remark 15 as each exceptional arc system with respect to a clover type II contains a standard arc. Because ${\psi }_{i+1}\ne 0$ by assumption, there exists a highly twisted exceptional arc $X\in \left[X_{2i+2;i+1}\right]$ (such arcs are the only highly twisted arcs with ${\psi }_{i+1}\ne 0$ and satisfying property P), each of which increases $M_1$ by 1. As $M_1=0$ for any other arc compatible with X we get ${ϵ}_i^{\prime }=N_i^{\prime }=min(M_1,p_1)$ as required.

□

Remark 16.

The proof of Lemma 10 shows that there exists compatible sets satisfying property P yet containing no exceptional arcs or arc systems. Such arc systems either contain $\{l_1,l_2\}$ or the arc $X_{2i+12i+2}=l_{14}$ together with an arc that satisfies ${\psi }_{i+1}\ne 0$ such as $\{l_5,l_{14}\}$ (note that $l_{14}$ contributes to both ${\lambda }_i$ and ${\Delta }_{i+1}\left(B\right)$). Using parameter $p_1$ and subtracting $X_{2i+12i+2}$ from ${\lambda }_i$ and ${\Delta }_{i+1}\left(B\right)$ rules out such arc systems, giving a way to compute only exceptional arcs or arc systems.

Remark 17.

Reflection in the horizontal diameter of the surface conjugates each crosscap transposition $u_i$ to $u_i^{-1}$. Therefore, a clover of type III is the reflection of a clover of type II along the horizontal diameter, and the corresponding transformation of generalized Dynnikov coordinates in max-plus notation is given by $[t_i;b_i]\mapsto [1/t_i;b_i]$. For example, for $n>0$

$$(t_1,\dots ,t_{g-1},b_1,\dots ,b_{n+g-2})\mapsto \left[(1/t_1,\dots ,1/t_{g-1},b_1,\dots ,b_{n+g-2})\right].$$

By Remark 17 we conclude that exceptional arcs with respect to a clover of type III can be obtained by reflecting exceptional arcs with respect to a clover of type II in the horizontal diameter. Therefore, replacing $u_i^{-1}$ with $u_i$ in Notation 10, we obtain the exceptional parameter $\overline{e_i}={ϵ}_i^{″}+{ϵ}_{i+1}^{″}$ for a clover of type III as given in Lemma 11 and Lemma 12.

Lemma 11.

Let $L_i$ be positive. Then ${\overline{e}}_i={ϵ}_i^{″}+{ϵ}_{i+1}^{″}$ where

$$\begin{array}{cc}\hfill {ϵ}_i^{″}& =min({\mathrm{\Lambda }}_i,{\psi }_{i+1},{\overline{\Delta }}_{i+1}\left(A\right),p_3);\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill {ϵ}_{i+1}^{″}& =min({\mathrm{\Lambda }}_{i+1},{\psi }_i,{\overline{\Delta }}_i\left(B\right),p_4)\hfill \end{array}$$

(50)

Lemma 12

(Equality for a clover of type III). Given a clover of type III we have

$$\begin{array}{c}\hfill 2{\beta }_{n+i}^{″}+C_i=max({\gamma }_{2i-1}+{\gamma }_{2i+2},{\gamma }_{2i-1}^{″}+{\gamma }_{2i+2}^{″})+2{\overline{e}}_i.\end{array}$$

(51)

3.1.3. Scale Equalities

Let $u_i^{-1}(\gamma ;\beta )=({\gamma }^{\prime };{\beta }^{\prime })$ and $u_i(\gamma ;\beta )=({\gamma }^{″};{\beta }^{″})$. A scale of type I has leaves ${\gamma }_{2i+1}$, ${\gamma }_{2i}$, ${\mathcal{C}}_i$, ${\beta }_{n+i+1}$; diagonals ${\gamma }_{2i+1}^{\prime }$ and ${\gamma }_{2i+2}$; and a scale of type II has leaves ${\gamma }_{2i+1}$, ${\gamma }_{2i}$, $C_i$, ${\beta }_{n+i-1}$; and diagonals ${\gamma }_{2i}^{\prime }$ and ${\gamma }_{2i-1}$. Reflecting these two scales along the horizontal diameter we respectively obtain a scale of type III and a scale of type IV (Figure 20). Observe that this is natural, as a scale of type III and a scale of type IV are the $u_i$ images of a scale of type I and a scale of type II, respectively (see Remark 17).

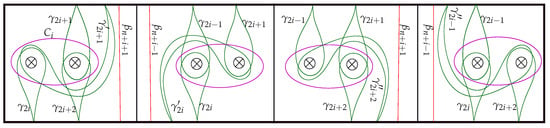
Figure 20. A scale of type I, type II, type III, and type IV from left to right.

Notation 13.

Let X be a component of $L_i$. In what follows we shall write $\lambda \left(X\right),{\lambda }_{c_k}\left(X\right),{\psi }_k\left(X\right)$ ($k=i,i+1$) to denote the number of non-core, core, and straight components of a given component X of $L\cap S_k^{\prime }$.

The key idea in the proof of Lemma 13 is that it is easy to find out which standard arcs satisfy equalities (52), (53), (54), and (55) as there are only finitely many standard arcs to check. Similarly, we call arcs that do not satisfy equalities (52), (53), (54), and (55) exceptional with respect to a scale of type I, type II, type III, and type IV, respectively.

$$\begin{array}{c}\hfill {\gamma }_{2i+1}^{\prime }+{\gamma }_{2i+2}=max({\gamma }_{2i+1}+{\gamma }_{2i},C_i+2{\beta }_{n+i+1})\end{array}$$

(52)

$$\begin{array}{c}\hfill {\gamma }_{2i}^{\prime }+{\gamma }_{2i-1}=max({\gamma }_{2i+1}+{\gamma }_{2i},C_i+2{\beta }_{n+i-1})\end{array}$$

(53)

$$\begin{array}{c}\hfill {\gamma }_{2i+2}^{″}+{\gamma }_{2i+1}=max({\gamma }_{2i+2}+{\gamma }_{2i-1},C_i+2{\beta }_{n+i+1})\end{array}$$

(54)

$$\begin{array}{c}\hfill {\gamma }_{2i-1}^{″}+{\gamma }_{2i}=max({\gamma }_{2i-1}+{\gamma }_{2i+2},C_i+2{\beta }_{n+i-1})\end{array}$$

(55)

We say that X is straight in $S_k^{\prime }$ ($k=i,i+1$) if ${\psi }_k\left(X\right)\ne 0$. Similarly, we say that X is $u_i$–straight in $S_k$ if ${\psi }_k\left(u_i\left(X\right)\right)\ne 0$ for some $k=i,i+1$. The definition for $u_i^{-1}$–straight arc in $S_k$ is similar.

Analysis of exceptional arcs with respect to a scale of type I shows that each standard component X of $L_i$ that is not straight in $S_{i+1}^{\prime }$ (i.e., those with ${\psi }_{i+1}=0$) satisfies equality (52). An analogous statement for a twisted component in the class of X is also true as each such component has the same number of intersections with ${\mathcal{C}}_i$ as X, and increases the number of intersections on each ${\gamma }_{2i+1}^{\prime }$, ${\gamma }_j(2i\le j\le 2i+2)$ and $2{\beta }_{n+i}$ (and hence $C_i+2{\beta }_{n+i+1}$) by the same amount. In addition, the only standard straight arcs in $S_{i+1}^{\prime }$ that satisfy equality (52) are $X_{2i+2;i+1}^{(0,1;-1,0)}$ and $X_{2i-1;i+1}$. That is, each standard straight arc in $S_{i+1}^{\prime }$ apart from $X_{2i+2;i+1}^{(0,1;-1,0)}$ and $X_{2i-1;i+1}$ is exceptional with respect to a scale of type I (top row of Figure 21). The only twisted arcs that are straight in $S_{i+1}^{\prime }$ are in the class of $\left[X_{k;i+1}\right]$ ($2i-1\le k\le 2i+2$) and $\left[X_i\right]$ (examples of which are as given on the bottom row of Figure 21). Each such exceptional arc X satisfies

$${\gamma }_{2i+1}^{\prime }+{\gamma }_{2i+2}=max({\gamma }_{2i+1}+{\gamma }_{2i},C_i+2{\beta }_{n+i+1})+2{\psi }_{i+1}\left(X\right)$$

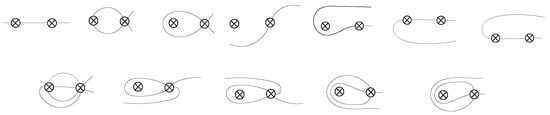
Figure 21. Standard arcs (top row) and examples for twisted arcs (bottom row) that are straight in $S_{i+1}^{\prime }$.

As a scale of type III is the $u_i$ image of a scale of type I, it follows from Remark 17 that each arc X with ${\psi }_{i+1}\left(X\right)\ne 0$ apart from $X_{2i+1;i+1}^{(0,1;-1,0)}$ and $X_{2i;i+1}$ is exceptional with respect to a scale of type III. For the same reason, each $u_i$–straight arc X in $S_{i+1}^{\prime }$ (Figure 22) apart from $X_{2i+12i+2}^{(1,0;-1,0)}$ and $X_{2i+2;i}$ is exceptional with respect to a scale of type I (Figure 23a,b show straight and $u_i$–straight arcs in $S_{i+1}^{\prime }$ which are not exceptional with respect to a scale of type I). Let us write ${\psi }_k\left(u_i\left(X\right)\right)={\psi }_k\left(X^{\prime }\right)$ and ${\psi }_k\left(u_i^{-1}\left(X\right)\right)={\psi }_k\left(X^{″}\right)$. Then for each $u_i$–straight arc X in $S_{i+1}^{\prime }$ we get

$${\gamma }_{2i+1}^{\prime }+{\gamma }_{2i+2}=max({\gamma }_{2i+1}+{\gamma }_{2i},C_i+2{\beta }_{n+i+1})+2{\psi }_{i+1}\left(X^{\prime }\right)$$

Write ${\psi }_k\left(u_i\left(L\right)\right)={\psi }_k^{\prime }$ and ${\psi }_k\left(u_i^{-1}\left(L\right)\right)={\psi }_k^{″}$ for a given $L\in {\mathcal{L}}_n$.

Figure 22. Examples for $u_i$–straight arcs in $S_{i+1}^{\prime }$.

Figure 23. (a) Straight and (b) $u_i$–straight arcs in $S_{i+1}^{\prime }$ that are not exceptional with respect to a scale of type I.

Then, setting

$$\begin{array}{c}\hfill f_i={\psi }_{i+1}-(X_{2i+2;i+1}^{(0,1;-1,0)}+X_{2i-1;i+1})+{\psi }_{i+1}^{\prime }-(X_{2i+12i+2}^{(1,0;-1,0)}+X_{2i+2;i})\end{array}$$

(56)

we obtain equality (60) given in Lemma 13. We call $f_i$ the exceptional parameter for a scale of type I. The exceptional arcs and hence the associated parameters for a scale of type II, type III, and type IV follow from symmetry:

$$\begin{array}{cc}\hfill g_i& ={\psi }_i-(X_{2i-1;i}^{(1,0;0,1)}+X_{2i+2;i})+{\psi }_i^{\prime }-(X_{2i-12i}^{(0,1;0,1)}+X_{2i-1;i+1})\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill \overline{f_i}& ={\psi }_{i+1}-(X_{2i+1;i+1}^{(0,1;-1,0)}+X_{2i;i+1})+{\psi }_{i+1}^{″}-(X_{2i+12i+2}^{(1,0;-1,0)}+X_{2i+1;i})\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill \overline{g_i}& ={\psi }_i-(X_{2i;i}^{(1,0;0,1)}+X_{2i+1;i})+{\psi }_i^{″}-(X_{2i-12i}^{(0,1;0,1)}+X_{2i;i+1})\hfill \end{array}$$

(59)

Hence, computing $f_i,\overline{f_i},g_i,\overline{g_i}$ in terms of generalized Dynnikov coordinates will require separate consideration of the arcs depicted in Figure 24 and given in Lemmas 14 and 15. We first state scale equalities in Lemma 13.

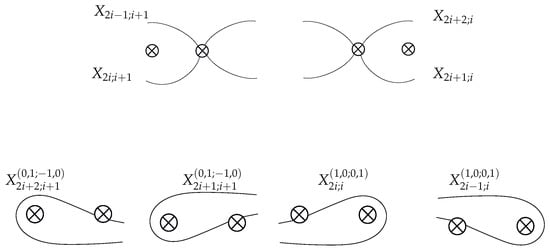
Figure 24. Arcs that are used in the computation of exceptional parameters $f_i,\overline{f_i},g_i,\overline{g_i}$.

Lemma 13.

Given a scale of type I, type II, type III, and type IV as shown in Figure 20, we have

$$\begin{array}{c}\hfill {\gamma }_{2i+1}^{\prime }+{\gamma }_{2i+2}=max({\gamma }_{2i+1}+{\gamma }_{2i},C_i+2{\beta }_{n+i+1})+2f_i\end{array}$$

(60)

$$\begin{array}{c}\hfill {\gamma }_{2i}^{\prime }+{\gamma }_{2i-1}=max({\gamma }_{2i+1}+{\gamma }_{2i},C_i+2{\beta }_{n+i-1})+2g_i\end{array}$$

(61)

$$\begin{array}{c}\hfill {\gamma }_{2i+2}^{″}+{\gamma }_{2i+1}=max({\gamma }_{2i+2}+{\gamma }_{2i-1},C_i+2{\beta }_{n+i+1})+2\overline{f_i}\end{array}$$

(62)

$$\begin{array}{c}\hfill {\gamma }_{2i-1}^{″}+{\gamma }_{2i}=max({\gamma }_{2i-1}+{\gamma }_{2i+2},C_i+2{\beta }_{n+i-1})+2\overline{g_i}\end{array}$$

(63)

Lemma 14.

Consider the arcs $X_{k;j}$ ($2i-1\le k\le 2i+2,j=i,i+1$) in Figure 24, and let $\chi \left(i\right)<1$. Then,

$$\begin{array}{cc}\hfill X_{2i-1;i+1}& =min\left({\psi }_{i+1},{\left[{\chi }_i\left(A\right)\right]}^{+}\right)X_{2i;i+1}=min\left({\psi }_{i+1},{\left[{\chi }_i\left(B\right)\right]}^{+}\right)\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill X_{2i+1;i}& =min\left({\psi }_i,{\left[{\chi }_{i+1}\left(A\right)\right]}^{+}\right)X_{2i+2;i}=min\left({\psi }_i,{\left[{\chi }_{i+1}\left(B\right)\right]}^{+}\right)\hfill \end{array}$$

(65)

Proof. 

We prove $X_{2i-1;i+1}=min\left({\psi }_{i+1},{\left[{\chi }_i\left(A\right)\right]}^{+}\right)$. The other equalities can be proved in a symmetric way. The proof is similar to the proof of Lemma 10, and is based on the following facts:

(1)

$X_{2i-1;i+1}$ increases ${\psi }_{i+1}$ and ${\chi }_i\left(A\right)$ by 1.

(2)

If X is compatible with $X_{2i-1;i+1}$ then ${\chi }_i\left(A\right)<1$.

Therefore, by fact $\left(1\right)$ if ${\psi }_{i+1}=0$ or ${\chi }_i\left(A\right)=0$, then $X_{2i-1;i+1}=0$. Similarly, by fact $\left(2\right)$ if $\chi \left(i\right)>1$ then $X_{2i-1;i+1}=0$. Suppose that ${\psi }_{i+1}\ne 0$ and ${\chi }_i\left(A\right)\ne 0$, and that $\chi \left(i\right)<1$, which is guaranteed by the assumption of the lemma. Let us say that an arc X has property Q if it satisfies ${\psi }_{i+1}\ne 0$, ${\chi }_i\left(A\right)\ne 0$ and $\chi \left(X\right)<1$, and that an arc is compatible with property Q if it is compatible with an arc that satisfies property Q. Figure 25 illustrates all arcs apart from $X_{2i-1;i+1}$ that are compatible with property Q. As ${\left[{\chi }_i\left(A\right)\right]}^{+}=0$ for each of these arcs $X_{2i-1;i+1}=min\left({\psi }_{i+1},{\left[{\chi }_i\left(A\right)\right]}^{+}\right)$ by fact $\left(1\right)$. □

Figure 25. Arcs compatible with property Q.

Lemma 15.

Consider the arcs $X_{k;j}^{v_i}$ ($2i-1\le k\le 2i+2,j=i,i+1$) in Figure 24. Let

$$\begin{array}{cc}\hfill M_1& =min({\mathrm{\Lambda }}_i,{\psi }_{i+1}-X_{2i-1;i+1},{\overline{\Delta }}_{i+1}\left(B\right));M_2=min({\mathrm{\Lambda }}_{i+1},{\psi }_i-X_{2i+2;i},{\overline{\Delta }}_i\left(A\right))\hfill \\ \hfill M_3& =min({\mathrm{\Lambda }}_i,{\psi }_{i+1}-X_{2i-1;i+1},{\overline{\Delta }}_{i+1}\left(B\right));M_4=min({\mathrm{\Lambda }}_{i+1},{\psi }_i-X_{2i+2;i},{\overline{\Delta }}_i\left(A\right))\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill X_{2i+2;i+1}^{(0,1;-1,0)}& =min\left(M_1,{\left(c_{i+1}-(c_i-|{\chi }_{i+1}\left(B\right)\left|\right)\right)}^{+},{\left(c_{i+1}-2{\left[{\chi }_{i+1}\left(B\right)\right]}^{+}\right)}^{+}\right)\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill X_{2i+1;i+1}^{(0,1;-1,0)}& =min(M_4,\left(c_{i+1}-{\left(c_i-|\left({\chi }_{i+1}\left(A\right)\right|)\right)}^{+},{\left(c_{i+1}-2{\left[{\chi }_{i+1}\left(A\right)\right]}^{+}\right)}^{+}\right)\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill X_{2i-1;i}^{(1,0;0,1)}& =min(M_2,\left(c_i-{\left(c_{i+1}-|{\chi }_i\left(A\right)\left|\right)\right)}^{+},{\left(c_i-2{\left[{\chi }_i\left(A\right)\right]}^{+}\right)}^{+}\right)\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill X_{2i;i}^{(1,0;0,1)}& =min(M_3,\left(c_i-{\left(c_{i+1}-|{\chi }_i\left(B\right)\left|\right)\right)}^{+},{\left(c_i-2{\left[{\chi }_i\left(B\right)\right]}^{+}\right)}^{+}\right)\hfill \end{array}$$

(69)

Proof. 

We compute $X_{2i+2;i+1}^{(0,1;-1,0)}$, which is a standard exceptional arc with respect to a clover of type II. Again, the other equalities can be proved in a symmetric way. To compute this arc separately, we need modification on the formulae given in Lemma 10 to eliminate the values $s_i^{\prime }$, $r_i^{\prime }$, $z_i^{\prime }$, which are parameters related with exceptional arc systems of type II, and the number of highly twisted exceptional arcs in the set $\left[X_{2i+2;i+1}\right]$. Using the value $X_{2i-1;i+1}-{\psi }_{i+1}$ in $M_1$ rules out the possibility of scissors and hence guarantees that $s_i^{\prime }=0$. Similarly, as ${\left(c_{i+1}-(c_i-|{\chi }_{i+1}\left(B\right)\left|\right)\right)}^{+}=0$ for anchors and ribbons we get $r_i^{\prime }=z_i^{\prime }=0$. Finally, for each highly twisted exceptional arc in $\left[X_{2i+2;i+1}^{(0,1;-1,0)}\right]$ we have $min\left({\left(c_{i+1}-(c_i-|{\chi }_{i+1}\left(B\right)\left|\right)\right)}^{+},{\left(c_{i+1}-2{\left[{\chi }_{i+1}\left(B\right)\right]}^{+}\right)}^{+}\right)=0$ (see, for instance, $l_{19}$ and $l_{20}$). As $X_{2i+2;i+1}^{(0,1;-1,0)}$ increases $M_1,{\left(c_{i+1}-(c_i-|{\chi }_{i+1}\left(B\right)\left|\right)\right)}^{+}$ and ${\left(c_{i+1}-2{\left[{\chi }_{i+1}\left(B\right)\right]}^{+}\right)}^{+}$ by one we conclude that $X_{2i+2;i+1}^{(0,1;-1,0)}$ is as given in Equation (66). □

If $L_i$ is mixed, $X_{2i+2;i+1}^{(0,1;-1,0)}=X_{2i;i}^{(1,0;0,1)}=X_{2i;i}^{(1,0;0,1)}=X_{2i+1;i+1}^{(0,1;-1,0)}=0$ by Remark 12. Otherwise they are as given in Lemma 15.

Lemma 16.

Let ${\psi }_k\left(u_i\left(L\right)\right)={\psi }_k^{\prime }$ and ${\psi }_k\left(u_i^{-1}\left(L\right)\right)={\psi }_k^{″}$ ($k=i,i+1$) denote the number of straight components of $u_i\left(L\right)\cap S_k^{\prime }$ and $u_i^{-1}\left(L\right)\cap S_k^{\prime }$, respectively.

Let $L_i$ be negative. Then

$${\psi }_{i+1}^{\prime }=\left\{\begin{array}{cc}{\lambda }_{c_i}^{-}+{\chi }_{i+1}\left(B\right)\hfill & if{\chi }_{i+1}\left(B\right))\le 0\hfill \\ {({\Delta }_{i+1}\left(B\right)-{\lambda }_i^{-})}^{+}\hfill & if{\chi }_{i+1}\left(B\right))>0\hfill \end{array}\right.and{\psi }_i^{\prime }=\left\{\begin{array}{cc}{\lambda }_{c_{i+1}}^{+}+{\chi }_i\left(A\right)\hfill & if{\chi }_i\left(A\right)\le 0\hfill \\ {({\Delta }_i\left(A\right)-{\lambda }_{i+1}^{+})}^{+}\hfill & if{\chi }_i\left(A\right)>0\hfill \end{array}\right.$$

Let $L_i$ be positive. Then,

$${\psi }_{i+1}^{″}=\left\{\begin{array}{cc}{\lambda }_{c_i}^{-}+{\chi }_{i+1}\left(A\right)\hfill & if{\chi }_{i+1}\left(A\right))\le 0\hfill \\ {({\Delta }_{i+1}\left(A\right)-{\lambda }_i^{-})}^{+}\hfill & if{\chi }_{i+1}\left(A\right))>0\hfill \end{array}\right.and{\psi }_i^{″}=\left\{\begin{array}{cc}{\lambda }_{c_{i+1}}^{+}+{\chi }_i\left(B\right)\hfill & if{\chi }_i\left(B\right)\le 0\hfill \\ {({\Delta }_i\left(B\right)-{\lambda }_{i+1}^{+})}^{+}\hfill & if{\chi }_i\left(B\right)>0\hfill \end{array}\right.$$

Proof. 

To compute the number ${\psi }_{i+1}^{\prime }$ of straight components of $u_i\left(L\right)\cap S_{i+1}^{\prime }$, we need to determine which arcs are $u_i$-straight in $S_{i+1}^{\prime }$. In order to do this, we first list all standard arcs that are straight in $S_{i+1}^{\prime }$ (there are finitely many of those) and take their inverse images under $u_i$ from which we obtain the arcs depicted in Figure 26. Using Notation 11, we write the following facts:

Figure 26. $u_i$-straight arcs in $S_{i+1}^{\prime }$.

• Each $u_i$-straight arc X is negative with ${\widehat{\chi }}_{i+1}\left(B\right)=0$ and ${\lambda }_{c_i}^{-}\left(X\right)\ne 0$ (i.e., X has a left core-loop in $S_i^{\prime }$). The converse is also true.
• ${\psi }_{i+1}\left(u_i\left(X\right)\right)$ equals the number of left core loops of $X\cap S_i^{\prime }$ that are entirely contained in below components of $X\cap S_{i+1}^{\prime }$.

We have the following cases:

• If ${\chi }_{i+1}\left(B\right)<0$, $L_i$ contains $X_{2i+22i+2}^{(1,0;-1,0)}$, which satisfies ${\lambda }_{c_i}^{-}\ne 0$, is not $u_i$-straight and not compatible with any highly twisted component. Therefore, by (1) and (2) we obtain ${\psi }_{i+1}^{\prime }={\lambda }_{c_i}^{-}-X_{2i+22i+2}^{(1,0;-1,0)}$. It is easy to show that $X_{2i+22i+2}^{(1,0;-1,0)}=-{\chi }_{i+1}\left(B\right)$ from which we get ${\psi }_{i+1}^{\prime }={\lambda }_{c_i}^{-}+{\chi }_{i+1}\left(B\right)$. Clearly, if ${\chi }_{i+1}\left(B\right)=0$, $L_i$ is some collection of arcs depicted in Figure 26, each of which satisfies ${\psi }_{i+1}^{\prime }={\lambda }_{c_i}^{-}={({\Delta }_{i+1}\left(B\right)-{\lambda }_i^{-})}^{+}$ by (2).
• If ${\chi }_{i+1}\left(B\right)>0$, $L_i$ contains a highly twisted component X, and only left core loops of $X\cap S_i$ that do not join right loop components of $X\cap S_{i+1}$ (i.e., those that are contained in ${\Delta }_{i+1}\left(B\right)$) can be mapped to a straight component of $X\cap S_{i+1}$. That is, for each such arc we have ${\psi }_{i+1}^{\prime }={({\Delta }_{i+1}\left(B\right)-{\lambda }_i^{-})}^{+}$.

□

Proof of Theorem 2.

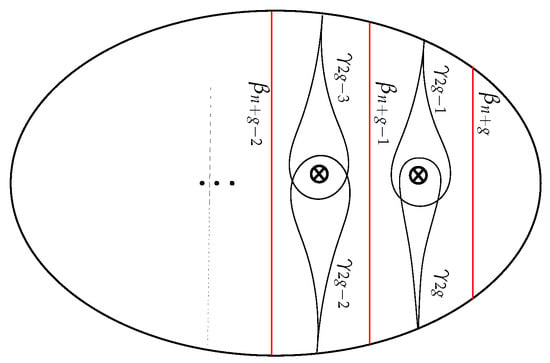
Let $n>0$ and ${\mathcal{A}}_{g,n}$ denote the set of arcs in Figure 1. $MCG\left(N_{g,n}\right)$ acts on both ${\mathcal{A}}_{g,n}$ and ${\mathfrak{L}}_{g,n}$, and hence $i(\mathcal{L},\xi )=i\left(\delta \right(\mathcal{L}),\delta (\xi \left)\right)$ for any $\delta \in MCG\left(N_{g,n}\right)$ and $\xi \in {\mathcal{A}}_{g,n}$. We also recall that the arcs ${\alpha }_i$ ($1\le i\le 2n-2$) and ${\beta }_i$ ($1\le i\le n$) are not affected by crosscap transpositions. For the crosscap transposition $u_i$, our approach is to compute the number of intersections of ${\gamma }_j^{\prime }=u_i^{-1}\left({\gamma }_j\right)$$(1\le j\le 2g-2)$ and ${\beta }_j^{\prime }=u_i^{-1}\left({\beta }_j\right)$$(1\le j\le n+g-1)$ with $\mathcal{L}$ instead of computing the number of intersections of $u_i\left(\mathcal{L}\right)$ with ${\gamma }_j$ and ${\beta }_j$. We have

$$t_j^{\prime }=\frac{{\gamma }_{2j}^{\prime }-{\gamma }_{2j-1}^{\prime }}{2}\mathrm{and}{b}_j^{\prime }=\frac{{\beta }_j^{\prime }-{\beta }_{j+1}^{\prime }}{2}.$$

We shall make use of clover and scale equalities given in Lemmas 5, 9, and 13. For computational convenience, we set $T_j=2t_j$ ($1\le j\le g+n-2$), $B_j=2b_j$ ($n\le j\le g+n-2$), $2{\beta }_{n+j}={\mathfrak{B}}_{n+j}(1\le j\le g-1)$ and $D_j=2d_j$, $E_j=2e_j$, $F_j=2f_j$, $G_j=2g_j$ ($1\le j\le g-1$), and work in the max-plus semiring as indicated in Remark 2. Therefore,

$$\begin{array}{c}\hfill T_j=\left[\frac{{\gamma }_{2j}}{{\gamma }_{2j-1}}\right]\mathrm{and}{B}_j=\left[\frac{{\beta }_j}{{\beta }_{j+1}}\right].\end{array}$$

(70)

and from the clover of type I equality (36),

$$\begin{array}{c}\hfill {\mathcal{C}}_i=\left[\frac{D_i({\gamma }_{2i-1}{\gamma }_{2i+2}+{\gamma }_{2i+1}{\gamma }_{2i})}{{\mathfrak{B}}_{n+i}}\right]\end{array}$$

(71)

We now consider the two separate cases of the statement.

Suppose that $1\le i<g+n-2$. Observe that ${\beta }_j^{\prime }={\beta }_j$ for $j\ne n+i$ and ${\gamma }_j^{\prime }={\gamma }_j$ for $j<2i-1$ and $j>2i+2$. Therefore, $T_j^{\prime }=T_j$ except for $j=i$ and $j=i+1$; and $B_j^{\prime }=B_j$ except for $j=n+i-1$ and $j=n+i$. Next we compute $T_i^{\prime }$, $T_{i+1}^{\prime }$, $B_{n+i-1}^{\prime }$, and $B_{n+i}^{\prime }$.

• We shall first compute $T_{i+1}^{\prime }=\left[\frac{{\gamma }_{2i+2}^{\prime }}{{\gamma }_{2i+1}^{\prime }}\right]$. We have ${\gamma }_{2i+2}^{\prime }={\gamma }_{2i}$. To compute ${\gamma }_{2i+1}^{\prime }$ we use the scale of type I equality (60) and obtain

  $$\begin{array}{c}\hfill {\gamma }_{2i+1}^{\prime }=\left[\frac{F_i({\mathcal{C}}_i{\mathfrak{B}}_{n+i+1}+{\gamma }_{2i}{\gamma }_{2i+1})}{{\gamma }_{2i+2}}\right].\end{array}$$

  (72)
  Then from (70), (71), and (72), we compute that

  $$\begin{array}{ccc}\hfill \left[\frac{1}{T_{i+1}^{\prime }}\right]& =& \left[F_i\left(\frac{D_i({\gamma }_{2i-1}{\gamma }_{2i+2}+{\gamma }_{2i+1}{\gamma }_{2i})}{{\mathfrak{B}}_{n+i}{\gamma }_{2i}{\gamma }_{2i+2}}{\mathfrak{B}}_{n+i+1}+\frac{{\gamma }_{2i}{\gamma }_{2i+1}}{{\gamma }_{2i}{\gamma }_{2i+2}}\right)\right]\mathrm{and}\mathrm{hence},\hfill \\ \hfill T_{i+1}^{\prime }& =& \left[\frac{T_i{T}_{i+1}{B}_{n+i}^2}{F_i\left(T_i(D_i+B_{n+i}^2)+D_i{T}_{i+1}\right)}\right].\mathrm{That}\mathrm{is},\hfill \\ \hfill T_{i+1}^{\prime }& =& T_i+T_{i+1}+2B_{n+i}-(F_i+max\left(T_i+max(D_i,2B_{n+i}),D_i+T_{i+1})\right)\hfill \end{array}$$
  Dividing both sides of the equation by 2, we get

  $$t_{i+1}^{\prime }=\left[\frac{t_i{t}_{i+1}{B}_{n+i}}{f_i\left(t_i(d_i+B_{n+i})+d_i{t}_{i+1}\right)}\right]=\left[\frac{t_i{t}_{i+1}{b}_{n+i}^2}{f_i(t_i(d_i+b_{n+i}^2)+d_i{t}_{i+1})}\right].$$
• We shall now compute $T_i^{\prime }=\left[\frac{{\gamma }_{2i}^{\prime }}{{\gamma }_{2i-1}^{\prime }}\right]$. We have ${\gamma }_{2i-1}^{\prime }={\gamma }_{2i+1}$. To compute ${\gamma }_{2i}^{\prime }$ we use the scale of type II equality (61) and obtain

  $${\gamma }_{2i}^{\prime }=\left[\frac{G_i({\gamma }_{2i}{\gamma }_{2i+1}+C_i{\mathfrak{B}}_{\mathfrak{n}+\mathfrak{i}-\mathfrak{1}})}{{\gamma }_{2i-1}}\right].$$
  Hence, from (71) we get

  $$t_i^{\prime }=\left[g_i\left(t_i(1+d_i{b}_{n+i-1}^2)+d_i{b}_{n+i-1}^2{t}_{i+1}\right)\right].$$
• We proceed with $B_{n+i}^{\prime }=\left[\frac{{\beta }_{n+i}^{\prime }}{{\beta }_{n+i+1}^{\prime }}\right]$. We have ${\beta }_{n+i+1}^{\prime }={\beta }_{n+i+1}$ and from the clover of type II equality (47),

  $${\mathfrak{B}}_{n+i}^{\prime }=\left[\frac{E_i({\gamma }_{2i}^{\prime }{\gamma }_{2i+1}^{\prime }+{\gamma }_{2i}{\gamma }_{2i+1})}{C_i}\right].$$
  Since ${\gamma }_{2i-1}^{\prime }={\gamma }_{2i+1}$ and ${\gamma }_{2i+2}^{\prime }={\gamma }_{2i}$

  $$\begin{array}{c}\hfill {\gamma }_{2i}^{\prime }=\left[T_i^{\prime }{\gamma }_{2i+1}\right]\mathrm{and}{\gamma }_{2i+1}^{\prime }=\left[\frac{{\gamma }_{2i}}{T_{i+1}^{\prime }}\right].\end{array}$$

  $$\begin{array}{cc}\hfill B_{n+i}^{\prime }& =\left[\frac{E_i\left(\frac{T_i^{\prime }}{T_{i+1}^{\prime }}{\gamma }_{2i}{\gamma }_{2i+1}+{\gamma }_{2i}{\gamma }_{2i+1}\right)}{C_i{\mathfrak{B}}_{n+i+1}}\right]=\left[\frac{E_i{\gamma }_{2i}{\gamma }_{2i+1}(\frac{T_i^{\prime }}{T_{i+1}^{\prime }}+1)}{\frac{D_i{\mathfrak{B}}_{n+i+1}}{{\mathfrak{B}}_{n+i}}({\gamma }_{2i-1}{\gamma }_{2i+2}+{\gamma }_{2i}{\gamma }_{2i+1})}\right]\hfill \\ \hfill & =\left[\frac{E_i}{D_i}{B}_{n+i}^2\left(\frac{T_i^{\prime }+T_{i+1}^{\prime }}{T_{i+1}^{\prime }}\right)\frac{1}{\frac{{\gamma }_{2i-1}{\gamma }_{2i+2}+{\gamma }_{2i}{\gamma }_{2i+1}}{{\gamma }_{2i}{\gamma }_{2i+1}}}\right]=\left[\frac{E_i}{D_i}{B}_{n+i}^2\left(\frac{T_i^{\prime }+T_{i+1}^{\prime }}{T_{i+1}^{\prime }}\right)\frac{T_i}{T_i+T_{i+1}}\right]\hfill \end{array}$$

  from which we get

  $$b_{n+i}^{\prime }=\left[\frac{e_i}{d_i}{b}_{n+i}^2\left(\frac{t_i^{\prime }+t_{i+1}^{\prime }}{t_{i+1}^{\prime }}\right)\frac{t_i}{t_i+t_{i+1}}\right].$$
• Now we shall compute $B_{n+i-1}^{\prime }=\left[\frac{{\beta }_{n+i-1}^{\prime }}{{\beta }_{n+i}^{\prime }}\right]$. We have

  $${\beta }_{n+i-1}^{\prime }={\beta }_{n+i-1},{\beta }_{n+i+1}^{\prime }={\beta }_{n+i+1}\mathrm{and}{B}_{n+i}^{\prime }=\left[\frac{{\beta }_{n+i}^{\prime }}{{\beta }_{n+i+1}^{\prime }}\right].$$
  Therefore, $B_{n+i-1}^{\prime }=\left[\frac{{\beta }_{n+i-1}}{B_{n+i}^{\prime }{\beta }_{n+i+1}}\right]$. Multiplying the numerator and denominator by ${\beta }_{n+i}$ gives $B_{n+i-1}^{\prime }=\left[\frac{B_{n+i}{B}_{n+i-1}}{B_{n+i}^{\prime }}\right]$. That is,

  $$b_{n+i-1}^{\prime }=\left[\frac{b_{n+i}{b}_{n+i-1}}{b_{n+i}^{\prime }}\right].$$

Now, suppose that $i=g-1$ (Figure 6). Observe as before that $t_j^{\prime }=t_j$ for all $j<g-1$ and $b_j^{\prime }=b_j$ for all $j<n+g-2$. As there are no teardrops encircling the last crosscap, our approach to compute $t_{g-1}^{\prime }$ and $b_{n+g-2}^{\prime }$ is to add dummy teardrops ${\gamma }_{2g-1}$, ${\gamma }_{2g}$, and ${\beta }_{n+g}$ as depicted in Figure 27, which enables us to make similar calculations as in the previous statement. We first note that ${\gamma }_{2g-1}={\gamma }_{2g}=\frac{{\beta }_{n+g-1}}{2}$ and ${\beta }_{n+g}=0$ hence we have $T_g=0$ and $B_{n+g-1}={\beta }_{n+g-1}$. Similar calculations give

$$t_{g-1}^{\prime }=\left[g_{g-1}\left(t_{g-1}+d_{g-1}{B}_{n+g-2}(1+t_{g-1})\right)\right]\mathrm{and}{B}_{n+g-2}^{\prime }=\left[\frac{d_{g-1}}{e_{g-1}}{B}_{n+g-2}\frac{1+t_{g-1}}{t_{g-1}(1+t_{g-1}^{\prime })}\right]$$

Figure 27. Dummy teardrops are used to compute $t_{g-1}^{\prime }$ and $b_{n+g-1}^{\prime }$.

Now let $n=0$. The formulae for $1<i\le g-2$ are obtained similarly, replacing i with $i-1$. For $i=1$, we add two dummy punctures around the first crosscap. Similar arguments give that

$$t_1^{\prime }=\left[\frac{t_1{B}_1}{f_0(1+B_1)+t_1}\right]\mathrm{and}{B}_1^{\prime }=\left[B_1{e}_0\frac{(1+t_1^{\prime })}{t_1^{\prime }}\frac{1}{(1+t_1)}\right]$$

For $i=g-1$, we note that rotation through $\pi$ about the center of the surface conjugates each crosscap generator $u_i$ to $u_{g-i}$, and the corresponding transformation of generalized Dynnikov coordinates in max-plus notation is given by

$$(t_1,\dots ,t_{g-2},b_1,\dots ,b_{g-2})\mapsto \left[(1/t_{g-2},\dots ,1/t_1,1/b_{g-2},\dots ,1/b_1)\right]$$

hence we get

$$\begin{array}{c}\hfill t_{g-2}^{\prime }=\left[g_{g-2}\left(t_{g-2}+d_{g-2}{B}_{g-2}(1+t_{g-2})\right)\right]\mathrm{and}{B}_{g-2}^{\prime }=\left[\frac{d_{g-2}}{e_{g-2}}{B}_{g-2}\frac{1+t_{g-2}}{t_{g-2}(1+t_{g-2}^{\prime })}\right]\end{array}$$

By Remark 17, we obtain the rules for $t_i^{″}$ and $b_i^{″}$ for each case by symmetry, conjugating the rules for $u_i$ by the involution (17). □

4. Conclusions

The method introduced in this paper can be used to provide an efficient way to solve on non-orientable surfaces many combinatorial and dynamical problems that were previously solved only on orientable surfaces [4,6,9,10]. However, to solve such problems not only for sequences of crosscap transpositions but also for any element of the mapping class group, we need to describe the action of of the other generators of the mapping class group $MCG\left(N_{g,n}\right)$ [3] on ${\mathfrak{L}}_{g,n}$ in terms of generalized Dynnikov coordinates, which require similar techniques to those introduced in this paper.