Asymptotic Behavior of a Surface Implicitly Defined

Abstract

In this paper, we introduce the notion of infinity branches and approaching surfaces. We obtain an algorithm that compares the behavior at the infinity of two given algebraic surfaces that are defined by an irreducible polynomial. Furthermore, we show that if two surfaces have the same asymptotic behavior, the Hausdorff distance between them is finite. All these concepts are new and represent a great advance for the study of surfaces and their applications.

1. Introduction

Algebraic curves and surfaces are essential entities for practical applications (see, for example [1,2]). In fact, one may find a lot of literature dealing with different problems related to curves defined by irreducible polynomials (see, e.g., [3,4]). In this paper, we introduce the concept of infinity branches for surfaces. Intuitively speaking, an infinity branch represents the behavior of an algebraic surface at the points with “sufficiently large coordinates”. Informally speaking and generalizing the situation of algebraic curves, an infinity branch is associated with a projective “place” centered at an “infinity point”, and it can be “parametrized” by means of “Puiseux series” (the formal definition of these notions can be seen in Section 2 and Section 3).

Infinity branches are necessary and essential for the study of surfaces since they reveal the behavior at a point at infinity of a real algebraic surface. For instance, the infinity branches of an implicit algebraic plane curve are an important tool to sketch its graph as well as to analyze its topology (see e.g., [5,6,7,8,9]). It should be mentioned that for the case of curves, in [10], the notion of a g-asymptote is introduced. A g-asymptote generalizes the well-known notion of linear asymptotes, and these asymptotes can be computed from the infinity branches. More precisely, we say that a curve $\overline{\mathcal{C}}$ is a generalized asymptote (or g-asymptote) of an input curve $\mathcal{C}$ if $\overline{\mathcal{C}}$ approaches $\mathcal{C}$ at some infinity branch. Furthermore, the input curve $\mathcal{C}$ cannot be approached by a new curve having a lower degree. In this paper, we generalize some of these notions introduced previously for curves in [5] to the case of surfaces.

The notion of an infinity branch allows us to define convergent branches and approaching surfaces (see Section 4). More precisely, we say that two infinity branches converge if they get closer as they tend to infinity. Furthermore, an algebraic surface $\overline{\mathcal{V}}$ approaches $\mathcal{V}$ at its infinity branch B if $\overline{\mathcal{V}}$ has another infinity branch $\overline{B}$ such that $\overline{B}$ is convergent with B. We obtain important results that characterize whether two algebraic surfaces are approaching.

Using these results, we obtain an algorithm that compares the the behavior of two surfaces at infinity (see Section 5). Finally, it is shown that if two algebraic surfaces defined implicitly have the same asymptotic behavior, then the Hausdorff distance between them is finite.

The results that we obtain in this paper (and also for the case of curves) are essential for some applications in the framework of computer-aided geometric design (CAGD) as, for instance, in the approximate parametrization problem (see [11]). This problem can be stated as follows: we are given a non-rational affine surface $\mathcal{V}$ (we assume that it is a perturbation of a rational surface), and we would like to compute, if it exists, a  parametrization of a new rational affine surface denoted by $\overline{\mathcal{V}}$, which is near to the input surface. The effectiveness of the algorithm depends on the closeness of $\mathcal{V}$ and $\overline{\mathcal{V}}$, and then, here, one needs to show that the Hausdorff distance between V and $\overline{V}$ is finite.

This paper is structured as follows: in Section 2, we present the notions and preliminaries that will be used throughout the paper. Section 3 introduces the concept of infinity branch, and here, we prove some important properties. Section 4 provides the notions of convergent branches and approaching surfaces. Additionally, we characterize whether or not two algebraic surfaces approach each other. The results presented in this section will be used in Section 5, where an algorithm to compare the asymptotic behavior of two algebraic surfaces is designed. Finally, we prove that if two given algebraic surfaces have the same asymptotic behavior, the Hausdorff distance between them is finite. We finish with a section for conclusions and future work (Section 6).

2. Preliminaries and Terminology

In the following, we present some concepts and notions that will be used throughout the paper. In particular, we introduce some previous results concerning local parametrizations and Puiseux series. For further details, one may see for instance, Section 2.5 in [3], Chapter 4 (Section 2) in [4], [12,13,14,15], etc.

We represent by $\mathbb{C}\left[\right[t\left]\right]$ the domain of formal power series in the variable t with coefficients in the field of complex numbers $\mathbb{C}$. That is, $\mathbb{C}\left[\right[t\left]\right]$ is the set of all the sums ${\sum }_{i=0}^{\infty }{a}_i{t}^i$, $a_i\in \mathbb{C}$. The quotient field of $\mathbb{C}\left[\right[t\left]\right]$ is the field of a formal Laurent series, which is denoted by $\mathbb{C}((t))$. Every non-zero formal Laurent series $A\in \mathbb{C}((t))$ can be written in the form $A(t)=t^k·(a_0+a_{1}t+a_2{t}^2+\cdots ),\mathrm{where}{a}_0\ne 0\mathrm{and}k\in \mathbb{Z}.$ Furthermore, the field $\mathbb{C}\ll t\gg :={\bigcup }_{n=1}^{\infty }\mathbb{C}((t^{1/n}))$ is the field of a formal Puiseux series. By Puiseux’s Theorem, one gets that the field $K\ll t\gg$ is algebraically closed. Observe that Puiseux series are power series with fractional exponents. Furthermore, given a Puiseux series, $\phi$, one has a bound for the denominators of exponents with non-vanishing coefficients of $\phi$. This bound is known as the ramification index of $\phi$, and we represent it as $\nu (\phi )$ (see [13]).

The order of a (Puiseux or Laurent) series A is the smallest exponent of a term with a non-vanishing coefficient in A. We represent it by $\mathrm{ord}(A)$, and we say that the order of 0 is ∞.

Let $Y(x)$ be a Puiseux series solving $f(x,y)=0$, $\mathrm{ord}(Y)>0$, and let n be the least integer for which $Y(x)\in \mathbb{C}((x^{\frac{1}{n}}))$ (i.e., $\nu (Y)=n$). We set $x^{\frac{1}{n}}=t$, and then $(t^n,Y(t^n))$ is a local parametrization with center at the origin. The solutions of $f(x,y)$ of order 0 are places with a center on the y-axis different from the origin. The solutions of negative order are places at infinity (that is, places with center at an infinity point).

Let $Y(x)={\sum }_{i\ge r}{a}_i{x}^{i/n}$ be a Puiseux series with $\nu (Y)=n$. The series ${\sigma }_{ϵ}(Y)$, ${ϵ}^n=1$ are defined as the conjugates of Y, where ${\sigma }_{ϵ}(Y)={\sum }_{i\ge r}{ϵ}^i{a}_i{x}^{i/n}.$ The set of all the conjugates of Y is called the conjugacy class of Y. The number of different conjugates of Y is $\nu (Y)$. Two Puiseux series provide the same place if they belong to the same conjugacy class (see [13,16]).

For the case of Puiseux power series in several variables, one may use the notation introduced in [14]. More precisely, let us fix a vector of variables $x=(x_1,\dots ,x_n),n>1$, and an integer $d>0$. We will use the lexicographic order ${\le }_{lex}$ on ${\mathbb{R}}^n$, which can be defined as follows: since we can assign to every monomial $x_1^{a_1}\cdots x_n^{a_n},a_i\in \mathbb{Z},i=1,\dots ,n,$ the vector $(a_1,\dots ,a_n)\in {\mathbb{Z}}^n$ of its exponents, we consider the lexicographic order of the group $M={\left\{x^a\right\}}_{\{a\in {\mathbb{Z}}^n\}}$ of monomials by writing

$$x_1^{a_1}\cdots x_n^{a_n}{\le }_{lex}{x}_1^{b_1}\cdots x_n^{b_n}\iff (a_1,\dots ,a_n){\le }_{lex}(b_1,\dots ,b_n).$$

This extension will also be called the lexocographic order for monomials, and it is a group order. The same argument follows for the group $M^{1/d}$, $d\in \mathbb{Z},d>0$ of monomials with vectors of exponents in $(1/d)·\mathbb{Z}$.

Let ${\mathcal{F}}_{n,d}$ be the set of all the functions $f:(1/d)·\mathbb{Z}\to \mathbb{C}$; then ${\mathcal{F}}_{n,d}$ is an abelian group with respect to the usual addition of functions. If we fix a vector x of variables, we may write every $f\in {\mathcal{F}}_{n,d}$ as a formal sum $f={\sum }_{a\in {\mathbb{Z}}^n}{f}_a{x}^{a/d}$ where $f_a=f(a/d)\in K$ and, if $a=(a_1,\dots ,a_n)$, then $x^{a/d}=x_1^{a_1/d}\cdots x_n^{a_n/d}$. In this case, we set ${\mathcal{F}}_{n,d}={\mathcal{F}}_{x,d}$. We call the support of f the set

$$E(f)=\{a/d\in (1/d)·\mathbb{Z}|a\in {\mathbb{Z}}^n,f_a\ne 0\}.$$

Finally, let us denote by $K_{x,d}$ the subgroup $K_{x,d}=\mathbb{C}((x_n^{1/d}))\cdots \mathbb{C}((x_1^{1/d}))$ of ${\mathcal{F}}_{x,d}$, which is a field constructed by induction (see [14]). Under these conditions, if $0\ne f\in {\mathcal{F}}_{x,d}$, then $f\in K_{x,d}$ if $E(f)$ is a well-ordered subset of $(1/d)·\mathbb{Z}$ for the lexicographic order. The elements of $K_{x,d}$ will be called generalized Puiseux power series.

In the next definition, we introduce the concept of projective local parametrization for a projective algebraic surface.

Definition 1.

Let ${\mathcal{V}}^{*}\subset {\mathbb{P}}^3(\mathbb{C})$ be a projective algebraic surface defined by the homogeneous polynomial $F(x,y,z,w)\in \mathbb{R}[x,y,z,w]$. Let $A^{*},B^{*},C^{*},D^{*}$ be series in $\mathbb{C}((t_1,t_2))$ such that: (i) $F(A^{*}(t_1,t_2):B^{*}(t_1,t_2):C^{*}(t_1,t_2):D^{*}(t_1,t_2))=0$ (where the three series converge), and (ii) there is no $K\in \mathbb{C}((t))\backslash \left\{0\right\}$ such that $K·(A^{*},B^{*},C^{*},D^{*})\in {\mathbb{C}}^4$. Then ${\mathcal{P}}^{*}=(A^{*}:B^{*}:C^{*}:D^{*})\in P^3(\mathbb{C}((t_1,t_2)))$ is called a projective local parametrization of ${\mathcal{C}}^{*}$.

One can always find such a parametrization such that $min\{\mathrm{ord}(A^{*}),\mathrm{ord}(B^{*}),\mathrm{ord}(C^{*}),$$\mathrm{ord}(D^{*})\}=0$, and the point ${\mathcal{P}}^{*}(0)\in {\mathcal{V}}^{*}$ is called the center of ${\mathcal{P}}^{*}$.

For a given affine surface, the previous notion can be stated as follows:

Definition 2.

Let $\mathcal{V}$ be a real algebraic surface over $\mathbb{C}$ implicitly defined by the irreducible polynomial $f(x,y,z)\in \mathbb{R}[x,y,z]$. Let $A,B,C$ be series in $\mathbb{C}((t_1,t_2))$ such that: (i) $f(A(t_1,t_2),B(t_1,t_2),$$C(t_1,t_2))=0$ (where the series converge), and (ii) not A and B and C, are constants. Then $\mathcal{P}=(A,B,C)$ is called an (affine) local parametrization of $\mathcal{V}$. If $\mathrm{ord}(A),\mathrm{ord}(B),\mathrm{ord}(C)\ge 0$, and the point $\mathcal{P}(0)=(a,b,c)\in \mathcal{V}$ is called the center of $\mathcal{P}$.

In the following, we deal with affine surfaces. The results and notions presented can be adapted easily for projective algebraic surfaces.

For our purposes, we will need a generalization of the above definition. More precisely, we will be in the conditions of Definition 2, but the place $\mathcal{P}(0,t_2)=(a(t_2),b(t_2),c(t_2))\in \mathcal{V},a(t_2),b(t_2),c(t_2)\in \mathbb{C}\ll t_2\gg ,$ will be the center of $\mathcal{P}$.

Definition 3.

An equivalence class of irreducible local parametrizations of the surface $\mathcal{V}$ is called a place of $\mathcal{V}$. The common center of the local parametrizations (if it exists) is the center of the place.

Now, we introduce the notion of a branch of a surface.

Definition 4.

Given a local parametrization $(X,Y,Z)$ of a surface $\mathcal{V}$, the set of all points $(X(t_1,t_2),$$Y(t_1,t_2),Z(t_1,t_2))$ obtained by allowing $t_1$ to vary within some neighborhood of 0 where $X(t_1,t_2)$ and $Y(t_1,t_2)$ and $Z(t_1,t_2)$ converge is called a branch of $\mathcal{V}$.

It can be proved that two equivalent local parametrizations provide the same branch. Hence, one gets a branch for each place of the input surface.

Furthermore, the center of a local parametrization of $\mathcal{V}$ is a point on $\mathcal{V}$. Reciprocally, from the following theorems, we also get that every point on $\mathcal{V}$ is the center of at least one place of $\mathcal{V}$.

Theorem 1.

Let $\mathcal{V}$ be a surface defined by $f(x,y,z)\in \mathbb{R}[x,y,z]$. To each root $(X(z),Y(z))\in \mathbb{C}\ll z\gg$ of $f(x,y,z)=0$ with $\mathrm{ord}(X)>,\mathrm{ord}(Y)>0,$ there corresponds a unique place of $\mathcal{V}$ with a center at the origin. Conversely, to each place $(X(t_1,t_2),Y(t_1,t_2),Z(t_1,t_2))$ of $\mathcal{V}$ with a center at the origin, there correspond $\mathrm{ord}(Z)$ roots of $f(x,y,z)=0$, each of order greater than zero.

3. Infinity Branches

In the following, we define an infinity branch (see Definition 5), and we get some important properties which will be essential for the results we will obtain.

For this purpose, let $\mathcal{V}$ be an algebraic affine surface over $\mathbb{C}$ implicitly defined by the irreducible polynomial $f(x,y,z)\in \mathbb{R}[x,y,z]$. Let ${\mathcal{V}}^{*}$ be its corresponding projective surface defined by the homogeneous polynomial $F(x,y,z,w)\in \mathbb{R}[x,y,z,w]$. In addition, let $p=(m_1(t_2),m_2(t_2))$, where $m_1(t_2),m_2(t_2)\in \mathbb{C}\ll t_2\gg ,$ be a local parametrization of an infinity curve of ${\mathcal{V}}^{*}$ implicitly defined by the irreducible polynomial $g(y,z,0)$ that divides $F(1:y:z:0)$ (see Definition 2). Observe that $F(1:m_1(t_2):m_2(t_2):0)=0$, and by abuse of notation, we refer to $P=(1:m_1(t_2):m_2(t_2):0)$ as an infinity point of the input surface ${\mathcal{V}}^{*}$.

We compute the series expansion for the solutions of $g(y,z,t_1)=0$ w.r.t $(y,z)$ in some neighborhood of $t_1=0$. We obtain solutions given by different Puiseux series that can be grouped into conjugacy classes. Let one of these solutions be given by the Puiseux series $\phi (t_1,t_2)=({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2))=$:

$$\left(m_1(t_2)+\sum _{N\in N^2}{h}_{1,N}{\xi }^{N/N},m_2(t_2)+\sum _{N\in N^2}{h}_{2,N}{\xi }^{N/N}\right)\in \mathbb{C}\ll t_1,t_2{\gg }^2,$$

where, for $j=1,2$, $N=(N_{j1},N_{j2}),{\xi }^{N/N}=t_1^{N_{j1}/N_1}{t}_2^{N_{j2}/N_2}$, ${\nu }_{t_i}(\phi )=N_i\in \mathbb{N}$, $i=1,2$, $N\in {\mathbb{N}}^2$, and the lexicographic order for monomials is considered. We have that $g({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2),t_1)=0$ in some neighborhood of $t_1=0$ where $\phi (t_1,t_2)$ converges. Then, there exists some $M\in {\mathbb{R}}^{+}$ such that

$$F(1:{\phi }_1(t_1,t_2):{\phi }_2(t_1,t_2):t_1)=g({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2),t_1)=0,$$

where $(t_1,t_2)\in {\mathbb{C}}^2$  and $|t_1|<M,$ which implies that

$$F(t_1^{-1}:t_1^{-1}{\phi }_1(t_1,t_2):t_1^{-1}{\phi }_2(t_1,t_2):1)=f(t_1^{-1},t_1^{-1}{\phi }_1(t_1,t_2),t_1^{-1}{\phi }_2(t_1,t_2))=0,$$

for $(t_1,t_2)\in {\mathbb{C}}^2$ and $0<|t_1|<M$. We set $t_1^{-1}\to t_1$, and we obtain that

$$f(t_1,r_1(t_1,t_2),r_2(t_1,t_2))=0,(t_1,t_2)\in {\mathbb{C}}^{2}and\left|t_1\right|>M^{-1},$$

where

$$r_j(t_1,t_2)=t_1{\phi }_j(t_1^{-1},t_2)=m_j(t_2)t_1+\sum _{N\in {\mathbb{N}}^2}{h}_{j,N}{\chi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

$N=(N_{j1},N_{j2}),{\chi }^{N/N}=t_1^{1-N_{j1}/N_1}{t}_2^{N_{j2}/N_2}$ for $j=1,2$.

Since ${\nu }_{t_1}(\phi )=N_1$, we get that there are $N_1$ different series in its conjugacy class (with respect to the variable $t_1$). Let ${\phi }_{11},\dots ,{\phi }_{1N_1}$ be these series, and $r_{1i}(t_1,t_2)=t_1{\phi }_{1i}(t_1^{-1},t_2)=$

$$m_1(t_2)t_1+a_1(t_2)c_i^{N_{11}}{t}_1^{1-N_{11}/N_1}+a_2(t_2)c_i^{N_{21}}{t}_1^{1-N_{21}/N_1}+a_3(t_2)c_i^{N_{31}}{t}_1^{1-N_{31}/N_1}+\cdots$$

(1)

where $c_1,\dots ,c_{N_1}$ are the $N_1$ complex roots of $x^{N_1}=1$. Similarly, one reasons for $r_{2i}(t_1,t_2)$. Now, we introduce the notion of an infinity branch.

Definition 5.

The set $B={\bigcup }_{i=1}^{N_1}{L}_i$ where

$$L_i=\{(t_1,r_{1i}(t_1,t_2),r_{2i}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M_i\}$$

is called an infinity branch of the affine surface $\mathcal{V}$. The subsets $L_1,\dots ,L_{N_1}$ are called the leaves of the infinity branch B.

Remark 1.

• Note that, up to conjugation, an infinity branch is uniquely determined from one leaf. That is, if $B={\bigcup }_{i=1}^{N_1}{L}_i$, where $L_i=\{(t_1,r_{1i}(t_1,t_2),r_{2i}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M_i\}$, and $r_{1i}(t_1,t_2)=t_1{\phi }_{1i}(t_1^{-1},t_2)=$

  $$m_1(t_2)t_1+a_1(t_2)t_1^{1-N_{11}/N_1}+a_2(t_2)t_1^{1-N_{21}/N_1}+a_3(t_2)t_1^{1-N_{31}/N_1}+\cdots$$

  then $r_{1j}=r_{1i},j=1,\dots ,N_1$, up to conjugation; i.e., $r_{1j}(t_1,t_2)=t_1{\phi }_{1j}(t_1^{-1},t_2)=$

  $$m_1(t_2)t_1+a_1(t_2)c_j^{N_{11}}{t}_1^{1-N_{11}/N_1}+a_2(t_2)c_j^{N_{21}}{t}_1^{1-N_{21}/N_1}+a_3(t_2)c_j^{N_{31}}{t}_1^{1-N_{31}/N_1}+\cdots$$

  where $c_j^{N_1}=1,j=1,\dots ,N_1$, and $N_1,N_{i1}\in \mathbb{N}$. Similarly, one reasons for $r_{2j}$.
• Let $M:=max\{M_1,\dots ,M_N\}$. In the following, we consider $L_i=\{(t_1,r_{1i}(t_1,t_2),r_{2i}(t_1,t_2))$$\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}$.

Let ${\phi }_{ji}(t_1,t_2)=m_j(t_2)+{\sum }_{N\in {\mathbb{N}}^2}{h}_{j,i,N}{\xi }^{N/N},j=1,2,$ be a series expansion for a solution of $g({\phi }_{1i}(t_1,t_2),{\phi }_{2i}(t_1,t_2),t_1)=0$. We consider ${\psi }_{ji}(t_1,t_2):={\phi }_{ji}(t_1^{N_1},t_2^{N_2}),$ and we observe that $(1:{\phi }_{1i}(t_1^{N_1},t_2^{N_2}),{\phi }_{2i}(t_1^{N_1},t_2^{N_2}):t_1^{N_1})$ is a local projective parametrization, with a center at $P=(1:m_1(t_2):m_2(t_2):0)$, of the projective surface ${\mathcal{V}}^{*}$.

Thus, from ${\psi }_{ji}(t_1,t_2):={\phi }_{ji}(t_1^{N_1},t_2^{N_2}),i=1,\dots ,N_1,j=1,2$ (${\phi }_{ji}$ are the $N_1$ different series in the conjugacy class of ${\phi }_{ji}$). We obtain $N_1$ equivalent local projective parametrizations, $(1:{\psi }_{1i}(t_1,t_2):{\psi }_{2i}(t_1,t_2):t_1^{N_1})$ (note that they are equivalent since ${\phi }_{j1},\dots {\phi }_{j{N}_1}$ belong to the same conjugacy class). Therefore, the leaves of B are all associated to a unique infinity place.

Conversely, from a given infinity place defined by a local projective parametrization $(1:{\phi }_1(t_1^{N_1},t_2^{N_2}),{\phi }_2(t_1^{N_1},t_2^{N_2}):t_1^{N_1})$, we obtain $N_1$ Puiseux series, ${\phi }_{ji}(t_1,t_2)=\psi (c_i{t_1}^{1/N_1}{t_1}^{1/N_1})$, $c_i^{N_1}=1$, that provide different expressions $r_{ji}(t_1,t_2)=t_1{\phi }_{ji}(t_1^{-1},t_2),i=1,\dots ,N_1,j=1,2$. Hence, the infinity branch B is defined by the leaves

$$L_j=\{(t_1,r_{1j}(t_1,t_2),r_{2j}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},j=1,\dots ,N_1.$$

From the previous disquisitions, we conclude that there exists a one-to-one relation between infinity places and infinity branches, and we may say that each infinity branch is associated with a unique infinity point (which is given by the center of the corresponding infinity place). Reciprocally, from the previous construction, we obtain that every infinity point has associated, at least, one infinity branch. Thus, every algebraic surface has, at least, one infinity branch. Furthermore, every algebraic surface has a finite number of branches.

The above process can be applied to an infinity point of the form $(a(t_2):b(t_2):c(t_2):0),a(t_2)=1$ that provides a local parametrization $(b(t_2),c(t_2))$ of an infinity curve. For the case that $b(t_2)=1$, we may reason similarly by considering the surface implicitly defined by the polynomial $F(x,1,z,w)$. Observe that $g(p,0)=0,$ where $p=(m_1(t_2),m_2(t_2))$, $m_1(t_2),m_2(t_2)\in \mathbb{C}\ll t_2\gg ,$ is a local parametrization of an infinity curve of ${\mathcal{V}}^{*}$ implicitly defined by the irreducible polynomial $g(x,z,0)$ that divides $F(x:1:z:0)$. In this case, $F(m_1(t_2):1:m_2(t_2):0)=0$, and by abuse of notation, we refer to $P=(m_1(t_2):1:m_2(t_2):0)$ as an infinity point of the input surface. In this situation, we get that there exists $M\in {\mathbb{R}}^{+}$ such that

$$F({\phi }_1(t_1,t_2),1,{\phi }_2(t_1,t_2),t_1)=h({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2),t_1)=0,$$

for  $(t_1,t_2)\in {\mathbb{C}}^2$  and $|t_1|<M$, where for $j=1,2,$

$${\phi }_j(t_1,t_2)=m_j(t_2)+\sum _{N\in {\mathbb{N}}^2}{h}_{j,N}{\xi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

$N=(N_{j1},N_{j2}),{\xi }^{N/N}=t_1^{N_{j1}/N_1}{t}_2^{N_{j2}/N_2}$, ${\nu }_{t_i}({\phi }_j)=N_i\in \mathbb{N}$, $N_{ji}\in \mathbb{N},i=1,\dots$ (and the lexicographic order for monomials is considered) is a series expansion for a solution of $h(x,z,t_1)=0$ with respect to $(x,z)$ in some neighborhood of $t_1=0$. We set $t_1\to t_1^{-1}$, and we get that

$$f(r_1(t_1,t_2),t_1,r_2(t_1,t_2))=0,(t_1,t_2)\in {\mathbb{C}}^2\mathrm{and}\left|t_1\right|>M^{-1},$$

where $r_j(t_1,t_2)=t_1{\phi }_j(t_1^{-1},t_2)$ for $j=1,2$.

Thus, we obtain an infinity branch $B={\bigcup }_{i=1}^{N_1}{L}_i$ whose leaves have the form:

$$L_i=\{(r_{1i}(t_1,t_2),t_1,r_{2i}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}.$$

Observe that we may apply this construction to any infinity point of the form $(a(t_2):b(t_2):c(t_2):0),b(t_2)\ne 0$.

Finally, for the case $c(t_2)=1$, we may consider the surface implicitly defined by the polynomial $F(x,y,1,w)$. Observe that $g(p,0)=0,$ where $p=(m_1(t_2),m_2(t_2))$, $m_1(t_2),m_2(t_2)\in \mathbb{C}\ll t_2\gg ,$ is a local parametrization of an infinity curve of ${\mathcal{V}}^{*}$ implicitly defined by the irreducible polynomial $g(x,y,0)$ that divides $F(x:y:1:0)$. In this case, $F(m_1(t_2):m_2(t_2):1:0)=0$, and by abuse of notation, we refer to $P=(m_1(t_2):m_2(t_2):1:0)$ as an infinity point of the input surface. In this situation, we get that there exists $M\in {\mathbb{R}}^{+}$ such that

$$F({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2),1,t_1)=h({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2),t_1)=0,$$

for  $(t_1,t_2)\in {\mathbb{C}}^2$  and $|t_1|<M$, where for $j=1,2,$

$${\phi }_j(t_1,t_2)=m_j(t_2)+\sum _{N\in {\mathbb{N}}^2}{h}_{j,N}{\xi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

$N=(N_{j1},N_{j2}),{\xi }^{N/N}=t_1^{N_{j1}/N_1}{t}_2^{N_{j2}/N_2}$, ${\nu }_{t_i}({\phi }_j)=N_i\in \mathbb{N}$, $N_{ji}\in \mathbb{N},i=1,\dots$ (and the lexicographic order for monomials is considered) is a series expansion for a solution of $h(x,y,w)=0$. We set $t_1\to t_1^{-1}$ and we get that

$$f(r_1(t_1,t_2),r_2(t_1,t_2),t_1)=0,(t_1,t_2)\in {\mathbb{C}}^{2}and\left|t_1\right|>M^{-1},where$$

$r_j(t_1,t_2)=t_1{\phi }_j(t_1^{-1},t_2)$ for $j=1,2$.

Thus, we obtain an infinity branch $B={\bigcup }_{i=1}^{N_1}{L}_i$ whose leaves have the form:

$$L_i=\{(r_{1i}(t_1,t_2),r_{2i}(t_1,t_2),t_1)\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}.$$

Observe that we may apply this construction to any infinity point of the form $(a(t_2):b(t_2):c(t_2):0),c(t_2)\ne 0$.

Definition 6.

Let $\mathcal{V}$ be an affine surface over $\mathbb{C}$ defined by an irreducible polynomial $f(x,y,z)\in \mathbb{R}[x,y,z]$.

• An infinity branch of $\mathcal{V}$ of type 1 associated with the infinity point $P=(1:m_1:m_2:0),m_1,m_2\in \mathbb{C}\ll t_2\gg$ is a set $B={\bigcup }_{i=1}^{N_1}{L}_i$, where $L_i=\{(t_1,r_{1i}(t_1,t_2),r_{2i}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}$,  $i=1,\dots ,N_1$, $M\in {\mathbb{R}}^{+}$, and $r_{11},\dots ,r_{1N_1}$ are the conjugates of

  $$r_1(t_1,t_2)=m_1(t_2)t_1+\sum _{N\in {\mathbb{N}}^2}{h}_N{\chi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

  $N=(N_{11},N_{12}),{\chi }^{N/N}=t_1^{1-N_{11}/N_1}{t}_2^{N_{12}/N_2}$ (similarly for $r_2$);
• An infinity branch of $\mathcal{V}$ of type 2 associated with the infinity point $P=(m_1:1:m_1:0),m_1,m_2\in \mathbb{C}\ll t_2\gg$ is a set $B={\bigcup }_{i=1}^{N_1}{L}_i$, where $L_i=\{(r_{1i}(t_1,t_2),t_1,r_{2i}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}$,  $i=1,\dots ,N_1$, $M\in {\mathbb{R}}^{+}$, and $r_{11},\dots ,r_{1N_1}$ are the conjugates of

  $$r_1(t_1,t_2)=m_1(t_2)t_1+\sum _{N\in {\mathbb{N}}^2}{h}_N{\chi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

  $N=(N_{11},N_{12}),{\chi }^{N/N}=t_1^{1-N_{11}/N_1}{t}_2^{N_{12}/N_2}$ (similarly for $r_2$);
• An infinity branch of $\mathcal{V}$ of type 3 associated with the infinity point $P=(m_1:m_2:1:0),m_1,m_2\in \mathbb{C}\ll t_2\gg$ is a set $B={\bigcup }_{i=1}^{N_1}{L}_i$, where $L_i=\{(r_{1i}(t_1,t_2),r_{2i}(t_1,t_2),t_1)\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}$,  $i=1,\dots ,N_1$, $M\in {\mathbb{R}}^{+}$, and $r_{11},\dots ,r_{1N_1}$ are the conjugates of

  $$r_1(t_1,t_2)=m_1(t_2)t_1+\sum _{N\in {\mathbb{N}}^2}{h}_N{\chi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

  $N=(N_{11},N_{12}),{\chi }^{N/N}=t_1^{1-N_{11}/N_1}{t}_2^{N_{12}/N_2}$ (similarly for $r_2$).

Remark 2.

• In the following, we work with the type 1 infinity branches of a given algebraic surface $\mathcal{V}$. Similarly, one can reason for the other infinity branches;
• We will say that $N_1$ is the ramification index of the branch B with respect to $t_1$, and we will write it as ${\nu }_{t_1}(B)=N_1$. Note that B has ${\nu }_{t_1}(B)$ leaves.

In the following examples, we compute the infinity branches for some given surfaces.

Example 1.

Let $\mathcal{V}$ be the a surface implicitly defined by the irreducible polynomial

$$f(x,y,z)=x^2+y^2-z^2-1\in \mathbb{R}[x,y,z].$$

The corresponding projective surface ${\mathcal{V}}^{*}$ is defined by

$$F(x:y:z:w)=x^2+y^2-z^2-w^2\in \mathbb{R}[x,y,z,w].$$

Note that $P=(1:-1/2(t_2-1)(t_2+1)/t_2:1/2(1+t_2^2)/t_2:0)$ is an infinity point of ${\mathcal{V}}^{*}$.

We determine the infinity branches associated with P. For this purpose, we consider the curve defined by the irreducible polynomial $g(y,z,w)=F(1:y:z:w)$, and we observe that $g(p,0)=0,$ where $p=(-1/2(t_2-1)(t_2+1)/t_2,1/2(1+t_2^2)/t_2)$ is a rational parametrization of the curve defined implicitly by $g(y,z,0)=F(1:y:z:0)=1+y^2-z^2$. Note that in this case, we have more than a local parametrization of $g(y,z,0)$ but a rational parametrization of $g(y,z,0)$.

Now, we compute the series expansion for the solutions of $g(y,z,t_1)=0$ with respect to $(y,z)$ around $t_1=0$. In this case, since $g(y,z,t_1)$ is rational over $\mathbb{C}(t_1)$, we compute a parametrization and we get that:

$${\phi }_1(t_1,t_2)=1/2(1-t_1^2-t_2^2)/t_2\in \mathbb{C}(t_1,t_2)\subset \mathbb{C}\ll t_1,t_2\gg ,and$$

$${\phi }_2(t_1,t_2)=1/2(1-t_1^2+t_2^2)/t_2\in \mathbb{C}(t_1,t_2)\subset \mathbb{C}\ll t_1,t_2\gg .$$

Observe that $p=({\phi }_1(0,t_2),{\phi }_2(0,t_2))$, and  $g({\phi }_1(t_1,t_2),{\phi }_2(t_1,t_2),t_1)=0$. Note that ${\nu }_{t_1}({\phi }_j)=1,j=1,2$, which implies that we only have one Puiseux series in the conjugacy class of ${\phi }_j,j=1,2$. Thus, we obtain one infinity branch:

$$B_1=L_1=\{(t_1,r_1(t_1,t_2),r_2(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

$$r_1(t_1,t_2)=t_1{\phi }_1(t_1^{-1},t_2)=1/2t_1{t}_2^{-1}-1/2t_1^{-1}{t}_2^{-1}-1/2t_1{t}_2,$$

$$r_2(t_1,t_2)=t_1{\phi }_2(t_1^{-1},t_2)=1/2t_1{t}_2^{-1}-1/2t_1^{-1}{t}_2^{-1}+1/2t_1{t}_2.$$

Example 2.

Let $\mathcal{V}$ be the surface implicitly defined by the irreducible polynomial

$$f(x,y,z)=x^2+z^2{x}^2+z{y}^3\in \mathbb{R}[x,y,z].$$

The corresponding projective surface ${\mathcal{V}}^{*}$ is defined by

$$F(x:y:z:w)=x^2{w}^2+z^2{x}^2+z{y}^3\in \mathbb{R}[x,y,z,w].$$

Note that $P_1=(1:t_2:-t_2^3:0)$ and $P_2=(1:t_2:0:0)$ are the two infinity points of ${\mathcal{V}}^{*}$. We determine the infinity branches associated with $P_1$ and $P_2$. For this purpose, we consider the curve defined by $g(y,z,w)=F(1:y:z:w)$, and we observe that $g(p_1,0)=0,$ where $p_1=(t_2,-t_2^3)$. Note that in this case, we have more than a local parametrization of $g(y,z,0)$ but a rational parametrization of $g(y,z,0)$.

Now, we compute the series expansion for the solutions of $g(y,z,t_1)=0$ with respect to $(y,z)$ around $t_1=0$. In this case, $g(y,z,t_1)$ is not rational over $\mathbb{C}(t_1)$; thus, we compute a local parametrization, and we get two different solutions:

• First, we get that ${\phi }_1(t_1,t_2)=({\phi }_{11}(t_1,t_2),{\phi }_{12}(t_1,t_2))$, where

  $${\phi }_{11}(t_1,t_2)=t_2\in \mathbb{C}(t_1,t_2)\subset \mathbb{C}\ll t_1,t_2\gg ,and$$

  $${\phi }_{12}(t_1,t_2)=-t_2^3+t_1^2/t_2^3+t_1^4/t_2^9+\cdots \in \mathbb{C}(t_1,t_2)\subset \mathbb{C}\ll t_1,t_2\gg .$$
  Observe that ${\phi }_1(0,t_2)=p_1$, and  $g({\phi }_1(t_1,t_2),t_1)=0$. Note that ${\nu }_{t_1}({\phi }_{1j})=1,j=1,2$, which implies that we only have one Puiseux series in the conjugacy class of ${\phi }_j,j=1,2$. Thus, we obtain one infinity branch:

  $$B_1=L_1=\{(t_1,r_{11}(t_1,t_2),r_{12}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

  $$r_{11}(t_1,t_2)=t_1{\phi }_{11}(t_1^{-1},t_2)=t_1{t}_2,$$

  $$r_{12}(t_1,t_2)=t_1{\phi }_{12}(t_1^{-1},t_2)=-t_1{t}_2^3+t_1^{-1}{t}_2^{-3}+t_1^{-3}{t}_2^{-9}+\cdots .$$
  In Figure 1, we plot the surface $\mathcal{V}$ and a surface, ${\mathcal{V}}_1$, constructed from the infinity branch $B_1$ that approach the input surface (see Section 4);
  

  Figure 1. Surface $\mathcal{V}$ (left), and surface ${\mathcal{V}}_1$ (right).
• We also get that ${\phi }_2(t_1,t_2)=({\phi }_{21}(t_1,t_2),{\phi }_{22}(t_1,t_2))$, where

  $${\phi }_{21}(t_1,t_2)=t_2\in \mathbb{C}(t_1,t_2)\subset \mathbb{C}\ll t_1,t_2\gg ,and$$

  $${\phi }_{22}(t_1,t_2)=-t_1^2/t_2^3-t_1^4/t_2^9+\cdots \in \mathbb{C}(t_1,t_2)\subset \mathbb{C}\ll t_1,t_2\gg .$$
  Observe that ${\phi }_2(0,t_2)=p_2$, and  $g({\phi }_2(t_1,t_2),t_1)=0$. Note that ${\nu }_{t_1}({\phi }_{2j})=1,j=1,2$, which implies that we only have one Puiseux series in the conjugacy class of ${\phi }_j,j=1,2$. Thus, we obtain one infinity branch:

  $$B_2=L_2=\{(t_1,r_{21}(t_1,t_2),r_{22}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

  $$r_{21}(t_1,t_2)=t_1{\phi }_{21}(t_1^{-1},t_2)=t_1{t}_2,$$

  $$r_{22}(t_1,t_2)=t_1{\phi }_{22}(t_1^{-1},t_2)=-t_1^{-1}{t}_2^{-3}-t_1^{-3}{t}_2^{-9}+\cdots .$$
  In Figure 2, we plot the surface $\mathcal{V}$ and a surface, ${\mathcal{V}}_2$, constructed from the infinity branch $B_2$ that approach the input surface (see Section 4). In  Figure 3, we plot the surface $\mathcal{V}$ and the surfaces ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$ together.
  

  Figure 2. Surface $\mathcal{V}$ (left), and surface ${\mathcal{V}}_2$ (right).
  

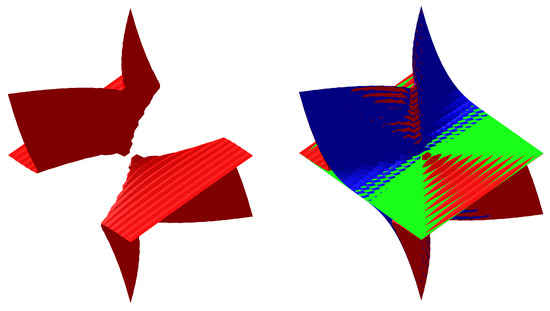  Figure 3. Surface $\mathcal{V}$ (left), surface $\mathcal{V}$ and surfaces ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$ (right).

Remark 3.

The computation of ${\phi }_i(t_1,t_2)\in \mathbb{C}\ll t_1,t_2\gg ,i=1,2,$ is not an easy question. In some cases, this problem can be easily solved as in Examples 1 and 2. For a more general cases, and also for the case of surfaces parametrically defined, we will deal with this question in a future work.

In the following, we prove that any point of the surface with sufficiently large coordinates belongs to some infinity branch. For this purpose, we recall that if h is a complex-valued function of a complex variable, $h:{\mathbb{C}}^3\to \mathbb{C}$, we say that the limit of $h(z_1,z_2,z_3)$ as $z_i$ approaches ∞ is L, written ${\displaystyle \underset{z\to \infty }{lim}h(z)=L}$. If whenever ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ is a sequence of points with ${\displaystyle \underset{n\to \infty }{lim}{z}_n=\infty }$, it holds that ${\displaystyle \underset{n\to \infty }{lim}h(z_n)=L}$ (see, e.g., [17] or [18]).

Lemma 1.

Let $\mathcal{V}$ be an algebraic surface. There exists $K\in {\mathbb{R}}^{+}$ such that for every $p=(a,b,c)\in \mathcal{V}$ with $\left|a\right|>K$, it holds that $p\in B_p$, where $B_p$ is an infinity branch of $\mathcal{C}$.

Proof. 

Let us assume that the lemma does not hold, and we consider a sequence ${\left\{K_n\right\}}_{n\in \mathbb{N}}\subset {\mathbb{R}}^{+}$ such that ${lim}_{n\to \infty }{K}_n=\infty$. Then, for every $n\in \mathbb{N}$, there exists a point $p_n=(a_n,b_n(t_2),$$c_n(t_2))\in \mathcal{V}$ such that $|a_n|>K_n$, and $p_n$ does not belong to any infinity branch of $\mathcal{V}$.

Let $P_n=(a_n:b_n(t_2):c_n(t_2):1)$. Since $F(P_n)=f(p_n)=0$, then ${lim}_{n\to \infty }F(P_n)=0$. Thus, we distinguish the following different cases:

(a)

If there exist two not-bounded monotone subsequences, ${\{b_{n_l}(t_2)/a_{n_l}\}}_{l\in \mathbb{N}}$ and ${\{b_{n_l}(t_2)/c_{n_l}(t_2)\}}_{l\in \mathbb{N}}$, we have that

$$\underset{l\to \infty }{lim}{b}_{n_l}(t_2)/a_{n_l}=\underset{l\to \infty }{lim}{b}_{n_l}(t_2)/c_{n_l}(t_2)=\infty ,$$

and then ${lim}_{l\to \infty }{a}_{n_l}/b_{n_l}(t_2)=0$ and ${lim}_{l\to \infty }{c}_{n_l}(t_2)/b_{n_l}(t_2)=0.$ Hence, ${lim}_{l\to \infty }F(Q_{n_l})=F(0:1:0:0)=0,$ where $Q_{n_l}=(a_{n_l}/b_{n_l}(t_2):1:c_{n_l}(t_2)/b_{n_l}(t_2):1/b_{n_l}(t_2))$, which implies that $P=(0:1:0:0)$ is an infinity point of ${\mathcal{V}}^{*}$;

(b)

If there exist a not-bounded monotone subsequence ${\{b_{n_l}(t_2)/a_{n_l}\}}_{l\in \mathbb{N}}$ and a bounded monotone subsequence ${\{b_{n_l}(t_2)/c_{n_l}(t_2)\}}_{l\in \mathbb{N}}$, we have that ${lim}_{l\to \infty }{b}_{n_l}(t_2)/a_{n_l}=\infty$ and ${lim}_{l\to \infty }{b}_{n_l}(t_2)/c_{n_l}(t_2)=m(t_2)$, and then ${lim}_{l\to \infty }{a}_{n_l}/b_{n_l}(t_2)=0$ and ${lim}_{l\to \infty }{c}_{n_l}(t_2)/b_{n_l}(t_2)=1/m(t_2):=m_2(t_2)$ (if $m(t_2)\ne 0$). Hence,

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(0:1:m_2(t_2):0)=0,$$

where $Q_{n_l}=(a_{n_l}/b_{n_l}(t_2):1:c_{n_l}(t_2)/b_{n_l}(t_2):1/b_{n_l}(t_2))$, which implies that $P=(0:1:m_2(t_2):0)$ is an infinity point of ${\mathcal{V}}^{*}$.

Note that if $m(t_2)=0$, then we consider ${lim}_{l\to \infty }{a}_{n_l}/c_{n_l}(t_2)=0$. Hence,

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(0:0:1:0)=0,$$

where $Q_{n_l}=(a_{n_l}/c_{n_l}(t_2):b_{n_l}/c_{n_l}(t_2):1:1/c_{n_l}(t_2))$, which implies that $P=(0:0:1:0)$ is an infinity point of ${\mathcal{V}}^{*}$;

(c)

If there exist two bounded monotone subsequences ${\{b_{n_l}(t_2)/a_{n_l}\}}_{l\in \mathbb{N}}$ and ${\{b_{n_l}(t_2)/c_{n_l}(t_2)\}}_{l\in \mathbb{N}}$, we have that ${lim}_{l\to \infty }{b}_{n_l}(t_2)/a_{n_l}=m_1(t_2)$ and

$$\underset{l\to \infty }{lim}{c}_{n_l}(t_2)/a_{n_l}=\underset{l\to \infty }{lim}(c_{n_l}(t_2)/b_{n_l}(t_2))/(b_{n_l}(t_2)/a_{n_l})=m(t_2)/m_1(t_2):=m_2(t_2)$$

(if $m_1(t_2)\ne 0$). Thus,

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(1:m_1(t_2):m_2(t_2):0)=0,$$

where $Q_{n_l}=(1:b_{n_l}(t_2)/a_{n_l}:c_{n_l}(t_2)/a_{n_l}:1/a_{n_l})$, which implies that $P=(1:m_1(t_2):m_2(t_2):0)$ is an infinity point of ${\mathcal{V}}^{*}$.

If $m_1(t_2)=0$, that is, ${lim}_{l\to \infty }{b}_{n_l}(t_2)/a_{n_l}=0$, since ${lim}_{l\to \infty }{b}_{n_l}(t_2)/c_{n_l}(t_2)=n(t_2)$ (we assume that $n(t_2)\ne 0$), we get that ${lim}_{l\to \infty }{c}_{n_l}(t_2)/a_{n_l}=0$. Thus,

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(1:0:0:0)=0,$$

where $Q_{n_l}=(1:b_{n_l}(t_2)/a_{n_l}:c_{n_l}(t_2)/a_{n_l}:1/a_{n_l})$, which implies that $P=(1:0:0:0)$ is an infinity point of ${\mathcal{V}}^{*}$.

If $m_1(t_2)=n(t_2)=0$, that is, ${lim}_{l\to \infty }{b}_{n_l}(t_2)/a_{n_l}={lim}_{l\to \infty }{b}_{n_l}(t_2)/c_{n_l}(t_2)=0$, then ${lim}_{l\to \infty }{c}_{n_l}(t_2)/a_{n_l}=n(t_2)$ or ${lim}_{l\to \infty }{a}_{n_l}/c_{n_l}(t_2)=m(t_2)$. Let us assume that ${lim}_{l\to \infty }{c}_{n_l}(t_2)/a_{n_l}=n(t_2)$. Then, since ${lim}_{l\to \infty }{b}_{n_l}(t_2)/a_{n_l}=0$, we get that

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(1:0:n(t_2):0)=0,$$

where $Q_{n_l}=(1:b_{n_l}(t_2)/a_{n_l}:c_{n_l}(t_2)/a_{n_l}:1/a_{n_l})$, which implies that $P=(1:0:n(t_2):0)$ is an infinity point of ${\mathcal{V}}^{*}$.

(d)

If there exist a bounded monotone subsequence ${\{b_{n_l}(t_2)/a_{n_l}\}}_{l\in \mathbb{N}}$ and a not-bounded monotone subsequence ${\{b_{n_l}(t_2)/c_{n_l}(t_2)\}}_{l\in \mathbb{N}}$, we have that

$$\underset{l\to \infty }{lim}{b}_{n_l}(t_2)/a_{n_l}=m_1(t_2)$$

and

$$\underset{l\to \infty }{lim}{c}_{n_l}(t_2)/a_{n_l}=\underset{l\to \infty }{lim}(c_{n_l}(t_2)/b_{n_l}(t_2))/(b_{n_l}(t_2)/a_{n_l})=0.$$

Thus,

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(1:m_1(t_2):0:0)=0,$$

where $Q_{n_l}=(1:b_{n_l}(t_2)/a_{n_l}:c_{n_l}(t_2)/a_{n_l}:1/a_{n_l})$, which implies that $P=(1:m_1(t_2):0:0)$ is an infinity point of ${\mathcal{V}}^{*}$.

Note that if ${lim}_{l\to \infty }{b}_{n_l}(t_2)/a_{n_l}=0$, then since ${lim}_{l\to \infty }{c}_{n_l}(t_2)/b_{n_l}(t_2)=0$, we get that ${lim}_{l\to \infty }{c}_{n_l}(t_2)/a_{n_l}=0$. Thus,

$$\underset{l\to \infty }{lim}F(Q_{n_l})=F(1:0:0:0)=0,$$

where $Q_{n_l}=(1:b_{n_l}(t_2)/a_{n_l}:c_{n_l}(t_2)/a_{n_l}:1/a_{n_l})$, which implies that $P=(1:0:0:0)$ is an infinity point of ${\mathcal{V}}^{*}$.

From both situations, we deduce that there exists a sequence ${\left\{Q_n\right\}}_{n\in \mathbb{N}}$ that approaches to an infinity point P as n tends to infinity; i.e., there exists $M\in {\mathbb{R}}^{+}$ such that $\parallel Q_n-P\parallel \le ϵ$ for $n\ge M$. Therefore, one may conclude that ${\left\{Q_n\right\}}_{n\in \mathbb{N},n\ge M}$ can be determined by a place centered at P. Thus, $p_n$ belongs to some infinity branch of $\mathcal{V}$, which contradicts the hypothesis.    □

Remark 4.

Reasoning as in Lemma 1; one gets that there exists $K\in {\mathbb{R}}^{+}$ satisfying that for every $p=(a,b,c)\in \mathcal{V}$,  $\left|b\right|>K$, it holds that $p\in B_p$, where $B_p$ is an infinity branch of $\mathcal{V}$. The reasoning is similar if $\left|c\right|>K$.

4. Convergent Branches and Approaching Surfaces

In the following, we define convergent branches and approaching surfaces. We say that two infinity branches converge if they get closer as they tend to infinity. This notion will allow us to analyze whether two surfaces approach each other at the infinity.

The results obtained in this section will be used in Section 5. In Section 5, we present a method that compares the asymptotic behavior of two surfaces implicitly defined.

Definition 7.

Given two leaves, $L=\{(t_1,r_1(t_1,t_2),r_2(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}$ and $\overline{L}=\{(t_1,{\overline{r}}_1(t_1,t_2),{\overline{r}}_2(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>\overline{M}\}$, we say that they are convergent if ${lim}_{t_1\to \infty }({\overline{r}}_i(t_1,t_2)-r_i(t_1,t_2))=0,$ for $i=1,2$.

Lemma 2.

Two leaves $L=\{(t_1,r_1(t_1,t_2),r_2(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}$ and $\overline{L}=\{(t_1,{\overline{r}}_1(t_1,t_2),{\overline{r}}_2(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>\overline{M}\}$ are convergent if and only if the monomials on the variable $t_1$ that have a non-negative exponent in the series $r_i(t_1,t_2)$ and ${\overline{r}}_i(t_1,t_2)$ are the same (for $i=1,2$).

Proof. 

Let

$$r_1(t_1,t_2)=m_1(t_2)t_1+\sum _{N\in {\mathbb{N}}^2}{h}_{1,N}{\chi }^{N/N}\in \mathbb{C}\ll t_1,t_2\gg ,$$

$N=(N_{11},N_{12}),{\chi }^{N/N}=t_1^{1-N_{11}/N_1}{t}_2^{N_{12}/N_2}$, and 

$${\overline{r}}_1(t_1,t_2)={\overline{m}}_1(t_2)t_1+\sum _{\overline{N}\in {\mathbb{N}}^2}{\overline{h}}_{1,\overline{N}}{\overline{\chi }}^{\overline{N}/\overline{N}}\in \mathbb{C}\ll t_1,t_2\gg ,$$

$\overline{N}=({\overline{N}}_{11},{\overline{N}}_{12}),{\overline{\chi }}^{\overline{N}/\overline{N}}=t_1^{1-{\overline{N}}_{11}/{\overline{N}}_1}{t}_2^{{\overline{N}}_{12}/{\overline{N}}_1}$. Then,

$$r_1(t_1,t_2)-{\overline{r}}_1(t_1,t_2)=m_1{t}_1-{\overline{m}}_1{t}_1+\sum _{N\in {\mathbb{N}}^2}{h}_{1,N}{\chi }^{N/N}-\sum _{\overline{N}\in {\mathbb{N}}^2}{\overline{h}}_{1,\overline{N}}{\overline{\chi }}^{\overline{N}/\overline{N}}.$$

Note that ${lim}_{t_1\to \infty }({\overline{r}}_1(t_1,t_2)-r_1(t_1,t_2))=0$ if and only if ${\overline{r}}_1(t_1,t_2)-r_1(t_1,t_2)$ has no monomials having a non-negative exponent. This situation holds if the monomials on the variable $t_1$ that have a non-negative exponent in both series, $r_1$ and ${\overline{r}}_1$, are the same.

One reasons similarly for $r_2$ and ${\overline{r}}_2$.    □

Remark 5.

• From Lemma 2, we deduce that $m_i(t_2)={\overline{m}}_i(t_2),i=1,2,$ and then, L and $\overline{L}$ are associated with the same infinity point;
• Note that the number of monomials with regard to $t_1$ that have a positive exponent in both series is finite.

Definition 8.

Two infinity branches, B and $\overline{B}$, are convergent if there exist two convergent leaves $L\subset B$ and $\overline{L}\subset \overline{B}$.

Remark 6.

Statement 1 in Remark 5 implies that two convergent infinity branches are associated with the same infinity point.

Proposition 1.

Two infinity branches B and $\overline{B}$ are convergent if and only if for each leaf $L\subset B$ there exists a leaf $\overline{L}\subset \overline{B}$ convergent with L, and reciprocally.

Proof. 

The proof follows reasoning similarly as in Proposition 4.6 in [5].    □

Remark 7.

Two convergent infinity branches may have different ramification indexes; that is, they may have different numbers of leaves. However, $n_1\in \mathbb{N}$, which is obtained by simplifying the non-negative exponents in the variable $t_1$, is the same in both branches. We refer to it as the degree of the infinity branch with respect to $t_1$. Note that from the proof of Proposition 1, we get that two convergent infinity branches have the same degree with respect to $t_1$.

Two convergent infinity branches may be contained in the same surface or they may belong to different surfaces. In this second case, we will say that those surfaces approach each other. In order to define this concept in a more formal way, we first introduce the following distance:

Definition 9.

Given an algebraic surface $\mathcal{V}$ over $\mathbb{C}$ and a point $p\in {\mathbb{C}}^3$, we define the distance from p to $\mathcal{V}$as $d(p,\mathcal{V})=min\{d(p,q):q\in \mathcal{V}\}.$

Remark 8.

We should note that since $\mathcal{V}$ is a closed set, this minimum exists.

Definition 10.

Let $\mathcal{V}$ be an algebraic surface over $\mathbb{C}$ with an infinity branch B. We say that a surface $\overline{\mathcal{V}}$ approaches $\mathcal{V}$ at its infinity branch B if there exists one leaf $L=\{(t_1,r_1(t_1,t_2),r_2(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\}\subset B$ such that ${lim}_{t_1\to \infty }d((t_1,r_1(t_1,t_2),r_2(t_1,t_2)),\overline{\mathcal{V}})=0.$

We will show that this condition is satisfied for one leaf of B if and only if it is satisfied for every leaf of B. It will be derived as a consequence of the following theorem.

Theorem 2.

Let $\mathcal{V}$ be an algebraic surface over $\mathbb{C}$ with an infinity branch B. An algebraic surface $\overline{\mathcal{V}}$ approaches $\mathcal{V}$ at B if and only if $\overline{\mathcal{V}}$ has an infinity branch, $\overline{B}$, such that B and $\overline{B}$ are convergent.

Proof. 

The proof follows reasoning similarly as in Theorem 4.11 in [5].    □

Remark 9.

• Theorem 2 implies that “proximity” is a symmetric relation. More precisely, the surface $\overline{\mathcal{V}}$ approaches the surface $\mathcal{V}$ at some infinity branch B if and only if $\mathcal{V}$ approaches $\overline{\mathcal{V}}$ at some infinity branch $\overline{B}$. In the following, we say that $\mathcal{V}$ and $\overline{\mathcal{V}}$ approach each other or that they are approaching surfaces ;
• From Theorem 2 and Remark 6, we get that two approaching surfaces have a common infinity point;
• Theorem 2 and Proposition 1 imply that $\overline{\mathcal{V}}$ approaches $\mathcal{V}$ at an infinity branch B if for every leaf

  $$L=\{(t_1,r_1(t_1,t_2),r_2(t_1,t_2))\in {\mathbb{C}}^3:t_1,t_2,\in \mathbb{C},|t_1|>M\}\subset B,$$

  it holds that ${\displaystyle \underset{z\to \infty }{lim}d((t_1,r_1(t_1,t_2),r_2(t_1,t_2)),\overline{\mathcal{V}})=0.}$

Corollary 1.

Let $\mathcal{V}$ be an algebraic surface with an infinity branch B. Let ${\overline{\mathcal{V}}}_1$ and ${\overline{\mathcal{V}}}_2$ be two different surfaces that approach $\mathcal{V}$ at B. Then, ${\overline{\mathcal{V}}}_1$ and ${\overline{\mathcal{V}}}_2$ approach each other.

Proof. 

From Theorem 2, there exist two infinity branches $B_1\subset {\overline{\mathcal{V}}}_1$ and $B_2\subset {\overline{\mathcal{V}}}_2$, convergent with B. Thus, for each leaf $L=\{(t_1,r_1(t_1,t_2),r_2(t_1,t_2))\in {\mathbb{C}}^3:t_i\in \mathbb{C},|t_1|>M\}\subset B$, there exist two leaves $L_1=\{(t_1,l_1(t_1,t_2),l_2(t_1,t_2))\in {\mathbb{C}}^2:t_i\in \mathbb{C},|t_1|>M_1\}\subset B_1$ and $L_2=\{(t_1,s_1(t_1,t_2),s_2(t_1,t_2))\in {\mathbb{C}}^3:t_i\in \mathbb{C},|t_1|>M_2\}\subset B_2$ such that ${lim}_{t_1\to \infty }(r_1(t_1,t_2)-l_1(t_1,t_2))=0$ and ${lim}_{t_1\to \infty }(r_1(t_1,t_2)-s_1(t_1,t_2))=0$. Then

$$|l_1(t_1,t_2)-s_1(t_1,t_2)|\le |l_1(z)-r_1(t_1,t_2)|+|r_1(t_1,t_2)-s_1(t_1,t_2){|}_{\overrightarrow{t_1\to \infty }}0$$

(one reasons similarly for $r_2$). Therefore, ${\overline{\mathcal{V}}}_1$ and ${\overline{\mathcal{V}}}_2$ approach each other.   □

In Example 3, we illustrate the above results.

Example 3.

Let $\mathcal{V}$ and $\overline{\mathcal{V}}$ be two surfaces implicitly defined by the polynomials

$$f(x,y,z)=x^2+z^2{x}^2+z{y}^3\in \mathbb{R}[x,y,z]and$$

$$\overline{f}(x,y,z)=x^2+z^2{x}^2+z{y}^3+x-2y-9\in \mathbb{R}[x,y,z],$$

respectively. Let us prove that $\mathcal{V}$ and $\overline{\mathcal{V}}$ approach each other at the infinity branch associated with the infinity points

$$P_1=(1:t_2:-t_2^3:0),P_2=(1:t_2:0:0)$$

(note that both surfaces have $P_1=(1:t_2:-t_2^3:0)$ and $P_2=(1:t_2:0:0)$ as infinity points). Reasoning as in Example 2, we get that the infinity branch of $\mathcal{V}$ associated with $P_1$ is given by

$$B_1=L_1=\{(t_1,r_{11}(t_1,t_2),r_{12}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},$$

where

$$r_{11}(t_1,t_2)=t_1{\phi }_{11}(t_1^{-1},t_2)=t_1{t}_2,$$

$$r_{12}(t_1,t_2)=t_1{\phi }_{12}(t_1^{-1},t_2)=-t_1{t}_2^3+t_1^{-1}{t}_2^{-3}+t_1^{-3}{t}_2^{-9}+\cdots .$$

The infinity branch of $\mathcal{V}$ associated with $P_2$ is given by

$$B_2=L_2=\{(t_1,r_{21}(t_1,t_2),r_{22}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},$$

where

$$r_{21}(t_1,t_2)=t_1{\phi }_{21}(t_1^{-1},t_2)=t_1{t}_2,$$

$$r_{22}(t_1,t_2)=t_1{\phi }_{22}(t_1^{-1},t_2)=-t_1^{-1}{t}_2^{-3}-t_1^{-3}{t}_2^{-9}+\cdots .$$

On the other hand, the infinity branch of $\overline{\mathcal{V}}$ associated with $P_1$ is given by

$${\overline{B}}_1={\overline{L}}_1=\{(t_1,{\overline{r}}_{11}(t_1,t_2),{\overline{r}}_{12}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},$$

where

$${\overline{r}}_{11}(t_1,t_2)=t_1{t}_2,$$

$${\overline{r}}_{12}(t_1,t_2)=-t_1{t}_2^3+t_1^{-1}{t}_2^{-3}-2t_1^{-2}{t}_2^{-3}+t_1^{-3}{t}_2^{-9}+\cdots .$$

The infinity branch of $\overline{\mathcal{V}}$ associated with $P_2$ is given by

$${\overline{B}}_2={\overline{L}}_2=\{(t_1,{\overline{r}}_{21}(t_1,t_2),{\overline{r}}_{22}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},$$

where

$${\overline{r}}_{21}(t_1,t_2)=t_1{t}_2,$$

$${\overline{r}}_{22}(t_1,t_2)=-t_1^{-1}{t}_2^{-3}-2t_1^{-2}{t}_2^{-2}-t_1^{-2}{t}_2^{-3}+\cdots .$$

From Lemma 2, we conclude that both branches converge, since the terms with non-negative exponent in both series, $r_{ij}$ and ${\overline{r}}_{ij}$, are the same.

Remark 10.

In the above example, the surfaces $\mathcal{V}$ and $\overline{\mathcal{V}}$ are approaching surfaces, since $\mathcal{V}$ approaches $\overline{\mathcal{V}}$ at one of its infinity branches reciprocally.

In fact, $\mathcal{V}$ approaches $\overline{\mathcal{V}}$ at all of its infinity branches and reciprocally. In this case, we say that both surfaces have the same asymptotic behavior. We focus on this special relation in the next section.

5. Asymptotic Behavior

From the results obtained previously, we obtain an algorithm that compares the asymptotic behavior of two surfaces implicitly defined. Two surfaces have the same asymptotic behavior if they approach each other at all of the infinity branches. Furthermore, we show that if two algebraic surfaces have the same asymptotic behavior, the Hausdorff distance between them is finite.

The algorithm developed, as well as the results presented in this section, provide essential tools in the frame of practical applications in computer-aided geometric design (CAGD) such as, for instance, the problem of the approximate parametrization (see Section 1).

To start with, we first introduce the following definition.

Definition 11.

We say that two algebraic surfaces, $\mathcal{V}$ and $\overline{\mathcal{V}}$, have the same asymptotic behavior if every infinity branch of $\mathcal{V}$ converges to another branch of $\overline{\mathcal{V}}$ and does so reciprocally.

Remark 11.

From Theorem 2, we get that $\mathcal{V}$ and $\overline{\mathcal{V}}$ have the same asymptotic behavior if $\mathcal{V}$ approaches $\overline{\mathcal{V}}$ at all its infinity branches and does so reciprocally.

Now, we recall the notion of Hausdorff distance.

Definition 12.

Given a metric space $(E,d)$ and two subsets $A,B\subset E\backslash \{\varnothing \}$, the Hausdorff distance between them is defined as:

$$d_H(A,B)=max\{\underset{x\in A}{sup}\underset{y\in B}{inf}d(x,y),\underset{y\in B}{sup}\underset{x\in A}{inf}d(x,y)\}.$$

If $E={\mathbb{C}}^3$ and d is the Euclidean distance, the Hausdorff distance between two surfaces $\mathcal{V}$ and $\overline{\mathcal{V}}$ can be expressed as:

$$d_H(\mathcal{V},\overline{\mathcal{V}})=max\{\underset{p\in \mathcal{V}}{sup}d(p,\overline{\mathcal{V}}),\underset{\overline{p}\in \overline{\mathcal{V}}}{sup}d(\overline{p},\mathcal{V})\}.$$

Proposition 2.

Let $\mathcal{V}$ and $\overline{\mathcal{V}}$ be two algebraic surfaces having the same asymptotic behavior.

Then, the Hausdorff distance between them is finite.

Proof. 

The proof follows reasoning similarly as in Proposition 5.4 in [5].    □

The following algorithm allows us to compare the asymptotic behavior of two surfaces $\mathcal{V}$ and $\overline{\mathcal{V}}$.

We assume that we have prepared $\mathcal{V}$ and $\overline{\mathcal{V}}$ such that by means of a suitable linear change of coordinates (the same change applied to both surfaces), $x=0$ is not a curve of infinity of ${\mathcal{V}}^{*}$ and ${\overline{\mathcal{V}}}^{*}$.

In Example 4, we illustrate the performance of Algorithm 1.

Algorithm 1 Asymptotic Behavior.

Given two implicit algebraic surfaces $\mathcal{V}$ and $\overline{\mathcal{V}}$, the algorithm decides whether $\mathcal{V}$ and $\overline{\mathcal{V}}$ have the same asymptotic behavior. 1. Compute the infinity curves of $\mathcal{V}$ and $\overline{\mathcal{V}}$. If they are not the same, Return the surfaces do not have the same asymptotic behavior (see Remark 6). Otherwise, let $P_1,\dots ,P_n$ be the infinity points corresponding to these infinity curves. 2. For each $P_k:=(1:m_{1k}:m_{2k}:0)$, $k=1,\dots ,n$ do: 2.1. Compute the infinity branches of $\mathcal{V}$ associated to $P_k$. Let $B_1,\dots ,B_{n_k}$ be these branches. For each $i=1,\dots ,n_k$, let $L_i=\{(t_1,r_{1i}(t_1,t_2),r_{2i}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M_i\}$ be any leaf of $B_i$. 2.2. Compute the infinity branches of $\overline{\mathcal{V}}$ associated with $P_k$. Let ${\overline{B}}_1,\dots ,{\overline{B}}_{l_k}$ be these branches. For each $j=1,\dots ,l_k$, let ${\overline{L}}_j=\{(t_1,r_{1j}(t_1,t_2),r_{2j}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M_j\}$ be any leaf of ${\overline{B}}_j$. 2.3. For each $B_i\subset \mathcal{V}$, find ${\overline{B}}_j\subset \overline{\mathcal{V}}$ such that the terms with a non-negative exponent in the variable $t_1$ in $r_{\ell i}$ and ${\overline{r}}_{\ell j}$ (for $\ell =1,2$) are the same up to conjugation. If there is not such a branch, Return the surfaces do not have the same asymptotic behavior (see Lemma 2). 2.4. For each ${\overline{B}}_j\subset \overline{\mathcal{V}}$, find $B_i\subset \mathcal{V}$ such that the terms with non-negative exponents in the variable $t_1$ in $r_{\ell i}$ and ${\overline{r}}_{\ell j}$ are the same up to conjugation. If there is not such a branch, Return the surfaces do not have the same asymptotic behavior (see Lemma 2). 3. Returnthe surfaces $\mathcal{V}$ and $\overline{\mathcal{V}}$ have the same asymptotic behavior.

Example 4.

Let $\mathcal{V}$ and $\overline{\mathcal{V}}$ be two surfaces implicitly defined by the polynomials

$$f(x,y,z)=xy-xz-y^4+y^{3}z+y{z}^2-z^3+1,and$$

$$\overline{f}(x,y,z)=xy-xz+y{z}^2-z^3-y^4+y^{3}z+5+2x-3y-x^2+2y^2,$$

respectively (see Figure 4).

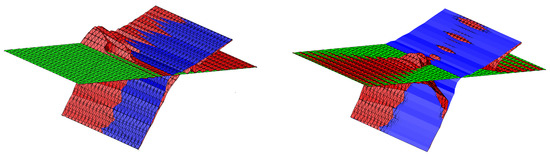
Figure 4. $\mathcal{V}$ (left) and $\overline{\mathcal{V}}$ (right).

We apply Algorithm 1 to decide whether $\mathcal{V}$ and $\overline{\mathcal{V}}$ have the same asymptotic behavior:

• Step 1: Compute the infinity points of $\mathcal{V}$ and $\overline{\mathcal{V}}$. We obtain that $\mathcal{V}$ and $\overline{\mathcal{V}}$ have the same infinity points that correspond to the curves defined implicitly by $y=0$ and $y-z=0$.
  We start by analyzing the infinity branches associated with $y=z$:
• Step 2.1: We reason similarly as in Example 1, and we get that the only infinity branch associated with $y=z$ in $\mathcal{V}$ is given by

  $$B_1=L_1=\{(t_1,r_{11}(t_1,t_2),r_{12}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

  $$r_{11}(t_1,t_2)=t_1{t}_2,r_{12}(t_1,t_2)=t_1{t}_2-t_1^{-3}{t}_2^{-3}-t_1^{-4}{t}_2^{-4}+\cdots .$$
• Step 2.2: We also have that there exists only one infinity branch associated with these curves of infinity in $\overline{\mathcal{V}}$. It is given by

  $${\overline{B}}_1={\overline{L}}_1=\{(t_1,{\overline{r}}_{11}(t_1,t_2),{\overline{r}}_{12}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

  $${\overline{r}}_{11}(t_1,t_2)=t_1{t}_2,$$

  $${\overline{r}}_{12}(t_1,t_2)=t_1{t}_2+t_1^{-1}{t}_2^{-3}-2t_1^{-1}{t}_2^{-1}+t_1^{-1}{t}_2^{-4}+t_1^{-2}{t}_2^{-2}-2t_1^{-2}{t}_2^{-3}+\cdots .$$
• Step 2.3 and Step 2.4: $r_{1i}(t_1,t_2)$ and ${\overline{r}}_{1i}(t_1,t_2),i=1,2,$ have the same terms with a non-negative exponent with respect to $t_1$. Thus, $B_1$ and ${\overline{B}}_1$ converge.
  In Figure 5, we plot the surfaces ${\mathcal{V}}_1$ constructed from the infinity branch $B_1$ that approach the input surface $\mathcal{V}$ (left), we plot the surfaces ${\overline{\mathcal{V}}}_1$ constructed from the infinity branch ${\overline{B}}_1$ that approach the input surface $\overline{\mathcal{V}}$ (right).
  

  Figure 5. Surface ${\mathcal{V}}_1$ (left), and surface ${\overline{\mathcal{V}}}_1$ (right).
  Now we analyze the infinity branches associated with $y=0$:
• Step 2.1: Reasoning as in Example 1, we get that the only infinity branch associated with $y=0$ in $\mathcal{V}$ is given by

  $$B_2=L_2=\{(t_1,r_{21}(t_1,t_2),r_{22}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

  $$r_{21}(t_1,t_2)=t_1{t}_2,$$

  $$r_{22}(t_1,t_2)=t_2^{3/2}{t}_1^{3/2}-1/2t_2^{-3/2}{t}_1^{-1/2}-1/8t_1^{-5/2}{t}_2^{-9/5}+1/2t_1^{-3}{t}_2^{-3}+\cdots .$$
• Step 2.2: The only infinity branch associated with $y=0$ in $\overline{\mathcal{V}}$ is given by

  $${\overline{B}}_2={\overline{L}}_2=\{(t_1,{\overline{r}}_{21}(t_1,t_2),{\overline{r}}_{22}(t_1,t_2))\in {\mathbb{C}}^3:(t_1,t_2)\in {\mathbb{C}}^2,|t_1|>M\},where$$

  $${\overline{r}}_{21}(t_1,t_2)=t_1{t}_2,$$
  ${\overline{r}}_{22}(t_1,t_2)=t_2^{3/2}{t}_1^{3/2}-1/2t_2^{-3/2}{t}_1^{-1/2}-1/2t_1^{-1}{t}_2^{-3}-t_1^{-1}{t}_2^{-1}-1/2t_1^{-3/2}{t}_2^{-7/2}+t_1^{-3/2}$$t_2^{-3/2}-1/2t_1^{-2}{t}_2^{-4}+\cdots .$

In Figure 6, we plot the surfaces ${\mathcal{V}}_2$ constructed from the infinity branch $B_2$ that approach the input surface $\mathcal{V}$ (left), and we plot the surfaces ${\overline{\mathcal{V}}}_2$ constructed from the infinity branch ${\overline{B}}_2$ that approach the input surface $\overline{\mathcal{V}}$ (right).

Figure 6. Surface ${\mathcal{V}}_2$ (left), and surface ${\overline{\mathcal{V}}}_2$ (right).

• Step 2.3 and Step 2.4: $r_{2i}(t_1,t_2)$ and ${\overline{r}}_{2i}(t_1,t_2),i=1,2,$ have the same terms with non-negative exponent s with regard to $t_1$. Thus, $B_2$ and ${\overline{B}}_2$ converge.

Since every infinity branch of $\mathcal{V}$ converges to another branch of $\overline{\mathcal{V}}$, and reciprocally, the algorithm returns that $\mathcal{V}$ and $\overline{\mathcal{V}}$ have the same asymptotic behavior.

In Figure 7, we plot the surfaces $\mathcal{V}$ and ${\mathcal{V}}_i,i=1,2$ together (left), and the surfaces $\overline{\mathcal{V}}$ and ${\overline{\mathcal{V}}}_i,i=1,2$ together (right).

Figure 7. Surfaces $\mathcal{V}$ and ${\mathcal{V}}_i,i=1,2$ (left), and surfaces $\overline{\mathcal{V}}$ and ${\overline{\mathcal{V}}}_i,i=1,2$ (right).

Remark 12.

• Once we have the infinity branches, we can compute surfaces having the same asymptotic behavior as the given surface at each of the infinity points. For this purpose, one simply has to remove the terms with negative exponents in the variable $t_1$ from $r_1$ and $r_2$. However, this problem, which will be dealt with in a future work, has to be carefully analyzed. Note that if we remove terms with negative exponents in the variable $t_1$, we could be removing necessary terms in the variable $t_2$;
• If we remove the terms with negative exponents in the variable $t_1$ from the series $r_1$ and $r_2$ defining the branch B, we obtain ${\tilde{r}}_1,{\tilde{r}}_2\in (\mathbb{C}\ll t_2\gg )\left[t_1\right]$. In a future work, we will analyze whether one may compute the surface ${\tilde{\mathcal{V}}}_i$ defined by the local parametrization

  $$(t_1^{N_1},{\tilde{r}}_1(t_1^{N_1},t_2),{\tilde{r}}_2(t_1^{N_1},t_2))\in (\mathbb{C}\ll t_2\gg )\left[t_1\right].$$
  In this case, $\tilde{\mathcal{V}}$ and $\mathcal{V}$ would have the same asymptotic behavior at B;
• For the computation of the series ${\phi }_i,i=1,2,$ we are considering $y=t_2$ and solving z by using Puiseux series (see Examples 1 and 2). This is not the best solution for some surfaces, and thus, this question should be deeply analyzed in a future work (see Remark 3).

6. Conclusions

In this paper, we introduce the notion of infinity branches and approaching surfaces for the case of a given algebraic surface implicitly defined. From these notions and the obtained properties, we present an algorithm that compares the behavior at the infinity of two algebraic surfaces defined implicitly. As a consequence and taking into account the case of curves (see [5]), we prove that if two algebraic surfaces have the same asymptotic behavior, the Hausdorff distance between them is finite.

As in the case of curves, this first paper opens some important questions that should be answered. In particular, the computation of surfaces having the same asymptotic behavior as the given surface at each of the infinity branches, the definition of a perfect surface, and the properties as well as the computation of the generalized asymptotes for implicitly and parametrically defined surfaces are important points that should be analyzed in a future work (see [10]).

Finally, we should remind the reader that, as we state in Remark 12, for the computation of the series ${\phi }_i,i=1,2,$ we are considering $y=t_2$ and solving z by using Puiseux series (see Examples 1 and 2). This is not the best solution for some surfaces, and thus, this question for the general case (and also for the case of surfaces defined by a rational parametrization) should be deeply analyzed in a future work (see Remark 3).