Minimum Zagreb Eccentricity Indices of Two-Mode Network with Applications in Boiling Point and Benzenoid Hydrocarbons

Abstract

A two-mode network is a type of network in which nodes can be divided into two sets in such a way that links can be established between different types of nodes. The relationship between two separate sets of entities can be modeled as a bipartite network. In computer networks data is transmitted in form of packets between source to destination. Such packet-switched networks rely on routing protocols to select the best path. Configurations of these protocols depends on the network acquirements; that is why one routing protocol might be efficient for one network and may be inefficient for a other. Because some protocols deal with hop-count (number of nodes in the path) while others deal with distance vector. This paper investigates the minimum transmission in two-mode networks. Based on some parameters, we obtained the minimum transmission between the class of all connected n-nodes in bipartite networks. These parameters are helpful to modify or change the path of a given network. Furthermore, by using least squares fit, we discussed some numerical results of the regression model of the boiling point in benzenoid hydrocarbons. The results show that the correlation of the boiling point in benzenoid hydrocarbons of the first Zagreb eccentricity index gives better result as compare to the correlation of second Zagreb eccentricity index. In case of a connected network, the first Zagreb eccentricity index ${\xi }_1(\aleph )$ is defined as the sum of the square of eccentricities of the nodes, and the second Zagreb eccentricity index ${\xi }_2(\aleph )$ is defined as the sum of the product of eccentricities of the adjacent nodes. This article deals with the minimum transmission with respect to ${\xi }_i(\aleph )$, for $i=1,2$ among all n-node extremal bipartite networks with given matching number, diameter, node connectivity and link connectivity.

1. Bipartite Network

In bipartite networks, nodes are divided into two disjoint sets where each link connects a node from one partition with a node from second partition.

Bipartite networks do not contain any odd cycle, (i.e., cycles that consist of an odd number of links). Hence, the bipartite networks do not contain triangular shapes because triangles have an odd number of links.

2. Preliminaries

In this article, connected, simple and undirected networks are considered. We denote $P_n$ for the path network, $K_n$ for the complete network and $K_{p,n-p}$ for the complete bipartite network with n nodes. We follow [1,2,3,4], for the notation and terminology which are not defined in this article.

Assume that $\aleph =(V_{\aleph },E_{\aleph })$ is a network having node set $V_{\aleph }$ which are connected by the link is denoted by $E_{\aleph }$. The cardinality of network W is denoted as $\left|W\right|$. Let $y\in V_{\aleph }$, then denote $N_{\aleph }\left(y\right)$ be the set of entire adjacent nodes with y in ℵ. We denote the degree of $y\in \aleph$ by $d_{\aleph }\left(y\right)=\left|N_{\aleph }\left(y\right)\right|$. The minimum degree of ℵ is denoted by $\delta (\aleph )$, and defined as $\delta (\aleph )=min\left\{d_{\aleph }\left(y\right)\right|y\in V_{\aleph }\}$. Let $\aleph \left[A\right]$ is a subset of $V_{\aleph }$ which is induced by A. The networks $\aleph -v$ and $\aleph -uv$ denote as any network construct from ℵ by removing the node $v\in V_{\aleph }$ and by removing the link $uv\in E_{\aleph }$, respectively. In the same way, $\aleph +uv$ can be determined from ℵ by adding a link $uv\notin E_{\aleph }$.

The quantity ${\aleph }_1\cup {\aleph }_2$ denotes the union of two networks ${\aleph }_1$ and ${\aleph }_2$ with $V_{{\aleph }_1\cup {\aleph }_2}=V_{{\aleph }_1}\cup V_{{\aleph }_2}$ and $E_{{\aleph }_1\cup {\aleph }_2}=E_{{\aleph }_1}\cup E_{{\aleph }_2}$. If ${\aleph }_1$ and ${\aleph }_2$ are disjoint nodes, then we let ${\aleph }_1\uplus {\aleph }_2$ denote the join of ${\aleph }_1$ and ${\aleph }_2$, which is the network obtained from ${\aleph }_1\cup {\aleph }_2$ by adding all the links between the nodes $x\in V_{{\aleph }_1}$ and $y\in V_{{\aleph }_2}$. For disjoint networks ${\aleph }_1,{\aleph }_2,\dots ,{\aleph }_k$ having $k\ge 3$, then the joining ${\aleph }_1\uplus {\aleph }_2\uplus \cdots \uplus {\aleph }_k$ is the network $({\aleph }_1\uplus {\aleph }_2)\cup ({\aleph }_2\uplus {\aleph }_3)\cup \cdots \cup ({\aleph }_{k-1}\uplus {\aleph }_k)$. In short, we indicate $k\aleph$ and $\left[k\right]\aleph$ for the union and for the joining of k time disjoint copies of ℵ, simultaneously. For instance, $k{K}_1\cong {\overline{K}}_k$ is exactly the k isolated nodes, whereas $\left[p\right]{\aleph }_1\uplus {\aleph }_2\uplus \left[q\right]{\aleph }_3$ is indicating the joining ${{\displaystyle \underbrace{{\aleph }_1\uplus {\aleph }_1\uplus \dots \uplus {\aleph }_1}}}_p\uplus {\aleph }_2\uplus {{\displaystyle \underbrace{{\aleph }_3\vee {\aleph }_3\uplus \dots \uplus {\aleph }_3}}}_q.$

For a network, the distance among x and y is denoted by $d_{\aleph }(x,y)$ and defined by the length of a shortest x-y path. Assume that $\epsilon$ denotes the eccentricity of a node, then it can be defined as ${\epsilon }_{\aleph }\left(x\right):={max}_{y\in V_{\aleph }}{d}_{\aleph }(x,y)$ be the eccentricity of x. Next, is the diameter of a network ℵ which is defined as diam$(\aleph )={max}_{x\in V_{\aleph }}{\epsilon }_{\aleph }\left(x\right).$ The path P is called a diametrical path of a network ℵ if it satisfies $|E_p|=\mathrm{diam}(\aleph )$.

Let ℵ be a simple network and $U_{\aleph }$ is the node set of ℵ. Then, $U_{\aleph }$ can be divided into two disjoint subsets $U_1$ and $U_2$ in such a way that there is at least one link between these two disjoint subsets, then ℵ is called a bipartite network. On the other hand if every node of $U_1$ is adjacent to every node of $U_2$ such network is called a complete bipartite network. Generally, it is denoted by $K_{n_1,n_2}$, where $n_1=\left|U_1\right|$, $n_2=\left|U_2\right|$. A node independent set of any network ℵ is the node subset in $V_{\aleph }$ which satisfies that any of the two distinct nodes in the set are not adjacent. The independence number is defined as the maximum cardinality in all of the independent sets of ℵ and it is denoted by $\alpha (\aleph )$.

Any two distinctive links of the set that are not incident with a common node is called a link independent set of any network ℵ. Similarly, a link independence number of any network ℵ is the maximum cardinalities among entire link independent sets. It is indicated as ${\alpha }^{\prime }(\aleph )$. The set of nodes (links) in which every link (node) of ℵ is incident with at least one node (link) of the set is called a node (link) cover of a network ℵ. The minimum of the cardinalities among entire node (link) covers is said to be the node (link) cover number of a given network ℵ and is indicated as $\beta (\aleph )\left({\beta }^{\prime }(\aleph )\right)$. In any connected network ℵ with order n, has a matching number ${\alpha }^{\prime }(\aleph )$ must fulfill $1\le {\alpha }^{\prime }(\aleph )\le \lfloor \frac{n}{2}\rfloor$. Meanwhile, in the case of a link cover of any network, one can constantly suppose that the network should consists no isolated node. It can easily be observed that for a network ℵ of order n, $\alpha (\aleph )+\beta (\aleph )=n$. Additionally, if ℵ has no isolated node, then one has ${\alpha }^{\prime }(\aleph )+{\beta }^{\prime }(\aleph )=n$. For a bipartite network ℵ, one has ${\alpha }^{\prime }(\aleph )=\beta (\aleph )$, and $\alpha (\aleph )={\beta }^{\prime }(\aleph )$.

For the sake of simplicity, we assume that ${\mathcal{A}}_n^q$ is the class of all bipartite networks with order n having matching number q. Whereas, ${\mathcal{B}}_n^d$ indicate the class of all bipartite networks with order n having diameter d. Similarly, ${\mathcal{C}}_n^s$ (resp. ${\mathcal{D}}_n^t$) be the class of all n-node bipartite networks with connectivity s (resp. link connectivity t).

We define $M_1(\aleph )={\displaystyle \sum _{u\in V(\aleph )}}{d}_{\aleph }^2\left(u\right)$ as the first Zagreb index of a network ℵ. Similarly, $M_2(\aleph )={\displaystyle \sum _{uv\in E(\aleph )}}{d}_{\aleph }\left(u\right)d_{\aleph }\left(v\right)$ is the second Zagreb index of a network ℵ, for further detail one can see [5].

Inspired from the above definitions Vukičević and Graovac [6], Ghorbani and Hosseinzadeh [7] invented another similar kinds of network invariant called the first (resp. second) Zagreb eccentricity index.

The first (resp. second) Zagreb eccentricity index of ℵ is denoted by ${\xi }_1(\aleph )$ (resp. ${\xi }_2(\aleph ))$ and defined as

$${\xi }_1(\aleph )=\sum _{x_1\in V(\aleph )}{\epsilon }^2\left(x_1\right),{\xi }_2(\aleph )=\sum _{x_1{x}_2\in E(\aleph )}\epsilon \left(x_1\right)\epsilon \left(x_2\right).$$

Some extremal problems related to first and second Zagreb eccentricity indices are presented by Das and Lee in [8]. In [9] the authors obtained trees having sharp lower bound of Zagreb eccentricity indices with given domination number, maximum degree, and bipartition size. Some extremal problems of unicyclic networks which minimize and maximize the first and second Zagreb eccentricity indices are considered by Qi and Zhou in [10]. The networks having maximum also second maximum with respect to the second Zagreb eccentricity index among entire n-node bicyclic networks figured out by Li and Zhang in [11]. The Zagreb eccentricity indices of generalized hierarchical product is computed by Luo and Wu in [12].

Studies given under [13,14,15,16,17] led us to consider the extremal problem on n-node bipartite networks with given matching number and diameter among ${\mathcal{A}}_n^q$ and ${\mathcal{B}}_n^d$. In order to formulate our main results, the following Lemma is helpful.

Lemma 1

([8], P:121). Let ℵ be any connected bipartite network with order n having bipartition $V(\aleph )=X_1\cup X_2$, $X_1\cap X_2=\varnothing$, $|X_1|=p$ and $|X_2|=q$. Then ${\xi }_i(\aleph )⩾{\xi }_i(K_{p,q}\backslash e)>{\xi }_i\left(K_{p,q}\right),$ where $i=1,2$ and $e\in K_{p,q}.$

3. Network Contain Minimum Zagreb Eccentricity Indices among All n-Node Bipartite Networks with Given Matching Number q

In this section, we characterize the networks among ${\mathcal{A}}_n^q$ having minimum Zagreb eccentricity indices.

Lemma 2.

Assume that ℵ be any connected bipartite network having $V_{\aleph }=(X,Y)$ with $\left|X\right|=n_1,\left|Y\right|=n_2$ and $n_1⩾n_2$.

(i)

If $n_1=1$, then ${\xi }_1(\aleph )=2$ and ${\xi }_2(\aleph )=1$, in this case $\aleph =K_2$.

(ii)

If $n_1>1$, and $n_2=1$ then ${\xi }_1(\aleph )=4n_1+1$ and ${\xi }_2(\aleph )=2n_1$, in this case $\aleph =K_{1,n_1}$.

(iii)

If $n_2>1$, then ${\xi }_1(\aleph )⩾4(n_1+n_2)$ and ${\xi }_2(\aleph )⩾4n_1{n}_2$, with equality if and only if $\aleph \cong K_{n_1,n_2}$.

Due to Lemma 2 we characterize all the bipartite networks which are connected and having order $n>2$.

Theorem 1.

Assume that ${\mathcal{A}}_n^q$ is an n-node bipartite network with matching number q, and $\aleph \in {\mathcal{A}}_n^q$.

(i)

If $q=1$, then ${\xi }_1(\aleph )=4n-3$ and ${\xi }_2(\aleph )=2n-2$, where $\aleph \cong K_{1,n-1}$.

(ii)

If $q>1$, then ${\xi }_1(\aleph )⩾4n$ and ${\xi }_2(\aleph )⩾4q(n-q)$. The equality holds if and only if $\aleph \cong K_{q,n-q}$.

Proof. 

By a direct calculation, one has

$${\xi }_1\left(K_{q,n-q}\right)=4n,{\xi }_2\left(K_{q,n-q}\right)=4q(n-q).$$

Hence, we only need to show that among ${\mathcal{A}}_n^q$ with minimum Zagreb eccentricity indices is a unique network $K_{q,n-q}$.

Choose ℵ, in ${\mathcal{A}}_n^q$ such that its first Zagreb eccentricity index and the second Zagreb eccentricity index are minimum. For $q=\lfloor \frac{n}{2}\rfloor$, due to Lemma 1 an extremal network is exactly $K_{\lfloor \frac{n}{2}\rfloor ,\lceil \frac{n}{2}\rceil }$ as desired. Therefore, we only consider the case $q<\lfloor \frac{n}{2}\rfloor$.

Let the bipartition node set in ℵ is denoted by $(X,Y)$, such that $\left|Y\right|⩾\left|X\right|⩾q$. Assume that M is a maximal matching in ℵ, then due to Lemma 1, the addition of new link(s) decreases the first Zagreb eccentricity index as well as the second Zagreb eccentricity index of a network. In what follows, if $\left|X\right|=q$, then the extremal network is $\aleph =K_{q,n-q}$. Hence, we consider the case $\left|X\right|>q$.

Assume that M is a matching set and $X_M$ (resp. $Y_M$) be the set of nodes of X (resp. Y) which are incident to the links of M. Therefore, $|X_M|=|Y_M|=q$. Keeping in mind that ℵ does not contain links between the nodes of $X\backslash X_M$ and the nodes of $Y\backslash Y_M$. Otherwise, any such link together with M producing the matching of cardinality more than as that in M, which contradicts the maximality in M.

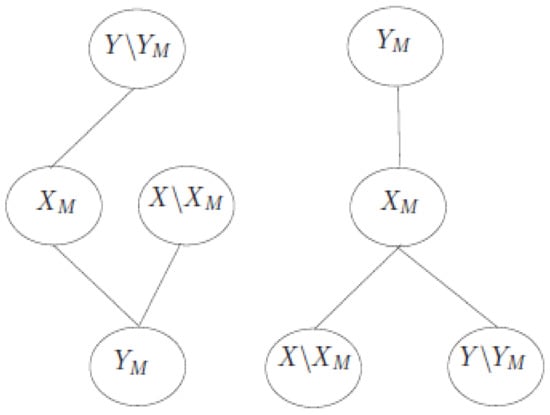
By adding entire potential links between the nodes of $X_M$ and $Y_M$, $X_M$ and $Y\backslash Y_M$, $X\backslash X_M$ and $Y_M$ we get a network ${\aleph }^{\prime }$ as depicted in Figure 1, with ${\xi }_1\left({\aleph }^{\prime }\right)<{\xi }_1(\aleph )$ and ${\xi }_2\left({\aleph }^{\prime }\right)<{\xi }_2(\aleph )$. It can be noticed that a matching number in ${\aleph }^{\prime }$ is at least $q+1$. Thus, ${\aleph }^{\prime }\notin {\mathcal{A}}_n^q$ and $\aleph \ncong {\aleph }^{\prime }$. Due to ${\aleph }^{\prime }$, one can build a new network, say ${\aleph }^{″}$, which is determine by keeping ${\aleph }^{\prime }$ in such a way that first delete entire links among $X\backslash X_M$ and $Y_M$, and then add entire links among $X\backslash X_M$ as well $X_M$, see Figure 1. Thereby, it is easy to see that ${\aleph }^{″}\cong K_{q,n-q}$.

Figure 1. Networks ${\aleph }^{\prime }$ and ${\aleph }^{″}$.

Assume that $|X\backslash X_M|=n_1$, $|Y\backslash Y_M|=n_2$ let $n_2⩾n_1$. We partition $V_{{\aleph }^{\prime }}=V_{{\aleph }^{\prime \prime }}$ into $X_M\cup Y_M\cup (X\backslash X_M)\cup (Y\backslash Y_M)$ as depicted in Figure 1. Through the direct calculation, for every $a\in Y\backslash Y_M,b\in X_M,c\in Y_M,d\in X\backslash X_M,$ one can see easily as

$${{\epsilon }^{\prime }}^2\left(a\right)=9,{{\epsilon }^{\prime }}^2\left(b\right)=4,{{\epsilon }^{\prime }}^2\left(c\right)=4,{{\epsilon }^{\prime }}^2\left(d\right)=9,{{\epsilon }^{″}}^2\left(a\right)=4,{{\epsilon }^{″}}^2\left(b\right)=4{{\epsilon }^{″}}^2\left(c\right)=4,{{\epsilon }^{″}}^2\left(d\right)=4$$

$$\begin{array}{cc}\hfill {\xi }_1\left({\aleph }^{\prime }\right)-{\xi }_1\left({\aleph }^{″}\right)& =\sum _{v_i\in V\left({\aleph }^{\prime }\right)}{{\epsilon }^{\prime }}^2\left(v_i\right)-\sum _{u_i\in V\left({\aleph }^{″}\right)}{{\epsilon }^{″}}^2\left(u_i\right)\hfill \\ \hfill & =9n_2+4q+4q+9n_1-4n_2-4q-4q-4n_1\hfill \\ \hfill & =5n_2+5n_1\hfill \\ \hfill & >0.\hfill \end{array}$$

(1)

By a similar argument as above, and by comparing the structure of networks ${\aleph }^{\prime }$ and ${\aleph }^{″}$, one has

$${\epsilon }^{\prime }\left(a\right){\epsilon }^{\prime }\left(b\right)=6,{\epsilon }^{\prime }\left(b\right){\epsilon }^{\prime }\left(c\right)=4,{\epsilon }^{\prime }\left(d\right){\epsilon }^{\prime }\left(c\right)=6,{\epsilon }^{″}\left(a\right){\epsilon }^{″}\left(b\right)=4,{\epsilon }^{″}\left(b\right){\epsilon }^{″}\left(c\right)=4,{\epsilon }^{″}\left(d\right){\epsilon }^{″}\left(b\right)=4.$$

This gives

$$\begin{array}{cc}\hfill {\xi }_2\left({\aleph }^{\prime }\right)-{\xi }_2\left({\aleph }^{″}\right)& =\sum _{uv\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(u\right){\epsilon }^{\prime }\left(v\right)-\sum _{uv\in V\left({\aleph }^{″}\right)}{\epsilon }^{″}\left(u\right){\epsilon }^{″}\left(v\right)\hfill \\ \hfill & =6n_{2}q+4q^2+6n_{1}q-4n_{2}q-4q^2-4n_{1}q\hfill \\ \hfill & =2n_{2}q+2n_{1}q\hfill \\ \hfill & >0,\hfill \end{array}$$

(2)

where the inequalities (1) and (2) follows from the fact that $n_1,n_2⩾1$, $q⩾1$. Hence we obtain that ${\xi }_i(\aleph )>{\xi }_i\left({\aleph }^{\prime }\right)>{\xi }_i\left({\aleph }^{\prime \prime }\right)$ for $i=1,2$, give contradiction. This completes our desired result. □

Keeping in mind the connections between the parameters such as $\alpha (\aleph ),{\alpha }^{\prime }(\aleph ),\beta (\aleph ),{\beta }^{\prime }(\aleph )$ of a bipartite network ℵ which is in fact a connected then, the following result is a straight analogous of Theorem 1.

Corollary 1.

A network $K_{\sigma ,n-\sigma }$ is the only network having minimum ${\xi }_i(\aleph )$, $i=1,2$, among all of the bipartite networks with order n having node cover number or node independence number or link cover number σ.

4. Network Having Minimum ${\mathbf{\xi }}_{\mathbf{i}}$-Value, $\mathbf{i}=\mathbf{1},\mathbf{2}$ w.r.t ${\mathcal{B}}_{\mathbf{n}}^{\mathbf{d}}$

In the current section, networks in ${\mathcal{B}}_n^d$ having minimum ${\xi }_i$-value is considered. Assume that every member in ${\mathcal{B}}_n^d$, has a diametrical path that is to say $P=v_0{v}_1\dots v_d$. Then for any $\aleph =(V_{\aleph },E_{\aleph })$ in ${\mathcal{B}}_n^d$, there is a partition $V_0,V_1,\dots V_d$ of $V_{\aleph }$ with $d(v_0,v)=i$ in every node $v\in V_i(i=0,1,2,\dots ,d)$. Named $V_i$ to distance layer in $V_{\aleph }$. If $|i-j|=1$ then the two distance layers $V_i$, $V_j$ in $V_{\aleph }$ are adjacent. Assume that $|V_i|=l_i$ throughout this section. Clearly, $l_0=\left|V_0\right|=1$.

If $3\le d\le n-1$, where d is odd, then suppose $\aleph (n,d):=\left[\frac{d-1}{2}\right]K_1+\lfloor \frac{n-d-1}{2}\rfloor K_1+\lceil \frac{n-d+1}{2}\rceil K_1+\left[\frac{d-1}{2}\right]K_1$. Whereas, if $4\le d\le n-1$, and d is even then, assume $\mathcal{H}(n,d)=\{H(n,d)=[\frac{d}{2}-1]K_1+a_1{K}_1+\lfloor \frac{n-d+2}{2}\rfloor K_1+a_2{K}_1+[\frac{d}{2}-1]K_1:a_1+a_2=\lceil \frac{n-d+2}{2}\rceil \}$.

Lemma 3.

For any network $\aleph \in {\mathcal{B}}_n^d$ with the above partition of $V_{\aleph }$, $\aleph \left[V_i\right]$ induces an empty network (i.e., containing no link) for each $i\in \{0,1,\dots ,d\}$.

Proof. 

It can be seen that $L_0=\left\{x_0\right\}$. There must be two paths P and Q such that $P=x_0\dots u$ and $Q=x_0\dots v$, once there exists a link $uv$ in $\aleph \left[L_i\right]$ for some $i\in \{0,1,\dots ,d\}$. Meanwhile, $P\cup Q+uv$ is an odd cycle in a network ℵ, if P and Q have no internal node in common, this gives a contradiction. Else, assume that $u_0$ is the last common internal node in P as well as Q. Thereby, $P(u_0,u)\cup Q(u_0,v)+uv$ again an odd cycle. This contradicts the statement that ℵ is a bipartite. □

Lemma 4.

A bipartite network $\aleph [L_{j-1}\cup L_j]$ is complete in which $j=1,2,\dots ,d$.

Proof. 

By Lemma 3, $\aleph \left[L_i\right]$ is an empty network for each $i\in \{1,2,\dots ,d\}$. In contrary, suppose that $\aleph [L_{j-1}\cup L_j]$ is not a complete bipartite network, then one can construct another network ${\aleph }^{\prime }$ with adding entire potential links among $L_{j-1}$ as well as $L_j$. Due to Lemma 1, one has ${\xi }_i\left({\aleph }^{\prime }\right)<{\xi }_i(\aleph )$, for $i=1,2$ a contradiction. Hence, $\aleph [L_{j-1}\cup L_j]$ is a complete bipartite network. Thus, we get our desired result. □

Theorem 2.

Assume that ℵ be any network in ${\mathcal{B}}_n^d$.

(i)

If $d=2$, then ${\xi }_1(\aleph )⩾4n$. The equality holds if and only if $\aleph \cong K_{n-t,t}$, and $\aleph \ncong S_n$.

(ii)

If $d=2$, then ${\xi }_2(\aleph )⩾4t(n-t)$. The equality holds if and only if $\aleph \cong K_{n-t,t}$, and $\aleph \ncong S_n$.

Proof. 

(i) Due to Lemma 1 we have $\aleph \cong K_{n-t,t}$, as $t,n-t⩾2$. Assume that $|Z_1|=n-t$, $|Z_2|=t$. Thereby, it is straightforward to see that for every x(resp. y) in $Z_1$(resp. $Z_2$), we have ${\epsilon }^2\left(x\right)={\epsilon }^2\left(y\right)=4$. This gives

$$\begin{array}{cc}\hfill {\xi }_1\left(K_{n-t,t}\right)=& \sum _{x\in V(\aleph )}{\epsilon }^2\left(x\right)+\sum _{y\in V(\aleph )}{\epsilon }^2\left(y\right)\hfill \\ \hfill =& 4t+4(n-t)\hfill \\ \hfill =& 4n.\hfill \end{array}$$

(3)

(ii) Similarly, if $d=2$, then due to Lemma 1 one has $\aleph \cong K_{n-t,t}$, as $t,n-t⩾2$. Assume that $|Z_1|=n-t,|Z_2|=t$. Thereby, one can check it easily that for every x (resp. y) in $Z_1$ (resp. $Z_2$), we have $\epsilon \left(x\right)=\epsilon \left(y\right)=2$. This gives

$$\begin{array}{cc}\hfill {\xi }_2\left(K_{n-t,t}\right)=& \sum _{xy\in E(\aleph )}\epsilon \left(x\right)\epsilon \left(y\right)\hfill \\ \hfill =& 4t(n-t).\hfill \end{array}$$

(4)

Note that, by the addition of any link(s) between any two nodes, does not increases the node eccentricity. Thus we have ${\epsilon }_i(\aleph +e)\le {\epsilon }_i(\aleph )$. Using this fact, one has ${\xi }_1(\aleph )⩾{\xi }_1(K_{n-t,t}\backslash \left\{e\right\})>{\xi }_1\left(K_{n-t,t}\right)=4n$ and ${\xi }_2(\aleph )⩾{\xi }_2(K_{n-t,t}\backslash \left\{e\right\})>{\xi }_2\left(K_{n-t,t}\right)=4t(n-t)$, where e is any link in $K_{n-t,t}$. Thus, we get our desired result. □

Theorem 3.

Assume that ℵ belongs to ${\mathcal{B}}_n^d$ with the minimum ${\xi }_1$-value. If $d⩾3$, then $\aleph \cong \aleph (n,d)$ for odd d, where $\aleph (n,d)$ is already defined.

Proof. 

We opt $\aleph \in {\mathcal{B}}_n^d$ such that its ${\xi }_1$-value is as small as possible. Let $v_0{v}_1\dots v_d$ is the diametrical path. Thereby, we partition $V_{\aleph }$ as $V_0\cup V_1\cup \cdots \cup V_d$. To complete the proof, we need the following claim. □

Claim 1. 

For odd d, one has

$$\begin{array}{c}\hfill |V_0|=|V_1|=\cdots =|V_{\frac{d-1}{2}-1}|=|V_{\frac{d+1}{2}+1}|=\cdots =|V_{d-1}|=|V_d|=1,||V_{\frac{d-1}{2}}|-|V_{\frac{d+1}{2}}\left|\right|\le 1.\end{array}$$

(5)

Proof of Claim 1. 

Note that $|V_0|=\left\{v_0\right\}$ and $|V_d|=\left\{v_d\right\}$. Here, we only need to prove that $|V_1|=1$ holds. In the same way, one can show that $|V_2|=\cdots =|V_{\frac{d-1}{2}-1}|=|V_{\frac{d+1}{2}+1}|=\cdots =|V_{d-1}|=1$, we omit the procedure here.

Since, for $d=3$, the desired result is trivial. In what follows we choose the case $d⩾5$, for odd d. In the case $|V_1|⩾2$, then we opt any $u\in V_1$ and let ${\aleph }^{\prime }=\aleph -u{v}_0+\{ux:x\in V_4\}$. Here, $\left\{v_0\right\}\cup (V_1\backslash \left\{u\right\})\cup V_2\cup (V_3\cup \left\{u\right\})\cup V_4\cup \dots \cup \left\{v_d\right\}$ is the node partition of ${\aleph }^{\prime }$; the choice of ℵ as well as in view of Lemma 4 i.e., for two of the neighbour blocks in $V_{{\aleph }^{\prime }}$ induces the complete bipartite subnetwork and $|V_d|=1$ for $d⩾5$.

By considering the construction of ℵ and ${\aleph }^{\prime }$, it is easy to verify that $\epsilon \left(u\right)⩾{\epsilon }^{\prime }\left(u\right)+1$, $\epsilon \left(x\right)={\epsilon }^{\prime }\left(x\right)$ for every $x\in V_{\aleph }\backslash \left\{u\right\}$. This gives

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{\prime }\right)& =\sum _{x\in V(\aleph )}{\epsilon }^2\left(x\right)+{\epsilon }^2\left(u\right)-\sum _{x\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(x\right)-{\epsilon }^{\prime 2}\left(u\right)\hfill \\ \hfill & ={\epsilon }^2\left(u\right)-{\epsilon }^{\prime 2}\left(u\right)\hfill \\ \hfill & ⩾{\epsilon }^2\left(u\right)-{(\epsilon \left(u\right)-1)}^2\hfill \\ \hfill & =2\epsilon \left(u\right)-1\hfill \\ \hfill & >0.\hfill \end{array}$$

(6)

The last inequality (6), follows by $d⩾5$ and $\epsilon \left(u\right)⩾4$. $i.e.$${\xi }_1\left({\aleph }^{\prime }\right)<{\xi }_1(\aleph ),$ which contradicts our selection of ℵ. Hence, $|V_1|=1$. In a similar manner one can also prove that $|V_2|=\cdots =|V_{\frac{d-1}{2}-1}|=|V_{\frac{d+1}{2}+1}|=\cdots =|V_{d-1}|=1$.

Next we show that if d is odd, then $\left|\right|V_{\frac{d-1}{2}}|-|V_{\frac{d+1}{2}}\left|\right|\le 1$. Without loss of generality, we assume that $|V_{\frac{d-1}{2}}|⩾|V_{\frac{d+1}{2}}|$. Then it suffices to show that $|V_{\frac{d-1}{2}}|-|V_{\frac{d+1}{2}}|\le 1.$ If this is not true, then $|V_{\frac{d-1}{2}}|-|V_{\frac{d+1}{2}}|⩾2.$ Choose $w\in V_{\frac{d-1}{2}},$ let

${\aleph }^{*}=\aleph -\{wx:x\in V_{\frac{d-3}{2}}\cup V_{\frac{d+1}{2}}\}+\{wy:y\in (V_{\frac{d-1}{2}}\backslash \left\{w\right\})\cup V_{\frac{d+3}{2}}\}.$

Then the node partition of ${\aleph }^{*}$ is $\left\{v_0\right\}\cup V_1\cup V_2\cup \dots \cup V_{\frac{d-3}{2}}\cup (V_{\frac{d-1}{2}}\backslash \left\{w\right\})\cup (V_{\frac{d+1}{2}}\cup \left\{w\right\})\cup V_{\frac{d+3}{2}}\cup \dots \cup \left\{v_d\right\}$ and every two adjacent blocks in $V_{{\aleph }^{*}}$ induce a complete bipartite network. Based on the constructions of ℵ and ${\aleph }^{*}$, it is straightforward to see that ${\epsilon }^2\left(v\right)={{\epsilon }^{*}}^2\left(v\right)$ for every $v\in V_{\aleph }$. Thus

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{*}\right)& =\sum _{v\in V(\aleph )}{\epsilon }^2\left(w\right)-\sum _{v\in V\left({\aleph }^{*}\right)}{{\epsilon }^{*}}^2\left(v\right)\hfill \\ \hfill & =0.\hfill \end{array}$$

This shows a class of networks such that $a+b=n-(d-1)$ where $a=|V_{\frac{d-1}{2}}|,$$b=|V_{\frac{d+1}{2}}|$, which contradicts the option of ℵ. Hence, this completes the proof of Claim 1.

Hence for odd d, by Lemma 4 and Equation (5), we obtain that $\aleph \cong \aleph (n,d)$, as desired. □

Theorem 4.

Let ℵ be in ${\mathcal{B}}_n^d$ with the minimum ${\xi }_1$-value. If $d\ge 4$, then $\aleph \cong \mathcal{H}(n,d)$ for even d, where $\mathcal{H}(n,d)$ is defined as above.

Proof. 

Without loss of generality, choose $\aleph \in {\mathcal{B}}_n^d$ such that its ${\xi }_1$-value is as small as possible. Let $v_0{v}_1\dots v_d$ is the diametrical path. We partition $V_{\aleph }$ as $V_0\cup V_1\cup \dots \cup V_d$. To fulfill all the conditions of the proof, we need to show the following claim.

Claim 2. 

For even d, one has

$$\begin{array}{c}\hfill |V_0|=|V_1|=\cdots =|V_{\frac{d-1}{2}-1}|=|V_{\frac{d+1}{2}+1}|=\cdots =|V_{d-1}|=|V_d|=1,|\left(\right|V_{\frac{d}{2}-1}|+|V_{\frac{d}{2}+1}\left|\right)-|V_{\frac{d}{2}}\left|\right|\le 1.\end{array}$$

(7)

Proof of Claim 2. 

By a similar argument as in Claim 1, it is straightforward to show that $|V_0|=|V_1|=\cdots =|V_{\frac{d-1}{2}-1}|=|V_{\frac{d+1}{2}+1}|=\cdots =|V_{d-1}|=|V_d|=1$. We only need to show that $\left|\right(|V_{\frac{d}{2}-1}|+|V_{\frac{d}{2}+1}\left|\right)-|V_{\frac{d}{2}}\left|\right|\le 1$. Suppose that $|V_{\frac{d}{2}-1}|+|V_{\frac{d}{2}+1}|<|V_{\frac{d}{2}}|$. Then, this is enough to see that $|V_{\frac{d}{2}}|-|V_{\frac{d}{2}-1}|-|V_{\frac{d}{2}+1}|\le 1$. If this is not true, then $|V_{\frac{d}{2}}|-|V_{\frac{d}{2}-1}|-|V_{\frac{d}{2}+1}|⩾2$. It is routine to check that at least one of $V_{\frac{d}{2}-1}$ and $V_{\frac{d}{2}+1}$ contains at least two nodes. Hence, we assume without loss of generality that $|V_{\frac{d}{2}-1}|⩾2$. Choose $w\in V_{\frac{d}{2}-1}$ and let

$${\aleph }^{*}=\aleph -\{wx:x\in V_{\frac{d}{2}-2}\cup V_{\frac{d}{2}}\}+\{wy:y\in V_{\frac{d}{2}-1}\cup V_{\frac{d}{2}+1}\}.$$

Then the node partition of ${\aleph }^{*}$ is $V_0\cup V_1\cup V_2\cup \dots \cup (V_{\frac{d}{2}-1}\backslash \left\{w\right\})\cup (V_{\frac{d}{2}}\cup \left\{w\right\})\cup V_{\frac{d}{2}+1}\cup \dots \cup V_d$ and every two adjacent blocks in $V_{{\aleph }^{*}}$ give a complete bipartite network. By direct calculation, we have ${\epsilon }^2\left(w\right)=\frac{1}{4}{(d+2)}^2,{\epsilon }^{*}{}^2\left(w\right)=\frac{1}{4}{d}^2$ all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{*}\right)& =\sum _{x\in V(\aleph )}{\epsilon }^2\left(x\right)+{\epsilon }^2\left(w\right)-\sum _{x\in V\left({\aleph }^{*}\right)}{\epsilon }^{*}{}^2\left(x\right)-{\epsilon }^{*}{}^2\left(w\right)\hfill \\ \hfill & =\frac{1}{4}{(d+2)}^2-\frac{1}{4}{d}^2\hfill \\ \hfill & =(d+1)\hfill \\ \hfill & >0,\hfill \end{array}$$

gives a contradiction to the choice of ℵ. Hence, we get our desired result.

Hence for even d, by Lemma 4 and Equation (7), we obtain that $\aleph \cong H(n,d)\in \mathcal{H}(n,d)$, as desired. □

In Theorem 3 (resp. Theorem 4), if d is odd (resp. even), the sharp lower bound for the second Zagreb eccentricity is not solved. Hence, we propose the following two research problems.

Problem 1.

Let ℵ be in ${\mathcal{B}}_n^d$. If d is odd, how to determine the sharp lower bound of the second Zagreb eccentricity.

Problem 2. 

Let ℵ be in ${\mathcal{B}}_n^d$. If d is even, how to determine the sharp lower bound of the second Zagreb eccentricity.

5. The Network with Minimum Zagreb Eccentricity Indices w.r.t ${\mathcal{C}}_{\mathbf{n}}^{\mathbf{s}}$(resp. ${\mathcal{D}}_{\mathbf{n}}^{\mathbf{t}}$)

This section deals with the sharp lower bounds on Zagreb eccentricity indices among ${\mathcal{C}}_n^s$ and ${\mathcal{D}}_n^t$, respectively.

In $K_{{\tau }_1,{\tau }_2}$, without loss of generality suppose that ${\tau }_1⩾{\tau }_2$. In case of $K_{{\tau }_1,0}$, ${\tau }_1⩾1,$ we assume that ${\tau }_1{K}_1$. Let us construct the networks ${\Phi }_s{\nabla }_1(K_{n_1,n_2}▵K_{m_1,m_2})$ and ${\Phi }_s{\nabla }_2(K_{n_1,n_2}▵K_{m_1,m_2})$. The notion Δ represents union between networks whereas ${\Phi }_s$ denote an empty network with order s and $s⩾1$. The notion ${\nabla }_1$ is any network operation that links entirely nodes in ${\Phi }_s$ with the nodes which belongs among the partitions of cardinality $n_1$ in $K_{n_1,n_2}$ (resp. $m_1$ in $K_{m_1,m_2}$). Similarly, an operator ${\nabla }_2$ represents a network operation which joins entirely nodes in ${\Phi }_s$ with nodes that belong to $n_2$ in $K_{n_1,n_2}$ (resp. $m_2$ in $K_{m_1,m_2}$). It can be noted that the operator ${\nabla }_2$ is expressed only if $n_2⩾1$ and $m_2⩾1$.

Lemma 5.

Let ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ and ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1+1,{\tau }_2-1})$ be two networks. Then

(i)

${\xi }_1\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})\right)>{\xi }_1\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1+1,{\tau }_2-1})\right).$

(ii)

If ${\tau }_1>\frac{3{\tau }_2+2s-3}{3}$ then ${\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})\right)>{\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1+1,{\tau }_2-1})\right).$

Proof. 

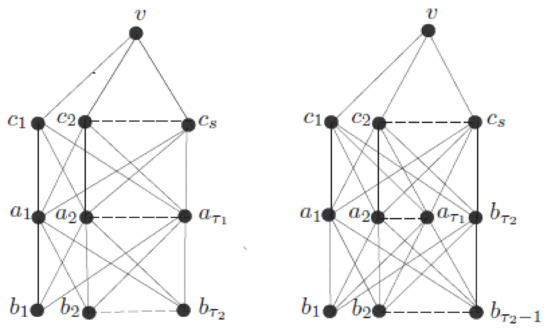
Assume that ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ belongs to ℵ and ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1+1,{\tau }_2-1})$ belongs to ${\aleph }^{\prime }$, respectively. Here ℵ and ${\aleph }^{\prime }$ are depicted in Figure 2. We partition $V_{\aleph }=V_{{\aleph }^{\prime }}$ with $\left\{v\right\}\cup {\Lambda }_1\cup {\Lambda }_2\cup {\Lambda }_3\cup \left\{b_{{\tau }_2}\right\}$, where ${\Lambda }_1=\{c_1,c_2,\dots ,c_s\}$, ${\Lambda }_2=\{a_1,a_2,\dots ,a_{{\tau }_1}\}$ and ${\Lambda }_3=\{b_1,b_2,\dots ,b_{{\tau }_2-1}\}$.

Figure 2. Networks ℵ and ${\aleph }^{*}$.

$\left(\mathrm{i}\right)$ By direct calculation we have

${\epsilon }^2\left(b_{{\tau }_2}\right)={{\epsilon }^{\prime }}^2\left(b_{{\tau }_2}\right)+5$ all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{\prime }\right)& =\sum _{b_{{\tau }_2}\in V(\aleph )}{\epsilon }^2\left(b_{{\tau }_2}\right)-\sum _{b_{{\tau }_2}\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(b_{{\tau }_2}\right)\hfill \\ \hfill & ={\epsilon }^2\left(b_{{\tau }_2}\right)-({\epsilon }^2\left(b_{{\tau }_2}\right)-5)\hfill \\ \hfill & >0\hfill \end{array}$$

Hence, $\left(\mathrm{i}\right)$ holds.

Now we prove $\left(\mathrm{ii}\right)$. By direct calculation we have $\epsilon \left(a\right)\epsilon \left(b_{{\tau }_2}\right)=6$, ${\epsilon }^{\prime }\left(b\right){\epsilon }^{\prime }\left(b_{{\tau }_2}\right)=6$, ${\epsilon }^{\prime }\left(c\right){\epsilon }^{\prime }\left(b_{{\tau }_2}\right)=4$, all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_2(\aleph )-{\xi }_2\left({\aleph }^{\prime }\right)& =\sum _{a{b}_{{\tau }_2}\in \epsilon (\aleph )}\epsilon \left(a\right)\epsilon \left(b_{{\tau }_2}\right)-\sum _{b{b}_{{\tau }_2}\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(b\right){\epsilon }^{\prime }\left(b_{{\tau }_2}\right)-\sum _{c{b}_{{\tau }_2}\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(c\right){\epsilon }^{\prime }\left(b_{{\tau }_2}\right)\hfill \\ \hfill & =6{\tau }_1-6({\tau }_2-1)-4s\hfill \\ \hfill & =6{\tau }_1-6{\tau }_2-4s+6\hfill \\ \hfill & >0.\hfill \end{array}$$

This completes the proof of $\left(\mathrm{ii}\right)$. □

Corollary 2.

Let ${\Phi }_s{\nabla }_2(K_1▵K_{{\tau }_1,{\tau }_2})$ and ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ be two networks. Then

(i)

${\xi }_1\left({\Phi }_s{\nabla }_2(K_1▵K_{{\tau }_1,{\tau }_2})\right)⩾{\xi }_1\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})\right)$

(ii)

${\xi }_2\left({\Phi }_s{\nabla }_2(K_1▵K_{{\tau }_1,{\tau }_2})\right)⩾{\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})\right).$

The equality holds in both cases if and only if ${\tau }_1={\tau }_2.$

Proof. 

Let $\aleph \in {\Phi }_s{\nabla }_2(K_1▵K_{{\tau }_1,{\tau }_2})$ and ${\aleph }^{\prime }\in {\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$. We partition $V_{\aleph }=V_{{\aleph }^{\prime }}$ with $\left\{v\right\}\cup {\Lambda }_1\cup {\Lambda }_2\cup {\Lambda }_3$, where ${\Lambda }_1=\{c_1,c_2,\dots ,c_s\}$, ${\Lambda }_2=\{a_1,a_2,\dots ,a_{{\tau }_1}\}$ and ${\Lambda }_3=\{b_1,b_2,\dots ,b_{{\tau }_2}\}$.

$\left(\mathrm{i}\right)$ By direct calculation we get

${\epsilon }^2\left(a\right)=4,{\epsilon }^2\left(b\right)=9,{{\epsilon }^{\prime }}^2\left(a\right)=9,{{\epsilon }^{\prime }}^2\left(b\right)=4$ all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{\prime }\right)& =\sum _{a\in V(\aleph )}{\epsilon }^2\left(a\right)+\sum _{b\in V(\aleph )}{\epsilon }^2\left(b\right)-\sum _{a\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(a\right)-\sum _{b\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(b\right)\hfill \\ \hfill & =4{\tau }_2+9{\tau }_1-9{\tau }_2-4{\tau }_1\hfill \\ \hfill & =5{\tau }_1-5{\tau }_2\hfill \\ \hfill & ⩾0.\hfill \end{array}$$

Hence, $\left(\mathrm{i}\right)$ holds.

Now we prove $\left(\mathrm{ii}\right)$. By direct calculation we have $\epsilon \left(c\right)\epsilon \left(a\right)=4,{\epsilon }^{\prime }\left(c\right){\epsilon }^{\prime }\left(b\right)=4$ all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_2(\aleph )-{\xi }_2\left({\aleph }^{\prime }\right)& =\sum _{ca\in \epsilon (\aleph )}\epsilon \left(c\right)\epsilon \left(a\right)-\sum _{cb\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(c\right){\epsilon }^{\prime }\left(b\right)\hfill \\ \hfill & =4s{\tau }_1-4s{\tau }_2\hfill \\ \hfill & =4s({\tau }_1-{\tau }_2)\hfill \\ \hfill & ⩾0.\hfill \end{array}$$

Hence, we get our desired result. □

Lemma 6.

Assume ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ and ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1-1,{\tau }_2+1})$ be the networks. Then

(i)

${\xi }_1\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})\right)>{\xi }_1\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1-1,{\tau }_2+1})\right)$

(ii)

${\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})\right)>{\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1-1,{\tau }_2+1})\right)$

Proof. 

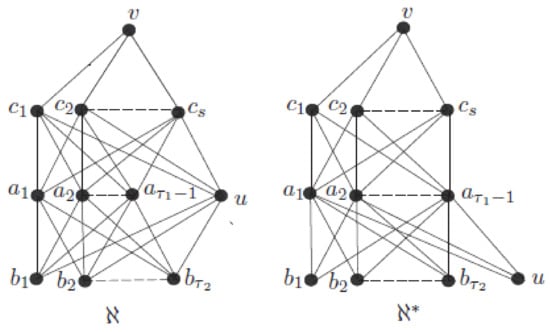
(i) Let us denote ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ by ℵ and ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1-1,{\tau }_2+1})$ by ${\aleph }^{\prime }$. We partition $V_{\aleph }=V_{{\aleph }^{\prime }}$ with $\left\{v\right\}\cup {\Lambda }_1\cup {\Lambda }_2\cup {\Lambda }_3\cup \left\{u\right\}$. We define ${\Lambda }_1,{\Lambda }_2$ and ${\Lambda }_3$ as ${\Lambda }_1=\{c_1,c_2,\dots ,c_s\}$, ${\Lambda }_2=\{a_1,a_2,\dots ,a_{{\tau }_1-1}\}$ and ${\Lambda }_3=\{b_1,b_2,\dots ,b_{{\tau }_2}\}$, respectively (see Figure 3).

Figure 3. Networks ℵ and ${\aleph }^{*}$.

Then by direct calculation we have ${\epsilon }^2\left(u\right)={{\epsilon }^{\prime }}^2\left(u\right)+5$ all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{\prime }\right)& =\sum _{u\in V(\aleph )}{\epsilon }^2\left(u\right)-\sum _{u\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(u\right)\hfill \\ \hfill & ={\epsilon }^2\left(u\right)-({\epsilon }^2\left(u\right)-5)\hfill \\ \hfill & =5\hfill \\ \hfill & >0.\hfill \end{array}$$

This completes the proof of $\left(\mathrm{i}\right)$.

$\left(\mathrm{ii}\right)$ Similar to $\left(\mathrm{i}\right)$, let us denote ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ by ℵ and ${\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1-1,{\tau }_2+1})$ by ${\aleph }^{\prime }$. We partition $V_{\aleph }=V_{{\aleph }^{\prime }}$ with $\left\{v\right\}\cup {\Lambda }_1\cup {\Lambda }_2\cup {\Lambda }_3\cup \left\{u\right\}$. We define ${\Lambda }_1,{\Lambda }_2$ and ${\Lambda }_3$ as ${\Lambda }_1=\{c_1,c_2,\dots c_s\}$, ${\Lambda }_2=\{a_1,a_2\dots ,a_{{\tau }_1-1}\}$ and ${\Lambda }_3=\{b_1,b_2,\dots ,b_{{\tau }_2}\}$ (see Figure 3).

Then by direct calculation we have

$\epsilon \left(u\right)\epsilon \left(c\right)=4$, $\epsilon \left(u\right)\epsilon \left(b\right)=6$, ${\epsilon }^{\prime }\left(u\right){\epsilon }^{\prime }\left(a\right)=6$ all other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_2(\aleph )-{\xi }_2\left({\aleph }^{\prime }\right)& =\sum _{uc\in \epsilon (\aleph )}\epsilon \left(u\right)\epsilon \left(c\right)+\sum _{ub\in \epsilon (\aleph )}\epsilon \left(u\right)\epsilon \left(b\right)-\sum _{ua\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(u\right){\epsilon }^{\prime }\left(a\right)\hfill \\ \hfill & =4s+6{\tau }_1-6({\tau }_2-1)\hfill \\ \hfill & =4s+6{\tau }_1-6{\tau }_2+6\hfill \\ \hfill & >0\hfill \end{array}$$

The last inequality holds as ${\tau }_1⩾{\tau }_2$. This completes the proof of $\left(\mathrm{ii}\right)$. □

Corollary 3.

Let $K_{s,n-s}$, ${\Phi }_s{\nabla }_1(K_1▵K_{1,n-s-2})$ and ${\Phi }_s{\nabla }_1(K_1▵K_{n-s-2,1})$ be the networks. Then

(i)

If $1\le s\le \lfloor \frac{4n-9{\tau }_2-13}{4}\rfloor ,$ then ${\xi }_1\left(K_{s,n-s}\right)⩾{\xi }_1\left({\Phi }_s{\nabla }_1(K_1▵K_{1,n-s-2})\right).$ The equality holds if and only if $n=\frac{4s+9{\tau }_2+13}{4}$.

(ii)

If $1\le s\le \lfloor \frac{3(n-2)}{4}\rfloor ,$ then ${\xi }_2\left(K_{s,n-s}\right)⩾{\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{n-s-2,1})\right),$ with equality if and only if $n=\frac{4}{3}s+2$.

Proof. 

(i) Let us denote $K_{s,n-s}$ by ℵ and ${\Phi }_s{\nabla }_1(K_1▵K_{1,n-s-2})$ by ${\aleph }^{\prime }$. We partition $V_{\aleph }=V_{{\aleph }^{\prime }}$ with $\left\{v\right\}\cup {\Lambda }_1\cup \left\{a\right\}\cup {\Lambda }_2$, where ${\Lambda }_1=\{c_1,c_2,\dots ,c_s\}$ and ${\Lambda }_2=\{b_1,b_2,\dots ,b_{{\tau }_2}\}$. Then by direct calculation we get ${\epsilon }^2\left(u\right)=4$, ${{\epsilon }^{\prime }}^2\left(v\right)=9$, ${{\epsilon }^{\prime }}^2\left(c\right)=4$, ${{\epsilon }^{\prime }}^2\left(a\right)=4$, ${{\epsilon }^{\prime }}^2\left(b\right)=9$

This gives

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{\prime }\right)& =\sum _{u\in V(\aleph )}{\epsilon }^2\left(u\right)-\sum _{v\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(v\right)-\sum _{c\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(c\right)-\sum _{a\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(a\right)-\sum _{b\in V\left({\aleph }^{\prime }\right)}{\epsilon }^{\prime 2}\left(b\right)\hfill \\ \hfill & =4n-9-4s-4-9{\tau }_2\hfill \\ \hfill & ⩾0.\hfill \end{array}$$

This completes the proof of $\left(\mathrm{i}\right)$.

$\left(\mathrm{ii}\right)$ Let us denote $K_{s,n-s}$ by ℵ and ${\Phi }_s{\nabla }_1(K_1▵K_{n-s-2,1})$ by ${\aleph }^{\prime }$. We partition $V_{\aleph }=V_{{\aleph }^{\prime }}$ with $\left\{v\right\}\cup {\Lambda }_1\cup {\Lambda }_2\cup \left\{b\right\}$, where ${\Lambda }_1=\{c_1,c_2,\dots ,c_s\}$ and ${\Lambda }_2=\{a_1,a_2,\dots ,a_{{\tau }_1}\}$. Then by direct calculation we get $\epsilon \left(u_1\right)\epsilon \left(u_2\right)=4$, ${\epsilon }^{\prime }\left(v\right){\epsilon }^{\prime }\left(c\right)=6$, ${\epsilon }^{\prime }\left(c\right){\epsilon }^{\prime }\left(a\right)=4$, ${\epsilon }^{\prime }\left(a\right){\epsilon }^{\prime }\left(b\right)=6$ This gives

$$\begin{array}{cc}\hfill {\xi }_2(\aleph )-{\xi }_2\left({\aleph }^{\prime }\right)& =\sum _{u_1{u}_2\in \epsilon (\aleph )}\epsilon \left(u_1\right)\epsilon \left(u_2\right)-\sum _{vc\in \epsilon (\aleph )}\epsilon \left(v\right)\epsilon \left(c\right)-\sum _{ca\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(c\right){\epsilon }^{\prime }\left(a\right)-\sum _{ab\in \epsilon \left({\aleph }^{\prime }\right)}{\epsilon }^{\prime }\left(a\right){\epsilon }^{\prime }\left(b\right)\hfill \\ \hfill & =4s(n-s)-6s-4s(n-s-2)-6(n-s-2)\hfill \\ \hfill & =8s-6n+12\hfill \\ \hfill & ⩾0.\hfill \end{array}$$

This completes the proof of $\left(\mathrm{ii}\right)$. □

Lemma 7.

Let $\aleph \in {\mathcal{C}}_n^s$ and $\aleph -W$ has two nontrivial components, where W is any node-cut set of order s in ℵ, then ℵ cannot be the network with minimum Zagreb eccentricity indices in $\aleph \in {\mathcal{C}}_n^s.$

Proof. 

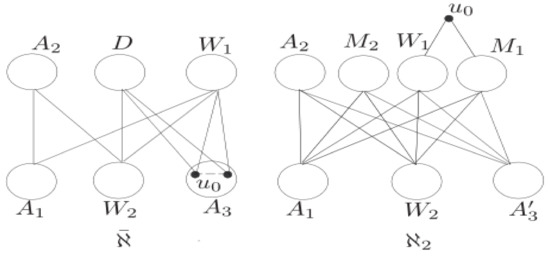
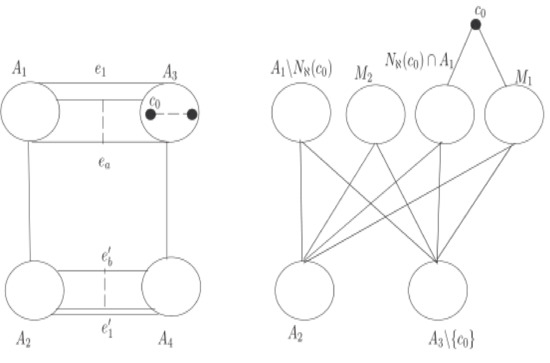
Assume that ${\aleph }_1$ and ${\aleph }_2$ are two nontrivial components of $\aleph -U$ having the two partitions $(A_1,A_2)$ and $(A_3,A_4)$, simultaneously. Suppose that $W=W_1\cup W_2$ be the two partitions of W which is induced from the bipartition of ℵ. Next, we join entire links among all the nodes of $A_1$ and $A_2$, $A_3$ and $A_4$, $W_1$ and $W_2$ we get a network $\overline{\aleph }\in {\mathcal{C}}_n^s$ which implies that ${\xi }_i(\aleph )⩾{\xi }_i\left(\overline{\aleph }\right)$, $i=1,2$. Therefore we suppose that $\aleph =\overline{\aleph }$; see Figure 4.

Figure 4. Networks $\overline{\aleph }$ and ${\aleph }_2$.

If it is possible that there exists any node w in $\aleph -W$ in such a way that $d_{\aleph }\left(w\right)=s$, in this situation we can obtain a complete bipartite network inside the nodes of $\aleph \backslash \left\{w\right\}$. Hence, it is easy to see that we can get a network in ${\mathcal{C}}_n^s$ which has smaller Zagreb eccentricity indices. Thereby, one can see that every node inside of $\aleph -W$ having degree more than s. Without loss of generality, $|A_1|=m_1$, $|A_2|=m_2$, $|A_3|=n_1$, $|A_4|=n_2$, $|W_1|=t$, $|W_2|=k$. Therefore, one can opt a node $u_0\in A_3$ and perceive that $d_{\aleph }\left(u_0\right)=t+\left|A_4\right|>s$, since $t(0\le t\le s)$ is the overall amount of links which join $u_0$ with the nodes of $W_1$. Note that $W_1\cup W_2$ represents the node-cut set with order s, hence $m_1,n_1>t$, $m_2,n_2>k$. Assume that $m_1=max\{m_1,m_2,n_1,n_2\}$ without loss of generality, note that $s⩾1$, $m_1⩾2$ and $m_1{m}_2+n_1{n}_2⩾2(m_2{n}_1+m_1{n}_2)$. Now, we opt a subset $M_2$ of $A_4$ in such a way $|M_2|=|A_4|-k>0$ hence, $n_2⩾2k$. Let

$${\aleph }^{*}=\aleph -\{u_{0}x:x\in M_2\}+\{bc:b\in A_2,c\in A_3\backslash \left\{u_0\right\}\}+\{{\tau }_1{\tau }_2:{\tau }_1\in A_4,{\tau }_2\in A\}.$$

It is routine to check that ${\aleph }^{*}\in {\mathcal{C}}_n^s$ having bipartition $(X,Y)$. The quantity $X=A_2\cup M_2\cup W_1\cup M_1$ and $Y=A_1\cup A_2\cup A_3^{\prime }\cup \left\{u_0\right\}$ with $|A_3^{\prime }|=n_1-1,\left|M_1\right|=k$, and $|M_2|=n_2-k$. Here, ${\aleph }^{*}$ is depicted in Figure 5. Notice that, for $a\in A_1(resp.b\in A_2,c\in A_3^{\prime },d\in A_4,d_1\in M_1,d_2\in M_2).$ By direct calculation we get

Figure 5. Networks $\overline{\aleph }$ and ${\aleph }^{*}$.

${\epsilon }^2\left(a\right)=9$, ${\epsilon }^2\left(d\right)=9$, ${\epsilon }^2\left(c\right)=9$, ${{\epsilon }^{*}}^2\left(a\right)=4$, ${{\epsilon }^{*}}^2\left(d_2\right)=9$, ${{\epsilon }^{*}}^2\left(d_1\right)=4$, ${{\epsilon }^{*}}^2\left(c\right)=4.$ All other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_1(\aleph )-{\xi }_1\left({\aleph }^{*}\right)& =9m_1+9n_2+9(n_1-1)-4m_1-9(n_2-k)-4k-4(n_1-1)\hfill \\ \hfill & =5m_1+5n_1-5+5k\hfill \\ \hfill & =5(m_1-1)+5(n_1+k)\hfill \\ \hfill & >0.\hfill \end{array}$$

By the similar argument as above, and by comparing the structure of networks ℵ and ${\aleph }^{*}$ one can see easily that

$\epsilon \left(b\right)\epsilon \left(a\right)=9$, $\epsilon \left(b\right)\epsilon \left(u_2\right)=6$, $\epsilon \left(d\right)\epsilon \left(u_2\right)=6$, $\epsilon \left(d\right)\epsilon \left(c\right)=9$, $\epsilon \left(d\right)\epsilon \left(u_0\right)=9$, $\epsilon \left(u_1\right)\epsilon \left(a\right)=6$, $\epsilon \left(u_1\right)\epsilon \left(u_2\right)=4$, $\epsilon \left(u_1\right)\epsilon \left(c\right)=6$, $\epsilon \left(u_1\right)\epsilon \left(u_0\right)=6$. ${\epsilon }^{*}\left(a\right){\epsilon }^{*}\left(b\right)=6$, ${\epsilon }^{*}\left(b\right){\epsilon }^{*}\left(u_2\right)=6$, ${\epsilon }^{*}\left(b\right){\epsilon }^{*}\left(c\right)=6$, ${\epsilon }^{*}\left(d_2\right){\epsilon }^{*}\left(a\right)=6$, ${\epsilon }^{*}\left(d_2\right){\epsilon }^{*}\left(u_2\right)=6$, ${\epsilon }^{*}\left(d_2\right){\epsilon }^{*}\left(c\right)=6$, ${\epsilon }^{*}\left(u_1\right){\epsilon }^{*}\left(a\right)=4$, ${\epsilon }^{*}\left(u_1\right){\epsilon }^{*}\left(u_2\right)=4$, ${\epsilon }^{*}\left(u_1\right){\epsilon }^{*}\left(c\right)=4$, ${\epsilon }^{*}\left(u_1\right){\epsilon }^{*}\left(u_0\right)=6$, ${\epsilon }^{*}\left(d_1\right){\epsilon }^{*}\left(a\right)=4$, ${\epsilon }^{*}\left(d_1\right){\epsilon }^{*}\left(u_2\right)=4$, ${\epsilon }^{*}\left(d_1\right){\epsilon }^{*}\left(c\right)=4$, ${\epsilon }^{*}\left(d_1\right){\epsilon }^{*}\left(u_0\right)=6.$ All other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_2(\aleph )-{\xi }_2\left({\aleph }^{*}\right)& =9m_1{m}_2+6m_{2}k+6n_{2}k+9n_2(n_1-1)+9n_2+6m_{1}t+4kt+6(n_1-1)t+6t\hfill \\ \hfill & -6m_1{m}_2-6m_{2}k-6m_2(n_1-1)-6(n_2-k)m_1-6(n_2-k)k-6(n_2\hfill \\ \hfill & -k)(n_1-1)-4t{m}_1-4kt-4t(n_1-1)-6t-4k{m}_1-4k^2-4k(n_1-1)-6k\hfill \\ \hfill & =3m_1{m}_2+3n_1{n}_2+2m_{1}t+2t{n}_1-6m_2{n}_1+6m_2-6m_1{n}_2+2k{m}_1+2k^2+6n_2+2k{n}_1-8k-2t\hfill \\ \hfill & =(3m_1{m}_2+3n_1{n}_2-6m_2{n}_1-6m_1{n}_2)+(2m_{1}t-2t)+(6n_2-8k)+2t{n}_1+6m_2\hfill \\ \hfill & +2k{m}_1+2k^2+2k{n}_1=3(m_1{m}_2+n_1{n}_2-2m_2{n}_1-2m_1{n}_2)\hfill \\ \hfill & +2t(m_1-1)+2(3n_2-4k)+2(t{n}_1+3m_2)+2k(m_1+k+n_1)\hfill \\ \hfill & >0.\hfill \end{array}$$

□

Lemma 8.

Let $\aleph \in {\mathcal{D}}_n^t$ and $\aleph -{\xi }_t$ has two nontrivial components, which implies that ${\xi }_t$ is any link cut-set of order t in ℵ. Then ℵ may not be the network having minimum Zagreb eccentricity indices in ${\mathcal{D}}_n^t$.

Proof. 

Assume that ${\aleph }_1$ and ${\aleph }_2$ be two nontrivial components of $\aleph -{\xi }_t$ having the two partitions $(A_1,A_2)$ and $(A_3,A_4)$, respectively. Now joining all possible links between the nodes of $A_1$ and $A_2$, $A_3$ and $A_4$ yields a network, say $\overline{\aleph }$, in ${\mathcal{D}}_n^t$ such that ${\xi }_i(\aleph )⩾{\xi }_i\left(\overline{\aleph }\right)$; $i=1,2$. Therefore, in ${\mathcal{D}}_n^t$ we suppose that $\aleph =\overline{\aleph }$; see Figure 5.

It can be noticed that for some node $v\in \aleph$ one has $d_{\aleph }\left(v\right)⩾t$. For the existence of some node w in ℵ we have $d_{\aleph }\left(w\right)=t$. By adding entirely probable links inside the subnetwork of ℵ which is induced from the nodes of $V_{\aleph }\backslash \left\{w\right\}$, then finally we would reach at a two partition network ${\aleph }^{\prime }$. For $\aleph \ne {\aleph }^{\prime }$, we have ${\xi }_i(\aleph )>{\xi }_i\left({\aleph }^{\prime }\right)$; $i=1,2$ in view of Lemma 1. Thereby, we suppose that every node in ℵ has degree more than t.

Assume that $|A_1|=m_1,|A_2|=m_2,|A_3|=n_1,\left|A_4\right|=n_2$ and the amount of links among $A_1$ and $A_3$(respectively $A_2$ and $A_4$), in ℵ, is i(resp. j).

Hence, it is easy to see that $m_1+m_2+n_1+n_2=n$ and $i+j=t$.

Choose any node $c_0\in A_3$ and perceive that $d_{\aleph }\left(c_0\right)={\tau }_2=h+\left|A_4\right|>i$, the quantity $h(0\le h\le i)$ is the overall amount of links which join $c_0$ with the nodes belongs to $A_1$. It can be noticed that ${\xi }_{\overline{\aleph }}[A_1,A_3]\cup {\xi }_{\overline{\aleph }}[A_2,A_4]$ is any link-cut set with size $i+j=t$, for further detail one can see Figure 6. Hence, $m_1,n_1>i,m_2,n_2>j$. Moreover, we opt a subset $M_2$ of $A_4$ which satisfies $|M_2|=|A_4|-({\tau }_2-h)>0$. Let

$${\aleph }^{*}=\overline{\aleph }-\{c_{0}x:x\in M_2\}+\{ac:a\in A_1,c\in A_3\backslash \left\{c_0\right\}\}+\{{\tau }_1{\tau }_2:{\tau }_1\in A_2,{\tau }_2\in A_4\}.$$

Figure 6. Graphs ${\aleph }_1^{*}$, ${\aleph }_2^{*}$ and ${\aleph }_3^{*}$.

It is easy to see that ${\aleph }^{*}\in {\mathcal{D}}_n^t$, for detail one can see the construction of Figure 5.

We denote the sets which are assumed to be the end-nodes of the links of ${\xi }_t$ in $A_1,A_2,A_3$ and $A_4$ by $S_1,S_2,S_3$, and $S_4$, respectively. Let $a\in A_1,b\in A_2,c\in A_3,d\in A_4,u\in S_1,v\in S_2,w\in S_3,z\in S_4,a_1\in A_1\backslash S_1,a_2\in A_2\backslash S_2,a_3\in A_3\backslash S_3,a_4\in A_4\backslash S_4,|S_1|=s_1,|S_2|=s_2,\left|S_3\right|=s_3$.

Moreover $m_1>s_1,m_2>s_2,n_1>s_3,n_2>s_4$ and note that $m_1{m}_2+n_1{n}_2⩾m_1{n}_1+m_2{n}_2,m_1+n_2⩾2{\tau }_2,{\tau }_2⩾2s_1,2s_4,s_1(s_2+9s_3)⩾4m_1{s}_2,s_4(s_3+9s_2)⩾4n_2{s}_3$. By direct calculation we get ${\overline{\epsilon }}^2\left(a_1\right)=16,{\overline{\epsilon }}^2\left(a_2\right)=16,{\overline{\epsilon }}^2\left(a_3\right)=16,{\overline{\epsilon }}^2\left(a_4\right)=16,{\overline{\epsilon }}^2\left(u\right)=9,{\overline{\epsilon }}^2\left(v\right)=9,{\overline{\epsilon }}^2\left(w\right)=9,{\overline{\epsilon }}^2\left(z\right)=9$, ${{\epsilon }^{*}}^2(a\backslash N_{\aleph }\left(c_0\right))=9,{{\epsilon }^{*}}^2\left(b\right)=4,{{\epsilon }^{*}}^2(c\backslash c_0)=4,{{\epsilon }^{*}}^2\left(c_0\right)=9,{{\epsilon }^{*}}^2\left(d_2\right)=9,{{\epsilon }^{*}}^2\left(d_1\right)=4,{{\epsilon }^{*}}^2(a\cap N_{\aleph }\left(c_0\right))=4.$ All other eccentricities are equal. Thus

$$\begin{array}{cc}\hfill {\xi }_1\left(\overline{\aleph }\right)-{\xi }_1\left({\aleph }^{*}\right)& =16(m_1-s_1)+16(m_2-s_2)+16(n_1-s_3)+16(n_2-s_4)+9s_1+9s_2+9s_3+9s_4\hfill \\ \hfill & -9(m_1-h)-4m_2-4(n_1-1)-9-9(n_2-({\tau }_2-h))-4({\tau }_2-h)-4h\hfill \\ \hfill & =7m_1-7s_1+12m_2-7s_2+12n_1-7s_3+7n_2-7s_4+5{\tau }_2-5\hfill \\ \hfill & >0.(\because {\tau }_2⩾1)\hfill \end{array}$$

By the similar argument as above, and by comparing the structure of networks $\overline{\aleph }$ and ${\aleph }^{*}$ one can see easily that $\overline{\epsilon }\left(a_1\right)\overline{\epsilon }\left(a_2\right)=16,\overline{\epsilon }\left(a_1\right)\overline{\epsilon }\left(v\right)=12,\overline{\epsilon }\left(u\right)\overline{\epsilon }\left(a_2\right)=12,\overline{\epsilon }\left(u\right)\overline{\epsilon }\left(v\right)=9,\overline{\epsilon }\left(u\right)\overline{\epsilon }\left(w\right)=9,\overline{\epsilon }\left(v\right)\overline{\epsilon }\left(z\right)=9,\overline{\epsilon }\left(a_3\right)\overline{\epsilon }\left(a_4\right)=16,\overline{\epsilon }\left(a_3\right)\overline{\epsilon }\left(z\right)=12,\overline{\epsilon }\left(w\right)\overline{\epsilon }\left(a_4\right)=12,\overline{\epsilon }\left(w\right)\overline{\epsilon }\left(z\right)=9;$ ${\epsilon }^{*}(a\backslash N_{\aleph }\left(c_0\right)){\epsilon }^{*}\left(b\right)=6,{\epsilon }^{*}(a\backslash N_{\aleph }\left(c_0\right)){\epsilon }^{*}(c\backslash c_0)=6,{\epsilon }^{*}\left(d_2\right){\epsilon }^{*}\left(b\right)=6,{\epsilon }^{*}\left(d_2\right){\epsilon }^{*}(c\backslash c_0)=6,{\epsilon }^{*}(a\cap N_{\aleph }\left(c_0\right)){\epsilon }^{*}(c\backslash c_0)=4,{\epsilon }^{*}(a\cap N_{\aleph }\left(c_0\right)){\epsilon }^{*}\left(b\right)=4,{\epsilon }^{*}\left(d_1\right){\epsilon }^{*}\left(b\right)=4,{\epsilon }^{*}\left(d_1\right){\epsilon }^{*}(c\backslash c_0)=4,{\epsilon }^{*}\left(c_0\right){\epsilon }^{*}(a\cap N_{\aleph }\left(c_0\right))=6,{\epsilon }^{*}\left(c_0\right){\epsilon }^{*}\left(d_1\right)=6.$ All other eccentricities are equal.

This gives

$$\begin{array}{cc}\hfill {\xi }_2\left(\overline{\aleph }\right)-{\xi }_2\left({\aleph }^{*}\right)& =16(m_1-s_1)(m_2-s_2)+12s_2(m_1-s_1)+12s_1(m_2-s_2)+9s_1{s}_2+9s_1{s}_3+9s_2{s}_4\hfill \\ \hfill & +16(n_1-s_3)(n_2-s_4)+12(n_1-s_3)s_4+12s_3(n_2-s_4)+9s_3{s}_4-6(m_1-h)m_2\hfill \\ \hfill & -6(m_1-h)(n_1-1)-6(n_2-({\tau }_2-h))m_2-6(n_2-({\tau }_2-h))(n_1-1)-4h(n_1-1)\hfill \\ \hfill & -4h{m}_2-4({\tau }_2-h)m_2-4({\tau }_2-h)(n_1-1)-6h-6\left(1\right)({\tau }_2-h)\hfill \\ \hfill & =10m_1{m}_2-4m_1{s}_2-4m_2{s}_1+s_1{s}_2+9s_1{s}_3+9s_2{s}_4+10n_1{n}_2-4n_1{s}_4-4n_2{s}_3+s_3{s}_4\hfill \\ \hfill & -6m_1{n}_1+6m_1-6m_2{n}_2+2{\tau }_2{m}_2+2{\tau }_2{n}_1+6n_2-8{\tau }_2\hfill \\ \hfill & =(10m_1{m}_2+10n_1{n}_2-6m_1{n}_1-6m_2{n}_2)+(2{\tau }_2{n}_1-4n_1{s}_4)+(6m_1+6n_2-8{\tau }_2)\hfill \\ \hfill & +(2{\tau }_2{m}_2-4m_2{s}_1)+(s_1{s}_2+9s_1{s}_3-4m_1{s}_2)+(s_3{s}_4+9s_1{s}_3-4n_2{s}_3)\hfill \\ \hfill & =2\left(5(m_1{m}_2+n_1{n}_2)-3(m_1{n}_1+m_2{n}_2)\right)+2n_1({\tau }_2-2s_4)+2(3(m_1+n_2)-4{\tau }_2)\hfill \\ \hfill & +2m_2({\tau }_2-2s_1)+\left(s_1(s_2+9s_3\right)-4m_1{s}_2)+(s_4(s_3+9s_2)-4n_2{s}_3)\hfill \\ \hfill & >0.\hfill \end{array}$$

□

Theorem 5.

Let ℵ be a network in ${\mathcal{C}}_n^s$ with minimum ${\xi }_1(\aleph )$ and ${\xi }_2(\aleph )$ with $1\le s\le \lfloor \frac{4n-9{\tau }_2-13}{4}\rfloor$ and $1\le s\le \lfloor \frac{3(n-2)}{4}\rfloor$ respectively. If n is odd then $\aleph \in \{{\aleph }_1^{*},{\aleph }_3^{*}\}$, otherwise $\aleph \cong {\aleph }_2^{*}$. In Fig.6, we have shown the networks ${\aleph }_1^{*},{\aleph }_2^{*}$ and ${\aleph }_3^{*}$.

Proof. 

Assume that ℵ be a network with minimum Zagreb eccentricity indices in ${\mathcal{C}}_n^s$. Let W be any node cut of ℵ which contains s number of nodes. By removing these nodes gives the components ${\aleph }_1,{\aleph }_2,...,{\aleph }_t$ in $\aleph -W$. The quantity t is greater than or equal to 2. Meanwhile, if any component ${\aleph }_i$ of $\aleph -W$ of has at least two nodes, then that should be a complete bipartite. Similarly, if few component ${\aleph }_i$ in $\aleph -W$ are singleton, that is to say ${\aleph }_i=\left\{u\right\}$, as a result u is connected to entire nodes of W; else $\kappa (\aleph )<s$. Thus, the subnetwork $\aleph \left[W\right]$ is induced from W which contains no links, and belongs with the alike partition of ℵ. To proceed further we need we need the following two cases.

Case 1. Entire components of $\aleph -W$ being singletons. In this case, one has $\aleph =K_{s,n-s}$ for $s=\lfloor \frac{n-1}{2}\rfloor$ or $\lfloor \frac{n-3}{2}\rfloor .$ It is straightforward to see that, if n is odd then $K_{s,n-s}\cong {\aleph }_1^{*}$, and otherwise $K_{s,n-s}\cong {\aleph }_2^{*}$ as desired. To prove the first Zagreb eccentricity index, let us assume that $1\le s\le \lfloor \frac{4n-9{\tau }_2-13}{4}\rfloor .$ Then by Corollary 3(i), ${\xi }_1\left(K_{s,n-s}\right)⩾{\xi }_1\left({\Phi }_s{\nabla }_1{\xi }_1(K_1▵K_{1,n-s-2})\right)$, this gives a contradiction to the minimality in ℵ. To prove the second Zagreb eccentricity index, let $1\le s\le \lfloor \frac{3(n-2)}{4}\rfloor .$ Then by Corollary 3(ii), ${\xi }_2\left(K_{s,n-s}\right)⩾{\xi }_2\left({\Phi }_s{\nabla }_1(K_1▵K_{n-s-2,1})\right)$, which also contradicts the minimality of ℵ. Thus, not every of the components in $\aleph -W$ are supposed to be singletons.

Case 2. Only single component in $\aleph -W$ that is to say ${\aleph }_1$, containing at least two nodes. In such situation, $\aleph -W$ containing exactly two components, else there is a complete bipartite network which consists the nodes of ${\aleph }_1\cup {\aleph }_2\cup ...{\aleph }_{t-1}$. Hence, one can construct a new network ${\aleph }^{*}$ from ℵ having smaller Zagreb eccentricity indices such that ${\aleph }^{*}\in {\mathcal{C}}_n^s$, which gives a contradiction. Let ${\aleph }_1,{\aleph }_2$ are the two components in $\aleph -W$. Due to Lemma 8, we have ${\aleph }_1=K_1$ or ${\aleph }_2=K_1$. Suppose that ${\aleph }_2=K_1=\left\{u\right\}$. In such scenario u is joining by entire nodes of W, and every node in W is joining each node of ${\aleph }_1$ these are under the same partition as that of u. It can be noticed that ℵ be any network with minimum Zagreb eccentricity indices, hence due to Corollary 3, $\aleph ={\Phi }_s{\nabla }_1(K_1▵K_{{\tau }_1,{\tau }_2})$ in few ${\tau }_1$ and ${\tau }_2$. One can notice that ${\tau }_1⩾s$, else s may not be the node connectivity in ℵ. The result follows for ${\xi }_2(\aleph )$ if $\frac{2s}{3}+{\tau }_2-1\le {\tau }_1\le \frac{3s}{2}+{\tau }_2+1$; and if ${\tau }_1⩾1$, then the result follows for ${\xi }_1(\aleph )$. Again, if $\frac{2s}{3}+{\tau }_2-1>{\tau }_1$, then applying Lemma 5(ii) multiple times we have $\aleph ={\aleph }_1^{*}$, for odd n, similarly $\aleph ={\aleph }_2^{*}$ for even n. At last, if ${\tau }_1>\frac{3s}{2}+{\tau }_2+1$, then by applying Lemma 7(ii) multiple times, one has ℵ in one hand ${\aleph }_2^{*}$ or on the other hand ${\aleph }_3^{*}$ depending on even n or odd n. This gives our desired result. □

The below result is similar to the proof of Theorem 5, so we omit its proof.

Theorem 6.

Assume that ℵ is any network in ${\mathcal{D}}_n^t$ with minimum ${\xi }_1(\aleph )$ and ${\xi }_2(\aleph )$ with $1⩽s⩽\lfloor \frac{4n-9{\tau }_2-13}{4}\rfloor$ and $1⩽s⩽\lfloor \frac{3(n-2)}{4}\rfloor$ respectively. For odd n we have $\aleph \in \{{\aleph }_1^{*},{\aleph }_3^{*}\}$, otherwise $\aleph \cong {\aleph }_2^{*}$. The networks ${\aleph }_1^{*},{\aleph }_2^{*}$ and ${\aleph }_3^{*}$ are shown inFigure 6.

6. Regression Model for Boiling Point

In this section, we study the correlation between the first and second Zagreb eccentricities of benzenoid hydrocarbons (depicted in Figure 7) and their boiling points (BP). The scatter plot between BP and ${\xi }_1$ and ${\xi }_2$ are shown in Figure 8 and Figure 9.

Figure 7. Molecular networks of benzenoid hydrocarbons.

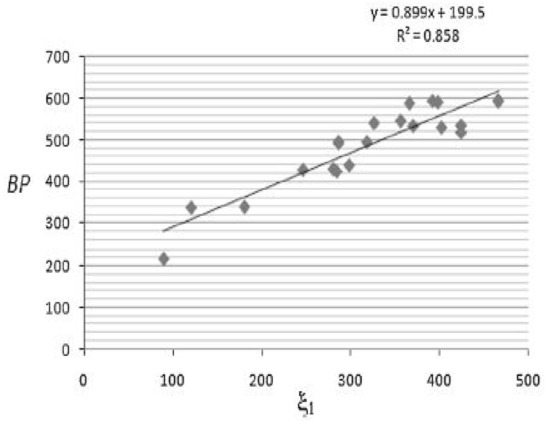
Figure 8. The scatter plot of $BP$ and ${\xi }_1$.

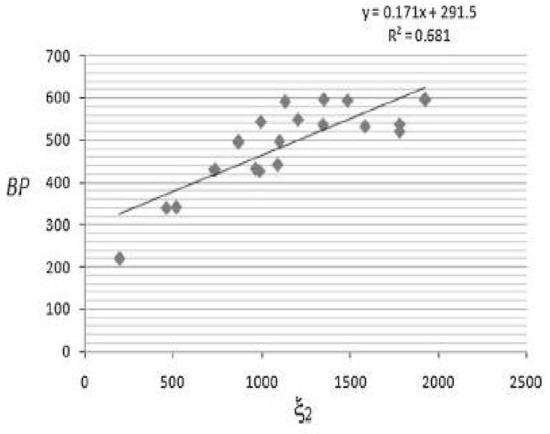
Figure 9. The scatter plot of $BP$ and ${\xi }_2$.

Linear regression models of a boiling point (BP) are obtained by considering the data given in Table 1 with the least square fitting method and calculated by SPSS Statistics programme as:

$$\begin{array}{c}\hfill BP=199.578(\pm 28.269)+0.899(\pm 0.084){\xi }_1\end{array}$$

(8)

$$\begin{array}{c}\hfill BP=291.549(\pm 33.537)+0.172(\pm 0.027){\xi }_2\end{array}$$

(9)

Table 1. Different values of BP, ${\xi }_1$ and ${\xi }_2$ of 21 benzenoid hydrocarbons.

BP	1	2	3	4	5	6	7	8	9	10	11
${\xi }_1$	89	120	180	280	284	246	298	318	286	286	356
${\xi }_2$	192	459	516	959	983	729	1085	1096	862	862	1201
BP	12	13	14	15	16	17	18	19	20	21
${\xi }_1$	326	370	424	402	424	366	398	466	466	392
${\xi }_2$	990	1344	1780	1584	1780	1128	1484	1926	1927	1349

The model (8) indicates that correlation of the boiling point in benzenoid hydrocarbons of ${\xi }_1$ gives a better (R = 0.927) result, as compare to the correlation of ${\xi }_2$ as given in Table 2.

Table 2. The correlation coefficient (R) and standard error estimation.

Index	The Correlation Coefficient (R)	The Standard Error of Estimation
${\xi }_1$	$0.927$	$38.525$
${\xi }_2$	$0.826$	$57.848$

7. Conclusions

This paper analyses the minimum transmission in two-mode networks. Based on some parameters, we obtained the minimum transmission between in the class of all connected n-nodes bipartite networks. The considered parameters are very useful to modify or to change the path of a given network. We determined the minimum transmission with respect to ${\xi }_i(\aleph )$, for $i=1,2$ among all n-node extremal two-mode networks with given matching number, diameter, node connectivity and link connectivity.