A Lower Bound for the Distance Laplacian Spectral Radius of Bipartite Graphs with Given Diameter

Abstract

Let G be a connected, undirected and simple graph. The distance Laplacian matrix $\mathcal{L}\left(G\right)$ is defined as $\mathcal{L}\left(G\right)=diag\left(Tr\right)-\mathcal{D}\left(G\right)$, where $\mathcal{D}\left(G\right)$ denotes the distance matrix of G and $diag\left(Tr\right)$ denotes a diagonal matrix of the vertex transmissions. Denote by ${\rho }_{\mathcal{L}}\left(G\right)$ the distance Laplacian spectral radius of G. In this paper, we determine a lower bound of the distance Laplacian spectral radius of the n-vertex bipartite graphs with diameter 4. We characterize the extremal graphs attaining this lower bound.

1. Introduction

The distance Laplacian and distance signless Laplacian matrices of a graph G proposed by Aouchiche and Hansen [1] are defined as $\mathcal{L}\left(G\right)=diag\left(Tr\right)-\mathcal{D}\left(G\right)$ and $\mathcal{Q}\left(G\right)=diag\left(Tr\right)+\mathcal{D}\left(G\right)$, respectively. Much attention has been paid to them since they were put forward. Aouchiche et al. [2] described some elementary properties of the distance Laplacian eigenvalues of graphs. Niu et al. [3] determined some extremal graphs minimizing the distance Laplacian spectral radius among bipartite graphs in terms of the matching number and the vertex connectivity, respectively. Nath and Paul [4] focused on the graph whose complement is a tree or a unicyclic graph and considered the second-smallest distance Laplacian eigenvalue. Lin and Zhou [5] determined some extremal graphs among several classes of graphs. Tian et al. [6] proved four conjectures put forward by Aouchiche and Hansen in [2]. One can refer to [7,8,9,10,11] for more details on the distance signless Laplacian spectral radius of graphs.

Although lots of conclusions have been obtained, many more problems remain unsolved. For instance, there are few papers focusing on the distance (signless) Laplacian spectral radius of graphs in terms of diameter, an important parameter of graphs. For adjacency matrices of graphs, several conclusions with respect to the diameter have been derived (e.g., [12,13,14]). In [12], the authors determined some extremal graphs with small diameter. Generally, the communication network is organized with small diameter to improve the quality of the service on the networks. Motivated by this, in the present paper, we deduce a lower bound of the distance Laplacian spectral radius among bipartite graphs with diameter 4, and we hope that it could be used to address a general case.

This paper is arranged as follows. In Section 2, some elementary notions and lemmas applied in the next parts are presented. In Section 3, the lower bound for the distance Laplacian spectral radius is obtained for bipartite graphs with diameter 4. Moreover, the extremal graph attaining the lower bound is determined.

2. Preliminaries

All graphs considered in this paper are undirected, connected and simple. By $V\left(G\right)$, we denote the vertex set of G, and the order of G is $\left|V\right(G\left)\right|$. Denote by $N_G\left(u\right)$ the set of vertices adjacent to u. If $N_G\left(u\right)=N_G\left(v\right)$ for $u,v\in V\left(G\right)$, then they are called twin points. Generally, a subset $S\subset V\left(G\right)$ is called a twin point set, if $N_G\left(u\right)=N_G\left(v\right)$ for any $u,v\in S$. The distance between $u,v\in V\left(G\right)$, denoted by $d(u,v)$, is the length of the shortest path between u and v. The diameter of graph G, written as $d\left(G\right)$ (d for short), is the maximum distance among all pairs of vertices of G. The chromatic number of G means the least number of colors required to color all the vertices of G such that each pair of adjacent vertices has different colors. The spanning subgraph of G is obtained by deleting some edges from G with order invariable. The transmission $T{r}_G\left(u\right)$ of a vertex u is referred to as the sum of the distances of u to all other vertices of $V\left(G\right)$, i.e., $T{r}_G\left(u\right)={\sum }_{v\in V\left(G\right)}d(v,u)$. $T{r}_{max}\left(G\right)$ means the maximal vertex transmission of G. Let ${\mathcal{B}}_{n,d}$ be the set of all n-vertex bipartite graphs with diameter d and ${\mathcal{C}}_{n,k}$ the set of all n-vertex graphs with chromatic number k.

Suppose $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$. The distance matrix $\mathcal{D}\left(G\right)$ of G is an $n\times n$ symmetric real matrix with $d(v_i,v_j)$ as the $(i,j)$-entry. Let the diagonal matrix $diag\left(Tr\right)$, called the vertex transmission matrix of G, be

$$diag\left(Tr\right)=diag(T{r}_G\left(v_1\right),T{r}_G\left(v_2\right),\dots ,T{r}_G\left(v_n\right)).$$

The largest eigenvalue of the distance Laplacian matrix $\mathcal{L}\left(G\right)$ is called the distance Laplacian spectral radius, written as ${\rho }_{\mathcal{L}}\left(G\right)$. For any matrix M, ${\lambda }_1\left(M\right)$ always denotes the largest eigenvalue of M.

A vector $x={(x_1,x_2,\dots ,x_n)}^T$ can be considered as a function defined on $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$, which maps $v_i$ to $x_i$, i.e., $x\left(v_i\right)=x_i$. Thus, for $\mathcal{L}\left(G\right)$,

$$\begin{array}{c}\hfill x^T\mathcal{L}\left(G\right)x=\sum _{\{u,v\}\subseteq V\left(G\right)}d(u,v){(x\left(u\right)-x\left(v\right))}^2.\end{array}$$

It is clear that $\mathbf{1}={(1,1,\dots ,1)}^T$ is an eigenvector corresponding to the eigenvalue zero of $\mathcal{L}\left(G\right)$. Thus, if $x={(x_1,x_2,\dots ,x_n)}^T$ is an eigenvector of $\mathcal{L}\left(G\right)$ corresponding to a nonzero eigenvalue, then ${\sum }_{i=1}^n{x}_i=0$.

Lemma 1

(Rayleigh’s Principal Theorem, p. 29, [15]). Let A be a symmetric real matrix and u any unit nonzero vector. Then ${\lambda }_1\left(A\right)\ge u^{T}Au$ with equality if and only if u is the eigenvector corresponding to ${\lambda }_1\left(A\right)$.

Lemma 2

(Courant-Weyl Inequality, p. 31, [15]). Let $A_1$ and $A_2$ be two symmetric real matrices of order n. Then

$${\lambda }_n\left(A_2\right)+{\lambda }_i\left(A_1\right)\le {\lambda }_i(A_1+A_2)\mathrm{for}1\le i\le n.$$

Lemma 3

(Interlacing Theorem, p. 30, [15]). Suppose A is a symmetric real matrix of order n and M a principal submatrix of A with order $s(\le n)$. Then

$$\begin{array}{c}\hfill {\lambda }_i\left(A\right)\ge {\lambda }_i\left(M\right),1\le i\le s.\end{array}$$

The next lemma follows from Lemma 3 immediately.

Lemma 4

(Proposition 2.11, [6]). Let G be an n-vertex graph and M a principal submatrix of $\mathcal{L}\left(G\right)$ with order $s\le n$. Then ${\lambda }_1\left(M\right)\le {\rho }_{\mathcal{L}}\left(G\right)$.

Lemma 5

(Theorem 3.5, [1]). Suppose $G+e_{uv}$ is the graph obtained from G by adding an edge $e_{uv}$ joining u and v. Then ${\rho }_{\mathcal{L}}\left(G\right)\ge {\rho }_{\mathcal{L}}(G+uv).$

3. The Lower Bound of the Distance Laplacian Spectral Radius of Graphs among ${\mathcal{B}}_{n,4}$

If $G\in {\mathcal{B}}_{n,d}$, then there exists a partition $\{V_0,V_1,\dots ,V_d\}$ of $V\left(G\right)$ such that $|V_0|=1$ and $d(u,v)=i$ for $u\in V_0$ and $v\in V_i$$(i=1,2,\dots ,d)$.

Lemma 6

(Lemma 2.1, [12]). Let $G\in {\mathcal{B}}_{n,d}$ with a vertex partition described as above. Then $G\left[V_i\right]$ induces an empty graph (i.e., containing no edge) for each $i\in \{0,1,\dots ,d\}$.

Lemma 7.

Let $d\ge 3$ and $G\in {\mathcal{B}}_{n,d}$. If $d(G+e)<d$ when any edge e is added to G, then $|V_d|=1$ and the induced subgraph $G[V_{i-1}\cup V_i](i=1,2,\dots ,d)$ is a complete bipartite graph.

Proof. 

From Lemma 6, it is clear that $G[V_{i-1}\cup V_i](i=1,2,\dots ,d)$ is a complete bipartite graph. Moreover, let $u\in V_d$ and $v\in V_{d-3}$. Assume, on the contrary, that $|V_d|\ge 2$, then the graph $G+e_{uv}\in {\mathcal{B}}_{n,d}$, a contradiction. □

Remark 1.

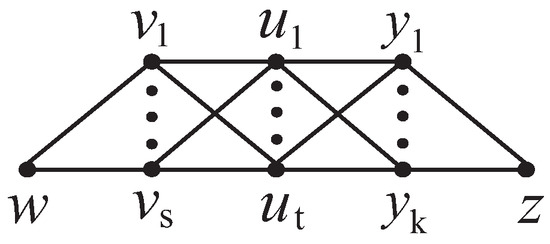
Denote a subset of ${\mathcal{B}}_{n,d}$ by $\widetilde{{\mathcal{B}}_{n,d}}$, consisting of all the graphs satisfying Lemma 7. For instance, if $G\in \widetilde{{\mathcal{B}}_{n,4}}$, then G is of the form shown in Figure 1. Then the partition of $V\left(G\right)$ can be written as $V_0=\left\{w\right\}$, $V_1=\{v_1,\dots ,v_s\}$, $V_2=\{u_1,\dots ,u_t\}$, $V_3=\{y_1,\dots ,y_k\}$ and $V_4=\left\{z\right\}$, where $s+t+k+2=n$ and $s,t,k\ge 1$.

Figure 1. A graph $G\in \widetilde{{\mathcal{B}}_{n,4}}$.

Before giving the main conclusion of this section, we first investigate the properties of the eigenvector corresponding to ${\rho }_{\mathcal{L}}\left(G\right)$ for $G\in \widetilde{{\mathcal{B}}_{n,4}}$.

Let $G\in \widetilde{{\mathcal{B}}_{n,4}}$ and the partition of $V\left(G\right)$ be arranged as in Remark 1. Without loss of generality, suppose $|V_3|\ge |V_1|\ge 1$ (i.e., $k\ge s\ge 1$).

Lemma 8.

Let the eigenvector corresponding to ${\rho }_{\mathcal{L}}\left(G\right)$ be x. Then

$$\left\{\begin{array}{c}x\left(v_i\right)=x\left(v_j\right)(1\le i,j\le s),\hfill \\ x\left(u_i\right)=x\left(u_j\right)(1\le i,j\le t),\hfill \\ x\left(y_i\right)=x\left(y_j\right)(1\le i,j\le k).\hfill \end{array}\right.$$

Proof. 

Since the proofs of the three results are parallel, here we only give the first one. As the vertices of $V_1$ are twin points (if $s>1$), $d(v,v_i)=d(v,v_j)$ for each $v\in V\left(G\right)\backslash \{v_i,v_j\}$, and thus $Tr\left(v_i\right)=Tr\left(v_j\right)=2s+t+2k+2$. Considering the characteristic equations indexed by $v_i$ and $v_j$, it is obtained that

$$\left\{\begin{array}{c}{\rho }_{\mathcal{L}}\left(G\right)·x\left(v_i\right)=\sum _{v\in V\left(G\right)}d(v_i,v)(x\left(v_i\right)-x\left(v\right))\hfill \\ {\rho }_{\mathcal{L}}\left(G\right)·x\left(v_j\right)=\sum _{v\in V\left(G\right)}d(v_j,v)(x\left(v_j\right)-x\left(v\right)).\hfill \end{array}\right.$$

Then it follows that ${\rho }_{\mathcal{L}}\left(G\right)·(x\left(v_i\right)-x\left(v_j\right))=(Tr\left(v_i\right)+2)(x\left(v_i\right)-x\left(v_j\right))$. From Lemma 4, we easily obtain

$$\begin{array}{ccc}\hfill {\rho }_{\mathcal{L}}\left(G\right)& \ge & T{r}_{max}=Tr\left(w\right)=s+2t+3k+4\hfill \\ \hfill & >& 2s+t+2k+4=Tr\left(v_i\right)+2.\hfill \end{array}$$

Thus, $x\left(v_i\right)=x\left(v_j\right)$ follows. □

For the eigenvector x in Lemma 8, suppose $x\left(w\right)=x_0$, $x\left(v_i\right)=x_1(1\le i\le s)$, $x\left(u_i\right)=x_2(1\le i\le t)$, $x\left(y_i\right)=x_3(1\le i\le k)$ and $x\left(z\right)=x_4$. Then x can be written as

$$x={(x_0,\underset{s}{\underbrace{x_1,\dots ,x_1}},\underset{t}{\underbrace{x_2,\dots ,x_2}},\underset{k}{\underbrace{x_3,\dots ,x_3}},x_4)}^T.$$

Lemma 9.

Let x be as just described. If $|V_1|=|V_3|$ (i.e., $s=k$), then

$$\left\{\begin{array}{c}{x}_0=-x_4\ne 0,\hfill \\ x_1=-x_3\ne 0,\hfill \\ x_2=0.\hfill \end{array}\right.$$

Proof. 

Applying Lemma 8, the characteristic equation $\mathcal{L}\left(G\right)·x={\rho }_{\mathcal{L}}\left(G\right)·x$ can be simplified in the conventional form as follows:

$$\left\{\begin{array}{c}{m}_0·x_0-s·x_1-2t·x_2-3k·x_3-4x_4={\rho }_{\mathcal{L}}\left(G\right)·x_0\hfill \\ -x_0+m_1·x_1-t·x_2-2k·x_3-3x_4={\rho }_{\mathcal{L}}\left(G\right)·x_1\hfill \\ -2x_0-s·x_1+m_2·x_2-k·x_3-2x_4={\rho }_{\mathcal{L}}\left(G\right)·x_2\hfill \\ -3x_0-2s·x_1-t·x_2+m_3·x_3-x_4={\rho }_{\mathcal{L}}\left(G\right)·x_3\hfill \\ -4x_0-3s·x_1-2t·x_2-k·x_3+m_4·x_4={\rho }_{\mathcal{L}}\left(G\right)·x_4,\hfill \end{array}\right.$$

(1)

where $m_0=Tr\left(w\right),m_1=Tr\left(v_i\right)-2(s-1),m_2=Tr\left(u_i\right)-2(t-1),m_3=Tr\left(y_i\right)-2(k-1)$ and $m_4=Tr\left(z\right)$.

The sum of the first equality and the fifth one gives

$$(n+t+2k+2)x_0-4(x_0+s{x}_1+t{x}_2+k{x}_3+x_4)+(n+t+2s+2)x_4={\rho }_{\mathcal{L}}\left(G\right)·(x_0+x_4).$$

(2)

Since $s=k$ and $x_0+s{x}_1+t{x}_2+k{x}_3+x_4=0$, we have

$$2n(x_0+x_4)={\rho }_{\mathcal{L}}\left(G\right)·(x_0+x_4).$$

(3)

Take a $2\times 2$ principal submatrix M of $\mathcal{L}\left(G\right)$, where $M=\left(\begin{array}{cc}Tr\left(w\right)& -4\\ -4& Tr\left(z\right)\end{array}\right).$ Note that $Tr\left(w\right)=Tr\left(z\right)=2n$ for $s=k$. Then, applying Lemma 4,

$${\rho }_{\mathcal{L}}\left(G\right)\ge {\lambda }_1\left(M\right)=Tr\left(w\right)+4=2n+4.$$

Thus, we obtain $x_0+x_4=0$, $i.e.,x_0=-x_4$ from (3). Similarly, from the second and the fourth equalities in (1), it follows that

$$-2(x_0+x_4)+(n+2)(x_1+x_3)={\rho }_{\mathcal{L}}\left(G\right)·(x_1+x_3).$$

Since $x_0+x_4=0$ and ${\rho }_{\mathcal{L}}\left(G\right)\ge 2n+4>n+2$, $x_1+x_3=0$, $i.e.,x_1=-x_3$. The fourth equality in (1) minus the second one indicates that

$$\begin{array}{ccc}\hfill 2(x_4-x_0)& =& [{\rho }_{\mathcal{L}}\left(G\right)-(2s+t+2k+4)](x_3-x_1)\hfill \\ \hfill & =& ({\rho }_{\mathcal{L}}\left(G\right)-2n+t)(x_3-x_1).\hfill \end{array}$$

(4)

If $x_0=0$, then $x_4=-x_0=0$. Further, from (4), it follows that $x_1=-x_3=0$ (note that ${\rho }_{\mathcal{L}}\left(G\right)\ge 2n+4$). Recalling that $x_0+s{x}_1+t{x}_2+k{x}_3+x_4=0$, we know $x_2=0$, and thus x is a zero vector, a contradiction. Hence, $x_0=-x_4\ne 0$. Similarly, $x_1=-x_3\ne 0$, which implies $x_2=0$. The proof is complete. □

For convenience, denote the graph $G\in \widetilde{{\mathcal{B}}_{n,4}}$ by $G(1,s,t,k,1)$ with vertex partition shown in Remark 1. We next determine the unique extremal graph minimizing the distance Laplacian spectral radius among $\widetilde{{\mathcal{B}}_{n,4}}$.

Theorem 1.

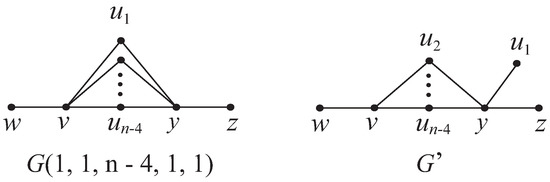
The graph $G(1,1,n-4,1,1)$ in Figure 2 is the unique graph with minimum distance Laplacian spectral radius among $\widetilde{{\mathcal{B}}_{n,4}}$.

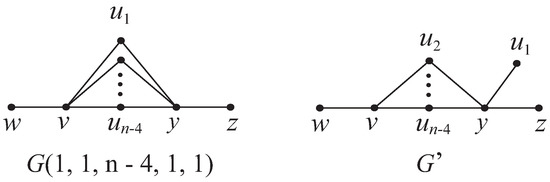
Figure 2. The graph $G(1,1,n-4,1,1)\in \widetilde{{\mathcal{B}}_{n,4}}$ and graph $G^{\prime }$.

Proof. 

Let $G_0=G(1,s,t,k,1)\in \widetilde{{\mathcal{B}}_{n,4}}$ with $s+t+k+2=n$ and $s,t,k\ge 1$. Without loss of generality, assume that $s\le k$. We proceed by proving the following three claims, which will imply the conclusion.

Claim 1. If $s\ge 2$ in graph $G_0$, then let $G_1=G(1,s-1,t,k+1,1)$. We claim that ${\rho }_{\mathcal{L}}\left(G_0\right)<{\rho }_{\mathcal{L}}\left(G_1\right)$.

In graph $G_0$, let $V\left(G_0\right)=\{V_0,\dots ,V_4\}$ and $V_i$ be expressed as that in Remark 1. Then we easily obtain

$$\left\{\begin{array}{cc}Tr\left(w\right)=s+2t+3k+4,\hfill & Tr\left(v_i\right)=Tr\left(y_i\right)=2s+t+2k+2,\hfill \\ Tr\left(u_i\right)=s+2t+k+2,\hfill & Tr\left(z\right)=3s+2t+k+4,\hfill \end{array}\right.$$

(5)

and the distance Laplacian matrix of $G_0$ is

$$\mathcal{L}\left(G_0\right)=\left(\begin{array}{ccccc}Tr\left(w\right)& -J_{1\times s}& -2J_{1\times t}& -3J_{1\times k}& -4\\ -J_{s\times 1}& (Tr\left(v_i\right)+2)I_s-2J_s& -J_{s\times t}& -2J_{s\times k}& -3J_{s\times 1}\\ -2J_{t\times 1}& -J_{t\times s}& (Tr\left(u_i\right)+2)I_t-2J_t& -J_{t\times k}& -2J_{t\times 1}\\ -3J_{k\times 1}& -2J_{k\times s}& -J_{k\times t}& (Tr\left(y_i\right)+2)I_k-2J_k& -J_{k\times 1}\\ -4& -3J_{1\times s}& -2J_{1\times t}& -J_{1\times k}& Tr\left(z\right)\end{array}\right).$$

Further, we have

$$|\lambda I_n-\mathcal{L}\left(G_0\right)|={(\lambda -Tr\left(v_i\right)-2)}^{s-1}{(\lambda -Tr\left(u_i\right)-2)}^{t-1}{(\lambda -Tr\left(y_i\right)-2)}^{k-1}·|\lambda I_5-R\left(G_0\right)|,$$

(6)

where

$$R\left(G_0\right)=\left(\begin{array}{ccccc}Tr\left(w\right)& -s& -2t& -3k& -4\\ -1& Tr\left(v_i\right)-2(s-1)& -t& -2k& -3\\ -2& -s& Tr\left(u_i\right)-2(t-1)& -k& -2\\ -3& -2s& -t& Tr\left(y_i\right)-2(k-1)& -1\\ -4& -3s& -2t& -k& Tr\left(z\right)\end{array}\right).$$

(7)

From the above, we say that the largest eigenvalue of $R\left(G_0\right)$ is the spectral radius of $G_0$. In fact, ${\lambda }_1\left(R\left(G_0\right)\right)\ge Tr\left(w\right)$ from Lemma 3, and $Tr\left(v_i\right)+2$, $Tr\left(y_i\right)+2$ and $Tr\left(u_i\right)+2$ are the eigenvalues of $\mathcal{L}\left(G_0\right)$ apart from those of $R\left(G_0\right)$ from (6). Furthermore, $Tr\left(w\right)>Tr\left(v_i\right)+2=Tr\left(y_i\right)+2$ and $Tr\left(w\right)>Tr\left(u_i\right)+2$ by (5) clearly. Thus, ${\lambda }_1\left(R\left(G_0\right)\right)={\rho }_{\mathcal{L}}\left(G_0\right)$ holds.

For graph $G_1$, we obtain the matrices $\mathcal{L}\left(G_1\right)$ and $R\left(G_1\right)$ by substituting $s-1$ and $k+1$ for s and k in $\mathcal{L}\left(G_0\right)$ and $R\left(G_0\right)$, respectively. Analogously, we have ${\lambda }_1\left(R\left(G_1\right)\right)={\rho }_{\mathcal{L}}\left(G_1\right)$. Denote the characteristic polynomials of $R\left(G_0\right)$ and $R\left(G_1\right)$ by ${\psi }_0\left(\lambda \right)$ and ${\psi }_1\left(\lambda \right)$, respectively. Next, we are aimed at proving

$${\psi }_1\left({\rho }_{\mathcal{L}}\left(G_0\right)\right)<0.$$

(8)

By using MATLAB, we obtain

$${\psi }_1\left(\lambda \right)-{\psi }_0\left(\lambda \right)=4(s-k-1)\lambda ({\lambda }^2-s\lambda -k\lambda -2n\lambda -4\lambda +6n+sn+kn+n^2).$$

(9)

Let $g\left(\lambda \right)=\lambda ({\lambda }^2-s\lambda -k\lambda -2n\lambda -4\lambda +6n+sn+kn+n^2).$ Then the derivative of $g\left(\lambda \right)$ is

$$g^{\prime }\left(\lambda \right)=3{\lambda }^2-(2s+2k+4n+8)\lambda +n^2+sn+kn+6n$$

with symmetry axis $\tilde{\lambda }=\frac{2n+s+k+4}{3}$. Since $s\le k$, $T{r}_{max}=Tr\left(w\right)=2n-s+k$ in graph $G_0$, and thus ${\rho }_{\mathcal{L}}\left(G_0\right)\ge T{r}_{max}=2n-s+k$ from Lemma 4. By simple calculation, we obtain $\tilde{\lambda }<2n-s+k$, and since $n\ge s+k+3$, we have

$$g^{\prime }(2n-s+k)=5n^2+(5k-11s-10)n+5s^2-6sk+8s+k^2-8k>0.$$

We now say that $g\left(\lambda \right)$ is strictly increasing for $\lambda \ge 2n-s+k$. Moreover, from $n\ge s+k+3$, it follows that

$$g(2n-s+k)=(2n-s+k)(n^2+kn-3sn-2n+4s-4k-2sk+2s^2)>0.$$

Note that $s-k-1<0$ in (9). Then we have

$$\begin{array}{ccc}\hfill {\psi }_1\left({\rho }_{\mathcal{L}}\left(G_0\right)\right)& =& {\psi }_1\left({\rho }_{\mathcal{L}}\left(G_0\right)\right)-{\psi }_0\left({\rho }_{\mathcal{L}}\left(G_0\right)\right)<{\psi }_1(2n-s+k)-{\psi }_0(2n-s+k)\hfill \\ \hfill & =& 4(s-k-1)·g(2n-s+k)<0,\hfill \end{array}$$

which establishes (8).

Applying (8), we can easily prove that ${\rho }_{\mathcal{L}}\left(G_0\right)<{\rho }_{\mathcal{L}}\left(G_1\right)$. Assume on the contrary that ${\rho }_{\mathcal{L}}\left(G_0\right)>{\rho }_{\mathcal{L}}\left(G_1\right)$ (noting that ${\rho }_{\mathcal{L}}\left(G_0\right)\ne {\rho }_{\mathcal{L}}\left(G_1\right)$ since ${\psi }_1\left({\rho }_{\mathcal{L}}\left(G_0\right)\right)<0$ and ${\psi }_1\left({\rho }_{\mathcal{L}}\left(G_1\right)\right)=0$). Observing that ${\psi }_1\left(\lambda \right)$ tends to infinity when $\lambda$ tends to infinity (as the leading coefficient of ${\psi }_1\left(\lambda \right)$ is 1), we can find a sufficiently large $q>{\rho }_{\mathcal{L}}\left(G_0\right)$ such that ${\psi }_1\left(q\right)>0$. As ${\psi }_1\left(\lambda \right)$ is a continuous function, from ${\psi }_1\left({\rho }_{\mathcal{L}}\left(G_0\right)\right)<0$ and ${\psi }_1\left(q\right)>0$, it follows that ${\psi }_1\left(p\right)=0$ for a positive number p between ${\rho }_{\mathcal{L}}\left(G_0\right)$ and q, which is a contradiction to the fact that ${\rho }_{\mathcal{L}}\left(G_1\right)$ is the largest root of ${\psi }_1\left(\lambda \right)=0$. Therefore, ${\rho }_{\mathcal{L}}\left(G_0\right)<{\rho }_{\mathcal{L}}\left(G_1\right)$.

Claim 2. Assume $G_2=G(1,s-1,t+2,k-1,1)$, where $k\ge s\ge 2$ and $t\ge 1$. Then we claim that ${\rho }_{\mathcal{L}}\left(G_0\right)>{\rho }_{\mathcal{L}}\left(G_2\right)$.

Let the unit eigenvector corresponding to ${\rho }_{\mathcal{L}}\left(G_2\right)$ be

$$x={(x_0,\underset{s-1}{\underbrace{x_1,\dots ,x_1}},\underset{t+2}{\underbrace{x_2,\dots ,x_2}},\underset{k-1}{\underbrace{x_3,\dots ,x_3}},x_4)}^T.$$

By Rayleigh’s principle,

$$\begin{array}{ccc}\hfill {\rho }_{\mathcal{L}}\left(G_0\right)-{\rho }_{\mathcal{L}}\left(G_2\right)& \ge & x^T·(\mathcal{L}\left(G_0\right)-\mathcal{L}\left(G_2\right))·x\hfill \\ \hfill & =& {\displaystyle \sum _{\{u,v\}\subseteq V\left(G_0\right)}}(d_{G_0}(u,v)-d_{G_2}(u,v)){(x\left(u\right)-x\left(v\right))}^2\hfill \\ \hfill & =& 2(s-1){(x_1-x_2)}^2+2(k-1){(x_3-x_2)}^2\ge 0.\hfill \end{array}$$

(10)

Next, we show that ${\rho }_{\mathcal{L}}\left(G_0\right)-{\rho }_{\mathcal{L}}\left(G_2\right)>0$. First, if $s=k$, then from Lemma 9, it follows that $x_1=-x_3\ne 0$ and $x_2=0$, and thus

$${\rho }_{\mathcal{L}}\left(G_0\right)-{\rho }_{\mathcal{L}}\left(G_2\right)\ge 4(s-1)x_1^2>0.$$

On the other hand, suppose $s<k$ and $2(s-1){(x_1-x_2)}^2+2(k-1){(x_3-x_2)}^2=0$ in (10). Then $x_1=x_2=x_3$. Substitute $t+2$ for t in (4), and then $x_0=x_4$ follows by applying $x_1=x_3$. In addition, by replacing s, k and t with $s-1$, $k-1$ and $t+2$ in (2), respectively, it gives

$${\rho }_{\mathcal{L}}\left(G_2\right)·x_0=2n·x_0,$$

and hence $x_0=0$ for the reason that ${\rho }_{\mathcal{L}}\left(G_2\right)\ge T{r}_{G_2}\left(w\right)=2n+k-s>2n.$ Recalling that $x_0+(s-1)x_1+(t+2)x_2+(k-1)x_3+x_4=0$, we have $x_1=x_2=x_3=0$, and then eigenvector x is the zero vector, a contradiction. Hence, if $s<k$, then

$$2(s-1){(x_1-x_2)}^2+2(k-1){(x_3-x_2)}^2>0.$$

In summary, ${\rho }_{\mathcal{L}}\left(G_0\right)-{\rho }_{\mathcal{L}}\left(G_2\right)>0$ holds.

Claim 3. If $s=k-1(\ge 1)$ in graph $G_0$, then let $G_3=G(1,s,t+1,k-1,1)$. We claim that ${\rho }_{\mathcal{L}}\left(G_0\right)>{\rho }_{\mathcal{L}}\left(G_3\right)$.

Let the unit eigenvector corresponding to ${\rho }_{\mathcal{L}}\left(G_3\right)$ be

$$x={(x_0,\underset{s}{\underbrace{x_1,\dots ,x_1}},\underset{t+1}{\underbrace{x_2,\dots ,x_2}},\underset{k-1=s}{\underbrace{x_3,\dots ,x_3}},x_4)}^T.$$

Then by Rayleigh’s principle and Lemma 9,

$$\begin{array}{ccc}\hfill {\rho }_{\mathcal{L}}\left(G\right)-{\rho }_{\mathcal{L}}\left(G_3\right)& \ge & x^T·(\mathcal{L}\left(G\right)-\mathcal{L}\left(G_3\right))·x\hfill \\ \hfill & =& {\displaystyle \sum _{\{u,v\}\subseteq V\left(G\right)}}(d_G(u,v)-d_{G_3}(u,v)){(x\left(u\right)-x\left(v\right))}^2\hfill \\ \hfill & =& {(x_0-x_2)}^2+s(x_1-x_2)-t{(x_2-x_2)}^2+s{(x_2-x_3)}^2-{(x_2-x_4)}^2\hfill \\ \hfill & =& 2s·x_1^2>0.\hfill \end{array}$$

Now we are in a position to complete the proof of the theorem.

For graph $G_0=G(1,s,t,k,1)\in \widetilde{{\mathcal{B}}_{n,4}}$, suppose $k\ge s$. If $k\ge 2$ and $(k-s)\equiv 0\left(mod2\right)$, then by Claim 1,

$${\rho }_{\mathcal{L}}\left(G_0\right)\ge {\rho }_{\mathcal{L}}\left(G(1,s+\frac{k-s}{2},t,k-\frac{k-s}{2},1)\right)={\rho }_{\mathcal{L}}\left(G(1,\frac{s+k}{2},t,\frac{s+k}{2},1)\right)$$

with equality if and only if $s=k$. Furthermore, from Claim 2, we have

$${\rho }_{\mathcal{L}}\left(G(1,\frac{s+k}{2},t,\frac{s+k}{2},1)\right)>{\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right).$$

On the other side, if $k\ge 3$ and $(k-s)\equiv 1\left(mod2\right)$, then by Claim 1,

$${\rho }_{\mathcal{L}}\left(G_0\right)\ge {\rho }_{\mathcal{L}}\left(G(1,s+\frac{k-s-1}{2},t,k-\frac{k-s-1}{2},1)\right)={\rho }_{\mathcal{L}}\left(G(1,\frac{s+k-1}{2},t,\frac{s+k+1}{2},1)\right),$$

with equality if and only if $k-s=1$. Moreover, from Claim 3,

$${\rho }_{\mathcal{L}}\left(G(1,\frac{s+k-1}{2},t,\frac{s+k+1}{2},1)\right)>{\rho }_{\mathcal{L}}\left(G(1,\frac{s+k-1}{2},t+1,\frac{s+k-1}{2},1)\right).$$

Finally, from Claim 2, it follows that

$${\rho }_{\mathcal{L}}\left(G(1,\frac{s+k-1}{2},t+1,\frac{s+k-1}{2},1)\right)>{\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right).$$

For the case of $s=1$ and $k=2$, from Claim 3, it is straightforward that

$${\rho }_{\mathcal{L}}\left(G(1,1,n-5,2,1)\right)>{\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right).$$

This completes the proof. □

From Theorem 1 and Lemma 5, we indicate that if $G\in {\mathcal{B}}_{n,d}$ is not a spanning subgraph of $G(1,1,n-4,1,1)$, then ${\rho }_{\mathcal{L}}\left(G\right)>{\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right)$. In addition, if $s=k=1$ and $t=n-4$ in (7), then we obtain ${\lambda }_1\left(R_0\right)=4+\frac{1}{2}(3n+\sqrt{n^2+16})$ by using MATLAB, i.e.,

$${\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right)=4+\frac{1}{2}(3n+\sqrt{n^2+16}).$$

Thus, we have the following theorem.

Theorem 2.

Let $G\in {\mathcal{B}}_{n,d}$. Then ${\rho }_{\mathcal{L}}\left(G\right)\ge 4+\frac{1}{2}(3n+\sqrt{n^2+16})$ with equality if and only if $G=G(1,1,n-4,1,1)$.

Proof. 

Denote the graph $G(1,1,n-4,1,1)-e_{v{u}_1}$ by $G^{\prime }$ (see Figure 2). First, we show that ${\rho }_{\mathcal{L}}\left(G^{\prime }\right)>{\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right)$. Take a $2\times 2$ principal submatrix $M=\left(\begin{array}{cc}Tr\left(w\right)& -4\\ -4& Tr\left(z\right)\end{array}\right)=\left(\begin{array}{cc}2n+2& -4\\ -4& 2n\end{array}\right)$ from $\mathcal{L}\left(G^{\prime }\right)$. By simple calculation, ${\lambda }_1\left(M\right)>2n+5>4+\frac{1}{2}(3n+\sqrt{n^2+16})$. From Lemma 4, it follows that

$${\rho }_{\mathcal{L}}\left(G^{\prime }\right)\ge {\lambda }_1\left(M\right)>2n+5>4+\frac{1}{2}(3n+\sqrt{n^2+16})={\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right).$$

Thus, we say that for any spanning subgraph $H\ne G(1,1,n-4,1,1)$ of $G(1,1,n-4,1,1)$, ${\rho }_{\mathcal{L}}\left(H\right)>{\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right)$ from Lemma 5.

Hence, now, it is clear from Theorem 1 and the above result that for any graph $G\in {\mathcal{B}}_{n,d}$,

$${\rho }_{\mathcal{L}}\left(G\right)\ge {\rho }_{\mathcal{L}}\left(G(1,1,n-4,1,1)\right)=4+\frac{1}{2}(3n+\sqrt{n^2+16})$$

with equality if and only if $G=G(1,1,n-4,1,1)$. □

4. Conclusions

In this paper, a lower bound of the distance Laplacian spectral radius of the n-vertex bipartite graphs with diameter 4 is obtained. The method used here is helpful for solving the general case and we conjecture that the graph $G(1,\dots ,1,n-d,1,\dots ,1)$ is the unique one minimizing the distance Laplacian spectral radius among n-vertex bipartite graphs with even diameter $d\ge 4$.