On the Number of Finite Fuzzy Subsets with Analysis of Integer Sequences

Abstract

This paper solves the issues of determining the number F_n of fuzzy subsets of a nonempty finite set $X$. To solve this, this paper incorporates the equivalence relation on the collection of all fuzzy subsets of $X$. We derive two closed explicit formulas for $F_n$, which is the sum of a finite series in the product of binomial numbers or the sum of $k$-level fuzzy subsets $F_{n,k}$ by introducing a classification technique. Moreover, these explicit formulas enable us to find the number of the maximal chains of crisp subsets of $X.$ Further, this paper presents some elementary properties of $F_{n,k}$ and $F_n$.

1. Introduction

The counting problem for the number of subsets in an ordinary finite set is simple. The challenges only occur when that set is infinite. By introducing the concept of aleph and aleph-null, Georg Cantor solved the problem of infiniteness [1,2]. However, in a fuzzy environment, the problem on counting becomes complicated due to the lack of sharp boundaries. This paper considers the counting problem in the case of fuzzy subsets, which becomes more complicated even if the set is finite. This is considered as a challenging problem due to the uncertainty in the membership values. Therefore, this paper tries to tackle the counting problems in the theory of fuzzy subsets under an equivalence relation.

Consider the sequence of numbers $1, 3, 11, 51, 299, 2163, 18,731, \cdots$, where the elements of this sequence correspond to the number of chains in the power set of $n$-set [3,4], where $n=0,1,2,3,4,5,6,\cdots$. This sequence is assigned with the identity number A007047 in the OEIS (On-Line Encyclopedia of Integer Sequences) [5]. The sequence A007047 is one of the most fundamental integer sequences in mathematics that plays a vital role in the area of combinatorics. It also has various interpretations that are connected to the familiar combinatorial integer sequences (see [4,6,7,8]). Essentially, Nelsen and Schmidt [3] introduced the family of exponential generating functions $P\left(x,t\right)=\frac{e^{tx}}{2-e^x}$, where $t=0, 1, 2, \cdots$. The generating functions for $t=0$ and $t=2$ have been shown to be the number of preferential arrangements of $X$ and the number of chains in the power set of $X$, respectively. Later, the family of generating functions $P\left(x,t\right)$ was briefly discussed for all non-negative integer values of $t$ in [4,6,9].

For readers, let us discuss an example; take $n=2$ and let the set $X_2=\left\{1,2\right\}$, the power set of $X_2$ is $\mathcal{P}\left(X_2\right)=\left\{\varnothing ,\left\{1\right\},\left\{2\right\}, \left\{1,2\right\}\right\}$. The number of chains in $\mathcal{P}\left(X_2\right)$ ordered by set inclusion is $\left|\varnothing ,\left\{1\right\},\left\{2\right\}, \left\{1,2\right\}, \varnothing \subset \left\{1\right\},\varnothing \subset \left\{2\right\},\varnothing \subset \left\{1,2\right\},\left\{1\right\}\subset \left\{1,2\right\},\left\{2\right\}\subset \left\{1,2\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,2\right\}\right|=11$. In [10], it is shown that there exists a bijection between the collection of all equivalence classes of fuzzy subsets of nonempty finite set $X$ and the collection of all chains in the power set of $X$. The fuzzy subsets have been used to characterize fuzzy matrices of a finite order [11,12], fuzzy subgroups (fuzzy normal subgroups) of a finite group [13,14,15,16,17,18,19,20].

In [21], Murali and Makamba determined the $n$-th term $F_n$ of the sequence A007047 by enumerating nonequivalent classes of fuzzy subsets and using the concept of flags, keychains, and pinned flags. Later, the recurrence relations satisfied by $F_n$, a closed formula, and a generating function for $F_n$ were derived by using ideas of $k$-level fuzzy subsets and Stirling numbers [10]. Since there can be many methods to solve a problem with each approach highlighting a different aspect of the problem, the issue of counting provides that opportunity to demonstrate the varieties of techniques from combinatorics. As a consequence, this paper provides more than one line of approach to most of our results. In this paper, we focus on the problem of computing the number of fuzzy subsets of $X$ from a different perspective using binomial numbers.

The paper first derives the formulas for the number of distinct unrooted and rooted $k$-level fuzzy subsets $F_{n,k},F_{n,k}^{\varnothing },$ and $F_{n,k}^X$. Then, it deduces the number of maximal chains of crisp subsets. Further, the total number of unrooted and rooted distinct fuzzy subsets of $X$ is also obtained. Throughout this paper, we mainly focus on the combinatorial connections between the existing and the obtained integer sequences in the OEIS.

The outline of this paper is organized as follows: Section 2 provides some known definitions, results, and existing works on the counting problem for the number of fuzzy subsets. Section 3 proposes the methods to classify fuzzy subsets of a finite set $X$ by a natural equivalence relation and the idea of $k$-level fuzzy subsets. The number of distinct unrooted and rooted $k$-level fuzzy subsets and the total number of distinct unrooted and rooted fuzzy subsets of any arbitrary finite set $X$ are determined using a new combinatorial technique in Section 4. Lastly, Section 5 contains the conclusions of the paper.

2. Preliminaries

In this section, we provided all necessary definitions and results to count the number of fuzzy subsets (see [22,23]).

2.1. Fuzzy Subsets

Throughout this paper, we assumed $X$ to be a nonempty finite set consisting of $n$ elements, where $n$ is a nonzero positive integer. A fuzzy subset $\tilde{A}$ of the set $X$ is defined by a membership function $\tilde{A}:X\to I,$where $I=\left[0, 1\right].$The set of all fuzzy subsets of $X$ is denoted by $I^X$, fuzzy subsets by $\tilde{A},\tilde{B},\tilde{C},$ etc., and its membership values by $\alpha ,\beta ,\gamma ,$ etc. The union $\left({\displaystyle \cup }\right)$ and intersection $\left({\displaystyle \cap }\right)$ of two fuzzy subsets were defined by using supremum and infimum pointwise, respectively, and the complementation ${(}^c)$ of a fuzzy subset by $1-\tilde{A}$ operator pointwise [22,24]. A fuzzy subset $\tilde{A}$ was stated to be contained in a fuzzy subset $\tilde{B}$, denoted by $\tilde{A}\subseteq \tilde{B},$ if $\tilde{A}\left(x\right)\le \tilde{B}\left(x\right),\forall x\in X$. A fuzzy subset $\tilde{A}$ was stated to be contained in a fuzzy subset $\tilde{B}$, denoted by $\tilde{A}\subseteq \tilde{B},$ if $\tilde{A}\left(x\right)\le \tilde{B}\left(x\right),\forall x\in X$. Through the support and core of a fuzzy subset of $\tilde{A}$, we mean the crisp subsets $Supp \left(\tilde{A}\right)=\{x\in X:\tilde{A}\left(x\right)>0\}$ and $Core \left(\tilde{A}\right)=\left\{x\in X:\tilde{A}\left(x\right)=0\right\}$, respectively. When stating the image of a fuzzy set $\tilde{A}$, we mean the set of membership values of $\tilde{A}$ denoted by$Im(\tilde{A})=\tilde{A}\left(X\right)$. Through an $\alpha$-cut [22,23] of a fuzzy subset $\tilde{A}$ for $\alpha$ belongs to $I,$ we had a crisp subset ${\tilde{A}}^{\alpha }=\left\{x\in X:\tilde{A}\left(x\right)\ge \alpha \right\}$ of $X$. This is called the weak $\alpha$-cuts. By strong $\alpha$-cuts, we mean ${\tilde{A}}_{\alpha }=\{x\in X:\tilde{A}\left(x\right)>\alpha \}$. In this paper, we were always dealt with weak $\alpha$-cuts. It was easy to verify that for $0\le \alpha \le \beta \le 1$, we had ${\tilde{A}}^{\beta }\subseteq {\tilde{A}}^{\alpha }$. For any arbitrary fuzzy subset $\tilde{A}$, we has a result as follows.

Proposition 1

([10], Proposition 1). For any fuzzy subset $\tilde{A},\tilde{A}=\underset{\alpha }{{\displaystyle \cup }}\left\{\alpha {\chi }_{{\tilde{A}}^{\alpha }}:0\le \alpha \le 1\right\}$

, where ${\chi }_{{\tilde{A}}^{\alpha }}$ denotes the characteristic function of the crisp subset ${\tilde{A}}^{\alpha }$.

2.2. Tool for Counting Methods

This subsection presents some known definitions and results in the area of combinatorics to deal with our main results.

Definition 1

([25]). The number of $m$-element subsets of an $n$-element set (that is, the number of ways we could select $m$-distinct elements from an $n$-element set) is called a binomial number or a binomial coefficient, denoted by $\left(\begin{array}{c}n\\ m\end{array}\right)$ (an alternative notation, $C\left(n,m\right)$).

We displayed some of its basic properties as follows:

• $\left(\begin{array}{c}n\\ 0\end{array}\right)=\left(\begin{array}{c}n\\ n\end{array}\right)=1$,
• $\left(\begin{array}{c}n\\ 1\end{array}\right)=\left(\begin{array}{c}n\\ n-1\end{array}\right)=n$,
• $\left(\begin{array}{c}n\\ m\end{array}\right)=\left(\begin{array}{c}n\\ n-m\end{array}\right)$, $0\le m\le n$ and
• $\left(\begin{array}{c}n\\ m\end{array}\right)=\left(\begin{array}{c}n-1\\ m\end{array}\right)+\left(\begin{array}{c}n-1\\ m-1\end{array}\right),1\le m<n$.

The fourth item is the most important recurrence relation for binomial numbers.

We provided a familiar formula for binomial numbers as follows (by definition, $0!=1$) (See Table 1):

Table 1. Binomial numbers, $\left(\begin{array}{c}n\\ m\end{array}\right); 0\le m\le n,$ for $n=0,1,\cdots ,9$.

	$\left(\begin{array}{c}\mathit{n}\\ \mathit{m}\end{array}\right); \mathit{m}$
$n$	0	1	2	3	4	5	6	7	8	9	$F_{n,0}$
0	1										1
1	1	1									2
2	1	2	1								4
3	1	3	3	1							8
4	1	4	6	4	1						16
5	1	5	10	10	5	1					32
6	1	6	15	20	15	6	1				64
7	1	7	21	35	35	21	7	1			128
8	1	8	28	56	70	56	28	8	1		256
9	1	9	36	84	126	126	84	36	9	1	512

Lemma 1

([25,26]). For $n\ge m\ge 0,$

$$\left(\begin{array}{c}n\\ m\end{array}\right)=\frac{n!}{m!\left(n-m\right)!}$$

with the convention that $\left(\begin{array}{c}n\\ m\end{array}\right)=0,$ for any $m>n.$

Next, we provided a famous theorem, known as the Binomial Theorem.

Theorem 1

([26], Binomial Theorem). For any integer $n\ge 0,$

$${(a+b)}^n={\displaystyle \sum }_{m=0}^n\left(\begin{array}{c}n\\ m\end{array}\right)a^m{b}^{n-m}$$

The binomial numbers can be put into a triangular array, which is called Pascal′s triangle. Pascal′s triangle was assigned by A007318 in the OEIS.

										1
									1		1
								1		2		1
							1		3		3		1
						1		4		6		4		1
					1		5		10		10		5		1
				1		6		15		20		15		6		1
			1		7		21		35		35		21		7		1
		1		8		28		56		70		56		28		8		1
	1		9		36		84		126		126		84		36		9		1

The row sums of Pascal′s triangle provided the sequence:

1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16,384, 32,768, 65,536,$\cdots$.

The elements of this sequence represented the number of subsets of an $n$-set, $n\in {\mathbb{N}}^{*}=\mathbb{N}{\displaystyle \cup }\left\{0\right\}$. This sequence was also assigned by A000079 in the OEIS.

Remark 1.

The first ten diagonals of Pascal′s triangle provided the following sequences in the OEIS: A000012 (the all one′s sequence), A000027 (the natural numbers), A000217 ($\left(\begin{array}{c}n+1\\ 2\end{array}\right), n\in {\mathbb{N}}^{*}$), A000292$(\left(\begin{array}{c}n+2\\ 3\end{array}\right), n\in {\mathbb{N}}^{*})$, A000332$(\left(\begin{array}{c}n\\ 4\end{array}\right), n\in {\mathbb{N}}^{*})$, A000389$(\left(\begin{array}{c}n\\ 5\end{array}\right), n\in {\mathbb{N}}^{*})$, A000579$(\left(\begin{array}{c}n\\ 6\end{array}\right), n\in {\mathbb{N}}^{*})$, A000580$(\left(\begin{array}{c}n\\ 7\end{array}\right), n\in {\mathbb{N}}^{*})$, A000581$(\left(\begin{array}{c}n\\ 8\end{array}\right), n\in {\mathbb{N}}^{*})$, A000582$(\left(\begin{array}{c}n\\ 9\end{array}\right), n\in {\mathbb{N}}^{*})$, and A001287$(\left(\begin{array}{c}n\\ 10\end{array}\right), n\in {\mathbb{N}}^{*})$.

2.3. Existing Works on Fuzzy Subsets

This section discusses the work related to the counting of fuzzy subsets. For more concepts, the reader can refer to [27,28,29].

In [28,30], Murali and Makamba introduced an equivalence relation ($\cong$) on $I^X$ by defining $\tilde{A}\cong \tilde{B}$ if $\tilde{A}\left(x\right)>\tilde{A}\left(y\right)\iff \tilde{B}\left(x\right)>\tilde{B}\left(y\right),\tilde{A}\left(x\right)=0\iff \tilde{B}\left(x\right)=0$, and $\tilde{A}\left(x\right)=1\iff \tilde{B}\left(x\right)=1$ for all $x,y\in X$. This equivalence relation agreed with the equality of crisp subsets when the binary values $\left\{0,1\right\}$ were used.

A fuzzy subset was represented by a pinned flag $\left(\mathfrak{F},\ell \right)$ through $\alpha$-cuts, which was written as follows:

$$X_0^1\subset X_0^{{\lambda }_1}\subset X_0^{{\lambda }_2}\subset \cdots \subset X_0^{{\lambda }_n} : {\displaystyle \cup }\left\{{\lambda }_i{\chi }_{X_i} : 0\le i\le 1\right\}=\tilde{A},$$

where $\mathfrak{F}$ is a flag on $X$, that is a chain $X_0\subset X_1\subset X_2\subset \cdots \subset X_n=X$ called the maximal chain (flag) of crisp subsets of $X,$ and $\ell$ is a keychain from $I$, i.e., $1\ge {\lambda }_0\ge {\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n\ge 0$ [30,31].

Let $F_n$ denote the number of distinct fuzzy subsets of $X$ over $\cong$. Through the detailed study of pinned flags, an explicit formula of $F_n$ was attained by accumulating all integer partitions $\tau ⊢n$. That is, $\tau ⊢n$ means that τ is a partition of the integer $n$.

Theorem 2

([21]). For any non-negative integer $n$, the number of distinct fuzzy subsets of $X$ with n-elements was given by the equality:

$$F_n={\displaystyle \sum }_{\tau ⊢n}\frac{4\left(k_1+k_2+k_3+\cdots +k_n\right)!n!}{\left(k_1!k_2!k_3!\cdots k_n!\right)\left(k_1{!}^{k_1}{k}_2{!}^{k_2}{k}_3{!}^{k_3}\cdots k_n{!}^{k_n}\right)}-1,$$

where $\tau$ runs overall non-negative integer solutions of $k_1+2k_2+3k_3+\cdots +n{k}_n=n$.

The formula as mentioned above is called the factorial summation formula for $F_n$. In [10], the author also discussed some different methods of counting the number of fuzzy subsets. This section presents some of the main results to focus our concepts.

Proposition 2

([10], Recurrence Relation 3.4). For any natural number $n$,

$$F_{n+1}={\displaystyle \sum }_{r=0}^n\left(\begin{array}{c}n+1\\ r\end{array}\right)F_r+2^{n+1}$$

with $F_0=1$.

A closed-form of $F_n$ was expressed by the following theorem.

Theorem 3

([10], Theorem 3.5). For a positive integer $n$, the number of distinct fuzzy subsets of $X$ with $n$-elements was given by the equality:

$$F_n=4\left({\displaystyle \sum }_{j=0}^n{\displaystyle \sum }_{i=0}^j{(-1)}^{j-1}\right(\begin{array}{c}j\\ i\end{array}\left)i^n\right)-1$$

observing that $j=0$ did not impact upon counting in the summation.

The expression as the infinite series for $F_n$ was given below.

Theorem 4

([10], Theorem 3.7). For a natural number$n$, the number of fuzzy subsets of $X$ with $n$-elements was given by the equality:

$$F_n={\displaystyle \sum }_{r=2}^{\infty }{r}^n{2}^{\left(1-r\right)}$$

Since permutations were taken, a significant role in the computation of an exponential generating function $F_n$, the function $F_n$ was derived in [10] as follows:

$$A\left(x\right)=\frac{e^{2x}}{2-e^x}.$$

3. Methodologies

In this section, we explored different methods to classify fuzzy subsets of a finite set $X$ using an equivalence relation and the idea of $k$-level fuzzy subsets.

3.1. An Equivalence Relation on Fuzzy Subsets

The idea of this subsection was to briefly discuss an equivalence relation $(\cong )$ on the set I^X. It was defined in the following way:

Definition 2

([31], Definition 3.1). Suppose $\tilde{A}$ and $\tilde{B}$ are two fuzzy subsets of $X$ , $\tilde{A}\cong \tilde{B}$ if and only if the following properties are satisfied for all $x,y\in X$:

a. 

$\tilde{A}\left(x\right)>\tilde{A}\left(y\right)$ iff $\tilde{B}\left(x\right)>\tilde{B}\left(y\right)$;

b. 

$\tilde{A}\left(x\right)=1$ iff $\tilde{B}\left(x\right)=1$; and

c. 

$\tilde{A}\left(x\right)=0$ iff $\tilde{B}\left(x\right)=0$.

Indeed, one can verify that this relation is an equivalence relation on $I^X$. This equivalence relation coincides with the equality of crisp subsets when the values of membership in $I=\left[0,1\right]$ are restricted to binary values $I^{\prime }=\left\{0,1\right\}$. Based on this equivalence relation, the equivalence class having $\tilde{A}$ was denoted by $\left[\tilde{A}\right]$. We stated that two fuzzy subsets $\tilde{A}$ and $\tilde{B}$ were distinct if $\tilde{A}$ and $\tilde{B}$ were not equivalent, that is, $\tilde{A}\ncong \tilde{B}$.

Remark 2.

1. 

In condition (a) the strict inequality ($>$) can be replaced by$\ge$inequality without disturbing the equivalence. It concludes that the same equivalence class of fuzzy subsets can be drawn by either of the inequalities.

2. 

$\tilde{A}\cong \tilde{B}$concludes that the cores of$\tilde{A}$and$\tilde{B}$are equal in the condition (b).

3. 

From condition (c) of the above definition, it can be merely followed that two equivalent fuzzy subsets are the equal support. This condition is an integral part of the above equivalence relation, i.e., it cannot be redundant.

4. 

If$\tilde{A}\cong \tilde{B}$, then$\left|Im\left(\tilde{A}\right)\right|=\left|Im\left(\tilde{B}\right)\right|$. However, the converse is not true, viz. if$\left|Im\left(\tilde{A}\right)\right|=\left|Im\left(\tilde{B}\right)\right|$or even if$Im(\tilde{A})=Im(\tilde{B})$,$Core \left(\tilde{A}\right)=Core\left(\tilde{B}\right)$and$Supp\left(\tilde{A}\right)=Supp\left(\tilde{B}\right)$, we count not confirm that$\tilde{A}\cong \tilde{B}.$

5. 

$\tilde{A}\cong \tilde{B}$if, and only if, for each$\alpha >0$there exists a$\beta >0$, such that${\tilde{A}}^{\alpha }={\tilde{B}}^{\beta }$.

Example 1.

Suppose$X$to be a set of four elements,$X=\left\{x_1,x_2,x_3,x_4\right\}$. Let us define fuzzy sets$\tilde{A}$and$\tilde{B}$ on$X$ in the following way.

$$\tilde{A}\left(x\right)=\{\begin{array}{c}\begin{array}{cc}1& \begin{array}{cc}\mathrm{if}& x=x_1,\end{array}\end{array}\\ \begin{array}{cc}\frac{1}{2}& \begin{array}{cc}\mathrm{if}& x=x_2\end{array}\end{array},\\ \begin{array}{cc}\frac{1}{4}& otherwise\end{array},\end{array} and\widetilde{ B}\left(x\right)=\{\begin{array}{c}\begin{array}{cc}1& \begin{array}{cc}\mathrm{if}& x=x_1,\end{array}\end{array}\\ \begin{array}{cc}\frac{1}{2}& \begin{array}{cc}\mathrm{if}& x=x_2\end{array},\end{array}\\ \begin{array}{cc}0& otherwise\end{array}.\end{array}$$

It is easy to see that$\tilde{A}\left(x\right)>\tilde{A}\left(y\right)$if$\tilde{B}\left(x\right)>\tilde{B}\left(y\right)$for all$x,y\in X,$but$Supp\left(\tilde{A}\right)\ne Supp\left(\tilde{B}\right)$.

Example 2.

Let$X$be a set of five elements labelled as$\left\{x_1,x_2,x_3,x_4,x_5\right\}$. Suppose we defined fuzzy sets$\tilde{A}$and$\tilde{B}$ onXas follows:

$$\tilde{A}\left(x\right)=\{\begin{array}{l}\begin{array}{cc}0& \begin{array}{cc}if& x=x_1,\end{array}\end{array}\\ \begin{array}{cc}1& \begin{array}{cc}if& x=x_2\end{array}\end{array},\\ \begin{array}{cc}\frac{1}{2}& \begin{array}{cc}if& x=x_3\end{array}\end{array}, \\ \begin{array}{cc}\frac{1}{4}& otherwise,\end{array}\end{array} and \tilde{B}\left(x\right)=\{\begin{array}{l}\begin{array}{cc}0& \begin{array}{cc}if& x=x_1,\end{array}\end{array}\\ \begin{array}{cc}1& \begin{array}{cc}if& x=x_2,\end{array}\end{array}\\ \begin{array}{cc}\frac{1}{2}& \begin{array}{cc}if& x=x_4\end{array}\end{array},\\ \begin{array}{cc}\frac{1}{4}& otherwise\end{array}.\end{array}$$

One could observe that, in this example,$Im\left(\tilde{A}\right)=Im\left(\tilde{B}\right),Core\left(\tilde{A}\right)=Core\left(\tilde{B}\right),$and$Supp\left(\tilde{A}\right)=Supp\left(\tilde{B}\right)$. However,$\tilde{A}\left(x_3\right)>\tilde{A}\left(x_4\right),$but$\tilde{B}\left(x_3\right)\ngtr \tilde{B}\left(x_4\right)$. Hence, it could be concluded that$\tilde{A}$is not equivalent to$\tilde{B}$.

3.2. A New Notion of Classifying Fuzzy Subsets

The motivation behind this subsection was to concentrate on classifying fuzzy subsets of $X$ using the idea of $k$-level fuzzy subsets. Now, we introduced some definitions to derive the main results of this paper in the next section.

Definition 3.

For$n\in \mathbb{N}$and$0\le k\le n$, a$k$-level fuzzy subset$\tilde{A}$means that$\tilde{A}$has$k$distinct membership values in the open unit interval I″, that is, I\{0,1}. Note that a 0-level fuzzy subset means a crisp subset.

One can see that for $\alpha \in I$ and $1\le k\le n$, $\alpha$-cuts of a $k$-level fuzzy subset $\tilde{A}$ of $X$ formed a chain of $\left(k+1\right)$-pair of crisp subsets of length k ordered by an usual set inclusion as follows:

$$\Lambda :{\tilde{A}}^{{\alpha }_0}\subset {\tilde{A}}^{{\alpha }_1}\subset {\tilde{A}}^{{\alpha }_2}\subset \cdots \subset {\tilde{A}}^{{\alpha }_k},$$

with:

$$1\ge {\alpha }_0>{\alpha }_1>{\alpha }_2>\cdots >{\alpha }_k\ge 0,$$

written in the magnitude of the descending order, not necessarily having $0$ and $1$.

That is, a fuzzy subset $\tilde{A}, \tilde{A}=\underset{{\alpha }_i}{{\displaystyle \cup }}\left\{{\alpha }_i{\chi }_{{\tilde{A}}^{{\alpha }_i}}:0\le {\alpha }_i\le 1\right\}$ had its ${\alpha }_i$-cuts equal to ${\tilde{A}}^{{\alpha }_i}$’s. Here, ${\tilde{A}}^{{\alpha }_i}$’s were various components of the above chain $\Lambda$. We stated that two $k$-level fuzzy subsets were distinct if they were not equivalent. Therefore, it could be concluded that $\tilde{A}\cong \tilde{B}$ if, and only if, $\tilde{A}$ and $\tilde{B}$ had the same chain of crisp subsets of type $\Lambda$.

A fuzzy subset of $X$ having $n$ elements could have maximum $n$-distinct membership values in $I$, and then the maximum number of distinct $\alpha$-cuts of a fuzzy subset of $X$ would be $n+1$. For $k=n$ in the above chain $\mathsf{\Lambda }$, one could obtain a maximal chain, which is called a flag. Therefore, the length of the flag for a fuzzy subset of $X$ is $n$.

For the sake of understanding Definition 4, let us illustrate the definition through the following example:

Example 3.

Suppose$X=\left\{x_1,x_2,x_3, x_4\right\}$and let us define that a fuzzy set$\tilde{A}$is given by

$$\tilde{A}=\{(x_1, 0.2), \left(x_2,0.7\right), \left(x_3,0.7\right),\left(x_4,1\right)\}.$$

Since$\tilde{A}$has two distinct membership values in$\left(0,1\right)$, we labeled$\tilde{A}$as a two-level fuzzy subset of$X$. The$\alpha$-cuts of a$two$-level fuzzy subset$\tilde{A}$of$X$are:

For$0.7<{\alpha }_0\le 1, 0.2<{\alpha }_1\le 0.7$, and $0\le {\alpha }_2\le 0.2$, we had${\tilde{A}}^{{\alpha }_0}=\left\{x_4\right\}$,${\tilde{A}}^{{\alpha }_1}=\left\{x_2,x_3, x_4\right\}$, and${\tilde{A}}^{{\alpha }_2}=\left\{x_1,x_2,x_3, x_4\right\}$, respectively. These$\alpha$-cuts also formed a chain of crisp subsets ordered by the usual set inclusion as follows:

$${\tilde{A}}^{{\alpha }_0}\subset {\tilde{A}}^{{\alpha }_1}\subset {\tilde{A}}^{{\alpha }_2}.$$

Definition 5.

A chain of crisp subsets of$X$ordered by the set inclusion was stated to be a$\varnothing$-rooted (respectively,$X$-rooted) if it contained$\varnothing$(respectively,$X$). Otherwise, it was stated as unrooted or simply called a chain of crisp subsets of$X$.

From the above discussions, it can be followed that there exists a bijection between the collection of all distinct $k$-level fuzzy subsets of $X$ and the collection of all chains of crisp of subsets of $X$ of length $k$ ordered by the set inclusion. Similarly, there was a bijection between the collection of all distinct $\varnothing$-rooted (respectively, $X$-rooted) $k$-level fuzzy subsets of $X$ and the set of all $\varnothing$-rooted (respectively, $X$-rooted) chains of crisp of subsets of $X$ of length $k$ ordered by the set inclusion, respectively.

Definition 6.

Suppose $n\in \mathbb{N}$ and$0\le k\le n$. Let$\mathcal{P}\left(X\right)$be the collection of all crisp subsets of$X$and let$\mathcal{C}$be the collection of all chains of crisp subsets of$X$ordered by the set inclusion. Now, we set:

${ℱ}_{n,k}=\{\Gamma \in \mathcal{C} :$ the length of$\Gamma$is$k$with the initial term and the terminal term of$\Gamma$are not necessarily be the null set$\varnothing$and the full set$X$, respectively},

${ℱ}_{n,k}^{\varnothing }=\{\Gamma \in \mathcal{C} :$the initial term of$\Gamma$is$\varnothing$of length$k\}$, and

${ℱ}_{n,k}^X=\{\Gamma \in \mathcal{C} :$the terminal term$\Gamma$is$X$of length$k\}$.

Note that if $\Gamma$ was a chain such that its initial term and the terminal term coincided, then $\Gamma$ was a chain of length $0$.

That is, ${ℱ}_{n,k}, {ℱ}_{n,k}^{\varnothing }$ and ${ℱ}_{n,k}^X$ were the collection of all chains of crisp subsets of $X$ of length $k$, the collection of all $\varnothing$-rooted chains of crisp subsets of $X$ of length $k,$ and the collection of all $X$-rooted chains of crisp subsets of $X$ of length $k$ ordered by the set inclusion, respectively. We used notations $F_{n,k},F_{n,k}^{\varnothing },$ and $F_{n.k}^X$ to denote the cardinal numbers of ${ℱ}_{n,k},{ℱ}_{n,k}^{\varnothing },$ and ${ℱ}_{n,k}^X$, respectively. Further we define $F_{0,0}=1, F_{0,0}^{\varnothing }=1$ and $F_{0,0}^X=1$.

Let ${ℱ}_n,{ℱ}_n^{\varnothing },$ and ${ℱ}_n^X$ be the set of all chains of crisp subsets of $X$, the set of all $\varnothing$-rooted chains of crisp subsets of $X$, and the set of all $X$-rooted chains of crisp subsets of $X$ ordered by the set inclusion, respectively. Take $F_n=\left|{ℱ}_n\right|,F_n^{\varnothing }=\left|{ℱ}_n^{\varnothing }\right|,$ and $F_n^X=\left|{ℱ}_n^X\right|$. Assume that $F_0=1,F_0^{\varnothing }=1,$ and $F_0^X=1$ for the counting formulas of $F_n,F_n^{\varnothing },$ and $F_n^X$ for $n=0$, respectively, as a fuzzy subset of the empty set has no conventional meaning. It can also be concluded that there also exists a bijection between the collection of all distinct fuzzy subsets of $X$ (respectively, distinct $\varnothing$-rooted fuzzy subsets of $X$, distinct $X$-rooted fuzzy subsets of $X$), and the collection of all chains of crisp subsets of $X$ (respectively, $\varnothing$-rooted chains of crisp subsets of $X,$ $X$-rooted chains of crisp subsets of $X$) ordered by the set inclusion.

4. Results

This section focused on the main objectives for finding the explicit formulas of $F_n,F_n^{\varnothing },$ and $F_n^X$. To attain this, we first determined the numbers $F_{n,k},F_{n,k}^{\varnothing },$ and $F_{n,k}^X$.

4.1. The Number of $k$-Level Fuzzy Subsets

This subsection drove the numbers $F_{n,k},F_{n,k}^{\varnothing },$ and $F_{n.k}^X$ in terms of binomial coefficients. To calculate these numbers, we first investigated one of them, e.g., $F_{n,k}$.

We took a set with three elements, e.g., $X_3=\left\{1, 2, 3\right\}.$ The lattice of $\mathcal{P}\left(X_3\right)$, denoted $L\left(\mathcal{P}\left(X_3\right)\right)$, was generated by the following subsets (See Figure 1):

$$\mathcal{P}\left(X_3\right)=\left\{\varnothing ,\left\{1\right\},\left\{2\right\},\left\{3\right\},\left\{1,2\right\},\left\{1,3\right\},\left\{2,3\right\},\left\{1,2,3\right\}\right\}.$$

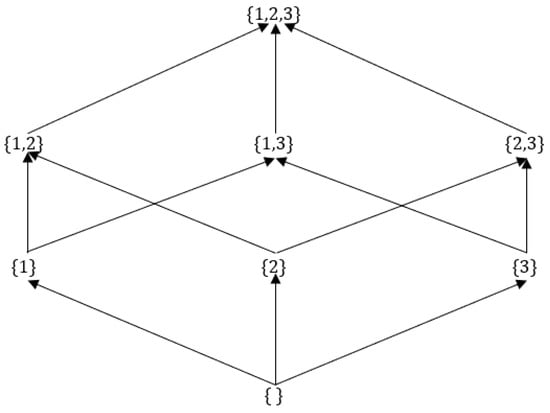
Figure 1. Chains in the power set of 3 elements.

It was essential to list these subsets because they were the key point in drawing a lattice diagram and for counting the number of chains of crisp subsets of $X_3$ (see Figure 1 and Figure 2). One could manually determine the number $F_3$ by describing all chains ordered by the set inclusion $(\subset )$ in the following four cases.

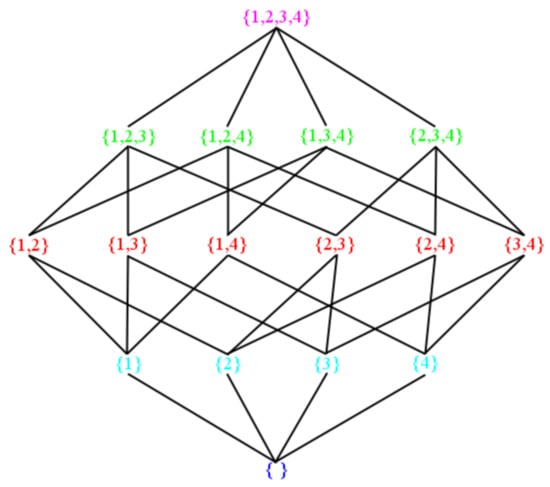
Figure 2. L($\mathcal{P}$({1,2,3,4})).

Case I

 

$$\begin{array}{}\left|{ℱ}_{3,0}\right|=\left|\left\{\varnothing ,\left\{1\right\},\left\{2\right\},\left\{3\right\},\left\{1,2\right\},\left\{1,3\right\},\left\{2,3\right\},\left\{1,2,3\right\}\right\}\right|=8,\\ \left|{ℱ}_{3,0}^{\varnothing }\right|=\left|\{\varnothing \}\right|=1,\\ \left|{ℱ}_{3,0}^X\right|=\left|\left\{\left\{1,2,3\right\}\right\}\right|=1;\end{array}$$

Case II

 

$$\begin{array}{}\left|{ℱ}_{3,1}\right|=\left|\right\{\varnothing \subset \left\{1\right\},\varnothing \subset \left\{2\right\},\varnothing \subset \left\{3\right\},\varnothing \subset \left\{1,2\right\},\varnothing \subset \left\{1,3\right\},\varnothing \subset \left\{2,3\right\},\varnothing \subset \left\{1,2,3\right\},\left\{1\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2\right\},\left\{1\right\}\subset \left\{1,3\right\},\left\{2\right\}\subset \left\{1,2\right\},\left\{2\right\}\subset \left\{2,3\right\},\left\{3\right\}\subset \left\{1,3\right\},\left\{3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{2,3\right\},\left\{1\right\}\subset \left\{1,2,3\right\}, \left\{2\right\}\subset \left\{1,2,3\right\},\left\{3\right\}\subset \left\{1,2,3\right\},\left\{1,2\right\}\subset \left\{1,2,3\right\},\left\{1,3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\left\{2,3\right\}\subset \left\{1,2,3\right\}\left\}\right|=19,\\ \left|{ℱ}_{3,1}^{\varnothing }\right|=\left|\left\{\varnothing \subset \left\{1\right\},\varnothing \subset \left\{2\right\},\varnothing \subset \left\{3\right\},\varnothing \subset \left\{1,2\right\},\varnothing \subset \left\{1,3\right\},\varnothing \subset \left\{2,3\right\},\varnothing \subset \left\{1,2,3\right\}\right\}\right|=7,\\ \left|{ℱ}_{3,1}^X\right|=\left|\right\{\varnothing \subset \left\{1,2,3\right\},\left\{1\right\}\subset \left\{1,2,3\right\},\left\{2\right\}\subset \left\{1,2,3\right\},\left\{3\right\}\subset \left\{1,2,3\right\},\left\{1,2\right\}\subset \left\{1,2,3\right\},\left\{1,3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\}, \left\{2,3\right\}\subset \left\{1,2,3\right\}\}|=7;\end{array}$$

Case III

 

$$\begin{array}{}\left|{ℱ}_{3,2}\right|=\left|\right\{\varnothing \subset \left\{1\right\}\subset \left\{1,2\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,3\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2\right\},\varnothing \subset \left\{2\right\}\subset \left\{2,3\right\},\varnothing \subset \left\{3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,3\right\},\varnothing \subset \left\{3\right\}\subset \left\{2,3\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,2\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\left\{1\right\}\subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\left\{1\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\}, \left\{2\right\}\subset \left\{1,2\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\left\{2\right\}\subset \left\{2,3\right\}\subset \left\{1,2,3\right\},\left\{3\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\left\{3\right\}\subset \left\{2,3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\}\left\}\right|=18,\\ \left|{ℱ}_{3,2}^{\varnothing }\right|=\left|\right\{\varnothing \subset \left\{1\right\}\subset \left\{1,2\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,3\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2\right\},\varnothing \subset \left\{2\right\}\subset \left\{2,3\right\},\varnothing \subset \left\{3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,3\right\},\varnothing \subset \left\{3\right\}\subset \left\{2,3\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,2\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\}\left\}\right|=12,\\ \left|{ℱ}_{3,2}^X\right|=\left|\right\{\left\{1\right\}\subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\left\{1\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\left\{2\right\}\subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\left\{2\right\}\subset \left\{2,3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\left\{3\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\left\{3\right\}\subset \left\{2,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,2\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,2,3\right\},\varnothing \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{3\right\}\subset \left\{1,2,3\right\}\left\}\right|=12;\end{array}$$

Case IV

 

$$\begin{array}{}\left|{ℱ}_{3,3}\right|=\left|\right\{\varnothing \subset \left\{1\right\}\subset \left\{1,2\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{1,2,3\right\},\varnothing \subset \left\{2\right\}\subset \left\{2,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{3\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\},\varnothing \subset \left\{3\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\subset \left\{2,3\right\}\subset \left\{1,2,3\right\}\left\}\right|=\left|F{S}_{3,3}^{\varnothing }\left(X\right)\right|=\left|F{S}_{3,3}^X\left(X\right)\right|=6.\end{array}$$

The total number $\left|{ℱ}_3\right|$ of distinct fuzzy subsets of $X_3$ was:

$$\left|{ℱ}_3\right|=\left|{ℱ}_{3,0}\right|+\left|{ℱ}_{3,1}\right|+\left|{ℱ}_{3,2}\right|+\left|{ℱ}_{3,3}\right|=8+19+18+6=51.$$

The total number of distinct rooted fuzzy subsets of $X_3$was:

$$F_3^{\varnothing }=1+7+12+6=26=F_3^X.$$

By examining the above discussions and analyzing Figure 1, one could conclude that the calculations manually consumed a lot of time, which is a difficult task. Therefore, it implied that a new technique was essential to solve these problems.

Lemma 2.

For each$n\in \mathbb{N}$and$k=0,1,2,\cdots ,n$, the number$F_{n,k}$of all the distinct$k$-level fuzzy subsets of$X$was given by the equality:

$$\begin{array}{}{F}_{n,0}={\displaystyle \sum }_{0\le i_0\le n}\left(\begin{array}{c}n\\ i_0\end{array}\right);\\ F_{n,1}={\displaystyle \sum }_{0\le i_0<i_1\le n}\left(\begin{array}{c}n\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right);\\ F_{n,2}={\displaystyle \sum }_{0\le i_0<i_1<i_2\le n}\left(\begin{array}{c}n\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right);\\ ⋮\\ F_{n,k}={\displaystyle \sum }_{0\le i_0<i_1<\cdots <i_k\le n}\left(\begin{array}{c}n\\ i_k\end{array}\right)\left(\begin{array}{c}{i}_k\\ i_{k-1}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right). \end{array}$$

Proof. 

We started the proof by determining an auxiliary construction. Let $X_k$ denote the set consisting of all the crisp subsets of $X$ with $k$-elements, $\left|X_k\right|=\left(\begin{array}{c}n\\ k\end{array}\right)$ for$n\in \mathbb{N}$ and $k=0,1,2,\cdots ,n$. Additionally, the crisp subsets$X_k$’s satisfied the following condition:

$$X_0\subset X_1\subset X_2\subset \cdots \subset X_k, \mathrm{for} k=0,1,2,\cdots ,n.$$

Now,

$$\begin{array}{}{ℱ}_{n,0}=\left\{X_k : 0\le k\le n\right\};\\ {ℱ}_{n,1}=\left\{X_i\subset X_k : 0\le i<k\le n\right\};\\ ⋮\\ {ℱ}_{n,k}=\left\{X_{i_0}\subset X_{i_1}\subset X_{i_2}\subset \cdots \subset X_{i_k} :0\le i_0<i_1<i_2<\cdots <i_k\le n\right\}.\end{array}$$

Next, we aimed to find the cardinality of ${ℱ}_{n,k}$ for $k=0,1,2,\cdots ,n$, and $n\in \mathbb{N}$.

It could be easily proved that $F_{n,0}=\left|{ℱ}_{n,0}\right|=2^n.$ Let $\Gamma$ be a chain of the crisp subsets in ${ℱ}_{n,k}$ for $k=0,1,2,\cdots ,n$ as follows:

$$\Gamma :X_0\subset X_1\subset X_2\subset \cdots \subset X_k.$$

Then, one could obtain the following $\left(k+1\right)$-dimensional vector as follows:

$$\alpha =\left(\left|X_0\right|,\left|X_1\right|,\left|X_2\right|,\cdots ,\left|X_k\right|\right).$$

For our convenience, we called $\alpha$ the order vector of $\Gamma$. Here, we considered

$$\Omega =\{\alpha :\alpha \mathrm{is} \mathrm{an} \mathrm{order} \mathrm{vector} \mathrm{of} \Gamma , \Gamma \in F_{n,k}\},$$

and for each $\alpha \in \Omega$,

$${ℱ}_{n,k}^{\alpha }=\{\Gamma \in {ℱ}_{n,k} :\mathrm{the}\mathrm{order}\mathrm{vector}\mathrm{of} \Gamma \mathrm{is} \alpha \}.$$

Then, it was very natural to conclude that:

$${ℱ}_{n,k}=\underset{\alpha \in \Omega }{{\displaystyle \cup }}{ℱ}_{n,k}^{\alpha },$$

and

$${ℱ}_{n,k}^{\alpha }{\displaystyle \cap }{ℱ}_{n,k}^{\beta }=\varnothing , \mathrm{if} \alpha \ne \beta .$$

Therefore,

$$F_{n,k}={{\displaystyle \sum }}_{\alpha \in \Omega }\left|{ℱ}_{n,k}^{\alpha }\right|.$$

Now, it was easy to find that:

$$\Omega =\left\{\alpha =\left(\left(\begin{array}{c}n\\ i_0\end{array}\right),\left(\begin{array}{c}n\\ i_1\end{array}\right),\left(\begin{array}{c}n\\ i_2\end{array}\right),\cdots ,\left(\begin{array}{c}n\\ i_k\end{array}\right)\right) : 0\le i_0<i_1<i_2<\cdots <i_k\le n\right\}.$$

Thus, for the order vector $\alpha$ of $\Gamma \in {ℱ}_{n,k}$, the number of choices for the first term, the second term, $\cdots$, and the k-th term of $\alpha$ were listed as follows:

$$\begin{array}{}\left(\begin{array}{c}n\\ i_k\end{array}\right),k\le i_k\le n;\\ \left(\begin{array}{c}{i}_k\\ i_{k-1}\end{array}\right),k-1\le i_{k-1}<i_k\le n;\\ \left(\begin{array}{c}{i}_{k-1}\\ i_{k-2}\end{array}\right),k-2\le i_{k-2}<i_{k-1}\le n-1;\\ ⋮\\ \left(\begin{array}{c}{i}_2\\ i_1\end{array}\right),1\le i_1<i_2\le n-k+2;\\ \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right),0\le i_0<i_1\le n-k+1.\end{array}$$

Therefore, we could precisely write the formula of $F_{n,k}$ as follows:

$$F_{n,k}={\displaystyle \sum }_{0\le i_0<i_1<\cdots <i_k\le n}\left(\begin{array}{c}n\\ i_k\end{array}\right)\left(\begin{array}{c}{i}_k\\ i_{k-1}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)$$

Hence, the lemma was proved. □

The following result can provide another version of Lemma 2.

Corollary 1.

Under the same requirements of Lemma 2, we had:

$$\begin{array}{}{F}_{n,0}={\displaystyle \sum }_{i_0=0}^n\left(\begin{array}{c}n\\ i_0\end{array}\right);\\ F_{n,1}={\displaystyle \sum }_{i_0=0}^{n-1}{\displaystyle \sum }_{i_1=1}^{n-i_0}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right);\\ F_{n,2}={\displaystyle \sum }_{i_0=0}^{n-2}{\displaystyle \sum }_{i_1=1}^{n-i_0-1}{\displaystyle \sum }_{i_2=1}^{n-i_0-i_1}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\left(\begin{array}{c}n-i_0-i_1\\ i_2\end{array}\right);\\ ⋮\\ F_{n,k}={\displaystyle \sum }_{i_0=0}^{n-k}{\displaystyle \sum }_{i_1=1}^{n-i_0-k+1}\cdots {\displaystyle \sum }_{i_k=1}^{n-i_0-i_1-i_2-\cdots -i_{k-1}}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\cdots \left(\begin{array}{c}n-i_0-i_1-i_2-\cdots -i_{k-1}\\ i_k\end{array}\right) \end{array}$$

The numbers $F_{n,k}$’s formed a triangular array and the rows for $n=0$ to 6 were shown below:

						1
					2		1
				4		5		2
			8		19		18		6
		16		65		110		84		24
	32		211		570		750		480		120
64		665		2702		5460		5880		3240		720

The above triangular array was assigned by identity number A038719 in the OEIS and its row sums gave the following sequence (see Theorem 5):

1, 3, 11, 51, 299, 2163, 18,731, 189,171, 2,183,339, 28,349,043, 408,990,251, ⋯.

The elements of the above sequence represent the number of fuzzy subsets of $n$-set, where $n\in {\mathbb{N}}^{*}$ and was assigned by A007047 in the OEIS.

Remark 3.

1. 

The first three diagonals of the triangular array A038719 gave the following sequences in the OEIS: A000079 (the number of subsets of an$n$-set,$n=0,1,2,3,\cdots )$, A001047$\left(3^n-2^n, n\in {\mathbb{N}}^{*}\right)$, and A038721 (the number of functions$f: \left\{1,2,\cdots ,n+1\right\}\to \left\{1,2,3,4\right\},$such that$Im\left(f\right)$contained$two$fixed elements,$n\ge 1$and$n\in \mathbb{N}$).

2. 

The last diagonal and next-to-last diagonal of the triangular array A038719 gave the sequences: A000142 (the number of permutations of$n$letters,$n\in {\mathbb{N}}^{*}$,or factorial numbers) and A038720$(n!\left(n+3\right)/2, n\in {\mathbb{N}}^{*} )$, respectively, in the OEIS.

The same methods as that in Lemma 2 were exemplified in the following two lemmas and two corollaries to derive the formulas of $F_{n,k}^{\varnothing }$ and $F_{n,k}^X$.

Lemma 3.

For each natural number$n$and$k=0,1,2,\cdots ,n$, the number$F_{n,k}^{\varnothing }$of all the distinct$\varnothing$-rooted$k$-level fuzzy subsets of$X$was given by the equality:

$$\begin{array}{}{F}_{n,1}^{\varnothing }={\displaystyle \sum }_{1\le i_0\le n}\left(\begin{array}{c}n\\ i_0\end{array}\right);\\ F_{n,2}^{\varnothing }={\displaystyle \sum }_{1\le i_0<i_1\le n}\left(\begin{array}{c}n\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right);\\ F_{n,3}^{\varnothing }={\displaystyle \sum }_{1\le i_0<i_1<i_2\le n}\left(\begin{array}{c}n\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right);\\ ⋮\\ F_{n,k}^{\varnothing }={\displaystyle \sum }_{1\le i_0<i_1<\cdots <i_{k-1}\le n}\left(\begin{array}{c}n\\ i_{k-1}\end{array}\right)\left(\begin{array}{c}{i}_{k-1}\\ i_{k-2}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right),\end{array}$$

with$F_{n,0}^{\varnothing }=1$for$n>0$.

Corollary 2.

Under the same assumptions of Lemma 3, we had:

$$\begin{array}{}{F}_{n,0}^{\varnothing }=1;\\ F_{n,1}^{\varnothing }={\displaystyle \sum }_{i_0=1}^n\left(\begin{array}{c}n\\ i_0\end{array}\right)\\ F_{n,2}^{\varnothing }={\displaystyle \sum }_{i_0=1}^{n-1}{\displaystyle \sum }_{i_1=1}^{n-i_0}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right);\\ ⋮\\ F_{n,k}^{\varnothing }={\displaystyle \sum }_{i_0=1}^{n-k+1}{\displaystyle \sum }_{i_1=1}^{n-i_0-k+2}\cdots {\displaystyle \sum }_{i_{k-1}=1}^{n-i_0-i_1-i_2-\cdots -i_{k-2}}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\cdots \left(\begin{array}{c}n-i_0-i_1-i_2-\cdots -i_{k-2}\\ i_{k-1}\end{array}\right).\end{array}$$

Lemma 4.

For any nonzero positive integers$n$and k,$0\le k\le n,$the number$F_{n.k}^X$of all the distinct$X$-rooted$k$-level fuzzy subsets of$X$ was given by the equality:

$$\begin{array}{}{F}_{n,0}^X=1;\\ F_{n,1}^X={\displaystyle \sum }_{0\le i_0\le n-1}\left(\begin{array}{c}n\\ i_0\end{array}\right);\\ F_{n,2}^X={\displaystyle \sum }_{0\le i_0<i_1\le n-1}\left(\begin{array}{c}n\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right);\\ F_{n,3}^X={\displaystyle \sum }_{0\le i_0<i_1<i_2\le n-1}\left(\begin{array}{c}n\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right);\\ ⋮\\ F_{n,k}^X={\displaystyle \sum }_{0\le i_0<i_1<\cdots <i_{k-1}\le n-1}\left(\begin{array}{c}n\\ i_{k-1}\end{array}\right)\left(\begin{array}{c}{i}_{k-1}\\ i_{k-2}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right),\end{array}$$

with$F_{n,0}^X=1$for$n>0$.

Corollary 3.

Under the same assumptions of Lemma 4, we had:

$$\begin{array}{}{F}_{n,0}^X=1;\\ F_{n,1}^X={\displaystyle \sum }_{i_0=0}^{n-1}\left(\begin{array}{c}n\\ i_0\end{array}\right);\\ F_{n,2}^X={\displaystyle \sum }_{i_0=0}^{n-2}{\displaystyle \sum }_{i_1=1}^{n-i_0-1}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right);\\ ⋮\\ F_{n,k}^X={\displaystyle \sum }_{i_0=0}^{n-k}{\displaystyle \sum }_{i_1=1}^{n-i_0-k+1}\cdots {\displaystyle \sum }_{i_{k-1}=1}^{n-i_0-i_1-i_2-\cdots -i_{k-2}-1}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\cdots \left(\begin{array}{c}n-i_0-i_1-i_2-\cdots -i_{k-2}\\ i_{k-1}\end{array}\right).\end{array}$$

The numbers satisfied by the formula of $F_{n,k}^{\varnothing }\left(=F_{n,k}^X\right)$ formed a triangle and the first few rows of the triangle were listed below:

						1
					1		1
				1		3		2
			1		7		12		6
		1		15		50		60		24
	1		31		180		390		360		120
1		63		602		2100		3360		2520		720

The above triangle was assigned by A028246 in the OEIS and its row sums gave the following sequence (see Theorems 6 and 7):

1, 2, 6, 26, 150, 1082, 9366, 94,586, 1,091,670, 14,174,522, 204,495,126, 3,245,265,146,$\cdots$.

The elements of this sequence correspond to the number of rooted fuzzy subsets of $n$-set, where $n\in {\mathbb{N}}^{*}$ and was assigned by the identity number A000629 in the OEIS.

Remark 4.

1. 

The first four diagonals of the triangle A028246 gave the following sequences in the OEIS: A000012 (the all one′s sequence), A000225 (the number of nonempty subsets of$n$-set, $n\in {\mathbb{N}}^{*}$), A028243 (the number of functions$f: \left\{1,2,\cdots ,n-1\right\}\to \left\{1,2,3\right\},$such that$Im\left(f\right)$contained two fixed elements,$n\ge 3$and$n\in \mathbb{N}$), and A028244 (the number of functions$f: \left\{1,2,\cdots ,n-1\right\}\to \left\{1,2,3,4\right\}$, such that$Im\left(f\right)$contained$three$fixed elements,$n\ge 4$and$n\in \mathbb{N}$).

2. 

The last seven external diagonals of the triangle A028246 gave the following sequences in the OEIS: A000142 (the number of permutations of$n$ letters,$n\in {\mathbb{N}}^{*}$) and A001710 (number of even permutations of $n$ letters, $n\in {\mathbb{N}}^{*}$), A005460 (essentially Stirling numbers of the second kind, offset: 0,2), A005461 (essentially Stirling numbers of the second kind, offset: 1,2), A005462 (essentially Stirling numbers of the second kind, offset: 3,2), A005463 (essentially Stirling numbers of the second kind, offset: 4,2), and A005464 (essentially Stirling numbers of the second kind, offset: 5,2), respectively, in the OEIS.

By taking $k=n$ in the explicit expression of $F_{n,k}$ in Lemma 2, we had an exciting result.

Corollary 4.

The number$F_{n,n}$of all the maximal chains of the crisp subsets of$X$was given by the equality:

$$F_{n,n}=n!.$$

Proof. 

The proof directly followed from the explicit formula of $F_{n,k}$ by substituting $k=n$

We had:

$$\begin{gathered} F_{n,n}=\left(\begin{array}{c}n\\ n\end{array}\right)\left(\begin{array}{c}n\\ n-1\end{array}\right)\left(\begin{array}{c}n-1\\ n-2\end{array}\right)\cdots \left(\begin{array}{c}2\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right) \\ =1\cdot n\cdot \left(n-1\right)\cdots 2\cdot 1 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=n! \end{gathered}$$

□

Corollary 5.

The numbers$F_{n,n}^{\varnothing }$and$F_{n,n}^X$of all the maximal chains of the crisp subsets of$X$were derived by the equality:

$$F_{n,n}^{\varnothing }=n!=F_{n,n}^X.$$

Proof. 

It could be proved similarly as in Corollary 4, by using Lemmas 3 and 4. □

Starting with $n=0$, the first few terms of the factorial of $n$ were:

$1, 1, 2, 6, 24, 120, 720, 5040, 40,320, 362,880, 3,628,800$.

This sequence was assigned by A000142 in the OEIS.

The formulas of $F_{n,n}$, $F_{n,n}^{\varnothing }$, and $F_{n,n}^X$ could also be justified by using Corollaries 1–3, respectively. To highlight and verify the above results, we illustrated them by the following example.

Example 4.

Determine the numbers$F_{4,4}$,$F_{4,4}^{\varnothing }$, and$F_{4,4}^X$.

Solution. 

One could calculate the numbers $F_{4,4}$, $F_{4,4}^{\varnothing }$, and $F_{4,4}^X$ in the following, by substituting $n=4$ and $k=4$ in Lemmas 2–4, respectively. We had:

$$\begin{array}{}{F}_{4,4}=\left(\begin{array}{c}4\\ 4\end{array}\right)\left(\begin{array}{c}4\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=1\times 4\times 3\times 2\times 1=24,\\ F_{4,4}^{\varnothing }=\left(\begin{array}{c}4\\ 4\end{array}\right)\left(\begin{array}{c}4\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)=1\times 4\times 3\times 2=24, \mathrm{and}\\ F_{4,4}^X=\left(\begin{array}{c}4\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 1\end{array}\right)=4\times 3\times 2\times 1=24.\end{array}$$

Hence, the formulas were verified.

As a verification of the above Corollaries 4 and 5, we manually computed all the maximal chains of the crisp subsets of $X_4=\left\{1,2,3,4\right\}$. We listed all the maximal chains, $F_{4,4}$, as follows:

$$\begin{gathered} \varnothing \subset \left\{1\right\}\subset \left\{1,2\right\}\subset \left\{1,2,3\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,2\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{1\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,3\right\}\subset \left\{1,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{1\right\}\subset \left\{1,4\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{1\right\}\subset \left\{1,4\right\}\subset \left\{1,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{2\right\}\subset \left\{1,2\right\}\subset \left\{1,2,3\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{2\right\}\subset \left\{1,2\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{2\right\}\subset \left\{2,3\right\}\subset \left\{1,2,3\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{2\right\}\subset \left\{2,3\right\}\subset \left\{2,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{2\right\}\subset \left\{2,4\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{2\right\}\subset \left\{2,4\right\}\subset \left\{2,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{3\right\}\subset \left\{1,3\right\}\subset \left\{1,2,3\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{3\right\}\subset \left\{1,3\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{3\right\}\subset \left\{2,3\right\}\subset \left\{1,2,3\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{3\right\}\subset \left\{2,3\right\}\subset \left\{2,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{3\right\}\subset \left\{3,4\right\}\subset \left\{1,3,4\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{3\right\}\subset \left\{3,4\right\}\subset \left\{2,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{4\right\}\subset \left\{1,4\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{4\right\}\subset \left\{1,4\right\}\subset \left\{1,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{4\right\}\subset \left\{2,4\right\}\subset \left\{1,2,4\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{4\right\}\subset \left\{2,4\right\}\subset \left\{2,3,4\right\}\subset \left\{1,2,3,4\right\}, \\ \varnothing \subset \left\{4\right\}\subset \left\{3,4\right\}\subset \left\{1,3,4\right\}\subset \left\{1,2,3,4\right\},\varnothing \subset \left\{4\right\}\subset \left\{3,4\right\}\subset \left\{2,3,4\right\}\subset \left\{1,2,3,4\right\}. \end{gathered}$$

These 24 maximal chains agreed with the numbers $F_{4,4},F_{4,4}^{\varnothing }$, and $F_{4,4}^X$.

We could have analyzed the time complexity of calculating $F_{n,n}$ as follows: The calculation of $\left(\begin{array}{c}r\\ r-1\end{array}\right)$, $r\in \mathbb{N}$ needed $\mathcal{O}\left(1\right)$. $F_{n,n}$ needed $n$ operations of the above calculation and multiplied them. Thus, its time complexity was $n\ast \mathcal{O}\left(1\right)+\mathcal{O}\left(n\right)$, which was $\mathcal{O}\left(n\right)$.

4.2. Explicit Formulas of $F_n,F_n^{\varnothing }$, and $F_n^X$

This subsection derived the explicit summation formulas of $F_n,F_n^{\varnothing }$, and $F_n^X$. Now, we gave the most important result in the following theorem.

Theorem 5.

The number$F_n$of all the distinct fuzzy subsets of$X$was given by the equality:

$$\begin{array}{}{F}_n={\displaystyle \sum }_{k=0}^n{F}_{n,k}={\displaystyle \sum }_{k=0}^n\left({\displaystyle \sum }_{0\le i_0<i_1<\cdots <i_k\le n}\left(\begin{array}{c}n\\ i_k\end{array}\right)\left(\begin{array}{c}{i}_k\\ i_{k-1}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\right), \end{array}$$

and

$$F_n={\displaystyle \sum }_{k=0}^n{F}_{n,k}={\displaystyle \sum }_{k=0}^n\left({\displaystyle \sum }_{i_0=0}^{n-k}{\displaystyle \sum }_{i_1=1}^{n-i_0-k+1}\cdots {\displaystyle \sum }_{i_k=1}^{n-i_0-i_1-i_2-\cdots -i_{k-1}}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\cdots \left(\begin{array}{c}n-i_0-i_1-i_2-\cdots -i_{k-1}\\ i_k\end{array}\right)\right)$$

where $n\ge 1$ is arbitrary.

Proof. 

By summing up all $\prime F_{n,k}$’s in Lemma 2 and Corollary 1, we had the required formula for $F_n$. □

For $0\le n\le 10$, the formula $F_n$ gave the following sequence with the initial terms (See Table 2):

Table 2. $F_{n,k}$ for $0\le k\le n,n\le 7$.

	$F_{n,k}; k$
$n$	0	1	2	3	4	5	6	7	$F_n$
0	1								1
1	2	1							3
2	4	5	2						11
3	8	19	18	6					51
4	16	65	110	84	24				299
5	32	211	570	750	480	120			2163
6	64	665	2702	5460	5880	3240	720		18,731
7	128	2059	12,138	35,406	57,120	52,080	25,200	5040	189,171

$1, 3, 11, 51, 299, 2163, 18,731, 189,171, 2,183,339, 28,167,603, 408,990,251.$ This sequence was assigned by A007047 in the OEIS.

One could have two immediate straightforward consequences of Theorem 5 in the following:

Theorem 6.

For a fixed value$n\in {\mathbb{Z}}^{+}$and$n\ge 1$, the number$F_n^{\varnothing }$of all the distinct$\varnothing$-rooted fuzzy subsets of$X$was given by the equality:

$$\begin{array}{}{F}_n^{\varnothing }={{\displaystyle \sum }}_{k=0}^n{F}_{n,k}^{\varnothing }=1+{{\displaystyle \sum }}_{k=1}^n\left({{\displaystyle \sum }}_{1\le i_0<i_1<\cdots <i_{k-1}\le n}\left(\begin{array}{c}n\\ i_{k-1}\end{array}\right)\left(\begin{array}{c}{i}_{k-1}\\ i_{k-2}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\right),\end{array}$$

and

$$\begin{array}{}{F}_n^{\varnothing }={\displaystyle \sum }_{k=0}^n{F}_{n,k}^{\varnothing }\\ =1+{\displaystyle \sum }_{k=1}^n\left({\displaystyle \sum }_{i_0=1}^{n-k+1}{\displaystyle \sum }_{i_1=1}^{n-i_0-k+2}\cdots {\displaystyle \sum }_{i_{k-1}=1}^{n-i_0-i_1-i_2-\cdots -i_{k-2}}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\cdots \left(\begin{array}{c}n-i_0-i_1-i_2-\cdots -i_{k-2}\\ i_{k-1}\end{array}\right)\right)\end{array}$$

with$F_0^{\varnothing }=1$.

Theorem 7.

The number$F_n^X$of all the distinct$X$-rooted fuzzy subsets of$X$with$n\ge 1$was given by the equality:

$$\begin{array}{}{F}_n^X={\displaystyle \sum }_{k=0}^n{F}_{n,k}^X=1+{\displaystyle \sum }_{k=1}^n\left({\displaystyle \sum }_{0\le i_0<i_1<\cdots <i_k\le n-1}\left(\begin{array}{c}n\\ i_k\end{array}\right)\left(\begin{array}{c}{i}_k\\ i_{k-1}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\right),\end{array}$$

and

$$\begin{array}{}{F}_n^X={\displaystyle \sum }_{k=0}^n{F}_{n,k}^X\\ =1+{\displaystyle \sum }_{k=1}^n\left({\displaystyle \sum }_{i_0=0}^{n-k}{\displaystyle \sum }_{i_1=1}^{n-i_0-k+1}\cdots {\displaystyle \sum }_{i_{k-1}=1}^{n-i_0-i_1-i_2-\cdots -i_{k-2}-1}\left(\begin{array}{c}n\\ i_0\end{array}\right)\left(\begin{array}{c}n-i_0\\ i_1\end{array}\right)\cdots \left(\begin{array}{c}n-i_0-i_1-i_2-\cdots -i_{k-2}\\ i_{k-1}\end{array}\right)\right),\end{array}$$

with$F_0^X=1$.

The beginning for $n=0$ to $10$, the results of theormula $F_n^{\varnothing } \left(=F_n^X\right)$ were shown below (see Table 3):

Table 3. $F_{n,k}^{\varnothing }\left(=F_{n,k}^X\right); k$ and $F_n^{\varnothing }(=F_n^X)$ for $0\le k\le n,n\le 7$.

	${\mathit{F}}_{\mathit{n},\mathit{k}}^{\varnothing }\left(={\mathit{F}}_{\mathit{n},\mathit{k}}^{\mathit{X}}\right);\mathit{k}$								$$\begin{gathered} {\mathit{F}}_{\mathit{n}}^{\varnothing } \\ (={\mathit{F}}_{\mathit{n}}^{\mathit{X}}). \end{gathered}$$
$\mathit{n}$	0	1	2	3	4	5	6	7
0	1								1
1	1	1							2
2	1	3	2						6
3	1	7	12	6					26
4	1	15	50	60	24				150
5	1	31	180	390	360	120			1082
6	1	63	602	2100	3360	2520	720		9366
7	1	127	1932	10,206	25,200	31,920	20,160	5040	94,586

$1, 2, 6, 26, 150, 1082, 9366, 94,586, 1,091,670, 14,174,522, 204,495,126.$

This sequence was assigned by A000629 in the OEIS.

The following observations gave the connections among the numbers of $F_n,F_n^{\varnothing }$, and $F_n^X$. It was similar to Proposition 1 in [32] and Theorem 1 in [33].

Proposition 3.

For any positive integer$n$, we had:

$$F_{n,k}=2F_{n,k}^{\varnothing }-1=2F_{n.k}^X-1.$$

To highlight and verify the above results, we illustrated it through an example in the following (see Figure 3):

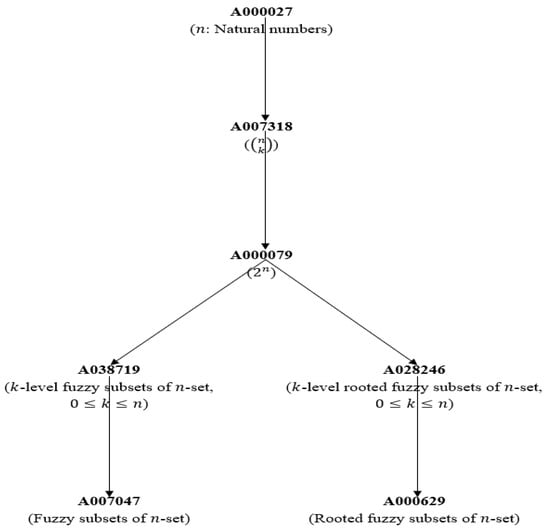
Figure 3. Connections between the sequences that are related to fuzzy subsets in the OEIS.

Example 5.

Find the numbers$F_3, F_3^{\varnothing }$, and$F_3^X$.

Solution. 

By taking $n=3$ in the explicit formulas of $F_n,F_n^{\varnothing }$, and $F_n^X$, we had $F_3, F_3^{\varnothing }$, and $F_3^X$ in the following way:

$$\begin{gathered} \begin{array}{ll}{F}_3={\displaystyle {\displaystyle \sum }_{k=0}^3}{F}_{3,k}=& F_{3,0}+F_{3,1}+F_{3,2}+F_{3,3} \\ & ={\displaystyle {\displaystyle \sum }_{0\le i_0\le 3}}\left(\begin{array}{c}3\\ i_0\end{array}\right)+{\displaystyle {\displaystyle \sum }_{0\le i_0<i_1\le 3}}\left(\begin{array}{c}3\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\\ & +{\displaystyle {\displaystyle \sum }_{0\le i_0<i_1<i_2\le 3}}\left(\begin{array}{c}3\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\\ & +{\displaystyle {\displaystyle \sum }_{0\le i_0<i_1<i_2<i_3\le 3}}\left(\begin{array}{c}3\\ i_3\end{array}\right)\left(\begin{array}{c}{i}_3\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\\ & =\left(\left(\begin{array}{c}3\\ 3\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)+\left(\begin{array}{c}3\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 0\end{array}\right)\right)\\ & +(\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)+\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 0\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 0\end{array}\right)\\ & +\left(\begin{array}{c}3\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right))\\ & +\left(\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 0\end{array}\right)+\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)\right)\\ & +\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)\\ & =\left(1+3+3+1\right)+\left(3+3+1+6+3+3\right)+(6+3+3\\ & +6)+6=51,\end{array} \\ \begin{array}{ll}{F}_3^{\varnothing }={\displaystyle {\displaystyle \sum }_{k=0}^3}{F}_{3,k}^{\varnothing }=& F_{3,0}^{\varnothing }+F_{3,1}^{\varnothing }+F_{3,2}^{\varnothing }+F_{3,3}^{\varnothing }\\ & =\left(\begin{array}{c}3\\ 0\end{array}\right)+{\displaystyle {\displaystyle \sum }_{1\le i_0\le 3}}\left(\begin{array}{c}3\\ i_0\end{array}\right)+{\displaystyle {\displaystyle \sum }_{1\le i_0<i_1\le 3}}\left(\begin{array}{c}3\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)+{\displaystyle {\displaystyle \sum }_{1\le i_0<i_1<i_2\le 3}}\left(\begin{array}{c}3\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\\ & =\left(\begin{array}{c}3\\ 0\end{array}\right)+\left(\left(\begin{array}{c}3\\ 3\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)+\left(\begin{array}{c}3\\ 1\end{array}\right)\right)+\left(\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)+\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)\right)\\ & +\left(\begin{array}{c}3\\ 3\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)=1+\left(1+3+3\right)+\left(3+3+6\right)+6=26,\end{array} \end{gathered}$$

and

$$\begin{array}{ll}{F}_3^X={\displaystyle {\displaystyle \sum }_{k=0}^n}{F}_{3,k}^X=& F_{3,0}^X+F_{3,1}^X+F_{3,2}^X+F_{3,3}^X\\ & =\left(\begin{array}{c}3\\ 3\end{array}\right)+{\displaystyle \sum }_{0\le i_0\le 2}\left(\begin{array}{c}3\\ i_0\end{array}\right)+{\displaystyle {\displaystyle \sum }_{0\le i_0<i_1\le 2}}\left(\begin{array}{c}3\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\\ & +{\displaystyle {\displaystyle \sum }_{0\le i_0<i_1<i_2\le 2}}\left(\begin{array}{c}3\\ i_2\end{array}\right)\left(\begin{array}{c}{i}_2\\ i_1\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)\\ & =\left(\begin{array}{c}3\\ 3\end{array}\right)+\left(\left(\begin{array}{c}3\\ 2\end{array}\right)+\left(\begin{array}{c}3\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 0\end{array}\right)\right)+\left(\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 0\end{array}\right)+\left(\begin{array}{c}3\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)\right)\\ & +\left(\begin{array}{c}3\\ 2\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)\\ & =1+\left(1+3+3\right)+\left(6+3+3\right)+6=26.\end{array}$$

We could have analyzed the time complexity of directly calculating $F_{n,k}$ as follows. The maximum time complexity for computing a binomial coefficient $\left(\begin{array}{c}n\\ k\end{array}\right), 0\le k\le n$ was $\mathcal{O}\left(n\right)$. For a $(k+1$)-tuple sequence $\left(i_0,i_1,\cdots ,i_k\right)$ satisfying $1\le i_0<i_1<\cdots <i_{k-1}\le n$, the time complexity for calculating $\left(\begin{array}{c}n\\ i_k\end{array}\right)\left(\begin{array}{c}{i}_k\\ i_{k-1}\end{array}\right)\cdots \left(\begin{array}{c}{i}_1\\ i_0\end{array}\right)$ was, thus, $\left(k+1\right)\ast \mathcal{O}\left(n\right)$. However, there were $\left(\begin{array}{c}n+1\\ k\end{array}\right)$ sequences in$F_{n,k}$; thus, the time complexity for $F_{n,k}$ was not polynomial.

5. Conclusions

This paper solved the counting problems for the number of fuzzy subsets of any arbitrary finite set by using binomial numbers. The explicit formulas of $F_n$ and $F_n^{\varnothing } \left(=F_n^X\right)$ for the numbers of distinct unrooted and rooted fuzzy subsets of a finite set $X$ were derived, respectively. Moreover, the combinatorial structures on the power set of $X$ were briefly studied. In addition, the paper gave the connection between the existing and obtained integer sequences in the OEIS that were strongly related to these numbers. This study could be successfully used to classify special classes of fuzzy matrices of finite order. It could also be extended to many other algebraic structures, such as subgroups of a finite group, ideals of a finite ring, and subfields of a finite field. This would surely indicate the way to further strengthen the research and lead to many novel findings in the area of artificial intelligence, clustering analysis, image processing, machine learning, neural networks, etc.

Moreover, as mentioned above, the time complexity of directly calculating $F_{n,k}$ was not polynomial. As future work, we could attempt to derive a better way to calculate $F_{n,k}$ such as designing a recursive way to obtain its value.