A Novel n-Point Newton-Type Root-Finding Method of High Computational Efficiency

Abstract

A novel Newton-type n-point iterative method with memory is proposed for solving nonlinear equations, which is constructed by the Hermite interpolation. The proposed iterative method with memory reaches the order $(2^n+2^{n-1}-1+\sqrt{2^{2n+1}+2^{2n-2}+2^n+1})/2$ by using n variable parameters. The computational efficiency of the proposed method is higher than that of the existing Newton-type methods with and without memory. To observe the stability of the proposed method, some complex functions are considered under basins of attraction. Basins of attraction show that the proposed method has better stability and requires a lesser number of iterations than various well-known methods. The numerical results support the theoretical results.

1. Introduction

Finding a solution a of nonlinear equation $f(x)=0$, where $f:D\subseteq \mathbb{R}\to \mathbb{R}$ is a sufficiently differentiable function in an open set D, is a difficult problem in the field of numerical analysis. Multipoint iterative methods with high computational efficiency were introduced by Traub [1] and Petković [2], which are very suitable for finding the solution of nonlinear equations. The design methods for multipoint iterative method include: the weight function method [3,4,5], the interpolation method [6,7], the rational function method [8,9], the undetermined coefficient method [10], the inverse interpolation function method [11,12] and the symbolic computation method [13]. Using these methods, many efficient multipoint iterative methods have been proposed for solving nonlinear equations, see [14,15,16,17,18,19,20] and the references therein. In those methods, the n-point iterative method is worth studying because of its high computational efficiency. The Kung–Traub’s method [14], Zheng’s method [15], Petković–Džunić’s method [16] and Wang–Zhang’s method [17] are well-known derivative-free n-point iterative methods. Furthermore, some efficient n-point Newton-type iterative methods with and without memory have been proposed. Kung and Traub [14] proposed an optimal $2^n$th order Newton-type method as follows:

$$\left\{\begin{array}{c}{y}_{k,1}=t_k-f(t_k)/f^{\prime }(t_k),\hfill \\ y_{k,j}=S_j(0),j=2,\dots ,n,\hfill \\ t_{k+1}=y_{k,n},\hfill \end{array}\right.$$

(1)

where the inverse interpolating polynomial is $S_j(y)$ such that $S_j(f(t_k))=t_k, S_j^{\prime }(f(t_k))=1/f^{\prime }(t_k),$$S_j(f(y_{k,j}))=y_{k,j}, (j=2,\dots ,n)$. Petković [18] derived the following n-point Newton-type method:

$$\left\{\begin{array}{c}{\varphi }_1(t)=t-\frac{f(t)}{f^{\prime }(t)},\hfill \\ {\varphi }_2(t)={\psi }_f(t),\hfill \\ {\varphi }_3(t)={\varphi }_2(t)-\frac{f({\varphi }_2(t))}{h_{(2)}^{\prime }({\varphi }_2(t))},\hfill \\ \cdots ,\hfill \\ {\varphi }_n(t)={\varphi }_{n-1}(t)-\frac{f({\varphi }_{n-1}(t))}{h_{(n-1)}^{\prime }({\varphi }_{(n-1)}(t))},\hfill \end{array}\right.$$

(2)

where $h_i^{\prime }(t),(i=2,3,\cdots ,n-1.)$ is the Hermite interpolation polynomial satisfying the conditions $f^{\prime }({\varphi }_0)=h_{m+1}^{\prime }({\varphi }_0),f({\varphi }_j)=h_{m+1}({\varphi }_j) and (j=0,1,\cdots ,n-1.)$, and ${\psi }_f(t)$ is an iterative function with an optimal order of 4. Cordero et al. [19] studied the stability of method (2) for $n=2,3.$ In [20], we obtained the following one-parameter n-point Newton-type method without memory:

$$\left\{\begin{array}{c}{t}_{k,1}=t_{k,0}-\frac{f(t_{k,0})}{f^{\prime }(t_{k,0})+Lf(t_{k,0})},\hfill \\ t_{k,2}=t_{k,1}-\frac{f(t_{k,1})}{f[t_{k,1},t_{k,0}]+f[t_{k,1},t_{k,0},t_{k,0}](t_{k,1}-t_{k,0})},\hfill \\ \dots ,\hfill \\ t_{k,n}=t_{k,n-1}-\frac{f(t_{k,n-1})}{N(t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0})},\hfill \end{array}\right.$$

(3)

where $N(t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0})=f[t_{k,n-1},t_{k,n-2}]+\cdots +f[t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0},$$t_{k,0}](t_{k,n-1}-t_{k,n-2})\cdots (t_{k,n-1}-t_{k,0}),t_{k,0}=t_k$, and $L\in \mathbb{R}$ is a constant. By replacing parameter L in (3) with a variable parameter $L_k$, method (3) can be transformed to the following one-parameter n-point Newton-type iterative method with memory:

$$\left\{\begin{array}{c}{t}_{k,1}=t_{k,0}-\frac{f(t_{k,0})}{f^{\prime }(t_{k,0})+L_{k}f(t_{k,0})},\hfill \\ t_{k,2}=t_{k,1}-\frac{f(t_{k,1})}{f[t_{k,1},t_{k,0}]+f[t_{k,1},t_{k,0},t_{k,0}](t_{k,1}-t_{k,0})},\hfill \\ \dots ,\hfill \\ t_{k,n}=t_{k,n-1}-\frac{f(t_{k,n-1})}{N(t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0})},\hfill \end{array}\right.$$

(4)

where $N(t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0})=f[t_{k,n-1},t_{k,n-2}]+\cdots +f[t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0},$$t_{k,0}](t_{k,n-1}-t_{k,n-2})\cdots (t_{k,n-1}-t_{k,0}),t_{k,0}=t_k$, $L_k=-H_4^{″}(y_{k,0})/(2f^{\prime }(y_{k,0}))$ and $H_4(x)$ is a Hermite’s interpolating polynomial with a degree of 4. Method (4) improved the convergence order of method (3) without any additional functional evaluations, which implied that the variable parameter can improve the computational efficiency of the Newton-type iterative method. Thus, we concluded that the convergence order of n-point Newton-type iterative method can be improved further by improving the number of variable parameters in the iterative scheme.

The aims of this work are to improve the computational efficiency and convergence order of n-point Newton-type method and produce a general n-point Newton-type iterative method with memory for solving nonlinear equations. The paper is organized as follows: In Section 2, we propose a general n-point Newton-type iterative method with optimal order $2^n$ by using Hermite’s interpolation polynomial. Based on the optimal n-point Newton-type iterative method, a general n-point Newton-type iterative method with memory is proposed by using n variable parameters in Section 3. The convergence order of the n-point Newton-type iterative method with memory is analyzed, which is higher than that of the existing Newton-type iterative methods. In Section 4, the stability of the presented iterative method is analyzed with the help of the basins of attraction. Several numerical tests are made to confirm the theoretical results in Section 5. Conclusions are given in Section 6.

2. The n-Parameter n-Point Newton-Type Method with Optimal Order 2ⁿ

Combining the first step of method (3) with Newton’s method [21,22], we construct the following one-parameter Newton-type method:

$$\left\{\begin{array}{c}{y}_k=t_k-\frac{f(t_k)}{L_{1}f(t_k)+f^{\prime }(t_k)},\hfill \\ t_{k+1}=y_k-\frac{f(y_k)}{f^{\prime }(y_k)},\hfill \end{array}\right.$$

(5)

where $L_1\in \mathbb{R}$ is a real parameter. To reduce the computational cost of method (5), we approximate $f(t)$ by Hermite’s interpolation polynomial $H_3(t)$. Interpolation polynomial $H_3(t)$ is given by:

$$\begin{array}{c}{H}_3(t)=f(y_k)+f[y_k,t_k](t-y_k)+f[y_k,t_k,t_k](t-y_k)(t-t_k)+L_2(t-y_k){(t-t_k)}^2,\hfill \end{array}$$

(6)

such that $H_3(t_k)=f(t_k),H_3(y_k)=f(y_k)$, $H_3^{\prime }(t_k)=f^{\prime }(t_k)$ and $L_2\in \mathbb{R}$. The derivative of $H_3(t)$ at $y_k$ is:

$$H_3^{\prime }(y_k)=f[y_k,t_k]+f[y_k,t_k,t_k](y_k-t_k)+L_2{(y_k-t_k)}^2.$$

(7)

Replacing $f^{\prime }(y_k)$ with $H_3^{\prime }(y_k)$ in (5), we obtain a two-parameter Newton-type method:

$$\left\{\begin{array}{c}{y}_k=t_k-\frac{f(t_k)}{L_{1}f(t_k)+f^{\prime }(t_k)},\hfill \\ t_{k+1}=y_k-\frac{f(y_k)}{f[y_k,t_k]+f[y_k,t_k,t_k](y_k-t_k)+L_2{(y_k-t_k)}^2},\hfill \end{array}\right.$$

(8)

where $f[y_k,t_k,t_k]=\frac{f[y_k,t_k]-f^{\prime }(t_k)}{y_k-t_k}$ and $L_2\in \mathbb{R}$ are real parameters. Combining method (8) with Newton’s method, we obtain the following three-step method:

$$\left\{\begin{array}{c}{y}_k=t_k-\frac{f(t_k)}{L_{1}f(t_k)+f^{\prime }(t_k)},\hfill \\ z_k=y_k-\frac{f(y_k)}{f[y_k,t_k]+f[y_k,t_k,t_k](y_k-t_k)+L_2{(y_k-t_k)}^2},\hfill \\ t_{k+1}=z_k-\frac{f(z_k)}{f^{\prime }(z_k)}.\hfill \end{array}\right.$$

(9)

We approximate $f(t)$ in (9) by the following interpolation polynomial $H_4(t)$ of a degree of four:

$$H_4(t)=f(z_k)+f[z_k,y_k](t-z_k)+f[z_k,y_k,t_k](t-z_k)(t-y_k)$$

$$+f[z_k,y_k,t_k,t_k](t-z_k)(t-y_k)(t-t_k)+L_3(t-z_k)(t-y_k){(t-t_k)}^2.$$

(10)

$H_4(t)$ satisfies interpolation conditions $H_4(t_k)=f(t_k)$, $H_4(y_k)=f(y_k)$, $H_4(z_k)=f(z_k)$ and $H_4^{\prime }(t_k)=f^{\prime }(t_k)$. The derivative of $H_4(t)$ at $z_k$ is:

$$H_4^{\prime }(z_k)=f[z_k,y_k]+f[z_k,y_k,t_k](z_k-y_k)+f[z_k,y_k,t_k,t_k]\times$$

$$(z_k-y_k)(z_k-t_k)+L_3(z_k-y_k){(z_k-t_k)}^2,$$

(11)

where $L_3\in \mathbb{R}$. Replacing $f^{\prime }(z_k)$ with $H_4^{\prime }(z_k)$ in (9), we obtain the following three-parameter method:

$$\left\{\begin{array}{c}{y}_k=t_k-\frac{f(t_k)}{L_{1}f(t_k)+f^{\prime }(t_k)},\hfill \\ z_k=y_k-\frac{f(y_k)}{f[y_k,t_k]+f[y_k,t_k,t_k](y_k-t_k)+L_2{(y_k-t_k)}^2},\hfill \\ t_{k+1}=z_k-\frac{f(z_k)}{H_4^{\prime }(z_k)},\hfill \end{array}\right.$$

(12)

where $H_4^{\prime }(z_k)=f[z_k,y_k]+f[z_k,y_k,t_k](z_k-y_k)+f[z_k,y_k,t_k,t_k](z_k-y_k)(z_k-t_k)+L_3(z_k-y_k){(z_k-t_k)}^2$ and $L_i\in \mathbb{R},(i=1,2,3)$.

Furthermore, we construct the following n-parameter n-point Newton-type method without memory:

$$\left\{\begin{array}{c}{t}_{k,1}=t_{k,0}-\frac{f(t_{k,0})}{L_{1}f(t_{k,0})+f^{\prime }(t_{k,0})},\hfill \\ t_{k,2}=t_{k,1}-\frac{f(t_{k,1})}{f[t_{k,1},t_{k,0}]+f[t_{k,1},t_{k,0},t_{k,0}](t_{k,1}-t_{k,0})+L_2{(t_{k,1}-t_{k,0})}^2},\hfill \\ t_{k,3}=t_{k,2}-\frac{f(t_{k,2})}{H_4^{\prime }(t_{k,2})},\hfill \\ \cdots ,\hfill \\ t_{k,n}=t_{k,n-1}-\frac{f(t_{k,n-1})}{H_{n+1}^{\prime }(t_{k,n-1})},\hfill \end{array}\right.$$

(13)

where

$$H_{n+1}^{\prime }(t_{k,n-1})=f[t_{k,n-1},t_{k,n-2}]+f[t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0},t_{k,0}]\prod _{j=2}^n(t_{k,n-1}-t_{k,n-j})$$

$$+\sum _{j=3}^n\left\{f[t_{k,n-1},t_{k,n-2},\cdots ,t_{k,n-j}]\prod _{i=2}^{j-1}(t_{k,n-1}-t_{k,n-i})\right\}+L_{n-1}(t_{k,n-1}-t_{k,0})\prod _{t=2}^n(t_{k,n-1}-t_{k,n-t}),$$

$t_{k,0}=t_k$ and $L_i\in \mathbb{R},(i=1,2\cdots ,n)$. The Petković’s method (2) and Wang’s method (3) are two special cases of method (13) for $L_i=0,(i=1,2,\cdots n)$ and $L_i=0,(i=2,3,\cdots n)$, respectively.

Theorem 1.

Let $a\in \mathbb{R}$ be a zero of a sufficiently differentiable function $f:D\subseteq \mathbb{R}\to \mathbb{R}$ in an open set D. Assume that initial approximation $t_0$ is sufficiently close to a. Then, method (8) reaches an optimal convergence order four and satisfies the following:

$$e_{k+1}=(c_2+L_1)[c_2(c_2+L_1)-c_3+\frac{L_2}{f^{\prime }(a)}]e_k^4+O(e_k^5).$$

(14)

where $c_n=(1/n!)f^{(n)}(a)/f^{\prime }(a),n\ge 2.$

Proof. 

Let $e_k=t_k-a$, $e{y}_k=y_k-a$, $e{z}_k=z_k-a$ and $c_n=(1/n!)f^{(n)}(a)/f^{\prime }(a),n\ge 2.$ Using the Taylor expansion of f at a, we obtain:

$$f(t_k)=f^{\prime }(a)(e_k+c_2{e}_k^2+c_3{e}_k^3+c_4{e}_k^4+c_5{e}_k^5+c_6{e}_k^6+c_7{e}_k^7+c_8{e}_k^8+O(e_k^9)),$$

(15)

and

$$f^{\prime }(t_k)=f^{\prime }(a)(1+2c_2{e}_k+3c_3{e}_k^2+4c_4{e}_k^3+5c_5{e}_k^4+6c_6{e}_k^5+7c_7{e}_k^6+8c_8{e}_k^7+O(e_k^8)).$$

(16)

According to (12), (15) and (16), we have:

$$e{y}_k=(c_2+L_1)e_k^2+(-2c_2^2+2c_3-2c_2{L}_1-L_1^2)e_k^3+(4c_2^3-7c_2{c}_3$$

$$+3c_4+5c_2^2{L}_1-4c_3{L}_1+3c_2{L}_1^2+L_1^3)e_k^4+O(e_k^5).$$

(17)

Using the Taylor expansion of $f(y_k)$ at a, we obtain:

$$f(y_k)=f^{\prime }(a)(e{y}_k+c_{2}e{y}_k^2+c_{3}e{y}_k^3+c_{4}e{y}_k^4+c_{5}e{y}_k^5+c_{6}e{y}_k^6+c_{7}e{y}_k^7+c_{8}e{y}_k^8++O(e{y}_k^9)),$$

(18)

and

$$f[y_k,t_k]=f^{\prime }(a)[1+c_2{e}_k+(c_2^2+c3+c2L_1)e_k^2+(-2c_2^3+3c_2{c}_3+c_4-2c_2^2{L}_1+c_3{L}_1-c_2{L}_1^2)e_k^3$$

$$+(4c_2^4+2c_3^2+c_5+5c_2^3{L}_1+c_4{L}_1+c_2^2(-8c_3+3L_1^2)+c_2(4c_4-4c_3{L}_1+L_1^3))e_k^4]+O(e_k^5).$$

(19)

From (16) and (19), we obtain:

$$f[y_k,t_k,t_k]=\frac{f[y_k,t_k]-f^{\prime }(t_k)}{y_k-t_k}$$

$$=f^{\prime }(a)(c_2+2c_3{e}_k+(c_2{c}_3+3c_4+c_3{L}_1)e_k^2+(-2c_2^2{c}_3+2c_3^2$$

$$+4c_5+2c_4{L}_1-c3L_1^2+2c_2(c_4-c_3{L}_1))e_k^3)+O(e_k^4).$$

(20)

Using (8) and (18)–(20), we attain:

$$e{z}_k=(c_2+L_1)[c_2(c_2+L_1)+\frac{L_2}{f^{\prime }(a)}-c_3]e_k^4+O(e_k^5).$$

(21)

This means that the convergence order of method (8) is four. This concludes the proof. □

For method (12), we can obtain the following convergence theorem.

Theorem 2.

Let $a\in \mathbb{R}$ be a zero of a sufficiently differentiable function $f:D\subseteq \mathbb{R}\to \mathbb{R}$ in an open set D. Assume that initial approximation $t_0$ is sufficiently close to a. Then, method (12) arrives the optimal order eight and satisfies the following error equation:

$$e_{k+1}={(c_2+L_1)}^2[c_2(c_2+L_1)-c_3+\frac{L_2}{f^{\prime }(a)}]\{c_2[c_2(c_2+L_1)-c_3+\frac{L_2}{f^{\prime }(a)}]+c_4-\frac{L_3}{f^{\prime }(a)}\}{e}_k^8+O(e_k^9),$$

(22)

where $c_n=(1/n!)f^{(n)}(a)/f^{\prime }(a),n\ge 2.$

Proof. 

Let $e_k=t_k-a$, $e{y}_k=y_k-a$, $e{z}_k=z_k-a$ and $c_n=(1/n!)f^{(n)}(a)/f^{\prime }(a),n\ge 2.$ Using the Taylor expansion of $f(z_k)$ at a, we obtain:

$$f(z_k)=f^{\prime }(a)(e{z}_k+c_{2}e{z}_k^2+c_{3}e{z}_k^3+c_{4}e{z}_k^4+c_{5}e{z}_k^5+O(e{z}_k^6)),$$

(23)

$$f[z_k,y_k]=f^{\prime }(a)+c_2{f}^{\prime }(a)(c_2+L_1)e_k^2-c_2{f}^{\prime }(a)(2c_2^2-2c_3+2c_2{L}_1+L_1^2)e_k^3$$

$$+(5c_2^4{f}^{\prime }(a)+7c_2^3{f}^{\prime }(a)L_1+c_3{f}^{\prime }(a)L_1^2+c_2^2(-7c_3{f}^{\prime }(a)+4f^{\prime }(a)L_1^2$$

$$+L_2)+c_2(3c_4{f}^{\prime }(a)+L_1(-3c_3{f}^{\prime }(a)+f^{\prime }(a)L_1^2+L_2)))e_k^4+O(e_k^5).$$

(24)

From (19) and (24), we obtain:

$$f[z_k,y_k,t_k]=\frac{f[z_k,y_k]-f[y_k,t_k]}{z_k-t_k}$$

$$=f^{\prime }(a)(c_2+c_3{e}_k+(c_2{c}_3+c_4+c_3{L}_1)e_k^2+(-2c_2^2{c}_3$$

$$+2c_3^2+c_5+c_4{L}_1-c_3{L}_1^2+c_2(c_4-2c_3{L}_1))e_k^3)+O(e_k^4).$$

(25)

Using (20) and (25), we have

$$f[z_k,y_k,t_k,t_k]=\frac{f[z_k,y_k,t_k]-f[y_k,t_k,t_k]}{z_k-t_k}$$

$$=f^{\prime }(a)(c_3+2c_4{e}_k+(c_2{c}_4+3c_5+c_4{L}_1)e_k^2+(-2c_2^2{c}_4+2c_3{c}_4$$

$$+4c_6+2c_5{L}_1-c_4{L}_1^2+2c_2(c_5-c_4{L}_1))e_k^3)+O(e_k^4).$$

(26)

Therefore, from (12), (25) and (26), we obtain:

$$e_{k+1}={(c_2+L_1)}^2[c_2(c_2+L_1)-c_3+\frac{L_2}{f^{\prime }(a)}]$$

$$\times \{c_2[c_2(c_2+L_1)-c_3+\frac{L_2}{f^{\prime }(a)}]+c_4-\frac{L_3}{f^{\prime }(a)}\}{e}_k^8+O(e_k^9).$$

(27)

This means that method (12) arrives at the optimal order eight. This concludes the proof. □

According to the above study, we can obtain the following convergence theorem.

Theorem 3.

Let $a\in \mathbb{R}$ be a zero of a sufficiently differentiable function $f:D\subseteq \mathbb{R}\to \mathbb{R}$ in an open set D. Assume that initial approximation $t_0$ is sufficiently close to a. Then, the n-parameter n-point Newton-type iterative scheme (13) without memory reaches the optimal order $2^n$ and its error relation is

$$e_{k+1}=e_{k,n}=t_{k,n}-\alpha =q_n{e}_{k,0}\prod _{i=0}^{n-1}{e}_{k,i}=q_n{q}_{n-1}{q}_{n-2}^2\cdots q_1^{2^{n-2}}{q}_0^{2^{n-1}}{e}_k^{2^n}+O(e_k^{2^n+1}),$$

(28)

where $e_{k,j}=t_{k,j}-a$, $(j=0,1,2,\cdots ,n),e_k=e_{k,0}=t_{k,0}-a,q_0=1,q_1=c_2+L_1$ and $q_n=c_n{q}_{n-1}+{(-1)}^{n-1}{c}_{n+1}+{(-1)}^n\frac{L_n}{f^{\prime }(a)},n=2,3,\cdots .$

Proof. 

Induction method is used to prove this Theorem. Form Theorem 1, we know that the Theorem is valid for $n=2$ and $n=3$. Suppose that Equation (28) is true for $n=N-1$, then we have the error relation

$$e_{k,N-1}=t_{k,N-1}-a=q_{N-1}{e}_{k,0}\prod _{i=0}^{N-2}{e}_{k,i}$$

$$=q_{N-1}{q}_{N-2}{q}_{N-3}^2\cdots q_1^{2^{N-3}}{q}_0^{2^{N-2}}{e}_k^{2^{N-1}}+O(e_k^{2^{N-1}+1}).$$

(29)

Noting that $e_{k,0}{e}_{k,0}{e}_{k,1}{e}_{k,2}\cdots e_{k,N-1}=O(e_k^{1+1+2+2^2+\cdots +2^{N-1}})=O(e_k^{2^N})$ and taking $n=N$, we obtain:

$$e_{k+1}=e_{k,N}=t_{k,N}-a=e_{k,N-1}-\frac{f[t_{k,N-1},a]e_{k,N-1}}{H_N^{\prime }(t_{k,N-1})}=e_{k,N-1}\left(\frac{H_N^{\prime }(t_{k,N-1})-f[t_{k,N-1},a]}{H_N^{\prime }(t_{k,N-1})}\right)$$

$$=e_{k,N-1}(f[t_{k,N-1},t_{k,N-2}]+f[t_{k,N-1},t_{k,N-2},t_{k,N-3}](t_{k,N-1}-t_{k,N-2})+\cdots$$

$$+f[t_{k,N-1},t_{k,N-2},\cdots ,t_{k,1},t_{k,0},t_{k,0}](t_{k,N-1}-t_{k,N-2})(t_{k,N-1}-t_{k,N-3})\cdots (t_{k,N-1}-t_{k,0})$$

$$+{(-1)}^N{L}_{N-1}{e}_{k,N-2}{e}_{k,N-3}\cdots e_{k,0}^2-f[t_{k,N-1},a]){[f^{\prime }(a)+O(e_k)]}^{-1}$$

$$=e_{k,N-1}\{f[t_{k,N-2},t_{k,N-1},a]e_{k,N-2}+f[t_{k,N-1},t_{k,N-2},t_{k,N-3}]e_{k,N-1}$$

$$-f[t_{k,N-1},t_{k,N-2},t_{k,N-3}]e_{k,N-2}+\cdots +{(-1)}^{N-1}f[t_{k,N-1},t_{k,N-2},\cdots ,t_{k,1},t_{k,0},t_{k,0}]$$

$$\times e_{k,N-2}{e}_{k,N-3}\cdots e_{k,0}+{(-1)}^N{L}_{N-1}{e}_{k,N-2}{e}_{k,N-3}\cdots e_{k,0}^2\}{\left[f^{\prime }\left(a\right)+O(e_k)\right]}^{-1}$$

$$=e_{k,N-1}\{f[t_{k,N-1},t_{k,N-2},t_{k,N-3}]e_{k,N-1}+{(-1)}^{N-1}f[t_{k,N-1},t_{k,N-2},\cdots ,t_{k,1},t_{k,0},t_{k,0},a]$$

$$\times e_{k,N-2}{e}_{k,N-3}\cdots e_{k,0}^2+{(-1)}^N{L}_{N-1}{e}_{k,N-2}{e}_{k,N-3}\cdots e_{k,0}^2+O(e_k^{2^{N-1}+1})\}{\left[f^{\prime }\left(a\right)+O(e_k)\right]}^{-1}$$

$$=e_{k,N-1}[c_2{q}_{N-1}{e}_{k,0}\prod _{i=0}^{N-2}{e}_{k,i}+{(-1)}^{N-1}{c}_{N+1}{e}_{k,0}\prod _{i=0}^{N-2}{e}_{k,i}+{(-1)}^N\frac{L_{N-1}}{f^{\prime }\left(a\right)}{e}_{k,0}\prod _{i=0}^{N-2}{e}_{k,i}+O(e_k^{2^{N-1}+1})]$$

$$=e_{k,0}\prod _{i=0}^{N-1}{e}_{k,i}[c_2{q}_{N-1}+{(-1)}^{N-1}{c}_{N+1}+{(-1)}^N\frac{L_{N-1}}{f^{\prime }\left(a\right)}]+O(e_k^{2^N+1})$$

$$=q_N{e}_{k,0}\prod _{i=0}^{N-1}{e}_{k,i}+O(e_k^{2^N+1}).$$

(30)

Hence, we obtain:

$$e_{k+1}=e_{k,n}=t_{k,n}-a=q_n{e}_{k,0}\prod _{i=0}^{n-1}{e}_{k,i}=q_n{q}_{n-1}{q}_{n-2}^2\cdots q_1^{2^{n-2}}{q}_0^{2^{n-1}}{e}_k^{2^n}+O(e_k^{2^n+1}).$$

(31)

The proof is completed. □

3. A General $\mathbf{n}$-Point Newton-Type Multipoint Iterative Method with Memory

Theorem 3 shows that the n-parameter n-point method (13) without memory reaches the optimal order $2^n$. Taking $L_1=-c_2$ and $L_i=\frac{f^{(i+1)}(a)}{(i+1)!},(i=2,3,\cdots ,n)$ in (13), the convergence order of method (13) can be improved. In this section, we replace the constant parameters $L_i,(i=1,2,\cdots ,n)$ of method (13) with the variable parameters $L_{k,i}$ and obtain a new n-parameter n-point method with memory. Variable parameters $L_{k,i}$ are constructed by the iterative sequences from current and previous iterations and satisfy the conditions $li{m}_{k\to \infty }{L}_{k,1}=-c_2=-\frac{f^{″}(a)}{2f^{\prime }(a)}$ and $li{m}_{k\to \infty }{L}_{k,i}=\frac{f^{(i+1)}(a)}{(i+1)!}$. To get the maximal order of convergence of the n-parameter n-point Newton-type method, we design the following variable parameters $L_{k,i},(i=1,\cdots ,n)$ by using Hermite’s interpolation polynomial

$$L_{k,1}=-\frac{H_{n+2}^{″}(t_{k,0})}{2f^{\prime }(t_{k,0})},$$

(32)

and

$$L_{k,i+1}=\frac{H_{n+i+2}^{(i+2)}(t_{k,i})}{(i+2)!},(0\le i\le n),$$

(33)

where

$$H_{n+2}(t)=H_{n+2}\left(t:t_{k,0},t_{k,0},t_{k-1,n-1},\cdots ,t_{k-1,0},t_{k-1,0}\right),$$

and

$$H_{n+i+2}(t)=H_{n+i+2}\left(t:t_{k,i},t_{k,i-1},\cdots ,t_{k,1},t_{k,0},t_{k,0},t_{k-1,n-1},\cdots ,t_{k-1,0},t_{k-1,0}\right).$$

Replacing the constant parameter $L_i$ with variable parameter $L_{k,i}$ in (13), we obtain: a general n-parameter n-point method with memory as follows:

$$\left\{\begin{array}{c}{t}_{k,1}=t_{k,0}-\frac{f(t_{k,0})}{L_{k,1}f(t_{k,0})+f^{\prime }(t_{k,0})},\hfill \\ t_{k,2}=t_{k,1}-\frac{f(t_{k,1})}{f\left[t_{k,1},t_{k,0}\right]+f\left[t_{k,1},t_{k,0},t_{k,0}\right](t_{k,1}-t_{k,0})+L_{k,2}{(t_{k,1}-t_{k,0})}^2},\hfill \\ \cdots ,\hfill \\ t_{k,n}=t_{k,n-1}-\frac{f(t_{k,n-1})}{H_n^{\prime }(t_{k,n-1})},\hfill \end{array}\right.$$

(34)

where $L_{k,i},(i=1,\cdots ,n)$ are the variable parameters constructed by (32)–(33) and $H_n^{\prime }(t_{k,n-1})$$=f[t_{k,n-1},t_{k,n-2}]+{\displaystyle \sum _{j=3}^n}\{f\left[t_{k,n-1},t_{k,n-2},\cdots ,t_{k,n-j}\right]{\displaystyle \prod _{i=2}^{j-1}}(t_{k,n-1}-t_{k,n-i})\}+(t_{k,n-1}-t_{k,0})$$L_{k,n-1}{\displaystyle \prod _{t=2}^n}(t_{k,n-1}-t_{k,n-t})+f\left[t_{k,n-1},t_{k,n-2},\cdots ,t_{k,1},t_{k,0},t_{k,0}\right]{\displaystyle \prod _{j=2}^n}(t_{k,n-1}-t_{k,n-j}),(n\ge 2)$.

From (14), (22) and (28), the error relations of method (34) can be obtained

$$e_{k,1}=(c_2+L_{k,1})e_k^2+O(e_k^3),$$

(35)

$$e_{k,2}=(c_2+L_{k,1})[c_2(c_2+L_{k,1})-c_3+\frac{L_{k,2}}{f^{\prime }(a)}]e_k^4+O(e_k^5),$$

(36)

and

$$e_{k,j}=t_{k,j}-a=q_{k,j}{e}_{k,0}\prod _{i=0}^{j-1}{e}_{k,i}=q_{k,j}{q}_{k,j-1}{q}_{k,j-2}^2\cdots q_{k,1}^{2^{j-2}}{q}_{k,0}^{2^{j-1}}{e}_k^{2^j}+O(e_k^{2^j+1}),2\le j\le n,$$

(37)

where $e_{k,j}=t_{k,j}-a,(j=0,1,2,\cdots ,n)$, $e_k=e_{k,0}=t_{k,0}-a$, $q_{k,0}=1$, $q_{k,1}=c_2+L_{k,1}$, $q_{k,n}={(-1)}^{n-1}{c}_{n+1}+{(-1)}^n\frac{L_{k,n}}{f^{\prime }(a)}+c_2{q}_{k,n-1},(n\ge 2)$.

The above consideration leads to the following Lemma.

Lemma 1.

Let $H_{n+i+2}(t),(i=0,1,2,\cdots ,n)$ be the Hermite interpolation polynomial of degree $n+i+2$ satisfying $H_{n+i+2}(t_{k,l})=f(t_{k,l}),(l=0,1,\cdots ,i)$, $H_{n+i+2}(t_{k-1,n-j})=f(t_{k-1,n-j}),$$(j=1,\cdots ,n)$, $H_{n+i+2}^{\prime }(t_{k,0})=f^{\prime }(t_{k,0})$ and $H_{n+i+2}^{\prime }(t_{k-1,0})=f^{\prime }(t_{k-1,0})$. Let $f(t)$ and its derivative $f^{(n+i+2)}$ be continuous in interval D. Nodes $t_{k,i},\cdots ,t_{k,1},t_{k,0},t_{k,0},t_{k-1,n-1},\cdots ,t_{k-1,1},t_{k-1,0},$$t_{k-1,0}$ are contained in interval D, which are sufficiently close to the simple zero a of $f(t)$. Define the error $e_{k,l}=t_{k,l}-a$ and assume that the condition $e_{k,l}=O(e_{k-1,n}\cdots e_{k-1,0}{e}_{k-1,0}),(0\le l\le n)$ holds. Then

$$H_{n+i+2}^{(i+2)}(t_{k,i})\sim (i+2)!f^{\prime }(a)\left[c_{i+2}-{(-1)}^{n+1}{c}_{n+i+3}{e}_{k-1,0}\prod _{j=1}^n{e}_{k-1,n-j}\right],(0\le i\le n).$$

(38)

Proof. 

The error relation of the Hermite’s interpolation polynomial $H_{n+i+2}(t)$ is given by

$$f(t)-H_{n+i+2}(t)=\frac{f^{(n+i+3)}(\eta )}{\left(n+i+3\right)!}[(t-t_{k,0})\prod _{l=0}^i(t-t_{k,l})][(t-t_{k-1,0})\prod _{j=1}^n(t-t_{k-1,n-j})],\eta \in D.$$

(39)

Differentiating (39) at t, we obtain:

$$f^{(i+2)}(t)-H_{n+i+2}^{(i+2)}(t)=\frac{1}{(n+i+3)!}\{[(t-t_{k,0})\prod _{l=0}^i(t-t_{k,l})][(t-t_{k-1,0})\prod _{j=1}^n(t-t_{k-1,n-j})]$$

$$\times \frac{d^{i+2}}{d{t}^{i+2}}[f^{(n+i+3)}(\eta )]+\sum _{m=1}^{i+1}{C}_{i+2}^m{[(t-t_{k,0})\prod _{l=0}^i(t-t_{k,l})(t-t_{k-1,0})\prod _{j=1}^n(t-t_{k-1,n-j})]}^{(m)}$$

$$\begin{array}{c}\times \frac{d^{i+2-m}}{d{t}^{i+2-m}}[f^{(n+i+3)}(\eta )]+{[(t-t_{k,0}){\displaystyle \prod _{l=0}^i}(t-t_{k,l})(t-t_{k-1,0}){\displaystyle \prod _{j=1}^n}(t-t_{k-1,n-j})]}^{(i+2)}{f}^{(n+i+3)}(\eta )\},\hfill \end{array}$$

(40)

and

$$f^{(i+2)}(t)-H_{n+i+2}^{(i+2)}(t)=\frac{1}{(n+i+3)!}\{(t-t_{k,0}){\displaystyle \prod _{l=0}^i}(t-t_{k,l})(t-t_{k-1,0}){\displaystyle \prod _{j=1}^n}(t-t_{k-1,n-j})$$

$$\times \frac{d^{i+2}}{d{t}^{i+2}}[f^{(n+i+3)}(\eta )]+{\displaystyle \sum _{m=1}^{i+1}}{C}_{i+2}^m{[(t-t_{k,0}){\displaystyle \prod _{l=0}^i}(t-t_{k,l})(t-t_{k-1,0}){\displaystyle \prod _{j=1}^n}(t-t_{k-1,n-j})]}^{(m)}$$

$$\begin{array}{c}\times \frac{d^{i+2-m}}{d{t}^{i+2-m}}[f^{(n+i+3)}(\eta )]+(i+2)![(t-t_{k-1,0}){\displaystyle \prod _{j=1}^n}(t-t_{k-1.n-j})+P_{n+1}(t)]f^{(n+i+3)}(\eta )\},\eta \in D,\hfill \end{array}$$

(41)

where $P_{n+1}(t)$ is a polynomial of degree $n+1$. Taylor’s series of $f(t)$ and its derivatives $f^{(i)}(t)$ at the points $t_{k,i}$ about zero a is

$$f^{\prime }(t_{k,i})=[1+2c_2{e}_{k,i}+3c_3{e}_{k,i}^2+O(e_{k,i}^3)]f^{\prime }(a),$$

(42)

$$f^{(i+2)}(t_{k,i})=[(i+2)!c_{i+2}+(i+3)!c_{i+3}{e}_{k,i}+O(e_{k,i}^2)]f^{\prime }(a),$$

(43)

and

$$f^{(n+i+3)}(\eta )=[(n+i+3)!c_{n+i+3}+(n+i+4)!c_{n+i+4}{e}_{\eta }+O(e_{\eta }^2)]f^{\prime }(a),$$

(44)

where $t_{k,i}\in D,\eta \in D$ and $e_{\eta }=\eta -a$.

Taking $t=t_{k,i}$ in (41) and using (44), we obtain:

$$H_{n+i+2}^{(i+2)}(t_{k,i})\sim f^{(i+2)}(t_{k,i})-(i+2)!\frac{f^{(n+i+3)}(\eta )}{(n+i+3)!}[P_{n+1}(t_{k,i})+(t_{k,i}-t_{k-1,0}){\displaystyle \prod _{j=1}^n}(t_{k,i}-t_{k-1,n-j})]$$

$$\begin{array}{c}\sim (i+2)!f^{\prime }(a)[c_{i+2}-{(-1)}^{n+1}{c}_{n+i+3}{e}_{k-1,0}{\displaystyle \prod _{j=1}^n}{e}_{k-1,n-j}].\hfill \end{array}$$

(45)

The proof is completed. □

From (33) and (45), we obtain:

$$L_{k,i+1}=\frac{H_{n+i+2}^{(i+2)}(t_{k,i})}{(i+2)!}\sim f^{\prime }(a)[c_{i+2}-{(-1)}^{n+1}{c}_{n+i+3}{e}_{k-1,0}{\displaystyle \prod _{j=1}^n}{e}_{k-1,n-j}],$$

(46)

and

$$c_{i+2}-\frac{L_{k,i+1}}{f^{\prime }(a)}\sim {(-1)}^{n+1}{c}_{n+i+3}{e}_{k-1,0}\prod _{j=1}^n{e}_{k-1,n-j}.$$

(47)

If sequence $\{t_n\}$ converges to the zero a with order r, we can get

$$e_{k+1}=e_{k+1,0}=e_{k,n}\sim Q_{k,n}{e}_{k,0}^r,$$

(48)

where $e_{k,n}=t_{k,n}-a$, and $Q_{k,n}$ is the asymptotic error constant. Suppose sequence $\{t_{k,j}\}$ has the convergence order $r_j$, we obtain:

$$e_{k,j}\sim Q_{k,j}{e}_{k,0}^{r_j},1\le j\le n-1,$$

(49)

and

$$c_{i+2}-\frac{L_{k,i+1}}{f^{\prime }(a)}\sim {(-1)}^{n+1}{c}_{n+i+3}{e}_{k-1,0}\prod _{j=1}^n{e}_{k-1,n-j}$$

$$\sim {(-1)}^{n+1}{c}_{n+i+3}{e}_{k-1,0}^{r_0+r_0+r_1+\cdots +r_{n-1}}\prod _{j=1}^n{Q}_{k-1,n-j}$$

$$\begin{array}{c}\sim T_{k,i+1}{e}_{k-1,0}^R,\hfill \end{array}$$

(50)

where $r_0=1,R=r_0+{\displaystyle \sum _{i=0}^{n-1}}{r}_i$ and $T_{k,i+1}={(-1)}^{n+1}{c}_{n+i+3}{\displaystyle \prod _{j=1}^n}{Q}_{k-1,n-j}.$

From (32) and (35), we obtain:

$$q_{k,1}=c_2+L_{k,1}\sim T_{k,1}{e}_{k-1,0}^R,$$

(51)

where $T_{k,1}={(-1)}^{n+1}{c}_{n+3}{\displaystyle \prod _{j=1}^n}{Q}_{k-1,n-j}$.

$$e_{k,1}\sim q_{k,1}{e}_{k,0}^2\sim T_{k,1}{e}_{k,0}^2{e}_{k-1,0}^R.$$

(52)

Lemma 2.

Let $a\in I$ be a simple zero of a sufficiently differentiable function f, then the $q_{k,j}$ in (37) such that

$$q_{k,j}\sim M_{k,j}{e}_{k-1,0}^R,(2\le j\le n),$$

(53)

where $r_0=1,R=r_0+{\displaystyle \sum _{i=0}^{n-1}}{r}_i,T_{k,i}={(-1)}^{n+1}{c}_{n+i+2}{\displaystyle \prod _{j=1}^n}{Q}_{k-1,n-j}$ and $M_{k,j}={\displaystyle \sum _{i=1}^j}{(-1)}^{i-1}$$c_2^{j-i}{T}_{k,i}$.

Proof. 

We proof the lemma by induction. Using (50)–(51) and taking $j=2$ in (37), we obtain:

$$e_{k,2}\sim q_{k,2}{e}_{k,1}{e}_{k,0}^2$$

$$\sim \{c_2{q}_{k,1}-c_3+\frac{L_{k,2}}{f^{\prime }(a)}\}{e}_{k,1}{e}_{k,0}^2$$

$$\begin{array}{c}\sim (c_2{T}_{k,1}-T_{k,2})e_{k,1}{e}_{k,0}^2{e}_{k-1,0}^R.\hfill \end{array}$$

(54)

Let $M_{k,2}=c_2{T}_{k,1}-T_{k,2}$ in (54), we obtain:

$$e_{k,2}\sim q_{k,2}{e}_{k,1}{e}_{k,0}^2\sim M_{k,2}{e}_{k,1}{e}_{k,0}^2{e}_{k-1,0}^R,$$

(55)

and

$$q_{k,2}\sim M_{k,2}{e}_{k-1,0}^R.$$

(56)

Using (50) and (51) and taking $j=3$ in (37), we get

$$e_{k,3}\sim q_{k,3}{e}_{k,2}{e}_{k,1}{e}_{k,0}^2$$

$$\sim \{c_2{q}_{k,2}+c_4-\frac{L_{k,2}}{f^{\prime }(a)}\}{e}_{k,2}{e}_{k,1}{e}_{k,0}^2$$

$$\begin{array}{c}\sim (c_2(c_2{T}_{k,1}-T_{k,2})+T_{k,3})e_{k,2}{e}_{k,1}{e}_{k,0}^2{e}_{k-1,0}^R.\hfill \end{array}$$

(57)

Let $M_{k,3}=c_2(c_2{T}_{k,1}-T_{k,2})+T_{k,3}$, we obtain:

$$e_{k,3}\sim q_{k,3}{e}_{k,2}{e}_{k,1}{e}_{k,0}^2$$

$$\begin{array}{c}\sim M_{K,3}{e}_{k,2}{e}_{k,1}{e}_{k,0}^2{e}_{k-1,0}^R,\hfill \end{array}$$

(58)

and

$$q_{k,3}{\sim M}_{k,3}{e}_{k-1,0}^R.$$

(59)

Assume that (53) holds for $j=n-1$, we obtain

$$q_{k,n-1}\sim M_{k,n-1}{e}_{k-1,0}^R.$$

(60)

Using (50) and (51) and taking $j=n$ in (37), we get

$$e_{k,n}\sim q_{k,n}{e}_{k,0}{\displaystyle \prod _{j=0}^{n-1}}{e}_{k,i}$$

$$\sim \{c_2{q}_{k,n-1}+{(-1)}^{n-1}{c}_{n+1}+{(-1)}^n\frac{L_{k,n-1}}{f^{\prime }(a)}\}{e}_{k,0}{\displaystyle \prod _{j=0}^{n-1}}{e}_{k,i}$$

$$\sim (T_{k,n}+c_2{M}_{k,n-1})e_{k,0}{\displaystyle \prod _{j=0}^{n-1}}{e}_{k,i}{e}_{k-1,0}^R$$

$$\begin{array}{c}\sim M_{k,n}{e}_{k,0}{\displaystyle \prod _{j=0}^{n-1}}{e}_{k,i}{e}_{k-1,0}^R,\hfill \end{array}$$

(61)

and

$$q_{k,n}\sim M_{k,n}{e}_{k-1,0}^R.$$

(62)

The proof is completed. □

According to the Lemma 1 and Lemma 2, we obtain: the convergence theorem as follows:

Theorem 4.

If $t_0$ is sufficiently close to a simple zero a of the sufficiently differentiable function $f(t)$ and the variable parameters $L_{k,1}$ and $L_{k,i},(2\le i\le n)$ of method (34) are calculated by (32) and (33), respectively. Then, the n-parameter n-point Newton-type iterative method (34) with memory reaches order $(2^n+2^{n-1}-1+\sqrt{2^{2n+1}+2^{2n-2}+2^n+1})/2$.

Proof. 

From (48) and (49), we obtain:

$$e_{k+1}=e_{k,n}\sim Q_{k,n}{(Q_{k-1,n}{e}_{k-1,0}^r)}^r\sim Q_{k,n}{Q}_{k-1,n}^r{e}_{k-1,0}^{r^2},e_{k,n}=x_{k,n}-a,$$

(63)

$$e_{k,j}\sim Q_{k,j}{(Q_{k-1,n}{e}_{k-1,0}^r)}^{r_j}\sim Q_{k,j}{Q}_{k-1,n}^{r_j}{e}_{k-1,0}^{r{r}_j},1\le j\le n-1.$$

(64)

Using (37) and (49), we arrive at:

$$e_{k,j}=t_{k,j}-a\sim q_{k,j}{e}_{k,0}\prod _{i=0}^{j-1}{e}_{k,i}$$

$$\sim q_{k,j}{e}_{k,0}^2\prod _{i=1}^{j-1}(Q_{k,i}{e}_{k,0}^{r_i})$$

$$\sim q_{k,j}{S}_{k,j}{e}_{k,0}^{2+r_1+r_2+\cdots r_{j-1}}$$

$$\sim M_{k,j}{e}_{k-1,0}^R{S}_{k,j}{e}_{k,0}^{2+r_1+r_2+\cdots r_{j-1}}$$

$$\sim M_{k,j}{e}_{k-1,0}^R{S}_{k,j}{Q}_{k-1,n}^{2+r_1+r_2+\cdots r_{j-1}}{e}_{k-1,0}^{r(2+r_1+r_2+\cdots r_{j-1})}$$

$$\begin{array}{c}\sim M_{k,j}{S}_{k,j}{Q}_{k-1,n}^{2+r_1+r_2+\cdots r_{j-1}}{e}_{k-1,0}^{R+r(2+r_1+r_2+\cdots r_{j-1})},\hfill \end{array}$$

(65)

where $S_{k,j}={\displaystyle \prod _{i=1}^{j-1}}{Q}_{k,i},2\le j\le n$.

According to (48) and (53), we have:

$$e_{k,1}\sim q_{k,1}{e}_{k,0}^2\sim T_{k,1}{e}_{k-1,0}^R{(Q_{k-1,n}{e}_{k-1,0}^r)}^2$$

$$\begin{array}{c}\sim T_{k,1}{Q}_{k-1,n}^2{e}_{k-1,0}^{2r+R}.\hfill \end{array}$$

(66)

Comparing the exponents of error $e_{k-1,0}$ in pairs of ((64), (66)) for $j=1$, ((63), (65)) for $j=n$ and ((64), (65)) for $2\le j\le n-1$, we obtain:

$$\left\{\begin{array}{c}{r}^2=r(2+r_1+r_2+\cdots +r_{n-1})+R=rR+R,\hfill \\ r{r}_{n-1}=r(2+r_1+r_2+\cdots +r_{n-2})+R,\hfill \\ r{r}_j=r(2+r_1+r_2+\cdots +r_{j-1})+R,(j=2,\cdots ,n-2),\hfill \\ r{r}_1=R+2r.\hfill \end{array}\right.$$

(67)

According to (67), we obtain:

$$\frac{r^2}{1+r}=R=2+r_1+r_2+\cdots r_{n-1},$$

(68)

$$r_j=2^{j-1}{r}_1,(j=2,\cdots ,n-1),$$

(69)

$$r=2r_{n-1},$$

(70)

$$r_1=2+\frac{r}{1+r}.$$

(71)

From (68) and (71), we obtain:

$$r^2-(2^n+2^{n-1}-1)r-2^n=0.$$

(72)

The solution of the Equation (72) is $(2^n+2^{n-1}-1+\sqrt{2^{2n+1}+2^{2n-2}+2^n+1})/2$. Thus, the n-parameter n-point Newton-type method with memory has the convergence order $(2^n+2^{n-1}-1+\sqrt{2^{2n+1}+2^{2n-2}+2^n+1})/2$. □

Remark 1.

According to Theorem 4, we conclude that the maximal order of n-parameter n-point Newton-type iterative method (34) with memory is $(2^n+2^{n-1}-1+\sqrt{2^{2n+1}+2^{2n-2}+2^n+1})/2$. The variable parameters $L_{k,i}$ of method (34) can be designed by simple interpolation polynomial, but this will decrease the order of convergence of method (34). Therefore, we do not discuss the low-order interpolation polynomial in this paper. For $n=2$, the order of method (34) with memory is $r=(5+\sqrt{41})/2\approx 5.701$. For $n=3$, the order of (34) with memory is $r=(11+\sqrt{153})/2\approx 11.684$.

4. Basins of Attraction

The basins of attraction can be applied to analyze the stability of the multipoint iterative method [23,24,25,26,27,28,29,30,31,32], which will help us to select the iterative schemes whose behaviors are better qualitatively. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show the basins of attraction of different methods. Our methods (13) (n = 3) and (34) (n = 2,3) are compared with methods (2) (n = 3), (3) (n = 3), (4) (n = 3), (73) and (76) for solving complex equations $z^n-1=0,$$(n=2,3,4,5,6)$. The field $D=[-5.0,5.0]\times [-5.0,5.0]\in C$ is divided into a grid of $500\times 500$ in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. The initial point $z_0$ will be painted with black after 25 iterations. If the sequence generated by the iterative method reaches a zero of the polynomial, the initial point $z_0$ will be painted in a color previously selected for this zero. In the same basin of attraction, the number of iterations needed to achieve the solution is shown in darker or brighter colors (the less iterations, the brighter the color). The tolerance is $|z-z^{*}|<{10}^{-3}$ in programs. Table 1, Table 2, Table 3, Table 4 and Table 5 show the average number of iterations(ANI) and the percentage of points (POP) which guarantee the convergence to the roots of complex equations $z^n-1=0,$$(n=2,3,4,5,6)$.

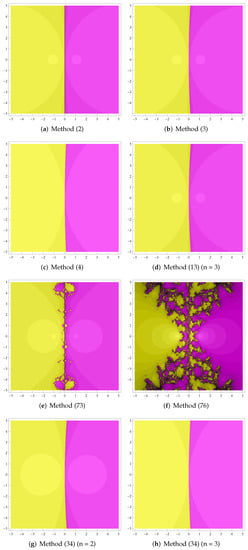
Figure 1. Dynamical planes for $z^2-1=0$.

Figure 2. Dynamical planes for $z^3-1=0$.

Figure 3. Dynamical planes for $z^4-1=0$.

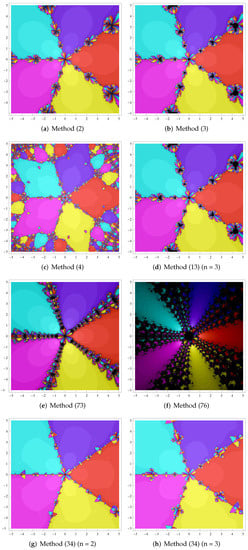
Figure 4. Dynamical planes for $z^5-1=0$.

Figure 5. Dynamical planes for $z^6-1=0$.

Table 1. Numerical results of different methods for $z^2-1=0$.

Methods	(2)	(3)	(4)	(13) (n = 3)	(73)	(76)	(34) (n = 2)	(34) (n = 3)
POP	99.80%	100%	100%	100%	99.80%	96.02%	100%	100%
ANI	2.2781	2.2415	1.1430	2.2233	3.4107	11.401	1.8806	1.1371

Table 2. Numerical results of different methods for $z^3-1=0$.

Methods	(2)	(3)	(4)	(13) (n = 3)	(73)	(76)	(34) (n = 2)	(34) (n = 3)
POP	100%	99.99%	100%	100%	99.62%	77.53%	100%	100%
ANI	2.6354	2.6416	1.3591	2.6386	4.4523	15.669	2.1994	1.3430

Table 3. Numerical results of different methods for $z^4-1=0$.

Methods	(2)	(3)	(4)	(13) (n = 3)	(73)	(76)	(34) (n = 2)	(34) (n = 3)
POP	99.60%	100%	100%	100%	97.10%	63.42%	100%	100%
ANI	3.5018	3.4208	2.1952	3.4200	6.3275	18.667	2.5931	1.9959

Table 4. Numerical results of different methods for $z^5-1=0$.

Methods	(2)	(3)	(4)	(13) (n = 3)	(73)	(76)	(34) (n = 2)	(34) (n = 3)
POP	99.83%	98.34%	99.98%	98.35%	95.75%	61.57%	99.99%	100%
ANI	4.2132	4.3115	3.5273	4.3119	6.9659	19.920	2.7746	2.2169

Table 5. Numerical results of different methods for $z^6-1=0$.

Methods	(2)	(3)	(4)	(13) (n = 3)	(73)	(76)	(34) (n = 2)	(34) (n = 3)
POP	99.60%	99.98%	98.09%	99.98%	94.27%	53.35%	99.92%	99.99%
ANI	4.6530	4.5337	5.1056	4.5347	7.8804	21.428	3.3563	2.4707

Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show that iterative methods without memory (2), (3) and (13) have similar convergence behavior. The black areas of basins of attraction for methods (73) and (76) are larger than in other methods. This implies that the convergence behavior of iterative methods with memory (73) and (76) are poor. The basins of attraction for method (34) with memory are brighter than the other methods with and without memory. This means that iterative method (34) requires a lesser number of iterations than other methods. Table 1, Table 2, Table 3, Table 4 and Table 5 show that, compared with other methods, our method (34) (n = 3) has the highest percentage of points which guarantee the convergence to the roots of complex equations and requires less number of iterations than various well-known methods. Thus, our method (34) (n = 3) has good stability for solving simple nonlinear equations.

5. Numerical Examples

The general n-parameter n-point Newton-type methods (13) and (34) are compared with Petković’s two-step Newton-type method with memory [12] (73), Wang’s Newton-type method with memory [33] (76), Petković’s n-point Newton-type method (2) without memory and Wang’s n-point Newton-type methods (3) and (4) for solving nonlinear functions.

Petković’s two-step Newton-type iterative method with memory is calculated as follows [12]:

$$\left\{\begin{array}{cc}\hfill y_k=& \varphi (y_{k-1})f{(t_k)}^2+M(t_k),\hfill \\ \hfill t_{k+1}=& \varphi (y_k)f{(t_k)}^2+M(t_k),\hfill \end{array}\right.$$

(73)

where

$$M(t_k)=t_k-\frac{f(t_k)}{f^{\prime }(t_k)},$$

(74)

$$\varphi (t)=\left(\frac{t-t_k}{f(t)-f(t_k)}-\frac{1}{f^{\prime }(t_k)}\right)\frac{1}{f(t)-f(t_k)}.$$

(75)

Wang’s Newton-type iterative method with memory is calculated as follows [33]:

$$\left\{\begin{array}{cc}\hfill z_k=& t_k-\frac{f(t_k)}{f^{\prime }(t_k)},\hfill \\ \hfill y_k=& t_k-\frac{(z_k-t_k)}{1-L_k(z_k-t_k)},\hfill \\ \hfill t_{k+1}=& y_k-\frac{f(y_k)f^{\prime }(t_k)}{f{[t_k,y_k]}^2},\hfill \end{array}\right.$$

(76)

where $L_k=\frac{t_k-z_{k-1}}{(z_k-t_{k-1})(t_k-t_{k-1})}.$

Iterative methods are applied to solve the following nonlinear equations:

$f_1(t)=cos(t)+t^2-t{e}^t=0,a\approx 0.63915409633200758$,  $t_0=0.5$,

$f_2(t)=t^4+log(t)-5=0,a\approx 1.4658939193282127$,  $t_0=1.6$,

$f_3(t)=-sin(t)+9t^2-1=0,a\approx 0.3918469070026$,    $t_0=0.3$.

$f_4(t)=t-\pi -t^3\sin (t)=0,a\approx 3.1415926535898$,    $t_0=2.9$.

The initial parameters $L=L_1=0.01$ and $L_{k,i}=0.01,(i=0,1,2)$ are used in the the iterative methods (3), (4), (13), (34) (73) and (76). Table 6, Table 7, Table 8 and Table 9 show the absolute error $|t_k-a|$ for the first four steps and the approximate computational order of convergence (ACOC) [34]:

$$R=\frac{ln(|t_{n+1}-t_n|/|t_n-t_{n-1}|)}{ln(|t_n-t_{n-1}|/|t_{n-1}-t_{n-2}|)}.$$

(77)

Table 6. Numerical results for $f_1(t)$.

Method	$\left|{\mathit{t}}_1-\mathit{a}\right|$	$\left|{\mathit{t}}_2-\mathit{a}\right|$	$\left|{\mathit{t}}_3-\mathit{a}\right|$	$\left|{\mathit{t}}_4-\mathit{a}\right|$	ACOC
(2) n = 2	0.51126 $\times {10}^{-4}$	0.97721 $\times {10}^{-18}$	0.13043 $\times {10}^{-72}$	0.41401 $\times {10}^{-292}$	4.0000003
(3) n = 2	0.54528 $\times {10}^{-4}$	0.13358 $\times {10}^{-17}$	0.48098 $\times {10}^{-72}$	0.80864 $\times {10}^{-290}$	4.0000000
(13) n = 2	0.52925 $\times {10}^{-4}$	0.11597 $\times {10}^{-17}$	0.26735 $\times {10}^{-72}$	0.75510 $\times {10}^{-291}$	4.0000000
(73)	0.44088 $\times {10}^{-5}$	0.64006 $\times {10}^{-25}$	0.44087 $\times {10}^{-115}$	0.32433 $\times {10}^{-526}$	4.5599449
(76)	0.27347 $\times {10}^{-3}$	0.29224 $\times {10}^{-16}$	0.13268 $\times {10}^{-70}$	0.60206 $\times {10}^{-301}$	4.2386945
(34) n = 2	0.52925 $\times {10}^{-4}$	0.21668 $\times {10}^{-27}$	0.48274 $\times {10}^{-159}$	0.86928 $\times {10}^{-910}$	5.7024880
(2) n = 3	0.40835 $\times {10}^{-8}$	0.24321 $\times {10}^{-68}$	0.38502 $\times {10}^{-550}$		8.0008692
(3) n = 3	0.45332 $\times {10}^{-8}$	0.61330 $\times {10}^{-68}$	0.68830 $\times {10}^{-547}$		8.0000000
(13) n = 3	0.44026 $\times {10}^{-8}$	0.47630 $\times {10}^{-68}$	0.89387 $\times {10}^{-548}$		8.0000000
(4) n = 3	0.45332 $\times {10}^{-8}$	0.14236 $\times {10}^{-85}$	0.62560 $\times {10}^{-861}$		10.004219
(34) n = 3	0.44026 $\times {10}^{-8}$	0.29405 $\times {10}^{-104}$	0.86439 $\times {10}^{-1222}$		11.619740

Table 7. Numerical results for $f_2(t)$.

Method	$\left|{\mathit{t}}_1-\mathit{a}\right|$	$\left|{\mathit{t}}_2-\mathit{a}\right|$	$\left|{\mathit{t}}_3-\mathit{a}\right|$	$\left|{\mathit{t}}_4-\mathit{a}\right|$	ACOC
(2) n = 2	0.11793 $\times {10}^{-3}$	0.84626 $\times {10}^{-16}$	0.22447 $\times {10}^{-64}$	0.11110 $\times {10}^{-258}$	4.0000000
(3) n = 2	0.12130 $\times {10}^{-3}$	0.97704 $\times {10}^{-16}$	0.41138 $\times {10}^{-64}$	0.12928 $\times {10}^{-257}$	4.0000000
(13) n = 2	0.12145 $\times {10}^{-3}$	0.98370 $\times {10}^{-16}$	0.42339 $\times {10}^{-64}$	0.14529 $\times {10}^{-257}$	4.0000000
(73)	0.62678 $\times {10}^{-5}$	0.88468 $\times {10}^{-24}$	0.18867 $\times {10}^{-109}$	0.41780 $\times {10}^{-500}$	4.5599373
(76)	0.31113 $\times {10}^{-3}$	0.69098 $\times {10}^{-15}$	0.29916 $\times {10}^{-64}$	0.23336 $\times {10}^{-273}$	4.2360780
(34) n = 2	0.12145 $\times {10}^{-3}$	0.42142 $\times {10}^{-24}$	0.33957 $\times {10}^{-142}$	0.70177 $\times {10}^{-815}$	5.6961912
(2) n = 3	0.15535 $\times {10}^{-7}$	0.72017 $\times {10}^{-63}$	0.15361 $\times {10}^{-505}$		8.0000000
(3) n = 3	0.16390 $\times {10}^{-7}$	0.11729 $\times {10}^{-62}$	0.80666 $\times {10}^{-504}$		8.0000000
(13) n = 3	0.16405 $\times {10}^{-7}$	0.11831 $\times {10}^{-62}$	0.86592 $\times {10}^{-504}$		8.0000000
(4) n = 3	0.16390 $\times {10}^{-7}$	0.46896 $\times {10}^{-79}$	0.17682 $\times {10}^{-794}$		9.9998487
(34) n = 3	0.16405 $\times {10}^{-7}$	0.65259 $\times {10}^{-95}$	0.93155 $\times {10}^{-1120}$		11.725876

Table 8. Numerical results for $f_3(t)$.

Method	$\left|{\mathit{t}}_1-\mathit{a}\right|$	$\left|{\mathit{t}}_2-\mathit{a}\right|$	$\left|{\mathit{t}}_3-\mathit{a}\right|$	$\left|{\mathit{t}}_4-\mathit{a}\right|$	ACOC
(2) n = 2	0.42633 $\times {10}^{-3}$	0.10988 $\times {10}^{-12}$	0.48611 $\times {10}^{-51}$	0.18620 $\times {10}^{-204}$	4.0000000
(3) n = 2	0.43209 $\times {10}^{-3}$	0.11749 $\times {10}^{-12}$	0.64401 $\times {10}^{-51}$	0.58130 $\times {10}^{-204}$	4.0000000
(13) n = 2	0.43241 $\times {10}^{-3}$	0.11792 $\times {10}^{-12}$	0.65398 $\times {10}^{-51}$	0.61858 $\times {10}^{-204}$	4.0000000
(73)	0.59903 $\times {10}^{-4}$	0.25674 $\times {10}^{-18}$	0.13907 $\times {10}^{-83}$	0.35294 $\times {10}^{-381}$	4.5597146
(76)	0.10103 $\times {10}^{-2}$	0.69855 $\times {10}^{-12}$	0.23785 $\times {10}^{-50}$	0.22107 $\times {10}^{-213}$	4.2381255
(34) n = 2	0.43241 $\times {10}^{-3}$	0.48374 $\times {10}^{-19}$	0.18668 $\times {10}^{-114}$	0.20222 $\times {10}^{-656}$	5.6801734
(2) n = 3	0.27207 $\times {10}^{-6}$	0.50023 $\times {10}^{-51}$	0.65317 $\times {10}^{-409}$		8.0000000
(3) n = 3	0.27947 $\times {10}^{-6}$	0.63668 $\times {10}^{-51}$	0.46203 $\times {10}^{-408}$		8.0000000
(13) n = 3	0.27977 $\times {10}^{-6}$	0.64293 $\times {10}^{-51}$	0.50004 $\times {10}^{-408}$		8.0000000
(4)n=3	0.27947 $\times {10}^{-6}$	0.14545 $\times {10}^{-67}$	0.21179 $\times {10}^{-680}$		10.000013
(34) n = 3	0.27977 $\times {10}^{-6}$	0.19008 $\times {10}^{-76}$	0.75443 $\times {10}^{-913}$		11.920006

Table 9. Numerical results for $f_4(t)$.

Method	$\left|{\mathit{t}}_1-\mathit{a}\right|$	$\left|{\mathit{t}}_2-\mathit{a}\right|$	$\left|{\mathit{t}}_3-\mathit{a}\right|$	$\left|{\mathit{t}}_4-\mathit{a}\right|$	ACOC
(2) n = 2	0.45791 $\times {10}^{-2}$	0.29033 $\times {10}^{-9}$	0.47507 $\times {10}^{-38}$	0.34058 $\times {10}^{-153}$	4.0000000
(3) n = 2	0.46989 $\times {10}^{-2}$	0.32946 $\times {10}^{-9}$	0.80651 $\times {10}^{-38}$	0.28961 $\times {10}^{-152}$	4.0000000
(13) n = 2	0.47013 $\times {10}^{-2}$	0.33026 $\times {10}^{-9}$	0.81472 $\times {10}^{-38}$	0.30172 $\times {10}^{-152}$	4.0000000
(73)	0.21843 $\times {10}^{-2}$	0.71702 $\times {10}^{-12}$	0.63014 $\times {10}^{-55}$	0.30506 $\times {10}^{-251}$	4.5595182
(76)	0.13208 $\times {10}^{-1}$	0.35938 $\times {10}^{-8}$	0.23138 $\times {10}^{-35}$	0.10762 $\times {10}^{-150}$	4.2415301
(34) n = 2	0.47013 $\times {10}^{-2}$	0.78035 $\times {10}^{-14}$	0.22231 $\times {10}^{-82}$	0.33152 $\times {10}^{-472}$	5.6871333
(2) n = 3	0.16926 $\times {10}^{-4}$	0.22742 $\times {10}^{-38}$	0.24157 $\times {10}^{-309}$		8.0000000
(3) n = 3	0.17852 $\times {10}^{-4}$	0.36590 $\times {10}^{-38}$	0.11400 $\times {10}^{-307}$		8.0000000
(13) n = 3	0.17864 $\times {10}^{-4}$	0.36802 $\times {10}^{-38}$	0.11943 $\times {10}^{-307}$		7.9999986
(4) n = 3	0.17852 $\times {10}^{-4}$	0.56501 $\times {10}^{-49}$	0.55091 $\times {10}^{-494}$		10.115357
(34) n = 3	0.17864 $\times {10}^{-4}$	0.38690 $\times {10}^{-57}$	0.18244 $\times {10}^{-682}$		11.873804

Table 6, Table 7, Table 8 and Table 9 show that the numerical results coincide with the theory developed in this paper. Our n-parameter n-point Newton-type method (34) has higher convergence order and computational accuracy than the existing Newton-type methods. Method (34) greatly improves the convergence order of method (13) by using n variable parameters. The variable parameters $L_{k,i}$ in method (34) are designed by using iteration sequences from current and previous iterations, which do not increase the computational cost of the iterative method. This implies that our method (34) with memory posses a very high computational efficiency.

6. Conclusions

In order to improve the convergence order of Newton-type multipoint iterative method, a general n-parameter n-point Newton-type iterative method with memory is designed in this paper. Firstly, an n-parameter n-point Newton-type multipoint method (13) with optimal order $2^n$ is proposed. Based on method (13), a general n-parameter n-point Newton-type multipoint iterative method (34) with n variable parameters is proposed for solving nonlinear equations. The maximal order of method (34) is superior to the existing Newton-type iterative methods with and without memory. The basins of attraction show that the proposed method (34) has the highest percentage of points, which guarantees the convergence to the roots of complex equations. The ANI of the proposed method (34) is less than that of other methods in Table 6, Table 7, Table 8 and Table 9. This implies that the proposed method (34) has good stability. The numerical results shows that the proposed method (34) greatly improves the computational efficiency and convergence order of the Newton-type iterative method.