Abstract
Ever since the appearance of quantum computers, prime factoring and discrete logarithm-based cryptography have been questioned, giving birth to the so-called post-quantum cryptography. The most prominent field in post-quantum cryptography is lattice-based cryptography, protocols that are proved to be as difficult to break as certain hard lattice problems like Learning with Errors (LWE) or Ring Learning with Errors (R-LWE). Furthermore, the application of cryptographic techniques to different areas, like electronic voting, has also nourished a great interest in distributed cryptography. In this work, we will give two original threshold protocols based in the lattice problem R-LWE: one for key generation and one for decryption. We will prove them both correct and secure under the assumption of hardness of some well-known lattice problems. Finally, we will give a rough implementation of the protocols in C to give some tentative results about their viability, in particular our model generates keys in the order of ms and decrypts and encrypts in the order of ms.
Keywords:
post-quantum cryptography; threshold cryptography; lattices; Ring Learning with Errors (R-LWE); R-LWE encryption MSC:
94A60; 68P25
1. Introduction
The appearance of the computer in the XXth century caused the explosion of cryptography, the safety of which enabled the huge development of the connected society (for example, recent cryptographic endeavours into facilitating the implementation of the Smart City model [1]). Similarly, the development of quantum computing and specifically Shor’s algorithm [2], which renders cryptography based on the discrete logarithm and prime factoring problems effectively useless against a quantum adversary, spawned new types of cryptography.
There are two main types of cryptography that have been developed to overcome the attacks of quantum computers: quantum and post-quantum cryptography. Quantum cryptography relies on quantum algorithms that cannot be broken by quantum adversaries, while post-quantum deals with classical (non-quantum) algorithms that cannot be broken by quantum adversaries. We focus on post-quantum cryptography given that widespread use of moderately powerful quantum computers seems unachievable in the short run. In this realm, the area that has had more recent advancements is lattice-based cryptography, as shown by the fact that in the Status Report on the Second Round of the National Institute of Standards and Technology (NIST) Post-Quantum Cryptography Standardization Process [3] most third-round finalists are lattice-based schemes. Within lattice based schemes, cryptography based in the Learning with Errors (LWE) problem and its variants is especially relevant. We will build our proposals around the Ring Learning with Errors (R-LWE) problem.
There are many applications of post-quantum cryptography, but the one we we focus on is electronic voting. Electronic voting is characterized by a significant lack of trust. The lack of trust in other entities is what initially spawned the concept of cryptography, thus going further in this direction is the next logical step to follow. Therefore, the aim is to “spread” that trust, so that one single corrupt player can no longer break the protocol. Distributed cryptography is this idea of spreading the tasks between several players so that only certain subsets of them can perform the cryptographic protocol. The interest in distributed cryptography, and in particular post-quantic distributed cryptography, can be seen in interesting recent advancements in the area like [4,5].
Adding post-quantum and distributed cryptography finally brings us to our main subject: R-LWE-based distributed key generation and threshold decryption.
1.1. State-of-the-Art
Despite the shown interest and potential usefulness of lattice-based threshold public key encryption cryptography, the amount of existing proposals is scarce, especially of proposals focusing on the R-LWE problem. Most of the existing proposals revolve around the LWE problem (see, for example, [5,6,7,8]), which has the potential problem of keys and ciphertexts growing with instead of with like the R-LWE variant (with n the dimension of the lattice), thus having a higher possibility to need a greater amount of operations and therefore computation time. In the world of threshold encryption based on R-LWE, as far as we know there is only one proposal given in [9], which is based on the homomorphic properties of the presented Fully Homomorphic Encryption scheme. However, this proposal does not come with a distributed key generation protocol (as it relies on a Trusted Third-Party (TTP) for that). Additionally, to the best of our knowledge, none of the mentioned proposals give an implementation to truly analyze computation times, even if implementations of post-quantic protocols is a hot topic, as shown by the Open Quantum Safe project [10]. Furthermore, the Open Quantum Safe project also shows us that despite recent developments, most applications are still on the prototype phase. A summary of the current state of the art can be found in Table 1.

Table 1.
State-of-the-art.
1.2. Contributions
In this work, we present original protocols of both distributed key generation and threshold decryption that, as far as we know, are the first R-LWE-based threshold protocols including both decryption and key generation. The protocols are based on the LWE proposal given by Bendlin and Damgård in [6], whose ideas are transported into the R-LWE setting. Furthermore, we prove these protocols both correct and secure, we give a set of parameters for which our protocols have more than 100 bits of security and we give a rough implementation in C of the protocols to analyze their performance.
1.3. Structure
In Section 2 we will give the preliminaries necessary to follow the work in the fields of cryptographic primitives, distributed cryptography, and Ring Learning with Errors. In Section 3, we present the protocols that act as the main contribution of this work, while in Section 4 we will prove their correctness, and in Section 5 we will prove them secure. Section 6 will be dedicated to analyzing the implementation in C of the protocols, and finally in Section 7 we will give our final concluding thoughts and possible future work. For the appendices, in Appendix A we give correctness and security proofs against an adversary acting actively in both protocols, in Appendix B we give the proofs for auxiliary results, and in Appendix C we give the link to a repository containing the relevant code of our implementation.
Most of the introduction has been taken from the introduction in the Master’s Thesis [11] by Ferran Alborch.
2. Preliminaries
2.1. Notation
Elements in , , or will be indicated as lower case letters (a, b, …), while elements in , , or will be indicated as bold lower case letters (). We will consider with the representatives in . Let X be a random variable, means X follows the probability distribution , means x is sampled from a random variable following the distribution , means Y is a vector such that every coordinate is independently sampled from the distribution and for any set , is the action of choosing j uniformly at random from . We will also identify any polynomial of degree , with the vector . A function g is said to be negligible over n () if such that . Finally, a function f is said to be if there exists and such that for all , while a function f is said to be if for all exists such that for all .
2.2. Cryptographic Primitives
We will start by giving some cryptographic primitives, well-known definitions, protocols, or techniques used in cryptography upon which we will build our encryption scheme and protocols. First, we will formally define what an encryption scheme is.
Definition 1.
An encryption scheme is a tuplesuch that:
- is a set called plaintext space.
- is a set called ciphertext space.
- is a set called key space. Generally a key generation procedure is also specified to generate.
- is a set of functionscalled encryption functions.is a randomness space to account for probabilistic encryption schemes.
- is a set of functionscalled decryption functions.
Note that ifanduse the same key, then we call it symmetric encryption; otherwise, we call it asymmetric or public key encryption. In public key encryption,can be divided into two different sets,, the secret key space, and, the public key space. The public key (known by all entities) is used to encrypt messages and the secret key (known only to the decrypting entity) is used to decrypt them.
Once we have defined a cryptosystem, we need to prove some properties about it to ensure it is useful. The most important of these properties are correctness and security, and from now on we will focus solely on public key encryption.
Definition 2.
Letbe an encryption scheme. The encryption scheme is said to be correct if for allexists some computablesuch that, given λ the security parameter, the probability
for all.
In contrast to the correctness of an encryption scheme, security can be defined in various ways. This is due to the fact that a decryption should always be correct (or always, except with negligible probability) but security depends on the properties of the adversary we want to protect us against (information available, computational power) and what we want to ensure (that the adversary cannot know what message was encrypted or that he cannot distinguish which message has been encrypted from a pool of plaintexts). In our case, we are interested in CPA security.
Attack Game 1
(Attack Games 5.2 and 11.2, [12]). Let be an encryption scheme. Given an adversary , the Chosen Plaintext Attack (CPA) attack game, has two experiments: Experiment 0 and Experiment 1. For we define Experiment b as
- The challenger choosesand sends it to the adversary.
- The adversary submits polynomially many queries to the challenger. For, submits two same-length messages. The challenger computesand sends it to the adversary.
- The adversary outputs a bit.
Letbe the event in whichoutputs 1 in the event b, then we define’s CPA advantage as
Definition 3
(Definitions 5.2 and 11.4, [12]). An encryption scheme is said to be CPA secure if for all efficient adversaries , the value is negligible.
Furthermore, security can be achieved against different types of adversaries depending on what capacities they have. We will focus basically on passive adversaries (also known as honest but curious), who can see all the information the corrupted players have but cannot make them deviate from the protocol, and active adversaries (also known as malicious), who can make the corrupted players deviate arbitrarily from the protocol. Another important distinction to make is whether it is a static adversary, who picks the subset of players it will corrupt prior to the start of the protocol; or a dynamic adversary, who can change the subset of corrupted players during the execution of the protocol. Our security model will be against static adversaries.
2.3. Distributed Cryptography
The specific branch of cryptography we are interested in this work is distributed cryptography.
Definition 4
([13]). A threshold secret sharing scheme of threshold t and u players is a scheme such that given some data D it divides it into u pieces such that:
- Knowledge ofor more piecesmakes D easily computable.
- Knowledge of t or less piecesleaves D completely undetermined (i.e., all its possible values are equally likely).
Definition 5.
We will call a threshold encryption scheme a secret sharing scheme where what we try to recover is a plaintext from a ciphertext.
One of the first secret sharing schemes and one of the most used up to this day due to its simplicity to compute and understand, is Shamir Secret Sharing. We will use it profusely throughout our work.
Technique 1
([13]). Shamir Secret Sharing over a field of a secret of threshold t works as follows:
- Choose t elementsand define the polynomial(i.e., choose a random polynomialsuch that).
- For every player, their share of the secret is, withbeing different for every player and agreed before-hand.
- Whenplayers want to recover the secret, they use Lagrange interpolation to findand then compute.
The convenience of this secret sharing scheme lays in two main properties: the recovery of the secret is done through Lagrange interpolation (which is easy to compute) and the shares are linear, which means that a linear combination of the shares is a share of the linear combination of secrets. Both of these properties will be used in our work.
Other distributed cryptographic tools we will use are the Pseudo-Random Secret Sharing (PRSS) and the Non-Interactive Verifiable Secret Sharing (NIVSS) techniques. These tools will be crucial in our proposal, as the security of our protocols is based on being able to mask the relevant information with noise in such a way that the adversary cannot retrieve it. To generate this noise we will use these two protocols.
Definition 6.
A Pseudo-Random Function (PRF),, is a deterministic function that maps two sets (domain and range) on the basis of a key, which when run multiple times with the same input gives the same output but given an arbitrary input the output seems random, i.e., one cannot distinguish the output of a given input from a random oracle. A random oracle is an oracle (a theoretical black box) that responds to every query with a (truly) random response chosen uniformly from its output domain. If a query is repeated, it responds the same way every time that query is submitted.
Technique 2
([14]). Pseudo-Random Secret Sharing in (PRSS) allows u players to non-interactively share a common random value x with a threshold of t players () given a pseudo-random function that with input a key and a value μ outputs values in the interval and whatever group of players of size less or equal than t cannot obtain relevant information on x. The algorithm works as follows:
- For each subset H of t players a TTP defines a keyuniformly at random.
- Each player is given such that .
- The pseudo-random number they are sharing isfor a value μ. Since there aresuch subsets H, we know.
- To computea Shamir share of x every player computeswhereis the unique degree-t polynomial (in our casewith q prime) such thatandfor all.
Technique 3
([14]). Non-Interactive Verifiable Secret Sharing in (NIVSS), allows a dealer D to share a secret s with u players with threshold t given a value μ and a pseudo-random function that with input a key and μ outputs values in the interval . It works very similarly to PRSS. The algorithm works as follows:
- For each subset H of t players the dealer D chooses a keyuniformly at random.
- The dealer D gives to playerall thesuch that.
- The dealer D reconstructs the pseudo-random value the players share, since he has all the keys.
- D broadcasts the value, and now all the players have a share of s by adding their shares of x to.
Finally, as we will be using distributed methods, one must ensure that the order in which the different players send information does not compromise the security of the scheme. Broadly speaking, the last player to send information would have an advantage with respect to the first one due to knowing more information when making its decision. To solve this problem, it is standard to use commitment schemes.
Definition 7
(Definition 8.8, [12]). Given a message space , a commitment scheme is a pair of efficient algorithms where C (the commiter) is an algorithm that given outputs a commitment c and an opening string o and V (the verifier) is a deterministic protocol that given outputs accept or reject, and such that it satisfies the following properties:
- Correctness: For all, if then
- Binding: This property is the notion that once a commitment c is generated, it should only commit for one message in. In particular, for every efficient adversarythat outputswe must have that
- Hiding: This property is the notion that the commitment c alone should not reveal any information about the message m. To properly define this, we use a semantic security attack game (see Attack Game 2.1, [12]) where instead of encrypting the messages we compute its commitment. What we ask is, ifdenotes the event that the adversary outputs 1 in experiment b, then
2.4. Ring Learning with Errors
The Learning with Errors (LWE) problem was introduced by Regev in 2005 in a previous version of [15] as a generalization of the parity learning problem, and gave both a cryptographic protocol based on it and a reduction of its security to a hard lattice problem (the GAP Shortest Vector Problem (GAPSVP)).
However, cryptosystems based on the LWE problem have several issues. For example, many of them need to encrypt bit by bit and, more importantly, the public keys required are very costly to store as they are usually (big) matrices of elements in . Coupling these two together we get that a lot of storage space is usually needed to encrypt small amounts of information.
To solve these problems, the Ring Learning with Errors variant was introduced by Lyubasevsky, Peikert and Regev in [16]. It is essentially a particular case of LWE but in polynomial rings over finite rings. The problem is over the polynomial ring , where is a monic polynomial in .
Given an element , one can see the principal ideal generated by
as an ideal lattice in , which we will note as . This correspondence is easy to see in the case (the particular we will use given its specific properties) due to the fact that the vector of coefficients of the product of polynomials in can be found through the anticyclic matrix as follows:
where and are the coefficients of and , respectively.
With this out of the way we can finally define the Ring Learning with Errors problem, on which a lot of lattice-based cryptography is based.
Definition 8.
Let χ be a probability distribution over and . Then, the R-LWE distribution is the distribution in given by , where is chosen uniformly at random, and all the operations to compute are made in .
Definition 9.
The decisional R-LWE problem is to distinguish samples from from the uniform distribution in with a probability that is non-negligibly bigger than .
Definition 10.
The search R-LWE problem is to find given a polynomial amount of samples from with non-negligible probability.
Therefore, a sample of the R-LWE distribution is a point of an ideal lattice that has been offset by a margin set by the distribution (which is normally taken such that the error is small). Therefore, the search R-LWE problem could be seen as finding a point in the ideal lattice (remember that a vector uniquely defines an ideal lattice through its anticyclic matrix) “close” to the sample, and the decision R-LWE could be seen as given an ideal lattice , decide whether the points given are all “close” to or are uniformly distributed.
When implementing LWE or R-LWE we will use a certain type of probability distribution over called discrete Gaussians, given their nice properties and ease in sampling values from them. There are several different definitions of discrete Gaussians but in our implementation we will use the following, given it is much easier to sample.
Definition 11
([15]). is the distribution in the torus obtained by sampling a Gaussian random variable centered in 0 and with standard deviation σ and then reducing modulo 1. Therefore,
Note that if , then with where reducing modulo 1 is taking only the decimal part of any real number.
Definition 12
([15]). The discretization to of any distribution in (), noted as is sampling from Ψ, multiplying by q, and then rounding to the closest integer. Therefore,
Note that if then with .
Definition 13.
We define the truncated Discrete Gaussian of parameters σ and κ as the distribution which samples from and rejects any sample bigger than κ, when seeing them with representatives in .
In particular, we will use such that
being λ the security parameter.
3. Encryption Scheme and Protocols
Having given all the necessary preliminaries, we can finally present our encryption scheme, threshold decryption protocol and distributed key generation protocol, which we will prove correct in Section 4, secure in Section 5, analyze its implementation in Section 6 and give some last thoughts and possible future work in Section 7.
We will use a version of the LPR encryption scheme presented in [16].
Encryption Scheme 1.Let , where u is the number of players, and χ be a distribution over . The encryption scheme and key generation we will be using is the following:
- . We will see every as an element in with being its vector of coefficients.
- .
- This is a public encryption scheme, we have and .
- –
- For any pair of keys we will have (meaning it is the sum of u samples of χ) and where and .
- such that given a message :wherewith.
- such that given a ciphertext :where we will recover every bit ofby rounding every coefficient ofto 0 or and then mapping 0 to 0 and to 1.
Now, we will define the Threshold Decryption Protocol based on this encryption scheme and a Distributed Key Generation protocol to work together with it. For clarity, we use a TTP to generate the keys in the encryption protocol, however, what we are looking for is a totally distributed scheme, so we also define a Distributed Key Generation Protocol to take the place of the TTP in the threshold decryption protocol.
Protocol 1.
Let χ be a distribution over and a pseudo-random function with image in , that is a vector of n coordinates with each coordinate being in an integer interval. Then the Threshold Decryption Protocol works as follows:
- A TTP generates the keys for every subset H of players of size t and distributes them according to the PRSS technique (Technique 2). It also generates the secret key and the public key as stated in the Encryption Scheme 1. Then, the TTP sends to the players and Shamir shares of . We call the Shamir share of of player , understood as a vector of Shamir shares on the coefficients of .
- Client receives ciphertext , and sends all players .
- Each player computes that is a Shamir share of with .
- Each player computes , as in the PRSS protocol but using (since it changes for every message and it is hard to distinguish from uniformly at random), its Shamir share of and gets Shamir share of .
- Client reconstructs for every allowed subset of players, picks whichever value is repeated more times, then for every coefficient returns 0 if is closer to 0 than to and returns 1 otherwise, and this is made public.
See Table 2.

Table 2.
Decryption protocol.
For the key generation protocol, we will assume a commitment scheme is used in the initial steps of interaction, when all the sampling is done and sent.
Protocol 2.
Let χ be a distribution over , , and a pseudo-random function with image in , where is an integer interval. The Distributed Key Generation Protocol works as follows:
- For the secret key , each player chooses its contribution with . Then, they act as the dealer in a NIVSS (Technique 3) to share every to all players. All players verify the value broadcast when doing the NIVSS () is in the interval . Now all players have shares of every and by their linearity also of . Then, is the polynomial in with coefficients .
- For the keys that will be used for the PRSS in the threshold decryption, for every subset H of t players each player chooses uniformly at random their contribution on these keys and shares it with all the players using Shamir secret sharing. Then, the players will have, by adding all the shares received by other players, Shamir shares of . Finally, all players send privately their shares on to all the players in A the complement of H, so they can recover .
- For the contributions to proceed identically to when generating .
- For every player chooses its share randomly in and does a Shamir share of it. Then, all players send to all players their share on all the so every player can recover (by adding the shares) . The polynomial in with these coefficients will be .
- Every player computes locally their Shamir shares on by performing these same operations with the shares they have on and .
- Finally, the public key is made public.
See Table 3 for a more detailed look into the steps of interaction needed. Note that we will denote with subindexes the additive contributions and with superindexes the Shamir shares.

Table 3.
Key Generation protocol.
4. Correctness
With all the preliminaries on hand and having defined both protocols we can now proceed to prove their correctness. We will give the proof for the case of a passive adversary in the Key Generation phase and an active (or passive) adversary in the Decryption phase, as this will be the case our implementation will use, the reasons for this decision will be explained in Section 6.1. The proof for the case where there is an active adversary during the Key Generation Protocol will be in Appendix A.1.
Theorem 1.
Let and u being the number of players. Let , be a pseudo-random function with image interval where
χ be a n-dimensional distribution obtained by n independent truncated Discrete Gaussian with parameters σ and κ and
Then Protocol 1 will have correct output against an active static adversary corrupting up to players.
Proof.
What we want to see first is that , where notes the coefficient i on the polynomial, given the way the decryption works in Encryption Scheme 1.
Let . Since the product in is done through the anticyclic matrix, we know that
and, therefore, as and , where every coefficient of is truncated by , we get that
Furthermore, given that there are keys , we know that
Adding both results, we then get that
as we wanted to see.
Finally, we just need to see that when the client reconstructs, there is indeed a majority of correct results, and this derives directly from having at most t corrupt players, therefore there will be a majority of subsets of players where they are all honest, and thus output the correct decryption. □
For the case where we combine both protocols, which means that we replace the TTP in Protocol 1 with Protocol 2, the outputs of this protocol and the TTP are equally generated for the case of a passive adversary in the Key Generation phase, as it cannot make any player deviate from the protocol. Therefore, we can directly apply Theorem 1. Furthermore, the same theorem and proof is valid against a passive adversary corrupting up to players, only noting that we will have all of the decryptions correct as a passive adversary cannot make any player deviate from the protocol.
5. Security
We will divide the proofs of security for the protocols into several theorems to ease the proofs. First, we will prove the CPA security of Encryption Scheme 1 as a one-player scheme, and then we will prove that no information is leaked when distributing the protocols. Finally, we will add everything to prove the CPA security of both protocols used together.
5.1. Security of Encryption Scheme
We will split the proof of security of Encryption Scheme 1 in three distinct parts: reducing the security of the encryption scheme to the decisional R-LWE problem, reducing the R-LWE problem with the distribution to the R-LWE problem with truncated discrete Gaussian, and finally reducing the decisional R-LWE problem to the Discrete Gaussian Sampling over K (K-DGS) with K the field such that R is its ring of integers, a well-known lattice problem assumed to be hard to solve. We will make this splitting because the first reduction will be for any distribution , while the second reduction will be specifically for the distribution . The first reduction follows the ideas from the reduction of Regev’s encryption scheme to LWE given in [15]. For the detailed proof see Appendix B.
Theorem 2.
Given χ a distribution over , there exists a reduction to the semantic security of the Encryption Scheme 1 from the decisional problem with distribution χ.
Note that the reduction is to the semantic security of the scheme and not the CPA security. However, it is well-known that in public key encryption both notions are equivalent (see, for example, Theorem 11.1 in [12]).
Second, we want to be able to ensure that if we know how to solve an instance of the decision R-LWE problem with a truncated discrete Gaussian we can solve an instance of the decision R-LWE problem with the distribution. This is clearly so given an instance of the decision R-LWE problem with the distribution one can see it as an instance with the truncated discrete Gaussian distribution except for a negligible amount of times. Therefore, the advantage of the adversary solving both instances will differ at most a negligible amount, as we needed.
Finally, we need to see that our R-LWE instance is as hard to solve as a lattice problem, in our case as hard to solve as K-DGS, where K is the field such that R is its ring of integers, in other words, (for more detail in the definition of K-DGS refer to Definition 2.10 and Section 2.3.3 in [17]). This job has already been done in [17], though to do so properly we need to give some clarifications about different ways to define the R-LWE distribution.
Let K be a number field with R its ring of integers. Let be the fractional co-differential ideal of K (), and let . Let be an integer modulus. Let us unpack this. First, in our specific case of K being a cyclotomic field with for some k, we have , so in turn it can be seen that is isomorphic to R. Second, which is isomorphic to , so looking it component by component could be seen as isomorphic to with . With this out of the way we can see their definition.
Definition 14
(Definition 2.14, [17]). For and an error distribution ψ over , the R-LWE distribution over is sampled by independently choosing and an error term , and outputting .
Now our postulate is that this definition taking as an n-dimensional spherical continuous Gaussian with parameter (which is a distribution used in [17]) and then raising it to again, is a more general definition to our Definition 8 using , in the sense that if we can solve an instance of the R-LWE problem defined with the distribution in Definition 8 we can solve an instance of the R-LWE problem with the distribution in Definition 14. It can be seen as one, as a spherical Gaussian in can be seen as the product of n independent Gaussians over with the same standard deviation. Then, in essence what we are doing in Definition 14 is multiply a times s, then divide the result by q (which we can as we are seeing the elements in which is a field) and adding the error distribution. Then, we reduce it modulo thus landing in . Now, if we look it component by component we have in essence computed and then added to each component a sample of , so when raising it again to (by multiplying by q and rounding) we get that and to every component we have added an independent sample taken from . Therefore, if is the spherical Gaussian with parameter , given an adversary who solves it is easy to give an adversary who solves .
Therefore, we can apply the result from [17], for which we need to give two quick lattice definitions.
Definition 15
([17]). The minimum distance of a lattice is the length of the shortest non-zero lattice vector
The dual lattice of a given lattice is defined as
Definition 16
(Definition 3.1, [18]). For a lattice , and a positive real , we define its smoothing parameter to be the smallest s such that , where for a lattice , and for some element .
Finally, we can give the following result.
Lemma 1
(Corollary 7.3, [17]). There is a polynomial-time quantum reduction from with function γ to the (average-case, decision) problem of solving using l samples with , and
as long as , where is an ideal lattice.
In conclusion, we have seen that breaking the security of Encryption Scheme 1 is at least as hard as solving the decision R-LWE problem with a truncated discrete Gaussian, which is at least as hard as solving the decision R-LWE problem with the distribution, which in turn is at least as hard as solving the K-DGS problem.
5.2. Non-Leakage of Information
In this section, we need to see that the adversary does not gain any extra information by interacting with the distributed protocol. We will start first with the Protocol 1, seeing that an adversary cannot distinguish between interacting with the protocol or with random inputs. Furthermore, we will also give the adversary the ability to choose its shares of the secret key and the PRSS keys, as it makes the game easier and it only serves to see that the protocol’s security is even stronger than what is usually required.
To appropriately do so we will need the following auxiliary lemmas about statistical distance, the proofs of which will be in Appendix B.
Lemma 2.
Let Y be a probability distribution over such that is bounded by κ and X be a discrete uniform distribution in the integer interval with . Then, , where .
Lemma 3.
Let be two probability distributions over a countable support such that , and with for some . Then .
With these auxiliary lemmas we can go ahead and prove the adversary cannot distinguish between interacting with the protocol and random values.
Theorem 3.
Assume that is a secure pseudo-random function modeled as a random oracle, that the keys have been securely generated and distributed, that the secret key s has been securely generated and shared and that the parameters follow the conditions of Theorem 1. Then, the Decryption Protocol (Protocol 1) is secure against a passive and static adversary, corrupting up to players.
Proof.
We want to construct an Attack Game in which the adversary cannot distinguish between the protocol executed correctly or with random values to show that the distribution does not leak anything about the secret key nor the error .
Let C denote the set of corrupted players and B the set of honest players. The Attack Game works as follows. Assume that the challenger knows the secret key and the such that (the keys that the adversary does not know) which have been securely generated. Assume that the challenger sends to the adversary the ciphertext and then submits as the challenge, where are the shares on the secret key of the corrupted players, are the keys such that (the keys knows) chosen by , and are the shares on the decryption of the corrupted players. Then, the challenger generates consistent shares on for the players not in C.
Once all these preliminaries are done, the challenger chooses and proceeds as following:
- If : The challenger uses the decryption protocol to compute the shares of the decryption for the honest players. It computes the decrypted message and outputs .
- If : The challenger computes for every H such that some element uniformly at random and we denote as the polynomial in with vector of coefficients . Then the challenger generates consistent shares of (the challenger knows as it can be computed using the protocol, given that everything needed is known) and outputs .
Finally outputs , meaning whether it thinks it has interacted with the protocol or with a simulation, and the Game concludes.
It is clear that will be correct in both cases given the proof of Theorem 1, and furthermore, will be an effective “decryption” of in the sense that every coefficient will be closer to 0 if and closer to if , because
Therefore we only need to see that are indistinguishable whether they are computed with or with . Let us see it. First of all, and are computationally indistinguishable to the adversary given the properties of pseudo-randomness of . We now want to see that the way and are distributed are at a negligible statistical distance. It is clear that is distributed in the interval (with values distributed uniformly in ) and as we have seen in the proof of Theorem 1 is in the interval . Therefore, as the distribution of every coefficient is identical and independent we have that by Lemma 2
and by Lemma 3
so the distribution of and are at a negligible statistical distance. Therefore, we get that and are computationally indistinguishable.
Finally, adding it all together we get that the output is computationally indistinguishable whether it has been computed with or with , so
as we wanted to see. □
After Theorem 3, we have only seen that Protocol 1 is secure when the keys are securely generated and against a passive adversary corrupting players, but it is standard to see that the same protocol is secure against an active adversary corrupting players if instead of the client reconstructs using the shares of all subsets of players, as that will give a majority of correct outputs.
The reason behind this is that we have already seen that no information is leaked, so we only need to see that the adversary cannot abort the protocol or cause an incorrect output. In case of an active adversary (who can cause players to deviate arbitrarily from the protocol), what is needed is that if all combinations of players are decrypting the message, there needs to be a majority of combinations of players with no corrupt players. This gives us that is enough.
Now, we need to see that Protocol 2 leaks no information against an adversary corrupting up to players. To do so we will once again see that the adversary cannot distinguish between interacting with the protocol or a simulation where the challenger sets before-hand the values of the keys.
Theorem 4.
Assuming that the image interval of the pseudo-random function is where
that is a commitment scheme such that it has a trapdoor and the parameters follow the conditions on Theorem of correctness, then the Key Generation Protocol (Protocol 2) is secure against a passive and static adversary, corrupting up to players.
Proof.
We want to construct an Attack Game in which the adversary cannot distinguish between the protocol executed correctly and a simulation where the challenger sets the values of and for all H before-hand.
Let C denote the set of corrupt players and B the set of honest players. The Attack Game works as follows. Assume that whenever a corrupt player needs to sample a uniform distribution it sends a query to the challenger for a random value from a random oracle. Let the challenge output by , the first step of the interaction in Protocol 2 as we can see in Table 3. Then, the challenger chooses and proceeds as follows:
- If : The challenger and the adversary follow Protocol 2 to generate and the shares and outputs .
- If : The challenger samples , and every and computes . Then he uses the trapdoor in the commitment scheme to recover , and proceeds as follows. We will divide the explanation depending on what he is simulating to ease comprehension, but everything will be done simultaneously, following the flow of information seen in Table 3.
- -
- For the “generation” of , the challenger will use the keys (of which he knows all of them given that they were generated through queries to the random oracle through the challenger) to recover , the contribution of the corrupt players to . With this information, the challenger can compute the contribution of the honest players to such that . With these values computed the challenger follows with the protocol.
- -
- For the “generation” of the challenger proceeds identically as with generating .
- -
- For the “generation” of , the challenger samples random values in for (the first step) and commits them. It then will receive from the adversary (the shares of pertaining to the corrupt players) and will compute consistent Shamir shares so that the players share . Then, as in the protocol, the challenger sends the shares to all players not in H.
- -
- For the “generation” of , the challenger samples random values in for (the first step) and commits them. It then will receive (the shares of pertaining to the corrupt players) and will compute consistent Shamir shares so that the players share . Then, as in the protocol, the challenger sends the shares to all players.
- -
- For the “generation” of the challenger outputs at the end of the protocol.
Then, the challenger outputs .
Finally, outputs , meaning whether it thinks it has interacted with the protocol or with the simulation, and the Game concludes.
It is clear that the flow of information is the same in both cases and that the values will be both correct and what the challenger sampled beforehand, so we just need to see that the adversary cannot distinguish between the values received when from the ones received when . For (and ) it is clear that they are indistinguishable, as we used the trapdoor in the commitment scheme to set the values necessary before any messages were sent from the adversary to the challenger. Furthermore, we know that no information was leaked in the NIVSS as because of Lemmas 2 and 3 we know that no information was leaked as in the proof of Theorem 3.
For (and in turn as they are analogous), we need to see that the adversary cannot distinguish from generated by the protocol or them being random in . To see this we will use the security of Shamir secret sharing, as the adversary can only control up to t players. Therefore, the value shared is completely undetermined by the shares of the corrupt players, so both cases ( and ) are indistinguishable to the adversary.
Finally, by adding everything up, we get that are indistinguishable whether we have or , so
as we wanted to see. □
As in Section 4, we have also proven the equivalent to this last theorem for an active adversary, however we will not use the result for the implementation, for reasons we will state in Section 6.1. The proof can be found in Appendix A.2.
Having proved the security of each protocol individually, we only need to see that using both protocols together still gives us an encryption scheme which is semantically secure.
Theorem 5.
Assume the conditions in Theorems 1 and 4 are fulfilled. Then, if K-DGS is hard, then encryption under keys generated by Protocol 2 and decryption following Protocol 1 is semantically secure against a static and passive adversary corrupting up to players acting through the Key Generation phase and the same adversary being active corrupting up to players in the Decryption phase.
Proof.
First, using the result in Theorem 4, we can see that the adversary cannot distinguish between executing both protocols, or replacing the key generation with keys generated by the challenger. Then, using Theorem 1, we can see that the adversary cannot distinguish between taking part in the decryption or having the challenger decrypt all by itself. Therefore, we get that the adversary cannot distinguish between the semantic security game when both distributed protocols are used from the basic semantic security game of Encryption Scheme 1. This means, using what we have seen in Section 5.1 that breaking semantic security when both protocols are being used is as hard as breaking semantic security of the encryption scheme, so using the reduction to K-DGS and that we assume this problem to be hard, we have that our protocols are semantically secure, as we wanted to see. □
6. Implementation
The first step for the implementation is finding good parameters that guarantee the security of the particular instance of the R-LWE problem. To verify it we will use the bounds on in Lemma 1 and the LWE hardness estimator given by Albrecht et al. in [19]. We use the LWE estimator because, as far as we know, no major attacks are known to exploit the particular properties of R-LWE, so the estimated hardness for LWE translates as estimated hardness for R-LWE.
6.1. Choosing Parameters
We set the security parameter . We need to find the following parameters: and which will then allow us to compute and . We will first leave everything in function of n and q, and we will then use the concrete hardness of an instance of the R-LWE problem to fix n and q.
Let and . Using the conditions on on Theorem 1 we get that
To find , we will use the following lemma, the proof of which is in Appendix B.
Lemma 4.
Let be a discrete Gaussian. Then, :
Using the bound on Definition 13 and Lemma 4 we can get the following bound:
which when isolating the gives us the following bound:
From here we will take the equality, as with a fixed q the larger the standard deviation the greater the hardness of that specific instance of the decision R-LWE problem.
Now, we can find n and q using the LWE hardness estimator, which given outputs the concrete hardness of that specific instance. We will set n as a power of 2, as it allows us to use more efficient multiplication algorithms and q as a prime near a power of 2. Using this, we implemented a Python algorithm to find these parameters. The code can be found in the repository in Appendix C. This has yielded the following results as parameters for and and more than 100 bits of security, as can be seen in Table 4.

Table 4.
Parameters for secure implementation.
In this code, there is also the computing of parameters for the case of an active adversary in Key Generation phase using the conditions on Theorem A1, meaning that to have 100 bits of security against this type of adversary we need to bump up to . This, as we will see with the results in Section 6.3, hurts the viability of the protocols, that is why we take our main proposal as secure against an adversary who acts passively in the Key Generation phase and actively in the Decryption phase.
6.2. Implementation Particulars
There are several implementation decisions we have taken and need to be discussed. First, we have not coded a truly interactive protocol between u different players, but rather a simulation where one processor computes all the steps simulating the interaction, in the sense that the protocols are divided by steps between communication phases where all computing can be done without the need to interact with other entities. Then, the program computes how much time every step costs for every player and picks the maximum as the “official” time for that step. As we only want to analyze roughly how viable our protocols are, this approximate works for us. This approximation also means that the execution of the simulation lasts considerably longer than the “real time” for the execution, thus limiting us with the amount of players we can reasonably use.
Second, to have the most compact possible form of Shamir Secret Sharing we have used Shamir over the field of instead of embed it in . This is the main reason why we have taken q prime, as none of the reductions require it.
Third, regarding the implementation of the PRF, we have used the main result in [20], which says that Hash-based Message Authentication Code (HMAC) is a PRF under the condition that the underlying compression function is a PRF. To ensure this condition is satisfied we have used the HMAC based around SHA-3.
Finally, regarding the Commitment Scheme we have used for the Key Generation protocol, we have used the hash of the message we want to send concatenated with a random string. We have used SHA-2 because, as far as we know, it is secure enough. However, should the need arise, it could be swapped for a more secure alternative. Furthermore, we only needed to use a commitment scheme after the first round where every player sets their values. This is so because once all the values have been set and all the shares sent, the contributions of the adversary are no longer needed, as the honest players can already generate a majority of correct values. And given that no other value needs to be set in a way the adversary cannot exploit (as the adversary becomes irrelevant), a commitment scheme in any further communication step seems unnecessary. However, this commitment phases could be added with no major change to the protocol nor the proof of security or correctness, only a slightly slower execution.
6.3. Results of the Simulation
In this final section, we will discuss the results we have obtained from the execution of the code for the simulation of both protocols. You can find the code in the repository linked in Appendix C. The specifications of the system where we have executed the programs are found in Table 5. Furthermore, we have used the following C libraries: FLINT (Fast Library for Number Theory) to ease computations in , which in turn uses the GMP and MPFR libraries to deal with multiple precision numbers, and OpenSSL library for cryptography-related functions like Hashes or HMACs. It is also worth mentioning that any result we obtain from the execution of the simulation has been found by averaging the times of 10,000 executions of the code, so as to better portray the results, getting rid of outliers.

Table 5.
Specifications of the system.
From what we have seen to this point there are two main dependencies: growth of time in respect to the threshold t and growth of time in respect to the dimension of the lattice. This is so because the threshold defines the minimum number of players needed (and vice versa, given a number of players we can get the maximum threshold it allows) depending if we are protecting ourselves against an active or a passive adversary. As we have seen in Section 6.1 given the adversary model, given an n we can find the rest of parameters that make the protocol secure (taking into account that there is a minimum n for which this analysis works).
In regards to the dependency on t, analyzing the protocols theoretically lets us see that when performing either the PRSS or the NIVSS there are different keys , meaning that the number of additions grows asymptotically with the value . This means that the dependency should be approximately exponential in the active case where and approximately linear in the passive case where . When obtaining results from the simulation, we have gathered results for the values of t most frequently used in real-life applications like electronic voting, which means against active adversaries and for passive adversaries. This decision is mainly due to how we have implemented the simulation, as instead of having the several players’ protocols being executed at the same time, we have them executed consecutively and then take the maximum time spent as the overall time. In the case of the Key Generation, as there are various steps of interaction, this process is applied to every one of the steps. Therefore, due to time constraints, we were limited in how many players we could simulate in the protocols while running 10,000 executions of the codes. Having said all that, the results we obtained for the dependency on t followed our predictions. In the active case they behaved greater than linearly in the three points we had, and in the passive case it behaved approximately linearly. A more in-depth analysis cannot be made unless more extensive data is gathered.
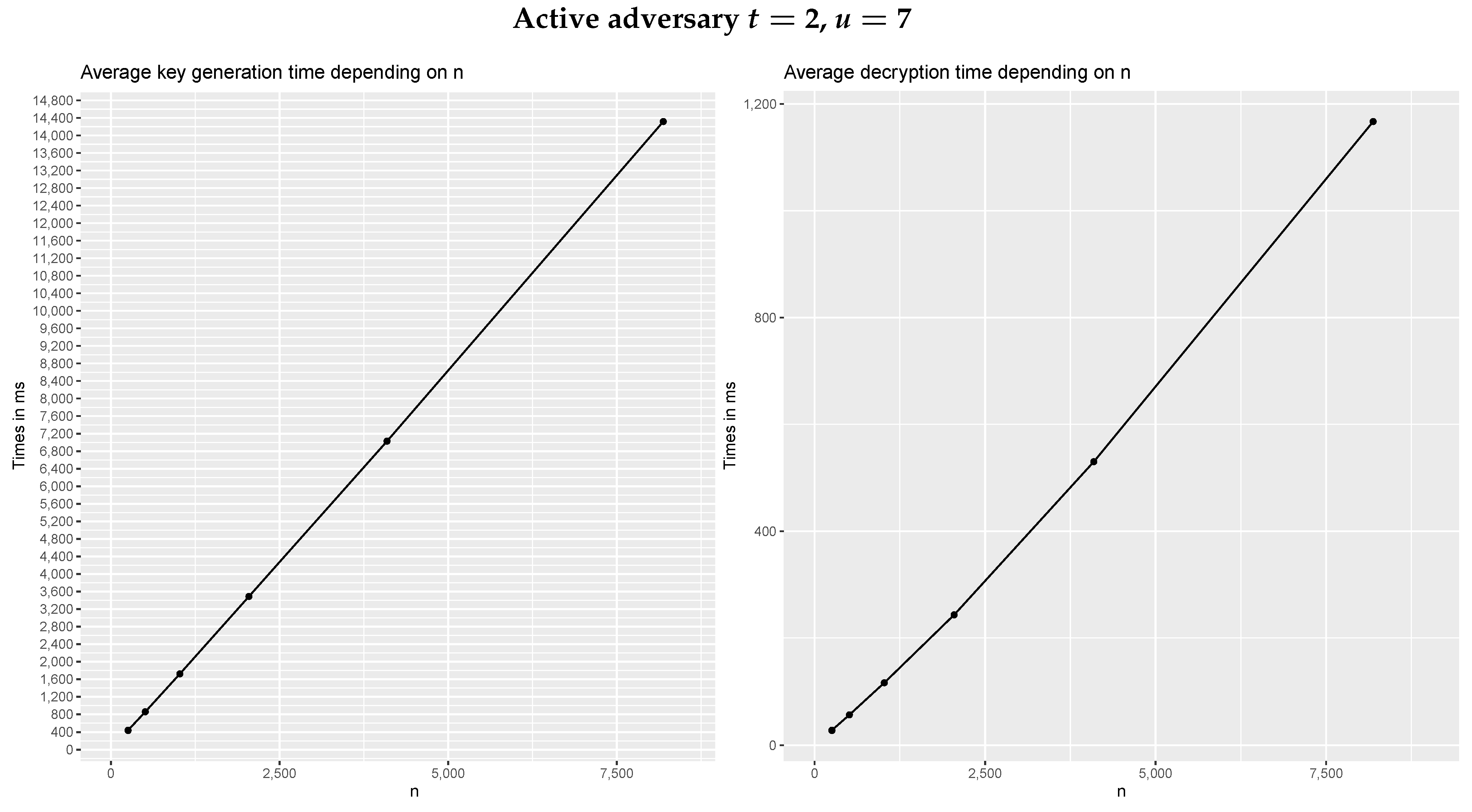
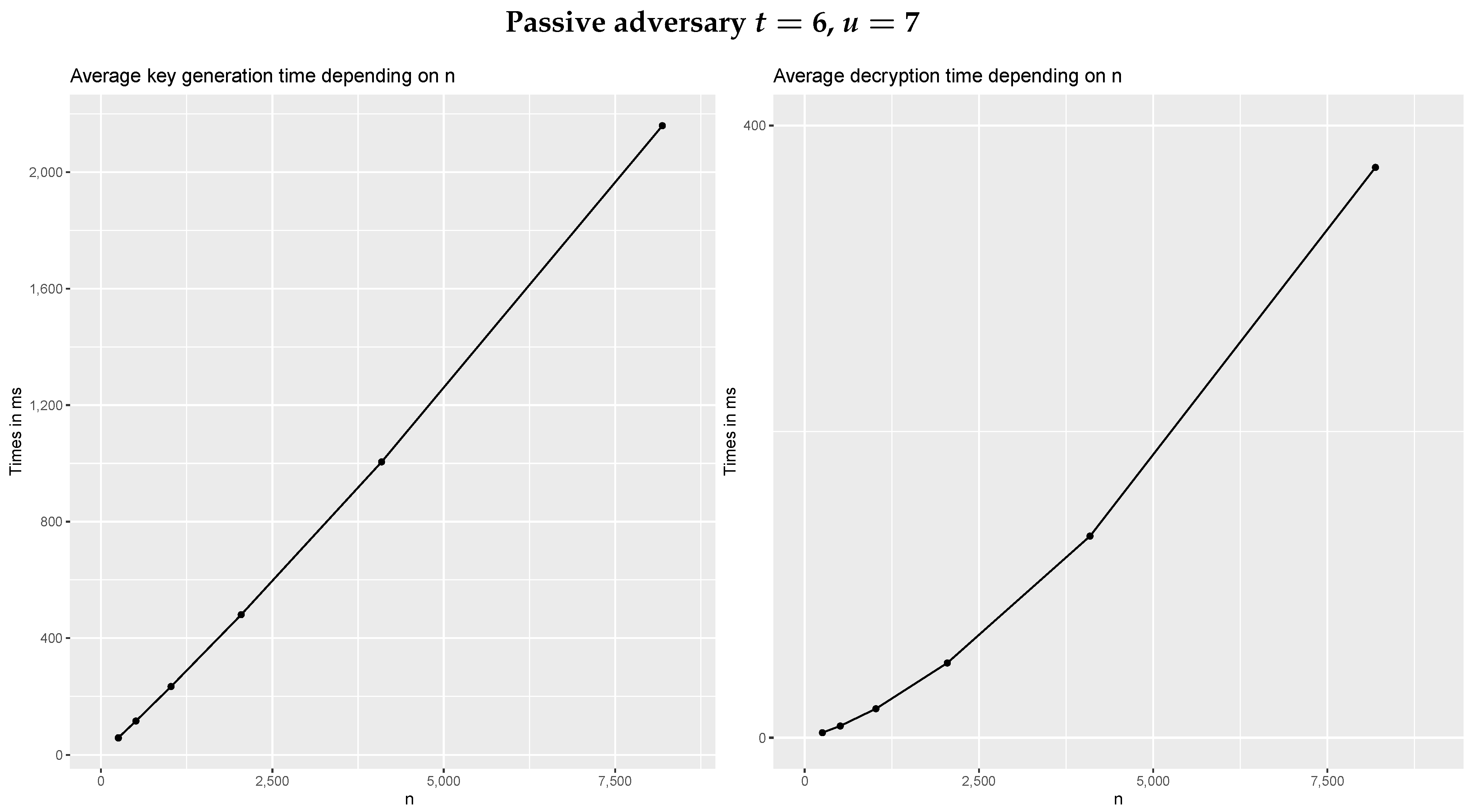
In regards to the dependency on n, given that there is multiplication of polynomials in both protocols, which is implemented using the Karatsuba algorithm that scales by the order of , the time grows asymptotically with this value. The results obtained for the dependency on n, which can be seen in Figure 1, show the expected results only in the decryption phase against a passive adversary. For the other cases, we see linear, or practically linear, behavior for the range of values of n we are interested in for real life applications. This is due to the fact that the protocols need to perform a much higher number of additions than products, and this difference ends up being high enough for the linear growth of the addition to offset the growth of the product at these values of n.
Figure 1.
Times of the simulation for .
Finally, we want to discuss the viability of the protocols. As we can see in Table 6, the Key Generation times are significantly slower than the Decryption time, between 4 and 7 times slower. This, however, does not pose a big problem, as by design in most implementations one round of Key Generation will be used to decrypt many messages; therefore, we can focus our main analysis in the decryption times. In that front, the 530.36 ms per decryption in the active case translates to approximately 7000 messages per hour, while the 131.73 ms per message in the passive case translates to approximately 27,000 messages per hour. As we can see it will be half these votes per hour with , which will be needed against an active adversary as we have said in Section 6.1.

Table 6.
Time comparison between active and passive adversary.
7. Conclusions and Future Work
For our concluding considerations, we would like to summarize the limitations that this work has and how it could be improved in future works, as well as to give some insight to some possible other uses outside the ones outlined above.
Construction-wise, our proposal has two main limiting factors: First, the fact that we compute the drowning noises through both the PRSS technique and NIVSS technique means that computation time will increase asymptotically exponentially with the number of players in an active adversary setting, which is not desirable. Should other techniques be used for non-interactively sharing the noise value, this could be avoided. Second, and more inherent to the structure of our protocols, is the fact that using noise drowning by itself causes our implementation to use very high dimensions for the lattices. This is due to the fact that to guarantee statistical indistinguishability we need the noise to be exponentially bigger than the secret while the LPR encryption scheme requires the noise to be smaller than , meaning that the parameter is proportionately very small compared to the modulus q. This then has an influence in the dimension of the lattice needed to ensure that the concrete instance of the R-LWE problem has the desired amount of bits of security. This limitation could only be avoided by using a different way to ensure security than noise drowning, which is a pivotal element in our proposal.
Implementation-wise, we would like to reiterate that our proposed codes are a proof of concept of approximate viability, and in no case an attempt to give a computationally secure and efficient program. As so, the codes should be carefully analyzed to ensure computational security (for example, some of the random samplings are not truly indistinguishable from uniformly at random) and that no other implementation based attacks (like side-channel attacks) can be performed. Furthermore, for any type of important practical application, the codes should be optimized in efficiency.
Finally, we would also want to state the fact that even if the protocols presented were thought of with the idea of using them together, their security proofs are independent, and therefore they can be used separately. This means that in a case where a TTP can be trusted with the key generation, only the decryption protocol may be used, and then make the process completely interactiveless. Additionally, while the key generation protocol is more particularly tailored to the needs of the encryption scheme, it would not be too hard to extract the main principles for generating the different types of elements, therefore being easily generalizable with a similar security proof. This opens the gateway to a whole new set of possibilities for applications.
Author Contributions
Conceptualization, R.M. and P.M.; methodology, R.M. and P.M.; software, F.A. and R.M.; validation, F.A.; formal analysis, F.A., R.M. and P.M.; investigation, F.A., R.M. and P.M.; resources, F.A., R.M. and P.M.; writing—original draft preparation, F.A.; writing—review and editing, F.A., R.M. and P.M.; supervision, P.M.; project administration, F.A., R.M. and P.M.; funding acquisition, P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been partially funded by the European Union PROMETHEUS project (Horizon 2020 Research and Innovation Program, grant 780701) and the Spanish Ministry of Economy and Competitiveness, through Project MTM2016-77213-R.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CPA | Chosen Plaintext Attack |
| GAPSVP | GAP Shortest Vector Problem |
| HMAC | Hash-based Message Authentication Code |
| K-DGS | Discrete Gaussian Sampling over K |
| LWE | Learning with Errors |
| NIST | National Institute of Standards and Technology |
| NIVSS | Non-Interactive Verifiable Secret Sharing |
| R-LWE | Ring Learning with Errors |
| PRF | Pseudo-Random Function |
| PRSS | Pseudo-Random Secret Sharing |
| TTP | Trusted Third-Party |
Appendix A. Correctness and Security against Active Adversaries
Appendix A.1. Correctness
We will prove correctness of the Decryption protocol against an active (or passive) adversary when the keys are generated by the Key Generation protocol against an active adversary.
Theorem A1.
Let be the number of coefficients in , be the number of players, be a pseudo-random function with image interval , χ be a distribution in where every coefficient is a truncated Discrete Gaussian with parameters σ and κ,
and
Then, Protocol 1 will have correct output except with probability against an active adversary corrupting up to players.
Proof.
What we want to see first, as before, is that , where notes the coefficient i on the polynomial, given the way the decryption works in Encryption Scheme 1.
Let . As the product in is done through the anticyclic matrix, we know that
Now, we still have but for t of the contributions we can only assure that they are in , so we get that
Furthermore, given that there are keys , we know that
Adding both results we then get that
as we wanted to see.
Finally, we just need to see that when the client reconstructs, there is indeed a majority of correct results, and this derives directly from having at most t corrupt players; therefore, there will be a majority of subsets of players where they are all honest, and thus output the correct decryption. □
As in Section 4, the same proof works against a passive adversary corrupting up to players.
However, in the case of dealing with an active adversary in the key generation phase, to have a truly correct scheme we need to see that the protocol cannot be halted by any actions performed by a malicious adversary. However, in the protocol, whenever a verification fails the protocol halts. To deal with these we implement the following dispute resolution policy, where a dispute is raised whenever a player receives a value that fails verification stating there which other player sent the values.
The policy works as follows, once the protocol is halted the players look at the disputes that have risen, and then “eliminate” all players involved in them, in the sense that a new execution of the key generation protocol will start without both players involved in every dispute, and in case a player is involved in more than one dispute only the first one will be analyzed. This policy ensures that the protocol will produce a correct output with at most t halts since no dispute can be risen between honest players, and given that the security of the scheme is based only on assuming that there is at least one contribution on and following the distribution, the output generates no problems. Finally, note that since in every dispute there is at most one honest player, the ratio of corrupt players will never go above .
Appendix A.2. Security
To be able to prove security when the Key Generation is against an active adversary, we will only need to reword the Theorem as follows.
Theorem A2.
Assuming that is a secure pseudo-random function modeled as a random oracle, that the keys have been securely generated and distributed, that the secret key s has been securely generated and shared, and that the parameters follow the conditions of Theorem A1, the Decryption Protocol (Protocol 1) is secure against an active and static adversary, corrupting up to players.
The proof is analogous to the proof of Theorem 1.
We will now prove that the Key Generation leaks no information when acting against an active adversary corrupting up to players. As before, we will prove that the adversary cannot distinguish between interacting with the protocol or a simulation where the challenger sets before-hand the values of the keys.
Theorem A3.
Assuming that the image interval of the pseudo-random function is where
that is a commitment scheme such that it has a trapdoor and the parameters follow the conditions on Theorem of correctness, then the Key Generation Protocol (Protocol 2) is secure against an active and static adversary, corrupting up to players.
Proof.
We want to construct an Attack Game in which the adversary cannot distinguish between the protocol executed correctly and a simulation where the challenger sets the values of and for all H beforehand.
Let C denote the set of corrupt players and B the set of honest players. The Attack Game works as follows. Assume that whenever a corrupt player needs to sample a uniform distribution it sends a query to the challenger for a random value from a random oracle. Let the challenge output by , the first step of the interaction in Protocol 2 as we can see in Table 3. Then, the challenger chooses and proceeds as follows:
- If : The challenger and the adversary follow Protocol 2 to generate and the shares and outputs .
- If : The challenger samples , and every and computes . Then he uses the trapdoor in the commitment scheme to recover , and proceeds as follows. We will divide the explanation depending on what he is simulating to ease comprehension, but everything will be done simultaneously, following the flow of information seen in Table 3.
- For the “generation” of , the challenger will use the keys (of which he knows all of them as he/she controls more than t players), to recover , the contribution of the corrupt players to . With this information, the challenger can compute the contribution of the honest players to such that . With these values computed, the challenger proceeds with the protocol.
- For the “generation” of the challenger proceeds identically as with generating .
- For the “generation” of , the challenger recovers (as it controls more than t players) the contribution of the corrupt players to . With this information, the challenger can compute the contribution of the honest players such that for all H. With these values computed, the challenger proceeds with the protocol.
- For the “generation” of , the challenger recovers (as it controls more than t players) the contribution of the corrupt players to . With this information, the challenger can compute the contribution of the honest players such that . With these values computed, the challenger proceeds with the protocol.
- For the “generation” of the challenger outputs at the end of the protocol.
Then, the challenger outputs .
Finally, outputs , meaning whether it thinks it has interacted with the protocol or with a simulation, and the Game concludes.
It is clear that the flow of information is the same in both cases and that the values will be correct and what the challenger has sampled beforehand, so we just need to see that the adversary cannot distinguish between the values received when from the ones received when . We can see they are indistinguishable as the challenger uses the trapdoor in the commitment scheme to get the values necessary before any message were sent from the challenger to the adversary. Moreover, once again, we know that no information was leaked in the NIVSS by the same reasoning from the proof of Theorem 4.
Therefore, are indistinguishable to the adversary whether they have been computed with or , so
as we wanted to see. □
Having proved the security of each protocol individually, we only need to see that using both protocols together still gives us an encryption scheme which is semantically secure.
Theorem A4.
Assume the conditions in Theorems A1 and A3 are fulfilled. Then, if K-DGS is hard, then encryption under keys generated by Protocol 2 and decryption following Protocol 1 is semantically secure against a static and passive adversary corrupting up to players acting through the Key Generation phase and the same adversary being active corrupting up to players in the Decryption phase.
Proof.
The proof is analogous to the proof of the Main Theorem but changing Theorems 1 and 4 for Theorems A1 and A3, respectively. □
Appendix B. Proofs of Auxiliary Theorems and Lemmas
Appendix B.1. Proof of Theorem 2
Theorem A5.
Given χ a distribution over , there exists a reduction to the semantic security of the Encryption Scheme 1 from the decisional problem.
Proof.
What we want to see is that given an efficient adversary who has non-negligible semantic security advantage, we can construct an efficient adversary with access to who given an instance of the decisional R-LWE problem, it can solve it with probability non-negligibly bigger than .
Let be an instance of the decisional R-LWE problem. What we need to do is to output whether a polynomial amount of instances are samples of the distribution or of the uniform distribution over , in other words, we want to know whether for some and .
Note that any adversary who breaks semantic security may be of one of two types. Either has non-negligible semantic security advantage against the encryption scheme when are generated independently uniformly at random (instead of having ) or it does not. We will construct two different adversaries for these cases.
Assume first that has a negligible semantic security advantage against the encryption scheme when are generated independently uniformly at random. Let be an instance of the problem, then we define the following attack game.
Attack Game A1.The attack game goes as follows:
- Set the public key to and send it to .
- Receive from the adversary, and choose .
- Compute and with , and send to .
- Receive from the adversary.
Then, will work as follows. When given the instances, it picks and performs the Attack Game 1 with a polynomial amount of times. Then, it computes the advantage
We know from how we have defined the adversary , as is non-negligible, if the instances follow the distribution then will be non-negligible and if the instances are uniform over then will be negligible. This means that with non-negligible probability can solve the decisional problem as we wanted.
Assume now that has a non-negligible semantic security advantage against the encryption scheme when are generated independently uniformly at random. Let, once again, and be two instances of the problem, then we define the following attack game.
Attack Game A2.The attack game goes as follows:
- Set the public key to and send it to the adversary.
- Receive from the adversary, and choose .
- and and send to .
- Receive from the adversary.
Then, will work as follows. When given the instances, it picks two of them and , and performs the Attack Game 2 with a polynomial amount of times. Then, it computes the advantage
We know from how we have defined the adversary , since is non-negligible, if the instances follow the distribution then will be non-negligible and if the instances are uniform over then will be negligible, since if are uniformly at random then is independent from the public key and . This means that with non-negligible probability can solve the decisional problem as we wanted, since it is possible to distinguish, with non-negligible probability, a negligible event from a non-negligible event. □
Appendix B.2. Proofs of Lemmas 2 and 3
Lemma A1.
Let Y be a probability distribution over such that is bounded by κ and X be a discrete uniform distribution in the integer interval with . Then, , where .
Proof.
The first thing to notice is that for any such that , we will clearly have , as the support of will only go from to . Furthermore, for , we can do the following analysis:
using that will always fall in the support of X (thus is never zero), that X is uniform and that Y only takes values in .
Now taking everything together we get from the definition of statistical distance:
□
Lemma A2.
Let be two probability distributions over a countable support such that , and with for some . Then .
Proof.
We define the n-dimensional distributions
where we have and . It is also clear that
Finally, because of the triangle inequality for distances
□
Appendix B.3. Proof of Lemma 4
To prove the lemma we will use another distribution called rounded discrete Gaussian.
Definition A1.
The rounded Gaussian distribution over with parameter is defined by the probability function
for with
The distribution we are interested in is , its standard reduction modulo q as it is defined as
It is clear once again from the definition that if , then with , hence the name rounded Gaussian.
Now, we can see the relation between and .
Lemma A3.
For any , we have that is indeed a random variable and in fact we have that .
Proof.
First, we need to see that is a random variable. Indeed,
Now, we can see that for all , and therefore as random variables.
where we have used the change of variables and the dominated convergence theorem. □
Therefore, if we know a bound for , we know a bound for . Given this result, we can now bound the distributions using the fact that is a rounded Gaussian and Mill’s inequality:
Lemma A4.
For all , then
Proof.
Let , then
where we have used Lemma A3, thus seeing what we wanted. □
Appendix C. Link to Repository
All relevant codes for the implementation can be found in the following GitHub repository, last update made on 20 December 2021: https://github.com/FerranAlborch/Implementation-RLWE-based-distributed-key-generation-and-threshold-decryption.
References
- Saračević, M.; Adamović, S.; Maček, N.; Elhoseny, M.; Sarhan, S. Cryptographic keys exchange model for smart city applications. IET Intell. Transp. Syst. 2020, 14, 1456–1464. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Alagic, G.; Alperin-Sheriff, J.; Apon, D.; Cooper, D.; Dang, Q.; Kelsey, J.; Liu, Y.K.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process; US Department of Commerce, NIST: Washington, DC, USA, 2020.
- De Feo, L.; Meyer, M. Threshold schemes from isogeny assumptions. In Proceedings of the IACR International Conference on Public-Key Cryptography, Edinburgh, UK, 4–7 May 2020; pp. 187–212. [Google Scholar]
- Devevey, J.; Libert, B.; Nguyen, K.; Peters, T.; Yung, M. Non-interactive CCA2-secure threshold cryptosystems: Achieving adaptive security in the standard model without pairings. In Proceedings of the IACR International Conference on Public-Key Cryptography, Virtual Event, 10–13 May 2021; pp. 659–690. [Google Scholar]
- Bendlin, R.; Damgård, I. Threshold decryption and zero-knowledge proofs for lattice-based cryptosystems. In Proceedings of the Theory of Cryptography Conference, Zurich, Switzerland, 9–11 February 2010; pp. 201–218. [Google Scholar]
- Singh, K.; Rangan, C.P.; Banerjee, A. Lattice-based identity-based resplittable threshold public key encryption scheme. Int. J. Comput. Math. 2016, 93, 289–307. [Google Scholar] [CrossRef]
- Boneh, D.; Gennaro, R.; Goldfeder, S.; Jain, A.; Kim, S.; Rasmussen, P.M.; Sahai, A. Threshold cryptosystems from threshold fully homomorphic encryption. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2018; pp. 565–596. [Google Scholar]
- Zhang, X.; Xu, C.; Jin, C.; Xie, R.; Zhao, J. Efficient fully homomorphic encryption from RLWE Ext. A Threshold Encryption Scheme. Future Gener. Comput. Syst. 2014, 36, 180–186. [Google Scholar] [CrossRef]
- OQS Development Team. Open Quantum Safe (OQS). Available online: https://openquantumsafe.org/ (accessed on 20 January 2022).
- Alborch Escobar, F. RLWE-Based Distributed Key Generation and Threshold Decryption. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2021. [Google Scholar]
- Boneh, D.; Shoup, V. A Graduate Course in Applied Cryptography (2020). Draft Version 0.5 2020. Available online: https://toc.cryptobook.us/book.pdf (accessed on 10 December 2021).
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Cramer, R.; Damgård, I.; Ishai, Y. Share conversion, pseudorandom secret-sharing and applications to secure computation. In Proceedings of the Theory of Cryptography Conference, Cambridge, MA, USA, 10–12 February 2005; pp. 342–362. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM (JACM) 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On ideal lattices and learning with errors over rings. J. ACM (JACM) 2013, 60, 1–35. [Google Scholar] [CrossRef]
- Peikert, C.; Regev, O.; Stephens-Davidowitz, N. Pseudorandomness of Ring-LWE for any ring and modulus. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, Montreal, ON, Canada, 19–23 June 2017; pp. 461–473. [Google Scholar]
- Micciancio, D.; Regev, O. Worst-case to average-case reductions based on Gaussian measures. SIAM J. Comput. 2007, 37, 267–302. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, M.R.; Player, R.; Scott, S. On the concrete hardness of learning with errors. J. Math. Cryptol. 2015, 9, 169–203. [Google Scholar] [CrossRef] [Green Version]
- Bellare, M. New proofs for NMAC and HMAC: Security without collision-resistance. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2006; pp. 602–619. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).