Abstract
This article establishes the vibrational behavior of functionally graded plates embedded in a viscoelastic medium. The quasi-3D elasticity equations are used for this purpose. The three-parameter Visco-Winkler-Pasternak model is employed to give the interaction between the viscoelastic foundation and the presented plate. Hamilton’s principle is applied to derive the governing dynamic equations. Many validation examples are presented. Additional benchmark results are tabulated for future comparisons. The effects of various parameters like geometrical, material properties, and viscoelastic foundations on the vibrational frequencies of homogeneous and functionally graded plates are investigated. The frequencies increase as all parameters increase except the functionally graded power-law index for which its increase causes a decrease in the frequency value.
1. Introduction
Functionally graded materials (FGMs), which were proposed by Koizumi [,], are widely used in many real-life engineering applications due to their distinct properties which cannot be achieved using traditional materials such as their capability to resist high temperature, high strength, mechanical, and chemical properties. The FGMs are produced by mixing ceramics and metals in which the ceramics and metals enhance the thermal properties and mechanical properties, respectively. Therefore, FGMs become favorable materials for designers in many applications such as aerospace, nuclear, marine, and lightweight structures.
Several structural applications use plates resting on elastic foundations and a lot of research has been conducted to investigate the vibration behavior of FGMs’ plates supported by elastic foundations. Here, we restrict our attention to the vibration analyses of different structures that rest on elastic foundations. The most famous model of the elastic foundations is known as the Winkler-Pasternak model or, for simplicity, Pasternak’s foundation model. It contains, of course, two parameters, the transverse stiffness coefficient of Winkler and the shear stiffness coefficient of Pasternak. Hosseini-Hashemi et al. [] presented an analytical solution for the free vibrational analyses of FG rectangular plates resting on Winkler or Pasternak elastic foundations using the first-order shear deformation plate theory (FSDT).
A layerwise finite element formulation was introduced by Pandey and Pradyumna [] for the free vibration analysis of FG sandwich plates with a nonlinear variation of the temperature through the thickness. Zenkour [] presented the free vibration of a microbeam resting on Pasternak’s foundation via the Green–Naghdi thermoelasticity theory without energy dissipation. The neutral surface concept using the higher-order shear deformation theory (HSDT) was used by Benferhat et al. [] to investigate the free vibration response of FGMs plates resting on elastic foundations. Zaoui et al. [] used the quasi-3D hybrid-type HSDT to study the free vibration of FG plates resting on Pasternak’s foundation. Zenkour and Radwan [] presented the free vibrational analysis of multilayered composite and softcore sandwich plates resting on Winkler-Pasternak foundations. Wang et al. [] analyzed the thermal vibration of FG graphene platelets reinforced composite annular plate supported by an elastic foundation. Sobhy and Zenkour [] discussed the vibration of FG graphene, platelet-reinforced, composite, doubly-curved, shallow shells resting on elastic foundations.
The HSDT and the two parameters, Pasternak and Winkler, as the elastic foundation were used by Kumar et al. [] to study the free vibration of tapered rectangular FG plates. Liu et al. [] used the FSDT and the multi-segment partition technique for the dynamic analysis of FG plates reinforced with graphene platelets resting on the two-parameter elastic foundation (Pasternak and Winkler). Arefi et al. [] presented the size-dependent free vibration of a three-layered exponentially graded (EG) nano-/micro-plate with piezomagnetic face sheets resting on Pasternak’s foundation via MCST. Furthermore, the two-parameter elastic foundation model was utilized by Tran et al. [] to investigate the vibration response of FG plates resting on an elastic foundation in a thermal environment. Li et al. [,] presented a new semi-analytical method to analyze the free vibration of uniform, stepped, and porous FG cylindrical shells under arbitrary boundary conditions. Radaković et al. [] presented a mathematical model to discuss the thermal buckling and free vibration of a functionally graded plate that includes interaction with an elastic foundation. Li et al. [] discussed the vibration analysis of rotating, functionally graded, nano-annular plates in a thermal environment. The edge-based smoothed, finite element method and a mixed interpolation of tensorial components were used by Nguyen et al. [] to study the free vibration of FG porous plates resting on a two-parameter elastic foundation. Tran et al. [] used a nonlocal theory based upon four unknowns to complete the analysis of FG porous nanoshells resting on an elastic foundation. Recently, Zenkour and El-Shahrany [] presented the forced vibration of a magnetoelastic, laminated, composite beam resting on Pasternak’s foundation.
If we add the effect of the damping coefficient to the above two-parameter elastic model, we can get the third viscoelastic foundation model. Several publications in the literature are made according to the inclusion of the third parameter to discuss the vibrational problems of structures resting on the viscoelastic foundation [,,,,]. The additional elastic foundation model is denoted by Kerr’s foundation model. A lot of articles are concerned with the force or the control of the hygrothermal vibration of sinusoidal FG nanobeams or viscoelastic magnetostrictive sandwich plates resting on a hybrid of Kerr’s foundation [,].
This paper, for the first time, uses the Visco-Winkler-Pasternak elastic foundation model in conjunction with a quasi-3D refined theory to study the vibration response of FG plates. The analytical solutions for the natural vibration analysis of FG plates are developed on the assumption that transverse shear displacements vary as a hyperbolic function through the thickness of the plate. In addition, the transverse normal strain is taken into consideration. Based on the present theory, comprehensive results of non-dimensional frequencies of homogeneous and FG plates with and without the inclusion of the three-parameter viscoelastic foundations are tabulated for future comparisons. Then fundamental/natural frequencies are found by solving the eigenvalue problem. To verify the accuracy of the present theory, many numerical examples are solved and compared with other published solutions in the literature. In addition to the two-parameter elastic foundation, the inclusion of a third damping parameter is also investigated.
2. Basic Equations
2.1. An FG Plate Structure
A functionally graded rectangular plate resting on a three-parameter elastic foundation and bounded by the coordinate planes , , , , and , , as shown in Figure 1, is considered. The Cartesian coordinates , , are chosen such as is placed on the middle plane of the FG plate. The FG plate is made from metal (Aluminum-Al) and ceramic (Alumina-Al2O3 or Zirconia-ZrO2) with the properties established in Section 3. The bottom surface of the FG plate is metal-rich, and the top surface is ceramic-rich while the middle is a mixture of both, which is varied using the following power-law function:
where the subscripts and denote metal and ceramic material properties, respectively, and is the gradient index that controls the smooth distribution of material through the thickness of the FG plate and is the distance from the neutral plane of the FG plate.
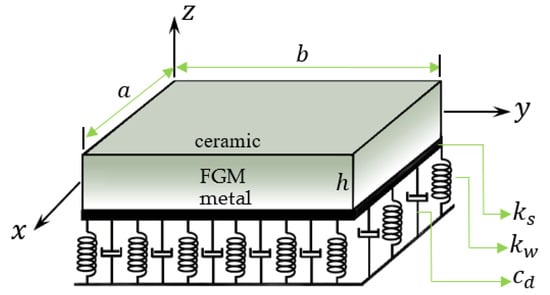
Figure 1.
The schematic diagram for the geometry of the FG plate resting on a Visco-Winkler-Pasternak foundation.
2.2. A Quasi 3-D Higher-Order Plate Theory
Let , , and denote the dynamic displacement components of a material point located at and time in the , , and directions, respectively. The in-plane displacements and transverse displacement are assumed according to the following refined quasi-3D plate theory:
where the above displacements contain six unknowns , , and as functions on . The effects due to transverse shear strain and normal deformations are both included. The function should be an odd function of while should be an even function. That is
No transversal shear correction factors are needed for the present model because a correct representation of the transversal shearing strain is given. In the displacement field in Equation (2), the strains are given by
where
In addition, the load-displacement formula between the plate and the supporting foundations is expressed according to the three-parameter Visco-Winkler-Pasternak model by
where is the foundation reaction per unit area, and are Winkler’s and Pasternak’s foundation stiffnesses, respectively, and represents Laplace’s operator. In addition, refers to the damping coefficient. Some special models may be simply obtained from the present models as:
Winkler’s model: , .
Pasternak’s model: , .
Winkler-Pasternak’s model: .
Visco–Winkler’s model: .
Visco–Pasternak’s model: .
2.3. Constitutive Equations
For transverse shear and normal strain in the FG plate coordinates, the stress-strain relationships can be expressed as
where are given by
in which is Young’s modulus and is Poisson’s ratio.
2.4. Stress Resultants
For transverse shear and normal strain in the FG plate coordinates, the stress-strain relationships can be expressed as
Using expressions (3)–(7) in Equation (8), expressions for stress resultants , moments , shape moments , and shear forces can be obtained. These expressions are given by:
where
in which , , … etc., are the plate stiffness, defined by
Hamilton’s principle can be written as
where the first variation of the kinetic energy is represented as
and is the total potential energy represented as
Using Equations (2), (4), (7), (17), and (18) in Equation (16) and carrying out the first variation allows us to get the following governing equations associated with the present quasi-3D plate theory:
where
The following closed-form solution is appropriate for such simply-supported plates and is seen to satisfy all governing equations:
where and . In addition, and represent the mode shapes of vibration and they indicate the number of half-waves in - and -directions, respectively. The stress and moment resultants in Equations (11)–(14) may be represented as
The governing Equations (19)–(24) after using Equations (26) and (27) are reduced to
where and the non-zero elements of the symmetric matrix and of the symmetric matrix are defined for FG plates by
3. Numerical Results and Discussion
This section presents some numerical examples for vibration frequencies of isotropic and FG rectangular plates. The accuracy and efficiency of the present quasi-3D refined theory in predicting fundamental and natural frequencies of simply-supported plates are discussed. The results due to the present theory are compared with those found in the literature using various theories. Different material properties are assumed as follows:
3.1. Isotropic Plate
3.2. Functionally Graded Plates
Numerical results concern values of dimensionless fundamental and natural frequencies are displayed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18. Different forms for dimensionless frequencies and foundation parameters are considered.
3.3. Analysis of Isotropic Plates
In this section, the special case of homogeneous isotropic plates is analyzed. Table 1, Table 2, Table 3 and Table 4 present the results of the non-dimensional natural frequency obtained by the present quasi-3D theory for square plates. In Table 1, Table 2, Table 3 and Table 4, the non-dimensional natural frequencies and nondimensional coefficients of foundations are utilized as
in which , , denote Young’s modulus, Poisson’s ratio, and density of the isotropic material.
Table 1 presents the natural frequencies of isotropic square plates due to the first eight modes. These frequencies are compared with the solutions of different authors: the 3D exact solutions by Leissa [], Zhou et al. [], Nagino et al. []; the FSDT using differential quadrature element method (DQM) by Liu and Liew []; and HDTs by Hosseini-Hashemi et al. [], Shufrin et al. [], Akavci [], and a quasi-3D hybrid type HSDT by Mantari et al. [].


Table 1.
Non-dimensional natural frequencies for isotropic square plates.
Table 1.
Non-dimensional natural frequencies for isotropic square plates.
| Theory | Mode | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (1,1) | (1,2) | (2,1) | (2,2) | (1,3) | (3,1) | (2,3) | (3,2) | ||
| 1000 | Leissa [] | 19.7392 | 49.3480 | 49.3480 | 78.9568 | 98.6960 | 98.6960 | 128.3021 | 128.3021 |
| Zhou et al. [] | 19.7115 | 49.3470 | 49.3470 | 78.9528 | 98.6911 | 98.6911 | 128.3048 | 128.3048 | |
| Akavci [] | 19.7391 | 49.3476 | 49.3476 | 78.9557 | 98.6943 | 98.6943 | 128.3020 | 128.3020 | |
| Mantari et al. [] | 19.7396 | 49.3482 | 49.3482 | 78.9568 | 98.6956 | 98.6956 | 128.3036 | 128.3036 | |
| Present | 19.73914 | 49.34760 | 49.34760 | 78.95574 | 98.69434 | 98.69434 | 128.30197 | 128.30197 | |
| 100 | Leissa [] | 19.7319 | 49.3027 | 49.3027 | 78.8410 | 98.5150 | 98.5150 | 127.9993 | 127.9993 |
| Nagino et al. [] | 19.7320 | 49.3050 | 49.3050 | 78.8460 | 98.5250 | 98.5250 | 128.0100 | 128.0100 | |
| Akavci [] | 19.7322 | 49.3045 | 49.3045 | 78.8456 | 98.5223 | 98.5223 | 128.0120 | 128.0120 | |
| Mantari et al. [] | 19.7326 | 49.3055 | 49.3055 | 78.8475 | 98.5250 | 98.5250 | 128.0156 | 128.0156 | |
| Present | 19.73231 | 49.30491 | 49.30491 | 78.84657 | 98.52386 | 98.52386 | 128.01415 | 128.01415 | |
| 10 | Liu et al. [] | 19.0584 | 45.4478 | 45.4478 | 69.7167 | 84.9264 | 84.9264 | 106.5154 | 106.5154 |
| Hosseini et al. [] | 19.0653 | 45.4869 | 45.4869 | 69.8093 | 85.0646 | 85.0646 | 106.7350 | 106.7350 | |
| Akavci [] | 19.0850 | 45.5957 | 45.5957 | 70.0595 | 85.4315 | 85.4315 | 107.3040 | 107.3040 | |
| Mantari et al. [] | 19.0901 | 45.6200 | 45.6200 | 70.1083 | 85.4964 | 85.4964 | 107.3896 | 107.3896 | |
| Present | 19.09028 | 45.62185 | 45.62185 | 70.11284 | 85.50305 | 85.50305 | 107.39973 | 107.39973 | |
| 5 | Shufrin et al. [] | 17.4524 | 38.1884 | 38.1884 | 55.2539 | 65.3130 | 65.3130 | 78.9864 | 78.9864 |
| Hosseini et al. [] | 17.4523 | 38.1883 | 38.1883 | 55.2543 | 65.3135 | 65.3135 | 78.9865 | 78.9865 | |
| Akavci [] | 17.5149 | 38.4722 | 38.4722 | 55.8358 | 66.1207 | 66.1207 | 80.1637 | 80.1637 | |
| Mantari et al. [] | 17.5271 | 38.4991 | 38.4991 | 55.8410 | 66.0874 | 66.0874 | 80.0364 | 80.0364 | |
| Present | 17.52821 | 38.50383 | 38.50383 | 55.84950 | 66.09809 | 66.09809 | 80.04976 | 80.04976 | |
It is clear from Table 1 that for the value of the side-to-thickness ratio (), the first mode of the present frequency is identical to those given by Leissa [] and Akavci [] and has proximity with the one obtained by Mantari et al. []. Additionally, the high modes of the present natural frequencies are identical to those given by Akavci [] and are very close to the ones obtained by Zhou et al. [], Leissa [], and Mantari et al. [] For the side-to-thickness ratio (), it is noted that the results are slightly less than those predicted by Mantari et al. [] and slightly greater than those predicted by Leissa [], Nagino et al. [], and Akavci []. For moderately thick plates (), the present natural frequencies are very close to those obtained by Mantari et al. [] and slightly greater than those predicted by Liu et al. [], Hosseini et al. [], and Akavci []. For thin plates (), the present natural frequencies are close to those obtained by Akavci [] and Mantari et al. []
In Table 2, Table 3 and Table 4, the outcomes of the non-dimensional natural frequency represented in Equation (34) for isotropic square plates resting on visco–Pasternak foundations are reported. The nondimensional coefficients of the three-parameter foundations are utilized as
The most important case is considered for isotropic square plates resting on the two-parameter Pasternak foundation. However, additional results for plates resting on three-parameter visco–Pasternak foundations are also included for future comparisons. Different values for the three-parameter coefficients , , and are discussed.



Table 2.
Non-dimensional fundamental frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, ).
Table 2.
Non-dimensional fundamental frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, ).
| Matsunaga [] | Thai and Choi [] | Mantari et al. [] | Present | |||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 17.5260 | 17.4523 | 17.5271 | 17.52821 | --- | --- | --- |
| 10 | 17.7847 | 17.7248 | 17.7858 | 17.78691 | 17.80266 | 17.85029 | 17.93085 | |
| 102 | 19.9528 | 20.0076 | 19.9613 | 19.96234 | 19.98001 | 20.03340 | 20.12372 | |
| 103 | 34.3395 | 35.5039 | 34.7796 | 34.78009 | 34.81060 | 34.90277 | 35.05861 | |
| 104 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 | |
| 105 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 | |
| 0 | 10 | 22.0429 | 22.2145 | 22.0707 | 22.07157 | 22.09109 | 22.15007 | 22.24983 |
| 10 | 22.2453 | 22.4286 | 22.2757 | 22.27657 | 22.29627 | 22.35578 | 22.45646 | |
| 102 | 23.9830 | 24.2723 | 24.0401 | 24.04090 | 24.06214 | 24.12631 | 24.23485 | |
| 103 | 36.6276 | 38.0650 | 37.2169 | 37.21732 | 37.24990 | 37.34833 | 37.51475 | |
| 104 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 | |
| 105 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 | |

Table 3.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
Table 3.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
| Matsunaga [] | Thai and Choi [] | Mantari et al. [] | Present | |||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 38.4827 | 38.1883 | 38.4991 | 38.50383 | --- | --- | --- |
| 10 | 38.5929 | 38.3098 | 38.6093 | 38.61403 | 38.75920 | 39.21005 | 40.01800 | |
| 102 | 39.5669 | 39.3895 | 39.5860 | 39.59068 | 39.73930 | 40.20086 | 41.02792 | |
| 103 | 47.8667 | 48.8772 | 48.1688 | 48.17300 | 48.35118 | 48.90436 | 49.89463 | |
| 104 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 | |
| 105 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 | |
| 0 | 10 | 43.4816 | 43.7943 | 43.5741 | 43.57850 | 43.74104 | 44.24576 | 45.14976 |
| 10 | 43.5747 | 43.9009 | 43.6701 | 43.67455 | 43.83742 | 44.34317 | 45.24900 | |
| 102 | 44.3994 | 44.8445 | 44.5241 | 44.52853 | 44.69434 | 45.20920 | 46.13126 | |
| 103 | 51.6029 | 53.3580 | 52.2029 | 52.20676 | 52.39828 | 52.99275 | 54.05639 | |
| 104 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 | |
| 105 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 | |
The first three non-dimensional natural frequencies of a thicker square plate () resting on the elastic foundation are presented in Table 2, Table 3 and Table 4. The first mode () fundamental frequencies are represented in Table 2 while natural frequencies and are presented in Table 3 and Table 4, respectively. In such tables, the frequencies are compared with the refined shear deformation theory given by Thai and Choi [], the HSDT proposed by Matsunaga [], and a quasi-3D hybrid type HSDT by Mantari et al. []


Table 4.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
Table 4.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
| Matsunaga [] | Thai and Choi [] | Mantari et al. [] | Present | |||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 65.9961 | 65.3135 | 66.0874 | 66.09809 | --- | --- | --- |
| 10 | 66.0569 | 65.3841 | 66.1481 | 66.15875 | 66.40586 | 67.17631 | 68.56834 | |
| 102 | 66.5995 | 66.0138 | 66.6907 | 66.70143 | 66.95005 | 67.72517 | 69.12547 | |
| 103 | 71.5577 | 72.0036 | 71.8192 | 71.83050 | 72.09271 | 72.90970 | 74.38380 | |
| 104 | 97.4964 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 | |
| 105 | 101.7992 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 | |
| 0 | 10 | 71.4914 | 71.9198 | 71.7485 | 71.75974 | 72.02177 | 72.83822 | 74.31135 |
| 10 | 71.5423 | 71.9839 | 71.8028 | 71.81402 | 72.07618 | 72.89304 | 74.36692 | |
| 102 | 71.9964 | 72.5554 | 72.2886 | 72.29990 | 72.56328 | 73.38389 | 74.86433 | |
| 103 | 76.1848 | 78.0290 | 76.9124 | 76.92383 | 77.19813 | 78.05223 | 79.59112 | |
| 104 | 99.0187 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 | |
| 105 | 101.7992 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 | |
The fundamental frequencies in Table 2 are close to those obtained by Matsunaga [] and Mantari et al. [] and slightly greater than those of Thai and Choi []. It is clear that the frequencies increase as the two-parameter coefficients increase. For higher values of the first parameter coefficient , the frequencies still have the same values. The inclusion of the third-parameter coefficient is also discussed here. It is interesting to see that the frequencies increase with the increase in the value of .
The natural frequencies in Table 3 and Table 4 are also closer to those obtained by Matsunaga [] and Mantari et al. [] and slightly greater than those of Thai and Choi []. Once again, the frequencies increase as the three-parameter coefficients increase. For higher values of the first parameter coefficient the frequencies still have the same values. It is to be noted that in Table 2, Table 3 and Table 4, as the mode increases, the frequency increases irrespective of the values of the three-parameter coefficients.
3.4. Analysis of FG Plates
Here, the non-dimensional fundamental frequencies of FG square plates are discussed in Table 5 and Table 6. The FG plates are fabricated of different materials. The mechanical properties of such materials are given in Equations (31)–(33). The non-dimensional frequency is utilized as
The non-dimensional fundamental frequencies for thicker () Aluminum-Zirconia (Al/ZrO2) FG square plates without elastic foundations are compared with the corresponding results in Table 5. Additional results for plates resting on Visco-Winkler-Pasternak foundations are also presented. The nondimensional coefficients of the three-parameter foundations are utilized as
In Table 5, the fundamental frequencies for three values of the FG power-law index are computed and compared with the 3D exact solution by Vel et al. [], quasi-3D sinusoidal and hyperbolic HSDTs by Neves et al. [,], a quasi-3D hybrid type HSDT by Mantari et al. [], and HSDTs by Akavci [], Hosseini-Hashemi et al. [], and Matsunaga []. The frequencies increase with the increase in the FG power-law index . Neglecting the three-parameter foundation coefficients shows that the present frequencies are identical to those of Mantari et al. []. In addition, the present frequencies agree well with the HSDTs’ frequencies. For the sake of future comparison, dome frequencies for plates on the Visco-Winkler-Pasternak foundation are also included in the same table. Once again, the frequencies increase with the increase in the three-parameter foundation coefficients.


Table 5.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates resting on Visco-Winkler-Pasternak foundations ().
Table 5.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates resting on Visco-Winkler-Pasternak foundations ().
| Theory | ||||
|---|---|---|---|---|
| 2 | 3 | 5 | ||
| Vel and Batra [] | 0.2197 | 0.2211 | 0.2225 | |
| Neves et al. () [] | 0.2189 | 0.2202 | 0.2215 | |
| Neves et al. () [] | 0.2198 | 0.2212 | 0.2225 | |
| Neves et al. () [] | 0.2191 | 0.2205 | 0.2220 | |
| Neves et al. () [] | 0.2201 | 0.2216 | 0.2230 | |
| Hosseini-Hashemi et al. [] | 0.2264 | 0.2276 | 0.2291 | |
| Akavci [] | 0.2263 | 0.2268 | 0.2277 | |
| Matsunaga [] | 0.2264 | 0.2270 | 0.2280 | |
| Mantari et al. [] | 0.2285 | 0.2290 | 0.2295 | |
| Present | 0.22848 | 0.22901 | 0.22952 | |
| , , | 0.23062 | 0.23130 | 0.23199 | |
| , , | 0.26937 | 0.27256 | 0.27610 | |
| , , | 0.26976 | 0.27301 | 0.27664 | |
| , , | 0.27095 | 0.27438 | 0.27825 | |
| , , | 0.28694 | 0.29132 | 0.29627 | |
The non-dimensional fundamental frequencies for Aluminum-Alumina (Al/Al2O3) FG rectangular plates are presented in Table 6. The frequencies are computed for four different values of the FG power-law index and compared with a quasi-3D hybrid type HSDT by Mantari et al. [] and a 3D exact solution proposed by Jin et al. []. Generally, the frequencies decrease with the increase in the FG power-law index . Additionally, the frequencies increase as both and decrease. Neglecting the three-parameter foundation coefficients shows that the present frequencies give good accuracy with those in [] and [] for square plates (). However, for rectangular plates (), the present frequencies are very close to those of Mantari et al. [] and slightly greater than those of Jin et al. [] For the sake of future comparison, some frequencies for plates on the Visco-Winkler-Pasternak foundation are also included in Table 6. The non-dimensional coefficients of the three-parameter foundations are given in Equation (37). For all cases studied, the frequencies increase with the increase in the three-parameter foundation coefficients.


Table 6.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations.
Table 6.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations.
| Theory | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | ||||
| 1 | 10 | Jin et al. [] | 0.1135 | 0.0870 | 0.0789 | 0.0741 | |
| Mantari et al. [] | 0.1135 | 0.0882 | 0.0806 | 0.0755 | |||
| Present | 0.11350 | 0.08818 | 0.08057 | 0.07553 | |||
| , , | 0.11627 | 0.09230 | 0.08533 | 0.08090 | |||
| , , | 0.11889 | 0.09613 | 0.08969 | 0.08578 | |||
| , , | 0.12152 | 0.09991 | 0.09397 | 0.09051 | |||
| 5 | Jin et al. [] | 0.4169 | 0.3222 | 0.2905 | 0.2676 | ||
| Mantari et al. [] | 0.4168 | 0.3260 | 0.2961 | 0.2722 | |||
| Present | 0.41685 | 0.32605 | 0.29613 | 0.27221 | |||
| , , | 0.42816 | 0.34278 | 0.31556 | 0.29463 | |||
| , , | 0.43885 | 0.35824 | 0.33329 | 0.31481 | |||
| , , | 0.44956 | 0.37344 | 0.35056 | 0.33425 | |||
| 2 | Jin et al. [] | 1.8470 | 1.4687 | 1.3095 | 1.1450 | ||
| Mantari et al. [] | 1.8505 | 1.4774 | 1.3219 | 1.1551 | |||
| Present | 1.85081 | 1.47762 | 1.32213 | 1.15544 | |||
| , , | 1.93506 | 1.59673 | 1.46375 | 1.33166 | |||
| , , | 2.01192 | 1.70066 | 1.58405 | 1.47548 | |||
| , , | 2.08633 | 1.79759 | 1.69386 | 1.60293 | |||
| 2 | 10 | Jin et al. [] | 0.0719 | 0.0550 | 0.0499 | 0.0471 | |
| Mantari et al. [] | 0.0718 | 0.0557 | 0.0510 | 0.0479 | |||
| Present | 0.07181 | 0.05573 | 0.05097 | 0.04794 | |||
| , , | 0.07614 | 0.06209 | 0.05824 | 0.05605 | |||
| , , | 0.07711 | 0.06348 | 0.05981 | 0.05778 | |||
| , , | 0.08115 | 0.06912 | 0.06611 | 0.06466 | |||
| 5 | Jin et al. [] | 0.2713 | 0.2088 | 0.1888 | 0.1754 | ||
| Mantari et al. [] | 0.2712 | 0.2115 | 0.1926 | 0.1786 | |||
| Present | 0.27124 | 0.21151 | 0.19262 | 0.17861 | |||
| , , | 0.28875 | 0.23709 | 0.22197 | 0.21183 | |||
| , , | 0.29268 | 0.24266 | 0.22828 | 0.21885 | |||
| , , | 0.30894 | 0.26520 | 0.25347 | 0.24662 | |||
| 2 | Jin et al. [] | 0.9570 | 0.7937 | 0.7149 | 0.6168 | ||
| Mantari et al. [] | 1.3040 | 1.0346 | 0.9293 | 0.8236 | |||
| Present | 1.30422 | 1.03469 | 0.92945 | 0.82385 | |||
| , , | 1.42513 | 1.20475 | 1.12760 | 1.06040 | |||
| , , | 1.45155 | 1.24029 | 1.16792 | 1.10679 | |||
| , , | 1.55824 | 1.37906 | 1.32259 | 1.28071 | |||
The non-dimensional fundamental frequencies for Aluminum-Zirconia (Al/ZrO2) FG square plates resting on Visco-Winkler-Pasternak foundations are reported in Table 7. When , the frequency parameter tends to . The frequencies, without the three-parameter foundation coefficients, are compared with the 3D exact solutions proposed by Vel and Batra [], HSDTs proposed by Akavci [], a quasi-3D hybrid type HSDT by Mantari et al. [], and Matsunaga []. In general, the frequencies increase as both and increase. The present frequencies are compared well with those reported in []. Additionally, the frequencies approach to the corresponding solutions obtained in [,,]. If the Visco-Winkler-Pasternak foundations are taken into account, the frequencies increase. Once again, the non-dimensional coefficients of the three-parameter foundations are given in Equation (37).


Table 7.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates on Visco-Winkler-Pasternak foundations.
Table 7.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates on Visco-Winkler-Pasternak foundations.
| Vel and Batra [] | Akavci [] | Matsunaga [] | Mantari et al. [] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (0,0,0) | (10,0,0.1) | (0,10,0.1) | (10,10,0.1) | ||||||
| 0 * | 4.6582 | 4.6569 | 4.6582 | 4.6601 | 4.66072 | 4.68987 | 5.20264 | 5.22844 | |
| 10 | 5.7769 | 5.7754 | 5.7769 | 5.7769 | 5.77698 | 5.80392 | 6.28692 | 6.31166 | |
| 1 | 5 | 5.4806 | 5.7110 | 5.7123 | 5.7501 | 5.75043 | 5.79726 | 6.61170 | 6.65231 |
| 10 | 5.9609 | 6.1924 | 6.1932 | 6.2365 | 6.23656 | 6.28244 | 7.08625 | 7.12659 | |
| 20 | 6.1076 | 6.3388 | 6.3390 | 6.3842 | 6.38419 | 6.42989 | 7.23208 | 7.27240 | |
| 2 | 5 | 5.4923 | 5.6593 | 5.6599 | 5.7115 | 5.71197 | 5.76558 | 6.68866 | 6.73430 |
| 3 | 5 | 5.5285 | 5.6718 | 5.6757 | 5.7246 | 5.72519 | 5.78258 | 6.76582 | 6.81423 |
| 5 | 5 | 5.5632 | 5.6941 | 5.7020 | 5.7376 | 5.73811 | 5.79984 | 6.85123 | 6.90276 |
* .
In Table 8, Table 9 and Table 10, the non-dimensional natural frequencies for Aluminum-Alumina (Al/Al2O3) FG rectangular plates () resting on Visco-Winkler-Pasternak foundations are reported. Three values of the side-to-thickness ratio , , are considered. The non-dimensional frequency and the non-dimensional coefficients of the three-parameter foundations are utilized as
Table 8, Table 9 and Table 10 present the first four non-dimensional natural frequencies , , and of FG plates for various values of the FG power-law index . Firstly, the frequencies increase as both the mode number and side-to-thickness ratio increase and as the FG power-law index decreases. For , the present frequencies are compared with the corresponding ones due to the HSDTs proposed by Akavci [], Thai et al. [], a quasi-3D hybrid type HSDT by Mantari et al. [], and the FSDT utilized by Hosseini-Hashemi et al. [] The present frequencies are very close to those in [,] and slightly greater than those in [,]. Furthermore, it is shown that for different values of the present frequencies get good agreements with the other theories. The frequencies, with the inclusion of the three-parameter foundation coefficients, are presented for future comparisons. The results represent benchmarks to help other investigators to assure their results for plates resting on three-parameter viscoelastic foundations. It is obvious that the frequency slightly increases when adding the three parameters of viscoelastic foundations one by one. The maximum frequencies occurred when all foundation coefficients are included.




Table 8.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
Table 8.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
| Mode | Theory | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | 8 | 10 | |||
| (1,1) | Akavci [] | 3.4495 | 2.6529 | 2.3989 | 2.2275 | 2.1724 | 2.1455 | |
| Thai et al. [] | 3.4412 | 2.6475 | 2.3949 | 2.2272 | 2.1697 | 2.1407 | ||
| Hosseini et al. [] | 3.4409 | 2.6473 | 2.4017 | 2.2528 | 2.1985 | 2.1677 | ||
| Mantari et al. [] | 3.4513 | 2.6913 | 2.4508 | 2.2725 | 2.2032 | 2.1689 | ||
| Present | 3.45145 | 2.69138 | 2.45102 | 2.27273 | 2.20328 | 2.16887 | ||
| , , | 3.57401 | 2.87249 | 2.66011 | 2.51080 | 2.45332 | 2.42438 | ||
| , , | 4.74470 | 4.43132 | 4.37556 | 4.37628 | 4.37573 | 4.37110 | ||
| , , | 4.83425 | 4.54296 | 4.49522 | 4.50341 | 4.50555 | 4.50200 | ||
| (1,2) | Akavci [] | 5.3003 | 4.0906 | 3.6900 | 3.3952 | 3.3031 | 3.2626 | |
| Thai et al. [] | 5.2813 | 4.0781 | 3.6805 | 3.3938 | 3.2964 | 3.2514 | ||
| Hosseini et al. [] | 5.2802 | 4.0773 | 3.6953 | 3.4492 | 3.3587 | 3.3094 | ||
| Mantari et al. [] | 5.3039 | 4.1487 | 3.7677 | 3.4633 | 3.3484 | 3.2955 | ||
| Present | 5.30428 | 4.14891 | 3.76818 | 3.46376 | 3.34863 | 3.29565 | ||
| , , | 5.38275 | 4.26554 | 3.90401 | 3.62103 | 3.51478 | 3.46565 | ||
| , , | 6.67940 | 6.03846 | 5.88419 | 5.81358 | 5.78825 | 5.77233 | ||
| , , | 6.74143 | 6.11832 | 5.97100 | 5.90714 | 5.88422 | 5.86923 | ||
| (1,3) | Akavci [] | 8.1179 | 6.2950 | 5.6614 | 5.1479 | 4.9921 | 4.9313 | |
| Thai et al. [] | 8.0749 | 6.2663 | 5.6390 | 5.1425 | 4.9758 | 4.9055 | ||
| Hosseini et al. [] | 8.0710 | 6.2636 | 5.6695 | 5.2579 | 5.1045 | 5.0253 | ||
| Mantari et al. [] | 8.1244 | 6.3814 | 5.7751 | 5.2484 | 5.0560 | 4.9747 | ||
| Present | 8.12516 | 6.38194 | 5.77596 | 5.24934 | 5.05661 | 4.97515 | ||
| , , | 8.17497 | 6.45589 | 5.86279 | 5.35193 | 5.16569 | 5.08687 | ||
| , , | 9.58143 | 8.41316 | 8.08122 | 7.86334 | 7.78824 | 7.75204 | ||
| , , | 9.62310 | 8.46823 | 8.14203 | 7.93018 | 7.85721 | 7.82177 | ||
| (2,1) | Akavci [] | 10.1828 | 7.9209 | 7.1105 | 6.4181 | 6.2111 | 6.1355 | |
| Thai et al. [] | 10.1164 | 7.8762 | 7.0751 | 6.4074 | 6.1846 | 6.0954 | ||
| Hosseini et al. [] | 9.7416 | 7.8711 | 7.1189 | 6.5749 | 5.9062 | 5.7518 | ||
| Mantari et al. [] | 10.1907 | 8.0264 | 7.2479 | 6.5397 | 6.2856 | 6.1833 | ||
| Present | 10.19182 | 8.02721 | 7.24906 | 6.54102 | 6.28651 | 6.18403 | ||
| , , | 10.23084 | 8.08500 | 7.31724 | 6.62262 | 6.37363 | 6.27329 | ||
| , , | 11.69616 | 10.13547 | 9.65993 | 9.31233 | 9.19418 | 9.14170 | ||
| , , | 11.72947 | 10.17994 | 9.70947 | 9.36749 | 9.25130 | 9.19949 | ||

Table 9.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
Table 9.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
| Mode | Theory | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | 8 | 10 | |||
| (1,1) | Akavci [] | 3.6542 | 2.7952 | 2.5376 | 2.3915 | 2.3418 | 2.3124 | |
| Thai et al. [] | 3.6518 | 2.7937 | 2.5364 | 2.3916 | 2.3411 | 2.3110 | ||
| Hosseini et al. [] | 3.6518 | 2.7937 | 2.5386 | 2.3998 | 2.3504 | 2.3197 | ||
| Mantari et al. [] | 3.6549 | 2.8365 | 2.5943 | 2.4398 | 2.3761 | 2.3398 | ||
| Present | 3.65486 | 2.83651 | 2.59442 | 2.43983 | 2.37599 | 2.33961 | ||
| , , | 3.77600 | 3.01640 | 2.80120 | 2.67192 | 2.61867 | 2.58757 | ||
| , , | 4.94508 | 4.58507 | 4.52571 | 4.53573 | 4.53665 | 4.53077 | ||
| , , | 5.03519 | 4.69835 | 4.64720 | 4.66450 | 4.66813 | 4.66344 | ||
| (1,2) | Akavci [] | 5.7754 | 4.4231 | 4.0118 | 3.7682 | 3.6864 | 3.6403 | |
| Thai et al. [] | 5.7694 | 4.4192 | 4.0090 | 3.7682 | 3.6846 | 3.6368 | ||
| Hosseini et al. [] | 5.7693 | 4.4192 | 4.0142 | 3.7881 | 3.7072 | 3.6580 | ||
| Mantari et al. [] | 5.7769 | 4.4881 | 4.1008 | 3.8443 | 3.7401 | 3.6827 | ||
| Present | 5.77698 | 4.48818 | 4.10112 | 3.84448 | 3.74004 | 3.68252 | ||
| , , | 5.85372 | 4.60305 | 4.23389 | 3.99463 | 3.89754 | 3.84363 | ||
| , , | 7.13799 | 6.38008 | 6.21360 | 6.16032 | 6.13672 | 6.11716 | ||
| , , | 7.20008 | 6.46117 | 6.30177 | 6.25482 | 6.23361 | 6.21512 | ||
| (1,3) | Akavci [] | 9.2029 | 7.0612 | 6.3959 | 5.9766 | 5.8388 | 5.7662 | |
| Thai et al. [] | 9.1880 | 7.0515 | 6.3886 | 5.9765 | 5.8341 | 5.7575 | ||
| Hosseini et al. [] | 9.1876 | 7.0512 | 6.4015 | 6.0247 | 5.8887 | 5.8086 | ||
| Mantari et al. [] | 9.2066 | 7.1643 | 6.5363 | 6.0976 | 5.9231 | 5.8315 | ||
| Present | 9.20678 | 7.16448 | 6.53682 | 6.09800 | 5.92308 | 5.83137 | ||
| , , | 9.25458 | 7.23620 | 6.62003 | 6.19285 | 6.02286 | 5.93351 | ||
| , , | 10.62513 | 9.17828 | 8.80991 | 8.61977 | 8.54454 | 8.49887 | ||
| , , | 10.66630 | 9.23397 | 8.87138 | 8.68657 | 8.61339 | 8.56863 | ||
| (2,1) | Akavci [] | 11.8560 | 9.1093 | 8.2428 | 7.6738 | 7.4892 | 7.3965 | |
| Thai et al. [] | 11.8315 | 9.0933 | 8.2309 | 7.6731 | 7.4813 | 7.3821 | ||
| Hosseini et al. [] | 11.8310 | 9.0928 | 8.2515 | 7.7505 | 7.5688 | 7.4639 | ||
| Mantari et al. [] | 11.8616 | 9.2416 | 8.4222 | 7.8291 | 7.5963 | 7.4783 | ||
| Present | 11.86203 | 9.24189 | 8.42299 | 7.82973 | 7.59651 | 7.47829 | ||
| , , | 11.89892 | 9.29724 | 8.48733 | 7.90347 | 7.67423 | 7.55787 | ||
| , , | 13.30715 | 11.31242 | 10.77355 | 10.45683 | 10.33484 | 10.26714 | ||
| , , | 13.33967 | 11.35714 | 10.82331 | 10.51139 | 10.39125 | 10.32437 | ||

Table 10.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
Table 10.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
| Mode | Theory | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | 8 | 10 | |||
| (1,1) | Akavci [] | 3.7129 | 2.8357 | 2.5774 | 2.4402 | 2.3924 | 2.3623 | |
| Thai et al. [] | 3.7123 | 2.8352 | 2.5771 | 2.4403 | 2.3923 | 2.3619 | ||
| Hosseini et al. [] | 3.7123 | 2.8352 | 2.5777 | 2.4425 | 2.3948 | 2.3642 | ||
| Mantari et al. [] | 3.7132 | 2.8777 | 2.6354 | 2.4892 | 2.4277 | 2.3908 | ||
| Present | 3.71313 | 2.87770 | 2.63557 | 2.48923 | 2.42750 | 2.39055 | ||
| , , | 3.83394 | 3.05727 | 2.84172 | 2.71973 | 2.66821 | 2.63648 | ||
| , , | 5.00322 | 4.62897 | 4.56905 | 4.58347 | 4.58523 | 4.57888 | ||
| , , | 5.09349 | 4.74266 | 4.69098 | 4.71261 | 4.71708 | 4.71193 | ||
| (1,2) | Akavci [] | 5.9215 | 4.5238 | 4.1108 | 3.8883 | 3.8112 | 3.7632 | |
| Thai et al. [] | 5.9199 | 4.5228 | 4.1100 | 3.8884 | 3.8107 | 3.7622 | ||
| Hosseini et al. [] | 5.9198 | 4.5228 | 4.1115 | 3.8939 | 3.8170 | 3.7681 | ||
| Mantari et al. [] | 5.9220 | 4.5909 | 4.2032 | 3.9665 | 3.8672 | 3.8084 | ||
| Present | 5.92192 | 4.59085 | 4.20342 | 3.96649 | 3.86700 | 3.80806 | ||
| , , | 5.99822 | 4.70524 | 4.33538 | 4.11474 | 4.02212 | 3.96672 | ||
| , , | 7.28089 | 6.48489 | 6.31643 | 6.27436 | 6.25285 | 6.23193 | ||
| , , | 7.34305 | 6.56631 | 6.40495 | 6.36905 | 6.34989 | 6.33007 | ||
| (1,3) | Akavci [] | 9.5711 | 7.3159 | 6.6453 | 6.2759 | 6.1488 | 6.0715 | |
| Thai et al. [] | 9.5669 | 7.3132 | 6.6433 | 6.2760 | 6.1476 | 6.0690 | ||
| Hosseini et al. [] | 9.5668 | 7.3132 | 6.6471 | 6.2903 | 6.1639 | 6.0843 | ||
| Mantari et al. [] | 9.5723 | 7.4242 | 6.7942 | 6.4023 | 6.2391 | 6.1440 | ||
| Present | 9.57223 | 7.42418 | 6.79463 | 6.40232 | 6.23878 | 6.14351 | ||
| , , | 9.61945 | 7.49521 | 6.87676 | 6.49490 | 6.33580 | 6.24279 | ||
| , , | 10.98422 | 9.43713 | 9.06263 | 8.90094 | 8.83088 | 8.78146 | ||
| , , | 11.02533 | 9.49302 | 9.124280 | 8.96765 | 8.89955 | 8.85106 | ||
| (2,1) | Akavci [] | 12.4633 | 9.5307 | 8.6542 | 8.1634 | 7.9954 | 7.8950 | |
| Thai et al. [] | 12.4562 | 9.5261 | 8.6509 | 8.1636 | 7.9934 | 7.8909 | ||
| Hosseini et al. [] | 12.4560 | 9.5261 | 8.6572 | 8.1875 | 8.0207 | 7.9166 | ||
| Mantari et al. [] | 12.4652 | 9.6715 | 8.8478 | 8.3279 | 8.1127 | 7.9888 | ||
| Present | 12.46522 | 9.67154 | 8.84835 | 8.32803 | 8.11232 | 7.98825 | ||
| , , | 12.50143 | 9.72605 | 8.91143 | 8.39926 | 8.18701 | 8.06469 | ||
| , , | 13.89984 | 11.73763 | 11.18768 | 10.91733 | 10.80357 | 10.72952 | ||
| , , | 13.93224 | 11.78246 | 11.23750 | 10.97160 | 10.85959 | 10.78637 | ||
Table 11, Table 12, Table 13 and Table 14 present the non-dimensional fundamental frequencies for Aluminum-Alumina (Al/Al2O3) FG rectangular plates resting on visco–Pasternak foundations (, ). Several values of the FG power-law index , aspect ratio , and side-to-thickness ratio are considered. In fact, there is no foundation in Table 11, and the inclusion of one-by-one elastic foundation is made in Table 12, Table 13 and Table 14. In such tables, the inclusion of the third-parameter coefficient is also discussed. The non-dimensional frequency and the non-dimensional third coefficient of the viscoelastic foundations are utilized as
and the other non-dimensional coefficients of the two-parameter foundations are given in Equation (37). In the absence of the third coefficient of the viscoelastic foundations , the present frequencies are compared with the HSDTs proposed by Thai and Choi [], Akavci [], and a quasi-3D hybrid type HSDT by Mantari et al. []



Table 11.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
Table 11.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
| Akavci [] | Thai and Choi [] | Mantari et al. [] | Present | |||
|---|---|---|---|---|---|---|
| 0.5 | 5 | 1 | 5.2122 | 5.2016 | 5.2875 | 5.28772 |
| 5 | 4.3763 | 4.3757 | 4.4648 | 4.46520 | ||
| 10 | 4.2153 | 4.2058 | 4.2611 | 4.26116 | ||
| 10 | 1 | 5.4918 | 5.4887 | 5.5728 | 5.57286 | |
| 5 | 4.6986 | 4.6987 | 4.7934 | 4.79350 | ||
| 10 | 4.5432 | 4.5404 | 4.5969 | 4.59661 | ||
| 20 | 1 | 5.5712 | 5.5704 | 5.6538 | 5.65379 | |
| 5 | 4.7943 | 4.7943 | 4.8906 | 4.89057 | ||
| 10 | 4.6411 | 4.6404 | 4.6971 | 4.69669 | ||
| 1 | 5 | 1 | 8.0368 | 8.0122 | 8.1509 | 8.15131 |
| 5 | 6.6705 | 6.6678 | 6.8043 | 6.80521 | ||
| 10 | 6.4099 | 6.3879 | 6.4746 | 6.47492 | ||
| 10 | 1 | 8.6899 | 8.6824 | 8.8178 | 8.81788 | |
| 5 | 7.4033 | 7.4034 | 7.5529 | 7.55319 | ||
| 10 | 7.1521 | 7.1453 | 7.2353 | 7.23501 | ||
| 20 | 1 | 8.8879 | 8.8859 | 9.0196 | 9.01959 | |
| 5 | 7.6393 | 7.6394 | 7.7929 | 7.79291 | ||
| 10 | 7.3934 | 7.3916 | 7.4823 | 7.48166 | ||
| 2 | 5 | 1 | 17.8289 | 17.7148 | 18.0607 | 18.06273 |
| 5 | 14.3625 | 14.3312 | 14.6274 | 14.63068 | ||
| 10 | 13.7120 | 13.6095 | 13.8083 | 13.81014 | ||
| 10 | 1 | 20.8487 | 20.8063 | 21.1501 | 21.15090 | |
| 5 | 17.5051 | 17.5028 | 17.8593 | 17.86082 | ||
| 10 | 16.8613 | 16.8232 | 17.0445 | 17.04463 | ||
| 20 | 1 | 21.9670 | 21.9548 | 22.2914 | 22.29144 | |
| 5 | 18.7946 | 18.7950 | 19.1737 | 19.17401 | ||
| 10 | 18.1727 | 18.1616 | 18.3877 | 18.38645 |

Table 12.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco-Winkler foundations (, ).
Table 12.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco-Winkler foundations (, ).
| Akavci [] | Thai and Choi [] | Mantari et al. [] | Present | ||||
|---|---|---|---|---|---|---|---|
| 0.5 | 5 | 1 | 5.8746 | 5.8654 | 5.9257 | 5.92588 | 5.92620 |
| 5 | 5.2360 | 5.2355 | 5.2934 | 5.29366 | 5.29417 | ||
| 10 | 5.1288 | 5.1212 | 5.1467 | 5.14660 | 5.14722 | ||
| 10 | 1 | 6.1393 | 6.1366 | 6.2077 | 6.20770 | 6.20801 | |
| 5 | 5.5276 | 5.5277 | 5.6038 | 5.60384 | 5.60430 | ||
| 10 | 5.4199 | 5.4176 | 5.4596 | 5.45931 | 5.45987 | ||
| 20 | 1 | 6.2152 | 6.2144 | 6.2883 | 6.28824 | 6.28829 | |
| 5 | 5.6156 | 5.6157 | 5.6969 | 5.69685 | 5.69692 | ||
| 10 | 5.5087 | 5.5080 | 5.5545 | 5.55415 | 5.55422 | ||
| 1 | 5 | 1 | 8.4748 | 8.4517 | 8.5671 | 8.56752 | 8.56801 |
| 5 | 7.2560 | 7.2534 | 7.3618 | 7.36260 | 7.36336 | ||
| 10 | 7.0373 | 7.0175 | 7.0758 | 7.07594 | 7.07683 | ||
| 10 | 1 | 9.1107 | 9.1035 | 9.2282 | 9.22829 | 9.22876 | |
| 5 | 7.9520 | 7.9521 | 8.0866 | 8.08681 | 8.08751 | ||
| 10 | 7.7356 | 7.7293 | 7.8067 | 7.80636 | 7.80720 | ||
| 20 | 1 | 9.3044 | 9.3025 | 9.4292 | 9.42918 | 9.42925 | |
| 5 | 8.1789 | 8.1790 | 8.3212 | 8.32122 | 8.32132 | ||
| 10 | 7.9658 | 7.9640 | 8.0468 | 8.04617 | 8.04629 | ||
| 2 | 5 | 1 | 18.0231 | 17.9108 | 18.2385 | 18.24050 | 18.24161 |
| 5 | 14.6363 | 14.6057 | 14.8810 | 14.88418 | 14.88578 | ||
| 10 | 14.0098 | 13.9101 | 14.0861 | 14.08780 | 14.08965 | ||
| 10 | 1 | 21.0241 | 20.9821 | 21.3187 | 21.31945 | 21.32062 | |
| 5 | 17.7396 | 17.7373 | 18.0843 | 18.08585 | 18.08761 | ||
| 10 | 17.1126 | 17.0751 | 17.2873 | 17.28741 | 17.28949 | ||
| 20 | 1 | 22.1378 | 22.1257 | 22.4585 | 22.45857 | 22.45967 | |
| 5 | 19.0187 | 19.0192 | 19.3921 | 19.39248 | 19.39408 | ||
| 10 | 18.4115 | 18.4005 | 18.6222 | 18.62087 | 18.62278 | ||
It can be seen from Table 11, Table 12, Table 13 and Table 14 that the present frequencies are in excellent agreement with the corresponding results of Mantari et al. [] and slightly more than those of Thai and Choi [] and Akavci []. The frequencies increase as both and increase and as decreases in case of neglecting the foundation medium. The frequency when is more than twice of this when .


Table 13.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco–Pasternak foundations (, ).
Table 13.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco–Pasternak foundations (, ).
| Akavci [] | Thai and Choi [] | Mantari et al. [] | Present | ||||
|---|---|---|---|---|---|---|---|
| 0.5 | 5 | 1 | 10.8489 | 10.8450 | 10.7649 | 10.76493 | 10.76552 |
| 5 | 10.9925 | 10.9919 | 10.9106 | 10.91023 | 10.91134 | ||
| 10 | 11.0818 | 11.0793 | 10.9611 | 10.96027 | 10.96164 | ||
| 10 | 1 | 11.0940 | 11.0926 | 11.1042 | 11.10417 | 11.10472 | |
| 5 | 11.2538 | 11.2538 | 11.2645 | 11.26443 | 11.26537 | ||
| 10 | 11.3313 | 11.3302 | 11.3190 | 11.31873 | 11.31989 | ||
| 20 | 1 | 11.1660 | 11.1656 | 11.1999 | 11.19984 | 11.20017 | |
| 5 | 11.3343 | 11.3343 | 11.3680 | 11.36794 | 11.36849 | ||
| 10 | 11.4093 | 11.4090 | 11.4236 | 11.42342 | 11.42390 | ||
| 1 | 5 | 1 | 14.3923 | 14.3818 | 14.2406 | 14.24088 | 14.24170 |
| 5 | 14.3071 | 14.3052 | 14.1562 | 14.15569 | 14.15721 | ||
| 10 | 14.3829 | 14.3759 | 14.1600 | 14.15860 | 14.16046 | ||
| 10 | 1 | 14.9443 | 14.9401 | 14.9631 | 14.96319 | 14.96395 | |
| 5 | 14.8693 | 14.8692 | 14.8895 | 14.88945 | 14.89075 | ||
| 10 | 14.9193 | 14.9162 | 14.8957 | 14.89520 | 14.89681 | ||
| 20 | 1 | 15.1189 | 15.1177 | 15.1825 | 15.18244 | 15.18316 | |
| 5 | 15.0607 | 15.0607 | 15.1251 | 15.12506 | 15.12623 | ||
| 10 | 15.1056 | 15.1047 | 15.1330 | 15.13257 | 15.13403 | ||
| 2 | 5 | 1 | 25.6912 | 25.6294 | 25.2563 | 25.25781 | 25.25932 |
| 5 | 24.3625 | 24.3453 | 23.8994 | 23.89854 | 23.90119 | ||
| 10 | 24.3109 | 24.2696 | 23.6297 | 23.62625 | 23.62944 | ||
| 10 | 1 | 28.2316 | 28.2023 | 28.2878 | 28.28833 | 28.28988 | |
| 5 | 26.7223 | 26.7201 | 26.7859 | 26.78627 | 26.78890 | ||
| 10 | 26.5586 | 26.5362 | 26.4775 | 26.47653 | 26.47974 | ||
| 20 | 1 | 29.2272 | 29.2181 | 29.4271 | 29.42715 | 29.42860 | |
| 5 | 27.7770 | 27.7772 | 27.9891 | 27.98915 | 27.99147 | ||
| 10 | 27.5919 | 27.5847 | 27.6803 | 27.67920 | 27.68203 | ||
In each table, in addition to the examination of the aspect ratios , thickness ratios , and the FG power-law index , we discussed several combinations of the foundation parameters and . Furthermore, different values of the third damping coefficient are considered. The results show that the three Visco-Winkler-Pasternak foundation parameters have effects of increasing the non-dimensional frequencies. The Pasternak parameter has more of an effect on increasing the frequencies than the Winkler parameter . However, the damping parameter has a little and sensitive effect on increasing the frequencies. It is interesting to discuss the effect of the FG power-law index on the non-dimensional frequencies. As shown in Table 11, the frequency parameter decreases with the increase in and this is irrespective of the values of and . Additionally, it is observed in Table 12 that if a plate is just rested on Winkler’s foundation or visco-Winkler foundations, the increase of the FG power-law index decreases the non-dimensional frequency. However, this situation is inversed if the plate is rested on Pasternak’s foundation regardless of the absence (Table 13) or presence (Table 14) of Winkler’s foundation or visco-Winkler foundations.


Table 14.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
Table 14.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
| Akavci [] | Thai and Choi [] | Mantari et al. [] | Present | ||||
|---|---|---|---|---|---|---|---|
| 0.5 | 5 | 1 | 11.1817 | 11.1780 | 11.0894 | 11.08946 | 11.09007 |
| 5 | 11.3598 | 11.3593 | 11.2700 | 11.26956 | 11.27071 | ||
| 10 | 11.4581 | 11.4558 | 11.3285 | 11.32767 | 11.32909 | ||
| 10 | 1 | 11.4284 | 11.4270 | 11.4358 | 11.43582 | 11.43638 | |
| 5 | 11.6243 | 11.6243 | 11.6322 | 11.63214 | 11.63311 | ||
| 10 | 11.7103 | 11.7093 | 11.6957 | 11.69536 | 11.69657 | ||
| 20 | 1 | 11.5008 | 11.5005 | 11.5331 | 11.53311 | 11.53346 | |
| 5 | 11.7054 | 11.7054 | 11.7374 | 11.73738 | 11.73796 | ||
| 10 | 11.7888 | 11.7886 | 11.8021 | 11.80186 | 11.80257 | ||
| 1 | 5 | 1 | 14.6407 | 14.6305 | 14.4792 | 14.47947 | 14.48030 |
| 5 | 14.5862 | 14.5843 | 14.4258 | 14.42519 | 14.42675 | ||
| 10 | 14.6702 | 14.6636 | 14.4366 | 14.43508 | 14.43698 | ||
| 10 | 1 | 15.1927 | 15.1887 | 15.2084 | 15.20848 | 15.20924 | |
| 5 | 15.1498 | 15.1497 | 15.1669 | 15.16678 | 15.16811 | ||
| 10 | 15.2075 | 15.2045 | 15.1810 | 15.18053 | 15.18217 | ||
| 20 | 1 | 15.3674 | 15.3663 | 15.4293 | 15.42927 | 15.43000 | |
| 5 | 15.3414 | 15.3414 | 15.4039 | 15.40390 | 15.40509 | ||
| 10 | 15.3938 | 15.3929 | 15.4198 | 15.41946 | 15.42094 | ||
| 2 | 5 | 1 | 25.8251 | 25.7640 | 25.3782 | 25.37974 | 25.38125 |
| 5 | 24.5206 | 24.5036 | 24.0450 | 24.04408 | 24.04674 | ||
| 10 | 24.4759 | 24.4352 | 23.7803 | 23.77672 | 23.77992 | ||
| 10 | 1 | 28.3613 | 28.3322 | 28.4137 | 28.41429 | 28.41586 | |
| 5 | 26.8763 | 26.8741 | 26.9360 | 26.93632 | 26.93896 | ||
| 10 | 26.7186 | 26.6964 | 26.6338 | 26.63282 | 26.63605 | ||
| 20 | 1 | 29.3557 | 29.3467 | 29.5539 | 29.55394 | 29.55539 | |
| 5 | 27.9292 | 27.9294 | 28.1392 | 28.13924 | 28.14156 | ||
| 10 | 27.7497 | 27.7426 | 27.8366 | 27.83544 | 27.83829 | ||
Table 15 presents the non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on viscoelastic foundations with and several values of . The non-dimensional frequency and the non-dimensional viscoelastic foundation coefficients are utilized as


Table 15.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
Table 15.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
| Theory | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 5 | |||||
| (0,0) | 0.5 | Akavci [] | 0.08018 | 0.06148 | 0.05215 | 0.04081 | |
| Hosseini et al. [] | 0.08006 | 0.06335 | 0.05379 | 0.04100 | |||
| Mantari et al. [] | 0.08021 | 0.06238 | 0.05321 | 0.04083 | |||
| Present | 0.080209 | 0.062382 | 0.053210 | 0.040825 | |||
| 1 | Akavci [] | 0.12508 | 0.09613 | 0.08089 | 0.06366 | ||
| Hosseini et al. [] | 0.12480 | 0.09644 | 0.08027 | 0.06335 | |||
| Mantari et al. [] | 0.12514 | 0.09753 | 0.08253 | 0.06370 | |||
| Present | 0.12514 | 0.09753 | 0.08253 | 0.063696 | |||
| 2 | Akavci [] | 0.28659 | 0.22189 | 0.18232 | 0.14587 | ||
| Hosseini et al. [] | 0.28513 | 0.20592 | 0.16315 | 0.14591 | |||
| Mantari et al. [] | 0.28682 | 0.22498 | 0.18592 | 0.14600 | |||
| Present | 0.286844 | 0.224999 | 0.185947 | 0.146000 | |||
| (100,10) | 0.5 | Baferani et al. [] | 0.12869 | 0.10498 | 0.09227 | --- | |
| Akavci [] | 0.12876 | 0.10388 | 0.09098 | 0.06554 | |||
| Hosseini et al. [] | 0.12870 | 0.10519 | 0.09223 | 0.06591 | |||
| Mantari et al. [] | 0.12804 | 0.10388 | 0.09118 | 0.06517 | |||
| Present | 0.128037 | 0.103883 | 0.091179 | 0.065169 | |||
| 0.128140 | 0.103981 | 0.091284 | 0.065243 | ||||
| 1 | Baferani et al. [] | 0.17020 | 0.13854 | 0.12077 | --- | ||
| Akavci [] | 0.17039 | 0.13592 | 0.11774 | 0.08673 | |||
| Hosseini et al. [] | 0.17020 | 0.13652 | 0.11786 | 0.08663 | |||
| Mantari et al. [] | 0.16931 | 0.13610 | 0.11825 | 0.08618 | |||
| Present | 0.169312 | 0.136102 | 0.118253 | 0.086178 | |||
| 0.169454 | 0.136236 | 0.118398 | 0.086279 | ||||
| 2 | Baferani et al. [] | 0.31449 | 0.26966 | 0.22932 | --- | ||
| Akavci [] | 0.32889 | 0.25901 | 0.21785 | 0.16741 | |||
| Hosseini et al. [] | 0.32768 | 0.24674 | 0.20359 | 0.16773 | |||
| Mantari et al. [] | 0.32670 | 0.25992 | 0.21953 | 0.16630 | |||
| Present | 0.326723 | 0.259934 | 0.219551 | 0.166298 | |||
| 0.327020 | 0.260213 | 0.219848 | 0.166511 | ||||
It is to be noted that when (ceramic plate), will tends to while when (metal plate) will tends to .
The present frequencies are compared with the corresponding ones of the FSDT of Hosseini-Hashemi et al. [], the HSDTs proposed by Akavci [] and Baferani et al. [], and a quasi-3D hybrid type HSDT by Mantari et al. [] It can be seen from this table that the present results are identical to those proposed by Mantari et al. [], close to the ones of Akavci [] and Mantari et al. [], and slightly more than those of Baferani et al. [] Once again, the frequencies increase with the inclusion of the damping coefficient .
Table 16 presents the non-dimensional fundamental frequencies for Aluminum-Zirconia (Al/ZrO2) FG rectangular plates () resting on viscoelastic foundations with several values of the side-to-thickness ratio . The non-dimensional frequency and the non-dimensional viscoelastic foundation coefficients are utilized as given in Equation (40). The present solution is compared with the corresponding ones of the theories presented in Table 15. In general, the frequencies are slightly decreasing as the FG power-law index increases while they rapidly increase as the side-to-thickness ratio increases. Furthermore, the inclusion of the viscoelastic foundations increases the values of the frequency parameter. Once again, the present results are identical to those proposed by Mantari et al. [] for free pleats or plates resting on elastic foundations. In the case of , the present frequencies are slightly greater than those proposed by Akavci [] and Hosseini et al. []. However, in the case of , , the present frequencies are slightly smaller than those proposed by Akavci [] and Hosseini et al. [], especially when . In the case of the viscoelastic coefficients, the frequencies increase with the inclusion of the damping coefficient .


Table 16.
Non-dimensional fundamental frequencies for Al/ZrO2 FG rectangular plates ().
Table 16.
Non-dimensional fundamental frequencies for Al/ZrO2 FG rectangular plates ().
| Theory | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 5 | |||||
| (0,0) | 20 | Akavci [] | 0.02393 | 0.02202 | 0.02244 | 0.02056 | |
| Hosseini et al. [] | 0.02392 | 0.02156 | 0.02180 | 0.02046 | |||
| Mantari et al. [] | 0.02393 | 0.02217 | 0.02260 | 0.02057 | |||
| Present | 0.023931 | 0.022174 | 0.022597 | 0.02056 | |||
| 10 | Akavci [] | 0.09203 | 0.08489 | 0.08576 | 0.07908 | ||
| Hosseini et al. [] | 0.09188 | 0.08155 | 0.08171 | 0.07895 | |||
| Mantari et al. [] | 0.09207 | 0.08549 | 0.08638 | 0.07911 | |||
| Present | 0.092068 | 0.085493 | 0.086386 | 0.079111 | |||
| 5 | Akavci [] | 0.32471 | 0.30152 | 0.31860 | 0.27902 | ||
| Hosseini et al. [] | 0.32284 | 0.29399 | 0.29099 | 0.27788 | |||
| Mantari et al. [] | 0.32498 | 0.30349 | 0.29990 | 0.27925 | |||
| Present | 0.325006 | 0.303514 | 0.299939 | 0.279268 | |||
| (250,25) | 20 | Baferani et al. [] | 0.03421 | 0.03249 | 0.03314 | --- | |
| Akavci [] | 0.03422 | 0.03213 | 0.03277 | 0.02940 | |||
| Hosseini et al. [] | 0.03421 | 0.03184 | 0.03235 | 0.02937 | |||
| Mantari et al. [] | 0.03417 | 0.03220 | 0.03283 | 0.02936 | |||
| Present | 0.034169 | 0.032200 | 0.032834 | 0.029361 | |||
| 0.034272 | 0.032213 | 0.032848 | 0.029395 | ||||
| 10 | Baferani et al. [] | 0.13365 | 0.12749 | 0.12950 | --- | ||
| Akavci [] | 0.13375 | 0.12585 | 0.12778 | 0.11492 | |||
| Hosseini et al. [] | 0.13365 | 0.12381 | 0.12533 | 0.11484 | |||
| Mantari et al. [] | 0.13302 | 0.12557 | 0.12755 | 0.11430 | |||
| Present | 0.133019 | 0.125569 | 0.127554 | 0.114299 | |||
| 0.133127 | 0.125707 | 0.127731 | 0.114495 | ||||
| 5 | Baferani et al. [] | 0.43246 | 0.46406 | 0.44824 | --- | ||
| Akavci [] | 0.50044 | 0.47298 | 0.47637 | 0.43000 | |||
| Hosseini et al. [] | 0.49945 | 0.46997 | 0.47400 | 0.43001 | |||
| Mantari et al. [] | 0.48945 | 0.46401 | 0.46838 | 0.42057 | |||
| Present | 0.489466 | 0.464028 | 0.468392 | 0.420583 | |||
| 0.489910 | 0.464595 | 0.469153 | 0.421389 | ||||
3.5. Parametric Studies
The above two sections are concerned with verifying the accuracy of the present model with the corresponding ones available in the literature. The present parametric studies are carried out to investigate the influences of the FG power-law index , aspect ratio , thickness ratio , and the two foundation parameters and on the natural frequency of Al/Al2O3 and Al/ZrO2 plates. In addition, the effect of the damping parameter is taken into consideration in most cases.
The variations of non-dimensional natural frequencies for Aluminum-Alumina (Al/Al2O3) FG rectangular plates concerning different parameters are presented in Table 17 and Table 18. The thickness and aspect ratios and the first mode number are fixed as , and , respectively. The effects of the FG power-law index , the second mode number , and the Visco-Winkler-Pasternak foundations , , and . The frequencies increase as all parameters increase, except the FG power-law index for which the frequencies decrease.



Table 17.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates (, ).
Table 17.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates (, ).
| Mode | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | |||||
| (1,1) | 0 | 0 | 0 | 0.46607 | 0.36775 | 0.33164 | 0.29787 | 0.23722 |
| 10 | 0 | 0.46741 | 0.36892 | 0.33283 | 0.29905 | 0.23790 | ||
| 1 | 0.46916 | 0.37056 | 0.33448 | 0.30070 | 0.23917 | |||
| 2 | 0.47462 | 0.37569 | 0.33960 | 0.30576 | 0.24314 | |||
| 100 | 0 | 0.47923 | 0.37925 | 0.34336 | 0.30943 | 0.24392 | ||
| 1 | 0.48103 | 0.38094 | 0.34506 | 0.31114 | 0.24521 | |||
| 2 | 0.48661 | 0.38621 | 0.35034 | 0.31638 | 0.24928 | |||
| 10 | 0 | 0 | 0.52750 | 0.42118 | 0.38575 | 0.35094 | 0.26849 | |
| 1 | 0.52947 | 0.42304 | 0.38766 | 0.35288 | 0.26990 | |||
| 2 | 0.53558 | 0.42886 | 0.39358 | 0.35885 | 0.27436 | |||
| 10 | 0 | 0.52866 | 0.42218 | 0.38676 | 0.35193 | 0.26908 | ||
| 1 | 0.53063 | 0.42405 | 0.38868 | 0.35387 | 0.27050 | |||
| 2 | 0.53675 | 0.42988 | 0.39461 | 0.35986 | 0.27496 | |||
| 100 | 0 | 0.53900 | 0.43112 | 0.39573 | 0.36066 | 0.24392 | ||
| 1 | 0.54101 | 0.43302 | 0.39769 | 0.36265 | 0.24521 | |||
| 2 | 0.54724 | 0.43897 | 0.40376 | 0.36879 | 0.24928 | |||

Table 18.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates (, ).
Table 18.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates (, ).
| Mode | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | |||||
| (1,2) | 0 | 0 | 0 | 1.17023 | 0.93832 | 0.83770 | 0.72561 | 0.59563 |
| 10 | 0 | 1.17072 | 0.93873 | 0.83813 | 0.72607 | 0.59588 | ||
| 1 | 1.17499 | 0.94280 | 0.84212 | 0.72977 | 0.59895 | |||
| 2 | 1.18832 | 0.95560 | 0.85469 | 0.74137 | 0.60870 | |||
| 100 | 0 | 1.17508 | 0.94244 | 0.84202 | 0.73020 | 0.59810 | ||
| 1 | 1.17935 | 0.94652 | 0.84602 | 0.73391 | 0.60117 | |||
| 2 | 1.19270 | 0.95933 | 0.85861 | 0.74557 | 0.61093 | |||
| 10 | 0 | 0 | 1.24726 | 1.00366 | 0.90580 | 0.79747 | 0.63484 | |
| 1 | 1.25160 | 1.00781 | 0.90995 | 0.80143 | 0.63796 | |||
| 2 | 1.26515 | 1.02085 | 0.92301 | 0.81384 | 0.64785 | |||
| 10 | 0 | 1.24769 | 1.00402 | 0.90618 | 0.79787 | 0.63506 | ||
| 1 | 1.25204 | 1.00818 | 0.91033 | 0.80183 | 0.63818 | |||
| 2 | 1.26558 | 1.02122 | 0.92339 | 0.81424 | 0.64807 | |||
| 100 | 0 | 1.25158 | 1.00731 | 0.90959 | 0.80144 | 0.63704 | ||
| 1 | 1.25593 | 1.01147 | 0.91375 | 0.80541 | 0.64016 | |||
| 2 | 1.26948 | 1.02452 | 0.92683 | 0.81787 | 0.65006 | |||
| (1,3) | 0 | 0 | 0 | 1.95174 | 1.58204 | 1.40727 | 1.19641 | 0.99341 |
| 10 | 0 | 1.95203 | 1.58228 | 1.40752 | 1.19669 | 0.99356 | ||
| 1 | 1.95889 | 1.58883 | 1.41381 | 1.20228 | 0.99849 | |||
| 2 | 1.98029 | 1.60940 | 1.43361 | 1.21989 | 1.01411 | |||
| 100 | 0 | 1.95461 | 1.58442 | 1.40979 | 1.19918 | 0.99487 | ||
| 1 | 1.96146 | 1.59097 | 1.41607 | 1.20477 | 0.99979 | |||
| 2 | 1.98282 | 1.61150 | 1.43585 | 1.22237 | 1.01539 | |||
| 10 | 0 | 0 | 2.04872 | 1.66250 | 1.49197 | 1.28918 | 1.04277 | |
| 1 | 2.05515 | 1.66863 | 1.49797 | 1.29470 | 1.04739 | |||
| 2 | 2.07508 | 1.68772 | 1.51677 | 1.31206 | 1.06190 | |||
| 10 | 0 | 2.04897 | 1.66271 | 1.49218 | 1.28941 | 1.04290 | ||
| 1 | 2.05539 | 1.66883 | 1.49818 | 1.29494 | 1.04751 | |||
| 2 | 2.07532 | 1.68792 | 1.51698 | 1.31230 | 1.06202 | |||
| 100 | 0 | 2.05118 | 1.66453 | 1.49410 | 1.29150 | 1.04402 | ||
| 1 | 2.05759 | 1.67064 | 1.50009 | 1.29702 | 1.04863 | |||
| 2 | 2.07747 | 1.68970 | 1.51886 | 1.31437 | 1.06311 | |||
4. Conclusions
In the present study, a refined quasi-3D elasticity theory is presented for natural vibration analysis of homogeneous and FG plates resting on Visco-Winkler-Pasternak foundations. The governing equations of motion are derived due to Hamilton’s principle. The closed-form solutions are obtained for different types of rectangular plates. A validation study is performed to verify the accuracy of the present frequencies. Furthermore, a parametric study is carried out to investigate the effects of various parameters on the natural frequencies of FG plates. Such parameters are the FG power-law index, aspect and thickness ratios, and foundation parameters, especially the inclusion of the third damping parameter. The following points can be outlined from the present study:
- The quasi-3D theory satisfies both the zero transverse and normal shear stress conditions on the plate surfaces and does not require any shear correction factor;
- Compared to other theories in the literature, the present quasi-3D theory produces accurate results for both thin and thick FG plates;
- One of the important notes is that Pasternak’s parameter has a greater effect on increasing the non-dimensional frequency than both the Winkler’s and visco-Winkler parameters;
- In general, in the inclusion of the viscoelastic foundation, increasing the value of Winkler, Pasternak, and damping coefficients causes an increase in the natural frequencies of FG plates;
- The FG power-law index affects reducing the non-dimensional frequencies of FG plates on visco-Winkler-Pasternak foundations.
Author Contributions
Conceptualization, A.M.Z. and M.A.A.; data curation, M.A.A.; funding acquisition, M.A.A.; investigation, A.M.Z.; methodology, A.M.Z.; project administration, A.M.Z.; resources, M.A.A.; software, M.A.A. and A.M.Z.; supervision, A.M.Z.; validation, A.M.Z.; visualization, A.M.Z.; writing—original draft preparation, M.A.A.; writing—review and editing, M.A.A. and A.M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IFPHI-198-135-2020) and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
Not applicable.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPHI-198-135-2020). Therefore, the authors gratefully acknowledge technical and financial support from the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koizumi, M. The concept of FGM ceramic transactions. Funct. Gradient Mater. 1993, 34, 3–10. [Google Scholar]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Taher, H.; Akhavan, H.; Omidi, M. Free vibration of functionally graded rectangular plates using first-order shear deformation plate theory. Appl. Math. Model. 2010, 34, 1276–1291. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. Free vibration of functionally graded sandwich plates in thermal environment using a layerwise theory. Europ. J. Mech.-A Solids 2015, 51, 55–66. [Google Scholar] [CrossRef]
- Zenkour, A.M. Free vibration of a microbeam resting on Pasternak’s foundation via the Green–Naghdi thermoelasticity theory without energy dissipation. J. Low Freq. Noise Vib. Act. Control 2016, 35, 303–311. [Google Scholar] [CrossRef] [Green Version]
- Benferhat, R.; Daouadji, T.; Mansour, M. Free vibration analysis of FG plates resting on an elastic foundation and based on the neutral surface concept using higher-order shear deformation theory. Comptes Rendus Mécanique 2016, 344, 631–641. [Google Scholar] [CrossRef]
- Zaoui, F.; Tounsi, A.; Ouinas, D. Free vibration of functionally graded plates resting on elastic foundations based on quasi-3D hybrid-type higher order shear deformation theory. Smart Struct. Syst. 2017, 20, 509–524. [Google Scholar]
- Zenkour, A.M.; Radwan, A.F. Free vibration analysis of multilayered composite and soft core sandwich plates resting on Winkler-Pasternak foundations. J. Sand. Struct. Mater. 2018, 20, 169–190. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, R.; Safarpour, M. Vibration analysis of FG-GPLRC annular plate in a thermal environment. Mech. Based Des. Struct. Mach. 2022, 50, 352–370. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Vibration analysis of functionally graded graphene platelet-reinforced composite doubly-curved shallow shells on elastic foundations. Steel Compos. Struct. 2019, 33, 195–208. [Google Scholar]
- Kumar, V.; Singh, S.; Saran, V.; Harsha, V. An analytical framework for rectangular FGM tapered plate resting on the elastic foundation. Mater. Today Proc. 2020, 28, 1719–1726. [Google Scholar] [CrossRef]
- Liu, J.; Deng, X.; Wang, Q.; Zhong, R.; Xiong, R.; Zhao, J. A unified modeling method for dynamic analysis of GPL-reinforced FGP plate resting on Winkler-Pasternak foundation with elastic boundary conditions. Compos. Struct. 2020, 244, 112217. [Google Scholar] [CrossRef]
- Arefi, M.; Kiani, M.; Zenkour, A.M. Size-dependent free vibration analysis of a three-layered exponentially graded nano-/micro-plate with piezomagnetic face sheets resting on Pasternak’s foundation via MCST. J. Sand. Struct. Mater. 2020, 22, 55–86. [Google Scholar] [CrossRef]
- Tran, T.; Nguyen, P.; Pham, Q. Vibration analysis of FGM plates in thermal environment resting on elastic foundation using ES-MITC3 element and prediction of ANN. Case Stud. Therm. Eng. 2021, 24, 100852. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Chen, H.; Du, Y. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos. Part B Eng. 2019, 164, 249–264. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Du, Y.; Gao, C. Free vibration analysis of uniform and stepped functionally graded circular cylindrical shells. Steel Compos. Struct. 2019, 33, 163–180. [Google Scholar] [CrossRef]
- Radaković, A.; Čukanović, D.; Bogdanović, G.; Blagojević, M.; Stojanović, B.; Dragović, D.; Manić, N. Thermal buckling and free vibration analysis of functionally graded plate resting on an elastic foundation according to high order shear deformation theory based on eew shape function. Appl. Sci. 2020, 10, 4190. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Yao, L. Analysis of the vibration behaviors of rotating composite nano-annular plates based on nonlocal theory and different plate theories. Appl. Sci. 2022, 12, 230. [Google Scholar] [CrossRef]
- Nguyen, P.; Pham, Q.; Tran, T.; Thoi, T. Effects of partially supported elastic foundation on free vibration of FGP plates using ES-MITC3 elements. Ain Shams Eng. J. 2021, 13, 101615. [Google Scholar]
- Tran, T.T.; Tran, V.K.; Pham, Q.-H.; Zenkour, A.M. Extended four-unknown higher-order shear deformation nonlocal theory for bending, buckling and free vibration of functionally graded porous nanoshell resting on elastic foundation. Compos. Struct. 2021, 264, 113737. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Forced vibration of a magnetoelastic laminated composite beam on Pasternak’s foundation. J. Comput. Appl. Mech. 2021, 52, 478–497. [Google Scholar]
- Zenkour, A.M. Vibration analysis of generalized thermoelastic microbeams resting on visco-Pasternak’s foundations. Adv. Aircr. Spacecr. Sci. 2017, 4, 269–280. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Size-dependent free vibration and dynamic analyses of piezo-electro-magnetic sandwich nanoplates resting on viscoelastic foundation. Appl. Phys. B 2017, 521, 188–197. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Vibration and bending analyses of magneto-electro-thermos-elastic sandwich microplates resting on viscoelastic foundation. Appl. Phys. A 2017, 123, 550. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Hygrothermal forced vibration of a viscoelastic laminated plate with magnetostrictive actuators resting on viscoelastic foundations. Int. J. Mech. Mater. Des. 2021, 17, 301–320. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Controlled motion of viscoelastic fiber-reinforced magnetostrictive sandwich plates resting on visco-Pasternak foundation. Mech. Adv. Mater. Struct. 2022, 2020, 1–10. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Forced vibration of sinusoidal FG nanobeams resting on hybrid Kerr foundation in hygro-thermal environments. Mech. Adv. Mater. Struct. 2018, 25, 669–680. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Control of hygrothermal vibration of viscoelastic magnetostrictive laminates resting on Kerr’s foundation. Mech. Based Des. Struct. Mach. 2021, 2021, 1–29. [Google Scholar] [CrossRef]
- Leissa, A.W. The Free vibration of rectangular plates. J. Sound Vib. 1973, 31, 257–293. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K.; Au, F.T.K.; Lo, S.H. Three-dimensional vibration analysis of thick rectangular plates using Chebyshev polynomial and Ritz method. Int. J. Solids Struct. 2002, 39, 6339–6353. [Google Scholar] [CrossRef]
- Nagino, H.; Mikami, T.; Mizusawa, T. Three-dimensional free vibration analysis of isotropic rectangular plates using the B-spline Ritz method. J. Sound Vib. 2008, 317, 329–353. [Google Scholar] [CrossRef]
- Liu, F.L.; Liew, K.M. Analysis of vibrating thick rectangular plates with mixed boundary constraints using differential quadrature element method. J. Sound Vib. 1999, 225, 915–934. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Fadaee, M.; Taher, H.R.D. Exact solutions for free flexural vibration of Lévy-type rectangular thick plates via third-order shear deformation plate theory. Appl. Math. Model. 2011, 35, 708–727. [Google Scholar] [CrossRef]
- Shufrin, I.; Eisenberger, M. Stability and vibration of shear deformable plates—First order and higher order analyses. Int. J. Solids Struct. 2005, 42, 1225–1251. [Google Scholar] [CrossRef]
- Akavci, S.S. An efficient shear deformation theory for free vibration of functionally graded thick rectangular plates on elastic foundation. Compos. Struct. 2014, 108, 667–676. [Google Scholar] [CrossRef]
- Mantari, J.L.; Granados, E.V.; Hinostroza, M.A.; Guedes Soares, C. Modelling advanced composite plates resting on elastic foundation by using a quasi-3D hybrid type HSDT. Compos. Struct. 2014, 118, 455–471. [Google Scholar] [CrossRef]
- Matsunaga, H. Vibration and stability of thick plates on elastic foundations. J. Eng. Mech. ASCE 2000, 126, 27–34. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. A refined shear deformation theory for free vibration of functionally graded plates on elastic foundation. Compos. Part B Eng. 2012, 43, 2335–2347. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plate. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Roque, C.M.C.; Cinefra, M.; Jorge, R.M.N.; Soares, C.M. A quasi-3D sinusoidal shear deformation theory for the static and free vibration analysis of functionally graded plates. Compos. Part B Eng. 2012, 43, 711–725. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Roque, C.M.C.; Jorge, R.M.N.; Soares, C.M. A quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. Compos. Struct. 2012, 94, 1814–1825. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Jin, G.; Su, Z.; Shi, S.; Ye, T.; Gao, S. Three-dimensional exact solution for the free vibration of arbitrarily thick functionally graded rectangular plates with general boundary conditions. Compos. Struct. 2014, 108, 565–577. [Google Scholar] [CrossRef]
- Thai, H.T.; Park, T.; Choi, D.H. An efficient shear deformation theory for vibration of functionally graded plates. Arch. Appl. Mech. 2013, 83, 137–149. [Google Scholar] [CrossRef]
- Hasani Baferani, A.; Saidi, A.R.; Ehteshami, H. Accurate solution for free vibration analysis of functionally graded thick rectangular plates resting on elastic foundation. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).