Abstract
This paper introduces a general stochastic game analysis of a network scenario consisting of a mix of cooperative and non-cooperative players (i.e., users) under incomplete game information. Users access a shared channel using the Slotted ALOHA mechanism combined with ZigZag Decoding (SAZD). Cooperative players seek to optimize the global utility of the system (e.g., throughput, delay, loss rate) regardless of their individual interests, whereas non-cooperative players act selfishly and optimize their own benefits irrespective of the impact of this behavior on others and on the entire network system. The game equilibrium is characterized by the social optimum and the Nash equilibrium, where the former is adopted by cooperative players and the latter is the equilibrium strategy of non-cooperative players. We undertake a comparative study across two game scenarios with different levels of cooperation and selfishness. Our results generally show that the information possessed by a player can determine the outcome. Furthermore, our findings show that the network performance is strongly influenced by selfish behavior, which can lead to a significant disruption of the entire system. Finally, we show a possible scenario in which the network could greatly benefit from this selfish behavior thanks to the ZigZag scheme.
1. Introduction
Random access mechanisms are the fundamental schemes for channel access under distributed access systems. These mechanisms can be divided into two categories: ALOHA and its enhanced variants [1,2,3,4,5] and Carrier Sense Multiple Access (CSMA)-based schemes [6]. Many approaches have been proposed over recent years to improve the performance of ALOHA, such as the Age of Information (AoI) threshold mechanism [7], Coded Slotted ALOHA (CSA) [5], Successive Interference Cancellation (SIC) [8], Capture Effect (CE) [9], and ZigZag Decoding (ZD) [10,11]. In ALOHA, users transmit whenever they generate a packet, whereas, in CSMA, users implement carrier sensing before accessing the channel. This paper focuses on the the Slotted ALOHA enhanced by ZigZag Decoding (SAZD). In slotted ALOHA (SA), users are allowed to transmit only at the beginning of a slot. This feature provides a peak throughput equal to compared with only for the pure ALOHA.
The game theory framework can be classified into two game categories: cooperative and non-cooperative games. In the cooperative game model, users know their neighbor’s action plan, strategy space, and utility functions. Thus, users cooperate to make decisions that lead to an equilibrium solution that makes the group satisfied. The cooperation leads to the best performance, whereas the non-cooperative game model yields the worst system performance [12].
The cooperative game framework provides highly effective approaches for modeling collaborative environments. It has been widely applied to solve various types of interactive situations such as channel access, resource management, and bandwidth allocation. In wireless networks, cooperation is performed by a central entity for optimizing the overall system performance, thus either maximizing the system throughput, minimizing the access channel delay, or minimizing the backlog level of the network.
In non-cooperative game models [4,13,14], each user attempts to maximize his utility without considering the potential impact on other users. Unfortunately, this selfish behavior usually leads to a dramatic degradation of the performance of all users. To address this issue, several approaches have been proposed in the literature. For example, in our previous work [12], we proposed to force the cooperation by associating a cost for every transmission attempt.
Most game theory models [13,14,15,16,17,18] consider that either all users cooperate or all users do not. However, in this paper, we propose a game theory model with both user categories. Thus, the proposed network scenario consists of cooperative and selfish users who share the same wireless channel. In this context, cooperative users behave for the benefit of the overall system. Consequently, they attempt to maximize the overall network performance. In contrast, selfish users are self-contained, and they act independently by trying to maximize their own utility instead of the utility of the overall system. This study aims to investigate the interaction between cooperative and non-cooperative users within the same wireless network, and also to evaluate the impact of selfish behavior on the performance of the cooperative users and on the overall system performance.
The main contributions of this paper are as follows:
- We propose a novel stochastic game model incorporating cooperative and non-cooperative players in the same game.
- We develop a bi-dimensional Markov chain to determine the system’s state in the stationary regime.
- We show that the game admits an equilibrium solution that integrates the Nash and social optimality concepts.
- We explore different performance metrics, such as throughput, delay, number of backlogged packets, and the equilibrium retransmission policy.
- We undertake a comparative study of two game scenarios with different levels of cooperation and selfishness.
The remainder of this paper is organized as follows. Section 2 presents some recent related works in the literature. In Section 3, we provide a brief overview of the SAZD mechanism. In Section 4, we describe the bi-dimensional Markov model and give the main performance metrics. Then, in Section 5, we develop the game model and find the corresponding equilibrium. In Section 6, we present the numerical results and discuss the main findings of the study. Finally, Section 7 concludes this paper.
2. Related Work
Slotted ALOHA is one of the most widely used random access schemes. Nowadays, it is implemented in many technologies, e.g., satellite networks [15], LoRaWAN networks [19,20,21], IoT applications [2], Machine-to-Machine (M2M) communications [3], and NOMA for the Next-Generation IoT [22].
2.1. Cooperative Game Models
Cooperative models study the situation of collaboration and coalition between users. In our previous work [12,23], we proposed a cooperative model of SA and SAZD. Our results showed that in both mechanisms, cooperation leads to the best results. We also showed that the SAZD mechanism outperforms the standard SA in terms of all performance metrics. However, in heavy-traffic conditions, the cooperation between users leads to unfair resource allocation due to the system specifications that allows newly arrived packets to be transmitted immediately after their arrival. Thus, even if the overall system performance is maximized, it is only used by newly arrived packets, making backlogged packets stay on hold for a very long time. To address this issue, we have proposed in [10] an enhanced pricing mechanism that allows us to guarantee a fairness level between newly arrived and backlogged packets.
The authors of [15] proposed a cooperative scheme for SA with power diversity transmission and an interference cancellation technique for multi-satellite networks. Using an optimization approach, they derived the optimal transmission power distribution. Their results show that the cooperative SA with optimized transmission power outperforms the SA with uniform power distribution. Even though their analysis and results focus mainly on the throughput, they investigated the access delay and energy consumption in [24].
The authors of [16] studied a cooperative SA full-duplex wireless network with two users. They found that they should only cooperate when the user has a higher successful transmission probability. However, the cooperation concept proposed in their study is a relay-based approach between a source and relay node, which could be extended to multiple user scenarios. The authors also proposed in [17] an optimal cooperation policy that outperforms, in some cases, the full-cooperation and non-cooperation policies.
In [18], the authors proposed a beamforming collision resolution scheme that exploits multiple satellites’ cooperation to decode the collided packets. The beamforming algorithm is used when a deadlock state is reached. Otherwise, they use the successive interference cancellation.
2.2. Non-Cooperative Game Models
Non-cooperative game theory provides a framework analysis of the interaction between selfish users. The Slotted ALOHA mechanism and its variants have been widely studied using non-cooperative models. In [4,12], we have proposed a stochastic game model of Slotted ALOHA combined with ZigZag Decoding. The model assumes that all users are selfish, and therefore they do not cooperate with each other. Compared with the cooperative model, we found that the selfish behavior of users yields the worst system performance, especially in the case of a large number of users.
In [13], the authors provided a non-cooperative game model for Slotted ALOHA. To achieve the desired throughput, they proposed to adjust users’ transmission probabilities at each iteration of the game. Then, they investigated the equilibrium of the game.
The authors of [14] proposed a non-cooperative game analysis of a network scenario operating using the carrier sense multiple access with collision avoidance (CSMA/CA) mechanism. Each user in the proposed scheme attempts to minimize the age of his information. They studied different profiles of pure and mixed strategies. They found that the collision length affects the dominant strategy of the game.
2.3. Mixed Game Models
The authors of [25] studied the cooperative and non-cooperative game models for Slotted ALOHA with channel capture. The optimal threshold strategy is used to characterize the equilibrium in the case of cooperation, whereas the non-cooperative equilibrium is given as the Bayesian Nash equilibrium. The authors showed that in the non-cooperative game, users transmit with a higher probability than the cooperative scenario. This aggressive behavior comes from the fact that in non-cooperative games, users consider only their own payoffs.
In [26], an extensive investigation of cooperation and selfishness was carried out using stochastic games and evolutionary game theory. According to the study, the system resource depends on the strategic choices of the users. Thus, it increases in the case of cooperation and decreases in the case of non-cooperation. The same behavior was found in SA and in SAZD systems [12].
The authors of [27] proposed a game model with a mix of cooperative and non-cooperative users for Wifi networks. They found that the cooperation is beneficial even if some users choose to deviate. Additionally, they claimed that most defected users are penalized by obtaining the worst signal-to-interference-plus-noise ratio (SINR). However, the results focus mainly on the SINR; and the impact of the mixed user scenario on other performance metrics, e.g., throughput and delay, is not investigated.
In [28], the authors developed an optimal caching algorithm using the social selfishness concept to achieve the best caching strategy for a mix of cooperative and non-cooperative users. The social selfishness concept adopted takes into account the social relationship between users. Thus, each user cares more about the cooperative users with whom he has a strong social relationship.
3. SAZD Overview
In this section, we outline the principle operation of the main access mechanism of this paper, namely, Slotted ALOHA combined with ZigZag decoding, which is a randomly distributed access mechanism for channel access in wireless networks. Due to its straightforward implementation, it can be widely implemented in many recent technologies. The proposed mechanism behaves exactly like the Slotted ALOHA mechanism. Thus, the time is divided into slots of the same length. Transmissions and retransmissions are allowed only at the beginning of the slot. Therefore, when a packet arrives during the current slot, it should be transmitted at the beginning of the next slot.
Furthermore, if a packet collides, it should be retransmitted later with a given probability . Unlike SA, in the proposed mechanism, the Access Point (AP) can decode two colliding packets thanks to the ZigZag decoding scheme. The AP can trigger the ZD only when it detects a collision of two packets [5], then it reserves the following slot to the same stations to collide again [29]. This feature does not introduce any overhead and does not require any change to the MAC layer.
Based on the received feedback, we can distinguish between four medium states.
- 0: when the medium is idle;
- 1: when one packet is successfully transmitted without interference;
- ZigZag: when the AP senses a simultaneous transmission of two packets;
- C: when three or more stations transmit at the same time slot.
4. Problem Formulation
In this section, we present an analytical model of the system’s state using a bidimensional Markov chain. This model allows us to derive all the performance metrics of interest in the stationary regime. This section introduces the theoretical framework and the basic requirements needed for the construction of the game theory model introduced in Section 5.
4.1. Model Description
We consider a wireless network consisting of two groups of users sharing a common transmission channel, as illustrated in Figure 1. Let us consider a case where the first group consists of cooperative users and let the second group be to the group of selfish users. Let M be the number of users in the first group and N the number of users in the second group, and let m and n be the number of backlogged users in each group. The arrival flow of packets to each source in each group follows a Bernoulli process with parameters and , respectively. Similarly, let and be the retransmission probability of backlogged users in each group.
Figure 1.
A scenario of a wireless network where M cooperative users share the same medium with N selfish users.
We define and as the transmission probability of i unbacklogged nodes in the first and the second groups, respectively.
Similarly, we define and as the retransmission probability of i backlogged nodes in the first and the second groups.
4.2. Analytical Model
In this section, we provide the theoretical model of the proposed mechanism. Let be the stochastic process representing the number of backlogged users in each group at the beginning of the time slot k. The reason behind using a bi-dimensional stochastic process comes from the subdivision of the users into two groups.
Theorem 1.
For any choice of values and , is Markovian with a unique stationary distribution.
Proof.
Consider the process , representing the number of backlogged nodes among cooperative and selfish users in a given slot time k. The state space is then
where M and N denote, respectively, the total number of cooperative and selfish users.
Let and denote the number of newly arrived packets, respectively, for cooperative and selfish users during slot and are scheduled for the first transmission attempt in slot k. Furthermore, let and , respectively, be the number of cooperative and selfish backlogged users that attempt to transmit in slot k. Thus, we have
Therefore, the number of transmissions occurring in a given slot k among cooperative and selfish users denoted, respectively, by and , can be expressed as follows:
The evolution of the number of backlogged nodes found in the system at the beginning of slot can now be expressed by the following equations:
where is the indicator function.
Thus, the number of backlogged nodes at the beginning of a given time slot depends not only on the number of arrivals and departures in previous slot k but also on the system state (i.e., the number of backlogged users). Therefore, the following Markov property holds since the future states of the process are independent of the past states.
For all and , we have:
where denotes the initial state of the Markov chain.
Now, let us assume that and . Then, the Markov chain has six absorbing states, namely, , , , , and . For and , all other states are transient. The absorbing states can be reached with positive probabilities and from any initial state, except from another absorbing state. Therefore, we shall exclude the case of and .
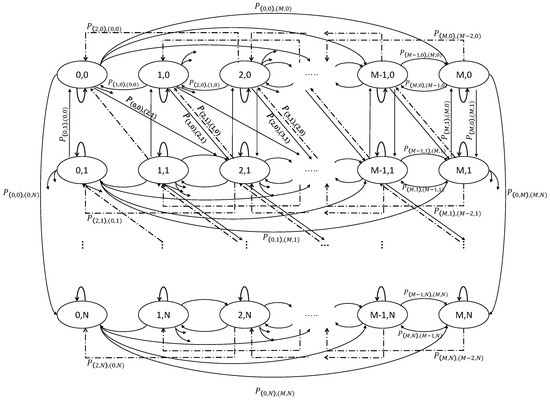
The stochastic process can now be described as a homogeneous finite Markov process with possible states, where the transition probabilities are given in the appendix. The transition diagram is given in Figure 2.

Figure 2.
Transition diagram of the Markov chain. The straight line corresponds to either a successful transmission or an increase in backlogged packets, whereas the dashed line represents a successful transmission with ZigZag.
Since all states communicate with each other and the state space is finite, the Markov chain is ergodic [30]. Therefore, the steady-state probability exists, and it is unique. We denote by the vector of the steady-state probability, where is the probability that the system contains i backlogged nodes of the cooperative group and j backlogged nodes of the selfish group. This steady-state distribution can be obtained by solving the following problem:
where P is the transition block matrix which is given in Appendix A. □
Note that the only absorbing state with no arrivals and no departures (i.e., deadlock state) is the state . Thus, from now on we consider and , and we choose such that .
4.3. Performance Evaluation
Proposition 1.
The average throughput of cooperative and non-cooperative users is given, respectively, as follows
Proof.
To derive the throughput expression, we need to define the packet’s transmission time .
The slots’ lengths in SA are of the same size. However, in SAZD, the slot duration depends on the stations’ transmission activities. In the case of ZigZag, the transmission duration takes two slots. Otherwise, the transmission takes one slot duration. Therefore, can be defined as follows
where is the probability that two packets are sent using ZD, and it is given by
is the indicator function, such that
Now, we can find the average throughput of cooperative users.
In the steady state, the average number of transmitted packets equals the average number of arrivals. Therefore, for a fixed value of m, the cooperative arrival rate in each state , where , is . Then, by taking all possible cases for m, we can derive the throughput of cooperative users as Equation (16) of the previous proposition. Similarly, the average number of arrival packets of non-cooperative users is , which yields Equation (17) by considering all the possible cases for n. □
Remark 1.
where and are the average number of successfully delivered packets among cooperative and non-cooperative users, respectively. They are given as follows
Proposition 2.
The average number of backlogged users is given by
Proof.
The backlogged users are the ones that have a packet on hold due to a previous collision. Thus, since the state of the Markov chain corresponds to the number of backlogged packets, then the average number of backlogged cooperative users can be derived by considering the current number of backlogged users m and taking the sum over all the possible states of the non-cooperative users which is given by
Then, we can sum all the possible states of m. Using a similar approach, we can derive the average number of backlogged nodes among non-cooperative users. □
Corollary 1.
Proof.
We can obtain the two results of the corollary by developing Equations (16) and (17) as follows:
and
□
Proposition 3.
The access delays of the transmitted packets of cooperative and non-cooperative users are given by
Proof.
According to Little’s result [30], the average number of packets in a stationary system is equal to the average effective throughput multiplied by the average time that a packet spends in the system. Note that the actual number of packets in the system includes the backlogged packets and transmitted packets. Thus, the packet delays for both users are:
□
In order to accurately evaluate the system implementation, we should explore the performance of the backlogged packets. The next proposition gives the average throughput of backlogged users.
Proposition 4.
Consider the transition matrix P, where is the transition probability from state to state . The average throughput of the backlogged packets transmitted by cooperative and non-cooperative users is given, respectively, as follows:
Proof.
In the stationary regime, the average number of backlogged packets that enter the system in a slot time corresponds to the average number of packets that leave the system in the same slot time, and thus to the backlogged throughput. Furthermore, for a given system state , the probability that k backlogged packets corresponding to cooperative users enter the system, or equivalently, the probability that cooperative-users packets become backlogged is given by . Thus, the number of backlogged packets that enter the system at a given state is , where .
Thus, by considering all possible states , , and , we can obtain the expression (40). A similar approach can be used to derive the second equation of Proposition 4. □
Corollary 2.
Proof.
When either a cooperative or a non-cooperative user transmits a backlogged packet, he will succeed if at most one other user transmits at the same time, which is given by the first term in Equations (44) and (45).
On the other hand, the second term of the previous equations comes from the fact that if two users transmit backlogged packets at the same time, they will all be successfully delivered thanks to ZigZag decoding. Finally, we can obtain the expression of the throughput of backlogged packets by normalizing by the slot time and taking all the possible cases of M and N. □
Proposition 5.
The access delays of backlogged packets of cooperative and non-cooperative users are given by
Proof.
The average number of backlogged packets includes the packets that are in the system and the transmitted ones. Thus, by applying Little’s result [30], the backlogged packets’ delay is obtained as follows:
□
5. Stochastic Game Formulation
To model the interaction between cooperative and selfish users, we define a finite stochastic game between a group of cooperative users and a group of non-cooperative users . All users access a shared wireless channel using the SAZD mechanism. Furthermore, we consider that the group plays a cooperative game with all users, and therefore they attempt to optimize the overall system’s performance, whereas each user in the group attempts to optimize his own performance.
We summarize the components of the game as follows:
- Players: The sets of cooperative and non-cooperative players are defined, respectively, as and . In what follows, we refer to the players as users.
- Strategy space: The set of strategies is the set of users’ actions. For each user i, we define the set of pure strategies as , where T represents the action “Transmit”, and W is the action “Wait”. Thus, at a given time slot, a user holding a packet can choose one action in . Furthermore, we define the mixed strategies as the set of all the distributions over , which is for a cooperative user i, and for a non-cooperative user j.
- Utility: The utility function corresponds to the user’s level of satisfaction, which can be, in the case of our study, the average throughput, the access delay, or any other performance metric of interest. Let denote the utility function of user i in . depends on the transmission probability of user i and the vector of others’ transmission probabilities. Thus, each non-cooperative user possesses his own utility function. On the other hand, let be the common utility function of all cooperative users among the set , which corresponds to the overall system performance.
- Game information: We assume that all players share a common knowledge, which is: the total number of players in the game, their own strategy space, and the strategy space of others, their utility, and the utility of others. On the other hand, we assume that cooperative players do not have the knowledge of the existence of selfish players among them. As a result, they behave cooperatively assuming that others will behave similarly. However, selfish users assume that everyone in the game is selfish, and therefore they behave selfishly.
In the mixed game defined in this paper, cooperative users are interested in maximizing the overall utility function (e.g., the system throughput), whereas selfish users maximize their own utility functions.
5.1. Basic Assumptions
Assumption 1.
We assume that each player considers a symmetric strategy profile. Thus, he chooses his actions expecting that others will behave similarly.
Assumption 2.
Cooperative players assume that everyone in the game is cooperating, whereas non-cooperative players assume that everyone is selfish. Therefore, we assume that cooperative players decide their actions based on the information they have about the game. Thus, since they assume that everyone in the game is cooperating (which is not always true since there may be some selfish players among them), they choose to cooperate expecting that others will do the same thing. Similarly, non-cooperative players decide to not cooperate due the information they have. Thus, they choose to act selfishly expecting that others will behave in a similar way.
Cooperative players choose a strategy that optimizes the expected utility of the system, which is the joint utility of all players. As a result, the equilibrium profile of cooperative players is defined by the social optimally concept. On the other hand, non-cooperative players attempt to optimize their own utility function which leads them to the Nash equilibrium.
5.2. Characterization of the Game Equilibrium
The game equilibrium is a situation where all users are satisfied with their action choices, and no one is interested in deviating. In game theory, an equilibrium is usually characterized by a strategy profile where different users (players) choose different actions [31]. However, for simplicity purposes, we focus on the symmetric strategy profile , where is the strategy chosen by all cooperative users, and is the strategy chosen by all non-cooperative users. Furthermore, we consider Markovian strategies that do not depend on past actions but only on the system state.
The equilibrium of the game can be obtained as a pair , where is the social optimal for cooperative users and is the Nash equilibrium for non-cooperative game. The following theorem provides the conditions for the existence of the equilibrium.
Theorem 2.
The pair is an equilibrium of the game if it satisfies:
Proof.
To prove the existence of an equilibrium profile, we should investigate the two games. First, let us consider the cooperative game where users of the set attempt to maximize the overall system performance . We emphasize that cooperative users are aware of the total number of users . Additionally, they assume that all users cooperate. Thus, the game from the point of view of users in is a cooperative game of users.
Therefore, the equilibrium is given by the social optimality concept, which is defined by the following optimization problem:
where and .
For any value , the steady-state probabilities are continuous functions. Therefore, a solution to the optimization problem (50) might not exist if we consider the non-closed interval . However, since we optimize on the closed interval , an optimal solution exists.
Let us now consider the game from the point of view of a selfish user. Each user in the set plays a non-cooperative game with all other users on the system, including users that choose to cooperate. Thus, selfish users assume that everyone is rational and attempt to optimize their own utility functions. Therefore, the game from the point of view of the set is a non-cooperative game of users. As a result, the equilibrium is obtained using the Nash concept, which satisfies for every user i in the following condition:
where , and .
According to Nash theorem, a mixed-strategy Nash equilibrium exists since the game includes a finite number of users and actions.
Let us now consider the set of the best response strategies of a user i in .
We are interested in a symmetric equilibrium where all selfish users use the same strategy. Thus, we have
□
Condition (49) means that is the best strategy for user i given that others will play the same strategy.
Remark 2.
The proposed stochastic game model is a generalisation of some models that have been proposed in the literature [19,32,33,34,35,36]. In the special case of , the game corresponds to the pure cooperative game, and the case is equivalent to a non-cooperative game model.
6. Numerical Results
In this section, we present the numerical results, and we discuss the main findings of this study. The overall system throughput is taken as the utility function of cooperative users , whereas the utility function of a single selfish user is the individual throughput.
We investigate and compare two game scenarios. First, we consider a network where the number of cooperative users exceeds the number of selfish users, and . Then, in the second game scenario, we consider the opposite case where the number of selfish is and the number of cooperative users is . In each scenario, we compare the performance of cooperative users and selfish users. Furthermore, we provide the performance of the overall system in each case. To maintain a fair channel condition, we set for all users the same arrival rate, i.e., . Finally, we take .
Figure 3 shows the game equilibrium as a function of the arrival rate , where and . The retransmission probabilities and represent the optimal retransmission probability of cooperative and selfish users, respectively. The results show that selfish users access the wireless channel more aggressively than cooperative users.
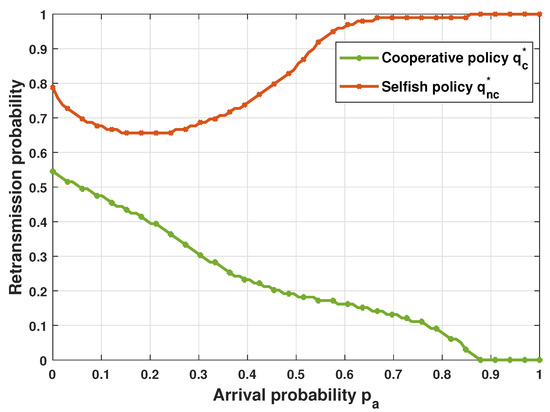
Figure 3.
Retransmission policy for cooperative users and selfish users.
Cooperative users use a high retransmission probability in light load conditions since the collision rate is meager. However, as the arrival rate increases, they lower their retransmission rate to reduce network congestion. In contrast, selfish users transmit with high probability than cooperative users. Moreover, they increase the transmission rate even in the case of high load conditions. Even though this aggressive behavior is not suitable for any user, selfish users cannot unilaterally deviate from their retransmission strategy due to the rationality concept.
Assuming that all others will cooperate, a selfish user could improve his utility function by choosing to cooperate. However, if he cooperates while the others defect, he will be heavily penalized. Thus, in such a situation, selfish users prefer to defect since they do not know the strategy chosen by others. This conflict situation is known in game theory as the prisoner dilemma. On the other hand, cooperative users assume that everyone is cooperating. Thus, they do not have any information about the existence of selfish users. Therefore, they play a cooperative game, assuming that everyone behaves similarly.
In the following results, we present the performance metrics at the equilibrium, i.e., when the cooperative and selfish users use the retransmission probability and , respectively. Figure 4 shows the throughput of cooperative and selfish users as well as the global system throughput. Furthermore, we compare two scenarios: (a) when the number of cooperative users exceeds the number of selfish users and (b) when the number of selfish users is greater than the number of cooperative users.
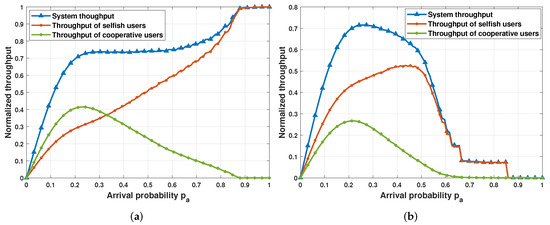
Figure 4.
Normalized throughput for different retransmission policies. (a) , , and (b) , .
Figure 4a shows that in light load conditions, cooperative users have a higher throughput than selfish users. This is because both users use a high retransmission probability. Even though the retransmission probability of selfish users is slightly higher, its impact is not significant in light load conditions. Thus, due to the dominant number of cooperative users, their throughput is slightly higher than that of selfish users. However, in high load conditions, selfish users get significantly better throughput since they transmit with higher probability and also because cooperative users lower their transmission probability as seen from Figure 3. In very high load conditions , cooperative users stop the retransmission of backlogged packets while selfish users transmit at the highest probability. This aggressive behavior allows selfish users to dominate the overall system throughput.
From the above results, it seems that the aggressive behavior of selfish users is beneficial for the system, even if it is done at the expense of the performance of cooperative users. However, it is not always the case, as shown in Figure 4b where the number of selfish users dominates over the number of cooperative users. Figure 4b shows that selfish users always get better throughput, not only because of their dominant number but also because of their aggressive behavior. However, when , the system throughput drops considerably due to the collisions caused by the selfish users.
Figure 5 shows the number of backlogged users as a function of the arrival rate. In the first game scenario Figure 5a, the cooperative users get heavily penalized by the aggressive behavior of selfish users since the number of their backlogged packets grows more rapidly as the traffic load increases.
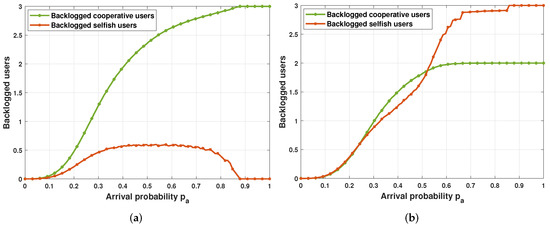
Figure 5.
Number of backlogged users for different retransmission policies. (a) , , and (b) , .
As for the selfish users, ≈30% of them get backlogged when . Note that when , cooperative users refrain from transmitting their backlogged packets, refer to Figure 3, as a result they all get backlogged, see Figure 5a. Indeed, due to the high arrival rate, cooperative users stay silent to allow the newly arrived packets to access the channel without any disturbance. On the other hand, selfish users take advantage of the situation and access the channel with the highest probability, i.e., , refer to Figure 3. Even in the presence of two selfish users, they reach the maximum throughput thanks to the ZigZag decoding technique that decodes all their collided packets.
In the second game scenario Figure 5b, selfish users are penalized by their aggressive behavior more than cooperative users because they collide very often, especially in high load conditions.
Figure 6 shows the access delay as a function of the arrival rate. The access delay represents the time in slots elapsed from the packet generating time and its successful transmission. The results show that the delay increases with the arrival rate. Furthermore, cooperative users exhibit the worst delay due to their low retransmission policy. For instance, under heavy load conditions, the delay reaches and slots in the first and second game scenarios, respectively. However, in the first game scenario, the delay of selfish users under the same load conditions is limited to 1 slot. That is to say, the selfish users are able to successfully transmit all their packets at the first attempt. On the other hand, selfish users experience a considerably high delay of slots in the second game scenario due to the increasing number of selfish users.
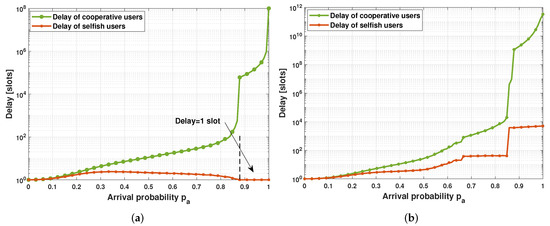
Figure 6.
Delay of transmitted packets for different retransmission policies. (a) , , and (b) , .
Figure 7 shows the delay of backlogged packets as a function of the arrival rate. Backlogged packets are the pending packets that went through a collision, and the ability to deliver backlogged packets is crucial for real-time traffic. Similar to the previous results, cooperative users have the worst delay. The first game scenario shows that backlogged packets get delayed more as the traffic load increases. However, as the arrival rate gets closer to 1, the backlogged packets of cooperative users become very large. In contrast, selfish users do not report any delay when since they do not possess any backlogged packet as shown in Figure 5a. On the other hand, both cooperative and selfish users suffer a longer delay when the load increases in the second game scenario (see Figure 7b). However, selfish users experience slightly higher backlogged delay than cooperative users due to their number and exaggerated aggressive behavior.
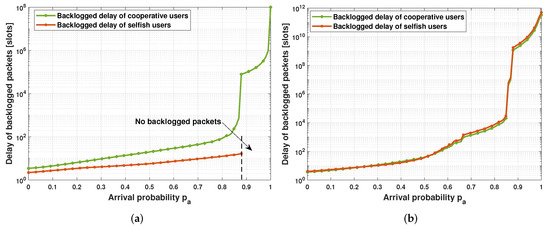
Figure 7.
Delay of backlogged packets for different retransmission policies. (a) , , and (b) , .
The mathematical and numerical models in this study provide the basis for the performance analysis and protocol design of future generation wireless networks and protocols. With the ever increasing number of interconnected wireless devices, there is an increasing need of developing more robust protocols capable of limiting the impact of interference over the network performance. Furthermore, the lack of cooperation of even a single user may result in the malfunctioning of the overall network.
In order to illustrate the potential use of our models in the context of the research and development efforts of future telecommunications systems, let us consider a network of and users. Table 1 shows the results as a function of the arrival probability . In the table, and indicate the throughput of a cooperative user and a non-cooperative user, respectively. As seen from the table, as the arrival probability increases, selfish users get more aggressive and attempt accessing the shared wireless channel using the highest probability . In contrast, the cooperative users lower their retransmission probability to avoid collisions for allowing everyone to use the network resources. Under very heavy load conditions (i.e., ), the cooperative users reduce drastically their retransmission probability while the two selfish users can successfully transmit all their packets thanks to the use of the ZigZag scheme. In fact, the impact of the ZigZag scheme can be particularly seen on all the performance metrics under very high load conditions. The last two rows of the table show that the delay experienced by the traffic of the cooperative users experience increases by several orders of magnitude as all the cooperative users get their packets backlogged, . On the contrary, the non-cooperative users benefit from the use of the ZigZag scheme by equally sharing the channel and are able to transmit practically all their packets at their first attempt, . The results also show that the collision probability resulting on packet losses reduces drastically to as the packets of the two non-cooperative users rarely collide with the packets of the cooperative users. Remember that by implementing the ZigZag code, the receiver may properly recover the information of up to two colliding packets. Even though the use of the ZigZag proves effective in improving the performance of the network, it also raises some concerns on the dangers of the misuse of such features. As seen from our results, non-cooperative users may take advantage of such a decoding scheme. Therefore, further studies are required to explore the use of such scheme even in the presence of non-cooperative users. One possible line of research will be a dynamic implementation of such code by enabling and disabling its operation as a means to discourage non-cooperative users.

Table 1.
Performance evaluation in the case of and . is the system collision probability, and are the individual throughputs of a cooperative user i and a selfish user j, respectively.
7. Conclusions
In this paper, we have presented a novel stochastic game analysis that considers the existence of cooperative and selfish users in the same game and studies the interaction between them. First, the system state evolution is modeled using a bi-dimensional Markov chain in which we derived different performance metrics. Then, we constructed the proposed stochastic game using cooperative and non-cooperative game theories. Finally, we showed that the game ends at an equilibrium that combines the social optimality and the Nash concept. This paper provides a comparative study between two game scenarios: (1) the case where the game consists mostly of cooperative users and (2) the opposite case where the game contains more selfish users. In each case, we highlighted the impact of the selfish behavior on the other users and on the overall system. Our results showed that the number of selfish users and the arrival rate significantly impact the system’s performance. The proposed model provides a general framework that can be implemented in a wide range of application areas, such as resource management, network architecture, and protocol design.
In our future work, we will develop and investigate a more complex system where each player can choose between multi-levels of cooperation and selfishness. We also plan to develop some approaches that help in getting rid of the non-desired selfish behavior.
Author Contributions
Conceptualization, A.B., A.Z. and A.H.; methodology, A.B. and A.Z.; software, A.B.; validation, all authors.; formal analysis, A.B., A.Z. and A.H.; investigation, all authors; writing—original draft preparation, A.B.; writing—review and editing, all authors; funding acquisition, L.O.-B. and A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Spanish Ministry of Science, Education and Universities, the European Regional Development Fund and the State Research Agency, Grant No. RTI2018-098156-B-C52. The first author was supported by the Erasmus+ program KA107.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Transition Probabilities
References
- Abramson, N. The ALOHA system: Another alternative for computer communications. In Proceedings of the Fall Joint Computer Conference, 1970, AFIPS ’70 (Fall), Houston, TX, USA, 17–19 November 1970; pp. 281–285. [Google Scholar]
- Oku, T.; Kimura, T.; Cheng, J. Performance Evaluation of Hierarchical Slotted ALOHA for IoT Applications. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), Taoyuan, Taiwan, 28–30 September 2020; pp. 1–2. [Google Scholar]
- Li, Y.; Zhan, W.; Dai, L. Rate-Constrained Delay Optimization for Slotted ALOHA. IEEE Trans. Commun. 2021, 69, 5283–5298. [Google Scholar] [CrossRef]
- Boujnoui, A.; Zaaloul, A.; Haqiq, A. A stochastic game analysis of the slotted ALOHA mechanism combined with zigzag decoding and transmission cost. In International Conference on Innovations in Bio-Inspired Computing and Applications; Springer International Publishing: Cham, Swiztherland, 2018; Volume 735, pp. 102–112. [Google Scholar]
- Oinaga, M.; Ogata, S.; Ishibashi, K. ZigZag decodable coded slotted ALOHA. In Proceedings of the 2018 15th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2018; pp. 1–6. [Google Scholar]
- Bianchi, G. Performance analysis of the IEEE 802.11 distributed coordination function. IEEE J. Sel. Areas Commun. 2000, 18, 535–547. [Google Scholar] [CrossRef]
- Ahmetoglu, M.; Yavascan, O.T.; Uysal, E. MiSTA: Threshold-ALOHA with Mini Slots. In Proceedings of the 2021 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Bucharest, Romania, 24–28 May 2021; pp. 1–6. [Google Scholar]
- Wang, H.; Fapojuwo, A.O. Design and performance evaluation of successive interference cancellation-based pure ALOHA for Internet-of-Things networks. IEEE Internet Things J. 2019, 6, 6578–6592. [Google Scholar] [CrossRef]
- Bankov, D.; Khorov, E.; Lyakhov, A. Mathematical model of LoRaWAN channel access with capture effect. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–5. [Google Scholar]
- Boujnoui, A.; Zaaloul, A.; Haqiq, A. Enhanced Pricing Strategy for Slotted ALOHA with ZigZag Decoding: A Stochastic Game Approach. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2021, 13, 160–171. [Google Scholar]
- Dai, M.; Mao, B.; Gong, X.; Sung, C.W.; Zhuang, W.; Lin, X. Zigzag-Division Multiple Access for Wireless Networks With Long and Heterogeneous Delays. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2822–2835. [Google Scholar] [CrossRef]
- Boujnoui, A.; Zaaloul, A.; Haqiq, A. Mathematical model based on game theory and Markov chains for analysing the transmission cost in SA-ZD mechanism. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2018, 10, 197–207. [Google Scholar]
- Jin, Y.; Kesidis, G. Equilibria of a noncooperative game for heterogeneous users of an ALOHA network. IEEE Commun. Lett. 2002, 6, 282–284. [Google Scholar]
- Gopal, S.; Kaul, S.K.; Chaturvedi, R.; Roy, S. A non-cooperative multiple access game for timely updates. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; pp. 924–929. [Google Scholar]
- Zhao, B.; Ren, G.; Zhang, H. Cooperative Contention Resolution Diversity Slotted ALOHA with Transmit Power Diversity for Multi-Satellite Networks. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–5. [Google Scholar]
- Vaezi, K.; Ashtiani, F. Delay-optimal cooperation policy in a slotted ALOHA full-duplex wireless network: Static approach. IEEE Syst. J. 2019, 14, 2257–2268. [Google Scholar] [CrossRef]
- Vaezi, K.; Akar, N.; Karasan, E. Age of Information in a Cooperative Slotted ALOHA Network: Marginal and Joint Distributions. TechRxiv. Preprint. 2021. Available online: https://www.techrxiv.org/articles/preprint/Age_of_Information_in_a_Cooperative_Slotted_Aloha_Network_Marginal_and_Joint_Distributions/16437330/1 (accessed on 1 February 2022).
- Liu, R.; Hong, T.; Ding, X.; Wang, Y.; Zhang, G. Multi-Satellite Cooperative Beamforming ALOHA for LEO Satellite IoT Networks. Front. Space Technol. 2021, 2, 9. [Google Scholar] [CrossRef]
- Cheikh, I.; Sabir, E.; Aouami, R.; Sadik, M.; Roy, S. Throughput-Delay Tradeoffs for Slotted-ALOHA-based LoRaWAN Networks. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; pp. 2020–2025. [Google Scholar]
- Beltramelli, L.; Mahmood, A.; Österberg, P.; Gidlund, M. LoRa beyond ALOHA: An investigation of alternative random access protocols. IEEE Trans. Ind. Inform. 2020, 17, 3544–3554. [Google Scholar] [CrossRef]
- Milarokostas, C.; Tsolkas, D.; Passas, N.; Merakos, L. A Comprehensive Study on LPWANs with a Focus on the Potential of LoRa/LoRaWAN Systems. TechRxiv. Preprint. 2021. Available online: https://www.techrxiv.org/articles/preprint/A_Comprehensive_Study_on_LPWANs_With_a_Focus_on_the_Potential_of_LoRa_LoRaWAN_Systems/16853893/1 (accessed on 1 February 2022).
- Tegos, S.A.; Diamantoulakis, P.D.; Lioumpas, A.S.; Sarigiannidis, P.G.; Karagiannidis, G.K. Slotted ALOHA with NOMA for the next generation IoT. IEEE Trans. Commun. 2020, 68, 6289–6301. [Google Scholar] [CrossRef]
- Boujnoui, A.; Zaaloul, A.; Haqiq, A. Cooperative Slotted ALOHA with ZigZag Decoding and a Pricing Mechanism. In International Conference on Innovations in Bio-Inspired Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1372, pp. 111–119. [Google Scholar]
- Zhao, B.; Ren, G.; Zhang, H. Slotted ALOHA Game for Medium Access Control in Satellite Networks. In Proceedings of the 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 11–13 August 2019; pp. 518–522. [Google Scholar]
- Cho, Y.; Tobagi, F.A. Cooperative and non-cooperative ALOHA games with channel capture. In Proceedings of the IEEE GLOBECOM 2008—2008 IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6. [Google Scholar]
- Hilbe, C.; Šimsa, Š.; Chatterjee, K.; Nowak, M.A. Evolution of cooperation in stochastic games. Nature 2018, 559, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Van Heesch, M.; Wissink, P.L.; Ranji, R.; Nobakht, M.; Den Hartog, F. Combining Cooperative With Non-Cooperative Game Theory to Model Wi-Fi Congestion in Apartment Blocks. IEEE Access 2020, 8, 64603–64616. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Y.; Chen, N.; Wang, K.; Chen, S.; Yao, S. LOCASS: Local optimal caching algorithm with social selfishness for mixed cooperative and selfish devices. IEEE Access 2018, 6, 30060–30072. [Google Scholar] [CrossRef]
- Gollakota, S.; Katabi, D. Zigzag decoding: Combating hidden terminals in wireless networks. In Proceedings of the ACM SIGCOMM 2008 conference on Data Communication, SIGCOMM ’08, Seattle, WA, USA, 22 August 2008; pp. 159–170. [Google Scholar]
- Allen, A.O. Probability, Statistics, and Queueing Theory; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- MacKenzie, A.B.; Wicker, S.B. Selfish users in ALOHA: A game-theoretic approach. In Proceedings of the IEEE 54th Vehicular Technology Conference, VTC Fall 2001, Proceedings (Cat. No. 01CH37211), Atlantic City, NJ, USA, 7–11 October 2001; Volume 3, pp. 1354–1357. [Google Scholar]
- Altman, E.; El Azouzi, R.; Jiménez, T. Slotted ALOHA as a game with partial information. Comput. Netw. 2004, 45, 701–713. [Google Scholar] [CrossRef][Green Version]
- El-Azouzi, R.; Sabir, E.; Jiménez, T.; Bouyakhf, E.H. Modeling slotted ALOHA as a stochastic game with random discrete power selection algorithms. J. Comput. Syst. Netw. Commun. 2009, 2009, 572650. [Google Scholar] [CrossRef]
- El-Azouzi, R.; Jiménez, T.; Sabir, E.; Benarfa, S.; Bouyakhf, E.H. Cooperative and non-cooperative control for slotted ALOHA with random power level selections algorithms. In Proceedings of the 2nd International Conference on Performance Evaluation Methodologies and Tools & Workshops, ValueTools ’07, Nantes, France, 22–27 October 2007; pp. 1–10. [Google Scholar]
- Karouit, A. Efficient Incentive Scheme forWireless Random Channel Access with Selfish Users. In International Symposium on Ubiquitous Networking; Springer: Berlin/Heidelberg, Germany, 2015; Volume 366, pp. 27–38. [Google Scholar]
- Sabir, E.; El-Azouzi, R.; Hayel, Y. Hierarchy sustains partial cooperation and induces a Braess-like paradox in slotted ALOHA-based networks. Comput. Commun. 2012, 35, 273–286. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).