Symmetry Analysis and Conservation Laws for a Time-Fractional Generalized Porous Media Equation

Abstract

The symmetry group method is applied to study a class of time-fractional generalized porous media equations with Riemann–Liouville fractional derivatives. All point symmetry groups and the corresponding optimal subgroups are determined. Then, the similarity reduction is performed to the given equation and some explicit solutions are derived. The asymptotic behaviours for the solutions are also discussed. Through the concept of nonlinear self-adjointness, the conservation laws arising from the admitted point symmetries are listed.

1. Introductions

The theory of differentiations and integrations of arbitrary order (real or complex) is named as fractional calculus, and was born on 30 September 1695 in a letter from Leibniz to L‘Hopital discussing the derivative of order $1/2$. The differential equation with arbitrary order derivatives, called a fractional differential equation (FDE), is a generalization of the differential equation with integer order derivatives, investigated by the theory of fractional calculus. FDEs are of considerable interest in various fields of science and engineering; in particular, modeling the phenomena relating hereditary, nonlocal and intrinsic memory properties (see [1,2,3] and references therein). Compared with integer order models, fractional order models can provide improved fits and induce sharp questions about the underlying conceptual models for the observed phenomena. Kac concluded that “success is characterized by the fidelity with which such models fit the observed phenomena, and by the sharpness of the questions they pose about the underlying physics.” [4]. In [5,6], for example, the authors demonstrated that the fractional Bloch–Torrey equation not only fits the diffusion data from human brain tissue precisely, but also affects the microscopic tissue structure. A lot of research activities have been performed on FDEs from points of theories and applications [7,8,9,10,11].

The Lie symmetry group is viewed as a powerful and widely applicable technique for investigating differential equations (DEs). The reason for the prevalence of the Lie symmetry group is its abilities to provide exact solutions and linearization mappings of DEs and to study the integrability, etc. [12,13]. Thus, questions about how the Lie symmetry group works for FDEs and whether the effectiveness of the Lie symmetry group for FDEs is the same as it for usual DEs arise. The study of Lie group theory for FDEs was initiated by Buckwar and Luchko in [14], where they mainly concentrated on the scaling invariance of a linear fractional diffusion equation and obtained several explicit solutions in terms of generalized Wright functions. Since then, a number of research papers, books and symbolic manipulation softwares have been dedicated to the study of Lie symmetry analysis. Following the established Lie symmetry schemas, symmetry reductions and group-invariant solutions were implemented to numerous kinds of FDEs, including scalar FDE [15,16,17,18], multidimensional time-fractional DEs [19,20] and coupled time-fractional DEs [21,22], etc. Based on the pioneer works on the symmetry analysis for FDEs, Singla and Gupta proposed the Lie group symmetry theories for space-time fractional systems and systems of FDEs with an arbitrary number of independent, as well as dependent, variables in [23,24]. Quite recently, Zhang and Zheng studied the symmetry structure to multidimensional time-fractional DEs and concluded that the corresponding infinitesimals could be determined by two elegant equivalent conditions [25]. To perform the symmetry group approach automatically, Jefferson and Carminati presented an algorithm named FracSym package in the platform MAPLE [26].

An important application of symmetry groups is to determine the conservation laws of DEs. For the DEs with a Lagrangian, the celebrated Noether theorem exhibits the correspondence between conservation laws and variational symmetries. However, many systems do not possess a variational principle and the variant integral is not invariant under the considered symmetry. Such dilemmas motivate scholars to develop other new techniques for the construction of conservation laws, such as the direct method [27], partial Lagrangian [28], multiplier method [29] and nonlinear self-adjointness method [30]. The research on conserved quantities of FDEs has also been explored. The fractional Noether theorem for FDEs was proved in [31], where the corresponding fractional conservation laws were also proposed. Moreover, in [32], Lukashchuk extended the nonlinear self-adjointness method to FDEs involving not only Riemann–Liouville fractional derivatives but also Caputo fractional derivatives. As a matter of fact, up to now, the nonlinear self-adjointness method has been widely used to construct the conservation laws for FDEs.

The present paper is devoted to studying the symmetry groups and conservation laws to a time-fractional generalized porous medium equation for $u=u(t,x)$, given by

$${\partial }_t^{\alpha }u={\left(u^n\right)}_{xx}+x^q{u}^s{u}_x+x^p{u}^m,0<\alpha <1,$$

(1)

with real constants $n\ne 0$, m, s, p and q, where ${\partial }_t^{\alpha }$ is the left Riemann–Liouville fractional differential operator of order $\alpha$ with respect to t [1]. The generalized porous medium equation with an integer order time derivative provides models of many interesting physical phenomena, such as the flow of liquids in porous media and transport of thermal energy in plasma, which has been investigated from several points of view [33,34,35,36,37]. Note that Equation (1) is linear when $sm(m-1)(n-1)=0$, which will be out of consideration in what follows.

This paper is structured as follows. In Section 2, we recall several definitions of fractional calculus. Section 3 provides the point symmetry groups admitted by Equation (1) and the corresponding optimal symmetry system. The symmetry reduction method is then applied to reduce Equation (1) and derive its explicit solutions in Section 4. Section 5 deals with the investigation of conservation laws for Equation (1) that arise from the obtained point symmetries. Finally, our conclusions are given in Section 6.

2. Preliminaries

Several definitions from fractional calculus theory are listed in this section. For more details, please refer to books and literatures [2].

Definition 1.

For function $f\left(t\right)\in L^1([0,T],{\mathbb{R}}_{+})$, the left-sided fractional integral operator of order $\mu >0$ is defined by

$${}_0{I}_t^{\mu }f\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\mu \right)}{\int }_0^t{(t-s)}^{\mu -1}f\left(s\right)ds,$$

(2)

and the right-sided fractional integral operator of order $\mu >0$ is defined by

$${}_t{I}_T^{\mu }f\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\mu \right)}{\int }_t^T{(s-t)}^{\mu -1}f\left(s\right)ds,$$

(3)

where and whereafter $\mathsf{\Gamma }\left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt$, $(\Re (z)>0)$ is the Euler–Gamma function. In particular, ${}_0{I}_t^{0}f\left(t\right)=f\left(t\right)$.

Definition 2.

For function $f\left(t\right)\in L^1([0,T],{\mathbb{R}}_{+})$, the left-sided Riemann–Liouville fractional derivative of order $\alpha >0$ is defined by

$${\partial }_t^{\alpha }f\left(t\right)=\frac{d^n}{d{t}^n}\left({}_0{I}_t^{n-\alpha }f\left(t\right)\right)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}\frac{d^n}{d{t}^n}{\int }_0^t{(t-s)}^{n-\alpha -1}f\left(s\right)ds,$$

(4)

and the right-sided Riemann–Liouville fractional derivative of order $\alpha >0$ is defined by

$${}_t{\partial }_T^{\alpha }f\left(t\right)={(-1)}^n\frac{d^n}{d{t}^n}\left({}_t{I}_T^{n-\alpha }f\left(t\right)\right)=\frac{{(-1)}^n}{\mathsf{\Gamma }(n-\alpha )}\frac{d^n}{d{t}^n}{\int }_t^T{(s-t)}^{n-\alpha -1}f\left(s\right)ds,$$

(5)

where $0\le n-1<\alpha <n$ and $n\in {\mathbb{Z}}^{+}$.

Definition 3.

For function $f\left(t\right)\in L^1([0,T],{\mathbb{R}}_{+})$, the left-sided Caputo fractional derivative of order $\alpha >0$ is defined by

$${}^C{\partial }_t^{\alpha }f\left(t\right)={}_0{I}_t^{n-\alpha }\left(\frac{d^n}{d{t}^n}f\left(t\right)\right)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_0^t{(t-s)}^{n-\alpha -1}\frac{d^n}{d{s}^n}f\left(s\right)ds,$$

(6)

and the right-sided Caputo fractional derivative of order $\alpha >0$ is defined by

$${}_t^C{\partial }_T^{\alpha }f\left(t\right)={(-1)}^n{}_t{I}_T^{n-\alpha }\left(\frac{d^n}{d{t}^n}f\left(t\right)\right)=\frac{{(-1)}^n}{\mathsf{\Gamma }(n-\alpha )}{\int }_t^T{(s-t)}^{n-\alpha -1}\frac{d^n}{d{s}^n}f\left(s\right)ds,$$

(7)

where $0\le n-1<\alpha <n$ and $n\in {\mathbb{Z}}^{+}$.

In literature, when one reads the Riemann–Liouville fractional derivative, it usually means the left Riemann–Liouville fractional derivative. In physics, if the time variable is denoted by variable t, then the right-sided Riemann–Liouville fractional derivative for $f\left(t\right)$ is interpreted as a future state of the process. Hence, the right derivative is usually omitted in applications when the present state of the process does not depend on the results of the future development. From a mathematical point of view, both derivatives appear naturally in the fractional calculus.

Definition 4.

The Erdélyi–Kober fractional differential operator is defined by

$$\left({\mathrm{P}}_{\delta }^{\beta ,\alpha }y\right)\left(z\right)=\prod _{j=0}^{l-1}\left(\beta +j-\frac{1}{\delta }z\frac{d}{dz}\right)\left({\mathrm{K}}_{\delta }^{\beta +\alpha ,l-\alpha }y\right)\left(z\right),\mathrm{with}l=\left\{\begin{array}{cc}\left[\alpha \right]+1,\hfill & \alpha \notin \mathbb{N};\hfill \\ \alpha ,\hfill & \alpha \in \mathbb{N},\hfill \end{array}\right.$$

(8)

where

$$\begin{array}{c}\hfill \left({\mathrm{K}}_{\delta }^{\beta ,\alpha }y\right)\left(z\right)=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_1^{\infty }{(s-1)}^{\alpha -1}{s}^{-\beta -\alpha }y\left(z{s}^{1/\delta }\right)ds,\hfill & \alpha >0;\hfill \\ y\left(z\right),\hfill & \alpha =0,\hfill \end{array}\right.\end{array}$$

(9)

is the Erdélyi–Kober fractional integral operator.

3. Point Symmetries and Optimal System

Given a one-parameter Lie group of transformation with group parameter $ϵ$:

$$\overline{t}=t+ϵ\tau (t,x,u)+O\left({ϵ}^2\right),\overline{x}=x+ϵ\xi (t,x,u)+O\left({ϵ}^2\right),\overline{u}=u+ϵ\eta (t,x,u)+O\left({ϵ}^2\right),$$

(10)

which is characterized by infinitesimal operator

$$\mathrm{X}=\tau (t,x,u){\partial }_t+\xi (t,x,u){\partial }_x+\eta (t,x,u){\partial }_u.$$

(11)

If the Lie group (10) leaves Equation (1) invariant, then the operator (11) satisfies two conditions:

$$\begin{array}{cc}\hfill & {\mathrm{pr}}^{(\alpha ,2)}\mathrm{X}({\partial }_t^{\alpha }u-{\left(u^n\right)}_{xx}-x^p{u}^m-x^q{u}^s{u}_x){|}_{\left(\right)}=0,\hfill \end{array}$$

(12)

and

$${\tau (t,x,u)|}_{t=0}=0.$$

(13)

In (12), ${\mathrm{pr}}^{(\alpha ,2)}$ is the $(\alpha ,2)$-th order prolongation of vector field (11)

$$\begin{array}{cc}\hfill & {\mathrm{pr}}^{(\alpha ,2)}\mathrm{X}=\mathrm{X}+{\eta }^{\alpha ,t}{\partial }_{{\partial }_t^{\alpha }u}+{\eta }^x{\partial }_{u_x}+{\eta }^{xx}{\partial }_{u_{xx}}.\hfill \end{array}$$

(14)

Here, ${\eta }^x$ and ${\eta }^{xx}$ are integer-order extended infinitesimals with respect to x [12,13] and ${\eta }^{\alpha ,t}$ is the extended infinitesimal of order $\alpha$ with respect to t [14,15], given by

$$\begin{array}{cc}\hfill {\eta }^{\alpha ,t}=& {\partial }_t^{\alpha }\eta +({\eta }_u-\alpha D_t\tau ){\partial }_t^{\alpha }u-u{\partial }_t^{\alpha }{\eta }_u+\sum _{i=1}^{\infty }\left(\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right){\partial }_t^i{\eta }_u-\left(\genfrac{}{}{0pt}{}{\alpha }{i+1}\right)D_t^{i+1}\tau \right){\partial }_t^{\alpha -i}u\hfill \\ & -\sum _{i=1}^{\infty }\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right)D_t^i\xi {\partial }_t^{\alpha -i}{u}_x+\nu ,\hfill \end{array}$$

(15)

where $D_t$ is the total derivative with respect to t, $D_t^{i+1}=D_t\left(D_t^i\right)$,

$$\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right)=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(i+1)\mathsf{\Gamma }(\alpha +1-i)},$$

(16)

and

$$\nu =\sum _{i=2}^{\infty }\sum _{l=2}^i\sum _{k=2}^l\sum _{h=0}^{k-l}\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right)\left(\genfrac{}{}{0pt}{}{i}{l}\right)\left(\genfrac{}{}{0pt}{}{k}{h}\right){(-1)}^h\frac{t^{i-\alpha }{u}^h{\partial }_t^l{u}^{k-h}}{k!\mathsf{\Gamma }(i+1-\alpha )}\frac{{\partial }^{i-l+k}\eta }{\partial t^{i-l}\partial u^k}.$$

(17)

The determining Equation (12) splits with respect to derivatives of u, yielding an overdetermined system for $\tau (t,x,u)$, $\xi (t,x,u)$ and $\eta (t,x,u)$, given by

$${\partial }_t^{\alpha }\eta -u{\partial }_t^{\alpha }{\eta }_u+x^p{u}^m({\eta }_u-\alpha {\tau }_t)-n{u}^{n-1}{\eta }_{xx}-x^q{u}^s{\eta }_x-m{x}^p{u}^{m-1}\eta -p{x}^{p-1}{u}^m\xi =0,$$

(18)

$$\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right){\partial }_t^i{\eta }_u-\left(\genfrac{}{}{0pt}{}{\alpha }{i+1}\right){\tau }_t^{(i+1)}=0,i=1,2,\dots ,$$

(19)

$${\tau }_x={\tau }_u={\xi }_t={\xi }_u=0,$$

(20)

$$(n-1)\eta +(\alpha {\tau }_t-2{\xi }_x)u=0,$$

(21)

$$u^2{\eta }_{uu}+(n-1)({\eta }_u+\alpha {\tau }_t-2{\xi }_x)u+(n-1)(n-2)\eta =0,$$

(22)

$$2n{u}^{n-1}{\eta }_{xu}+2n(n-1)u^{n-2}{\eta }_x+s{x}^q{u}^{s-1}\eta +x^q{u}^s(\alpha {\tau }_t-{\xi }_x)-n{u}^{n-1}{\xi }_{xx}+q{x}^{q-1}{u}^s\xi =0.$$

(23)

Solving the determining Equations (18)–(23) associated with condition (13) yields the following result:

Equation (1) with $sm(m-1)(n-1)\ne 0$ possesses point symmetries

$${\mathrm{X}}_1={\partial }_x,\mathrm{for}p=q=0,$$

(24)

$${\mathrm{X}}_2=\alpha x{\partial }_x+2t{\partial }_t,\mathrm{for}m=n=s+1,q=-1,p=-2,n\ne -1,-2/3,1/3,$$

(25)

$${\mathrm{X}}_3=\alpha (m-s-1)x{\partial }_x+(ps-(q-1)(m-1))t{\partial }_t-\alpha (p-q+1)u{\partial }_u,\mathrm{for}(p+2)(n-s-1)=(n-m)(q+1),$$

(26)

$${\mathrm{X}}_4=t^2{\partial }_t+(\alpha -1)tu{\partial }_u,\mathrm{for}m=n=s+1=(1-\alpha )/(1+\alpha ),$$

(27)

$${\mathrm{X}}_5=e^x{\partial }_x-e^{x}u{\partial }_u,\mathrm{for}m=-n=1,s=-2,p=q=0,$$

(28)

$${\mathrm{X}}_6=x(lnx){\partial }_x-(1+lnx)u{\partial }_u,\mathrm{for}m=n=q=-1,s=p=-2,ł$$

(29)

$${\mathrm{X}}_7=x(lnx){\partial }_x-3(1+lnx)u{\partial }_u,\mathrm{for}m=n=1/3,s=-2/3,q=-1,p=-2,$$

(30)

$${\mathrm{X}}_8=x^{5/2}{\partial }_x-3x^{3/2}u{\partial }_u,\mathrm{for}m=n=-2/3,s=-5/3,q=-1,p=-2,$$

(31)

$${\mathrm{X}}_9=(n+1)x^{2-3n}{\partial }_x-2x^{1-3n}u{\partial }_u,\mathrm{for}2(m-1)=p(1\pm \frac{1}{\sqrt{3}}),n=\pm \frac{1}{\sqrt{3}},s=-1\pm \frac{1}{\sqrt{3}},q=-1,$$

(32)

$${\mathrm{X}}_{10}=n(3n+1)e^{\frac{(1-n)x}{n(3n+1)}}{\partial }_x-2e^{\frac{(1-n)x}{n(3n+1)}}u{\partial }_u,\mathrm{for}m=n=s+1,9n^3+6n^2-n-2=0,p=q=0.$$

(33)

The optimal symmetry system is the maximal set of one-dimensional point symmetry subgroups that are conjugacy inequivalent in the full Lie group of point symmetries admitted by Equation (1). The reduction under such a system could lead to all group-invariant solutions. The optimal symmetry system can be attacked by considering a general operator in Lie algebra and subjecting it to various adjoint transformations to simplify it as much as possible [12,27]. The adjoint action is defined by

$$\begin{array}{c}\hfill \mathrm{Ad}(exp\left(ϵ{\mathrm{X}}_i\right)){\mathrm{X}}_j={\mathrm{X}}_j-ϵ[{\mathrm{X}}_i,{\mathrm{X}}_j]+\frac{{ϵ}^2}{2}[{\mathrm{X}}_i,[{\mathrm{X}}_i,{\mathrm{X}}_j]]-\cdots ,\end{array}$$

where $[{\mathrm{X}}_i,{\mathrm{X}}_j]$ is the commutator of the Lie algebra and $ϵ$ is a parameter. Through a systematic calculation, we obtain the one-dimensional optimal symmetry of Equation (1) as follows.

Theorem 1.

The one-dimensional optimal system of Equation (1) in the case of $m+n=2(s+1)$ and $p=q=0$ is spanned by (24) and (26). For the case of $m=n=s+1=(1+\alpha )/(1-\alpha )$, the one-dimensional optimal system of Equation (1) is spanned by (26) and (27). For the case of $m=n=s+1$, $q=-1$ and $p=-2$, the one-dimensional optimal system of Equation (1) is spanned by (25) and (26). For the case of $2(m-1)=p(1\pm \frac{1}{\sqrt{3}})$, $n=\pm \frac{1}{\sqrt{3}}$, $s=-1\pm \frac{1}{\sqrt{3}}$ and $q=-1$, the one-dimensional optimal system of Equation (1) is spanned by (26) and (32). For the case of $m=-n=1$, $s=-2$ and $p=q=0$, the one-dimensional optimal system of Equation (1) is spanned by (24) and (28). For the case of $m=n=s+1=(1+\alpha )/(1-\alpha )$, $q=-1$ and $p=-2$, the one-dimensional optimal system of Equation (1) is spanned by

$${\mathrm{X}}_3,{\mathrm{X}}_4,{\mathrm{X}}_2+a_1{\mathrm{X}}_3,$$

(34)

with parameter $-\infty <a_1<\infty$. For the case of $m=n=q=-1$ and $s=p=-2$, the one-dimensional optimal system of Equation (1) is generated by

$${\mathrm{X}}_2,{\mathrm{X}}_6+a_1{\mathrm{X}}_3,$$

(35)

with parameter $-\infty <a_1<\infty$. For the case of $m=n=1/3$, $s=-2/3$, $q=-1$ and $p=-2$, the one-dimensional optimal system of Equation (1) is generated by

$${\mathrm{X}}_2,{\mathrm{X}}_7+a_1{\mathrm{X}}_3,$$

(36)

with parameter $-\infty <a_1<\infty$. For the case of $m=n=-2/3$, $s=-5/3$, $q=-1$ and $p=-2$, the one-dimensional optimal system of Equation (1) is spanned by

$${\mathrm{X}}_3,{\mathrm{X}}_2+a_1{\mathrm{X}}_3,{\mathrm{X}}_8+a_2{\mathrm{X}}_3,$$

(37)

with parameters $-\infty <a_i<\infty$ and $(i=1,2)$. For the case of $m=n=s+1$, $9n^3+6n^2-n-2=0$ and $p=q=0$, the one-dimensional optimal system of Equation (1) is generated by

$${\mathrm{X}}_3,{\mathrm{X}}_1+a_1{\mathrm{X}}_3,{\mathrm{X}}_{10}+a_2{\mathrm{X}}_3,$$

(38)

with parameters $-\infty <a_i<\infty$ and $(i=1,2)$. For the case of $m=n=s+1=(1+\alpha )/(1-\alpha )$, $9n^3+6n^2-n-2=0$ and $p=q=0$, the one-dimensional optimal system of Equation (1) is generated by

$${\mathrm{X}}_4,{\mathrm{X}}_1+a_1{\mathrm{X}}_3,{\mathrm{X}}_1+a_2{\mathrm{X}}_4,{\mathrm{X}}_3+a_3{\mathrm{X}}_{10},{\mathrm{X}}_{10}+a_4{\mathrm{X}}_4,$$

(39)

with parameters $-\infty <a_i<\infty$ and $(i=1,2,3,4)$.

Proof. 

Here, we just consider the case of $m=n=s+1=(1+\alpha )/(1-\alpha )$, $9n^3+6n^2-n-2=0$ and $p=q=0$. In this case, Equation (1) admits symmetries ${\mathrm{X}}_1$, ${\mathrm{X}}_3$, ${\mathrm{X}}_4$ and ${\mathrm{X}}_{10}$ with nonzero commutators

$$[{\mathrm{X}}_1,{\mathrm{X}}_{10}]=\frac{1-n}{n(1+3n)}{\mathrm{X}}_{10},[{\mathrm{X}}_3,{\mathrm{X}}_4]=(n-1){\mathrm{X}}_4.$$

(40)

With the help of (40), the corresponding adjoint action can be evaluated, as shown in Table 1. □

Table 1. Adjoint action of ${\mathrm{X}}_1$, ${\mathrm{X}}_3$, ${\mathrm{X}}_4$ and ${\mathrm{X}}_{10}$.

Ad	${\mathbf{X}}_1$	${\mathbf{X}}_3$	${\mathbf{X}}_4$	${\mathbf{X}}_{10}$
${\mathrm{X}}_1$	${\mathrm{X}}_1$	${\mathrm{X}}_3$	${\mathrm{X}}_4$	$e^{\frac{ϵ(n-1)}{n(1+3n)}}{\mathrm{X}}_{10}$
${\mathrm{X}}_3$	${\mathrm{X}}_1$	${\mathrm{X}}_3$	$e^{ϵ(1-n)}{\mathrm{X}}_4$	${\mathrm{X}}_{10}$
${\mathrm{X}}_4$	${\mathrm{X}}_1+\frac{ϵ(1-n)}{n(1+3n)}{\mathrm{X}}_{10}$	${\mathrm{X}}_3$	${\mathrm{X}}_4$	${\mathrm{X}}_{10}$
${\mathrm{X}}_{10}$	${\mathrm{X}}_1$	${\mathrm{X}}_3+ϵ(n-1){\mathrm{X}}_4$	${\mathrm{X}}_4$	${\mathrm{X}}_{10}$

Let $\mathrm{X}$ be the most general vector, namely $\mathrm{X}=a_1{\mathrm{X}}_1+a_2{\mathrm{X}}_3+a_3{\mathrm{X}}_4+a_4{\mathrm{X}}_{10}$, where $a_i$ and $(i=1,\dots ,4)$, are arbitrary constants. Next, we will simplify $\mathrm{X}$ by utilizing suitable adjoint maps. To achieve this, we need to distinguish three cases: $a_1{a}_2\ne 0$, $a_1=0$ and $a_2=0$.

Case 1. $a_1{a}_2\ne 0$. Without a loss of generality, we assume $a_1=1$. Referring to Table 1, we act on such a $\mathrm{X}$ by $\mathrm{Ad}(exp\left({ϵ}_2\right){\mathrm{X}}_4)\circ \mathrm{Ad}(exp\left({ϵ}_1\right){\mathrm{X}}_{10})$ with ${ϵ}_1=n(1+3n)a_4/(n-1)$ and ${ϵ}_2=(1-n)a_4/a_2$, yielding

$$\begin{array}{c}\hfill \tilde{\mathrm{X}}=\mathrm{Ad}(exp\left({ϵ}_2\right){\mathrm{X}}_4)\circ \mathrm{Ad}(exp\left({ϵ}_1\right){\mathrm{X}}_{10})\mathrm{X}={\mathrm{X}}_1+a_2{\mathrm{X}}_3.\end{array}$$

Case 2. $a_1=0$. To proceed, we consider two cases: $a_2\ne 0$ and $a_2=0$. When $a_2\ne 0$, we assume $a_2=1$ and apply $\mathrm{Ad}(exp(a_3/(1-n)){\mathrm{X}}_4)$ to the corresponding vector $\mathrm{X}$, leading to

$$\begin{array}{c}\hfill \tilde{\mathrm{X}}=\mathrm{Ad}(exp(a_3/(1-n))){\mathrm{X}}_4)\mathrm{X}={\mathrm{X}}_3+a_4{\mathrm{X}}_{10}.\end{array}$$

when $a_2=0$, we scale $a_4(\ne 0)$ to $a_4=1$ by action $\mathrm{Ad}(exp(n(1+3n)ln{a}_4/(1-n)){\mathrm{X}}_1)$ so that the vector $\mathrm{X}$ is equivalent to ${\mathrm{X}}_{10}+a_3{\mathrm{X}}_4$. If $a_4=0$, the vector $\mathrm{X}$ is equivalent to ${\mathrm{X}}_4$.

Case 3. $a_2=0$. Analogous to the earlier analysis, two cases, $a_1\ne 0$ and $a_1=0$, arise. When $a_1\ne 0$, we assume $a_1=1$. Then, the action $\mathrm{Ad}(exp(n(1+3n)a_4/(1-n)){\mathrm{X}}_{10})$ on the corresponding vector $\mathrm{X}$ gives

$$\begin{array}{c}\hfill \tilde{\mathrm{X}}=\mathrm{Ad}(exp(n(1+3n)a_4/(1-n)){\mathrm{X}}_{10})\mathrm{X}={\mathrm{X}}_1+a_3{\mathrm{X}}_4.\end{array}$$

When $a_1=0$, the result for simplification is the same as the one for case 2 with $a_2=0$.

After renaming the constants, we can obtain the result in (39). For the other cases, one can obtain the results in a similar manner. □

4. Symmetry Reductions

Each point symmetry of the optimal system in Theorem 1 can be used to obtain group-invariant solutions of the Equation (1) by the well-known symmetry reduction method (see Refs. [12,13]). Suppose that not both of the independent variables t and x are invariant under the given symmetry $\mathrm{X}$; thus, the group-invariant solutions have the form

$$u=\mathsf{\Phi }(t,x,U(z\left)\right),$$

(41)

in terms of invariants

$$z=z(t,x),U=U(t,x,u),$$

(42)

determined by characteristic equations

$$\mathrm{X}z=\mathrm{X}U=0,$$

(43)

where $U\left(z\right)$ satisfies a fractional ordinary differential equation (ODE) obtained by the reduction of Equation (1). In what follows, we will run the reduction under each symmetry group in Theorem 1, where the parameters $a_i$ and $(i=1,2,3,4)$ will be replaced by parameter $\lambda$ for convenience.

4.1. Reduction by Generator X${}_1$

When $m+n=2(s+1)$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_1$ describes a space translation transformation. It has invariants

$$z=t,U=u.$$

(44)

Hence,

$$u(t,x)=U\left(z\right),$$

(45)

yields the corresponding group-invariant solution. Inserting (44) and (45) into Equation (1), we know that the invariant function $U\left(z\right)$ satisfies a fractional ODE

$${\partial }_z^{\alpha }U=U^m,$$

(46)

which has solutions

$$\begin{array}{c}\hfill U={\left(\frac{\mathsf{\Gamma }(1+\alpha /(1-m\left)\right)}{\mathsf{\Gamma }(1-m\alpha /(1-m\left)\right)}\right)}^{1/(m-1)}{z}^{\alpha /(1-m)},\mathrm{for}m<1+\alpha ;\end{array}$$

(47)

$$\begin{array}{c}\hfill U=c_1{z}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(z^{\alpha }\right),\mathrm{for}m=1.\end{array}$$

(48)

In (48), ${\mathrm{E}}_{\alpha ,\beta }\left(s\right)={\sum }_{j=0}^{\infty }\frac{s^j}{\mathsf{\Gamma }(\alpha j+\beta )}$ is the Mittag–Leffler function [1]. Then, the Equation (1) with $m+n=2(s+1)$ and $p=q=0$ possesses solutions

$$\begin{array}{c}\hfill u={\left(\frac{\mathsf{\Gamma }(1+\alpha /(1-m\left)\right)}{\mathsf{\Gamma }(1-m\alpha /(1-m\left)\right)}\right)}^{1/(m-1)}{t}^{\alpha /(1-m)},\mathrm{for}m<1+\alpha ;\end{array}$$

(49)

$$\begin{array}{c}\hfill u=c_1{t}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(t^{\alpha }\right),\mathrm{for}m=1,\end{array}$$

(50)

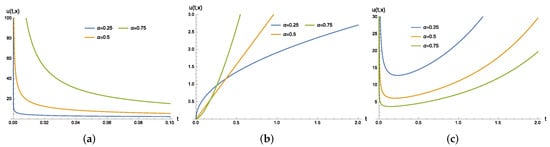
where and whereafter $c_i$ and $(i\in {\mathbb{Z}}^{+})$ are arbitrary constants. It is worth noting that, when $1<m<1+\alpha$, solution (49) is dispersive as $t\to +\infty$, and blows up at $t=0$. Figure 1 shows the behaviors of solutions (49) and (50) with respect to time variable t.

Figure 1. Behaviors of (a) solution (49) with $m=2$, (b) solution (49) with $m=0.5$ and (c) solution (50) with $c_1=2$.

4.2. Reduction by Generator X${}_3$

When $m+n=2(s+1)$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_3$ describes a scaling transformation. It has invariants

$$z=x{t}^{\frac{-\alpha (m-s-1)}{ps-(q-1)(m-1)}},U=u{t}^{\frac{\alpha (p-q+1)}{ps-(q-1)(m-1)}}.$$

(51)

Thus, the invariant solution has the form

$$u(t,x)=t^{-\frac{\alpha (p-q+1)}{ps-(q-1)(m-1)}}U\left(z\right).$$

(52)

Under the change in variables (51) and (52), ${\partial }_t^{\alpha }u$ with $0<\alpha <1$ in (4) can be rewritten as

$${\partial }_t^{\alpha }u=\frac{\partial }{\partial t}\left(\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t{(t-s)}^{-\alpha }{s}^{-\frac{\alpha (p-q+1)}{ps-(m-1)(q-1)}}U\left(x{s}^{-\frac{\alpha (m-s-1)}{ps-(m-1)(q-1)}}\right)ds\right).$$

(53)

Let $s=t/y$ and $ds=-(t/y^2)dy$; then, Equation (53) is transformed to

$$\begin{array}{cc}\hfill {\partial }_t^{\alpha }u& =\frac{\partial }{\partial t}\left(\frac{t^{\beta -\alpha }}{\mathsf{\Gamma }(1-\alpha )}{\int }_1^{\infty }{(y-1)}^{-\alpha }{y}^{\alpha -\beta -1}U\left(z{y}^{1/\delta }\right)dy\right)\hfill \\ & =\frac{\partial }{\partial t}\left(t^{\beta -\alpha }\left({\mathrm{K}}_{\delta }^{\beta ,1-\alpha }U\right)\left(z\right)\right),\hfill \end{array}$$

(54)

where $\beta =1-\frac{\alpha (p-q+1)}{ps-(m-1)(q-1)}$, $\gamma =\beta -\alpha$ and $\delta =\frac{ps-(m-1)(q-1)}{\alpha (m-s-1)}$, and $\left({\mathrm{K}}_{\delta }^{\beta ,\alpha }U\right)\left(z\right)$ is the Erdélyi–Kober fractional integral operator, defined by (9). In view of $\frac{\partial }{\partial t}U\left(z\right)=-\frac{z}{\delta t}\frac{d}{dz}U\left(z\right)$, the expression in (54) becomes

$$\begin{array}{cc}\hfill \frac{\partial }{\partial t}\left(t^{\beta -\alpha }\left({\mathrm{K}}_{\delta }^{\beta ,1-\alpha }U\right)\left(z\right)\right)& =t^{\beta -\alpha -1}\left(\beta -\alpha -\frac{z}{\delta }\frac{d}{dz}\right)\left({\mathrm{K}}_{\delta }^{\beta ,1-\alpha }U\right)\left(z\right).\hfill \\ & =t^{\beta -\alpha -1}\left({\mathrm{P}}_{\delta }^{\beta -\alpha ,\alpha }U\right)\left(z\right),\hfill \end{array}$$

(55)

where and whereafter $\left({\mathrm{P}}_{\delta }^{\beta ,\alpha }U\right)\left(z\right)$ is the Erdélyi–Kober fractional differential operator, defined by (8). Thus, the transformed expression of the right hand side to Equation (1) under transformations (51) and (52) associated with (55) leads to the reduced fractional ODE for invariant function $U\left(z\right)$, given by

$$\left({\mathrm{P}}_{\frac{ps-(q-1)(m-1)}{\alpha (m-s-1)}}^{1-\alpha -\frac{\alpha (p-q+1)}{ps-(q-1)(m-1)},\alpha }U\right)\left(z\right)=n{U}^{n-1}{U}^{\prime \prime }+n(n-1)U^{n-2}{U}^{\prime 2}+z^q{U}^s{U}^{\prime }+z^p{U}^m.$$

(56)

4.3. Reduction by Generator X${}_4$

When $m=n=s+1=(1+\alpha )/(1-\alpha )$, $p=-2$ and $q=-1$, the optimal symmetry generator ${\mathrm{X}}_4$ has invariants

$$z=x,U=u{t}^{\frac{2\alpha }{1-n}}.$$

(57)

Hence,

$$u(t,x)=t^{\frac{2\alpha }{n-1}}U\left(z\right),$$

(58)

yields the corresponding group-invariant solution. Inserting (57) and (58) into Equation (1), we know that the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$n{U}^{n-1}{U}^{″}+n(n-1)U^{n-2}{U}^{\prime 2}+z^{-1}{U}^{n-1}{U}^{\prime }+z^{-2}{U}^n=0,$$

(59)

which has solutions

$$\begin{array}{c}\hfill U=c_1{z}^{\frac{n-1-\sqrt{(n+1)(1-3n)}}{2n^2}}{\left(z^{\frac{\sqrt{(n+1)(1-3n)}}{n}}+c_2\right)}^{1/n},\mathrm{for}n\ne 1/3;\end{array}$$

(60)

$$\begin{array}{c}\hfill U=c_1{z}^{-3}{(c_2+lnz)}^3,\mathrm{for}n=1/3.\end{array}$$

(61)

Then, the Equation (1) with $m=n=s+1=(1+\alpha )/(1-\alpha )$, $p=-2$ and $q=-1$ possesses solutions

$$\begin{array}{c}\hfill u=c_1{t}^{\frac{-2}{n+1}}{x}^{\frac{n-1-\sqrt{(n+1)(1-3n)}}{2n^2}}{\left(x^{\frac{\sqrt{(n+1)(1-3n)}}{n}}+c_2\right)}^{1/n},\mathrm{for}n\ne 1/3;\end{array}$$

(62)

$$\begin{array}{c}\hfill u=c_1{t}^{-\frac{3}{2}}{x}^{-3}{(c_2+lnx)}^3,\mathrm{for}n=1/3.\end{array}$$

(63)

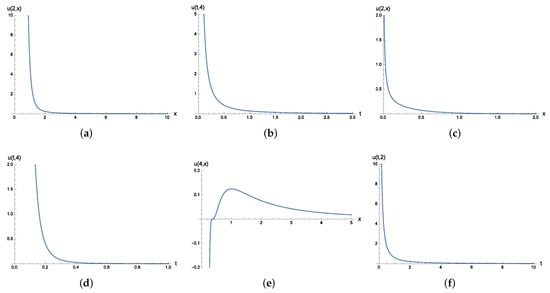
Note that solutions (62) and (63) are separable solutions. When $-1<n<1/3$, solution (62) is singular at $x=0$ and dispersive as $t\to \infty$, possessing a blow-up at $t=0$. For solution (63), u is singular at $x=0$. It also displays dispersion for a long time as $t\to \infty$ and blows up at $t=0$. Figure 2 exhibits the behaviors of solutions (62) and (63).

Figure 2. Behaviors of (a,b) solution (62) with $n=0.75$ and $c_1=c_2=1$, (c,d) solution (62) with $n=-0.5$ and $c_1=c_2=1$ and (e,f) solution (63) with $c_1=c_2=1$.

4.4. Reduction by Generator X${}_9$

When $2(m-1)=p(1\pm \frac{1}{\sqrt{3}})$, $n=\pm \frac{1}{\sqrt{3}}$, $s=-1\pm \frac{1}{\sqrt{3}}$ and $q=-1$, the optimal symmetry generator ${\mathrm{X}}_9$ has invariants

$$z=t,U=u{x}^{3\mp \sqrt{3}}.$$

(64)

Then, the invariant solution is given by

$$u(t,x)=x^{-3\pm \sqrt{3}}U\left(z\right),$$

(65)

where the invariant function $U\left(z\right)$ satisfies Equation (46) with solutions (47) and (48). Thus, when $2(m-1)=p(1\pm \frac{1}{\sqrt{3}})$, $n=\pm \frac{1}{\sqrt{3}}$, $s=-1\pm \frac{1}{\sqrt{3}}$ and $q=-1$, Equation (1) possesses solutions

$$\begin{array}{c}\hfill u={\left(\frac{\mathsf{\Gamma }(1+\alpha /(1-m\left)\right)}{\mathsf{\Gamma }(1-m\alpha /(1-m\left)\right)}\right)}^{1/(m-1)}{x}^{-3\pm \sqrt{3}}{t}^{\alpha /(1-m)},\mathrm{for}m<1+\alpha ;\end{array}$$

(66)

$$\begin{array}{c}\hfill u=c_1{x}^{-3\pm \sqrt{3}}{t}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(t^{\alpha }\right),\mathrm{for}m=1.\end{array}$$

(67)

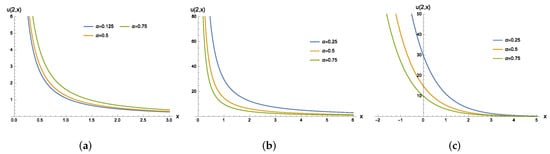
Solutions (66) and (67) are separable solutions. It is easily seen that solutions (66) and (67) are singular at $x=0$. Observe that, for a fixed value of x, solutions (66) and (67) are, respectively, the same as solutions (49) and (50) up to a constant. For such a reason, the behaviors of solutions (66) and (67) on time variable t are exhibited by Figure 1. The behaviors of solutions (66) and (67) on space variable x are depicted in Figure 3a,b.

Figure 3. Behaviors of (a) solution (66) with $m=2$, (b) solution (67) with $c_1=1$ and (c) solution (71) with $c_1=1$.

4.5. Reduction by Generator X${}_5$

When $m=-n=1$, $s=-2$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_5$ has invariants

$$z=t,U=u{e}^x.$$

(68)

Hence, the invariant solution has the form

$$u(t,x)=e^{-x}U\left(z\right),$$

(69)

where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$${\partial }_z^{\alpha }U=U.$$

(70)

Observe that Equation (70) has solution (48). Then, Equation (1) with $m=-n=1$, $s=-2$ and $p=q=0$ possesses solution

$$\begin{array}{c}\hfill u=c_1{e}^{-x}{t}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(t^{\alpha }\right),\end{array}$$

(71)

which is a separable solution. Figure 3c depicts the behavior of solution (71) related to space variable x, whereas the behaviors of solution (71) related to time variable t are shown in Figure 1a,b, since, for a fixed x, solution (71) is exactly solution (49) up to a constant.

4.6. Reduction by Generator X${}_1$ + $\lambda$X${}_3$

When $m=n=s+1$, $9n^3+6n^2-n-2=0$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_1+\lambda {\mathrm{X}}_3$ in (38) and (39) has invariants

$$z=texp\left(\lambda (1-n)x/\alpha \right),U=u{t}^{\alpha /(n-1)}.$$

(72)

Then,

$$u(t,x)=t^{\alpha /(1-n)}U\left(z\right),$$

(73)

is the invariant solution, where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill \left({\mathrm{P}}_{-1}^{1-\frac{n\alpha }{n-1},\alpha }U\right)\left(z\right)=& -\frac{2{\lambda }^2}{{\alpha }^2}(12n^2-5n+1)z^{2}U{U}^{″}+\frac{{\lambda }^2}{27{\alpha }^2}(150n^2-32n-198)U^{\prime 2}\hfill \\ & -\frac{\lambda }{9{\alpha }^2}(24\lambda n^2-(10\lambda -9\alpha )n-2\lambda -9\alpha )zU{U}^{\prime }+U^2.\hfill \end{array}$$

(74)

The obtainment of Equation (74) is achieved in a similar manner as for Equation (56).

4.7. Reduction by Generator X${}_1$ + $\lambda$X${}_4$

When $m=n=s+1=(1+\alpha )/(1-\alpha )$, $9n^3+6n^2-n-2=0$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_1+\lambda {\mathrm{X}}_4$ in (39) has invariants

$$z=\frac{t}{1+\lambda (n-1)xt},U=u{\left(\frac{t}{1+\lambda (n-1)xt}\right)}^{2\alpha /(1-n)}.$$

(75)

Then,

$$u(t,x)={\left(\frac{t}{1+\lambda (1-n)xt}\right)}^{2\alpha /(1-n)}U\left(z\right),$$

(76)

is the invariant solution, where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill {\partial }_z^{\alpha }U=& n{\lambda }^2{(n-1)}^2{z}^4{U}^{n-1}{U}^{\prime }+n{\lambda }^2{(n-1)}^3{z}^4{U}^{n-2}{U}^{\prime 2}\hfill \\ & +\frac{\lambda (n-1)}{n+1}{z}^2\left(\frac{4\lambda }{3}(1+2n)(1-3n)z-n-1\right)U^{n-1}{U}^{\prime }\hfill \\ & +\left(1-\frac{2\lambda (n-1)}{n+1}z+\frac{2{\lambda }^2(1+3n){(n-1)}^2}{{(n+1)}^2}{z}^2\right)U^n.\hfill \end{array}$$

(77)

4.8. Reduction by Generator X${}_2$ + $\lambda$$X_3$

When $m=n=s+1$, $q=-1$, $p=-2$ and $(n+2/3)\left(n-\frac{1+\alpha }{1-\alpha }\right)=0$, the optimal symmetry generator ${\mathrm{X}}_2+\lambda {\mathrm{X}}_3$ in (34) and (37) has invariants

$$z=x{t}^{-\alpha /(2+(n-1\left)\lambda \right)},U=u{t}^{-\alpha /(2+(n-1\left)\lambda \right)}.$$

(78)

Thus, Equation (1) has an invariant solution

$$u(t,x)=t^{\alpha /(2+(n-1\left)\lambda \right)}U\left(z\right),$$

(79)

where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill \left({\mathrm{P}}_{\frac{2+(n-1)\lambda }{\alpha }}^{1-\frac{\alpha (2+n\lambda )}{2+(n-1)\lambda },\alpha }U\right)\left(z\right)=& n{U}^{n-1}{U}^{″}+n(n-1)U^{n-2}{U}^{\prime 2}+z^{-1}{U}^{n-1}{U}^{\prime }+z^{-2}{U}^n.\hfill \end{array}$$

(80)

Here, Equation (80) is derived by a similar procedure as before.

4.9. Reduction by Generator X${}_6$ + $\lambda$X${}_3$

When $m=n=q=-1$ and $s=p=-2$, the optimal symmetry generator ${\mathrm{X}}_6+\lambda {\mathrm{X}}_3$ in (35) has invariants

$$z=t{(lnx)}^{2\lambda /\alpha },U=ux{(lnx)}^{1+\lambda }.$$

(81)

Thus, the invariant solution reads as

$$u(t,x)=x^{-1}{(lnx)}^{-1-\lambda }U\left(z\right).$$

(82)

With a similar analysis as aforementioned, we find the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill \left({\mathrm{P}}_{-1}^{1-\alpha ,l-\alpha }U\right)\left(z\right)=& -\frac{\lambda }{{\alpha }^2}{z}^{\alpha }{U}^{-3}(4\lambda z^{2}U{U}^{″}-8\lambda z^2{U}^{\prime 2}+2(2\lambda \alpha +\alpha +2\lambda )zU{U}^{\prime }\hfill \\ & -{\alpha }^2(\lambda +1)U^2).\hfill \end{array}$$

(83)

4.10. Reduction by Generator X${}_7$ + $\lambda$$X_3$

When $m=n=1/3$, $s=-2/3$, $q=-1$ and $p=-2$, the optimal symmetry generator ${\mathrm{X}}_7+\lambda {\mathrm{X}}_3$ in (36) has invariants

$$z=t{(lnx)}^{2\lambda /\left(3\alpha \right)},U=u{x}^3{(lnx)}^{3+\lambda }.$$

(84)

Thus, the invariant solution takes the form

$$u(t,x)=x^{-3}{(lnx)}^{-3-\lambda }U\left(z\right),$$

(85)

where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill \left({\mathrm{P}}_{-1}^{1-\alpha ,l-\alpha }U\right)\left(z\right)=& ({\alpha }^{-2}/81)z^{\alpha }{U}^{-5/3}(12{\lambda }^2{z}^{2}U{U}^{″}-8{\lambda }^2{z}^2{U}^{\prime 2}-6\lambda (2\lambda \alpha +9\alpha -2\lambda )zU{U}^{\prime }\hfill \\ & +9{\alpha }^2(\lambda +6)(\lambda +3)U^2).\hfill \end{array}$$

(86)

For the obtainment of Equation (86), we achieved this in a similar manner as earlier.

4.11. Reduction by Generator X${}_8$ + $\lambda$X${}_3$

When $m=n=-2/3$, $s=-5/3$, $q=-1$ and $p=-2$, the optimal symmetry generator ${\mathrm{X}}_8+\lambda {\mathrm{X}}_3$ in (37) has invariants

$$z=texp\left(-10\lambda x^{-3/2}/\left(9\alpha \right)\right),U=u{x}^{3}exp\left(-(2/3)\lambda x^{-3/2}\right).$$

(87)

The invariant solution is of the form

$$u(t,x)=x^{-3}exp\left((2/3)\lambda x^{-3/2}\right)U\left(z\right).$$

(88)

Analogous to the earlier analysis, we deduce that the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{c}\hfill \left({\mathrm{P}}_{-1}^{1-\alpha ,l-\alpha }U\right)\left(z\right)=-\frac{2{\lambda }^2}{81{\alpha }^2}{z}^{\alpha }{U}^{-\frac{8}{3}}\left(75z^{2}U{U}^{″}-125z^2{U}^{\prime 2}+15(4\alpha +5)zU{U}^{\prime }-18{\alpha }^2{U}^2\right).\end{array}$$

(89)

4.12. Reduction by Generator X${}_{10}$ + $\lambda$X${}_3$

When $m=n=s+1$, $9n^3+6n^2-n-2=0$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_{10}+\lambda {\mathrm{X}}_3$ in (38) and (39) has invariants

$$z=texp\left(-\frac{n(3n+1)\lambda }{\alpha }exp\left(\frac{(n-1)}{n(3n+1)}x\right)\right),$$

(90)

$$U=uexp\left(\frac{2}{n(3n+1)}x+\frac{\lambda n(3n+1)}{n-1}exp\left(\frac{n-1}{n(3n+1)}x\right)\right).$$

(91)

Then, the invariant solution is given by

$$u(t,x)=exp\left(\frac{-2}{n(3n+1)}x-\frac{\lambda n(3n+1)}{n-1}exp\left(\frac{n-1}{n(3n+1)}x\right)\right)U\left(z\right),$$

(92)

where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill \left({\mathrm{P}}_{-1}^{1-\alpha ,l-\alpha }U\right)\left(z\right)=& \frac{n{\lambda }^2}{{\alpha }^2}{z}^{\alpha }({(n-1)}^2{z}^2{U}^{n-1}{U}^{″}+{(n-1)}^3{z}^2{U}^{n-2}{U}^{\prime 2}\hfill \\ & +(n-1)(2n\alpha +n-1)z{U}^{n-1}{U}^{\prime }+n{\alpha }^2{U}^n).\hfill \end{array}$$

(93)

Equation (93) is obtained in a similar manner as before.

4.13. Reduction by Generator X${}_{10}$ + $\lambda$X${}_4$

When $m=n=s+1=(1+\alpha )/(1-\alpha )$, $9n^3+6n^2-n-2=0$ and $p=q=0$, the optimal symmetry generator ${\mathrm{X}}_{10}+\lambda {\mathrm{X}}_4$ in (39) has invariants

$$z=\frac{t}{1+\lambda texp\left(\frac{(n-1)x}{n(1+3n)}\right)},U=u{(-t)}^{\frac{2\alpha }{n-1}}exp\left(\frac{2x}{n(1+3n)}\right).$$

(94)

Then, the invariant solution is given by

$$u(t,x)={(-t)}^{\frac{2\alpha }{1-n}}exp\left(\frac{-2x}{n(1+3n)}\right)U\left(z\right),$$

(95)

where the invariant function $U\left(z\right)$ satisfies a fractional ODE

$$\begin{array}{cc}\hfill {\partial }_z^{\alpha }U=& \frac{{(n-1)}^2{\lambda }^2}{n{(1+3n)}^2}{z}^{\frac{n+3}{n+1}}\left(z{U}^{n-1}{U}^{″}+(n-1)z{U}^{n-2}{U}^{\prime 2}+2U^{n-1}{U}^{\prime }\right).\hfill \end{array}$$

(96)

5. Conservation Law

A conservation law of the Equation (1) is a space-time divergence equation

$$\left(D_t{C}^t+D_x{C}^x\right){|}_{\mathcal{E}}=0,$$

(97)

where $\mathcal{E}$ denotes the solution space of Equation (1), $C^t$ is the conserved density and $C^x$ is the spacial flux, which are functions of t, x, u and all derivatives of u.

To begin, we introduce a formal Lagrangian of Equation (1)

$$\mathcal{L}=v(t,x)\left({\partial }_t^{\alpha }u-{\left(u^n\right)}_{xx}-x^q{u}^s{u}_x-x^p{u}^m\right),$$

(98)

where $v(t,x)$ is a new dependent variable, and define a function

$$\begin{array}{cc}\hfill & F^{*}(t,x,u,v,u_x,v_x,u_{xx},v_{xx})=\frac{\delta \mathcal{L}}{\delta u},\hfill \end{array}$$

(99)

where $\frac{\delta }{\delta u}$ is the Euler–Lagrange operator with respect to variable u, given by

$$\begin{array}{c}\hfill \frac{\delta }{\delta u}=\frac{\partial }{\partial u}+{}_t^C{\partial }_T^{\alpha }\frac{\partial }{\partial \left({\partial }_t^{\alpha }u\right)}-D_x\frac{\partial }{\partial u_x}+D_x^2\frac{\partial }{\partial u_{xx}}.\end{array}$$

(100)

In (100), ${}_t^C{\partial }_T^{\alpha }$ is the right-sided Caputo fractional derivative operator of order $\alpha$, defined by (7). Then,

$$\begin{array}{cc}\hfill & F^{*}(t,x,u,v,u_x,v_x,u_{xx},v_{xx})=0,\hfill \end{array}$$

(101)

is the adjoint equation of Equation (1). Equation (1) is called nonlinearly self-adjoint if the adjoint Equation (99) is satisfied for all solutions of Equation (1) upon a substitution $v=\varphi (t,x,u)$, i.e., condition

$$\begin{array}{c}\hfill \frac{\delta \mathcal{L}}{\delta u}{|}_{\mathcal{E}}=\mu ({\partial }_t^{\alpha }u-{\left(u^n\right)}_{xx}-x^q{u}^s{u}_x-x^p{u}^m),\end{array}$$

(102)

holds for a unknown coefficient $\mu$. Splitting the determining Equation (102) with $v=\varphi (t,x,u)$ leads to an overdetermined system for $\varphi$, given by

$${\varphi }_u-\mu =0,$$

(103)

$$u{\varphi }_{uu}-(n-1)\mu =0,$$

(104)

$$2n{u}^{n-s-1}{\varphi }_{xu}-x^q{\varphi }_u-\mu x^q=0,$$

(105)

$${}_t^C{\partial }_T^{\alpha }\varphi -n{u}^{n-1}{\varphi }_{xx}+x^q{u}^s{\varphi }_x+q{x}^{q-1}{u}^s\varphi -m{x}^p{u}^{m-1}=\mu {\partial }_t^{\alpha }u-\mu x^p{u}^m.$$

(106)

Now, let us solve system (103)–(106). It is easy to see that $\mu =0$ from Equations (103) and (105). Thus, system (103)–(106) is reduced to Equation (106) with $\mu =0$ for $\varphi =\varphi (t,x)$. As mentioned before, the case of $sm(m-1)(n-1)=0$ is out of our consideration. To proceed, we consider the following three cases. When $n=m\ne s+1$, the reduced system is of the form

$$\begin{array}{c}\hfill {\varphi }_{xx}+x^p=0,x{\varphi }_x+q\varphi =0,{}_t^C{\partial }_T^{\alpha }\varphi =0,\end{array}$$

which has solution

$$\varphi =-\frac{x^{p+2}}{q(q+1)},\mathrm{for}p+q+2=0,q(q+1)\ne 0.$$

(107)

When $m=s+1\ne n$, the reduced system is given by

$$\begin{array}{c}\hfill {\varphi }_{xx}=0,x^q{\varphi }_x+q{x}^{q-1}\varphi -m{x}^p=0,{}_t^C{\partial }_T^{\alpha }\varphi =0.\end{array}$$

Solving this system, we immediately obtain

$$\varphi =-\frac{m(p-2q)}{q(q+1)}{x}^{p-q+1},\mathrm{for}(p-q)(p-q+1)=0.$$

(108)

When $n=m=s+1$, the reduced system reads as

$$\begin{array}{c}\hfill n{\varphi }_{xx}-x^q{\varphi }_x-q{x}^{q-1}\varphi +n{x}^p=0,{}_t^C{\partial }_T^{\alpha }\varphi =0,\end{array}$$

which can be solved explicitly in terms of special elementary functions, given by

$$\begin{array}{c}\hfill \varphi =c_{1}x+c_2{x}^{1/n}-\frac{n}{(p+1)(np+2n-1)}{x}^{p+2},\mathrm{for}q=1,\end{array}$$

(109)

$$\begin{array}{c}\hfill \varphi =c_{1}x+c_2{x}^{1/n}+\frac{n}{{(n-1)}^2}x(n+(1-n)lnx),\mathrm{for}p=q=-1,\end{array}$$

(110)

$$\begin{array}{c}\hfill \varphi =c_{1}x+c_2{x}^{1/n}+\frac{n}{n-1}{x}^{1/n}lnx,\mathrm{for}p=-2+1/n,q=-1.\end{array}$$

(111)

In [30,32], it is shown that the conserved density $C^t$ and spacial flux $C^x$ in (97) are determined by

$$\begin{array}{c}\hfill C^x=W\left(\frac{\partial \mathcal{L}}{\partial u_x}-D_x\left(\frac{\partial \mathcal{L}}{\partial u_{xx}}\right)\right)+D_x\left(W\right)\frac{\partial \mathcal{L}}{\partial u_{xx}},\end{array}$$

(112)

$$\begin{array}{c}\hfill C^t=\sum _{k=0}^{l-1}{(-1)}^k{\partial }_t^{\alpha -1-k}\left(W\right)D_t^k\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_t^{\alpha }u\right)}\right)-{(-1)}^{l}I\left(W,D_t^l\left(\frac{\partial \mathcal{L}}{\partial \left({\partial }_t^{\alpha }u\right)}\right)\right),\end{array}$$

(113)

where $W=\eta -\xi u_x-\tau u_t$ is the characteristic function of symmetry generator $\mathrm{X}=\xi {\partial }_x+\tau {\partial }_t+\eta {\partial }_u$ and integral $I(f,g)$ is defined by

$$I(f,g)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t{\int }_t^T{(\rho -\sigma )}^{-\alpha }f(\sigma ,x)g(\rho ,x)d\rho d\sigma .$$

(114)

Now, let us use the point symmetries in Theorem 1 to construct all conservation laws of Equation (1). In view of the expressions for $\varphi$ in (107)–(111), symmetry (28) cannot generate any conservation law.

5.1. Conservation Law Generated by Symmetry X${}_1$

The characteristic function corresponding to symmetry (24) is easily seen to be $W_a=-u_x$. From the expressions of $\varphi$, we note that, when $\varphi =x$, Equation (1) with $p=q=0$ and $s=m-1$ admits a conservation law. The corresponding two components obtained from (112) and (113) are

$$C^x=nx{u}^{n-1}{u}_{xx}+n(n-1)x{u}^{n-2}{u}_x^2-n{u}^{n-1}{u}_x+x{u}^{m-1}{u}_x,$$

(115)

$$C^t=-x{}_0{I}_t^{1-\alpha }\left(u_x\right).$$

(116)

5.2. Conservation Laws Generated by Symmetry $X_2$

The characteristic function corresponding to symmetry (25) is given by $W_b=-\alpha x{u}_x-2t{u}_t$. From the expressions of $\varphi$, there are three cases to be considered.

Case 1. $\varphi =1$. In this case, Equation (1) with $m=n=s+1$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=2nt{u}^{n-1}{u}_{tx}+n\alpha x{u}^{n-1}{u}_{xx}+2n(n-1)t{u}^{n-2}{u}_t{u}_x+\alpha n(n-1)x{u}^{n-2}{u}_x^2+\alpha (n+1)u^{n-1}{u}_x+2t{x}^{-1}{u}^{n-1}{u}_t,$$

(117)

$$C^t=-{}_0{I}_t^{1-\alpha }(\alpha x{u}_x+2t{u}_t).$$

(118)

Case 2. $\varphi =x$. In this case, Equation (1) with $m=n=s+1$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=2ntx{u}^{n-1}{u}_{tx}+n\alpha x^2{u}^{n-1}{u}_{xx}+2n(n-1)tx{u}^{n-2}{u}_t{u}_x+\alpha n(n-1)x^2{u}^{n-2}{u}_x^2+\alpha x{u}^{n-1}{u}_x-2(n-1)t{u}^{n-1}{u}_t,$$

(119)

$$C^t=-x{}_0{I}_t^{1-\alpha }(\alpha x{u}_x+2t{u}_t).$$

(120)

Case 3. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=s+1$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=x^{1/n}{u}^{n-2}\left(2ntu{u}_{tx}+\alpha nxu{u}_{xx}+2n(n-1)t{u}_x{u}_t+\alpha n(n-1)x{u}_x^2\right),$$

(121)

$$C^t=-x^{1/n}{}_0{I}_t^{1-\alpha }(\alpha x{u}_x+2t{u}_t).$$

(122)

5.3. Conservation Laws Generated by Symmetry $X_3$

The characteristic function corresponding to symmetry (26) is given by $W_c=-\alpha (p-q+1)u-\alpha (m-s-1)x{u}_x-(ps-(q-1)(m-1))t{u}_t$. From the expressions of $\varphi$, the following five cases are needed to be considered.

Case 1. $\varphi =x$. In this case, Equation (1) with $m=n=s+1$ and $q=-1$ admits a conservation law with two components

$$C^x=(p+2)\left(n(n-1)tx{u}^{n-1}{u}_{tx}+n{(n-1)}^{2}tx{u}^{n-2}{u}_x{u}_t-{(n-1)}^{2}t{u}^{n-1}{u}_t+\alpha n^{2}x{u}^{n-1}{u}_x-\alpha (n-1)u^n\right),$$

(123)

$$C^t=-(p+2)x{}_0{I}_t^{1-\alpha }(\alpha u+(n-1)t{u}_t).$$

(124)

Case 2. $\varphi =x^{p+2}$. In this case, Equation (1) with $m=n=s+1$, $q=-1$ or $n-m=p+q+2=0$ admits a conservation law with two components

$$\begin{array}{c}{C}^x=(2p+3)(n(n-1)t{x}^{2p+3}u{u}_{tx}+n{(n-1)}^{2}t{x}^{p+2}{u}_x{u}_t-(n-1)t\left(n(p+2)x^{p+1}-1\right)u{u}_t\hfill \\ +\alpha n^2{x}^{p+2}u{u}_x-\alpha \left(n(p+2)x^{p+1}-1\right)u^2)u^{n-2},\hfill \end{array}$$

(125)

$$C^t=-x^{p+2}{}_0{I}_t^{1-\alpha }\left(\alpha (p-q+1)u+\alpha (m-s-1)x{u}_x+(ps-(q-1)(m-1))t{u}_t\right).$$

(126)

Case 3. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=s+1$ and $q=-1$ admits a conservation law with two components

$$C^x=(p+2)x^{1/n}{u}^{n-2}\left(n(n-1)t{u}_{tx}+n{(n-1)}^{2}t{u}_t{u}_x+\alpha n^{2}u{u}_x\right),$$

(127)

$$C^t=-(p+2)x^{1/n}{}_0{I}_t^{1-\alpha }\left(\alpha u+(n-1)t{u}_t\right).$$

(128)

Case 4. $\varphi =xlnx$. In this case, Equation (1) with $m=n=s+1$ and $p=q=-1$ admits a conservation law with two components

$$\begin{array}{c}{C}^x=n(n-1)tx(lnx)u^{n-1}{u}_{tx}+n{(n-1)}^{2}tx{u}^{n-2}{u}_x{u}_t-(n-1)t(n+(n-1)lnx)u^{n-1}{u}_t\hfill \\ -\alpha n^{2}xlnx{u}^{n-1}{u}_x-\alpha (n+(n-1)lnx)u^n,\hfill \end{array}$$

(129)

$$C^t=-xlnx{}_0{I}_t^{1-\alpha }\left(\alpha u+(n-1)t{u}_t\right).$$

(130)

Case 5. $\varphi =x^{1/n}lnx$. In this case, Equation (1) with $m=n=s+1=1/(p+2)$ and $q=-1$ admits a conservation law with two components

$$\begin{array}{c}{C}^x=(n-1)t{x}^{1/n}lnx{u}^{n-1}{u}_{tx}+{(n-1)}^{2}t{x}^{1/n}lnx{u}_t{u}_x-(n-1)t{x}^{-1+1/n}{u}^{n-1}{u}_t\hfill \\ +\alpha n{x}^{1/n}lnx{u}^{n-1}{u}_x-\alpha x^{-1+1/n}{u}^n,\hfill \end{array}$$

(131)

$$C^t=-\frac{1}{n}{x}^{1/n}lnx{}_0{I}_t^{1-\alpha }\left((n-1)t{u}_t+\alpha u\right).$$

(132)

5.4. Conservation Laws Generated by Symmetry $X_4$

The characteristic function corresponding to symmetry (27) is given by $W_d=(\alpha -1)tu-t^2{u}_t$. In view of the expressions of $\varphi$, we need to consider the following six cases.

Case 1. $\varphi =1$. In this case, Equation (1) with $m=n=s+1=(1-\alpha )/(1+\alpha )$ and $q=-1$ admits a conservation law with two components

$$C^x=n(n-1)t^2{u}^{n-1}{u}_{tx}+n{(n-1)}^2{t}^2{u}^{n-2}{u}_t{u}_x+(n-1)t^2{x}^q{u}^{n-1}{u}_t+2\alpha n^{2}t{u}^{n-1}{u}_x+2\alpha t{x}^q{u}^n,$$

(133)

$$C^t=-{}_0{I}_t^{1-\alpha }(2\alpha tu+(n-1)t^2{u}_t).$$

(134)

Case 2. $\varphi =x$. In this case, Equation (1) with $m=n=s+1=(1-\alpha )/(1+\alpha )$ and $q=-1$ admits a conservation law with two components

$$C^x=n(n-1)x{t}^2{u}^{n-1}{u}_{tx}+n{(n-1)}^{2}x{t}^2{u}^{n-2}{u}_t{u}_x+{(n-1)}^2{t}^2{u}^{n-1}{u}_t+2\alpha n^{2}xt{u}^{n-1}{u}_x-2\alpha (n-1)t{u}^n,$$

(135)

$$C^t=-x{}_0{I}_t^{1-\alpha }(2\alpha tu+(n-1)t^2{u}_t).$$

(136)

Case 3. $\varphi =x^{p+2}$. In this case, Equation (1) with $m=n=s+1=(1-\alpha )/(1+\alpha )$ and $q=-1$ admits a conservation law with two components

$$C^x=t{x}^{p+1}{u}^n\left(n(n-1)xtu{u}_{tx}+n{(n-1)}^{2}xt{u}_t{u}_x-(n-1)(pn+2n-1)tu{u}_t+2\alpha n^{2}xu{u}_x-2\alpha (pn+2n-1)t{u}^2\right),$$

(137)

$$C^t=-x^{p+2}{}_0{I}_t^{1-\alpha }(2\alpha tu+(n-1)t^2{u}_t).$$

(138)

Case 4. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=s+1=(1-\alpha )/(1+\alpha )$ and $q=-1$ admits a conservation law with two components

$$C^x=nt{x}^{1/n}{u}^{n-2}\left((n-1)tu{u}_{tx}+{(n-1)}^{2}t{u}_t{u}_x+2\alpha nu{u}_x\right),$$

(139)

$$C^t=-x^{1/n}{}_0{I}_t^{1-\alpha }(2\alpha tu+(n-1)t^2{u}_t).$$

(140)

Case 5. $\varphi =xlnx$. In this case, Equation (1) with $m=n=s+1=(1-\alpha )/(1+\alpha )$ and $q=-1$ admits a conservation law with two components

$$\begin{array}{c}{C}^x=n(n-1)x(lnx)t^2{u}^{n-1}{u}_{tx}+n{(n-1)}^{2}x(lnx)t^2{u}^{n-2}{u}_t{u}_x-(n-1)(n+(n-1)lnx)t^2{u}^{n-1}{u}_t\hfill \\ +2\alpha n^{2}x(lnx)t{u}^{n-1}{u}_x-2\alpha (n+(n-1)lnx)t{u}^n,\hfill \end{array}$$

(141)

$$C^t=-xlnx{}_0{I}_t^{1-\alpha }(2\alpha tu+(n-1)t^2{u}_t).$$

(142)

Case 6. $\varphi =x^{1/n}lnx$. In this case, Equation (1) with $m=n=s+1=(1-\alpha )/(1+\alpha )=1/(p+2)$ and $q=-1$ admits a conservation law with two components

$$\begin{array}{c}{C}^x=n(n-1)x^{1/n}(lnx)t^2{u}^{n-1}{u}_{tx}+n{(n-1)}^2{x}^{1/n}(lnx)t^2{u}^{n-2}{u}_t{u}_x-n(n-1)x^{-1+1/n}{t}^2{u}^{n-1}{u}_t\hfill \\ +2\alpha n^2{x}^{1/n}(lnx)t{u}^{n-1}{u}_x-2n\alpha x^{-1+1/n}t{u}^n,\hfill \end{array}$$

(143)

$$C^t=-x^{1/n}lnx{}_0{I}_t^{1-\alpha }(2\alpha tu+(n-1)t^2{u}_t).$$

(144)

5.5. Conservation Laws Generated by Symmetry $X_6$

The characteristic function corresponding to symmetry (29) is $W_f=-(1+lnx)u-xlnx{u}_x$. From the solutions of $\varphi$, we have the following three cases.

Case 1. $\varphi =1$. In this case, Equation (1) with $m=n=q=-1$ and $s=p=-2$ admits a conservation law with two components

$$C^x=(lnx)\left(-x{u}^{-2}{u}_{xx}+2x{u}^{-3}{u}_x^2+u^{-3}{u}_x+x^{-1}{u}^{-1}\right),$$

(145)

$$C^t=-{}_0{I}_t^{1-\alpha }\left((1+lnx)u+x(lnx)u_x\right).$$

(146)

Case 2. $\varphi =x$. In this case, Equation (1) with $m=n=q=-1$ and $s=p=-2$ admits a conservation law with two components

$$C^x=-x^2(lnx)u^{-2}{u}_{xx}+2x^2(lnx)u^{-3}{u}_x^2+2x(lnx)u^{-2}{u}_x+2(1+lnx)u^{-1},$$

(147)

$$C^t=-x{}_0{I}_t^{1-\alpha }\left((1+lnx)u+xlnx{u}_x\right).$$

(148)

Case 3. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=q=-1$ and $s=p=-2$ admits a conservation law with two components

$$C^x=-(lnx)u^{-2}{u}_{xx}+2(lnx)u^{-3}{u}_x^2-x^{-2}{u}^{-1},$$

(149)

$$C^t=-x^{-1}{}_0{I}_t^{1-\alpha }\left((1+lnx)u+xlnx{u}_x\right).$$

(150)

5.6. Conservation Laws Generated by Symmetry $X_7$

The characteristic function corresponding to symmetry (30) is given by $W_g=-3(1+lnx)u-xlnx{u}_x$. With the expressions of $\varphi$, we arrive at three cases, which are as follows.

Case 1. $\varphi =1$. In this case, Equation (1) with $m=n=1/3$, $s=-2/3$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=\frac{1}{3}x(lnx)u^{-2/3}{u}_{xx}-\frac{2}{9}x(lnx)u^{-5/3}{u}_x^2+\frac{1}{3}(2+5lnx)u^{-2/3}{u}_x+x^{-1}(4+3lnx)u^{1/3},$$

(151)

$$C^t=-{}_0{I}_t^{1-\alpha }\left(3(1+lnx)u+x(lnx)u_x\right).$$

(152)

Case 2. $\varphi =x$. In this case, Equation (1) with $m=n=1/3$, $s=-2/3$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=\frac{1}{3}{x}^2(lnx)u^{-2/3}{u}_{xx}-\frac{2}{9}{x}^2(lnx)u^{-5/3}{u}_x^2+\frac{2}{3}x(1+2lnx)u^{-2/3}{u}_x+(3+2lnx)u^{1/3},$$

(153)

$$C^t=-x{}_0{I}_t^{1-\alpha }\left(3(1+lnx)u+x(lnx)u_x\right).$$

(154)

Case 3. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=1/3$, $s=-2/3$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=\frac{1}{3}{x}^4(lnx)u^{-2/3}{u}_{xx}-\frac{2}{9}{x}^4(lnx)u^{-5/3}{u}_x^2+\frac{2}{3}{x}^3(1+lnx)u^{-2/3}{u}_x+x^2{u}^{1/3},$$

(155)

$$C^t=-x^3{}_0{I}_t^{1-\alpha }\left(3(1+lnx)u+x(lnx)u_x\right).$$

(156)

5.7. Conservation Laws Generated by Symmetry $X_8$

The characteristic function corresponding to symmetry (31) is $W_h=-3x^{3/2}u-x^{5/2}{u}_x$. From the expressions of $\varphi$, the following three cases arise.

Case 1. $\varphi =1$. In this case, Equation (1) with $m=n=-2/3$, $s=-5/3$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=-\frac{2}{3}{x}^{5/2}{u}^{-5/3}{u}_{xx}+\frac{10}{9}{x}^{5/2}{u}^{-8/3}{u}_x^2+\frac{2}{3}{x}^{3/2}{u}^{-5/3}{u}_x,$$

(157)

$$C^t=-{}_0{I}_t^{1-\alpha }\left(3x^{3/2}u+x^{5/2}{u}_x\right).$$

(158)

Case 2. $\varphi =x$. In this case, Equation (1) with $m=n=-2/3$, $s=-5/3$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=-\frac{2}{3}{x}^{7/2}{u}^{-5/3}{u}_{xx}+\frac{10}{9}{x}^{7/2}{u}^{-8/3}{u}_x^2+\frac{4}{3}{x}^{5/2}{u}^{-5/3}{u}_x+2x^{3/2}{u}^{-2/3},$$

(159)

$$C^t=-x{}_0{I}_t^{1-\alpha }\left(3x^{3/2}u+x^{5/2}{u}_x\right).$$

(160)

Case 3. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=-2/3$, $s=-5/3$, $q=-1$ and $p=-2$ admits a conservation law with two components

$$C^x=-\frac{2}{3}x{u}^{-5/3}{u}_{xx}+\frac{10}{9}x{u}^{-8/3}{u}_x^2-\frac{1}{3}{u}^{-5/3}{u}_x-3x^{-1}{u}^{-2/3},$$

(161)

$$C^t=-x^{-2/3}{}_0{I}_t^{1-\alpha }\left(3x^{3/2}u+x^{5/2}{u}_x\right).$$

(162)

5.8. Conservation Laws Generated by Symmetry $X_9$

The characteristic function corresponding to symmetry (32) is given by $W_i=-2x^{1-3n}u-(n+1)x^{2-3n}{u}_x$. In view of the expressions of $\varphi$, we need to consider the following three cases.

Case 1. $\varphi =x$. In this case, Equation (1) with $m=n=s-1=\pm 1/\sqrt{3}$, $q=-1$ and $p=\frac{2(n-1)}{n+1}$ admits a conservation law with two components

$$C^x=n(n+1)x^{3-3n}{u}^{n-1}{u}_{xx}+n{(n-1)}^2{x}^{3-3n}{u}^{n-2}{u}_x^2-(n-1)(3n+2)x^{2-3n}{u}^{n-1}{u}_x,$$

(163)

$$C^t=-x{}_0{I}_t^{1-\alpha }\left(2x^{1-3n}u+(n+1)x^{2-3n}{u}_x\right).$$

(164)

Case 2. $\varphi =x^{p+2}$. In this case, Equation (1) with $m=n=s-1=\pm 1/\sqrt{3}$, $q=-1$ and $p=\frac{2(n-1)}{n+1}$ admits a conservation law with two components

$$C^x=n(n+1)x^{\frac{1+3n}{1+n}}{u}^{n-1}{u}_{xx}-\frac{2n}{3}{x}^{\frac{1+3n}{1+n}}{u}^{n-2}{u}_x^2+2n{x}^{\frac{2n}{1+n}}{u}^{n-1}{u}_x-\frac{2(1-n)}{1+n}{u}^n,$$

(165)

$$C^t=x^{4n/(n+1)}{}_0{I}_t^{1-\alpha }\left(2x^{1-3n}u+(n+1)x^{2-3n}{u}_x\right).$$

(166)

Case 3. $\varphi =x^{1/n}$. In this case, Equation (1) with $m=n=s-1=\pm 1/\sqrt{3}$, $q=-1$ and $p=\frac{2(n-1)}{n+1}$ admits a conservation law with two components

$$C^x=n(n+1)x^2{u}^{n-1}{u}_{xx}-\frac{2n}{3}{x}^2{u}^{n-2}{u}_x^2+n(n+1)x{u}^{n-1}{u}_x-2(1-n)u^n,$$

(167)

$$C^t=-x^{1/n}{}_0{I}_t^{1-\alpha }\left(2x^{1-3n}u+(n+1)x^{2-3n}{u}_x\right).$$

(168)

5.9. Conservation Laws Generated by Symmetry $X_{10}$

The characteristic function corresponding to symmetry (33) is given by $W_j=-e^{\frac{(1-n)x}{n(3n+1)}}\left(2u+n(3n+1)u_x\right)$. We note that, when $\varphi =x$, Equation (1) with $m=n=s+1$, $9n^3+6n^2-n-2=0$ and $p=q=0$ admits a conservation law. The corresponding two components are given by

$$C^x=e^{\frac{(1-n)x}{n(3n+1)}}\left(n^2(3n+1)x{u}^{n-1}{u}_{xx}+n^2(n-1)(3n+1)x{u}^{n-2}{u}_x^2+2n(1+2n)u^{n-1}{u}_x-\frac{4(1+n)}{3n+1}x{u}^n\right),$$

(169)

$$C^t=-x{e}^{\frac{(1-n)x}{n(3n+1)}}{}_0{I}_t^{1-\alpha }\left(2u+n(3n+1)u_x\right).$$

(170)

6. Conclusions

In this paper, we perform a complete symmetry and conservation law analysis to the time-fractional generalized porous medium Equation (1). Equation (1) admits affluent symmetry groups. Altogether, there are ten symmetry generators shown in Theorem 1. Then, the one-dimensional optimal system of Lie subalgebra is constructed and used to reduce Equation (1) to a fractional ODE. Some solutions for Equation (1) are derived due to the reductions, such as time-dependent solutions and separable solutions. They have several interesting dynamic behaviors: they are dispersive, blow-up and singular. Furthermore, the concept of nonlinear self-adjointness is adopted to derive the conservation laws of Equation (1).

In the process of this study, we realise that Lie symmetry analysis is an effective technique for solving fractional PDEs. A challenging problem is how to solve fractional ODEs with an Erdélyi–Kober fractional differential operator.

For future work, we will still focus on the study of FDEs; for example, how to generalize the group-foliation method [38] to FDEs and whether the theories for higher-order symmetry groups in [39] and potential symmetry groups in [40] can be extended to nonlinear FDEs.