Global Dynamics of a Vibro-Impact Energy Harvester

Abstract

In this paper, we consider a two-sided vibro-impact energy harvester described as a forced cylindrical capsule inclined at a horizontal angle, and the motion of the ball inside the capsule follows from the impacts with the capsule ends and gravity. Two distinct cases of dynamical behavior are investigated: the nondissipative and dissipative cases, where the dissipation is given by a restitution coefficient of impacts. We show that the dynamics of the system are described by the use of a 2D implicit map written in terms of the variables’ energy and time when the ball leaves the moving capsule ends. More precisely, in the nondissipative case, we analytically show that this map is area-preserving and the existence of invariant curves for some rotation number with Markoff constant type is proved according to Moser’s twist theorem in high energy. The existence of invariant curves implies that the kinetic energy of the ball is always bounded, and hence, the structure of system is not destroyed by the impacts of the ball. Furthermore, by numerical analysis we also show that the dynamical behavior of this system is regular, mainly containing periodic points, invariant curves and Aubry–Mather sets. After introducing dissipation, the dissipation destroys the regular dynamical behavior of the nondissipative case, and a periodic point with low energy is generated.

1. Introduction

Energy harvesting (EH) refers to the process of converting various renewable energy sources such as wind, solar, wave, and vibration into electrical energy, which usually can be used to complement and substitute other sources of energy [1]. In recent years, a number of well-known conventional transduction methods of converting various energy into electrical energy were explored and developed, including piezoelectric [2], electromagnetic [3], electrostatic [4], and triboelectric [5].

To efficiently capture energy, various mechanical systems and energy conversion methods based on single-degree-of-freedom and multiple-degrees-of-freedom were developed. Linear systems are generally not suitable as EH devices under excitation with varying frequencies, since the high-power output required by the system can only be achieved by near resonance, leading to reliability and fatigue issues [6,7]. Due to these limitations, parametric excitation and nonlinearities are often introduced into systems to improve their performance and amplify their response [8,9,10]. In addition, due to the high efficiency of EH, multistable equilibria systems became increasingly popular in various realistic applications [11,12,13]. The study of vibro-impact (VI) systems for EH and the benefits of exploiting their dynamical behavior were proposed in [14,15]. The study of VI systems is both challenging and fascinating to scientists for two main reasons. The first one is that the simplest VI system has extremely complicated dynamical behavior. The best way to explain this behavior is with the impact-pair model, which is described as the ball of a point mass moving freely inside a 1D box and reflecting when hitting the boundary of the box. Due to the existence of the impacts, it has extremely complicated dynamical behavior, such as grazing bifurcation, singularity, and chaotic attractor [16,17,18,19]. The second is that a proper approach to studying VI systems is to attempt to establish its discrete Poincaré map (sometimes called the first return map). However, this map usually cannot be solved explicitly, thereby presenting the main difficulty with obtaining further analytical results.

Recently, a new type of VI-EH device was proposed in [20,21,22]. The device consists of a forced cylinder and a ball that moves freely inside the cylinder. Both ends of the cylinder are covered with membranes consisting of DE material that is sandwiched between two compliant electrodes, thereby acting as a variable capacitance capacitor. The principle of EH is that the ball impacts against one of the membranes and causes it to deform, resulting in a change in capacitance between the initial and deformed stated, leading to EH. Thus, the kinetic energy is converted through the impacts of the potential energy of the deformed membrane, and then into electrical energy. Here, we consider a VI-EH system described as as a small ball rolling inside a forced cylindrical capsule that is reflected after hitting the capsule ends. The main contribution of this paper is that we prove that the structure of the system is not destroyed by the impact of the ball. More precisely, in the nondissipative case, a proof of the existence of invariant curves is proved according to Moser’s twist theorem, which in turn proves that the kinetic energy of the ball is always bounded. Moreover, through the numerical simulation results, we find that in the nondissipative case, the energy of the ball is dissipative; i.e., infinite energy cannot also appear. Therefore, the structure of the system is not destroyed. The rest of this paper is organized as follows. In Section 2, we present a VI-EH and establish its Poincaré map. In Section 3, the existence of invariant curves is proved according to a version of Morser’s twist theorem. In Section 4, the global dynamical behavior of the system is investigated by numerical simulations, and the theoretical results are further verified. We draw the conclusions of this paper in Section 5.

2. Statement of the Problem

The VI-EH system can be modeled as a small ball of unitary mass rolling inside a forced cylindrical capsule that is inclined at a horizontal angle of $\beta (0<\beta <\frac{\pi }{2})$, along with two DE membranes $\partial B$ and $\partial T$ for harvesting energy from ambient vibrations at the bottom and top of the capsule at distance L apart. The friction between the ball and the capsule is neglected, thus the motion of the ball is driven purely by impacts with one of the DE membranes and gravity. The elastic restitution coefficient for impacts between the ball and the DE membranes is $e\in (0,1]$, and the mass of the capsule is huge with respect to the mass of the ball, which means that the impacts do not affect the motion of the capsule. Assume that the capsule moves periodically according to a $C^6$ and 1-periodic function $p\left(t\right)$, i.e., $p(t+1)=p\left(t\right)$, see Figure 1.

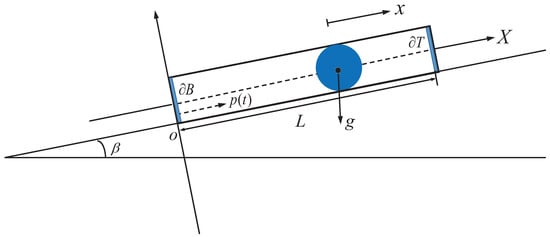
Figure 1. Schematic for vibro-impact energy harvesting (VI-EH) system.

Using the absolute coordinates, under the influence of the gravity and inclined angle, the motion of the ball moving inside the capsule satisfies as

$$\begin{array}{c}\hfill \ddot{x}=-gsin\beta ,\end{array}$$

(1)

where g is the gravitational acceleration. Assume that the motion equation of $\partial B$ is

$$\begin{array}{c}\hfill X\left(t\right)=p\left(t\right),\end{array}$$

(2)

then, the motion equation of $\partial T$ is $X\left(t\right)=p\left(t\right)+L$.

Assuming that the impact occurs at instant $\tau$, we consider the following problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\ddot{x}=-gsin\beta ,p\left(t\right)\le x\left(t\right)\le p\left(t\right)+L,\hfill \\ x\left(\tau \right)=p\left(\tau \right)\mathrm{or}x\left(\tau \right)=p\left(\tau \right)+L\Rightarrow \dot{x}\left({\tau }^{+}\right)=-e\dot{x}\left({\tau }^{-}\right)+(1+e)\dot{p}\left(\tau \right),\hfill \end{array}\right.\end{array}$$

(3)

where $\dot{x}\left({\tau }^{+}\right)$ and $\dot{x}\left({\tau }^{-}\right)$ are the velocity of the ball before and after the impact at $\tau$, respectively.

Remark 1.

Note that the grazing and chattering phenomenons can also occur in this system, but we do not discuss them here because the research required to analyze them needs different approaches.

The problem (3) can usually be formulated in discrete form. Let $v=\dot{x}\left(t\right)$ denote the velocity of the ball. Suppose that at time t the ball impacts with $\partial B$ and attains a velocity v after impact. Then, it moves from $\partial B$ to $\partial T$ and reaches $\partial T$ at time $\tilde{t}$ with the velocity $\tilde{v}$. After impact with $\partial T$, the ball attains a velocity $\widehat{v}$. Continuing this process, the ball moves from $\partial T$ to $\partial B$ and reaches $\partial T$ at time $t^{\prime }$ with the velocity $\overline{v}$. After impacts with $\partial T$, the ball attains a velocity $v^{\prime }$. Based on the above analysis, we obtain

$$\begin{array}{c}\hfill p\left(\tilde{t}\right)-p\left(t\right)+L=v(\tilde{t}-t)-\frac{gsin\beta }{2}{(\tilde{t}-t)}^2\end{array}$$

(4)

and

$$\begin{array}{c}\hfill \tilde{v}=v-\frac{gsin\beta }{2}(\tilde{t}-t).\end{array}$$

(5)

The relative velocity of the ball and $\partial T$ before and after an impact is related by

$$\begin{array}{c}\hfill \frac{\widehat{v}-\dot{p}\left(\tilde{t}\right)}{\tilde{v}-\dot{p}\left(\tilde{t}\right)}=-e.\end{array}$$

It gives

$$\begin{array}{c}\hfill \widehat{v}=-e\tilde{v}+(1+e)\dot{p}\left(\tilde{t}\right).\end{array}$$

(6)

Then, by (5) and (6), we have

$$\begin{array}{c}\hfill \widehat{v}=-ev+\frac{gesin\beta }{2}(\tilde{t}-t)+(1+e)\dot{p}\left(\tilde{t}\right).\end{array}$$

(7)

Completely similar to the above analysis, we have

$$\begin{array}{c}\hfill p\left(\tilde{t}\right)-p\left(t^{\prime }\right)+L=-\tilde{v}(t^{\prime }-\tilde{t})+\frac{gsin\beta }{2}(t^{\prime }-\tilde{t})\end{array}$$

(8)

and

$$\begin{array}{c}\hfill \overline{v}=\widehat{v}-\frac{gsin\beta }{2}(t^{\prime }-\tilde{t}).\end{array}$$

(9)

The relative velocities of the ball and $\partial B$ before and after an impact are related by

$$\begin{array}{c}\hfill \frac{v^{\prime }-\dot{p}\left(t^{\prime }\right)}{\overline{v}-\dot{p}\left(t^{\prime }\right)}=-e.\end{array}$$

It gives that

$$\begin{array}{c}\hfill v^{\prime }=-e\overline{v}+(1+e)\dot{p}\left(t^{\prime }\right).\end{array}$$

(10)

Then, we obtain from (8)–(10) that

$$\begin{array}{c}\hfill \begin{array}{cc}{v}^{\prime }\hfill & =-e\widehat{v}+\frac{gesin\beta }{2}(\tilde{t}-t)-\frac{gsin\beta }{2}(t^{\prime }-\tilde{t})+(1+e)\dot{p}\left(t^{\prime }\right)\hfill \\ & =e^{2}v+\frac{gesin\beta }{2}(t^{\prime }-\tilde{t}-e(\tilde{t}-t))-(1+e)(\dot{p}\left(t^{\prime }\right)-\dot{p}\left(\tilde{t}\right)).\hfill \end{array}\end{array}$$

(11)

A good strategy to describe the motion of the ball at the moments of impact with the same moving membranes $\partial B$ (or $\partial T$) in problem (3) is to define a Poincaré map P that sends the couple $(t,v)$ to $(t^{\prime },v^{\prime })$. In the following, we introduce a notion to construct the map P.

Define the sections

$$\begin{array}{c}\hfill {\mathsf{\Pi }}_1=\{(x,v,t)\in {\mathbb{R}}^3|x=X\left(t\right)\}\end{array}$$

and

$$\begin{array}{c}\hfill {\mathsf{\Pi }}_2=\{(x,v,t)\in {\mathbb{R}}^3|x=X\left(t\right)+L\}.\end{array}$$

Moreover, define the sections

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_1=\left\{(t,v)\right|(p\left(t\right),v,t)\in {\mathsf{\Pi }}_1\}\end{array}$$

and

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_2=\left\{(t,v)\right|(p\left(t\right)+L,v,t)\in {\mathsf{\Pi }}_2\}.\end{array}$$

The section ${\mathsf{\Lambda }}_1$ (or ${\mathsf{\Lambda }}_2$) can be interpreted as the Poincaré section. Thus, we obtain four basic maps $P_1:{\mathsf{\Lambda }}_1\to {\mathsf{\Lambda }}_2$, $P_2:{\mathsf{\Lambda }}_2\to {\mathsf{\Lambda }}_2$, $P_3:{\mathsf{\Lambda }}_2\to {\mathsf{\Lambda }}_1$, $P_4:{\mathsf{\Lambda }}_1\to {\mathsf{\Lambda }}_1$, which is defined by

$$\begin{array}{cc}{P}_1(t,v):=(t_0,v_0)\hfill & =(\tilde{t},\tilde{v}),\hfill \\ P_2(t_0,v_0):=(t_1,v_1)\hfill & =(\tilde{t},\widehat{v}),\hfill \\ P_3(t_1,v_1):=(t_2,v_2)\hfill & =(t^{\prime },\overline{v}),\hfill \\ P_4(t_2,v_2):=(t_5,v_3)\hfill & =(t^{\prime },v^{\prime }),\hfill \end{array}$$

respectively, see Figure 2.

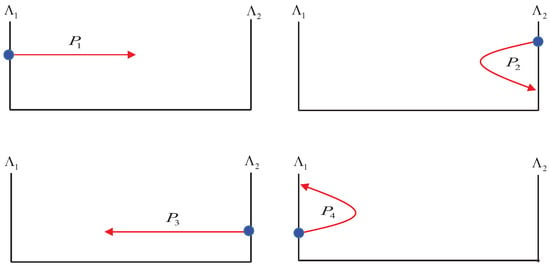
Figure 2. Schematic for four basic maps.

Define the composition map $P=P_4\circ P_3\circ P_2\circ P_1:{\mathsf{\Lambda }}_1\to {\mathsf{\Lambda }}_1$, and then P is regarded as a Poincaré map of problem (3).

Lemma 1.

The Poincaré map P has the expansion

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle t^{\prime }=t+\frac{L+(p\left(\tilde{t}\right)-p\left(t\right))}{v}+\frac{-L+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right))}{\tilde{v}}+\mathcal{K}(g,\beta ),}\hfill \\ {\displaystyle v^{\prime }=e^{2}v+\frac{gesin\beta }{2}(t^{\prime }-\tilde{t}-e(\tilde{t}-t))-(1+e)(\dot{p}\left(t^{\prime }\right)-\dot{p}\left(\tilde{t}\right)),}\hfill \end{array}\right.\end{array}$$

(12)

where

$$\begin{array}{c}{\displaystyle \mathcal{K}(g,\beta )=\frac{-{\alpha }_1(p\left(\tilde{t}\right)-p\left(t\right)+L)}{v(2v+{\alpha }_1)}+\frac{{\alpha }_2(p\left(\tilde{t}\right)-p\left(t^{\prime }\right)+L)}{\tilde{v}(2\tilde{v}+{\alpha }_2)},}\hfill \\ {\displaystyle {\alpha }_1=\frac{{\mathcal{K}}_1(g,\beta )}{\sqrt{v^2+{\mathcal{K}}_1(g,\beta )}+v},{\alpha }_2=\frac{{\mathcal{K}}_2(g,\beta )}{\sqrt{{\tilde{v}}^2+{\mathcal{K}}_2(g,\beta )}+\tilde{v}},}\hfill \\ {\displaystyle {\mathcal{K}}_1(g,\beta )=-2gsin\beta (p\left(\tilde{t}\right)-p\left(t\right)+L),{\mathcal{K}}_2(g,\beta )=2gsin\beta (p\left(\tilde{t}\right)-p\left(t^{\prime }\right)+L).}\hfill \end{array}$$

Proof. 

By (4), we have

$$\frac{gsin\beta }{2}{(\tilde{t}-t)}^2-v(\tilde{t}-t)+(p\left(\tilde{t}\right)-p\left(t\right)+L)=0.$$

It gives

$$\begin{array}{c}\hfill \begin{array}{cc}\tilde{t}-t\hfill & =\frac{2(p\left(\tilde{t}\right)-p\left(t\right)+L)}{v+\sqrt{v^2-\frac{gsin\beta }{2}(p\left(\tilde{t}\right)-p\left(t\right)+L)}}\hfill \\ & =\frac{p\left(\tilde{t}\right)-p\left(t\right)+L}{v}+\left(\frac{2(p\left(\tilde{t}\right)-p\left(t\right)+L)}{v+\sqrt{v^2-\frac{gsin\beta }{2}(p\left(\tilde{t}\right)-p\left(t\right)+L)}}-\frac{p\left(\tilde{t}\right)-p\left(t\right)+L}{v}\right).\hfill \end{array}\end{array}$$

(13)

Then, we have

$$\tilde{t}-t=\frac{p\left(\tilde{t}\right)-p\left(t\right)+L}{v}+(p\left(\tilde{t}\right)-p\left(t\right)+L){\mathcal{Q}}_1,$$

(14)

where

$$\begin{array}{cc}{\mathcal{Q}}_1\hfill & =\frac{2}{v+\sqrt{v^2-\frac{gsin\beta }{2}(p\left(\tilde{t}\right)-p\left(t\right)+L)}}-\frac{1}{v}\hfill \\ & =\frac{2}{v+\sqrt{v^2+{\mathcal{K}}_1(g,\beta )}}-\frac{1}{v}\hfill \\ & =\frac{-{\mathcal{K}}_1(g,\beta )}{v(2v+\sqrt{v^2+{\mathcal{K}}_1(g,\beta )})+{\mathcal{K}}_1(g,\beta )}\hfill \\ & =\frac{-1}{v\left(\frac{2v+\sqrt{v^2+{\mathcal{K}}_1(g,\beta )}}{{\mathcal{K}}_1(g,\beta )}\right)+1}=\frac{-{\alpha }_1}{v(2v+{\alpha }_1)}\hfill \end{array}$$

with ${\mathcal{K}}_1(g,\beta ):=-2gsin\beta (p\left(\tilde{t}\right)-p\left(t\right)+L)$ and ${\alpha }_1=\frac{{\mathcal{K}}_1(g,\beta )}{\sqrt{v^2+{\mathcal{K}}_1(g,\beta )}+v}$.

Similarly, we have

$$t^{\prime }-\tilde{t}=\frac{-L+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right))}{\tilde{v}}+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right)-L){\mathcal{Q}}_2,$$

(15)

where ${\mathcal{Q}}_2=\frac{{\alpha }_2}{\tilde{v}(2\tilde{v}+{\alpha }_2)}$ with ${\alpha }_2=\frac{{\mathcal{K}}_2(g,\beta )}{\sqrt{{\tilde{v}}^2+{\mathcal{K}}_2(g,\beta )}+\tilde{v}}$, ${\mathcal{K}}_2(g,\beta )=2gsin\beta (p\left(\tilde{t}\right)-p\left(t^{\prime }\right)+L)$.

Thus, by (14) and (15), we get

$$\begin{array}{c}\hfill {\displaystyle t^{\prime }=t+\frac{L+(p\left(\tilde{t}\right)-p\left(t\right))}{v}+\frac{-L+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right))}{\tilde{v}}+\mathcal{K}(g,\beta ),}\end{array}$$

where $\mathcal{K}(g,\beta )=(p\left(\tilde{t}\right)-p\left(t\right)+L){\mathcal{Q}}_1+(p\left(\tilde{t}\right)-p\left(t^{\prime }\right)+L){\mathcal{Q}}_2$. □

Lemma 2.

There is a sufficiently large constant $v^{*}>0$ such that if the initial velocity $v>v^{*}$ and for every $t\in \mathbb{R}$, then the Poincaré map P is well defined and belongs to a class of functions of $C^6$.

Proof. 

By (12), we have

$$\begin{array}{cc}\hfill \tilde{t}-t& =\frac{2(p\left(\tilde{t}\right)-p\left(t\right)+L)}{v+\sqrt{v^2-\frac{gsin\beta }{2}(p\left(\tilde{t}\right)-p\left(t\right)+L)}}.\end{array}$$

(16)

Consider the function

$$F(\tilde{t},t,v)=t^{\prime }-t-\left(\frac{L+(p\left(\tilde{t}\right)-p\left(t\right))}{v}+\frac{-L+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right))}{\tilde{v}}+\mathcal{K}(g,\beta )\right).$$

Then, for sufficiently large v, we have

$${\partial }_{\tilde{t}}F(\tilde{t},t,v)=1-O\left(\frac{1}{v}\right)>0.$$

Thus, when v is large enough, for every couple $(t,v)$ we get a unique $\tilde{t}=\tilde{t}(t,v)$ that satisfies (16). By using the implicit function theorem, we obtain by uniqueness that $\tilde{t}(t,v)$ is a $C^6$ function. Then, by (12) we conclude that the Poincaré map P is well defined and belongs to a class of function of $C^6$. □

Remark 2.

Note that P is a 2D implicit map written in terms of the variables’ energy and time when the ball leaves the moving capsule ends, which usually give rise to the main difficulties for analytical investigation.

Lemma 3.

There exists a constant sufficiently large constant $v^{*}>0$ and $t\in \mathbb{R}$ such that the Poincaré map P is an area-preserving map in the nondissipative case, i.e., the elastic restitution coefficient $e=1$.

Proof. 

When $r=1$, by Lemma 1, the Poincaré map P is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle t^{\prime }=t+\frac{L+(p\left(\tilde{t}\right)-p\left(t\right))}{v}+\frac{-L+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right))}{\tilde{v}}+\mathcal{K}(g,\beta ),}\hfill \\ {\displaystyle v^{\prime }=v+\frac{gsin\beta }{2}(t^{\prime }-2\tilde{t}+t)-2\dot{p}\left(\tilde{t}\right)+2\dot{p}\left(t^{\prime }\right).}\hfill \end{array}\right.\end{array}$$

(17)

Let $X=p\left(t\right)$, $H(X,v)=v^2/2+Xgsin\beta$, $X_2=p\left(t_1\right)+L=p\left(t_2\right)+L$, $X_3=X_4=p\left(t_3\right)=p\left(t_4\right)$. For the maps $P_1$ and $P_3$, the integral invariant of Poincaré–Cartan (c.f. [23]) yields

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\oint }_{\mathsf{\Gamma }}vdX-H(X,v)dt={\oint }_{P_1\left(\mathsf{\Gamma }\right)}{v}_{1}d{X}_1-H(X_1,v_1)d{t}_1,}\hfill \\ {\displaystyle {\oint }_{P_2\circ P_1\left(\mathsf{\Gamma }\right)}{v}_{2}d{X}_2-H(X_2,v_2)d{t}_2={\oint }_{P_3\circ P_2\circ P_1\left(\mathsf{\Gamma }\right)}{v}_{3}d{X}_3-H(X_3,v_3)d{t}_3,}\hfill \end{array}\end{array}$$

(18)

where $\mathsf{\Gamma }=\{(t,\mu \left(t\right)):t\in \mathbb{R},\mu \left(t\right)>v^{*}\}$ is any a $C^1$ Jordan curve in the definition region P.

Set $dX=\dot{p}\left(t\right)dt$, $d{X}_1=d{X}_2=\dot{p}\left(t_1\right)d{t}_1=\dot{p}\left(t_2\right)d{t}_2$, $d{X}_3=\dot{p}\left(t_3\right)d{t}_3$. This transforms Equation (18) to

$$\begin{array}{c}\hfill \begin{array}{c}{\oint }_{\mathsf{\Gamma }}(v\dot{p}\left(t\right)dt-\frac{v^2}{2}-p\left(t\right)Xgsin\beta )dt={\oint }_{P_1\left(\mathsf{\Gamma }\right)}(v_1\dot{p}\left(t_1\right)d{t}_1-\frac{v_1^2}{2}-p\left(t_1\right)X_{1}gsin\beta )d{t}_1,\hfill \\ {\oint }_{P_2\circ P_1\left(\mathsf{\Gamma }\right)}(v_2\dot{p}\left(t_2\right)d{t}_2-\frac{v_2^2}{2}-p\left(t_2\right)X_{2}gsin\beta )d{t}_2={\oint }_{P_3\circ P_2\circ P_1\left(\mathsf{\Gamma }\right)}(v_3\dot{p}\left(t_3\right)d{t}_3-\frac{v_3^2}{2}-p\left(t_1\right)X_{3}gsin\beta )d{t}_3.\hfill \end{array}\end{array}$$

(19)

Taking into account both (7) and (8), we obtain

$$\begin{array}{c}\hfill \begin{array}{c}{\oint }_{P_1\left(\mathsf{\Gamma }\right)}(v_1\dot{p}\left(t_1\right)d{t}_1-\frac{v_1^2}{2}-p\left(t_1\right)X_{1}gsin\beta )d{t}_1={\oint }_{P_2\circ P_1\left(\mathsf{\Gamma }\right)}(v_2\dot{p}\left(t_2\right)d{t}_2-\frac{v_2^2}{2}-p\left(t_2\right)X_{2}gsin\beta )d{t}_2,\hfill \\ {\oint }_{P_3\circ P_2\circ P_1\left(\mathsf{\Gamma }\right)}(v_3\dot{p}\left(t_3\right)d{t}_3-\frac{v_3^2}{2}-p\left(t_1\right)X_{3}gsin\beta )d{t}_3={\oint }_{P\left(\mathsf{\Gamma }\right)}(v^{\prime }\dot{p}\left(t^{\prime }\right)d{t}^{\prime }-\frac{v^{\prime 2}}{2}-p\left(t^{\prime }\right)X^{\prime }gsin\beta )d{t}^{\prime }.\hfill \end{array}\end{array}$$

(20)

From (19) and (20), we get

$$\begin{array}{c}\hfill {\oint }_{\mathsf{\Gamma }}(v\dot{p}\left(t\right)-\frac{v^2}{2}-p\left(t\right)gsin\beta )dt={\oint }_{P\left(\mathsf{\Gamma }\right)}(v^{\prime }\dot{p}\left(t^{\prime }\right)-\frac{v^{\prime 2}}{2}-p\left(t^{\prime }\right)gsin\beta )d{t}^{\prime }.\end{array}$$

(21)

It is obvious that the curves $\mathsf{\Gamma }$ and $P\left(\mathsf{\Gamma }\right)$ either intersect or one of them goes around the other. Suppose that the later case occurs and let $\mathcal{R}$ denote the domain that is bounded by $\mathsf{\Gamma }$ and $P\left(\mathsf{\Gamma }\right)$. When $v^{}$ is sufficiently large, by Green’s formula (c.f. [23]) and (21), we have ${\int \int }_{\mathcal{R}}(\dot{p}\left(t\right)-v)dtdv=0.$ In fact, when $v^{*}$ is sufficiently large, we also have ${\int \int }_{\mathcal{R}}(\dot{p}\left(t\right)-v)dtdv<0.$ This naturally leads to a contradiction; thus, the intersection of the curves $\mathsf{\Gamma }$ and $P\left(\mathsf{\Gamma }\right)$ is nonempty (called Moser’s intersection property) and the Poincarḿap P is an area-preserving map. □

3. The Existence of Invariant Curves

In this section, a proof of the existence of invariant curves for the system is given, based on Moser’s twist theorem in the nondissipative case. To illustrate the main results below, we first briefly review some of the definitions and results of Moser’s twist theorem investigations into area-preserving maps [23,24,25].

By [26], we know that an irrational number $\alpha$ is said to be a type of constant $\gamma$. If $\gamma$ is defined by

$$\begin{array}{c}\hfill \gamma =inf\left\{q^2|\alpha -\frac{p}{q}|:p,q\in \mathbb{Z},q\ge 1\right\}\end{array}$$

then it is strictly positive and $\gamma$ is called the Markoff constant of $\alpha$.

Lemma 4.

In choosing a 1D interval $[a,b]\subset [0,1]$ with $b-a\ge \epsilon >0$ on the real-number axial, there exists a constant type $\alpha \in [a,b]/\mathbb{Q}$ such that the corresponding Markoff constant satisfies $\frac{\epsilon }{16}\le \gamma \le \frac{\epsilon }{4}$.

Theorem 1.

(Moser’s twist theorem) Assume that the operator $\mathsf{\Phi }:\mathbb{R}\times [-1,1]\to \mathbb{R}\times \mathbb{R}$ is a diffeomorphism that belongs to a class of functions of $C^5$ and is a 1-periodic function with respect to the variable θ. Moreover, assume that the specific form of Φ is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\theta }^{\prime }=\theta +\alpha +\delta r+\delta \phi (\theta ,r),\hfill \\ r^{\prime }=r+\delta \varphi (\theta ,r),\hfill \end{array}\right.\end{array}$$

(22)

where $0<\delta <2$ and α is an irrational number of constant type with Markoff constant γ, thereby satisfying

$$\begin{array}{c}\hfill \gamma \le \delta \le b\gamma \end{array}$$

(23)

for some fixed b. We also assume that the operator Φ has Moser’s intersection property (see the proof of Lemma 2.3), i.e., for any parameterized $C^1$ Jordan curve $\mathsf{\Gamma }=\left\{\right(\theta ,\mu \left(\theta \right)):\theta \in \mathbb{R}\}$ located in region $\mathbb{R}\times [-1,1]$ that satisfies $\mathsf{\Gamma }\cap \mathsf{\Phi }\left(\mathsf{\Gamma }\right)\ne \varnothing$, there is a positive constant C that depends only on fixed b, such that if

$$\begin{array}{c}\hfill {\parallel \phi (\theta ,r)\parallel }_{C^5}+{\parallel \varphi (\theta ,r)\parallel }_{C^5}\le C,\end{array}$$

then there exists $\mu \in C^3\left({\mathbb{S}}^1\right)$ such that $\mathsf{\Gamma }=\{\theta ,\mu (\theta ):\theta \in \mathbb{R}\}$ is invariant under the action of operator Φ, and the rotation number of ${\mathsf{\Phi }|}_{\mathsf{\Gamma }}$ is α.

Remark 3.

The proofs of Lemma 3.1 and Theorem 3.1 were given in [26,27], respectively, so we do not repeat them. These theories were applied to the study of different dynamical systems, such as breathing circle billiard [28], piece-wise linear oscillator [29], and so on.

We are now ready to prove the main result of this paper, say

Theorem 2.

There exists a constant number $\kappa >0$ such that if the function p satisfies

$$\begin{array}{c}\hfill \left|\frac{d^{k}p\left(t\right)}{d{t}^k}\right|<\kappa ,\forall t\in \mathbb{R},k=0,1,\cdots ,6,\end{array}$$

then there exist curves $\mathsf{\Gamma }=\left\{\right(t,\mu \left(t\right)):t\in \mathbb{R}\}$ with $\mu \in C^3\left({\mathbb{S}}^1\right)$ that are invariant under the Poincaré map P, resulting in the energy of the ball always being bounded.

Proof. 

Let

$$\left\{\begin{array}{c}{\displaystyle \mathcal{F}(t,v)=\frac{-L+(p\left(t^{\prime }\right)-p\left(\tilde{t}\right))}{\tilde{v}}+\mathcal{K}(g,\beta ),}\hfill \\ {\displaystyle \mathcal{G}(t,v)=\frac{gsin\beta }{2}(t^{\prime }-2\tilde{t}+t)-2\dot{p}\left(\tilde{t}\right)+2\dot{p}\left(t^{\prime }\right).}\hfill \end{array}\right.$$

Then, by (17), the map P has the expansion

$$\left\{\begin{array}{c}{\displaystyle t^{\prime }=t+\frac{L+(p\left(\tilde{t}\right)-p\left(t\right))}{v}+\mathcal{F}(t,v),}\hfill \\ {\displaystyle v^{\prime }=v+\mathcal{G}(t,v).}\hfill \end{array}\right.$$

By Lemma 4, we get a sequence $\left\{{\alpha }_n\right\}$ of irrational numbers of constant type converging to 0, and this satisfies

$$\begin{array}{c}\hfill \frac{1}{2n}\le {\alpha }_n\le \frac{1}{n},\frac{1}{32n}\le M_n\le \frac{1}{8n}.\end{array}$$

Define ${\epsilon }_n$ by ${\alpha }_n=\frac{4(L+(p\left(\tilde{t}\right)-p\left(t\right)))}{n{\epsilon }_n}$ and consider transformation

$$\begin{array}{c}\hfill U_n:\left(\theta ,\frac{n{\epsilon }_n}{r+4}\right)\mapsto (t,v).\end{array}$$

The transformation $U_n$ maps the region $D=\left\{\right(\theta ,r):\theta \in \mathbb{R},r\in [-1,1\left]\right\}$ to the region $D_n=\{(t,v):t\in \mathbb{R},v\in [\frac{n{\epsilon }_n}{5},\frac{n{\epsilon }_n}{3}]\}$. Since $n{\epsilon }_n=\frac{4(L+(p\left(\tilde{t}\right)-p\left(t\right)))}{{\alpha }_n}$, the distance from the region $D_n$ to the line $v=0$ goes to infinity when $n\to \infty$. Let

$$P_n=U_n^{-1}\circ P\circ U_n:D\to {\mathbb{R}}^2.$$

We obtain

$$\begin{array}{c}\hfill P_n:\left\{\begin{array}{c}{\displaystyle {\theta }^{\prime }=\theta +{\alpha }_n+{\delta }_{n}r+{\delta }_n{\phi }_n({\theta }_n,r_n),}\hfill \\ {\displaystyle r^{\prime }=r+{\delta }_n{\varphi }_n({\theta }_n,r_n),}\hfill \end{array}\right.\end{array}$$

where ${\delta }_n=\frac{{\alpha }_n}{4},{\phi }_n({\theta }_n,r_n)=\frac{1}{{\delta }_n}\mathcal{F}\left(\theta ,\frac{n{\epsilon }_n}{r+4}\right),$ ${\varphi }_n({\theta }_n,r_n)=\mathcal{G}\left(\theta ,\frac{n{\epsilon }_n}{r+4}\right)\frac{{(r+4)}^2{(L+p\left(\tilde{t}\right)-p\left(t\right))}^{-1}}{1+\mathcal{G}\left(\theta ,\frac{n{\epsilon }_n}{r+4}\right)(r+4)n^{-1}{\epsilon }_n^{-1}}.$

Since the map P satisfies the Moser’s intersection property (see the proof of Lemma 3) and $P_n$ is homeomorphic to P, we can conclude that $P_n$ also satisfies Moser’s intersection property. Since (23) holds for $b=8$, then we can apply Theorem 1 as soon as both $\parallel \phi (\theta ,r)$ and ${\parallel }_{C^5},{\parallel \varphi (\theta ,r)\parallel }_{C^5}$ are sufficiently small. The case is held because we chose an n that is sufficiently large and assumed that ${\parallel p\parallel }_{C^6}$ is sufficiently small. Thus, by Theorem 1, $P_n$ has an invariant curve. We then obtain a curve ${\mathsf{\Gamma }}_n=\{(t,{\mu }_n\left(t\right)):t\in \mathbb{R}\}$ with ${\mu }_n\in C^3\left({\mathbb{S}}^1\right)$ via the transformation $U_n$, which is also invariant under the action of P. After passing to a subsequence ${\left\{{\mu }_n\right\}}_{n\ge 1}$, we assume that ${\mu }_n\left(t\right)\le {\mu }_{n+1}\left(t\right)$ and ${lim}_{n\to \infty }{\mu }_n\left(t\right)=\infty$ uniformly with respect to $t\in \mathbb{R}$. Define a region

$$\begin{array}{c}\hfill B_n=\{(t,v):t\in \mathbb{R},{\mu }_n\left(t\right)\le v\le {\mu }_{n+1}\left(t\right)\}\end{array}$$

for $n\ge 1$. The region $B_n$ is homomorphically mapped to its image by P, and the boundary of $B_n$ is invariant. Thus, $B_n$ must be invariant under the action of P. Let $v^{*}$ be a constant such that $\{(t,v):v\ge v^{*}\}\subset {\cup }_{n\ge 1}{B}_n$. When $v\ge v^{*}$, it follows that $(t,v)\in B_N$ for some $N\ge 1$. By invariance of $B_N$, the orbit $\left\{P^n(t,v)\right\}$ is completely contained in $B_N$. Therefore, we conclude that $\left\{P^n(t,v)\right\}$ is bounded, i.e., the energy of the ball is bounded. □

Remark 4.

According to Theorem 3.2, the existence of invariant curves also provides the stability results of the problem (3): if the initial condition of the system is on an invariant curve, then the future dynamical evolution will stay confined to that invariant curve forever; if the initial condition of the system lies between two invariant curves, the future dynamical evolution will stay bounded between them forever. Moreover, the existence of invariant curves also ensures that the kinetic energy of the ball is always bounded, and hence, the structure of VI-EH is not destroyed by the impact of the ball.

Remark 5.

The symmetry of the system is mainly reflected in two aspects: on the one hand, it refers to the geometric symmetry of the system; on the other hand, it refers to the symmetry of the dynamical behavior of the system. The geometric symmetry is obvious. If the DE materials covered in both ends of the cylinder capsule are different, that is, the restitution coefficients of the collisions are different, then the dynamic behavior of the system is asymmetric (see [30] for a similar analysis). If the restitution coefficients of the collisions are the same and $p\left(t\right)$ is chosen as a class of specific functions that satisfies $p(t+n/2)=-p\left(t\right)$ (n is odd integer), then the Poincaré map P of problem (3) has the property of symmetry, such that if Γ is an invariant curve of P, then $P\left(\mathsf{\Gamma }\right)$ is also an invariant curve of P (c.f. [31,32]).

Remark 6.

If $\beta =0$, then the cylindrical capsule moves along the horizontal direction, and Theorem 2 still holds in this case.

4. Numerical Simulations

In this section, we discuss the numerical simulations results obtained from the VI-EH system to further verify our theoretical results. We first discuss the dynamical behavior of the system in the nondissipative case, and then discuss the dissipative case.

Choose $p\left(t\right)=\zeta sint,\zeta =0.1$, $\beta =\pi /8$, $e=1,L=6$ m and v change from 50 m/s to 52 m/s. We find that the system exhibits regular dynamic behavior, mainly containing periodic points (Birkhoff type), invariant curves, and Aubry–Mather sets (the definition of Aubry–Mather sets can be found in [33]), see Figure 3. Moreover, the existence of invariant curves also ensures that the kinetic energy of the ball is always bounded. For the same parameter condition, i.e., only choosing $v=52$ m/s, e = 0.99, the dissipation introduced by the coefficient of restitution e destroys the regular dynamic behavior in the nondissipative case and generates a low-energy periodic point, see Figure 4.

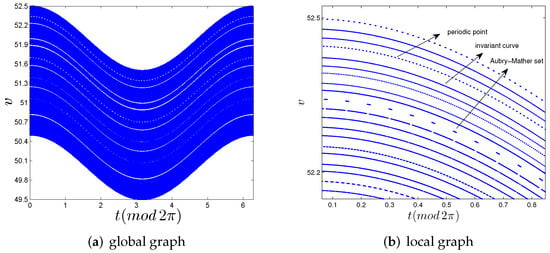
Figure 3. Regular dynamic behavior containing reriodic points, invariant curves, and Aubry–Mather sets.

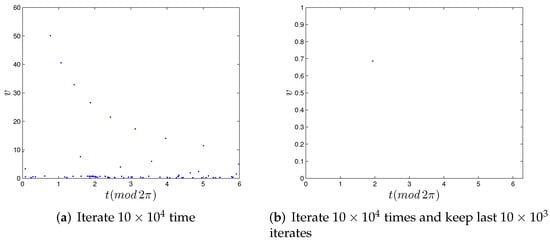
Figure 4. A low-energy periodic point.

5. Conclusions

In this work, we consider a two-sided vibro-impact energy harvester (VI-EH) system. Our main objective is to investigate whether the structure of the system will be destroyed by the impact of the ball. For this objective, we study the nondissipative and dissipative cases of the system, respectively. We show that the dynamics of the system are described by the use of a 2D implicit map, and the existence of invariant curves in the nondissipative case is proved by using Moser’s twist theorem. Thus, in nondissipative case, the kinetic energy of the ball is always bounded, and the structure of system is not destroyed by the impacts of the ball. Furthermore, by numerical analysis we also obtain that the dynamical behavior of this system is regular. After the introduction of dissipation, the dissipation destroys the regular dynamical behavior in the nondissipative case, and a periodic point with low energy appears. In summary, the structure of the system was not destroyed, and the theoretical analysis shows that this is mainly related to the smoothness of the system.