Bayes and Maximum Likelihood Estimation of Uncertainty Measure of the Inverse Weibull Distribution under Generalized Adaptive Progressive Hybrid Censoring

Abstract

The inverse Weibull distribution (IWD) can be applied to a various situations, including applications in reliability and medicine. In a reliability and medicine test, it is generally known that the results of test units may not be recorded. Recently, the generalized adaptive progressive hybrid censoring (GAPHC) scheme was introduced. In this paper, therefore, we consider the classical estimators (maximum likelihood estimator (MLE) and maximum product spacings estimator (MPSE)) and Bayes estimators (BayEsts) of the uncertainty measure of the IWD under GAPHC scheme. We derive the BayEsts of the uncertainty measure based on flexible (symmetrical and asymmetrical) priors. Additionally, we derive the Bayes estimators using the Tierney and Kadane approximation (TiKa) and importance sampling methods. In particular, the importance sampling method is used to obtain the credible interval for the uncertainty measure of the IWD under the GAPHC scheme. To compare the proposed estimators (classical and BayEsts), the Monte Carlo simulation method is conducted. Finally, the real dataset based on GAPHC scheme is analyzed.

1. Introduction

Entropy, which is one of the important terms in statistical mechanics, was originally defined in physics. Shannon [1] re-defined it and introduced the idea of entropy into information theory to quantify information uncertainty. Differential entropy is defined by Cover and Thomas [2] to be

$$\begin{array}{c}\hfill \mathbb{H}(\Theta )=-{\int }_{-\infty }^{\infty }f(x;\Theta )logf(x;\Theta )dx,\end{array}$$

where $f(x;\Theta )$ denotes a probability density function (pdf) of random variable X. Entropy measurement is a crucial concept in a variety of fields. More entropy indicates that there is less information in the sample.

The estimation of entropy has been studied by many researchers. Cho et al. [3] provided the estimators of entropy of a Rayleigh distribution under doubly generalized hybrid censoring. Cho et al. [4] provided the classical and BayEsts of entropy of a Weibull distribution (WD) under generalized progressive hybrid censoring (GPHC). Recently, Attoui et al. [5] provided the Bayes premium estimators for a mixture of two gamma distributions under squared error (SELF), entropy (GELF), and Linex (LLF) loss functions. Xu and Gui [6] provided the classical and BayEsts of entropy of a IWD under adaptive progressive hybrid censoring (APHC). Yu et al. [7] provided the classical and BayEsts of entropy of a IWD under progressive first-failure censoring. Shi et al. [8] provided the estimator for entropy of generalized Bilal distribution under APHC. Shrahili et al. [9] provided the estimator for the entropy of log-logistic distribution under progressive censoring (PrC).

The IWD can be readily applied to a wide range of situations, including applications in reliability and medicine [10,11,12,13,14]. The cumulative distribution function (cdf) and pdf of IWD are given by

$$\begin{array}{c}\hfill F(x;\Theta )=exp\left(-{\theta }_2{x}^{-{\theta }_1}\right),x>0,{\theta }_1>0,{\theta }_2>0,\end{array}$$

(1)

and

$$\begin{array}{c}\hfill f(x;\Theta )={\theta }_1{\theta }_2{x}^{-({\theta }_1+1)}exp\left(-{\theta }_2{x}^{-{\theta }_1}\right),x>0,{\theta }_1>0,{\theta }_2>0,\end{array}$$

(2)

where $\Theta =({\theta }_1,{\theta }_2)$, ${\theta }_1$ and ${\theta }_2$ are the scale and shape parameters, respectively. Note that when ${\theta }_1=1$, we have the Frechet distribution. Additionally, when ${\theta }_2=1$ and ${\theta }_2=2$, the IWDs are referred to as the inverse exponential and inverse Raleigh distribution, respectively [15,16]. Then, the differential entropy of X is given by

$$\begin{array}{c}\hfill \mathbb{H}(\Theta )=E[-logf(x;\Theta )]=-{\int }_0^{\infty }f(x;\Theta )logf(x;\Theta )dx=-{\theta }_1{\theta }_2[A_1+A_2+A_3],\end{array}$$

where $A_1$, $A_2$ and $A_3$ are obtained below:

$$\begin{array}{cc}\hfill A_1& ={\int }_0^{\infty }log\left({\theta }_1{\theta }_2\right)x^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}^{-{\theta }_1}}dx=\frac{log\left({\theta }_1{\theta }_2\right)}{{\theta }_1{\theta }_2},\hfill \\ \hfill A_2& =-({\theta }_1+1){\int }_0^{\infty }log\left(x\right)x^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}^{-{\theta }_1}}dx\hfill \\ \hfill & =\frac{{\theta }_1+1}{{\theta }_1^2}{\int }_0^{\infty }log\left(u_1\right)e^{-{\theta }_2{u}_1}d{u}_1=-\frac{{\theta }_1+1}{{\theta }_1^2{\theta }_2}\left(\gamma +log{\theta }_2\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill A_3& =-{\theta }_2{\int }_0^{\infty }{x}^{-2{\theta }_1-1}{e}^{-{\theta }_2{x}^{-{\theta }_1}}dx\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =-\frac{{\theta }_2}{{\theta }_1}{\int }_0^{\infty }{u}_1{e}^{-{\theta }_2{u}_1}d{u}_1=-\frac{1}{{\theta }_1{\theta }_2},\hfill \end{array}$$

where $\gamma$ is the Euler–Mascheroni constant. Finally, entropy reduces to

$$\begin{array}{c}\hfill \mathbb{H}(\Theta )=1+\left(1+\frac{1}{{\theta }_1}\right)\left(\gamma +log{\theta }_2\right)-log\left({\theta }_1{\theta }_2\right).\end{array}$$

(3)

On the other hand, in a life-testing and reliability test, it is generally known that the lifetimes of test units may not be recorded. Additionally, there are situations wherein the withdrawal of units prior to failure is pre-arranged in order to reduce the cost or time. This case is called a typical censoring scheme. However, one of the drawbacks of a typical censoring scheme is that it does not allow units to be removed from the test at a point other than the end point of the test. For this reason, reliability theoreticians considered the progressive censoring (PC) scheme [17]. Consider a life-testing experiment in which n identical units are put to the test. In the PC scheme, if the 1st failure is observed ($X_{1:m:n}$), the ${\Re }_1$ survival units are removed randomly from the test. Furthermore, if the 2nd failure is observed ($X_{2:m:n}$), the ${\Re }_2$ survival units are removed randomly from the test. Finally, if the m-th failure is observed ($X_{m:m:n}$), all the survival units (${\Re }_m=n-{\Re }_1-\cdots -{\Re }_{m-1}-m$) are removed from the test. In this test, the PC scheme $𝕽=\left({\Re }_1,{\Re }_2,\cdots ,{\Re }_m\right)$ and $m\in \{1,2,\cdots ,n\}$ are pre-fixed integers satisfying ${\sum }_{i=1}^m{\Re }_i+m=n$. The m-ordered time of observed failure ($X_{1:m:n},X_{2:m:n},\cdots ,X_{m:m:n}$) is called the PC data.

However, the time of test under the PC scheme can be long. Hence, Ng et al. [18] suggest an adaptive progressive hybrid censoring (APHC) scheme. In the APHC scheme, the PC scheme is pre-assigned, but the values of some of the ${\Re }_i$ may change accordingly during the test. Suppose the experimenter provides a pre-assigned ideal total time on test ($\mathcal{T}$). If the $X_{m:m:n}$ occurs before pre-assigned time $\mathcal{T}$, the test stops at the $X_{m:m:n}$. Otherwise, once the test time passes the pre-assigned time $\mathcal{T}$ but the number of failures has not reached m, the experimenter would want to terminate the test as soon as possible (assume that we still allow the experiment to run over time $\mathcal{T}$). After the test passed pre-assigned time $\mathcal{T}$, therefore, Ng et al. [18] set ${\Re }_{\mathcal{D}+1}=\cdots ={\Re }_{m-1}=0$ and ${\Re }_m=n-{\sum }_{i=1}^{\mathcal{D}}{\Re }_i-m$.

However, the time of the test under APHCS also can be long. For this reason, Lee and Lee [19] suggested a GAPHC scheme in which the test is assured to end at a pre-assigned time. The GAPHC scheme can be explained as follows. Let ${\mathcal{T}}_1,{\mathcal{T}}_2({\mathcal{T}}_1<{\mathcal{T}}_2<\infty )$ be a pre-fixed time point. Additionally, let ${\mathcal{D}}_i$ represent the number of failures up to the pre-assigned times ${\mathcal{T}}_i$. Likewise, let $d_i$ be the observed value of ${\mathcal{D}}_i$. If $X_{m:m:n}<{\mathcal{T}}_1$, terminate the test at $X_{m:m:n}$ (Case I). If ${\mathcal{T}}_1<X_{m:m:n}<{\mathcal{T}}_2$, then instead of terminating the test by removing all the survival units at ${\mathcal{T}}_1$, continue to observe failures, without any removals (${\Re }_{d_1+1}=\cdots ={\Re }_{m-1}=0$), up to time m-th failure (Case II). If ${\mathcal{T}}_2<X_{m:m:n}$, terminate the test at ${\mathcal{T}}_2$ (Case III). This GAPHC scheme modifies the APHC scheme by guaranteeing that the test will be completed by time ${\mathcal{T}}_2$. In the GAPHC scheme (Figure 1), there are Cases I, II and III as follows:

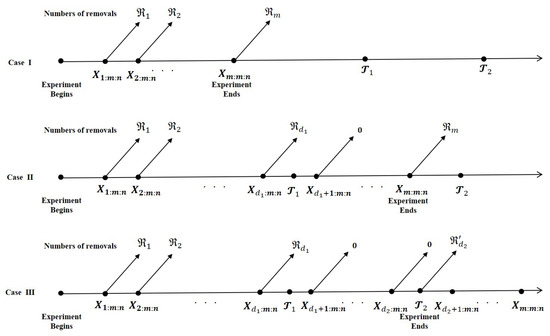
Figure 1. A schematic representation of GAPHC scheme.

CasesI: 

$\{X_{1:m:n},X_{2:m:n},\cdots ,X_{m:m:n}\}$, if $X_{m:m:n}<{\mathcal{T}}_1$.

CasesII: 

$\{X_{1:m:n},X_{2:m:n},\cdots ,X_{d_1:m:n},\cdots ,X_{m:m:n}\}$, if ${\mathcal{T}}_1<X_{m:m:n}<{\mathcal{T}}_2,{\Re }_{d_1+1}=\cdots ={\Re }_{m-1}=0$.

CasesIII: 

$\{X_{1:m:n},X_{2:m:n},\cdots ,X_{d_1:m:n},\cdots ,X_{d_2:m:n}\}$, if $X_{m:m:n}>{\mathcal{T}}_2,{\Re }_{d_1+1}=\cdots ={\Re }_{d_2-1}=0$.

Here, $X_{d_1:m:n}<{\mathcal{T}}_1<X_{d_1+1:m:n}$ and $X_{d_2:m:n}<{\mathcal{T}}_2<X_{d_2+1:m:n}$. A schematic representation of the GAPHC scheme is presented in Figure 1.

Therefore, the aim of this paper is to propose the classical and BayEsts of the entropy of a IWD under GAPHC scheme. However, we observed that the classical estimators of the entropy cannot be derived in closed form. Therefore, we have to obtain them by solving non-linear equations simultaneously. Further, we derive the BayEsts of the entropy based on various priors—SELF, GELF and LLF are derived. However, we observe that the BayEsts cannot be derived in closed form, and we propose the Tierney and Kadane approximate method and importance sampling procedure of the BayEsts. Moreover, the importance sampling procedure is used to obtain the HPD credible interval for the entropy of a IWD under the GAPHC scheme.

In Section 2, Section 3 and Section 4, we derive the classical and BayEsts of the entropy of IWD based on the GAPHC scheme. To compare the proposed estimators (classical and BayEsts), the Monte Carlo simulation method is conducted in Section 5. Finally, a real dataset based on GAPHC scheme is analyzed.

2. Maximum Likelihood Estimation

2.1. Maximum Likelihood Estimator

This section deals with deriving MLE of the unknown parameters of a IWD. As a consequence, MLEs of entropy will also be obtained. Using Lee and Lee [19], the likelihood functions of $\Theta =({\theta }_1$, ${\theta }_2$) under the GAPHC scheme are given by

$$\begin{array}{c}\hfill \mathbb{L}(\Theta )=\left\{\begin{array}{c}\left[\prod _{j=1}^m\sum _{k=j}^m\left({\Re }_k+1\right)\right]\prod _{j=1}^{m}f\left(x_{j:m:n}\right){\left[1-\mathcal{F}\left(x_{j:m:n}\right)\right]}^{{\Re }_j},\hfill \\ \hfill & \\ \left[\prod _{j=1}^m\sum _{k=j}^m\left({\Re }_k+1\right)\right]\prod _{j=1}^{m}f\left(x_{j:m:n}\right)\prod _{j=1}^{d_1}{\left[1-\mathcal{F}\left(x_{j:m:n}\right)\right]}^{{\Re }_j}{\left[1-\mathcal{F}\left(x_{m:m:n}\right)\right]}^{{\Re }_m},\hfill \\ \hfill & \\ \left[\prod _{j=1}^{d_2}\sum _{k=j}^m\left({\Re }_k+1\right)\right]\prod _{j=1}^{d_2}f\left(x_{j:m:n}\right)\prod _{j=d_1+1}^{d_2}{\left[1-\mathcal{F}\left(x_{j:m:n}\right)\right]}^{{\Re }_j}{\left[1-\mathcal{F}\left({\mathcal{T}}_2\right)\right]}^{{\Re }_{d_2}^{\prime }},\hfill \end{array}\right.\end{array}$$

(4)

where ${\Re }_{d_2}^{\prime }=n-{\sum }_{i=1}^{d_1}{\Re }_i-d_2$. Utilizing Equations (1), (2) and (4), the likelihood function of ${\theta }_1$ and ${\theta }_2$ under GAPHC are given by

$$\begin{array}{c}\hfill \mathbb{L}(\Theta )=\left\{\begin{array}{c}\left[\prod _{j=1}^m\sum _{k=j}^m\left({\Re }_k+1\right)\right]{\left({\theta }_1{\theta }_2\right)}^m\prod _{i=1}^m{x}_{i:m:n}^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i},\hfill \\ \hfill & \\ \left[\prod _{j=1}^m\sum _{k=j}^m\left({\Re }_k+1\right)\right]{\left({\theta }_1{\theta }_2\right)}^m\prod _{i=1}^m{x}_{i:m:n}^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\prod _{i=1}^{d_1}{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\hfill \\ \times {\left[1-e^{-{\theta }_2{x}_{m:m:n}^{-{\theta }_1}}\right]}^{{\Re }_m},\hfill \\ \hfill & \\ \left[\prod _{j=1}^{d_2}\sum _{k=j}^m\left({\Re }_k+1\right)\right]{\left({\theta }_1{\theta }_2\right)}^{d_2}\prod _{i=1}^{d_2}{x}_{i:m:n}^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\prod _{i=d_1+1}^{d_2}{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\hfill \\ \times {\left[1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right]}^{R_{d_2}^{\prime }}.\hfill \end{array}\right.\end{array}$$

Therefore, the above equations can be combined as

$$\begin{array}{c}\hfill \mathbb{L}(\Theta )=\left[\prod _{j=1}^{\tau }\sum _{k=j}^m\left({\Re }_k+1\right)\right]{\left({\theta }_1{\theta }_2\right)}^{\tau }\prod _{i=1}^{\tau }{x}_{i:m:n}^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\zeta (\Theta ;{\mathcal{T}}_2),\end{array}$$

(5)

where $\tau =m$ and $\zeta (\Theta ;{\mathcal{T}}_2)=1$ for Case I, $\tau =m$, $\zeta (\Theta ;{\mathcal{T}}_2)=1$ and ${\Re }_{d_1+1}=\cdots ={\Re }_{m-1}=0$ for Case II, $\tau =d_2$, ${\Re }_{d_1+1}=\cdots ={\Re }_{d_2}=0$ and $\zeta (\Theta ;{\mathcal{T}}_2)={[1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}]}^{{\Re }_{d_2}^{\prime }}$ for Case III. Hence, the log-likelihood function becomes

$$\begin{array}{cc}\hfill \mathcal{L}(\Theta )\propto & \tau log{\theta }_1{\theta }_2-({\theta }_1+1)\sum _{i=1}^{\tau }log{x}_{i:m:n}-{\theta }_2\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}+\sum _{i=1}^{\tau }{\Re }_{i}log\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]\hfill \\ \hfill & +log\zeta (\Theta ;{\mathcal{T}}_2).\hfill \end{array}$$

(6)

On differentiating Equation (5) with respect to ${\theta }_1$ and ${\theta }_2$ and then equating to zero, we have

$$\begin{array}{cc}\hfill \frac{\partial \mathcal{L}(\Theta )}{\partial {\theta }_1}=& \frac{\tau }{{\theta }_1}+\sum _{i=1}^{\tau }\left[{\theta }_2{x}_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}-log{x}_{i:m:n}-{\Re }_i\frac{x_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}\right]\hfill \\ \hfill & +{\zeta }_{{\theta }_1}^1(\Theta ;{\mathcal{T}}_2)=0,\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill 1-1\frac{\partial \mathcal{L}(\Theta )}{\partial {\theta }_2}=& \frac{\tau }{{\theta }_2}-\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}+\sum _{i=1}^{\tau }{\Re }_i\frac{x_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}+{\zeta }_{{\theta }_2}^1(\Theta ;{\mathcal{T}}_2)=0.\hfill \end{array}$$

(8)

Here, for Case III,

$$\begin{array}{cc}\hfill {\zeta }_{{\theta }_1}^1(\Theta ;{\mathcal{T}}_2)& =-{\Re }_{d_2}^{\prime }\frac{{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}log{\mathcal{T}}_2{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}}{1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}}\mathrm{and}{\zeta }_{{\theta }_2}^1(\Theta ;{\mathcal{T}}_2)={\Re }_{d_2}^{\prime }\frac{{\mathcal{T}}_2^{-{\theta }_1}{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}}{1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}},\hfill \end{array}$$

for Cases I and II,

$$\begin{array}{cc}\hfill {\zeta }_{{\theta }_1}^1(\Theta ;{\mathcal{T}}_2)& ={\zeta }_{{\theta }_2}^1(\Theta ;{\mathcal{T}}_2)=0.\hfill \end{array}$$

The MLEs of $\Theta =({\theta }_1,{\theta }_2)$ are the solution of Equations (7) and (8). Therefore, we propose to use the Newton–Raphson algorithm to solve it. Using the MLEs of $\Theta =({\theta }_1,{\theta }_2)$, say $\widehat{\Theta }=({\widehat{\theta }}_1,{\widehat{\theta }}_2)$, the MLE of entropy function is obtained as

$$\begin{array}{c}\hfill \widehat{\mathbb{H}}=1+\left(1+\frac{1}{{\widehat{\theta }}_1}\right)\left(\gamma +log{\widehat{\theta }}_2\right)-log\left({\widehat{\theta }}_1{\widehat{\theta }}_2\right).\end{array}$$

2.2. Approximate Confidence Interval

In this subsection, we obtain the $100(1-\alpha )\%$ approximate CI of the entropy. By using Equations (7) and (8), the second derivatives of Equation (5) with respect to ${\theta }_1$ and ${\theta }_2$ are given by

$$\begin{array}{cc}\hfill {\mathcal{L}}_{20}=\frac{{\partial }^2\mathcal{L}(\Theta )}{\partial {\theta }_1^2}=& -\frac{\tau }{{\theta }_1^2}-{\theta }_2\sum _{i=1}^{\tau }[{\Re }_i{x}_{i:m:n}^{-{\theta }_1}{\left(log{x}_{i:m:n}\right)}^2{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\frac{{\theta }_2{x}_{i:m:n}^{-{\theta }_1}+e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-1}{{\left(1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right)}^2}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +x_{i:m:n}^{-{\theta }_1}{\left(log{x}_{i:m:n}\right)}^2]+{\zeta }_{{\theta }_1}^2(\Theta ;{\mathcal{T}}_2),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{02}=\frac{{\partial }^2\mathcal{L}(\Theta )}{\partial {\theta }_2^2}=& -\frac{\tau }{{\theta }_2^2}-\sum _{i=1}^{\tau }{\Re }_i\frac{x_{i:m:n}^{-2{\theta }_1}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{{\left(1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right)}^2}+{\zeta }_{{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)\hfill \end{array}$$

(10)

and

$$\begin{array}{cc}\hfill {\mathcal{L}}_{11}=\frac{{\partial }^2\mathcal{L}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}=& \sum _{i=1}^{\tau }{\Re }_i{x}_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\frac{{\theta }_2{x}_{i:m:n}^{-{\theta }_1}+e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-1}{{\left(1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right)}^2}\hfill \\ \hfill & +\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}+{\zeta }_{{\theta }_1{\theta }_2}^2(\Theta ;{\mathcal{T}}_2).\hfill \end{array}$$

(11)

Here, for Case III,

$$\begin{array}{cc}\hfill {\zeta }_{{\theta }_1}^2(\Theta ;{\mathcal{T}}_2)& =-{\theta }_2{\Re }_{d_2}^{*}{\mathcal{T}}_2^{-{\theta }_1}{\left(log{\mathcal{T}}_2\right)}^2{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\frac{{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}+e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}-1}{{\left[1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right]}^2},\hfill \\ \hfill {\zeta }_{{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)& =-{\Re }_{d_2}^{*}\frac{{\mathcal{T}}_2^{-2{\theta }_1}{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}}{{\left(1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right)}^2},\hfill \\ \hfill {\zeta }_{{\theta }_1{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)& ={\Re }_{d_2}^{*}{\mathcal{T}}_2^{-{\theta }_1}log{\mathcal{T}}_2{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\frac{{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}+e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}-1}{{\left[1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right]}^2},\hfill \end{array}$$

for Case I and Case II,

$$\begin{array}{cc}\hfill {\zeta }_{{\theta }_1}^2(\Theta ;{\mathcal{T}}_2)& ={\zeta }_{{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)={\zeta }_{{\theta }_1{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)=0.\hfill \end{array}$$

Let $I\left(\Theta \right)$ denote the Fisher information matrix of the $\Theta =({\theta }_1,{\theta }_2)$. Under some mild regularity conditions, $\widehat{\Theta }=({\widehat{\theta }}_1,{\widehat{\theta }}_2)$ is approximately bivariately normal with mean $\Theta$ and covariance matrix $I^{-1}(\Theta )$. In practice, we usually estimate $I^{-1}(\Theta )$ by $I^{-1}\left(\widehat{\Theta }\right)$. A simpler and equally valid procedure is to use the approximation

$$\begin{array}{c}\hfill \widehat{\Theta }\sim N\left(\Theta ,I^{-1}\left(\widehat{\Theta }\right)\right),\end{array}$$

where

$$\begin{array}{c}\hfill I^{-1}\left(\widehat{\Theta }\right)={\left(\begin{array}{cc}-{\mathcal{L}}_{20}& -{\mathcal{L}}_{11}\\ -{\mathcal{L}}_{11}& -{\mathcal{L}}_{02}\end{array}\right)}_{\Theta =\widehat{\Theta }}^{-1}.\end{array}$$

(12)

In order to find the approximate estimate of the variance of entropy, we use the delta method. Let

$$\begin{array}{c}\hfill {\Psi }^{\prime }=\left(\frac{\partial \mathbb{H}}{\partial {\theta }_1},\frac{\partial \mathbb{H}}{\partial {\theta }_2}\right),\end{array}$$

where

$$\begin{array}{c}\hfill \frac{\partial \mathbb{H}}{\partial {\theta }_1}=-\frac{1}{{\theta }_1^2}({\theta }_1+\gamma +log{\theta }_2),\frac{\partial \mathbb{H}}{\partial {\theta }_2}=\frac{1}{{\theta }_1{\theta }_2}.\end{array}$$

Then, the approximate estimate of variance of entropy is given by

$$\widehat{var}\left(\widehat{\mathbb{H}}\right)=[{\Psi }^{\prime }{I}^{-1}\left(\widehat{\Theta }\right)\Psi ]$$

Thus, asymptotically,

$$\frac{\widehat{\mathbb{H}}-\mathbb{H}}{\sqrt{\widehat{var}\left(\widehat{\mathbb{H}}\right)}}\sim N(0,1).$$

These results yield the $100(1-\alpha )$% approximate CIs for entropy given by

$$\begin{array}{c}\hfill \left(\widehat{\mathbb{H}}-Z_{\alpha /2}\sqrt{\widehat{var}\left(\widehat{\mathbb{H}}\right)},\widehat{\mathbb{H}}+Z_{\alpha /2}\sqrt{\widehat{var}\left(\widehat{\mathbb{H}}\right)}\right),\end{array}$$

where $Z_{\alpha /2}$ is the percentile of the standard normal distribution with right-tail probability $\alpha /2$.

3. Maximum Product Spacings Estimation

The limitation of MLE is that it cannot work for heavy tailed distribution. Additionally, it creates problem in mixture of distributions. In order to overcome these problems, Cheng and Amin [20] introduced the MPSE as an alternative to MLE. Cheng and Amin [20] proposed to replace the likelihood function by the product of spacings (PSs) and insisted that it preserves the properties of the MLE.

For GAPHC samples, the PS to be maximized is

$$\begin{array}{c}\hfill \mathbb{S}(\Theta )\propto \prod _{i=1}^{\tau +1}[\mathcal{F}\left(x_{i:m:n}\right)-\mathcal{F}\left(x_{i-1:m:n}\right)]\prod _{i=1}^{\tau }{[1-\mathcal{F}\left(x_{i:m:n}\right)]}^{{\Re }_i}\zeta (\Theta ;{\mathcal{T}}_2),\end{array}$$

(13)

where $\mathcal{F}\left(x_{0:m:n}\right)\equiv 0$, $\mathcal{F}\left(x_{\tau +1:m:n}\right)\equiv 1$. Then, taking the logarithm of $\mathbb{S}(\Theta )$, we obtain

$$\begin{array}{cc}\hfill \mathcal{S}(\Theta )\propto & -{\theta }_2{x}_{1:m:n}^{-{\theta }_1}+\sum _{i=2}^{\tau }log\left[e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-e^{-{\theta }_2{x}_{i-1:m:n}^{-{\theta }_1}}\right]+log[1-e^{-{\theta }_2{x}_{\tau :m:n}^{-{\theta }_1}}]\hfill \\ \hfill & +\sum _{i=1}^{\tau }{\Re }_{i}log\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]+log\zeta (\Theta ;{\mathcal{T}}_2).\hfill \end{array}$$

After differentiating the above equation with respect to parameters and then equating it to zero, we have

$$\begin{array}{cc}\hfill \frac{\partial \mathcal{S}(\Theta )}{\partial {\theta }_1}=& -{\theta }_2{x}_{1:m:n}^{-{\theta }_1}log{x}_{1:m:n}-\frac{{\theta }_2{x}_{\tau :m:n}^{-{\theta }_1}log{x}_{\tau :m:n}{e}^{-{\theta }_2{x}_{\tau :m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{\tau :m:n}^{-{\theta }_1}}}\hfill \\ \hfill & +{\theta }_2\sum _{i=2}^{\tau }\frac{x_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-x_{i-1:m:n}^{-{\theta }_1}log{x}_{i-1:m:n}{e}^{-{\theta }_2{x}_{i-1:m:n}^{-{\theta }_1}}}{e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-e^{-{\theta }_2{x}_{i-1:m:n}^{-{\theta }_1}}}\hfill \\ \hfill & -\sum _{i=1}^{\tau }{\Re }_i\frac{{\theta }_2{x}_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}+{\zeta }_{{\theta }_1}^1(\Theta ;{\mathcal{T}}_2)=0\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill \frac{\partial \mathcal{S}(\Theta )}{\partial {\theta }_2}=& -x_{1:m:n}^{-{\theta }_1}-\sum _{i=2}^{\tau }\frac{x_{i:m:n}^{-{\theta }_1}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-x_{i-1:m:n}^{-{\theta }_1}{e}^{-{\theta }_2{x}_{i-1:m:n}^{-{\theta }_1}}}{e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-e^{-{\theta }_2{x}_{i-1:m:n}^{-{\theta }_1}}}+\frac{x_{\tau :m:n}^{-{\theta }_1}{e}^{-{\theta }_2{x}_{\tau :m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{\tau :m:n}^{-{\theta }_1}}}\hfill \\ \hfill & +\sum _{i=1}^{\tau }{\Re }_i\frac{x_{i:m:n}^{-{\theta }_1}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}+{\zeta }_{{\theta }_2}^1(\Theta ;{\mathcal{T}}_2)=0.\hfill \end{array}$$

(15)

The MPSEs of $\Theta$ are the solution of Equations (14) and (15). Therefore, we propose to use the Newton–Raphson algorithm to solve it. Using the MPSEs of $\Theta$, say ${\widehat{\Theta }}_P=({\widehat{{\theta }_1}}_P,{\widehat{{\theta }_2}}_P)$, the MPSE of entropy function is obtained as

$$\begin{array}{c}\hfill {\widehat{\mathbb{H}}}_P=1+\left(1+\frac{1}{{\widehat{{\theta }_1}}_P}\right)\left(\gamma +log{\widehat{{\theta }_2}}_P\right)-log\left({\widehat{{\theta }_1}}_P{\widehat{{\theta }_2}}_P\right).\end{array}$$

4. Bayes Estimation

In this section, we obtain the BayEsts for the entropy of the IWD under GAPHC scheme. We obtain the BayEst under three different loss functions—SELF, GELF and LLF. Additionally, we assume that priors of $\Theta =({\theta }_1,{\theta }_2)$ are independent, and the $\Theta$ follow the gamma prior distributions (${\theta }_1\sim$ GAM$(a_1,b_1)$ and ${\theta }_2\sim$ GAM$(a_2,b_2)$). Therefore, the joint prior distribution of $\Theta$ is obtained as

$$\begin{array}{c}\hfill \pi (\Theta )\propto {\theta }_1^{a_1-1}{\theta }_2^{a_2-1}{e}^{-b_1{\theta }_1-b_2{\theta }_2},{\theta }_1>0,{\theta }_2>0.\end{array}$$

Then, the joint posterior distribution of the $\Theta$ given the $\mathit{X}$ is obtained

$$\begin{array}{cc}\hfill \pi \left(\Theta |\mathit{X}\right)\propto & {\theta }_1^{\tau +a_1-1}{\theta }_2^{\tau +a_2-1}\prod _{i=1}^{\tau }{x}_{i:m:n}^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}-b_1{\theta }_1-b_2{\theta }_2}{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\zeta (\Theta ;{\mathcal{T}}_2),\hfill \end{array}$$

(16)

where $\mathit{X}=\left(X_{1:m:n},X_{2:m:n},\cdots ,X_{\tau :m:n}\right)$. However, it is impossible to obtain the marginal posterior distribution of the entropy function. Therefore, we propose the use of TK approximation procedure and the importance sampling procedure to obtain the BayEsts of entropy function under three different loss functions.

4.1. Tierney and Kadane Approximation

For TiKa method, let g be a smooth, positive function on the parameter space (Tierney and Kadane [21]). The posterior expectation of $g(\Theta )$ is obtained as

$$\begin{array}{c}\hfill \widehat{g}=E\left(g(\Theta )\right|\mathit{X})=\int \int g(\Theta )\pi (\Theta |\mathit{X})d{\theta }_{1}d{\theta }_2=\frac{\int \int e^{n{\kappa }^{*}(\Theta )}d{\theta }_{1}d{\theta }_2}{\int \int e^{n\kappa (\Theta )}d{\theta }_{1}d{\theta }_2},\end{array}$$

where

$$\begin{array}{c}\hfill \kappa (\Theta )=\frac{log\mathbb{L}(\Theta )+log\pi (\Theta )}{n}\mathrm{and}{\kappa }^{*}(\Theta )=\kappa (\Theta )+\frac{logg(\Theta )}{n}.\end{array}$$

For the $\Theta =({\theta }_1,{\theta }_2)$, the BayEst using TiKa of $g(\Theta )$ can be obtained as

$$\begin{array}{c}\hfill \widehat{g}(\Theta )=\sqrt{\frac{|{\Sigma }^{*}|}{|\Sigma |}}{e}^{n{\kappa }^{*}({\widehat{\theta }}_1{}_{{\kappa }^{*}},{\widehat{\theta }}_2{}_{{\kappa }^{*}})-n\kappa ({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })},\end{array}$$

(17)

where $({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })$ and $({\widehat{\theta }}_1{}_{{\kappa }^{*}},{\widehat{\theta }}_2{}_{{\kappa }^{*}})$ maximize the $\kappa (\Theta )$ and ${\kappa }^{*}(\Theta )$, respectively. $|{\Sigma }^{*}|$ and $|\Sigma |$ denote the minus of inverse of Hessians of $\kappa (\Theta )$ and ${\kappa }^{*}(\Theta )$ at $({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })$ and $({\widehat{\theta }}_1{}_{{\kappa }^{*}},{\widehat{\theta }}_2{}_{{\kappa }^{*}})$, respectively. In our problem, we observe that

$$\begin{array}{cc}\hfill \kappa (\Theta )=& \frac{1}{n}\left[(\tau +a_1-1)log{\theta }_1+(\tau +a_2-1)log{\theta }_2-({\theta }_1+1)\sum _{i=1}^{\tau }log{x}_{i:m:n}-{\theta }_2\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}\right.\hfill \\ \hfill & \left.+\sum _{i=1}^{\tau }{\Re }_{i}log\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]+log\zeta (\Theta ;{\mathcal{T}}_2)-(b_1{\theta }_1+b_2{\theta }_2)\right].\hfill \end{array}$$

Then, $({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })$ is computed by solving the following equations:

$$\begin{array}{cc}\hfill \frac{\partial \kappa (\Theta )}{\partial {\theta }_1}=& -b_1+\frac{\tau +a_1-1}{{\theta }_1}-\sum _{i=1}^{\tau }log{x}_{i:m:n}+{\zeta }_{{\theta }_1}^1(\Theta ;{\mathcal{T}}_2)\hfill \\ \hfill & +{\theta }_2\sum _{i=1}^{\tau }\left[x_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}-{\Re }_i\frac{x_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}\right]=0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \frac{\partial \kappa (\Theta )}{\partial {\theta }_2}=& -b_2+\frac{\tau +a_2-1}{{\theta }_2}-\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}+\sum _{i=1}^{\tau }{\Re }_i\frac{x_{i:m:n}^{-{\theta }_1}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}+{\zeta }_{{\theta }_2}^1(\Theta ;{\mathcal{T}}_2)=0.\hfill \end{array}$$

Additionally, we compute $|\Sigma |$, and it is given by

$$\begin{array}{c}\hfill |\Sigma |={\left[\frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1^2}\frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_2^2}-\frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1\partial {\theta }_2}\frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_2\partial {\theta }_1}\right]}^{-1},\end{array}$$

where

$$\begin{array}{cc}\hfill \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1^2}=& \frac{1}{n}[-\frac{\tau +a_1-1}{{\theta }_1^2}-{\theta }_2\sum _{i=1}^{\tau }\{{\Re }_i{x}_{i:m:n}^{-{\theta }_1}{\left(log{x}_{i:m:n}\right)}^2{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\frac{{\theta }_2{x}_{i:m:n}^{-{\theta }_1}+e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-1}{{\left(1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right)}^2}\hfill \\ \hfill & +x_{i:m:n}^{-{\theta }_1}{\left(log{x}_{i:m:n}\right)}^2\}+{\zeta }_{{\theta }_1^2}^2(\Theta ;{\mathcal{T}}_2)],\hfill \\ \hfill \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_2^2}=& \frac{1}{n}[-\frac{\tau +a_2-1}{{\theta }_2^2}-\sum _{i=1}^{\tau }{\Re }_i\frac{x_{i:m:n}^{-2{\theta }_1}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}}{{\left(1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right)}^2}+{\zeta }_{{\theta }_2^2}^2(\Theta ;{\mathcal{T}}_2)]\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill 1-1\frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1\partial {\theta }_2}=& \frac{1}{n}[\sum _{i=1}^{\tau }{\Re }_i{x}_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\frac{{\theta }_2{x}_{i:m:n}^{-{\theta }_1}+e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}-1}{{\left(1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right)}^2}+\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}log{x}_{i:m:n}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\zeta }_{{\theta }_1{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)].\hfill \end{array}$$

Here, for Case III,

$$\begin{array}{cc}\hfill {\zeta }_{{\theta }_1^2}^2(\Theta ;{\mathcal{T}}_2)& =-{\theta }_2{\Re }_{d_2}^{\prime }{\mathcal{T}}_2^{-{\theta }_1}{\left(log{\mathcal{T}}_2\right)}^2{e}^{-{\theta }_2{T}^{-{\theta }_1}}\frac{{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}+e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}-1}{{\left[1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right]}^2},\hfill \\ \hfill {\zeta }_{{\theta }_2^2}^2(\Theta ;{\mathcal{T}}_2)& =-{\Re }_{d_2}^{\prime }\frac{{\mathcal{T}}_2^{-2{\theta }_1}{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}}{{\left(1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right)}^2},\hfill \\ \hfill {\zeta }_{{\theta }_1{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)& ={\Re }_{d_2}^{\prime }{\mathcal{T}}_2^{-{\theta }_1}log{\mathcal{T}}_2{e}^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\frac{{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}+e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}-1}{{\left[1-e^{-{\theta }_2{\mathcal{T}}_2^{-{\theta }_1}}\right]}^2},\hfill \end{array}$$

for Cases I and II,

$$\begin{array}{cc}\hfill 1-1{\zeta }_{{\theta }_1}^2(\Theta ;{\mathcal{T}}_2)& ={\zeta }_{{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)={\zeta }_{{\theta }_1{\theta }_2}^2(\Theta ;{\mathcal{T}}_2)=0.\hfill \end{array}$$

In order to compute BayEst of entropy under SELF, we take $g(\Theta )=1+(1+1/{\theta }_1)(\gamma +log{\theta }_2)-log\left({\theta }_1{\theta }_2\right)$. Then, ${\kappa }_S^{*}(\Theta )$ is obtained as

$$\begin{array}{c}\hfill {\kappa }_S^{*}(\Theta )=\kappa (\Theta )+\frac{1}{n}log\left[1+\left(1+\frac{1}{{\theta }_1}\right)(\gamma +log{\theta }_2)-log\left({\theta }_1{\theta }_2\right)\right].\end{array}$$

Now solving the following equation

$$\begin{array}{cc}\hfill \frac{\partial {\kappa }_S^{*}(\Theta )}{\partial {\theta }_1}=& \frac{\partial \kappa (\Theta )}{\partial {\theta }_1}-\frac{1}{n{\theta }_1^2}\frac{{\theta }_1+\gamma +log{\theta }_2}{H\left(f\right)}=0\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \frac{\partial {\kappa }_S^{*}(\Theta )}{\partial {\theta }_2}=& \frac{\partial \kappa (\Theta )}{\partial {\theta }_2}+\frac{1}{n{\theta }_1{\theta }_{2}H\left(f\right)}=0,\hfill \end{array}$$

We obtain $({\widehat{\theta }}_1{}_{{\kappa }_S^{*}},{\widehat{\theta }}_2{}_{{\kappa }_S^{*}})$. Then, we compute $|{\Sigma }_S^{*}|$ and it is given by

$$\begin{array}{c}\hfill |{\Sigma }_S^{*}|={\left[\frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_1^2}\frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_2^2}-\frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}\frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_2\partial {\theta }_1}\right]}^{-1},\end{array}$$

where

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_1^2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1^2}+\frac{1}{n}\left[\frac{{\theta }_1+2\gamma +2log{\theta }_2}{{\theta }_1^{3}H\left(f\right)}-{\left(\frac{{\theta }_1+\gamma +log{\theta }_2}{{\theta }_1^{2}H\left(f\right)}\right)}^2\right],\hfill \\ \hfill \frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_2^2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_2^2}-\frac{1}{n{\theta }_1^2{\theta }_2^{2}H{\left(f\right)}^2}\left({\theta }_{1}H\left(f\right)-1\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill 1-1\frac{{\partial }^2{\kappa }_S^{*}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1\partial {\theta }_2}-\frac{1}{n{\theta }_1^3{\theta }_{2}H{\left(f\right)}^2}\left[{\theta }_{1}H\left(f\right)-({\theta }_1+\gamma +log{\theta }_2)\right].\hfill \end{array}$$

Then, the BayEst of entropy is obtained by

$$\begin{array}{c}\hfill {\widehat{\mathbb{H}}}_S=\sqrt{\frac{|{\Sigma }_S^{*}|}{|\Sigma |}}{e}^{n{\kappa }_S^{*}({\widehat{\theta }}_1{}_{{\kappa }_S^{*}},{\widehat{\theta }}_2{}_{{\kappa }_S^{*}})-n\kappa ({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })}.\end{array}$$

(18)

Next, in order to compute BayEst of entropy under GELF, we take $g(\Theta )={[1+(1+1/{\theta }_1)(\gamma +log{\theta }_2)-log\left({\theta }_1{\theta }_2\right)]}^{-q}$. Then, ${\kappa }_E^{*}(\Theta )$ is obtained as

$$\begin{array}{c}\hfill {\kappa }_E^{*}(\Theta )=\kappa (\Theta )-\frac{q}{n}log\left[1+\left(1+\frac{1}{{\theta }_1}\right)(\gamma +log{\theta }_2)-log\left({\theta }_1{\theta }_2\right)\right].\end{array}$$

Now solving the following equation

$$\begin{array}{cc}\hfill \frac{\partial {\kappa }_E^{*}(\Theta )}{\partial {\theta }_1}=& \frac{\partial \kappa (\Theta )}{\partial {\theta }_1}+\frac{q}{n{\theta }_1^2}\frac{{\theta }_1+\gamma +log{\theta }_2}{H\left(f\right)}=0\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill 1-1\frac{\partial {\kappa }_E^{*}(\Theta )}{\partial {\theta }_2}=& \frac{\partial \kappa (\Theta )}{\partial {\theta }_2}-\frac{q}{n{\theta }_1{\theta }_{2}H\left(f\right)}=0,\hfill \end{array}$$

We obtain $({\widehat{\theta }}_1{}_{{\kappa }_E^{*}},{\widehat{\theta }}_2{}_{{\kappa }_E^{*}})$. Then, we compute $|{\Sigma }_E^{*}|$ and it is given by

$$\begin{array}{c}\hfill |{\Sigma }_E^{*}|={\left[\frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_1^2}\frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_2^2}-\frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}\frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_2\partial {\theta }_1}\right]}^{-1},\end{array}$$

where

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_1^2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1^2}-\frac{q}{n}\left[\frac{{\theta }_1+2\gamma +2log{\theta }_2}{{\theta }_1^{3}H\left(f\right)}-{\left(\frac{{\theta }_1+\gamma +log{\theta }_2}{{\theta }_1^{2}H\left(f\right)}\right)}^2\right],\hfill \\ \hfill \frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_2^2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_2^2}+\frac{q}{n{\theta }_1^2{\theta }_2^{2}H{\left(f\right)}^2}({\theta }_{1}H\left(f\right)+1)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\kappa }_E^{*}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1\partial {\theta }_2}+\frac{q}{n{\theta }_1^3{\theta }_{2}H{\left(f\right)}^2}[{\theta }_{1}H\left(f\right)-({\theta }_1+\gamma +log{\theta }_2)].\hfill \end{array}$$

Then, the BayEst of entropy under GELF is obtained by

$$\begin{array}{c}\hfill {\widehat{\mathbb{H}}}_E={\left[\sqrt{\frac{|{\Sigma }_E^{*}|}{|\Sigma |}}{e}^{n{\kappa }_E^{*}({\widehat{\theta }}_1{}_{{\kappa }_E^{*}},{\widehat{\theta }}_2{}_{{\kappa }_E^{*}})-n\kappa ({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })}\right]}^{-1/q}.\end{array}$$

(19)

In order to compute BayEst of entropy function under LLF, we take $g(\Theta )=exp\{-c[1+(1+1/{\theta }_1)(\gamma +log{\theta }_2)-log\left({\theta }_1{\theta }_2\right)]\}$. Then, ${\kappa }_L^{*}(\Theta )$ is obtained as

$$\begin{array}{c}\hfill {\kappa }_L^{*}(\Theta )=\kappa (\Theta )-\frac{c}{n}\left[1+\left(1+\frac{1}{{\theta }_1}\right)(\gamma +log{\theta }_2)-log\left({\theta }_1{\theta }_2\right)\right].\end{array}$$

Now solving the following equation

$$\begin{array}{cc}\hfill \frac{\partial {\kappa }_L^{*}(\Theta )}{\partial {\theta }_1}=& \frac{\partial \kappa (\Theta )}{\partial {\theta }_1}+\frac{c}{n{\theta }_1^2}({\theta }_1+\gamma +log{\theta }_2)=0\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill 1-1\frac{\partial {\kappa }_L^{*}(\Theta )}{\partial {\theta }_2}=& \frac{\partial \kappa (\Theta )}{\partial {\theta }_2}-\frac{c}{n{\theta }_1{\theta }_2}=0,\hfill \end{array}$$

We obtain $({\widehat{\theta }}_1{}_{{\kappa }_L^{*}},{\widehat{\theta }}_2{}_{{\kappa }_L^{*}})$. Then, we compute $|{\Sigma }_L^{*}|$ and it is given by

$$\begin{array}{c}\hfill |{\Sigma }_L^{*}|={\left[\frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_1^2}\frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_2^2}-\frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}\frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_2\partial {\theta }_1}\right]}^{-1},\end{array}$$

where

$$\begin{array}{cc}\hfill \frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_1^2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1^2}-\frac{c}{n{\theta }_1^3}({\theta }_1+2\gamma +2log{\theta }_2),\hfill \\ \hfill \frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_2^2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_2^2}+\frac{c}{n{\theta }_1{\theta }_2^2}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill 1-1\frac{{\partial }^2{\kappa }_L^{*}(\Theta )}{\partial {\theta }_1\partial {\theta }_2}=& \frac{{\partial }^2\kappa (\Theta )}{\partial {\theta }_1\partial {\theta }_2}+\frac{c}{n{\theta }_1^2{\theta }_2}.\hfill \end{array}$$

Then, the BayEst of entropy function under LLF is obtained by

$$\begin{array}{c}\hfill {\widehat{\mathbb{H}}}_L=-\frac{1}{c}log\left[\sqrt{\frac{|{\Sigma }_L^{*}|}{|\Sigma |}}{e}^{n{\kappa }_L^{*}({\widehat{\theta }}_1{}_{{\kappa }_L^{*}},{\widehat{\theta }}_2{}_{{\kappa }_L^{*}})-n\kappa ({\widehat{\theta }}_1{}_{\kappa },{\widehat{\theta }}_2{}_{\kappa })}\right].\end{array}$$

(20)

4.2. Importance Sampling

The drawback of the TiKa method is that it cannot be used to construct an HPD credible interval. Therefore, we propose to use the importance sampling procedure similarly to Lee and Cho [22] to compute simulation consistent Bayes estimates (BEs) of the entropy and also to construct associated HPD credible interval.

To implement the importance sampling procedure, we re-write Equation (16) as follows:

$$\begin{array}{cc}\hfill \pi (\Theta |\mathit{X})\propto & {\theta }_1^{\tau +a_1-1}{\theta }_2^{\tau +a_2-1}\prod _{i=1}^{\tau }{x}_{i:m:n}^{-({\theta }_1+1)}{e}^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}-b_1{\theta }_1-b_2{\theta }_2}{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\zeta (\Theta ;{\mathcal{T}}_2)\hfill \\ \hfill \propto & {\theta }_1^{\tau +a_1-1}exp\left[-{\theta }_1\left(b_1+\sum _{i=1}^{\tau }log{x}_{i:m:n}\right)\right]{\theta }_2^{\tau +a_2-1}exp\left[-{\theta }_2\left(b_2+\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}\right)\right]\hfill \\ \hfill & \times exp\left[-\sum _{i=1}^{\tau }log{x}_{i:m:n}\right]{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\zeta (\Theta ;{\mathcal{T}}_2)\hfill \\ \hfill \propto & GAM\left({\theta }_1;\tau +a_1,b_1+\sum _{i=1}^{\tau }log{x}_{i:m:n}\right)GAM\left({\theta }_2;\tau +a_2,b_2+\sum _{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1}\right)k(\Theta )\hfill \end{array}$$

where

$$\begin{array}{c}\hfill k(\Theta )=\frac{exp\left[-{\sum }_{i=1}^{\tau }log{x}_{i:m:n}\right]{\prod }_{i=1}^{\tau }{\left[1-e^{-{\theta }_2{x}_{i:m:n}^{-{\theta }_1}}\right]}^{{\Re }_i}\zeta (\Theta ;{\mathcal{T}}_2)}{{\left[b_1+{\sum }_{i=1}^{\tau }log{x}_{i:m:n}\right]}^{\tau +a_1}}.\end{array}$$

Samples are generated using the following steps.

• Step 1. Generate ${\theta }_1$ from $GAM(\tau +a_1,b_1+{\sum }_{i=1}^{\tau }log{x}_{i:m:n})$.
• Step 2. Given ${\theta }_1$ generated in Step 1, generate ${\theta }_2$ from $GAM(\tau +a_2,b_2+{\sum }_{i=1}^{\tau }{x}_{i:m:n}^{-{\theta }_1})$
• Step 3. Repeat Steps 1 and 2 to generate (${{\theta }_1}_1$,${{\theta }_2}_1$), (${{\theta }_1}_2$,${{\theta }_2}_2$), ⋯, (${{\theta }_1}_N$,${{\theta }_2}_N$).
• Step 4. The BEs of entropy under SELF, GELF and LLF can be obtained as follow

  $$\begin{array}{cc}\hfill & {\widehat{\mathbb{H}}}_{IS}=\frac{{\sum }_{i=1}^N\mathbb{H}\left({\Theta }_i\right)k\left({\Theta }_i\right)}{{\sum }_{i=1}^{N}k\left({\Theta }_i\right)},\hfill \\ \hfill & {\widehat{\mathbb{H}}}_{IE}={\left[\frac{{\sum }_{i=1}^N{\mathbb{H}\left({\Theta }_i\right)}^{-q}k\left({\Theta }_i\right)}{{\sum }_{i=1}^{N}k\left({\Theta }_i\right)}\right]}^{-\frac{1}{q}},\hfill \\ \hfill & {\widehat{\mathbb{H}}}_{IL}=-\frac{1}{c}log\left[\frac{{\sum }_{i=1}^N{e}^{-c\mathbb{H}\left({\Theta }_i\right)}k\left({\Theta }_i\right)}{{\sum }_{i=1}^{N}k\left({\Theta }_i\right)}\right],\hfill \end{array}$$

  where $\mathbb{H}\left({\Theta }_i\right)=1+\left(1+\frac{1}{{{\theta }_1}_i}\right)\left(\gamma +log{{\theta }_2}_i\right)-log\left({{\theta }_1}_i{{\theta }_2}_i\right)$.

Next we obtain the HPD credible interval of entropy using the generated importance sample. We consider the procedure of obtaining the HPD credible interval for entropy. Suppose $a_p$ is such that $P[\mathbb{H}\le a_p|\mathit{X}]=p$. Then an approximate BE of $a_p$ under the SELF can be obtained from the generated sample (${\mathbb{H}}_1$, ${\mathbb{H}}_2$, ⋯, ${\mathbb{H}}_N$) as follows.

Define

$$\begin{array}{c}\hfill v_i=\frac{k({{\theta }_1}_i,{{\theta }_2}_i)}{{\sum }_{i=1}^{N}k({{\theta }_1}_i,{{\theta }_2}_i)},i=1,2,\cdots ,N.\end{array}$$

Rearrange {(${\mathbb{H}}_1$,$v_1$), (${\mathbb{H}}_2$,$v_2$), ⋯, (${\mathbb{H}}_N$,$v_N$)} as {(${\mathbb{H}}_{\left(1\right)}$,$v_{\left(1\right)}$), (${\mathbb{H}}_{\left(2\right)}$,$v_{\left(2\right)}$), ⋯, (${\mathbb{H}}_{\left(N\right)}$,$v_{\left(N\right)}$)}, where ${\mathbb{H}}_{\left(1\right)}<\cdots <{\mathbb{H}}_{\left(N\right)}$. Note that $v_{\left(i\right)}$’s are not ordered, they are just associated with ${\mathbb{H}}_{\left(i\right)}$. Then the BE of $a_p$ is ${\widehat{a}}_p={\mathbb{H}}_{\left(N_p\right)}$, where $N_p$ is the integer satisfying

$$\begin{array}{c}\hfill \sum _{i=1}^{N_p}{v}_{\left(i\right)}\le p<\sum _{i=1}^{N_p+1}{v}_{\left(i\right)}.\end{array}$$

Hence, using the above procedure, a $100(1-\alpha )\%$ HPD credible interval of $\mathbb{H}$ can be obtained as $({\widehat{a}}_{\delta },{\widehat{a}}_{\delta +1-\alpha })$, for $\delta$ = $v_{\left(1\right)}$, $v_{\left(1\right)}+v_{\left(2\right)}$, ⋯, ${\sum }_{i=1}^{N_{\alpha }}{v}_{\left(i\right)}$. Therefore, a $100(1-\alpha )\%$ HPD credible interval of $\mathbb{H}$ becomes $({\widehat{a}}_{{\delta }^{*}},{\widehat{a}}_{{\delta }^{*}+1-\alpha })$, where ${\delta }^{*}$ is such that ${\widehat{a}}_{{\delta }^{*}+1-\alpha }-{\widehat{a}}_{{\delta }^{*}}\le {\widehat{a}}_{\delta +1-\alpha }-{\widehat{a}}_{\delta }$ for all $\delta$.

5. Example and Simulation Results

5.1. Example—Aircraft Windshields

In order to analyze the real life data set, we use the proposed estimators in the above section. The real-life dataset was from the data on failure times of aircraft windshields (see Blischke and Murthy [23]). Blischke and Murthy [23] examined the goodness-of-fit of the data to IWD and they found that the IWD fits the data. The ordered data are as follows: 0.301, 0.309, 0.557, 0.943, 1.070, 1.124, 1.248, 1.281, 1.281, 1.303, 1.432, 1.480, 1.505, 1.506, 1.568, 1.615, 1.619, 1.652, 1.652, 1.757, 1.795, 1.866, 1.876, 1.899, 1.911, 1.912, 1.914, 1.981, 2.010, 2.038, 2.085, 2.089, 2.097, 2.135, 2.154, 2.190, 2.194, 2.223, 2.224, 2.229, 2.300, 2.324, 2.349, 2.385, 2.481, 2.610, 2.625, 2.632, 2.646, 2.661, 2.688, 2.823, 2.890, 2.902, 2.934, 2.962, 2.964, 3.000, 3.103, 3.114, 3.117, 3.166, 3.344, 3.376, 3.385, 3.443, 3.467, 3.478, 3.578, 3.595, 3.699, 3.779, 3.924, 4.035, 4.121, 4.167, 4.240, 4.255, 4.278, 4.305, 4.376, 4.449, 4.485, 4.570, 4.602, 4.663, 4.694.

Here, we consider the case when the data are PrC with the following schemes: $n=87$, $m=70$ and ${\Re }_1=\cdots ={\Re }_{53}=0$, ${\Re }_{54}=\cdots ={\Re }_{70}=1$. We take Sch. a: ${\mathcal{T}}_1=4.0$ and ${\mathcal{T}}_2=5.0$, Sch. b: ${\mathcal{T}}_1=2.0$ and ${\mathcal{T}}_2=4.0$ and Sch. c: ${\mathcal{T}}_1=2.0$ and ${\mathcal{T}}_2=3.0$. The BEs based on the non-informative prior $(a_1=a_2=b_1=b_2=0.00001)$ are obtained. And, the BEs based on the GELF with q = −0.25, 1.25, and LLF with c = −0.25, 1.25 are obtained. Table 1 shows the estimates of the entropy under the GAPHC scheme.

Table 1. Classical and Bayes estimates of entropy for example.

Sch.	$\widehat{\mathbb{H}}$	${\widehat{\mathbb{H}}}_{\mathit{P}}$	${\widehat{\mathbb{H}}}_{\mathit{S}}$	${\widehat{\mathbb{H}}}_{\mathit{E}}$		${\widehat{\mathbb{H}}}_{\mathit{L}}$
				$\mathit{c}=-\mathbf{0.25}$	$\mathit{c}=\mathbf{1.25}$	$\mathit{q}=-\mathbf{0.25}$	$\mathit{q}=\mathbf{1.25}$
a	2.369661	2.362360	2.365983	2.370594	2.363953	2.368730	2.368096
			2.369481	2.374308	2.365666	2.370388	2.346619
b	2.401055	2.393866	2.397353	2.402497	2.395123	2.400103	2.399451
			2.401296	2.402141	2.377641	2.406237	2.397509
c	2.574591	2.568136	2.571705	2.585728	2.566123	2.575513	2.574599
			2.578135	2.582959	2.546323	2.582959	2.572144

In Table 1, we tabulate the entropy of the respective MLE and MPSE in the third and fourth columns of the table, respectively. In the other columns, the BEs of entropy under SELF, GELF, LLF are tabulated. In BEs, the two values are BE using the TiKa method and MCMC estimate of entropy, respectively. In Table 1, we observe that the BEs of entropy under GELF are marginally smaller than the corresponding BEs of entropy under SELF and LLF. Additionally, we observe that the MPSEs of entropy are smaller than the corresponding MLE of entropy.

5.2. Simulation Results

In this subsection, we use Monte Carlo simulations to compare the proposed estimators. First of all, we consider various n, m, ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$, and four different PrC schemes, namely; Sch. a: ${\Re }_m=n-m$ and ${\Re }_i=0$ for $i\ne m$. Sch. b: ${\Re }_1={\Re }_m=(n-m)/2$ and ${\Re }_i=0$ for $i\ne 1,m$. Sch. c: ${\Re }_{m/2}=n-m$ and ${\Re }_i=0$ for $i\ne m/2$. Sch. d: ${\Re }_1=n-m$ and ${\Re }_i=0$ for $i\ne 1$.

In each cases, we take ${\theta }_1=2$ and ${\theta }_2=2$. We replicate the process 1000 times. The associated classical estimates are computed using a Newton–Raphson method. All BEs are calculated with respect to the non-informative prior distribution $(a_1=a_2=b_1=b_2={10}^{-6})$. BEs of entropy are obtained with respect to SELF, GELF and LLF. BEs under GELF and LLF are obtained for two distinct values of $q=-0.25,1.25$ and $c=-0.25,1.25$, respectively. Various schemes have been taken into consideration to calculate MSE and the bias of the proposed classical and BEs (Table 2 and Table 3).

Table 2. The relative MSEs and biases of entropy estimators with classical and BayEst (${\mathcal{T}}_1=1.5$ and ${\mathcal{T}}_2=2.0$).

n	m	Sch.	$\widehat{\mathbb{H}}$	${\widehat{\mathbb{H}}}_{\mathit{P}}$	${\widehat{\mathbb{H}}}_{\mathit{S}}$	${\widehat{\mathbb{H}}}_{\mathit{L}}$		${\widehat{\mathbb{H}}}_{\mathit{E}}$
						$\mathit{c}=-\mathbf{0.25}$	$\mathit{c}=\mathbf{1.25}$	$\mathit{q}=-\mathbf{0.25}$	$\mathit{q}=\mathbf{1.25}$
20	18	a	0.1484 (−0.0513) ${}^{†}$	0.1689 (0.1536)	0.1435 (0.0416)	0.1511 (0.0738)	0.1424 (0.0580)	0.1426 (0.0381)	0.1411 (0.0312)
					0.1207 (0.0944)	0.1256 (0.1052)	0.0881 (0.0193)	0.1204 (0.1029)	0.0795 (0.2193)
		b	0.1528 (−0.0602)	0.1733 (0.1509)	0.1451 (0.0354)	0.1527 (0.0693)	0.1438 (0.0527)	0.1443 (0.0318)	0.1429 (0.0246)
					0.1226 (0.0910)	0.1274 (0.1020)	0.0897 (0.0134)	0.1225 (0.1009)	0.0801 (0.0378)
		c	0.1515 (−0.0346)	0.1769 (0.1770)	0.1476 (0.0608)	0.1559 (0.0944)	0.1466 (0.0778)	0.1467 (0.0573)	0.1450 (0.0501)
					0.1255 (0.1128)	0.1309 (0.1239)	0.0883 (0.0339)	0.1226 (0.1217)	0.0860 (0.0691)
		d	0.1627 (−0.0622)	0.1878 (0.1574)	0.1618 (0.0395)	0.1716 (0.0757)	0.1595 (0.0576)	0.1608 (0.0357)	0.1588 (0.0280)
					0.1321 (0.0938)	0.1369 (0.1052)	0.0896 (0.0090)	0.1385 (0.1049)	0.0891 (0.0455)
	16	a	0.1538 (−0.0462)	0.1717 (0.1597)	0.1528 (0.0432)	0.1603 (0.0753)	0.1517 (0.0595)	0.1519 (0.0397)	0.1504 (0.0329)
					0.1220 (0.0863)	0.1271 (0.0984)	0.0900 (0.0097)	0.1224 (0.0888)	0.0894 (0.0308)
		b	0.1623 (−0.0445)	0.2005 (0.1778)	0.1614 (0.0510)	0.1717 (0.0872)	0.1600 (0.0689)	0.1603 (0.0471)	0.1583 (0.0395)
					0.1383 (0.0973)	0.1449 (0.1107)	0.1128 (0.0155)	0.1382 (0.1000)	0.1100 (0.0441)
		c	0.1583 (−0.0143)	0.1973 (0.2119)	0.1595 (0.0834)	0.1688 (0.1195)	0.1586 (0.1016)	0.1584 (0.0796)	0.1566 (0.0720)
					0.1385 (0.1244)	0.1446 (0.1375)	0.0955 (0.0370)	0.1324 (0.1280)	0.0949 (0.0690)
		d	0.1759 (−0.0538)	0.2267 (0.1891)	0.1722 (0.0491)	0.1840 (0.0901)	0.1702 (0.0692)	0.1710 (0.0448)	0.1687 (0.0362)
					0.1486 (0.0973)	0.1559 (0.1120)	0.1000 (0.0020)	0.1507 (0.1004)	0.0959 (0.1891)
	14	a	0.1621 (−0.0744)	0.1758 (0.1324)	0.1614 (0.0242)	0.1767 (0.0567)	0.1595 (0.0412)	0.1609 (0.0207)	0.1589 (0.0138)
					0.1386 (0.0603)	0.1398 (0.0709)	0.1141 (−0.0157)	0.1319 (0.0670)	0.1115 (0.0117)
		b	0.1712 (−0.0714)	0.2051 (0.1601)	0.1706 (0.0359)	0.1796 (0.0741)	0.1686 (0.0551)	0.1697 (0.0319)	0.1660 (0.0239)
					0.1500 (0.1004)	0.1486 (0.1101)	0.1211 (0.0178)	0.1456 (0.1271)	0.1208 (0.0981)
		c	0.2091 (−0.0394)	0.2397 (0.2085)	0.1985 (0.0769)	0.2071 (0.1175)	0.1958 (0.0977)	0.1975 (0.0727)	0.1939 (0.0643)
					0.1728 (0.1318)	0.1762 (0.1421)	0.1230 (0.0420)	0.1697 (0.1592)	0.1219 (0.1549)
		d	0.2164 (−0.0783)	0.2676 (0.1848)	0.2034 (0.0428)	0.2182 (0.0900)	0.1995 (0.0653)	0.2018 (0.0378)	0.1960 (0.0280)
					0.2057 (0.1123)	0.1950 (0.1226)	0.1382 (0.0070)	0.2002 (0.1784)	0.1358 (0.0738)
30	28	a	0.0876 (−0.0374)	0.0948 (0.1097)	0.0847 (0.0175)	0.0871 (0.0388)	0.0852 (0.0322)	0.0846 (0.0160)	0.0842 (0.0131)
					0.0766 (0.0429)	0.0785 (0.0520)	0.0637 (−0.0101)	0.0765 (0.0417)	0.0622 (−0.0005)
		b	0.0897 (−0.0411)	0.0968 (0.1090)	0.0864 (0.0149)	0.0887 (0.0369)	0.0868 (0.0301)	0.0862 (0.0134)	0.0859 (0.0104)
					0.0778 (0.0406)	0.0797 (0.0500)	0.0646 (−0.0138)	0.0777 (0.0392)	0.0635 (−0.0043)
		c	0.0866 (−0.0196)	0.0982 (0.1308)	0.0852 (0.0363)	0.0882 (0.0581)	0.0861 (0.0513)	0.0850 (0.0348)	0.0846 (0.0317)
					0.0781 (0.0609)	0.0804 (0.0702)	0.0636 (0.0059)	0.0781 (0.0594)	0.0626 (0.0161)
		d	0.0913 (−0.0438)	0.0985 (0.1094)	0.0874 (0.0134)	0.0898 (0.0362)	0.0877 (0.0291)	0.0873 (0.0118)	0.0869 (0.0087)
					0.0787 (0.0395)	0.0807 (0.0491)	0.0653 (−0.0165)	0.0786 (0.0377)	0.0645 (−0.0071)
	24	a	0.0926 (−0.0392)	0.0988 (0.1072)	0.0894 (0.0158)	0.0916 (0.0370)	0.0897 (0.0304)	0.0892 (0.0143)	0.0889 (0.0114)
					0.0807 (0.0409)	0.0827 (0.0499)	0.0674 (−0.0119)	0.0806 (0.0398)	0.0662 (−0.0019)
		b	0.1000 (−0.0380)	0.1098 (0.1192)	0.0968 (0.0207)	0.0997 (0.0444)	0.0973 (0.0369)	0.0966 (0.0191)	0.0962 (0.0158)
					0.0868 (0.0466)	0.0892 (0.0565)	0.0708 (−0.0117)	0.0864 (0.0448)	0.0691 (−0.0010)
		c	0.1167 (0.0111)	0.1353 (0.1747)	0.1103 (0.0717)	0.1218 (0.0960)	0.1087 (0.0882)	0.1070 (0.0701)	0.1063 (0.0668)
					0.1084 (0.0933)	0.1116 (0.1034)	0.0865 (0.0320)	0.1083 (0.0906)	0.0861 (0.0443)
		d	0.1114 (−0.0378)	0.1227 (0.1304)	0.1090 (0.0255)	0.1132 (0.0524)	0.0997 (0.0437)	0.1087 (0.0237)	0.0982 (0.0200)
					0.0976 (0.0506)	0.1006 (0.0618)	0.0775 (−0.0150)	0.0969 (0.0475)	0.0763 (−0.0040)
	20	a	0.1048 (−0.0344)	0.1111 (0.1152)	0.1005 (0.0211)	0.1026 (0.0429)	0.0905 (0.0362)	0.1004 (0.0196)	0.0953 (0.0180)
					0.0979 (0.0371)	0.0997 (0.0466)	0.0844 (−0.0179)	0.0992 (0.0347)	0.0834 (−0.0091)
		b	0.1165 (−0.0293)	0.1325 (0.1376)	0.1140 (0.0314)	0.1181 (0.0572)	0.1047 (0.0489)	0.1137 (0.0296)	0.1033 (0.0260)
					0.1036 (0.0565)	0.1067 (0.0673)	0.0828 (−0.0074)	0.1035 (0.0535)	0.0809 (0.0033)
		c	0.1606 (−0.0007)	0.1796 (0.1888)	0.1581 (0.0694)	0.1629 (0.0985)	0.1486 (0.0892)	0.1578 (0.0674)	0.1473 (0.0635)
					0.1429 (0.0886)	0.1468 (0.1002)	0.1148 (0.0188)	0.1431 (0.0825)	0.1097 (0.2591)
		d	0.1426 (−0.0354)	0.1687 (0.1581)	0.1382 (0.0337)	0.1447 (0.0663)	0.1390 (0.0552)	0.1378 (0.0315)	0.1370 (0.0270)
					0.1243 (0.0562)	0.1288 (0.0696)	0.0960 (−0.0217)	0.1231 (0.0508)	0.0917 (−0.0072)
40	38	a	0.0687 (−0.0317)	0.0700 (0.0842)	0.0666 (0.0075)	0.0677 (0.0234)	0.0570 (0.0198)	0.0665 (0.0066)	0.0564 (0.0050)
					0.0619 (0.0249)	0.0629 (0.0320)	0.0551 (−0.0146)	0.0620 (0.0236)	0.0500 (−0.0078)
		b	0.0710 (−0.0314)	0.0728 (0.0865)	0.0688 (0.0084)	0.0701 (0.0248)	0.0593 (0.0210)	0.0688 (0.0076)	0.0587 (0.0059)
					0.0640 (0.0260)	0.0651 (0.0332)	0.0567 (−0.0145)	0.0640 (0.0245)	0.0519 (−0.0076)
		c	0.0671 (−0.0156)	0.0717 (0.1023)	0.0661 (0.0241)	0.0676 (0.0403)	0.0568 (0.0366)	0.0660 (0.0233)	0.0558 (0.0216)
					0.0621 (0.0411)	0.0633 (0.0483)	0.0542 (0.0004)	0.0621 (0.0396)	0.0493 (0.0076)
		d	0.0726 (−0.0307)	0.0750 (0.0894)	0.0705 (0.0098)	0.0719 (0.0266)	0.0610 (0.0227)	0.0704 (0.0089)	0.0603 (0.0072)
					0.0654 (0.0274)	0.0666 (0.0348)	0.0576 (−0.0142)	0.0654 (0.0257)	0.0531 (−0.0072)
	34	a	0.0720 (−0.0426)	0.0729 (0.0724)	0.0708 (−0.0028)	0.0714 (0.0130)	0.0609 (0.0095)	0.0698 (−0.0036)	0.0607 (−0.0053)
					0.0658 (0.0157)	0.0665 (0.0226)	0.0605 (−0.0229)	0.0659 (0.0145)	0.0552 (−0.0162)
		b	0.0736 (−0.0437)	0.0733 (0.0775)	0.0704 (−0.0019)	0.0713 (0.0153)	0.0625 (0.0114)	0.0703 (−0.0027)	0.0612 (−0.0045)
					0.0644 (0.0169)	0.0653 (0.0243)	0.0577 (−0.0247)	0.0645 (0.0153)	0.0552 (−0.0170)
		c	0.0787 (−0.0003)	0.0852 (0.1239)	0.0781 (0.0421)	0.0801 (0.0594)	0.0691 (0.0554)	0.0780 (0.0412)	0.0648 (0.0395)
					0.0739 (0.0584)	0.0754 (0.0659)	0.0640 (0.0151)	0.0742 (0.0563)	0.0610 (0.0229)
		d	0.0822 (−0.0449)	0.0828 (0.0832)	0.0787 (−0.0009)	0.0799 (0.0179)	0.0689 (0.0135)	0.0786 (−0.0018)	0.0655 (−0.0037)
					0.0722 (0.0178)	0.0734 (0.0259)	0.0641 (−0.0273)	0.0723 (0.0156)	0.0611 (−0.0202)
	30	a	0.0748 (−0.0224)	0.0783 (0.0941)	0.0734 (0.0159)	0.0746 (0.0317)	0.0639 (0.0281)	0.0733 (0.0150)	0.0632 (0.0134)
					0.0699 (0.0322)	0.0689 (0.0393)	0.0630 (−0.0077)	0.0700 (0.0307)	0.0579 (−0.0010)
		b	0.0756 (−0.0252)	0.0803 (0.1014)	0.0737 (0.0162)	0.0754 (0.0343)	0.0644 (0.0301)	0.0737 (0.0152)	0.0635 (0.0134)
					0.0690 (0.0332)	0.0703 (0.0412)	0.0601 (−0.0119)	0.0690 (0.0309)	0.0594 (−0.0049)
		c	0.1048 (0.0248)	0.1167 (0.1615)	0.1009 (0.0694)	0.1090 (0.0887)	0.0974 (0.0841)	0.0957 (0.0684)	0.0953 (0.0665)
					0.1010 (0.0819)	0.1031 (0.0903)	0.0861 (0.0331)	0.1013 (0.0782)	0.0811 (0.0407)
		d	0.0886 (−0.0250)	0.0966 (0.1151)	0.0868 (0.0204)	0.0892 (0.0417)	0.0777 (0.0365)	0.0866 (0.0193)	0.0764 (0.0171)
					0.0811 (0.0363)	0.0829 (0.0457)	0.0695 (−0.0161)	0.0811 (0.0327)	0.0709 (−0.0088)
50	40	a	0.0521 (−0.0189)	0.0640 (0.0784)	0.0510 (0.0109)	0.0518 (0.0235)	0.0514 (0.0213)	0.0510 (0.0103)	0.0509 (0.0093)
					0.0484 (0.0239)	0.0491 (0.0298)	0.0440 (−0.0077)	0.0485 (0.0226)	0.0472 (−0.0025)
		b	0.0574 (−0.0205)	0.0711 (0.0836)	0.0561 (0.0112)	0.0570 (0.0253)	0.0566 (0.0227)	0.0561 (0.0107)	0.0560 (0.0095)
					0.0532 (0.0245)	0.0539 (0.0309)	0.0480 (−0.0104)	0.0532 (0.0227)	0.0518 (−0.0049)
		c	0.0776 (0.0352)	0.1036 (0.1449)	0.0793 (0.0684)	0.0817 (0.0831)	0.0808 (0.0803)	0.0792 (0.0678)	0.0790 (0.0666)
					0.0771 (0.0787)	0.0785 (0.0853)	0.0672 (0.0413)	0.0772 (0.0762)	0.0732 (0.0477)
		d	0.0662 (−0.0219)	0.0828 (0.0903)	0.0646 (0.0121)	0.0658 (0.0279)	0.0652 (0.0250)	0.0646 (0.0115)	0.0645 (0.0102)
					0.0612 (0.0250)	0.0621 (0.0322)	0.0548 (−0.0140)	0.0612 (0.0226)	0.0596 (−0.0083)
60	20	a	0.0988 (−0.0746)	0.1046 (0.0766)	0.0872 (−0.0237)	0.0851 (0.0001)	0.0848 (−0.0035)	0.0873 (−0.0244)	0.0869 (−0.0275)
					0.0848 (−0.0243)	0.0849 (−0.0151)	0.0846 (−0.0729)	0.0832 (−0.0321)	0.0944 (−0.0772)
		b	0.0888 (−0.0523)	0.0969 (0.0766)	0.0812 (−0.0127)	0.0802 (0.0074)	0.0798 (0.0042)	0.0813 (−0.0133)	0.0815 (−0.0146)
					0.0798 (−0.0156)	0.0799 (−0.0071)	0.0780 (−0.0602)	0.0819 (−0.0222)	0.0862 (−0.0592)
		c	0.1185 (−0.0733)	0.1458 (0.1298)	0.1072 (−0.0125)	0.1071 (0.0200)	0.1058 (0.0144)	0.1073 (−0.0136)	0.1060 (−0.0214)
					0.1019 (−0.0131)	0.1032 (−0.0005)	0.0972 (−0.0793)	0.1039 (−0.0304)	0.1115 (−0.0864)
		d	0.1327 (−0.0207)	0.1830 (0.1494)	0.1275 (0.0235)	0.1327 (0.0551)	0.1296 (0.0487)	0.1273 (0.0224)	0.1270 (0.0203)
					0.1228 (−0.0050)	0.1251 (0.0092)	0.1086 (−0.0775)	0.1231 (−0.0155)	0.1242 (−0.0716)
100	50	a	0.0298 (−0.0287)	0.0311 (0.0393)	0.0283 (−0.0109)	0.0280 (−0.0028)	0.0280 (−0.0035)	0.0283 (−0.0110)	0.0283 (−0.0114)
					0.0280 (−0.0112)	0.0280 (−0.0076)	0.0281 (−0.0298)	0.0283 (−0.0134)	0.0292 (−0.0285)
		b	0.0325 (−0.0126)	0.0377 (0.0561)	0.0320 (0.0042)	0.0322 (0.0126)	0.0321 (0.0118)	0.0320 (0.0040)	0.0320 (0.0037)
					0.0316 (0.0096)	0.0318 (0.0135)	0.0302 (−0.0108)	0.0317 (0.0082)	0.0315 (−0.0079)
		c	0.0446 (−0.0267)	0.0517 (0.0689)	0.0430 (−0.0025)	0.0431 (0.0097)	0.0430 (0.0086)	0.0430 (−0.0027)	0.0430 (−0.0032)
					0.0418 (0.0004)	0.0421 (0.0056)	0.0405 (−0.0263)	0.0420 (−0.0047)	0.0426 (−0.0262)
		d	0.0475 (−0.0133)	0.0574 (0.0745)	0.0466 (0.0075)	0.0472 (0.0198)	0.0470 (0.0185)	0.0466 (0.0073)	0.0466 (0.0068)
					0.0455 (0.0100)	0.0459 (0.0157)	0.0428 (−0.0195)	0.0456 (0.0073)	0.0453 (−0.0159)
200	100	a	0.0147 (−0.0170)	0.0151 (0.0227)	0.0142 (−0.0084)	0.0142 (−0.0043)	0.0142 (−0.0045)	0.0142 (−0.0084)	0.0142 (−0.0085)
					0.0142 (−0.0085)	0.0142 (−0.0067)	0.0143 (−0.0178)	0.0143 (−0.0096)	0.0145 (−0.0171)
		b	0.0153 (−0.0104)	0.0169 (0.0301)	0.0152 (−0.0021)	0.0152 (0.0020)	0.0152 (0.0019)	0.0152 (−0.0021)	0.0152 (−0.0022)
					0.0150 (0.0010)	0.0150 (0.0029)	0.0148 (−0.0090)	0.0150 (0.0004)	0.0150 (−0.0076)
		c	0.0210 (−0.0217)	0.0226 (0.0340)	0.0204 (−0.0100)	0.0203 (−0.0039)	0.0203 (−0.0041)	0.0204 (−0.0100)	0.0204 (−0.0101)
					0.0201 (−0.0086)	0.0201 (−0.0060)	0.0201 (−0.0218)	0.0202 (−0.0111)	0.0205 (−0.0218)
		d	0.0236 (−0.0127)	0.0264 (0.0399)	0.0232 (−0.0022)	0.0233 (0.0039)	0.0233 (0.0036)	0.0232 (−0.0022)	0.0232 (−0.0023)
					0.0229 (0.0004)	0.0230 (0.0030)	0.0224 (−0.0143)	0.0230 (−0.0009)	0.0230 (−0.0124)

^† MSE (Bias).

Table 3. The relative MSEs and biases of entropy estimators with classical and BayEst (${\mathcal{T}}_1=1.5$ and ${\mathcal{T}}_2=2.5$).

n	m	Sch.	$\widehat{\mathbb{H}}$	${\widehat{\mathbb{H}}}_{\mathit{P}}$	${\widehat{\mathbb{H}}}_{\mathit{S}}$	${\widehat{\mathbb{H}}}_{\mathit{L}}$		${\widehat{\mathbb{H}}}_{\mathit{E}}$
						$\mathit{c}=-\mathbf{0.25}$	$\mathit{c}=\mathbf{1.25}$	$\mathit{q}=-\mathbf{0.25}$	$\mathit{q}=\mathbf{1.25}$
20	18	a	0.1201 (−0.0476) ${}^{†}$	0.1260 (0.1258)	0.1127 (0.0236)	0.1153 (0.0485)	0.1115 (0.0367)	0.1124 (0.0209)	0.1119 (0.0153)
					0.1144 (0.1367)	0.1140 (0.1414)	0.0843 (0.0895)	0.1183 (0.1627)	0.0789 (0.1335)
		b	0.1237 (−0.0551)	0.1288 (0.1240)	0.1151 (0.0186)	0.1176 (0.0448)	0.1137 (0.0325)	0.1149 (0.0157)	0.1143 (0.0099)
					0.1138 (0.1388)	0.1127 (0.1429)	0.0876 (0.0928)	0.1150 (0.1713)	0.0792 (0.1582)
		c	0.1310 (0.0081)	0.1543 (0.1926)	0.1303 (0.0821)	0.1357 (0.1086)	0.1300 (0.0956)	0.1296 (0.0791)	0.1284 (0.0732)
					0.1182 (0.2022)	0.1176 (0.2063)	0.0816 (0.1499)	0.1110 (0.2435)	0.0827 (0.1965)
		d	0.1343 (−0.0572)	0.1382 (0.1275)	0.1252 (0.0195)	0.1284 (0.0474)	0.1234 (0.0341)	0.1249 (0.0164)	0.1242 (0.0102)
					0.1231 (0.1446)	0.1208 (0.1484)	0.0899 (0.0948)	0.1269 (0.1900)	0.0888 (0.1740)
	16	a	0.1267 (−0.0481)	0.1328 (0.1269)	0.1200 (0.0218)	0.1223 (0.0470)	0.1182 (0.0352)	0.1197 (0.0190)	0.1162 (0.0134)
					0.1189 (0.0964)	0.1203 (0.1046)	0.0872 (0.0431)	0.1193 (0.1059)	0.0846 (0.0735)
		b	0.1371 (−0.0493)	0.1423 (0.1354)	0.1306 (0.0247)	0.1343 (0.0527)	0.1287 (0.0393)	0.1302 (0.0216)	0.1264 (0.0154)
					0.1254 (0.1266)	0.1280 (0.1339)	0.1032 (0.0730)	0.1296 (0.1438)	0.0993 (0.1189)
		c	0.1413 (0.0558)	0.1618 (0.2593)	0.1368 (0.1328)	0.1454 (0.1626)	0.1323 (0.1475)	0.1258 (0.1295)	0.1298 (0.1230)
					0.1296 (0.2312)	0.1333 (0.2388)	0.0920 (0.1644)	0.1245 (0.2576)	0.0895 (0.2870)
		d	0.1501 (−0.0521)	0.1538 (0.1442)	0.1434 (0.0281)	0.1485 (0.0603)	0.1411 (0.0447)	0.1429 (0.0247)	0.1388 (0.0177)
					0.1353 (0.1391)	0.1361 (0.1464)	0.0906 (0.0848)	0.1278 (0.1694)	0.0893 (0.1336)
	14	a	0.1392 (−0.0858)	0.1494 (0.0954)	0.1306 (−0.0041)	0.1403 (0.0227)	0.1223 (0.0106)	0.1206 (−0.0071)	0.1207 (−0.0130)
					0.1316 (0.0233)	0.1302 (0.0328)	0.1097 (−0.0449)	0.1305 (0.0278)	0.1038 (−0.0256)
		b	0.1436 (−0.0708)	0.1453 (0.1228)	0.1405 (0.0133)	0.1530 (0.0434)	0.1340 (0.0292)	0.1303 (0.0101)	0.1298 (0.0035)
					0.1448 (0.1092)	0.1411 (0.1152)	0.1135 (0.0489)	0.1431 (0.1308)	0.1096 (0.0924)
		c	0.1709 (0.0487)	0.1920 (0.2771)	0.1618 (0.1428)	0.1718 (0.1776)	0.1594 (0.1599)	0.1605 (0.1391)	0.1482 (0.1316)
					0.1611 (0.2776)	0.1642 (0.2770)	0.1153 (0.2125)	0.1597 (0.4182)	0.1132 (0.3023)
		d	0.1755 (−0.0769)	0.1878 (0.1449)	0.1748 (0.0183)	0.1750 (0.0553)	0.1564 (0.0374)	0.1593 (0.0143)	0.1554 (0.0063)
					0.1864 (0.1649)	0.1677 (0.1650)	0.1270 (0.0951)	0.1876 (0.2551)	0.1251 (0.3153)
30	28	a	0.0706 (−0.0385)	0.0698 (0.0858)	0.0671 (0.0039)	0.0677 (0.0204)	0.0668 (0.0154)	0.0670 (0.0027)	0.0669 (0.0003)
					0.0603 (0.0631)	0.0617 (0.0696)	0.0496 (0.0236)	0.0611 (0.0674)	0.0463 (0.0367)
		b	0.0750 (−0.0374)	0.0748 (0.0900)	0.0716 (0.0060)	0.0724 (0.0233)	0.0714 (0.0180)	0.0715 (0.0048)	0.0714 (0.0023)
					0.0648 (0.0656)	0.0663 (0.0723)	0.0531 (0.0245)	0.0656 (0.0697)	0.0505 (0.0379)
		c	0.0773 (0.0116)	0.0872 (0.1416)	0.0769 (0.0551)	0.0803 (0.0725)	0.0787 (0.0670)	0.0777 (0.0538)	0.0773 (0.0513)
					0.0765 (0.1134)	0.0786 (0.1203)	0.0602 (0.0696)	0.0777 (0.1174)	0.0597 (0.0847)
		d	0.0764 (−0.0402)	0.0758 (0.0902)	0.0725 (0.0043)	0.0733 (0.0221)	0.0722 (0.0167)	0.0725 (0.0030)	0.0723 (0.0004)
					0.0654 (0.0640)	0.0668 (0.0710)	0.0536 (0.0218)	0.0661 (0.0681)	0.0515 (0.0353)
	24	a	0.0791 (−0.0417)	0.0765 (0.0829)	0.0744 (0.0013)	0.0748 (0.0180)	0.0739 (0.0130)	0.0744 (0.0001)	0.0713 (−0.0023)
					0.0741 (0.0492)	0.0751 (0.0560)	0.0645 (0.0084)	0.0755 (0.0526)	0.0534 (0.0206)
		b	0.0862 (−0.0380)	0.0863 (0.0957)	0.0820 (0.0077)	0.0830 (0.0263)	0.0817 (0.0206)	0.0819 (0.0063)	0.0788 (0.0037)
					0.0744 (0.0670)	0.0760 (0.0741)	0.0632 (0.0247)	0.0754 (0.0713)	0.0584 (0.0473)
		c	0.0927 (0.0770)	0.1338 (0.2238)	0.0910 (0.1253)	0.0922 (0.1455)	0.0888 (0.1388)	0.0866 (0.1239)	0.0838 (0.1210)
					0.0948 (0.1802)	0.1086 (0.1878)	0.0835 (0.1282)	0.0969 (0.1840)	0.0778 (0.1558)
		d	0.0948 (−0.0407)	0.0964 (0.1039)	0.0931 (0.0087)	0.0914 (0.0298)	0.0898 (0.0232)	0.0900 (0.0072)	0.0868 (0.0042)
					0.0795 (0.0691)	0.0815 (0.0770)	0.0671 (0.0229)	0.0802 (0.0734)	0.0666 (0.0423)
	20	a	0.0945 (−0.0522)	0.0868 (0.0817)	0.0856 (−0.0042)	0.0849 (0.0146)	0.0840 (0.0091)	0.0856 (−0.0055)	0.0809 (−0.0068)
					0.0889 (0.0047)	0.0891 (0.0130)	0.0835 (−0.0430)	0.0916 (0.0038)	0.0789 (−0.0354)
		b	0.0995 (−0.0351)	0.1007 (0.1071)	0.0942 (0.0128)	0.0953 (0.0334)	0.0937 (0.0270)	0.0941 (0.0114)	0.0911 (0.0084)
					0.0930 (0.0595)	0.0946 (0.0678)	0.0790 (0.0092)	0.0949 (0.0614)	0.0729 (0.0220)
		c	0.1425 (0.0534)	0.1695 (0.2274)	0.1329 (0.1116)	0.1382 (0.1367)	0.1136 (0.1285)	0.1325 (0.1099)	0.1019 (0.1063)
					0.1389 (0.1643)	0.1332 (0.1730)	0.0974 (0.1087)	0.1342 (0.1671)	0.0896 (0.1352)
		d	0.1218 (−0.0335)	0.1299 (0.1322)	0.1163 (0.0213)	0.1190 (0.0474)	0.1060 (0.0390)	0.1161 (0.0195)	0.1028 (0.0158)
					0.1032 (0.0789)	0.1061 (0.0886)	0.0883 (0.0227)	0.1056 (0.0831)	0.0844 (0.0611)
40	38	a	0.0582 (−0.0290)	0.0558 (0.0698)	0.0560 (0.0014)	0.0564 (0.0139)	0.0460 (0.0111)	0.0560 (0.0008)	0.0420 (−0.0006)
					0.0512 (0.0420)	0.0520 (0.0474)	0.0451 (0.0107)	0.0516 (0.0440)	0.0401 (0.0195)
		b	0.0603 (−0.0303)	0.0576 (0.0701)	0.0579 (0.0007)	0.0583 (0.0135)	0.0478 (0.0106)	0.0579 (0.0000)	0.0449 (−0.0014)
					0.0530 (0.0412)	0.0538 (0.0467)	0.0466 (0.0091)	0.0534 (0.0432)	0.0428 (0.0179)
		c	0.0613 (0.0079)	0.0648 (0.1096)	0.0612 (0.0388)	0.0625 (0.0517)	0.0519 (0.0487)	0.0612 (0.0381)	0.0510 (0.0367)
					0.0592 (0.0787)	0.0605 (0.0843)	0.0502 (0.0452)	0.0598 (0.0806)	0.0454 (0.0551)
		d	0.0620 (−0.0317)	0.0593 (0.0705)	0.0596 (−0.0002)	0.0599 (0.0129)	0.0494 (0.0100)	0.0595 (−0.0010)	0.0485 (−0.0024)
					0.0545 (0.0402)	0.0553 (0.0459)	0.0480 (0.0075)	0.0549 (0.0421)	0.0435 (0.0163)
	34	a	0.0615 (−0.0421)	0.0672 (0.0560)	0.0585 (−0.0112)	0.0584 (0.0012)	0.0482 (−0.0015)	0.0575 (−0.0119)	0.0455 (−0.0133)
					0.0544 (0.0298)	0.0549 (0.0351)	0.0500 (−0.0006)	0.0549 (0.0319)	0.0436 (0.0076)
		b	0.0666 (−0.0449)	0.0720 (0.0583)	0.0633 (−0.0125)	0.0632 (0.0010)	0.0529 (−0.0020)	0.0623 (−0.0132)	0.0503 (−0.0146)
					0.0575 (0.0303)	0.0581 (0.0360)	0.0525 (−0.0021)	0.0580 (0.0323)	0.0467 (0.0065)
		c	0.0685 (0.0551)	0.0849 (0.1651)	0.0680 (0.0885)	0.0706 (0.1028)	0.0594 (0.0994)	0.0678 (0.0878)	0.0555 (0.0863)
					0.0686 (0.1278)	0.0704 (0.1338)	0.0541 (0.0899)	0.0696 (0.1292)	0.0525 (0.1013)
		d	0.0695 (−0.0444)	0.0783 (0.0650)	0.0681 (−0.0100)	0.0690 (0.0049)	0.0586 (0.0015)	0.0660 (−0.0108)	0.0540 (−0.0123)
					0.0626 (0.0334)	0.0633 (0.0395)	0.0573 (−0.0014)	0.0632 (0.0353)	0.0531 (0.0079)
	30	a	0.0696 (−0.0268)	0.0769 (0.0738)	0.0601 (0.0038)	0.0673 (0.0166)	0.0569 (0.0137)	0.0591 (0.0031)	0.0540 (0.0017)
					0.0592 (0.0294)	0.0597 (0.0352)	0.0543 (−0.0037)	0.0601 (0.0303)	0.0491 (0.0038)
		b	0.0724 (−0.0255)	0.0818 (0.0829)	0.0672 (0.0069)	0.0707 (0.0213)	0.0602 (0.0180)	0.0652 (0.0061)	0.0571 (0.0046)
					0.0592 (0.0453)	0.0591 (0.0516)	0.0589 (0.0093)	0.0586 (0.0467)	0.0539 (0.0180)
		c	0.0995 (0.0887)	0.1025 (0.2129)	0.0934 (0.1250)	0.0974 (0.1414)	0.0855 (0.1374)	0.0932 (0.1242)	0.0827 (0.1224)
					0.0916 (0.1585)	0.0943 (0.1655)	0.0785 (0.1141)	0.0927 (0.1584)	0.0727 (0.1267)
		d	0.0720 (−0.0316)	0.0814 (0.0881)	0.0690 (0.0041)	0.0696 (0.0210)	0.0619 (0.0171)	0.0679 (0.0032)	0.0589 (0.0014)
					0.0627 (0.0427)	0.0638 (0.0499)	0.0590 (0.0013)	0.0630 (0.0434)	0.0571 (0.0105)
50	40	a	0.0424 (−0.0218)	0.0484 (0.0613)	0.0410 (0.0014)	0.0411 (0.0114)	0.0409 (0.0097)	0.0410 (0.0010)	0.0409 (0.0001)
					0.0399 (0.0288)	0.0403 (0.0334)	0.0366 (0.0031)	0.0402 (0.0298)	0.0391 (0.0093)
		b	0.0456 (−0.0217)	0.0529 (0.0671)	0.0441 (0.0030)	0.0443 (0.0142)	0.0441 (0.0122)	0.0441 (0.0025)	0.0440 (0.0016)
					0.0409 (0.0333)	0.0414 (0.0384)	0.0368 (0.0052)	0.0411 (0.0343)	0.0396 (0.0118)
		c	0.0966 (0.0888)	0.1268 (0.1867)	0.1000 (0.1154)	0.1027 (0.1276)	0.1018 (0.1252)	0.0998 (0.1149)	0.0996 (0.1138)
					0.1008 (0.1417)	0.1026 (0.1472)	0.0870 (0.1082)	0.1016 (0.1418)	0.0950 (0.1175)
		d	0.0540 (−0.0221)	0.0633 (0.0742)	0.0522 (0.0046)	0.0526 (0.0172)	0.0523 (0.0149)	0.0522 (0.0041)	0.0522 (0.0030)
					0.0483 (0.0348)	0.0490 (0.0404)	0.0432 (0.0031)	0.0486 (0.0353)	0.0467 (0.0101)
60	20	a	0.0988 (−0.0746)	0.1046 (0.0766)	0.0872 (−0.0237)	0.0851 (0.0001)	0.0848 (−0.0035)	0.0873 (−0.0244)	0.0870 (−0.0274)
					0.0848 (−0.0243)	0.0849 (−0.0151)	0.0846 (−0.0729)	0.0856 (−0.0281)	0.0944 (−0.0772)
		b	0.0855 (−0.0552)	0.0912 (0.0727)	0.0775 (−0.0158)	0.0761 (0.0041)	0.0758 (0.0010)	0.0775 (−0.0164)	0.0778 (−0.0177)
					0.0758 (−0.0191)	0.0757 (−0.0106)	0.0752 (−0.0631)	0.0780 (−0.0255)	0.0829 (−0.0623)
		c	0.1145 (−0.0650)	0.1394 (0.1289)	0.1044 (−0.0102)	0.1042 (0.0194)	0.1031 (0.0145)	0.1045 (−0.0111)	0.1034 (−0.0175)
					0.0939 (0.0038)	0.0956 (0.0150)	0.0866 (−0.0561)	0.0946 (−0.0103)	0.0995 (−0.0594)
		d	0.1151 (−0.0234)	0.1450 (0.1261)	0.1097 (0.0129)	0.1120 (0.0391)	0.1103 (0.0342)	0.1096 (0.0120)	0.1095 (0.0102)
					0.1034 (−0.0008)	0.1046 (0.0110)	0.0937 (−0.0618)	0.1043 (−0.0069)	0.1056 (−0.0549)
100	50	a	0.0298 (−0.0287)	0.0311 (0.0392)	0.0282 (−0.0110)	0.0280 (−0.0028)	0.0280 (−0.0035)	0.0283 (−0.0111)	0.0283 (−0.0114)
					0.0280 (−0.0113)	0.0279 (−0.0077)	0.0281 (−0.0299)	0.0283 (−0.0135)	0.0291 (−0.0286)
		b	0.0287 (−0.0236)	0.0302 (0.0395)	0.0275 (−0.0088)	0.0273 (−0.0014)	0.0273 (−0.0021)	0.0275 (−0.0090)	0.0275 (−0.0093)
					0.0275 (−0.0050)	0.0275 (−0.0014)	0.0273 (−0.0231)	0.0278 (−0.0056)	0.0283 (−0.0203)
		c	0.0385 (−0.0270)	0.0434 (0.0623)	0.0369 (−0.0057)	0.0369 (0.0051)	0.0368 (0.0041)	0.0369 (−0.0059)	0.0368 (−0.0063)
					0.0352 (0.0037)	0.0354 (0.0083)	0.0341 (−0.0202)	0.0354 (−0.0003)	0.0357 (−0.0196)
		d	0.0410 (−0.0136)	0.0472 (0.0632)	0.0401 (0.0031)	0.0403 (0.0131)	0.0402 (0.0121)	0.0401 (0.0029)	0.0401 (0.0025)
					0.0385 (0.0132)	0.0388 (0.0180)	0.0364 (−0.0117)	0.0387 (0.0123)	0.0384 (−0.0075)
200	100	a	0.0147 (−0.0171)	0.0151 (0.0227)	0.0142 (−0.0084)	0.0141 (−0.0044)	0.0141 (−0.0045)	0.0142 (−0.0085)	0.0142 (−0.0085)
					0.0142 (−0.0086)	0.0141 (−0.0067)	0.0142 (−0.0179)	0.0143 (−0.0096)	0.0145 (−0.0171)
		b	0.0143 (−0.0139)	0.0148 (0.0234)	0.0140 (−0.0066)	0.0139 (−0.0029)	0.0139 (−0.0030)	0.0140 (−0.0066)	0.0140 (−0.0067)
					0.0140 (−0.0048)	0.0140 (−0.0030)	0.0140 (−0.0138)	0.0141 (−0.0050)	0.0142 (−0.0123)
		c	0.0186 (−0.0203)	0.0198 (0.0316)	0.0181 (−0.0099)	0.0180 (−0.0045)	0.0180 (−0.0048)	0.0181 (−0.0100)	0.0181 (−0.0101)
					0.0176 (−0.0056)	0.0176 (−0.0033)	0.0176 (−0.0175)	0.0177 (−0.0076)	0.0179 (−0.0172)
		d	0.0188 (−0.0136)	0.0204 (0.0321)	0.0185 (−0.0052)	0.0185 (−0.0003)	0.0185 (−0.0005)	0.0185 (−0.0053)	0.0185 (−0.0054)
					0.0180 (0.0012)	0.0181 (0.0036)	0.0177 (−0.0110)	0.0181 (0.0010)	0.0181 (−0.0088)

^† MSE (Bias).

In Table 2 and Table 3, MSEs and biases of all estimates of entropy are presented for various n, m, ${\mathcal{T}}_1$, ${\mathcal{T}}_2$ and PrC schemes. We tabulated MSE and bias of the respective MLE in the fourth column of Table 2 and Table 3. We also tabulated MSE and bias of the respective MPSE in the fifth column. Uniformly, all other columns contain two values. The 1st values represent the MSE and bias of BEs by using the importance sampling procedure. The 2nd values represent the MSE and bias of BEs by using the TiKa method.

In Table 4, interval estimates for entropy are tabulated for various n, m, ${\mathcal{T}}_1$, ${\mathcal{T}}_2$ and PrC schemes. Approximate CI is computed using the normality property of MLE. Estimates of HPD credible interval using importance sampling method are also tabulated in Table 4. In Table 4, we also tabulate the coverage probability (CP) for the interval estimates.

Table 4. The relative CLs and CPs of entropy estimators with classical and BayEst.

n	m	Sch.	${\mathcal{T}}_1=1.5$, ${\mathcal{T}}_2=2.0$				${\mathcal{T}}_1=1.5$, ${\mathcal{T}}_2=2.5$
			$\widehat{\mathbb{H}}$	${\widehat{\mathbb{H}}}_{\mathit{S}}$	${\widehat{\mathbb{H}}}_{\mathit{L}}$	${\widehat{\mathbb{H}}}_{\mathit{E}}$	$\widehat{\mathbb{H}}$	${\widehat{\mathbb{H}}}_{\mathit{S}}$	${\widehat{\mathbb{H}}}_{\mathit{L}}$	${\widehat{\mathbb{H}}}_{\mathit{E}}$
20	18	a	1.4083 (92.3) ${}^{†}$	1.4688 (96.5)	1.4794 (96.8)	1.4422 (96.0)	1.2816 (92.5)	1.3244 (95.6)	1.3321 (95.4)	1.3024 (95.3)
		b	1.4455 (91.2)	1.5081 (95.9)	1.5192 (96.2)	1.4807 (95.8)	1.3076 (92.2)	1.3537 (96.1)	1.3620 (95.8)	1.3308 (95.8)
		c	1.4487 (92.0)	1.5104 (96.2)	1.5213 (96.7)	1.4832 (95.3)	1.3425 (93.6)	1.3890 (96.0)	1.3973 (95.8)	1.3657 (95.4)
		d	1.4837 (91.3)	1.5521 (96.0)	1.5640 (96.4)	1.5232 (95.3)	1.3432 (92.0)	1.3937 (96.1)	1.4027 (96.3)	1.3696 (95.9)
	16	a	1.4171 (93.1)	1.4746 (96.9)	1.4848 (96.7)	1.4483 (96.7)	1.2865 (92.9)	1.3303 (95.9)	1.3381 (95.5)	1.3081 (95.9)
		b	1.4958 (92.1)	1.5636 (96.3)	1.5755 (96.7)	1.5347 (96.1)	1.3481 (92.9)	1.3984 (96.0)	1.4074 (95.8)	1.3743 (95.9)
		c	1.5006 (93.2)	1.5684 (97.8)	1.5802 (97.6)	1.5395 (97.1)	1.4255 (92.0)	1.4792 (94.4)	1.4887 (94.0)	1.4537 (94.1)
		d	1.5764 (91.7)	1.6577 (97.0)	1.6716 (97.6)	1.6255 (96.7)	1.4286 (93.1)	1.4892 (97.1)	1.4998 (96.9)	1.4623 (96.7)
	14	a	1.4185 (90.8)	1.4767 (96.7)	1.4870 (97.1)	1.4503 (96.3)	1.2961 (90.3)	1.3457 (96.5)	1.3544 (96.8)	1.3225 (96.3)
		b	1.5173 (92.5)	1.5922 (97.4)	1.6050 (97.2)	1.5618 (96.6)	1.3771 (90.8)	1.4339 (97.1)	1.4439 (97.5)	1.4084 (96.2)
		c	1.5615 (93.5)	1.6459 (97.4)	1.6599 (97.2)	1.6138 (96.5)	1.5104 (89.6)	1.5793 (90.9)	1.5910 (90.4)	1.5504 (91.1)
		d	1.6679 (92.9)	1.7705 (97.4)	1.7873 (97.6)	1.7339 (96.8)	1.5089 (90.8)	1.5852 (97.1)	1.5982 (97.3)	1.5548 (96.7)
30	28	a	1.1364 (92.3)	1.1651 (95.1)	1.1704 (95.0)	1.1475 (94.9)	1.0334 (94.5)	1.0550 (96.1)	1.0588 (95.9)	1.0400 (95.5)
		b	1.1550 (93.4)	1.1852 (97.0)	1.1907 (97.0)	1.1671 (96.1)	1.0520 (94.0)	1.0748 (96.1)	1.0789 (95.9)	1.0594 (95.3)
		c	1.1586 (92.0)	1.1883 (96.7)	1.1937 (96.8)	1.1703 (96.5)	1.0731 (94.2)	1.0958 (95.7)	1.0998 (95.9)	1.0802 (95.8)
		d	1.1720 (92.3)	1.2038 (96.7)	1.2096 (96.6)	1.1851 (96.4)	1.0680 (93.9)	1.0919 (96.2)	1.0962 (95.8)	1.0761 (95.8)
	24	a	1.1394 (93.1)	1.1683 (95.3)	1.1735 (95.4)	1.1506 (95.0)	1.0342 (92.6)	1.0562 (96.0)	1.0601 (96.2)	1.0411 (95.7)
		b	1.1955 (93.5)	1.2290 (95.5)	1.2352 (95.3)	1.2098 (95.5)	1.0874 (92.6)	1.1127 (95.4)	1.1173 (95.3)	1.0964 (95.2)
		c	1.2206 (92.3)	1.2547 (94.6)	1.2609 (94.5)	1.2351 (94.8)	1.1616 (91.6)	1.1888 (94.1)	1.1937 (94.0)	1.1714 (94.4)
		d	1.2663 (93.0)	1.3063 (95.9)	1.3136 (95.8)	1.2850 (95.2)	1.1498 (92.6)	1.1800 (95.4)	1.1855 (95.1)	1.1620 (95.7)
30	20	a	1.1495 (94.3)	1.1955 (96.1)	1.2030 (96.3)	1.1750 (96.1)	1.0721 (91.8)	1.1136 (94.8)	1.1201 (95.2)	1.0948 (94.5)
		b	1.2471 (93.5)	1.2875 (95.1)	1.2947 (95.1)	1.2666 (94.9)	1.1352 (92.2)	1.1669 (95.5)	1.1724 (95.2)	1.1489 (95.3)
		c	1.3096 (94.6)	1.3631 (94.3)	1.3720 (94.4)	1.3392 (94.6)	1.2545 (92.2)	1.3006 (94.0)	1.3082 (94.7)	1.2788 (94.3)
		d	1.3843 (93.7)	1.4380 (95.6)	1.4475 (95.0)	1.4129 (95.4)	1.2641 (92.5)	1.3053 (94.8)	1.3127 (94.7)	1.2839 (94.4)
40	38	a	0.9743 (93.2)	0.9923 (94.8)	0.9955 (95.0)	0.9788 (94.6)	0.8880 (92.9)	0.9016 (95.2)	0.9039 (95.4)	0.8900 (95.1)
		b	0.9920 (92.9)	1.0107 (95.0)	1.0140 (95.1)	0.9968 (94.7)	0.9042 (92.3)	0.9184 (95.1)	0.9208 (95.0)	0.9065 (94.3)
		c	0.9934 (93.4)	1.0118 (95.9)	1.0150 (96.0)	0.9980 (95.4)	0.9180 (93.7)	0.9322 (94.4)	0.9345 (94.2)	0.9202 (94.4)
		d	1.0048 (93.2)	1.0243 (95.4)	1.0277 (95.7)	1.0101 (94.7)	0.9147 (92.3)	0.9294 (94.7)	0.9319 (94.6)	0.9173 (94.2)
	34	a	0.9798 (93.4)	0.9979 (95.3)	1.0010 (95.5)	0.9843 (94.7)	0.8940 (92.4)	0.9077 (95.6)	0.9099 (95.6)	0.8960 (95.4)
		b	1.0107 (92.8)	1.0309 (95.0)	1.0345 (94.9)	1.0165 (94.3)	0.9199 (93.5)	0.9351 (94.6)	0.9377 (94.6)	0.9228 (94.6)
		c	1.0256 (93.2)	1.0458 (94.5)	1.0493 (94.2)	1.0312 (94.3)	0.9690 (91.8)	0.9849 (91.7)	0.9876 (91.2)	0.9720 (91.6)
		d	1.0513 (92.4)	1.0742 (94.3)	1.0783 (94.4)	1.0587 (94.0)	0.9588 (93.6)	0.9762 (95.2)	0.9791 (95.0)	0.9629 (94.8)
	30	a	0.9827 (93.6)	1.0007 (95.3)	1.0038 (95.8)	0.9871 (95.1)	0.9020 (92.4)	0.9162 (94.5)	0.9185 (94.8)	0.9043 (93.7)
		b	1.0439 (93.1)	1.0656 (95.3)	1.0695 (95.5)	1.0505 (95.1)	0.9529 (93.5)	0.9694 (95.4)	0.9723 (95.3)	0.9565 (95.1)
		c	1.0813 (91.7)	1.1044 (92.8)	1.1085 (92.6)	1.0887 (92.8)	1.0363 (93.3)	1.0552 (94.7)	1.0585 (94.7)	1.0409 (94.3)
		d	1.1237 (93.4)	1.1510 (95.5)	1.1559 (95.7)	1.1338 (95.1)	1.0220 (92.8)	1.0427 (95.4)	1.0464 (95.5)	1.0281 (95.3)
50	40	a	0.8757 (93.6)	0.8883 (95.1)	0.8902 (95.7)	0.8770 (94.8)	0.7987 (94.1)	0.8083 (95.6)	0.8096 (95.6)	0.7986 (95.0)
		b	0.9186 (93.6)	0.9332 (95.4)	0.9357 (95.5)	0.9211 (94.8)	0.8383 (93.8)	0.8495 (95.1)	0.8511 (95.6)	0.8390 (95.3)
		c	0.9462 (93.7)	0.9613 (92.9)	0.9637 (92.6)	0.9488 (92.8)	0.8970 (86.6)	0.9090 (86.2)	0.9108 (84.7)	0.8978 (85.9)
		d	0.9700 (93.5)	0.9873 (95.2)	0.9903 (94.8)	0.9740 (94.8)	0.8871 (93.4)	0.9004 (94.7)	0.9025 (94.7)	0.8888 (94.7)
60	20	a	1.0932 (91.2)	1.0579 (95.2)	1.0440 (95.3)	1.0485 (94.2)	1.0932 (91.2)	1.0579 (95.2)	1.0440 (95.3)	1.0485 (94.2)
		b	1.0435 (92.0)	1.0697 (94.8)	1.0741 (94.9)	1.0539 (94.4)	1.0380 (92.0)	1.0640 (95.0)	1.0684 (95.0)	1.0483 (94.8)
		c	1.2757 (91.8)	1.9607 (96.0)	2.1076 (96.2)	1.7751 (95.8)	1.2259 (91.6)	1.9053 (95.5)	2.0512 (95.8)	1.7213 (95.3)
		d	1.3373 (92.8)	1.3839 (94.9)	1.3923 (94.8)	1.3606 (95.2)	1.2321 (92.9)	1.2690 (94.4)	1.2757 (94.5)	1.2487 (94.2)
100	50	a	0.6751 (94.0)	0.6809 (96.5)	0.6814 (96.1)	0.6735 (95.9)	0.6749 (94.0)	0.6808 (96.6)	0.6812 (96.2)	0.6733 (96.0)
		b	0.7031 (94.4)	0.7095 (95.6)	0.7100 (95.4)	0.7016 (95.5)	0.6662 (94.3)	0.6718 (96.1)	0.6721 (95.9)	0.6645 (96.0)
		c	0.8068 (93.5)	0.8168 (95.0)	0.8182 (95.3)	0.8069 (94.7)	0.7655 (94.2)	0.7741 (95.5)	0.7751 (95.5)	0.7650 (95.3)
		d	0.8446 (94.3)	0.8558 (95.1)	0.8575 (95.0)	0.8452 (95.2)	0.7789 (94.3)	0.7877 (95.1)	0.7880 (95.2)	0.7784 (95.1)
200	100	a	0.4778 (94.6)	0.4799 (95.4)	0.4793 (95.3)	0.4755 (95.0)	0.4778 (94.6)	0.4799 (95.4)	0.4793 (95.3)	0.4754 (95.0)
		b	0.4945 (95.2)	0.4967 (95.5)	0.4962 (95.3)	0.4921 (95.2)	0.4713 (95.2)	0.4732 (95.9)	0.4727 (95.5)	0.4689 (95.3)
		c	0.5692 (94.4)	0.5726 (95.4)	0.5724 (95.4)	0.5669 (94.9)	0.5409 (94.3)	0.5438 (95.2)	0.5435 (95.3)	0.5385 (95.3)
		d	0.5933 (95.3)	0.5972 (94.7)	0.5971 (95.0)	0.5911 (94.8)	0.5473 (95.1)	0.5504 (95.5)	0.5501 (95.9)	0.5450 (95.3)

^† CL (CP).

5.3. Discussion

This study deals with the classical and BayEsts of the entropy of a IWD under GAPHC scheme. For BayEsts, the performance depends on the loss function assumed. In practice, the loss function is often not symmetric. Therefore, we consider the BayEsts of the entropy based on flexible loss functions. In the above subsection, it is revealed that the BayEst under asymmetric loss is more efficient than the BayEst under symmetry loss function.

In general, the MSE and bias decrease as the sample size (n) and progressive censored sample size (m) increase. For fixed sample size and progressive censored sample size, generally, the MSE and bias decrease as the longest test time (${\mathcal{T}}_2$) increases. Additionally, the estimates for Sch. b and c behave quite similarly in terms of bias and MSE. The proposed classical and BayEsts for Sch. a have a smaller MSE than the corresponding proposed classical and BayEsts for the other Sch. b, c and d.

Additionally, among the classical estimators, we observe that MLE are superior to the respective MPSE in terms of MSE and bias. Furthermore, we can observe that the BEs of entropy under SELF and GELF for the choice $q=-0.25$ behave almost similarly in terms of MSE and bias. However, we can observe that BEs of entropy under GELF are better than the BEs of entropy under other loss functions in terms of MSE. We observe that the TiKa method perform better compared to the classical estimates. The problem of selecting a loss function is concerned; it can be seen that GELF emerges as the best loss function. Among BEs of entropy, we observe that BEs obtained using the GELF and LLF for the choice $q=1.25$ and $c=1.25$ have overall lower MSE, respectively.

In general, the average confidence length (CL) of the approximate CI and HPD credible interval using importance sampling method tends to decrease with the effective increase in sample size and progressive censored data size. We observe that the average CL of credible interval is wider than the corresponding average CL of approximate CI. CP of approximate CI is mostly below 95%. In the case of the credible interval, however, in some cases, CP lies below 95%, and for some schemes it lies above 95%.

6. Conclusions

In this paper, we consider the MLE, MPSE and BayEst of the entropy of a IWD under GAPHC scheme. We observe that the classical estimators of the entropy cannot be derived in closed form. The associated classical estimates are computed using a Newton–Raphson method. Additionally, we propose the TiKa method and importance sampling procedure of the BayEsts. Moreover, the importance sampling procedure is used to obtain the credible interval for the entropy of the IWD under GAPHC scheme. Among the classical estimators, we observe that MLE are superior to the respective MPSE in terms of MSE and bias. We can also observe that BEs of entropy under GELF are better than the BEs of entropy under other loss functions in terms of MSE. Among the BayEsts, the choices $q=1.25$ and $c=1.25$ seem to be reasonable under GELF and LLF, respectively. In the interval estimation, we observe that the average CL of credible interval is wider than the corresponding average CL of approximate CI. Although we focus on the entropy estimate of the IWD based on the GAPHC scheme, the Bayes estimation can be applied to any other distributions. The estimation of the uncertainty measure from other distributions based on the GAPHC scheme is of potential interest for future research.