A Guaranteed Approximation Algorithm for QoS Anypath Routing in WMNs

Abstract

Anypath routing is a hot research topic for QoS guarantee in wireless mesh networks (WMNs). According to time-varying characteristics of WMNs and the idea of anypath routing, a system network modeling method is proposed to address the multiple constrained optimization anypath problem. It focuses on the application of WMNs; under various QoS constraints, it satisfies a specific constraint and approaches other QoS constraints from an approximate perspective. A heuristic multi-constrained anypath algorithm with a time complexity as Dijkstra is proposed for the problem, and the algorithm is proved to be a K-1 approximation algorithm. The feasibility of the algorithm is verified, then its computational efficiency and performance are evaluated through simulation experiments, respectively. According to the application characteristics of wireless networks, the algorithm is suitable for WMNs and has good compatibility with existing routing protocols.

1. Introduction

In the process of the rapid development of the Internet of Things, new wireless mesh networks (WMNs) are generated by the convergence of WLAN and ad-hoc networks due to the presence of a large number of sensors and corresponding communication methods [1,2,3]. In recent years, a large number of applications of WMNs have appeared in people’s life, such as wireless telemedicine, wireless online shopping, wireless video on demand, wireless multi-party voice conferences, and so on. As a result, people are very concerned about the quality of service (QoS) of WMNs, such as the delay, delay jitter, cost, bandwidth, and so on. In WMNs, to find the optimal path (minimum delay, minimum cost, or maximum bandwidth) from the source node to the destination node, many researchers have continued to conduct relevant studies [4,5,6,7,8,9,10,11,12]. In [13], the lowest cost anypath routing (LCAR) method was discussed, which was applied to low-power and low-rate wireless communications, then a new wireless link layer technology with high stability and robustness was introduced in combination with anypath routing to reduce transmission costs. On this basis, a new paradigm of wireless multi-hop network anypath routing was proposed [14]. They were all concerned about the guarantee of a certain QoS and mainly used unicast routing algorithms. In multi-rate routing, each node uses a set of next hops and a selected transmission rate to forward packets; thus, two polynomial time algorithms proved to be optimal and suitable for deployment in routing protocols are proposed. The LCAR method was extended to support multicast anypath routing from one source to multiple destinations [15], which can be used to calculate the multicast cost metrics and determine the forwarding policy for the forwarding set, so that the packets can effectively reach all destination nodes. Furthermore, the spatial diversity and broadcast properties of wireless media were used to improve the performance of unreliable wireless networks [16]. Considering the anypath routing with multiple constraints, a K approximation algorithm was proposed to approximate all constraints simultaneously [16]. The advantage of this method is that it runs very fast; however, on a small-scale network, the error of the optimal solution could not be guaranteed. Recently, the anypath routing method was proposed to improve the reliability of multi-hop vehicular ad-hoc network (vanet) communication [17]. It was the first time to solve the link stability firstly and propose a stable life path of the long lifecycle of the anypath routing method, which was better than the classic Shortest Anypath First (SAF) method. Considering that the spatial reusability of wireless communication media can greatly improve the end-to-end throughput of multi-hop wireless networks, a spatial reusable awareness of single-path routing and anypath routing protocol was proposed in [18], which significantly improved the performance on the basics of an existing protocol. Unfortunately, there was no literature on QoS guarantee algorithm for wireless multimedia applications based on this protocol. Moreover, the routing problem in a multi-hop cognitive network (CR) with the newly proposed CR as an example was studied in [19]. Considering the typical spectrum uncertainties of CR and the unreliable transmission of wireless media, an anypath routing scheme based on spectrum recognition was proposed.

In the above research on WMNs, hot research on anypath routing is emerging, which aims to find an anypath routing method which ensures the optimal performance of one or more QoS metrics (such as delay, bandwidth, and power consumption). Previous research on anypath routing focused on considering a QoS metric constraint, calculating anypath routing with the minimum delay or minimum power consumption, or searching for anypath routing to ensure that one of the QoS parameters is optimal [17,18,19]. So far, there is minimal literature on anypath routing involve propagation delay, energy consumption, minimum bandwidth, delay jitter, and other QoS constraints. Only the Decision version of Multiple Constrained Anypath Problem (DMCAP) was proposed for the first time, and then the Optimized version of Multiple Constrained Anypath Problem (OMCAP) was studied in the literature [16]. Thus, the previous research on anypath routing of multi-constrained QoS has mainly focused on finding an anypath routing method with one optimal QoS parameter or approximating all constraints from an approximate perspective in the ideal state.

There has been a lot of research on the multi-constrained single-path routing problem with good performance [20,21]. The previous research is all aimed at general multimedia service applications, but may not be suitable for specific wireless multimedia applications. As far as we know, there is no research on the guarantee of multi-constraint anypath routing under the premise of satisfying one QoS. Therefore, we need to develop a new QoS guarantee scheme for specific wireless multimedia application services.

However, in wireless multimedia applications, one of the QoS parameters needs to be guaranteed while others need to be optimized. For example, real-time services such as voice and video have strict requirements on delay jitter, but also need to provide as large transmission bandwidth and as small transmission delay as possible. Thus, the Multiple Constrained Optimization Anypath Problem (MCOAP) is addressed in this paper. Different from previous studies, a Heuristic Multi-constrained Anypath Algorithm (HMAA) with a guaranteed constraint while approximating $K-1(K\ge 3)$ QoS constraints, compatible with existing wireless routing protocols, is developed to provide a fast and efficient solution for WMNs applications. This paper has three major contributions, which are as follows.

• The MCOAP model is proposed from an approximate point of view. In the case that most important service performance of WMNs is guaranteed, the model can also consider multiple QoS metrics in WMNs;
• The problem of MCOAP is formulated, then an approximation algorithm called HMAA, which approximates $K-1(K\ge 3)$ QoS constraints with a specific constraint, is developed;
• The theoretical properties of the proposed algorithm are analyzed. The analysis results show that the proposed algorithm achieves lower complexity and approximate optimal solution for WMNs.

The rest is arranged as follows: the second section formally sets out the problem to be studied and the symbols to be used in subsequent sections. The third section presents the approximation algorithm and theoretical analysis of anypath routing under multiple QoS constraints. In Section 4, simulation results obtained from special networks are reported to verify the algorithm. Finally, the fifth section summarizes the paper.

2. Problem Description and Related Works

This paper is based on the weight of node v in the network, and the weight on the edge represents the forwarding probability. In the existing study of routing protocol [22,23,24], there are at least three Media Access Control (MAC) layer protocols that can support anypath routing. The anypath routing for WMNs and the Expected Weight of Anypath Transmissions (EWATX) were modeled in [16], based on which the research of this paper is carried out. First, the basic anypath routing DMCAP is introduced, and then the MCOAP studied in this paper is proposed. Frequently used notations are shown in Table 1.

Table 1. Frequently used notations.

s, t	the source node and the destination node, respectively
m, n	the edge and the node number of graph G, respectively
$w_i(v)$	ith weight of node v
$p(v,u)$	forwarding probability from node v to node u
F	forwarding sets of node v
$p(v,F)$	forwarding probability from node v to forwarding sets F
K	the number of QoS requirements
$\stackrel{\rightharpoonup }{W}$	the set of weights of the edges
$\stackrel{\rightharpoonup }{L}$	the set of constraints
$L_i$	ith QoS requirement
$P_s$	the anypath routing from source node s to destination node t
$P_s{}^{opt}$	the optimal anypath routing
$P_s{}^{*}$	the approximate optimal anypath routing
$w_i(v,P_s)$	ith weight from node v to destination node t along $P_s$
$w_{\mathrm{M}}(v)$	the maximum weight of node v
$w_{{}_{\mathrm{M}}}(v,P_s)$	the maximum weight from node v to destination node t along $P_s$
$w_{{}_{\mathrm{M}}}(F,P_s)$	the maximum weight from forwarding sets F to destination node t along $P_s$

Definition 1.

DMCAP Problem. Consider a directed and connected graph$G(V,E,\stackrel{\rightharpoonup }{W},\stackrel{\rightharpoonup }{L},\stackrel{\rightharpoonup }{p})$, where$\left|V\right|=n$is the set of vertices in the figure, $\left|E\right|=m$is the set of edges, $p\left(e\right)\in (0,1]$is the probability of packet forwarding on one edge, the ith weight on a node$v\in V$is$w_i\left(v\right)$, $\stackrel{\rightharpoonup }{W}=\left\{w_i\left(v\right)\right\}|w_i\left(v\right)\ge 0$is the set of total weights on node v; the positive matrix$\stackrel{\rightharpoonup }{L}=(L_1,L_2,\dots ,L_{\mathrm{K}})$is a set of$\mathrm{K}(\mathrm{K}\ge 3)$QoS constraints. The DMCAP problem is to find an anypath routing from s to t to satisfy the condition.

$$w_i(s,P_s)\le L_i,\forall 1\le i\le \mathrm{K}.$$

(1)

An anypath routing that satisfies formula (1) is called a feasible solution to the DMCAP problem, thus all feasible anypath routing in graph G are expressed as $\left\{P_s\right\}$. However, a feasible solution to the DMCAP problem is computationally very complex, and the literature [16] proves that it is a NP-hard problem.

Definition 2.

MCOAP Problem. The MCOAP problem is to find an optimal anypath among all the anypath routing$\left\{P_s\right\}$from s to t that satisfies the constraints and minimizes the other values of the anypath routing.

The computing performance of the routing adapters in WMNs is limited, so it seems unrealistic to run an intelligent algorithm and spend a lot of time on finding a feasible solution to the DMCAP problem. In wireless multimedia applications, more and more business application requirements turn out to be mandatory to meet a QoS constraint while approximating the remaining QoS constraints from an approximate perspective. This paper introduces the anypath auxiliary length value $\widehat{w}(v,P_s)$ shown in Equation (2)

$$\widehat{w}(v,P_s)=\underset{2\le i\le \mathrm{K}}{\max }\frac{w_i(v,P_s)}{L_i}.$$

(2)

Definition 3.

$\alpha (\alpha \ge 1)$approximation algorithm. If an algorithm finds an anypath$P_s^{*}$from s to t that satisfies the condition$\widehat{w}(s,P_s^{*})\le \alpha \cdot \widehat{w}(s,P_s^{opt}),s.t.w_1(v,P_s^{opt})\le L_1$, we say it is an approximation algorithm for MCOAP problems.

Definition 4.

Auxiliary Anyptah Weight (AAW) for EWATX [16]. The AAW along anypath routing from node v to t is

$$w_m(v,P_s)=\frac{w_m(v)}{p(v,F(v,P_s))}+w_m(F(v,P_s),P_s).$$

(3)

Remark 1.

The OMCAP problem has been proposed in [16], thus the anypath routing of the multi-constrained QoS was studied in an ideal state from an approximate perspective. Differing from previous studies, this paper examines the MCOAP problem: looking for an anypath routing$P_s^{*}$that satisfies a specific QoS constraint such as tightly limited transmission times, limited transmission power, limited bandwidth, etc., while approximating other QoS constraints.

3. An Anypath Routing Approximation Algorithm for QoS

In this paper, the HMAA is proposed to calculate an anypath routing from s to t from an approximate perspective in a reasonable time. In order to simplify the operation, the weight $w_i\left(v\right)$ of all nodes $v\in V$ are normalized as $w_i\left(v\right)/L_i,\forall 2\le i\le \mathrm{K}$, thus the corresponding constraints become $L_2=\mathrm{\dots }{L}_{\mathrm{K}}=1$.

3.1. Design of HMAA Algorithm

The design of HMAA algorithm is described below. Each node $v\in V$ has an auxiliary variable ${\widehat{w}}_m(v)$, a forwarding set $\widehat{F}(v,P)$, and K value ${\widehat{w}}_i(v)$, which represents the current calculated value from v to t along anypath, respectively. The algorithm uses two data queues P and Q. P is a linked list that stores the shortest anypath routing node found by HMAA and outputs $P_s{}^{*}$ at the end. Q is a priority queue where each node is sorted according to the existing values ${\widehat{w}}_m(v)$. In addition, ${\widehat{w}}_m(F)$ and ${\widehat{w}}_i(F)$ are the AAW and the ith weight of forwarding set F are currently calculated, respectively.

3.1.1. HMAA Algorithm Implementation Steps Are as Follows

Step 1: Initialize all nodes $v\in V$ in the graph $G(V,E,\stackrel{\rightharpoonup }{W},\stackrel{\rightharpoonup }{L},\stackrel{\rightharpoonup }{p})$ and give the currently calculated value ${\widehat{w}}_m(v)$ and $\widehat{F}(v,P)$ the initial value;

Step 2: If $Q\ne \varnothing$ and $w_1(s,P)\le L_1$, all of the nodes in the link matrix $Q\leftarrow Q-\left\{u\right\}$ are traversed: the node u with the smallest AAW is added to the current anypath P, then the AAW value of the current node u is calculated; otherwise, skip to Step 5.

Step 3: The neighbor node of the minimum AAW node is traversed, the value ${\widehat{w}}_m{}^{\prime }(v)$ of the neighbor node is calculated by the Equation (9), then the K-1 value ${\widehat{w}}_i(v)$ of the node is calculated.

Step 4: If $j>\mathrm{K}$, skip to Step 5; otherwise, make $j=j+1$, and repeat Step 2.

Step 5: Check the first weight of the current anypath P. If $w_1(s,P)\le L_1$, output anypath $P_s{}^{*}=P$ found by HMAA; otherwise, output “NO Feasible Anypath”.

3.1.2. Detailed Procedure of HMAA Algorithm

The detailed procedure of HMAA algorithm is shown in Algorithm 1.

Algorithm 1. HMAA algorithm.

Input:$G(V,E,\stackrel{\rightharpoonup }{W},\stackrel{\rightharpoonup }{L},\stackrel{\rightharpoonup }{p})$, the source node s, the destination node t

Output: Anypath $P_s{}^{*}$

1.      for each $v\in V$ in $G(V,E,\stackrel{\rightharpoonup }{W},\stackrel{\rightharpoonup }{L},\stackrel{\rightharpoonup }{p})$ do

2.            $w_m(v)={\max }_{2\le i\le \mathrm{K}}{w}_i(v);$

3.            ${\widehat{w}}_m(v)\leftarrow \infty ;$

4.            $\widehat{F}(v,P)\leftarrow \varnothing ;$

5.      end for

6.      ${\widehat{w}}_m(t)=0;$

7.      $P\leftarrow \varnothing ;$

8.      $Q\leftarrow V;$

9.      while $Q\ne \varnothing$ & $w_1(s,P)\le L_1$ do

10.            $u\leftarrow \mathrm{Min}(Q);$

11.            $P\leftarrow P\cup \left\{u\right\};$

12.            $\widehat{w}(u,P)\leftarrow {\max }_{2\le i\le \mathrm{K}}{\widehat{w}}_i(u);$

13.              for each incoming link $(v,u)$ in E do

14.                    $F\leftarrow \widehat{F}(v,P)\cup \left\{u\right\};$

15.                    ${\widehat{w}}_m{}^{\prime }(v)\leftarrow \frac{w_m(v)}{p(v,F)}+{\widehat{w}}_m(F);$

16.                    if ${\widehat{w}}_m{}^{\prime }(v)<{\widehat{w}}_m(v)$ then

17.                       ${\widehat{w}}_m(v)\leftarrow {\widehat{w}}_m{}^{\prime }(v);$

18.                       $Q\leftarrow Q-\left\{u\right\};$

19.                       $\widehat{F}(v,P)\leftarrow F;$

20.                          for $i=2:\mathrm{K}$ do

21.                             ${\widehat{w}}_i(v)\leftarrow \frac{w_i(v)}{p(v,\widehat{F}(v,P))}+{\widehat{w}}_i(\widehat{F}(v,P));$

22.                          end for

23.                    end if

24.            end for

25.      end while

26.      if $w_1(s,P)\le L_1$

27.               $P_s{}^{*}\leftarrow P$; OUTPUT $P_s{}^{*}$;

28.      else Output NO Feasible Anypath;

29.      end if

30.     END

3.1.3. An Example of HMAA Algorithm

The implementation process of HMAA algorithm is described by an example. As shown in Figure 1, the source node s and the destination node t are in WMNs, then the anypath routing $P_s{}^{*}$ is calculated by HMAA algorithm. The system initializes the constraint value $L_1=18$ for a given mandatory QoS. Figure 1a–f demonstrate the operation of the algorithm, where Figure 1f shows the anypath routing $P_s{}^{*}$ in WMNs found by HMAA. According to the operation of HMAA, we introduce the process of adding each node to anypath P:

Figure 1. An example of the anypath computed by HMAA algorithm.

(a)

In system initialization, the first node t is cleared to zero, then added to the anypath P;

(b)

After the node t is added to the queue P, ${\widehat{w}}_i(v)$ and ${\widehat{w}}_m(v)$ of the neighbors of node t (cyan nodes u₄, u₃ and u₅) are updated by the red dotted arrows, respectively, so that ${\widehat{w}}_2(u_4)=\frac{2}{0.5}+0=4,{\widehat{w}}_3(u_4)=\frac{2}{0.5}+0=4$ and ${\widehat{w}}_m(u_4)=4$. Thus, the values of the other two nodes (blue font marked next to the node) can be obtained in the same way;

(c)

Compare the values of nodes (u₃, u₄, u₅), the smallest node is u₄, which is added to queue P, then the determined edge link is updated as shown in bold arrows. Update ${\widehat{w}}_i(v)$ and ${\widehat{w}}_m(v)$ of neighbor nodes (u₁, u₃) of u₄, it can obtain ${\widehat{w}}_2(u_1)=\frac{1}{0.2}+4=9,{\widehat{w}}_3(u_1)=\frac{2}{0.2}+4=14,{\widehat{w}}_m(u_1)=14$, ${\widehat{w}}_2(u_3)=\frac{2+0.5\cdot 0+0.4\cdot (1-0.5)\cdot 4}{1-(1-0.4)(1-0.5)}=4$, ${\widehat{w}}_3(u_3)=5.43$, ${\widehat{w}}_m(u_3)=5.43$;

(d)

Compare the values of nodes (u₁, u₃), the smallest node is u₃, which is added to queue P. Update ${\widehat{w}}_i(v)$ and ${\widehat{w}}_m(v)$ of neighbor node u₁, it can obtain ${\widehat{w}}_2(u_1)=\frac{1+0.5\cdot 4+0.2\cdot (1-0.5)\cdot 4}{1-(1-0.2)(1-0.5)}=5.67$, ${\widehat{w}}_3(u_1)=8.52$, ${\widehat{w}}_m(u_1)=8.52$. Thus, the values of node u₂ can also be obtained (blue font marked above the node);

(e)

Compare the values of nodes (u₁, u₂), the smallest node is u₁, which is added to queue P. Update ${\widehat{w}}_i(v)$ and ${\widehat{w}}_m(v)$ of neighbor node s, it can obtain ${\widehat{w}}_2(s)=\frac{3}{0.5}+5.67=11.67$, ${\widehat{w}}_3(s)=\frac{3}{0.5}+8.52=14.52$, ${\widehat{w}}_m(s)=14.52$;

(f)

Through the reverse order search, the source node s is finally added to the queue P, and the anypath routing $P=\{s,u_1,u_3,u_4,t\}$ is found. Thus, the first weight can be obtained by ${\widehat{w}}_1(u_4)=8,{\widehat{w}}_1(u_3)=\frac{46}{7},{\widehat{w}}_1(u_1)=13\frac{10}{21}$ and ${\widehat{w}}_1(s)=\frac{2}{0.5}+13\frac{10}{21}=17\frac{10}{21}$. Check the first constraint that ${\widehat{w}}_1(s,P)=17\frac{10}{21}\le L_1=18$, then the HMAA algorithm ends and the anypath routing $P_s{}^{*}=P$ is found, where ${\widehat{w}}_m(s,P_s{}^{*})=14.52$.

Remark 2.

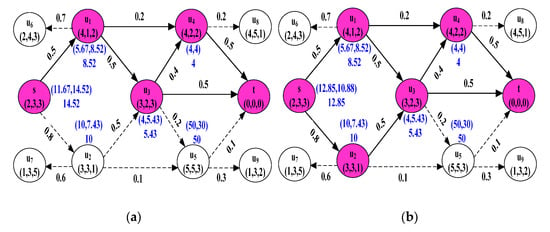
As shown in Figure 2a, the anypath routing $P_s{}^{*}$found by HMAA algorithm can calculate the AAW value of 14.52; Figure 2b shows the actual optimal anypath routing$P_s{}^{opt}$in WMNs, thus the AAW value can be calculated by ${\widehat{w}}_m(s,P_s{}^{opt})=12.85$. According to Definition 3, we can observe that$\alpha ={\widehat{w}}_m(s,P_s{}^{*})/{\widehat{w}}_m(s,P_s{}^{opt})=14.52/12.85\approx 1.13$, so the solution found in this example by HMAA is a 1.13-approximation optimal anypath routing.

Figure 2. (a) Anypath $P_s{}^{*}$ by HMAA and (b) optimal Anypath $P_s{}^{opt}$.

3.2. Analysis of HMAA Algorithm

In this paper, we first discuss the time complexity of the proposed HMAA algorithm, which can find a feasible solution to the MCOAP problem in a reasonable time. Secondly, we prove that HMAA is a K-1 approximation algorithm for the MCOAP problem.

Theorem 1.

The time complexity of HMAA algorithm is $\mathrm{O}(n\log n+\mathrm{K}m)$.

Proof. 

The proof of this theorem and the problems studied in [6] are somewhat different, but the logic between them is consistent. There are three stages for HMAA algorithm:

In the first stage, AAW is calculated for each node in graph G and the data structure is initialized (Lines 1–8 of HMAA) with a time complexity of $\mathrm{O}(\mathrm{K})$.

In the second phase, it calculates the AAW value (Lines 9–25 of HMAA) of the shortest anypath from all of the nodes to the destination node t, and the same time complexity as the traditional Dijkstra algorithm is $\mathrm{O}(n\log n+\mathrm{K}m)$.

In the third stage, it checks if the AAW value of the anypath routing P found by HMAA satisfies the first mandatory constraint (Lines 26–29 of HMAA), where the time complexity is $\mathrm{O}(m)$.

The time complexity of HMAA above three stages is $\mathrm{O}(\mathrm{K}+n\log n+\mathrm{K}m+m)=\mathrm{O}(n\log n+\mathrm{K}m)$, so Theorem 1 is proven.

The proposed HMAA algorithm has the same time complexity as the traditional Dijkstra algorithm. On one hand, it has good compatibility with existing routing protocols. On the other hand, it is faster and computationally suitable for time-varying WMNs to find a feasible solution in a reasonable time. Theorem 1 indicates that $P_s{}^{*}$ is the shortest AAW anypath. In other words, the forwarding set of each node calculated by HMAA algorithm is actually the optimal forwarding set based on AAW value. The HMAA algorithm is proposed in this chapter to identify the efficiency of the solution.

Theorem 2.

The anypath found by HMAA algorithm is at least a K-1 approximation solution and subject to$\widehat{w}(s,P_s^{*})\le (\mathrm{K}-1)\cdot \widehat{w}(s,P_s^{opt}),s.t.w_1(v,P_s^{opt})\le L_1$.

Proof. 

According to the implementation steps of HMAA algorithm, the nodes join the queue P one by one. All of the nodes are indexed on the path $P_v^{*}$ in this order, the index value of node t is 0, and node v with maximum index value finally joins queue P. It will be proved that the formula (4) is established for all of the nodes v by mathematical induction

$$\widehat{w}(v,P_v^{*})\le w_m(v,P_v^{*}).$$

(4)

For a node $v_1$, only the destination node t is its forwarding set, so

$$w_m(v_1,P_v^{*})=\frac{w_m(v_1)}{p(v_1,t)}+w_m(<t>,P_v^{*})=\frac{w_m(v_1)}{p(v_1,t)} =\underset{2\le i\le \mathrm{K}}{\max }\frac{w_i(v_1)}{p(v_1,t)}.$$

(5)

On the other hand, according to the definition of anypath routing length AAW, it can obtain

$$\widehat{w}(v_1,P_v^{*})=\underset{2\le i\le \mathrm{K}}{\max }{w}_i(v_1,P_v^{*})=\underset{2\le i\le \mathrm{K}}{\max }\frac{w_i(v_1)}{p(v_1,t)}+w_m(<t>,P_v^{*})=\underset{2\le i\le \mathrm{K}}{\max }\frac{w_i(v_1)}{p(v_1,t)}.$$

(6)

Thus, a node $v_1$ satisfying the Formula (7)

$$\widehat{w}(v_1,P_v^{*})\le w_m(v_1,P_v^{*}).$$

(7)

Assuming that all nodes with subscripts [1, r], the following inequality holds

$$\widehat{w}(v_r,P_v^{*})\le w_m(v_r,P_v^{*}).$$

(8)

Next prove that it is also satisfied for $v_{r+1}$. According to the definition of the variable $w_m$, it can obtain

$$w_m(v_{r+1},P_v^{*})=\frac{w_m(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{*}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{*})}\beta (u_j,P_v^{*})}{w}_m(u_j,P_v^{*}).$$

(9)

According to the implementation of HMAA algorithm, all of the nodes (including neighbor nodes $u_j$) on the path $P_v^{*}$ are added to the queue P before the node $v_{r+1}$ joins it. For all nodes with subscripts [1, r], the inequality (8) is true. So, there is

$$w_m(u_j,P_v^{*})\ge \widehat{w}(u_j,P_v^{*})=\underset{2\le i\le \mathrm{K}}{\max }{w}_i(u_j,P_v^{*}),\forall u_j\in F(v_{r+1},P_v^{*}).$$

(10)

According to the definition of Formula (2), it can obtain

$$\begin{array}{cc}\widehat{w}(v_{r+1},P_v^{*})& =\underset{2\le i\le \mathrm{K}}{\max }{w}_i(v_{r+1},P_v^{*})\hfill \\ & =\underset{2\le i\le \mathrm{K}}{\max }\left(\frac{w_i(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{*}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{*})}\beta (u_j,P_v^{*})}{w}_i(u_j,P_v^{*})\right)\hfill \\ & =\underset{2\le i\le \mathrm{K}}{\max }\left(\frac{w_i(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{*}))}\right)+\underset{2\le i\le \mathrm{K}}{\max }\left({\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{*})}\beta (u_j,P_v^{*})}{w}_i(u_j,P_v^{*})\right)\hfill \\ & \le \frac{w_m(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{*}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{*})}\beta (u_j,P_v^{*})}\underset{2\le i\le \mathrm{K}}{\max }{w}_i(u_j,P_v^{*})\hfill \end{array}$$

(11)

By comparing Equations (9)–(11), it can obtain

$$\widehat{w}(v_{r+1},P_v^{*})\le w_m(v_{r+1},P_v^{*}).$$

(12)

So, the inequality (4) is true for node v on the anypath $P_v^{*}$.

Since the anypath routing is directed and acyclic, HMAA algorithm indexes all of the nodes in reverse order along the optimal anypath $P_v^{*}$. The index value of t is 0, and v is the largest one. Moreover, the index value of each node is larger than that of its forwarding set. The mathematical induction is used to prove that the following inequality holds for any node v on the optimal path $P_v^{opt}$

$$w_m(v,P_v^{opt})\le {\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v,P_v^{opt})}.$$

(13)

For the node $v_1$, since only t is its forwarding set, it can obtain

$$w_m(v_1,P_v^{opt})=\frac{w_m(v_1)}{p(v_1,t)}+w_m(<t>,P_v^{opt})=\frac{\underset{2\le i\le \mathrm{K}}{\max }{w}_i(v_1)}{p(v_1,t)}.$$

(14)

$${\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v_1,P_v^{opt})}={\displaystyle \sum _{i=2}^{\mathrm{K}}\frac{w_i(v_1)}{p(v_1,t)}}+w_i(<t>,P_v^{opt}) =\frac{{\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v_1)}}{p(v_1,t)}.$$

(15)

From the above two inequalities, it is easy to find the following relationship for the node $v_1$,

$$w_m(v_1,P_v^{opt})\le {\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v_1,P_v^{opt})}.$$

(16)

Assuming that the inequality (13) is true for all nodes with subscripts $[1,r]$, it will prove that the inequality is still true for the node $v_{r+1}$. For node $v_{r+1}$, it has the following relationship.

$$\begin{array}{cc}{\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v_{r+1},P_v^{opt})}& ={\displaystyle \sum _{i=2}^{\mathrm{K}}\left(\frac{w_i(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{opt}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{opt})}\beta (u_j,P_v^{opt})}{w}_i(u_j,P_v^{opt})\right)}\hfill \\ & \ge \underset{2\le i\le \mathrm{K}}{\max }\frac{w_i(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{opt}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{opt})}\beta (u_j,P_v^{opt})}{\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(u_j,P_v^{opt})}\hfill \\ & \ge \frac{w_m(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{opt}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{opt})}\beta (u_j,P_v^{opt})}{\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(u_j,P_v^{opt})}\hfill \end{array}$$

(17)

Since the index value of the forwarding node $u_j$ is smaller than that of the node $v_{r+1}$, assuming that the inequality (13) is true for all nodes in the subscript range, the following relationship holds

$${\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(u_j,P_v^{opt})}\ge w_m(u_j,P_v^{opt}),\forall u_j\in F(v_{r+1},P_v^{opt}).$$

(18)

Define the following relationship according to Formula (2)

$$w_m(v_{r+1},P_v^{opt})=\frac{w_m(v_{r+1})}{p(v_{r+1},F(v_{r+1},P_v^{opt}))}+{\displaystyle \sum _{u_j\in F(v_{r+1},P_v^{opt})}\beta (u_j,P_v^{opt})}{w}_m(u_j,P_v^{opt}).$$

(19)

According to the above inequalities (17), (18) and (19), the following holds for the node

$$w_m(v_{r+1},P_v^{opt})\le {\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v_{r+1},P_v^{opt})}.$$

(20)

Substituting $v_{r+1}$ in the inequality (20) with v, thus it proves that the inequality (13) holds. In addition, according to the definition of $\widehat{w}(v,P_v^{opt})$, it holds

$$w_i(v,P_v^{opt})\le \widehat{w}(v,P_v^{opt}).$$

(21)

Combine the inequalities (13) and (21), it can obtain

$$w_m(v,P_v^{opt})\le {\displaystyle \sum _{i=2}^{\mathrm{K}}{w}_i(v,P_v^{opt})}\le (\mathrm{K}-1)\cdot \widehat{w}(v,P_v^{opt}).$$

(22)

For any node v in WMNs, define $P_v^{*}$ as the anypath routing from v to t calculated by HMAA, $P_v^{opt}$ as the optimal solution to MCOAP. Theorem 1 indicates that an anypath $P_v^{*}$ from v to t is the shortest AAW, so the following inequality holds

$$w_m(v,P_v^{*})\le w_m(v,P_v^{opt}).$$

(23)

According to the inequalities (4), (22) and (23), it holds

$$\widehat{w}(v,P_v^{*})\le (\mathrm{K}-1)\cdot \widehat{w}(v,P_v^{opt}).$$

(24)

Replace the node v in the above inequalities with s, then the HAMA algorithm (Lines 26–29) checks if it is feasible for the first parameter that $w_1(v,P_s^{opt})\le L_1$, thus it can obtain

$$\widehat{w}(s,P_s^{*})\le (\mathrm{K}-1)\cdot \widehat{w}(s,P_s^{opt}),s.t. w_1(v,P_s^{opt})\le L_1.$$

(25)

That is, HMAA algorithm finds a K-1 approximate solution to the MCOAP problem, thus Theorem 2 is proven.

4. Simulation Experiment and Performance Evaluation

In this section, we run HMAA to check if it can find a feasible solution in a reasonable time and evaluate its operational efficiency. According to the quality of the anypath routing in this experiment, the efficieney and performance of HMAA are evaluated. First of all, a large-scale random network (RNET) is produced by the Waxman model [20], which is used to perform the simulation experiment in this section. Secondly, in order to further verify the performance and efficiency of our proposed algorithm, the real WMNs network of wireless multimedia service (NTT) mentioned in the literature [16] is used for simulation calculation. All of the above simulations are run on a computer with 8GB of RAM and a 1.66GHz clock Core Duo CPU.

4.1. Experiment and Analysis of HMAA Algorithm Operation Efficiency

At present, there is no literature on the MCOAP problem. The existing intelligent algorithms such as the genetic algorithm and the ant colony algorithm are almost solely concerned with the optimal solution, thus its consuming time increases exponentially with the increase in network scale, which is not suitable for WMNs with strong time-varying characteristics. In this section, the MAP algorithm [16] and the deformation of the SAF algorithm [17] are used to the OMCAP problem, thus the HMAA, MAP and SAF algorithms are compared in this experiment. The Waxman model [20] is used to generate a network called RNET with 500 nodes. The RNET network is set up according to the above-described protocol. Three QoS constraints, source node s and destination node t are randomly generated. Three algorithms are used to find the anypath routing and record the running time, respectively (run 10 times to find ATC according to Formula (26)). The ATC of the three algorithms is recorded 20 times and shown in Figure 3.

$$\mathrm{ATC}=\frac{\mathrm{Total} \mathrm{time} \mathrm{consuming}}{\mathrm{Number} \mathrm{of} \mathrm{running}}$$

(26)

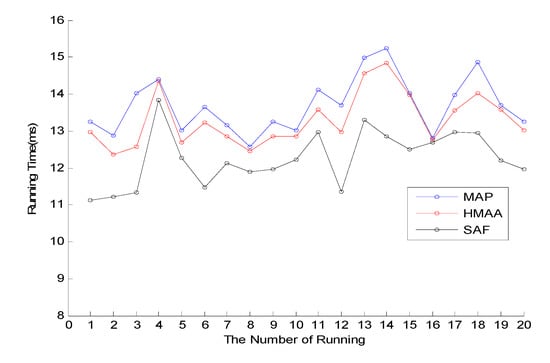
Figure 3. Running Time vs. the number of running for MAP, HMAA and SAF.

It can be seen from the records shown in Figure 3 that: ① In the RNET network with 500 nodes, regardless of the source node and the destination node, the overall consuming time of the three algorithms is kept within the range [11,16], and the running time is all within 16ms; ② When the source node s and the destination node t are the same, the running time of the three algorithms to find anypath routing is compared: the running time of HMAA is in the middle, MAP [16] is about 5% more, and SAF [17] is about 15% less.

The experimental results show that: ① MAP is an anypath routing algorithm to OMCAP, which has the same time complexity as HMAA to MCOAP. SAF with a single metric also has the same time complexity. Therefore, the running time trends of the three algorithms are consistent. ② MAP is to find the approximate solution where K = 3, which is slightly more than that of HMAA finding the approximate solution where K-1 in the actual calculation. SAF is a single metric anypath routing algorithm, which is equivalent to the case of K = 1, and the running time is relatively short in practical calculation. According to the simulation experiment data shown in Figure 4, HMAA proposed in this paper is evaluated by analyzing the principle and operation mechanism of the three algorithms. For WMNs with strong time-varying characteristics, the optimal solution to the MCOAP problem can be found in a reasonable time.

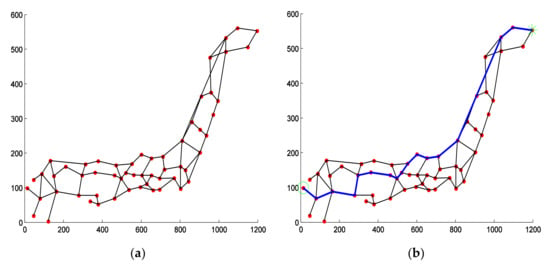
Figure 4. Experiment on real WMNs network. (a) the NTT network topology. (b) Anypath $P_{\mathrm{s}}^{*}$ found by HMAA.

4.2. Experiment on Real WMNs Network for HMAA Algorithm

Figure 4a shows the static WMNs network structure diagrams of the simulation experiments. The NTT network has 57 nodes and 81 edges. Each link in these networks has three weights, which corresponds to Cost, Delay and Jitter. All of the parameters in these networks can be found at the following URL: http://code.google.com/p/efptas/downloads/list (accessed on 13 October 2022). All of the red points are denoted as nodes of the network, the black wires as the wireless links of WMNs in Figure 4a. The green circle denotes the source node S and the green star denotes the destination node T in Figure 4b, respectively. The final anypath $P_{\mathrm{s}}^{*}$, the blue path shown in Figure 4b, is obtained by running proposed HMAA algorithm. At the same time, we also ran two other algorithms on this real WMNs network. The final result is the same that the anypath path obtained by running SAF and MAP algorithms is also the blue path in Figure 4b. Therefore, we can draw a conclusion that in the real wireless multimedia network, the proposed HMAA algorithm is as effective as the existing SAF and MAP algorithms in finding the anypath path.

4.3. Experiment and Analysis of HMAA Algorithm

In the network, the source node s and the destination node t are randomly selected, then the anypath routing is found by MAP, HMAA and SAF, respectively (SAF with the single metric “time”), in order to compare and analyze the efficiency of the three algorithms. As shown in Figure 3, according to the experimental steps, three networks with a different number of nodes are generated randomly, so are the constraints, the source node s and the destination node t subsequently. Then, the three algorithms are run and the anypath routing is recorded (run for 10 times on average). For simplicity, the weights of nodes in the network are normalized (equivalent to 1), thus the recorded data is shown in Figure 5.

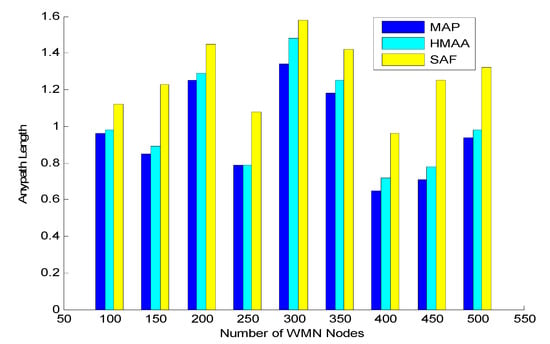
Figure 5. Anypath Length vs. number of nodes for MAP, HMAA and SAF.

As shown in Figure 5, the QoS constraints of each network are random. The number of normalized network nodes has no effect on the length of anypath routing. In the same network, the length of the anypath routing by three algorithms are compared. The length of MAP is the smallest, followed by HMAA, and SAF is the largest. Since MAP approximates all of the constraints of the OMCAP problem, the length of anypath routing obtained is minimal. HMAA approximates the constraint when K−1 = 2, and its length is slightly larger than MAP. SAF is a metric used to find an anypath routing, which cannot guarantee any other constraints on the anypath routing, so it has a larger length compared to the other two algorithms. ③When the anypath routing found by MAP satisfies the constraints, anypath routing found by HMAA also meets the constraints, while SAF cannot guarantee other QoS constraints.

The following approximation rate IAR (ratio of optimal value to the sub-optimal value) [21] is used to evaluate the performance of HMAA proposed in this paper. In other words, if the approximation rate IAR is equal to 1, it means that the optimal anypath is found, and if the approximation rate is less than 1, it means that the solution found is sub-optimal. Therefore, the approximation rate IAR indicates the quality of the solution found by HMAA. As we know that finding the optimal solution to MCOAP is NP-hard, $P_s^{opt}$ is replaced by the solution obtained by the intelligent algorithm proposed in [20]. Therefore, IAR is obtained by comparing the value $P_s^{*}$ calculated by HMAA with that by [20]. The network with different nodes is calculated 20 times, respectively, thus the approximation rate IAR (blue dot) is recorded in Figure 6.

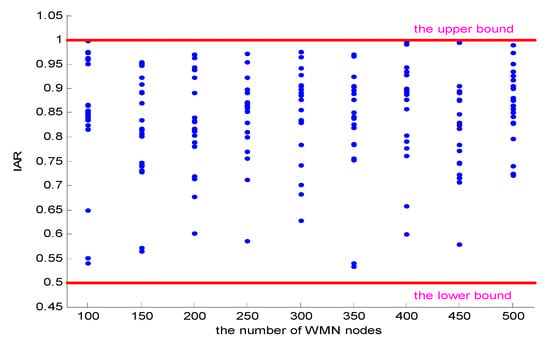
Figure 6. Analysis of the approximation ratio.

As can be seen from Figure 6, no more than 70% of IAR fall between [0.75, 0.95], and all the IAR fall within the range of [0.5,1] regardless of how many nodes there are in the network. HMAA proposed in this paper focuses on the MCOAP problem and finds the anypath routing in a reasonable time from an approximate perspective. Theorem 2 proves that the upper bound of HMAA is the K-1 approximation (here it is the 2 approximation), then the following simulation experiments also show that its approximation to the optimal solution is very high, so it is reasonable and feasible in wireless multimedia applications.

HMAA has a slightly longer running time than SAF, but the quality of the solution is good for multiple QoS constraints. MAP is a solution to OMCAP problem and tries to satisfy all constraints in an ideal state, but HMAA guarantees a specific QoS constraint while approaching other QoS constraints, so it is more in line with the business requirements in wireless multimedia applications. For example, if real-time voice services have strict delay jitter constraints, HMAA can guarantee its performance, but MAP cannot.

To sum up, in our network simulation experiment above, we compare the proposed algorithm HMAA with the best SAF and MAP algorithms. These three algorithms are oriented to different wireless multimedia applications. SAF focuses on the running time of the algorithm, and MAP focuses on the quality of all of the solutions. The algorithm we proposed is suitable for multimedia services. In wireless multimedia applications that need to guarantee a specific QoS, our algorithm is the best.

Remark 3.

The simulation experiments and analysis above reveal that HMAA proposed in this paper is a “trade-off” algorithm in a sense, which can find a better balance between the running time and the quality of the solution. The simulation experiment verifies that the running time of HMAA is reasonable and the quality of the solution can meet the business requirements.

5. Conclusions

This paper addresses the anypath routing problem that guarantees QoS in WMNs. According to the time-varying characteristics of WMNs, combined with the idea of anypath routing, the system network modeling is described, and the MCOAP problem is discussed. This paper focuses on the wireless multimedia applications: under a variety of QoS constraints, it is mandatory to meet a specific constraint while approaching other QoS constraints from an approximate perspective. The HMAA algorithm is proposed for the MCOAP problem. The time complexity of HMAA is consistent with that of Dijkstra algorithm, and it is proved to be K-1 approximation. The feasibility of the algorithm is verified by simulation, then its computational efficiency and performance are evaluated. HMAA proposed in this chapter is suitable for WMNs, conforms to wireless multimedia applications, and has good compatibility with existing routing protocols.

As for future research work, we plan to study an even better solution and faster algorithm for the MCOAP problem according to the time-varying characteristics of wireless networks based on the existing research. An investigation of the comparison of the HMAA with other algorithms [25,26,27] would also be interesting.