On the Order of Convergence of the Noor–Waseem Method

Abstract

In 2009, Noor and Waseem studied an important third-order iterative method. The convergence order is obtained using Taylor expansion and assumptions on the derivatives of order up to four. In this paper, we have obtained convergence order three for this method using assumptions on the first and second derivatives of the involved operator. Further, we have extended the method to obtain a fifth- and a sixth-order methods. The dynamics of the methods are also provided in this study. Numerical examples are included. The same technique can be used to extend the utilization of other single or multistep methods.

1. Introduction

Due to its wide application in various fields, such as Engineering [1], Applied sciences [2,3], Mathematics [4], Medicine and Scientific computing [5,6], finding a solution of the nonlinear equation

$$F\left(x\right)=0,$$

(1)

is an important problem in computational mathematics. Here, $F:\mathsf{\Omega }\subset T\to T_1$ is a Fréchet differentiable operator between Banach spaces T and $T_1$ and $\mathsf{\Omega }$ is an open convex set. Since a closed form solution for (1) is difficult to obtain (in general), iterative methods are usually employed to approximate the solution $x^{*}$ of (1). While studying iterative methods, the order of convergence is an important concern. In this paper, we consider the iterative method studied in [7] by Noor and Waseem. The method in [7] is defined for $n=0,1,2,\dots$ by

$$\begin{array}{ccc}\hfill y_n& =& x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =& x_n-4A_n^{-1}F\left(x_n\right),\hfill \end{array}$$

(2)

where $A_n=3F^{\prime }\left(\frac{2x_n+y_n}{3}\right)+F^{\prime }\left(y_n\right)$.

Noor and Waseem in [7] obtained a convergence order three for (2) using Taylor expansion. The analysis in [7] uses assumptions on the derivatives of F of order up to four.

Recall [4,8] that an iterative method is of order $p>0$ if

$$\parallel x_{n+1}-x^{*}\parallel \le c\parallel x_n-x^{*}{\parallel }^p,$$

where c is called an asymptotic error constant or rate of convergence.

Observe that the assumption on the derivative of F up to order four reduces the applicability of the method to the problems involving operator, whose higher order derivatives are not bounded. For example, let $f:[-\frac{1}{2},\frac{3}{2}]$ be defined by

$$\begin{array}{c}\hfill f\left(x\right)=\left\{\begin{array}{cc}\frac{1}{20}(x^{4}log{x}^2+x^6-x^5)\hfill & ifx\ne 0\hfill \\ 0\hfill & ifx=0.\hfill \end{array}\right.\end{array}$$

Then, we obtain by this definition

$$\begin{array}{ccc}\hfill f^{\prime }\left(x\right)& =& \frac{1}{20}(2x^3+4x^{3}log{x}^2+6x^5-5x^4)\hfill \\ \hfill f^{″}\left(x\right)& =& \frac{1}{20}(14x^2+12x^{2}log{x}^2+30x^4-20x^3)\hfill \\ \hfill f^{‴}\left(x\right)& =& \frac{1}{20}(52x+24xlog{x}^2+120x^3-60x^2)\hfill \\ \hfill f^{IV}\left(x\right)& =& \frac{1}{20}(24log{x}^2+360x^2-120x+100).\hfill \end{array}$$

Note that the fourth derivative of the function f is not bounded.

Later, in [9], the convergence of method (2) is proved using the assumptions only on the first derivative of F. However, the order of convergence is not obtained in [9].

Since the order of convergence is an important matter, our goal in this paper is to obtain the convergence order of (2), without using higher-order derivatives. In this direction, we obtain the convergence order three for (2) using assumptions on the derivatives of F of order up to two. Indeed, this is a considerable achievement. Note that, we are not using Taylor series expansion in our studies. Our new idea can be used to study and obtain convergence order of the other similar methods as well [1,2,6,10,11,12,13,14]. It is envisioned to study such similar methods in the future, since our technique does not depend on the method but only on the inverses of the linear operators involved.

Further, we extended the order of method (2) to five and six using the Cordero et al. [1,3] technique. The new methods are defined for $n=0,1,2,\dots$ as follows:

$$\begin{array}{ccc}\hfill y_n& =& x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill z_n& =& x_n-4A_n^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =& z_n-F^{\prime }{\left(y_n\right)}^{-1}F\left(z_n\right)\hfill \end{array}$$

(3)

and

$$\begin{array}{ccc}\hfill y_n& =& x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill z_n& =& x_n-4A_n^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =& z_n-F^{\prime }{\left(z_n\right)}^{-1}F\left(z_n\right),\hfill \end{array}$$

(4)

where $A_n=3F^{\prime }\left(\frac{2x_n+y_n}{3}\right)+F^{\prime }\left(y_n\right)$.

The rest of the paper is organized as follows. In Section 2, Section 3 and Section 4, we provide the convergence analysis of the methods in (2), (3) and (4), respectively. Numerical examples are provided in Section 5. The dynamics of the methods (2), (3) and (4) are given in Section 6. Finally, the paper ends with the conclusions in Section 7.

2. Convergence Analysis of (2)

For our convergence analysis, we introduce some functions and scalars. Let $L>0,L_1>0$ and $L_2>0$ be the given parameters. Let the functions $\phi ,{\phi }_1,h_i,i=1,2:[0,\frac{1}{L})⟶\mathbb{R}$ be defined by

$$\phi \left(t\right)=\frac{L}{2(1-Lt)},$$

$${\phi }_1\left(t\right)=\frac{L}{2}(1+\frac{L}{2(1-Lt)}t),$$

and let $h_1\left(t\right)=\phi \left(t\right)t-1,h_2\left(t\right)={\phi }_1\left(t\right)t-1.$ Then, $h_i,i=1,2$ are nondecreasing and continuous functions. Further, $h_i\left(0\right)=-1<0$ and ${lim}_{t⟶{\frac{1}{L}}^{-}}{h}_i\left(t\right)=+\infty .$ Therefore, there exist smallest zeros $r_1,r_2\in (0,\frac{1}{L})$ for the equations $h_i\left(t\right)=0.$

Let the functions ${\phi }_2,h_3:[0,r_2)⟶\mathbb{R}$ be defined by

$${\phi }_2\left(t\right)=\frac{1}{12(1-{\phi }_1\left(t\right)t)}((6L_1+L_{2}t)\phi \left(t\right)+L_2),$$

and $h_3\left(t\right)={\phi }_2\left(t\right)t^2-1.$ Then, $h_3$ is a nondecreasing and continuous function, $h_3\left(0\right)=-1<0$ and ${lim}_{t⟶r_2^{-}}{h}_3\left(t\right)=+\infty .$ Therefore, $h_3$ has the smallest zero $r_3\in (0,r_2).$

Let

$$r=min\{r_1,r_3\}.$$

(5)

Then, for all $t\in [0,r),$ we have

$$0\le \phi \left(t\right)t<1,$$

(6)

$$0\le {\phi }_1\left(t\right)t<1,$$

(7)

and

$$0\le {\phi }_2\left(t\right)t^2<1.$$

(8)

Throughout the paper, $B(x^{*},\rho )=\{x\in T:\parallel x-x_0\parallel <\rho \}$ and $\overline{B}(x^{*},\rho )=\{x\in T:\parallel x-x_0\parallel \le \rho \}$ for some $\rho >0.$

Our analysis is based on the following assumptions:

(a1) $x^{*}$ is a simple solution of (1) and $F^{\prime }{\left(x^{*}\right)}^{-1}\in \mathcal{L}(T_1,T)$;

(a2) $\parallel F^{\prime }{\left(x^{*}\right)}^{-1}(F^{\prime }\left(x\right)-F^{\prime }\left(y\right))\parallel \le L\parallel x-y\parallel \forall x,y\in B(x^{*},r)$;

(a3) $\parallel F^{\prime }{\left(x^{*}\right)}^{-1}(F^{″}\left(u\right)-F^{″}\left(v\right))\parallel \le L_2\parallel u-v\parallel \forall u,v\in B(x^{*},r)$;

(a4) $\parallel F^{\prime }{\left(x^{*}\right)}^{-1}{F}^{″}\left(y\right)\parallel \le L_1\forall y\in B(x^{*},r)$;

(a5) $\parallel F^{\prime }{\left(u\right)}^{-1}(F^{\prime }\left(u\right)-F^{\prime }\left(v\right))\parallel \le L_3\parallel u-v\parallel \forall u,v\in B(x^{*},r).$

 Theorem 1. 

Suppose the conditions (a1)–(a4) hold. Then, the sequence $\left\{x_n\right\}$ defined by (2), starting from $x_0\in B(x^{*},r)-\left\{x^{*}\right\}$ is well defined and remains in $\overline{B}(x^{*},r)$ for $n=0,1,2,\dots$ and converges to a solution $x^{*}$ of (1). Moreover, we have the following estimates

$$\parallel y_n-x^{*}\parallel \le \phi \left(r\right)\parallel x_n-x^{*}{\parallel }^2$$

(9)

and

$$\parallel x_{n+1}-x^{*}\parallel \le {\phi }_2\left(r\right){\parallel x_n-x^{*}\parallel }^3.$$

(10)

Proof. 

The proof is by induction. Suppose $x\in B(x^{*},r).$ Then by (a2), we have

$$\parallel F^{\prime }{\left(x^{*}\right)}^{-1}(F^{\prime }\left(x\right)-F^{\prime }\left(x^{*}\right))\parallel \le L\parallel x-x^{*}\parallel \le Lr<1.$$

By the Banach Lemma on invertible operators [4], we have

$$\parallel F^{\prime }{\left(x\right)}^{-1}{F}^{\prime }\left(x^{*}\right)\parallel \le \frac{1}{1-L\parallel x-x^{*}\parallel }.$$

(11)

Using the Mean Value Theorem, we have

$$\begin{array}{c}\hfill F\left(x_0\right)=F\left(x_0\right)-F\left(x^{*}\right)={\int }_0^1{F}^{\prime }(x^{*}+t(x_0-x^{*}))dt(x_0-x^{*}).\end{array}$$

(12)

Next, since $y_0=x_0-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right),$ we have

$$\begin{array}{ccc}\hfill \parallel y_0-x^{*}\parallel & =& \parallel x_0-x^{*}-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\parallel \hfill \\ & =& ∥(x_0-x^{*})-F^{\prime }{\left(x_0\right)}^{-1}{\int }_0^1{F}^{\prime }(x^{*}+t(x_0-x^{*}))dt(x_0-x^{*})∥\hfill \\ & =& ∥\left({\int }_0^1{F}^{\prime }{\left(x_0\right)}^{-1}(F^{\prime }\left(x_0\right)-F^{\prime }(x^{*}+t(x_0-x^{*})))dt\right)(x_0-x^{*})∥\hfill \\ & \le & {\int }_0^1\parallel F^{\prime }{\left(x_0\right)}^{-1}(F^{\prime }\left(x_0\right)-F^{\prime }(x^{*}+t(x_0-x^{*})))\parallel dt\parallel x_0-x^{*}\parallel \hfill \\ & =& {\int }_0^1\parallel F^{\prime }{\left(x_0\right)}^{-1}{F}^{\prime }\left(x^{*}\right)F^{\prime }{\left(x^{*}\right)}^{-1}(F^{\prime }\left(x_0\right)-F^{\prime }(x^{*}+t(x_0-x^{*})))dt\parallel \parallel x_0-x^{*}\parallel .\hfill \end{array}$$

Thus, by (11) and (a2), we obtain

$$\begin{array}{ccc}\hfill \parallel y_0-x^{*}\parallel & \le & \frac{L}{2(1-L\parallel x_0-x^{*}\parallel )}{\parallel x_0-x^{*}\parallel }^2\hfill \\ & \le & \phi (\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}{\parallel }^2<\parallel x_0-x^{*}\parallel <r.\hfill \end{array}$$

(13)

Then, the iteratation $y_0\in B(x^{*},r)$ and (9) holds for $n=0.$

Next, we shall prove $A_0^{-1}$ is well defined. Note that

$$4F^{\prime }\left(x^{*}\right)-A_0=3(F^{\prime }\left(x^{*}\right)-F^{\prime }(\frac{2x_0+y_0}{3}))-(F^{\prime }\left(y_0\right)-F^{\prime }\left(x^{*}\right)).$$

Hence, by (a2) we get

$$\begin{array}{ccc}\hfill \parallel {\left(4F^{\prime }\left(x^{*}\right)\right)}^{-1}(A_0-4F^{\prime }\left(x^{*}\right))\parallel & \le & \frac{1}{4}\left[3\parallel F^{\prime }{\left(x^{*}\right)}^{-1}(F^{\prime }(\frac{2x_0+y_0}{3})-F^{\prime }\left(x^{*}\right))\parallel \right.\hfill \\ & & +\left.\parallel F^{\prime }{\left(x^{*}\right)}^{-1}(F^{\prime }\left(y_0\right)-F^{\prime }\left(x^{*}\right))\parallel \right]\hfill \\ & \le & \frac{L}{4}\left[3\parallel \frac{2x_0+y_0}{3}-x^{*}\parallel +\parallel y_0-x^{*}\parallel \right]\hfill \\ & \le & \frac{L}{4}\left[\right(2\parallel x_0-x^{*}\parallel +\parallel y_0-x^{*}\parallel )+\parallel y_0-x^{*}\parallel ]\hfill \\ & \le & \frac{L}{4}[2+\frac{2L}{2(1-L\parallel x_0-x^{*}\parallel )}\parallel x_0-x^{*}\parallel ]\parallel x_0-x^{*}\parallel \hfill \\ & \le & \frac{L}{2}[1+\frac{L}{2(1-L\parallel x_0-x^{*}\parallel )}\parallel x_0-x^{*}\parallel ]\parallel x_0-x^{*}\parallel \hfill \\ & \le & {\phi }_1(\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel <1.\hfill \end{array}$$

Therefore,

$$\parallel A_0^{-1}{F}^{\prime }\left(x^{*}\right)\parallel \le \frac{1}{4(1-{\phi }_1(\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel )}.$$

(14)

Let

$$G_0=F^{″}\left(x^{*}+t(x_0-x^{*})+\theta \left(\frac{2x_0+y_0}{3}-x^{*}-t(x_0-x^{*})\right)\right)$$

and

$$H_0=F^{″}\left(x^{*}+t(x_0-x^{*})+\theta \left(y_0-x^{*}-t(x_0-x^{*})\right)\right).$$

Then, by (2) and (12), we have

$$\begin{array}{ccc}\hfill x_1-x^{*}& =& x_0-x^{*}-4A_0^{-1}{\int }_0^1{F}^{\prime }(x^{*}+t(x_0-x^{*}))dt(x_0-x^{*})\hfill \\ & =& A_0^{-1}\left[A_0-4{\int }_0^1{F}^{\prime }(x^{*}+t(x_0-x^{*}))dt\right](x_0-x^{*})\hfill \\ & =& A_0^{-1}\left[{\int }_0^{1}3F^{\prime }(\frac{2x_0+y_0}{3})+F^{\prime }\left(y_0\right)-4{\int }_0^1{F}^{\prime }(x^{*}+t(x_0-x^{*}))dt\right](x_0-x^{*})\hfill \\ & =& A_0^{-1}[{\int }_0^{1}3\left(F^{\prime }(\frac{2x_0+y_0}{3})-F^{\prime }(x^{*}+t(x_0-x^{*}))\right)dt\hfill \\ & & +{\int }_0^1\left(F^{\prime }\left(y_0\right)-F^{\prime }(x^{*}+t(x_0-x^{*}))\right)dt](x_0-x^{*}).\hfill \end{array}$$

Then, by the Mean Value Theorem for second derivatives, we can write in turn that

$$\begin{array}{ccc}\hfill x_1-x^{*}& =& 3A_0^{-1}[{\int }_0^1{\int }_0^1{F}^{″}\left(x^{*}+t(x_0-x^{*})+\theta \left(\frac{2x_0+y_0}{3}-x^{*}-t(x_0-x^{*})\right)\right)d\theta \hfill \\ & & \times \left(\frac{2x_0+y_0}{3}-x^{*}-t(x_0-x^{*})\right)dt\hfill \\ & & +{\int }_0^1{\int }_0^1{F}^{″}(x^{*}+t(x_0-x^{*})+\theta (y_0-x^{*}-t(x_0-x^{*})))d\theta \hfill \\ & & (y_0-x^{*}-t(x_0-x^{*}))dt](x_0-x^{*})\hfill \\ & =& [3A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta \left(\frac{2x_0+y_0}{3}-x^{*}-t(x_0-x^{*})\right)dt\hfill \\ & & +A_0^{-1}{\int }_0^1{\int }_0^1{H}_{0}d\theta (y_0-x^{*}-t(x_0-x^{*}))dt](x_0-x^{*})\hfill \\ & =& [A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta \left(2x_0+y_0-3x^{*}-3t(x_0-x^{*})\right)dt\hfill \\ & & +A_0^{-1}{\int }_0^1{\int }_0^1{H}_{0}d\theta (y_0-x^{*}-t(x_n-x^{*}))dt](x_0-x^{*})\hfill \\ & =& A_0^{-1}[{\int }_0^1{\int }_0^1{G}_{0}d\theta (y_0-x^{*})dt+{\int }_0^1{\int }_0^1{G}_0(2-3t)(x_0-x^{*})dt\hfill \\ & & +{\int }_0^1{\int }_0^1{H}_{0}d\theta (y_0-x^{*})dt-{\int }_0^1{\int }_0^1{H}_{0}d\theta t(x_0-x^{*})dt](x_0-x^{*})\hfill \\ & =& \left[A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta (y_0-x^{*})dt+A_0^{-1}{\int }_0^1{\int }_0^1{H}_{0}d\theta (y_0-x^{*})dt\right](x_0-x^{*})\hfill \\ & & +[A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta (2-4t)(x_0-x^{*})dt+A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta t(x_0-x^{*})dt\hfill \\ & & -A_0^{-1}{\int }_0^1{\int }_0^1{H}_{0}d\theta t(x_0-x^{*})dt](x_0-x^{*})\hfill \\ & =& {\mathsf{\Gamma }}_1+A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta (2-4t)dt{(x_0-x^{*})}^2+{\mathsf{\Gamma }}_2+{\mathsf{\Gamma }}_3,\hfill \end{array}$$

(15)

where

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_1& :=& \left[A_0^{-1}{\int }_0^1{\int }_0^1{G}_{0}d\theta (y_0-x^{*})dt\right](x_0-x^{*}),\hfill \\ \hfill {\mathsf{\Gamma }}_2& :=& \left[A_0^{-1}{\int }_0^1{\int }_0^1{H}_{0}d\theta (y_0-x^{*})dt\right](x_0-x^{*})\hfill \end{array}$$

and

$${\mathsf{\Gamma }}_3:=\left[A_0^{-1}{\int }_0^1{\int }_0^1(G_0-H_0)d\theta tdt\right]{(x_0-x^{*})}^2.$$

Observe that by (14) and (a4), we have

$$\begin{array}{cc}\hfill \parallel {\mathsf{\Gamma }}_1\parallel & =\parallel \left[A_0^{-1}{F}^{\prime }\left(x^{*}\right){\int }_0^1{\int }_0^1{F}^{\prime }{\left(x^{*}\right)}^{-1}{G}_{0}d\theta (y_0-x^{*})dt\right](x_0-x^{*})\parallel \\ & \le \frac{L_1}{4(1-{\phi }_1(\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel )}\parallel y_0-x^{*}\parallel \parallel x_0-x^{*}\parallel .\end{array}$$

(16)

Similarly, we obtain

$$\begin{array}{cc}\hfill \parallel {\mathsf{\Gamma }}_2\parallel & \le \frac{L_1}{4(1-{\phi }_1(\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel )}\parallel y_0-x^{*}\parallel \parallel x_0-x^{*}\parallel .\end{array}$$

(17)

To compute the second term in (15), we observe that

$$\begin{array}{ccc}\hfill & & \parallel {\int }_0^1{\int }_0^1{A}_0^{-1}{G}_{0}d\theta (2-4t)dt{(x_0-x^{*})}^2\parallel \hfill \\ \hfill & \le & ∥\underset{t\in [0,1]}{max}{\int }_0^1\parallel A_0^{-1}{G}_{0}d\theta \parallel {\int }_0^1(2-4t)dt{(x_0-x^{*})}^2∥\hfill \\ \hfill & =& 0.\hfill \end{array}$$

(18)

Notice that

$$\begin{array}{ccc}\hfill G_0-H_0& =& F^{″}\left(X\right)-F^{″}\left(Y\right),\hfill \end{array}$$

(19)

where

$$\begin{array}{ccc}\hfill X& =& \left(x^{*}+t(x_0-x^{*})+\theta \left(\frac{2x_0+y_0}{3}-x^{*}-t(x_0-x^{*})\right)\right),\hfill \\ \hfill Y& =& \left(x^{*}+t(x_0-x^{*})+\theta \left(y_0-x^{*}-t(x_0-x^{*})\right)\right).\hfill \end{array}$$

Note that again

$$X-Y=\frac{2\theta }{3}[x_0-x^{*}-(y_0-x^{*})]$$

(20)

and hence by (14) and (a3), we have

$$\begin{array}{ccc}\hfill \parallel {\mathsf{\Gamma }}_3\parallel & =& \parallel \left[A_0^{-1}{F}^{\prime }\left(x^{*}\right){\int }_0^1{\int }_0^1{F}^{\prime }{\left(x^{*}\right)}^{-1}(G_0-H_0)d\theta tdt\right]{(x_0-x^{*})}^2\parallel \hfill \\ \hfill & \le & \frac{L_2}{4(1-{\phi }_1(\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel )}{\int }_0^1{\int }_0^1\parallel X-Y\parallel d\theta dt\parallel x_0-x^{*}{\parallel }^2\hfill \\ \hfill & \le & \frac{L_2}{12(1-{\phi }_1(\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel )}[1+\phi (\parallel x_0-x^{*}\parallel )\parallel x_0-x^{*}\parallel ]\parallel x_0-x^{*}{\parallel }^3.\hfill \\ \hfill \end{array}$$

(21)

Combining (15)–(21), we get

$$\parallel x_1-x^{*}\parallel \le {\phi }_2\left(r\right){\parallel x_0-x^{*}\parallel }^3.$$

Then, since ${\phi }_2\left(r\right)r^2<1$, we have $\parallel x_1-x^{*}\parallel <\parallel x_0-x^{*}\parallel <r,$ so the iteratate $x_1\in B(x^{*},r).$

Replacing $x_0,y_0$ and $x_1$ in the earlier estimates by $x_n,y_n$ and $x_{n+1}$, respectively, completes the induction for (9) and (10). □

 Remark 1. 

We have obtained the order of convergence three for the method (2) without using Taylor expansion and making assumptions only on derivatives of F up to order two. Thus, our analysis extends the applicability of the method (2).

3. Convergence Analysis of (3)

Let ${\phi }_3,h_4:[0,r_2)⟶\mathbb{R}$ be defined by

$${\phi }_3\left(t\right)=L_3(\phi \left(t\right)+\frac{1}{2}{\phi }_2\left(t\right)t){\phi }_2\left(t\right)$$

and $h_4\left(t\right)={\phi }_3\left(t\right)t^4-1.$ Then, $h_4\left(0\right)=-1$ and $h_4\left(t\right)⟶+\infty$ as $t⟶r_2^{-}.$ Therefore, $h_4$ has the smallest zero $r_4\in (0,r_2).$

Let

$$R=min\{r,r_4\}.$$

(22)

Then, for $t\in [0,R),$ we have

$$0\le {\phi }_3\left(t\right)t^4<1.$$

We have the following theorem for method (3).

 Theorem 2. 

Suppose the conditions (a1)–(a5) hold. Then, the sequence $\left\{x_n\right\}$ defined by (3), starting from $x_0\in B(x^{*},R)-\left\{x^{*}\right\}$ is well defined and remains in $\overline{B}(x^{*},R)$ for $n=0,1,2,\dots$ and converges to a solution $x^{*}$ of (1). Moreover, we have the following estimates

$$\parallel y_n-x^{*}\parallel \le \phi \left(R\right)\parallel x_n-x^{*}{\parallel }^2,$$

(23)

$$\parallel z_n-x^{*}\parallel \le {\phi }_2\left(R\right){\parallel x_n-x^{*}\parallel }^3$$

(24)

and

$$\parallel x_{n+1}-x^{*}\parallel \le {\phi }_3\left(R\right){\parallel x_n-x^{*}\parallel }^5.$$

(25)

Proof. 

Observe that by taking $r=R$ and $x_{n+1}=z_n$ in Theorem 1, we have

$$\parallel z_n-x^{*}\parallel \le {\phi }_2(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}{\parallel }^3$$

(26)

and the iterate $z_n\in B(x^{*},R).$ Note that

$$\begin{array}{ccc}\hfill x_{n+1}-x^{*}& =& z_n-x^{*}-F^{\prime }{\left(y_n\right)}^{-1}F\left(z_n\right)\hfill \\ & =& F^{\prime }{\left(y_n\right)}^{-1}{\int }_0^1[F^{\prime }\left(y_n\right)-F^{\prime }(x^{*}+t(z_n-x^{*}))]dt(z_n-x^{*})\hfill \\ & =& {\int }_0^1{F}^{\prime }{\left(y_n\right)}^{-1}[F^{\prime }\left(y_n\right)-F^{\prime }(x^{*}+t(z_n-x^{*}))]dt(z_n-x^{*}).\hfill \end{array}$$

Thus, by (a5), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{*}\parallel & \le & L_3(\parallel y_n-x^{*}\parallel +\frac{1}{2}\parallel z_n-x^{*}\parallel )\parallel z_n-x^{*}\parallel \hfill \\ & \le & L_3\left(\phi \right(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}{\parallel }^2\hfill \\ & & +\frac{1}{2}{\phi }_2(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}{\parallel }^3){\phi }_2(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}{\parallel }^3\hfill \\ & \le & L_3\left(\phi \right(\parallel x_n-x^{*}\parallel )\hfill \\ & & +\frac{1}{2}{\phi }_2(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}\parallel ){\phi }_2(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}{\parallel }^5\hfill \\ & \le & {\phi }_3\left(R\right){\parallel x_n-x^{*}\parallel }^5.\hfill \end{array}$$

□

4. Convergence Analysis of (4)

Let ${\phi }_4,h_5:[0,r_2)⟶\mathbb{R}$ be defined by

$${\phi }_4\left(t\right)=\frac{L_3}{2}{\left({\phi }_2\left(t\right)\right)}^2$$

and $h_5\left(t\right)={\phi }_4\left(t\right)t^5-1.$ Then, $h_5\left(0\right)=-1$ and $h_5\left(t\right)⟶+\infty$ as $t⟶r_2^{-}.$ Therefore, $h_5$ has a smallest zero $r_5\in (0,r_2).$

Let

$$R_1=min\{r,r_5\}.$$

(27)

Then, for $t\in [0,R_1),$ we have

$$0\le {\phi }_4\left(t\right)t^5<1.$$

We have the following theorem for method (4).

 Theorem 3. 

Suppose conditions (a1)–(a5) hold. Then, the sequence $\left\{x_n\right\}$ defined by (4), starting from $x_0\in B(x^{*},R_1)-\left\{x^{*}\right\}$ is well defined and remains in $\overline{B}(x^{*},R_1)$ for $n=0,1,2,\dots$ and converges to a solution $x^{*}$ of (1). Moreover, we have the following estimates

$$\parallel y_n-x^{*}\parallel \le \phi \left(R_1\right){\parallel x_n-x^{*}\parallel }^2,$$

(28)

$$\parallel z_n-x^{*}\parallel \le {\phi }_2\left(R_1\right){\parallel x_n-x^{*}\parallel }^3$$

(29)

and

$$\parallel x_{n+1}-x^{*}\parallel \le {\phi }_4\left(R_1\right){\parallel x_n-x^{*}\parallel }^6.$$

(30)

 Proof. 

Notice that (28) and (29) follows as in Theorem 2. Further,

$$\begin{array}{ccc}\hfill x_{n+1}-x^{*}& =& z_n-x^{*}-F^{\prime }{\left(z_n\right)}^{-1}F\left(z_n\right)\hfill \\ & =& F^{\prime }{\left(z_n\right)}^{-1}{\int }_0^1[F^{\prime }\left(z_n\right)-F^{\prime }(x^{*}+t(z_n-x^{*}))]dt(z_n-x^{*})\hfill \\ & =& {\int }_0^1{F}^{\prime }{\left(z_n\right)}^{-1}[F^{\prime }\left(z_n\right)-F^{\prime }(x^{*}+t(z_n-x^{*}))]dt(z_n-x^{*}).\hfill \end{array}$$

Hence, by (a5), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x^{*}\parallel & \le & \frac{L_3}{2}{\parallel z_n-x^{*}\parallel }^2\hfill \\ & \le & \frac{L_3}{2}({\phi }_2(\parallel x_n-x^{*}{\parallel \left)\right)}^2{\parallel x_n-x^{*}\parallel }^6\hfill \\ & \le & {\phi }_4\left(R_1\right){\parallel x_n-x^{*}\parallel }^6.\hfill \end{array}$$

□

We complete this section by providing a result for the uniqueness of the solution $x^{*}$, that applies to all the methods given in this paper.

 Proposition 1. 

Suppose:

(1) There exist a simple solution $x^{*}\in B(x^{*},\rho )$ of the Equation (1) for some $\rho >0$ and a parameter $K>0$ such that

$$\parallel F^{\prime }{\left(x^{*}\right)}^{-1}(F^{\prime }\left(x^{*}\right)-F^{\prime }\left(x\right))\parallel \le K\parallel x^{*}-x\parallel$$

(31)

for each $x\in B(x^{*},\rho ).$

(2) There exists ${\rho }_1\ge \rho$ such that

$${\rho }_1<\frac{2}{K}.$$

(32)

Set $S=\overline{B}(x^{*},{\rho }_1)\cap \mathsf{\Omega }.$ Then, Equation (1) is uniquely solvable at $x^{*}$ in the region $S.$

 Proof. 

Let $\gamma \in S$ be a solution of Equation (1). Define the linear operator M as $M={\int }_0^1{F}^{\prime }(x^{*}+\tau (\gamma -x^{*}))d\tau .$ By applying the conditions (31) and (32), we obtain in turn that

$$\begin{array}{ccc}\hfill \parallel F^{\prime }{\left(x^{*}\right)}^{-1}(M-F^{\prime }\left(x^{*}\right))\parallel & \le & K{\int }_0^1\tau \parallel x^{*}-\gamma \parallel d\tau \hfill \\ & \le & \frac{K}{2}{\rho }_1<1.\hfill \end{array}$$

That is, the linear operator M is invertible. Then, the identity

$$\gamma -x^{*}=M^{-1}(F\left(\gamma \right)-F\left(x^{*}\right))=M^{-1}\left(0\right)=0$$

leads to the conclusion that $\gamma =x^{*}.$ □

 Remark 2. 

The efficiency index $E_I$ and the informational efficiency $I_E$ are defined as $E_I=o^{\frac{1}{m}}$ [15] and $I_E=\frac{o}{m}$ [14], respectively, where o is the order of convergence and m is the number of functions (and derivatives). The $E_I$ and $I_E$ of the methods (2), (3) and (4) are $3^{1/4}=1.316,\frac{3}{4}=0.75;5^{1/5}=1.3797,\frac{5}{5}=1$ and $6^{1/6}=1.348,6/6=1,$ respectively.

5. Examples

Three examples are presented in this section.

 Example 1. 

Let $T=T_1={\mathbb{R}}^3,D=\overline{B}(0,1),x^{*}={(0,0,1)}^{Tr}.$ Define the function F on D for $w={(x,y,z)}^{Tr}$ by

$$F(w)={(sinx,\frac{y^2}{5}+y,z)}^{Tr}.$$

Then, the Fréchet-derivatives are given by

$$F^{\prime }\left(w\right)=\left[\begin{array}{ccc}cosx& 0& 0\\ 0& \frac{2y}{5}+1& 0\\ 0& 0& 1\end{array}\right]$$

and

$$F^{″}\left(w\right)=\left[\begin{array}{ccccccccc}-sinx& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{2}{5}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right].$$

The conditions (a1)–(a5) are validated if $L=L_2=L_3=1$ and $L_1=\frac{2}{5}.$ Then, the parameters are:

$$r_1=0.6667,r_2=0.7639,r=R_1=r_3=0.6588,R=r_4=0.6260,r_5=0.7469.$$

 Example 2. 

Let $T=T_1=C[0,1],$ the space of continuous functions defined on $[0,1]$ and be equipped with the max norm. Let $D=\overline{B}(0,1).$ Define the function F on D by

$$F\left(\phi \right)\left(x\right)=\phi \left(x\right)-5{\int }_0^{1}x\theta \phi {\left(\theta \right)}^{3}d\theta .$$

(33)

We have that

$$F^{\prime }\left(\phi \left(\xi \right)\right)\left(x\right)=\xi \left(x\right)-15{\int }_0^{1}x\theta \phi {\left(\theta \right)}^2\xi \left(\theta \right)d\theta ,for each\xi \in D.$$

Then, we get that for $x^{*}=0,$ the conditions (a1)-(a5) hold, provided $L=L_3=15$ and $L_2=8.5$ and $L_1=31.$ Then the parameters are:

$$r_1=0.0444,r_2=0.0509,r=R_1=r_3=0.0380,R=r_4=0.0378,r_5=0.0457.$$

 Example 3. 

Getting back to the motivational example at the introduction of this paper, we have $L=45.9234=L_1,L_2=125.7312,L_3=100.6338.$ Then the parameters are:

$$r=R_1=r_1=r_3=0.0145,r_2=0.0166,R=r_4=0.0125,r_5=0.0156.$$

In the next example, we compare method (3) with the fifth-order iterative method studied in [16]. Furthermore, we provide the iterates for the methods (2) and (3).

 Example 4. 

Consider the system of equations

$$\begin{array}{ccc}\hfill 3x_1^2{x}_2+x^2& =& 1\hfill \\ \hfill x_1^4+x_1{x}_2^3& =& 1.\hfill \end{array}$$

Note that the solutions are $(-1,0.2),(-0.4,-1.3)$ and $(0.9,0.3).$ We approximate the solution $(0.9,0.3)$ using the methods (2), (3) (4) and the fifth-order method considered in [16], with the initial point $(2,-1).$ The obtained results are provided in Table 1 and Table 2.

Table 1. Method (3).

k	Fifth Order Method in [16]	Method (3)
	${\mathit{x}}_{\mathit{k}}=({\mathit{x}}_{\mathbf{1}}^{\mathit{k}},{\mathit{x}}_{\mathbf{2}}^{\mathit{k}})$	${\mathit{x}}_{\mathit{k}}=({\mathit{x}}_{\mathbf{1}}^{\mathit{k}},{\mathit{x}}_{\mathbf{2}}^{\mathit{k}})$
0	$(2.000000000000000000,-1.000000000000000000)$	$(2.000000000000000000,-1.000000000000000000)$
1	$(1.082281042482679530,0.123366196386319406)$	$(0.97999747117802393781,0.31079296183420979104)$
2	$(0.992837748938471569,0.306361894605406281)$	$(0.99252009675815366929,0.30661919359513767346)$
3	$(0.992779994851123249,0.306440446511020432)$	$(0.99277988170910103082,0.30644055554978738564)$
4	$(0.992779994851123249,0.306440446511020432)$	$(0.99277999485110035582,0.30644044651104612730)$

Table 2. Method (2) and Method (4).

k	Method (2)	Method (4)
	${\mathit{x}}_{\mathit{k}}=({\mathit{x}}_{\mathbf{1}}^{\mathit{k}},{\mathit{x}}_{\mathbf{2}}^{\mathit{k}})$	${\mathit{x}}_{\mathit{k}}=({\mathit{x}}_{\mathbf{1}}^{\mathit{k}},{\mathit{x}}_{\mathbf{2}}^{\mathit{k}})$
0	$(2.000000000000000000,-1.000000000000000000)$	$(2.000000000000000000,-1.000000000000000000)$
1	$(1.019623593558109941,0.265386054724064790)$	$(1.03759994297628344028,0.26149549469920185806)$
2	$(0.992853658605661104,0.306346433846240717)$	$(0.99619799193796287894,0.30257508692302936825)$
3	$(0.992779994852644009,0.306440446509150976)$	$(0.99277999575683006927,0.30644044541552573068)$
4	$(0.992853658605661104,0.306346433846240717)$	$(0.0.99277999485112322641,0.3064404465110204256)$
5	$(0.992779994852644009,0.306440446509150976)$	$(0.0.99277999485112322641,0.3064404465110204256)$

6. Basins of Attractions

In this section, we study the basin of attraction and Julia sets corresponding to methods (2), (3) and (4). Recall that the collection of all initial points from which the iterative method converges to a solution of a given equation are called the basins of attraction or Fatou sets, of an iterative method [11]. The complement of the Fatou set is known as a Julia set. We provide the basins of attraction associated with the roots of the following three systems of equations.

 Example 5. 

$\left\{\begin{array}{c}{x}^3-y=0\hfill \\ y^3-x=0\hfill \end{array}\right.$

with solutions { $(-1,-1),(0,0),(1,1)$}.

 Example 6. 

$\left\{\begin{array}{c}3x^{2}y-y^3=0\hfill \\ x^3-3x{y}^2-1=0\hfill \end{array}\right.$

with solutions { $(-\frac{1}{2},-\frac{\sqrt{3}}{2}),(-\frac{1}{2},\frac{\sqrt{3}}{2}),(1,0)$}.

 Example 7. 

$\left\{\begin{array}{c}{x}^2+y^2-4=0\hfill \\ 3x^2+7y^2-16=0\hfill \end{array}\right.$

with solutions { $(\sqrt{3},1),(-\sqrt{3},1),(\sqrt{3},-1),(-\sqrt{3},-1)$}.

For generating the basin of attraction associated with each root of a given system of nonlinear equations, we consider the rectangular region $\mathcal{R}=\{(x,y)\in {\mathbb{R}}^2:-2\le x\le 2,-2\le y\le 2\}$, which contains all the roots of test problems. We consider an equidistant grid of $401\times 401$ points in $\mathcal{R}$ and choose these points as the initial guess $x_0$, for the methods (2), (3) and (4). A fixed tolerance ${10}^{-8}$ and a maximum of 50 iterations are used for all the cases. A color is being assigned to each attracting basin corresponding to each root. If we do not obtain the desired tolerance with the fixed iterations, we do not continue and we decide that the iterative method starting at $x_0$ does not converge to any of the roots and assign black color to those points. In this way, we distinguish the basins of attraction by their respective colors for distinct roots of each method.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 demonstrates the basin of attraction corresponding to each root of above Examples (Examples 5–7) for the methods (2), (3) and (4). The Julia set (black region), which contains all the initial points from which the iterative method does not converge to any of the roots, can easily be observed in the figure.

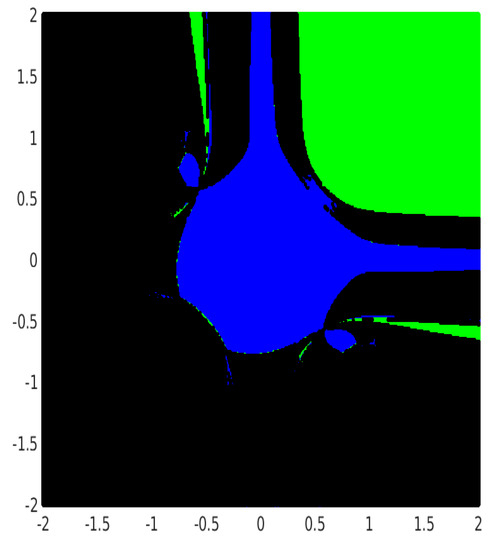
Figure 1. Dynamical plane of the methods (2) with basins of attraction for the Example 5.

Figure 2. Dynamical plane of the methods (3) (left) and (4) (right) with basins of attraction for the Example 5.

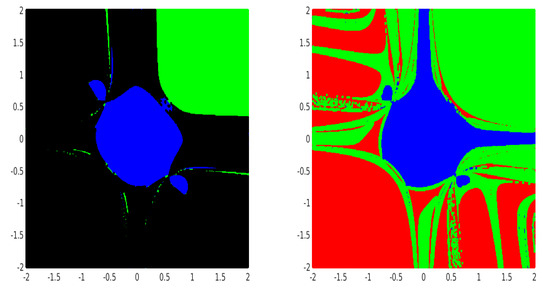
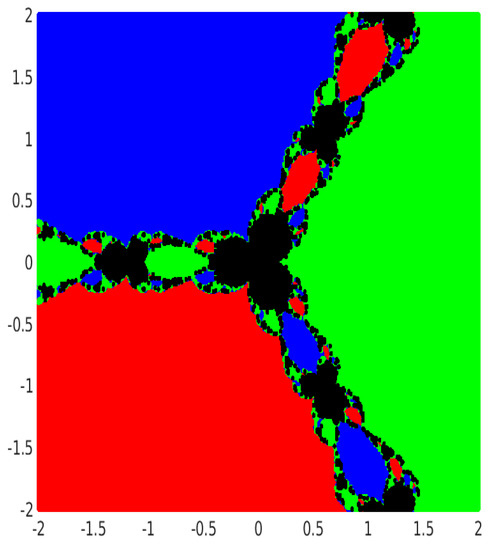
Figure 3. Dynamical plane of the methods (2) with basins of attraction for Example 6.

Figure 4. Dynamical plane of the methods (3) (left) and (4) (right) with basins of attraction for Example 6.

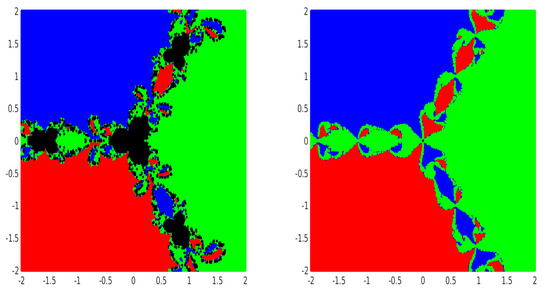
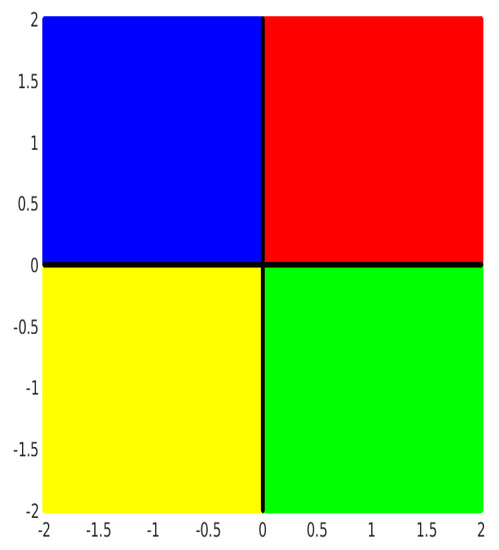
Figure 5. Dynamical plane of method (2) with basins of attraction for Example 7.

Figure 6. Dynamical plane of the methods (3) (left) and (4) (right) with basins of attraction for Example 7.

The figures presented in this work were created on a 16-core 64 bit Windows machine with Intel Core i7-10700 CPU @ 2.90GHz using MATLAB programming language.

 Remark 3. 

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 above, clearly show that method (4) has a larger basin of attraction compared to method (2) and method (3).

7. Conclusions

A process is developed to determine the convergence order of method (2), method (3) and method (4). The analysis involves only the first and second derivative in contrast to the earlier works using the fourth derivative [7]. Moreover, computable error distances are also provided, which are not given before [7]. Hence, the applicability of these methods is extended. The new process does not depend on these methods. Therefore, it can also be used to extend the usage of other methods of higher order using inverses of linear operators. This is our future topic of research.