Self-Adapting Spherical Search Algorithm with Differential Evolution for Global Optimization

Abstract

The spherical search algorithm is an effective optimizer to solve bound-constrained non-linear global optimization problems. Nevertheless, it may fall into the local optima when handling combination optimization problems. This paper proposes an enhanced self-adapting spherical search algorithm with differential evolution (SSDE), which is characterized by an opposition-based learning strategy, a staged search mechanism, a non-linear self-adapting parameter, and a mutation-crossover approach. To demonstrate the outstanding performance of the SSDE, eight optimizers on the CEC2017 benchmark problems are compared. In addition, two practical constrained engineering problems (the welded beam design problem and the pressure vessel design problem) are solved by the SSDE. Experimental results show that the proposed algorithm is highly competitive compared with state-of-the-art algorithms.

1. Introduction

In the field of science and engineering, single-objective optimization problems are often characterized as discontinuities, multi-variable, and non-differentiable [1,2,3,4]. Solutions to these optimization problems are divided into local optima and global optima. Some algorithms may be trapped in local optima and cannot find the global optima, while other algorithms can find the global optima [5]. Deciding how to design an algorithm that can find the global optima for an optimization problem more efficiently has become a hot research topic [6].

In the literature, there are usually two ways to solve optimization problems. One is to use deterministic methods and the other is to employ stochastic algorithms. Most deterministic methods find solutions by utilizing derivative information of the objective functions [7,8,9]. However, not all problems’ objective functions are differentiable. Examples are economic dispatch problems [10,11], unit commitment problems [12], electromagnetic optimization problems [13], job shop problems [14], industrial scheduling problems [15,16,17,18], and disassembly line balancing problems [19,20,21,22,23]. As a result, stochastic optimization algorithms have received a lot of attention recently [24,25,26,27]. These algorithms do not require objective functions to be differentiable, instead, they use the ability of exploration and exploitation to search multiple randomly selected spaces [28]. Specifically, during the exploration, the goal is to explore a promising region in the search space, and for exploitation, the goal is to excavate the previous promising region carefully.

Over the past few decades, researchers have designed many stochastic optimization algorithms by mimicking the lifestyles or activities of natural creatures. Some well-known algorithms, such as the genetic algorithm (GA) [29], particle swarm optimization (PSO) [30], differential evolution (DE) [31], whale optimization algorithm (WOA) [32], grey wolf optimizer (GWO) [33], artificial bee colony optimization (ABC) [34], salp swarm algorithm (SSA) [35], polar bear optimization (PBO) [36], moth-flame optimization algorithm (MFO) [37], and dragonfly algorithm (DA) [38] have been proposed. In addition, some researchers have also improved the performance of stochastic optimization algorithms. Rizk-Allah et al. [39] integrated the ant colony optimization and firefly algorithm, and firefly worked as a local search to refine the positions found by the ants. Liang et al. [40] proposed a comprehensive learning PSO to improve the global search ability of PSO. Ghosh et al. [41] presented a novel, simple, and efficient mutation formulation by archiving and reusing the most promising difference vectors from past generations to disturb the base individual. Singh et al. [42] presented WOA–differential evolution and genetic algorithm (WOADEGA), appending DE and GA with WOA, and solved the unit commitment scheduling problem. Sumit et al. [43] proposed and investigated a novel, simple, and robust decomposition-based multi-objective heat transfer search for solving real-world structural problems. Betul et al. [44] proposed a new metaheuristic dubbed as the chaotic lévy flight distribution algorithm, to address physical world engineering optimization problems that incorporate chaotic maps in the elementary lévy flight distribution. In addition, a novel hybrid metaheuristic algorithm [45] based on the artificial hummingbird algorithm and simulated annealing problem is proposed to improve the performance of the artificial hummingbird algorithm. The reason for the new variety of stochastic algorithms is out of the no free lunch (NFL) theorem [46], which points out that no single algorithm can perfectly solve all optimization problems.

A spherical search (SS) algorithm [47] was introduced by Kumar, Das, and Zelinka in 2019. To solve global optimization problems more efficiently, a self-adaptive spherical search algorithm (SASS) is proposed [48]. The SASS is a swarm-based meta-heuristic algorithm and has been applied in solving non-linear bound-constrained global optimization problems. SASS has a rigorous mathematical derivation process, and it exhibits some good characteristics similar to other popular algorithms. For example, it is swarm-based; it checks for the stop condition; it has no special requirements for objective functions; and it is not restricted to specific issues. SASS uses a successful history-based parameter adaptation tuning procedure, which enhances the performance of the algorithm.

As an optimization algorithm proposed in recent years, the SASS has the following advantages: (a) a few parameters that need to be debugged, (b) strong exploitation capacity, and (c) high diversity during the search process [48]. However, due to the weak exploration ability of the SASS, it is easy for the algorithm to fall into local optimal in the late iteration [49]. The motivation of this work is to enhance the exploration capability of the SASS so that the algorithm can better balance global exploration and local mining throughout the search process. Thus, in this paper, we propose an enhanced self-adaptive spherical search algorithm with differential evolution (SSDE). The contributions of this paper are as follows:

• The opposition-based learning strategy is used in the initialization phase, which can enhance the quality of the initial solution.
• To balance the exploration and exploitation of the algorithm in the search process, we divide the whole search process into three stages. In addition, we propose three search strategies, with individuals using different search strategies at different stages.
• To effectively prevent the algorithm from falling into local optimal, we propose a non-line parameter.
• According to the mutation strategy in DE, we propose a new mutation strategy. The mutation strategy can help the algorithm achieve a faster convergence speed and find the optimal solution more effectively.
• Experimental results on 29 functions from the standard IEEE CEC 2017 test functions and four constrained practical engineering problems show that the performance of the SSDE is significantly superior to SASS and other state-of-the-art algorithms.

The rest of this paper is organized as follows. Section 2 introduces the original SS and the SASS. Section 3 describes the issues with SASS and presents the novel SSDE. Experiments testing the performance of the SSDE are discussed in Section 4. Finally, Section 5 concludes this paper and discusses future work.

2. Spherical Search Algorithm

2.1. Original Spherical Search Algorithm

The spherical search (SS) algorithm is a swarm-based meta-heuristic proposed to solve non-linear bound-constrained global optimization problems [47]. In the SS, the search space is represented in the form of vector space in which the location of each individual is a position vector representing a candidate solution to the problem.

In a D-dimensional search space, for each individual, before generating its trial location, spherical boundaries are created in advance depending on the individual’s destination direction in every iteration. Here, the destination direction is the main axis of the spherical boundary, and the individual lies on the surface of the spherical boundary [47]. An example of a two-dimensional search space is depicted in Figure 1. The spherical boundary for each individual is drawn as “–”, the target location is drawn as “☆”, and each spherical boundary is generated using the axis obtained by the individual locations and the target locations. Trial solutions appear on the spherical boundary. Thus, in each iteration, the trial location for each individual is generated on the surface of the spherical boundary.

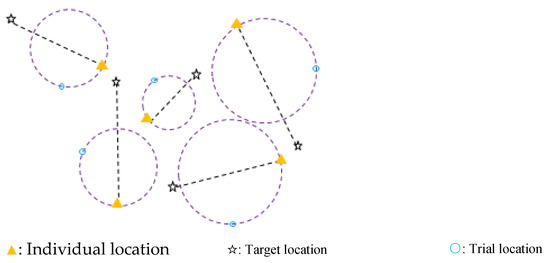
Figure 1. Demonstrating the spherical (circular) boundary of the SS in a two-dimensional search space.

In the SS, the initial population is randomly generated in the search space. Let

$$P_x^{\left(k\right)}=\left[{\overline{x}}_1^{\left(k\right)},{\overline{x}}_2^{\left(k\right)},\dots \dots {\overline{x}}_N^{\left(k\right)}\right]$$

(1)

$${\overline{x}}_i^{\left(k\right)}={\left[x_{i,1}^{\left(k\right)},x_{i,2}^{\left(k\right)},\dots \dots .x_{i,D}^{\left(k\right)}\right]}^T$$

(2)

where $P_x^{\left(k\right)}$ is the population at the kth iteration, N is the number of individuals, and $x_{i,j}^{\left(k\right)}$ is the value of the jth element (parameter) of the ith solution. At the kth iteration, $x_{i,j}^0$ is initialized as follows:

$$x_{i,j}^0=\left(x_{uj}-x_{lj}\right)rand\left(0,1\right)+x_{lj}$$

(3)

where x_uj and x_lj represent the upper and lower bounds of the jth constituent, respectively.

In the SS, the following equation is used to generate a trial solution corresponding to the ith solution.

$${\overline{y}}_i^{\left(k\right)}={\overline{x}}_i^{\left(k\right)}+c_i^{\left(k\right)}{Q}_i^{\left(k\right)}{\overline{z}}_i^{\left(k\right)}$$

(4)

where $Q_i^{\left(k\right)}$ is a projection matrix, which decides the value of ${\overline{y}}_i^{\left(k\right)}$ on the spherical boundary [47], $c_i^{\left(k\right)}$ is a step-size control parameter. At the start of the kth iteration, the value of $c_i{}^{\left(k\right)}$ is selected randomly in the range of [0.5, 0.7] [47]. ${\overline{z}}_i^{\left(k\right)}$ represents the search direction. The SS calculates the search direction in two ways, namely towards-rand and towards-best. With towards-rand, the search direction ${\overline{z}}_i^{\left(k\right)}$ for the ith solution at the kth iteration is calculated by using the following equation:

$${\overline{z}}_i^{\left(k\right)}={\overline{x}}_a^{\left(k\right)}+{\overline{x}}_b^{\left(k\right)}-{\overline{x}}_c^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}$$

(5)

While with towards-best, the search direction ${\overline{z}}_i^{\left(k\right)}$ is calculated as:

$${\overline{z}}_i^{\left(k\right)}={\overline{x}}_{pbest}^{\left(k\right)}+{\overline{x}}_b^{\left(k\right)}-{\overline{x}}_c^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}$$

(6)

In Equations (5) and (6), ${\overline{x}}_i$ represents the current individual position, a, b, and c are randomly selected indices from 1 to N such that a ≠ b ≠ c ≠ i, and ${\overline{x}}_{pbest}$ represents the randomly selected individual among a certain number of top solutions searched so far.

The projection matrix $Q$ is used in Equation (4) to generate the trial solution ${\overline{y}}_i$. Here, $Q=A^{\prime }diag\left({\overline{b}}_i\right)A$, A and${\overline{b}}_i$ are the orthogonal matrix and binary vector, respectively. $diag\left({\overline{b}}_i\right)$ represents the binary diagonal matrix formed by placing the elements of the vector ${\overline{b}}_i$ at the diagonal position. The binary diagonal matrix $diag\left({\overline{b}}_i\right)$ is generated randomly, such that

$$0<rank\left(diag\left({\overline{b}}_i\right)\right)<D$$

(7)

The pseudo code of the SS is shown in Algorithm 1.

Algorithm 1: SS
1	Inputs: The population size N and maximum number of calculations T;
2	Outputs: The global optima and its fitness;
3	Initialize N D-dimensional individuals and calculate their fitness;
4	while t < T do
5	A $\leftarrow$ Compute Orthogonal Matrix;
6	for i = 1 to N do
7		c = rand;
8		rk = rand;
9		for j = 1 to D do
10			if rand < rk then
11				${\overline{b}}_{i,j}$ = 1;
12			else
13				${\overline{b}}_{i,j}$ = 0;
14			end
15		end
16		if i < 0.5 × N then
17			${\overline{z}}_i^{\left(k\right)}={\overline{x}}_a^{\left(k\right)}+{\overline{x}}_b^{\left(k\right)}-{\overline{x}}_d^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}$;
18		else
19			${\overline{z}}_i^{\left(k\right)}={\overline{x}}_{pbest}^{\left(k\right)}+{\overline{x}}_b^{\left(k\right)}-{\overline{x}}_d^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}$;
20		end
21		${\overline{y}}_i \leftarrow {\overline{x}}_i+c{A}^{\prime }diag\left({\overline{b}}_i\right)A{\overline{z}}_i$;
22		$O{f}_i \leftarrow \mathit{O}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{v}\mathit{e}\mathit{F}\mathit{u}\mathit{n}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left({\overline{y}}_i\right)$;
23		$t \leftarrow t+1$;
24		${\overline{x}}_i \leftarrow \mathit{g}\mathit{r}\mathit{e}\mathit{e}\mathit{d}\mathit{S}\mathit{e}\mathit{l}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left({\overline{x}}_i , {\overline{y}}_i\right)$;
25	end
26	end
27	Return the global optima

2.2. Self-Adaptive Spherical Search Algorithm

To more effectively reach globally optimal solutions, Kumar, Das, and Zelinka propose the SASS algorithm [48], in which they use the successful history-based strategy to reset the parameters in the SS.

The success history-based parameter adaptation (SHPA) method [50] is proposed to adapt two control parameters, rk and c. As shown in Table 1, a historical memory that deserves H historical value of rk and c is set. In each generation, rk and c randomly select an element L_rk,j and L_c,j from L_rk and L_c, respectively, with j ∈ [1, H], which are calculated by Equations (8) and (9), respectively.

$$r{k}_i^{\left(k\right)}=Binornd\left(D, L_{1,j}\right)$$

(8)

$$c_i{}^{\left(k\right)}=Cauchyrand\left(L_{2,j}, 0.1\right)$$

(9)

Table 1. The historical memory of L_rk and L_c.

Index	1	2	H−1	H
Lrk	Lrk,1	Lrk,2	Lrk,H-1	Lrk,H
Lc	Lc,1	Lc,2	Lc,H-1	Lc,H

In the beginning, the values of L_rk,s and L_c,s (s = 1, 2, …, H) are all initialized to 0.5. The rk and c values used by successful individuals are recorded in S_r and S_c, and at the end of the generation, the contents of memory are updated as follows:

$$L_{rk,h}^{\left(k+1\right)}=\{\begin{array}{ll}mea{n}_{WL}\left(S_r\right),& \mathrm{if} S_r\ne 0\\ L_{rk,h}^{\left(k\right)}& \mathrm{otherwise}\end{array}$$

(10)

$$L_{c,h}^{\left(k+1\right)}=\{\begin{array}{ll}mea{n}_{WL}\left(S_c\right),& \mathrm{if} S_c\ne 0\\ L_{c,h}^{\left(k\right)}& \mathrm{otherwise}\end{array}$$

(11)

Here, an index h (h = 1, 2, …, H) determines the position in the memory to update, and h is increased progressively. If the value of h exceeds H, h is reset to 1. Furthermore, h is used to update the mean values by using the Lehmer mean ($mea{n}_{WL}$) as follows.

$$\mu ran{k}_h^{\left(k+1\right)}=mea{n}_{WL}\left(S_r\right)$$

(12)

$$\mu c_h^{\left(k+1\right)}=mea{n}_{WL}\left(S_c\right)$$

(13)

$$mea{n}_{WL}\left(S_r\right)=\frac{{{\displaystyle \sum }}_{h=1}^{\left|S_r^{\left(k\right)}\right|}{w}_h^{\left(k\right)}{r}_h^{\left(k\right)2}}{{{\displaystyle \sum }}_{h=1}^{\left|S_r^{\left(k\right)}\right|}{w}_h^{\left(k\right)}{r}_h^{\left(k\right)}}$$

(14)

$$mea{n}_{WL}\left(S_c\right)=\frac{{{\displaystyle \sum }}_{h=1}^{\left|S_c^{\left(k\right)}\right|}{w}_h^{\left(k\right)}{c}_h^{\left(k\right)2}}{{{\displaystyle \sum }}_{h=1}^{\left|S_c^{\left(k\right)}\right|}{w}_h^{\left(k\right)}{c}_h^{\left(k\right)}}$$

(15)

$$w_h^{\left(k\right)}=\frac{f_h^{\left(k\right)}-f_h^{\left(k-1\right)}}{{{\displaystyle \sum }}_{g=1}^{\left|S_r^{\left(k\right)}\right|}(f_g^{\left(k\right)}-f_g^{\left(k-1\right)})}$$

(16)

where $\left|S_r^{\left(k\right)}\right|$ and $\left|S_c^{\left(k\right)}\right|$ are the length of vectors $S_r^{\left(k\right)}$ and $S_c^{\left(k\right)}$, respectively.

3. Proposed Algorithm

Compared with other swarm-based meta-heuristic algorithms, the SASS is very efficient in exploring the new search regions of the solution space. However, it has weak exploration capability, and in some cases, its ability to escape from local optima is limited. Based on an in-depth study of the SASS, the following modifications are introduced to improve its search performance.

3.1. Population Initialization

The opposition-based learning (OBL) strategy [51] is an optimization technique to improve the quality of initial solutions by diversifying them, which has been used by many studies [52,53,54,55,56,57]. The OBL strategy is to search in two directions in the search space, including an original solution and its opposite solution. Finally, the OBL strategy takes the fittest solutions from all solutions. To enhance population diversity and improve the quality of solutions, the OBL strategy is used in the proposed algorithm.

The opposite number of x is, denoted by $\tilde{x}$, calculated as:

$$\tilde{x}=l+u–x$$

(17)

where x is defined as a real number over the interval x ∈ [l, u]. Equation (17) is also applicable to multi-dimensional search space. Therefore, to generalize it, every search-agent position and its opposite position can be represented as

$$x=\left[x_1,x_2,x_3,\dots \dots ,x_D\right]$$

(18)

$$\tilde{x}=\left[{\tilde{x}}_1,{\tilde{x}}_2,{\tilde{x}}_3,\dots \dots ,{\tilde{x}}_D\right]$$

(19)

The values of all elements in $\tilde{x}$ can be determined by

$${\tilde{x}}_j=l_j+u_j–x_j$$

(20)

The procedure for integrating the OBL with the SASS is summarized as follows:

• Step 1. Initialize the population P as x_i, i = 1, 2, …, n.
• Step 2. Determine the opposite population $OP$ as ${\tilde{x}}_i$ using Equation (20), i = 1, 2, …, n.
• Step 3. Select the n fittest individuals from {P ∪ OP}, which represents the new initial population of the SSDE.

3.2. Modifying the Search Direction

Assume that in the entire search process, we evaluate the objective function for T times. The proposed SSDE divides the search process into three phases based on the times of objective evaluation.

Phase 1 The first one-third of the calculation times of the objective evaluations constitutes the first phase. To prevent the algorithm from converging too fast and falling into local optima, the following search direction is proposed to improve the exploration performance of the algorithm:

$${\overline{z}}_i^{\left(k\right)}={\overline{x}}_{r1}^{\left(k\right)}+{\overline{x}}_{r2}^{\left(k\right)}-{\overline{x}}_{r3}^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}+R\ast \left({\overline{x}}_{pbest}^{\left(k\right)}-{\overline{x}}_{r2}^{\left(k\right)}\right)$$

(21)

where ${\overline{x}}_{r1}$, ${\overline{x}}_{r2}$, and ${\overline{x}}_{r3}$ are three different individuals randomly selected from the current population, and ${\overline{x}}_{pbest}$ represents the randomly selected individual from the top p% solutions searched so far. The parameter R changes linearly, and is expressed by the following equation:

$$R=t/T$$

(22)

where t is the times of objective evaluation conducted so far. In this phase, the value of R is small (not greater than 1/3). Therefore, the difference item ${\overline{x}}_{pbest}^{\left(k\right)}-{\overline{x}}_{r2}^{\left(k\right)}$ has less effect.

Phase 2 The middle one-third of the calculation times of the objective evaluations constitute the second phase. We hope that the algorithm can find the optima and balance the global exploration and the local exploitation in the search space. Therefore, the search direction is represented as follows:

$${\overline{z}}_i^{\left(k\right)}={\overline{x}}_{pbest}^{\left(k\right)}+{\overline{x}}_{r2}^{\left(k\right)}-{\overline{x}}_{r3}^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}+R\ast \left({\overline{x}}_{pbest}^{\left(k\right)}-{\overline{x}}_{r2}^{\left(k\right)}\right)$$

(23)

In this phase, the value of R is between 1/3 and 2/3. Therefore, Equation (23) can help the algorithm better balance global exploration and local exploitation.

Phase 3 This phase corresponds to the last one-third of the calculation times of the objective evaluations. In this phase, we improve the exploitation ability and accelerate the convergence of the algorithm. Hence, we update the search direction as follows:

$${\overline{z}}_i^{\left(k\right)}={\overline{x}}_{pbesti}^{\left(k\right)}+{\overline{x}}_{r2}^{\left(k\right)}-{\overline{x}}_{r3}^{\left(k\right)}-{\overline{x}}_i^{\left(k\right)}+R\ast \left({\overline{x}}_{pbest}^{\left(k\right)}-{\overline{x}}_{r2}^{\left(k\right)}\right)$$

(24)

where${\overline{x}}_{pbesti}^{\left(k\right)}$ is the best individual in the current population. The difference item ${\overline{x}}_{pbest}^{\left(k\right)}-{\overline{x}}_{r2}^{\left(k\right)}$ has a great impact, which can help the algorithm converge fast and find the global optima.

3.3. Non-Linear Transition Parameter

In the SASS, the step-size control parameter c is generated from the Cauchy distribution at each iteration. However, a lot of problems require the parameter to change non-linearly changes in the exploratory and exploitative behaviors of an algorithm to avoid local optimal solutions [58,59,60,61]. An appropriate selection of this parameter is necessary to balance global exploration and local exploitation. To spend more time on the exploration phase than exploitation in the proposed algorithm, a non-linear self-adapting parameter c is used and given by

$$c=e^{{\left(-\frac{0.5t}{T}\right)}^2}$$

(25)

Figure 2 shows the change of c when the total times of objective function evaluation are set to 20,000. In fact, c controls the diameter of the spherical boundary. A slightly larger c at the later stage of iteration means that the spherical boundary becomes larger, and the individual can get closer to the global optima faster.

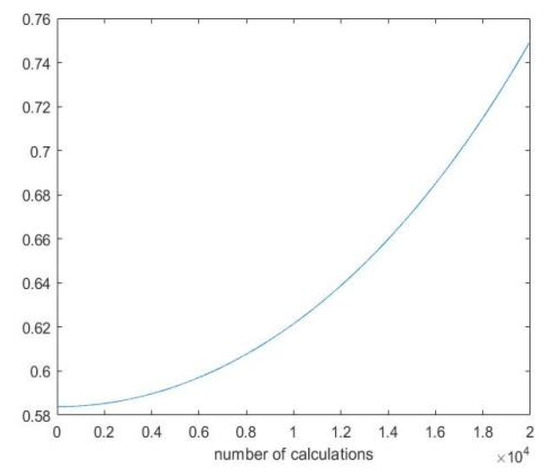
Figure 2. The change of c when the total times of objective function evaluation are set to 20,000.

3.4. Mutation and Crossover Strategies

Inspired by DE, we add the mutation and crossover strategies to the SSDE.

(1)

Mutation strategy. For each individual $x_i^{\left(k\right)}$ in the current population, a mutation individual ${\overline{v}}_i^{\left(k+1\right)}=\left(v_{i,1}^{\left(k+1\right)},v_{i,2}^{\left(k+1\right)},\dots ,v_{i,D}^{\left(k+1\right)}\right)$ is produced through a mutation operation. Inspired by common mutation strategies, a new mutation strategy is introduced, represented by the following equation:

$${\overline{v}}_i^{\left(k+1\right)}={\overline{x}}_{r1}^{\left(k\right)}+R\ast \left({\overline{x}}_{best}^{\left(k\right)}-{\overline{x}}_{r2}^{\left(k\right)}\right)+R\ast \left({\overline{x}}_{best}^{\left(k\right)}-{\overline{x}}_{r3}^{\left(k\right)}\right)$$

(26)

where ${\overline{x}}_{r1}$, ${\overline{x}}_{r2}$, and ${\overline{x}}_{r3}$ are three different individuals randomly selected from the current population. The parameter R is a scale factor given by Equation (22), and ${\overline{x}}_{best}$ is the optimal solution for the current population.

(2)

Crossover strategy. For the target individual ${\overline{x}}_i^{\left(k\right)}$ and its associated mutation individual $v_i^{\left(k+1\right)}$, a trial individual ${\overline{u}}_i^{\left(k+1\right)}=\left(u_{i,1}^{\left(k+1\right)},u_{i,2}^{\left(k+1\right)},\dots ,u_{i,D}^{\left(k+1\right)}\right)$ is generated using the binomial crossover:

$$u_{i,j}^{\left(k+1\right)}=\{\begin{array}{c}{v}_{i,j}^{\left(k+1\right)} ,\hspace{1em}\mathrm{if} rand\le P_{CR} \mathrm{or} j=j_0\\ x_{i,j}^{\left(k\right)}, \mathrm{otherwise}\end{array}$$

(27)

where P_CR ∈ [0, 1] is a crossover probability, and j₀ is a randomly generated index from {1, 2, …, N}.

Due to the impact of mutation, it is possible that some elements of trial individual ${\overline{u}}_i^{\left(k+1\right)}$ may deviate from the feasible solution space. Therefore, the infeasible elements should be reset as follows.

$$u_{i,j}^{\left(k+1\right)}=\{\begin{array}{c}\left(x_{uj}-x_{lj}\right)\times rand\left(0,1\right)+x_{lj},\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} u_{i,j}^{\left(k+1\right)}\notin \left[x_{lj},x_{uj}\right]\\ u_{i,j}^{\left(k+1\right)} \mathrm{otherwise}\end{array}$$

(28)

In the SASS, if the offspring value is not as good as the parent solution, the algorithm does not replace its parent solution with the offspring solution, and the offspring solution is discarded. This will slow the convergence of the search process. To overcome this shortcoming, we add the above mutation and crossover strategies to the SSDE. In the proposed algorithm, if an offspring solution is worse than its parent solution, the algorithm uses mutation and crossover strategies to produce a new one. It will replace the parent solution if it is better than the parent. Otherwise, the parent solution will be reserved for the next iteration. In this way, the SSDE can find the optimal solution more efficiently and has a faster convergence speed.

The flowchart of the proposed SSDE with all the above-mentioned strategies is shown in Figure 3, and the pseudo code is presented in Algorithm 2.

Algorithm 2: SSDE
1	Inputs: The population size N and maximum number of calculations T;
2	Outputs: The global optima and its fitness;
3	Initialize N D-dimensional individuals with the OBL strategy and calculate their fitness;
4	Set all values in Lrk to 0.5, h = 1;
5	while t < T do
6	Sr = ϕ;
7	$c=e^{{(-\frac{0.5t}{T})}^2}$;
8	A $\leftarrow$ Compute Orthogonal Matrix;
9	for i = 1 to N do
10		j = select from [1, H] randomly;
11		rk = Binornd(D, Lrk,j);
12		for k = 1 to D do
13			if rand < rk then
14				${\overline{b}}_{i,k}$ = 1;
15			else
16				${\overline{b}}_{i,k}$ = 0;
17			end
18		end
19		if t < (1/3) × T then
20			Using Equation (21);
21		else if (1/3) × T < t < (2/3) × T then
22			Using Equation (23);
23		else
24			Using Equation (24);
25		end
26		${\overline{y}}_i \leftarrow x_i+c{A}^{\prime }diag\left({\overline{b}}_i\right)A{\overline{z}}_i$;
27		$O{f}_i \leftarrow \mathit{O}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{v}\mathit{e}\mathit{F}\mathit{u}\mathit{n}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left({\overline{y}}_i\right)$;
28		$t \leftarrow t+1$;
29		if $O{f}_i^{k+1}>O{f}_i^k$ then
30			New solution $u_i$ is produced using Equations (26)–(28);
31			$Of{u}_i \leftarrow \mathit{O}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{v}\mathit{e}\mathit{F}\mathit{u}\mathit{n}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(u_i\right)$;
32			$t \leftarrow t+1$;
33			${\overline{y}}_i \leftarrow \mathit{g}\mathit{r}\mathit{e}\mathit{e}\mathit{d}\mathit{S}\mathit{e}\mathit{l}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(u_i, {\overline{y}}_i\right)$;
34		else
35			rk is recorded in Sr;
36		end
37		${\overline{x}}_i \leftarrow \mathit{g}\mathit{r}\mathit{e}\mathit{e}\mathit{d}\mathit{S}\mathit{e}\mathit{l}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left({\overline{x}}_i, {\overline{y}}_i\right)$;
38	end
39	if Sr ≠ ϕ
40		update Lrk,h;
41		h = h + 1;
42		if h > H then, h is set to 1; end
43	end
44	${\overline{x}}_{pbest}$ = top p% solution searched so far;
45	${\overline{x}}_{best}$= best solution searched so far;
46	end
47	Return ${\overline{x}}_{best}$

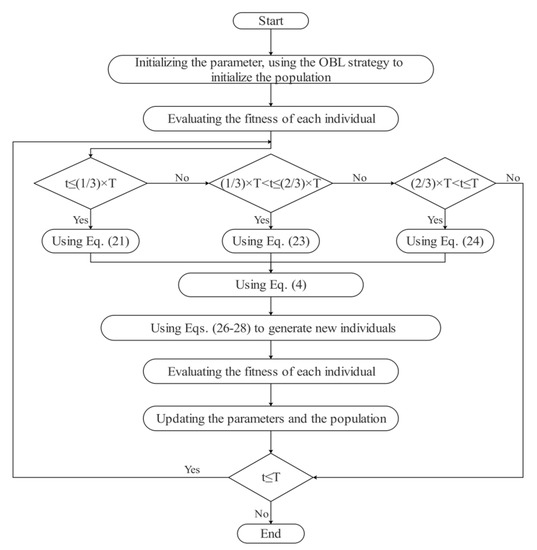
Figure 3. The flowchart of the SSDE.

4. Experimental Results and Discussion

To test and verify the performance of the SSDE, a variety of experiments are conducted. Given the randomness of the optimization algorithm, to ensure that the superior results of the proposed algorithm do not happen by accident, we use the standard IEEE CEC 2017 [62] and two practical engineering problems to test the SSDE. In addition, to evaluate the strength of the SSDE, we compare the SSDE with the SASS and seven state-of-the-art algorithms: WOA, DE, PSO, SSA, SCA [63], GWO, and MSCA [59].

4.1. Experimental Analysis of Standard IEEE CEC2017 Benchmark Functions

The well-known 29 benchmark functions from a special session of IEEE CEC 2017 [62] are considered to analyze the performance of the SSDE and for comparison with the other state-of-the-art algorithms. Detailed information and characteristics of these problems are available in [64]. The CEC 2017 test functions are categorized into four groups: unimodal (F1–F3), multimodal (F4–F10), hybrid (F11–F20), and composite (F21–F30).

For any benchmark test function, each algorithm runs 30 times independently and the population size is set to 25. The algorithm will stop when the times of function evaluation reach 20,000, i.e., T = 20,000. Other parameters are the same as the original algorithm to ensure the fairness of comparison. The obtained results on these test functions corresponding to 10-dimensional search space are recorded in Table 2. The Wilcoxon sign rank test is also utilized to judge whether the improvements are significant in Table 3. The experimental results of 30 and 50 dimensions on these test functions are shown in Table 4 and Table 5.

Table 2. Experimental results of IEEE CEC 2017 test problems with 10 dimensions.

Functions (D = 10)		Algorithm
		SSDE	PSO	SASS	GWO	SCA	DE	MSCA	SSA	WOA
F1	mean	100	34,246.02	100	1.05 × 108	1.15 × 109	5448.92	3664.507	24,203,215	8.38 × 108
	std	2.01 × 10−14	171,407.2	9.67 × 10−14	1.86 × 108	4.05 × 108	5201.572	3234.143	22,487,065	1.06 × 109
	best	100	118.7576	100	14,778.19	3.55 × 108	220.9604	237.4083	1,988,914	1.06 × 108
	Rank1	1	5	2	7	9	4	3	6	8
F3	mean	300	300.7913	1138.779	2238.573	4236.662	7253.396	300	5875.853	3475.632
	std	4.95 × 10−14	1.509412	2288.111	1982.749	2129.628	3102.121	2.77 × 10−9	5808.211	3071.002
	best	300	300.0005	300	359.4759	1312.951	1960.043	300	888.7846	578.2727
	Rank3	1	3	4	5	7	9	2	8	6
F4	mean	400.0219	404.5307	400	415.0882	473.5321	405.9912	408.0454	437.4486	462.495
	std	0.11985	0.612478	4.13 × 10−9	14.76518	29.69938	1.207048	13.95554	40.45976	39.25786
	best	400	403.075	400	406.7814	432.424	403.6232	400.03	403.3351	412.0046
	Rank4	2	3	1	6	9	4	5	7	8
F5	mean	504.1737	510.1823	504.4146	516.7324	558.6243	509.3172	527.1079	558.9709	551.671
	std	1.482855	5.344041	1.646337	6.990039	7.613383	1.601565	13.05469	21.72435	12.64874
	best	501.9909	501.9899	501.9906	506.2205	545.5591	506.5302	501.9899	526.2454	527.0799
	Rank5	1	4	2	5	8	3	6	9	7
F6	mean	600	600.0003	600.0004	602.2146	625.3604	600	613.4951	636.182	624.5874
	std	1.27 × 10−13	0.000993	0.000864	2.650979	4.661668	2.37 × 10−6	8.010433	14.06836	9.986023
	best	600	600	600	600.0678	616.3785	600	601.3978	618.1464	610.5589
	Rank6	1	3	4	5	8	2	6	9	7
F7	mean	714.8522	724.2474	714.9653	736.7176	790.4605	722.8071	739.8617	787.2327	781.6688
	std	1.609563	5.469394	3.322038	12.47522	13.39333	3.076604	12.51864	25.10096	17.50719
	best	711.8061	711.3336	704.8283	716.4962	760.2025	716.2453	714.5461	737.5685	749.4585
	Rank7	1	4	2	5	9	3	6	8	7
F8	mean	804.701	813.6163	805.0716	816.892	849.0973	811.994	825.0484	836.6839	836.2285
	std	1.656063	7.877355	1.685183	8.4292	9.080428	2.299403	11.59091	17.12915	7.340493
	best	802.0046	804.9748	801.991	802.5454	831.3656	809.2004	808.9546	813.0176	822.9558
	Rank8	1	4	2	5	9	3	6	8	7
F9	mean	900	900.0879	900.1864	934.5943	1104.827	900.0001	1047.683	1410.488	1330.281
	std	2.11 × 10−14	0.404123	0.314037	50.45165	89.7745	0.000171	299.4402	366.8872	376.2577
	best	900	900	900	900.088	956.9951	900	900.0895	998.8913	927.6632
	Rank9	1	3	4	5	7	2	6	9	8
F10	mean	1134.713	1495.179	1256.386	1796.312	2635.735	1542.551	1936.831	2213.272	2330.367
	std	88.28647	288.4056	142.717	319.0949	190.7183	114.0585	328.1472	314.9542	324.9352
	best	1007.486	1023.597	1018.805	1311.315	2284.22	1284.388	1140.263	1280.863	1582.587
	Rank10	1	3	2	5	9	4	6	7	8
F11	mean	1102.601	1106.031	1103.253	1140.468	1259.909	1106.775	1172.451	1218.709	1183.353
	std	1.190558	3.386216	2.922299	21.90572	70.28524	2.648874	47.15133	96.45727	37.38167
	best	1100	1100.998	1100	1112.843	1150.03	1101.271	1108.662	1125.791	1141.456
	Rank11	1	3	2	5	9	4	6	8	7
F12	mean	1274.532	20,345.78	1660.864	965,440.8	40,400,247	496,575.2	2,743,075	4,899,297	6,880,265
	std	78.44183	17,273.06	406.3034	100,3047	37,161,505	540,438.6	3,234,578	6,224,999	76,269,77
	best	1200.004	1575.165	1211.418	6749.233	6,603,427	40,376.35	3702.779	7901.736	203,108.8
	Rank12	1	3	2	5	9	4	6	7	8
F13	mean	1305.445	11,113.62	1306.601	14,533.95	119,429.2	6181.118	17,463.51	19,650.27	21,048.3
	std	2.384138	10,694.13	3.441744	11,524.87	105,367.8	3366.069	12,367.83	16,747.16	12,152.58
	best	1300.117	1312.298	1300	1828.208	12,509.54	1842.88	2088.414	2151.667	6093.469
	Rank13	1	4	2	5	9	3	6	7	8
F14	mean	1400.522	1511.187	1407.851	3533.604	2627.875	1520.076	2172.1	2421.396	2562.814
	std	0.49147	104.8579	8.766021	1966.26	1179.53	390.6259	1292.342	1298.167	1235.804
	best	1400	1425.245	1400	1455.971	1520.056	1403.497	1462.936	1458.809	1503.306
	Rank14	1	3	2	9	8	4	5	6	7
F15	mean	1500.445	2042.943	1501.95	5169.392	5965.438	1546.768	6180.33	9219.764	4895.496
	std	0.489679	1176.53	3.921523	2530.107	5849.843	72.37771	6123.108	6315.789	4511.734
	best	1500.003	1515.284	1500.064	1604.607	1953.085	1504.481	1591.059	1809.038	1767.368
	Rank15	1	4	2	6	7	3	8	9	5
F16	mean	1600.942	1659.691	1627.424	1802.864	1865.585	1632.984	1768.699	1946.426	1823.735
	std	0.525412	75.70036	49.93683	163.011	105.2517	27.02148	112.2436	153.2795	141.0026
	best	1600.292	1600.132	1600.331	1603.509	1668.016	1603.396	1608.566	1634.709	1640.371
	Rank16	1	4	2	6	8	3	5	9	7
F17	mean	1701.406	1731.113	1703.412	1772.365	1801.509	1704.984	1810.436	1825.534	1782.034
	std	3.380266	35.43425	5.760702	40.88989	17.46695	2.485578	56.40685	61.64626	23.99218
	best	1700	1701.329	1700.042	1734.619	1768.94	1701.633	1725.249	1744.71	1752.695
	Rank17	1	4	2	5	7	3	8	9	6
F18	mean	1800.529	10,423.56	1816.007	28,248.12	758,555.4	2405.031	23,139.23	18,720.76	65,853.29
	std	0.478062	7086.168	14.36381	17,002.95	917142.4	1143.299	12,870.63	13,400.16	38,095.21
	best	1800	1887.071	1800.006	1931.84	57847.29	1827.836	3409.868	3069.755	11,041.02
	Rank18	1	4	2	7	9	3	6	5	8
F19	mean	1900.054	3411.068	1900.984	8940.802	24,764.73	1987.064	5369.088	192,681.6	9705.1
	std	0.178498	2135.486	1.390807	7437.749	49,828.33	288.102	4220.804	471,066	9028.701
	best	1900	1903.401	1900.019	1914.999	2094.819	1901.246	1944.284	2300.063	2059.191
	Rank19	1	4	2	6	8	3	5	9	7
F20	mean	2000.148	2029.8	2000.213	2103.169	2148.39	2000.202	2095.97	2193.77	2122.105
	std	0.235108	36.40018	0.321892	67.14641	52.07042	0.200424	52.81643	88.90603	51.33178
	best	2000	2000.312	2000	2026.95	2060.707	2000	2028.461	2069.93	2047.836
	Rank20	1	4	3	6	8	2	5	9	7
F21	mean	2249.172	2298.152	2305.789	2310.329	2286.841	2277.222	2278.58	2328.93	2311.639
	std	56.87799	38.48879	13.25438	29.5534	67.71513	33.14775	59.4237	54.60013	58.35942
	best	2103.689	2200.313	2237.741	2200.788	2208.559	2209.234	2200.332	2209.009	2207.643
	Rank21	1	5	6	7	4	2	3	9	8
F22	mean	2284.712	2299.63	2297.656	2339.026	2435.404	2298.944	2302.143	2388.957	2404.186
	std	26.87408	13.03449	15.50953	129.3929	52.13074	13.36789	11.16604	263.1557	108.7401
	best	2226.929	2230.856	2215.56	2301.077	2309.092	2256.914	2244.413	2267.231	2276.428
	Rank22	1	4	2	6	9	3	5	7	8
F23	mean	2608.025	2611.863	2607.06	2622.234	2666.615	2612.679	2625.155	2654.057	2649.126
	std	2.203656	5.358664	2.543877	10.0788	8.691642	2.365113	10.4542	22.94077	11.3572
	best	2604.091	2604.247	2602.934	2605.363	2648.471	2608.393	2608.111	2621.33	2629.261
	Rank23	2	3	1	5	9	4	6	8	7
F24	mean	2600.746	2742.297	2720.518	2741.83	2790.578	2669.078	2742.707	2776.592	2783.652
	std	114.8247	6.794553	56.46529	37.98631	44.31915	63.34987	46.94934	64.50508	11.23809
	best	2500	2732.27	2500	2553.705	2562.116	2544.42	2500	2541.384	2766.408
	Rank24	1	5	3	4	9	2	6	7	8
F25	mean	2902.837	2928.617	2921.399	2939.774	2985.776	2918.014	2927.671	2964.687	2966.392
	std	13.84709	24.26633	23.74803	19.55005	26.19457	13.92404	24.11831	22.0164	38.20065
	best	2897.743	2898.329	2897.743	2904.455	2941.482	2899.959	2897.787	2933.205	2906.368
	Rank25	1	5	3	6	9	2	4	7	8
F26	mean	2856.544	3161.183	2942.878	3191.133	3165.533	2891.744	2989.896	3777.01	3231.533
	std	95.96362	455.5761	171.0177	420.925	45.93121	95.44366	308.2803	535.3961	308.7191
	best	2600	2800	2900	2816.189	3077.831	2670.471	2600	2908.449	2952.377
	Rank26	1	5	3	7	6	2	4	9	8
F27	mean	3078.178	3098.001	3090.875	3102.384	3108.466	3094.847	3094.87	3149.297	3101.021
	std	6.203248	3.107609	2.352379	16.29375	4.111021	2.014573	2.826782	49.41694	5.843989
	best	3070.577	3092.021	3089.006	3089.533	3102.329	3090.161	3089.955	3098.249	3094.08
	Rank27	1	5	2	7	8	3	4	9	6
F28	mean	3119.618	3296.094	3277.862	3389.683	3376.754	3257.482	3329.95	3501.928	3299.904
	std	77.75105	150.7798	145.4635	78.42421	106.0469	92.68148	138.3757	149.7309	0.34587
	best	2800	3100	3100	3169.614	3205.987	3088.754	3164.612	3217.055	3298.161
	Rank28	1	4	3	8	7	2	6	9	5
F29	mean	3154.113	3192.162	3157.096	3207.68	3287.239	3184.21	3240.789	3352.915	3270.3
	std	7.624298	39.60988	19.21254	42.65411	56.20661	11.52755	51.96886	111.779	58.6343
	best	3138.788	3135.933	3132.054	3147.649	3210.817	3168.743	3155.891	3198.503	3178.055
	Rank29	1	4	2	5	8	3	6	9	7
F30	mean	3428.451	818,861	430,950	698,032.7	1,617,495	66,110.84	885,587.4	1,465,661	770,843.4
	std	204.8178	1,076,251	549,727.1	117,2826	898,592.4	73,780.6	1,217,842	1,935,629	695,539
	best	3232.172	8976.342	3399.592	5507.622	259,891.8	3922.918	5349.961	14,653.59	9622.095
	Rank30	1	6	3	4	9	2	7	8	5
Result	w/t/l	--	29/0/0	27/0/2	29/0/0	29/0/0	29/0/0	29/0/0	29/0/0	29/0/0
	Total	31	115	72	167	235	91	206	157	231
	Rank	1	4	2	6	9	3	7	5	8

Table 3. The calculated p-values for the SSDE algorithm versus other competitors on CEC2017.

	DE	PSO	SASS	GWO	MSCA	SCA	SSA	WOA
F1	1.24 × 10−11	1.24 × 10−11	0.053459	1.24 × 10−11	1.24 × 10−11	1.24 × 10−11	1.24 × 10−11	1.24 × 10−11
F3	1.33 × 10−11	1.33 × 10−11	0.238288	1.33 × 10−11	1.33 × 10−11	1.33 × 10−11	1.33 × 10−11	1.33 × 10−11
F4	3 × 10−11	3 × 10−11	0.009197	3 × 10−11	3 × 10−11	3 × 10−11	3.32 × 10−11	3 × 10−11
F5	1.33 × 10−10	1.16 × 10−7	0.695215	4.08 × 10−11	3.02 × 10−11	3.02 × 10−11	6.12 × 10−10	3.02 × 10−11
F6	1.83 × 10−11	1.83 × 10−11	1.56 × 10−9	1.83 × 10−11	1.83 × 10−11	1.83 × 10−11	1.83 × 10−11	1.83 × 10−11
F7	5.49 × 10−11	1.2 × 10−8	0.3871	4.98 × 10−11	3.02 × 10−11	3.02 × 10−11	1.61 × 10−10	3.02 × 10−11
F8	3.02 × 10−11	3.2 × 10−9	0.717189	4.57 × 10−9	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F9	1.72 × 10−12	1.91 × 10−12	0.000224	1.72 × 10−12	1.72 × 10−12	1.72 × 10−12	1.72 × 10−12	1.72 × 10−12
F10	4.08 × 10−11	6.53 × 10−7	0.001004	4.08 × 10−11	3.02 × 10−11	3.02 × 10−11	1.46 × 10−10	3.34 × 10−11
F11	1.01 × 10−8	5.46 × 10−6	0.911707	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F12	3.02 × 10−11	3.02 × 10−11	3.5 × 10−9	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F13	3.02 × 10−11	3.02 × 10−11	0.102326	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F14	3 × 10−11	3 × 10−11	6.95 × 10−8	3 × 10−11	3 × 10−11	3 × 10−11	3 × 10−11	3 × 10−11
F15	3.02 × 10−11	3.02 × 10−11	5.61 × 10−5	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F16	3.02 × 10−11	0.000268	0.001236	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F17	5.57 × 10−10	1.78 × 10−10	0.019883	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F18	3.02 × 10−11	3.02 × 10−11	7.69 × 10−8	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F19	3.02 × 10−11	3.02 × 10−11	1.6 × 10−7	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11
F20	0.000207	2.02 × 10−11	0.001452	1.33 × 10−11	1.33 × 10−11	1.33 × 10−11	1.33 × 10−11	1.33 × 10−11
F21	0.016283	6.76 × 10−5	0.00238	9.53 × 10−7	3.32 × 10−6	0.000856	0.055542	1.6 × 10−7
F22	6.04 × 10−7	9.75 × 10−10	0.000744	3.02 × 10−11	2.61 × 10−10	3.02 × 10−11	3.47 × 10−10	2.03 × 10−9
F23	2.02 × 10−8	0.004033	0.10869	1.47 × 10−7	3.02 × 10−11	3.02 × 10−11	9.92 × 10−11	3.02 × 10−11
F24	0.005569	5.09 × 10−8	0.005321	4.11 × 10−7	3.02 × 10−11	1.09 × 10−10	2.92 × 10−9	3.82 × 10−10
F25	5.86 × 10−8	4.56 × 10−8	0.003802	9.44 × 10−10	3.05 × 10−10	3.93 × 10−11	8.02 × 10−7	3.93 × 10−11
F26	0.001113	6.7 × 10−8	0.004197	6.06 × 10−9	2.45 × 10−11	2.45 × 10−11	3.46 × 10−6	3 × 10−11
F27	7.39 × 10−11	4.08 × 10−11	1.75 × 10−9	7.39 × 10−11	3.02 × 10−11	3.02 × 10−11	1.09 × 10−10	3.02 × 10−11
F28	1.99 × 10−7	1.23 × 10−7	0.000205	8.54 × 10−11	2.58 × 10−11	5.75 × 10−11	1.99 × 10−7	3.49 × 10−11
F29	3.34 × 10−11	6.74 × 10−6	0.841801	2.03 × 10−9	3.02 × 10−11	3.02 × 10−11	8.99 × 10−11	3.02 × 10−11
F30	3.34 × 10−11	3.02 × 10−11	3.15 × 10−5	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11	3.02 × 10−11

Table 4. Experimental results of IEEE CEC 2017 test problems with 30 dimensions.

Functions (D = 30)		Algorithm
		SSDE	PSO	SASS	GWO	SCA	DE	MSCA	SSA	WOA
F1	mean	1214.735	318,302.5	2693.978	2.82 × 109	2.22 × 1010	12,563.19	5223.161	3.59 × 109	2.17 × 1010
	std	1916.514	923,540.7	3913.923	2.08 × 109	4.21 × 109	8193.083	5908.148	1.59 × 109	6.92 × 109
	best	100.3902	9751.81	100.2905	1.48 × 108	1.56 × 1010	1654.601	103.4057	1.06 × 109	1.17 × 1010
	Rank1	1	5	2	6	9	4	3	7	8
F3	mean	23,942.32	78,837.2	42,182.59	55,596.32	101,154.3	127,579.3	59,609.19	270,390.1	66,569.37
	std	47,823.35	22,596.9	61,202.19	9755.418	22,800.18	14,988.43	17,367.13	61,032.97	11,111.25
	best	312.0746	40,892.75	619.905	37470.61	61,308.36	96,613.94	36,118.38	117,354.1	47,422.39
	Rank3	1	6	2	3	7	8	4	9	5
F4	mean	477.5421	584.6983	492.8606	640.4271	3844.283	533.7523	516.188	1078.833	3294.031
	std	28.39	47.56279	20.51791	119.8701	1317.736	15.39032	34.12509	233.7412	2145.133
	best	404.175	511.2588	464.1175	520.2232	2003.569	504.5435	470.4384	731.5059	1012.88
	Rank4	1	5	2	6	9	4	3	7	8
F5	mean	541.1189	599.017	538.4414	629.5262	841.6137	651.2377	668.2491	858.1546	814.4567
	std	8.045002	33.68432	10.49185	38.88677	28.08444	13.63791	55.7492	67.7493	33.88972
	best	522.7386	550.3528	522.2036	581.0746	788.7319	622.5741	568.652	721.9649	738.2459
	Rank5	2	3	1	4	8	5	6	9	7
F6	mean	600.0039	602.528	600.2777	612.5991	669.0795	600.0082	652.9687	679.6934	667.5183
	std	0.008565	1.378882	0.438796	6.121403	7.042164	0.002077	13.12979	11.80915	8.267706
	best	600.0004	600.6673	600	604.2167	652.7276	600.0034	632.1626	657.8453	645.9588
	Rank6	1	4	3	5	8	2	6	9	7
F7	mean	775.2795	881.503	787.2502	919.7737	1285.993	888.1853	956.0451	1308.173	1224.209
	std	16.48145	49.83537	19.57216	54.13244	65.95231	13.59312	79.08342	81.07318	76.88078
	best	757.2861	801.8672	758.8045	836.5483	1152.906	867.2314	854.5204	1100.308	1101.11
	Rank7	1	3	2	5	8	4	6	9	7
F8	mean	844.1768	893.1935	840.06	899.8351	1105.645	946.507	965.2352	1045.259	1062.671
	std	8.777689	38.9006	8.483102	22.11481	25.00203	13.3735	35.6698	40.9629	34.7959
	best	827.7551	833.2403	821.5657	850.7726	1062.461	915.0619	889.5461	978.6451	1006.401
	Rank8	2	3	1	4	9	5	6	7	8
F9	mean	919.6242	1683.255	1085.664	2688.093	9186.586	1483.405	5623.1	11,401.85	8956.392
	std	36.31226	787.6032	146.1299	951.3941	1632.926	186.5288	1491.474	3965.377	2088.556
	best	900.4476	996.241	939.3865	1398.808	5138.516	1127.085	3257.784	5980.982	5290.591
	Rank9	1	4	2	5	8	3	6	9	7
F10	mean	3726.802	6691.426	3407.903	5195.362	8993.712	6486.723	5210.946	7253.927	8421.412
	std	575.5629	1061.329	261.9461	1455.201	376.3233	259.5786	710.2808	746.1995	533.4861
	best	2917.698	4836.995	2930.748	3619.285	8129.568	6050.648	4142.074	5854.345	6927.831
	Rank10	2	6	1	3	9	5	4	7	8
F11	mean	1140.347	1320.516	1322.513	2364.29	4760.276	1859.169	1373.355	8087.669	3316.554
	std	20.36572	104.5667	347.068	958.5571	954.0125	463.6676	90.97094	3374.625	1222.641
	best	1117.047	1137.171	1194.979	1391.704	3079.215	1343.659	1250.336	3360.885	1785.524
	Rank11	1	2	3	6	8	5	4	9	7
F12	mean	43,717.07	1,988,534	36,057.54	1.5 × 108	3.07 × 109	7,677,616	24,697,429	3.81 × 108	1.83 × 109
	std	37,087.48	1,773,727	24,241.95	1.38 × 108	8.47 × 108	4,064,328	22,967,506	3.16 × 108	1.53 × 109
	best	7949.39	108,045.5	3249.557	4,734,442	1.45 × 109	2,390,306	2,251,356	47,322,980	5.48 × 108
	Rank12	2	3	1	6	9	4	5	7	8
F13	mean	3531.069	705,732.4	8064.486	22,037,460	1.5 × 109	947,794.8	138,573.4	4,918,600	3.97 × 108
	std	3488.159	2,749,256	8177.317	77,719,596	8.14 × 108	844,674.9	111,150.2	3,516,607	5.37 × 108
	best	1474.154	1386.979	1659.798	40,467.39	1.39 × 108	59,000.31	17,081.68	865,684.1	52,349,332
	Rank13	1	4	2	7	9	5	3	6	9
F14	mean	1446.482	69,556.08	1570.81	656,694.1	901,895.8	401,921.7	90,460.76	2,752,249	569,586.4
	std	7.968351	55,613.53	52.4077	940,302.1	794,882.7	396,702.5	85,656.52	3,133,303	787,998.3
	best	1435.379	9310.253	1490.805	9446.702	138,704.7	21,388.36	3498.422	82,958.11	60,570.56
	Rank14	1	3	2	7	8	5	4	9	6
F15	mean	1556.968	47,813.5	1845.443	803,138.2	87,958,238	419,127.2	76,523.86	5,796,479	9,350,120
	std	38.97468	156,431.1	146.3524	1,341,614	73,896,549	420,663.5	43,124.8	8,303,473	17,402,550
	best	1515.419	1756.559	1648.858	13,934.78	9,648,115	57,658.67	21,269.03	76,385.59	275,388.4
	Rank15	1	3	2	6	9	5	4	7	8
F16	mean	2221.167	2565.365	2241.364	2553.444	4240.757	2723.693	2921.968	3991.564	3705.815
	std	140.402	397.9829	211.967	352.4102	309.5066	150.0677	398.0898	406.954	377.177
	best	1963.154	1805.894	1769.643	1972.211	3678.952	2467.829	2259.218	3211.533	2634.415
	Rank16	1	4	2	3	9	5	6	8	7
F17	mean	1840.45	2042.891	1902.922	2103.255	2857.21	2047.113	2383.156	2805.449	2483.9
	std	98.47333	145.0102	100.0874	205.1428	201.3401	129.0857	238.3734	333.7176	254.3479
	best	1744.649	1803.566	1743.749	1811.528	2385.028	1831.617	1930.647	2066.67	2081.961
	Rank17	1	3	2	5	9	4	6	8	7
F18	mean	20,906.56	2,166,180	28,696.89	2,934,427	16,318,884	973,410.4	1,139,948	15,215,895	5,935,632
	std	73,358.83	191,4316	57,525.82	4,611,271	10,007,632	419,581.2	1,332,961	13,620,010	5,591,938
	best	2188.267	211,402	3048.483	66,331.88	1,243,929	379,075.2	152,080.6	360,024.9	296,456.5
	Rank18	1	5	2	6	9	3	4	8	7
F19	mean	1930.22	17,744.62	2068.848	13,299,474	1.07 × 108	275,197.4	5,126,766	15,094,397	16,986,271
	std	16.01712	14,939.43	80.06088	59,558,539	59,641,706	163,253.4	2,529,800	16,442,760	15,601,603
	best	1913.57	2348.125	1944.216	6842.181	18,005,102	74,784.85	24,544.21	496,822.1	2,666,205
	Rank19	1	3	2	6	9	4	5	7	9
F20	mean	2216.252	2322.75	2319.041	2439.469	2970.974	2397.494	2647.471	2972.125	2790.858
	std	87.59456	172.2885	113.6932	140.5444	149.0737	131.8006	184.2347	199.8384	176.1902
	best	2050.566	2066.665	2083.616	2245.655	2680.631	2129.798	2233.401	2582.163	2404.303
	Rank20	1	3	2	5	8	4	6	9	7
F21	mean	2343.467	2426.937	2339.381	2414.536	2607.462	2448.681	2447.039	2639.353	2585.115
	std	8.241865	46.62559	10.57509	44.33458	26.14788	11.47136	38.6798	69.74984	41.49378
	best	2328.879	2337.667	2321.327	2363.062	2568.479	2424.392	2369.108	2496.43	2511.827
	Rank21	2	4	1	3	8	6	5	9	7
F22	mean	2473.439	5652.81	2966.603	4948.645	9959.929	3238.169	5521.019	8073.984	6039.086
	std	644.3842	2823.078	1191.037	2084.618	1497.375	965.042	2233.659	1534.083	2269.538
	best	2300	2300.849	2300	2472.702	4108.188	2554.987	2300	3813.058	3541.608
	Rank22	1	6	2	4	9	3	5	8	7
F23	mean	2694.51	2778.312	2689.808	2803.913	3100.924	2793.002	2800.372	3162.298	2999.109
	std	9.586829	52.55253	11.05885	49.34804	45.49504	12.89897	32.89713	122.019	48.65913
	best	2677.852	2693.384	2667.751	2734.785	3010.326	2764.933	2747.02	2935.069	2926.217
	Rank23	2	3	1	6	8	4	5	9	7
F24	mean	2872.644	3000.303	2861.901	2955.733	3273.588	2999.539	2942.244	3272.308	3159.839
	std	12.13741	44.55668	10.88099	55.7742	45.64415	16.18424	35.35299	98.53333	39.1045
	best	2851.211	2888.587	2842.809	2885.773	3178.396	2969.582	2880.505	3101.388	3091.326
	Rank24	2	6	1	4	9	5	3	8	7
F25	mean	2883.204	2925.359	2892.012	3027.803	3741.007	2895.714	2937.38	3179.153	3530.672
	std	4.094973	22.64489	9.703009	77.37472	280.4763	5.090101	29.95837	70.39087	369.0774
	best	2878.559	2895.079	2883.577	2942.089	3245.769	2888.45	2897.385	3075.699	3139.248
	Rank25	1	4	2	6	9	3	5	7	8
F26	mean	4005.809	4752.348	4084.703	4948.957	8141.935	5175.481	4808.641	8334.316	7416.938
	std	352.4129	458.7195	283.9643	416.4842	573.9177	179.6555	1375.728	1030.117	917.7473
	best	2946.438	3952.01	2900	4210.652	7206.439	4421.83	2800.003	6375.017	4954.286
	Rank26	1	3	2	5	8	6	4	9	7
F27	mean	3167.077	3271.651	3224.05	3270.916	3587.553	3233.091	3272.817	3450.364	3200.007
	std	17.85653	13.94893	11.04673	33.47732	67.7237	4.500357	26.4086	133.9828	5.69 × 10−5
	best	3149.654	3241.91	3204.144	3228.391	3492.889	3224.026	3221.789	3282.479	3200.007
	Rank27	1	7	3	6	9	4	8	9	2
F28	mean	3219.938	3283.913	3213.903	3527.571	4635.833	3276.004	3291.582	3685.491	3942.116
	std	17.43694	51.06665	34.09523	135.0544	425.5092	16.82819	49.82494	166.5222	503.9273
	best	3191.581	3214.369	3103.489	3343.43	3971.405	3251.315	3212.987	3422.978	3300.007
	Rank28	2	4	1	6	9	3	5	7	8
F29	mean	3412.507	3750.909	3520.708	3959.045	5304.486	3810.176	4351.165	5455.996	4698.575
	std	106.4616	205.2828	123.2694	174.7359	321.4533	116.1537	297.7375	616.7706	339.5266
	best	3223.4	3392.091	3420.051	3641.181	4731.91	3583.597	3950.985	4593.54	4197.895
	Rank29	1	3	2	5	8	4	6	9	7
F30	mean	4033.791	43,027.72	8536.308	10,706,158	2.15 × 108	408,820.2	8,095,003	41,773,732	85,625,341
	std	1154.468	43,625.64	2734.866	7,789,367	80,801,991	266,148.9	9,599,077	35,119,267	1.35 × 108
	best	3306.365	9118.613	5678.458	1,281,587	60,685,335	93,028.28	1,110,624	4,883,074	17,289,597
	Rank30	1	3	2	6	9	4	5	7	8
Result	w/t/l	--	29/0/0	22/0/7	29/0/0	29/0/0	29/0/0	29/0/0	29/0/0	29/0/0
	Total	37	115	53	148	248	126	206	141	232
	Rank	1	3	2	6	9	4	7	5	8

Table 5. Experimental results of IEEE CEC 2017 test problems with 50 dimensions.

Functions (D = 50)		Algorithm
		SSDE	PSO	SASS	GWO	SCA	DE	MSCA	SSA	WOA
F1	mean	160,040.1	83,816,607	37,769.75	1.21 × 1010	6.81 × 1010	6,368,259	19,689.12	1.54 × 1010	6.08 × 1010
	std	255,904.1	74,836,778	70,041.99	4.32 × 109	7.7 × 109	4,700,698	16,075.46	5.25 × 109	9.73 × 109
	best	2,383.752	22,174,240	998.4982	4.35 × 109	5.54 × 1010	887,502.7	2427.805	5.95 × 109	4.38 × 1010
	Rank1	3	5	2	6	9	4	1	7	8
F3	mean	144,425.8	231,808.8	97,778.43	145,251.8	247,232.1	264,154.2	210,666.4	262,500.5	274,011
	std	122,797.2	42,660.59	116,067.7	26,098.69	59,051.09	24,106.16	56,598.77	83,641.74	65,130.97
	best	8756.673	150,191.4	14,854.17	88,714.33	135,558.1	216,181.2	99,179.91	156,782.9	168,215.3
	Rank3	2	5	1	3	6	8	4	7	9
F4	mean	563.4389	865.9641	570.2304	1794.099	15,244.81	720.9505	657.3554	4171.72	9862.004
	std	38.3144	86.96939	34.1682	783.2679	3936.418	34.22491	56.74416	1189.223	3317.268
	best	483.3184	692.5565	500.1854	916.2366	9241.854	659.414	541.5919	2115.72	4586.732
	Rank4	1	5	2	6	9	4	3	7	8
F5	mean	609.1139	754.296	608.9462	767.6637	1152.156	857.7253	869.0674	1094.501	1096.084
	std	15.7284	65.10729	17.71183	72.10621	52.95093	18.18453	73.06895	71.52161	45.22095
	best	576.1027	625.1969	582.1629	690.8143	1051.823	822.5183	683.1291	984.4831	989.5952
	Rank5	2	3	1	4	9	5	6	7	8
F6	mean	600.0644	612.1176	600.6146	627.597	688.5384	600.2636	665.5699	696.7489	687.409
	std	0.044523	4.955531	0.806076	5.332059	5.295189	0.051763	8.985297	10.65182	9.908688
	best	600.0078	604.6244	600.0074	616.4867	677.5548	600.1688	644.0729	678.1152	668.2738
	Rank6	1	4	3	5	8	2	6	9	7
F7	mean	880.5744	1191.008	1021.791	1142.076	1937.808	1138.399	1263.074	1885.375	1731.548
	std	23.7209	85.17833	71.9527	83.99404	131.4321	24.97392	106.9297	105.2404	131.0099
	best	835.5122	1004.495	896.6846	1034.807	1697.98	1080.656	1107.863	1679.258	1551.675
	Rank7	1	5	2	4	9	3	6	8	7
F8	mean	921.2497	1066.191	907.3805	1074.321	1460.664	1146.493	1176.299	1385.169	1397.617
	std	19.5574	82.65143	16.34292	52.61749	52.71699	18.47602	76.33376	74.80728	53.97892
	best	888.8279	971.3557	870.3604	992.8811	1353.775	1106.121	1065.656	1249.613	1313.653
	Rank8	2	3	1	4	9	5	6	7	8
F9	mean	1412.333	5480.861	2991.801	11,052.81	34,679.93	6795.157	16,355.47	37,586.35	34,539.55
	std	495.727	3296.784	985.7353	4244.007	9045.246	1448.893	4025.936	9850.894	5219.874
	best	995.3209	2034.324	1691.405	5229.652	26,413.03	4094.415	8798.012	20,735.18	26,045.19
	Rank9	1	3	2	5	8	4	6	9	7
F10	mean	7093.192	12,900.77	5764.667	7858.367	15,594.09	12,264.75	8490.3	13,052.32	14,486.5
	std	1924.157	1793.787	564.3154	1771.865	510.6293	401.7407	883.006	833.3803	1169.602
	best	5896.744	7827.275	4498.347	4746.18	14,312.54	11,588.88	5919.189	10,665.27	11,105.17
	Rank10	2	6	1	3	9	5	4	7	8
F11	mean	1254.725	1751.054	1703.735	7621.173	13,828.47	5745.791	2148.195	6830.475	10351.51
	std	38.40966	248.5979	1328.703	2386.969	3470.773	1907.337	302.7066	1772.24	2933.496
	best	1165.867	1441.506	1240.107	2973.89	7754.411	2149.673	1526.061	3356.958	6522.884
	Rank11	1	3	2	7	9	5	4	6	8
F12	mean	734,149.2	55,926,301	1,557,291	1.4 × 109	2.45 × 1010	89,967,534	1.6 × 108	3.4 × 109	2.01 × 1010
	std	496,001.1	81,107,893	1,115,693	1.4 × 109	5.06 × 109	28,900,372	1.27 × 108	2.06 × 109	9.89 × 109
	best	174,350.8	6,257,004	144,848.6	92,314,702	1.69 × 1010	27,427,763	12,493,547	1.36 × 109	7 × 109
	Rank12	1	3	2	6	9	4	5	7	8
F13	mean	7439.863	15,365.51	8842.93	3.91 × 108	6.97 × 109	2,679,217	190,278.7	3.83 × 108	5.04 × 109
	std	5123.696	10,781.5	6870.112	5.9 × 108	2.51 × 109	2,150,450	144,813.6	3.33 × 108	5.09 × 109
	best	2821.949	3639.404	1950.086	1,963,443	1.8 × 109	455,066	72,156.51	94,994,576	8.59 × 108
	Rank13	1	3	2	7	9	5	4	6	8
F14	mean	4594.115	674,107.6	4618.996	2,308,778	10,405,138	2,671,752	528,649.7	57,940,77	3,459,594
	std	6782.695	848,590.7	3788.043	2,869,654	5,403,053	1,529,607	402,306.7	6,847,417	32,22,689
	best	1580.336	22,251.52	1822.55	56,354.43	2,989,443	430,466	77,318.69	562,022.4	652,244
	Rank14	1	4	2	5	9	6	3	8	7
F15	mean	3785.082	370,299.8	5498.761	62,711,090	1.24 × 109	712,076.6	48,610.56	34,504,385	8.11 × 108
	std	2045.124	1,981,117	4485.737	1.68 × 108	4.68 × 108	606,712	25,318.35	43,748,718	8.01 × 108
	best	1785.634	1812.885	1952.803	41,470.58	5.24 × 108	56,815.32	12,340	694,819.6	1.14 × 108
	Rank15	1	4	2	7	9	5	3	6	8
F16	mean	2908.88	3930.433	2878.641	3315.169	6455.368	3977.644	4216.451	6069.888	5495.542
	std	233.188	843.3878	257.8198	398.216	392.0204	215.397	590.2684	1074.047	606.1609
	best	2340.389	2559.447	2333.153	2667.632	5679.954	3413.761	3084.595	4556.372	3843.73
	Rank16	2	4	1	3	9	5	6	8	7
F17	mean	2612.689	3493.388	2755.448	3172.129	5171.268	3181.951	3441.805	4485.392	4650.444
	std	222.0672	526.5409	234.8515	384.2505	371.4599	166.1484	389.5048	555.7028	639.3884
	best	2236.986	2701.92	2080.731	2256.339	4593.159	2899.997	2604.831	3624.638	2863.535
	Rank17	1	6	2	3	9	4	5	7	8
F18	mean	44,476.42	9,172,805	86,070.94	11,218,011	82,158,263	7,903,020	5,090,083	58,424,018	33,301,861
	std	27,086.57	5,987,197	68,108.23	16,053,459	34,936,797	3,854,796	3,368,815	47,631,090	27,229,155
	best	14,218.74	1,217,649	18,142.11	764,212	28,872,177	3,385,313	290,550.4	5,368,797	6,220,737
	Rank18	1	5	2	6	9	4	3	8	7
F19	mean	4052.642	15,870.31	9225.733	11,981,185	7.6 × 108	250,229.3	5,200,376	12,761,399	3.5 × 108
	std	3350.075	14,778.03	8474.828	26,973,964	4.23 × 108	171,284.4	4,702,120	14,802,670	4.4 × 108
	best	2049.646	2014.774	2225.641	36,809.24	2.69 × 108	51,196.96	67,850.08	588,590.3	24,579,022
	Rank19	1	3	2	6	9	4	5	7	8
F20	mean	2782.932	3452.745	2911.381	3092.161	4370.176	3372.192	3368.785	3940.622	4001.329
	std	149.4499	488.2344	215.8694	359.998	231.2428	206.6125	277.2094	285.4438	322.0493
	best	2513.971	2651.273	2465.509	2421.917	3882.355	2884.49	2787.481	3223.969	3446.798
	Rank20	1	6	2	3	9	5	4	7	8
F21	mean	2409.828	2569.347	2404.947	2556.275	2978.951	2663.81	2657.033	3060.36	2929.424
	std	18.27525	71.73672	14.30392	40.98694	53.04955	16.46424	70.65938	94.70003	51.1834
	best	2374.74	2456.706	2383.381	2471.171	2838.375	2629.915	2510.799	2842.394	2793.713
	Rank21	2	4	1	3	8	6	5	9	7
F22	mean	8470.196	14,382.24	7217.277	10,472.02	17,251.58	13,660.3	9922.052	14,461.53	16,578.4
	std	1784.287	2216.171	1913.248	2605.891	360.4047	1776.577	979.7037	1002.945	648.1354
	best	2444.946	9508.853	2336.512	5580.485	16650.2	7007.212	8298.5	11,364.53	15,460.79
	Rank22	2	6	1	4	9	5	3	7	8
F23	mean	2852.142	3065.972	2880.053	3028.135	3742.085	3101.649	3093.348	3807.263	3513.509
	std	19.42229	94.97247	35.1143	75.71468	68.9404	14.9897	84.67721	141.2651	92.50664
	best	2817.652	2887.066	2812.069	2905.931	3585.678	3071.253	2970.319	3520.783	3314.798
	Rank23	1	4	2	3	8	6	5	9	7
F24	mean	3021.403	3306.473	3027.097	3241.076	3921.9	3321.153	3215.953	3854.304	3640.405
	std	24.31475	66.75373	36.82324	108.1628	88.96247	22.38882	67.1197	165.1063	65.41181
	best	2983.797	3126.976	2972.508	3126.764	3666.68	3253.487	3110.428	3582.654	3505.107
	Rank24	1	5	2	4	9	6	3	8	7
F25	mean	3079.962	3239.503	3049.626	4075.648	10,148.56	3150.719	3146.483	4832.814	7691.827
	std	43.56151	57.82701	24.74167	492.702	1469.036	23.947	46.4501	456.7395	1331.49
	best	2942.342	3130.835	3018.356	3412.728	7455.292	3114.948	3051.057	4063.383	5794.234
	Rank25	2	5	1	6	9	4	3	7	8
F26	mean	5086.365	6626.045	5218.613	7165.184	14,044.5	7368.264	7112.548	14,681.55	13,357.54
	std	263.035	933.7976	325.803	871.938	853.3066	166.2529	2885.302	1567.436	1267.231
	best	4612.36	5100.881	4808.421	5971.109	12,159.99	6974.289	3224.77	12,113.75	10,480.64
	Rank26	1	3	2	5	8	6	4	9	7
F27	mean	3230.909	3649.338	3439.495	3703.738	5098.034	3515.148	3676.093	4872.919	3200.012
	std	59.67202	127.795	78.18665	94.56336	254.3151	45.383	122.3547	543.6804	5.07 × 10−5
	best	3179.71	3461.754	3329.639	3504.913	4631.486	3424.278	3421.085	3915.975	3200.012
	Rank27	2	5	3	7	9	4	6	8	1
F28	mean	3348.06	3503.853	3333.202	4851.69	9401.737	3424.222	3445.855	5867.225	6266.111
	std	40.52479	95.32536	33.84948	468.2387	819.4306	29.10061	67.3916	511.7105	1947.186
	best	3269.514	3363.045	3269.456	4069.568	8166.799	3369.191	3351.506	5005.094	3300.012
	Rank28	2	5	1	7	9	3	4	7	8
F29	mean	3713.312	4587.843	4029.481	4891.197	9596.822	4528.614	5825.732	9322.998	7410.649
	std	184.3058	474.9608	287.7496	372.0875	1898.422	136.2945	525.7357	1596.468	1028.2
	best	3356.793	3848.854	3525.472	4275.774	7205.861	4182.824	4892.185	6780.624	5831.023
	Rank29	1	4	2	5	9	3	6	8	7
F30	mean	4465.658	6,172,326	957,425	1.57 × 108	1.54 × 109	6597827	1.55 × 108	2.83 × 108	1.14 × 109
	std	1062.473	2,464,594	250,214.9	94,243,881	5.76 × 108	2287863	48074715	1.72 × 108	1.2 × 109
	best	3403.683	3,082,660	698,238.6	70,520,643	6.92 × 108	3871480	78380292	66080463	2.73 × 108
	Rank30	1	3	2	6	9	4	5	7	8
Result	w/t/l	--	29/0/0	20/0/8	29/0/0	29/0/0	29/0/0	28/0/1	29/0/0	28/0/1
	Total	41	124	51	142	253	134	215	128	217
	Rank	1	3	2	6	9	5	8	4	7

In 0, we can see that the SSDE achieves the best accuracy on all test functions except F1 and F23. This shows that the SSDE has strong competitiveness in unimodal functions, multimodal functions, hybrid functions, and composite functions. Specifically, the SSDE uses the OBL strategy, staged search mechanism, and non-linear self-adapting parameters to explore the wider unknown area of the search space. These strategies help the SSDE avoid premature convergence and accelerate convergence by taking full advantage of the global optimal individual’s information at the later search stage. From Table 3, it can be seen that most of the p-values are less than 0.05, indicating that the performance of the SSDE on all the test functions is significantly improved compared with SASS and other competitors.

We can see from Table 4 that the SSDE remains very competitive with other algorithms at 30 dimensions. Results show that the SSDE is significantly better than PSO, SASS, GWO, SCA, DE, MSCA, SSA, and WOA on a total of 29, 22, 29, 29, 29, 29, 29, and 29 test functions, respectively. The competitive results on all functions reveal that the SSDE can find the optimal solution more effectively. In addition, from Table 5, the SSDE performs better than all of the compared algorithms on F4, F6–7, F9, F11–F15, F17–F20, F23–24, F26, F29, and F30. On F1 and F3 the SSDE is slightly lower than that of some compared algorithms and ranks third and second, respectively. As for the multimodal functions, the SSDE shows good performance, while it obtains no-best results only on F5, F8, and F10. On all 20 hybrid and composite functions, the SSDE obtains the optimal solution on all 14 functions. Compared with the SASS, the SSDE ranks first on 11 functions while SASS ranks first on five functions. It indicates that the proposed algorithm can deal with the combination functions more effectively.

Thus, from the results presented in these tables, we conclude that all employed strategies in Section 3 have shown their impact on improving the search mechanism of the SASS for obtaining better solution accuracy. Furthermore, to analyze the convergence rates of WOA, DE, PSO, SSA, SCA, GWO, and MSCA, Figure 4, Figure 5 and Figure 6 plot the evolution curve of the best value.

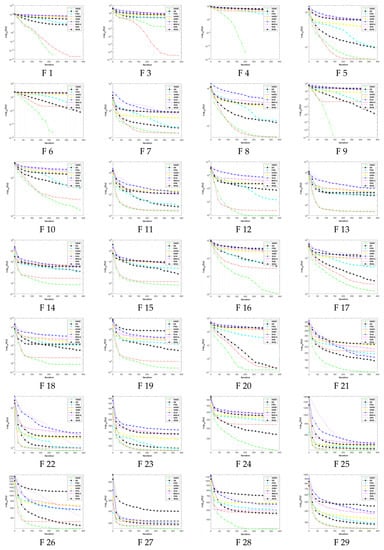
Figure 4. Evolutionary curves of SSDE, DE, PSO, SASS, GWO, SCA, MSCA, SSA, and WOA on the CEC 2017 test functions in 10 dimensions.

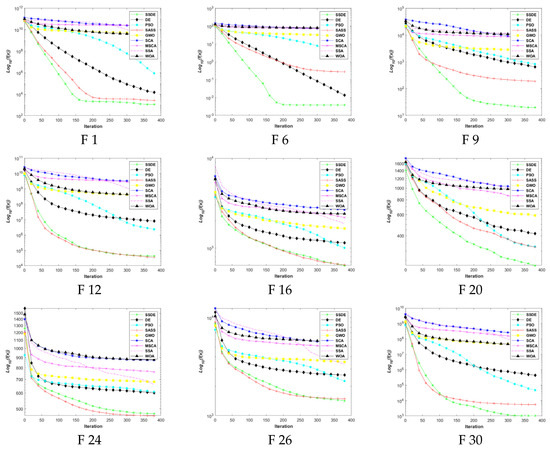
Figure 5. Evolutionary curves of SSDE, DE, PSO, SASS, GWO, SCA, MSCA, SSA, and WOA on the CEC 2017 test functions in 30 dimensions.

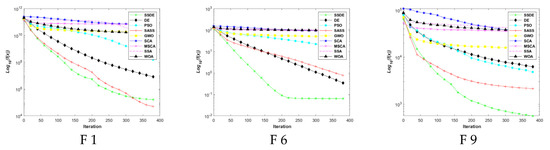
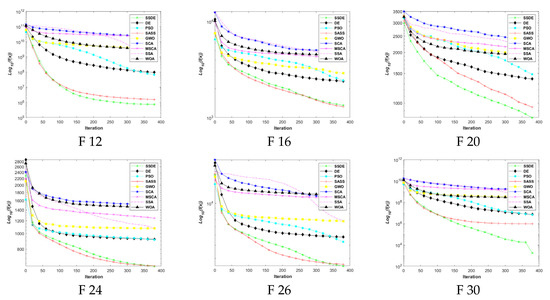
Figure 6. Evolutionary curves of SSDE, DE, PSO, SASS, GWO, SCA, MSCA, SSA, and WOA on the CEC 2017 test functions in 50 dimensions.

The convergence diagrams of 10 dimensions on the CEC2017 test functions for the SSDE and other comparison algorithms are shown in Figure 4. These diagrams show that the SSDE has much higher accuracy than SASS, indicating that the optimization capability of SASS has been improved considerably with the introduction of the OBL, phased search, mutation and crossover strategies, and the non-linear parameter. Figure 4 shows that the SSDE with the fastest convergence speed outperforms all other optimizers in dealing with F3, F5–F11, F13–F21, F24, and F26–F30.

In Figure 5 and Figure 6, we select some representative functions and expose a convergence diagram of the SSDE and the algorithms for comparison. These representative functions come from all four types of CEC2017 test functions. It can be found that the SSDE converges on F3 at 50 dimensions second only to the SASS. However, the initial solution of the SSDE is better at the beginning. In other functions, SSDE has a much faster convergence speed than SASS and the other competitors. The obtained results show that the SSDE is competitive in dealing with multi-dimensional problems.

4.2. Practical Engineering Design Problem

In this section, we study the performance of the SSDE in solving practical engineering problems. Two constrained practical engineering problems are considered, namely a welded beam design problem and a pressure vessel design problem. The optimization results with the SSDE are to be compared with the results of several well-regarded algorithms for an unbiased conclusion. Since the two engineering problems are constrained problems, a classic penalty method is used to handle the constraints [64].

4.2.1. Welded Beam Design

The goal of this problem is to minimize the manufacturing cost of the welded beam under four constraints including shear stress ($\tau$), bending stress ($\theta$), buckling load ($P_c$), and deflection ($\delta$) [65]. As shown in Figure 7, there are four variables involved in this problem: welding seam thickness ($h$), welding joint length ($l$), beam width ($t$), and beam thickness ($b$). The mathematical model can be described as follows:

Consider	$\stackrel{\rightharpoonup }{x}=\left[x_1 x_2 x_3 x_4\right]=\left[h l t b\right]$
Minimize	$f\left(\stackrel{\rightharpoonup }{x}\right)=1.10471x_1^2{x}_2+0.04811x_3{x}_4\left(14.0+x_2\right)$
Subject to	$g_1\left(\stackrel{\rightharpoonup }{x}\right)=\tau \left(\stackrel{\rightharpoonup }{x}\right)-{\tau }_{max}\le 0$
	$g_2\left(\stackrel{\rightharpoonup }{x}\right)=\sigma \left(\stackrel{\rightharpoonup }{x}\right)-{\sigma }_{max}\le 0$
	$g_3\left(\stackrel{\rightharpoonup }{x}\right)=x_1-x_4\le 0$
	$g_4\left(\stackrel{\rightharpoonup }{x}\right)=\delta \left(\stackrel{\rightharpoonup }{x}\right)-{\delta }_{max}\le 0$
	$g_5\left(\stackrel{\rightharpoonup }{x}\right)=P-P_c\left(\stackrel{\rightharpoonup }{x}\right)\le 0$
	$g_6\left(\stackrel{\rightharpoonup }{x}\right)=0.125-x_1\le 0$
	$g_7\left(\stackrel{\rightharpoonup }{x}\right)=1.10471x_1^2{x}_2+0.04811x_3{x}_4\left(14.0+x_2\right)-5.0\le 0$
Variable ranges:	$0.1\le x_1\le 2$$; 0.1\le x_2\le 10; 0.1\le x_3\le 10; 0.1\le x_4\le 2$

where

$$\tau \left(\stackrel{\rightharpoonup }{x}\right)=\sqrt{{\left({\tau }^{\prime }\right)}^2+2{\tau }^{\prime }{\tau }^{″}\frac{x_2}{2R}+{\left({\tau }^{″}\right)}^2}, {\tau }^{\prime }=\frac{P}{\sqrt{2}{x}_1{x}_2}$$

$${\tau }^{″}=\frac{MR}{J}, M=P\left(L+\frac{x_2}{2}\right), R=\sqrt{\frac{x_2^2}{4}+{\left(\frac{x_1+x_3}{2}\right)}^2}$$

$$J=2\left\{\sqrt{2}{x}_1{x}_2\left[\frac{x_2^2}{12}+{\left(\frac{x_1+x_3}{2}\right)}^2\right]\right\}, \sigma \left(\stackrel{\rightharpoonup }{x}\right)=\frac{6PL}{x_4{x}_3^2}$$

$$P_c\left(\stackrel{\rightharpoonup }{x}\right)=\frac{4.013E\sqrt{\frac{x_3^2{x}_4^6}{36}}}{L^2}\left(1-\frac{x_3}{2L}\sqrt{\frac{E}{4G}}\right), \delta \left(\stackrel{\rightharpoonup }{x}\right)=\frac{4P{L}^3}{E{x}_3^3{x}_4}$$

P = 6000lb, L = 14in, E = 30$\times {10}^6$ psi, G = 12$\times {10}^6$ psi, ${\tau }_{max}$= 30,600 psi, ${\sigma }_{max}$= 30,000, ${\delta }_{max}$= 0.23in.

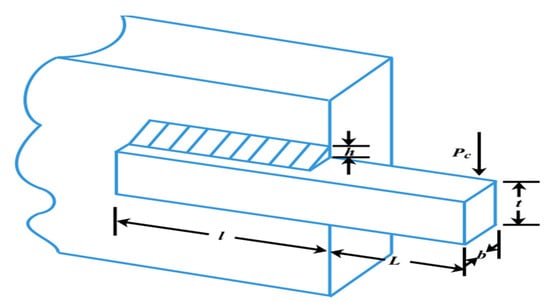
Figure 7. Design of a welded beam problem.

On this subject, Goello and Montes [66], Deb [65,67] use GA to solve it. Lee and Geem [68] use HS to optimize this problem. Radgsdell and Phillips [69] employ mathematical approaches including Richardson’s random method, Simplex method, Davidon–Fletcher–Powell, Griffith, and Stewart’s successive linear approximation. The results are provided in Table 6, which show that the SSDE algorithm finds a solution with the minimum cost compared with others. We conclude that the SSDE algorithm solves the welded beam design problem brilliantly.

Table 6. Comparison of results of the welded beam design problem.

Algorithm	Optimum Variables				Optimum Cost
	h	l	t	b
SSDE	0.2057295	3.4704909	9.0366263	0.2057296	1.72485271
GA (Goello) [67]	/	/	/	/	1.824500
GA (Deb) [66]	0.248900	6.17300	8.178900	0.253300	2.433116
GA (Deb) [68]	/	/	/	/	2.3800
HS (Lee et al.) [69]	0.2442	6.2231	8.2915	0.2443	2.3807
MVO (Mirjalili) [70]	0.2055	3.4732	9.0445	0.2057	1.7265
WOA (Mirjalili) [32]	0.2054	3.4843	9.0374	0.2063	1.7305
Random	0.4575	4.7313	5.0853	0.6600	4.1185
Simplex	0.2792	5.6256	7.7512	0.2796	2.5307
David	0.2434	6..2552	8.2915	0.2444	2.3841
APPROX	0.2444	6.2189	8.2915	0.2444	2.3815

4.2.2. Pressure Vessel Design

The goal of this problem is to minimize the total cost consisting of material, forming, and welding of a cylindrical vessel. As shown in Figure 8, there are four decision variables involved in this problem: the thickness of the shell ($T_s$), the thickness of the head ($T_h$), inner radius ($R$), and length of the cylindrical section of the vessel ($L$). The mathematical model is described as follows:

Consider	$\stackrel{\rightharpoonup }{x}=\left[x_1 x_2 x_3 x_4\right]=\left[T_s T_h R L\right]$
Minimize	$f\left(x\right)=0.6624x_1{x}_3{x}_4+1.7781x_2{x}_3^2+3.1661x_4{x}_1^2+19.84x_1^2{x}_3$
Subject to	$g_1\left(\stackrel{\rightharpoonup }{x}\right)=-x_1+0.0193x_3\le 0$
	$g_2\left(\stackrel{\rightharpoonup }{x}\right)=-x_3+0.00954x_3\le 0$
	$g_3\left(\stackrel{\rightharpoonup }{x}\right)=-\pi x_3^2{x}_4-\frac{4}{3}\pi x_3^3+1296000\le 0$
	$g_4\left(x\right)=x_4-240\le 0$
Variable ranges:	$0\le x_1,x_2\le 99$$, 0\le x_3,x_4\le 200$

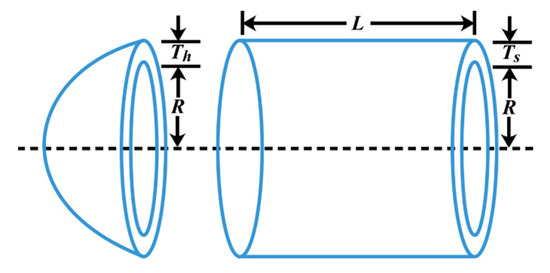
Figure 8. Design of a pressure vessel problem.

This optimization problem has been well studied. He and Wang [71] use PSO to solve this problem while Deb [72] uses GA. In addition, ES [73], DE [31], and two mathematical methods in [74,75], are all adopted to crack this problem. The results are provided in Table 7. The SSDE outperforms all the other algorithms. The results prove that the SSDE is a highly competitive candidate for solving the welded beam design problem.

Table 7. Comparison of results of the pressure vessel design problem.

Algorithm	Optimum Variables				Optimum Cost
	${\mathit{T}}_{\mathit{s}}$	${\mathit{T}}_{\mathit{h}}$	R	L
SSDE	0.806139	0.398485	41.768839	180.764404	5934.8828
PSO (He et al.) [72]	0.812500	0.437500	42.091266	176.746500	6061.0777
GA (Deb et al.) [73]	0.937500	0.500000	48.329000	112.679000	6410.3811
DE (Huang et al.) [31]	0.812500	0.437500	42.098411	176.637690	6059.7340
ES (Montes et al.) [74]	0.812500	0.437500	42.098087	176.640518	6059.7456
WOA (Mirjalili) [32]	0.812500	0.437500	42.098269	176.638998	6059.7410
iDEaSm (Awad) [76]	0.778198	0.384665	40.321054	199.98023	5988.027532
MVO (Mirjalili) [71]	0.812500	0.437500	42.090738	176.73869	6060.8066
Lagrangian Multipier (Kannan)	1.125000	0.625000	58.291000	43.690000	7198.0428
Branch-bound (Sandgren)	1.125000	0.625000	47.700000	117.701000	8129.1036

4.2.3. Tension/Compression Spring Design

This problem is described in [33]. The goal of this problem is to minimize the weight of the spring. As shown in Figure 9, there are three decision variables in this problem, which are wire diameter (d), mean coil diameter (D), and the number of active coils (N). This problem has four inequality constraints, which are mathematically expressed as follows:

Consider	$\overrightarrow{x}=\left[x_1,x_2,x_3\right]=\left[d D N\right]$
Minimize	$f\left(\overrightarrow{x}\right)=\left(x_3+2\right)x_2{x}_1^2$
Subject to	$g_1\left(\overrightarrow{x}\right)=1-\frac{x_2^3{x}_3}{71785x_1^4}\le 0$
	$g_2\left(\overrightarrow{x}\right)=\frac{4x_2^2-x_1{x}_2}{12566\left(x_2{x}_1^3-x_1^4\right)}+\frac{1}{5108x_1^2}\le 0$
	$g_3\left(\overrightarrow{x}\right)=1-\frac{140.45x_1}{x_2^2{x}_3}\le 0$
	$g_4\left(\overrightarrow{x}\right)=\frac{x_1+x_2}{1.5}-1\le 0$
0.05 ≤ x1 ≤ 2.00, 0.25 ≤ x2 ≤ 1.30, 2.00 ≤ x3 ≤ 15.0

Figure 9. Design of a tension/compression spring problem.

The comparison results between SSDE and other state-of-art algorithms are given in Table 8. From this table, it is clear that SSDE achieves the best results with x* = (0.051785958, 0.3590533, 11.15334) and object function f(x) = 0.012665403. Compared with the results obtained by other algorithms, SSDE can deal with this problem well.

Table 8. Comparison of results of the tension/compression spring problem.

Algorithms	Optimum Variables			Optimal Cost
	d	D	N
SSDE	0.051785958	0.3590533	11.15334	0.012665403
GWO (Mirjalili) [33]	0.05169	0.356737	11.28885	0.012666
WOA (Mirjalili) [32]	0.051207	0.345215	12.004032	0.0126763
HHO (Heidari) [77]	0.051796393	0.359305355	11.138859	0.012665443
SSA (Mirjalili) [35]	0.051207	0.345215	12.004032	0.0126763
MFO (Mirjalili) [37]	0.051994457	0.36410932	10.868422	0.0126669
AEO (Zhao) [78]	0.051897	0.361751	10.879842	0.0126662

4.2.4. Cantilever Beam Design

The cantilever beam problem is shown in Figure 10. This problem includes five hollow blocks, so the number of variables is five [32]. The objective is to minimize the weight of the beam. The problem formulation is as follows:

Consider	$\overrightarrow{x}=\left[x_1 x_2 x_3 x_4 x_5\right]=\left[h_1 h_2 h_3 h_4 h_5\right]$
Minimize	$f\left(\overrightarrow{x}\right)=0.0624\left(x_1+x_2+x_3+x_4+x_5\right)$
Subject to	$g_1\left(\overrightarrow{x}\right)=\frac{61}{x_1^3}+\frac{37}{x_2^3}+\frac{19}{x_3^3}+\frac{7}{x_4^3}+\frac{1}{x_5^3}-1\le 0$
0 ≤ xi ≤ 100, i = 1, 2, …, 5

Many algorithms have been used to solve the cantilever beam design problem, and the results of the comparison are shown in Table 9. From Table 9, we can see that SSDE achieves the best results. Thus, SSDE is a better optimizer for solving this problem.

Table 9. Comparison of results of the cantilever beam problem.

Algorithm	Optimum Variables					Optimal Cost
	x1	x2	x3	x4	x5
SSDE	6.016016	5.30917382	4.4943296	3.50147497	2.1526653	1.33995636
ISA (Jahangiri) [79]	6.0246	5.2958	4.4790	3.5146	2.1600	1.33996
WOA (Mirjalili) [32]	5.5638	6.0809	4.6858	3.2263	2.2467	1.36055
ABC (Karaboga) [34]	5.9638	5.3312	4.5122	3.4744	2.1952	1.34004
GWO (Mirjalili) [33]	6.0189	5.3173	4.4922	3.5014	2.1440	1.33997
AEO (Zhao) [78]	6.02885	5.31652	4.46265	3.50846	2.15776	1.33997
GBO (Ahmadianfar) [80]	6.0124	5.3129	4.4941	3.5036	2.1506	1.33996

Table 9. Comparison of results of the cantilever beam problem.

Algorithm	Optimum Variables					Optimal Cost
	x1	x2	x3	x4	x5
SSDE	6.016016	5.30917382	4.4943296	3.50147497	2.1526653	1.33995636
ISA (Jahangiri) [79]	6.0246	5.2958	4.4790	3.5146	2.1600	1.33996
WOA (Mirjalili) [32]	5.5638	6.0809	4.6858	3.2263	2.2467	1.36055
ABC (Karaboga) [34]	5.9638	5.3312	4.5122	3.4744	2.1952	1.34004
GWO (Mirjalili) [33]	6.0189	5.3173	4.4922	3.5014	2.1440	1.33997
AEO (Zhao) [78]	6.02885	5.31652	4.46265	3.50846	2.15776	1.33997
GBO (Ahmadianfar) [80]	6.0124	5.3129	4.4941	3.5036	2.1506	1.33996

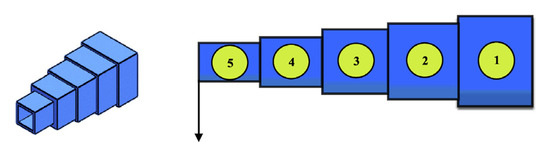
Figure 10. Design of a cantilever beam problem [80].

4.3. Computation Cost of the SSDE

The running time of the SSDE and the algorithms for comparison on the 29 benchmark problems at 10 dimensions are shown in Figure 11. It is clear that the computation cost of the SSDE is higher than those of the other eight algorithms. Specifically, the average running time that the SSDE spends at 10 dimensions is 0.84, and the average running time of SASS, PSO, GWO, SCA, DE, SSA, WOA, and MSCA are 0.268, 0.04, 0.102, 0.052, 0.092, 0.111, 0.085, and 0.166, respectively. The reason for the longer running time of the SSDE is that its search process is divided into three stages, and the mutation and crossover strategies are applied at the end of the algorithm. However, although the SSDE takes more time than other algorithms, it can find optimal solutions.

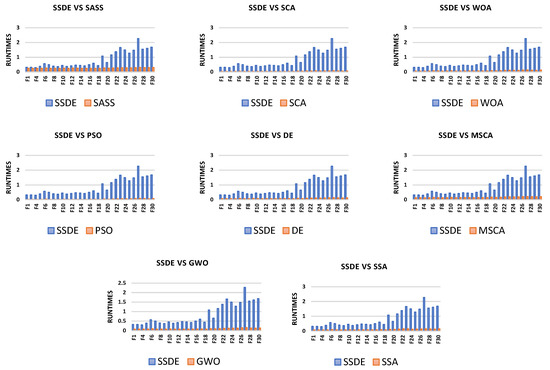
Figure 11. Running time comparison in 10 dimensions.

5. Conclusions

This paper proposes a new swarm-based heuristic algorithm named SSDE. It divides the search process in search space into three phases. Each phase uses a different search rule. A non-linear self-adapting parameter is proposed. These strategies help the SSDE algorithm find the optimal solution more effectively. To verify its performance, we test 10 dimensions, 30 dimensions, and 50 dimensions of objective functions on the CEC 2017 test functions. Numerical results show that the SSDE is a competitive SASS variant in most functions. Compared with the other seven most popular algorithms, the SSDE exhibits stronger performance. In addition, the SSDE is also used to solve two popular practical engineering design problems, including the welded beam design problem and the pressure vessel design problem, which further demonstrate the power of the proposed algorithm in solving these kinds of engineering problems.

In future work, we will further enhance the performance of the SSDE algorithm. Orthogonal learning, levy flight, ranking-based schemes, multi-population structures, and their various combinations may be applied. We will use the SSDE in various applications, such as constrained optimization, parameter optimization, and feature selection. In addition, the proposed algorithm can also be reconstructed as a multi-objective technique based on the Pareto condition to further improve its performance.