Equivalence, Partial Order and Lattice of Neighborhood Sequences on the Triangular Grid

Abstract

In (digital) grids, neighbor relation is a crucial concept; digital distances are based on paths through neighbor points. Digital distances are significant, e.g., in digital image processing for giving an approximation of the Euclidean distance and allowing incremental algorithms on images. Neighborhood sequences (i.e., infinite sequences of the possible types of neighbors) are defining digital distances with a lower rotational dependency than the distances based only on a sole neighborhood. They allow one to change the used neighborhood condition in every step along a path. They are defined in various grids, and they can be periodic. Generalized neighborhood sequences do not need to be periodic. In this paper, the triangular grid is studied. An equivalence and two partial order relations on the set of generalized and periodic neighborhood sequences are shown on this grid. The first partial order, the “faster” relation, is based on distances defined by neighborhood sequences, and it does not provide a lattice but gives a relatively complex relation for neighborhood sequences with a short period. The other partial order, the relation “componentwise dominate”, defines a complete distributive lattice on the set of generalized neighborhood sequences. Finally, a relation of the above-mentioned relations is established. Important differences regarding the cases of the square and triangular grids are also highlighted.

1. Introduction

The present paper has various roots in mathematics. On the one hand, digital geometry (a field that is closely connected to graph theory, geometry and combinatorics and that has applications in crystallography, image processing and computer graphics [1,2]), including the theory of digital (path-based) distances on various grids, was started by the seminal works of Rosenfeld and Pfaltz in the 1960s. They defined the two basic movements (steps) on the square grid (see [3,4]): the cityblock (also called the Manhattan taxicab) motion that allows horizontal and vertical steps only, while the chessboard motion allows diagonal steps also as when a king moves on the chessboard.

In digital spaces, e.g., on a computer screen, the geometry is not the same as in the continuous spaces: instead of the Euclidean geometry, digital geometry is applied. There is an underlying grid, and pixels or gridpoints are arranged accordingly; the neighborhood relation is crucial, while no neighbor points exist in Euclidean geometry. Consequently, digital distances are based on the steps/moves to neighbor pixels/points. However, the digital distances based on the cityblock or on the chessboard moves are a rough approximation of the Euclidean distance and have a large rotational dependency, i.e., to go in different directions, e.g., horizontal and diagonal (0 and ${45}^{\circ }$, respectively), the same number of steps leads to connected points with a Euclidean distance of a $\sqrt{2}$ factor.

Therefore, Rosenfeld and Pflatz previously coined the idea of alternating use of these two motions to have a digital distance with a lower rotational dependency [4]. These octagonal distances are obtained by the mixed use of the two basic motions. The theory was further developed when arbitrarily long periodic sequences of cityblock and chessboard steps, named neighborhood sequences, were studied in [5,6] (to distinguish those neighborhood sequences. Some more general ones were introduced later on, and we refer to these as periodic neighborhood sequences throughout this paper).

Digital distances are useful for stepwise approximations and simulations with incremental algorithms, e.g., computing distance transform in digital image processing and various algorithms in computer graphics. Moreover, as these distances always have integer values, it is easy to use them without rounding errors. Das et al. also provided a formula for calculating the distance between two arbitrary gridpoints based on any periodic neighborhood sequence. Based on this formula, a partial order relation on the set of periodic neighborhood sequences was investigated in [7].

This result connects our topic to other fields of mathematics. When there is a set of objects, e.g., the set of neighborhood sequences (and distance functions based on them), one may be interested to know how the objects of the set are related to each other. Various relations and algebraic concepts are known to help to describe the inner structure of a set. Now, we come back to the history of neighborhood sequences in the next section with a brief literature review.

In this paper, we use both periodic and generalized neighborhood sequences. Our motivation here is to show that similar algebraic concepts can be studied on sets of neighborhood sequences on a triangular grid and a square grid; thus, our results are somewhat analogous to the results of [7,8] with some interesting and remarkable differences. Moreover, a better understanding of the structure of the sets of neighborhood sequences allows us to know more about the distances based on them and also helps to find adequate neighborhood sequences and/or distances based on them in various applications.

On the triangular grid, there is also a natural equivalence relation on the sets of neighborhood sequences based on the distance function that they define; thus, after recalling the necessary definitions and preliminaries, we start our results with this equivalence relation. Although this result appears to be an easy consequence of some previous studies (see, e.g., [9]), we present it for the following two reasons.

On the one hand, it highlights an important difference between the square and triangular grids, which has various interesting consequences later on. On the other hand, the partial order that we consider first is a relation on the above-mentioned equivalence sets. This partial order and equivalence relation have a close connection to the distances defined by the neighborhood sequences. Further, another partial order relation is also studied. By this second partial order relation, lattice structures can also be obtained with some additional properties.

We also highlight the main differences between the cases of square and triangular grids in view of the mentioned relations and their analogous relations on the other grid, as the latter one is, in fact, not a point lattice (i.e., the triangular grid is not translation invariant to all grid vectors). Our last two theorems establish some connections among the considered relations. More precisely, our results are as follows. (For a better explanation, see Section 4).

The first two results are more or less the rephrasing or formal stating of known things:

• On the set T of generalized neighborhood sequences of the triangular grid, the relation of defining the same distance function is an equivalence relation (Theorem 1).
• The faster relation is a partial order both on the equivalence classes of T and of the set $T^{\prime }$ of periodic neighborhood sequences on the triangular grid (Theorem 2).

The following results are our main results:

• The set $T^{\prime }$ does not form a lattice under the faster relation (Theorem 3).
• The set T does not form a lattice under the faster relation (Theorem 4).
• Incomparability of two generalized neighborhood sequences of the square grid under the componentwise dominate relation implies that the given neighborhood sequences cannot have the same speed, i.e., it cannot happen that both of them are faster than the other (Proposition 5).
• The set S of generalized neighborhood sequences of the square grid is a Boolean lattice under the componentwise dominate relation (Theorem 5).
• The set T is a complete distributive lattice under the componentwise dominate relation (Theorem 6); however, it is not a Boolean lattice (Proposition 7).
• The set $T^{\prime }$ is a distributive lattice under the componentwise dominate relation (Theorem 7); however, it may not be complete (Theorem 10).
• The maximal equivalent neighborhood sequence of any generalized neighborhood sequence of T is defined and computed (in the proof of Theorem 8).
• The relations faster and componentwise dominate have more complex and sophisticated structures on T than do their analogous relations on S (Theorems 11 and 12).

In the next section, a brief literature review is given allowing the reader to better understand and place our results. Then, in Section 3, necessary definitions and preliminaries are recalled about the triangular grid itself, about the neighborhood sequences on the triangular grid and about lattice theory. These parts before starting with the real results in Section 4 may seem lengthy; however, we would like to have the paper self-consistent such that readers without much background in these fields can also read and understand how the results are connected to these fields. Section 5 shows how our results can be applied, and our concluding section summarizes our results and also give links to future works.

2. Literature Review

Here, we recall parts of the history of digital distances. As we previously mentioned, Rosenfeld and Pfaltz defined the first digital distances. Around the same time when Das and their co-authors conducted their fundamental studies regarding periodic neighborhood sequences in the 1980s, a similar type of generalization of the basic digital distances was introduced under the same “neighborhood sequence” name [10,11] using some more general predefined motions (but still restricting the work to periodic sequences).

In [8,12], the concept of neighborhood sequences appeared with another type of generalization that also allowed non-periodic infinite neighborhood sequences. In [8], partial order relations were introduced, and the lattice properties of the set of these neighborhood sequences were analyzed extending the results of [7]. In [13,14], a greedy shortest path algorithm, a necessary and sufficient condition for neighborhood sequences to define metrical distances and a formula to compute distances between any pair of points was proven.

Higher dimensional extensions of these digital distances were also studied, see, e.g., [15]. Approximation of the Euclidean distance has been studied in [6,16,17,18] in various dimensions. Various image processing algorithms, e.g., distance transforms [19,20,21], have been developed; moreover, the distances based on neighborhood sequences have a close connection to integer sequences [22].

A generalization giving various real-valued weights to the diagonal steps was also investigated to give perfect approximation of the Euclidean distance on a perimeter of a square [23,24], while another type of generalization using a larger set of neighbor relations was developed under the name “broadcasting sequences” [25,26,27]. These papers show that neighborhood sequences have already been efficiently applied on a square grid.

Another way to have a digital distance with a lower rotational dependency is to use a non-traditional grid instead of the traditional (i.e., the square/rectangular) grid. The hexagonal and the triangular grids also provide regular tiling of the plane, and moreover they have better symmetric properties compared with the square grid [28,29,30].

In [31], Deutsch described the basic three types of neighborhoods in a triangular grid. Stojmenovic and Nagy, in [32] and in [9,33], respectively, used three coordinate values to represent a honeycomb grid and triangular tiling of the plane. These are dual notations of the same structure. In this paper, we use a triangular grid with triangle pixels (trixels for short). For defining digital distances on this grid, the concept of a generalized neighborhood sequence was used in [9,33]. The applicability of the neighborhood sequences and of the distances based on them is shown in [34,35], where applications in image processing and in networking are presented.

3. Basic Definitions and Preliminaries

To allow us to formally write our results, in this section, we provide the basic definitions and notations. In this paper, $\mathbb{N},{\mathbb{N}}_0$ and $\mathbb{Z}$ denote the set of positive integers, nonnegative integers and integers, respectively. We also recall some basic facts about the neighborhood sequences and the distances based on them.

First, we recall the description of the triangular grid using three coordinate values to address the cells of the triangular grid, i.e., trixels.

3.1. Description of the Triangular Grid

Figure 1 (right) shows a part of the grid with coordinate axes and coordinate triplets for the points of the grid (for details, we refer to [9,33,36]). The coordinate system reflects the symmetry of the grid. The points are represented by trixels; however, throughout the paper, we usually refer to them as points.

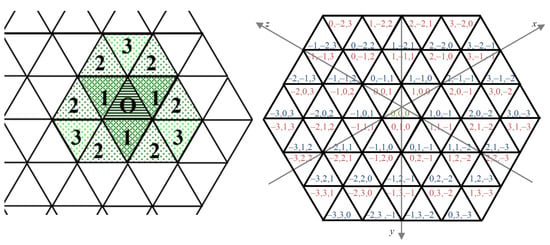
Figure 1. Various (strict) neighborhood relations (left) and a part of the grid with the symmetric coordinate system (right).

If the sum of the coordinates of a point p is 0, then we call this point even. If the sum is 1, then we call this point odd. Graphically, the even points (as triangles) have the same orientation as the origin, and the odd points (triangles) have the opposite orientation.

Since we have two types of points, the triangular grid is not a point lattice, e.g., not every grid vector transforms the grid to itself.

Definition 1.

Let p and q be two points in the triangular grid (plane). The i-th coordinate of the point p is indicated by $p\left(i\right)$. Let m be 1, 2 or 3. The points p and q are m-neighbors, if the following two conditions hold:

• $\left|p\right(i)-q(i\left)\right|\le 1$for$1\le i\le 3$,
• ${\sum }_{i=1}^3|p\left(i\right)-q\left(i\right)|\le m$.

In the case of equality at the second condition, we use the term strict m-neighbors as well.

The coordinate-values of the points and the definition of neighborhood relation harmonize (see Figure 1) and return the same neighborhood relations as the ones used in [31].

On the square grid, the description of neighborhood relations is similar to Definition 1 using the Cartesian coordinate system and addressing the points of grid by the elements of ${\mathbb{Z}}^2$. Accordingly, the one-neighbor relation corresponds to the cityblock neighborhood, while the two-neighbor relation corresponds to the chessboard neighborhood.

Now, we recall some known parts of the theory of neighborhood sequences concentrating on the triangular grid.

3.2. Neighborhood Sequences

We start this subsection with the definition of neighborhood sequences for both square (see, e.g., [5,8,12]) and triangular grids ([9,33,34]).

Definition 2.

A neighborhood sequence on the triangular grid (on the square grid) is an infinite sequence $B={\left(b\left(i\right)\right)}_{i=1}^{\infty }$, where $b\left(i\right)\in \{1,2,3\}$ ($b\left(i\right)\in \{1,2\}$, resp.) for all $i\in \mathbb{N}$. If there exists $l\in \mathbb{N}$ such that $\forall i\in \mathbb{N}$, $b\left(i\right)=b(i+l)$, then B is periodic (with period l). In this case, the abbreviation $B=\left(b\right(1),\cdots ,b(l\left)\right)$ is used.

Let T (S) and $T^{\prime }$ ($S^{\prime }$) denote the sets of general and periodic neighborhood sequences on the triangular (square) grid, respectively.

In some papers, to distinguish the general scenario, when non-periodic neighborhood sequences can also be used, the term “generalized neighborhood sequence” is used [8,12]; however, here and on the triangular grid in general, if we do not restrict ourselves to only periodic ones, we may simply use the term “neighborhood sequence”. We use neighborhood sequences to define path-based (digital) distances as follows.

Definition 3.

Let p and q be two points (in the triangular grid or in the square grid), and let $B={\left(b\left(i\right)\right)}_{i=1}^{\infty }$ be a neighborhood sequence (respectively). The point sequence $\mathrm{\Pi }(p,q;B)$ of the form $(p=p_0),p_1,\cdots ,(p_m=q)$, with $b\left(i\right)$-neighbor points $p_{i-1}$ and $p_i$ for each $i\in \{1,\cdots ,m\}$, is called a B-path, i.e., a path from p to q with respect the neighborhood sequence B. Further, the length $\left|\mathrm{\Pi }\right(p,q;B\left)\right|$ of the path $\mathrm{\Pi }(p,q;B)$ is m. Let a B-path from p to q with minimum length (with respect to B) be denoted by ${\mathrm{\Pi }}^{*}(p,q;B)$. The distance from p to q is defined as the length of such a shortest path and is written as $d(p,q;B)=|{\mathrm{\Pi }}^{*}(p,q;B)|.$ Since the distance is defined by B, it is called the B-distance.

The above-defined distance functions may not satisfy the metric properties. On the rectangular grid, there are already neighborhood sequences that define distances without satisfying the triangular inequality; however, these distances are always symmetric on that grid. Here, we show that the case of the triangular grid is more interesting and challenging.

Example 1.

Let $B=(3,1)$, $p=(0,0,0)$, $q=(-1,1,1)$ and $r=(-2,2,1)$. In this case, $d(p,q;B)=1$, $d(q,r;B)=1$ but $d(p,r;B)=3$. Thus, this distance does not meet the triangular inequality. Furthermore, there is a property of B-distances of a triangular grid that does not occur in the rectangular case; it is possible that the B-distance is non-symmetric. Let $s=(0,1,0)$, $t=(1,-1,1)$, then $d(s,t;B)=3$ opposite to $d(t,s;B)=2$.

To use the neighborhood sequences in various applications, a/the shortest B-path and the B-distance are computed from any point to any other and necessary and sufficient conditions are proven for a neighborhood sequence to define a metric (see [12,13,14] for these results on the rectangular grids and [9,33,37] on the triangular grid).

The following fact about B-distances on the square grid can be shown, e.g., based on the algorithm providing a short/the shortest B-path. This is connected to one of the important differences between B-distances on the two grids.

Proposition 1.

On the square grid, each neighborhood sequence defines a unique distance function injectively, i.e., if $B_1,B_2$ are two different neighborhood sequences ($B_1\ne B_2$), then there are points $p,q\in {\mathbb{Z}}^2$ such that $d(p,q;B_1)\ne d(p,q;B_2)$.

This is not the case on the triangular grid; thus, we require some further notions. The next concept, the minimal equivalent neighborhood sequence, and the related result are recalled from [9].

Definition 4.

Let $B={\left(b\left(i\right)\right)}_{i=1}^{\infty }$ and $B_m={\left(b_m\left(i\right)\right)}_{i=1}^{\infty }$ be two neighborhood sequences. $B_m$ is the minimal equivalent neighborhood sequence of B if the following conditions hold:

• $d(p,q;B)=d(p,q;B_m)$for all points$p,q$; and
• for each neighborhood sequence$B^{\prime }$, if $d(p,q;B)=d(p,q;B^{\prime })$for all points$p,q$, then$b_m\left(i\right)\le b^{\prime }\left(i\right)$for all$i\in \mathbb{N}$.

Lemma 1

(Nagy [9]). The minimal equivalent neighborhood sequence $B_m$ of B is uniquely determined and is given by

• $b_m\left(i\right)=b\left(i\right),$if$b\left(i\right)<3$;
• $b_m\left(i\right)=3$, if$b\left(i\right)=3$and if there is no$j<i$, such that$b_m\left(j\right)=3$;
• $b_m\left(i\right)=3$, if$b\left(i\right)=3$and there are some$b_m\left(l\right)=3$with$l<i$and$\sum _{k=j+1}^{i-1}{b}_m\left(k\right)$is odd, where$j=max\left\{\left.l\right|l<i,b_m\left(l\right)=3\right\};$
• $b_m\left(i\right)=2$, otherwise.

As we shall see later, this concept and result has a good connection with the “componentwise dominate” relation (that we recall formally in Definition 9). By that terminology, one can say that any neighborhood sequence B componentwise dominates its minimal equivalent neighborhood sequence.

Now, we recall the main theorem of [37]. First, we need some further notions and notations.

For a neighborhood sequence B, let $B_m$ be the minimal equivalent neighborhood sequence of B, and let $B_m^{\prime }$ be the neighborhood sequence that is obtained from $B_m$ by replacing its first value 3 by 2 (if it has any value 3). Further, the sequence obtained from B by replacing all its values of 3 with values of 2 is denoted by $B^{\left(2\right)}={\left(b^2\left(i\right)\right)}_{i=1}^{\infty }$. Thus, $B^{\left(2\right)}=B_m^{\left(2\right)}={\left(B_m^{\prime }\right)}^{\left(2\right)}={\left(min\{b_m\left(i\right),2\}\right)}_{i=1}^{\infty }$.

For two points $p=\left(p\right(1),p(2),p(3\left)\right)$ and $q=\left(q\right(1),q(2),q(3\left)\right)$, let $x\left(1\right)=p\left(1\right)-q\left(1\right),x\left(2\right)=p\left(2\right)-q\left(2\right),x\left(3\right)=p\left(3\right)-q\left(3\right)$ and $w=\left(w\right(1),w(2),w(3\left)\right)$ be defined as the sorted difference vector of p and q: let $w\left(1\right)$ be the value with highest absolute value among $\left\{x\right(1),x(2),x(3\left)\right\}$, let $w\left(3\right)$ be the value with the smallest absolute value among these values, and let $w\left(2\right)$ be the third value. (For disambiguation, if the largest absolute value appears twice, let the positive one be $w\left(1\right)$ and the negative one be $w\left(2\right)$.)

Now, we are ready to recall the formula for computing the B-distance.

Lemma 2

(Nagy [37]). Let two points $p=\left(p\right(1),p(2),p(3\left)\right)$ and $q=\left(q\right(1),q(2),q(3\left)\right)$ and a neighborhood sequence $B={\left(b\left(i\right)\right)}_{i=1}^{\infty }$ be given. Let the sequences $B_m$, $B_m^{\prime }$ and $B^{\left(2\right)}$ be given accordingly. Further, let $Z=\sum _{i=1}^{k-1}b\left(i\right)$ where k is the index of the first element 3 of B (if there is no value 3 in B, then $Z=\infty$).

Now, let

$$\begin{gathered} \begin{array}{c}D\left(B\right)=\end{array} \\ max\left\{\left|w\left(1\right)\right|,max\left\{i\left|\left|w\left(1\right)\right|+\left|w\left(2\right)\right|>\sum _{j=1}^{i-1}{b}^{\left(2\right)}\left(j\right)\right.\right\},max\left\{i\left|\sum _{j=1}^3\left|w\left(j\right)\right|>\sum _{j=1}^{i-1}b\left(j\right)\right.\right\}\right\}. \end{gathered}$$

The B-distance from p to q can be computed by the following formula

$$d(p,q;B)=\left\{\begin{array}{cc}\hfill D\left(B_m^{\prime }\right),& \mathit{if}p\mathit{is}\mathit{even},Z\mathit{is}\infty \mathit{or}\mathit{even}\mathit{and}w\mathit{contains}\mathit{two}\mathit{negative}\mathit{values};\hfill \\ \hfill D\left(B_m^{\prime }\right),& \mathit{if}p\mathit{is}\mathit{odd},Z\mathit{is}\infty \mathit{or}\mathit{odd}\mathit{and}w\mathit{contains}\mathit{two}\mathit{negative}\mathit{values};\hfill \\ \hfill D\left(B_m^{\prime }\right),& \mathit{if}p\mathit{is}\mathit{odd},Z\mathit{is}\infty \mathit{or}\mathit{even}\mathit{and}w\mathit{contains}\mathit{two}\mathit{positive}\mathit{values};\hfill \\ \hfill D\left(B_m^{\prime }\right),& \mathit{if}p\mathit{is}\mathit{even},Z\mathit{is}\infty \mathit{or}\mathit{odd}\mathit{and}w\mathit{contains}\mathit{two}\mathit{positive}\mathit{values};\hfill \\ \hfill D\left(B_m\right),& \mathit{otherwise}.\hfill \end{array}\right.$$

The concept of digital disks based on neighborhood sequences is also recalled (see, e.g., [34]).

Definition 5.

Let B be a neighborhood sequence on the triangular grid. Then, for any point p of the grid and for any natural number $r\in \mathbb{N}$,

$${\Delta }_p(B,r)=\left\{q\right|d(p,q;B)\le r\}$$

denotes the digital disk (based on the B-distance) with center p and radius r. In the case where p is the origin, the notation can be simplified to $\Delta (B,r)$.

We note here that the digital disk with a radius r depends only on the first r elements of B.

3.3. Lattice Theory

We assume that the reader is familiar with the basic concepts of lattice theory, otherwise they aer referred to review the following concepts in [38,39] or another standard textbook on the topic. Here, we list them to show the notation we use:

• Equivalence relation $(P,\sim )$ with equivalence classes $\overline{x}=\left\{y\right|x\sim y\}$.
• Partially ordered set $(P,\le )$.
• Supremum (least upper bound, $x\vee y$ for any $x,y\in P$) of a set.
• Infimum (greatest lower bound $x\wedge y$) of a set.
• Lattice, distributive lattice.
• Complete lattice (with a supremum $\bigvee X$ and an infimum $\bigwedge X$ for any $X\subset P$).
• Complete distributive lattice and Boolean lattice (Boolean algebra).

4. Relations on the Set of Neighborhood Sequences in the Triangular Grid

The results of the paper are shown in this section. First, the equivalence relation and the partial order relation “faster” on the equivalence classes of neighborhood sequences are shown, and then some algebraic properties of this partial order relation are presented. Finally, the “componentwise dominate” relation will be investigated with details.

4.1. An Equivalence Relation

In this section, we formally establish the equivalence relation among the neighborhood sequences that has been previously mentioned.

Definition 6.

Let $B_1$ and $B_2$ be two neighborhood sequences in T. We say that they are equivalent, i.e., $B_1\sim B_2$, if, for every pair of points $p,q$, $d(p,q;B_1)=d(p,q;B_2$).

Based on the definition of minimal equivalent neighborhood sequences, we may establish the following statement.

Lemma 3.

For any two neighborhood sequences $B_1$ and $B_2$, $B_1\sim B_2$, if and only if their minimal equivalent sequences coincide.

Based on that, we can conclude the following result.

Theorem 1.

The relation ∼ is an equivalence relation on the set T of generalized neighborhood sequences.

Proof. 

Using Definition 6, ∼ is reflexive, symmetric and transitive, and therefore it is an equivalence relation. □

By comparing this result to the square and nD rectangular grids, it is important to note that there are no two different neighborhood sequences that generate the same distance function on those grids. By the mirror of this fact, the forthcoming relations on the neighborhood sequences on the triangular grid also have some interesting properties in which the case of the triangular grid differs from the case of rectangular grids.

For further purposes, we fix the following notation.

Definition 7.

Let $\overline{B}$ denote the equivalence class of neighborhood sequences defined by ∼:

$$\overline{B}=\left\{B^{\prime }\right|B\sim B^{\prime }\}.$$

We say that B is a representative of the set $\overline{B}$ or that B represents this class.

There exists neighborhood sequence B for which the class $\overline{B}$ contains only the neighborhood sequence B itself and no other neighborhood sequences. One can obtain neighborhood sequences with this property based on Lemma 1, e.g., every neighborhood sequence without containing any value of 3 is satisfying this property.

4.2. A Partial Order Defined by B-Distances

Since there are several, there are actually infinitely many distance functions that are defined by neighborhood sequences; thus, the question arises of how they are related to each other. The next definition is recalled from [9].

Definition 8.

For any $B_1,B_2\in T$, we define the relation “faster” denoted by ${\ge }^{*}$ in the following way:

$$B_1{\ge }^{*}{B}_2\iff d(p,q;B_1)\le d(p,q;B_2)$$

for all points $p,q$.

The relation ${\ge }^{*}$ can be understood on the set of equivalence classes of neighborhood sequences as well; however, for simplicity, we use the above notations, where $B_1$ and $B_2$ represent their equivalence sets, respectively. When we are talking about periodic neighborhood sequences, then only the elements of $\overline{B}\cap T^{\prime }$ are counted.

Notice that equality is allowed by the relation ${\ge }^{*}$; thus, the term “is faster than or has the same speed” would match better to it; however, for traditional reasons, we use the short term “faster”.

Similarly, the relation ${\ge }^{*}$ is defined on the sets of S and $S^{\prime }$, and it was studied in [8,13] as it also plays an important role in the metricity condition.

Proposition 2

(Fazekas et. al. [8]). On the square grid $\left(S,{\ge }^{*}\right)$ forms a complete distributive lattice. On the other hand, $\left(S^{\prime },{\ge }^{*}\right)$ is not a lattice.

The equivalence classes for the neighborhood sequences on the square grid are singleton sets, i.e., each of them has exactly one element, and therefore this element can be used to represent this class or used instead of the class itself.

The next examples demonstrate the non-triviality of our partial order for the case of periodic neighborhood sequences.

Example 2.

Let $B_1,B_2\in T^{\prime }$ such that $B_1=(1,2)$, $B_2=(1,1,2,2,2)$. Further, let the points $o=(0,0,0)$, $p=(2,-1,0)$, $q=(1,0,0)$ and $r=(4,-4,0)$. Then, $d(o,p;B_1)=2<3=d(o,p;B_2)$, $d(o,q;B_1)=1=d(o,q;B_2)$ but $d(o,r;B_1)=6>5=d(o,r;B_2)$. Therefore, the functions $B_1$-distance and $B_2$-distance are not comparable, in general.

We should note here that similar examples can also be constructed on the square and other grids using B-distances. Our next example, however, does not work on point lattices but does work on the triangular grid.

Example 3.

Let $B_1=(1,3)$, $B_2=(3,1)$ and the points $p=(0,0,0)$, $q=(1,1,-2)$ and $r=(-1,-1,2)$. Then, one may see that $d(p,q;B_1)=3>2=d(p,q;B_2)$ but $d(p,r;B_1)=2<3=d(p,r;B_2)$.

This example shows that, although we have the same sum of the values in the sequences, (i.e., $b_1\left(1\right)+b_1\left(2\right)=b_2\left(1\right)+b_2\left(2\right)=4$), their order makes a difference on the distance: the steps of a shortest path may not commute [33]. We note here that, on the square- and nD grids the B-distance of the point-pair $p,q$ depends only on the multiset of used elements of the neighborhood sequence and does not depend on the order of the first $d(p,q;B)-1$ elements of the neighborhood sequence [13,14].

Now, after these introductory examples and thoughts, let us see how and which neighborhood sequences are comparable on the triangular grid.

Theorem 2.

The relation ${\ge }^{*}$ is a partial order on the sets of equivalence classes of T and $T^{\prime }$.

Proof. 

By definition, the relation ${\ge }^{*}$ is reflexive and transitive. In defining it for the equivalence sets, it is clear that, if $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$, then $d(p,q;B_1)=d(p,q;B_2)$, and thus $\overline{B_1}=\overline{B_2}$; therefore, they represent the same class. □

As we have previously seen in Example 3, the neighborhood sequences $(1,3)$ and $(3,1)$ are not comparable under the relation ${\ge }^{*}$. In terms of digital disks, this means that $\Delta \left(\right(1,3),2)\not\subset \Delta \left(\right(3,1),2)$ and $\Delta \left(\right(1,3),2)\not\supset \Delta \left(\right(3,1),2)$; see also Figure 2, where digital disks with radii up to 3 are presented with the (periodic) neighborhood sequences $(3,1)$, $\left(2\right)$ and $(1,3)$.

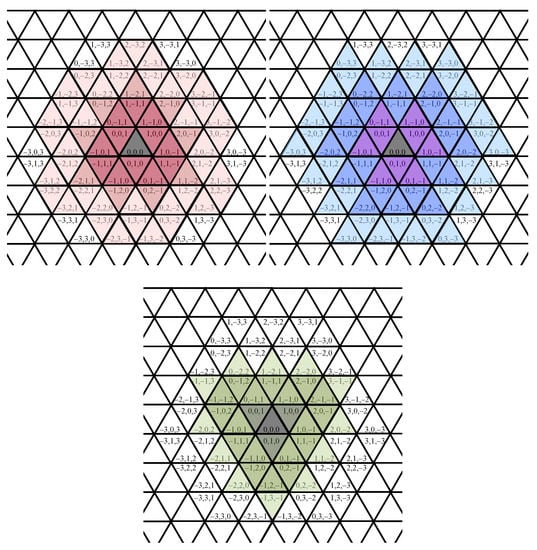
Figure 2. Digital disks with neighborhood sequence $(3,1)$ on the left, with $\left(2\right)$ on the right and with $(1,3)$ at the bottom. The origin is marked with gray color, disks with radius 1 are dark shaded, disks with radius 2 are (dark and) medium color, while for disks with radius 3, all shaded pixels are counted.

Based on Lemma 2, and by observing the digital disks obtained by neighborhood sequences (see [34,35,40] for details), we may consider the following important observations.

Proposition 3.

In the triangular grid, from any point

(a) 

By a 2-step, exactly the same region (i.e., set of points) is reached as by two consecutive 1-steps.

(b) 

By two consecutive 2-steps, a larger region can be reached than by using a 1-step and a 3-step in any order.

We can transform part (b) of the above proposition into the next lemma about the partial order ${\ge }^{*}$.

Lemma 4.

The following statements hold for the specific periodic neighborhood sequences mentioned below.

$$\begin{array}{c}\left(2\right){\ge }^{*}(1,3).\\ (1,2,2,2){\ge }^{*}(1,1,2,3,1).\end{array}$$

However, $\left(2\right){\ngeqq }^{*}(3,1)$ and $(3,1){\ngeqq }^{*}\left(2\right)$.

Proof. 

The first and the second statements follow from the formula of Lemma 2.

The first part of the last statement of the lemma is proven, for instance, by looking the points that can be reached in one step: in one step, a larger set of points is reached by $(3,1)$ than by $\left(2\right)$, i.e., $\Delta \left(\right(2),1)\subset \Delta \left(\right(3,1),1)$. To prove the other part, consider the B-distances of the points $p=(0,0,0)$ and $q=(2,-1,-1)$. By the formula of Lemma 2, $d(p,q;(2\left)\right)=2$ and $d(p,q;(3,1\left)\right)=3$, proving the incomparability of the neighborhood sequences $(3,1)$ and $\left(2\right)$ under ${\ge }^{*}$ on the triangular grid. □

Now, we establish our results on the structure of T and $T^{\prime }$ under ${\ge }^{*}$. Some of the results may seem simple or easy to prove; however, they give important information about the sets T and $T^{\prime }$ of neighborhood sequences. They also underline the differences between the distances defined on the square and on the triangular grids. Figure 3 shows the partial order ${\ge }^{*}$ on the sets of periodic neighborhood sequences with periods 1, 2 and 3 for both of the square and triangular grids. As one can observe, the diagram of $T^{\prime }$ with period 2 already appears more complicated than the diagram of $S^{\prime }$ with period 3 (the diagrams on the top are recalled from [7]). The Hasse diagrams shown here compress a number of comparisons of B-distances.

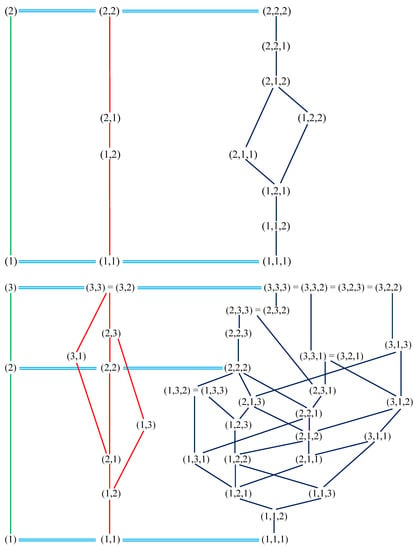
Figure 3. The Hasse diagrams of the partial orders $(S^{\prime },{\ge }^{*})$ (top) and $(T^{\prime },{\ge }^{*})$ (bottom) restricted to neighborhood sequences with periods 1, 2 and 3, from left to right, respectively.

One can observe on Figure 3, bottom-right, that, for instance, the neighborhood sequence $\left(2\right)=(2,2,2)$ is faster than $(1,3,2)$, $(1,3,3)$, $(2,1,3)$, $(2,2,1)$ and all the neighborhood sequences below them, i.e., $(1,3,1)$, $(1,2,3)$, $(1,2,2)$, $(2,1,2)$, $(2,1,1)$, $(1,2,1)$, $(1,1,3)$, $(1,1,2)$ and $\left(1\right)=(1,1,1)$. By, e.g., the formula of Lemma 2, one can see that there is no point that can be reached in one step by any of the listed neighborhood sequences B but not with the neighborhood sequence $\left(2\right)$. That could be the base of the induction. The inheritance can be proven for each particular case (applying also, e.g., Proposition 3) by checking the sums of the prefix of the (minimal equivalent) neighborhood sequence B and comparing the same length prefix of $\left(2\right)$, i.e., to the number that is twice the length of the prefix.

On the other hand, $(3,3,3)$, $(3,3,2)$, $(3,2,3)$, $(3,2,2)$, $(2,3,3)$, $(2,3,2)$ and $(2,2,3)$ are faster than $\left(2\right)$. All those relations can be seen since any path defined by $\left(2\right)$ is also a path with any of the listed neighborhood sequences; thus, the distance determined by $\left(2\right)$ cannot be smaller than the B-distance defined by another neighborhood sequence in this list. (Trivially, $\left(2\right)$ is faster than itself. We mention this only for the sake of completeness).

Further, there are neighborhood sequences such that they are incomparable with $\left(2\right)$ under the relation faster. Each of those neighborhood sequences B are listed below with two points such that the B-distance of exactly one of the points, p, is smaller from the origin than its $\left(2\right)$-distance, while, for the second point, q, its B-distance is larger than its $\left(2\right)$-distance from the origin.

• $B=(3,1,1)$, $p=(1,-1,1)$ and $q=(2,-3,1)$;
• $B=(3,1,2)$, $p=(1,-1,1)$ and $q=(-3,3,0)$;
• $B=(2,3,1)$, $p=(2,-2,1)$ and $q=(-3,3,0)$;
• $B=(3,3,1)$, $p=(1,-1,1)$ and $q=(-3,3,0)$;
• $B=(3,2,1)$, same points as above;
• $B=(3,1,3)$, $p=(1,-1,1)$ and $q=(-3,0,3)$.

The relations among other neighborhood sequences can be shown in a similar manner.

Now, as the first of our main theoretical results about ${\ge }^{*}$, we show the following.

Theorem 3.

The set of periodic neighborhood sequences $\left(T^{\prime },{\ge }^{*}\right)$ is not a lattice.

Proof. 

Let $B_1=(2,1,1)$ and $B_2=(1,3,2)$ be periodic neighborhood sequences. Notice that $\overline{B_1}=\left\{B_1\right\}$, while

$$\overline{B_2}=\left\{{\left(b_y\left(i\right)\right)}_{i=1}^{\infty }\left|\begin{array}{cc}\hfill b_y\left(i\right)=1,& if i\equiv 1(mod3)\\ \hfill b_y\left(i\right)=3,& if i\equiv 2(mod3)\\ \hfill b_y\left(i\right)\ge 2,& if i\equiv 0(mod3)\end{array}\right.\right\}.$$

The least upper bound of these sequences in $\left(T,{\ge }^{*}\right)$ can be written as

$B=(2,2,2,1,3,2,1,3,2,1,3,2,\cdots )$, which belongs to the equivalence set

$$\overline{B}=\left\{{\left(b\left(i\right)\right)}_{i=1}^{\infty }\left|\begin{array}{cc}\hfill b\left(i\right)=2,& if i\in \{1,2,3\}\hfill \\ \hfill b\left(i\right)=1,& if i>3,i\equiv 1(mod3)\\ \hfill b\left(i\right)=3,& if i>3,i\equiv 2(mod3)\\ \hfill b\left(i\right)\ge 2,& if i>3,i\equiv 0(mod3)\end{array}\right.\right\}.$$

Notice that $B_M=(2,2,2,1,3,3,1,3,3,1,3,3,1,3,3,\cdots )\in \overline{B}$ contains only three values of 2. Clearly, there is no element of $\overline{B}$ that is in $T^{\prime }$. Now, let us suppose, on the contrary, that there is a neighborhood sequence $B^{\prime }=B_1\vee B_2$ in $T^{\prime }$ and $B^{\prime }=(b^{\prime }\left(1\right),\cdots ,b^{\prime }\left(l\right))$ for some value $l\in \mathbb{N}$. Then, $B^{\prime }{\ge }^{*}B$ in T but $B^{\prime }\notin \overline{B}$; therefore, there must be $i\in \mathbb{N}$ such that $b^{\prime }\left(i\right)>b_M\left(i\right)$ holds.

• $B^{\prime }$ may contain an element larger than 2 among its first three elements. (Clearly, it cannot contain values smaller than 2 at these positions without contradicting the fact that $B^{\prime }{\ge }^{*}B$.) However, in this case, for the periodic sequence $B^{″}=\left(2\right)$, we have $B^{\prime }{\ge }^{*}{B}^{″}$ (and $B^{″}{\ngeqq }^{*}{B}^{\prime }$), but (as one can easily check) $B^{″}{\ge }^{*}{B}_1$ and $B^{″}{\ge }^{*}{B}_2$. That leads to a contradiction.
• In the other case, it means that there is a value $i=3j+1$ (for a value $j\in \mathbb{N}$) such that $b_M\left(i\right)=1$; however, $b^{\prime }\left(i\right)>1$. Without loss of generality, suppose that, for all $j<i$: $b^{\prime }\left(j\right)=b\left(j\right)$ holds. Then, defining $b^{″}\left(k\right)=b\left(k\right)$ for $1\le k\le i+5$ and $B^{″}=(b^{″}\left(1\right),\cdots ,b^{″}(i+5))$ as a periodic neighborhood sequence with period $i+5$, clearly $B^{″}{\ge }^{*}{B}_1$ and $B^{″}{\ge }^{*}{B}_2$. However, in this case, $B^{″}{\ngeqq }^{*}{B}^{\prime }$, which leads to a contradiction.

Therefore, $B^{\prime }=B_1\vee B_2$ cannot be in $T^{\prime }$. □

By the previous proof, we demonstrated the following fact.

Corollary 1.

Even if the supremum of two periodic neighborhood sequences exists, it may not be periodic.

By the following theorem, we show the case with the set of general neighborhood sequences.

Theorem 4.

The set of neighborhood sequences on the triangular grid $\left(T,{\ge }^{*}\right)$ is not a lattice.

Proof. 

Let

$$B_1=\{3,2,1,1,1,3,1,3,1,3,1,3,1,\cdots \},$$

$$B_2=\{2,2,1,2,1,2,2,2,2,2,2,2,2,\cdots \},$$

$$B_3=\{2,2,1,1,1,3,1,3,1,3,1,3,1,\cdots \}$$

and

$$B_4=\{2,2,1,1,1,1,3,1,3,1,3,1,3,\cdots \}.$$

(The last two values are repeated for each of these sequences up to infinity). Observe that $B_1,B_2,B_3$ and $B_4$ form a singleton equivalence set under ∼. Clearly, $B_1{\ge }^{*}{B}_3$ and $B_2{\ge }^{*}{B}_3$. Let $B_5\in T$ such that $B_1{\ge }^{*}{B}_5$ and $B_2{\ge }^{*}{B}_5$. Then, one can easily infer that $B_5{\ngeqq }^{*}{B}_3$. Further, the first two elements of $B_5$ can be at most 2. Let us assume that the first difference of $B_3={\left(b_3\left(k\right)\right)}_{k=1}^{\infty }$ and $B_5={\left(b_5\left(k\right)\right)}_{k=1}^{\infty }$ occurs at their $(i+1)$st position, i.e., $b_3\left(k\right)=b_5\left(k\right)$ for all $k\le i$; however, $b_3(i+1)\ne b_5(i+1)$. Then, $B_5{\ge }^{*}{B}_3$ would imply that $b_5(i+1)>b_3(i+1)$. It can only be if $b_3(i+1)=1$ and $b_5(i+1)\ge 2$, which contradicts $B_1{\ge }^{*}{B}_5$.

Clearly, $B_1{\ge }^{*}{B}_4,B_2{\ge }^{*}{B}_4$ but $B_3{\ngeqq }^{*}{B}_4$ (since the order of elements 1 and 3 matters). Therefore, $B_1$ and $B_2$ have no greatest lower bound, completing the proof that T is not a lattice. □

In the previous proof, we used non-periodic sequences. Thus, it seems that none of T and $T^{\prime }$ form a lattice under the relation ${\ge }^{*}$. This also highlights an important difference between the square and the triangular grid. In the next subsection, another relation will be investigated on T and $T^{\prime }$.

4.3. Lattices

The results of the previous subsection recommend that, instead of the relation ${\ge }^{*}$, we may use another relation to find some structure in T and in $T^{\prime }$. Now, we adopt another partial order relation that was investigated in [8] for S and $S^{\prime }$ and is called “componentwise dominates” in [5] for some subsets of $S^{\prime }$. We have also seen that it plays a natural role when we defined and used minimal equivalent neighborhood sequences in T.

Definition 9.

For any two neighborhood sequences $B_1={\left(b_1\left(i\right)\right)}_{i=1}^{\infty }$, $B_2={\left(b_2\left(i\right)\right)}_{i=1}^{\infty }$, the relation ⊒ is defined in the following way:

$$B_1⊒B_2\iff b_1\left(i\right)\ge b_2\left(i\right),\mathit{for}\mathit{every}i\in \mathbb{N}.$$

Let us have a more detailed view of the structure that this relation gives to the sets S and $S^{\prime }$ on the square grid. It should be noted that ${\ge }^{*}$ is a proper refinement of ⊒ in S and $S^{\prime }$; more formally, we can state the following results (based, e.g., on the formula to compute B-distances on the square grid [14] or on the properties of a faster relation from [13]).

Proposition 4.

Let $B_1,B_2\in S$. If $B_1⊒B_2$, then $B_1{\ge }^{*}{B}_2$. Furthermore, if $B_1⊒B_2$ and $B_1\ne B_2$, then $B_2⋣B_1$.

Proof. 

It is a corollary of the formula to compute B-distances on the square grid; see Proposition 1 and Definition 9. □

Moreover, we state the following.

Proposition 5.

Let $B_1,B_2\in S$. If $B_1⋣B_2$ and $B_2⋣B_1$, then $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ cannot be at the same time, i.e., at most, one of them may hold.

Proof. 

Generally, for $B_1,B_2\in S$, there could be three cases, either both $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ hold, or maybe exactly one of them, or maybe none of them.

If the condition $B_1⋣B_2$ and $B_2⋣B_1$ holds:

• We may have that $B_1$ and $B_2$ are incomparable under ${\ge }^{*}$. Let us consider, e.g., $B_1=(1,1,2,2,2)$ and $B_2=(1,2,1,1,1)$. Then, considering the points $(0,0)$ and $(1,2)$, their $B_2$-distance is 2; however, their $B_1$-distance is 3. On the other hand, by considering $(0,0)$ and $(4,2)$, their $B_1$-distance is 4, while their $B_2$-distance is 5.
• However, it may also happen that, e.g., $B_1{\ge }^{*}{B}_2$, and we check the case, e.g., with $B_1=(1,2,2,1,2)$ and $B_2=(1,1,1,2,1)$. (By changing the role of $B_1$ and $B_2$, the opposite relation can be fulfilled.)

Now, to complete the proof, let us assume that $B_1⋣B_2$ and $B_2⋣B_1$ for $B_1={\left(b_1\left(i\right)\right)}_{i=1}^{\infty },B_2={\left(b_2\left(i\right)\right)}_{i=1}^{\infty }\in S$. It follows that $B_1\ne B_2$. Thus, there is a position i where the first mismatch occurs in these two sequences, i.e., $b_1\left(j\right)=b_2\left(j\right)$ for all $j<i$ but $b_1\left(i\right)\ne b_2\left(i\right)$. Then, considering the points $(0,0)$ and $(i,k+1)$ with $k=\left|\left\{j\right|b_1\left(j\right)=2,j<i\}\right|$, i.e., k is the number of 2s among the first $i-1$ elements of $B_1$ (and also of $B_2$ since their $i-1$ long prefix sequence are identical). Then, one of the $B_1$- and $B_2$-distances of these points is i, the other is $i+1$, and hence it cannot be that both $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ hold. □

Moreover, the following results are known.

Proposition 6

(Fazekas et al. [8]). $\left(S,⊒\right)$ is a complete distributive lattice with the greatest lower bound $\bigwedge S=\left(1\right)$ and least upper bound $\bigvee S=\left(2\right)$.

$\left(S^{\prime },⊒\right)$ is a distributive lattice with the greatest lower bound $\bigwedge S^{\prime }=\left(1\right)$ and least upper bound $\bigvee S^{\prime }=\left(2\right)$; however, it is not a complete lattice.

Our first result in this subsection is a kind of strengthening of (the first part of) the previous result on the square grid.

Theorem 5.

$(S,⊒)$ is a Boolean lattice (Boolean algebra).

Proof. 

A Boolean algebra, by definition, is a complemented distributive lattice. By Proposition 6, $(S,⊒)$ is a complete distributive lattice, and we need to show only that it is also complemented. Having exactly two types of neighborhood, the complementary relation can easily be defined on them: with 1 and 2 as complements of each other. This complementarity relation can also be extended to the neighborhood sequences: the complement of the neighborhood sequence $B={\left(b\left(i\right)\right)}_{i=1}^{\infty }$, $B^c={(3-b\left(i\right))}_{i=1}^{\infty }$ contains the opposite element in every of its positions. In this way, both the axioms of complements: $B\vee B^c=\left(2\right)$ and $B\wedge B^c=\left(1\right)$ are satisfied for every neighborhood sequence B on the square grid. Thus, the statement is proven. □

Now, we turn to analyze the componentwise dominate relation on neighborhood sequences of the triangular grid. In the following part, the sets T and $T^{\prime }$ are analyzed under ⊒.

Theorem 6.

$\left(T,⊒\right)$ is a complete distributive lattice with the greatest lower bound $\bigwedge T=\left(1\right)$ and least upper bound $\bigvee T=\left(3\right)$.

Proof. 

By Definition 9, ⊒ is a partial order on T. Moreover, for any $B_1={\left(b_1\left(i\right)\right)}_{i=1}^{\infty }$, $B_2={\left(b_2\left(i\right)\right)}_{i=1}^{\infty }\in T$, we can define $B_1\wedge B_2$ as ${\left(min\{b_1\left(i\right),b_2\left(i\right)\}\right)}_{i=1}^{\infty }$ and $B_1\vee B_2$ as ${\left(max\{b_1\left(i\right),b_2\left(i\right)\}\right)}_{i=1}^{\infty }$. Furthermore, for any set P of neighborhood sequences $B_1,B_2,\cdots$, their greatest lower bound

$\bigwedge P={\left(min\left\{b_j\left(i\right)\right|B_j\in P,B_j={\left(b_j\left(k\right)\right)}_{k=1}^{\infty }\}\right)}_{i=1}^{\infty }$ and least upper bound

$\bigvee P={\left(max\left\{b_j\left(i\right)\right|B_j\in P,B_j={\left(b_j\left(k\right)\right)}_{k=1}^{\infty }\}\right)}_{i=1}^{\infty }$ is determined; thus, the completeness of the lattice is shown. This implies also that $\bigwedge T=\left(1\right)$ and $\bigvee T=\left(3\right)$. Finally, the distributivity of the lattice is straightforward. □

However, there is a remarkable difference between the T and S under ⊒.

Proposition 7.

$\left(T,⊒\right)$ is not a Boolean lattice with $B_1\wedge B_2={\left(min\{b_1\left(i\right),b_2\left(i\right)\}\right)}_{i=1}^{\infty }$ and $B_1\vee B_2={\left(max\{b_1\left(i\right),b_2\left(i\right)\}\right)}_{i=1}^{\infty }$ where $B_1={\left(b_1\left(i\right)\right)}_{i=1}^{\infty }$ and $B_2={\left(b_2\left(i\right)\right)}_{i=1}^{\infty }$.

Proof. 

In the proof of the previous theorem, we previously proved that $\left(T,⊒\right)$ is a distributive lattice with the given operators. We need to show that the complement operation cannot be introduced on T fulfilling the required axioms. Let $B=\left(2\right)$, if there is its complement $B^c\in T$, then both $B\wedge B^c=\left(1\right)$ and $B\vee B^c=\left(3\right)$ would be fulfilled. However, then $B_c=\left(1\right)$ should be to make $B\wedge B^c=\left(1\right)$ true; however, $B_c=\left(3\right)$ would be required to fulfill $B\vee B^c=\left(3\right)$. This contradiction proves the result. □

Now, we continue with a result on $T^{\prime }$.

Theorem 7.

$\left(T^{\prime },⊒\right)$ is a distributive lattice with the greatest lower bound $\bigwedge T^{\prime }=\left(1\right)$ and least upper bound $\bigvee T^{\prime }=\left(3\right)$.

Proof. 

The proof is similar to the proof of the previous theorem except the completeness by noting that the constructions mentioned there provide periodic neighborhood sequences with period of the least common multiplier of the periods of the given neighborhood sequences. □

In the next part of the paper, we establish connections on the relations studied in this paper. Let us see how the ordering ⊒ and the sets T and $T^{\prime }$ can be connected to the B-distances. First, we use the relation ⊒ on specific subsets of T.

Theorem 8.

Let B be any neighborhood sequence in T. The relation ⊒ defines a complete distributive lattice on $\overline{B}$.

Proof. 

The reflexivity, the antisymmetry and the transitivity follows from the the definition of ⊒. Therefore, $\left(\overline{B},⊒\right)$ is a partially ordered set for any $B\in T$.

It is clear that, for every $B_1,B_2\in \overline{B}$, $B_1\wedge B_2$ and $B_1\vee B_2$ exist in T and can be defined as $B_1\wedge B_2={(min\{b_1\left(i\right),b_2\left(i\right)\})}_{i=1}^{\infty }$, and $B_1\vee B_2={(max\{b_1\left(i\right),b_2\left(i\right)\})}_{i=1}^{\infty }$.

It can be checked (e.g., by using Lemma 1) that both $B_1\wedge B_2$ and $B_1\vee B_2$ are in $\overline{B}$. Thus, $\left(\overline{B},⊒\right)$ is a lattice.

Let $X=\left\{B_k\right|B_k\in \overline{B},k\in K\}$ be a subset of $\overline{B}$ with some index set K. Let now, $b^{\prime }\left(i\right)={max}_{k\in K}\left\{b_k\left(i\right)\right\}$. Clearly, $B^{\prime }={\left(b^{\prime }\left(i\right)\right)}_{i=1}^{\infty }$ is the least upper bound of the subset X, and thus $(\overline{B},⊒)$ is a complete lattice.

The statement that this lattice is distributive is trivial. Moreover, $\bigwedge \overline{B}=B_m$, the minimal equivalent neighborhood sequence for B, and

$\bigvee \overline{B}=$

${\left(b_M\left(i\right)=\left\{\begin{array}{cc}\hfill b\left(i\right),& \mathrm{if} b\left(i\right)=1 \mathrm{or} b\left(i\right)=3,\hfill \\ \hfill 2,& \mathrm{if} b\left(i\right)=2 \mathrm{and} \mathrm{there} \mathrm{is} \mathrm{no} j<i,\mathrm{such} \mathrm{that} b_M\left(j\right)=3,\hfill \\ \hfill 3,& \mathrm{if} b\left(i\right)=2 \mathrm{and} \mathrm{there} \mathrm{are} \mathrm{some} b_M\left(l\right)=3\mathrm{with} l<i,\mathrm{and} \hfill \\ & \left|\right\{k|b_M\left(k\right)=1,j<k<i\}|\mathrm{is} \mathrm{even},\hfill \\ & \mathrm{where} j=max\left\{\left.l\right|l<i,b_M\left(l\right)=3\right\},\hfill \\ \hfill 2,& \mathrm{otherwise}.\hfill \end{array}\right.\right)}_{i=1}^{\infty }$

Thus, the proof of the theorem is completed. □

The neighborhood sequence defined by the last formula of the previous proof can be called the maximal equivalent neighborhood sequence $B_M$ of B. Analogously to Lemma 1, it can be shown that it is uniquely defined for every $B\in T$. The case of periodic neighborhood sequences is more interesting due to the fact that there are periodic neighborhood sequences such that their minimal/maximal equivalent neighborhood sequences are not periodic and vice versa.

Example 4.

$B=\left(3\right)$ is periodic. It is the same as its maximal equivalent neighborhood sequence. However, its minimal equivalent neighborhood sequence is not periodic, it is $(3,2,2,2,2,2,2,\cdots )$ (having only 2’s after the first 3). The next non-periodic neighborhood sequence belongs to the same equivalence class: $(3,2,2,3,2,2,2,2,3,2,2,\cdots )$ having 3 at every place i where $i=j^2$ for some $j\in \mathbb{N}$.

Example 5.

Let $B=(2,1,3)$, and then its minimal equivalent neighborhood sequence is the same; however, its maximal equivalent neighborhood sequence,

$B_M=(2,1,3,3,1,3,3,1,3,3,1,3,3,1,3,\cdots )$, is not periodic (having exactly one value 2).

Therefore, it is interesting to analyze what we can say about subsets of T containing only periodic neighborhood sequences.

Theorem 9.

Let B be any neighborhood sequence in $T^{\prime }$. The relation ⊒ defines a distributive lattice on $\overline{B}\cap T^{\prime }$ that may not be complete.

Proof. 

Since ⊒ is a partial order on any set $\overline{B}$ (see (the proof of) Theorem 8), it is a partial order on the subset $\overline{B}\cap T^{\prime }$. Now, we show that, for any two representatives $B_1$ and $B_2$ of the class $\overline{B}\cap T^{\prime }$ have $B_1\wedge B_2$ and $B_1\vee B_2$ elements in $\overline{B}\cap T^{\prime }$. Let $l_1$ and $l_2$ be the periods of $B_1$ and $B_2$, respectively. For simplicity, let $l=l_1·l_2$. (The least common multiplier of $l_1$ and $l_2$ suffices.) Then, let us construct $B_1\wedge B_2$ with period l: ${(min\{b_1\left(i\right),b_2\left(i\right)\})}_{i=1}^l$. Similarly, the construction $B_1\vee B_2={(max\{b_1\left(i\right),b_2\left(i\right)\})}_{i=1}^l$.

Therefore, $(\overline{B}\cap T^{\prime },⊒)$ form a lattice for any $B\in T^{\prime }$. By the constructions above, it is clear that this lattice is distributive.

Now, we show an example for $(\overline{B}\cap T^{\prime },⊒)$ that proves that this lattice is not complete.

Let $B^{@}=\left(3\right)$. Then, $\overline{B^{@}}$ contains every neighborhood sequence $B^{\prime }$ that have the following properties: $b^{\prime }\left(1\right)=3$, and $b^{\prime }\left(i\right)\ge 2$ for every $i\in \mathbb{N}$.

Now, a monotonously increasing and a monotonously decreasing sequence in $\overline{B^{@}}$ will be shown, such that they have a common “limit sequence” $B_{lim}$ but $B_{lim}$ is not in $\overline{B^{@}}\cap T^{\prime }$. In this way, we show that $\left(\overline{B^{@}},⊒\right)$ is not complete. For technical purposes, we introduce the following notation. Any periodic neighborhood sequence $B=(b\left(1\right),\cdots ,b\left(l\right))\in T^{\prime }$ can also be written in the form having period $2l$: $\left(b\right(1),\cdots ,b(l),b(1),\cdots ,b(l\left)\right)$, and this form is denoted by $B^2\left(l\right)$.

Now, for any neighborhood sequence $B\in \overline{B^{@}}$ that has period l, i.e., $B=\left(b\right(1),\cdots ,b(l\left)\right)$, and for any $i\mathbb{N}$ with $1\le i\le l$ let $B^{⟨i⟩}\left(l\right)=(b^{\prime }\left(1\right),\cdots ,b^{\prime }\left(l\right))$ defined with the elements $b^{\prime }\left(j\right)=b\left(j\right)$ for $j\ne i$ and $b^{\prime }\left(i\right)=5-b\left(i\right)$. In this way, only the i-th (modulo l) element of B is changed from 2 to 3 or vice versa, each other element remains the same.

Further, for any $k\in {\mathbb{N}}_0$, we say that k is even-square-bounded (ESB) if there is an even $j\in {\mathbb{N}}_0$ such that $j^2\le k<{(j+1)}^2$, else k is odd-square-bounded (OSB). Clearly, the even-square-bounded and the odd-square-bounded numbers form longer and longer intervals in ${\mathbb{N}}_0$ as they are growing. Let $B_{-1}^{\downarrow }=\left(3\right)$, $B_{-1}^{\uparrow }=\left(2\right)$, and now we define the sequences $B_k^{\downarrow }$ and $B_k^{\uparrow }$ in $T^{\prime }$ as follows. For an ESB $k\in {\mathbb{N}}_0$, use $B_k^{\downarrow }={\left(B_{k-1}^{\downarrow }\right)}^2\left(2^k\right)$ and $B_k^{\uparrow }={\left({\left(B_{k-1}^{\uparrow }\right)}^2\left(2^k\right)\right)}^{⟨2^k⟩}\left(2^{k+1}\right)$, else (in case k is OSB) let $B_k^{\downarrow }={\left({\left(B_{k-1}^{\downarrow }\right)}^2\left(2^k\right)\right)}^{⟨2^k⟩}\left(2^{k+1}\right)$ and $B_k^{\uparrow }={\left(B_{k-1}^{\uparrow }\right)}^2\left(2^k\right)$.

In this way, to describe $B_k^{\downarrow }$ and $B_k^{\uparrow }$, we give the $2^k$ long periods of $B_{k-1}^{\downarrow }$ and $B_{k-1}^{\uparrow }$ after $B_{k-1}^{\downarrow }$ and $B_{k-1}^{\uparrow }$, respectively, such that exactly one of the $2^{k+1}$-th long periods is modified at the $2^k$-th position; where the modified period depends on the ESBness of k. For the sake of a better view, we show some of the first constructed values of these sequences:

$B_0^{\downarrow }=(3,3)$,

$B_1^{\downarrow }=(3,2,3,3)$,

$B_2^{\downarrow }=(3,2,3,2,3,2,3,3)$,

$B_3^{\downarrow }=(3,2,3,2,3,2,3,2,3,2,3,2,3,2,3,3)$

$B_4^{\downarrow }=(3,2,3,2,3,2,3,2,3,2,3,2,3,2,3,3,3,2,3,2,3,2,3,2,3,2,3,2,3,2,3,3)$

and

$B_0^{\uparrow }=(3,2)$,

$B_1^{\uparrow }=(3,2,3,2)$,

$B_2^{\uparrow }=(3,2,3,2,3,2,3,2)$,

$B_3^{\uparrow }=(3,2,3,2,3,2,3,2,3,2,3,2,3,2,3,2)$,

$B_4^{\uparrow }=(3,2,3,2,3,2,3,2,3,2,3,2,3,2,3,3,3,2,3,2,3,2,3,2,3,2,3,2,3,2,3,2)$.

As one may observe, and as can also be seen from the construction, every element of both sequences for $k\ge 0$ is in $\overline{B^{@}}$, i.e., $B_k^{\downarrow }\in \overline{B^{@}}$ and $B_k^{\uparrow }\in \overline{B^{@}}$ for all non-negative values of k. It is also clear that $B_k^{\uparrow }⊒B_{k-1}^{\uparrow }$ and $B_{k-1}^{\downarrow }⊒B_k^{\downarrow }$ for every non-negative k, moreover, in both sequences, there are strict inequalities infinitely often. However, by comparing the elements of the two sequences with the same index k, from the construction, we have the following. They both have $2^{k+1}$ long periods, i.e., $B_k^{\downarrow }=(b_k^{\downarrow }\left(1\right),\cdots ,b_k^{\downarrow }\left(2^{k+1}\right))$ and $B_k^{\uparrow }=(b_k^{\uparrow }\left(1\right),\cdots ,b_k^{\uparrow }\left(2^{k+1}\right))$.

Moreover, their elements $b_k^{\downarrow }\left(i\right)=b_k^{\uparrow }\left(i\right)$ for every $1\le i<2^{k+1}$ and $b_k^{\uparrow }\left(2^{k+1}\right)<b_k^{\downarrow }\left(2^{k+1}\right)$ for every $k\in {\mathbb{N}}_0\cup \{-1\}$ (the mismatch is at the last position of the $2^{k+1}$ long period). Then, for each $i\in \mathbb{N}$, let us choose a value $k\in \mathbb{N}$ with $2^{k+1}>i$ and let $b_{lim}\left(i\right)=b_k^{\uparrow }\left(i\right)$ and, further, $B_{lim}={\left(b_{lim}\left(i\right)\right)}_{i=1}^{\infty }$. By the previously analyzed property of the sequences $B_k^{\downarrow }$ and $B_k^{\uparrow }$, the sequence $B_{lim}$ is well-defined. It is clear that $B_{lim}\in \overline{B^{@}}$ holds. Now, we prove that $B_{lim}$ is not periodic.

The definitions of $B_k^{\downarrow }$ and $B_k^{\uparrow }$ imply that, for each non-negative j$b_{lim}\left(i\right)=b_{lim}(i+nt)$ with $t=2^{\left(j^2\right)}$, $1\le i\le t$ and $0\le n\le 2^{2j+1}-1$, but $b_{lim}\left(2^{\left(j^2\right)}\right)\ne b_{lim}\left(2^{{(j+1)}^2}\right)$. However, there is no periodic sequence with this property.

Finally, let $X=\left\{B_k^{\uparrow }\right|k\ge 0\}$. It is clear that $X\subset \overline{B^{@}}$. Now, suppose that $B^{\vee }=\bigvee X$ in $\overline{B^{@}}\cap T^{\prime }$ for some $B^{\vee }=(b^{\vee }\left(1\right),\cdots ,b^{\vee }\left(l\right))$. However, in this case, in $\overline{B^{@}}$ (such as in T) $B^{\vee }⊒B_{lim}$ but $B^{\vee }\ne B_{lim}$; therefore, there is $i\in \mathbb{N}$ such that $b^{\vee }\left(i\right)>b_{lim}\left(i\right)$. However, this would yield $B_k^{\downarrow }⋣B^{\vee }$ in $\overline{B^{@}}\cap T^{\prime }$, if $2^{k+1}>i$.

However, by $B_k^{\downarrow }⊒B_j^{\uparrow }$, for each $j\ge 0$, which contradicts $B^{\vee }=\bigvee X$ in $T^{\prime }$. Thus, there is no least upper bound for X in $\overline{B^{@}}\cap T^{\prime }$; therefore, $\left(\overline{B^{@}}\cap T^{\prime },⊒\right)$ is not complete. □

Now, we are ready to complement the results of Theorem 7.

Theorem 10.

$\left(T^{\prime },⊒\right)$ is not a complete lattice.

Proof. 

Observe that, in the previous proof, we demonstrated that $(\overline{B}\cap T^{\prime })$ is not complete as all the neighborhood sequences constructed were in $T^{\prime }$; however, as $B_{lim}\notin T^{\prime }$, the mentioned property is also inherited to $T^{\prime }$ itself. □

Thus, the sets T and $T^{\prime }$ have some similar properties under the partial order ⊒ as S and $S^{\prime }$ with the differences mentioned.

We are closing in on results that connect the orderings ${\ge }^{*}$ and ⊒ on the triangular grid. These results, with respect to Propositions 4 and 5, show that these relations give a more complex (theoretical) structure on the triangular grid compared with on the square grid.

Theorem 11.

Let $B_1,B_2\in T$. The following statements hold:

(a) 

If $B_1⊒B_2$, then $B_1{\ge }^{*}{B}_2$.

(b) 

Moreover, $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ both may hold, even if $B_1⊒B_2$ and $B_1\ne B_2$.

(c) 

Further, if none of $B_1⊒B_2$ and $B_2⊒B_1$ hold, all the following possibilities may occur:

• both $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ hold, i.e., $B_1$ and $B_2$ have the same “speed” according to the faster relation;
• exactly one of $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ holds, i.e., one of them is (really) faster (and not equally fast) compared with the other; or
• none of $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ hold: $B_1$ and $B_2$ are also incomparable under the faster relation.

Proof. 

From Part (a) from $B_1⊒B_2$, it follows that every $B_2$-path is also a $B_1$-path, and thus $B_1{\ge }^{*}{B}_2$ is immediately proven.

If the class $\overline{B}$ contains more than one element, then one can easily pick two elements from there, e.g., the minimal and the maximal equivalent neighborhood sequences $B_m$ and $B_M$, respectively. Then, clearly $B_m\ne B_M$, but $B_M⊒B_m$. On the other hand, since these neighborhood sequences are equivalent ($B_m\sim B_M$; they provide the same distance function), both $B_m{\ge }^{*}{B}_M$ and $B_m{\ge }^{*}{B}_M$ hold.

Finally, the proof of part (c) is by examples.

Considering $B_1=(3,2,3)$ and $B_2=(3,3,2)$, it is clear that none of $B_1⊒B_2$ and $B_2⊒B_1$ hold; however, they provide the same distance function with their minimal equivalent neighbor sequence $B_m=(3,2,2,2,2,\cdots )$ with exactly one value of 3 and all other values are 2. Thus, both $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ hold in this case.

Now, consider $B_1=(1,3,3,3,3)$ and $B_2=(2,3,2,2,2)$. Clearly, $B_1⋣B_2$ and $B_2⋣B_1$. On the other hand, the minimal equivalent neighborhood sequence of $B_1$ is $B_m=(1,3,2,2,2,2,2,\cdots )$ contains exactly one value of 1 and exactly one value of 3 and then only 2s. The minimal equivalent neighborhood sequence of $B_2$ is itself. These facts imply that $B_2$ is faster than $B_1$ but not vice versa, i.e., $B_2{\ge }^{*}{B}_1$ and $B_1{\ngeqq }^{*}{B}_2$.

To show the last possibility, let $B_1=(1,2,2)$ and $B_2=(2,1,1)$. One may observe, e.g., on the bottom right of Figure 3 that these two neighborhood sequences are incomparable under the faster relation, i.e., $B_1{\ngeqq }^{*}{B}_2$ and $B_2{\ngeqq }^{*}{B}_1$. □

In the next result, the equivalence relation ∼ is also involved.

Theorem 12.

Let every class $\overline{B}$ be represented by the minimal (maximal) equivalent neighborhood sequence $B_m$ ($B_M$, respectively) of the class. Then, the relation ⊒ provides a proper refinement of ${\ge }^{*}$ defined on the sets of these classes of T, i.e., for any two neighborhood sequences $B_1,B_2$ that are minimal (resp. maximal) equivalent neighborhood sequences of themselves $B_1⊒B_2$ implies that $B_1{\ge }^{*}{B}_2$. However, it may occur that $B_1{\ge }^{*}{B}_2$ holds without $B_1⊒B_2$.

Proof. 

Let $B_1$ and $B_2$ be two neighborhood sequences such that both of them are equivalent to their minimal (maximal, resp.) neighborhood sequences. Assume that $B_1⊒B_2$ holds. Let p and q be any two points of the grid. Then, let $d(p,q;B_2)$ be determined by a short/the shortest $B_2$-path $\mathrm{\Pi }$. Observe that, by the definition of $B_1⊒B_2$, the $B_2$-path $\mathrm{\Pi }$ is also a $B_1$ path from p to q, but then $d(p,q;B_1)\le d(p,q;B_2)$ clearly holds.

It is also clear from the definitions that $B_1⊒B_2$ and $B_2⊒B_1$ if and only if $B_1=B_2$, and then both $B_1{\ge }^{*}{B}_2$ and $B_2{\ge }^{*}{B}_1$ trivially hold.

The refinement is proper, since there are neighborhood sequences $B_1$ and $B_2$, such that $B_1{\ge }^{*}{B}_2$ but $B_1⋣B_2$. Let $B_1=(2,2,2,1)$ and $B_2=(1,1,1,2)$. Notice that each of these sequences defines a singleton equivalence class, therefore $\overline{B_1}=\left\{B_1\right\}$ and $\overline{B_2}=\left\{B_2\right\}$, and thus $B_{1,m}=B_{1,M}=B_1$ and $B_{2,m}=B_{2,M}=B_2$. □

We need to note that the previous proof works for any representatives of the classes. On the other hand, this last result shows also one of the good applicability features of our result, and this will lead us to the next section.

5. Applications

This paper is of theoretical nature; however, in this section, our aim is to briefly show how our results can be applied.

In [35], neighborhood sequences were used in communication networks in various scenarios. The case of periodic neighborhood sequences were studied as special cases, as it is sufficient to attach a period-long part of the neighborhood sequence along the signal. Based on our equivalence relation described in this paper, one may easily find a periodic equivalent neighborhood sequence to the original sequence (if such equivalent exists) even if the original sequence is not a periodic one.

Example 6.

Let $B_1=(1,3,1,1,3,1,1,2,1,1,2,1,1,3,1,\cdots )$ be a neighborhood sequence defined by $b\left(i\right)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}i\equiv 1(mod3);\hfill \\ 3,\hfill & \mathit{if}i=3\left(n^2\right)+2,\mathit{for}n\in {\mathbb{N}}_0;\hfill \\ 2,\hfill & \mathit{if}i\equiv 2(mod3)\mathit{but}i\notin \{3\left(n^2\right)+2|n\in {\mathbb{N}}_0\};\mathit{and}\hfill \\ 1,\hfill & \mathit{if}i\equiv 0(mod3).\hfill \end{array}\right.$It is easy to see that $B_1$ is not periodic. However, one can see that $B_1$ is equivalent to $B_2=(1,3,1)$, and this latter is periodic with period 3, which makes it possible to use the distance function defined by $B_1$ in communication schemes that require periodic neighborhood sequences. The minimal equivalent neighborhood sequence of $B_1$ is not periodic, but $B_2$ is its maximal equivalent neighborhood sequence (which we defined in this paper).

Another possible application can be in the approximation of Euclidean disks on the triangular grid: We recall here the fact that there are digital disks with the same radius that are incomparable under set theoretic inclusion on the triangular grid also yields to advanced types of approximation of the Euclidean disks based on neighborhood sequences that is impossible on the square grid: it uses the intersection of two disks; see, e.g., in [41].

To make such approximations allowed and efficient, one requires two such neighborhood sequences, let us say $B_1$ and $B_2$, that are not in any of the relations that we have studied, i.e., none of the following is true for them: $B_1\sim B_2$, $B_1{\ge }^{*}{B}_2$, $B_2{\ge }^{*}{B}_1$, $B_1⊒B_2$, and $B_2⊒B_1$. If any of these relations were true, then the intersection of the disks after each step will be the same as one of the disks based on one of the neighborhood sequences, and one will not gain anything by using the other neighborhood sequence.

From an application point of view, it is essential to be able to decide if two given neighborhood sequences are in any of the studied relations. Regarding our equivalence relation studied in Section 4.1, one can use Lemma 1 and the fact that equivalent neighborhood sequences have the same minimal equivalent neighborhood sequence.

For the faster relation, the decision is based on the comparisons of formulae of Lemma 2; finally, it is clear to see which neighborhood sequence componentwise dominates another neighborhood sequence by the definition of the relation.

On the other hand, based on our results, we may also able to decide about the faster relation based on Theorem 12: using an arbitrary representative of an equivalent class, it could happen that $B_1⊒B_2$ does not hold, even if it could hold for some of their other representatives. This causes the possibilities listed in Theorem 11. We highlight again the difference between neighborhood sequences on the square and on the triangular grid with the following example: $B_1=(2,3,2,2,2)$ and $B_2=(1,3,3,3,1)$. If there are representatives $B_1^{\prime }\in \overline{B_1}$ and $B_2^{\prime }\in \overline{B_2}$ of these classes for which $B_1^{\prime }⊒B_2^{\prime }$ holds, then it is easy to see that it also holds for their minimal/maximal equivalent neighborhood sequences, and thus $B_1{\ge }^{*}{B}_2$ can be more easily deducted by using these special representatives.

6. Conclusions

We investigated various relations among the neighborhood sequences on a triangular grid with various properties. There are specific equivalence and partial order relations, and we also proved a distributive lattice structure. More precisely, we characterized and described the equivalent neighborhood sequences that define the same distance function and characterized the partial order relation “faster” on the aforementioned equivalence classes.

Further, among other results, we showed that the relation “componentwise dominate” gives a lattice structure to the sets T and $T^{\prime }$ of general and periodic neighborhood sequences. Based on our results, we can say that the structure of the set of neighborhood sequences on the triangular grid is proven to be more interesting than the structure of the set of neighborhood sequences on the square grid. This is based, e.g., on the fact that there are various neighborhood sequences that define the same distance function. Thus, the minimal and the newly investigated maximal equivalent neighborhood sequences play crucial roles not only in the computation of B-distances and in various applications of them but also in the description of various relations among the neighborhood sequences.

Further, by viewing the digital disks (circles) of the same radius, they do not form a well-ordered set on the triangular grid for a fixed radius [34,35,40], and the order that the elements of the neighborhood sequence takes also matters. As we also presented, our results could be applied in communication networks with a honeycomb structure in a similar way as to the examples shown in [35]. Our theoretical results can help to find appropriate neighborhood sequences with some desired properties and relations.

On the one hand, it is a future task to develop further applications in the field of image processing, computer imaging and/or in networking where the appropriate neighborhood sequences are selected based on the algebraic relations that we investigated. On the other hand, in [35], a possible generalization of the faster relation was also defined where some parameters were also added to make theoretical investigations on these relations a possible future work.