Abstract
The current work aims to investigate elasto-thermodiffusive wave propagation in a homogeneous, isotropic, and thermally conducting excited semiconductor medium. The two-temperature theory is utilized in the context of the linear photo-thermoelasticity (PTE) theory of semiconductors. Thermal and elastic memories found in the equations for heat, motion, and charge carrier field are taken into account. The governing equations are applied according to the mass-diffusion transport processes in one dimension (1D), under the influence of optoelectronics with a non-Gaussian laser pulse. Laplace transforms for dimensionless quantities are utilized to obtain the analytical linear solutions for the main quantities during thermoelastic (TD) and electronic (ED) deformation. The numerical approximations solutions of the primary relevant relations are done in the Laplace inverse time domain to observe the exact expressions of the main physical quantities according to some boundary surface conditions. The physical parameters of silicon (Si) semiconductor material are used to obtain the numerical computational results. According to the difference of the thermal memories and two-temperature parameters, the wave propagation of the physical fields is obtained graphically and the results are discussed and analyzed theoretically.
Keywords:
electrons; diffusion; two-temperature theory; elastic waves; thermal memories; semiconductors MSC:
74A15
1. Introduction
Under normal conditions, semiconductor materials are insulators, but when they are exposed to the thermal action of light, their physical characteristics alter. Due to this phenomenon, semiconductors are used and useful as raw materials in numerous modern industries, particularly those related to electronics, clean energy, and electronic circuits. The internal resistance of a semiconductor gradually decreases as temperature rises, allowing current to flow through it. When the electrons become extremely excited, they travel to the surface; this is referred to as the electronic deformation process (ED). Furthermore, the interior particles vibrate and collide as a result of the temperature rise, permitting the appearance of thermoelastic deformation (TE). In this case, it is possible to study semiconductor materials as elastic materials. The so-called photo-thermoelasticity theory can be used to study these materials during the ED and TE deformation processes. The study of the phenomenon of wave propagation through materials such as semiconductors has become very important to the study of the physical changes of these materials, which enables maximizing their use in modern electronic industries, including in sensors and the development of clean energy.
Biot [1] established the concepts of elastic and thermoelastic wave propagation when he introduced the coupled-dynamic (CD) thermoelasticity theory. Moreover, by adding thermal memories into the heat equation and the equation of motion for elastic bodies, Lord and Shulman (LS) [2] and Green and Lindsay (GL) [3] produced novel models of the thermoelasticity theory. In these models, the generalized thermoelastic theory, which resolves all of the paradoxes in the theory of uncoupled thermoelasticity, is linked to the heat equation with the governing equations for elastic materials. Many scientists have recently extended the generalized thermoelastic theory, which has numerous applications [4,5,6]. By examining the interference between electromagnetic, mechanical, and thermal-elastic waves, the effect of the magnetic field on elastic solid objects was also investigated [7,8]. The variable thermal conductivity of the two-dimensional generalized magneto-thermoelastic problem was investigated by Abbas et al. [9,10] using the laser pulse during thermal shock problem. A new concept for elastic materials presented by Chen et al. [11,12,13] was based on thermodynamic temperature and conductive temperature. It was discovered that the distinction between the two temperatures is directly proportional to the heat supply when the locations of the elastic particles are independent of time, but they are identical when heat is not present. In contrast, the two temperatures are generally different for problems that depend on time, especially those that are involved with investigating the propagation of waves, whether a heat source is present or not. In the context of the generalized thermoelasticity theory, Youssef et al. [14,15] presented an innovative model that made use of the two-temperature theory.
New theoretical model considerations that describe the interaction of the elastic, thermal, and charge carrier fields in elastic semiconductors were presented by Maruszewski [16,17]. Recent research [18,19] has examined the thermal diffusivity of semiconductors during heat and mass transfer processes according to the overlap between thermal, elastic, and plasma waves. Modern research on sensitive photoacoustic processes in semiconductor materials uses the photothermal (PT) approach [20]. The PT mechanism, which is utilized to determine semiconductors’ physical properties, is dependent on both TE and ED deformation. A semiconductor medium’s response to a laser beam, electromagnetic radiation, and acoustic waves was investigated [21]. Numerous writers [22,23,24] examined various issues related to elastic semiconductor materials within the framework of the photo-thermoelasticity theory. When thermal conductivity changes during PT transport operations, the absorbed optical energy on the free surface of homogeneous and non-homogenous semiconductor materials is investigated [25,26,27,28,29]. When studying semiconductors in PT theory, the interaction between electrons and holes is disregarded in all of the aforementioned experiments. However, in the absence of a heat source, the impact of two separate temperatures is disregarded. In contrast, Sarkar et al. [30,31,32,33,34,35] analyze semiconducting nonlocal media with memory-dependent derivatives via the two-temperature theory by studying a variety of generalized thermoelasticity theories.
Studying the impact of electron diffusion in the presence of two different temperatures—the thermodynamic temperature and the conductive temperature—is the primary goal of this investigation. During a photo-generated excitation, the homogeneous, isotropic semiconductor medium is employed to study the propagation of elasto-thermodiffusive waves. A brand-new mathematical photo-thermoelasticity model with two temperature dimensions is created. Laplace transforms for the partial differential governing equation is employed analytically under the right circumstances. To obtain the entire solutions of the major quantities (displacement, two temperatures, stress, holes, and carrier density) in this issue, the reversal of the Laplace transform is used in mathematics. Finally, by presenting the results of the physical field quantities graphically, analytical verification can be made. Thermal memory of silicon media is explored, as well as the effects of the two-temperature parameters. The numerical results have been presented graphically.
2. Basic Equations
Consider an elastic n-type semiconductor rod that is extrinsic, homogenous, isotropic, thermally conducting, and initially at a reference temperature when . In 1D deformation, the Cartesian coordinate is used. In this case, all field quantities are independent of the and coordinates. The non-dimensional governing field equations for temperature change , the conductive temperature , displacement and carrier density (electron diffusion field) in the linear theory of thermoelasticity for semiconductors depend on the time t and the -axis (semiconductor rod). In the absence of body forces, electro-magnetic pressure, and heat sources, the main equations for when the charge carrier mass is ignored according to the two-temperature theory under the non-Gaussian laser pulses effect can be obtained as in [9]:
The following pattern includes the temporal period of a laser pulse, which can be seen in Figure 1.
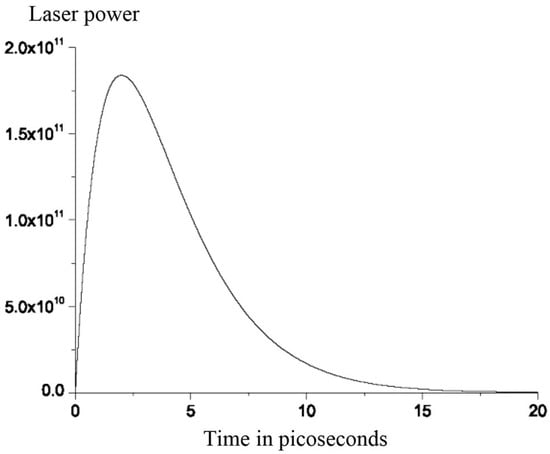
Figure 1.
Temporal profile of the laser pulse.
According to the two-temperature theory, the relation between and can be written in the following form [11,12]:
The other notations correspond as: , , , .
According to [28], the constitutive equation for the effects of the electron carrier field in 1D is as follows:
For more simplicity, the following dimensionless quantities can be used to transform the main equations as shown in [29]:
The main equations can be expressed in the following manner, even if the primes are ignored for convenience:
where
The quantity in Equation (7) can be referred to as the coupling thermoelastic parameter. For this issue, the following initial conditions that can be represented as follows should be considered:
3. The Mathematical Solutions
Using the given initial conditions, the Laplace transform is used in the time-space domain to convert the partial differential equations to ordinary differential equations (ODE). The function according to Laplace transform can be created as follows:
The Laplace transform Equation (12) can be used to derive the following equations:
where , , , ,
By applying the method of elimination between the quantities and in the previous equations, we obtain the following differential equation:
where
By presenting the characteristic equation of the differential equation in the following form:
Since the roots of the characteristic equation are , which is chosen as real (when ).
The following is a representation of the general linear solutions of Equation (18) for thermodynamic temperature:
where .
On the other hand, the mathematical methodology can be used to represent the linear solutions of the other significant physical quantities:
where and are parameters dependent on , which can be determinate from the surface conditions, and the other coefficients can be represented as: , , , .
4. Boundary Conditions
When the values of the unknown parameters are determined, full solutions to the significant physical fields can be achieved. Accordingly, some thermal changes and mechanical strains are applied at the medium’s boundary during plasma (carrier density, electronic diffusion, electron concentration) recombination processes.
- (I)
- When , the thermally gradient temperature can be used to depict the pulsating heat flow boundary condition in the following ways:
When applied to a thermal condition load at the time of pulse heat flux with the constant , the Laplace transforms yield:
- (II)
- When using the Laplace transform, the load force is considered to be a mechanical condition at the boundary and can be stated as follows:
- (III)
- Recombination processes occur during electron excitation and transport activities as a result of the thermal effect of the light surface temperature at . In this case, the carrier density diffusive is used to derive the plasma condition under the Laplace transform, which is represented as follows:
- (IV)
- The displacement distribution’s final condition can be stated as:
The function refers to the Heaviside unit step function and represents an arbitrary parameter.
5. Inversion of Laplace Transform
When the converse of the Laplace transform is used, the complete solutions in 1D for the main dimensionless physical fields in the time domain can be found. Laplace transformations are inverted using a numerical approach and the Riemann-sum approximation method. This is how the function can be reversed in the Laplace time domain:
In this case, (). In , the Fourier series is utilized to expand the function to get the following form:
where and represents the real part. For convergence, is chosen freely when [12].
6. Validation
6.1. The Thermoelasticity with Two-Temperature Models
When the carrier density is omitted, the thermoelasticity models can be produced (i.e., ). The main Equations (1)–(4) in this instance are simplified to the generalized two-temperature thermoelasticity theory in one dimension, as shown in [7,8]:
The thermal memories are: , the dual phase lag (DPL) can be obtained. On the other hand, the Lord and Șhulman (LS) model is observed when and . However, the coupled thermos-elasticity (CT) theory is produced at .
6.2. The Influence of the Two-Temperature Parameter
The set of equations expresses the case of the generalized photo-thermoelasticity theory when taking into account the interaction between elastic, thermal, and electronic waves when the thermodynamic temperature and the conductive temperature are equal. The heat equation and the system of four primary equations can be rewritten as follows [36]:
To determine the one-temperature solution in this situation, the above two equations can be solved.
6.3. The Non-Gaussian Laser Pulses Impact
The previous fundamental equations illustrate the impact of the non-Gaussian laser pulses. However, the model under consideration changes into a model of the photo-thermoelasticity theory under the influence of two-temperature theory when the power intensity of the effect of the laser pulses is ignored (i.e., ) [37,38,39,40].
7. Numerical Results and Discussions
To confirm the validity of the derived theoretical and analytical results, and to contrast them with earlier findings. The propagation of waves in important physical fields is simulated numerically. It is possible to graphically depict the elastic wave (displacement), plasma wave (electron diffusion), mechanical wave (stress), and thermal wave (temperature and conductive) that are produced for a small amount of time. The Matlab (2022a) program is used to graph the distribution of the principal waves while taking into account the input parameters in the SI unit of the semiconductor silicon (Si) materials. Table 1 lists the physical constants of Si as follows [41,42]:

Table 1.
The SI units of the physical constants of Si material.
7.1. The Photo-Thermoelasticity Models
Figure 2a–d shows the change in the distribution of basic physical quantities under the influence of different relaxation times according to models based on the theory of photo-thermoelasticity with increasing distance in the semiconductor medium. In this group, the numerical calculations of the real dimensional quantities are done when taking a very small time under the influence of laser pulses when in the presence of the two-temperature theory (). As can be seen from the diagram, the solid line represents the theory of coupled thermoelasticity (CT when ), the dotted line represents the Lord and Shulman (LS, and ) model, and the dual phase lag (DPL, ) model is represented by the dashed line. Figure 2a represents the distribution of the thermal wave, which is represented by the temperature distribution, where the distribution starts from the positive value on the surface, fulfilling the boundary condition [43]. As a direct result of the laser pulse effect, the thermal wave distribution increases near the surface to reach the maximum value and then gradually decreases, taking the form of an exponential function. In the end, the distribution converges with the zero line to reach the state of equilibrium by going deeper into the surface, where the effect of the laser pulses decreases. These results are in agreement with what has been observed through practical experiments [44,45]. Figure 2b shows the change in the elastic wave that is represented using the displacement distribution with increasing distance. The distribution starts at the surface from the zero value, fulfilling the boundary condition, decreasing sharply down to the absolute minimum value near the edge. Then the distribution increases suddenly in a less severe way to reach the maximum value before decreasing and increasing again periodically until the state of equilibrium inside the semiconductor medium. This apparent disturbance in the elastic wave distribution is due to the increased collisions between the inner particles as a direct result of the thermal effect of the laser pulses. Figure 2c shows the change in the mechanical wave, which is represented using the normal stress distribution () with increasing distance. The distribution begins because of the mechanical load applied at the surface from the positive value, fulfilling the boundary condition, so that the distribution decreases smoothly until the minimum value in the first range near the edge. Then the distribution increases smoothly, as well, taking a curve in the form of a wave distribution and reaching the state of equilibrium inside the semiconductor medium. This apparent behavior in the mechanical wave distribution is due to the effect of the mechanical load used, as well as the thermal effect of the laser pulses. Figure 2d shows the distribution of plasma waves that are represented by the diffusive of electrons or carrier density with increasing distance. This distribution starts from the positive value at the surface, fulfilling the boundary condition during the recombination processes, where the diffusive of electrons begins to increase on the surface as a result of the increasing temperature rise from the effect of laser pulses, until they reach the maximum value. In the case of moving away from the surface, the distribution begins to decrease gradually, taking the form of an exponential function, until it reaches the state of equilibrium by the zero line inside the semiconductor medium, which is consistent with the experimental results [44,45].
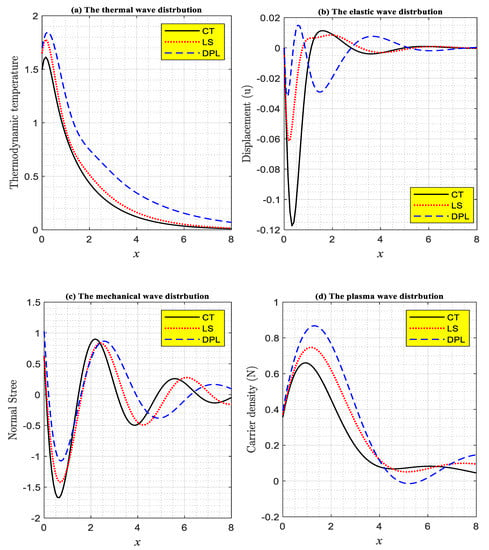
Figure 2.
According to the two-temperature theory, the primary field distributions change with horizontal distance at various thermal memory (thermal relaxation durations) under the impact of laser pulses.
7.2. The Laser Pulses Effect
Figure 3a–d illustrates how the principal fields in this phenomenon vary depending on the various values of the laser pulses based on the power intensity against a horizontal distance . According to the DPL model, the numerical simulation is conducted during thermoelastic and electronic deformations over a small amount of time under the effect of the two-temperature theory. This category includes two examples, the first of which is the disappearance of the laser pulse effect. The other example is subject to the effect of the laser pulses, where it appears to be clear that the thermal effect of laser pulses changes the behavior of wave propagation in a visible way, which is what prompted us to study the effect of laser pulses with this model of equations.
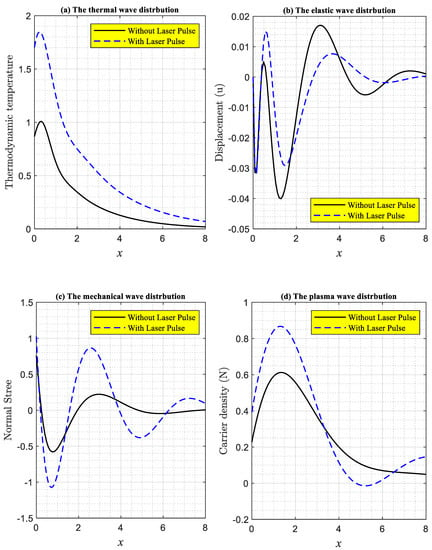
Figure 3.
According to the DPL model, the main field distributions in two temperature fields under the impact of laser pulses and without them change with horizontal distance.
7.3. The Effect of the Two-Temperature Parameter
According to the various values of the two-temperature parameter measured against the horizontal distance, the third group (Figure 4a–d) depicts the fluctuations of the main fields in this occurrence. According to the DPL model, a numerical simulation is conducted during electronic diffusion caused by laser pulses for a small time. This category includes two examples, the first of which is the disappearance of the two-temperature parameter. The one-temperature example is represented in this case by the equality of the thermodynamic and conductive temperatures . The photo-thermoelasticity theory is investigated in the one-temperature example [38]. On the other hand, wave propagations have different behavior in all distributions. The magnitude of all field distributions from this category is significantly influenced by the two-temperature parameter. In two instances of two-temperature parameters, the physical fields meet the boundary criteria at the surface.
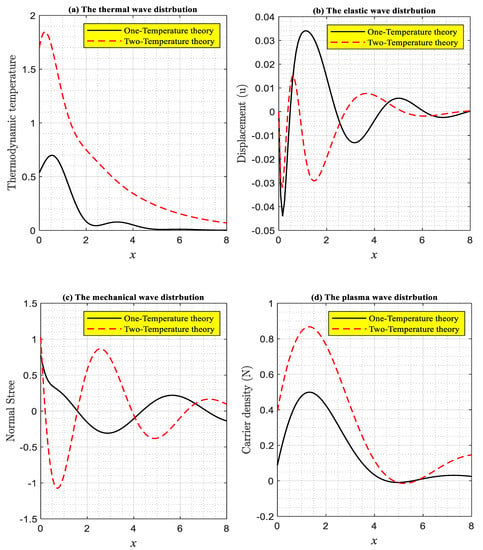
Figure 4.
The main field distributions in distinct two-temperature cases under the influence of laser pulses vary with horizontal distance in accordance with the DPL model.
8. Conclusions
In this work, we have introduced the influence of thermal memories and mechanical loading on the characteristics of generalized photo-thermoelasticity in an n-type silicon semiconductor under the impact of laser pulses. When the material is photoexcited during an elasto-thermodiffusive process, the overlap between thermo-elastic-mechanical-plasma waves is explored. When used in the framework of the two-temperature theory, the innovative model is investigated in 1D during electronic diffusion. According to thermal relaxation times, the disparity between the photo-thermoelasticity theories is taken into account. All of the main physical distribution wave propagations are significantly impacted by the action of thermal memories. However, the strength of the laser pulses and the two-temperature parameter also has a significant effect on all wave propagations. The creation of elastic waves as a result of a material’s transient thermal heating is quickly developing into a powerful method for characterizing the material’s impact on its microstructure as a semiconductor. Due to the widespread use of semiconductors in the production of electronics and medical equipment, the fact that these waves propagate at speeds of only a few kilometers per second is notable. Interest in studying the properties of semiconductors leads to improving their properties to maximize their use in the future. The model used in this study can be developed to study changes in thermal conductivity, as well as other physical constants that change when laser beams fall on semiconductors. Furthermore, the energy of these waves being concentrated near the upper portion of the device’s surface, and the direct possibility of generation, detection, and control that is used in the photovoltaic cell, make this type of problem important to study.
Author Contributions
Conceptualization, K.L.; methodology, K.L.; software, H.M.A.: validation, investigation; data curation, K.L.; writing—original draft preparation, H.M.A.: visualization, K.L.; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia has funded this project, under grant no. (FP-166-43).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request. The information applied in this research is ready from the authors at request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Elastic Lame’s parameters (). | |
| Deformation potential difference between conduction and valence band (). | |
| The electronic deformation coefficient ED () | |
| Reference temperature in its natural state () | |
| Volume thermal expansion (). | |
| Stress tensor () | |
| The density of the sample () | |
| Linear thermal expansion () | |
| Equilibrium carrier concentration | |
| Specific heat at constant strain () | |
| Thermal conductivity of the semiconductor medium () | |
| The electrons relaxation time () | |
| The lifetime of photogenerated carriers () | |
| Energy gap () | |
| Components of the strain tensor | |
| Peltier-Seebeck- Dufour-Soret-like constants | |
| The flux-like constants | |
| Thermal and elastic relaxation times () | |
| The positive two-temperature parameter | |
| The power intensity of the laser | |
| The optical absorption coefficient | |
| The pulse parameter | |
| Recombination velocities () |
References
- Biot, M. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solid. 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.; Lindsay, K. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Thermoelasticity with second sound: A review. Appl. Mech. Rev. 1986, 39, 355–376. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Hyperbolic Thermoelasticity: A review of recent literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Sharma, J.N.; Kumar, V.; Dayal, C. Reflection of generalized thermoelastic waves from the boundary of a half-space. J. Therm. Stress. 2003, 26, 925–942. [Google Scholar] [CrossRef]
- Lotfy, K.; Abo-Dahab, S. Two-dimensional problem of two temperature generalized thermoelasticity with normal mode analysis under thermal shock problem. J. Comput. Theor. Nanosci. 2015, 12, 1709–1719. [Google Scholar] [CrossRef]
- Othman, M.; Lotfy, K. The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation. J. Comp. Theor. Nanosci. 2015, 12, 2587–2600. [Google Scholar] [CrossRef]
- Abbas, I.; Marin, M. Analytical solutions of a two-dimensional generalized thermoelastic diffusions problem due to laser pulse. Iran J. Sci. Technol. Trans. Mech. Eng. 2018, 42, 57–71. [Google Scholar] [CrossRef]
- Abo-Dahab, S.; Abbas, I. LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Appl. Math. Model. 2011, 35, 3759–3768. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. A note on non-simple heat conduction. J. Appl. Math. Phys. (ZAMP) 1968, 19, 969–970. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. On the thermodynamics of non-simple elastic materials with two temperatures. J. Appl. Math. Phys. (ZAMP) 1969, 20, 107–112. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Tham, C.L. Ultrafast thermoelasticity for short-pulse laser heating. Int. J. Eng. Sci. 2004, 42, 793–807. [Google Scholar] [CrossRef]
- Youssef, H. Theory of two-temperature-generalized thermoelasticity. IMA J. Appl. Math. 2006, 71, 383–390. [Google Scholar] [CrossRef]
- Youssef, H.; Al-Lehaibi, E. State-space approach of two-temperature generalized thermoelasticity of one-dimensional problem. Int. J. Solids Struct. 2007, 44, 1550–1562. [Google Scholar] [CrossRef]
- Maruszewski, B. Electro-magneto-thermo-elasticity of Extrinsic Semiconductors, Classical Irreversible Thermodynamic Approach. Arch. Mech. 1986, 38, 71–82. [Google Scholar]
- Maruszewski, B. Electro-magneto-thermo-elasticity of Extrinsic Semiconductors, Extended Irreversible Thermodynamic Approach. Arch. Mech. 1986, 38, 83–95. [Google Scholar]
- Sharma, J.; Nath, J.; Naveen, T. Plane harmonic elasto-thermodiffusive waves in semiconductor materials. J. Mech. Mater. Struct. 2006, 1, 813–835. [Google Scholar] [CrossRef]
- Mandelis, A. Photoacoustic and Thermal Wave Phenomena in Semiconductors; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Almond, D.; Patel, P. Photothermal Science and Techniques; Springer Science & Business Media: Berlin, Germany, 1996. [Google Scholar]
- Gordon, J.P.; Leite, R.C.C.; Moore, R.S.; Porto, S.P.S.; Whinnery, J.R. Long-transient effects in lasers with inserted liquid samples. Bull. Am. Phys. Soc. 1964, 119, 501–510. [Google Scholar] [CrossRef]
- Lotfy, K. Effect of Variable Thermal Conductivity during the Photothermal Diffusion Process of Semiconductor Medium. Silicon 2019, 11, 1863–1873. [Google Scholar] [CrossRef]
- Lotfy, K. A novel model of magneto photothermal diffusion (MPD) on polymer nano-composite semiconductor with initial stress. Waves Ran. Comp. Med. 2021, 31, 83–100. [Google Scholar] [CrossRef]
- Hobinya, A.; Abbas, I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys. 2019, 15, 102588. [Google Scholar] [CrossRef]
- Abbas, I.; Alzahrani, F.; Elaiw, A. A DPL model of photothermal interaction in a semiconductor material. Waves Rand. Comp. Media 2019, 29, 328–343. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I. Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model. Mathematics 2020, 8, 585. [Google Scholar] [CrossRef]
- Song, Y.Q.; Todorovic, D.M.; Cretin, B.; Vairac, P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 2010, 47, 1871. [Google Scholar] [CrossRef]
- Yadav, A. Photothermal plasma wave in the theory of two-temperature with multi-phase-lag thermo-elasticity in the presence of magnetic field in a semiconductor with diffusion. Waves Random Complex Media 2022, 32, 2416–2444. [Google Scholar] [CrossRef]
- Tam, A.C. Ultrasensitive Laser Spectroscopy; Academic Press: New York, NY, USA, 1983; 108p. [Google Scholar]
- Sarkar, N.; Mondal, S. Transient responses in a two-temperature thermoelastic infinite medium having cylindrical cavity due to moving heat source with memory-dependent derivative. Z. Angew. Math. Mech. 2019, 99, e201800343. [Google Scholar] [CrossRef]
- Lotfy, K.; Sarkar, N. Memory-dependent derivatives for photothermal semiconducting medium in generalized thermoelasticity with two-temperature. Mech Time-Depend Mater. 2017, 21, 519–534. [Google Scholar] [CrossRef]
- Sarkar, N.; Mondal, S.; Othman, M. L–S theory for the propagation of the photo-thermal waves in a semiconducting nonlocal elastic medium. Waves Random Complex Media 2022, 32, 2622–2635. [Google Scholar] [CrossRef]
- Sarkar, N.; Ghosh, D.; Lahiri, A. A two-dimensional magneto-thermoelastic problem based on a new two-temperature generalized thermoelasticity model with memory-dependent derivative. Mech. Adv. Mater. Struct. 2019, 26, 957–966. [Google Scholar] [CrossRef]
- Sarkar, N. Wave propagation in an initially stressed elastic half-space solids under time-fractional order two-temperature magneto-thermoelasticity. Eur. Phys. J. Plus. 2017, 132, 154. [Google Scholar] [CrossRef]
- Marin, M.; Lupu, M. On harmonic vibrations in thermoelasticity of micropolar bodies. J. Vibrat. Control 1998, 4, 507–518. [Google Scholar] [CrossRef]
- Marin, M.; Stan, G. Weak solutions in Elasticity of dipolar bodies with stretch. Carpath. J. Math. 2013, 29, 33–40. [Google Scholar] [CrossRef]
- Marin, M. Harmonic Vibrations in Thermoelasticity of Microstretch Materials. J. Vib. Acoust. Trans. ASME 2010, 132, 044501. [Google Scholar] [CrossRef]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381. [Google Scholar] [CrossRef]
- Lotfy, K. A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci. Rep. 2019, 9, 3319. [Google Scholar] [CrossRef]
- Ismail, G.M.; Lotfy, K.; El-Bary, A. Response of thermo-mechanical waves of an excited microelongated semiconductor layer according to photothermal transport processes. Eur. J. Mech. —A/Solids 2022, 96, 104714. [Google Scholar] [CrossRef]
- Mondal, S.; Sur, A. Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves Ran. Comp. Med. 2021, 31, 1835–1858. [Google Scholar]
- Aldwoah, K.; Lotfy, K.; Mhemdi, A.; El-Bary, A. A novel magneto-photo-elasto-thermodiffusion electrons-holes model of excited semiconductor. Case Stud. Therm. Eng. 2022, 32, 101877. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459–468. [Google Scholar] [CrossRef]
- Xiao, Y.; Shen, C.; Zhang, W.B. Screening and prediction of metal-doped α-borophene monolayer for nitric oxide elimination. Mater. Today Chem. 2022, 25, 100958. [Google Scholar] [CrossRef]
- Liu, J.; Han, M.; Wang, R.; Xu, S.; Wang, X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 2022, 131, 065107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).