Orthogonal Learning Rosenbrock’s Direct Rotation with the Gazelle Optimization Algorithm for Global Optimization

Abstract

An efficient optimization method is needed to address complicated problems and find optimal solutions. The gazelle optimization algorithm (GOA) is a global stochastic optimizer that is straightforward to comprehend and has powerful search capabilities. Nevertheless, the GOA is unsuitable for addressing multimodal, hybrid functions, and data mining problems. Therefore, the current paper proposes the orthogonal learning (OL) method with Rosenbrock’s direct rotation strategy to improve the GOA and sustain the solution variety (IGOA). We performed comprehensive experiments based on various functions, including 23 classical and IEEE CEC2017 problems. Moreover, eight data clustering problems taken from the UCI repository were tested to verify the proposed method’s performance further. The IGOA was compared with several other proposed meta-heuristic algorithms. Moreover, the Wilcoxon signed-rank test further assessed the experimental results to conduct more systematic data analyses. The IGOA surpassed other comparative optimizers in terms of convergence speed and precision. The empirical results show that the proposed IGOA achieved better outcomes than the basic GOA and other state-of-the-art methods and performed better in terms of solution quality.

1. Introduction

In recent years, numerous disciplines, including data science, systems engineering, mathematical optimization, and their applications, have focused on real-world optimization challenges [1,2]. Traditional and meta-heuristic methods are the two main approaches for handling these issues. Newton and gradient descent are two simple examples of the first category of techniques [3]. The time-consuming nature of these procedures is, however, a disadvantage. Additionally, there is only one solution for each run. The effectiveness of these methods depends on the issues being addressed, as well as the restrictions, objective functions, search methods, and variables [4,5].

Numerous optimization techniques have been created, and optimization issues are frequently encountered in engineering and scientific study disciplines [6]. The search space generation and local optimal stagnation are two fundamental problems with current optimization paradigms [7]. Consequently, stochastic optimization techniques have received much attention in recent years. Because stochastic optimization methods merely modify the inputs, monitor the outputs of a given system for objective outcomes, and consider the optimization problem a “black box”, they can skip deriving the computational formula [8]. Additionally, stochastic optimization techniques can randomly complete optimization problems, giving them an inherent advantage over traditional optimization algorithms in their capacity for optimal local avoidance [9]. Stochastic optimization algorithms can be categorized into population-based and individual-based techniques depending on how many solutions are produced at each iteration of the entire process. Population-based methods have many random solutions and promote them throughout the optimization procedure [10,11]. In contrast, individual-based methods only produce one candidate solution at a time.

Nature-inspired stochastic techniques have received much interest recently [12,13,14]. Such optimization frequently imitates the social or individual behavior of a population of animals or other natural occurrences. Such algorithms begin the optimization process by generating several random solutions, which they then enhance as potential answers to a specific issue [15]. Stochastic optimization algorithms are used in various sectors because they outperform mathematical optimization methods. Despite the enormous number of suggested ways in the optimization area, it is crucial to understand why we require different optimization techniques. The no free lunch (NFL) theorem can be used to justify this problem [16]. It logically supports the idea that one method cannot provide an efficient solution for resolving any optimization issue. In other words, it cannot be guaranteed that an algorithm’s success in addressing a specific set of issues would enable it to solve all optimization problems of all types and natures. This theorem allows researchers to suggest brand-new optimization strategies or enhance the existing algorithms to solve various issues.

As mentioned above, hard optimization problems need powerful search methods to find the optimal solutions for different problems. Thus, the basic method faces several problems during the search process, which are premature convergence, a lack of balance between the search methods, and low convergence behavior. The gazelle optimization algorithm (GOA) is a global stochastic optimizer that is straightforward and has a powerful search capability. Nevertheless, the GOA requires a deep investigation to improve its search abilities and address various multimodal–hybrid functions and data mining problems efficiently. Therefore, this paper proposes a new hybrid method, called (IGOA), based on using the orthogonal learning (OL) method with Rosenbrock’s direct rotational strategy. This modification aims to improve the basic GOA performance and sustain solution varieties. We performed comprehensive experiments based on various functions, including 23 classical and IEEE CEC2017 problems. Moreover, eight data clustering problems taken from the UCI repository were tested to further verify the proposed method’s performance. The IGOA was compared with several other proposed meta-heuristic algorithms. Moreover, the Wilcoxon signed-rank test further assessed the experimental results to conduct more systematic data analyses. The IGOA surpassed other comparative optimizers in terms of convergence speed and precision. The empirical results show that the proposed IGOA achieved better results compared to the basic GOA and other state-of-the-art methods, and it obtained higher performance in terms of solution quality.

The remainder of this paper is structured as follows. In Section 2, the related works are presented. Section 3 presents the main procedure of the used original GOA. Section 4 presents the proposed IGOA method. Section 5 presents the experiments and the obtained results by the comparative methods. The results are presented in Section 6. Finally, the conclusion and potential future research directions are presented in Section 7.

2. Related Works

In this section, the related search methods that were used to solve various problems with their modifications are presented.

A popular technique inspired by nature, called moth–flame optimization (MFO), is straightforward. However, MFO may struggle with convergence or tend to slip into local optima for some complicated optimization tasks, particularly high-dimensional and multimodal issues. The integration of MFO with the Gaussian mutation (GM), the Cauchy mutation (CM), the Lévy mutation (LM), or the combination of GM, CM, and LM, is presented in [17] to address these constraints. To specifically enhance neighborhood-informed capabilities, GM is added to the fundamental MFO. On an extensive collection of 23 benchmark issues and 30 CEC2017 benchmark tasks, the most acceptable variation of MFO was evaluated to 15 cutting-edge methods and 4 well-known sophisticated optimization techniques. The extensive experiments show that there are three ways to considerably increase the basic MFO exploration and exploitation capabilities.

To direct the swarm, further enhance the balance between the integrated exploratory and neighborhood-informed capacities of the traditional process, and explore the core (in an attempt to search the abilities of the whale optimization algorithm (WOA) in dealing with optimal control tasks), two novel and appropriate strategies (made up of Lévy flight and chaotic local search) are instantaneously presented into the WOA [18]. Unimodal, multimodal, and fixed-dimension multimodal problems are in the benchmark tasks. The study and practical findings show that the suggested method can surpass its rivals in terms of convergence speed and rate. The proposed approach may be a powerful and valuable supplemental tool for more complicated optimization problems.

Implementing effective software products is becoming increasingly difficult due to the high-performance computing (HPC) industry’s rapidly changing hardware environment and growing specialization. Software abstraction is one approach to overcoming these difficulties. A parallel algorithm paradigm is proposed that enables both optimum mappings to be various and complex architectures with global control of their synchronization and parallelization [19]. The model that is provided distinguishes between an algorithm’s structure and its functional execution. It preserves them in an abstract pattern tree. It uses a hierarchical breakdown of parallel process models while building blocks for computational frameworks (APT). Based on the APT, a data-centric flow graph is created that serves as an intermediary description for complex and automatic structural changes. Three example algorithms are used to illustrate the usability of this paradigm, which results in runtime speedups between 1.83 and 2.45 on a typical mixed CPU/GPU system.

One of the recently developed algorithms, the salp swarm algorithm (SSA), is based on the simulated behavior of salps. However, it faces local optima stagnation and slow convergence (similar to most meta-heuristic methods). These issues were recently satisfactorily resolved using chaos theory. A brand-new hybrid approach built on SSA and the chaos theory was put forth in this work [20]. A total of 20 benchmark datasets and 14 benchmark unimodal and multimodal optimization tasks were used to test the proposed chaotic salp swarm algorithm (CSSA). Ten distinct chaotic maps were used to increase the convergence rate and ensuing precision. The suggested CSSA is an algorithm with promise, according to the simulation findings. The outcomes also demonstrate CSSA’s capacity to identify an ideal feature subset that maximizes classification performance while using the fewest possible features. Additionally, the results show that the chaotic logistic map is the best of the ten maps utilized and may significantly improve the effectiveness of the original SSA.

The sine–cosine algorithm, newly created to handle global optimization issues, is based on the properties of the sine and cosine trigonometric functions. The sine–cosine technique is modified in this study [21], improving the solution’s ability to be exploited while lowering the diversity overflow in traditional SCA search equations. ISCA is the suggested algorithm’s name. Its standout feature is the presented algorithm’s fusion of crossover skills with individual optimal states of unique solutions and a combination of self-learning and global search methods. A traditional collection of common benchmark issues, the IEEE CEC2014 benchmark test, and a more recent group of benchmark functions, the IEEE CEC2017 benchmark exam, have been used to assess these skills in ISCA. ISCA has used several performance criteria to guarantee the robustness and effectiveness of the method. In the study, five well-known engineering optimization problems were also solved using the suggested technique, ISCA. The proposed approach is also employed for multilayer thresholding in picture segmentation toward the study’s conclusion.

The WOA, a novel and competitive population-based optimization technique, beats specific previous biologically inspired algorithms in terms of ease of use and effectiveness [22]. However, for massive global optimization (LSGO) issues, WOA will become entangled in local optima and lose accuracy. To solve LSGO difficulties, a modified version of the whale optimization algorithm (MWOA) is suggested. A nonlinear dynamic method based on a differential operator is provided to update the controller parameters to equilibrium regarding the exploration and exploitation capacities. The algorithm is forced to leave local optima by employing a Lévy flight technique. Additionally, the population’s leader is subjected to a quadratic extrapolation approach, which increases the precision of the solution and the effectiveness of local exploitation. A total of 25 well-known benchmark problems varying from 100 to 1000 were used to evaluate MWOA. The experimental findings show that MWOA on LSGO perform better than other cutting-edge optimization methods in terms of solution correctness, fast convergence, and reliability.

3. Gazelle Optimization Algorithm: Procedure and Presentation

This section introduces the gazelle optimization algorithm (GOA) and formulates the suggested procedures for optimization.

The family of the genus Gazella includes the gazelles. The drylands throughout most of Asia, including China, the Arabian Peninsula, and a portion of the Sahara Desert in northern Africa, are home to gazelles. Additionally, they may be found in eastern Africa and the sub-Saharan Sahel, which stretches from Tanzania to the Horn of Africa. The majority of predators frequently hunt on gazelles. There are about 19 different species of gazelles, ranging in size from the little Thomson’s and Speke’s gazelle to the enormous Dama gazelle. The gazelle’s hearing, sight, and smell are keen, and they move quickly. These evolutionary traits enable them to flee from predators, making up for their chronic weaknesses. In nature, gazelles and their peculiar characteristics may be seen [23].

3.1. Initialization

The GOA is a population-based optimization technique that employs gazelles (X) with randomly initialized search parameters. According to Equation (1), the search agents are represented by an n-by-d matrix of the potential solution. The GOA leverages the issue’s upper bound (UB) and lower limit (LB) constraints to determine the possible values for the population matrix stochastically.

$$X=\left[\begin{array}{cccccc}{X}_{1,1}& X_{1,2}& \cdots & X_{1,j}& X_{1,1-d}& X_{1,d}\\ X_{2,1}& X_{2,2}& \cdots & X_{2,j}& X_{2,1-d}& X_{2,d}\\ \cdots & \cdots & \cdots & ⋮& \cdots & \cdots \\ ⋮& \cdots & \cdots & X_{i,j}& ⋮& \cdots \\ X_{n-1,1}& X_{n-1,2}& \cdots & X_{n-1,j}& \cdots & X_{n-1,d}\\ X_{n,1}& X_{n,2}& \cdots & \cdots & X_{n,d-1}& X_{n,d}\end{array}\right]$$

(1)

where X is the matrix of the solution locations, each location is stochastically yielded by Equation (2), $X_{i,j}$ is the jth randomly induced location of the ith solution, n denotes the number of gazelles, and d is the specified search space.

$$X_{i,j}=rand\ast (U{B}_j-L{B}_j)+L{B}_j$$

(2)

Each iteration has a candidate location for each $X_{i,j}$, where $rand$ is a random numeral, $U{B}_j$−$L{B}_j$ are the upper and lower bounds of the specified search space, respectively. The best-obtained solution is appointed as a top gazelle to create an elite matrix (n × d) as given in Equation (3). This matrix is employed to explore and discover the gazelle’s next iteration.

$$Elite=\left[\begin{array}{cccccc}{X}_{1,1}^{\prime }& X_{1,2}^{\prime }& \cdots & X_{1,j}^{\prime }& X_{1,1-d}^{\prime }& X_{1,d}^{\prime }\\ X_{2,1}^{\prime }& X_{2,2}^{\prime }& \cdots & X_{2,j}^{\prime }& X_{2,1-d}^{\prime }& X_{2,d}^{\prime }\\ \cdots & \cdots & \cdots & ⋮& \cdots & \cdots \\ ⋮& \cdots & \cdots & X_{i,j}^{\prime }& ⋮& \cdots \\ X_{n-1,1}^{\prime }& X_{n-1,2}^{\prime }& \cdots & X_{n-1,j}^{\prime }& \cdots & X_{n-1,d}^{\prime }\\ X_{n,1}^{\prime }& X_{n,2}^{\prime }& \cdots & \cdots & X_{n,d-1}^{\prime }& X_{n,d}^{\prime }\end{array}\right]$$

(3)

where $X_{i,j}^{\prime }$ denotes the locations of the top gazelle. The predator and gazelles are indeed regarded as search agents by the GOA. Since the gazelles are already running in unison for refuge by the time a predator is observed stalking them, the predator would have already searched the area when the gazelles flee. If the superior gazelle replaces the top gazelle, the elite will change after each iteration.

3.2. The Brownian Motion

A seemingly random movement when the displacement conforms to a standard (Gaussian) probability distribution function with a median and variance of $\mu$ = 0 and ${\sigma }^2$ = 1, respectively. Equation (4) defines the normal Brownian motion at location M [23].

$$f_B(x;\mu ,\sigma )=\frac{1}{\sqrt{2\mu {\sigma }^2}}exp\left(-\frac{{(x-\mu )}^2}{2{\sigma }^2}\right)=\frac{1}{\sqrt{2\mu }}exp\left(-\frac{x^2}{2}\right)$$

(4)

3.3. The Lévy Flight

The Lévy distribution from Equation (5) is used by the Lévy flight to conduct a random walk [24].

$$L\left(X_j\right)={\left|X_j\right|}^{1-\alpha }$$

(5)

where $X_j$ indicates the flight space, and $\alpha$ = (1, 2) indicates the power law exponent. Equation (6) indicates the Lévy regular operation [25].

$$f_L(x;\alpha ,\nu )=\frac{1}{n}{\int }_{\infty }^{0}exp(-\nu q^{\alpha })cos\left(qx\right)\delta q$$

(6)

This work utilized an algorithm that yields a stable Lévy motion. The algorithm employed within the range of 0.3–1.99, represented in Equation (7), where $\alpha$ is the distribution index that handles the motion processes, and $\nu$ denotes the scale unit.

$$Levy\left(\alpha \right)=0.05\ast \frac{x}{{\left|y\right|}^{\frac{1}{\alpha }}}$$

(7)

where $\alpha$, x, and y are described as follows:

$$x=Normal(0,{\sigma }_x^2)$$

(8)

$$y=Normal(0,{\sigma }_x^2)$$

(9)

$${\sigma }_x=\left[\frac{\mathsf{\Gamma }(1-\alpha )sin\left(\frac{\pi \alpha }{2}\right)}{\mathsf{\Gamma }(\frac{1+\alpha }{2})\alpha 2^{\frac{\alpha -1}{2}}}\right]$$

(10)

where ${\sigma }_y$ = 1 and $\alpha$ = 1.5.

3.4. Modeling the Basic GOA

The developed GOA algorithm mimics the way that gazelles survive. The optimization process entails grazing without a predator and fleeing to a refuge when one is seen. As a result, there are two steps to the described GOA algorithm optimization procedure [23].

3.4.1. Exploitation

In this stage, it is assumed that there is no predator present or that the predator is only stalking the gazelles while they calmly graze. During this phase, neighborhood regions of the domain are efficiently covered using the Brownian motion, characterized by uniform and controlled steps. As shown in Figure 1, it is expected that the gazelles walk in a Brownian motion during grazing.

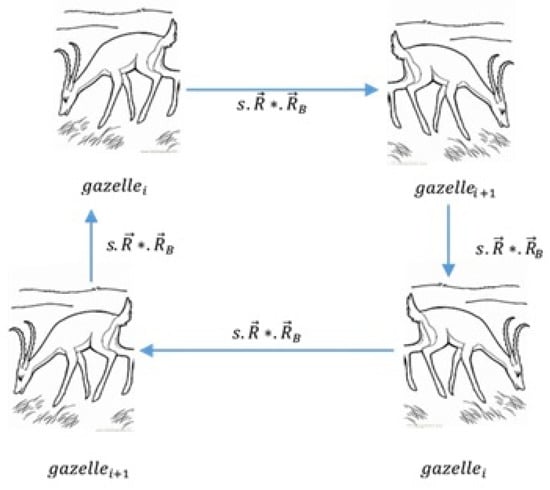
Figure 1. The gazelle’s grazing pattern denotes exploitation.

Equation (11) illustrates the mathematical formula of this phenomenon.

$$gazell{e}_{i+1}=gazell{e}_i+s.R\ast R_B\ast (Elite-R_B\ast gazell{e}_i)$$

(11)

where $gazell{e}_{i+1}$ is the solution for the following iteration, $gazell{e}_i$ is the solution for the current iteration, s is the pace at which the gazelles graze, $R_B$ is a vector of constant random integers [0, 1], and R is a vector of different random numbers reflecting the Brownian motion.

3.4.2. Exploration

When a predator is seen, the exploring phase begins. The 2 m height is mimicked by scaling the 2 m height to a figure between 0 and 1. Gazelles respond to danger by flicking their tail, stomping their feet, or stotting up to 2 m in the air with all four feet. This algorithm phase uses the Lévy flight, which involves a series of little steps and sporadic large jumps. This strategy has enhanced searchability in the literature on optimization. In Figure 2, the exploring phase is shown. Once the predator is seen, the gazelle flees, and the predator pursues. Both runs exhibit a sharp turn in travel direction, symbolized by the $mu$. This study assumed that this direction shift happens every iteration; when the iteration number is odd, the gazelle moves in one direction, and when it is even, it moves in the opposite direction. We hypothesized that because the gazelle reacts first, it uses the Lévy flight to move. The study assumed that the predator would lift off utilizing Brownian motion and switch to Lévy flight since the predator would respond later.

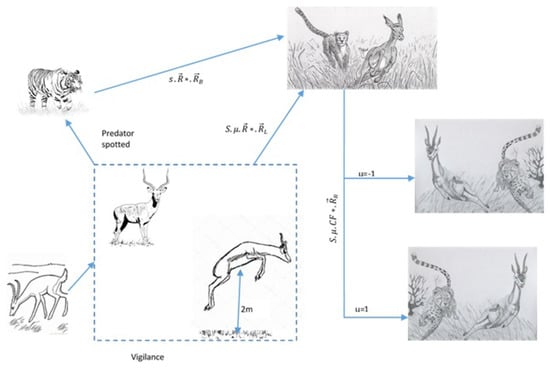
Figure 2. Gazelles fleeing the predator is a sign of exploration.

Equation (12) illustrates the computational formula of the gazelle’s behavior after spotting the predator.

$$\overrightarrow{gazell{e}_{i+1}}=\overrightarrow{gazell{e}_i}+S.\mu .\overrightarrow{R_L}\ast (\overrightarrow{Elit{e}_i}-\overrightarrow{R_L}\ast \overrightarrow{gazell{e}_i})$$

(12)

where S represents the fastest the gazelle can go, and $\overrightarrow{R_L}$ is a vector of random integers generated using Lévy distributions. Equation (13) illustrates the computational formula for the predator’s pursuit of the gazelle.

$$\overrightarrow{gazell{e}_{i+1}}=\overrightarrow{gazell{e}_i}+S.\mu .CF.R\ast \overrightarrow{R_B}\ast (\overrightarrow{Elit{e}_i}-\overrightarrow{R_L}\ast \overrightarrow{gazell{e}_i})$$

(13)

where,

$$CF={(1-\frac{iter}{max\_iter})}^{\left(2\frac{iter}{max\_iter}\right)}$$

(14)

The research on Mongolian gazelles also claimed that even though the animals are not endangered, they have annual survivorship of 0.66, which translates to just 0.34 instances where predators are effective. PSRs, which stand for predator success rates, impact the gazelle’s capacity to flee. Therefore, the method prevents becoming stuck in a local minimum. Equation (15) models the impact of PSRs.

$$\overrightarrow{gazell{e}_{i+1}}=\left\{\begin{array}{cc}\overrightarrow{gazell{e}_i}+CF\left[\overrightarrow{LB}+\overrightarrow{R}\ast (\overrightarrow{UB}-\overrightarrow{LB})\ast \overrightarrow{U}\right],\hfill & \mathrm{if}r\le PSRs\hfill \\ \overrightarrow{gazell{e}_i}+\left[PSRs(1-r)+r\right](\overrightarrow{gazell{e}_{r1}}-\overrightarrow{gazell{e}_{r2}}),\hfill & \mathrm{else}\hfill \end{array}\right.$$

(15)

$$\overrightarrow{U}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}r<0.34\hfill \\ 1\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(16)

The main procedure of the basic IGOA is presented in Figure 3.

Figure 3. Procedure of the basic GOA.

4. The Proposed Method

In this section, the proposed IGOA is presented according to its main search procedures.

4.1. Orthogonal Learning (OL)

A fractional experiment holds the secret to the orthogonal design. Finding the optimum level combination may be accomplished fast by utilizing the features of a fractional experiment to produce all possible level combinations. The standard approach to finding the best level for each variable is to cycle via all levels, supposing that the experimental findings of the objective issue rely on the K factor, which may be split into Q levels. When there are a few factors involved, this strategy works quite well. However, when many factors are involved, it becomes very challenging to reach every level. This traversal approach differs from orthogonal design. Through an orthogonal array, it mixes various elements and stories. As an illustration, the construction procedure follows: build the introductory column first, then the nonbasic column [26,27]. The following Equation describes how to create an orthogonal array of $L_{10}\left(3^4\right)$.

$$L_{10}\left(3^4\right)=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 2& 2& 2\\ 1& 3& 3& 3\\ 2& 1& 2& 3\\ 2& 2& 3& 1\\ 2& 3& 1& 2\\ 3& 1& 3& 2\\ 3& 2& 1& 3\\ 3& 3& 2& 1\\ 4& 1& 1& 1\end{array}\right]$$

(17)

4.2. Rosenbrock’s Direct Rotational (RDR)

The coordinate axes are used as the initial search path in Rosenbrock’s direct rotation (RDR) local search technology, which then rotates along these directions before moving to a new arrangement point where effective steps are produced until at least one effective process and one failed step has been made in each search direction [28]. In this scenario, the present phase will end, and the orthonormal basis will be revised to account for the cumulative impact of all successful steps in all dimensions [29]. Equation (18) displays the orthonormal basis update.

$$x^{k+1}-x^{k+}=\sum _{i=1}^n{\lambda }_i{d}_i$$

(18)

Equation (19) defines the new set of guidelines. Where ${\lambda }_i$ is the total number of successful design variables, the most beneficial search direction at this point is $x^{k+1}-x^{k+}$; hence, it must be included in the revised search direction.

$$p_i=\left\{\begin{array}{cc}{d}_i,\hfill & {\lambda }_i=0\hfill \\ \sum _{j=0}^n{\lambda }_j{d}_j,\hfill & {\lambda }_i\ne 0\hfill \end{array}\right.$$

(19)

The search results are then updated using the Gram–Schmidt orthonormalization process as given in Equation (20).

$$q_i=\left\{\begin{array}{cc}{p}_i,\hfill & i=1\hfill \\ p_i-\sum _{j=1}^{i-1}\frac{q_j^T{p}_i}{q_j^T{q}_j},\hfill & i\ge 2\hfill \end{array}\right.$$

(20)

Equation (21) displays the modified search instructions upon normalization.

$$d_i=\frac{q_i}{∥q_i∥},i=1,2,3,....,n.$$

(21)

The technique searches once more along the new opposite manner after updating the local search, continuing until the end condition is fulfilled.

4.3. Procedure of the Proposed IGOA

The suggested IGOA is presented in this section to demonstrate its primary process and structure. The three primary methods—GOA, OL, and RDR—are employed in the suggested technique, subject to three phases following a transition mechanism. The suggested IGOA modifies the placements of the solutions in accordance with an assumption (IF $rand$ < 0.2). The search procedure is checked at the end to see if it may be terminated or kept on. The search operations of the OL will be carried out if this is the case; otherwise, IF $rand$< 0.5, the search processes of the RDR will be carried out. If not, the search procedures will be excused in accordance with the GOA’s exploration and exploitation. The main procedure of the proposed IGOA is presented in Figure 4.

Figure 4. Procedure of the proposed IGOA.

By creating a novel arrangement (transition mechanism) and utilizing three integrated approaches, the suggested method addresses the shortcomings of the conventional methods (i.e., GOA, LO, and RDR). The traditional approach, such as GOA, has problems with quick convergence rates, saturation in the immediate search region, and an imbalance between the search stages (exploration and exploitation). One of the critical issues with the GOA is that the variety of possible solutions is possibly low. In order to solve clustering difficulties more effectively, the suggested technique has an appropriate arrangement among the existing methods to meet these issues.

In conclusion, we demonstrate how the flaws were fixed. The first step is to address the imbalance between the search processes by doing an exploration search of OL and RDR for half of the iterations and an exploitation search of GOA for the other half. Thus, the suggested force arrangement may balance the search processes and increase variety in the candidate solutions by selecting one exploration or exploitation process out of three approaches in each iteration. Second, adjustments in the search procedure made in accordance with the suggested transition mechanism would regulate the pace of convergence. This impacts the optimization process by causing it to avoid the local search region and continue searching for the optimal answer. Finally, using various updating mechanisms per the suggested methodology will preserve the diversity of the solutions employed.

4.4. Computational Complexity of the Proposed IGOA

The suggested IGOA’s total computing complexity is provided according to the initialization of the candidate solutions, the objective function of the existing solutions, and the updating of the candidate solutions.

Assume that N is the number of all utilized solutions, and O(N) is the complexity time of the solutions’ initialization. The time complexity of the solutions’ updating is O(T × N) + O(T × N × $Dim$), where T is the total number of used iterations. $Dim$ is the location size of the problem. Therefore, the time complexity of the presented IGOA is given as follows.

$$O\left(IGOA\right)=\left(N\right)\times O\left(GOA\right)+O\left(OL\right)+O\left(RDR\right)$$

(22)

The time complexity of the proposed method depends on three main search operators; GOA, OL, and RDR. These methods’ complexity times are calculated as follows.

$$O\left(OL\right)=O(N\times (max\_iter\times Dim+1\left)\right)$$

(23)

$$O\left(GOA\right)=O(N\times (max\_iter\times Dim+1\left)\right)$$

(24)

$$O\left(RDR\right)=O(N\times Dim)$$

(25)

Therefore, the total time complexity of the IGOA is given as follows.

$$O\left(IGOA\right)=O(max\_iter\times N\times (Dim+1)+(N\times Dim)+(N\times Dim\left)\right)$$

(26)

$$O\left(IGOA\right)=O\left(max\_iter\times N\times \left(Dim+N\right)\right)$$

(27)

5. Experiments and Results

The suggested approach (IGOA) is tested in this part to solve the optimization problems (data clustering problems). The outcomes are assessed using various metrics. Additionally, the suggested method’s considerable benefits over previous comparative approaches in the literature are demonstrated using the Friedman ranking test (FRT) and Wilcoxon signed-rank (WRT) test.

To evaluate the outcomes of the suggested strategy, a number of optimizers are employed as comparing techniques.

These methods are the salp swarm algorithm (SSA) [30], whale optimization algorithm (WOA) [31], sine–cosine algorithm (SCA) [32], dragonfly algorithm (DA) [33], grey wolf optimizer (GWO) [34], equilibrium optimizer (EO) [35], particle swarm optimizer (PSO) [36], Aquila optimizer (AO) [37], ant lion optimizer (ALO) [38], marine predators algorithm (MPA) [39], and gazelle optimization algorithm (GOA).

The findings are reported after 30 separate runs of each comparison approach with a population size of 30 and 1000 iterations. The parameters for the comparison approaches are set out in Table 1 in the ’Parameter’ column. Table 2 lists the specifics of the computers that were used.

Table 1. Setting of the comparative methods’ parameters.

No.	Algorithm	Reference	Parameter	Value
1	SSA	[32]	$v_0$	0
2	WOA	[40]	$\alpha$	Decreased from 2 to 0
			b	2
3	SCA	[41]	$\alpha$	0.05
4	DA	[33]	w	0.2–0.9
			s, a, and c	0.1
			f and e	1
5	GWO	[34]	Convergence parameter (a)	Linear reduction from 2 to 0
6	PSO	[36]	Topology	Fully connected
			Cognitive and social constant	(C1, C2) 2, 2
			Inertia weight	Linear reduction from 0.9 to 0.1
			Velocity limit	10% of dimension range
7	ALO	[38]	$\alpha$	∈ [0 1]
8	MPA	[39]	$\gamma$	$\gamma$ > 1
			P	0.0
9	EO	[35]	r	0.5
			a	4
			$GP$	0.5
10	AO	[37]	$\alpha$	0.1
			$\delta$	0.1

Table 2. Details of the utilized computers.

Name	Setting
Software
- Operating system	64-Bit
- Windows	Windows 10
- Language	MATLAB R2015a
Hardware
- CPU	Intel(R) Core(TM) i7 processor
- Frequency	2.3 GHz
- RAM	16 GB
- Hard disk	1000 GB

5.1. Experiments Series 1: Classical Benchmark Problems

In this section, the performance of the proposed method is evaluated using a set of 23 classical benchmark functions.

The mathematical representation and classifications of the applied 23 benchmark functions are shown in Table 3. The benchmark functions are unimodal (F1–F7); they are used to assess the exploitation capability of the proposed method as they have one optimal solution. Multimodal (F8–F13) has several local optima and one global optimum used to evaluate the algorithm’s exploration. The fixed-dimension multimodal has a limited search space to assess the equilibrium between exploration and exploitation.

Table 3. Classical benchmark functions.

Function	Description	Dimensions	Range	${\mathit{f}}_{\mathbf{min}}$
F1	$f\left(x\right)={\sum }_{i=1}^n{x}_i^2$	10, 50, 100, 500	[−100, 100]	0
F2	$f\left(x\right)={\sum }_{i=0}^n|x_i|+{\prod }_{i=0}^n\left|x_i\right|$	10, 50, 100, 500	[−10, 10]	0
F3	$f\left(x\right)={\sum }_{i=1}^d{\left({\sum }_{j=1}^i{x}_j\right)}^2$	10, 50, 100, 500	[−100, 100]	0
F4	$f\left(x\right)=ma{x}_i\left\{\right|x_i|,1\le i\le n\}$	10, 50, 100, 500	[−100, 100]	0
F5	$f\left(x\right)={\sum }_{i=1}^{n-1}[100{(x_i^2-x_{i+1})}^2+{(1-x_i)}^2]$	10, 50, 100, 500	[−30, 30]	0
F6	$f\left(x\right)={\sum }_{i=1}^n{\left([x_i+0.5]\right)}^2$	10, 50, 100, 500	[−100, 100]	0
F7	$f\left(x\right)={\sum }_{i=0}^{n}i{x}_i^4+\mathrm{random}[0,1)$	10, 50, 100, 500	[−128, 128]	0
F8	$f\left(x\right)={\sum }_{i=1}^n(-x_{i}sin\left(\sqrt{|x_i|}\right))$	10, 50, 100, 500	[−500, 500]	−418.9829 × n
F9	$f\left(x\right)={\sum }_{i=1}^n[x_i^2-10cos\left(2\pi x_i\right)+10]$	10, 50, 100, 500	[−5.12, 5.12]	0
F10	$f\left(x\right)=-20exp(-0.2\sqrt{\frac{1}{n}{\sum }_{i=1}^n{x}_i^2})-exp\left(\frac{1}{n}{\sum }_{i=1}^{n}cos\left(2\pi x_i\right)\right)+20+e$	10, 50, 100, 500	[−32, 32]	0
F11	$f\left(x\right)=1+\frac{1}{4000}{\sum }_{i=1}^n{x}_i^2-{\prod }_{i=1}^{n}cos\left(\frac{x_i}{\sqrt{i}}\right)$	10, 50, 100, 500	[−600, 600]	0
F12	$f\left(x\right)=\frac{\pi }{n}\left\{10sin\left(\pi y_1\right)\right\}+{\sum }_{i=1}^{n-1}{(y_i-1)}^2[1+10si{n}^2\left(\pi y_{i+1}\right)+{\sum }_{i=1}^{n}u(x_i,10,100,4)]$, where $y_i=1+{\displaystyle \frac{x_i+1}{4}},u(x_i,a,k,m)\left\{\begin{array}{cc}K{(x_i-a)}^m\hfill & \mathrm{if}{x}_i>a\hfill \\ 0\hfill & -a\le x_i\ge a\hfill \\ K{(-x_i-a)}^m\hfill & -a\le x_i\hfill \end{array}\right.$	10, 50, 100, 500	[−50, 50]	0
F13	$f\left(x\right)=0.1(si{n}^2\left(3\pi x_1\right)+{\sum }_{i=1}^n{(x_i-1)}^2[1+si{n}^2(3\pi x_i+1)]+{(x_n-1)}^{2}1+si{n}^2\left(2\pi x_n\right))+{\sum }_{i=1}^{n}u(x_i,5,100,4)$	10, 50, 100, 500	[−50, 50]	0
F14	$f\left(x\right)={\left(\frac{1}{500}+{\sum }_{j=1}^{25}\frac{1}{j+{\sum }_{i=1}^2}(x_i-a_{ij})\right)}^{-1}$	2	[−65, 65]	1
F15	$f\left(x\right)={\sum }_{i=1}^{11}{\left[a_i-\frac{x_1(b_i^2+b_i{x}_2)}{b_i^2+b_i{x}_3+x_4}\right]}^2$	4	[−5, 5]	0.00030
F16	$f\left(x\right)=4x_1^2-2.1x_1^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^4$	2	[−5, 5]	−1.0316
F17	$f\left(x\right)={\left(x_2-\frac{5.1}{4{\pi }^2}{x}_1^2+\frac{5}{\pi }{x}_1-6\right)}^2+10(1-\frac{1}{8\pi })cos$ $x_1+10$	2	[−5, 5]	0.398
F18	$f\left(x\right)=\left[1+{(x_1+x_2+1)}^2(19-14x_1+3x_1^2-14x_2+6x_1{x}_2+3x_2^2)\right]\times \left[30+{(2x_1-3x_2)}^2\times (18-32x_i+12x_1^2+48x_2-36x_1{x}_2+27x_2^2)\right]$	2	[−2, 2]	3
F19	$f\left(x\right)=-{\sum }_{i=1}^4{c}_{i}exp\left(-{\sum }_{i=1}^3{a}_{ij}{(x_j-p_{ij})}^2\right)$	3	[−1, 2]	−3.86
F20	$f\left(x\right)=-{\sum }_{i=1}^4{c}_{i}exp\left(-{\sum }_{i=1}^6{a}_{ij}{(x_j-p_{ij})}^2\right)$	6	[0, 1]	−0.32
F21	$f\left(x\right)=-{\sum }_{i=1}^5{\left[(X-a_i){(X-a_i)}^T+c_i\right]}^{-1}$	4	[0, 1]	−10.1532
F22	$f\left(x\right)=-{\sum }_{i=1}^7{\left[(X-a_i){(X-a_i)}^T+c_i\right]}^{-1}$	4	[0, 1]	−10.4028
F23	$f\left(x\right)=-{\sum }_{i=1}^{10}{\left[(X-a_i){(X-a_i)}^T+c_i\right]}^{-1}$	4	[0, 1]	−10.5363

Note: Unimodal functions are from F1–F7, multimodal functions are from F8–F13, and fixed-dimension multi-modal functions are from F14–F23.

To find the best number of used candidate solutions of the proposed method, experiments were conducted as shown in Figure 5. The influence of the number of solutions (i.e., N) is examined on the classical test functions (23 benchmark functions). According to the literature, several numbers were taken to choose the population size; these numbers were 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50, comparing the changes in the number of solution parameters throughout iterations (i.e., 500 iterations).

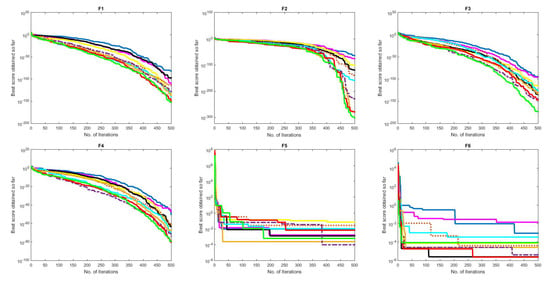
Figure 5. The influence of the population size tested on the classical test functions.

Usually, the used solution numbers range from 5 to 50. For example, if we look at F5, F6, F7, and F9, we find slight differences between the solutions used, as 30 is almost the best-utilized number. This size had the best results on average as this value can be considered the smallest number of the used best numbers (30 solutions), as given in F17–F22. The best number of solutions between several values is the smallest one, to maintain low computational time and obtain the maximum performance. It can be observed from the obtained results in Figure 5 that when these many population sizes are used, the proposed IGOA method keeps its advantages, which means that IGOA is more robust and less overwhelmed by population size. The proposed IGOA is more stable when the population changes, such as F10, F16, F17, F18, F19, F21, F22, and F23. In other words, the best number of solutions is 50 in most of the used benchmark functions (i.e., F1, F6, F9, F10, F11, etc.). However, because there is little difference between the given number of solutions, the claim as mentioned earlier is supported.

Deep investigations were conducted to show the performance of the proposed method compared to the original methods as given in Figure 6. In this Figure, in each row, four sub-figures are given: function topology, trajectory of the first dimension, average fitness values, and convergence curves of the tested methods.

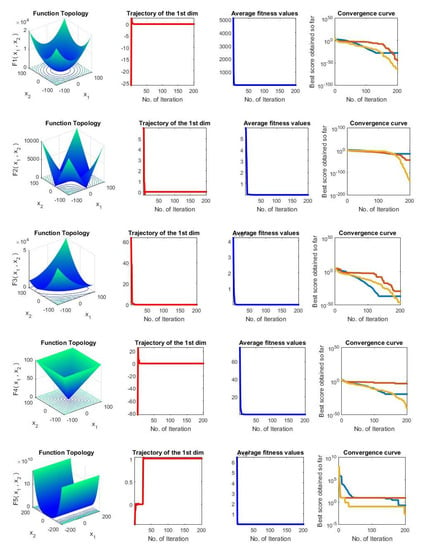
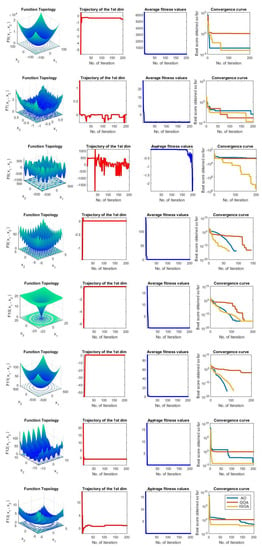
Figure 6. Qualitative results of the proposed method.

In the first column in Figure 6, the standard 2D designs of the fitness function are provided. The second column presents the first position story collected by the proposed IGOA through the optimization process. IGOA examines promising areas in the assigned search space for the used problems. Unique positions are given in a broad search space, while the largest is developed around the local region for the provided problems because of these difficulty levels. The second column, trajectory patterns, shows that the solution achieves significant and acute changes in the optimization’s first actions. This operation can confirm that the proposed IGOA can ultimately meet the optimal position. The third column presents the average fitness value of the used candidate solutions in each repetition. The curves display shrinking behaviors on the employed problems. This proves that the proposed IGOA enhances the performance of the search process for iterations. In the fourth column, the objective function value of the best-obtained solution in each repetition is presented. Consequently, the proposed IGOA has preferred exploration and exploitation aptitudes.

The results of the proposed IGOA, compared to the other comparative methods using classical (F1–F13) benchmark functions, where the dimension size is 10, are given in Table 4. A very impressive indication is observed when the proposed method achieved all of the best results in the tested cases (F1–F13). According to the FRT, the proposed method ranked first, followed by AO, MPA, GOA, EO, WOA, GWO, PSO, SCA, SSA, ALO, and DE. In Table 5, the results of the proposed IGOA are compared to other comparative methods using classical benchmark functions (F14–F23), where the dimension size was fixed. From this table, we notice that the proposed method had the best results in almost all of the tested problems, except F15, where it obtained the second-best results. So, the archived results prove that the proposed IGOA has a promising ability to solve the benchmark problems. According to the FRT, the proposed IGOA ranked first, followed by MPA, SSA, GWO, EO, AO, ALO, PSO, DA, WOA, SCA, and GOA.

Table 4. The results of the proposed IGOA and other comparative methods using classical benchmark functions (F1–F13), where the dimension size is 10.

Measure	Comparative Algorithms
	SSA	WOA	SCA	DA	GWO	PSO	ALO	MPA	EO	AO	GOA	IGOA
F1
Max	5.6687E-06	3.0768E-29	9.2720E-03	3.7901E+02	4.5916E-18	6.0401E-03	5.2574E-01	1.9657E-29	3.8998E-26	9.5870E-81	1.6001E-40	4.0016E-111
Mean	1.6182E-06	7.6986E-30	2.3193E-03	2.5349E+02	1.5936E-18	1.6560E-03	1.3154E-01	9.7494E-30	1.6302E-26	2.4125E-81	4.0002E-41	1.0004E-111
Min	1.4128E-07	1.4455E-36	9.0439E-08	1.0313E+02	1.2000E-19	7.8798E-06	7.9433E-05	4.8694E-30	3.6988E-27	1.4810E-85	1.6323E-122	2.5272E-123
Std	2.7047E-06	1.5380E-29	4.6352E-03	1.2133E+02	2.0273E-18	2.9346E-03	2.6280E-01	6.9322E-30	1.5858E-26	4.7830E-81	8.0003E-41	2.0008E-111
Ranking	8	4	10	12	7	9	11	5	6	2	3	1
F2
Max	7.7959E+00	2.1492E-29	1.1036E-04	2.2195E+01	3.3639E-11	1.6219E-01	1.9575E+01	2.6474E-16	1.4528E-14	7.8147E-44	6.4440E-71	0.0000E+00
Mean	3.0662E+00	5.9613E-30	4.4043E-05	1.1944E+01	1.2412E-11	1.1260E-01	8.5054E+00	1.4902E-16	3.8156E-15	2.0429E-44	1.6110E-71	0.0000E+00
Min	5.4086E-01	3.1640E-34	5.9247E-06	3.0554E+00	1.8400E-12	9.3967E-03	1.4917E+00	1.7669E-17	2.9474E-17	1.0185E-49	3.4455E-95	0.0000E+00
Std	3.3581E+00	1.0413E-29	4.6685E-05	7.8998E+00	1.4482E-11	7.0423E-02	7.7648E+00	1.0159E-16	7.1434E-15	3.8512E-44	3.2220E-71	0.0000E+00
Ranking	10	4	8	12	7	9	11	5	6	3	2	1
F3
Max	1.2878E+03	3.1583E+03	7.2366E+01	6.6942E+03	3.5163E-07	3.4736E+00	5.4055E+03	8.8765E-13	2.7141E-11	4.1515E-79	4.0712E-09	1.8119E-94
Mean	5.0275E+02	1.7896E+03	3.3041E+01	4.9705E+03	1.2577E-07	1.5269E+00	3.5168E+03	2.3968E-13	1.0682E-11	1.0379E-79	1.0178E-09	4.5299E-95
Min	6.5881E+01	7.8867E+02	1.0676E-01	3.4937E+02	1.0960E-08	4.5930E-02	2.0838E+03	6.1340E-17	4.4484E-13	1.3725E-90	0.0000E+00	1.4890E-115
Std	5.5639E+02	1.0134E+03	3.7958E+01	3.0848E+03	1.5853E-07	1.4318E+00	1.3815E+03	4.3327E-13	1.1833E-11	2.0757E-79	2.0356E-09	9.0597E-95
Ranking	9	10	8	12	6	7	11	3	4	2	5	1
F4
Max	1.1350E+01	2.4947E+01	5.2459E-01	3.4546E+01	7.0394E-06	2.5740E-01	2.5872E+01	5.0672E-13	6.4122E-08	7.0382E-40	1.9988E-23	9.7425E-52
Mean	4.7755E+00	1.0417E+01	3.4400E-01	1.8807E+01	2.2793E-06	1.6819E-01	1.8858E+01	3.1893E-13	1.8603E-08	1.8001E-40	4.9970E-24	2.4506E-52
Min	1.0957E+00	2.8202E+00	1.5933E-01	8.1766E+00	2.3154E-07	9.0260E-02	1.2936E+01	5.3543E-14	7.8747E-10	1.2170E-48	1.8617E-77	3.5318E-62
Std	4.5106E+00	1.0221E+01	1.9127E-01	1.1584E+01	3.1913E-06	6.8608E-02	5.7790E+00	2.1383E-13	3.0477E-08	3.4929E-40	9.9939E-24	4.8613E-52
Ranking	9	10	8	11	6	7	12	4	5	2	3	1
F5
Max	2.4884E+03	8.9652E+00	8.9499E+00	3.9872E+04	8.0846E+00	9.6438E+01	2.9905E+04	8.5294E+00	8.7210E+00	1.9262E-01	8.5801E+00	3.4160E-02
Mean	1.1873E+03	8.8175E+00	8.4259E+00	2.4852E+04	7.6262E+00	3.5639E+01	8.2018E+03	7.2907E+00	7.7837E+00	8.6155E-02	8.2137E+00	1.8406E-02
Min	7.7911E+00	8.5543E+00	8.0821E+00	1.3031E+04	7.1861E+00	7.4127E+00	2.5891E+02	6.2748E+00	7.1336E+00	2.0769E-06	7.7814E+00	1.4281E-03
Std	1.3156E+03	1.9212E-01	3.6921E-01	1.1143E+04	5.0584E-01	4.1800E+01	1.4479E+04	9.2936E-01	7.5787E-01	9.7685E-02	3.4581E-01	1.5032E-02
Ranking	10	8	7	12	4	9	11	3	5	2	6	1
F6
Max	1.8987E-02	7.1473E-01	1.4622E+00	2.5496E+02	7.5229E-01	8.3608E-04	1.2734E-02	7.7604E-02	4.9193E-01	3.3793E-04	4.6477E-01	3.2478E-04
Mean	6.9763E-03	4.8733E-01	1.0843E+00	2.1284E+02	3.7321E-01	3.8147E-04	3.2223E-03	1.9401E-02	1.2318E-01	1.9276E-04	3.4021E-01	9.2145E-05
Min	1.1915E-06	3.2553E-01	8.8693E-01	1.8611E+02	1.4414E-05	1.9334E-05	2.9475E-05	9.0157E-10	2.0808E-05	5.9616E-06	2.5929E-01	4.4427E-08
Std	9.0313E-03	1.7744E-01	2.6857E-01	3.1781E+01	3.2201E-01	3.6694E-04	6.3413E-03	3.8802E-02	2.4583E-01	1.4224E-04	9.4276E-02	1.5640E-04
Ranking	5	10	11	12	9	3	4	6	7	2	8	1
F7
Max	9.4570E-02	5.1017E-02	1.3523E-02	4.6264E-01	5.0253E-03	1.6015E-01	7.5349E-01	1.4525E-03	4.0995E-03	1.5900E-03	1.0205E-03	1.4519E-04
Mean	7.4271E-02	1.3559E-02	7.8508E-03	2.1954E-01	3.0991E-03	8.1841E-02	4.5660E-01	1.1726E-03	1.8678E-03	5.9058E-04	5.0738E-04	9.7675E-05
Min	5.6938E-02	6.9400E-04	4.3940E-03	9.3729E-02	2.1818E-03	3.0057E-02	8.7673E-02	8.4107E-04	9.6380E-04	1.7258E-05	2.2784E-04	4.4478E-05
Std	1.9462E-02	2.4974E-02	4.2216E-03	1.6841E-01	1.3158E-03	6.1565E-02	2.7498E-01	2.9914E-04	1.4989E-03	7.0301E-04	3.6238E-04	4.4662E-05
Ranking	9	8	7	11	6	10	12	4	5	3	2	1
F8
Max	−2.2734E+03	−1.8870E+03	−1.6176E+03	−1.8505E+03	−2.1174E+03	−1.2648E+03	−1.9152E+03	−2.8653E+03	−2.4220E+03	−1.6770E+03	−2.0896E+03	−2.7694E+07
Mean	−2.5962E+03	−2.7810E+03	−1.9484E+03	−2.1719E+03	−2.4186E+03	−1.4903E+03	−2.0689E+03	−3.3299E+03	−2.8783E+03	−2.4188E+03	−2.2345E+03	−1.2332E+08
Min	−3.1435E+03	−3.4289E+03	−2.3834E+03	−2.7042E+03	−2.6000E+03	−1.6333E+03	−2.3523E+03	−3.5369E+03	−3.4762E+03	−4.1864E+03	−2.3109E+03	−2.5083E+08
Std	3.8896E+02	6.4835E+02	3.2334E+02	3.7546E+02	2.0990E+02	1.6288E+02	2.0383E+02	3.1353E+02	4.4133E+02	1.1838E+03	9.9463E+01	1.0036E+08
Ranking	5	4	11	9	7	12	10	2	3	6	8	1
F9
Max	3.6813E+01	1.5062E+00	1.2066E+00	7.0022E+01	4.7147E+00	3.0419E+01	7.6611E+01	1.4211E-14	3.0381E+00	2.6242E-01	0.0000E+00	0.0000E+00
Mean	2.5869E+01	3.7655E-01	3.0890E-01	5.7496E+01	2.6264E+00	1.7201E+01	5.7956E+01	3.5527E-15	1.0083E+00	6.5605E-02	0.0000E+00	0.0000E+00
Min	1.5920E+01	0.0000E+00	2.0227E-06	4.7361E+01	4.2633E-14	5.9917E+00	3.7810E+01	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Std	9.0092E+00	7.5310E-01	5.9859E-01	1.0614E+01	1.9778E+00	1.0360E+01	1.7468E+01	7.1054E-15	1.4322E+00	1.3121E-01	0.0000E+00	0.0000E+00
Ranking	10	6	5	11	8	9	12	3	7	4	1	1
F10
Max	1.9965E+01	4.3521E-14	1.3360E+01	1.5782E+01	3.2645E-10	2.3169E+00	1.5140E+01	7.9936E-15	7.6827E-13	8.8818E-16	8.8818E-16	8.8818E-16
Mean	7.0934E+00	1.6875E-14	3.3500E+00	1.0033E+01	2.0063E-10	5.8999E-01	1.2971E+01	5.3291E-15	2.7711E-13	8.8818E-16	8.8818E-16	8.8818E-16
Min	1.6466E+00	8.8818E-16	4.6053E-05	3.4909E+00	4.7813E-11	3.8237E-03	9.6145E+00	4.4409E-15	5.0626E-14	8.8818E-16	8.8818E-16	8.8818E-16
Std	8.6251E+00	1.8687E-14	6.6735E+00	5.0775E+00	1.3298E-10	1.1513E+00	2.3725E+00	1.7764E-15	3.3477E-13	0.0000E+00	0.0000E+00	0.0000E+00
Ranking	10	5	9	11	7	8	12	4	6	1	1	1
F11
Max	1.9439E-01	0.0000E+00	4.7522E-01	7.2161E+00	6.3368E-02	5.2703E+00	5.5890E-01	1.7339E-02	2.6300E-02	0.0000E+00	3.5947E-02	0.0000E+00
Mean	1.5599E-01	0.0000E+00	3.1614E-01	4.3403E+00	3.9139E-02	2.1440E+00	2.5481E-01	4.3347E-03	9.0506E-03	0.0000E+00	8.9867E-03	0.0000E+00
Min	9.1527E-02	0.0000E+00	5.0005E-02	2.1045E+00	2.6828E-02	2.9533E-01	3.7795E-02	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Std	4.8640E-02	0.0000E+00	1.9205E-01	2.1867E+00	1.6448E-02	2.1658E+00	2.3401E-01	8.6694E-03	1.2411E-02	0.0000E+00	1.7973E-02	0.0000E+00
Ranking	8	1	10	12	7	11	9	4	6	1	5	1
F12
Max	1.1753E+01	2.6635E-01	1.8565E+00	1.7519E+01	1.5264E-01	6.1327E-04	4.0024E+01	1.5225E-02	2.0023E-02	3.8124E-04	3.3640E-01	2.5541E-04
Mean	5.2622E+00	2.2869E-01	6.9748E-01	7.8833E+00	7.3856E-02	1.8414E-04	1.5694E+01	3.8159E-03	8.8384E-03	2.1247E-04	2.8413E-01	1.7172E-04
Min	1.2927E+00	1.8560E-01	1.4509E-01	1.5513E+00	4.2429E-02	5.1148E-06	6.8637E+00	2.2171E-09	5.5321E-06	8.5093E-05	2.0181E-01	7.8122E-05
Std	4.6576E+00	3.5965E-02	7.8947E-01	6.8630E+00	5.3004E-02	2.8779E-04	1.6242E+01	7.6063E-03	1.0349E-02	1.2764E-04	5.7632E-02	7.3077E-05
Ranking	10	7	9	11	6	2	12	4	5	3	8	1
F13
Max	2.5967E+00	5.1313E-01	9.8470E-01	3.6598E+05	5.2436E-01	1.0989E-02	1.7543E+01	5.4243E-02	2.4034E-01	7.9376E-03	9.9617E-01	6.4710E-04
Mean	6.9400E-01	4.6523E-01	6.8633E-01	9.1861E+04	2.9147E-01	2.7604E-03	8.9895E+00	1.8705E-02	1.6238E-01	1.9946E-03	8.1993E-01	2.2333E-04
Min	2.8184E-02	4.4162E-01	5.5358E-01	2.2382E+00	1.0911E-01	2.5130E-07	3.0920E-02	1.7929E-08	1.0272E-01	1.1894E-05	6.8063E-01	4.5897E-05
Std	1.2691E+00	3.3200E-02	2.0330E-01	1.8275E+05	1.7691E-01	5.4854E-03	8.3440E+00	2.5601E-02	5.9648E-02	3.9620E-03	1.3519E-01	2.8682E-04
Ranking	9	7	8	12	6	3	11	4	5	2	10	1
Friedman test
Mean Rank	8.62	6.46	8.54	11.38	6.62	7.62	10.62	3.92	5.38	2.54	4.77	1.00
Final Ranking	10	6	9	12	7	8	11	3	5	2	4	1

Table 5. The results of the proposed IGOA and other comparative methods using classical benchmark functions (F14–F23), where the dimension size is a fixed size.

Measure	Comparative Algorithms
	SSA	WOA	SCA	DA	GWO	PSO	ALO	MPA	EO	AO	GOA	IGOA
F14
Max	2.9821E+00	1.0763E+01	2.9821E+00	1.5504E+01	1.0763E+01	1.5504E+01	2.3809E+01	1.2671E+01	1.0763E+01	1.2671E+01	1.2671E+01	1.9920E+00
Mean	1.4940E+00	3.9616E+00	2.4866E+00	5.3690E+00	8.8179E+00	1.1203E+01	1.0637E+01	5.1574E+00	4.6720E+00	7.0828E+00	1.2194E+01	1.2465E+00
Min	9.9800E-01	9.9800E-01	1.0001E+00	9.9800E-01	2.9821E+00	5.9288E+00	3.9683E+00	1.9920E+00	9.9800E-01	9.9800E-01	1.0763E+01	9.9800E-01
Std	9.9205E-01	4.6251E+00	9.9101E-01	6.8049E+00	3.8905E+00	5.0297E+00	9.0070E+00	5.0305E+00	4.6790E+00	6.4649E+00	9.5366E-01	4.9701E-01
Ranking	2	4	3	7	9	11	10	6	5	8	12	1
F15
Max	1.7018E-03	4.3071E-03	1.5907E-03	2.7670E-02	1.4827E-03	1.7771E-03	1.8452E-02	3.3202E-04	2.0363E-02	1.2317E-03	8.9716E-02	6.4899E-04
Mean	1.5560E-03	1.6586E-03	1.3341E-03	1.2183E-02	6.4339E-04	1.0875E-03	7.7714E-03	3.1617E-04	1.0343E-02	7.0995E-04	4.7898E-02	5.0192E-04
Min	1.4119E-03	3.3772E-04	8.9731E-04	6.5750E-04	3.1075E-04	7.6724E-04	2.9649E-03	3.0749E-04	3.0935E-04	3.3906E-04	2.9486E-02	4.4828E-04
Std	1.5860E-04	1.7941E-03	3.0634E-04	1.1296E-02	5.6338E-04	4.7034E-04	7.3060E-03	1.1593E-05	1.1570E-02	4.0040E-04	2.8449E-02	9.8118E-05
Ranking	7	8	6	11	3	5	9	1	10	4	12	2
F16
Max	−1.0316E+00	−1.0316E+00	−1.0000E+00	−1.0308E+00	−1.0316E+00	−1.0291E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0096E+00	−1.0316E+00	−1.0316E+00
Mean	−1.0316E+00	−1.0316E+00	−1.0236E+00	−1.0313E+00	−1.0316E+00	−1.0308E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0198E+00	−1.0316E+00	−1.0316E+00
Min	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0316E+00	−1.0249E+00	−1.0316E+00	−1.0316E+00
Std	1.1358E-13	9.0053E-06	1.5707E-02	3.2551E-04	7.7555E-08	1.1721E-03	6.8452E-13	1.8559E-13	3.4995E-14	7.0603E-03	2.2852E-07	0.0000E+00
Ranking	4	8	11	9	6	10	5	3	2	12	7	1
F17
Max	3.9789E-01	4.2689E-01	4.3137E-01	3.9874E-01	3.9795E-01	4.8050E-01	3.9789E-01	3.9789E-01	3.9789E-01	4.0216E-01	1.5356E+00	3.9789E-01
Mean	3.9789E-01	4.0740E-01	4.1413E-01	3.9832E-01	3.9791E-01	4.2242E-01	3.9789E-01	3.9789E-01	3.9789E-01	3.9922E-01	9.0263E-01	3.9789E-01
Min	3.9789E-01	3.9866E-01	3.9906E-01	3.9789E-01	3.9789E-01	3.9863E-01	3.9789E-01	3.9789E-01	3.9789E-01	3.9790E-01	4.4057E-01	3.9789E-01
Std	1.6369E-14	1.3370E-02	1.6334E-02	3.5436E-04	2.6611E-05	3.8869E-02	4.9152E-13	5.5505E-13	2.7422E-09	2.0199E-03	5.2840E-01	0.0000E+00
Ranking	2	9	10	7	6	11	4	3	5	8	12	1
F18
Max	3.0000E+00	3.0579E+01	3.0022E+00	3.0021E+00	8.4001E+01	3.0542E+00	3.0000E+00	3.0000E+00	3.0000E+00	3.6799E+00	8.4339E+01	3.0000E+00
Mean	3.0000E+00	1.6688E+01	3.0013E+00	3.0010E+00	3.0001E+01	3.0141E+00	3.0000E+00	3.0000E+00	3.0000E+00	3.3010E+00	2.4463E+01	3.0000E+00
Min	3.0000E+00	3.0053E+00	3.0007E+00	3.0001E+00	3.0001E+00	3.0000E+00	3.0000E+00	3.0000E+00	3.0000E+00	3.0190E+00	3.0000E+00	3.0000E+00
Std	6.2815E-13	1.5784E+01	6.6423E-04	9.1491E-04	3.8184E+01	2.6794E-02	2.6479E-11	2.2338E-13	3.8520E-07	2.7651E-01	3.9974E+01	1.4950E-15
Ranking	3	10	7	6	12	8	4	2	5	9	11	1
F19
Max	−3.8572E+00	−3.0723E+00	−3.8398E+00	−3.6103E+00	−3.8549E+00	−3.5817E+00	−3.8596E+00	−3.0898E+00	−3.8609E+00	−3.7221E+00	−3.8227E+00	−3.8628E+00
Mean	−3.8596E+00	−3.2723E+00	−3.8494E+00	−3.7415E+00	−3.8601E+00	−3.7763E+00	−3.8610E+00	−3.6695E+00	−3.8623E+00	−3.7943E+00	−3.8444E+00	−3.8628E+00
Min	−3.8627E+00	−3.8468E+00	−3.8573E+00	−3.8471E+00	−3.8628E+00	−3.8468E+00	−3.8628E+00	−3.8628E+00	−3.8628E+00	−3.8522E+00	−3.8587E+00	−3.8628E+00
Std	2.5466E-03	3.8304E-01	7.7153E-03	1.1360E-01	3.6683E-03	1.2987E-01	1.3784E-03	3.8651E-01	9.5396E-04	6.3004E-02	1.5338E-02	4.4409E-16
Ranking	5	12	6	10	4	9	3	11	2	8	7	1
F20
Max	−3.1979E+00	−1.7529E+00	−1.2348E+00	−3.1440E+00	−2.2762E+00	−3.2031E+00	−2.5329E+00	−3.3220E+00	−3.2030E+00	−2.5225E+00	−2.6051E+00	−3.3220E+00
Mean	−3.2609E+00	−2.7847E+00	−2.2059E+00	−3.1943E+00	−2.9987E+00	−3.2328E+00	−2.7032E+00	−3.3220E+00	−3.2328E+00	−2.8380E+00	−2.8984E+00	−3.3220E+00
Min	−3.3220E+00	−3.1841E+00	−3.0581E+00	−3.3162E+00	−3.3219E+00	−3.3220E+00	−2.8814E+00	−3.3220E+00	−3.3220E+00	−3.1264E+00	−3.0035E+00	−3.3220E+00
Std	7.0573E-02	6.8900E-01	9.4395E-01	8.1983E-02	4.8517E-01	5.9447E-02	1.6440E-01	4.0937E-10	5.9494E-02	2.6187E-01	1.9564E-01	1.7172E-10
Ranking	3	10	12	6	7	4	11	2	5	9	8	1
F21
Max	−2.6305E+00	−4.8157E+00	−3.5065E-01	−5.0500E+00	−5.0966E+00	−2.6829E+00	−2.6305E+00	−4.9540E+00	−8.8199E-01	−9.2575E+00	−1.5798E+00	−1.0153E+01
Mean	−7.0094E+00	−4.8932E+00	−7.5598E-01	−6.8195E+00	−8.8813E+00	−8.0375E+00	−5.7235E+00	−8.0029E+00	−4.0233E+00	−9.7647E+00	−2.4100E+00	−1.0153E+01
Min	−1.0153E+01	−5.0032E+00	−1.3155E+00	−8.6125E+00	-1.0150E+01	−1.0153E+01	−1.0153E+01	−9.9566E+00	−5.1007E+00	-1.0152E+01	−3.5016E+00	−1.0153E+01
Std	3.7676E+00	7.9719E-02	4.3024E-01	2.0287E+00	2.5232E+00	3.6003E+00	3.1666E+00	2.2399E+00	2.0943E+00	4.3512E-01	8.3575E-01	1.3286E-08
Ranking	6	9	12	7	3	4	8	5	10	2	11	1
F22
Max	−2.7519E+00	−9.0585E-01	−9.0510E-01	−1.8369E+00	−1.0393E+01	−1.8376E+00	−5.1288E+00	−5.0801E+00	−5.0877E+00	−5.0645E+00	−1.2329E+00	−1.0403E+01
Mean	−6.8205E+00	−5.1360E+00	−1.4838E+00	−3.3195E+00	−1.0399E+01	−4.4431E+00	−9.0844E+00	−8.7305E+00	−6.4165E+00	−9.0095E+00	−2.1487E+00	−1.0403E+01
Min	−1.0403E+01	−1.0235E+01	−2.4565E+00	−5.0164E+00	−1.0403E+01	−1.0403E+01	−1.0403E+01	−1.0272E+01	−1.0403E+01	−1.0399E+01	−3.0909E+00	−1.0403E+01
Std	4.1556E+00	3.8525E+00	7.4057E-01	1.3673E+00	4.3456E-03	3.9973E+00	2.6371E+00	2.4694E+00	2.6576E+00	2.6311E+00	8.0696E-01	1.5991E-08
Ranking	6	8	12	10	2	9	3	5	7	4	11	1
F23
Max	−2.8711E+00	−2.2850E+00	−1.8691E+00	−1.8570E+00	−5.0079E+00	−2.8711E+00	−2.4217E+00	−3.8354E+00	−3.8354E+00	−1.0183E+01	−3.4634E+00	−1.0522E+01
Mean	−7.2799E+00	−3.8940E+00	−2.0020E+00	−4.1990E+00	−7.5155E+00	−6.9448E+00	−4.4504E+00	−8.8612E+00	−7.1852E+00	−1.0361E+01	−5.1392E+00	−1.0526E+01
Min	−1.0536E+01	−5.0669E+00	−2.0959E+00	−1.0215E+01	−1.0019E+01	−1.0536E+01	−1.0536E+01	−1.0536E+01	−1.0536E+01	−1.0515E+01	−8.7041E+00	−1.0532E+01
Std	3.8762E+00	1.3956E+00	1.1257E-01	4.0177E+00	2.8379E+00	4.1658E+00	4.0573E+00	3.3505E+00	3.8680E+00	1.3645E-01	2.4546E+00	4.4536E-03
Ranking	5	11	12	10	4	7	9	3	6	2	8	1
Friedman test
Mean Rank	3.91	8.09	8.27	7.55	5.09	7.09	6.00	3.73	5.18	6.00	9.00	1.00
Final Ranking	3	10	11	9	4	8	6	2	5	6	12	1

For further investigation, the WRT was applied in Table 6 to find the significant improvements that cases obtained in the proposed IGOA compared to the comparative methods (i.e., SSA, WOA, SCA, DA, GWO, PSO, ALO, MPA, EO, AO, and GOA). The proposed method had 16 significant improvements out of 23 compared to SSA; it obtained 14 significant improvements out of 23 compared to WOA; it obtained 17 significant improvements out of 23 compared to SSA; it obtained 19 significant improvements out of 23 compared to SCA; it obtained 16 significant improvements out of 23 compared to DA; it obtained 16 significant improvements out of 23 compared to GWO; it obtained 15 significant improvements out of 23 compared to PSO; it obtained 15 significant improvements out of 23 compared to ALO; it obtained 14 significant improvements out of 23 compared to MPA; it obtained 11 significant improvements out of 23 compared to EO; and it obtained 17 significant improvements out of 23 compared to GOA.

Table 6. The results of the Wilcoxon ranking test of the comparative methods using 23 classical benchmark functions.

Measure	Comparative Algorithms
	SSA	WOA	SCA	DA	GWO	PSO	ALO	MPA	EO	AO	GOA
F1
p-value	2.7661E-02	3.5541E-02	3.5559E-01	5.8221E-03	1.6699E-02	3.0216E-02	4.3554E-02	3.0643E-02	3.5536E-02	3.5201E-01	3.5592E-01
Sign	1	1	0	1	1	1	1	1	1	0	0
F2
p-value	1.1761E-02	2.9581E-01	1.0812E-02	2.3280E-02	1.3734E-01	1.8648E-02	4.1002E-02	2.6155E-02	3.2647E-02	3.2957E-02	3.5592E-02
Sign	1	0	1	1	0	1	1	1	1	1	1
F3
p-value	1.2074E-02	1.2344E-02	1.3234E-02	1.8078E-02	1.6370E-01	4.6919E-02	2.2403E-03	3.1094E-01	1.2106E-02	3.5592E-02	3.5592E-02
Sign	1	1	1	1	0	1	1	0	1	1	1
F4
p-value	7.8557E-02	8.7641E-02	1.1406E-02	1.7528E-02	2.0308E-01	2.7028E-03	6.1763E-04	2.4542E-02	2.6797E-01	3.4241E-01	3.5592E-01
Sign	0	0	1	1	0	1	1	1	0	0	0
F5
p-value	1.2113E-01	1.1615E-10	7.5441E-09	4.2798E-03	8.9790E-08	1.3920E-02	3.0048E-01	4.3146E-06	8.7920E-07	2.1946E-01	5.9453E-09
Sign	0	1	1	1	1	1	0	1	1	0	1
F6
p-value	1.7828E-01	1.6523E-03	2.0092E-04	1.0725E-05	4.3337E-02	1.9479E-01	5.2165E-01	4.5575E-02	3.8125E-01	1.8377E-01	4.1149E-04
Sign	0	1	1	1	1	0	0	1	0	0	1
F7
p-value	2.7429E-04	3.3626E-01	1.3366E-02	4.0602E-02	8.9881E-03	3.8431E-02	1.6060E-02	2.9906E-02	1.2811E-01	8.4033E-01	6.5965E-02
Sign	1	0	1	1	1	1	1	1	0	0	0
F8
p-value	4.9287E-02	4.9287E-02	4.9286E-02	4.9286E-02	4.9287E-02	4.9285E-02	4.9286E-02	4.9288E-02	4.9287E-02	4.9287E-02	4.9286E-02
Sign	1	1	1	1	1	1	1	1	1	1	1
F9
p-value	1.2123E-03	3.5592E-01	3.4183E-01	3.6625E-05	3.7729E-02	1.5993E-02	5.6505E-04	3.5592E-01	2.0877E-01	3.5592E-01	1.2452E-02
Sign	1	0	0	1	1	1	1	0	0	0	1
F10
p-value	1.5111E-02	1.3792E-02	3.5415E-02	7.5193E-03	2.3472E-02	3.4494E-01	3.4726E-05	2.4523E-03	1.4998E-01	3.8431E-02	7.5441E-09
Sign	1	1	1	1	1	0	1	1	0	1	1
F11
p-value	6.7778E-04	1.0725E-05	1.6568E-02	7.3688E-03	3.1295E-03	4.5040E-02	7.2286E-02	3.5592E-01	1.9499E-01	4.3146E-06	3.5592E-01
Sign	1	1	1	1	1	1	0	0	0	1	0
F12
p-value	4.5898E-02	1.4565E-05	1.2774E-01	4.1330E-02	3.1982E-02	9.3609E-01	1.0150E-01	3.7499E-02	1.4498E-01	5.9953E-01	6.2976E-05
Sign	1	1	0	1	1	0	0	1	0	0	1
F13
p-value	3.1619E-01	1.3697E-07	5.1562E-04	3.5354E-01	1.6561E-02	3.9124E-01	7.4624E-02	1.9893E-01	1.6070E-03	4.0685E-01	1.9106E-05
Sign	0	1	1	0	1	0	0	0	1	0	1
F14
p-value	2.0296E-02	7.3831E-01	3.3765E-02	2.9617E-02	2.9344E-02	1.4011E-02	3.2899E-02	1.7275E-02	8.9226E-01	4.6549E-02	3.3358E-02
Sign	1	0	1	1	1	1	1	1	0	1	1
F15
p-value	2.8670E-05	2.4533E-01	2.0663E-03	4.1099E-02	4.6384E-02	4.0643E-02	9.3738E-02	1.3982E-01	9.3964E-03	3.5181E-01	1.5768E-02
Sign	1	0	1	1	1	1	0	0	1	0	1
F16
p-value	2.2168E-01	2.2493E-01	3.9237E-01	4.9464E-02	2.2172E-01	2.2168E-01	2.2168E-01	2.2168E-01	2.2168E-01	2.1779E-02	2.2188E-01
Sign	0	0	0	1	0	0	0	0	0	1	0
F17
p-value	2.5376E-02	4.9263E-02	7.0800E-01	2.6141E-02	2.5417E-02	2.5376E-02	2.5376E-02	2.5376E-02	2.5376E-02	2.7835E-02	1.1982E-02
Sign	1	1	0	1	1	1	1	1	1	1	1
F18
p-value	3.3442E-02	1.3387E-02	3.7619E-02	3.6649E-01	2.0723E-02	3.3442E-02	3.3442E-02	3.3442E-02	3.3443E-02	4.4389E-02	3.2447E-02
Sign	1	1	1	0	1	1	1	1	1	1	1
F19
p-value	2.4717E-02	4.7013E-02	3.0434E-02	6.9990E-01	2.4501E-02	2.3149E-02	2.4026E-02	6.1910E-01	2.3379E-02	8.1141E-01	3.3805E-02
Sign	1	1	1	0	1	1	1	0	1	0	1
F20
p-value	7.8799E-04	8.2574E-01	3.3926E-01	1.7493E-03	2.9256E-01	9.1595E-04	2.8465E-04	2.8465E-04	9.1707E-04	4.1671E-01	1.7737E-01
Sign	1	0	0	1	0	1	1	1	1	0	0
F21
p-value	6.6625E-03	3.2211E-02	7.1209E-04	4.6331E-02	6.2122E-01	9.8752E-01	2.8439E-02	1.0326E-02	4.0904E-02	1.7348E-01	3.3997E-03
Sign	1	1	1	1	0	0	1	1	1	0	1
F22
p-value	4.5947E-01	1.6723E-02	1.3534E-03	8.6195E-03	2.2524E-01	1.1780E-02	8.5115E-01	2.2436E-02	2.4921E-02	1.8822E-02	2.2948E-03
Sign	0	1	1	1	0	1	0	1	1	1	1
F23
p-value	9.2506E-01	6.1916E-02	8.1461E-03	2.2618E-01	4.8084E-02	8.2839E-01	2.6193E-02	5.6241E-01	2.8950E-02	2.2042E-02	2.5223E-02
Sign	0	0	1	0	1	0	1	0	1	1	1
Total	16	14	17	19	16	16	15	15	14	11	17

Figure 7 shows the convergence behaviors of the comparative algorithms on classical test functions (F1–F23), where the functions from 1–13 are fixed to 10 dimensions. These figures illustrate the optimization process during the iterations. It is clear that the proposed method finds the best solutions in all of the test cases, and it performs very well according to its convergence curves. For example, in the first test case (F1), the proposed IGOA presents good behavior through the optimization process. It had the best results in a smooth curve and faster compared to all comparative methods. The proposed IGOA in F16 obtained the best solution contrary to all comparison methods; the speed of the most significant difference is apparent.

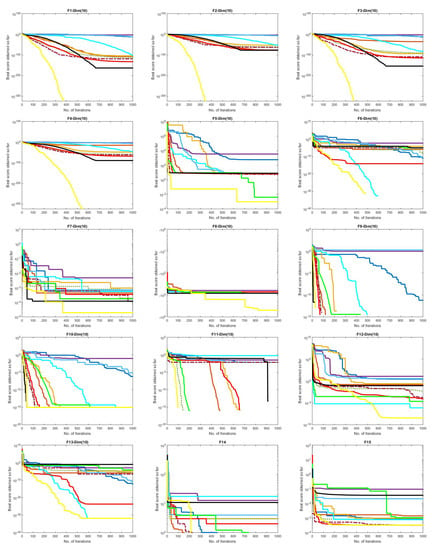
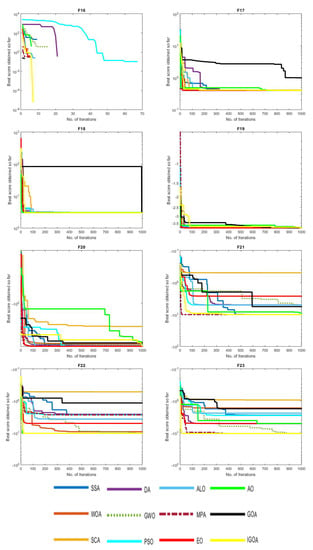
Figure 7. Convergence behaviors of the comparative algorithms on classical test functions (F1–F23).

Table 7 shows the results of the proposed IGOA compared to other comparative methods using classical benchmark functions (F1–F13), where the dimension size is 50. High-dimensional problems are used to validate the performance of the proposed IGOA compared to other methods. The proposed IGOA obtained better results than other methods, except the F8, which brought the best results in all of the test cases. The performance of the IGOA is excellent for solving high-dimensional problems. According to the FRT, the IGOA ranked first, followed by AO, MPA, EO, WOA, GOA, GWO, PSO, SSA, SCA, DA, and ALO. In Table 8, the results of the proposed IGOA compared to other comparative methods are presented using classical benchmark functions (F1–F13), where the dimension size is 100. Moreover, the proposed IGOA had the best results in all of the test cases, and it recorded the new best results in some cases. According to the FRT, the IGOA ranked first, followed by AO, MPA, WOA, EO, GOA, GWO, PSO, ALO, SSA, and SCA.

Table 7. The results of the proposed IGOA and other comparative methods using classical benchmark functions (F1–F13), where the dimension size is 50.

Measure	Comparative Algorithms
	SSA	WOA	SCA	DA	GWO	PSO	ALO	MPA	EO	AO	GOA	IGOA
F1
Max	1.6218E+04	2.1984E-21	5.5910E+03	1.6915E+04	1.2783E-06	1.8019E+02	2.8149E+04	3.6023E-23	1.3670E-13	5.3554E-79	6.6370E-03	1.5722E-79
Mean	1.1851E+04	5.4959E-22	2.4330E+03	1.1095E+04	6.6143E-07	8.8624E+01	2.1047E+04	1.1866E-23	4.4250E-14	1.3389E-79	3.1433E-03	3.9304E-80
Min	6.9875E+03	4.3444E-35	9.0817E+02	4.7960E+03	2.2679E-07	3.1343E+01	1.4298E+04	1.5924E-24	4.0144E-16	1.0172E-86	5.1212E-05	2.7584E-106
Std	3.8851E+03	1.0992E-21	2.1585E+03	5.0664E+03	4.8487E-07	6.3910E+01	6.5360E+03	1.6212E-23	6.3336E-14	2.6777E-79	3.4204E-03	7.8608E-80
Ranking	11	4	9	10	6	8	12	3	5	2	7	1
F2
Max	1.4023E+05	6.2386E-23	7.3347E+00	1.5847E+02	2.6315E-04	5.9956E+01	2.0823E+02	5.0305E-13	8.1913E-09	1.4280E-39	9.0945E-42	4.7159E-42
Mean	4.9211E+04	1.5787E-23	4.5222E+00	1.1268E+02	1.3932E-04	3.9135E+01	1.6509E+02	1.7435E-13	5.4547E-09	4.1641E-40	2.2736E-42	1.2189E-42
Min	1.3926E+02	4.2176E-30	6.1124E-01	6.7739E+01	4.5768E-05	2.2800E+01	7.3738E+01	2.9129E-14	2.6583E-09	1.1092E-42	4.7221E-59	1.8606E-51
Std	6.6198E+04	3.1067E-23	3.0088E+00	4.3988E+01	9.3082E-05	1.5398E+01	6.3429E+01	2.2192E-13	2.2952E-09	6.7921E-40	4.5473E-42	2.3326E-42
Ranking	12	4	8	10	7	9	11	5	6	3	2	1
F3
Max	6.5413E+04	6.8367E+05	1.0594E+05	2.4096E+05	1.7714E+03	1.4516E+04	1.5527E+05	1.9532E+00	6.2031E+01	1.0137E-76	4.8398E-01	3.9901E-84
Mean	5.8588E+04	4.5196E+05	7.2010E+04	1.8319E+05	8.7469E+02	1.0734E+04	1.2098E+05	6.1570E-01	1.7256E+01	2.5343E-77	2.4046E-01	9.9751E-85
Min	5.1191E+04	1.8831E+05	4.2268E+04	1.1646E+05	1.4849E+02	8.7526E+03	1.0824E+05	5.9612E-04	1.3599E-02	8.5573E-100	1.4096E-01	1.5318E-116
Std	6.2005E+03	2.3483E+05	3.3319E+04	5.1089E+04	6.8684E+02	2.6554E+03	2.2920E+04	9.2270E-01	2.9999E+01	5.0687E-77	1.6308E-01	1.9950E-84
Ranking	8	12	9	11	6	7	10	4	5	2	3	1
F4
Max	6.8899E+01	9.1800E+01	8.6073E+01	9.1337E+01	6.4686E+00	2.6396E+01	6.6814E+01	7.2917E-09	1.7832E-03	1.7153E-40	7.7673E-02	5.5416E-47
Mean	6.3772E+01	7.8942E+01	8.1343E+01	5.4232E+01	4.5319E+00	2.4381E+01	5.5044E+01	3.3935E-09	7.1452E-04	4.2899E-41	7.2182E-02	1.4531E-47
Min	6.0251E+01	4.1870E+01	7.4059E+01	2.3414E+01	2.8701E+00	2.2176E+01	4.2960E+01	1.6458E-09	2.1465E-04	2.7587E-52	6.7869E-02	2.8523E-65
Std	3.6504E+00	2.4719E+01	5.2408E+00	2.8233E+01	1.7816E+00	1.7632E+00	1.0941E+01	2.6186E-09	7.2951E-04	8.5756E-41	4.1536E-03	2.7287E-47
Ranking	10	11	12	8	6	7	9	3	4	2	5	1
F5
Max	1.1466E+07	4.8878E+01	2.5207E+07	2.0836E+07	4.8797E+01	6.0770E+04	3.2361E+07	4.8543E+01	4.8836E+01	9.2352E-01	4.8946E+01	7.5327E-02
Mean	8.1869E+06	4.8787E+01	1.4245E+07	1.1847E+07	4.8365E+01	3.2787E+04	2.1723E+07	4.8080E+01	4.8736E+01	2.6935E-01	4.8824E+01	2.3955E-02
Min	4.7476E+06	4.8704E+01	1.8179E+05	3.5789E+06	4.7957E+01	7.7683E+03	9.9082E+06	4.7882E+01	4.8561E+01	9.5134E-04	4.8635E+01	2.7754E-04
Std	3.1123E+06	8.7276E-02	1.1337E+07	7.0631E+06	4.0259E-01	2.6510E+04	1.1468E+07	3.1421E-01	1.2161E-01	4.3930E-01	1.4145E-01	3.5332E-02
Ranking	9	6	11	10	4	8	12	3	5	2	7	1
F6
Max	1.9156E+04	8.1525E+00	7.6716E+03	2.0207E+04	8.4984E+00	1.2644E+02	2.4720E+04	3.9668E+00	6.4815E+00	1.2152E-02	9.1091E+00	1.0081E-01
Mean	1.2957E+04	7.3447E+00	3.6820E+03	1.5112E+04	7.6074E+00	9.2171E+01	1.9583E+04	3.6884E+00	6.0817E+00	3.7421E-03	8.7934E+00	4.2876E-02
Min	1.0247E+04	6.2648E+00	6.0131E+02	4.7529E+03	7.0766E+00	4.9020E+01	1.4009E+04	3.3131E+00	5.8648E+00	3.6313E-07	8.0696E+00	2.7665E-03
Std	4.1735E+03	7.8671E-01	2.9352E+03	7.0247E+03	6.2472E-01	3.2030E+01	4.5631E+03	2.8150E-01	2.7298E-01	5.6647E-03	4.8543E-01	4.1387E-02
Ranking	10	5	9	11	6	8	12	3	4	1	7	2
F7
Max	2.9031E+01	3.1956E-02	9.8864E+00	2.2178E+01	3.0870E-02	4.9951E+02	3.9801E+01	3.1534E-03	1.7831E-02	8.0405E-04	1.2233E-03	6.5384E-04
Mean	1.6099E+01	1.6597E-02	4.9402E+00	1.4279E+01	1.7940E-02	1.8972E+02	2.6277E+01	2.3485E-03	9.1412E-03	3.8734E-04	6.6861E-04	3.0638E-04
Min	8.8668E+00	8.2613E-04	1.0335E+00	5.3067E+00	8.2160E-03	4.6662E+01	8.5259E+00	1.8104E-03	4.3024E-03	1.0980E-04	1.3892E-04	4.0132E-05
Std	8.8703E+00	1.6283E-02	3.6637E+00	7.6343E+00	1.0628E-02	2.0972E+02	1.3917E+01	5.8897E-04	6.3451E-03	2.9642E-04	4.8153E-04	2.6922E-04
Ranking	10	6	8	9	7	12	11	4	5	2	3	1
F8
Max	−8.7775E+03	−1.3214E+04	−3.8859E+03	−3.8665E+03	−7.1314E+03	−2.7860E+03	−9.0295E+03	−1.0965E+04	−9.4877E+03	−4.1272E+03	−5.6384E+03	−2.7814E+06
Mean	−9.4181E+03	−1.7744E+04	−4.1214E+03	−4.6595E+03	−8.3000E+03	−4.1270E+03	−9.0295E+03	−1.1250E+04	−1.0613E+04	−4.7543E+03	−6.0615E+03	−1.9399E+09
Min	−1.0788E+04	−2.0805E+04	−4.3281E+03	−6.2820E+03	−9.1511E+03	−5.2134E+03	−9.0295E+03	−1.1795E+04	−1.2302E+04	−6.1055E+03	−6.6070E+03	−5.7275E+09
Std	9.2277E+02	3.6361E+03	1.9671E+02	1.1238E+03	9.8483E+02	1.0172E+03	0.0000E+00	3.7047E+02	1.1959E+03	9.1748E+02	4.6042E+02	2.6775E+09
Ranking	5	2	12	10	7	11	6	3	4	9	8	1
F9
Max	4.0940E+02	6.7153E-07	2.2995E+02	6.3180E+02	2.1152E+01	4.0120E+02	3.6963E+02	0.0000E+00	2.8863E+00	0.0000E+00	0.0000E+00	0.0000E+00
Mean	3.8197E+02	1.6788E-07	1.4151E+02	5.6403E+02	9.0516E+00	3.5740E+02	3.3235E+02	0.0000E+00	7.2156E-01	0.0000E+00	0.0000E+00	0.0000E+00
Min	3.6797E+02	0.0000E+00	4.2817E+01	5.1762E+02	1.6947E+00	3.3564E+02	3.0105E+02	0.0000E+00	5.6843E-13	0.0000E+00	0.0000E+00	0.0000E+00
Std	1.9120E+01	3.3576E-07	7.7491E+01	4.8844E+01	8.4071E+00	2.9652E+01	3.3984E+01	0.0000E+00	1.4431E+00	0.0000E+00	0.0000E+00	0.0000E+00
Ranking	11	5	8	12	7	10	9	1	6	1	1	1
F10
Max	1.9306E+01	6.9722E-13	2.0650E+01	1.9961E+01	3.4051E-04	6.9781E+00	1.8075E+01	5.3024E-13	2.0638E-08	8.8818E-16	1.3498E-08	8.8818E-16
Mean	1.8195E+01	1.8741E-13	1.8678E+01	1.7540E+01	2.0529E-04	5.4526E+00	7.9782E+00	3.7126E-13	1.1748E-08	8.8818E-16	3.3745E-09	8.8818E-16
Min	1.7747E+01	4.4409E-15	1.2972E+01	1.6521E+01	6.9576E-05	4.3857E+00	8.8818E-16	2.2116E-13	4.6971E-09	8.8818E-16	8.8818E-16	8.8818E-16
Std	7.4469E-01	3.4025E-13	3.8039E+00	1.6273E+00	1.2266E-04	1.1117E+00	8.7915E+00	1.3779E-13	6.6047E-09	0.0000E+00	6.7490E-09	0.0000E+00
Ranking	11	3	12	10	7	8	9	4	6	1	5	1
F11
Max	1.7362E+02	1.1102E-16	1.0601E+01	4.3677E+02	7.4534E-02	1.9413E+02	3.1461E+02	0.0000E+00	1.0418E-02	0.0000E+00	3.4754E+02	0.0000E+00
Mean	1.2334E+02	5.5511E-17	6.9297E+00	2.3595E+02	1.8637E-02	1.3345E+02	1.9353E+02	0.0000E+00	2.6046E-03	0.0000E+00	2.1478E+02	0.0000E+00
Min	9.4444E+01	0.0000E+00	1.2481E+00	1.1602E+02	4.0480E-07	1.0472E+02	9.0246E+01	0.0000E+00	1.9984E-15	0.0000E+00	1.2010E+02	0.0000E+00
Std	3.4603E+01	6.4099E-17	4.2980E+00	1.4060E+02	3.7264E-02	4.2027E+01	9.7164E+01	0.0000E+00	5.2092E-03	0.0000E+00	9.6724E+01	0.0000E+00
Ranking	8	4	7	12	6	9	10	1	5	1	11	1
F12
Max	6.6041E+06	7.6181E-01	1.7325E+08	2.9504E+06	8.7300E-01	1.2819E+01	2.4959E+07	2.8493E-01	4.6137E-01	7.7594E-05	9.6619E-01	5.2576E-05
Mean	4.7716E+06	6.7329E-01	8.5889E+07	1.3861E+06	5.2826E-01	8.2059E+00	9.8564E+06	2.0643E-01	3.9241E-01	3.0632E-05	9.3607E-01	2.1443E-05
Min	7.2951E+05	4.2717E-01	5.0216E+07	6.7839E+05	4.0129E-01	3.6242E+00	1.9815E+06	1.1744E-01	3.2544E-01	1.9160E-06	9.0405E-01	3.9386E-07
Std	2.7700E+06	1.6419E-01	5.8718E+07	1.0568E+06	2.2999E-01	4.0047E+00	1.0301E+07	6.8716E-02	6.0555E-02	3.2779E-05	2.8743E-02	2.5393E-05
Ranking	10	6	12	9	5	8	11	3	4	2	7	1
F13
Max	1.8640E+08	4.0618E+00	3.5703E+08	5.1925E+07	4.5126E+00	9.2536E+01	1.3806E+08	4.6401E+00	3.9209E+00	7.1058E-03	5.0124E+00	5.0486E-04
Mean	7.4528E+07	3.2654E+00	1.3817E+08	2.0251E+07	4.1590E+00	7.7931E+01	9.0749E+07	4.1691E+00	3.6951E+00	3.4706E-03	4.9641E+00	1.9322E-04
Min	2.7158E+07	2.5325E+00	3.4788E+06	7.2943E+06	3.7958E+00	3.5409E+01	6.6837E+07	3.7053E+00	3.4860E+00	3.5106E-04	4.9044E+00	3.0919E-05
Std	7.5206E+07	8.1278E-01	1.6310E+08	2.1185E+07	3.3293E-01	2.8350E+01	3.3005E+07	3.8267E-01	1.7869E-01	2.9141E-03	5.0203E-02	2.1632E-04
Ranking	10	3	12	9	5	8	11	6	4	2	7	1
Friedman test
Mean Rank	9.62	5.46	9.92	10.08	6.08	8.69	10.23	3.31	4.85	2.31	5.62	1.08
Final Ranking	9	5	10	11	7	8	12	3	4	2	6	1

Table 8. The results of the proposed IGOA and other comparative methods using classical benchmark functions (F1–F13), where the dimension size is 100.

Measure	Comparative Algorithms
	SSA	WOA	SCA	DA	GWO	PSO	ALO	MPA	EO	AO	GOA	IGOA
F1
Max	6.4450E+04	2.2100E-25	1.8971E+04	6.1119E+04	1.9274E-03	2.6248E+03	1.0401E+05	2.1620E-21	1.7958E-11	4.7366E-83	6.4311E-02	3.2757E-97
Mean	5.8329E+04	6.0754E-26	1.5087E+04	3.0927E+04	1.2495E-03	1.8935E+03	8.6209E+04	8.2788E-22	8.9226E-12	1.1847E-83	4.5752E-02	8.1893E-98
Min	4.6369E+04	6.0190E-30	1.0715E+04	7.4207E+03	8.4757E-04	1.2104E+03	5.7437E+04	5.0547E-23	8.6992E-13	3.0147E-93	3.5219E-02	4.1461E-126
Std	8.2402E+03	1.0732E-25	4.0115E+03	2.3071E+04	4.9092E-04	6.0029E+02	2.0334E+04	9.2942E-22	9.1868E-12	2.3680E-83	1.3744E-02	1.6379E-97
Ranking	11	3	9	10	6	8	12	4	5	2	7	1
F2
Max	1.1688E+25	3.4538E-23	4.4337E+01	3.2154E+02	7.1401E-03	2.2877E+02	4.8464E+02	7.1408E-13	9.6007E-08	1.0283E-44	1.4934E-12	7.6707E-49
Mean	2.9221E+24	8.6966E-24	3.5901E+01	2.8186E+02	4.9435E-03	1.9384E+02	4.0496E+02	3.6888E-13	6.5048E-08	3.7138E-45	4.0823E-13	1.9177E-49
Min	3.6567E+07	4.6747E-27	2.3812E+01	2.0375E+02	3.8459E-03	1.5887E+02	2.2760E+02	1.6618E-13	5.5969E-09	5.0295E-54	5.8608E-24	2.8573E-57
Std	5.8441E+24	1.7228E-23	9.0612E+00	5.3474E+01	1.5476E-03	3.1984E+01	1.1956E+02	2.4632E-13	4.1719E-08	4.5717E-45	7.2438E-13	3.8354E-49
Ranking	12	3	8	10	7	9	11	4	6	2	5	1
F3
Max	3.0940E+05	2.9857E+06	4.5705E+05	7.2240E+05	2.6564E+04	9.1971E+04	5.1265E+05	1.6998E+02	1.3121E+04	9.4571E-79	2.1274E+00	9.9554E-97
Mean	2.3669E+05	1.7822E+06	2.9752E+05	6.5700E+05	1.9553E+04	8.5210E+04	4.3074E+05	5.5700E+01	4.8385E+03	2.3644E-79	8.8560E-01	5.5818E-97
Min	1.6464E+05	9.4484E+05	2.0399E+05	5.8488E+05	1.2861E+04	7.6831E+04	3.9466E+05	2.5961E-01	9.3275E+01	3.7128E-93	3.2007E-01	4.0772E-112
Std	6.7513E+04	9.2686E+05	1.1076E+05	6.5245E+04	6.5376E+03	6.8786E+03	5.5000E+04	7.7934E+01	6.1542E+03	4.7284E-79	8.4679E-01	4.1342E-97
Ranking	8	12	9	11	6	7	10	4	5	2	3	1
F4
Max	8.9996E+01	9.5933E+01	9.7350E+01	9.0926E+01	3.6873E+01	4.2037E+01	9.2671E+01	7.6362E-08	4.6973E+00	4.0962E-40	1.3932E-01	5.7872E-40
Mean	8.1540E+01	8.5303E+01	9.5168E+01	7.3538E+01	3.0380E+01	3.8428E+01	7.3165E+01	3.6609E-08	1.3036E+00	1.0252E-40	1.1315E-01	1.4468E-40
Min	7.1679E+01	6.9219E+01	9.2087E+01	5.7173E+01	2.7215E+01	3.6876E+01	5.9800E+01	9.5124E-09	1.5244E-02	9.4961E-61	8.1765E-02	7.0045E-51
Std	7.5223E+00	1.1439E+01	2.2576E+00	1.5401E+01	4.4120E+00	2.4303E+00	1.4777E+01	2.8403E-08	2.2658E+00	2.0473E-40	2.7412E-02	2.8936E-40
Ranking	10	11	12	9	6	7	8	3	5	1	4	2
F5
Max	1.3626E+08	9.8819E+01	2.9568E+08	1.6827E+08	9.9508E+01	2.3804E+06	2.1146E+08	9.8561E+01	9.8782E+01	1.2431E+00	9.9003E+01	1.0128E+00
Mean	1.1233E+08	9.8685E+01	1.8065E+08	1.3770E+08	9.8798E+01	1.6261E+06	1.3225E+08	9.8410E+01	9.8675E+01	6.8750E-01	9.8967E+01	2.5496E-01
Min	9.6365E+07	9.8552E+01	1.0803E+08	9.1133E+07	9.7860E+01	1.1455E+06	7.1318E+07	9.7992E+01	9.8452E+01	2.2469E-01	9.8940E+01	7.9814E-04
Std	1.7408E+07	1.1599E-01	8.7119E+07	3.6996E+07	6.8924E-01	5.3146E+05	5.8216E+07	2.7899E-01	1.5157E-01	4.5514E-01	2.7347E-02	5.0525E-01
Ranking	9	5	12	11	6	8	10	3	4	2	7	1
F6
Max	8.9225E+04	1.7458E+01	4.4523E+04	4.8419E+04	1.8732E+01	4.5079E+03	1.1998E+05	1.5020E+01	1.8757E+01	4.8547E-02	2.0854E+01	9.9236E-02
Mean	6.7793E+04	1.5675E+01	2.2272E+04	3.1812E+04	1.7622E+01	2.3132E+03	8.8804E+04	1.4006E+01	1.7521E+01	1.4148E-02	2.0176E+01	3.3483E-02
Min	5.0618E+04	1.4788E+01	5.6090E+03	1.7590E+04	1.6555E+01	8.9842E+02	5.7004E+04	1.2863E+01	1.5730E+01	4.5258E-06	1.9503E+01	2.3732E-03
Std	1.6012E+04	1.2371E+00	1.8107E+04	1.4850E+04	8.8996E-01	1.5634E+03	3.2783E+04	9.4087E-01	1.3357E+00	2.3070E-02	6.8445E-01	4.4461E-02
Ranking	11	4	9	10	6	8	12	3	5	1	7	2
F7
Max	2.7204E+02	1.8463E-02	3.9305E+02	3.0559E+02	1.0116E-01	2.0273E+03	2.0268E+02	4.6610E-03	1.1035E-02	1.8323E-03	8.5588E-04	1.0198E-03
Mean	1.4734E+02	9.5542E-03	1.6825E+02	1.9049E+02	5.8300E-02	1.7556E+03	1.3493E+02	2.3908E-03	8.0461E-03	8.9543E-04	5.3393E-04	3.7064E-04
Min	7.9767E+01	6.0216E-03	7.5642E+01	1.0019E+02	2.5231E-02	1.4554E+03	5.2479E+01	1.5111E-03	6.0757E-03	6.8527E-06	1.7860E-05	2.0470E-05
Std	8.6798E+01	5.9534E-03	1.5044E+02	8.9961E+01	3.5648E-02	2.5530E+02	6.5760E+01	1.5163E-03	2.2743E-03	8.5082E-04	3.6001E-04	4.6821E-04
Ranking	9	6	10	11	7	12	8	4	5	3	2	1
F8
Max	−1.3646E+04	−2.1492E+04	−5.3732E+03	−6.6223E+03	−1.1677E+04	−5.1598E+03	−1.8059E+04	−1.6364E+04	−1.4114E+04	−4.9756E+03	−7.1045E+03	−4.9875E+06
Mean	−1.5292E+04	−2.7471E+04	−5.9623E+03	−7.6416E+03	−1.3239E+04	−5.9618E+03	−1.8059E+04	−1.8456E+04	−1.7127E+04	-6.9425E+03	−7.5314E+03	−1.1856E+11
Min	−1.6871E+04	−3.7725E+04	−6.2835E+03	−8.9144E+03	−1.4785E+04	−7.7160E+03	−1.8059E+04	−2.0714E+04	−2.1019E+04	−8.8904E+03	−8.5248E+03	−4.7145E+11
Std	1.3184E+03	7.0723E+03	4.0828E+02	1.0152E+03	1.3767E+03	1.1981E+03	0.0000E+00	1.9681E+03	3.0433E+03	1.7483E+03	6.7273E+02	2.3526E+11
Ranking	6	2	11	8	7	12	4	3	5	10	9	1
F9
Max	9.9339E+02	0.0000E+00	4.8313E+02	1.1884E+03	9.8581E+01	1.1115E+03	9.3285E+02	0.0000E+00	2.4728E+00	0.0000E+00	0.0000E+00	0.0000E+00
Mean	8.7313E+02	0.0000E+00	3.2001E+02	1.1454E+03	5.4544E+01	9.7640E+02	8.0171E+02	0.0000E+00	8.7120E-01	0.0000E+00	0.0000E+00	0.0000E+00
Min	7.9510E+02	0.0000E+00	1.4363E+02	1.0557E+03	2.8686E+01	9.0364E+02	6.9063E+02	0.0000E+00	1.3642E-12	0.0000E+00	0.0000E+00	0.0000E+00
Std	8.6539E+01	0.0000E+00	1.6490E+02	6.0815E+01	3.0661E+01	9.8033E+01	1.0578E+02	0.0000E+00	1.1695E+00	0.0000E+00	0.0000E+00	0.0000E+00
Ranking	10	1	8	12	7	11	9	1	6	1	1	1
F10
Max	1.9126E+01	3.5039E-12	2.0689E+01	1.9743E+01	6.6654E-03	1.0103E+01	1.8613E+01	2.2462E-12	2.5460E-07	4.4409E-15	4.8293E-03	8.8818E-16
Mean	1.8807E+01	9.2015E-13	2.0650E+01	1.6857E+01	4.6223E-03	9.7618E+00	9.3010E+00	1.7613E-12	1.4055E-07	1.7764E-15	2.4339E-03	8.8818E-16
Min	1.8189E+01	1.5099E-14	2.0599E+01	1.4417E+01	2.2334E-03	9.3897E+00	8.8818E-16	1.4539E-12	6.4001E-08	8.8818E-16	3.7348E-06	8.8818E-16
Std	4.1994E-01	1.7234E-12	3.7988E-02	2.5906E+00	2.0241E-03	3.1516E-01	1.0740E+01	3.4094E-13	8.0772E-08	1.7764E-15	2.2733E-03	0.0000E+00
Ranking	11	3	12	10	7	9	8	4	5	2	6	1
F11
Max	7.6438E+02	0.0000E+00	2.4170E+02	5.5599E+02	1.3725E-01	3.4697E+02	8.8736E+02	0.0000E+00	4.4995E-11	0.0000E+00	1.5563E+03	0.0000E+00
Mean	6.6258E+02	0.0000E+00	1.2059E+02	3.2260E+02	6.7813E-02	2.9022E+02	7.4397E+02	0.0000E+00	1.5632E-11	0.0000E+00	1.2242E+03	0.0000E+00
Min	5.0940E+02	0.0000E+00	6.7609E+01	9.6513E+01	3.6218E-04	2.6014E+02	4.8176E+02	0.0000E+00	3.2496E-13	0.0000E+00	9.8697E+02	0.0000E+00
Std	1.0973E+02	0.0000E+00	8.1316E+01	1.9609E+02	7.7747E-02	3.9246E+01	1.8275E+02	0.0000E+00	2.0097E-11	0.0000E+00	2.4182E+02	0.0000E+00
Ranking	10	1	7	9	6	8	11	1	5	1	12	1
F12
Max	1.0867E+08	6.2302E-01	1.1473E+09	1.3795E+07	7.8790E-01	8.7761E+04	1.9343E+08	4.1403E-01	6.5971E-01	3.2853E-05	1.1572E+00	1.3334E-05
Mean	7.7271E+07	5.0075E-01	7.2816E+08	7.4978E+06	6.9134E-01	3.0279E+04	1.2189E+08	3.6533E-01	6.2007E-01	1.5033E-05	1.0648E+00	7.0284E-06
Min	5.3628E+07	2.8339E-01	2.5478E+08	2.0035E+06	5.7241E-01	1.1431E+03	4.8932E+07	3.3838E-01	5.4336E-01	1.5344E-06	1.0026E+00	7.4445E-09
Std	2.4450E+07	1.5492E-01	3.7221E+08	5.3527E+06	1.0843E-01	4.0208E+04	6.2288E+07	3.4113E-02	5.3034E-02	1.5254E-05	6.7986E-02	7.2560E-06
Ranking	10	4	12	9	6	8	11	3	5	2	7	1
F13
Max	6.1786E+08	9.3496E+00	1.0303E+09	5.1763E+08	1.0134E+01	9.1508E+05	7.5026E+08	9.7839E+00	9.2059E+00	4.2178E-02	1.0028E+01	2.5780E-02
Mean	3.3934E+08	8.5770E+00	8.8837E+08	2.0178E+08	9.4544E+00	4.9212E+05	4.8928E+08	9.6897E+00	8.9239E+00	1.1599E-02	9.9911E+00	7.5849E-03
Min	1.6900E+08	8.0494E+00	6.4915E+08	3.6750E+07	8.8932E+00	1.1739E+05	2.9431E+08	9.5922E+00	8.5903E+00	5.6404E-04	9.9129E+00	1.2093E-05
Std	1.9376E+08	5.5539E-01	1.7019E+08	2.1606E+08	5.2363E-01	3.3819E+05	2.0447E+08	1.0628E-01	2.6804E-01	2.0401E-02	5.3388E-02	1.2292E-02
Ranking	10	3	12	9	5	8	11	6	4	2	7	1
Friedman test
Mean Rank	9.77	4.46	10.08	9.92	6.31	8.85	9.62	3.31	5.00	2.38	5.92	1.15
Final Ranking	10	4	12	11	7	8	9	3	5	2	6	1

Figure 8 illustrates the convergence behaviors of the comparative algorithms on classical test functions (F1–F13) with higher dimensional sizes (i.e., 100). Obviously, the proposed IGOA has the best solutions in all of the test high-dimensional problems, and it shows promising behavior according to the given convergence curves. For example, in the third test case (F3), the proposed IGOA shows stable and smooth convergence behavior through the optimization rule. It is faster than all of the comparative methods in solving high-dimensional problems.

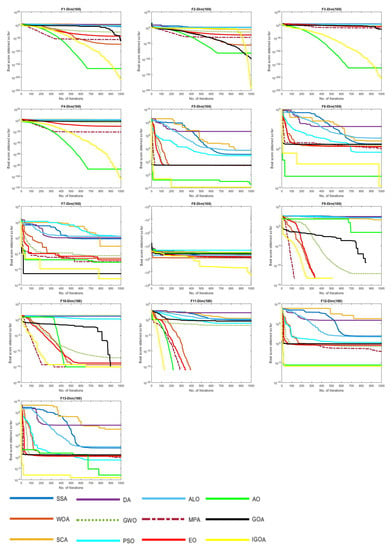
Figure 8. Convergence behaviors of the comparative algorithms on classical test functions (F1–F13) with higher dimensional sizes (i.e., 100).

Figure 9 shows the exploration and exploitation of the optimization processes. This figure shows the division of the search tools and how to exploit them during the optimization process, which indicates the distribution between the search tools of exploitation and exploration; this enhances the ability of the proposed algorithm to find new solutions in the available search space.

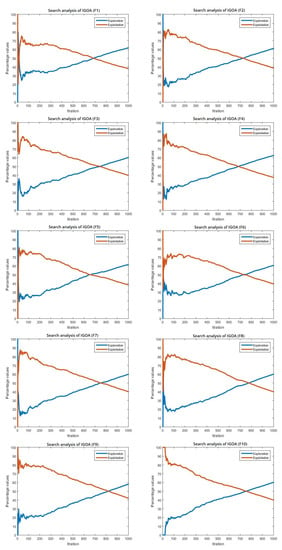
Figure 9. The exploration and exploitation of the optimization processes.

5.2. Experiments Series 2: Advanced CEC2017 Benchmark Problems

In this section, the proposed IGOA is tested further using a set of 30 advanced CEC2017 benchmark functions.

The types and descriptions of the used CEC2017 benchmark functions are presented in Table 9. The benchmark functions are unimodal (F1–F3) and multimodal (F4–F10), which are shifted and rotated functions. Hybrid functions range from F11 to F20. Composition functions range from F21 to F30. These functions are usually used to test the exploration and exploitation search processes and their equilibrium. The primary setting of the experiment in this section is the same as in the previous section.

Table 9. Description of CEC2017 functions.

No.	Type	Description	Fi*
1	Unimodal functions	SAR Bent Cigar Function	100
2		SAR Sum of Different Power Functions	200
3		SAR Zakharov Function	300
4	Simple Multimodal Functions	SAR Rosenbrock’s Function	400
5		SAR Rastrigin’s Function	500
6		SAR Expanded Schaffer’s F6 Function	600
7		SAR Lunacek’s Bi-Rastrigin Function	700
8		SAR Non-Continuous Rastrigin’s Function	800
9		SAR Lévy Function	900
10		SAR Schwefel’s Function	1000
11	Hybrid functions	HF1 (N = 3)	1100
12		HF2 (N = 3)	1200
13		HF3 (N = 3)	1300
14		HF4 (N = 4)	1400
15		HF5 (N = 4)	1500
16		HF6 (N = 4)	1600
17		HF6 (N = 5)	1700
18		HF6 (N = 5)	1800
19		HF6 (N = 5)	1900
20		HF6 (N = 6)	2000
21	Composition Functions	CF1 (N = 3)	2100
22		CF2 (N = 3)	2200
23		CF3 (N = 4)	2300
24		CF4 (N = 4)	2400
25		CF5 (N = 5)	2500
26		CF6 (N = 5)	2600
27		CF7 (N = 6)	2700
28		CF8 (N = 6)	2800
29		CF9 (N = 3)	2900
30		CF10 (N = 3)	3000

Note: SAR = shifted and rotated, HF = hybrid function, CF = composition function.

The proposed IGOA is compared with other state-of-the-art methods using CEC2017, including the dimension-decided Harris hawks optimization (GCHHO) [42], multi-strategy mutative whale-inspired optimization (CCMWOA) [43], balanced whale optimization algorithm (BMWOA) [18], reinforced whale optimizer (BWOA) [44], hybridizing sine–cosine differential evolution (SCADE) [45], Cauchy and Gaussian sine–cosine algorithm (CGSCA) [46], improved opposition-based sine–cosine optimizer (OBSCA) [47], hybrid grey wolf differential evolution (HGWO) [48], mutation-driven salp chains-inspired optimizer (CMSSA) [49], and dynamic Harris hawks optimization (DHHOM) [50].

The results of the proposed IGOA compared to other comparative state-of-the-art methods are presented in Table 10 using 30 CEC2017 benchmark functions. This table shows that the proposed IGOA method obtained perfect results compared to other methods. In most of the best CEC2017 problems, the IGOA obtained better results and delivered high-quality solutions to solve mathematical problems. FRT was conducted in Table 11 to rank the comparative methods for solving the CEC2017 problems to support our claim. In Table 11, the proposed IGOA is ranked first, followed by GCHHO, CMSSA, DHHOM, HGWO, BMWOA, BWOA, CGSCA, OBSCA, SCADE, and CCMWOA. So, the obtained results proved that the performance of the IGOA is promising compared to other comparative methods. Since these mathematical problems are complex, it is challenging to reach the optimal solutions for such problems. Since the proposed method obtained a set of optimal solutions, this confirms its efficiency in solving complex and different CEC2017 problems, improving its ability to avert from local optima and increase population diversity.

Table 10. The results of the proposed IGOA and other comparative methods using 30 CEC2017 benchmark functions.

Measure	Comparative Algorithms
	GCHHO	CCMWOA	BMWOA	BWOA	SCADE	CGSCA	OBSCA	HGWO	CMSSA	DHHOM	IGOA
F1
Mean	3.30940E+03	2.02540E+10	2.37560E+08	1.57600E+08	2.01310E+10	1.42880E+10	1.67810E+10	8.13100E+09	1.35370E+09	1.34700E+07	3.25100E+03
Std	4.00990E+03	4.34540E+09	1.12730E+08	9.52730E+07	2.37100E+09	1.99070E+09	2.57230E+09	1.16330E+09	8.03300E+08	2.56170E+06	4.65850E+04
F2
Mean	1.42050E+06	7.75550E+37	2.63340E+22	1.86990E+26	1.55760E+36	1.78980E+35	3.60910E+35	1.18990E+34	7.57370E+31	7.66760E+15	1.32600E+03
Std	4.35570E+06	2.78850E+38	1.01970E+23	7.00190E+26	4.19900E+36	4.60380E+35	8.75620E+35	2.40170E+34	3.86780E+32	2.11000E+16	4.23561E+06
F3
Mean	5.72480E+02	7.75120E+04	6.95490E+04	5.78200E+04	5.93160E+04	4.18320E+04	6.17240E+04	7.78820E+04	5.91790E+04	1.54280E+04	5.72000E+02
Std	2.29300E+02	6.00500E+03	8.30380E+03	1.08020E+04	6.77840E+03	7.55140E+03	5.80660E+03	5.29540E+03	7.90900E+03	3.37440E+03	2.15410E+04
F4
Mean	4.92330E+02	3.37030E+03	6.13220E+02	6.11720E+02	3.69940E+03	1.71050E+03	2.67520E+03	8.98810E+02	6.97120E+02	5.38890E+02	4.93000E+02
Std	2.20920E+01	1.07380E+03	4.52740E+01	7.44420E+01	7.85300E+02	3.16700E+02	8.37710E+02	1.21710E+02	1.25430E+02	3.28540E+01	2.15000E+02
F5
Mean	7.16920E+02	8.35120E+02	7.94230E+02	7.67440E+02	8.28150E+02	7.89630E+02	8.06510E+02	7.50670E+02	7.16280E+02	7.35870E+02	7.15000E+02
Std	3.58460E+01	3.41570E+01	4.81890E+01	3.47290E+01	2.18030E+01	2.43770E+01	2.45210E+01	1.39620E+01	5.00250E+01	3.09490E+01	1.21456E+01
F6
Mean	6.52280E+02	6.68500E+02	6.64740E+02	6.67190E+02	6.60110E+02	6.54060E+02	6.57370E+02	6.37400E+02	6.52630E+02	6.62000E+02	6.37322E+02
Std	7.04260E+00	7.43640E+00	1.22790E+01	4.92080E+00	5.71150E+00	6.12160E+00	5.42690E+00	2.75530E+00	1.67270E+01	6.79720E+00	1.23549E+01
F7
Mean	1.07440E+03	1.28440E+03	1.18850E+03	1.23650E+03	1.17650E+03	1.14720E+03	1.17170E+03	1.03810E+03	9.80550E+02	1.23790E+03	9.80003E+02
Std	9.50300E+01	7.86780E+01	1.04810E+02	7.38450E+01	3.21420E+01	5.09880E+01	3.47780E+01	2.95840E+01	6.57600E+01	7.19790E+01	2.15648E+01
F8
Mean	9.51300E+02	1.05130E+03	1.01270E+03	9.77110E+02	1.08420E+03	1.05910E+03	1.06590E+03	1.00090E+03	9.89580E+02	9.53930E+02	9.50548E+02
Std	2.50210E+01	3.14490E+01	3.44830E+01	2.20290E+01	1.78760E+01	2.15500E+01	1.96760E+01	1.30390E+01	3.35310E+01	2.24990E+01	1.23684E+01
F9
Mean	4.99930E+03	7.99490E+03	7.26070E+03	6.21960E+03	8.16870E+03	6.13090E+03	6.89320E+03	3.48300E+03	4.79750E+03	7.15890E+03	3.48226E+03
Std	6.67700E+02	1.18910E+03	1.33260E+03	8.87330E+02	1.20850E+03	1.22730E+03	1.13440E+03	4.07920E+02	1.93030E+03	7.65270E+02	1.85667E+02
F10
Mean	4.93970E+03	7.11260E+03	7.41370E+03	6.54980E+03	8.23470E+03	8.14170E+03	7.36950E+03	6.65980E+03	6.29020E+03	5.52560E+03	4.93911E+03
Std	7.02370E+02	6.56310E+02	7.24060E+02	9.75090E+02	2.22270E+02	2.97070E+02	3.50750E+02	4.53880E+02	6.78770E+02	5.45470E+02	1.98266E+02
F11
Mean	1.22750E+03	3.51630E+03	1.63860E+03	1.74140E+03	3.43800E+03	2.24610E+03	2.69610E+03	5.03510E+03	2.11820E+03	1.25990E+03	1.22636E+03
Std	4.61680E+01	7.12600E+02	1.73870E+02	2.18240E+02	6.15770E+02	2.93550E+02	5.75960E+02	9.23410E+02	3.80140E+02	4.31720E+01	3.26710E+01
F12
Mean	1.18910E+06	2.18990E+09	7.96980E+07	1.34760E+08	1.92660E+09	1.43190E+09	2.04570E+09	5.89000E+08	1.78120E+08	1.54720E+07	1.18237E+06
Std	1.05870E+06	1.40780E+09	6.51450E+07	8.69410E+07	4.82420E+08	3.09240E+08	6.73740E+08	1.53340E+08	1.86560E+08	1.09180E+07	1.53623E+04
F13
Mean	1.51460E+04	8.10180E+07	3.16270E+05	2.49390E+05	6.42760E+08	5.11870E+08	6.32870E+08	3.06160E+08	7.74430E+05	4.53100E+05	1.51413E+04
Std	1.55350E+04	1.01880E+08	2.76180E+05	1.49100E+05	2.80990E+08	1.88770E+08	2.45500E+08	1.52570E+08	3.73460E+06	3.41790E+05	1.23633E+04
F14
Mean	4.37800E+04	1.36190E+06	4.51810E+05	9.58570E+05	3.42730E+05	1.83780E+05	2.12560E+05	7.58740E+05	3.33800E+05	1.26670E+05	4.36933E+04
Std	3.37360E+04	1.06020E+06	2.97310E+05	1.03090E+06	1.51470E+05	1.04920E+05	1.04490E+05	6.32210E+05	3.16240E+05	1.06830E+05	1.54932E+04
F15
Mean	7.98250E+03	6.08890E+06	8.76670E+04	1.20450E+05	8.49960E+06	1.02240E+07	1.38510E+07	1.27440E+07	2.58440E+04	6.76810E+04	7.98191E+03
Std	7.03540E+03	7.18430E+06	9.03590E+04	8.97940E+04	5.00020E+06	1.16050E+07	1.72250E+07	1.57900E+07	2.18710E+04	4.31430E+04	7.54535E+03
F16
Mean	2.75590E+03	3.82030E+03	3.29790E+03	3.67160E+03	3.91670E+03	3.76790E+03	3.84600E+03	3.29040E+03	3.18600E+03	3.27670E+03	2.75461E+03
Std	3.40700E+02	5.19220E+02	3.55500E+02	5.13770E+02	2.38250E+02	2.22570E+02	2.22620E+02	1.67740E+02	3.03380E+02	2.92610E+02	1.33951E+02
F17
Mean	2.32790E+03	2.74680E+03	2.37630E+03	2.60050E+03	2.52920E+03	2.46670E+03	2.60340E+03	2.41310E+03	2.38060E+03	2.61210E+03	2.32751E+03
Std	2.20580E+02	3.49430E+02	2.56110E+02	2.84310E+02	1.63110E+02	1.85890E+02	1.61410E+02	1.69650E+02	1.98150E+02	2.77480E+02	1.25317E+02
F18
Mean	2.25110E+05	8.74010E+06	2.91200E+06	3.17660E+06	3.73710E+06	3.13090E+06	4.22870E+06	1.46490E+06	2.46650E+06	1.09400E+06	2.25110E+05
Std	1.61650E+05	8.78500E+06	2.41540E+06	3.06640E+06	2.58540E+06	1.39660E+06	2.36190E+06	1.30980E+06	3.60400E+06	9.71750E+05	1.65429E+04
F19
Mean	6.63810E+03	5.12680E+06	7.74970E+05	3.48230E+06	2.33610E+07	2.46870E+07	4.16280E+07	1.38590E+07	6.29370E+06	4.04430E+05	6.63798E+03
Std	7.38500E+03	7.32160E+06	8.59610E+05	3.12020E+06	1.15100E+07	1.22460E+07	2.74960E+07	1.55780E+07	5.81650E+06	2.62140E+05	4.62325E+03
F20
Mean	2.56010E+03	2.70240E+03	2.76650E+03	2.79680E+03	2.74110E+03	2.62520E+03	2.70000E+03	2.65430E+03	2.60240E+03	2.71820E+03	2.55955E+03
Std	2.02220E+02	2.16930E+02	1.62670E+02	2.18290E+02	1.08830E+02	1.38560E+02	1.31380E+02	1.30220E+02	2.05090E+02	1.30250E+02	1.12149E+02
F21
Mean	2.48850E+03	2.61950E+03	2.53510E+03	2.57030E+03	2.57740E+03	2.56520E+03	2.44250E+03	2.50510E+03	2.46770E+03	2.55420E+03	2.48749E+03
Std	3.85930E+01	5.12580E+01	4.56750E+01	5.02670E+01	2.56880E+01	3.32110E+01	8.21800E+01	1.56890E+01	5.50670E+01	4.03780E+01	1.51456E+02
F22
Mean	4.62350E+03	7.04850E+03	5.53390E+03	6.18390E+03	4.59700E+03	3.93100E+03	4.11250E+03	3.23580E+03	2.94720E+03	6.79490E+03	2.94754E+03
Std	2.41780E+03	1.54310E+03	3.21560E+03	2.48410E+03	2.19660E+02	2.56550E+02	3.62170E+02	2.77220E+02	1.26680E+03	1.67410E+03	3.20515E+02
F23
Mean	2.92700E+03	3.18090E+03	2.99450E+03	3.08030E+03	3.01140E+03	3.00190E+03	3.01420E+03	2.90250E+03	2.84090E+03	3.16020E+03	2.99325E+03
Std	7.37890E+01	1.18160E+02	8.17800E+01	1.07680E+02	3.48820E+01	3.15550E+01	4.54740E+01	1.68870E+01	6.23460E+01	1.38630E+02	2.35565E+02
F24
Mean	3.08380E+03	3.30380E+03	3.09670E+03	3.19780E+03	3.16640E+03	3.14920E+03	3.18440E+03	3.05480E+03	2.95410E+03	3.44050E+03	2.95326E+03
Std	5.04200E+01	1.16420E+02	7.36580E+01	8.09340E+01	3.72610E+01	2.53380E+01	3.43000E+01	2.60000E+01	3.86290E+01	1.45780E+02	3.52588E+01
F25
Mean	2.90010E+03	3.44510E+03	3.02210E+03	3.01640E+03	3.45100E+03	3.28120E+03	3.38280E+03	3.08930E+03	3.09440E+03	2.91640E+03	3.00055E+03
Std	1.49490E+01	1.41040E+02	3.39370E+01	4.69270E+01	9.77010E+01	1.02840E+02	1.57830E+02	3.12340E+01	5.98770E+01	2.30520E+01	1.22550E+01
F26
Mean	5.65890E+03	9.01340E+03	6.69870E+03	8.11220E+03	7.41680E+03	7.13610E+03	7.05350E+03	5.92290E+03	5.48950E+03	7.64800E+03	5.47518E+03
Std	1.72280E+03	1.03630E+03	9.25950E+02	7.67280E+02	2.41560E+02	3.74440E+02	5.36350E+02	4.49190E+02	1.27270E+03	1.08640E+03	4.52201E+02
F27
Mean	3.26360E+03	3.63050E+03	3.31650E+03	3.39200E+03	3.44060E+03	3.38790E+03	3.45800E+03	3.31450E+03	3.33700E+03	3.38570E+03	3.26194E+03
Std	2.42390E+01	1.79580E+02	7.97790E+01	8.83970E+01	5.54960E+01	4.08300E+01	5.42170E+01	2.33400E+01	8.83800E+01	9.26590E+01	5.66982E+01
F28
Mean	3.21950E+03	4.67320E+03	3.39180E+03	3.38910E+03	4.37540E+03	3.89120E+03	4.18740E+03	3.60200E+03	3.52070E+03	3.27420E+03	3.29525E+03
Std	2.31010E+01	4.05870E+02	4.45990E+01	4.22080E+01	2.39090E+02	1.21840E+02	1.91430E+02	4.75420E+01	1.14230E+02	2.25600E+01	2.35466E+01
F29
Mean	4.04170E+03	5.18310E+03	4.78350E+03	5.07360E+03	5.08210E+03	4.76980E+03	4.94150E+03	4.48290E+03	4.76470E+03	4.49320E+03	4.04055E+03
Std	2.30680E+02	4.91440E+02	4.43160E+02	5.09510E+02	2.77570E+02	2.08340E+02	2.10560E+02	1.72000E+02	4.50640E+02	3.90420E+02	2.35486E+02
F30
Mean	1.15970E+04	5.82960E+07	7.26090E+06	1.50610E+07	8.68650E+07	8.04480E+07	1.16700E+08	7.21540E+07	2.47330E+07	2.64540E+06	1.93215E+05
Std	4.23300E+03	5.37510E+07	5.42220E+06	1.03830E+07	3.83730E+07	2.22460E+07	4.32210E+07	3.48540E+07	2.61650E+07	1.50810E+06	6.45852E+05

Table 11. The results of the Friedman ranking test of the comparative methods using 30 CEC2017 benchmark functions.

Measure	Comparative Algorithms
	GCHHO	CCMWOA	BMWOA	BWOA	SCADE	CGSCA	OBSCA	HGWO	CMSSA	DHHOM	IGOA
F1	2	11	5	4	10	8	9	7	6	3	1
F2	2	11	4	5	10	8	9	7	6	3	1
F3	2	10	9	5	7	4	8	11	6	3	1
F4	1	10	5	4	11	8	9	7	6	3	2
F5	3	11	8	6	10	7	9	5	2	4	1
F6	3	11	9	10	7	5	6	2	4	8	1
F7	4	11	8	9	7	5	6	3	2	10	1
F8	2	8	7	4	11	9	10	6	5	3	1
F9	4	10	9	6	11	5	7	2	3	8	1
F10	2	7	9	5	11	10	8	6	4	3	1
F11	2	10	4	5	9	7	8	11	6	3	1
F12	2	11	4	5	9	8	10	7	6	3	1
F13	2	7	4	3	11	9	10	8	6	5	1
F14	2	11	8	10	7	4	5	9	6	3	1
F15	2	7	5	6	8	9	11	10	3	4	1
F16	2	9	6	7	11	8	10	5	3	4	1
F17	2	11	3	8	7	6	9	5	4	10	1
F18	2	11	6	8	9	7	10	4	5	3	1
F19	2	6	4	5	9	10	11	8	7	3	1
F20	2	7	10	11	9	4	6	5	3	8	1
F21	4	11	6	9	10	8	1	5	2	7	3
F22	7	11	8	9	6	4	5	3	1	10	2
F23	3	11	5	9	7	6	8	2	1	10	4
F24	4	10	5	9	7	6	8	3	2	11	1
F25	1	10	5	4	11	8	9	6	7	2	3
F26	3	11	5	10	8	7	6	4	2	9	1
F27	2	11	4	8	9	7	10	3	5	6	1
F28	1	11	5	4	10	8	9	7	6	2	3
F29	2	11	7	9	10	6	8	3	5	4	1
F30	1	7	4	5	10	9	11	8	6	3	2
Summation	73	294	181	202	272	210	246	172	130	158	42
Mean Rank	2.4333	9.8	6.033	6.733	9.066	7.00	8.200	5.733	4.333	5.266	1.400
Final Ranking	2	11	6	7	10	8	9	5	3	4	1

5.3. Experiments Series 3: Data Clustering Problems

The proposed method was further tested on real-world problems (data clustering) to prove its searchability.

5.3.1. Description of the Data Clustering Problem

Suppose we have a collection of objects (N) that has to be divided into predetermined clusters (K). To reduce the Euclidean distance between the provided objects and the centroids of the clusters, which refer to each specified item, the clustering procedure allocates each object (O) to a specific cluster. Equation (28) is the distance metric used to evaluate the similarity (connection) between data objects. The issue is primarily described as follows:

$$ED(O,Z)=\sum _{i=1}^N\sum _{j=1}^K{w}_{ij}\left|\right|O_i-Z_j{\left|\right|}^2$$

(28)

where $\left|\right|O_i-Z_j\left|\right|$ is the distance measure between the ith object ($O_i$) and the jth cluster centroid ($Z_j$). N is the number of given objects, and K is the number of clusters. $w_{ij}$ is the weight of the ith object ($O_i$) associated with the jth cluster ($Z_j$), which is either 1 or 0.

5.3.2. Results of the Data Clustering Problems

This experiment tests the proposed IGOA using eight different UCI datasets, namely Cancer, Vowels, CMC, Iris, Seeds, Glass, Heart, and Water. The details of these datasets are presented in Table 12.

Table 12. UCI data clustering benchmark datasets.

Dataset	Features No.	Instances No.	Classes No.
Cancer	9	683	2
CMC	10	1473	3
Glass	9	214	7
Iris	4	150	3
Seeds	7	210	3
Heart	13	270	2
Vowels	6	871	3
Water	13	178	3

Table 13 shows the obtained results by the proposed IGOA compared to other comparative methods using various data clustering problems. It is clear from the results presented in this table that the modification made in the proposed method effectively affected the ability of the basic algorithm. This modification helped the proposed algorithm obtain impressive results compared with the basic (and other) methods. The proposed method had the best results in most cases, with a clear difference, as it received new results in some cases. Thus, it was found that the proposed algorithm is able to deal with such complex problems and solve them efficiently.

Table 13. The obtained results by the comparative methods using the data clustering problems.

Dataset	Metric	Comparative Algorithms
		AOA	PSO	GWO	SCA	PDOA	RSA	GOA	IGOA
Cancer	Worst	3.34E+03	2.01E+03	2.95E+03	3.47E+03	3.50E+03	3.55E+03	3.48E+03	3.73E+02
	Average	3.28E+03	1.12E+03	2.81E+03	3.16E+03	3.23E+03	3.38E+03	3.18E+03	2.49E+02
	Best	3.19E+03	5.62E+02	2.48E+03	2.88E+03	3.06E+03	3.05E+03	2.94E+03	1.54E+02
	STD	7.93E+01	5.98E+02	1.92E+02	2.85E+02	2.10E+02	1.90E+02	2.35E+02	9.07E+01
CMC	Worst	3.33E+02	9.60E+01	3.11E+02	3.35E+02	3.35E+02	3.35E+02	3.35E+02	8.08E+01
	Average	3.33E+02	8.95E+01	3.08E+02	3.33E+02	3.35E+02	3.34E+02	3.34E+02	7.76E+01
	Best	3.32E+02	8.14E+01	3.01E+02	3.32E+02	3.34E+02	3.33E+02	3.32E+02	7.43E+01
	STD	5.34E-01	6.48E+00	4.21E+00	9.86E-01	2.03E-01	8.63E-01	1.12E+00	2.77E+00
Glass	Worst	3.48E+01	1.08E+01	3.07E+01	3.49E+01	3.52E+01	3.43E+01	3.51E+01	1.23E+00
	Average	3.42E+01	6.40E+00	2.89E+01	3.44E+01	3.49E+01	3.37E+01	3.44E+01	7.67E-01
	Best	3.36E+01	0.00E+00	2.74E+01	3.37E+01	3.44E+01	3.23E+01	3.37E+01	0.00E+00
	STD	4.65E-01	4.20E+00	1.40E+00	4.16E-01	3.35E-01	8.74E-01	6.66E-01	4.62E-01
Iris	Worst	2.39E+01	6.19E+00	1.66E+01	2.43E+01	2.47E+01	2.47E+01	2.48E+01	2.16E+00
	Average	2.37E+01	4.48E+00	1.54E+01	2.37E+01	2.37E+01	2.40E+01	2.44E+01	1.60E+00
	Best	2.33E+01	6.16E-01	1.42E+01	2.29E+01	2.27E+01	2.33E+01	2.39E+01	9.03E-01
	STD	2.68E-01	2.23E+00	1.07E+00	5.47E-01	8.98E-01	5.31E-01	3.39E-01	5.38E-01
Seeds	Worst	4.92E+01	1.96E+01	4.52E+01	5.02E+01	5.01E+01	5.06E+01	5.04E+01	6.65E+00
	Average	4.86E+01	1.69E+01	3.89E+01	4.86E+01	4.92E+01	4.99E+01	4.97E+01	6.28E+00
	Best	4.80E+01	1.56E+01	3.59E+01	4.74E+01	4.78E+01	4.84E+01	4.82E+01	5.95E+00
	STD	5.41E-01	1.60E+00	3.65E+00	1.12E+00	9.53E-01	8.76E-01	9.81E-01	2.55E-01
Statlog (Heart)	Worst	1.66E+03	4.06E+02	9.85E+02	1.69E+03	1.69E+03	1.67E+03	1.66E+03	3.53E+01
	Average	1.58E+03	2.72E+02	9.14E+02	1.65E+03	1.59E+03	1.49E+03	1.60E+03	2.12E+01
	Best	1.50E+03	7.35E+01	7.40E+02	1.61E+03	1.48E+03	1.39E+03	1.43E+03	0.00E+00
	STD	6.06E+01	1.28E+02	1.01E+02	2.97E+01	7.84E+01	1.09E+02	9.47E+01	1.38E+01
Vowels	Worst	1.53E+02	2.51E+01	1.53E+02	1.53E+02	1.53E+02	1.53E+02	1.53E+02	2.10E+01
	Average	1.52E+02	2.05E+01	1.37E+02	1.53E+02	1.53E+02	1.52E+02	1.53E+02	1.97E+01
	Best	1.52E+02	1.56E+01	1.28E+02	1.52E+02	1.53E+02	1.51E+02	1.52E+02	1.85E+01
	STD	4.75E-01	5.43E+00	1.00E+01	2.97E-01	1.20E-01	4.95E-01	3.70E-01	1.04E+00
Water	Worst	3.91E+03	1.66E+03	2.91E+03	4.02E+03	3.94E+03	3.91E+03	3.98E+03	3.63E+02
	Average	3.87E+03	1.20E+03	2.52E+03	3.91E+03	3.87E+03	3.83E+03	3.84E+03	3.08E+02
	Best	3.78E+03	8.05E+02	2.20E+03	3.79E+03	3.72E+03	3.77E+03	3.42E+03	2.48E+02
	STD	5.49E+01	3.39E+02	3.29E+02	9.24E+01	9.02E+01	5.02E+01	2.31E+02	4.17E+01

In Table 14, it was found that the proposed method obtained significantly better results than the comparative methods according to the tests used. According to the Wilcoxon rank test, it was found that the results were substantially better. The improvement rates were significant, which indicates the ability of the proposed algorithm to solve such problems more efficiently compared to others. Based on the Friedman ranking test examination in Table 14, the proposed algorithm’s order is in the first place. The PSO algorithm is in second place, the GWO algorithm is in third place, the AOA algorithm is in fourth place, the SCA and RSA algorithms are in fifth place, and the GOA algorithm is in seventh place. Figure 10 indicates that the proposed algorithm is able to achieve results that exceed other algorithms in most of the cases used in these experiments.

Table 14. The statistical test using the p-value, Wilcoxon rank test, and Friedman ranking test.

Dataset	Metric	Comparative Algorithms
		AOA	PSO	GWO	SCA	PDOA	RSA	GOA	IGOA
Cancer	p-value	1.11E-11	0.012455	3.83E-09	2.12E-08	2.11E-09	7.38E-10	5.2E-09	1
	h	1	1	1	1	1	1	1	NaN
	Rank	7	2	3	4	6	8	5	1
CMC	p-value	4.01E-16	0.005429	9.41E-14	5.47E-16	3.34E-16	4.8E-16	6.09E-16	1
	h	1	1	1	1	1	1	1	NaN
	Rank	4	2	3	5	8	7	6	1
Glass	p-value	3.93E-14	0.017665	1.01E-10	2.43E-14	1.1E-14	1.19E-12	2.02E-13	1
	h	1	1	1	1	1	1	1	NaN
	Rank	5	2	3	6	8	4	7	1
Iris	p-value	5.39E-13	0.022566	5.6E-09	3.76E-12	4.45E-11	2.96E-12	6.55E-13	1
	h	1	1	1	1	1	1	1	NaN
	Rank	4	2	3	5	6	7	8	1
Seeds	p-value	2.85E-15	4.65E-07	4.18E-08	5.38E-13	1.39E-13	6.58E-14	1.58E-13	1
	h	1	1	1	1	1	1	1	NaN
	Rank	5	2	3	4	6	8	7	1
Statlog (Heart)	p-value	1.15E-11	0.00248	4.79E-08	4.89E-14	7.74E-11	1.68E-09	3.2E-10	1
	h	1	1	1	1	1	1	1	NaN
	Rank	5	2	3	8	6	4	7	1
Vowels	p-value	5.48E-17	0.965425	5.32E-09	3.43E-17	2.6E-17	5.98E-17	4E-17	1
	h	1	1	1	1	1	1	1	NaN
	Rank	5	2	3	6	8	4	7	1
Water	p-value	3.56E-14	0.000384	4.03E-07	7.09E-13	6.53E-13	2.47E-14	6.74E-10	1
	h	1	1	1	1	1	1	1	NaN
	Rank	6	2	3	8	7	4	5	1
Mean	Ranking	5.125	2.000	3.000	5.750	6.875	5.750	6.500	1.000
Final	Ranking	4	2	3	5	8	5	7	1

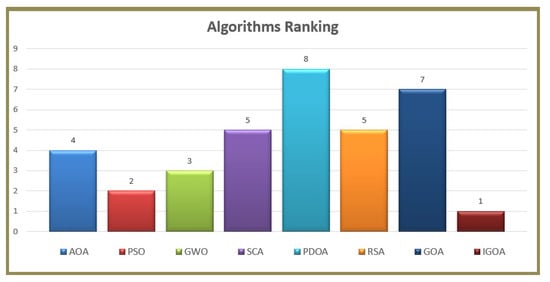
Figure 10. The ranking of the tested methods for the data clustering problems.

6. Discussions

In the tests indicated above, the OL technique and RDR method were incorporated in order to improve the performance of the original GOA method, and the improved resultant IGOA was thoroughly examined. Using benchmark datasets for clustering, the effectiveness of IGOA was evaluated.

We realize that the IGOA presents significantly superior outcomes for multi-dimensional classical test problems than other well-known optimization algorithms through results in earlier sections. The effectiveness of other algorithms significantly diminishes by expanding the dimension space. The results revealed that the proposed IGOA can maintain the equipoise between the exploratory and exploitative abilities on the problem’s nature with a high-dimension space.

From the results of the F1–F13 classical test functions, one can see a clear significant gap among the results of the comparative algorithms, with superior solutions obtained from the proposed IGOA solution. As a result, the IGOA convergence speed is greatly improved. This observation proves the superior exploitative qualities of the IGOA. According to the obtained solution for multimodal and fixed dimensional multimodal functions, we conclude that IGOA achieved superior solutions in most cases (and in competitive solutions in some cases) according to the equilibrium between the explorative and exploitative capabilities, as well as a smooth change among the searching methods.

In addition, the performance of IGOA was tested using 30 advanced CEC2017 benchmark functions for further judgment. In the first part, regarding CEC2017 unimodal functions (F1–F3), IGOA has excellent results and optimization efficiency because the OL and RDR strategies supplement the diversity of the solutions of the conventional GOA and increase its likelihood of taking the local optimal section. In contrast, the DE has different distribution properties that allow the conventional GOA to obtain a good stability point in the search mechanisms (exploration and exploitation), increasing the optimizer’s accuracy.

The importance of the proposed method is further validated in the CEC2017 multimodal functions (F4–F10). First, it can be recognized that the IGOA strategies thoroughly allow the search solutions at various regions to be determined. Then the data (from the solutions’ positions) interact with each other. As a result, it is hard for the implied areas to be trapped quickly. Furthermore, when the GOA is trapped with local optima, the stochastic disturbance of the OL can dramatically improve the GOA and its search accuracy. Finally, by combining the two strategies (OL and RDR) into the GOA, IGOA works well in the multimodal functions.

The combinations of CEC2017 unimodal and CEC2017 multimodal functions, called hybrid functions (F11–F20), were used to analyze the accuracy of the proposed IGOA. The RDR encourages the GOA to obtain the possibly optimal region faster. On the other hand, the OL encourages the GOA to obtain a potentially more reliable solution in the adjacent area. Nevertheless, due to the hardness of some problems, the combination of two search strategies (RDR and OL) interacting together leads to good results.

CEC2017 composite functions (F21–F30) examine the proposed IGOA’s ability to change between the search phases. Such benchmark analyses place more critical needs on the optimization process. For example, the OL principally assists in enhancing the ability in the exploration aspect, which enables IGOA to come near the better region quickly. Contrarily, the RDR encourages determining a more suitable solution close to the current best solution. However, the overall performance of IGOA was developed.

IGOA is shown to be highly effective since the precision of the final findings is improved when compared to well-known cutting-edge methodologies in the literature. IGOA’s efficacy is further demonstrated in clustering application challenges. Additionally, it can be shown from the outcomes of the two clustering issues (data clustering) that IGOA also performs remarkably well in locating ideal clusters and centroids.

To demonstrate its efficacy concerning convergence acceleration and optimization accuracy, the suggested approach presents a better form of the GOA when compared with well-known methods and state-of-the-art methods. When using the suggested IGOA to solve actual clustering issues, whether they include data or text, we also compare it to alternative optimization techniques. Researchers will understand how to implement the suggested optimizer to minimize and maximize the costs of clustering applications as we reduce the difficulties with data clustering and maximize the issues with text document clustering. In essence, one may obtain managerial recommendations from this document. An earlier subsection described this experimental configuration.

7. Conclusions and Future Works

An effective optimization technique is required to handle challenging problems and identify the best solution. Optimization problems can take many different routes in a variety of disciplines. It is challenging to solve several problems using the same approach since the nature of these problems varies. One simple–global stochastic optimizer with strong search capabilities is the GOA. However, the GOA is inadequate for multi-modality, hybrid functions, and data mining.

To enhance the GOA and maintain diversity in solutions, the current article suggests combining Rosenbrock’s direct rotational (RDR) technique with the orthogonal learning (OL) method (IGOA). We carried out extensive tests based on several functions, including 23 classical and IEEE CEC2017 challenges. Several other suggested meta-heuristic algorithms were contrasted with the IGOA. To further confirm the effectiveness of the proposed strategy, 8 data clustering issues collected from the UCI repository were tested. The Wilcoxon signed-rank test also evaluated the experimental findings for a more organized data analysis. Other comparison optimizers could not compete with the IGOA’s convergence speed and accuracy. The empirical results demonstrate that the suggested IGOA outperformed different comparative approaches and the basic GOA regarding outcomes and solution quality.

In future work, the proposed method can be improved using other search operators. Moreover, the proposed method can be tested to solve other hard problems, such as text clustering problems, scheduling problems, industrial engineering problems, advanced mathematical problems, parameter extraction problems, forecasting problems, feature selection problems, multi-objective problems, and others. Moreover, a deep investigation is needed to determine the main reasons for the current weaknesses in some cases.