Abstract
Numerical and analytical investigations were performed to study the panel flutter generated by the coupling of elastic and aerodynamic loads with thermal loads. Based on large deflection theory and piston aerodynamic theory, the nonlinear dynamic differential equations of heated panels with pre-stretch displacement are derived. The Galerkin method is applied to transform the continuous partial differential equations into a nonlinear system of ordinary differential equations. The analytical expressions of the flutter critical dynamic pressure and flutter frequency, the static divergence stability boundary and the Hopf bifurcation fluttering stability boundary for the initial equilibrium of the panel can be obtained through the algebraic criterion of the Hopf bifurcation. The results show that, compared to the non-pre-stretch condition, when the pre-strain of the panel was merely 0.0328%, the flutter critical dynamic pressure and flutter frequency increased by 380.78% and 223.43%, respectively. Moreover, the pre-stretching method can significantly enhance the capacity of the supersonic panel to sustain temperature loads.
MSC:
34D20
1. Introduction
It is critical to take into account the flutter caused by the coupling of elastic and aerodynamic loads with inertial forces during supersonic flight, besides satisfying the static stiffness and dynamic strength within the aircraft panel structure design. Numerous supersonic aircraft accidents occurred regarding the panel flutter in the last few decades, including NACA’s P-80s, several experienced US aircraft from the 1950s, the hypersonic X-15, the rocket Saturn V, the US Apollo spacecraft, the F-16, F-18, F-117A, F-22, etc. Flutter can result in loss of control, failure of hydraulic lines, and a dramatic increase in background noise inside the aircraft, besides the individual panel destruction at wings and tails (Kehoe [1]). Since panel flutter generally leads to fatigue damage and affects flight stability, it is a priority to determine the stability boundary for panel flutter and to improve panel stability.
For panel flutter, the flutter boundary is typically determined by the eigenvalues of the model, which is more convenient for Hopf bifurcation theory than other methods. According to Hopf bifurcation theory, balance points shift from stable to unstable and limit cycles emerge when parameters of the nonlinear system vary slightly near the critical values. To improve the criterion of Hopf bifurcation theory, it makes sense to determine the sign of the real part of the eigenvalues of Jacobi matrices. Zhang [2] investigated the Hopf bifurcation solution and stability of a two-dimensional nonlinear viscoelastic panel using Maple and normal form theory, based on the property that the eigenvalue equation possesses a pair of purely imaginary eigenvalues and a pair of complex conjugate eigenvalues with negative real parts. Wang et al. [3] proposed a nonlinear flutter analysis for viscoelastic heated panels. With aerodynamic loads applied on both sides, a static divergence stability boundary for the initial plane equilibrium and an elastic/viscoelastic flutter stability boundary can be obtained using the Routh–Hurwitz criterion. Cao and Yao [4] studied the flutter stability of heated panels in a supersonic airflow using the Hopf bifurcation algebraic criterion. The analytical expressions of the flutter critical dynamic pressure and the critical vibration frequency of the panels, as well as the demonstration procedures of the theorem, are supplemented. Through the improvement of the Hopf bifurcation algebraic criterion by the above scholars, the flutter boundary can be conveniently derived. In this study, the Hopf bifurcation algebraic criterion is adopted to obtain flutter boundaries and flutter frequencies, and to analyze the number and stability of equilibrium points in each region on the parameter plane formed by the static divergence stable boundary and the Hopf bifurcation flutter stable boundary.
In panel flutter analysis, in addition to the effects of classical parameters, such as physical materials, geometric models, and boundary conditions, on flutter, more factors and complex physical environments have been taken into account in recent decades, such as aerodynamic uncertainties, new composite materials, aerodynamic thermoelastic coupling, and composite boundary layers. Considering the problem of heat generation in supersonic flight, it is inevitable to take the effect of thermal loads into account in the analysis of panel flutter. Li et al. [5] considered the historical effects of aerodynamic heating and an improved aero-thermoelastic dynamics model for infinitely long isotropic panels and demonstrated them mathematically. The results indicated that aerodynamic heating induced, exacerbated, or modified the vibrational behavior of the panels. Hosseini and Fazelzadeh [6] explored temperature-dependent material properties and investigated the post-critical behavior of functionally graded plates in supersonic airflows based on a power law distribution of volume fraction relationships in the thickness direction. Stanford and Beran [7] developed a SIMP-based framework for the topology optimization of sheet metal structures under aerodynamic, inertial, elastic, and thermal loads and proposed a flutter optimization topology for unheated sheets, a thermal bending optimization topology, and a flutter optimization result for heated panels. Guimaraes et al. [8] evaluated the difference in nonlinear flutter behavior and post-flutter motion between single-panel and multi-compartment panels under the thermal effects of adjacent panel interactions. Their results showed that the thermal loads have a significant effect on panel flutter: as the temperature gradient increases, the flutter critical dynamic pressure decreases, and as the temperature gradient decreases, the flutter critical dynamic pressure increases.
To improve the stability of the panel (flutter critical dynamic pressure), numerous scholars have conducted thorough research. Arena et al. [9] investigated the effect of various carbon nanotube weight fractions in composite panels on flutter and post-flutter states from a new materials perspective, concluding that minor carbon nanotube weight fractions can remarkably raise the flutter critical velocity by up to 28% and reduce the limit cycle oscillation amplitude. Samadpour et al. [10] researched the nonlinear aerothermal flutter instability of shape memory alloy (SMA) fiber-reinforced composite beams under thermal and aerodynamic loading. The results showed that embedding SMA fibers can significantly improve the aerothermal flutter characteristics of laminated beams. They improved the stability of the panels by using new functional materials. Kassem et al. [11] designed an active dynamic vibration absorber using a cantilever beam combined with a microfiber composite (MFC) and lumped mass experiments. Closed-loop control can raise the critical speed of the wing flutter by 42.9% and effectively suppress the amplitude. Basta et al. [12] utilized the conserved mass metamaterials concept to fabricate shock absorbers, enabling an 84% improvement in wing flutter speed through a distributed array of shock absorbers with appropriate stiffness. Zhao and Cao [13] studied, in detail, the effect of different stiffening schemes and the geometric size of the stiffeners on the critical dynamic pressure and transverse vibration amplitude of panels. The critical dynamic pressure for panel flutter can be greatly increased with appropriate stiffening. They utilized active dynamic dampers and reinforced structures to suppress vibrations and enhance the stability of the panels.
Whereas the methods described above can effectively improve the flutter critical velocity, the new materials used are costly and the designs of additional supports and absorbers are complex. The simplest, lowest-cost method currently available is to pre-stretch the structure. Amirzadegan et al. [14] studied the vibration of a rectangular isotropic thin panel in a supersonic flow and indicated that compressive stress would lead to an increase in the dynamic instability of the panel, while tensile stress would increase the stability. Wang et al. [15] investigated the nonlinear behavior of stiffened panels with initial stresses. As the bending stiffness of the stiffening ribs increased with tensile stresses and played a dominant role in the overall stiffened panel structure, the nonlinear behavior of the stiffened panel became weaker, and vice versa. Rasool and Singha [16] researched the constant and variable stiffness of composite panels through finite element methods and concluded that in-plane compressive stresses reduce the flutter velocity of cantilever plates, while the initial in-plane traction forces opposite to the airflow increase it.
Hitherto, there have been no simultaneous studies on the effect of pre-stretching and thermal loading on panel flutter. Yet, in practical situations (e.g., panels on the wings of supersonic aircraft), thermal loads on the wings and panels are inevitable in flight. Since thermal loads drastically affect the flutter boundary and stability of the panel, it is essential to take both pre-stretching and thermal loads into account in the structural design of supersonic aircraft. In this study, pre-stretch displacement is applied to a heated plate in a hypersonic airflow, and a nonlinear dynamic differential equation is derived based on the equilibrium equation according to the large deflection theory of the thin panel. Analytic expressions for the critical dynamic pressure and flutter frequency in a supersonic airflow are calculated using the algebraic criterion of Hopf bifurcation. Nonlinear dynamic characteristics are obtained through numerical analysis, which is of significance for practical engineering applications.
2. Governing Equations
The structure we consider is a simply supported isotropic panel subjected to pre-stretch displacement and thermal loads in a supersonic aerodynamic airflow, as shown in Figure 1.
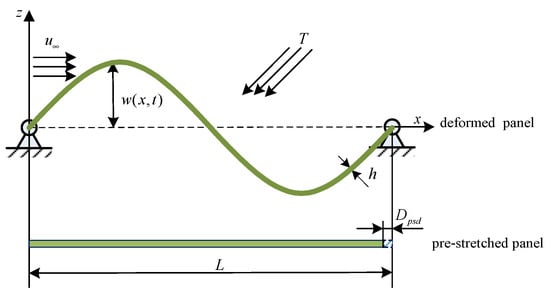
Figure 1.
Sketch of a two-dimensional nonlinear heated pre-stretched panel in a supersonic airflow.
The pre-stretch displacement produced by stretching the panel is , the chord length after stretching is , the thickness is , the span is , and the density is . The upper surface of the panel is subject to a supersonic airflow along the x-direction with density , speed , and Mach number . is the temperature elevation, and the reference temperature is , .
2.1. Geometrical Relationship of Deformation
It is assumed that the temperature distribution over the entire panel is uniform and stable. Under the condition of uniform temperature variation and large deflection, based on large deflection theory, the displacements of the pre-stretched panel are defined as
where and are the lateral and longitudinal mid-plane displacements in the x- and z-directions; is the rotational angle of a cross-section; is the coefficient of thermal expansion.
The strain–displacement relation and constitutive equation of the pre-stretched panel can be described by Equations (2) and (3), respectively.
where is Young’s modulus and is Poisson’s ratio.
2.2. Differential Equilibrium Equation
The force and deformation of the infinitesimal element on the x-z plane are shown in Figure 2.
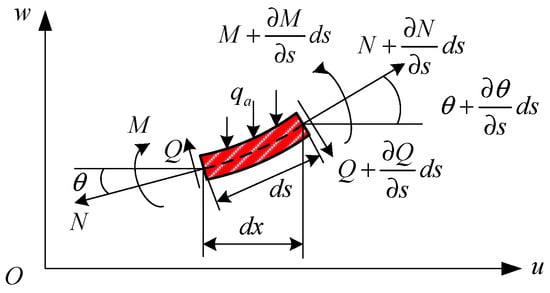
Figure 2.
Force diagram of microelements taken out from the plate.
Considering the force equilibrium in the z-direction, the transversal dynamic equation of the infinitesimal element can be given in the following form:
where , is the panel cross-section , is the shear force in the panel element and is the in-plane force in the panel element.
The moment at the left end of the infinitesimal element is , the moment at the right end is and the moment of shear force Q about the right endpoint is . Ignoring the moment of inertia, the moment balance equation about the right endpoint can be simplified as
The shear force can be obtained as
By substituting Equation (6) into Equation (4), the transversal dynamic equation can be simplified as
Based on the deformation of the infinitesimal element shown in Figure 2, we assume that
The force perpendicular to the section is simplified to the midline, and the force and moment perpendicular to the cross-section can be obtained using Equations (9) and (10), respectively.
where is the bending stiffness.
It is assumed that the in-plane force is uniformly distributed along the length, considering the boundary condition ,. By substituting Equation (3) into Equation (9) and performing integration yields, the in-plane force can be simplified as
where
By substituting Equations (8), (10), and (11) into Equation (7), the transversal dynamic equation can be simplified as
2.3. Aerodynamic Equations
The aerodynamic force can be obtained based on first-order piston theory as
where is the airflow pressure, is the Prandtl–Glauert factor, and , and are the mass density, velocity, and Mach number of the airflow, respectively.
2.4. Governing Equation
For convenient analysis, the dimensionless parameters are incorporated and given by
Then, the dimensionless differential equation for the oscillation of two-dimensional heated panels with pre-stretch displacement in a supersonic airflow can be derived as
where the aerodynamic stiffness coefficient , and the aerodynamic damping coefficient .
When is greater than one, the aerodynamic damping coefficient can be simplified as
Boundary conditions are described as
3. Solution Methodology
3.1. Routh–Hurwitz Algebraic Criterion
Using the Hopf bifurcation algebraic criterion, the stable boundaries under different temperatures and pre-stretch displacements are obtained. Based on the Galerkin principle, can be truncated as
where is the Galerkin truncated order, is the i-th trial function that satisfies the simply supported boundary conditions, is the i-th general coordinates, and are orthogonal to each other, satisfying and .
Then, Equation (18) can be written as
where
By multiplying and integrating over the range , Equation (16) can be derived as
Let . Equation (20) can be transformed into the matrix form as
where is the Jacobi matrix.
The equilibrium point and the vector have the same dimension. The characteristic equation of the Jacobi matrix at the equilibrium point can be derived as
The necessary and sufficient conditions for the real coefficient of the algebraic Equation (22) to have a pair of pure imaginary zeros and the remaining n-2 roots to have negative real parts can be expressed as
The critical flutter dynamic pressure is computed in Section 3.2 for when is equal to zero. If Equation (22) has a pair of pure imaginary zeros, according to Cao and Yao [4], the flutter frequency can be computed as
when , there is , , , and the system is stable; when , the system is unstable; when , the system presents a Hopf bifurcation. This will be uncovered in the next section.
3.2. Flutter Boundary
The Hopf bifurcation is influenced by the eigenvalues of the Jacobi matrix of Equation (20) for the nonlinear system at the balance point. The character equation of the Jacobi matrix has the same order as the Jacobi matrix, but when the order is larger than five, there is no analytical solution of eigenvalues. To obtain analytical eigenvalues, we should make . Equation (20) can be obtained as
Equation (21) can be expressed as
The coefficients of Equation (22) can be expressed as
The Hurwitz determinant derived from can be given by
As and , Equation (23), and can be satisfied. Then, the critical dynamic pressure can be computed as follows, on the basis of :
where
According to Equation (25), the flutter frequency can be calculated as
When the coefficients of Equation (22) have only zero real roots, based on , the airflow pressure can be solved as
When is equal to , the airflow pressure can be obtained as
According to Wang et al. [3] and Equations (30), (32), and (33), the parameter plane () is divided into five regions, as shown in Figure 3, where .
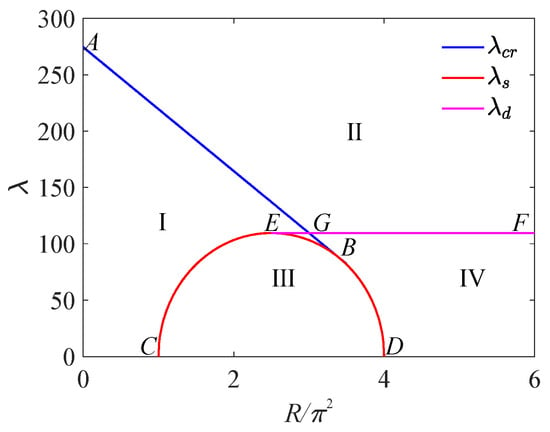
Figure 3.
Bifurcation boundaries in the parameters of the elastic panel, vs. .
When the airflow pressure is equal to , Equation (27) has only one balance point . When the parameters are in regions EBG and IV of Figure 3, the equilibrium points of the panel change to five equilibrium points, and the additional equilibrium point is set as (), which can be calculated by substituting it into Equation (27), obtained as
where
The Jacobi matrix at the equilibrium point can be obtained as
where
The stability of each region and the number of equilibrium points will be analyzed in detail in the next section.
3.3. Nonlinear Post-Flutter Response
We obtained the numerical results of the post-flutter response to Equation (27) for heated large deflection panels with pre-stretch displacement in a supersonic airflow via the Runge–Kutta method. Time-domain curves, phase trajectories, and bifurcation plots are more adapted to analyze the post-flutter response of panels with variable parameters such as the pre-stretch displacement and temperature increment. The time domain of the ODE numerical algorithm is calculated for a time increment step Δt = 0.001 s and 40,000 integration steps. The time-domain curves, phase trajectories, and bifurcation diagrams presented in the next chapter are located at the dimensionless position , with the most representative point of the maximum deflection amplitude.
4. Results and Discussion
This section discusses the nonlinear flutter characteristics of the pre-stretched panel in the thermal environment in detail. Firstly, a comparative study is conducted to verify the accuracy of the proposed model and the MATLAB numerical solution. Then, the flutter boundary and stability are analyzed using the Routh–Hurwitz algebraic criterion, and the parameters are discussed using the Galerkin method to determine the effect of pre-stretch displacement and temperature variation on the nonlinear thermal flutter behavior of the simply supported panel in a supersonic airflow.
4.1. Verification
Dowell [17] initially performed the nonlinear analysis of a two-dimensional flutter panel considering in-plane loads. The changes in aerodynamic deflection at different airflow pressures and the results of the flutter boundary vs. temperature are compared in Figure 4. It should be noted here that, for the thermal load , due to the temperature change and the in-plane compressive load in Xue and Mei [18], the relation can be obtained. The panel deflection shapes shown in Figure 5 are in excellent agreement with the results from Dowell [17], and the MATLAB code used in the numerical simulation is accurate.
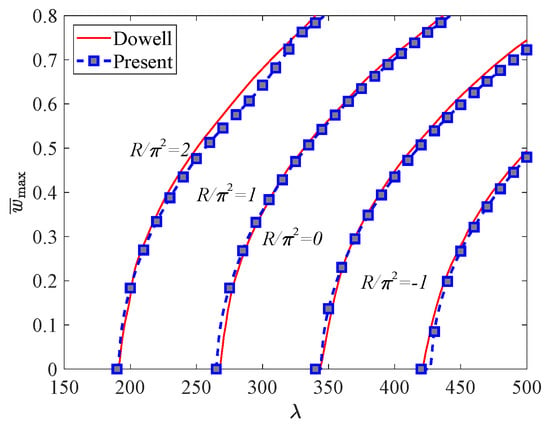
Figure 4.
Limit cycle amplitude. vs. dynamic pressure.
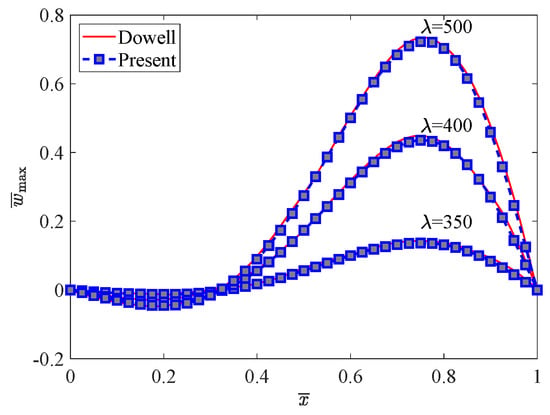
Figure 5.
Panel deflection shapes.
4.2. Numerical Results
The oscillation of heated aluminum alloy panels in a supersonic airflow is treated in this section. Table 1 shows the mechanical properties. For example, the length and thickness of the panel specimen studied are and , respectively, assuming the mass density of the airflow parameters and the speed of sound . For aeronautical applications under a supersonic airflow, is usually in the range of 0.01–0.04.

Table 1.
The mechanical properties of the panel.
When , , and the aerodynamic stiffness coefficient , according to Equations (28)–(32), the coefficients on the quartic polynomial equation of and the Hurwitz determinant are computed as follows:
It is clear that the results satisfy Equations (23) and (24), as all coefficients are greater than zero. Moreover, when , the critical dynamic pressure , and the flutter frequency .
The influence of pre-stretch displacement on the critical dynamic pressure under different values is shown in Figure 6. As (the Mach number of the airflow ) increases, the critical dynamic pressure at the same pre-stretch displacement decreases slightly, and, overall, has a minor effect on the critical dynamic pressure. During the following analysis, takes the value of 0.01.
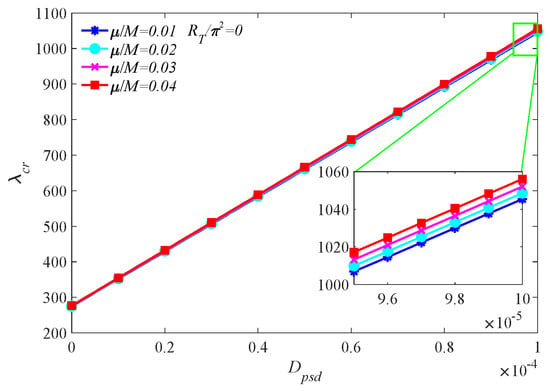
Figure 6.
Critical dynamic pressure vs. pre-stretch displacement under different values of .
The influence of pre-stretch displacement on the critical dynamic pressure of the panel under different temperature elevations, where , is shown in Figure 7. In this case, , the critical dynamic pressure drops drastically with the temperature increase and increases sharply with the temperature decrease, where . This result agrees with that described by Xue and Mei [18] using the finite element method. Under various temperature gradients, the critical dynamic pressure increases rapidly with the increase in the minimum of the pre-stretch displacement. When the pre-stretch displacement and , the pre-stretch strain can be computed as , and the critical dynamic pressure increases sharply by 380.78% compared to that at .
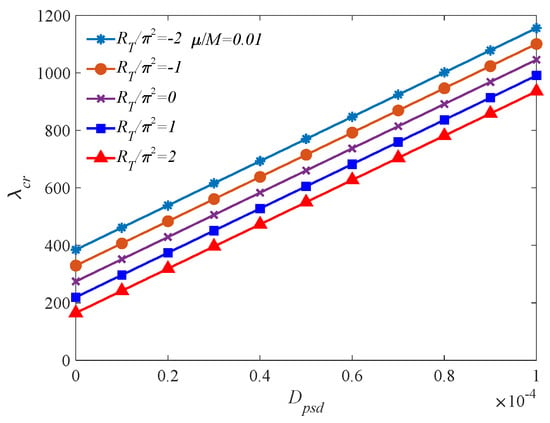
Figure 7.
Critical dynamic pressure vs. pre-stretch displacement under different temperature elevations.
Compared to Amirzadegan et al. [14], Wang et al. [15] and Rasool and Singha [16], although the models analyzed are different, the results are consistent in that the critical dynamic pressure of the structure increases by pre-stretching the structure and decreases by compressing it. According to Wang et al. [15], the upper surface skin of the wing is compressed and the lower surface is stretched as the aircraft wing bends upward due to lift force. The most critical region is located on the upper skin near the wing root, which leads to a significant reduction in the flutter critical dynamic pressure during supersonic flight, while the safest region is located on the bottom skin near the wing root. The application of pre-stretching should be considered in the structural design of the aircraft. Xue and Mei [18] investigated the fatigue life of two-dimensional panels with temperature effects. As the temperature increases, the in-plane pressure increases, while the fatigue life then decreases sharply. Compressive stress induced by temperature rise can be counteracted through pre-stretching the structure, thus improving fatigue life.
The influence of pre-stretch displacement on the flutter frequency of the panel under different temperature elevations is shown in Figure 8, where . For heated panels, the temperature rise reduces the flutter frequency of the panel and the temperature drop increases the flutter frequency. When the pre-stretch displacement and , the flutter frequency increases sharply by 223.42% compared to that at . Compared with other methods in the literature, such as those of Arena et al. [9] and Zhao and Cao [13], the increase in the critical dynamic pressure and flutter frequency by applying pretension to the panel in this paper is highly remarkable.
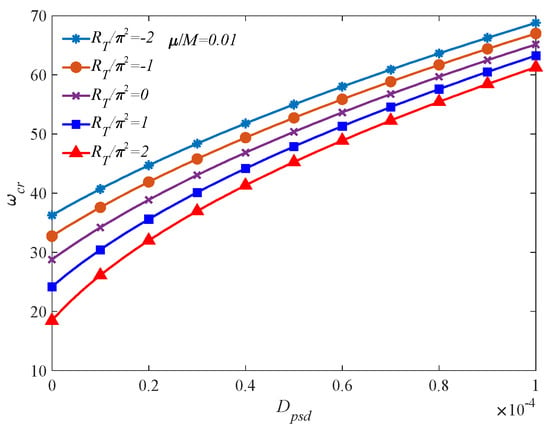
Figure 8.
Flutter frequency vs. pre-stretch displacement under different temperature elevations.
The eigenvalues of the Jacobi matrix for the equilibrium points of each region in Figure 3 are shown in Table 2. In region I, the system has only one equilibrium point and all four eigenvalues have negative real parts. Therefore, the equilibrium point is stable. The displacement response gradually converges to a straight line in the time history diagram, and the phase trajectory of the system converges to a stable point corresponding to the equilibrium point , as shown in Figure 9a,b. In region II, the system has only one equilibrium point , where one pair of four complex eigenvalues has negative real parts and the other pair has positive real parts. Therefore, the equilibrium point is unstable, and the phase trajectory of the system generates limit cycles near the point , as shown in Figure 9c.

Table 2.
The eigenvalues of the Jacobi matrix at the equilibrium point in each region.
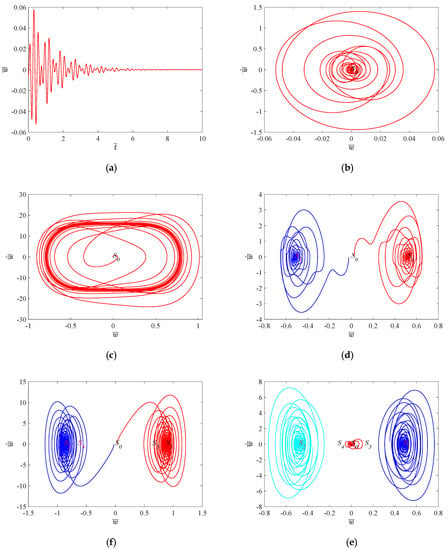
Figure 9.
Time history diagrams and phase trajectories for . (a) Region I time history diagrams. (b) Region I phase trajectories and stable point. (c) Region II phase trajectories and stable point. (d) Region III phase trajectories and stable point. (e) Region IV phase trajectories and stable point. (f) Region EDG phase trajectories and stable point.
Similarly, we can determine that the system in region III has three equilibrium points , and , where the equilibrium point is unstable, while and are stable. When the initial value is , the phase trajectory of the system converges to a stable point corresponding to the equilibrium point . When the initial value is , the phase trajectory of the system converges to a stable point corresponding to the equilibrium point , as shown in Figure 9d.
The system in region IV has five equilibrium points , , , , and , where equilibrium points and are stable, while , and are unstable. When the initial value is , the system phase trajectory converges to a stable point corresponding to the equilibrium point . When the initial value is , the system phase trajectory converges to a stable point corresponding to the equilibrium point , as shown in Figure 9e. The system in region EDG has five equilibrium points , , , and , where equilibrium points , and are stable, while equilibrium points and are unstable. When the initial values are , and , the phase trajectories of the system converge to the stable points , and corresponding to the equilibrium points , and , respectively, as shown in Figure 9f.
5. Conclusions
The main purpose of this paper was to analyze the flutter of a heated panel in a supersonic airflow under pre-stretch displacement based on large deflection theory for a thin panel under the assumption of a quasi-steady-state temperature field. In this paper, an analytical expression for the critical flutter dynamic pressure and flutter frequency under panel flutter was obtained using the Hopf bifurcation algebraic criterion. It is demonstrated that increasing the Mach number of the airflow will lead to a decrease in the critical dynamic pressure of the chattering. Moreover, in the pre-stretch displacement (the pre-strain ) condition, the critical dynamic pressure increases dramatically by 380.78%, and the flutter frequency increases sharply by 223.42%, compared to the non-pre-stretch conditions. The critical dynamic pressure and flutter frequency drop drastically with the temperature increase and increase sharply with the temperature decrease. The stability of the equilibrium points in each region of the bifurcation boundary of the elastic panel is verified by the eigenvalue properties at the equilibrium points, and the time-domain curves and phase trajectories under different initial conditions are used for verification.
Author Contributions
Conceptualization, M.W.; Methodology, M.W.; Software, G.-F.Y. and K.-Y.G.; Formal analysis, Y.-C.Z. and K.-Y.G.; Resources, Q.H.; Writing–original draft, Y.-C.Z. and K.-Y.G.; Writing–review & editing, M.W. and Q.H.; Funding acquisition, G.-F.Y. All the authors contributed equally and significantly to writing this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the finding of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kehoe, M.W. A historical overview of flight flutter testing. In Proceedings of the AGARD Structures and Materials Panel Meeting, Banff, AB, Canada, 4–5 October 1995. [Google Scholar]
- Zhang, X. Local bifurcations of nonlinear viscoelastic panel in supersonic flow. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1931–1938. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Wang, W.; Tian, W. Nonlinear viscoelastic heated panel flutter with aerodynamic loading exerted on both surfaces. J. Sound Vib. 2017, 409, 306–317. [Google Scholar] [CrossRef]
- Cao, L.-N.; Yao, G. Hopf Bifurcation of Heated Panels Flutter in Supersonic Flow. Mathematics 2019, 7, 787. [Google Scholar] [CrossRef]
- Li, K.; Zhang, J.; Mei, G. Aerothermoelastic model of panel flutter with consideration of the history effects of aerodynamic heating. Int. J. Appl. Mech. 2012, 4, 3. [Google Scholar] [CrossRef]
- Hosseini, M.; Fazelzadeh, S.A. Aerothermoelastic Post-Critical and Vibration Analysis of Temperature-Dependent Functionally Graded Panels. J. Therm. Stress. 2010, 33, 1188–1212. [Google Scholar] [CrossRef]
- Stanford, B.; Beran, P. Aerothermoelastic topology optimization with flutter and buckling metrics. Struct. Multidiscip. Optim. 2013, 48, 149–171. [Google Scholar] [CrossRef]
- Guimarães, T.A.; Sanches, L.; Marques, F.D. Nonlinear supersonic post-flutter motion of panels with adjacent bays and thermal effects. Int. J. Non-Linear Mech. 2020, 125, 103545. [Google Scholar] [CrossRef]
- Arena, A.; Taló, M.; Snyder, M.P.; Lacarbonara, W. Enhancing flutter stability in nanocomposite thin panels by harnessing CNT/polymer dissipation. Mech. Res. Commun. 2020, 104, 103495. [Google Scholar] [CrossRef]
- Samadpour, M.; Asadi, H.; Wang, Q. Nonlinear aero-thermal flutter postponement of supersonic laminated composite beams with shape memory alloys. Eur. J. Mech. A/Solids 2016, 57, 18–28. [Google Scholar] [CrossRef]
- Kassem, M.; Yang, Z.; Gu, Y.; Wang, W.; Safwat, E. Active dynamic vibration absorber for flutter suppression. J. Sound Vib. 2019, 469, 115110. [Google Scholar] [CrossRef]
- Basta, E.; Ghommem, M.; Emam, S. Flutter control and mitigation of limit cycle oscillations in aircraft wings using distributed vibration absorbers. Nonlinear Dyn. 2021, 106, 1975–2003. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, D. A study on the aero-elastic flutter of stiffened laminated composite panel in the supersonic flow. J. Sound Vib. 2013, 332, 4668–4679. [Google Scholar] [CrossRef]
- Amirzadegan, S.; Safavi, S.M.M.; Jafarzade, A. Supersonic Panel Flutter Analysis Assuming Effects of Initial Structural Stresses. J. Inst. Eng. Ser. C 2019, 100, 833–839. [Google Scholar] [CrossRef]
- Wang, T.-Q.; Wang, R.-H.; Ma, N.-J. Nonlinear Vibration of a Stiffened Plate Considering the Existence of Initial Stresses. KSCE J. Civ. Eng. 2019, 23, 2303–2312. [Google Scholar] [CrossRef]
- Rasool, M.; Singha, M.K. Aeroelastic analysis of pre-stressed variable stiffness composite panels. J. Vib. Control 2019, 26, 724–734. [Google Scholar] [CrossRef]
- Dowell, E. Nonlinear oscillations of a fluttering plate. AIAA J. 1966, 4, 1267–1275. [Google Scholar] [CrossRef]
- Xue, D.Y.; Mei, C. Finite element nonlinear flutter and fatigue life of two-dimensional panels with temperature effects. J. Aircr. 1993, 30, 993–1000. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).