Global Stability of a Reaction–Diffusion Malaria/COVID-19 Coinfection Dynamics Model

Abstract

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is a new virus which infects the respiratory system and causes the coronavirus disease 2019 (COVID-19). The coinfection between malaria and COVID-19 has been registered in many countries. This has risen an urgent need to understand the dynamics of coinfection. In this paper, we construct a reaction–diffusion in-host malaria/COVID-19 model. The model includes seven-dimensional partial differential equations that explore the interactions between seven compartments, healthy red blood cells (RBCs), infected RBCs, free merozoites, healthy epithelial cells (ECs), infected ECs, free SARS-CoV-2 particles, and antibodies. The biological validation of the model is confirmed by establishing the nonnegativity and boundedness of the model’s solutions. All equilibrium points with the corresponding existence conditions are calculated. The global stability of all equilibria is proved by picking up appropriate Lyapunov functionals. Numerical simulations are used to enhance and visualize the theoretical results. We found that the equilibrium points show the different cases when malaria and SARS-CoV-2 infections occur as mono-infection or coinfection. The shared antibody immune response decreases the concentrations of SARS-CoV-2 and malaria merozoites. This can have an important role in reducing the severity of SARS-CoV-2 if the immune response works effectively.

1. Introduction

The coronavirus disease 2019 (COVID-19) is a viral disease that appeared in China at the end of 2019 and spread to most countries of the world. The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is the cause of COVID-19. Malaria-endemic regions face a great challenge due to the possibility of coinfection between malaria and other viral diseases. Indeed, malaria/COVID-19 coinfection has been founded in several countries [1]. This has increased the necessity to understand the dynamics of the coinfection and its effect on the patient.

SARS-CoV-2 is an RNA virus and belongs to the family Coronaviridae [2]. It uses the angiotensin-converting enzyme 2 (ACE2) receptor to step into the ECs [3]. Such receptor is expressed in kidney, heart, gastrointestinal tract, blood vessels, and other organs [4]. The human-to-human transmission of SARS-CoV-2 occurs via respiratory droplets containing viruses [5]. Eleven vaccines for COVID-19 were approved by the World Health Organization (WHO) for emergency use. These include Novavax/Nuvaxovid, Bharat Biotech/Covaxin, CanSino/Convidecia, Pfizer/BioNTech/Comirnaty, Moderna/Spikevax, Serum Institute of India COVOVAX (Novavax formulation), Janssen (Johnson & Johnson)/Jcovden, Oxford/AstraZeneca/Vaxzevria, Serum Institute of India Covishield (Oxford/AstraZeneca formulation), Sinopharm (Beijing)/Covilo, and Sinovac/CoronaVac [6]. There are a number of other effective vaccines that are not yet approved by the WHO. On 22 October 2020, the U.S. Food and Drug Administration (FDA) approved the antiviral drug Veklury (remdesivir) for the treatment of COVID-19 cases who need hospitalization [7]. It is utilized for adults and pediatric patients 12 years of age and older (with weight ≥ 40 kg) [7].

On the other hand, malaria is a parasitic disease attributable to Plasmodium parasites [5,8]. There are five types of Plasmodium parasites: P. malariae, P. knowlesi, P. vivax, P. falciparum, and P. ovale. However, P. falciparum is the deadliest malaria parasite. Infected Anopheles mosquitoes transmit the malaria parasite to humans [8]. There are two stages for malaria infection in the body: the liver stage and the blood stage [8]. The blood stage is responsible for most of the clinical symptoms. At the blood stage, the parasites, in the form of a merozoite attack, infect the red blood cells (RBCs) [8]. After rupturing a cell, 8–32 daughter merozoites are produced [8]. Preventive chemotherapies are utilized to treat malaria infection and their consequences [9]. In this paper, we focus on the blood stage of malaria infection.

Malaria and COVID-19 have common symptoms including fever, headache, fatigue, myalgia and difficulty in breathing [10,11,12]. This can cause difficulty in the clinical diagnosis of malaria and SARS-CoV-2 coinfection [4,5]. Wrong or late diagnosis of coinfection can have a bad effect on the health of the patient [13]. The incubation periods for Plasmodium falciparum malaria and SARS-CoV-2 are 7–14 days and 2–17 days, respectively, and this enhances the possibility of coinfection [5,13]. In fact, malaria/COVID-19 coinfection has been found in several countries [13,14,15]. Some studies indicated that the coinfection could increase the severity of SARS-CoV-2 infection [1,13]. Wilairatana et al. [1] presented a review article and identified studies of malaria/COVID-19 coinfection and compared them from several aspects including: the possible correlations between COVID-19 and malaria, the prevalence of malaria infection among COVID-19 patients, the risk of oxidative stress in the malaria/COVID-19 coinfection, the role of sex in the malaria/COVID-19 coinfection, the effect of malaria coinfection on the clearance of SARS-CoV-2 in COVID-19 patients, the clinical severity of COVID-19, treatment of COVID-19, mean duration of the hospitalized and the underlying comorbidities. Hussein et al. [16] reported that coinfection with malaria and COVID-19 is associated with increased all-cause in-hospital mortality compared to a single-infection with SARS-CoV2. Nevertheless, several studies mentioned that the neutralizing antibodies against Plasmodium falciparum can also be effective against SARS-CoV-2 particles. This can minimize the severity of SARS-CoV-2 infection in coinfected patients [4,17,18,19]. Thus, understanding the dynamics of coinfection is very crucial in order to find better ways to deal with and treat this group of patients.

Mathematical modeling is considered as one of the most substantial tools that is used to support medical studies during epidemics. Malaria models at the blood stage have been explored in many works (see for example [20,21,22,23,24,25,26]). In addition, many COVID-19 models have been formulated and studied. These models can be classified into epidemiological models and in-host models. Epidemiological models study the transmission of COVID-19 between individuals (see for example [27,28,29,30,31,32]). On the other hand, in-host models study the interactions between SARS-CoV-2 and cells inside the body (see for example [33,34,35,36,37,38]). In fact, in-host models have received less attention than between-host models. In a recent work [39], the malaria/SARS-CoV-2 coinfection model has been developed and investigated. All the above-mentioned models assume that parasites, viruses, and cells are distributed homogeneously in the body. However, this assumption is not realistic in biological systems as the diffusion of particles causes spatial variations within the body. Considering spatial diffusion converts the ODE model into a PDE model, which allows the compartments to vary in space and time. This will give a more accurate description of the model’s dynamics. Therefore, some malaria models (see for example [8,40]) and SARS-CoV-2 models (see for example [39,41]) are formulated using partial differential equations (PDEs) to take into account the diffusion of some components in the model. Actually, the coinfection of COVID-19 with malaria is an active area of research. Current studies are trying to deeply understand the dynamics of this coinfection. This will help to effectively treat coinfected patients and save their lives. Mathematical modeling can support these studies and reduce the number of experiments needed to test hypotheses. We noted that a diffusive malaria/COVID-19 coinfection model has not yet been considered. In this paper, we formulate a reaction–diffusion malaria/COVID-19 model. This model considers the interactions between healthy RBCs, infected RBCs, free merozoites, healthy ECs, infected ECs, free SARS-CoV-2 particles, and antibodies. For this model, we (i) validate the boundedness and nonnegativity of solutions, (ii) calculate all model’s equilibria and extract the conditions of their existence, (iii) show the global stability of equilibria, and (iv) enhance the analytical results by executing some numerical simulations.

The paper is written as follows: Section 2 gives a description for the proposed model. Section 3 shows the properties of the model’s solutions. Furthermore, it calculates all models’ equilibria. Section 4 introduces the Lyapunov method to establish the global stability of all model’s equilibria. Section 5 is devoted for numerical simulations. Finally, the results are discussed and some future research points are suggested in Section 6.

2. Reaction–Diffusion Malaria/COVID-19 Model with Immune Response

In this section, we give a detailed description of the proposed model. We construct the malaria/COVID-19 coinfection model as a system of seven PDEs:

$$\left\{\begin{array}{c}\frac{\partial U(x,t)}{\partial t}=D_U\Delta U(x,t)+{\sigma }_1-{\beta }_{m}U(x,t)M(x,t)-d_{1}U(x,t),\hfill \\ \frac{\partial I(x,t)}{\partial t}=D_I\Delta I(x,t)+{\beta }_{m}U(x,t)M(x,t)-d_{2}I(x,t),\hfill \\ \frac{\partial M(x,t)}{\partial t}=D_M\Delta M(x,t)+\eta d_{2}I(x,t)-q_{1}M(x,t)Z(x,t)-d_{3}M(x,t),\hfill \\ \frac{\partial Y(x,t)}{\partial t}=D_Y\Delta Y(x,t)+{\sigma }_2-{\beta }_{v}Y(x,t)V(x,t)-d_{4}Y(x,t),\hfill \\ \frac{\partial N(x,t)}{\partial t}=D_N\Delta N(x,t)+{\beta }_{v}Y(x,t)V(x,t)-d_{5}N(x,t),\hfill \\ \frac{\partial V(x,t)}{\partial t}=D_V\Delta V(x,t)+eN(x,t)-q_{2}V(x,t)Z(x,t)-d_{6}V(x,t),\hfill \\ \frac{\partial Z(x,t)}{\partial t}=D_Z\Delta Z(x,t)+p_{1}M(x,t)Z(x,t)+p_{2}V(x,t)Z(x,t)-d_{7}Z(x,t),\hfill \end{array}\right.$$

(1)

for $t>0$ and $x\in \mathsf{\Gamma }$, where $U(x,t)$, $I(x,t)$, $M(x,t)$, $Y(x,t)$, $N(x,t)$, $V(x,t)$, and $Z(x,t)$ stand for the concentrations of healthy RBCs, infected RBCs, free merozoites, healthy ECs, infected ECs, free SARS-CoV-2 particles, and antibodies. Healthy RBCs are generated at a constant rate ${\sigma }_1$, get infected by merozoites at rate ${\beta }_{m}UM$, and die at rate $d_{1}U$. Infected RBCs die at rate $d_{2}I$ and burst to generate $\eta$ merozoites per infected cell. Free merozoites die at rate $d_{3}M$ and are cleared by antibodies at rate $q_{1}MZ$. Healthy ECs are recruited from its source at rate ${\sigma }_2$, get infected by SARS-CoV-2 at rate ${\beta }_{v}YV$ and die at rate $d_{4}Y$. Infected ECs die at rate $d_{5}N$ and release SARS-CoV-2 at rate $eN$. SARS-CoV-2 particles are eliminated by antibodies at rate $q_{2}VZ$ and die at rate $d_{6}V$. Antibodies die at a natural death rate $d_{7}Z$ and are stimulated to target malaria merozoites and SARS-CoV-2 at rates $p_{1}MZ$ and $p_{2}VZ$, respectively. The spatial domain $\mathsf{\Gamma }$ is continuous, bounded and its boundary $\partial \mathsf{\Gamma }$ is smooth. $\Delta =\frac{{\partial }^2}{\partial x^2}$ is the Laplacian operator. We assume that each component $C(x,t)$ of the model diffused in the domain with a diffusion coefficient $D_C$. The initial conditions (ICs) of model (1) are defined as the following:

$$\begin{array}{cc}U(x,0)\hfill & ={\gamma }_1\left(x\right),I(x,0)={\gamma }_2\left(x\right),M(x,0)={\gamma }_3\left(x\right),Y(x,0)={\gamma }_4\left(x\right),\hfill \\ N(x,0)\hfill & ={\gamma }_5\left(x\right),V(x,0)={\gamma }_6\left(x\right),Z(x,0)={\gamma }_7\left(x\right),{\gamma }_i\left(x\right),i=1,2,\dots ,7,x\in \overline{\mathsf{\Gamma }}.\hfill \end{array}$$

(2)

The boundary conditions are given by the following Neumann boundary conditions (NBCs):

$$\frac{\partial U}{\partial \overrightarrow{\upsilon }}=\frac{\partial I}{\partial \overrightarrow{\upsilon }}=\frac{\partial M}{\partial \overrightarrow{\upsilon }}=\frac{\partial Y}{\partial \overrightarrow{\upsilon }}=\frac{\partial N}{\partial \overrightarrow{\upsilon }}=\frac{\partial V}{\partial \overrightarrow{\upsilon }}=\frac{\partial Z}{\partial \overrightarrow{\upsilon }}=0,t>0,x\in \partial \mathsf{\Gamma },$$

(3)

where ${\displaystyle \frac{\partial }{\partial \overrightarrow{\upsilon }}}$ is the outward normal derivative on $\partial \mathsf{\Gamma }$. This type of boundary condition simulates a natural barrier that prevents cells and viruses from crossing the boundary.

3. Properties of Solutions

In this section, we verify the basic properties of model (1) including the existence, nonnegativity, and boundedness of the solutions. Furthermore, we evaluate all possible equilibrium points with their conditions of existence.

Let $\mathbb{H}={\mathbb{C}}_b\left(\overline{\mathsf{\Gamma }},{\mathbb{R}}^7\right)$ be the set of all bounded and continuous functions from $\overline{\mathsf{\Gamma }}$ to ${\mathbb{R}}^7$, and ${\mathbb{H}}_{+}={\mathbb{C}}_b\left(\overline{\mathsf{\Gamma }},{\mathbb{R}}_{+}^7\right)\subset \mathbb{H}$. The positive cone ${\mathbb{H}}_{+}$ induces a partial order on $\mathbb{H}$. Let ${\parallel \varphi \parallel }_{\mathbb{H}}=\underset{x\in \overline{\mathsf{\Gamma }}}{sup}\left|\varphi \left(x\right)\right|$, where $|·|$ is the Euclidean norm on ${\mathbb{R}}^7$. This reveals that $\left({\mathbb{H},\parallel ·\parallel }_{\mathbb{H}}\right)$ is a Banach lattice [42,43].

Theorem 1. 

Assume that $D_U=D_I$, $D_Y=D_N$, and $D_M=D_V=D_Z$. Then, model (1) has a unique, nonnegative and bounded solution defined on $\overline{\mathsf{\Gamma }}\times [0,+\infty )$ for any initial conditions satisfying (2).

Proof. 

For any $\gamma ={({\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4,{\gamma }_5,{\gamma }_6,{\gamma }_7)}^T\in {\mathbb{H}}_{+}$, we define $A=(A_1,A_2,A_3,A_4,A_5,A_6$, $A_7{)}^T:{\mathbb{H}}_{+}\to \mathbb{H}$ by

$$\left\{\begin{array}{c}{A}_1\left(\gamma \right)\left(x\right)={\sigma }_1-{\beta }_m{\gamma }_1\left(x\right){\gamma }_3\left(x\right)-d_1{\gamma }_1\left(x\right),\hfill \\ A_2\left(\gamma \right)\left(x\right)={\beta }_m{\gamma }_1\left(x\right){\gamma }_3\left(x\right)-d_2{\gamma }_2\left(x\right),\hfill \\ A_3\left(\gamma \right)\left(x\right)=\eta d_2{\gamma }_2\left(x\right)-q_1{\gamma }_3\left(x\right){\gamma }_7\left(x\right)-d_3{\gamma }_3\left(x\right),\hfill \\ A_4\left(\gamma \right)\left(x\right)={\sigma }_2-{\beta }_v{\gamma }_4\left(x\right){\gamma }_6\left(x\right)-d_4{\gamma }_4\left(x\right),\hfill \\ A_5\left(\gamma \right)\left(x\right)={\beta }_v{\gamma }_4\left(x\right){\gamma }_6\left(x\right)-d_5{\gamma }_5\left(x\right),\hfill \\ A_6\left(\gamma \right)\left(x\right)=e{\gamma }_5\left(x\right)-q_2{\gamma }_6\left(x\right){\gamma }_7\left(x\right)-d_6{\gamma }_6\left(x\right),\hfill \\ A_7\left(\gamma \right)\left(x\right)=p_1{\gamma }_3\left(x\right){\gamma }_7\left(x\right)+p_2{\gamma }_6\left(x\right){\gamma }_7\left(x\right)-d_7{\gamma }_7\left(x\right).\hfill \end{array}\right.$$

We note that A is locally Lipschitz on ${\mathbb{H}}_{+}$. We rewrite system (1)–(3) as the abstract differential equation

$$\left\{\begin{array}{c}\frac{dQ}{dt}=DQ+A\left(Q\right),t>0,\hfill \\ Q_0=\gamma \in {\mathbb{H}}_{+},\hfill \end{array}\right.$$

where $Q={(U,I,M,Y,N,V,Z)}^T$ and $DQ=(D_U\Delta U,D_I\Delta I,D_M\Delta M,D_Y\Delta Y,D_N\Delta N,D_V\Delta V$, $4D_Z{\Delta Z)}^T$. It is possible to show that

$$\underset{h\to 0^{+}}{lim}\frac{1}{h}\mathrm{dist}\left(\gamma +hA\left(\gamma \right),{\mathbb{H}}_{+}\right)=0,\gamma \in {\mathbb{H}}_{+}.$$

According to [42,43,44], systems (1)–(3) have a unique nonnegative mild solution on $[0,T_x)$, which is the maximal existence time interval. Next, we show that the solutions of model (1) are bounded. We define

$${\mathsf{\Theta }}_1(x,t)=U(x,t)+I(x,t).$$

Since $D_U=D_I$, we obtain that

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Theta }}_1(x,t)}{\partial t}-D_U\Delta {\mathsf{\Theta }}_1(x,t)=& {\sigma }_1-d_{1}U(x,t)-d_{2}I(x,t)\hfill \\ \hfill \le & {\sigma }_1-{\zeta }_1\left[U(x,t)+I(x,t)\right]\hfill \\ \hfill =& {\sigma }_1-{\zeta }_1{\mathsf{\Theta }}_1(x,t),\hfill \end{array}$$

where ${\zeta }_1=min\left\{d_1,d_2\right\}$. Thus, ${\mathsf{\Theta }}_1(x,t)$ satisfies the following system:

$$\left\{\begin{array}{c}\frac{\partial {\mathsf{\Theta }}_1(x,t)}{\partial t}-D_U\Delta {\mathsf{\Theta }}_1(x,t)\le {\sigma }_1-{\zeta }_1{\mathsf{\Theta }}_1(x,t),\hfill \\ \frac{\partial {\mathsf{\Theta }}_1}{\partial \overrightarrow{\upsilon }}=0,\hfill \\ {\mathsf{\Theta }}_1(x,0)={\gamma }_1\left(x\right)+{\gamma }_2\left(x\right)\ge 0.\hfill \end{array}\right.$$

Let ${\tilde{\mathsf{\Theta }}}_1\left(t\right)$ be a solution to the following ODE

$$\left\{\begin{array}{c}\frac{d{\tilde{\mathsf{\Theta }}}_1\left(t\right)}{dt}={\sigma }_1-{\zeta }_1{\tilde{\mathsf{\Theta }}}_1\left(t\right),\hfill \\ {\tilde{\mathsf{\Theta }}}_1\left(0\right)=\underset{x\in \overline{\mathsf{\Gamma }}}{\max }{\mathsf{\Theta }}_1(x,0).\hfill \end{array}\right.$$

Thus, ${\tilde{\mathsf{\Theta }}}_1\left(t\right)\le \max \left\{{\displaystyle \frac{{\sigma }_1}{{\zeta }_1}},\underset{x\in \overline{\mathsf{\Gamma }}}{\max }{\mathsf{\Theta }}_1(x,0)\right\}$. Comparison principle [45] provides that ${\mathsf{\Theta }}_1(x,t)\le {\tilde{\mathsf{\Theta }}}_1\left(t\right)$. Therefore, we have

$${\mathsf{\Theta }}_1(x,t)\le \max \left\{{\displaystyle \frac{{\sigma }_1}{{\zeta }_1}},\underset{x\in \overline{\mathsf{\Gamma }}}{\max }{\mathsf{\Theta }}_1(x,0)\right\}:={\kappa }_1.$$

Accordingly, $U(x,t)$ and $I(x,t)$ are bounded. Let

$${\mathsf{\Theta }}_2(x,t)=Y(x,t)+N(x,t).$$

As $D_Y=D_N$, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Theta }}_2(x,t)}{\partial t}-D_Y\Delta {\mathsf{\Theta }}_2(x,t)=& {\sigma }_2-d_{4}Y(x,t)-d_{5}N(x,t)\hfill \\ \hfill \le & {\sigma }_2-{\zeta }_2\left[Y(x,t)+N(x,t)\right]\hfill \\ \hfill =& {\sigma }_2-{\zeta }_2{\mathsf{\Theta }}_2(x,t),\hfill \end{array}$$

where ${\zeta }_2=min\left\{d_4,d_5\right\}$. Comparison principle [45] implies that

$${\mathsf{\Theta }}_2(x,t)\le \max \left\{{\displaystyle \frac{{\sigma }_2}{{\zeta }_2}},\underset{x\in \overline{\mathsf{\Gamma }}}{\max }{\mathsf{\Theta }}_2(x,0)\right\}:={\kappa }_2.$$

This proves the boundedness of $Y(x,t)$ and $N(x,t)$. Finally, we define a function

$${\mathsf{\Theta }}_3(x,t)=M(x,t)+\frac{q_1{p}_2}{p_1{q}_2}V(x,t)+\frac{q_1}{p_1}Z(x,t).$$

Since $D_M=D_V=D_Z$, $I(x,t)\le {\kappa }_1$, and $N(x,t)\le {\kappa }_2$, we have

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Theta }}_3(x,t)}{\partial t}-D_M\Delta {\mathsf{\Theta }}_3(x,t)=& \eta d_{2}I(x,t)+\frac{e{q}_1{p}_2}{p_1{q}_2}N(x,t)-d_{3}M(x,t)-\frac{q_1{p}_2{d}_6}{p_1{q}_2}V(x,t)-\frac{q_1{d}_7}{p_1}Z(x,t)\hfill \\ \hfill \le & \eta d_2{\kappa }_1+\frac{e{q}_1{p}_2}{p_1{q}_2}{\kappa }_2-{\zeta }_3\left[M(x,t)+\frac{q_1{p}_2}{p_1{q}_2}V(x,t)+\frac{q_1}{p_1}Z(x,t)\right]\hfill \\ \hfill =& \eta d_2{\kappa }_1+\frac{e{q}_1{p}_2}{p_1{q}_2}{\kappa }_2-{\zeta }_3{\mathsf{\Theta }}_3(x,t),\hfill \end{array}$$

where ${\zeta }_3=min\left\{d_3,d_6,d_7\right\}$. Based on the comparison principle [45], we obtain

$${\mathsf{\Theta }}_3(x,t)\le \max \left\{\frac{\eta d_2{\kappa }_1}{{\zeta }_3}+\frac{e{q}_1{p}_2{\kappa }_2}{p_1{q}_2{\zeta }_3},\underset{x\in \overline{\mathsf{\Gamma }}}{\max }{\mathsf{\Theta }}_3(x,0)\right\}.$$

Thus, $M(x,t)$, $V(x,t)$, and $Z(x,t)$ are bounded. Consequently, all solutions are bounded on $[0,T_x)$. Based on the standard theory for semi-linear parabolic systems [46], the solutions are bounded on $\overline{\mathsf{\Gamma }}\times [0,+\infty )$. □

Proposition 1. 

There exist positive parameters ${\mathcal{R}}_{0m}$, ${\mathcal{R}}_{1m}$, ${\mathcal{R}}_p$ ${\mathcal{R}}_{0v}$, and ${\mathcal{R}}_{1v}$ such that model (1) admits seven equilibria as:

(1) 

The uninfected equilibrium $E_0$ always exists;

(2) 

The SARS-CoV-2-free equilibrium without immune response $E_1$ exists if ${\mathcal{R}}_{0m}>1$;

(3) 

The SARS-CoV-2-free equilibrium $E_2$ exists if ${\mathcal{R}}_{1m}>1$;

(4) 

The malaria-free equilibrium without immune response $E_3$ exists if ${\mathcal{R}}_{0v}>1$;

(5) 

The malaria-free equilibrium $E_4$ exists if ${\mathcal{R}}_{1v}>1$;

(6) 

The malaria/COVID-19 coinfection immune-free equilibrium $E_5$ exists if ${\mathcal{R}}_{0m}>1$ and ${\mathcal{R}}_{0v}>1$;

(7) 

The malaria/COVID-19 coinfection equilibrium $E_6$ exists if ${\mathcal{R}}_p>1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$, ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}>1+{\displaystyle \frac{e{\beta }_v{q}_1{\sigma }_2{p}_2}{q_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)}}$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}>1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$.

Proof. 

Each equilibrium of system (1) satisfies the following algebraic system:

$$\left\{\begin{array}{c}0={\sigma }_1-{\beta }_{m}UM-d_{1}U,\hfill \\ 0={\beta }_{m}UM-d_{2}I,\hfill \\ 0=\eta d_{2}I-q_{1}MZ-d_{3}M,\hfill \\ 0={\sigma }_2-{\beta }_{v}YV-d_{4}Y,\hfill \\ 0={\beta }_{v}YV-d_{5}N,\hfill \\ 0=eN-q_{2}VZ-d_{6}V,\hfill \\ 0=p_{1}MZ+p_{2}VZ-d_{7}Z.\hfill \end{array}\right.$$

(4)

By solving (4), we obtain the following equilibria:

(1)

The uninfected equilibrium $E_0=(U_0,0,0,Y_0,0,0,0)$, where

$$U_0=\frac{{\sigma }_1}{d_1}>0,Y_0=\frac{{\sigma }_2}{d_4}>0.$$

Thus, the equilibrium $E_0$ always exists.

(2)

The malaria single-infection without immunity equilibrium is given by $E_1=(U_1,I_1$, $M_1,Y_1,0,0,0)$, where

$$U_1=\frac{d_3}{\eta {\beta }_m},I_1=\frac{d_1{d}_3}{\eta {\beta }_m{d}_2}\left({\mathcal{R}}_{0m}-1\right),M_1=\frac{d_1}{{\beta }_m}\left({\mathcal{R}}_{0m}-1\right),Y_1=\frac{{\sigma }_2}{d_4},$$

where ${\mathcal{R}}_{0m}={\displaystyle \frac{\eta {\beta }_m{\sigma }_1}{d_1{d}_3}}$. We note that $U_1$ and $Y_1$ are positive, while $I_1$ and $M_1$ are positive for ${\mathcal{R}}_{0m}>1$. Thus, $E_1$ exists when ${\mathcal{R}}_{0m}>1$. Here, ${\mathcal{R}}_{0m}$ is a threshold parameter, which specifies the establishment of malaria infection.

(3)

The malaria single-infection with immunity equilibrium $E_2=\left(U_2,I_2,M_2,Y_2,0,0,Z_2\right)$. The components are given by

$$U_2=\frac{{\sigma }_1{p}_1}{p_1{d}_1+{\beta }_m{d}_7},I_2=\frac{{\beta }_m{\sigma }_1{d}_7}{d_2(p_1{d}_1+{\beta }_m{d}_7)},M_2=\frac{d_7}{p_1},Y_2=\frac{{\sigma }_2}{d_4},Z_2=\frac{d_3}{q_1}\left({\mathcal{R}}_{1m}-1\right),$$

where ${\mathcal{R}}_{1m}={\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1}{d_3(p_1{d}_1+{\beta }_m{d}_7)}}$. We see that $U_2$, $I_2$, $M_2$ and $Y_2$ are always positive, while $Z_2>0$ when ${\mathcal{R}}_{1m}>1$. Therefore, $E_2$ exists if ${\mathcal{R}}_{1m}>1$. ${\mathcal{R}}_{1m}$ is a threshold parameter which sets the initiation of antibody immune response against malaria merozoites.

(4)

The SARS-CoV-2 single-infection without immunity equilibrium is defined as $E_3=(U_3,0,0,Y_3,N_3,V_3,0)$. The components are given by

$$U_3=\frac{{\sigma }_1}{d_1},Y_3=\frac{d_5{d}_6}{e{\beta }_v},N_3=\frac{d_4{d}_6}{e{\beta }_v}\left({\mathcal{R}}_{0v}-1\right),V_3=\frac{d_4}{{\beta }_v}\left({\mathcal{R}}_{0v}-1\right),$$

where ${\mathcal{R}}_{0v}={\displaystyle \frac{e{\beta }_v{\sigma }_2}{d_4{d}_5{d}_6}}$. Notably, $U_3$ and $Y_3$ are always positive, while $N_3$ and $V_3$ are positive when ${\mathcal{R}}_{0v}>1$. Here, ${\mathcal{R}}_{0v}$ is a threshold parameter which determines the establishment of SARS-CoV-2 infection.

(5)

The SARS-CoV-2 single-infection with immunity is given by $E_4=(U_4,0,0,Y_4,N_4,V_4$, $Z_4)$, where

$$U_4=\frac{{\sigma }_1}{d_1},Y_4=\frac{{\sigma }_2{p}_2}{p_2{d}_4+{\beta }_v{d}_7},N_4=\frac{{\beta }_v{\sigma }_2{d}_7}{d_5(p_2{d}_4+{\beta }_v{d}_7)},V_4=\frac{d_7}{p_2},Z_4=\frac{d_6}{q_2}\left({\mathcal{R}}_{1v}-1\right),$$

where ${\mathcal{R}}_{1v}={\displaystyle \frac{e{\beta }_v{\sigma }_2{p}_2}{d_5{d}_6(p_2{d}_4+{\beta }_v{d}_7)}}$. We see that $U_4$, $Y_4$, $N_4$ and $V_4$ are always positive, while $Z_4>0$ if ${\mathcal{R}}_{1v}>1$. Hence, $E_4$ exists if ${\mathcal{R}}_{1v}>1$. The threshold parameter ${\mathcal{R}}_{1v}$ marks the establishment of antibody immunity against SARS-CoV-2 infection.

(6)

The malaria/SARS-CoV-2 coinfection without immunity equilibrium is given by $E_5=(U_5,I_5,M_5$, $Y_5,N_5,V_5,0)$, where

$$\begin{array}{cc}& U_5=\frac{d_3}{\eta {\beta }_m},I_5=\frac{d_1{d}_3}{\eta {\beta }_m{d}_2}\left({\mathcal{R}}_{0m}-1\right),M_5=\frac{d_1}{{\beta }_m}\left({\mathcal{R}}_{0m}-1\right),\hfill \\ & Y_5=\frac{d_5{d}_6}{e{\beta }_v},N_5=\frac{d_4{d}_6}{e{\beta }_v}\left({\mathcal{R}}_{0v}-1\right),V_5=\frac{d_4}{{\beta }_v}\left({\mathcal{R}}_{0v}-1\right).\hfill \end{array}$$

The components $U_5$ and $Y_5$ are always positive. $I_5$ and $M_5$ are positive when ${\mathcal{R}}_{0m}>1$, while $N_5$ and $V_5$ are positive when ${\mathcal{R}}_{0v}>1$. Consequently, $E_5$ exists when ${\mathcal{R}}_{0m}>1$ and ${\mathcal{R}}_{0v}>1$.

(7)

The malaria/SARS-CoV-2 coinfection with immunity equilibrium is given by $E_6=(U_6,I_6,M_6$, $Y_6,N_6,V_6,Z_6)$, where

$$\begin{array}{cc}& U_6=\frac{{\sigma }_1{p}_1}{p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)},I_6=\frac{{\sigma }_1{\beta }_m(d_7-p_2{V}_6)}{d_2\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]},M_6=\frac{d_7-p_2{V}_6}{p_1},\hfill \\ & Y_6=\frac{q_2{d}_3{d}_5(p_1{d}_1+{\beta }_m{d}_7)\left({\mathcal{R}}_{1m}-1\right)+{\beta }_m{p}_2{q}_2{d}_3{d}_5{V}_6+d_5{q}_1{d}_6\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]}{e{q}_1{\beta }_v\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]},\hfill \\ & N_6=\frac{q_2{d}_3(p_1{d}_1+{\beta }_m{d}_7)\left({\mathcal{R}}_{1m}-1\right)+{\beta }_m{p}_2{q}_2{d}_3{V}_6+q_1{d}_6\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]}{e{q}_1\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]}{V}_6,\hfill \\ & Z_6=\frac{d_3(p_1{d}_1+{\beta }_m{d}_7)\left({\mathcal{R}}_{1m}-1\right)+{\beta }_m{p}_2{d}_3{V}_6}{q_1\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]}.\hfill \end{array}$$

By substituting $Y_6$ in the fourth equation of model (1), we obtain

$$\begin{array}{cc}& e{\beta }_v{q}_1{\sigma }_2\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right]-d_4{d}_5\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right][q_1{d}_6-q_2{d}_3]-\eta {\beta }_m{\sigma }_1{p}_1{q}_2{d}_4{d}_5\hfill \\ & -{\beta }_v{d}_5{V}_6\left[p_1{d}_1+{\beta }_m(d_7-p_2{V}_6)\right](q_1{d}_6-q_2{d}_3)-\eta {\beta }_m{\beta }_v{\sigma }_1{p}_1{q}_2{d}_5{V}_6=0.\hfill \end{array}$$

Thus, $V_6$ fulfills the following equation

$$\begin{array}{cc}& {\beta }_m{\beta }_v{p}_2{d}_5(q_1{d}_6-q_2{d}_3){V_6}^2+({\beta }_m{q}_1{p}_2{d}_4{d}_5{d}_6+{\beta }_v{p}_1{d}_1{q}_2{d}_3{d}_5+{\beta }_m{\beta }_v{q}_2{d}_3{d}_5{d}_7-e{\beta }_m{\beta }_v{q}_1{\sigma }_2{p}_2\hfill \\ & -{\beta }_m{p}_2{q}_2{d}_3{d}_4{d}_5-{\beta }_v{p}_1{q}_1{d}_1{d}_5{d}_6-{\beta }_m{\beta }_v{q}_1{d}_5{d}_6{d}_7-\eta {\beta }_m{\beta }_v{\sigma }_1{p}_1{q}_2{d}_5)V_6+e{\beta }_v{p}_1{q}_1{d}_1{\sigma }_2\hfill \\ & +e{\beta }_m{\beta }_v{q}_1{\sigma }_2{d}_7+p_1{d}_1{q}_2{d}_3{d}_4{d}_5+{\beta }_m{q}_2{d}_3{d}_4{d}_5{d}_7-p_1{d}_1{q}_1{d}_4{d}_5{d}_6-{\beta }_m{q}_1{d}_4{d}_5{d}_6{d}_7-\eta {\beta }_m{\sigma }_1{p}_1{q}_2{d}_4{d}_5=0.\hfill \end{array}$$

Let us define a function $G\left(V\right)$ as follows:

$$G\left(V\right)=a{V}^2+bV+c,$$

where

$$\begin{array}{cc}\hfill a=& {\beta }_m{\beta }_v{p}_2{d}_5(q_1{d}_6-q_2{d}_3),\hfill \\ \hfill b=& {\beta }_m{q}_1{p}_2{d}_4{d}_5{d}_6+{\beta }_v{p}_1{d}_1{q}_2{d}_3{d}_5+{\beta }_m{\beta }_v{q}_2{d}_3{d}_5{d}_7-e{\beta }_m{\beta }_v{q}_1{\sigma }_2{p}_2-{\beta }_m{p}_2{q}_2{d}_3{d}_4{d}_5\hfill \\ & -{\beta }_v{p}_1{q}_1{d}_1{d}_5{d}_6-{\beta }_m{\beta }_v{q}_1{d}_5{d}_6{d}_7-\eta {\beta }_m{\beta }_v{\sigma }_1{p}_1{q}_2{d}_5,\hfill \\ \hfill c=& e{\beta }_v{p}_1{q}_1{d}_1{\sigma }_2+e{\beta }_m{\beta }_v{q}_1{\sigma }_2{d}_7+p_1{d}_1{q}_2{d}_3{d}_4{d}_5+{\beta }_m{q}_2{d}_3{d}_4{d}_5{d}_7-p_1{d}_1{q}_1{d}_4{d}_5{d}_6\hfill \\ & -{\beta }_m{q}_1{d}_4{d}_5{d}_6{d}_7-\eta {\beta }_m{\sigma }_1{p}_1{q}_2{d}_4{d}_5.\hfill \end{array}$$

By computing the value of $G\left(V\right)$ at $V=0$, we obtain

$$\begin{array}{cc}\hfill G\left(0\right)=& e{\beta }_v{q}_1{\sigma }_2(p_1{d}_1+{\beta }_m{d}_7)+q_2{d}_3{d}_4{d}_5(p_1{d}_1+{\beta }_m{d}_7)-q_1{d}_4{d}_5{d}_6(p_1{d}_1+{\beta }_m{d}_7)-\eta {\beta }_m{\sigma }_1{p}_1{q}_2{d}_4{d}_5\hfill \\ \hfill =& q_1{d}_4{d}_5{d}_6(p_1{d}_1+{\beta }_m{d}_7)\left[\frac{e{\beta }_v{q}_1{\sigma }_2+q_2{d}_3{d}_4{d}_5}{q_1{d}_4{d}_5{d}_6}-1-\frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}\right]\hfill \\ \hfill =& q_1{d}_4{d}_5{d}_6(p_1{d}_1+{\beta }_m{d}_7)\left[{\mathcal{R}}_p-1-\frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}\right],\hfill \end{array}$$

where ${\mathcal{R}}_p={\displaystyle \frac{e{\beta }_v{q}_1{\sigma }_2+q_2{d}_3{d}_4{d}_5}{q_1{d}_4{d}_5{d}_6}}$. We note that $G\left(0\right)>0$ if

$${\mathcal{R}}_p>1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}.$$

(5)

In addition, we find that

$$\begin{array}{cc}\hfill G\left(\frac{d_7}{p_2}\right)=& \frac{-1}{p_2}\left[\eta {\beta }_m{\sigma }_1{p}_1{q}_2{d}_5(p_2{d}_4+{\beta }_v{d}_7)+p_1{q}_1{d}_1{d}_5{d}_6(p_2{d}_4+{\beta }_v{d}_7)-p_1{d}_1{q}_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)-e{\beta }_v{p}_1{q}_1{d}_1{\sigma }_2{p}_2\right]\hfill \\ \hfill =& -\frac{p_1{d}_1{q}_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)}{p_2}\left[{\mathcal{R}}_{0m}+\frac{q_1{d}_6}{q_2{d}_3}-1-\frac{e{\beta }_v{q}_1{\sigma }_2{p}_2}{q_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)}\right]\hfill \end{array}$$

Thus, $G\left({\displaystyle \frac{d_7}{p_2}}\right)<0$ if

$${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}>1+\frac{q_1{d}_6}{q_2{d}_3}{\mathcal{R}}_{1v}.$$

(6)

This implies that there exists a root $0<V^{*}<{\displaystyle \frac{d_7}{p_2}}$ such that $G\left(V^{*}\right)=0$. Let $V_6=V^{*}$ and observe that for $0<V_6<{\displaystyle \frac{d_7}{p_2}}$ and ${\mathcal{R}}_{1m}>1$ (${\mathcal{R}}_{1m}>1$ is naturally satisfied at $E_6$ because $E_2$ coexists with $E_6$ when ${\mathcal{R}}_{1m}>1$, but it will not be stable as can be concluded from Theorem 4), we have $U_6>0$, $I_6>0$, $M_6>0$, $Y_6>0$, $N_6>0$ and $Z_6>0$. Similarly, to find the third existence condition of $E_6$, we form a function of Z and extract the conditions at which there is a positive root. This will give

$${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}>1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}.$$

(7)

It follows that $E_6$ exists if conditions (5), (6), and (7) are met. □

4. Global Stability of Equilibria

This section confirms the global stability of all equilibrium points by building appropriate Lyapunov functionals. Define a Lyapunov functional

$${\Delta }_i\left(t\right)={\int }_{\mathsf{\Gamma }}{\tilde{\Delta }}_i(x,t)\mathrm{d}x,$$

and let $K_i^{{}^{\prime }}$ be the largest invariant subset of $K_i=\left\{(U,I,M,Y,N,V,Z)|{\displaystyle \frac{d{\Delta }_i}{dt}}=0\right\},i=0,1,\cdots ,6.$

Theorem 2. 

The uninfected equilibrium $E_0$ is globally asymptotically stable (GAS) when ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{0v}\le 1$.

Proof. 

Define

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_0(x,t)=& U_0\left(\frac{U}{U_0}-1-ln\frac{U}{U_0}\right)+I+\frac{1}{\eta }M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_0\left(\frac{Y}{Y_0}-1-ln\frac{Y}{Y_0}\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}N+\frac{q_1{p}_2}{\eta p_1{q}_2}V+\frac{q_1}{\eta p_1}Z.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_0}{\partial t}=& \left(1-\frac{U_0}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+D_I\Delta I+{\beta }_{m}UM-d_{2}I\hfill \\ \hfill & +\frac{1}{\eta }\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_0}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ \hfill & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ \hfill & +\frac{q_1}{\eta p_1}\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right)\hfill \\ \hfill =& \left(1-\frac{U_0}{U}\right)\left({\sigma }_1-d_{1}U\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_0}{Y}\right)\left({\sigma }_2-d_{4}Y\right)+\left({\beta }_m{U}_0-\frac{d_3}{\eta }\right)M\hfill \\ \hfill & +\left(\frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_0-\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\right)V-\frac{q_1{d}_7}{\eta p_1}Z+\left(1-\frac{U_0}{U}\right)D_U\Delta U+D_I\Delta I+\frac{1}{\eta }{D}_M\Delta M\hfill \\ \hfill & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_0}{Y}\right)D_Y\Delta Y+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N\Delta N+\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V\Delta V+\frac{q_1}{\eta p_1}{D}_Z\Delta Z.\hfill \end{array}$$

By calculating the time derivative of ${\Delta }_0\left(t\right)$, we have

$$\begin{array}{cc}\hfill \frac{d{\Delta }_0}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_0\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_0\right)}^2}{Y}\mathrm{d}x+\frac{d_3}{\eta }\left({\mathcal{R}}_{0m}-1\right){\int }_{\mathsf{\Gamma }}M\mathrm{d}x\hfill \\ \hfill & +\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left({\mathcal{R}}_{0v}-1\right){\int }_{\mathsf{\Gamma }}V\mathrm{d}x-\frac{q_1{d}_7}{\eta p_1}{\int }_{\mathsf{\Gamma }}Z\mathrm{d}x+D_U{\int }_{\mathsf{\Gamma }}\left(1-\frac{U_0}{U}\right)\Delta U\mathrm{d}x+D_I{\int }_{\mathsf{\Gamma }}\Delta I\mathrm{d}x\hfill \\ \hfill & +\frac{1}{\eta }{D}_M{\int }_{\mathsf{\Gamma }}\Delta M\mathrm{d}x+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{\int }_{\mathsf{\Gamma }}\left(1-\frac{Y_0}{Y}\right)\Delta Y\mathrm{d}x+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N{\int }_{\mathsf{\Gamma }}\Delta N\mathrm{d}x\hfill \\ \hfill & +\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V{\int }_{\mathsf{\Gamma }}\Delta V\mathrm{d}x+\frac{q_1}{\eta p_1}{D}_Z{\int }_{\mathsf{\Gamma }}\Delta Z\mathrm{d}x.\hfill \end{array}$$

(8)

Depending on the Divergence theorem and NBCs, we have

$$\begin{array}{cc}\hfill 0=& {\int }_{\partial \mathsf{\Gamma }}\nabla \chi ·\overrightarrow{\upsilon }\mathrm{d}x={\int }_{\mathsf{\Gamma }}\mathrm{div}(\nabla \chi )\mathrm{d}x={\int }_{\mathsf{\Gamma }}\Delta \chi \mathrm{d}x,\hfill \\ \hfill 0=& {\int }_{\partial \mathsf{\Gamma }}\frac{1}{\chi }\nabla \chi ·\overrightarrow{\upsilon }\mathrm{d}x={\int }_{\mathsf{\Gamma }}\mathrm{div}(\frac{1}{\chi }\nabla \chi )\mathrm{d}x={\int }_{\mathsf{\Gamma }}\left[\frac{\Delta \chi }{\chi }-\frac{{\parallel ▿\chi \parallel }^2}{{\chi }^2}\right]\mathrm{d}x,\mathrm{for}\chi \in \{U,I,M,Y,N,V,Z\}.\hfill \end{array}$$

This implies that

$$\begin{array}{cc}& {\int }_{\mathsf{\Gamma }}\Delta \chi \mathrm{d}x=0,\hfill \\ & {\int }_{\mathsf{\Gamma }}\frac{\Delta \chi }{\chi }\mathrm{d}x={\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿\chi \parallel }^2}{{\chi }^2}\mathrm{d}x,\mathrm{for}\chi \in \{U,I,M,Y,N,V,Z\}.\hfill \end{array}$$

(9)

By applying (9) to (8), we obtain

$$\begin{array}{cc}\hfill \frac{d{\Delta }_0}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_0\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_0\right)}^2}{Y}\mathrm{d}x+\frac{d_3}{\eta }\left({\mathcal{R}}_{0m}-1\right){\int }_{\mathsf{\Gamma }}M\mathrm{d}x\hfill \\ \hfill & +\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left({\mathcal{R}}_{0v}-1\right){\int }_{\mathsf{\Gamma }}V\mathrm{d}x-\frac{q_1{d}_7}{\eta p_1}{\int }_{\mathsf{\Gamma }}Z\mathrm{d}x-D_U{U}_0{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_0{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x.\hfill \end{array}$$

We note that ${\displaystyle \frac{d{\Delta }_0}{dt}}\le 0$ when ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{0v}\le 1$. In addition, ${\displaystyle \frac{d{\Delta }_0}{dt}}=0$ when $U=U_0$, $Y=Y_0$, and $M=V=Z=0$. The solutions tend to $K_0^{{}^{\prime }}$ which contains elements with $M=V=0$ and then ${\displaystyle \frac{dM}{dt}}=0$ and ${\displaystyle \frac{dV}{dt}}=0$. The third and sixth equations of system (1) imply that $I=N=0$. Then, $K_0^{{}^{\prime }}=\left\{E_0\right\}$ and thus LaSalle’s invariance principle (LIP) [47] assures the global asymptotic stability of $E_0$ when ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{0v}\le 1$. □

Theorem 3. 

Assume that ${\mathcal{R}}_{0m}>1$. Then, the malaria single-infection without immunity equilibrium $E_1$ is GAS if ${\mathcal{R}}_{0v}\le 1$ and ${\mathcal{R}}_{1m}\le 1$.

Proof. 

Define

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_1(x,t)=& U_1\left(\frac{U}{U_1}-1-ln\frac{U}{U_1}\right)+I_1\left(\frac{I}{I_1}-1-ln\frac{I}{I_1}\right)+\frac{1}{\eta }{M}_1\left(\frac{M}{M_1}-1-ln\frac{M}{M_1}\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_1\left(\frac{Y}{Y_1}-1-ln\frac{Y}{Y_1}\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}N+\frac{q_1{p}_2}{\eta p_1{q}_2}V+\frac{q_1}{\eta p_1}Z.\hfill \end{array}$$

Then, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_1}{\partial t}=& \left(1-\frac{U_1}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+\left(1-\frac{I_1}{I}\right)\left(D_I\Delta I+{\beta }_{m}UM-d_{2}I\right)\hfill \\ & +\frac{1}{\eta }\left(1-\frac{M_1}{M}\right)\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_1}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ & +\frac{q_1}{\eta p_1}\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right).\hfill \end{array}$$

(10)

The equilibrium conditions at $E_1$ are

$$\left\{\begin{array}{c}{\sigma }_1={\beta }_m{U}_1{M}_1+d_1{U}_1,\hfill \\ {\beta }_m{U}_1{M}_1=d_2{I}_1,\hfill \\ d_2{I}_1=\frac{d_3}{\eta }{M}_1,\hfill \\ {\sigma }_2=d_4{Y}_1.\hfill \end{array}\right.$$

(11)

By utilizing (11) to collect terms of Equation (10), we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_1}{\partial t}=& \left(1-\frac{U_1}{U}\right)\left(d_1{U}_1-d_{1}U\right)+3{\beta }_m{U}_1{M}_1-{\beta }_m{U}_1{M}_1\frac{U_1}{U}-{\beta }_m{U}_1{M}_1\frac{U{I}_{1}M}{U_{1}I{M}_1}\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_1}{Y}\right)\left(d_4{Y}_1-d_{4}Y\right)-{\beta }_m{U}_1{M}_1\frac{I{M}_1}{I_{1}M}+\left(\frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_1-\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\right)V\hfill \\ & +\left(\frac{q_1}{\eta }{M}_1-\frac{q_1{d}_7}{\eta p_1}\right)Z+\left(1-\frac{U_1}{U}\right)D_U\Delta U+\left(1-\frac{I_1}{I}\right)D_I\Delta I+\frac{1}{\eta }\left(1-\frac{M_1}{M}\right)D_M\Delta M\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_1}{Y}\right)D_Y\Delta Y+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N\Delta N+\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V\Delta V+\frac{q_1}{\eta p_1}{D}_Z\Delta Z.\hfill \end{array}$$

By computing ${\displaystyle \frac{d{\Delta }_1}{dt}}$, we obtain

$$\begin{array}{cc}\hfill \frac{d{\Delta }_1}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_1\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_1\right)}^2}{Y}\mathrm{d}x+{\beta }_m{U}_1{M}_1{\int }_{\mathsf{\Gamma }}\left(3-\frac{U_1}{U}-\frac{I{M}_1}{I_{1}M}-\frac{U{I}_{1}M}{U_{1}I{M}_1}\right)\mathrm{d}x\hfill \\ & +\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left({\mathcal{R}}_{0v}-1\right){\int }_{\mathsf{\Gamma }}V\mathrm{d}x+\frac{q_1(p_1{d}_1+{\beta }_m{d}_7)}{\eta p_1{\beta }_m}\left({\mathcal{R}}_{1m}-1\right){\int }_{\mathsf{\Gamma }}Z\mathrm{d}x+D_U{\int }_{\mathsf{\Gamma }}\left(1-\frac{U_1}{U}\right)\Delta U\mathrm{d}x\hfill \\ & +D_I{\int }_{\mathsf{\Gamma }}\left(1-\frac{I_1}{I}\right)\Delta I\mathrm{d}x+\frac{1}{\eta }{D}_M{\int }_{\mathsf{\Gamma }}\left(1-\frac{M_1}{M}\right)\Delta M\mathrm{d}x+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{\int }_{\mathsf{\Gamma }}\left(1-\frac{Y_1}{Y}\right)\Delta Y\mathrm{d}x\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N{\int }_{\mathsf{\Gamma }}\Delta N\mathrm{d}x+\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V{\int }_{\mathsf{\Gamma }}\Delta V\mathrm{d}x+\frac{q_1}{\eta p_1}{D}_Z{\int }_{\mathsf{\Gamma }}\Delta Z\mathrm{d}x\hfill \\ \hfill =& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_1\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_1\right)}^2}{Y}\mathrm{d}x+{\beta }_m{U}_1{M}_1{\int }_{\mathsf{\Gamma }}\left(3-\frac{U_1}{U}-\frac{I{M}_1}{I_{1}M}-\frac{U{I}_{1}M}{U_{1}I{M}_1}\right)\mathrm{d}x\hfill \\ & +\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left({\mathcal{R}}_{0v}-1\right){\int }_{\mathsf{\Gamma }}V\mathrm{d}x+\frac{q_1(p_1{d}_1+{\beta }_m{d}_7)}{\eta p_1{\beta }_m}\left({\mathcal{R}}_{1m}-1\right){\int }_{\mathsf{\Gamma }}Z\mathrm{d}x-D_U{U}_1{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x\hfill \\ & -D_I{I}_1{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}x-\frac{1}{\eta }{D}_M{M}_1{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿M\parallel }^2}{M^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_1{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x.\hfill \end{array}$$

Thus, we see that ${\displaystyle \frac{d{\Delta }_1}{dt}}\le 0$ if ${\mathcal{R}}_{0v}\le 1$ and ${\mathcal{R}}_{1m}\le 1$. In addition, ${\displaystyle \frac{d{\Delta }_1}{dt}}=0$ when $U=U_1$, $I=I_1$, $M=M_1$, $Y=Y_1$, and $V=Z=0$. The solutions tend to $K_1^{{}^{\prime }}$, which has $V=0$ and then ${\displaystyle \frac{dV}{dt}}=0$. From the sixth equation of (1), we obtain $N=0$. Hence, $K_1^{{}^{\prime }}=\left\{E_1\right\}$. Accordingly, LIP proves the global asymptotic stability of $E_1$ if ${\mathcal{R}}_{0m}>1$, ${\mathcal{R}}_{0v}\le 1$ and ${\mathcal{R}}_{1m}\le 1$. □

Theorem 4. 

Suppose that ${\mathcal{R}}_{1m}>1$. Then, the malaria single-infection with immunity equilibrium $E_2$ is GAS when ${\mathcal{R}}_p\le 1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$.

Proof. 

Consider

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_2(x,t)=& U_2\left(\frac{U}{U_2}-1-ln\frac{U}{U_2}\right)+I_2\left(\frac{I}{I_2}-1-ln\frac{I}{I_2}\right)+\frac{1}{\eta }{M}_2\left(\frac{M}{M_2}-1-ln\frac{M}{M_2}\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_2\left(\frac{Y}{Y_2}-1-ln\frac{Y}{Y_2}\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}N+\frac{q_1{p}_2}{\eta p_1{q}_2}V+\frac{q_1}{\eta p_1}{Z}_2\left(\frac{Z}{Z_2}-1-ln\frac{Z}{Z_2}\right).\hfill \end{array}$$

Then, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_2}{\partial t}=& \left(1-\frac{U_2}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+\left(1-\frac{I_2}{I}\right)\left(D_I\Delta I+{\beta }_{m}UM-d_{2}I\right)\hfill \\ & +\frac{1}{\eta }\left(1-\frac{M_2}{M}\right)\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_2}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ & +\frac{q_1}{\eta p_1}\left(1-\frac{Z_2}{Z}\right)\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right).\hfill \end{array}$$

(12)

The equilibrium conditions at $E_2$ are computed as

$$\left\{\begin{array}{c}{\sigma }_1={\beta }_m{U}_2{M}_2+d_1{U}_2,\hfill \\ {\beta }_m{U}_2{M}_2=d_2{I}_2,\hfill \\ d_2{I}_2=\frac{d_3}{\eta }{M}_2+\frac{q_1}{\eta }{M}_2{Z}_2,\hfill \\ {\sigma }_2=d_4{Y}_2,\hfill \\ \frac{q_1}{\eta }{M}_2{Z}_2=\frac{q_1{d}_7}{\eta p_1}{Z}_2.\hfill \end{array}\right.$$

After using the equilibrium conditions to collect terms of Equation (12), we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_2}{\partial t}=& \left(1-\frac{U_2}{U}\right)\left(d_1{U}_2-d_{1}U\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_2}{Y}\right)\left(d_4{Y}_2-d_{4}Y\right)+3{\beta }_m{U}_2{M}_2-{\beta }_m{U}_2{M}_2\frac{U_2}{U}\hfill \\ & -{\beta }_m{U}_2{M}_2\frac{U{I}_{2}M}{U_{2}I{M}_2}-{\beta }_m{U}_2{M}_2\frac{I{M}_2}{I_{2}M}+\left(\frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_2-\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}-\frac{q_1{p}_2}{\eta p_1}{Z}_2\right)V+\left(1-\frac{U_2}{U}\right)D_U\Delta U\hfill \\ & +\left(1-\frac{I_2}{I}\right)D_I\Delta I+\frac{1}{\eta }\left(1-\frac{M_2}{M}\right)D_M\Delta M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_2}{Y}\right)D_Y\Delta Y+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N\Delta N\hfill \\ & +\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V\Delta V+\frac{q_1}{\eta p_1}\left(1-\frac{Z_2}{Z}\right)D_Z\Delta Z.\hfill \end{array}$$

By using the values of $Y_2$ and $Z_2$, we have

$$\begin{array}{cc}\hfill \frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_2-\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}-\frac{q_1{p}_2}{\eta p_1}{Z}_2=& \frac{e{\beta }_v{q}_1{\sigma }_2{p}_2}{\eta p_1{q}_2{d}_4{d}_5}-\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}-\frac{q_1{p}_2\left(\eta {\beta }_m{\sigma }_1{p}_1-p_1{d}_1{d}_3-{\beta }_m{d}_3{d}_7\right)}{\eta p_1{q}_1(p_1{d}_1+{\beta }_m{d}_7)}\hfill \\ \hfill =& \frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left[\frac{e{\beta }_v{q}_1{\sigma }_2+q_2{d}_3{d}_4{d}_5}{q_1{d}_4{d}_5{d}_6}-1-\frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}\right]\hfill \\ \hfill =& \frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left[{\mathcal{R}}_p-1-\frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}\right].\hfill \end{array}$$

Accordingly, ${\displaystyle \frac{d{\Delta }_2}{dt}}$ is given by

$$\begin{array}{cc}\hfill \frac{d{\Delta }_2}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_2\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_2\right)}^2}{Y}\mathrm{d}x+{\beta }_m{U}_2{M}_2{\int }_{\mathsf{\Gamma }}\left(3-\frac{U_2}{U}-\frac{I{M}_2}{I_{2}M}-\frac{U{I}_{2}M}{U_{2}I{M}_2}\right)\mathrm{d}x\hfill \\ & +\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}\left({\mathcal{R}}_p-1-\frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}\right){\int }_{\mathsf{\Gamma }}V\mathrm{d}x-D_U{U}_2{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x\hfill \\ & -D_I{I}_2{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}x-\frac{1}{\eta }{D}_M{M}_2{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿M\parallel }^2}{M^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_2{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x\hfill \\ & -\frac{q_1}{\eta p_1}{D}_Z{Z}_2{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Z\parallel }^2}{Z^2}\mathrm{d}x.\hfill \end{array}$$

We observe that ${\displaystyle \frac{d{\Delta }_2}{dt}}\le 0$ if ${\mathcal{R}}_p\le 1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$. In addition, ${\displaystyle \frac{d{\Delta }_2}{dt}}=0$ when $U=U_2$, $I=I_2$, $M=M_2$, $Y=Y_2$, and $V=0$. We can prove that the elements of $K_2^{{}^{\prime }}$ satisfy $N=0$ and $Z=Z_2$. Consequently, $K_2^{{}^{\prime }}=\left\{E_2\right\}$. Therefore, the global asymptotic stability of $E_2$ is followed by LIP when ${\mathcal{R}}_{1m}>1$ and ${\mathcal{R}}_p\le 1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$. □

Theorem 5. 

Assume that ${\mathcal{R}}_{0v}>1$. Then, the SARS-CoV-2 single-infection without immunity equilibrium $E_3$ is GAS when ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{1v}\le 1$.

Proof. 

Define

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_3(x,t)=& U_3\left(\frac{U}{U_3}-1-ln\frac{U}{U_3}\right)+I+\frac{1}{\eta }M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_3\left(\frac{Y}{Y_3}-1-ln\frac{Y}{Y_3}\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{N}_3\left(\frac{N}{N_3}-1-ln\frac{N}{N_3}\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}{V}_3\left(\frac{V}{V_3}-1-ln\frac{V}{V_3}\right)+\frac{q_1}{\eta p_1}Z.\hfill \end{array}$$

Then, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_3}{\partial t}=& \left(1-\frac{U_3}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+D_I\Delta I+{\beta }_{m}UM-d_{2}I\hfill \\ & +\frac{1}{\eta }\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_3}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_3}{N}\right)\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_3}{V}\right)\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ & +\frac{q_1}{\eta p_1}\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right).\hfill \end{array}$$

(13)

By using the equilibrium conditions at $E_3$

$$\left\{\begin{array}{c}{\sigma }_1=d_1{U}_3,\hfill \\ {\sigma }_2={\beta }_v{Y}_3{V}_3+d_4{Y}_3,\hfill \\ \frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_3{V}_3=\frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_3,\hfill \\ \frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_3=\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}{V}_3,\hfill \end{array}\right.$$

the partial derivative in (13) is transformed to

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_3}{\partial t}=& \left(1-\frac{U_3}{U}\right)\left(d_1{U}_3-d_{1}U\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_3}{Y}\right)\left(d_4{Y}_3-d_{4}Y\right)+3\frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_3{V}_3\hfill \\ & -\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_3{V}_3\frac{Y_3}{Y}-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_3{V}_3\frac{N{V}_3}{N_{3}V}-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_3{V}_3\frac{Y{N}_{3}V}{Y_{3}N{V}_3}+\left({\beta }_m{U}_3-\frac{d_3}{\eta }\right)M\hfill \\ & +\left(\frac{q_1{p}_2}{\eta p_1}-\frac{q_1{d}_7}{\eta p_1}\right)Z+\left(1-\frac{U_3}{U}\right)D_U\Delta U+D_I\Delta I+\frac{1}{\eta }{D}_M\Delta M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_3}{Y}\right)D_Y\Delta Y\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_3}{N}\right)D_N\Delta N+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_3}{V}\right)D_V\Delta V+\frac{q_1}{\eta p_1}{D}_Z\Delta Z.\hfill \end{array}$$

Accordingly, ${\displaystyle \frac{d{\Delta }_3}{dt}}$ is given by

$$\begin{array}{cc}\hfill \frac{d{\Delta }_3}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_3\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_3\right)}^2}{Y}\mathrm{d}x+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_3{V}_3{\int }_{\mathsf{\Gamma }}\left(3-\frac{Y_3}{Y}-\frac{N{V}_3}{N_{3}V}-\frac{Y{N}_{3}V}{Y_{3}N{V}_3}\right)\mathrm{d}x\hfill \\ & +\frac{d_3}{\eta }\left({\mathcal{R}}_{0m}-1\right){\int }_{\mathsf{\Gamma }}M\mathrm{d}x+\frac{q_1(p_2{d}_4+{\beta }_v{d}_7)}{\eta p_1{\beta }_v}\left({\mathcal{R}}_{1v}-1\right){\int }_{\mathsf{\Gamma }}Z\mathrm{d}x-D_U{U}_3{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x\hfill \\ & -\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_3{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N{N}_3{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿N\parallel }^2}{N^2}\mathrm{d}x-\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V{V}_3{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿V\parallel }^2}{V^2}\mathrm{d}x.\hfill \end{array}$$

This implies that ${\displaystyle \frac{d{\Delta }_3}{dt}}\le 0$ if ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{1v}\le 1$. In addition, one can show that ${\displaystyle \frac{d{\Delta }_3}{dt}}=0$ when $U=U_3$, $I=0$, $M=0$, $Y=Y_3$, $N=N_3$, $V=V_3$, and $Z=0$. Thus, $K_3^{{}^{\prime }}=\left\{E_3\right\}$. As a result, LIP insures the global asymptotic stability of $E_3$ when ${\mathcal{R}}_{0v}>1$, ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{1v}\le 1$. □

Theorem 6. 

Assume that ${\mathcal{R}}_{1v}>1$. Then, the SARS-CoV-2 single-infection with immunity equilibrium $E_4$ is GAS if ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}\le 1+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}$.

Proof. 

Consider

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_4(x,t)=& U_4\left(\frac{U}{U_4}-1-ln\frac{U}{U_4}\right)+I+\frac{1}{\eta }M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_4\left(\frac{Y}{Y_4}-1-ln\frac{Y}{Y_4}\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{N}_4\left(\frac{N}{N_4}-1-ln\frac{N}{N_4}\right)\hfill \\ & +\frac{q_1{p}_2}{\eta p_1{q}_2}{V}_4\left(\frac{V}{V_4}-1-ln\frac{V}{V_4}\right)+\frac{q_1}{\eta p_1}{Z}_4\left(\frac{Z}{Z_4}-1-ln\frac{Z}{Z_4}\right).\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_4}{\partial t}=& \left(1-\frac{U_4}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+D_I\Delta I+{\beta }_{m}UM-d_{2}I\hfill \\ & +\frac{1}{\eta }\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_4}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_4}{N}\right)\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_4}{V}\right)\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ & +\frac{q_1}{\eta p_1}\left(1-\frac{Z_4}{Z}\right)\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right).\hfill \end{array}$$

(14)

The equilibrium conditions at $E_4$ can be written as

$$\left\{\begin{array}{c}{\sigma }_1=d_1{U}_4,\hfill \\ {\sigma }_2={\beta }_v{Y}_4{V}_4+d_4{Y}_4,\hfill \\ \frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_4{V}_4=\frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_4,\hfill \\ \frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_4=\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}{V}_4+\frac{q_1{p}_2}{\eta p_1}{V}_4{Z}_4,\hfill \\ \frac{q_1{p}_2}{\eta p_1}{V}_4{Z}_4=\frac{q_1{d}_7}{\eta p_1}{Z}_4.\hfill \end{array}\right.$$

(15)

By utilizing Equation (15) to collect terms of Equation (14), we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_4}{\partial t}=& -\frac{d_1{\left(U-U_4\right)}^2}{U}-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}\frac{{\left(Y-Y_4\right)}^2}{Y}+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_4{V}_4\left(3-\frac{Y_4}{Y}-\frac{N{V}_4}{N_{4}V}-\frac{Y{N}_{4}V}{Y_{4}N{V}_4}\right)\hfill \\ & +\left({\beta }_m{U}_4-\frac{d_3}{\eta }-\frac{q_1}{\eta }{Z}_4\right)M+\left(1-\frac{U_4}{U}\right)D_U\Delta U+D_I\Delta I+\frac{1}{\eta }{D}_M\Delta M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_4}{Y}\right)D_Y\Delta Y\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_4}{N}\right)D_N\Delta N+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_4}{V}\right)D_V\Delta V+\frac{q_1}{\eta p_1}\left(1-\frac{Z_4}{Z}\right)D_Z\Delta Z.\hfill \end{array}$$

By using Equation (9), ${\displaystyle \frac{d{\Delta }_4}{dt}}$ is computed as

$$\begin{array}{cc}\hfill \frac{d{\Delta }_4}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_4\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_4\right)}^2}{Y}\mathrm{d}x+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_4{V}_4{\int }_{\mathsf{\Gamma }}\left(3-\frac{Y_4}{Y}-\frac{N{V}_4}{N_{4}V}-\frac{Y{N}_{4}V}{Y_{4}N{V}_4}\right)\mathrm{d}x\hfill \\ & +\frac{d_3}{\eta }\left({\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}-1-{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}\right){\int }_{\mathsf{\Gamma }}M\mathrm{d}x-D_U{U}_4{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_4{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x\hfill \\ & -\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N{N}_4{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿N\parallel }^2}{N^2}\mathrm{d}x-\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V{V}_4{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿V\parallel }^2}{V^2}\mathrm{d}x-\frac{q_1}{\eta p_1}{D}_Z{Z}_4{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Z\parallel }^2}{Z^2}\mathrm{d}x.\hfill \end{array}$$

Therefore, ${\displaystyle \frac{d{\Delta }_4}{dt}}\le 0$ if ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}\le 1+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}$. Furthermore, ${\displaystyle \frac{d{\Delta }_4}{dt}}=0$ when $U=U_4$, $M=0$, $Y=Y_4$, $N=N_4$, and $V=V_4$. One can show that $K_4^{{}^{\prime }}=\left\{E_4\right\}$. By LIP, the equilibrium $E_4$ is GAS if ${\mathcal{R}}_{1v}>1$ and ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}\le 1+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}$. □

Theorem 7. 

Assume that ${\mathcal{R}}_{0m}>1$ and ${\mathcal{R}}_{0v}>1$. Then, the malaria/SARS-CoV-2 coinfection without immunity equilibrium $E_5$ is GAS if ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}\le 1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$.

Proof. 

Define

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_5(x,t)=& U_5\left(\frac{U}{U_5}-1-ln\frac{U}{U_5}\right)+I_5\left(\frac{I}{I_5}-1-ln\frac{I}{I_5}\right)+\frac{1}{\eta }{M}_5\left(\frac{M}{M_5}-1-ln\frac{M}{M_5}\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_5\left(\frac{Y}{Y_5}-1-ln\frac{Y}{Y_5}\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{N}_5\left(\frac{N}{N_5}-1-ln\frac{N}{N_5}\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}{V}_5\left(\frac{V}{V_5}-1-ln\frac{V}{V_5}\right)+\frac{q_1}{\eta p_1}Z.\hfill \end{array}$$

Then, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_5}{\partial t}=& \left(1-\frac{U_5}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+\left(1-\frac{I_5}{I}\right)\left(D_I\Delta I+{\beta }_{m}UM-d_{2}I\right)\hfill \\ & +\frac{1}{\eta }\left(1-\frac{M_5}{M}\right)\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_5}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_5}{N}\right)\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_5}{V}\right)\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ & +\frac{q_1}{\eta p_1}\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right).\hfill \end{array}$$

(16)

The equilibrium conditions at $E_5$ can be written as

$$\left\{\begin{array}{c}{\sigma }_1=d_1{U}_5+{\beta }_m{U}_5{M}_5,\hfill \\ {\beta }_m{U}_5{M}_5=d_2{I}_5,\hfill \\ d_2{I}_5=\frac{d_3}{\eta }{M}_5,\hfill \\ {\sigma }_2={\beta }_v{Y}_5{V}_5+d_4{Y}_5,\hfill \\ \frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_5{V}_5=\frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_5,\hfill \\ \frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_5=\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}{V}_5.\hfill \end{array}\right.$$

By using the above conditions, the derivative in (16) becomes

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_5}{\partial t}=& -\frac{d_1{\left(U-U_5\right)}^2}{U}-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}\frac{{\left(Y-Y_5\right)}^2}{Y}+{\beta }_m{U}_5{M}_5\left(3-\frac{U_5}{U}-\frac{I{M}_5}{I_{5}M}-\frac{U{I}_{5}U}{U_{5}I{M}_5}\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_5{V}_5\left(3-\frac{Y_5}{Y}-\frac{N{V}_5}{N_{5}V}-\frac{Y{N}_{5}V}{Y_{5}N{V}_5}\right)+\left(\frac{q_1}{\eta }{M}_5+\frac{q_1{p}_2}{\eta p_1}{V}_5-\frac{q_1{d}_7}{\eta p_1}\right)Z\hfill \\ & +\left(1-\frac{U_5}{U}\right)D_U\Delta U+\left(1-\frac{I_5}{I}\right)D_I\Delta I+\frac{1}{\eta }\left(1-\frac{M_5}{M}\right)D_M\Delta M+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_5}{Y}\right)D_Y\Delta Y\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_5}{N}\right)D_N\Delta N+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_5}{V}\right)D_V\Delta V+\frac{q_1}{\eta p_1}{D}_Z\Delta Z.\hfill \end{array}$$

(17)

To evaluate the fifth term in (17), we calculate

$$\begin{array}{cc}\hfill \frac{q_1}{\eta }{M}_5+\frac{q_1{p}_2}{\eta p_1}{V}_5-\frac{q_1{d}_7}{\eta p_1}=& \frac{q_1{\sigma }_1}{d_3}+\frac{e{q}_1{\sigma }_2{p}_2}{\eta p_1{d}_5{d}_6}-\frac{q_1{d}_1}{\eta {\beta }_m}-\frac{q_1{p}_2{d}_4}{\eta p_1{\beta }_v}-\frac{q_1{d}_7}{\eta p_1}\hfill \\ \hfill =& \frac{q_1{d}_1}{\eta {\beta }_m}\left[\frac{\eta {\sigma }_1{\beta }_m}{d_1{d}_3}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}-1-{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}\right]\hfill \\ \hfill =& \frac{q_1{d}_1}{\eta {\beta }_m}\left[{\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}-1-{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}\right].\hfill \end{array}$$

Accordingly, ${\displaystyle \frac{d{\Delta }_5}{dt}}$ is provided as

$$\begin{array}{cc}\hfill \frac{d{\Delta }_5}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_5\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_5\right)}^2}{Y}\mathrm{d}x+{\beta }_m{U}_5{M}_5{\int }_{\mathsf{\Gamma }}\left(3-\frac{U_5}{U}-\frac{I{M}_5}{I_{5}M}-\frac{U{I}_{5}M}{U_{5}I{M}_5}\right)\mathrm{d}x\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_5{V}_5{\int }_{\mathsf{\Gamma }}\left(3-\frac{Y_5}{Y}-\frac{N{V}_5}{N_{5}V}-\frac{Y{N}_{5}V}{Y_{5}N{V}_5}\right)\mathrm{d}x+\left({\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}-1-{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}\right){\int }_{\mathsf{\Gamma }}Z\mathrm{d}x\hfill \\ & -D_U{U}_5{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x-D_I{I}_5{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}x-\frac{1}{\eta }{D}_M{M}_5{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿M\parallel }^2}{M^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_5{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x\hfill \\ & -\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N{N}_5{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿N\parallel }^2}{N^2}\mathrm{d}x-\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V{V}_5{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿V\parallel }^2}{V^2}\mathrm{d}x.\hfill \end{array}$$

Hence, we have ${\displaystyle \frac{d{\Delta }_5}{dt}}\le 0$ if ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}\le 1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$. In addition, ${\displaystyle \frac{d{\Delta }_5}{dt}}=0$ when $U=U_5$, $I=I_5$, $M=M_5$, $Y=Y_5$, $N=N_5$, $V=V_5$, and $Z=0$. Thus, $K_5^{{}^{\prime }}=\left\{E_5\right\}$ and, according to LIP, $E_5$ is GAS if ${\mathcal{R}}_{0m}>1$, ${\mathcal{R}}_{0v}>1$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}\le 1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$. □

Theorem 8. 

Suppose that ${\mathcal{R}}_p>1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$, ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}>1+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}>1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$. Then, the malaria/SARS-CoV-2 coinfection with immunity equilibrium $E_6$ is GAS.

Proof. 

Consider

$$\begin{array}{cc}\hfill {\tilde{\Delta }}_6(x,t)=& U_6\left(\frac{U}{U_6}-1-ln\frac{U}{U_6}\right)+I_6\left(\frac{I}{I_6}-1-ln\frac{I}{I_6}\right)+\frac{1}{\eta }{M}_6\left(\frac{M}{M_6}-1-ln\frac{M}{M_6}\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{Y}_6\left(\frac{Y}{Y_6}-1-ln\frac{Y}{Y_6}\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{N}_6\left(\frac{N}{N_6}-1-ln\frac{N}{N_6}\right)\hfill \\ & +\frac{q_1{p}_2}{\eta p_1{q}_2}{V}_6\left(\frac{V}{V_6}-1-ln\frac{V}{V_6}\right)+\frac{q_1}{\eta p_1}{Z}_6\left(\frac{Z}{Z_6}-1-ln\frac{Z}{Z_6}\right).\hfill \end{array}$$

Then, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\tilde{\Delta }}_6}{\partial t}=& \left(1-\frac{U_6}{U}\right)\left(D_U\Delta U+{\sigma }_1-{\beta }_{m}UM-d_{1}U\right)+\left(1-\frac{I_6}{I}\right)\left(D_I\Delta I+{\beta }_{m}UM-d_{2}I\right)\hfill \\ & +\frac{1}{\eta }\left(1-\frac{M_6}{M}\right)\left(D_M\Delta M+\eta d_{2}I-q_{1}MZ-d_{3}M\right)+\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{Y_6}{Y}\right)\left(D_Y\Delta Y+{\sigma }_2-{\beta }_{v}YV-d_{4}Y\right)\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}\left(1-\frac{N_6}{N}\right)\left(D_N\Delta N+{\beta }_{v}YV-d_{5}N\right)+\frac{q_1{p}_2}{\eta p_1{q}_2}\left(1-\frac{V_6}{V}\right)\left(D_V\Delta V+eN-q_{2}VZ-d_{6}V\right)\hfill \\ & +\frac{q_1}{\eta p_1}\left(1-\frac{Z_6}{Z}\right)\left(D_Z\Delta Z+p_{1}MZ+p_{2}VZ-d_{7}Z\right).\hfill \end{array}$$

By using the equilibrium conditions at $E_6$,

$$\left\{\begin{array}{c}{\sigma }_1=d_1{U}_6+{\beta }_m{U}_6{M}_6,\hfill \\ {\beta }_m{U}_6{M}_6=d_2{I}_6,\hfill \\ d_2{I}_6=\frac{d_3}{\eta }{M}_6+\frac{q_1}{\eta }{M}_6{Z}_6,\hfill \\ {\sigma }_2={\beta }_v{Y}_6{V}_6+d_4{Y}_6,\hfill \\ \frac{e{q}_1{p}_2{\beta }_v}{\eta p_1{q}_2{d}_5}{Y}_6{V}_6=\frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_6,\hfill \\ \frac{e{q}_1{p}_2}{\eta p_1{q}_2}{N}_6=\frac{q_1{p}_2{d}_6}{\eta p_1{q}_2}{V}_6+\frac{q_1{p}_2}{\eta p_1}{V}_6{Z}_6,\hfill \\ \frac{q_1}{\eta }{M}_6{Z}_6+\frac{q_1{p}_2}{\eta p_1}{V}_6{Z}_6=\frac{q_1{d}_7}{\eta p_1}{Z}_6,\hfill \end{array}\right.$$

and the ${\displaystyle \frac{d{\Delta }_6}{dt}}$ is given by

$$\begin{array}{cc}\hfill \frac{d{\Delta }_6}{dt}=& -d_1{\int }_{\mathsf{\Gamma }}\frac{{\left(U-U_6\right)}^2}{U}\mathrm{d}x-\frac{e{q}_1{p}_2{d}_4}{\eta p_1{q}_2{d}_5}{\int }_{\mathsf{\Gamma }}\frac{{\left(Y-Y_6\right)}^2}{Y}\mathrm{d}x+{\beta }_m{U}_6{M}_6{\int }_{\mathsf{\Gamma }}\left(3-\frac{U_6}{U}-\frac{I{M}_6}{I_{6}M}-\frac{U{I}_{6}M}{U_{6}I{M}_6}\right)\mathrm{d}x\hfill \\ & +\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{\beta }_v{Y}_6{V}_6{\int }_{\mathsf{\Gamma }}\left(3-\frac{Y_6}{Y}-\frac{N{V}_6}{N_{6}V}-\frac{Y{N}_{6}V}{Y_{6}N{V}_6}\right)\mathrm{d}x-D_U{U}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}x-D_I{I}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}x\hfill \\ & -\frac{1}{\eta }{D}_M{M}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿M\parallel }^2}{M^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_Y{Y}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Y\parallel }^2}{Y^2}\mathrm{d}x-\frac{e{q}_1{p}_2}{\eta p_1{q}_2{d}_5}{D}_N{N}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿N\parallel }^2}{N^2}\mathrm{d}x\hfill \\ & -\frac{q_1{p}_2}{\eta p_1{q}_2}{D}_V{V}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿V\parallel }^2}{V^2}\mathrm{d}x-\frac{q_1}{\eta p_1}{D}_Z{Z}_6{\int }_{\mathsf{\Gamma }}\frac{{\parallel ▿Z\parallel }^2}{Z^2}\mathrm{d}x.\hfill \end{array}$$

Therefore, we have ${\displaystyle \frac{d{\Delta }_6}{dt}}\le 0$. Furthermore, we have ${\displaystyle \frac{d{\Delta }_6}{dt}}=0$ when $U=U_6$, $I=I_6$, $M=M_6$, $Y=Y_6$, $N=N_6$, $V=V_6$, and $Z=Z_6$. Thus, $K_6^{{}^{\prime }}=\left\{E_6\right\}$. It follows from LIP that $E_6$ is GAS when ${\mathcal{R}}_p>1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$, ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}>1+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}>1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$. □

5. Numerical Simulations

In this section, we execute some numerical simulations to visualize the analytical results gained previously. The MATLAB PDE solver (pdepe) is used to solve the equations (see the Supplementary File S1 pdex30.m). The spatial domain is selected as $\mathsf{\Gamma }=[0,2]$ with step size $\Delta x=0.02$ and time step size $\Delta t=0.1$. The initial conditions of model (1) are taken as:

$$\begin{array}{cc}& U(x,0)=5(1+0.2{cos}^2\left(\pi x\right)),I(x,0)=0.0001(1+0.2{cos}^2\left(\pi x\right)),M(x,0)=0.0002(1+0.2{cos}^2\left(\pi x\right)),\hfill \\ & Y(x,0)=10(1+0.2{cos}^2\left(\pi x\right)),N(x,0)=0.02(1+0.2{cos}^2\left(\pi x\right))V(x,0)=0.01(1+0.2{cos}^2\left(\pi x\right)),\hfill \\ & Z(x,0)=0.1\times {10}^{10}(1+0.2{cos}^2\left(\pi x\right)),x\in [0,2].\hfill \end{array}$$

The values are assumed based on previous studies [8,48]. The results are classified into seven cases corresponding to the global stability of each equilibrium point. These cases are obtained by varying five parameters ${\beta }_m$, ${\beta }_v$, $p_1$, $p_2$, and $d_7$, while the rest of the parameters take fixed values as shown in Table 1. We used the values of some parameters which are given in the literature to perform our numerical simulations. We mention that these values are taken from studies for SARS-CoV-2 single-infection and malaria single-infection. To the best of our knowledge, till now, there has been no available data (e.g., the concentrations of SARS-CoV-2 particles, merozoites, antibodies, etc.) from SARS-CoV-2 and malaria coinfection patients. Therefore, estimating the parameters of the coinfection model is sill open for future work.

Table 1. Model parameters.

Parameter	Definition	Value	Reference
${\sigma }_1$	Production rate of healthy RBCs	$2.5\times {10}^8$	[21]
${\sigma }_2$	Recruitment rate of healthy ECs	0.02241	[33]
${\beta }_m$	Incidence rate constant of RBCs	Varied	–
${\beta }_v$	Incidence rate constant of ECs	Varied	–
$\eta$	Number of merozoites produced from an infected RBC	16	[20]
$q_1$	Removal rate constant of merozoites by antibodies	${10}^{-8}$	[21]
$q_2$	Removal rate constant of SARS-CoV-2 particles by antibodies	$4.88\times {10}^{-8}$	[49]
e	Generation rate constant of SARS-CoV-2 by infected ECs	0.24	[33]
$p_1$	Proliferation rate constant of antibodies by merozoites	Varied	–
$p_2$	Proliferation rate constant of antibodies by SARS-CoV-2	Varied	–
$d_1$	Death rate constant of healthy RBCs	0.025	[21]
$d_2$	Death rate constant of infected RBCs	0.5	[26]
$d_3$	Death rate constant of merozoites	48	[21]
$d_4$	Death rate constant of healthy ECs	${10}^{-3}$	[33]
$d_5$	Death rate constant of infected ECs	$0.11$	[33]
$d_6$	Death rate constant of SARS-CoV-2 particles	5.36	[33]
$d_7$	Death rate constant of antibodies	Varied	–
$D_U$	Diffusion coefficient of healthy RBCs	0.1	Assumed
$D_I$	Diffusion coefficient of infected RBCs	0.1	Assumed
$D_M$	Diffusion coefficient of merozoites	0.2	Assumed
$D_Y$	Diffusion coefficient of healthy ECs	0.01	Assumed
$D_N$	Diffusion coefficient of infected ECs	0.01	Assumed
$D_V$	Diffusion coefficient of SARS-CoV-2 particles	0.2	Assumed
$D_Z$	Diffusion coefficient of antibodies	0.2	Assumed

Now, we have the following cases:

(1)

The varied parameters are $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-10},0.1,3\times {10}^{-8},0.96,0.2)$. This yields ${\mathcal{R}}_{0m}=0.6667<1$ and ${\mathcal{R}}_{0v}=0.9122<1$. This implies that the equilibrium $E_0=(10\times {10}^9,0,0,22.41,0,0,0)$ is GAS (see Figure 1), which agrees with Theorem 2. This simulates an individual who has recovered from both malaria and SARS-CoV-2 infections.

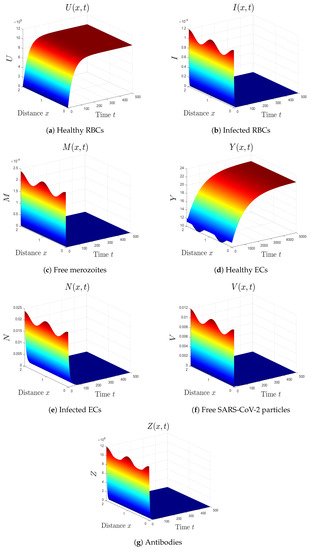Figure 1. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-10},0.1,3\times {10}^{-8},0.96,0.2)$. The uninfected equilibrium $E_0=(10\times {10}^9,0,0,22.41,0,0,0)$ is GAS.

(2)

The selected parameters are $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-9},0.1,2\times {10}^{-9},0.96,0.2)$. Then, we obtain ${\mathcal{R}}_{0m}=6.6667>1$, ${\mathcal{R}}_{0v}=0.9122<1$, and ${\mathcal{R}}_{1m}=0.7407<1$. Figure 2 shows that the numerical results agree with the analytical results of Theorem 4. The equilibrium $E_1=(1.5\times {10}^9,4.25\times {10}^8,7.08\times {10}^7,22.41,0,0,0)$ is GAS. This case describes a patient who only has malaria with inactive antibody immune response.

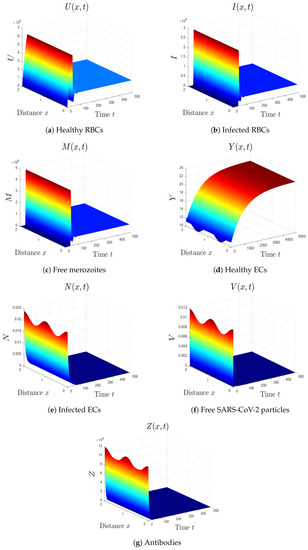Figure 2. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-9},0.1,2\times {10}^{-9},0.96,0.2)$. The equilibrium $E_1=(1.5\times {10}^9,4.25\times {10}^8,7.08\times {10}^7,22.41,0,0,0)$ is GAS.

(3)

The varied parameters are $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-9},0.1,3\times {10}^{-8},0.96,0.2)$. This yields ${\mathcal{R}}_{1m}=4.3478>1$ and ${\mathcal{R}}_p=44.6137<1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}=191.0065$. From Figure 3, we see that the equilibrium $E_2=(6.522\times {10}^9,1.739\times {10}^8,6.667\times {10}^6,22.41,0,0,1.607\times {10}^{10})$ is GAS, which illustrates Theorem 4. This case represents a patient who has only malaria with an active antibody immune response.

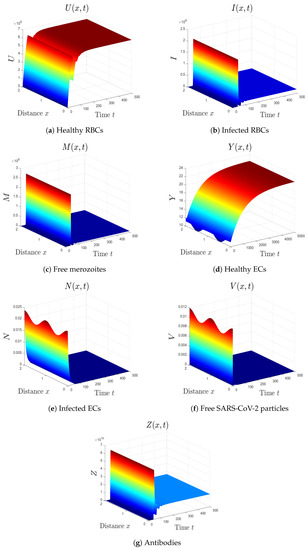Figure 3. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-9},0.1,3\times {10}^{-8},0.96,0.2)$. The equilibrium $E_2=(6.522\times {10}^9,1.739\times {10}^8,6.667\times {10}^6,22.41,0,0,1.607\times {10}^{10})$ is GAS.

(4)

By choosing $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-10},0.9,3\times {10}^{-8},0.96,0.2)$, we obtain ${\mathcal{R}}_{0v}=8.2099>1$, ${\mathcal{R}}_{0m}=0.6667<1$, and ${\mathcal{R}}_{1v}=0.0436<1$. Figure 4 illustrates the global asymptotic stability of the equilibrium $E_3=(10\times {10}^9,0,0,2.73,0.1789,0.008,0)$ as given by Theorem 5. The patient in this situation suffers from SARS-CoV-2 single-infection with inactive immunity.

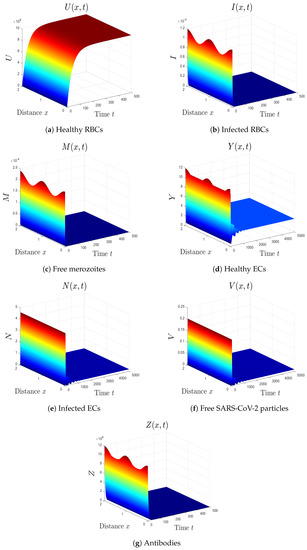Figure 4. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-10},0.9,3\times {10}^{-8},0.96,0.2)$. The equilibrium $E_3=(10\times {10}^9,0,0,2.73,0.1789,0.008,0)$ is GAS.

(5)

By selecting $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-10},0.9,3\times {10}^{-8},3.9,0.01)$ we obtain ${\mathcal{R}}_{1v}=2.4821>1$, ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}=0.6895<1+{\displaystyle \frac{e{\beta }_v{q}_1{\sigma }_2{p}_2}{q_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)}}=1.0568$. Accordingly, the equilibrium $E_4=(10\times {10}^9,0,0,6.775,0.1421,0.0026,1.628\times {10}^8)$ is GAS (see Figure 5). This result comes in agreement with Theorem 6. The patient in this situation has SARS-CoV-2 single-infection with active immunity. The activation of the antibody immunity causes a reduction in the number of SARS-CoV-2 particles.

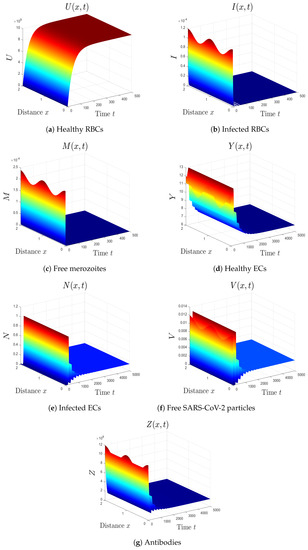Figure 5. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(2\times {10}^{-10},0.9,3\times {10}^{-8},3.9,0.01)$. The equilibrium $E_4=(10\times {10}^9,0,0,6.775,0.1421,0.0026,1.628\times {10}^8)$ is GAS.

(6)

We take $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(4\times {10}^{-10},0.9,3\times {10}^{-8},0.96,0.8)$. This gives ${\mathcal{R}}_{0m}=1.3333>1$, ${\mathcal{R}}_{0v}=8.2099>1$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}=1.338<1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}=1.4272$. Thus, the equilibrium $E_5=(7.5\times {10}^9,1.25\times {10}^8,2.08\times {10}^7,2.73,0.1789,0.008,0)$ is GAS (see Figure 6), which agrees with Theorem 7. Here, the coinfection of malaria and COVID-19 occurs but with inactive antibody immunity. The inactivation of immunity enhances the replication of both SARS-CoV-2 particles and malaria merozoites, which worsens the health state of the patient.

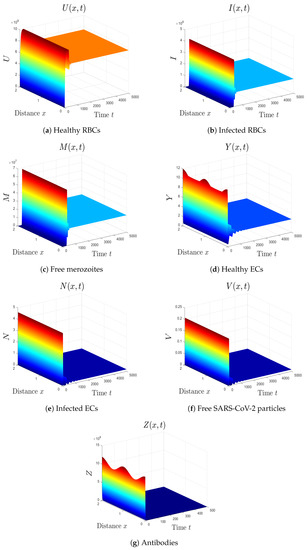Figure 6. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(4\times {10}^{-10},0.9,3\times {10}^{-8},0.96,0.8)$. The equilibrium $E_5=(7.5\times {10}^9,1.25\times {10}^8,2.08\times {10}^7,2.73,0.1789,0.008,0)$ is GAS.

(7)

We select $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(4\times {10}^{-10},3.9,3\times {10}^{-8},0.5,0.4)$. In this case, the threshold parameters are given as ${\mathcal{R}}_p=79.2777>1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}=49.0236$, ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}=1.3562>1+{\displaystyle \frac{e{\beta }_v{q}_1{\sigma }_2{p}_2}{q_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)}}=1.0003$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}=1.3358>1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}=1.2134$. In line with Theorem 8, the equilibrium $E_6=(8.244\times {10}^9,8.78\times {10}^7,1.33\times {10}^7,3.36,0.17,0.0015,4.76\times {10}^8)$ is GAS (see Figure 7). Under these circumstances, the coinfection of malaria and COVID-19 occurs with active antibody immunity. This action works on reducing the concentrations of both malaria merozoites and SARS-CoV-2 particles.

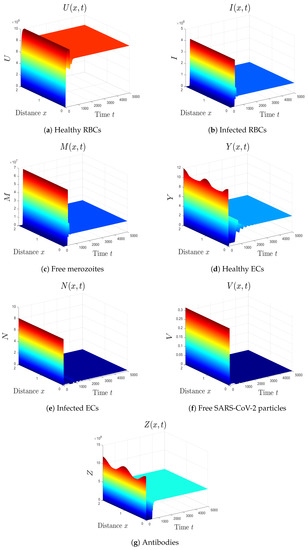Figure 7. Simulation of system (1) for $({\beta }_m,{\beta }_v,p_1,p_2,d_7)=(4\times {10}^{-10},3.9,3\times {10}^{-8},0.5,0.4)$. The equilibrium $E_6=(8.244\times {10}^9,8.78\times {10}^7,1.33\times {10}^7,3.36,0.17,0.0015,4.76\times {10}^8)$ is GAS.

5.1. Sensitivity Analysis

Sensitivity analysis evaluates a relative change in a variable when a parameter changes. We execute sensitivity analysis for ${\mathcal{R}}_{0m}$ and ${\mathcal{R}}_{0v}$ as they are the main determinants for the stability of the uninfected equilibrium $E_0$. The normalized forward sensitivity index of a differentiable function $\theta$ with respect to a parameter p is defined as

$${\mathsf{\Gamma }}_p^{\theta }=\frac{\partial \theta }{\partial p}·\frac{p}{\theta }.$$

5.1.1. Sensitivity Analysis of ${\mathcal{R}}_{0m}$

The normalized forward sensitivity index of ${\mathcal{R}}_{0m}$ is given by

$${\mathsf{\Gamma }}_p^{{\mathcal{R}}_{0m}}=\frac{\partial {\mathcal{R}}_{0m}}{\partial p}·\frac{p}{{\mathcal{R}}_{0m}}.$$

We calculate the sensitivity indices of ${\mathcal{R}}_{0m}$ with respect to each parameter using the values provided in Table 1. The results are listed in Table 2. We note that the sensitivity indices of ${\mathcal{R}}_{0m}$ do not depend on any parameters. For instance, the sensitivity index of ${\mathcal{R}}_{0m}$ with respect to $\eta$ is

$${\mathsf{\Gamma }}_{\eta }^{{\mathcal{R}}_{0m}}=\frac{\partial {\mathcal{R}}_{0m}}{\partial \eta }·\frac{\eta }{{\mathcal{R}}_{0m}}={\displaystyle \frac{{\beta }_m{\sigma }_1}{d_1{d}_3}}·{\displaystyle \frac{\eta d_1{d}_3}{\eta {\beta }_m{\sigma }_1}}=1.$$

Table 2. Sensitivity indices of ${\mathcal{R}}_{0m}$.

Parameter	Sensitivity Index
$\eta$	1
${\beta }_m$	1
${\sigma }_1$	1
$d_1$	$-1$
$d_3$	$-1$

Therefore, it is useful to justify the sign of the sensitivity indices of ${\mathcal{R}}_{0m}$. According to Table 2, the number of merozoites produced per infected cell, $\eta$, the infection rate of RBCs, ${\beta }_m$, and the recruitment rate of healthy RBCs, ${\sigma }_1$, are the parameters that increase malaria infection in the body. Conversely, the death rate of uninfected RBCs, $d_1$, and the death rate of merozoites, $d_3$, are the parameters that have a crucial role in eliminating malaria infection from the body.

5.1.2. Sensitivity Analysis of ${\mathcal{R}}_{0v}$

The normalized forward sensitivity index of ${\mathcal{R}}_{0v}$ is given by

$${\mathsf{\Gamma }}_p^{{\mathcal{R}}_{0v}}=\frac{\partial {\mathcal{R}}_{0v}}{\partial p}·\frac{p}{{\mathcal{R}}_{0v}}.$$

As for ${\mathcal{R}}_{0m}$, we calculate the sensitivity index of each parameter in ${\mathcal{R}}_{0v}$ using the values given in Table 1. The results are presented in Table 3. We see that, when one of the parameters with a positive index (e, ${\beta }_v$, or ${\sigma }_2$) is increased while the other parameters remain constant, this raises the value of ${\mathcal{R}}_{0v}$. In other words, these parameters lead to the growth of SARS-CoV-2. Conversely, the parameters with negative indices have a role in eliminating SARS-CoV-2 infection from the body.

Table 3. Sensitivity indices of ${\mathcal{R}}_{0v}$.

Parameter	Sensitivity Index
e	1
${\beta }_v$	1
${\sigma }_2$	1
$d_4$	$-1$
$d_5$	$-1$
$d_6$	$-1$

6. Results and Discussion

Malaria/COVID-19 coinfection represents a true concern especially in malaria-endemic regions. Therefore, there is an urgent need to understand the dynamics of this coinfection within a human body. In this paper, we develop a reaction–diffusion in-host malaria/COVID-19 coinfection model. This model considers the interactions between healthy RBCs, infected RBCs, free merozoites, healthy ECs, infected ECs, free SARS-CoV-2 particles and antibodies. We show that the system admits seven equilibrium points and we prove the following:

(1)

The uninfected equilibrium $E_0$ always exists. Moreover, $E_0$ is GAS if ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{0v}\le 1$. This situation represents an individual who recovered from both malaria and SARS-CoV-2 infections.

(2)

The malaria single-infection without immunity equilibrium $E_1$ exists if ${\mathcal{R}}_{0m}>1$. In addition, $E_1$ is GAS if ${\mathcal{R}}_{0v}\le 1$ and ${\mathcal{R}}_{1m}\le 1$. This simulates the situation of malaria mono-infection patient with inactive immunity.

(3)

The malaria single-infection with immunity equilibrium $E_2$ exists if ${\mathcal{R}}_{1m}>1$. Moreover, $E_2$ is GAS if ${\mathcal{R}}_p\le 1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$. At this point, the antibody immune response is activated to eradicate malaria merozoites.

(4)

The SARS-CoV-2 single-infection without immunity equilibrium $E_3$ exists if ${\mathcal{R}}_{0v}>1$. In addition, $E_3$ is GAS if ${\mathcal{R}}_{0m}\le 1$ and ${\mathcal{R}}_{1v}\le 1$. This point simulates the situation of a patient who is only infected by SARS-CoV-2 and the immune response is inactive.

(5)

The SARS-CoV-2 single-infection with immunity equilibrium $E_4$ exists if ${\mathcal{R}}_{1v}>1$. It is GAS when ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}\le 1+{\displaystyle \frac{e{\beta }_v{q}_1{\sigma }_2{p}_2}{q_2{d}_3{d}_5(p_2{d}_4+{\beta }_v{d}_7)}}$. The immune response is activated in the SARS-CoV-2 mono-infection patient.

(6)

The malaria/COVID-19 coinfection without immunity equilibrium $E_5$ exists if ${\mathcal{R}}_{0m}>1$ and ${\mathcal{R}}_{0v}>1$. It is GAS when ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}\le 1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$. Here, the coinfection occurs with inactive immune response.

(7)

The malaria/COVID-19 coinfection with immunity equilibrium $E_6$ exists, and it is GAS if ${\mathcal{R}}_p>1+{\displaystyle \frac{\eta {\beta }_m{\sigma }_1{p}_1{q}_2}{q_1{d}_6(p_1{d}_1+{\beta }_m{d}_7)}}$, ${\mathcal{R}}_{0m}+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}>1+{\displaystyle \frac{q_1{d}_6}{q_2{d}_3}}{\mathcal{R}}_{1v}$, and ${\mathcal{R}}_{0m}+{\displaystyle \frac{e{\beta }_m{\sigma }_2{p}_2}{p_1{d}_1{d}_5{d}_6}}>1+{\displaystyle \frac{{\beta }_m(p_2{d}_4+{\beta }_v{d}_7)}{{\beta }_v{p}_1{d}_1}}$. This point represents the occurrence of malaria/COVID-19 coinfection with an active antibody immune response.

The numerical results agree with the analytical results. Based on our results, we assume that the malaria/COVID-19 coinfection can be protective as the shared antibody immune response works on clearing SARS-CoV-2. This can decrease the severity of COVID-19. This result comes in agreement with some studies that reported the positive impact of the shared antibody immune response [4,17,18,19]. However, other studies suggested that there is an increased risk of death in malaria patients with SARS-CoV-2 infection [1,13]. Therefore, more studies are required to investigate the impact of coinfection between malaria and COVID-19, to evaluate the effect of the immune system during the coinfection, and to find the suitable ways for treating the coinfected patients. The main limitation of this research work is that we did not estimate the values of the model’s parameters using real data. The reasons are as follows: (1) The data on malaria/COVID-19 coinfection are still very limited; (2) Comparing our results with a small number of real studies may not be very precise; (3) Collecting real data from patient coinfected with malaria and SARS-CoV-2 is not an easy process; (4) Working on experiments to obtain data is beyond the scope of this paper. Thus, the theoretical results obtained in this paper need to be tested against empirical findings when real data become available.

6.1. Conclusions

Malaria/COVID-19 coinfection has been reported in many countries. In this paper, we formulated a reaction–diffusion in-host model to study the coinfection between malaria and COVID-19. We assumed that the shared antibody immune response decreases the concentrations of SARS-CoV-2 and malaria merozoites. This can reduce the severity of SARS-CoV-2 in coinfected patients. The principal limitation of this paper is that we did not use real data to estimate the values of parameters or to compare the results due to the scarcity of data. Therefore, our results need to be validated when real data become available.

6.2. Future Works

The model developed in this work can be improved by (i) using real data to find a good estimation of the parameters’ values, (ii) examining the influence of time delays that may occur during infection or production of SARS-CoV-2 particles and malaria merozoites, (iii) considering viral mutations [41,50,51], (iv) considering the effect of treatments on the progression of both diseases, (v) incorporating the role of CTLs in killing infected RBCs or ECs, and (vi) considering an age-structured model to account for the age structure in the infected cells compartments, which can lead to important observations.