Fixed Points on Covariant and Contravariant Maps with an Application

Abstract

Fixed-point results on covariant maps and contravariant maps in a $C^{★}$-algebra-valued bipolar metric space are proved. Our results generalize and extend some recently obtained results in the existing literature. Our theoretical results in this paper are supported with suitable examples. We have also provided an application to find an analytical solution to the integral equation and the electrical circuit differential equation.

1. Introduction

The Banach contraction principle [1] of 1922 forms the basis for metric fixed-point theory. The principle is not just a source of inspiration but also a point of origin for establishing the fixed-point results both of Hausdorff and of non-Hausdorff topological spaces with vast applications not just in science, technology, engineering, and mathematics (STEM) but also in economics, game theory, and other fields as well. Using this principle, fixed-point results have been established in various topological spaces. Due to its generalized nature, metric space is the obvious choice for any mathematician for applications in real-life situations.

Metric fixed-point theory is used to solve different types of mathematical problems such as dynamic programming, variational inequalities, nonlinear differential equations, fractal dynamics, and satellite launch. It also ensures that patients receive the most appropriate diagnosis, and it examines the intensity of the spread of contagious diseases in a variety of cities.

The study of new space discoveries in mathematics and their basic properties are always favorite topics of interest among the mathematical research community. In this context, the concept of 2-metric spaces was introduced initially by Gahler [2] in his series of papers, and it drew attention to new dimensions for ordinary metric spaces. Since the metric for a pair of points is non-negative real, i.e., $[0,+\infty )$, it has wide scope for further study.

Various types of distances such as those between points of a set are considered in metric spaces and their generalization. However, we come across situations where distances arise between elements of two different sets rather than between points of a unique set, wherein the distances between the same type of points are either not known or not defined, due to lack of data. In a Euclidean space, the distance between points and lines; in a metric space, the distance between sets and points; and the reaction rates of pairs from disjoint sets of chemical substances are some examples of such distances. The concept of probabilistic metric spaces in which the probabilistic distance between two points is considered has provided a new dimension for the study of stars in the universe.

Mutlu et al. [3] formalized these types of distances as the bipolar metric, considering them only isometrically without analyzing their topological structures in detail. They introduced the concept of bipolar metric spaces (bpms) and proved certain fixed-point theorems.

Definition 1 

([3]). Let Φ and Λ be non empty sets. Let $\mathfrak{d}:\Phi \times \mathsf{\Lambda }\to (0,\infty )$ be a map satisfying:

(a) 

$\mathfrak{d}(\vartheta ,\varpi )=0$ if and only if $\vartheta =\varpi$, for all $(\vartheta ,\varpi )\in \Phi \times \mathsf{\Lambda }$

(b) 

$\mathfrak{d}(\vartheta ,\varpi )=\mathfrak{d}(\varpi ,\vartheta )$, for all $(\vartheta ,\varpi )\in \Phi \times \mathsf{\Lambda }$

(c) 

$\mathfrak{d}(\vartheta ,\varpi )$ = $\mathfrak{d}(\varpi ,\vartheta )$ for all $(\vartheta ,\varpi )\in \Phi \bigcap \mathsf{\Lambda }$

(d) 

$\mathfrak{d}(\vartheta ,\varpi )\le \mathfrak{d}(\vartheta ,\sigma )+\mathfrak{d}({\vartheta }_1,\sigma )+\mathfrak{d}({\vartheta }_1,\varpi )$, for all $\vartheta ,{\vartheta }_1\in \Phi$ and $\sigma ,\varpi \in \mathsf{\Lambda }$.

The pair $(\Phi ,\mathsf{\Lambda },\mathfrak{d})$ is a bpms.

Remark 1. 

Suppose (a) in the above definition is replaced with $\left(a^{*}\right)$ as: $\vartheta =\varpi$ implies $\mathfrak{d}(\vartheta ,\varpi )=0$; then, $(\Phi ,\mathsf{\Lambda },\mathfrak{d})$ is a bipolar pseudo-metric space.

In the recent past, mathematicians have established many fixed-point results under various contractive conditions in the setting of bpms (see [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]).

Ma et al. [26] defined the concept of ${\mathcal{C}}^{★}$-algebra-valued metric space and proved Banach’s contraction principle. Later, fixed-point results in the setting of a ${\mathcal{C}}^{★}$-valued contractive-type map were established by Batul and Kamran [27]. For further details on ${\mathcal{C}}^{★}$-algebra, please refer to [28,29,30,31]. Recently, Guna et al. [25] introduced the notion of ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space and proved fixed-point results therein. Inspired by the proven results, we establish fixed-point results in the setting of ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space and find its application to prove the existence of unique solutions to integral equations.

The rest of the paper is organized as follows: In Section 2, we present certain basic concepts and monographs that are required for our main result. In Section 3, we present our main result of establishing the fixed-point results for covariant and contravariant maps in the setting of ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space. We support our main results with suitable non-trivial examples. We present an application to analyze the applicability of our main result for finding the existence of a unique common solution for an integral equation and a voltage differential equation in an electric circuit.

2. Preliminaries

Let us begin with some basic concepts and definitions, which are very essential in the sequel.

An algebra $\mathbb{A}$, with a conjugate linear involution map $\eta ⟼{\eta }^{★}$, is called a ★-algebra, if ${\left(\eta \varrho \right)}^{★}={\varrho }^{★}{\eta }^{★}$ and ${\left({\eta }^{★}\right)}^{★}=\eta$ for all $\varrho ,\eta \in \mathbb{A}$. If $\mathbb{A}$ contains the identity element $1_{\mathbb{A}}$∈$\mathbb{A}$, then $(\mathbb{A},★)$ is a unital ★-algebra. A complete normed unital ★-algebra is called a Banach ★-algebra $(\mathbb{A},★)$ where the norm on $\mathbb{A}$ is sub-multiplicative and satisfies $\parallel {\eta }^{★}\parallel =\parallel \eta \parallel$ for all $\eta \in \mathbb{A}$. If $\parallel {\eta }^{★}\eta \parallel =\parallel \eta {\parallel }^2$ for all $\eta \in \mathbb{A}$, in a Banach ★-algebra $(\mathbb{A},★)$, then $\mathbb{A}$ is known as a ${\mathcal{C}}^{★}$-algebra. $\eta \in \mathbb{A}$ is called a positive element, if $\eta ={\eta }^{★}$ and its spectrum $\sigma \left(\eta \right)\subset {\mathbb{R}}_{+}$, where $\sigma \left(\eta \right)$ = $\{\mu \in \mathbb{R}:\mu 1_{\mathbb{A}}-\eta \mathrm{is}\mathrm{non}\text{-}\mathrm{invertible}\}$.

${\mathbb{A}}_{+}$ denotes the collection of all positive elements that defines a partial order ⪰ on $\mathbb{A}$. That is,

$$\begin{array}{c}\hfill \varrho ⪰\eta iff\varrho -\eta \in {\mathbb{A}}_{+}.\end{array}$$

Let $0_{\mathbb{A}}$ be the zero element. Then, $\eta ⪰0_{\mathbb{A}}$, if $\eta$ is positive. Each positive element $\eta$ of a ${\mathcal{C}}^{★}$-algebra $\mathbb{A}$ has a unique positive square root denoted by ${\eta }^{\frac{1}{2}}$ in $\mathbb{A}$.

Hereafter, $\mathbb{A}$ represents a unital ${\mathcal{C}}^{★}$-algebra with identity element $1_{\mathbb{A}}$. Additionally, ${\mathbb{A}}_{+}$ = $\{\eta \in \mathbb{A}:\eta ⪰0_{\mathbb{A}}\}$ and ${\left({\eta }^{★}\eta \right)}^{1/2}$ =$\left|\right|\eta \left|\right|$.

Definition 2 

([26]). Let $\mathbb{A}$ be a ${\mathcal{C}}^{*}$-algebra, and Φ, Λ≠ϕ. Let $\mathfrak{d}:\Phi \times \mathsf{\Lambda }\to {\mathbb{A}}_{+}$ be a map satisfying

(a) 

$\mathfrak{d}(\vartheta ,\varpi )=0$ iff $\vartheta =\varpi$, for all $(\vartheta ,\varpi )\in \Phi \times \mathsf{\Lambda }$

(b) 

$\mathfrak{d}(\vartheta ,\varpi )=\mathfrak{d}(\varpi ,\vartheta )$, for all $(\vartheta ,\varpi )\in \Phi \times \mathsf{\Lambda }$

(c) 

$\mathfrak{d}(\vartheta ,\varpi )\le \mathfrak{d}(\vartheta ,\gamma )+\mathfrak{d}({\vartheta }_1,\gamma )+\mathfrak{d}({\vartheta }_1,\varpi )$, for all $\vartheta ,{\vartheta }_1\in \Phi$ and $\gamma ,\varpi \in \mathsf{\Lambda }$.

The 4-tuple $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is a ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space.

Lemma 1 

([29,31]). Let $\mathbb{A}$ be a unital ${\mathcal{C}}^{★}$-algebra, where $1_{\mathbb{A}}$ is the identity element.

(A1) 

If $\vartheta \in {\mathbb{A}}_{+}$, then $\vartheta ⪯1_{\mathbb{A}}$ if and only if $\left|\right|\vartheta \left|\right|\le 1$.

(A2) 

If $\delta \in {\mathbb{A}}_{+}$ with $\left|\right|\delta \left|\right|<\frac{1}{2}$, then $(1_{\mathbb{A}}-\delta )$ is invertible and $\left|\right|\delta {(1_{\mathbb{A}}-\delta )}^{-1}\left|\right|<1$.

(A3) 

Suppose that $\delta ,\varrho \in \mathbb{A}$ with $\delta \varrho ⪰\theta$ and $\delta \varrho =\varrho \delta$, then $\varrho \delta ⪰\theta$.

(A4) 

By ${\mathbb{A}}^{\prime }$, we denote the set $\{\delta \in \mathbb{A}:\delta \varrho =\varrho \delta ,$ for all $\varrho \in \mathbb{A}\}$. Let $\delta \in {\mathbb{A}}^{\prime }$, if $\varrho ,\mathfrak{c}\in \mathbb{A}$ with $\varrho ⪰\mathfrak{c}⪰\theta$, and $1_{\mathbb{A}}-\delta \in {\mathbb{A}}_{+}^{\prime }$ is an invertible operator, then

$$\begin{array}{c}\hfill {(1_{\mathbb{A}}-\delta )}^{-1}\varrho ⪰{(1_{\mathbb{A}}-\delta )}^{-1}\mathfrak{c}.\end{array}$$

Remark 2. 

It may be noted that in a ${\mathcal{C}}^{★}$-algebra, if $\theta ⪯\delta ,\varrho$, one cannot conclude that $\theta ⪯\delta \varrho$.

Definition 3. 

Let $({\Phi }_1,{\mathsf{\Lambda }}_1,\mathbb{A},\mathfrak{d})$ and $({\Phi }_2,{\mathsf{\Lambda }}_2,\mathbb{A},\mathfrak{d})$ be two ${\mathcal{C}}^{★}$-algebra-valued bipolar metric spaces and given a map ${\rm Y}:{\Phi }_1\cup {\mathsf{\Lambda }}_1\to {\Phi }_2\cup {\mathsf{\Lambda }}_2$.

(B1) 

If ${\rm Y}\left({\Phi }_1\right)\subseteq {\Phi }_2$ and ${\rm Y}\left({\mathsf{\Lambda }}_1\right)\subseteq {\mathsf{\Lambda }}_2$, then Υ is called a covariant map, or a map from $({\Phi }_1,{\mathsf{\Lambda }}_1,\mathbb{A},{\mathfrak{d}}_1)$ to $({\Phi }_2,{\mathsf{\Lambda }}_2,\mathbb{A},{\mathfrak{d}}_2)$, and this is written as

${\rm Y}:({\Phi }_1,{\mathsf{\Lambda }}_1,\mathbb{A},{\mathfrak{d}}_1)$⇉$({\Phi }_2,{\mathsf{\Lambda }}_2,\mathbb{A},{\mathfrak{d}}_2)$.

(B2) 

If ${\rm Y}\left({\Phi }_1\right)\subseteq {\mathsf{\Lambda }}_2$ and ${\rm Y}\left({\mathsf{\Lambda }}_1\right)\subseteq {\Phi }_2$, then Υ is called a contravariant map from $({\Phi }_1,{\mathsf{\Lambda }}_1,\mathbb{A},{\mathfrak{d}}_1)to({\Phi }_2,{\mathsf{\Lambda }}_2,\mathbb{A},{\mathfrak{d}}_2)$, and this is denoted as:

${\rm Y}:({\Phi }_1,{\mathsf{\Lambda }}_1,\mathbb{A},{\mathfrak{d}}_1)\leftrightarrows ({\Phi }_2,{\mathsf{\Lambda }}_2,\mathbb{A},{\mathfrak{d}}_2)$.

Definition 4. 

Let $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ be a ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space.

(C1) 

A sequence $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ on the set $\Phi \times \mathsf{\Lambda }$ is called a bisequence on $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$.

(C2) 

A point $\vartheta \in \Phi \cup \mathsf{\Lambda }$ is said to be a left point, if $\vartheta \in \Phi$, a right point if $\vartheta \in \mathsf{\Lambda }$ and a central point if $\vartheta \in \Phi \cap \mathsf{\Lambda }$. Similarly, a sequence $\left\{{\vartheta }_{\mathfrak{n}}\right\}$ on the set Φ and a sequence $\left\{{\varpi }_{\mathfrak{n}}\right\}$ on the set Λ are called left and right sequence, respectively, with respect to $\mathbb{A}$.

(C3) 

A sequence $\left\{{\vartheta }_{\mathfrak{n}}\right\}$ converges to a point ϖ (with respect to $\mathbb{A}$) if $\left\{{\vartheta }_{\mathfrak{n}}\right\}$ is a left sequence, ϖ is a right point, and $\underset{\mathfrak{n}\to \infty }{lim}\mathfrak{d}({\vartheta }_{\mathfrak{n}},\varpi )=0_{\mathbb{A}}$, or if

$\left\{{\vartheta }_{\mathfrak{n}}\right\}$ is a right sequence, ϖ is a left point, and $\underset{\mathfrak{n}\to \infty }{lim}\mathfrak{d}(\varpi ,{\vartheta }_{\mathfrak{n}})=0_{\mathbb{A}}$.

(C4) 

If both $\left\{{\vartheta }_{\mathfrak{n}}\right\}$ and $\left\{{\varpi }_{\mathfrak{n}}\right\}$ converge (with respect to $\mathbb{A}$), then the bisequence $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ is said to be convergent (with respect to $\mathbb{A}$). If $\left\{{\vartheta }_{\mathfrak{n}}\right\}$ and $\left\{{\varpi }_{\mathfrak{n}}\right\}$ both converge (with respect to $\mathbb{A}$) to a same point $u\in \Phi \cap \mathsf{\Lambda }$, then this bisequence is said to be biconvergent (with respect to $\mathbb{A}$).

(C5) 

A bisequence $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ on $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is said to be a Cauchy bisequence (with respect to $\mathbb{A}$), if $\underset{\mathfrak{n},\mathfrak{m}\to \infty }{lim}\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{m}})=0_{\mathbb{A}}$.

(C6) 

$(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is complete if every Cauchy bisequence (with respect to $\mathbb{A}$) is convergent.

3. Main Results

Now, we present our first fixed-point result using covariant maps in the setting of bpms.

Theorem 1. 

Let $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ be a complete ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space. Suppose ${\rm Y},\Omega :(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})\rightrightarrows (\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ are covariant maps such that

$$\begin{array}{c}\hfill \mathfrak{d}({\rm Y}\left(\vartheta \right),\Omega \left(\varpi \right))⪯{\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu \mathit{for}\mathit{all}\vartheta \in \Phi ,\varpi \in \mathsf{\Lambda },\end{array}$$

where $\mu \in \mathbb{A}$ with ${\left|\right|\mu \left|\right|}^2<1$. Then, ${\rm Y},\Omega :\Phi \cup \mathsf{\Lambda }\to \Phi \cup \mathsf{\Lambda }$ have a unique common fixed point.

Proof. 

If $\mathbb{A}=\left\{0_{\mathbb{A}}\right\}$, then we are done. Suppose not. Let ${\vartheta }_0\in \Phi$ and ${\varpi }_0\in \mathsf{\Lambda }$. For each $\mathfrak{n}\in \mathbb{N}$, define ${\rm Y}\left({\vartheta }_{2\mathfrak{n}}\right)={\vartheta }_{2\mathfrak{n}+1}$, $\Omega \left({\vartheta }_{2\mathfrak{n}+1}\right)={\vartheta }_{2\mathfrak{n}+2}$ and ${\rm Y}\left({\varpi }_{2\mathfrak{n}}\right)={\varpi }_{2\mathfrak{n}+1}$, $\Omega \left({\varpi }_{2\mathfrak{n}+1}\right)={\varpi }_{2\mathfrak{n}+2}$$(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ is a bisequence on $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$. Let $\mathcal{M}:=\mathfrak{d}({\vartheta }_0,{\varpi }_1)+\mathfrak{d}({\vartheta }_0,{\varpi }_0)$ and $\mathcal{S}:=\mathfrak{d}({\vartheta }_1,{\varpi }_0)+\mathfrak{d}({\vartheta }_0,{\varpi }_0)$. Then, for each $\mathfrak{n},\mathfrak{p}\in {\mathbb{Z}}^{+}$,

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{2\mathfrak{n}+1},{\varpi }_{2\mathfrak{n}+2})& =\mathfrak{d}({\rm Y}{\vartheta }_{2\mathfrak{n}},\Omega {\varpi }_{2\mathfrak{n}+1})\hfill \\ \hfill & ⪯{\mu }^{★}\mathfrak{d}({\vartheta }_{2\mathfrak{n}},{\varpi }_{2\mathfrak{n}+1})\mu \hfill \\ \hfill & ={\mu }^{★}\mathfrak{d}({\rm Y}{\vartheta }_{2\mathfrak{n}-1},\Omega {\varpi }_{2\mathfrak{n}})\mu \hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^2\mathfrak{d}({\vartheta }_{2\mathfrak{n}-1},{\varpi }_{2\mathfrak{n}}){\mu }^2\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^3\mathfrak{d}({\vartheta }_{2\mathfrak{n}-2},{\varpi }_{2\mathfrak{n}-1}){\mu }^3\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_1){\mu }^{2\mathfrak{n}+1},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{2\mathfrak{n}+2},{\varpi }_{2\mathfrak{n}+1})& =\mathfrak{d}({\rm Y}{\vartheta }_{2\mathfrak{n}+1},\Omega {\varpi }_{2\mathfrak{n}})\hfill \\ \hfill & ⪯{\mu }^{★}\mathfrak{d}({\vartheta }_{2\mathfrak{n}+1},{\varpi }_{2\mathfrak{n}})\mu \hfill \\ \hfill & ={\mu }^{★}\mathfrak{d}({\rm Y}{\vartheta }_{2\mathfrak{n}},\Omega {\varpi }_{2\mathfrak{n}-1})\mu \hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^2\mathfrak{d}({\vartheta }_{2\mathfrak{n}},{\varpi }_{2\mathfrak{n}-1}){\mu }^2\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^3\mathfrak{d}({\vartheta }_{2\mathfrak{n}-1},{\varpi }_{2\mathfrak{n}-2}){\mu }^3\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{1}},{\varpi }_0){\mu }^{2\mathfrak{n}+1},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{2\mathfrak{n}+1},{\varpi }_{2\mathfrak{n}+1})& =\mathfrak{d}({\rm Y}{\vartheta }_{2\mathfrak{n}},\Omega {\varpi }_{2\mathfrak{n}})\hfill \\ \hfill & ⪯{\mu }^{★}\mathfrak{d}({\vartheta }_{2\mathfrak{n}},{\varpi }_{2\mathfrak{n}})\mu \hfill \\ \hfill & ={\mu }^{★}\mathfrak{d}({\rm Y}{\vartheta }_{2\mathfrak{n}-1},\Omega {\varpi }_{2\mathfrak{n}-1})\mu \hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^2\mathfrak{d}({\vartheta }_{2\mathfrak{n}-1},{\varpi }_{2\mathfrak{n}-1}){\mu }^2\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^3\mathfrak{d}({\vartheta }_{2\mathfrak{n}-2},{\varpi }_{2\mathfrak{n}-2}){\mu }^3\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}})& ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}})\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+1})+{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{M}{\mu }^{\mathfrak{n}}\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+2})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+2})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{M}{\mu }^{\mathfrak{n}}\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+2})+{\left({\mu }^{★}\right)}^{\mathfrak{n}+1}\mathcal{M}{\mu }^{\mathfrak{n}+1}+{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{M}{\mu }^{\mathfrak{n}}\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+\mathfrak{p}})+{\left({\mu }^{★}\right)}^{\mathfrak{n}+\mathfrak{p}-1}\mathcal{M}{\mu }^{\mathfrak{n}+\mathfrak{p}-1}+\cdots +{\left({\mu }^{★}\right)}^{\mathfrak{n}+1}\mathcal{M}{\mu }^{\mathfrak{n}+1}+{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{M}{\mu }^{\mathfrak{n}}\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{\mathfrak{n}+\mathfrak{p}}\mathcal{M}{\mu }^{\mathfrak{n}+\mathfrak{p}}+{\left({\mu }^{★}\right)}^{\mathfrak{n}+\mathfrak{p}-1}\mathcal{M}{\mu }^{\mathfrak{n}+\mathfrak{p}-1}+\cdots +{\left({\mu }^{★}\right)}^{\mathfrak{n}+1}\mathcal{M}{\mu }^{\mathfrak{n}+1}+{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{M}{\mu }^{\mathfrak{n}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left({\mu }^{★}\right)}^{\mathfrak{k}}\mathcal{M}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left({\mu }^{★}\right)}^{\mathfrak{k}}{\mathcal{M}}^{\frac{1}{2}}{\mathcal{M}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left({\mathcal{M}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right)}^{★}{\mathcal{M}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left|{\mathcal{M}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right|}^2\hfill \\ \hfill & ⪯\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}\left|\right|{\mathcal{M}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}\left|\right|\mathcal{M}\left|\right|\left|\right|{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\left|\right|\mathcal{M}\left|\right|\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}\left|\right|{\mu }^2{\left|\right|}^{\mathfrak{k}}{1}_{\mathbb{A}}\to 0\mathrm{as}\mathfrak{n},\mathfrak{p}\to +\infty \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}+\mathfrak{p}})& ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathfrak{d}({\vartheta }_0,{\varpi }_0){\mu }^{\mathfrak{n}}+{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathfrak{d}({\vartheta }_1,{\varpi }_0){\mu }^{\mathfrak{n}}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{S}{\mu }^{\mathfrak{n}}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{S}{\mu }^{\mathfrak{n}}+{\left({\mu }^{★}\right)}^{\mathfrak{n}+1}\mathcal{S}{\mu }^{\mathfrak{n}+1}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{S}{\mu }^{\mathfrak{n}}+{\left({\mu }^{★}\right)}^{\mathfrak{n}+1}\mathcal{S}{\mu }^{\mathfrak{n}+1}+\cdots +{\left({\mu }^{★}\right)}^{\mathfrak{n}+\mathfrak{p}-1}\mathcal{S}{\mu }^{\mathfrak{n}+\mathfrak{p}-1}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{\mathfrak{n}}\mathcal{S}{\mu }^{\mathfrak{n}}+{\left({\mu }^{★}\right)}^{\mathfrak{n}+1}\mathcal{S}{\mu }^{\mathfrak{n}+1}+\cdots +{\left({\mu }^{★}\right)}^{\mathfrak{n}+\mathfrak{p}-1}\mathcal{S}{\mu }^{\mathfrak{n}+\mathfrak{p}-1}+{\left({\mu }^{★}\right)}^{\mathfrak{n}+\mathfrak{p}}\mathcal{S}{\mu }^{\mathfrak{n}+\mathfrak{p}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left({\mu }^{★}\right)}^{\mathfrak{k}}\mathcal{S}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left({\mu }^{★}\right)}^{\mathfrak{k}}{\mathcal{S}}^{\frac{1}{2}}{\mathcal{S}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left({\mathcal{S}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right)}^{★}{\mathcal{S}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ⪯\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}\left|\right|{\mathcal{S}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}\left|\right|{\mathcal{S}}^{\frac{1}{2}}{\left|\right|}^2\left|\right|{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\left|\right|{\mathcal{S}}^{\frac{1}{2}}{\left|\right|}^2\sum _{\mathfrak{k}=\mathfrak{n}}^{\mathfrak{n}+\mathfrak{p}}{\left|\right|\mu \left|\right|}^{2\mathfrak{k}}{1}_{\mathbb{A}}\hfill \\ \hfill & \to 0\mathrm{as}\mathfrak{n},\mathfrak{p}\to +\infty .\hfill \end{array}$$

Therefore, $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ is a Cauchy bisequence in $\Phi$ with regard to $\mathbb{A}$. By the completeness of $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$, we have, ${\vartheta }_{\mathfrak{n}}\to \varphi$ and ${\varpi }_{\mathfrak{n}}\to \varphi$, where $\varphi \in \Phi \cap \mathsf{\Lambda }$. Since $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ is a Cauchy bisequence, we have $\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}})\prec ϵ$. Now,

$$\begin{array}{cc}\hfill \mathfrak{d}({\rm Y}\varphi ,\varphi )& ⪯\mathfrak{d}({\rm Y}\varphi ,{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\hfill \\ \hfill & ⪯\mathfrak{d}({\rm Y}\varphi ,\Omega {\varpi }_{\mathfrak{n}})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\hfill \\ \hfill & ⪯{\mu }^{*}\mathfrak{d}(\varphi ,{\varpi }_{\mathfrak{n}})\mu +\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\hfill \\ \hfill & \prec {\mu }^{*}\mathfrak{d}(\varphi ,{\varpi }_{\mathfrak{n}})\mu +ϵ+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi ).\hfill \end{array}$$

As $\mathfrak{n}\to +\infty$,

$$\begin{array}{c}\hfill \mathfrak{d}({\rm Y}\varphi ,\varphi )\prec ϵ.\end{array}$$

Therefore, ${\rm Y}\left(\varphi \right)=\varphi$.

Note that,

$$\begin{array}{c}\hfill \mathfrak{d}(\varphi ,\Omega \varphi )=\mathfrak{d}({\rm Y}\varphi ,\Omega \varphi )⪯{\mu }^{*}\mathfrak{d}(\varphi ,\varphi )\mu =0.\end{array}$$

Therefore, $\Omega \left(\varphi \right)=\varphi$. Hence, $\varphi$ is the common fixed point of ${\rm Y}$ and $\Omega$. To prove uniqueness, suppose that $\psi \in \Phi \cup \mathsf{\Lambda }$ is another common fixed point of $\Phi$ and $\mathsf{\Lambda }$ such that $\Omega \psi ={\rm Y}\psi =\psi$. Then,

$$\begin{array}{c}\hfill 0_{\mathbb{A}}⪯\mathfrak{d}(\varphi ,\psi )=\mathfrak{d}({\rm Y}\varphi ,\Omega \psi )⪯{\mu }^{*}\mathfrak{d}(\varphi ,\psi )\mu .\end{array}$$

From the norm of $\mathbb{A}$,

$$\begin{array}{c}\hfill 0\le \parallel \mathfrak{d}(\varphi ,\psi )\parallel \le \parallel {\mu }^{*}\mathfrak{d}(\varphi ,\psi )\mu \parallel \le \parallel {\mu }^{*}\parallel \parallel \mathfrak{d}(\varphi ,\psi )\parallel \parallel \mu \parallel =\parallel \mu {\parallel }^2\parallel \mathfrak{d}(\varphi ,\psi )\parallel .\end{array}$$

The above inequality holds only when $\mathfrak{d}(\varphi ,\psi )=0_{\mathbb{A}}$. Hence, $\varphi =\psi$. □

Example 1. 

Let $\Phi =[0,2]$, $\mathsf{\Lambda }=\left\{0\right\}\cup \mathbb{N}-\{1,2\}$, and $\mathbb{A}={\mathcal{M}}_2\left(\mathbb{C}\right)$. Define $\mathfrak{d}:\Phi \times \mathsf{\Lambda }\to \mathbb{A}$ by

$$\mathfrak{d}(\vartheta ,\varpi )=\left(\begin{array}{c}\begin{array}{cc}|\vartheta -\varpi |& 0\\ 0& \alpha |\vartheta -\varpi |\end{array}\end{array}\right)$$

for all $\vartheta \in \Phi$ and $\varpi \in \mathsf{\Lambda }$, where $\alpha \ge 0$ is a constant. Consider the partial ordering ⪯ on $\mathbb{A}$ such that,

$$\begin{array}{c}\hfill ({\delta }_1,{\varrho }_1)⪯({\delta }_2,{\varrho }_2)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{\delta }_1\le {\delta }_2\mathrm{a}nd{\varrho }_1\le {\varrho }_2.\end{array}$$

Then, $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is a complete $C^{★}$-algebra-valued bipolar metric space.

Define ${\rm Y},\Omega :\Phi \cup \mathsf{\Lambda }\rightrightarrows \Phi \cup \mathsf{\Lambda }$ by

$${\rm Y}\left(\vartheta \right)=\left\{\begin{array}{cc}\frac{\vartheta }{4},\hfill & \mathrm{if}\vartheta \in [0,2],\hfill \\ \frac{\vartheta }{6},\hfill & \mathrm{if}\vartheta \in \mathbb{N}-\{1,2\},\hfill \end{array}\right.$$

and

$$\Omega \left(\vartheta \right)=\left\{\begin{array}{cc}\frac{\vartheta }{6},\hfill & \mathrm{if}\vartheta \in [0,2],\hfill \\ \frac{\vartheta }{4},\hfill & \mathrm{if}\vartheta \in \mathbb{N}-\{1,2\},\hfill \end{array}\right.$$

for all $\vartheta \in \Phi \cup \mathsf{\Lambda }$. Now, we consider two cases:

Case 1: Let $\vartheta \in [0,2]$ and $\varpi \in \mathbb{N}-\{1,2\}$, then

$$\begin{array}{c}\hfill \mathfrak{d}({\rm Y}\vartheta ,\Omega \varpi )=\left(\begin{array}{c}\begin{array}{cc}|{\rm Y}\vartheta -\Omega \varpi |& 0\\ 0& \alpha |{\rm Y}\vartheta -\Omega \varpi |\end{array}\end{array}\right)\\ \hfill =\left(\begin{array}{cc}& \begin{array}{cc}|\frac{\vartheta }{4}-\frac{\varpi }{4}|& 0\\ 0& \alpha |\frac{\vartheta }{4}-\frac{\varpi }{4}|\end{array}\end{array}\right)\\ \hfill =\frac{1}{4}\left(\begin{array}{cc}& \begin{array}{cc}|\vartheta -\varpi |& 0\\ 0& \alpha |\vartheta -\varpi |\end{array}\end{array}\right)\\ \hfill ={\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu ,\end{array}$$

where

$$\mu =\left(\begin{array}{c}\begin{array}{cc}\frac{1}{4}& 0\\ 0& \frac{1}{4}\end{array}\end{array}\right)$$

and $\left|\right|\mu \left|\right|=\frac{1}{4}<1$.

Case 2: Let $\varpi \in [0,2]$ and $\vartheta \in \mathbb{N}-\{1,2\}$, then

$$\begin{array}{c}\hfill \mathfrak{d}({\rm Y}\vartheta ,\Omega \varpi )=\left(\begin{array}{c}\begin{array}{cc}|{\rm Y}\vartheta -\Omega \varpi |& 0\\ 0& \alpha |{\rm Y}\vartheta -\Omega \varpi |\end{array}\end{array}\right)\\ \hfill =\left(\begin{array}{cc}& \begin{array}{cc}|\frac{\vartheta }{6}-\frac{\varpi }{6}|& 0\\ 0& \alpha |\frac{\vartheta }{6}-\frac{\varpi }{6}|\end{array}\end{array}\right)\\ \hfill =\frac{1}{6}\left(\begin{array}{cc}& \begin{array}{cc}|\vartheta -\varpi |& 0\\ 0& \alpha |\vartheta -\varpi |\end{array}\end{array}\right)\\ \hfill ={\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu ,\end{array}$$

where

$$\mu =\left(\begin{array}{c}\begin{array}{cc}\frac{1}{6}& 0\\ 0& \frac{1}{6}\end{array}\end{array}\right)$$

and $\left|\right|\mu \left|\right|=\frac{1}{6}<1$. Both the cases satisfy Theorem 1, and $\vartheta =0$ is the unique fixed point of Υ.

Now, we prove a similar result for contravariant maps.

Theorem 2. 

Let $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ be a complete ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space. Suppose ${\rm Y},\Omega :(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})\leftrightarrows (\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ are contravariant maps such that

$$\begin{array}{c}\hfill \mathfrak{d}({\rm Y}\left(\varpi \right),\Omega \left(\vartheta \right))⪯{\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu \mathrm{for}\mathrm{all}\vartheta \in \Phi ,\varpi \in \mathsf{\Lambda },\end{array}$$

where $\mu \in \mathbb{A}$ with ${\left|\right|\mu \left|\right|}^2<1$. Then, ${\rm Y},\Omega :\Phi \cup \mathsf{\Lambda }\to \Phi \cup \mathsf{\Lambda }$ have a unique common fixed point.

Proof. 

If $\mathbb{A}=\left\{0_{\mathbb{A}}\right\}$, then we are done. Suppose not. Let ${\vartheta }_0\in \Phi$ and ${\varpi }_0\in \mathsf{\Lambda }$. For each $\mathfrak{n}\in \mathbb{N}$, define ${\rm Y}\left({\vartheta }_{2\mathfrak{n}}\right)={\varpi }_{2\mathfrak{n}}$, $\Omega \left({\vartheta }_{2\mathfrak{n}+1}\right)={\varpi }_{2\mathfrak{n}+1}$ and ${\rm Y}\left({\varpi }_{2\mathfrak{n}}\right)={\vartheta }_{2\mathfrak{n}+1}$, $\Omega \left({\varpi }_{2\mathfrak{n}+1}\right)={\vartheta }_{2\mathfrak{n}+2}$. Then, $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ bisequence on $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$. Let $\mathcal{G}:=\mathfrak{d}({\vartheta }_0,{\varpi }_0)$. Then, for each $\mathfrak{n},\mathfrak{p}\in {\mathbb{Z}}^{+}$,

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{2\mathfrak{n}+1},{\varpi }_{2\mathfrak{n}+1})=& \mathfrak{d}({\rm Y}{\varpi }_{2\mathfrak{n}},\Omega {\vartheta }_{2\mathfrak{n}+1})\hfill \\ \hfill & ⪯{\mu }^{★}\mathfrak{d}({\vartheta }_{2\mathfrak{n}+1},{\varpi }_{2\mathfrak{n}})\mu \hfill \\ \hfill & ={\mu }^{★}\mathfrak{d}({\rm Y}{\varpi }_{2\mathfrak{n}},\Omega {\vartheta }_{2\mathfrak{n}})\mu \hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^2\mathfrak{d}({\vartheta }_{2\mathfrak{n}},{\varpi }_{2\mathfrak{n}}){\mu }^2\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^4\mathfrak{d}({\vartheta }_{2\mathfrak{n}-1},{\varpi }_{2\mathfrak{n}-1}){\mu }^4\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{4\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{4\mathfrak{n}+2},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{2\mathfrak{n}+1},{\varpi }_{2\mathfrak{n}})=& \mathfrak{d}({\rm Y}{\varpi }_{2\mathfrak{n}},\Omega {\vartheta }_{2\mathfrak{n}})\hfill \\ \hfill & ⪯{\mu }^{★}\mathfrak{d}({\vartheta }_{2\mathfrak{n}},{\varpi }_{2\mathfrak{n}})\mu \hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{4\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{4\mathfrak{n}+1},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}})& ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}})\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+1})+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+2})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+2})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+1})+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2}\hfill \\ \hfill & +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+2})+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+4}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+4}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+3}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+3}\hfill \\ \hfill & +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2}\hfill \\ \hfill & +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+\mathfrak{p}-1})+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2\mathfrak{p}-2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2\mathfrak{p}-2}\hfill \\ \hfill & +\cdots +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2\mathfrak{p}-1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2\mathfrak{p}-1}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2\mathfrak{p}-2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2\mathfrak{p}-2}\hfill \\ \hfill & +\cdots +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}+1}^{2\mathfrak{n}+2\mathfrak{p}-1}{\left({\mu }^{★}\right)}^{\mathfrak{k}}\mathcal{G}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}+1}^{2\mathfrak{n}+2\mathfrak{p}-1}{\left({\mu }^{★}\right)}^{\mathfrak{k}}{\mathcal{G}}^{\frac{1}{2}}{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}+1}^{2\mathfrak{n}+2\mathfrak{p}-1}{\left({\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right)}^{★}{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}+1}^{2\mathfrak{n}+2\mathfrak{p}-1}{\left|{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right|}^2\hfill \\ \hfill & ⪯\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}-2}\left|\right|{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ⪯\sum _{\mathfrak{k}=2\mathfrak{n}+1}^{2\mathfrak{n}+2\mathfrak{p}-1}\left|\right|\mathcal{G}\left|\right|\left|\right|{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\left|\right|\mathcal{G}\left|\right|\sum _{\mathfrak{k}=2\mathfrak{n}+1}^{2\mathfrak{n}+2\mathfrak{p}-1}\left|\right|{\mu }^2{\left|\right|}^{\mathfrak{k}}{1}_{\mathbb{A}}\to 0\mathrm{as}\mathfrak{n},\mathfrak{p}\to +\infty ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}+\mathfrak{p}})& ⪯\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})\hfill \\ \hfill & +\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2}\hfill \\ \hfill & +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+3}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+3}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+2},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2}\hfill \\ \hfill & +\cdots +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2\mathfrak{p}-1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2\mathfrak{p}-1}+\mathfrak{d}({\vartheta }_{\mathfrak{n}+\mathfrak{p}},{\varpi }_{\mathfrak{n}+\mathfrak{p}})\hfill \\ \hfill & ⪯{\left({\mu }^{★}\right)}^{2\mathfrak{n}}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+1}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2}\hfill \\ \hfill & +\cdots +{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2\mathfrak{p}-1}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2\mathfrak{p}-1}+{\left({\mu }^{★}\right)}^{2\mathfrak{n}+2\mathfrak{p}}\mathfrak{d}({\vartheta }_{\mathfrak{0}},{\varpi }_{\mathfrak{0}}){\mu }^{2\mathfrak{n}+2\mathfrak{p}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}{\left({\mu }^{★}\right)}^{\mathfrak{k}}\mathcal{G}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}{\left({\mu }^{★}\right)}^{\mathfrak{k}}{\mathcal{G}}^{\frac{1}{2}}{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}{\left({\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right)}^{★}{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\hfill \\ \hfill & =\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}{\left|{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}\right|}^2\hfill \\ \hfill & ⪯\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}\left|\right|{\mathcal{G}}^{\frac{1}{2}}{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}\left|\right|\mathcal{G}\left|\right|\left|\right|{\mu }^{\mathfrak{k}}{\left|\right|}^2{1}_{\mathbb{A}}\hfill \\ \hfill & ⪯\left|\right|\mathcal{G}\left|\right|\sum _{\mathfrak{k}=2\mathfrak{n}}^{2\mathfrak{n}+2\mathfrak{p}}\left|\right|{\mu }^2{\left|\right|}^{\mathfrak{k}}{1}_{\mathbb{A}}\to 0\mathrm{as}\mathfrak{n},\mathfrak{p}\to +\infty .\hfill \end{array}$$

Therefore, $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ is a Cauchy bisequence in $\Phi$ with respect to $\mathbb{A}$. By the completeness of $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$, it follows that ${\vartheta }_{\mathfrak{n}}\to \varphi$ and ${\varpi }_{\mathfrak{n}}\to \varphi$, where $\varphi \in \Phi \cap \mathsf{\Lambda }$. Since $(\left\{{\vartheta }_{\mathfrak{n}}\right\},\left\{{\varpi }_{\mathfrak{n}}\right\})$ is a Cauchy bisequence, we have $\mathfrak{d}({\vartheta }_{\mathfrak{n}},{\varpi }_{\mathfrak{n}})\prec ϵ$. Now,

$$\begin{array}{cc}\hfill \mathfrak{d}(\Omega \varphi ,\varphi )& ⪯\mathfrak{d}(\Omega \varphi ,{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\hfill \\ \hfill & ⪯\mathfrak{d}(\Omega \varphi ,{\rm Y}{\vartheta }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\hfill \\ \hfill & ⪯{\mu }^{*}\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\mu +\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},{\varpi }_{\mathfrak{n}+1})+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\hfill \\ \hfill & \prec {\mu }^{*}\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi )\mu +ϵ+\mathfrak{d}({\vartheta }_{\mathfrak{n}+1},\varphi ).\hfill \end{array}$$

As $\mathfrak{n}\to +\infty$,

$$\begin{array}{c}\hfill \mathfrak{d}(\Omega \varphi ,\varphi )\prec ϵ.\end{array}$$

Therefore, $\Omega \left(\varphi \right)=\varphi$. Note that,

$$\begin{array}{c}\hfill \mathfrak{d}(\varphi ,{\rm Y}\varphi )=\mathfrak{d}(\Omega \varphi ,{\rm Y}\varphi )⪯{\mu }^{*}\mathfrak{d}(\varphi ,\varphi )\mu =0.\end{array}$$

Therefore, $\Omega \left(\varphi \right)=\varphi$. Hence, $\varphi$ is a common fixed point of ${\rm Y}$ and $\Omega$. Let $\psi \in \Phi \cup \mathsf{\Lambda }$ be a another common fixed point of $\Phi$ and $\mathsf{\Lambda }$ such that $\Omega \psi ={\rm Y}\psi =\psi$. Then,

$$\begin{array}{c}\hfill 0_{\mathbb{A}}⪯\mathfrak{d}(\varphi ,\psi )=\mathfrak{d}(\Omega \varphi ,{\rm Y}\psi )⪯{\mu }^{*}\mathfrak{d}(\varphi ,\psi )\mu .\end{array}$$

Using the norm of $\mathbb{A}$, we have

$$\begin{array}{c}\hfill 0\le \parallel \mathfrak{d}(\varphi ,\psi )\parallel \le \parallel {\mu }^{*}\mathfrak{d}(\varphi ,\psi )\mu \parallel \le \parallel {\mu }^{*}\parallel \parallel \mathfrak{d}(\varphi ,\psi )\parallel \parallel \mu \parallel =\parallel \mu {\parallel }^2\parallel \mathfrak{d}(\varphi ,\psi )\parallel .\end{array}$$

The above inequality holds only when $\mathfrak{d}(\varphi ,\psi )=0_{\mathbb{A}}$. Hence, $\varphi =\psi$. □

Example 2. 

Let $\Phi =\{0,1,2,7\}$, $\mathsf{\Lambda }=\{0,\frac{1}{4},\frac{1}{2},3\}$, $\mathbb{A}={\mathcal{M}}_2\left(\mathbb{C}\right)$, and $\mathfrak{d}:\Phi \times \mathsf{\Lambda }\to \mathbb{A}$ be defined by

$$\mathfrak{d}(\vartheta ,\varpi )=\left(\begin{array}{c}\begin{array}{cc}|\vartheta -\varpi |& 0\\ 0& \alpha |\vartheta -\varpi |\end{array}\end{array}\right)$$

for all $\vartheta \in \Phi$ and $\varpi \in \mathsf{\Lambda }$, where $\alpha \ge 0$ is a constant. Let ⪯ be the partial order on $\mathbb{A}$ given by

$$\begin{array}{c}\hfill ({\delta }_1,{\varrho }_1)⪯({\delta }_2,{\varrho }_2)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{\delta }_1\le {\delta }_2\mathrm{a}nd{\varrho }_1\le {\varrho }_2.\end{array}$$

Then, $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is a complete $C^{★}$-algebra-valued bipolar metric space. Define ${\rm Y}:\Phi \cup \mathsf{\Lambda }\leftrightarrows \Phi \cup \mathsf{\Lambda }$ by

$${\rm Y}\left(\vartheta \right)=\left\{\begin{array}{cc}\frac{\vartheta }{5},\hfill & \mathrm{if}\vartheta \in \{0,7,2\},\hfill \\ \frac{\vartheta }{7},\hfill & \mathrm{if}\vartheta \in \{\frac{1}{4},\frac{1}{2},1,3\},\hfill \end{array}\right.$$

$$\Omega \left(\vartheta \right)=\left\{\begin{array}{cc}\frac{\vartheta }{7},\hfill & \mathrm{if}\vartheta \in \{0,7,2\},\hfill \\ \frac{\vartheta }{5},\hfill & \mathrm{if}\vartheta \in \{\frac{1}{4},\frac{1}{2},1,3\},\hfill \end{array}\right.$$

for all $\vartheta \in \Phi \cup \mathsf{\Lambda }$. We have the following two cases:

Case 1: Let $\vartheta \in \{0,7,2\}$ and $\varpi \in \{\frac{1}{4},\frac{1}{2},1,3\}$; then,

$$\begin{array}{cc}\hfill \mathfrak{d}({\rm Y}\varpi ,\Omega \vartheta )=& \left(\begin{array}{c}\begin{array}{cc}|{\rm Y}\varpi -\Omega \vartheta |& 0\\ 0& \alpha |{\rm Y}\varpi -\Omega \vartheta |\end{array}\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{cc}& \begin{array}{cc}|\frac{\vartheta }{7}-\frac{\varpi }{7}|& 0\\ 0& \alpha |\frac{\vartheta }{7}-\frac{\varpi }{7}|\end{array}\end{array}\right)\hfill \\ \hfill =& \frac{1}{7}\left(\begin{array}{cc}& \begin{array}{cc}|\vartheta -\varpi |& 0\\ 0& \alpha |\vartheta -\varpi |\end{array}\end{array}\right)\hfill \\ \hfill =& {\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu ,\hfill \end{array}$$

where

$$\mu =\left(\begin{array}{c}\begin{array}{cc}\frac{1}{7}& 0\\ 0& \frac{1}{7}\end{array}\end{array}\right)$$

and $\left|\right|\mu \left|\right|=\frac{1}{7}<1$.

Case 2: Let $\varpi \in \{0,7,2\}$ and $\vartheta \in \{\frac{1}{4},\frac{1}{2},1,3\}$; then,

$$\begin{array}{cc}\hfill \mathfrak{d}({\rm Y}\vartheta ,\Omega \varpi )=& \left(\begin{array}{c}\begin{array}{cc}|{\rm Y}\vartheta -\Omega \varpi |& 0\\ 0& \alpha |{\rm Y}\vartheta -\Omega \varpi |\end{array}\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{cc}& \begin{array}{cc}|\frac{\vartheta }{5}-\frac{\varpi }{5}|& 0\\ 0& \alpha |\frac{\vartheta }{5}-\frac{\varpi }{5}|\end{array}\end{array}\right)\hfill \\ \hfill =& \frac{1}{5}\left(\begin{array}{cc}& \begin{array}{cc}|\varpi -\vartheta |& 0\\ 0& \alpha |\varpi -\vartheta |\end{array}\end{array}\right)\hfill \\ \hfill =& {\mu }^{★}\mathfrak{d}(\varpi ,\vartheta )\mu ,\hfill \end{array}$$

where

$$\mu =\left(\begin{array}{c}\begin{array}{cc}\frac{1}{5}& 0\\ 0& \frac{1}{5}\end{array}\end{array}\right)$$

and $\left|\right|\mu \left|\right|=\frac{1}{5}<1$.

The above two cases satisfy Theorem 2, and $\vartheta =0$ is the unique fixed point of Υ.

4. Application

Now, we present an application of Theorem 1 to integral equations.

Theorem 3. 

Consider the equations

$$\begin{array}{c}\hfill \vartheta \left(\mathfrak{t}\right)=\varrho \left(\mathfrak{t}\right)+{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{\mathcal{G}}_1(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))d\mathfrak{s},\mathfrak{t}\in {\mathcal{Z}}_1\cup {\mathcal{Z}}_2\end{array}$$

$$\begin{array}{c}\hfill and\\ \hfill \vartheta \left(\mathfrak{t}\right)=\varrho \left(\mathfrak{t}\right)+{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{\mathcal{G}}_2(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))d\mathfrak{s},\mathfrak{t}\in {\mathcal{Z}}_1\cup {\mathcal{Z}}_2,\end{array}$$

where ${\mathcal{Z}}_1\cup {\mathcal{Z}}_2$ is a Lebesgue measurable set. Suppose

(T1) 

${\mathcal{G}}_1,{\mathcal{G}}_2:({\mathcal{Z}}_1^2\cup {\mathcal{Z}}_2^2)\times [0,\infty )\to [0,\infty )$ and $b\in L^{\infty }\left({\mathcal{Z}}_1\right)\cup L^{\infty }\left({\mathcal{Z}}_2\right)$,

(T2) 

there is a continuous function $\theta :{\mathcal{Z}}_1^2\cup {\mathcal{Z}}_2^2\to [0,\infty )$ and $\mu \in (0,1)$ such that

$$\begin{array}{c}\hfill |{\mathcal{G}}_1(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))-{\mathcal{G}}_2(\mathfrak{t},\mathfrak{s},\varpi \left(\mathfrak{s}\right)|\le \mu \left|\theta (\mathfrak{t},\mathfrak{s})\right||\vartheta \left(\mathfrak{s}\right)-\varpi \left(\mathfrak{s}\right)|,\end{array}$$

for $\mathfrak{t},\mathfrak{s}\in {\mathcal{Z}}_1^2\cup {\mathcal{Z}}_2^2$,

(T3) 

${sup}_{\mathfrak{t}\in {\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\theta (\mathfrak{t},\mathfrak{s})d\mathfrak{s}\le 1$.

Then, the integral equations have a unique common solution in $L^{\infty }\left({\mathcal{Z}}_1\right)\cup L^{\infty }\left({\mathcal{Z}}_2\right)$.

Proof. 

Consider two normed linear spaces $\Phi =L^{\infty }\left({\mathcal{Z}}_1\right)$ and $\mathsf{\Lambda }=L^{\infty }\left({\mathcal{Z}}_2\right)$, where ${\mathcal{Z}}_1,{\mathcal{Z}}_2$ are Lebesgue measurable sets and $m({\mathcal{Z}}_1\cup {\mathcal{Z}}_2)<\infty$. Let $\mathbb{A}=L^2\left({\mathcal{Z}}_1\right)\cup L^2\left({\mathcal{Z}}_2\right)$. Consider $\mathfrak{d}:\Phi \times \mathsf{\Lambda }\to L\left(\mathbb{A}\right)$ defined by $\mathfrak{d}(\vartheta ,\varpi )={\pi }_{|\vartheta -\varpi |}$, where ${\pi }_{\mathfrak{h}}:\mathbb{A}\to \mathbb{A}$ is the multiplication operator defined by ${\pi }_{\mathfrak{h}}\left(\sigma \right)=\mathfrak{h}.\sigma$ for $\sigma \in \mathbb{A}$. Then, $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is a complete ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space.

Define the covariant maps ${\rm Y},\Omega :L^{\infty }\left({\mathcal{Z}}_1\right)\cup L^{\infty }\left({\mathcal{Z}}_2\right)\to L^{\infty }\left({\mathcal{Z}}_1\right)\cup L^{\infty }\left({\mathcal{Z}}_2\right)$ by

$$\begin{array}{c}\hfill {\rm Y}\left(\vartheta \left(\mathfrak{t}\right)\right)=\varrho \left(\mathfrak{t}\right)+{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{\mathcal{G}}_1(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))d\mathfrak{s},\mathfrak{t}\in {\mathcal{Z}}_1\cup {\mathcal{Z}}_2.\end{array}$$

$$\begin{array}{c}\hfill \Omega \left(\vartheta \left(\mathfrak{t}\right)\right)=\varrho \left(\mathfrak{t}\right)+{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{\mathcal{G}}_2(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))d\mathfrak{s},\mathfrak{t}\in {\mathcal{Z}}_1\cup {\mathcal{Z}}_2.\end{array}$$

Set $\mathcal{B}=\mu I$, then $\mathcal{B}\in L{\left(\mathbb{A}\right)}_{+}$ and $\left|\right|\mathcal{B}\left|\right|=\mu <1$. For any $\mathfrak{h}\in \mathbb{A}$,

$$\begin{array}{cc}\hfill \left|\right|\mathfrak{d}({\rm Y}\vartheta ,\Omega \varpi )\left|\right|& =\underset{\parallel \mathfrak{h}\parallel =1}{sup}({\pi }_{|{\rm Y}\vartheta -\Omega \varpi |}\mathfrak{h},\mathfrak{h})\hfill \\ \hfill & =\underset{\parallel \mathfrak{h}\parallel =1}{sup}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\left[{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}|{\mathcal{G}}_1(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))-{\mathcal{G}}_2(\mathfrak{t},\mathfrak{s},\varpi \left(\mathfrak{s}\right))|d\mathfrak{s}\right]\mathfrak{h}\left(\mathfrak{t}\right)\overline{\mathfrak{h}\left(\mathfrak{t}\right)}\mathfrak{d}\mathfrak{t}\hfill \\ \hfill & \le \underset{\parallel \mathfrak{h}\parallel =1}{sup}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\left[{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}|{\mathcal{G}}_1(\mathfrak{t},\mathfrak{s},\vartheta \left(\mathfrak{s}\right))-{\mathcal{G}}_2(\mathfrak{t},\mathfrak{s},\varpi \left(\mathfrak{s}\right))|d\mathfrak{s}\right]{\left|\mathfrak{h}\left(\mathfrak{t}\right)\right|}^2\mathfrak{d}\mathfrak{t}\hfill \\ \hfill & \le \underset{\parallel \mathfrak{h}\parallel =1}{sup}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\left[{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\mu \left|\theta (\mathfrak{t},\mathfrak{s})\right||\vartheta \left(\mathfrak{s}\right)-\varpi \left(\mathfrak{s}\right)|d\mathfrak{s}\right]{\left|\mathfrak{h}\left(\mathfrak{t}\right)\right|}^2\mathfrak{d}\mathfrak{t}\hfill \\ \hfill & \le \mu \underset{\parallel \mathfrak{h}\parallel =1}{sup}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\left[{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\left|\theta (\mathfrak{t},\mathfrak{s})\right|d\mathfrak{s}\right]{\left|\mathfrak{h}\left(\mathfrak{t}\right)\right|}^2\mathfrak{d}\mathfrak{t}.\left|\right|\vartheta -{\varpi \left|\right|}_{\infty }\hfill \\ \hfill & \le \mu \underset{\mathfrak{t}\in {\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{sup}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}\left|\theta (\mathfrak{t},\mathfrak{s})\right|d\mathfrak{s}.\underset{\parallel \mathfrak{h}\parallel =1}{sup}{\int }_{{\mathcal{Z}}_1\cup {\mathcal{Z}}_2}{\left|\mathfrak{h}\left(\mathfrak{t}\right)\right|}^2\mathfrak{d}\mathfrak{t}.\left|\right|\vartheta -{\varpi \left|\right|}_{\infty }\hfill \\ \hfill & \le \mu \left|\right|\vartheta -{\varpi \left|\right|}_{\infty }\hfill \\ \hfill & =\left|\right|\mathcal{B}\left|\right|\left|\right|\mathfrak{d}(\vartheta ,\varpi )\left|\right|.\hfill \end{array}$$

One can easily see that Theorem 1 is satisfied as $\left|\right|\mathcal{B}\left|\right|<1$, and hence the integral equations have a unique common solution. □

5. Application to Electric Circuit Differential Equation

In this section, we study the existence and unique solution to an electric circuit differential equation as an application of Theorem 1.

Let us consider a series electric circuit that contains a resistor ($\mathcal{R}$, Ohms), a capacitor ($\mathcal{C}$, Faradays), an inductor ($\mathcal{L}$, Henries), a voltage ($\mathcal{V}$, Volts), and an electromotive force ($\mathcal{E}$, Volts), as in the following scheme, Figure 1.

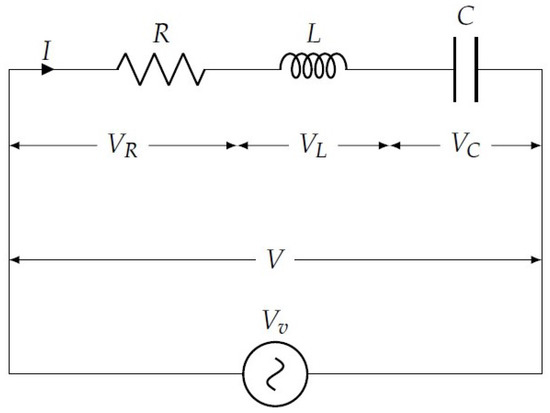
Figure 1. RLC circuit in series.

Considering the definition of the intensity of electric currents ${\mathcal{I}}_{\mathfrak{i}}=\frac{\mathrm{d}{\mathfrak{q}}_{\mathfrak{i}}}{\mathrm{d}\mathfrak{t}}$, $\mathfrak{i}=1,2$ where ${\mathfrak{q}}_{\mathfrak{i}}$ denote the electric charges and $\mathfrak{t}$ the time, let us recall the following usual formulas:

• ${\mathcal{V}}_{\mathcal{R}}={\mathcal{I}}_{\mathfrak{i}}\mathcal{R};$
• ${\mathcal{V}}_{\mathcal{C}}=\frac{{\mathfrak{q}}_{\mathfrak{i}}}{\mathcal{C}}$
• ${\mathcal{V}}_{\mathcal{L}}=\mathcal{L}\frac{\mathrm{d}{\mathcal{I}}_{\mathfrak{i}}}{\mathrm{d}\mathfrak{t}}$

In a series circuit, the current flowing through the circuit is uniform. So, ${\mathcal{I}}_{\mathfrak{i}}$ have the same value throughout the entire circuit.

One of the fundamental laws of circuit theory is Kirchhoff’s voltage law. It states that the algebraic sum of all the voltages around any closed loop in a circuit is equal to zero. Kirchhoff’s Voltage Law is based on the fact that while moving along a closed loop or a circuit, one can find that the starting and ending points are the same. The voltage drop in the circuit equals the voltage source. This implies that there is no voltage loss in the circuit. Voltage drop, if any, will be equal to the voltage source encountered along the way. Mathematically, the sum of the voltage drops equals the sum of the voltage rises across any circuit. Accordingly, we have the following:

$$\begin{array}{c}\hfill {\mathcal{I}}_{\mathfrak{i}}\mathcal{R}+\frac{{\mathfrak{q}}_{\mathfrak{i}}}{\mathcal{C}}+\mathcal{L}\frac{\mathrm{d}{\mathcal{I}}_{\mathfrak{i}}}{\mathrm{d}\mathfrak{t}}=\mathcal{V}={\mathcal{V}}_v\left(\mathfrak{t}\right),\mathfrak{i}=1,2.\end{array}$$

The above voltage equation can be expressed as follows:

$$\begin{array}{c}\hfill \mathcal{L}\frac{{\mathrm{d}}^2{\mathfrak{q}}_{\mathfrak{i}}}{\mathrm{d}{\mathfrak{t}}^2}+\mathcal{R}\frac{\mathrm{d}{\mathfrak{q}}_{\mathfrak{i}}}{\mathrm{d}\mathfrak{t}}+\frac{{\mathfrak{q}}_{\mathfrak{i}}}{\mathcal{C}}={\mathcal{V}}_v\left(\mathfrak{t}\right),\mathrm{with}\mathrm{the}\mathrm{initial}\mathrm{conditions},{\mathfrak{q}}_{\mathfrak{i}}\left(0\right)=0,{\mathfrak{q}}_{\mathfrak{i}}^{{}^{\prime }}\left(0\right)=0,\mathfrak{i}=1,2\end{array}$$

(1)

where $\mathcal{C}=\frac{4\mathcal{L}}{{\mathcal{R}}^2}$ and $\tau =\frac{\mathcal{R}}{2\mathcal{L}}$ - the nondimensional time for the resonance case in physics.

Moreover,

$$\begin{array}{c}\hfill \mathcal{G}(\mathfrak{t},\mathfrak{s})=\left\{\begin{array}{c}-\mathfrak{s}{\mathfrak{e}}^{-\tau (\mathfrak{s}-\mathfrak{t})},if0\le \mathfrak{s}\le \mathfrak{t}\le 1;\hfill \\ -\mathfrak{t}{\mathfrak{e}}^{-\tau (\mathfrak{s}-\mathfrak{t})},if0\le \mathfrak{t}\le \mathfrak{s}\le 1,\hfill \end{array}\right.\end{array}$$

where, $\mathcal{G}(\mathfrak{t},\mathfrak{s})$ represents the Green function associated with the second order differential Equation (1).

In these conditions, Equation (1) can be expressed as the following set of integral equations.

$$\begin{array}{c}\hfill \vartheta \left(\mathfrak{t}\right)={\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s}){\mathfrak{f}}_1(\mathfrak{s},\vartheta \left(\mathfrak{s}\right))\mathrm{d}\mathfrak{s},\mathrm{where}\mathfrak{t}\in [0,1]\end{array}$$

(2)

$$\begin{array}{c}\hfill \vartheta \left(\mathfrak{t}\right)={\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s}){\mathfrak{f}}_2(\mathfrak{s},\vartheta \left(\mathfrak{s}\right))\mathrm{d}\mathfrak{s},\mathrm{where}\mathfrak{t}\in [0,1]\end{array}$$

(3)

and ${\mathfrak{f}}_{\mathfrak{i}}(\mathfrak{s},·):[0,1]\times \mathbb{R}\to \mathbb{R}$ is a monotonically nondecreasing map for all $\mathfrak{s}\in [0,1]$.

Let $\Phi =\left(C\right[0,1],[0,+\infty \left)\right)$ be the set of all continuous functions defined in $[0,1]$ with values in the interval $[0,+\infty )$, and let $\mathsf{\Lambda }=\left(C\right[0,1],(-\infty ,0\left]\right)$ be the set of all continuous functions defined on $[0,1]$ with values in the interval $(-\infty ,0]$. Let $\mathbb{A}={\mathcal{M}}_2\left(\mathbb{C}\right)$ and $\mathfrak{d}:\Phi \times \mathsf{\Lambda }\to {\mathbb{A}}_{+}$ be defined by

$$\mathfrak{d}(\vartheta ,\varpi )=\left[\begin{array}{c}\begin{array}{cc}\underset{\mathfrak{t}\in [0,1]}{sup}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|& 0\\ 0& \mathbb{k}\underset{\mathfrak{t}\in [0,1]}{sup}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|\end{array}\end{array}\right]$$

for all $\vartheta \in \Phi$ and $\varpi \in \mathsf{\Lambda }$, where $\mathbb{k}\ge 0$ is a constant. Then, $(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ is a complete ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space.

Now, let us give the main result of this section.

Theorem 4. 

Let ${\rm Y},\Omega :(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})\rightrightarrows (\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ be maps such that the following assertions hold:

(i) 

$\mathcal{G}:{[0,1]}^2\to [0,\infty )$ is a continuous function;

(ii) 

${\mathfrak{f}}_{\mathfrak{i}}(\mathfrak{s},·):[0,1]\times \mathbb{R}\to \mathbb{R}$, $\mathfrak{i}=1,2$ is a monotonically non-decreasing function for all $\mathfrak{s}\in [0,1]$ such that for $(\vartheta ,\varpi )\in (\Phi ,\mathsf{\Lambda })$, we have the inequality:

$$\begin{array}{c}\hfill |{\mathfrak{f}}_1(\mathfrak{t},\vartheta )-{\mathfrak{f}}_2(\mathfrak{t},\varpi )|\le \frac{1}{2}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|;\end{array}$$

(iii) 

${sup}_{\mathfrak{t}\in [0,1]}{\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s})\le 1$.

Then, the voltage differential Equation (1) has a unique common solution.

Proof. 

Define the covariant maps ${\rm Y},\Omega :(\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})\rightrightarrows (\Phi ,\mathsf{\Lambda },\mathbb{A},\mathfrak{d})$ by

$$\begin{array}{c}\hfill {\rm Y}\vartheta \left(\mathfrak{t}\right)={\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s}){\mathfrak{f}}_1(\mathfrak{s},\vartheta \left(\mathfrak{s}\right))\mathrm{d}\mathfrak{s}.\end{array}$$

and

$$\begin{array}{c}\hfill \Omega \vartheta \left(\mathfrak{t}\right)={\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s}){\mathfrak{f}}_2(\mathfrak{s},\vartheta \left(\mathfrak{s}\right))\mathrm{d}\mathfrak{s}.\end{array}$$

Now,

$$\begin{array}{cc}\hfill \mathfrak{d}({\rm Y}\vartheta ,\Omega \varpi )& =\left[\begin{array}{c}\begin{array}{cc}\underset{\mathfrak{t}\in [0,1]}{sup}|{\rm Y}\vartheta \left(\mathfrak{t}\right)-\Omega \varpi \left(\mathfrak{t}\right)|& 0\\ 0& \mathbb{k}\underset{\mathfrak{t}\in [0,1]}{sup}|{\rm Y}\vartheta \left(\mathfrak{t}\right)-\Omega \varpi \left(\mathfrak{t}\right)|\end{array}\end{array}\right]\hfill \\ & \le \left[\begin{array}{cc}& \begin{array}{c}\underset{\mathfrak{t}\in [0,1]}{sup}{\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s})|{\mathfrak{f}}_1(\mathfrak{s},\vartheta \left(\mathfrak{s}\right))-{\mathfrak{f}}_2(\mathfrak{s},\varpi \left(\mathfrak{s}\right))|\mathrm{d}\mathfrak{s}0\\ \\ 0\mathbb{k}\underset{\mathfrak{t}\in [0,1]}{sup}{\int }_0^{\mathfrak{t}}\mathcal{G}(\mathfrak{t},\mathfrak{s})|{\mathfrak{f}}_1(\mathfrak{s},\vartheta \left(\mathfrak{s}\right))-{\mathfrak{f}}_2(\mathfrak{s},\varpi \left(\mathfrak{s}\right))|\mathrm{d}\mathfrak{s}\end{array}\end{array}\right]\hfill \\ \\ & \le \left[\begin{array}{cc}& \begin{array}{cc}\frac{1}{2}\underset{\mathfrak{t}\in [0,1]}{sup}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|& 0\\ 0& \mathbb{k}\frac{1}{2}\underset{\mathfrak{t}\in [0,1]}{sup}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|\end{array}\end{array}\right]\hfill \\ & =\frac{1}{2}\left[\begin{array}{cc}& \begin{array}{cc}\underset{\mathfrak{t}\in [0,1]}{sup}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|& 0\\ 0& \mathbb{k}\underset{\mathfrak{t}\in [0,1]}{sup}|\vartheta \left(\mathfrak{t}\right)-\varpi \left(\mathfrak{t}\right)|\end{array}\end{array}\right]\hfill \\ & ={\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu ,\hfill \end{array}$$

where

$$\mu =\left[\begin{array}{c}\begin{array}{cc}\frac{1}{\sqrt{2}}& 0\\ 0& \frac{1}{\sqrt{2}}\end{array}\end{array}\right]$$

and $\left|\right|\mu \left|\right|=\frac{1}{\sqrt{2}}<1$. Therefore,

$$\begin{array}{c}\hfill \mathfrak{d}({\rm Y}\vartheta ,\Omega \varpi )\le {\mu }^{★}\mathfrak{d}(\vartheta ,\varpi )\mu .\end{array}$$

All conditions of Theorem 1 are satisfied. Hence, the differential voltage Equation (1) has a unique common solution. □

6. Conclusions

It has been established that the generalization of the Banach contraction principle in various topological spaces helps in establishing fixed-point results under varius contractive conditions. We established fixed-point results using covariant and contravariant maps in the setting of the ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space, supplemented with suitable examples. The derived results have been applied to analyze the existence of the unique common solution to integral equations and the voltage differential equations of electric circuits. This research explores the possibility of establishing fixed-point results using the Ćirić type, the Nadler type, the Prešić type, and the Meir–Keeler type of contractions, in the setting of ${\mathcal{C}}^{★}$-algebra-valued bipolar metric space and its applications therein.