The Leader Property in Quasi Unidimensional Cases

Abstract

The following problem was studied: let ${\left({\mathbf{Z}}_j\right)}_{j\ge 1}$ be a sequence of i.i.d. d-dimensional random vectors. Let F be their probability distribution and for every $n\ge 1$ consider the sample ${\mathcal{S}}_n=\{{\mathbf{Z}}_1,{\mathbf{Z}}_2,\dots ,{\mathbf{Z}}_n\}.$ Then ${\mathbf{Z}}_j$ was called a “leader” in the sample ${\mathcal{S}}_n$ if ${\mathbf{Z}}_j\ge {\mathbf{Z}}_k,$$\forall k\in \{1,2,\dots ,n\}$ and ${\mathbf{Z}}_j$ was an “anti-leader” if ${\mathbf{Z}}_j\le {\mathbf{Z}}_k,$$\forall k\in \{1,2,\dots ,n\}$. The comparison of two vectors was the usual one: if ${\mathbf{Z}}_j=\left(Z_j^{\left(1\right)},Z_j^{\left(2\right)},\dots ,Z_j^{\left(d\right)}\right),$$j\ge 1,$ then ${\mathbf{Z}}_j\ge {\mathbf{Z}}_k$ means $Z_j^{\left(i\right)}\ge Z_k^{\left(i\right)},$ while ${\mathbf{Z}}_j\le {\mathbf{Z}}_k$ means $Z_j^{\left(i\right)}\le Z_k^{\left(i\right)},$$\forall 1\le i\le d,$$\forall j,k\ge 1.$ Let $a_n$ be the probability that ${\mathcal{S}}_n$ has a leader, $b_n$ be the probability that ${\mathcal{S}}_n$ has an anti-leader and $c_n$ be the probability that ${\mathcal{S}}_n$ has both a leader and an anti-leader. Sometimes these probabilities can be computed or estimated, for instance in the case when F is discrete or absolutely continuous. The limits $a=liminf{a}_n,$$b=liminf{b}_n,$$c=liminf{c}_n$ were considered. If $a>0$ it was said that F has the leader property, if $b>0$ they said that F has the anti-leader property and if $c>0$ then F has the order property. In this paper we study an in-between case: here the vector $\mathbf{Z}$ has the form $\mathbf{Z}=\mathit{f}\left(X\right)$ where $\mathit{f}=\left(f_1,\dots ,f_d\right):\left[0,1\right]\to {\mathbb{R}}^d$ and X is a random variable. The aim is to find conditions for $\mathit{f}$ in order that $a>0,b>0$ or $c>0$. The most examples will focus on a more particular case $\mathbf{Z}=\left(X,f_2\left(X\right),\dots ,f_d\left(X\right)\right)$ with X uniformly distributed on the interval $[0,1]$.

1. Introduction

In a previous paper [1], the following problem was studied: what is the probability $a_n$ that a “leader” exists in a set ${\left({\mathbf{Z}}_j\right)}_{1\le j\le n}$ of n i.i.d. d-dimensional random vectors, $d\ge 2$. Various formulae were established. In most cases, $a_n\to 0$ as $n\to \infty .$ If $liminf{a}_n>0$, it is said that “$\mathbf{Z}$ has the leader property”. This property is, rather, an exception, not a rule, among the d-dimensional probability distributions.

The problem was prompted by the relevance of various rankings, which are fashionable today and which are obtained by the unidimensionalization of a data set using different algorithms. For instance: the ranking of the countries by HDI—human development index or by corruption index, of musical hits, of universities, of researchers, or of scientific journals by various ISI factors.

The topic the Pareto maxima or minima in random sets is approached in several articles, such as [2,3].

A series of papers study the expected number of maximal vectors in a set of n elements from a d-dimensional space: in [4], this is derived a recurrence relation for computing the average number of maximal vectors under the assumption that all ${(n!)}^d$ relative orderings are equally probable, while in [5], the expected number of maximal vectors is determined explicitly for any n and d assuming that the vectors are distributed identically and that the d components of each vector are distributed independently and continuously. See other similar results in [6].

The asymptotic behaviour of this quantity as n tends to infinity has also been investigated. For instance, in [7], the authors proved that the number of maximal points is approximately normally distributed, under given conditions. In addition, see [4] or [8].

On the other hand, in [9] is presented an exact expression for the variance in the number of maxima in a three-dimensional cube.

In [10], the authors derive a general asymptotic formula for the variance in the number of maxima in a set of independent and identically distributed random vectors in ${\mathbb{R}}^d$, where the components of each vector are independently and continuously distributed.

However, the authors in [1] were not interested in finding Pareto maxima or minima but in the existence of real maximum or minimum in a finite random set. That is, in the existence of a first or last element.

In [1], the focus was on discrete or absolutely continuous vectors $\mathbf{Z}.$.

Here, we consider an in-between case: suppose that there exists an imponderable (meaning that it cannot be measured) uni-dimensional random variable $X$ which determines the ranking.

Next, suppose that we can measure various effects of X assumed to be functions $f_j\left(X\right).$ In this case, the vector $\mathbf{Z}$ becomes $\mathbf{Z}=\mathit{f}\left(X\right),\mathit{f}=\left(f_1,\dots ,f_d\right)$. We may hope that now it is easier to compute the probabilities $a_n,b_n,c_n$ and to decide their limits $a,b,c.$

It is well-known (see [11]) that we can always replace the random variable X by $F_X^{-1}\left(U\right)$ where U is uniformly distributed on $[0,1]$ and $F_X^{-1}$ is the quantile of the distribution function of X. Thus, there is no restriction if we consider that X itself is uniformly distributed.

The challenge is to determine the properties of $\mathit{f}$ for which $\mathbf{Z}$ has a leader.

2. Stating of the Problem

Let $X:\mathsf{\Omega }\to \mathbb{R}$ be a random variable uniformly distributed on $[0,1],$ let $\mathit{f}=\left(f_1,\dots ,f_d\right):\left[0,1\right]\to {\mathbb{R}}^d,$$d\ge 2$ be a measurable function and let $\mathbf{Z}=\mathit{f}\left(X\right).$ We shall denote by the same letter F both the probability distribution of $\mathbf{Z}$ (which is a measure on the borelian subsets of ${\mathbb{R}}^d$) and its distribution function. Thus

$$F\left(\mathbf{z}\right)=P\left(\mathbf{Z}\le \mathbf{z}\right)=P\left(f_i\left(X\right)\le z_i,\forall 1\le i\le d\right)$$

(1)

for any $\mathbf{z}=\left(z_1,z_2,\dots ,z_d\right)\in {\mathbb{R}}^d.$

There should be no danger of confusion since in an integral of the form $\int n{F}^{n-1}\left(\mathbf{y}\right)dF\left(\mathbf{y}\right)$ the first F is a function an the last F is a measure. Moreover, the integral is a Lebesgue integral.

Let us denote

$$F^{*}:{\mathbb{R}}^d\to \left[0,1\right],F^{*}\left(\mathbf{z}\right)=P\left(\mathbf{Z}\ge \mathbf{z}\right)=P\left(f_i\left(X\right)\ge z_i,\forall 1\le i\le d\right)$$

(2)

for any $\mathbf{z}=\left(z_1,z_2,\dots ,z_d\right)\in {\mathbb{R}}^d$ and

$$\mathsf{\Phi }:{\mathbb{R}}^d\times {\mathbb{R}}^d\to [0,1],\mathsf{\Phi }\left(\mathbf{x},\mathbf{y}\right)=P\left(\mathbf{x}\le \mathbf{Z}\le \mathbf{y}\right)=P\left(x_i\le f_i\left(X\right)\le y_i,\forall 1\le i\le d\right),$$

(3)

$\forall \mathbf{x}=\left(x_1,x_2,\dots ,x_d\right),$$\mathbf{y}=\left(y_1,y_2,\dots ,y_d\right)\in {\mathbb{R}}^d.$

If the function $\mathit{f}$ is one to one, then F is a continuous distribution, meaning that $F\left(C\right)=0$ for any, at most, countable Borel set C from ${\mathbb{R}}^d.$ For continuous distributions, the general formulae established in [1] were

$$a_n=E\left[n{F}^{n-1}\left(\mathbf{Z}\right)\right]=\int n{F}^{n-1}\left(\mathbf{y}\right)dF\left(\mathbf{y}\right),\forall n\ge 2$$

(4)

$$b_n=E\left[n{\left(F^{*}\right)}^{n-1}\left(\mathbf{Z}\right)\right]=\int n{\left(F^{*}\right)}^{n-1}\left(\mathbf{x}\right)dF\left(\mathbf{x}\right),\forall n\ge 2$$

(5)

$$c_n=E\left[n\left(n-1\right){\mathsf{\Phi }}^{n-2}\left(\mathbf{Z}\right)\right]=\int \int n\left(n-1\right){\mathsf{\Phi }}^{n-2}\left(\mathbf{x},\mathbf{y}\right)dF\left(\mathbf{y}\right)dF\left(\mathbf{x}\right),\forall n\ge 3.$$

(6)

 Remark 1. 

It is important to notice that $a_2=b_2=c_2$ means the probability that two i.i.d. F-distributed vectors ${\mathbf{Z}}_1$ and ${\mathbf{Z}}_2$ are comparable.

 Remark 2. 

Clearly, $c_3$ is the probability that a set of three random vectors ${\left({\mathbf{Z}}_j\right)}_{1\le j\le 3}$ are ordered.

 Remark 3. 

Recall that a function $\mathit{g}:{\mathbb{R}}^d\to {\mathbb{R}}^d$ is called strongly increasing (see [1]) if $\mathit{g}\left(\mathbf{x}\right)\le \mathit{g}\left(\mathbf{y}\right)$ if and only if$\mathbf{x}\le \mathbf{y}.$ Of course, in the one-dimensional case, “strongly increasing" and “non-decreasing" is the same thing. Obviously, $a_n,b_n,c_n$ remain the same if we replace $\mathit{f}$ by $\mathit{g}\left(\mathit{f}\right).$

In our special case, when X is uniformly distributed on $\left[0,1\right],$ the integration formula becomes

E$u\left(\mathbf{Z}\right)=$ E$u\left(\mathit{f}\left(X\right)\right)={\int }_0^{1}u\left(\mathit{f}\left(x\right)\right)dx$ for any integrable function $u:{\mathbb{R}}^d\to [0,1]$; hence,

$$a_n={\int }_0^{1}n{F}^{n-1}\left(\mathit{f}\left(y\right)\right)dy,\forall n\ge 1$$

(7)

$$b_n={\int }_0^{1}n{\left(F^{*}\right)}^{n-1}\left(\mathit{f}\left(x\right)\right)dx,\forall n\ge 1$$

(8)

$$c_n={\int }_0^1{\int }_x^{1}n\left(n-1\right){\mathsf{\Phi }}^{n-2}\left(\mathit{f}\left(x\right),\mathit{f}\left(y\right)\right)dydx,\forall n\ge 3.$$

(9)

Let $h:I\to \mathbb{R}$ with $I\subset \mathbb{R}$ interval and $x,y\in I$ arbitrary. We denote

$$\begin{array}{cc}\hfill L_y\left(h\right)& =\{t\in I:h\left(t\right)\le h\left(y\right)\},L_y^0\left(h\right)=\{t\in I:h\left(t\right)<h\left(y\right)\}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill H_x\left(h\right)& =\{t\in I:h\left(t\right)\ge h\left(x\right)\},H_x^0\left(h\right)=\{t\in I:h\left(t\right)>h\left(x\right)\}\hfill \end{array}$$

(11)

and let $\lambda :\mathcal{B}\left(\mathbb{R}\right)\to \mathbb{R}$ be the Lebesgue measure.

 Proposition 1. 

If X is uniformly distributed on $\left[0,1\right],$

$$F\left(\mathit{f}\left(y\right)\right)=\lambda \left(\bigcap _{i=1}^d{L}_y\left(f_i\right)\right)$$

(12)

$$F^{*}\left(\mathit{f}\left(x\right)\right)=\lambda \left(\bigcap _{i=1}^d{H}_x\left(f_i\right)\right)$$

(13)

$$\mathsf{\Phi }\left(\mathit{f}\left(x\right),\mathit{f}\left(y\right)\right)=\lambda \left(\bigcap _{i=1}^d{L}_y\left(f_i\right)\cap \bigcap _{i=1}^d{H}_x\left(f_i\right)\right)$$

(14)

 Proof. 

With $X\sim U\left([0,1]\right),$ one can easily find the probability:

$F\left(\mathit{f}\left(y\right)\right)=P\left(\mathbf{Z}\le \mathit{f}\left(y\right)\right)=P\left(\mathit{f}\left(X\right)\le \mathit{f}\left(y\right)\right)=\lambda \left(\{t\in [0,1]:f_i\left(t\right)\le f_i\left(y\right),\forall 1\le i\le d\}\right)$

$=\lambda \left(\bigcap _{i=1}^d{L}_y\left(f_i\right)\right)$

$F^{*}\left(\mathit{f}\left(x\right)\right)=P\left(\mathbf{Z}\ge \mathit{f}\left(x\right)\right)=P\left(\mathit{f}\left(X\right)\ge \mathit{f}\left(x\right)\right)=\lambda \left(\{t\in [0,1]:f_i\left(t\right)\ge f_i\left(x\right),\forall 1\le i\le d\}\right)$

$=\lambda \left(\bigcap _{i=1}^d{H}_x\left(f_i\right)\right)$

$\mathsf{\Phi }\left(\mathit{f}\left(x\right),\mathit{f}\left(y\right)\right)=P\left(\mathit{f}\left(x\right)\le \mathbf{Z}\le \mathit{f}\left(y\right)\right)=P\left(\mathit{f}\left(x\right)\le \mathit{f}\left(X\right)\le \mathit{f}\left(y\right)\right)=$

$=\lambda \left(\{t\in [0,1]:f_i\left(x\right)\le f_i\left(t\right)\le f_i\left(y\right),\forall 1\le i\le d\}\right)=$

$=\lambda \left(\{t\in [0,1]:t\in L_y\left(f_i\right)\cap H_x\left(f_i\right),\forall 1\le i\le d\}\right)=\lambda \left(\bigcap _{i=1}^d{L}_y\left(f_i\right)\cap \bigcap _{i=1}^d{H}_x\left(f_i\right)\right).$□

Next, if $\mathit{f}=\left(f_1,\dots ,f_d\right):\left[0,1\right]\to {\mathbb{R}}^d$ and $x,y\in [0,1]$, define the functions ${\varphi }_{\mathit{f}},$${\psi }_{\mathit{f}}:\left[0,1\right]\to \left[0,1\right]$ and ${\eta }_{\mathit{f}}:\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right]$ using

$${\varphi }_{\mathit{f}}\left(y\right)=F\left(\mathit{f}\left(y\right)\right),{\psi }_{\mathit{f}}\left(x\right)=F^{*}\left(\mathit{f}\left(x\right)\right)\mathrm{and}{\eta }_{\mathit{f}}\left(x,y\right)=\mathsf{\Phi }\left(\mathit{f}\left(x\right),\mathit{f}\left(y\right)\right).$$

(15)

Therefore, we can rewrite relations (7), (8), (9) as

$$a_n={\int }_0^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(y\right)dy$$

(16)

$$b_n={\int }_0^{1}n{\psi }_{\mathit{f}}^{n-1}\left(x\right)dx$$

(17)

$$c_n={\int }_0^1{\int }_x^{1}n\left(n-1\right){\eta }_{\mathit{f}}^{n-2}\left(x,y\right)dydx$$

(18)

Let us denote

$$a=liminf{a}_n,b=liminf{b}_n,c=liminf{c}_n.$$

(19)

Thus, the problem is: compute $a_n,b_n,c_n.$ If not, find conditions for $\mathit{f}$ such that the limits $a,b,c$ are positive.

3. General Results

Here we show some results that hold without any restrictions on the dimension d of the space. The function $\mathit{f}:\left[0,1\right]\to {\mathbb{R}}^d$ is supposed to be bounded measurable and injective.

 Definition 1. 

A partially ordered set C has the property L if it has a last element, that is, if there exists $c\in C$ such that $c\ge x$ for every $x\in C.$ We say that C has the property F if it has a first element, that is, if there exists an element $c\in C$ such that $c\le x$ for every $x\in C.$ Finally, the set C has the property FL if it has both a first element and a last element.

One of the results from [1], namely, Proposition 2, p. 5, is that: if a distribution F has the leader/anti-leader/order property, its support $C=Supp\left(F\right)$ must have the properties L/F/FL.

The support of the distribution F, denoted by $C=Supp\left(F\right),$ is defined to be the intersection of all closed sets M with $F\left(M\right)=1.$

In our case, if $\mathbf{Z}=\mathit{f}\left(X\right)$, it is more or less obvious that the support of F is the closure of the image of $\mathit{f}$: $Supp\left(F\right)=Cl\left(\mathit{f}\left([0,1]\right)\right).$

Thus,

 Proposition 2. 

Let $X:\mathsf{\Omega }\to \mathbb{R}$ is a random variable uniformly distributed on $[0,1]$, let $\mathit{f}:[0,1]\to {\mathbb{R}}^d$ be a bounded measurable function. Let F be the distribution of $\mathbf{Z}=\mathit{f}\left(X\right).$ Then, the following assertions hold:

• If $a=liminf{a}_n>0$ then there exists ${\mathbf{z}}_0\in Supp\left(F\right)$ such that ${\mathbf{z}}_0\ge \mathit{f}\left(t\right)$ for all $t\in \left[0,1\right].$ If ${\mathbf{z}}_0\in \mathit{f}\left([0,1]\right)$ then there exists $t_0\in \left[0,1\right]$ such that $\mathit{f}\left(t_0\right)\ge \mathit{f}\left(t\right)$ for all $t\in \left[0,1\right].$ In the particular case when $f_1$ is increasing then $t_0=1.$ Otherwise written, the function $\mathit{f}$ must have a global maximum. If $f_1$ is increasing, this is at $t=1.$
• If $b=liminf{b}_n>0$ then there exists ${\mathbf{z}}_0\in Supp\left(F\right)$ such that ${\mathbf{z}}_0\le \mathit{f}\left(t\right)$ for all $t\in \left[0,1\right].$ If ${\mathbf{z}}_0\in \mathit{f}\left([0,1]\right)$ then there exists $t_0\in \left[0,1\right]$ such that $\mathit{f}\left(t_0\right)\le \mathit{f}\left(t\right)$ for all $t\in \left[0,1\right].$ In the particular case when $f_1$ is increasing then $t_0=0.$ Otherwise written, the function $\mathit{f}$ must have a global minimum. If $f_1$ is increasing, this is at $t=0.$
• If $c=liminf{c}_n>0$ then there exists ${\mathbf{z}}_0,{\mathbf{z}}_1\in Supp\left(F\right)$ such that ${\mathbf{z}}_0\le \mathit{f}\left(t\right)\le {\mathbf{z}}_1$ for all $t\in \left[0,1\right].$ If ${\mathbf{z}}_0,{\mathbf{z}}_1\in \mathit{f}\left([0,1]\right)$ then there exist $t_0,t_1\in \left[0,1\right]$ such that $\mathit{f}\left(t_0\right)\le \mathit{f}\left(t\right)\le \mathit{f}\left(t_1\right)$ for all $t\in \left[0,1\right].$ Otherwise written, the function $\mathit{f}$ must have both a global maximum and a global minimum. In the particular case when $f_1$ is increasing then $t_0=1,$$t_1=1.$

 Proof. 

Obvious. The set $Supp\left(F\right)=Cl\left(\mathit{f}\left([0,1]\right)\right)$ has a last element if there exists ${\mathbf{z}}_0\in \mathit{f}\left([0,1]\right)$ such that ${\mathbf{z}}_0\ge \mathbf{z}$ for all $\mathbf{z}\in \mathit{f}\left([0,1]\right).$ However, that is equivalent to the fact that ${\mathbf{z}}_0\ge \mathbf{z}$ for all $\mathbf{z}\in \mathit{f}\left([0,1]\right)$ or, which is the same thing, that ${\mathbf{z}}_0\ge \mathit{f}\left(t\right)$ for all $t\in \left[0,1\right].$ Now, if ${\mathbf{z}}_0\in \mathit{f}\left([0,1]\right)$ then $z_0=\mathit{f}\left(t_0\right)$ for some $t_0\in \left[0,1\right].$ □

The next result establishes some relations between the functions defined in (15).

 Proposition 3. 

For an arbitrary function $\mathit{f}:\left[0,1\right]\to$${\mathbb{R}}^d$, consider the functions defined by relation (15). Then, the following hold:

 1. 

${\psi }_{\mathit{f}}\left(x\right)={\varphi }_{-\mathit{f}}\left(x\right)={\varphi }_{\alpha -\mathit{f}}\left(x\right)$ where $\alpha =\left({\alpha }_1,\dots ,{\alpha }_d\right)$ is a constant.

 2. 

${\eta }_{\mathit{f}}\left(x,y\right)\ge {\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-1$ for any $x,y\in \left[0,1\right].$ The equality is possible if and only if $\left(\bigcap _{i=1}^d{L}_y\left(f_i\right)\right)\cup \left(\bigcap _{i=1}^d{H}_x\left(f_i\right)\right)=\left[0,1\right]$ a.s.

 Proof. 

Let the constant $\alpha =\left({\alpha }_1,\dots ,{\alpha }_d\right)\in {\mathbb{R}}^d$ and $x,y\in \left[0,1\right]$ arbitrarily. Then:

• ${\psi }_{\mathit{f}}\left(x\right)=\lambda \left(\{t\in [0,1]:f_i\left(t\right)\ge f_i\left(x\right),\forall i=\overline{1,d}\}\right)=$
  $=\lambda \left(\{t\in [0,1]:-f_i\left(t\right)\le -f_i\left(x\right),\forall i=\overline{1,d}\}\right)=$
  $=\lambda \left(\{t\in [0,1]:{\alpha }_i-f_i\left(t\right)\le {\alpha }_i-f_i\left(x\right),\forall i=\overline{1,d}\}\right)={\varphi }_{\alpha -\mathit{f}}\left(x\right).$
• Write relations (15) as ${\varphi }_{\mathit{f}}\left(y\right)=\lambda \left(A\right),$${\psi }_{\mathit{f}}\left(x\right)=\lambda \left(B\right)$, ${\eta }_{\mathit{f}}\left(x,y\right)=\lambda \left(A\cap B\right)$ with $A=\bigcap _{i=1}^d{L}_y\left(f_i\right),$$B=\bigcap _{i=1}^d{H}_x\left(f_i\right).$ Remark that ${\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-{\eta }_{\mathit{f}}\left(x,y\right)=\lambda \left(A\cup B\right)\le \lambda \left(\left[0,1\right]\right)=1$ and that is all. The equality occurs if and only if $A\cup B=\left[0,1\right]$ a.s. or if $L_y\left(f_i\right)\cup H_x\left(f_j\right)=\left[0,1\right]$ a.s. for all $i,j\in \left\{1,\dots ,d\right\}.$

Let $\mathit{f}:\left[0,1\right]\to$${\mathbb{R}}^d$ such that $f_1$ is an increasing function. The following are obvious:

 Remark 4. 

$$\begin{array}{cc}\hfill {\varphi }_{\mathit{f}}\left(0\right)& =0,{\varphi }_{\mathit{f}}\left(y\right)\le y,\forall y\in \left(0,1\right)\hfill \\ \hfill {\psi }_{\mathit{f}}\left(1\right)& =0,{\psi }_{\mathit{f}}\left(x\right)\le 1-x,\forall x\in \left(0,1\right)\hfill \\ \hfill {\eta }_{\mathit{f}}\left(x,y\right)& \le y-x,\forall x,y\in \left(0,1\right).\hfill \end{array}$$

(20)

 Remark 5. 

If$\mathit{f}\left(0\right)=0$and$\mathit{f}\left(1\right)=1$then

$${\eta }_{\mathit{f}}\left(x,1\right)={\psi }_{\mathit{f}}\left(x\right)\mathrm{and}{\eta }_{\mathit{f}}\left(0,y\right)={\varphi }_{\mathit{f}}\left(y\right),\forall x,y\in \left(0,1\right)$$

(21)

 Remark 6. 

If $a,b>0$ then $af+b$ has the same $\varphi ,\psi ,\eta$ as $f:$ for instance ${\varphi }_{af+b}={\varphi }_f$ and so on.

 Remark 7. 

Obviously, if f is non-decreasing then $a_n=b_n=c_n=1,$$\forall n\ge 1.$

Actually, this is a good opportunity to check formulae (4)–(6):

Indeed, ${\varphi }_{\mathit{f}}\left(y\right)=F\left(\mathit{f}\left(y\right)\right)=P\left(\mathit{f}\left(X\right)\le \mathit{f}\left(y\right)\right)\ge P\left(X\le y\right)=y.$

In the same way, ${\psi }_{\mathit{f}}\left(x\right)=F^{*}\left(\mathit{f}\left(x\right)\right)=P\left(\mathit{f}\left(X\right)\ge \mathit{f}\left(x\right)\right)\ge P\left(X\ge x\right)=1-x.$

In addition, according to Proposition 3 (2), ${\eta }_{\mathit{f}}\left(x,y\right)\ge {\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-1=y-x.$

Thus, $a_n={\int }_0^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(y\right)dy\ge {\int }_0^{1}n{y}^{n-1}dy=1,b_n={\int }_0^{1}n{\psi }_{\mathit{f}}^{n-1}\left(x\right)dx\ge {\int }_0^{1}n{\left(1-x\right)}^{n-1}dx=1$ and $c_n\ge {\int }_0^1{\int }_x^{1}n\left(n-1\right){\left(y-x\right)}^{n-2}dydx=1.$

If we are interested only in $a,b,c$ and not in $a_n,b_n,c_n$, then the following result may help.

 Proposition 4. 

Suppose that $\mathit{f}:\left[0,1\right]\to$${\mathbb{R}}^d$ has the property that $f_1$ is an increasing function. Then for every $\epsilon >0$ the following are true

$$\begin{array}{cc}\hfill a& =liminf{\int }_{1-\epsilon }^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(y\right)dy\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill b& =liminf{\int }_0^{\epsilon }n{\psi }_{\mathit{f}}^{n-1}\left(y\right)dy\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill c& =liminf{\int }_0^{\epsilon }{\int }_{1-\epsilon }^{1}n\left(n-1\right){\eta }_{\mathit{f}}^{n-2}\left(x,y\right)dydx.\hfill \end{array}$$

(24)

Proof. 

Obvious. If $f_1$ is increasing then ${\varphi }_{\mathit{f}}\left(y\right)\le y,$${\psi }_{\mathit{f}}\left(x\right)\le 1-x$ and ${\eta }_{\mathit{f}}\left(x,y\right)\le y-x.$ As the probabilities defined in $\left(16\right)$ and $\left(17\right)$ verify $a_n=a_{n,1}+a_{n,2}$ with $a_{n,1}={\int }_0^{1-\epsilon }n{\varphi }_{\mathit{f}}^{n-1}\left(y\right)dy$ and $a_{n,2}={\int }_{1-\epsilon }^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(y\right)dy$ and $a_{n,1}\le {\int }_0^{1-\epsilon }n{y}^{n-1}dy\le {\left(1-\epsilon \right)}^n\to 0$ as $n\to \infty$, it is obvious that $a=liminf\left(a_{n,1}+a_{n,2}\right)=liminf{a}_{n,2}=liminf{\int }_{1-\epsilon }^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(y\right)dy.$

The same holds for b and $c.$ □

Finally, we will need the following result ([1], Lemma 5, p. 18).

 Proposition 5. 

 1. 

Let $g:\left[0,1\right]\to [0,\infty )$ be continuous at $x=1$. Then ${\displaystyle \underset{n}{lim}}n{\int }_{1-\epsilon }^1{x}^{n-1}g\left(x\right)dx=g\left(1\right)$ for any $\epsilon >0.$

 2. 

Let $G:\left[0,1\right]\to [0,1]$ be increasing and differentiable such that $G\left(1\right)=1,G^{\prime }\left(1\right)>0$ and let g be as above. Then ${\displaystyle \underset{n}{lim}}n{\int }_{1-\epsilon }^1{G}^{n-1}\left(x\right)g\left(x\right)dx=\frac{g\left(1\right)}{G^{\prime }\left(1\right)}$ for any $\epsilon >0.$

 3. 

Let $\varphi :{\left[0,1\right]}^2\to [0,\infty )$ be continuous.

Then ${\displaystyle \underset{n}{lim}}n\left(n-1\right){\int }_0^{\epsilon }{\int }_{1-\epsilon }^1{\left(y-x\right)}_{+}^{n-2}\varphi \left(x,y\right)dydx=\varphi \left(0,1\right)$ for any $\epsilon >0.$

Now we can prove the general result.

 Theorem 1. 

Let $\mathit{f}:\left[0,1\right]\to {\mathbb{R}}^d$ be measurable bounded function with the properties: $f_1$ is increasing; ${\varphi }_{\mathit{f}}$ is differentiable, increasing in a neighborhood of $t=1$ and such that ${\varphi }_{\mathit{f}}^{\prime }$ is continuous $;{\psi }_{\mathit{f}}$ is differentiable, decreasing in a neighborhood of $t=0$ and such that its derivative is continuous. The following assertions hold.

 (i) 

If ${\varphi }_{\mathit{f}}\left(1\right)<1,$$a=0.$ If ${\varphi }_{\mathit{f}}\left(1\right)=1$ then $a=\frac{1}{{\varphi }_{\mathit{f}}^{\prime }\left(1\right)}.$

 (ii) 

If ${\psi }_{\mathit{f}}\left(0\right)<1,$$b=0.$ If ${\psi }_{\mathit{f}}\left(0\right)=1$ then $b=-\frac{1}{{\psi }_{\mathit{f}}^{\prime }\left(0\right)}.$

 (iii) 

Always $c\ge ab.$

 (iv) 

If there exists $\epsilon >0$ such that $\eta \left(x,y\right)=\varphi \left(y\right)+\psi \left(x\right)-1$ for $x\in \left[0,\epsilon \right],y\in \left[1-\epsilon ,1\right]$ then $c=ab.$

 Proof. 

If ${\varphi }_f\left(1\right)<1$ then we may choose an $\epsilon >0$ small enough such that ${\displaystyle \underset{x\in \left[1-\epsilon ,1\right]}{sup}}{\varphi }_f\left(x\right)\stackrel{not}{=}\beta <1$ thus, $a=lim{\int }_{1-\epsilon }^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(x\right)dx\le limn{\beta }^{n-1}=0.$

If ${\varphi }_f\left(1\right)=1$ then let $\epsilon >0$ be small enough so that on the interval $\left[1-\epsilon ,1\right]$ the mapping ${\varphi }_{\mathit{f}}$ is an increasing differentiable, and on the interval $\left[0,\epsilon \right]$, the function ${\psi }_{\mathit{f}}$ is a decreasing differentiable.

Then $a=lim{\int }_{1-\epsilon }^{1}n{\varphi }_{\mathit{f}}^{n-1}\left(x\right)dx.$ Let $t={\varphi }_{\mathit{f}}\left(x\right)$; hence, $dt={\varphi }_{\mathit{f}}^{\prime }\left(x\right)dx.$

It follows that $a=lim{\int }_{{\varphi }_{\mathit{f}}\left(1-\epsilon \right)}^1\frac{n{t}^{n-1}\left(x\right)}{{\varphi }_{\mathit{f}}^{\prime }\left(x\left(t\right)\right)}dt=\frac{1}{{\varphi }_{\mathit{f}}^{\prime }\left(1\right)}$ according to Proposition 5 (2).

Next $b=lim{\int }_0^{\epsilon }n{\psi }_{\mathit{f}}^{n-1}\left(x\right)dx.$ Let $t={\psi }_{\mathit{f}}\left(x\right)$; hence, $dt=-{\psi }_{\mathit{f}}^{\prime }\left(x\right)dx.$ The same trick.

Finally, $c=lim{\int }_0^{\epsilon }{\int }_{1-\epsilon }^{1}n\left(n-1\right){\eta }_{\mathit{f}}^{n-2}\left(x,y\right)dydx.$ If $a=0$ or $b=0$ there is nothing to prove.

If $a>0$ and $b>0$, then $c\ge lim{\int }_0^{\epsilon }{\int }_{1-\epsilon }^{1}n\left(n-1\right){\left({\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-2}dydx$ according to Proposition 3 (2). For any $\epsilon >0$ we shall denote

$${\int }_0^{\epsilon }{\int }_{1-\epsilon }^{1}n\left(n-1\right){\left({\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-2}dydx\stackrel{not}{=}{J}_{\epsilon }\left(n\right)$$

(25)

If ${\varphi }_f\left(1\right)=1$ then let $\delta >0$ be fixed. Let $\epsilon >0$ be small enough such that the mapping ${\varphi }_{\mathit{f}}$ is increasing and differentiable on the interval $\left[1-\epsilon ,1\right]$ and $\left|{\varphi }_f^{\prime }\left(y\right)-{\varphi }_f^{\prime }\left(1\right)\right|<\delta$ for every $y\in \left[1-\epsilon ,1\right]$, the function ${\psi }_{\mathit{f}}$ is decreasing, and differentiable on the interval $\left[0,\epsilon \right]$. We shall denote

$${\int }_{1-\epsilon }^1\left(n-1\right){\left({\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-2}dy=I_{n,\epsilon }\left(x\right),n\ge 2,x\in [0,\epsilon ].$$

(26)

Let $t={\varphi }_{\mathit{f}}\left(y\right)+{\psi }_{\mathit{f}}\left(x\right)-1.$ Thus, $dt={\varphi }_{\mathit{f}}^{\prime }\left(y\right)dy$ and $I_{n,\epsilon }\left(x\right)={\int }_{{\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1}^{{\psi }_{\mathit{f}}\left(x\right)}\left(n-1\right)$$t^{n-2}\frac{dt}{{\varphi }_{\mathit{f}}^{\prime }\left(y\left(t\right)\right)}$. As $y\left(t\right)\in \left[1-\epsilon ,1\right]$ then $\left|{\varphi }_f^{\prime }\left(y\right)-{\varphi }_f^{\prime }\left(1\right)\right|<\delta$. It follows that

$$\frac{1}{{\varphi }_f^{\prime }\left(1\right)+\delta }{\int }_{{\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1}^{{\psi }_{\mathit{f}}\left(x\right)}\left(n-1\right)t^{n-2}dt\le I_{n,\epsilon }\left(x\right)\le \frac{1}{{\varphi }_f^{\prime }\left(1\right)-\delta }{\int }_{{\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1}^{{\psi }_{\mathit{f}}\left(x\right)}\left(n-1\right)t^{n-2}dt$$

or,

$\frac{{\psi }_{\mathit{f}}^{n-1}\left(x\right)-{\left({\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-1}}{{\varphi }_f^{\prime }\left(1\right)+\delta }\le I_{n,\epsilon }\left(x\right)\le \frac{{\psi }_{\mathit{f}}^{n-1}\left(x\right)-{\left({\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-1}}{{\varphi }_f^{\prime }\left(1\right)-\delta }.$

As $J_{\epsilon }\left(n\right)={\int }_0^{\epsilon }n{I}_{n,\epsilon }\left(x\right)dx$ it results that $lim{\int }_0^{\epsilon }n\frac{{\psi }_{\mathit{f}}^{n-1}\left(x\right)-{\left({\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-1}}{{\varphi }_f^{\prime }\left(1\right)+\delta }dx\le lim{J}_{\epsilon }\left(n\right)$

$\le lim{\int }_0^{\epsilon }n\frac{{\psi }_{\mathit{f}}^{n-1}\left(x\right)-{\left({\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-1}}{{\varphi }_f^{\prime }\left(1\right)-\delta }dx.$ But ${\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1<1-\epsilon ;$ thus,

$lim{\int }_0^{\epsilon }n\frac{{\left({\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-1}}{{\varphi }_f^{\prime }\left(1\right)+\delta }dx=lim{\int }_0^{\epsilon }n\frac{{\left({\varphi }_{\mathit{f}}\left(1-\epsilon \right)+{\psi }_{\mathit{f}}\left(x\right)-1\right)}^{n-1}}{{\varphi }_f^{\prime }\left(1\right)-\delta }dx=0$ and it remains that $lim{\int }_0^{\epsilon }n\frac{{\psi }_{\mathit{f}}^{n-1}\left(x\right)}{{\varphi }_f^{\prime }\left(1\right)+\delta }dx\le lim{J}_{\epsilon }\left(n\right)\le lim{\int }_0^{\epsilon }n\frac{{\psi }_{\mathit{f}}^{n-1}\left(x\right)}{{\varphi }_f^{\prime }\left(1\right)-\delta }dx.$ According to (ii), these inequalities can be written as:

$$\frac{-1}{\left({\varphi }_f^{\prime }\left(1\right)+\delta \right){\psi }^{\prime }\left(0\right)}\le lim{J}_{\epsilon }\left(n\right)\le \frac{-1}{\left({\varphi }_f^{\prime }\left(1\right)-\delta \right){\psi }^{\prime }\left(0\right)}.$$

(27)

As $\delta$ is arbitrarily small, we infer that $lim{J}_{\epsilon }\left(n\right)=\frac{-1}{{\varphi }_f^{\prime }\left(1\right){\psi }^{\prime }\left(0\right)}=ab.$

To conclude, $c\ge ab.$

(iv). An immediate consequence of the proof of (iii). □

 Remark 8. 

In the above theorem, it is important that at least one of the components of $\mathit{f}=\left(f_1,\dots ,f_d\right)$ is increasing. Otherwise, all the assertions fail to be true. Consider for example the case when $\mathit{f}:\left[0,1\right]\to {\mathbb{R}}^d$ is measurable non decreasing and $g:\left[0,1\right]\to \left[0,1\right]$ is any measurable function. If $\mathbf{Z}=\mathit{f}\left(g\left(X\right)\right)$ all the quantities $a_n,b_n,c_n$ are always equal to 1. The reason is that the image of $\mathit{f}\circ g$ is an increasing curve: if $g\left(x_1\right)\le g\left(x_2\right)$ then $\mathit{f}\left(g\left(x_1\right)\right)\le \mathit{f}\left(g\left(x_2\right)\right).$ Many similar examples could be constructed.

4. The Bidimensional Case

We study the case $\mathbf{Z}=\left(X,f\left(X\right)\right)$ with $X:\mathsf{\Omega }\to [0,1]$ as a uniformly distributed random variable and $f:[0,1]\to [0,\infty )$ a measurable function. Therefore, the function $\mathit{f}$ from the previous section is $\mathit{f}\left(x\right)=\left(x,f\left(x\right)\right)$ and $Supp\left(F_{\mathbf{Z}}\right)=Cl\left(Graph\left(f\right)\right).$

We shall consider the functions defined in relations $\left(1\right),\left(2\right),\left(3\right).$ More exactly, let

$$\begin{array}{cc}\hfill F& :[0,1]\times [0,\infty )\to [0,1],F\left(y,f\left(y\right)\right)=P\left(X\le y,f\left(X\right)\le f\left(y\right)\right)\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill F^{*}& :[0,1]\times [0,\infty )\to [0,1],F^{*}\left(x,f\left(x\right)\right)=P\left(X\ge x,f\left(X\right)\ge f\left(x\right)\right)\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill \mathsf{\Phi }& :{\left([0,1]\times [0,\infty )\right)}^2\to [0,1],\mathsf{\Phi }\left(x,f\left(x\right),y,f\left(y\right)\right)=P\left(x\le X\le y,f\left(x\right)\le f\left(X\right)\le f\left(y\right)\right)\hfill \end{array}$$

(30)

for each $x,y\in [0,1]$.

Let us denote

$$\begin{array}{cc}\hfill {\varphi }_f& :[0,1]\to [0,1],{\varphi }_f\left(y\right)=F\left(y,f\left(y\right)\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\psi }_f& :[0,1]\to [0,1],{\psi }_f\left(x\right)=F^{*}\left(x,f\left(x\right)\right)\mathrm{and}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\eta }_f& :[0,1]\times [0,1]\to [0,1],{\eta }_f\left(x,y\right)=\mathsf{\Phi }\left(x,f\left(x\right),y,f\left(y\right)\right)\hfill \end{array}$$

(33)

for each $x,y\in [0,1].$

The next result is a consequence of Proposition 1.

 Lemma 1. 

Let λ be the Lebesgue measure and the functions ${\varphi }_f,$${\psi }_f,$${\eta }_f$ defined according to (31), (32) and (33).

Then

$$\begin{array}{cc}\hfill {\varphi }_f\left(y\right)& =\lambda \left(\left[0,y\right]\cap L_y\left(f\right)\right),1-{\varphi }_f\left(y\right)=\lambda \left((y,1]\cup H_y^0\left(f\right)\right)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill {\psi }_f\left(x\right)& =\lambda \left(\left[x,1\right]\cap H_x\left(f\right)\right),1-{\psi }_f\left(x\right)=\lambda \left([0,x\right)\cup L_x^0\left(f\right))\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\eta }_f\left(x,y\right)& =\lambda \left(\left[x,y\right]\cap L_y\left(f\right)\cap H_x\left(f\right)\right),1-{\eta }_f\left(x,y\right)=\lambda \left([0,x\right)\cup L_x^0\left(f\right)\cup (y,1]\cup H_y^0\left(f\right))\hfill \end{array}$$

(36)

$\forall x,y\in [0,1],$ where the sets $L_y\left(f\right),$$L_x^0\left(f\right),$$H_x\left(f\right)$ and $H_y^0\left(f\right)$ are defined by notation $\left(10\right)$ and $\left(11\right).$

 Proof. 

As X is uniformly distributed, it follows that $P\left(X\in C\right)=\lambda \left(C\cap \left[0,1\right]\right)$ for any borel set $C.$ Therefore, ${\varphi }_f\left(y\right)=F\left(y,f\left(y\right)\right)=P\left(X\le y,f\left(X\right)\le f\left(y\right)\right)=\lambda \left(\left\{s\le y:f\left(x\right)\le f\left(y\right)\right\}\right)$$=\lambda \left(\left[0,y\right]\cap L_y\left(f\right)\right),$$\forall y\in [0,1].$ Next

$1-{\varphi }_f\left(y\right)=\lambda \left(\left[0,1\right]\setminus \left(\left[0,y\right]\cap L_y\left(f\right)\right)\right)=\lambda \left(\left[0,1\right]\setminus \left[0,y\right]\cup \left[0,1\right]\setminus L_y\left(f\right)\right)$

$=\lambda \left((y,1]\cup \left\{t\in \left[0,1\right]:f\left(t\right)>f\left(y\right)\right\}\right)=\lambda \left((y,1]\cup H_y^0\left(f\right)\right)$ proving the assertion (34).

The proof of (35) is the same.

Regarding (36),

$1-{\eta }_f\left(x,y\right)=\lambda \left(\left[0,1\right]\setminus \left(\left[x,y\right]\cap A_y\cap B_x\right)\right)=\lambda \left([0,x)\cup L_x^0\left(f\right)\cup (y,1]\cup H_y^0\left(f\right)\right)$. □

 Definition 2. 

Let $f:[0,1]\to [0,\infty )$ be a measurable function and the functions ${\phi }_f,{\psi }_f,{\eta }_f$ defined according to (31), (32), (33). We shall say that

f is L-acceptable  if $a:={\displaystyle \underset{n\to \infty }{lim}}n{\int }_0^1{\phi }_f^{n-1}\left(y\right)dy>0$

f is F-acceptable  if ${\displaystyle \underset{n\to \infty }{b:=lim}}n{\int }_0^1{\psi }_f^{n-1}\left(y\right)dy>0$

f is F, L-acceptable  if $c:={\displaystyle \underset{n\to \infty }{lim}}{\int }_0^1{\int }_x^{1}n\left(n-1\right){\eta }_f^{n-2}\left(x,y\right)dydx>0.$

In words, if $\mathbf{Z}=\left(X,f\left(X\right)\right)$ with $X\sim U\left([0,1]\right)$ then f is L-acceptable if $F,$ the distribution function of $\mathbf{Z}$, has the leader property. In addition, f is F-acceptable if F has the anti-leader property and f is F, L-acceptable if F has the order property.

Obviously, if f is L-acceptable then $sup{\phi }_f=1$ because otherwise if $sup{\phi }_f=M<1$ then $n{\int }_0^1{\phi }_f^{n-1}\left(y\right)dy<n{M}^{n-1}\to 0$. In the same way, if f is F-acceptable then $sup{\psi }_f=1$ and if f is F,L-acceptable then $sup{\eta }_f=1.$

According to Proposition 2, if f is L-acceptable then $Supp\left(F\right)=Cl\left(Graph\left(f\right)\right)$ must have a last element.

 Remark 9. Let us mention the following interesting fact:

• A function f is F,L-acceptable if and only if f is both F-acceptable and L -acceptable.
• Indeed, if f is F-acceptable then $b>0$ and if f is L-acceptable then $a>0.$
• According to Theorem 1 (3), $c\ge ab$. Therefore, if f is both F-acceptable and L-acceptable it results that $c>0$ and by definition this means that f is F,L-acceptable.

It is known (see [1]) that $a>0$ implies that $Supp\left(F\right)$ has a last element. Thus, a natural question is:

If $Supp\left(F\right)$ has a last element is it true or not that f is L-acceptable?

For general distribution functions F we know from [1] that the answer is no. However, this is a particular case and one could expect that in particular cases the answer is yes.

The answer is still no.

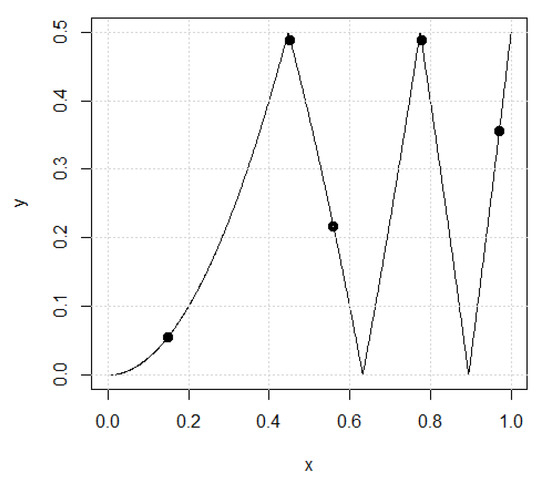
 Counterexample 1. 

Let $f:[0,1]\to [0,1],$ defined by $f\left(x\right)=min\left(1,max\left(0,\frac{3}{2}-\left|5x-\frac{3}{2}\right|\right)\right)+max\left(0,5x-4\right)$

In this case, $Supp\left(F\right)$ has $\left(1,1\right)$ as last element and $\left(0,0\right)$ as first element (see Figure 1), but f is neither F-acceptable nor L-acceptable.

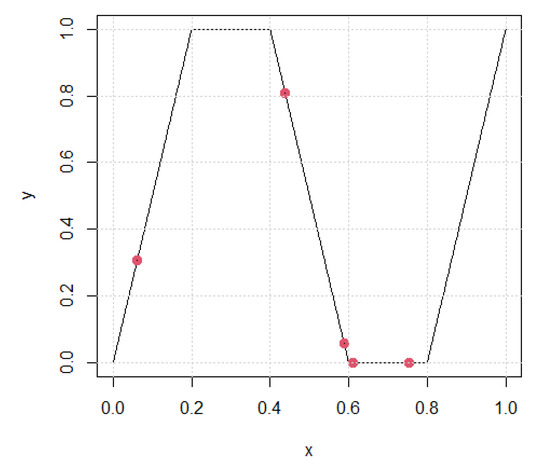
Figure 1. $Supp\left(F\right)$ has $\left(1,1\right)$ as last element and $\left(0,0\right)$ as first element, but f is not F,L-acceptable. The marked set of five points has neither first nor last element.

Indeed, writing the functions (29), (30) and (31) as ${\phi }_f\left(y\right)=\lambda \left([0,y]\cap L_y\left(f\right)\right)=$$=y{1}_{[0,\frac{2}{5}]}\left(y\right)+\left(\frac{3}{5}-y\right)1_{(\frac{2}{5},\frac{3}{5}]}\left(y\right)+\left(y-\frac{3}{5}\right)1_{[\frac{3}{5},\frac{4}{5}]}\left(y\right)+\left(3y-\frac{11}{5}\right)1_{[\frac{4}{5},1)}\left(y\right)$${\psi }_f\left(x\right)=\lambda \left([x,1]\cap H_x\left(f\right)\right)=$$=\left(\frac{4}{5}-3x\right)1_{[0,\frac{1}{5}]}\left(x\right)+\left(\frac{2}{5}-x\right)1_{[\frac{1}{5},\frac{2}{5}]}\left(x\right)+\left(x-\frac{2}{5}\right)1_{[\frac{2}{5},\frac{3}{5}]}\left(x\right)+\left(1-x\right)1_{(\frac{3}{5},1]}\left(x\right)$

It follows that

$a_n={\left(\frac{2}{5}\right)}^n+{\left(\frac{1}{5}\right)}^n+{\left(\frac{1}{5}\right)}^n+\frac{1}{3}\left({\left(\frac{4}{5}\right)}^n-{\left(\frac{1}{5}\right)}^n\right)$$b_n=\frac{1}{3}\left({\left(\frac{4}{5}\right)}^n-{\left(\frac{1}{5}\right)}^n\right)+{\left(\frac{1}{5}\right)}^n+{\left(\frac{1}{5}\right)}^n+{\left(\frac{2}{5}\right)}^n.$

Thus $a_n=b_n,$$a={\displaystyle \underset{n\to \infty }{lim}}{a}_n=0,$ $b={\displaystyle \underset{n\to \infty }{lim}}{b}_n=0,$ meaning that f is not L-acceptable neither F-acceptable. The fact that $a_n=b_n$ should be obvious due to the symmetry of the graph of f with respect to the point $C\left(\frac{1}{2},\frac{1}{2}\right).$

The probability that ${\mathbf{Z}}_1$ and ${\mathbf{Z}}_2$ are comparable is equal to $a_2=\frac{11}{25}$ and the probability that ${\mathbf{Z}}_1,{\mathbf{Z}}_2,{\mathbf{Z}}_3$ are ordered is equal to $c_3=a_3{b}_3={\left(\frac{31}{125}\right)}^2=0.0615\dots$

After all, this is not surprising because ${\displaystyle \underset{y\in (0,1)}{sup}}{\phi }_f\left(y\right)={\displaystyle \underset{y\in (0,1)}{sup}}{\psi }_f\left(y\right)=0.8<1.$

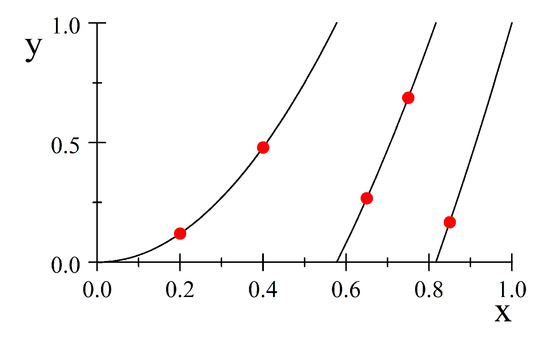
 Counterexample 2. 

We define the function f as follows:

Let $q\in \left(0,1\right),$$p=1-q,$ let the sequence ${\left({\alpha }_k\right)}_{k\ge 0}$ with ${\alpha }_k=1-q^k,\forall k\ge 0.$

Let $f:[0,1]\to [0,1]$ defined by

$f\left(y\right)=\frac{y-{\alpha }_{k-1}}{{\alpha }_k-{\alpha }_{k-1}},\forall y\in [{\alpha }_{k-1},{\alpha }_k]$ for each $k\ge 1.$

In this case, $Supp\left(F\right)$ contains the segment $\left\{1\right\}\times [0,1]$; hence, it has a last element: the point $\left(1,1\right).$ (see Figure 2)

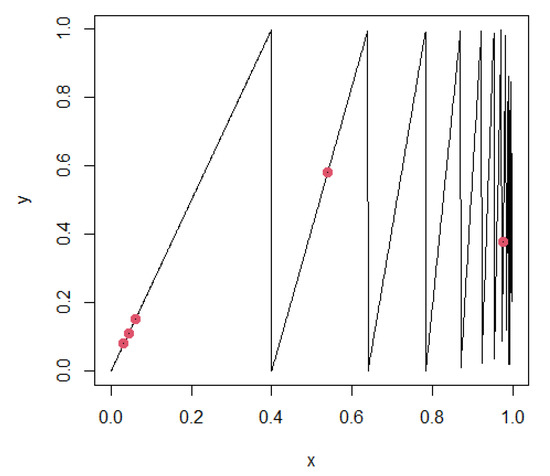
Figure 2. f is not L-acceptable. The set of marked points has a first element, but does not have a last element.

After some calculus, the value of the function ${\phi }_f$ for $y\in [{\alpha }_k,{\alpha }_k+\epsilon ],$$k\ge 0$ and $\epsilon \in \left(0,{\alpha }_{k+1}-{\alpha }_k\right)$ becomes

${\phi }_f\left(y\right)=\left(y-{\alpha }_k\right)\left(1+\frac{1}{q}+\frac{1}{q^2}+\dots +\frac{1}{q^k}\right)=\left(y-{\alpha }_k\right)\left(\frac{1-q^{k+1}}{q-q^{k+1}}\right).$ Then,

${\int }_{{\alpha }_k}^{{\alpha }_{k+1}}n{\phi }_f^{n-1}\left(y\right)dy={\int }_{{\alpha }_k}^{{\alpha }_{k+1}}n{\left(\left(y-{\alpha }_k\right)\left(\frac{1-q^{k+1}}{q-q^{k+1}}\right)\right)}^{n-1}dy={\left(\frac{1-q^{k+1}}{q-q^{k+1}}p{q}^k\right)}^{n-1}p{q}^k$.

Let us notice that $\frac{1-q^{k+1}}{q-q^{k+1}}p{q}^k<1.$ Indeed, this inequality is equivalent to

$p{q}^k-p{q}^{2k+1}<q-q^{k+1}\iff p{q}^{k-1}-p{q}^{2k}<1-q^k\iff \left(1-q\right)q^{k-1}-p{q}^{2k}<1-q^k\iff$

$q^{k-1}-p{q}^{2k}<1$, which is obvious.

Notice that ${\phi }_f\left({\alpha }_k\right)=0$ and ${\phi }_f\left({\alpha }_{k+1}-0\right)=p{q}^k\frac{1-q^{k+1}}{q-q^{k+1}}=1-q^{k+1},$$\forall k\ge 0.$ Thus

$sup{\phi }_f=1.$ It follows that

$a_n={\int }_0^{1}n{\phi }_f^{n-1}\left(y\right)dy={\displaystyle \sum _{k=0}^{\infty }}{\int }_{{\alpha }_k}^{{\alpha }_{k+1}}n{\phi }_f^{n-1}\left(y\right)dy={\displaystyle \sum _{k=0}^{\infty }}{\left(\frac{1-q^{k+1}}{q-q^{k+1}}p{q}^k\right)}^{n-1}p{q}^k.$

Moreover, the sequence of functions ${\left(g_n\right)}_n$ defined by $g_n\left(k\right)=$${\left(\frac{1-q^{k+1}}{q-q^{k+1}}p{q}^k\right)}^{n-1}$ is decreasing to 0 as $n\to \infty$. It follows that the sequence ${\left(a_n\right)}_n$ itself is decreasing and $a_1=1.$

According to the monotone convergence theorem ( Beppo Levi), $a=lim{a}_n={\displaystyle \sum _{k=0}^{\infty }}lim{g}_n\left(k\right)p{q}^k=0.$

To conclude, although $Supp\left(F\right)$ has a last element and $sup{\phi }_f=1,$f is not L-acceptable.

The following simple result gives necessary conditions for f to be L (or F or F,L)-acceptable.

 Proposition 6. 

Let $f:[0,1]\to [0,1]$ be a measurable function and ${\phi }_f,{\psi }_f,{\eta }_f:[0,1]\to [0,1]$ defined in (31)–(33).

 (a) 

If $f\left(1\right)=maxf$ and there exists an $\epsilon >0$ with the property that ${\phi }_f{\mid }_{[1-\epsilon ,1]}$ is differentiable and increasing, then $a=\frac{1}{{\phi }_f^{{}^{\prime }}\left(1\right)}.$ If ${\phi }_f^{{}^{\prime }}\left(1\right)<\infty$ then f is L-acceptable.

 (b) 

If $f\left(0\right)=minf$ and there exists an $\epsilon >0$ with the property that ${\psi }_f{\mid }_{[0,\epsilon ]}$ is differentiable and decreasing, then $b=-\frac{1}{{\psi }_f^{{}^{\prime }}\left(0\right)}.$ If ${\psi }_f^{{}^{\prime }}\left(0\right)>-\infty$ then f is F-acceptable.

 (c) 

If there exists an $\epsilon >0$ with the property $f\left(x\right)\le f\left(y\right)$$\forall x\in [0,\epsilon ],$$y\in [1-\epsilon ,1]$ then ${\eta }_f\left(x,y\right)={\phi }_f\left(y\right)+{\psi }_f\left(x\right)-1$ hence, according to Theorem 1, $c=ab.$

Proof. (a) We shall find the exact value of the limit a.

According to (22), $a={\displaystyle \underset{n\to \infty }{liminf}}{\int }_{1-\epsilon }^{1}n{\phi }_f^{n-1}\left(y\right)dy.$ Notice that ${\phi }_f\left(1\right)=1$ since, according to our hypothesis, $f\left(t\right)\le f\left(1\right)=maxf$ for all $t\in [0,1].$

Let us change the variable to $t={\phi }_f\left(y\right).$ We can write

${\displaystyle \underset{n\to \infty }{lim}}{\int }_{1-\epsilon }^{1}n{\phi }_f^{n-1}\left(y\right)dy={\displaystyle \underset{n\to \infty }{lim}}{\int }_{{\phi }_f\left(1-\epsilon \right)}^{1}n{t}^{n-1}\frac{dt}{{\phi }_f^{\prime }\left(y\left(t\right)\right)}.$ Let $g\left(t\right)=\frac{1}{{\phi }_f^{\prime }\left(y\left(t\right)\right)}.$

As $y\left(1\right)=1,$$g\left(1\right)=\frac{1}{{\phi }_f^{\prime }\left(1\right)};$ thus, according to Proposition 5 (1) $a=\frac{1}{{\phi }_f^{{}^{\prime }}\left(1\right)}.$

The proof for (b) is similar.

(c) Let $\epsilon >0$ and $x\in [0,\epsilon ],$$y\in [1-\epsilon ,1]$ be fixed.

We have ${\phi }_f\left(y\right)=\lambda \left([0,y]\cap L_y\left(f\right)\right),$${\psi }_f\left(x\right)=\lambda \left([x,1]\cap H_x\left(f\right)\right).$

Denote $A=[0,y]\cap L_y\left(f\right),$$B=[x,1]\cap H_x\left(f\right).$

Then ${\phi }_f\left(y\right)=\lambda \left(A\right),{\psi }_f\left(x\right)=\lambda \left(B\right)$ and ${\eta }_f\left(x,y\right)=\lambda \left(A\cap B\right).$ According to Proposition 3 (2), in order to check that ${\eta }_f\left(x,y\right)={\phi }_f\left(y\right)+{\psi }_f\left(x\right)-1$, it is enough to verify that $A\cup B=[0,1].$

Let $t<x.$ If we take into account that $f\left(x\right)\le f\left(y\right)$$\forall \left(x,y\right)\in [0,\epsilon ]\times [1-\epsilon ,1]$, it follows that $f\left(t\right)\le f\left(y\right)$; thus, $t\in A$ and $[0,x]\subset A.$

In the same way we obtain that $[y,1]\subset B.$

Let $x\le t\le y.$ Then either $f\left(t\right)\le f\left(y\right)$ or $f\left(t\right)\ge f\left(x\right)$ because otherwise, we have that $f\left(x\right)>f\left(t\right)>f\left(y\right)$ which is a contradiction of the hypothesis $f\left(x\right)\le f\left(y\right)$ $\forall \left(x,y\right)\in [0,\epsilon ]\times [1-\epsilon ,1].$ It follows that $A\cup B=[0,1].$ □

 Example 1. 

f is L-acceptable but is not F-acceptable.

Let $f:[0,1]\to [-1,1],$$f\left(x\right)=sin\left(\frac{5\pi x}{2}\right).$ The support of F (meaning the graph of f) has the last element $\left(1,1\right),$ but it does not have a first element since $f\left(0\right)>minf.$ Here, $b=0=c.$ Regarding $a,$ it can be calculated.

Elementary computations yield ${\varphi }_f\left(y\right)=y{1}_{[0,\frac{1}{5}]}\left(y\right)+\left(\frac{2}{5}-y\right)1_{[\frac{1}{5},\frac{2}{5}]}\left(y\right)+\left(2y-\frac{6}{5}\right)1_{[\frac{3}{5},\frac{4}{5}]}\left(y\right)$

$+\left(3y-2\right)1_{[\frac{4}{5},1]}\left(y\right).$ Thus $a_n=\frac{1}{5^n}+\frac{1}{5^n}+\frac{2^{n-1}}{5^n}+\frac{1}{3}\left(1-\frac{2^n}{5^n}\right)=\frac{1}{3}+\frac{2}{5^n}+\frac{3·2^{n-1}-2^n}{3·5^n}=$

$=\frac{1}{3}+\frac{6+2^{n-1}}{3·5^n}$ and $a=\frac{1}{3}.$ On the other hand, ${\psi }_f\left(x\right)\le \frac{3}{5}<1$ hence $b=0.$

 Example 2. 

A family of functions where all cases may occur.

Let $\alpha ,\beta >0$ and the function $f:[0,1]\to$$[0,1]$ be defined as:

$f\left(x,\alpha ,\beta \right)=\left\{\begin{array}{ccc}2{\left(2^{-\alpha }-x^{\alpha }\right)}^{1/\alpha }& if& 0\le x\le \frac{1}{2}\\ 2{\left(2^{-\beta }-{\left(1-x\right)}^{\beta }\right)}^{1/\beta }& if& \frac{1}{2}\le x\le 1\end{array}\right.$

In order to compute $a_n$, let $\epsilon >0$ be small enough.Then

${\varphi }_f\left(1-\epsilon \right)=1-\epsilon -{\left(2^{-\alpha }-{\left(2^{-\beta }-{\epsilon }^{\beta }\right)}^{\alpha /\beta }\right)}^{1/\alpha }$ and ${\varphi }_f^{\prime }\left(1\right)=1+L$ with

$$L={\displaystyle \underset{\epsilon \to 0}{lim}}\frac{{\left(2^{-\alpha }-{\left(2^{-\beta }-{\epsilon }^{\beta }\right)}^{\alpha /\beta }\right)}^{1/\alpha }}{\epsilon }$$

(37)

If we put $\epsilon =t/2,$ it follows that $L={\displaystyle \underset{t\to 0}{lim}}\frac{{\left(1-{\left(1-t^{\beta }\right)}^{\alpha /\beta }\right)}^{1/\alpha }}{t}$

Change the variable to $z={\left(1-t^{\beta }\right)}^{1/\beta }.$ Then, $L={\displaystyle \underset{z\uparrow 1}{lim}}\frac{{\left(1-z^{\alpha }\right)}^{1/\alpha }}{{\left(1-z^{\beta }\right)}^{1/\beta }}$

There are two cases:

A. $\alpha$ and $\beta$ are commensurable: $\frac{\alpha }{\beta }=\frac{m}{n},$ $m,n$ are natural numbers. Then, $\alpha =ms,\beta =ns,s>0.$ If $u=z^s,$ the limit becomes $L={\displaystyle \underset{u\uparrow 1}{lim}}\frac{{\left(1-u^m\right)}^{1/\alpha }}{{\left(1-u^n\right)}^{1/\beta }}={\displaystyle \underset{u\uparrow 1}{lim}}\frac{{\left(1-u\right)}^{1/\alpha }{\left(1+u+\dots +u^{m-1}\right)}^{1/\alpha }}{{\left(1-u\right)}^{1/\beta }{\left(1+u+\dots +u^{n-1}\right)}^{1/\beta }}={\displaystyle \underset{u\uparrow 1}{lim}}\frac{{\left(1-u\right)}^{1/\alpha -1/\beta }{m}^{1/\alpha }}{n^{1/\beta }}$

Thus, in this case, $L=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\alpha <\beta \hfill \\ 1\hfill & \mathrm{if}\alpha =\beta \hfill \\ \infty \hfill & \mathrm{if}\alpha >\beta \hfill \end{array}\right.$

B. $\alpha$ and $\beta$ are not commensurable. In that case, there exist positive integers $m,n$ such that $\beta \frac{m}{n}<\alpha <\beta \frac{m+1}{n}$

$\frac{{\left(1-z^{\beta \frac{m}{n}}\right)}^{1/\alpha }}{{\left(1-z^{\beta }\right)}^{1/\beta }}<\frac{{\left(1-z^{\alpha }\right)}^{1/\alpha }}{{\left(1-z^{\beta }\right)}^{1/\beta }}<\frac{{\left(1-z^{\beta \frac{m+1}{n}}\right)}^{1/\alpha }}{{\left(1-z^{\beta }\right)}^{1/\beta }}.$ For $z=u^{n/\beta }$ we get $\frac{{\left(1-u^m\right)}^{1/\alpha }}{{\left(1-u^n\right)}^{1/\beta }}<\frac{{\left(1-z^{\alpha }\right)}^{1/\alpha }}{{\left(1-z^{\beta }\right)}^{1/\beta }}<\frac{{\left(1-u^{m+1}\right)}^{1/\alpha }}{{\left(1-u^n\right)}^{1/\beta }}$

If $z\to 1$ then $u\to 1$ hence ${\displaystyle \underset{u\uparrow 1}{lim}}\frac{{\left(1-u^m\right)}^{1/\alpha }}{{\left(1-u^n\right)}^{1/\beta }}\le {\displaystyle \underset{z\uparrow 1}{lim}}\frac{{\left(1-z^{\alpha }\right)}^{1/\alpha }}{{\left(1-z^{\beta }\right)}^{1/\beta }}\le {\displaystyle \underset{u\uparrow 1}{lim}}\frac{{\left(1-u^{m+1}\right)}^{1/\alpha }}{{\left(1-u^n\right)}^{1/\beta }}$ and the result is the same.

To conclude, $a=lim{a}_n=\frac{1}{{\varphi }_f^{\prime }\left(1\right)}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\alpha <\beta \hfill \\ 1/2\hfill & \mathrm{if}\alpha =\beta \hfill \\ 0\hfill & \mathrm{if}\alpha >\beta \hfill \end{array}\right.$(see Figure 3)

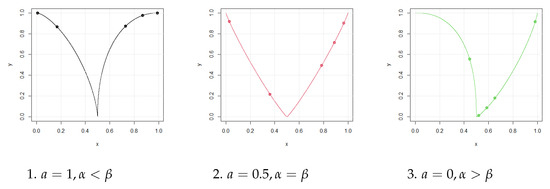
Figure 3. Example 2.

Therefore if $\alpha >\beta ,$F has no leader even if $Supp\left(F\right)$ has the last element $(1,f\left(1\right))$ and f is not L- acceptable. What is interesting is that if $\alpha <\beta$ then $a=1,$ meaning that, in the long run, the occurrence of a leader is sure.

If the function f is not increasing, but it lies in-between two increasing differentiable functions $f_1,f_2$, the following result might help.

 Theorem 2. 

Let $f:[0,1]\to [0,1]$ and $f_1,f_2:[0,1]\to [0,1]$ be increasing and derivable functions such as $f_1\le f\le f_2$.

1. If $f_1\left(1\right)=f\left(1\right)=f_2\left(1\right)$ then

$$a\ge \frac{f_2^{{}^{\prime }}\left(1\right)}{f_1^{{}^{\prime }}\left(1\right)}.$$

2. If $f_1\left(0\right)=f\left(0\right)=f_2\left(0\right)$ then

$$b\ge \frac{f_1^{{}^{\prime }}\left(0\right)}{f_2^{{}^{\prime }}\left(0\right)}.$$

 Proof. 

1. Let $y\in [0,1]$ be fixed and $x\in [0,1]$ such that $f_2\left(x\right)\le f_1\left(y\right).$ The relation $f_1\le f\le f_2$ implies that $f\left(x\right)\le f_2\left(x\right)\le f_1\left(y\right)\le f\left(y\right)$; thus, $f\left(x\right)\le f\left(y\right).$ Then $\{x\mid x\in [0,1],$$f_2\left(x\right)\le f_1\left(y\right)\}\subset \{x\mid x\in [0,1],$$f\left(x\right)\le f\left(y\right)\}\Rightarrow$

$\lambda \left([0,y]\cap \{x\mid x\in [0,1],f_2\left(x\right)\le f_1\left(y\right)\}\right)\le \lambda \left([0,y]\cap \{x\mid x\in [0,1],f\left(x\right)\le f\left(y\right)\}\right)$

However, $\lambda \left([0,y]\cap \{x\mid x\in [0,1],f\left(x\right)\le f\left(y\right)\}\right)=\lambda \left(\{x\le y\mid f\left(x\right)\le f\left(y\right)\}\right)={\phi }_f\left(y\right)$; therefore,

${\phi }_f\left(y\right)\ge \lambda \left(\{x\in [0,y]\mid f_2\left(x\right)\le f_1\left(y\right)\}\right)=\lambda \left(\{x\in [0,y]\mid x\le f_2^{-1}\left(f_1\left(y\right)\right)\}\right)=$

$=min\left(y,f_2^{-1}\left(f_1\left(y\right)\right)\right)=f_2^{-1}\left(f_1\left(y\right)\right)$ (since $f_1,f_2$ are increasing and $f_1\left(y\right)\le f_2\left(y\right)$ ) $\Rightarrow {\phi }_f\left(y\right)\ge f_2^{-1}\left(f_1\left(y\right)\right).$ It results that

$a_n={\int }_0^{1}n{\phi }_f^{n-1}\left(y\right)dy\ge {\int }_0^{1}n{\left(f_2^{-1}\left(f_1\left(y\right)\right)\right)}^{n-1}dy$ and, if we denote $t=f_2^{-1}\left(f_1\left(y\right)\right),$

$a_n\ge {\int }_0^{1}n{t}^{n-1}\frac{f_2^{{}^{\prime }}\left(f_2^{-1}\left(f_1\left(y\left(t\right)\right)\right)\right)}{f_1^{{}^{\prime }}\left(y\left(t\right)\right)}dt={\int }_0^{1}n{t}^{n-1}g\left(t\right)dt$ with $g:[0,1]\to [0,1],$$g\left(t\right)=\frac{f_2^{{}^{\prime }}\left(f_2^{-1}\left(f_1\left(y\left(t\right)\right)\right)\right)}{f_1^{{}^{\prime }}\left(y\left(t\right)\right)}.$

According to Proposition 5 (2) mentioned above, ${\int }_0^{1}n{t}^{n-1}g\left(t\right)dt=g\left(1\right)=\frac{f_2^{{}^{\prime }}\left(1\right)}{f_1^{{}^{\prime }}\left(1\right)}.$ It follows that $a\ge \frac{f_2^{{}^{\prime }}\left(1\right)}{f_1^{{}^{\prime }}\left(1\right)}.$

2. Let $x\in [0,1]$ be fixed and $t\in [0,1]$ such that $f_1\left(t\right)\ge f_2\left(x\right)$. Then $f\left(t\right)\ge f_1\left(t\right)\ge f_2\left(x\right)\ge f\left(x\right)$ and

${\psi }_f\left(x\right)\ge \lambda \left(\{t\ge x\mid f_1\left(t\right)\ge f_2\left(x\right)\}\right)=\lambda \left(\{t\ge x\mid t\ge f_1^{-1}\left(f_2\left(x\right)\right)\}\right)=$

$=1-max\left(x,f_1^{-1}\left(f_2\left(x\right)\right)\right)=1-f_1^{-1}\left(f_2\left(x\right)\right).$

It follows that

$b_n={\int }_0^{1}n{\psi }_f^{n-1}\left(x\right)dx\ge {\int }_0^{1}n{\left(1-f_1^{-1}\left(f_2\left(x\right)\right)\right)}^{n-1}dy$ and, if we denote $t=1-f_1^{-1}\left(f_2\left(x\right)\right),$

$b_n\ge {\int }_0^{1}n{t}^{n-1}\frac{f_1^{{}^{\prime }}\left(f_1^{-1}\left(f_2\left(x\left(t\right)\right)\right)\right)}{f_2^{{}^{\prime }}\left(x\left(t\right)\right)}dt={\int }_0^{1}n{t}^{n-1}h\left(t\right)dt$ with $h:[0,1]\to [0,1],$$h\left(t\right)=\frac{f_1^{{}^{\prime }}\left(f_1^{-1}\left(f_2\left(x\left(t\right)\right)\right)\right)}{f_2^{{}^{\prime }}\left(x\left(t\right)\right)}$ and

$h\left(1\right)=\frac{f_1^{{}^{\prime }}\left(f_1^{-1}\left(f_2\left(x\left(1\right)\right)\right)\right)}{f_2^{{}^{\prime }}\left(x\left(1\right)\right)}=\frac{f_1^{{}^{\prime }}\left(f_1^{-1}\left(f_2\left(0\right)\right)\right)}{f_2^{{}^{\prime }}\left(0\right)}=\frac{f_1^{{}^{\prime }}\left(f_1^{-1}\left(\left(f_1\left(0\right)\right)\right)\right)}{f_2^{{}^{\prime }}\left(0\right)}=\frac{f_1^{{}^{\prime }}\left(0\right)}{f_2^{{}^{\prime }}\left(0\right)}.$ Thus (see Proposition 5 (2)) $b\ge \frac{f_1^{{}^{\prime }}\left(0\right)}{f_2^{{}^{\prime }}\left(0\right)}.$ □

 Example 3. 

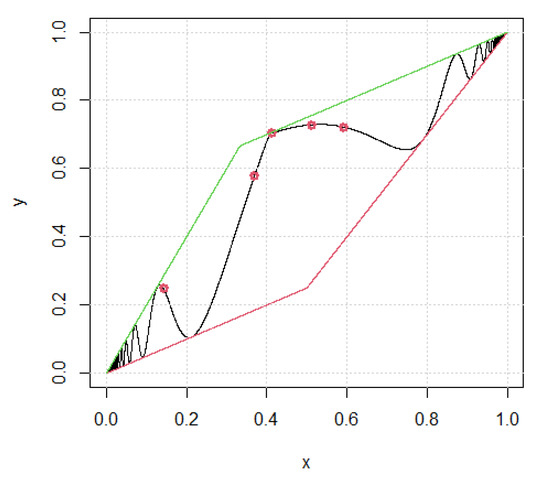
Let $f\left(x\right)=\left\{\begin{array}{ccc}\frac{x}{4}\left(3sin\frac{1}{x}+5\right)& \mathrm{if}& 0\le x\le \alpha \\ x+\frac{1-x}{2}sin\left(\frac{1}{1-x}\right)& \mathrm{if}& \alpha \le x\le 1\end{array}\right.$ where α is the solution of the equation $\frac{x}{4}\left(3sin\frac{1}{x}+5\right)-\left(x+\frac{1-x}{2}sin\left(\frac{1}{1-x}\right)\right)=0$, more exactly $\alpha \approx 0.40691.$

$f_1\left(x\right)=\left\{\begin{array}{ccc}\frac{x}{2}& if& 0\le x\le \frac{1}{2}\\ \frac{3x-1}{2}& if& \frac{1}{2}\le x\le 1\end{array}\right.$$f_2\left(x\right)=\left\{\begin{array}{ccc}2x& if& 0\le x\le \frac{1}{3}\\ \frac{x+1}{2}& if& \frac{1}{3}\le x\le 1\end{array}\right.$ (see Figure 4)

Figure 4. Example 3.

$f\left(x\right)=f_1\left(x\right)\iff \frac{x}{4}\left(3sin\frac{1}{x}+5\right)=\frac{x}{2}\Rightarrow x=\frac{2}{3\pi }\stackrel{not}{=}{\epsilon }_0$

$f\left(y\right)=f_2\left(y\right)\iff y+\frac{1-y}{2}sin\left(\frac{1}{1-y}\right)=\frac{y+1}{2}\iff sin\left(\frac{1}{1-y}\right)=1=sin\frac{\pi }{2}\iff y_k=1-\frac{1}{\frac{\pi }{2}+2k\pi }\stackrel{not}{=}{\epsilon }_1$

$\epsilon \stackrel{not}{=}min\left(\frac{2}{3\pi },1-\frac{2}{\pi }\right)=\frac{2}{3\pi }=0.21221$

${\varphi }_f\left(y\right)=y$

Then $a\ge \frac{\frac{1}{2}}{\frac{3}{2}}=\frac{1}{3}$ while $b\ge \frac{\frac{1}{2}}{2}=\frac{1}{4}.$

Next, we present a class of functions having the property F,L-acceptable.

5. Functions with the Property F, L-Acceptable: Piecewise Monotonous Functions

 Definition 3. 

The function $f:[0,1]\to \mathbb{R}$ is called piecewise monotonous if there exist $0={\alpha }_0<{\alpha }_1<\dots <{\alpha }_N=1$ such that the restrictions of f on the interval $({\alpha }_j,{\alpha }_{j+1}),$ denoted by $f_j,$ are monotonous; $0\le j\le N-1.$

We study two extreme cases.

The first one: alternate monotonicity.

All the restrictions ${\left(f_{2k+1}\right)}_{1\le k\le m}$ are non-decreasing, while all ${\left(f_{2k}\right)}_{1\le k\le m}$ are non-increasing, with $N=2m+1$ an odd number.

 Proposition 7. 

Let $f:[0,1]\to \mathbb{R}$ such that $f\left(0\right)=minf,$$f\left(1\right)=max\left(f\right)$. Suppose that there exists $0={\alpha }_0<{\alpha }_1<\dots <{\alpha }_N=1$ with $N=2m+1$ such that the functions $f_i\stackrel{not}{=}f{\mid }_{[{\alpha }_{i-1},{\alpha }_i]}$, $1\le i\le N,$ are differentiable, increasing for odd i and decreasing for even $i.$ Let $I=\{j\mid f\left({\alpha }_j\right)=f\left(1\right)\},$$I^{*}=I-\{2m+1\},$$J=\{j\mid f\left({\alpha }_j\right)=f\left(0\right)\},$ $J^{*}=J-\left\{0\right\}$ then, as long as the formulae (38)–(40) make sense,

$$\begin{array}{cc}\hfill a& =\frac{1}{1+f_N^{{}^{\prime }}\left(1\right){\displaystyle \sum _{j\in I^{*}}}\left(\frac{1}{f_j^{\prime }\left({\alpha }_j-0\right)}-\frac{1}{f_{j+1}^{\prime }\left({\alpha }_j+0\right)}\right)}\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill b& =\frac{1}{1+f_1^{\prime }\left(0\right){\displaystyle \sum _{j\in J^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left({\alpha }_j+0\right)}-\frac{1}{f_j^{\prime }\left({\alpha }_j-0\right)}\right)}\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill c& =ab\hfill \end{array}$$

(40)

 Proof. 

Let $0<\epsilon <min\left({\alpha }_1,1-{\alpha }_{2m}\right)$ and $y\in$ $\left(1-\epsilon ,1\right)$ be fixed. We want to calculate ${\varphi }_f\left(y\right)=\lambda \left(\{t\mid t\in [0,y],f\left(t\right)\le f\left(y\right)\}\right)$ and $a={\displaystyle \underset{n\to \infty }{lim}}$${\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy.$

For $k\in I$ let $y_k\in [{\alpha }_{k-1},{\alpha }_k]$ be such that $f_k\left(y_k\right)=f_N\left(y\right)$ or, equivalent, $y_k=f_k^{-1}\left(f_N\left(y\right)\right).$ Then

${\varphi }_f\left(y\right)=y-{\displaystyle \sum _{j\in I^{*}}}\left(f_{j+1}^{-1}\left(f_N\left(y\right)\right)-f_j^{-1}\left(f_N\left(y\right)\right)\right).$ For $y>1-\epsilon$ the derivative is

${\varphi }_f^{\prime }\left(y\right)=1-f_N^{{}^{\prime }}\left(y\right){\displaystyle \sum _{j\in I^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_N\left(y\right)\right)\right)}-\frac{1}{f_j^{\prime }\left(f_j^{-1}\left(f_N\left(y\right)\right)\right)}\right).$ As $N=2m+1$ is odd, $f_N$ is increasing; hence, $f_N^{{}^{\prime }}\left(y\right)\ge 0.$ Moreover, $f_j^{-1}\left(f_N\left(y\right)\right)$ lies between ${\alpha }_{j-1}$ and ${\alpha }_j$ and j is odd. As on the interval $\left({\alpha }_{j-1},{\alpha }_j\right)$ the function $f_j$ is increasing it follows that $f_j^{\prime }\left(f_j^{-1}\left(f_N\left(y\right)\right)\right)\ge 0.$

On the other hand, $f_{j+1}^{-1}\left(f_N\left(y\right)\right)$ lies between ${\alpha }_j$ and ${\alpha }_{j+1}$ and j is odd. On the interval $\left({\alpha }_j,{\alpha }_{j+1}\right)$ the function $f_j$ is decreasing hence $f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_N\left(y\right)\right)\right)\le 0.$ Therefore ${\varphi }_f^{\prime }\left(y\right)>0.$

We have $a=lim{\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy.$ Let $t={\varphi }_f\left(y\right).$ The integral becomes

${\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy={\int }_{{\varphi }_f\left(1-\epsilon \right)}^{{\varphi }_f\left(1\right)}\frac{n{t}^{n-1}}{1-f_N^{{}^{\prime }}\left(y\left(t\right)\right){\displaystyle \sum _{j\in I^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_N\left(y\left(t\right)\right)\right)\right)}-\frac{1}{f_j^{\prime }\left(f_j^{-1}\left(f_N\left(y\left(t\right)\right)\right)\right)}\right)}dt$

According to Proposition 5 (2),

${\displaystyle \underset{n\to \infty }{lim}}$${\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy=\frac{1}{1-f_N^{{}^{\prime }}\left(1\right){\displaystyle \sum _{j\in I^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_N\left(1\right)\right)\right)}-\frac{1}{f_j^{\prime }\left(f_j^{-1}\left(f_N\left(1\right)\right)\right)}\right)}.$

On the other hand ${\psi }_f\left(x\right)=\lambda \left(\{t\mid t\in [x,1],f\left(t\right)\ge f\left(x\right)\}\right)$ where $0\le x\le \epsilon$ is fixed.

We shall follow the same procedure: for $j\in J$ let $x_j\in \left({\alpha }_j,{\alpha }_{j+1}\right)$ such as $f_{j+1}\left(x_j\right)=f_1\left(x\right)$$\forall 1\le j\le 2m.$ Then

${\psi }_f\left(x\right)=1-x-{\displaystyle \sum _{j\in J^{*}}}\left(f_{j+1}^{-1}\left(f_1\left(x\right)\right)-f_j^{-1}\left(f_1\left(x\right)\right)\right)$ and the derivative is

${\psi }_f^{\prime }\left(x\right)=-1-f_1^{\prime }\left(x\right){\displaystyle \sum _{j\in J^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_1\left(x\right)\right)\right)}-\frac{1}{f_j^{\prime }\left(f_j^{-1}\left(f_1\left(x\right)\right)\right)}\right).$

With the change in variable ${\psi }_f\left(x\right)=t,$ the integral becomes

${\int }_0^{\epsilon }n{\psi }_f^{n-1}\left(x\right)dx=-{\int }_{{\psi }_f\left(\epsilon \right)}^{{\psi }_f\left(0\right)}n{t}^{n-1}\frac{1}{-1-f_1^{\prime }\left(x\right){\displaystyle \sum _{j\in J^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_1\left(x\left(t\right)\right)\right)\right)}-\frac{1}{f_j^{\prime }\left(f_j^{-1}\left(f_1\left(x\left(t\right)\right)\right)\right)}\right)}dt.$

According to Proposition 5 (2), we find that $b=lim{\int }_0^{\epsilon }n{\psi }_f^{n-1}\left(x\right)dx=\frac{1}{1+f_1^{\prime }\left(0\right){\displaystyle \sum _{j\in J^{*}}}\left(\frac{1}{f_{j+1}^{\prime }\left({\alpha }_{j+1}+0\right)}-\frac{1}{f_j^{\prime }\left({\alpha }_{j+1}+0\right)}\right)}.$

Next, in order to prove that $c=ab$ one should check that ${\eta }_f\left(x,y\right)={\varphi }_f\left(y\right)+{\psi }_f\left(x\right)-1,$ for x and $1-y$ small enough and that is true according to Proposition 6 (c). □

 Example 4. In the particular case that $f_j$ are affine, it is easy to see that $a=1-p_N$ and $b=p_1$ with $p_j={\alpha }_j-{\alpha }_{j-1}$, $1\le j\le N.$

Another example (see Figure 5): $f\left(x\right)=\left|\frac{5x^2}{2}-⌊\frac{5x^2}{2}+.5⌋\right|$. Here ${\alpha }_j=\sqrt{\frac{j}{5}},$$0\le j\le 5,$ $I=\{1,3,5\},I^{*}=\{1,3\}$$J=\{0,2,4\},J^{*}$={2,4}

Figure 5. $a=\frac{1}{1+2\left(\sqrt{5}+\sqrt{\frac{5}{3}}\right)}=0.12416,$$b=1$.

The second case: the same monotonicity.

 Proposition 8. 

Let $f:[0,1]\to \mathbb{R}$ such that $f\left(0\right)=minf,$$f\left(1\right)=max\left(f\right)$. Suppose that there exist $0={\alpha }_0<{\alpha }_1<\dots <{\alpha }_N=1$ such that the functions $f_i\stackrel{not}{=}f{\mid }_{({\alpha }_{i-1},{\alpha }_i)}$, $1\le i\le N,$ are differentiable, increasing for every $i.$ If $I=\{j\mid f\left({\alpha }_j-0\right)=f\left(1\right)\},$ $I^{*}=I-\left\{N\right\},$$J=\{j\mid f\left({\alpha }_j+0\right)=f\left(0\right)\},$$J^{*}=J-\left\{0\right\}$ then, as long as the formulae (41)–(43) make sense,

$$\begin{array}{cc}\hfill a& =\frac{1}{1+f_N^{{}^{\prime }}\left(1\right){\displaystyle \sum _{k\in I^{*}}}\frac{1}{f_k^{\prime }\left({\alpha }_k-0\right)}}\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill b& =\frac{1}{1+f_1^{\prime }\left(0\right){\displaystyle \sum _{j\in J^{*}}}\frac{1}{f_{j+1}^{\prime }\left({\alpha }_{j+1}+0\right)}}\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill c& =ab.\hfill \end{array}$$

(43)

 Proof. 

Let $0<\epsilon <min\left({\alpha }_1,1-{\alpha }_{2m}\right)$ and $y\in$ $\left(1-\epsilon ,1\right)$ be fixed.

We want to calculate ${\varphi }_f\left(y\right)=\lambda \left(\{t\mid t\in [0,y],f\left(t\right)\le f\left(y\right)\}\right).$

For $k\in I$ let $y_k\in ({\alpha }_{k-1},{\alpha }_k)$ be such that $f_k\left(y_k\right)=f_N\left(y\right)$ or, equivalent, $y_k=f_k^{-1}\left(f_N\left(y\right)\right).$ Then

${\varphi }_f\left(y\right)=y-{\displaystyle \sum _{k\in I^{*}}}\left({\alpha }_k-f_k^{-1}\left(f_N\left(y\right)\right)\right).$ For $y>1-\epsilon$ the derivative is

${\varphi }_f^{\prime }\left(y\right)=1+f_N^{{}^{\prime }}\left(y\right){\displaystyle \sum _{k\in I^{*}}}\frac{1}{f_k^{\prime }\left(f_k^{-1}\left(f_N\left(y\right)\right)\right)}.$ As $f_N$ is increasing $f_N^{{}^{\prime }}\left(y\right)\ge 0.$ Therefore, ${\varphi }_f^{\prime }\left(y\right)>0.$

We have $a=lim{\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy.$ Let $t={\varphi }_f\left(y\right).$ The integral becomes

${\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy={\int }_{{\varphi }_f\left(1-\epsilon \right)}^{{\varphi }_f\left(1\right)}\frac{n{t}^{n-1}}{1+f_N^{{}^{\prime }}\left(y\right){\displaystyle \sum _{k\in I^{*}}}\frac{1}{f_k^{\prime }\left(f_k^{-1}\left(f_N\left(y\right)\right)\right)}}dt$

In the same way as in the previous proposition

$a={\displaystyle \underset{n\to \infty }{lim}}$${\int }_{1-\epsilon }^{1}n{\varphi }_f^{n-1}\left(y\right)dy=\frac{1}{1+f_N^{{}^{\prime }}\left(1\right){\displaystyle \sum _{k\in I^{*}}}\frac{1}{f_k^{\prime }\left(f_k^{-1}\left(f_N\left(1\right)\right)\right)}}=\frac{1}{1+f_N^{{}^{\prime }}\left(1\right){\displaystyle \sum _{k\in I^{*}}}\frac{1}{f_k^{\prime }\left({\alpha }_k-0\right)}}.$

On the other hand ${\psi }_f\left(x\right)=\lambda \left(\{t\mid t\in [x,1],f\left(t\right)\ge f\left(x\right)\}\right)$ where $0\le x\le \epsilon$ is fixed.

We shall follow the same procedure: for $j\in J$ let $x_j\in \left({\alpha }_j,{\alpha }_{j+1}\right)$ such as $f_{j+1}\left(x_j\right)=f_1\left(x\right).$ Then

${\psi }_f\left(x\right)=1-x-{\displaystyle \sum _{j\in J^{*}}}\left(f_{j+1}^{-1}\left(f_1\left(x\right)\right)-{\alpha }_j\right)$ and the derivative is

${\psi }_f^{\prime }\left(x\right)=-1-f_1^{\prime }\left(x\right){\displaystyle \sum _{j\in J^{*}}}\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_1\left(x\right)\right)\right)}.$

With the change in variable ${\psi }_f\left(x\right)=t,$ the integral becomes

${\int }_0^{\epsilon }n{\psi }_f^{n-1}\left(x\right)dx=-{\int }_{{\psi }_f\left(\epsilon \right)}^{{\psi }_f\left(0\right)}n{t}^{n-1}\frac{1}{-1-f_1^{\prime }\left(x\right){\displaystyle \sum _{j\in J^{*}}}\frac{1}{f_{j+1}^{\prime }\left(f_{j+1}^{-1}\left(f_1\left(x\right)\right)\right)}}dt.$ Therefore

$b=lim{\int }_0^{\epsilon }n{\psi }_f^{n-1}\left(x\right)dx=\frac{1}{1+f_1^{\prime }\left(0\right){\displaystyle \sum _{j\in J^{*}}}\frac{1}{f_{j+1}^{\prime }\left({\alpha }_{j+1}+0\right)}}.$

The fact that $c=ab$ is motivated in the same way as in proposition 7. □

 Example 5. 

In the particular case that $f_j$ are affine, it is easy to see that $a=1-p_N$ and $b=p_1$ with $p_j={\alpha }_j-{\alpha }_{j-1}$, $1\le j\le N.$

Another example (see Figure 6): $f\left(x\right)=3x^2-\lfloor 3x^2\rfloor$.

Figure 6. $a=\frac{\sqrt{3}-1}{2}=0.36603,$$b=1$

Here ${\alpha }_j=\sqrt{\frac{j}{3}},$$0\le j\le 3,$ $I=\{1,3\},I^{*}=\left\{1\right\},$$J=\{0,2\},J^{*}$={2}.

 Remark 10. 

Actually, we do not need all the functions $f_k$ to be differentiable, or even continuous. The only functions that matter are $f_k$ for $k\in I\cup J.$

 Remark 11. 

In general, various situations may occur: some of the functions $f_k$ could be increasing, others could be decreasing. Moreover, some of them could be non-increasing or non-decreasing. In all these situations, formulae can be computed but they are very cumbersome and we decided not to consider them.

6. Conclusions and Open Problems

In the paper [1], the authors tried to characterize the d-dimensional distributions F that have the leader property. Some sufficient conditions or necessary conditions were found, but only in two cases: if F is either discrete or continuous. In the unidimensional case, any probability distribution is a mixture between a discrete and an absolutely continuous one. However, in the d-dimensional case, things are much more complicated. Here, we tried to perform a characterization of the distributions with the leader property that are quasi-unidimensional. We found necessary (Proposition 2) or sufficient conditions (Theorem 1, Theorem 2, Proposition 7, Proposition 8). As usual, many open problems appeared:

• We were not able to find examples with c different to $ab$.
• How to find a computable criterion to decide if f is L (F, F-L) acceptable. More generally, we say that $\mathit{f}=\left(f_1,\dots f_d\right)$ is L (F,F-L)-acceptable if $\mathbf{Z}=\mathit{f}\left(X\right)$ has the leader, first element, or order property.
• How to characterize the set of L-acceptable functions? A sufficient condition is that $\mathit{f}$ is continuous and $\mathit{f}\left(t_0\right)=sup\left(\mathit{f}\right)$ for some $t_0$ in $\left[0,1\right]$.

Let $\mathit{f}=\left(f_1,f_2,f_3\right):\left[0,1\right]\to$${\mathbb{R}}^3$ with $f_1,f_2,f_3$ as in the next Figure 7.

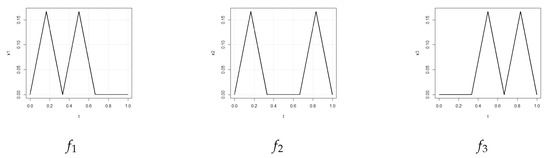
Figure 7. An example of functions $f_1,f_2,f_3$ such as the pairs $\left(f_1,f_2\right)$, $\left(f_2,f_3\right)$, $\left(f_3,f_1\right)$ have leader, but the vector $\left(f_1,f_2,f_3\right)$ has no leader.

Then the functions ${\varphi }_{1,2}$, ${\varphi }_{2,3}$, ${\varphi }_{3,1}$ are as follows (Figure 8):

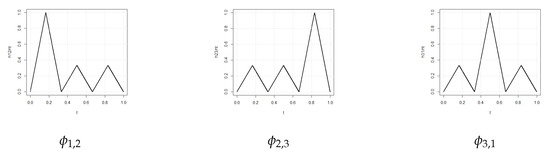
Figure 8. Comparison between pairs of functions.