Adaptive Neural Backstepping Control Approach for Tracker Design of Wheelchair Upper-Limb Exoskeleton Robot System

Abstract

In this study, the desired tracking control of the upper-limb exoskeleton robot system under model uncertainty and external disturbance is investigated. For this reason, an adaptive neural network using a backstepping control strategy is designed. The difference between the actual values of the upper-limb exoskeleton robot system and the desired values is considered as the tracking error. Afterward, the auxiliary variable based on the tracking error is defined and the virtual control input is obtained. Then, by using the backstepping control procedure and Lyapunov stability concept, the convergence of the position tracking error is proved. Moreover, for the compensation of the model uncertainty and the external disturbance that exist in the upper-limb exoskeleton robot system, an adaptive neural-network procedure is adopted. Furthermore, for the estimation of the unknown coefficient related to the parameters of the neural network, the adaptive law is designed. Finally, the simulation results are prepared for demonstration of the effectiveness of the suggested method on the upper-limb exoskeleton robot system.

1. Introduction

A wheelchair is usually used by disabled and elderly people due to its significant features, including it being easy to operate and energy efficient on flat roads. However, there exist some difficulties for wheelchair users such as the restricted driving of them on rough roads and the ability to climb stairs [1,2,3,4,5]. Thus, recent technologies have been taken into consideration and expanded on by researchers to boost the efficiency of the wheelchair system [6,7,8]. The exoskeleton system is a technical and an assistive robot which allows disabled people to experience better movement in their daily life [9,10,11,12]. The wheelchair upper-limb exoskeleton robot is one of the popular kinds of exoskeleton, which owns noteworthy features and offers many important applications. The main application of the wheelchair upper-limb exoskeleton is the assistance of the physically weak person, and so, a professional and up-to-date controller should be designed to boost the power assistance of these kinds of robots [10,13,14].

The position of each joint of the wheelchair upper-limb exoskeleton robot system is the chief parameter which needs to be controlled [15]. Then, an efficient control procedure should be designed and implemented with the aim of the position tracking control of the wheelchair upper-limb exoskeleton system [16,17,18]. Due to the existence of the nonlinear dynamics, the model’s uncertainty and the external disturbance in the dynamical model of the wheelchair upper-limb exoskeleton robot system, a Lyapunov-based control technique can be employed in the design of the controller for this system [19,20]. In [21], the tracking control of the exoskeleton robot system is investigated by using a sliding mode control scheme. In addition, at the aim of the optimal performance of this system, a genetic algorithm is used to regulate the control parameters optimally. Although, the rejection of the model’s uncertainty and the external disturbance is not examined in these articles. One of the best control schemes is the backstepping control technique which presents a systematic and recursive design procedure which can break down the complicated nonlinear systems into simple subsystems to realize the stabilization and tracking purposes [22,23]. In any physical system, the unknown dynamics such as model uncertainties, external disturbances, and unmodeled dynamics can always diminish the performance level of the system, and so, the compensator system should be designed to reject the unknown dynamics. In [24], the backstepping sliding mode control using a disturbance observer is offered for the control of the exoskeleton robot system. Additionally, the disturbance observer procedure is used to compensate for the uncertainty and external disturbance that exist in the exoskeleton robot system. In [25], the non-singular fast terminal sliding mode tracker that is based on a disturbance observer is used with the aim of tracking the control of the exoskeleton system. In [26,27], the fractional-order terminal sliding tracker for an exoskeleton robot system is proposed. However, in these studies, the adaptive neural network procedure which has a better performance when it is compared to the disturbance observer is not used for the rejection of the unknown dynamics. Therefore, one of the best methods for the rejection of the unknown dynamics is the adaptive neural network technique for the intelligent learning of unknown dynamics [28,29]. In [30], a backstepping sliding mode control tracker using the adaptive neural network approach is suggested for the exoskeleton robot system. In [31], the sliding mode control tracker via the usage of the adaptive neural network is offered for an exoskeleton robot system.

According to the above-mentioned discussion for the design of the controller for the position tacking control of the wheelchair upper-limb exoskeleton robot system, it can be concluded that this research field is still being discussed in the literature. Thus, in this paper, an adaptive neural network control strategy using backstepping control technique is presented with the aim of the position tracking control of the upper-limb exoskeleton robot system. So, the fundamental contributions of this paper can be summarized as follows:

(i).

Presentation of the dynamical model of the upper-limb exoskeleton robot system using a common model of the robot system;

(ii).

Using backstepping control strategy based on a virtual control input for the demonstration of the convergence of the position tracking error;

(iii).

Proposition of the adaptive neural network for the rejection of the model uncertainty and external disturbance;

(iv).

Adoption of the adaptation law for the estimation of the unknown constant parameter existed in the neural network process.

Now, the rest of this paper is organized as follows: In Section 2, the dynamical model of the upper-limb exoskeleton robot system is obtained. Some preliminaries are given in Section 3. The adaptive neural network using the backstepping control procedure is presented in Section 4. The simulation outcomes and some conclusions are provided in Section 5 and Section 6, respectively.

2. Model Description of Wheelchair Upper-Limb Exoskeleton System

Every wheelchair upper-limb exoskeleton robot system possesses a schematic as shown in Figure 1 and also owns two chief parts. The first part is related to upper-limb exoskeleton robot which includes three-degrees-of-freedom from joint 1 to joint 4 which are used for adduction/abduction, internal/external rotation, flexion/extension, and elbow flexion/extension functions, respectively [16].

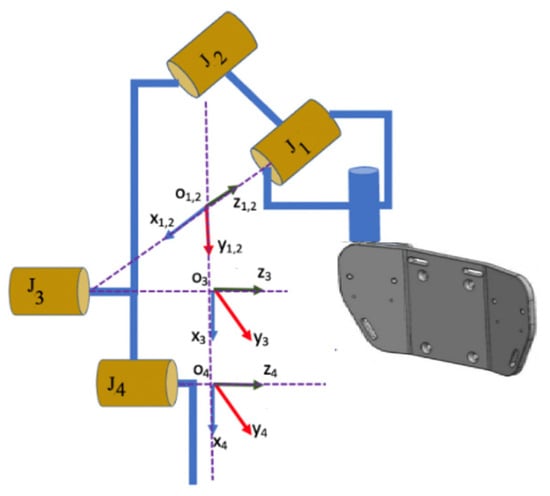
Figure 1. Review of wheelchair upper-limb exoskeleton robot system.

According to the remark mentioned in [16], for the design of the controller for the wheelchair upper-limb exoskeleton robot system, the free typical dynamical model of the robot system is considered as

$$M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+{\tau }_g=\tau$$

(1)

where $q$, $\dot{q}$, and $\ddot{q}$ are the position, velocity, and accelerations of the robot system, respectively. The expressions $M\left(q\right)$, $C\left(q,\dot{q}\right)$, and ${\tau }_g$ are the inertia, Coriolis and centrifugal forces, and gravitational forces, respectively, which are defined as

$$M\left(q\right)=\left[\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right]$$

(2)

$$C\left(q,\dot{q}\right)=\left[\begin{array}{cc}-h{\dot{q}}_2& -h\left({\dot{q}}_1-{\dot{q}}_2\right)\\ h{\dot{q}}_1& 0\end{array}\right]+\left[\begin{array}{cc}{v}_1& 0\\ 0& v_2\end{array}\right]$$

(3)

$${\tau }_g=\left[\begin{array}{cc}{F}_{c1}& 0\\ 0& F_{c2}\end{array}\right]\left[\begin{array}{c}sgn\left({\dot{q}}_1\right)\\ sgn\left({\dot{q}}_2\right)\end{array}\right]$$

(4)

with $m_{11}=a_1+2a_3\cos \left(q_2\right)-2a_4\sin \left(q_2\right)$, $m_{12}=m_{21}=a_2+a_3\cos \left(q_2\right)+a_4\sin \left(q_2\right)$, and $m_{22}=a_2$ and $h=a_3\sin \left(q_2\right)-a_4\cos \left(q_2\right)$. Furthermore, the parameter $\tau$ indicates the control input. Moreover, the constants parameters of the upper-limb exoskeleton robot system are considered as Table 1. By doing some mathematical calculations, the dynamical model (1) can be rewritten under the model uncertainty ${\mathsf{\Lambda }}_1$ and the external disturbance of ${\mathsf{\Lambda }}_2$ as

$$\ddot{q}=-M^{-1}\left(q\right)C\left(q,\dot{q}\right)\dot{q}-M^{-1}\left(q\right){\tau }_g+M^{-1}\left(q\right)\tau +{\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2$$

(5)

Table 1. Parameters of the upper-limb exoskeleton robot system.

$m_1=1 \mathrm{kg}$	$v_2=2.7 {\mathrm{kgm}}^2/\mathrm{s}$	$l_{ce}=0.25 \mathrm{m}$	$a_2=0.375 {\mathrm{kgm}}^2$
$m_e=2 \mathrm{kg}$	$I_1=0.12 {\mathrm{kgm}}^2$	$F_{c1}=F_{c2}=5 \mathrm{Nm}$	$a_3=0.433 {\mathrm{kgm}}^2$
$l_1=1 \mathrm{m}$	$I_2=0.25 {\mathrm{kgm}}^2$	$v_1=5.5 {\mathrm{kgm}}^2/\mathrm{s}$	$a_4=0.25 {\mathrm{kgm}}^2$
$l_{c1}=0.5 \mathrm{m}$	$a_1=2.745 {\mathrm{kgm}}^2$

3. Preliminaries

In this section, some assumptions and Lemmas are expressed for their usage in the design of the proposed control strategy.

Lemma 1

[32]. For any homogeneous continuous function $f(.):\left[0,+\infty \right)\to ℝ$ on $t\ge 0$, it can be said that $\underset{t\to +\infty }{\lim }f\left(t\right)=0$ if its integration $\underset{t\to +\infty }{\lim }{{\displaystyle \int }}_0^{t}f\left(\tau \right)d\tau =0$ exists and is infinite.

Lemma 2

[33]. For any $\zeta \in ℝ$ and $\eta \in {ℝ}_{+}$, the following inequality realizes

$$0\le \left|\zeta \right|-\zeta sat\left(\frac{\zeta }{\eta }\right)\le \rho \eta$$

(6)

where $sat(.)$ denotes the saturation function.

4. Main Results

The main purpose of this part is the design of the adaptive neural-based backstepping control method for the position tracking control of the upper-limb exoskeleton robot system. Hence, the tracking error is defined as

$$\begin{gathered} e_1=q-q_d \\ {e}_2=\dot{q}-{\dot{q}}_d \end{gathered}$$

(7)

where $q_d$ is the desired position. Now, the supplementary variable $s$ is defined as

$$s_i=e_i-{\alpha }_{i-1}, \forall i=1,2$$

(8)

where ${\alpha }_0=0$ and ${\alpha }_1$ is the virtual control input.

• Step 1: Taking the time-derivative of Equation (8) for $i=1$ results in

  $${\dot{s}}_1={\dot{e}}_1$$

  (9)

With a substitution from (7) into (9) and in consideration of the equation, one can find

$${\dot{s}}_1=\dot{q}-{\dot{q}}_d$$

(10)

whereas ${\dot{q}}_d=\dot{q}-e_2$, we obtain that

$${\dot{s}}_1=e_2$$

(11)

with $e_2=s_2+{\alpha }_1$, it can attain that

$${\dot{s}}_1=s_2+{\alpha }_1$$

(12)

Moreover, the virtual control input ${\alpha }_1$ is designed as

$${\alpha }_1=-k_1{s}_1$$

(13)

where $k_1>0$.

Consider the Lyapunov function $V_1=0.5s_1{}^2$. By taking the time-derivative, ${\dot{V}}_1=s_1{\dot{s}}_1$ and a substitution from Equation (12), we have

$${\dot{V}}_1=s_1\left(s_2+{\alpha }_1\right)$$

(14)

Using Equation (13), it can gain

$${\dot{V}}_1\le -k_1{s}_1{}^2+s_1{s}_2$$

(15)

• Step 2: Taking the time-derivative of Equation (8) for $i=2$ results in

  $${\dot{s}}_2={\dot{e}}_2-{\dot{\alpha }}_1$$

  (16)

With a substitution from (7) to (5), one can obtain

$${\dot{s}}_2=-M^{-1}\left(q\right)C\left(q,\dot{q}\right)\dot{q}-M^{-1}\left(q\right){\tau }_g+M^{-1}\left(q\right)\tau +{\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2-{\ddot{q}}_d-{\dot{\alpha }}_1$$

(17)

Because the terms ${\mathsf{\Lambda }}_1$ and ${\mathsf{\Lambda }}_2$ are unknown, the adaptive neural network technique is used to estimate them. Hence, the adaptive neural network law is adopted as

$${\mathsf{\Lambda }}_1={\theta }_1^T{\Phi }_1\left(X\right)+{ℰ}_1$$

(18)

$${\mathsf{\Lambda }}_2={\theta }_2^T{\Phi }_2\left(X\right)+{ℰ}_2$$

(19)

where ${\theta }_1=\left[{\theta }_{11 } {\theta }_{12 }\right]\in R^{m\times 2}$ and ${\theta }_2=\left[{\theta }_{21 } {\theta }_{22 }\right]\in R^{m\times 2}$ denote the ideal weight matrices such that ${\theta }_{1i },{\theta }_{2i }\in R^m, \forall i=1,2$ are the ideal weight vectors related to the neural network estimate for $i^{th}$ element of ${\mathsf{\Lambda }}_1$ and ${\mathsf{\Lambda }}_2$, respectively. ${\Phi }_1\left(X\right)={\left[{\mathsf{\Phi }}_{11 }\left(X\right),\dots , {\mathsf{\Phi }}_{1m }\left(X\right)\right]}^T\in R^m$ and ${\Phi }_2\left(X\right)={\left[{\mathsf{\Phi }}_{21 }\left(X\right),\dots , {\mathsf{\Phi }}_{2m }\left(X\right)\right]}^T\in R^m$ indicate the corresponding basic function vectors, $X={\left[x_{1 } x_{2 }\right]}^T\in R^4$ signifies neural network input and ${\epsilon }_1={\left[{\epsilon }_{11 } {\epsilon }_{12 }\right]}^T\in R^2$ and ${\epsilon }_2={\left[{\epsilon }_{21 } {\epsilon }_{22 }\right]}^T\in R^2$ are the estimation error vectors and their upper boundary are ${ϵ}_1={\left[{ϵ}_{11 } {ϵ}_{12 }\right]}^T$ and ${ϵ}_2={\left[{ϵ}_{21 } {ϵ}_{22 }\right]}^T.$ We define

$$\{\begin{array}{c}{\widehat{\theta }}_{1i}={\left[{\theta }_{1i }{}^T {ϵ}_{1i }\right]}^T\in R^{m+1} \& {\widehat{\theta }}_{2i}={\left[{\theta }_{2i }{}^T {ϵ}_{2i }\right]}^T\in R^{m+1}\\ {\overline{\theta }}_1=\left[{\overline{\theta }}_{11 } {\overline{\theta }}_{12 }\right]\in R^{\left(m+1\right)\times 2} \& {\overline{\theta }}_2=\left[{\overline{\theta }}_{21 } {\overline{\theta }}_{22 }\right]\in R^{\left(m+1\right)\times 2}\\ \Phi ={\left[{\Phi }_1{}^T 1\right]}^T\in R^{m+1}\& \Phi ={\left[{\Phi }_2{}^T 1\right]}^T\in R^{m+1}\end{array}$$

(20)

with

$$\left|{\mathsf{\Lambda }}_1\right|=\left|{\theta }_1^T{\Phi }_1\left(X\right)+{ℰ}_1\right|\le \left|{\theta }_1^T{\Phi }_1\left(X\right)\right|\le \left|{\theta }_1^T\right|\left|{\Phi }_1\left(X\right)\right|\le {\nu }_1\sqrt{m+1}$$

(21)

$$\left|{\mathsf{\Lambda }}_2\right|=\left|{\theta }_2^T{\Phi }_2\left(X\right)+{ℰ}_2\right|\le \left|{\theta }_2^T{\Phi }_2\left(X\right)\right|\le \left|{\theta }_2^T\right|\left|{\Phi }_2\left(X\right)\right|\le {\nu }_2\sqrt{m+1}$$

(22)

where ${\nu }_1$ and ${\nu }_2$ are the unknown maximum eigenvalues of matrix ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$, respectively, which are estimated by adaptive law as

$${\dot{\hat{\nu }}}_1={\lambda }_1\sqrt{m+1}{s}_{2}sat\left(\frac{s_2}{\eta }\right)-{\lambda }_1\eta {\hat{\nu }}_1$$

(23)

$${\dot{\hat{\nu }}}_2={\lambda }_2\sqrt{m+1}{s}_{2}sat\left(\frac{s_2}{\eta }\right)-{\lambda }_2\eta {\hat{\nu }}_2$$

(24)

where ${\lambda }_1, {\lambda }_2>0$.

When we consider the Lyapunov function as

$$V_2=V_1+0.5s_2{}^2+0.5{\lambda }_1{}^{-1}{\tilde{v}}_1{}^2+0.5{\lambda }_2{}^{-1}{\tilde{v}}_2{}^2$$

(25)

With taking time-derivative from above Lyapunov function, we have

$${\dot{V}}_2={\dot{V}}_1+s_2{\dot{s}}_2+{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}$$

(26)

With substitution of Equation (15) in the above equation, it can gain

$${\dot{V}}_2\le -k_1{s}_1{}^2+s_1{s}_2+s_2{\dot{s}}_2+{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}$$

(27)

Now, the expression is substituted in above equation which results in

$${\dot{V}}_2\le -k_1{s}_1{}^2+s_1{s}_2+s_2\left\{-M^{-1}\left(q\right)C\left(q,\dot{q}\right)\dot{q}-M^{-1}\left(q\right){\tau }_g+M^{-1}\left(q\right)\tau +{\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2-{\ddot{q}}_d-{\dot{\alpha }}_1\right\}+{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}$$

(28)

The control input is designed as

$$\begin{gathered} \tau =M\left(M^{-1}\left(q\right)C\left(q,\dot{q}\right)\dot{q}+M^{-1}\left(q\right){\tau }_g+{\ddot{q}}_d+{\dot{\alpha }}_1-s_1-k_2{s}_2 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\hat{\nu }}_1\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)-{\hat{\nu }}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)\right) \end{gathered}$$

(29)

With substitution of the control input $\tau$ in (28), we have

$${\dot{V}}_2\le -k_1{s}_1{}^2-k_2{s}_2{}^2+s_2\left\{-{\hat{\nu }}_1\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)-{\hat{\nu }}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)\right\}+\left|s_2\right|\left|{\mathsf{\Lambda }}_1\right|+\left|s_2\right|\left|{\mathsf{\Lambda }}_2\right|+{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}$$

(30)

From Equations (21) and (22), we can observe that

$$\begin{gathered} {\dot{V}}_2\le -k_1{s}_1{}^2-k_2{s}_2{}^2+s_2\left\{-{\hat{\nu }}_1\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)-{\hat{\nu }}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)\right\}+\left|s_2\right|{\nu }_1\sqrt{m+1}+\left|s_2\right|{\nu }_2\sqrt{m+1} \\ +{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

(31)

Based on Lemma 2 $\left(\left|s_2\right|\le s_{2}sat\left(\frac{s_2}{\eta }\right)+\rho \eta \right)$, we have

$$\begin{gathered} {\dot{V}}_2\le -k_1{s}_1{}^2-k_2{s}_2{}^2+s_2\left\{-{\hat{\nu }}_1\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)-{\hat{\nu }}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)\right\}+\left[s_{2}sat\left(\frac{s_2}{\eta }\right)+2\rho \eta \right]{\nu }_1\sqrt{m+1} \\ +\left[s_{2}sat\left(\frac{s_2}{\eta }\right)+2\rho \eta \right]{\nu }_2\sqrt{m+1}+{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

(32)

By adding and subtracting of the terms of $s_{2}sat\left(\frac{s_2}{\eta }\right){\hat{\nu }}_1\sqrt{m+1}$ and $s_{2}sat\left(\frac{s_2}{\eta }\right){\hat{\nu }}_2\sqrt{m+1}$, one can find

$$\begin{gathered} {\dot{V}}_2\le -k_1{s}_1^2-k_2{s}_2^2+s_2\left\{-{\hat{\nu }}_1\sqrt{m+1}\mathit{sat}\left(\frac{s_2}{\eta }\right)-{\hat{\nu }}_2\sqrt{m+1}\mathit{sat}\left(\frac{s_2}{\eta }\right)\right\}+\left[s_2\mathit{sat}\left(\frac{s_2}{\eta }\right)+2\rho \eta \right]{\nu }_1\sqrt{m+1} \\ \hspace{1em}\hspace{1em}\hspace{1em}+\left[s_2\mathit{sat}\left(\frac{s_2}{\eta }\right)+2\rho \eta \right]v_2\sqrt{m+1}+{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}+s_2\mathit{sat}\left(\frac{s_2}{\eta }\right){\hat{\nu }}_1\sqrt{m+1} \\ -s_2\mathit{sat}\left(\frac{s_2}{\eta }\right){\hat{\nu }}_1\sqrt{m+1}+s_2\mathit{sat}\left(\frac{s_2}{\eta }\right){\hat{\nu }}_2\sqrt{m+1}-s_2\mathit{sat}\left(\frac{s_2}{\eta }\right){\hat{\nu }}_2\sqrt{m+1} \end{gathered}$$

(33)

With consideration of ${\tilde{v}}_1$ = ${\hat{\nu }}_1-v_1$ and ${\tilde{v}}_2$=${\hat{\nu }}_2-v_2$, we can obtain

$$\begin{gathered} {\dot{V}}_2\le -k_2{s}_2{}^2-k_1{s}_1{}^2-s_2{\tilde{v}}_1\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)+2\rho \eta {\nu }_1\sqrt{m+1}-s_2{\tilde{v}}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)+2\rho \eta {\nu }_2\sqrt{m+1} \\ +{\lambda }_1{}^{-1}{\tilde{v}}_1\dot{{\tilde{v}}_1}+{\lambda }_2{}^{-1}{\tilde{v}}_2\dot{{\tilde{v}}_2}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

(34)

Now, the adaptation laws (23) and (24) are substituted in above equation and the following result is obtained:

$$\begin{gathered} {\dot{V}}_2\le -k_2{s}_2{}^2-k_1{s}_1{}^2-s_2{\tilde{v}}_1\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)+2\rho \eta {\nu }_1\sqrt{m+1}-s_2{\tilde{v}}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta }\right)+2\rho \eta {\nu }_2\sqrt{m+1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\lambda }_1{}^{-1}{\tilde{v}}_1\left\{{\lambda }_1\sqrt{m+1}{s}_{2}sat\left(\frac{s_2}{\eta }\right)-{\lambda }_1\eta {\hat{\nu }}_1\right\}+{\lambda }_2{}^{-1}{\tilde{v}}_2\left\{{\lambda }_2\sqrt{m+1}{s}_{2}sat\left(\frac{s_2}{\eta }\right)-{\lambda }_2\eta {\hat{\nu }}_2\right\} \end{gathered}$$

(35)

After doing some simplification, we have

$${\dot{V}}_2\le -k_1{s}_1{}^2-k_2{s}_2{}^2-\eta \left({\tilde{v}}_1{\hat{\nu }}_1+{\tilde{v}}_2{\hat{\nu }}_2\right)+2\rho \eta \sqrt{m+1}\left({\nu }_1+{\nu }_2\right)$$

(36)

Theorem 1.

Consider the upper-limb exoskeleton robot system (5)with uncertainty and external disturbance. Based on the virtual control input (13) and control input (29) and parameter adaptation laws (23) and (24). Then, all of the signals in the closed-loop system are globally bounded, and furthermore, the tracking errors $e_1$and$e_2$converge to zero.

Proof. 

Considering the Young’s inequality as $-\tilde{x}\widehat{x}=-\tilde{x}\left(\tilde{x}+x\right)\le -0.5{\tilde{x}}^2+0.5x^2\le 0.5x^2$, we have

$${\tilde{v}}_1{\hat{\nu }}_1\le 0.5{\nu }_1{}^2$$

(37)

$${\tilde{v}}_2{\hat{\nu }}_2\le 0.5{\nu }_2{}^2$$

(38)

Hence, Equation (36) is converted to

$$\begin{gathered} {\dot{V}}_2\le -k_1{s}_1{}^2-k_2{s}_2{}^2+\eta \left[0.5\left({\nu }_1{}^2+{\nu }_2{}^2\right)+2\rho \eta \sqrt{m+1}\left({\nu }_1+{\nu }_2\right)\right] \\ {\dot{V}}_2\le -k_1{s}_1{}^2-k_2{s}_2{}^2+\eta \mathsf{\Theta } \end{gathered}$$

(39)

where $\mathsf{\Theta }=\left[0.5\left({\nu }_1{}^2+{\nu }_2{}^2\right)+2\rho \eta \sqrt{m+1}\left({\nu }_1+{\nu }_2\right)\right]$. By taking integrator from both side of Equation (39), we have

$$\begin{gathered} V_2\left(t\right)\le V_2\left(0\right)-{{\displaystyle \int }}_0^t{\displaystyle \sum }_{i=1}^2{k}_i{s}_i{}^2\left(\tau \right)d\tau +\eta \mathsf{\Theta }\le V_2\left(0\right)+\eta \mathsf{\Theta } \\ {{\displaystyle \int }}_0^t{\displaystyle \sum }_{i=1}^2{k}_i{s}_i{}^2\left(\tau \right)d\tau \le V_2\left(0\right)-V_2\left(t\right)+\eta \mathsf{\Theta }\le V_2\left(0\right)+\eta \mathsf{\Theta } \end{gathered}$$

(40)

It means that $s_i$ and ${\nu }_i, \forall i=1,2$ are bounded and based on the Barbalat Lemma $\underset{t\to +\infty }{\lim }{s}_1=0$, so, $e_1=q-q_d=0$, hence, $q=q_d$. Therefore, the position tracking control is realized. □

Remark 1.

As it is obvious, thediscontinuous function $sign\left(s_i\left(t\right)\right)$results in the chattering phenomenon of the control inputs. Due to this reason, $sign\left(s_i\left(t\right)\right)$can be replaced by $tanh\left(\frac{s_i}{{\Im }_i}\right)$, where ${\Im }_i$is the boundary layer thickness coefficient [34]. Thus, the control inputs can be rewritten as follows:

$$\begin{gathered} \tau =M\left(M^{-1}\left(q\right)C\left(q,\dot{q}\right)\dot{q}+M^{-1}\left(q\right){\tau }_g+{\ddot{q}}_d+{\dot{\alpha }}_1-s_1-k_2{s}_2 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\hat{\nu }}_1\sqrt{m+1}tanh\left(\frac{s_2}{\eta {\Im }_2}\right)-{\widehat{\nu }}_2\sqrt{m+1}sat\left(\frac{s_2}{\eta {\Im }_2}\right)\right) \end{gathered}$$

(41)

5. Main Results

In this section, in order to investigate the proficiency of the adaptive neural-network mixed with the backstepping control strategy for desired tracking control of the upper limb exoskeleton robot system in the existence of model uncertainty and external disturbance, the simulation results have been obtained in two different scenarios with different desired values, various model uncertainties, and external disturbances. In each scenario, the simulation results were implemented using various initial conditions. All of the simulation results are modeled in the MATLAB (Simulink environment) software. Additionally, the desired values, control parameter, model uncertainty, external disturbance, and different initial conditions for each scenario are given in Table 2, Table 3, Table 4 and Table 5, respectively.

Table 2. Desired values.

Scenario 1	$q_d={\left[\pi \left(sin\left(t\right)-cos\left(t\right)\right),\pi \left(sin\left(t\right)-cos\left(t\right)\right)\right]}^T$
Scenario 2	$q_d={\left[\frac{\pi }{2}\left(\sin \left(t\right)-cos\left(t\right)\right),\frac{\pi }{2}\left(\sin \left(t\right)-cos\left(t\right)\right)\right]}^T$

Table 3. Design parameters.

$k_1=k_2=10$

${\lambda }_1={\lambda }_2=1$

$m=20$

$\eta ={\left(1+t^2\right)}^{-1}$

Table 4. Model uncertainty and external disturbance.

Scenario $1$	${\mathsf{\Lambda }}_1={\left[0.1\ast e^{-t},0.1\ast e^{-t}\right]}^T$ ${\mathsf{\Lambda }}_2={\left[0.1\ast sin\left(t\right),0.1\ast sin\left(t\right)\right]}^T$
Scenario $2$	${\mathsf{\Lambda }}_1={\left[1+e^{-2t},1+e^{-2t}\right]}^T$ ${\mathsf{\Lambda }}_2={\left[0.5\ast sin\left(2\ast t\right),0.5\ast sin\left(2\ast t\right)\right]}^T$

Table 5. Considered initial conditions.

Number	Initial Condition
1	$q\left(0\right)={\left[0.3,0.3\right]}^T$
2	$q\left(0\right)={\left[0.6,0.6\right]}^T$
3	$q\left(0\right)={\left[0.9,0.9\right]}^T$

As it can be observed, the simulation results based on the Scenarios 1 and 2 are provided in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. The desired tracking of the upper-limb exoskeleton robot system based on Scenario 1 and Scenario 2 is depicted in Figure 2 and Figure 8. As one can observe, the upper limb exoskeleton robot system tracks as desired, completely. The trajectories of the tracking error based on Scenario 1 and Scenario 2 are illustrated in Figure 3 and Figure 9, respectively. From these figures, we can observe the that desired tracking has been performed accurately. Moreover, the sliding surfaces based on Scenario 1 and Scenario 2 are displayed in Figure 4 and Figure 10, respectively, and it is obvious that the sliding surfaces converge to zero eventually. From the figures related to the desired tracking, tracking error, and sliding surface, it can be found that under different initial conditions, the proposed control method is robust and offers an acceptable performance. Additionally, the control inputs, which are obtained based on Scenarios 1 and 2, are shown in Figure 5 and Figure 11, respectively. Lastly, the adaptation laws based on the neural network are displayed in Figure 6, Figure 7, Figure 12 and Figure 13. As one can observe, the approximation of the upper bounds of the model uncertainty and external disturbance are accomplished appropriately. Therefore, from the simulation results, we can observe that the designed method proposes a robust and productive performance under different initial conditions, a diverse model uncertainty and external disturbance, and various desired values.

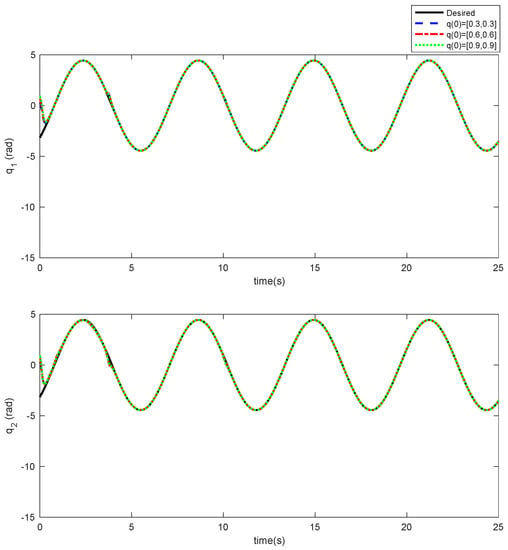
Figure 2. Desired tracking based on Scenario 1.

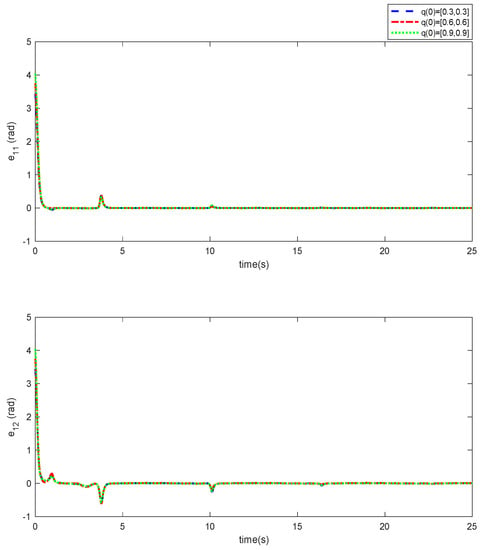
Figure 3. Trajectory of the tracking error based on Scenario 1.

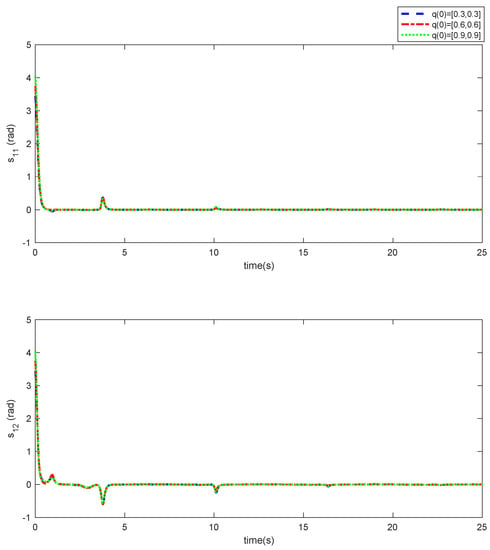
Figure 4. Sliding surface in Scenario 1.

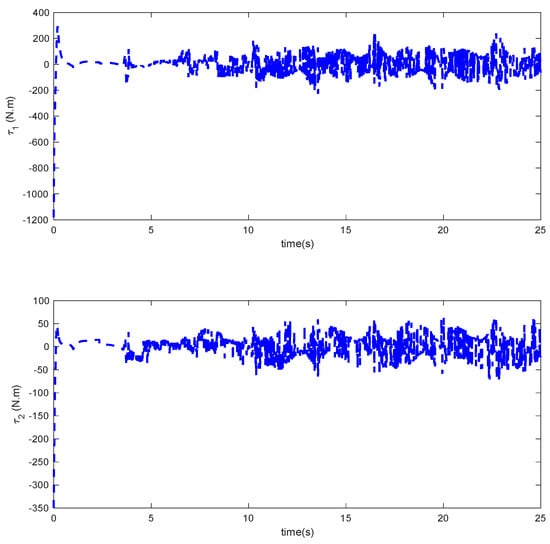
Figure 5. Control input in Scenario 1.

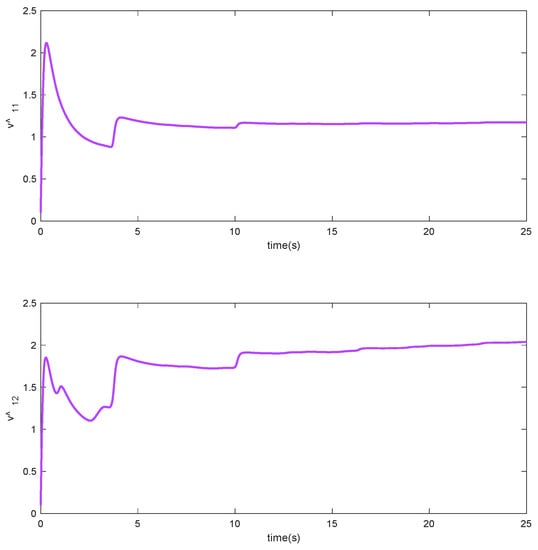
Figure 6. Adaptation laws ${\hat{\nu }}_{11}$, ${\hat{\nu }}_{12}$ in Scenario 1.

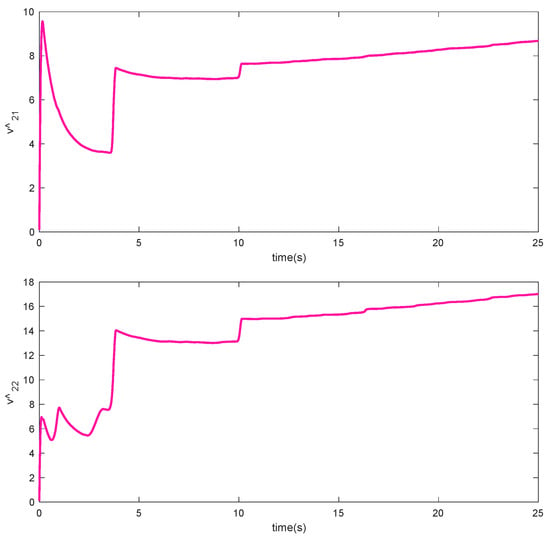
Figure 7. Adaptation laws ${\hat{\nu }}_{21}$, ${\hat{\nu }}_{22}$ in Scenario 1.

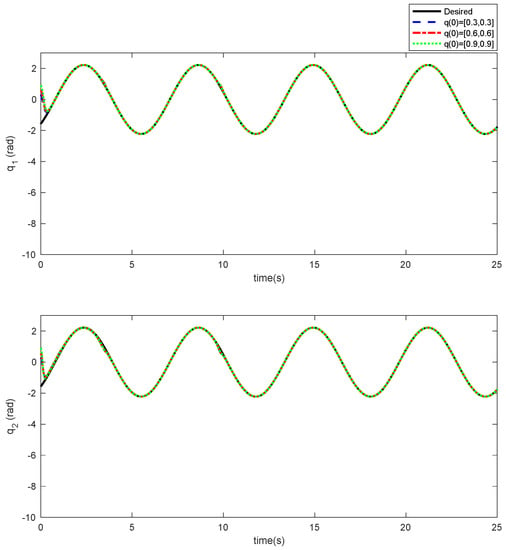
Figure 8. Desired tracking based on Scenario 2.

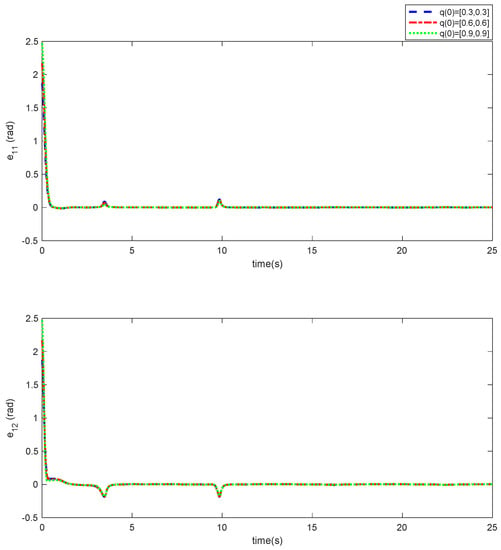
Figure 9. Trajectory of the tracking error based on Scenario 2.

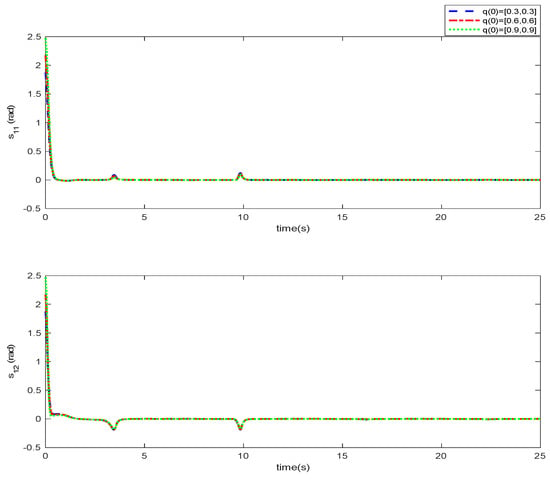
Figure 10. Sliding surface in Scenario 2.

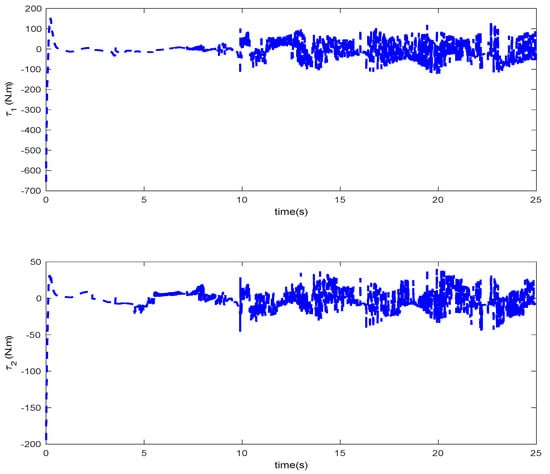
Figure 11. Control input in Scenario 2.

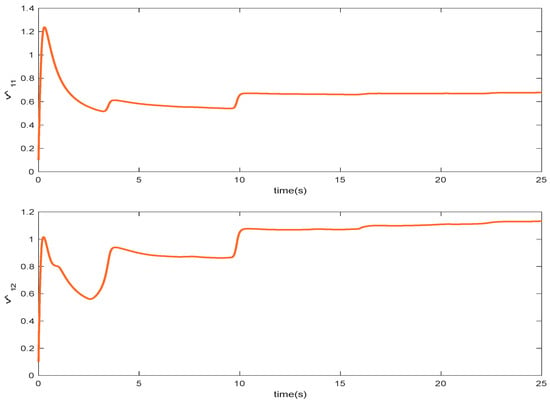
Figure 12. CAdaptation laws ${\hat{\nu }}_{11}$, ${\hat{\nu }}_{12}$ in Scenario 2.

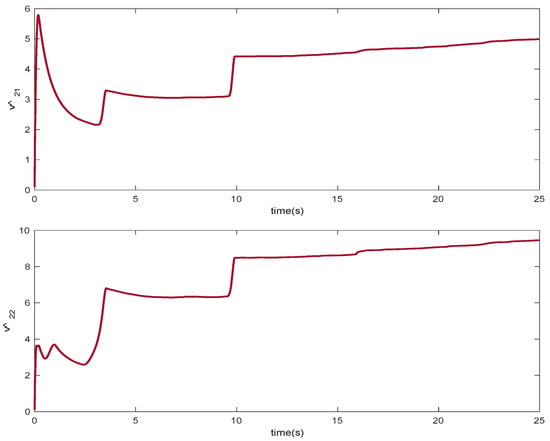
Figure 13. Adaptation laws ${\hat{\nu }}_{21}$, ${\hat{\nu }}_{22}$ in Scenario 2.

6. Conclusions

In this paper, the position tracking control of the upper-limb exoskeleton robot system in the appearance of the model’s uncertainty and external disturbance has been examined. Due to this reason, one control method based on the adaptive neural network using the backstepping control technique has been developed. Hence, using the backstepping control approach accompanied by the Lyapunov stability theory, the convergence of the position tracking error has been demonstrated. Afterward, the compensation of the model’s uncertainty and external disturbance has been accomplished using the adaptive neural network method. Due to the existence of some uncertainties related to the parameters of the neural network, the adaptation law has been used for the approximation of these uncertainties at any moment. Lastly, the simulation results have been prepared to show that the recommended method is applicable and useful over the upper-limb exoskeleton robot system. Moreover, the development of the adaptive neural network procedure for the upper-limb exoskeleton robot system under the input saturation condition and providing some experimental results are considered to be our future research work.