On the Global Behaviour of Solutions for a Delayed Viscoelastic-Type Petrovesky Wave Equation with p-Laplacian Operator and Logarithmic Source

Abstract

This research is concerned with a nonlinear p-Laplacian-type wave equation with a strong damping and logarithmic source term under the null Dirichlet boundary condition. We establish the global existence of the solutions by using the potential well method. Moreover, we prove the stability of the solutions by the Nakao technique. An example with illustrative figures is provided as an application.

1. Introduction

Many dynamical systems in physics and engineering have been designed and proposed by means of semilinear hyperbolic equations. For instance, logarithmic nonlinearity has received a great deal of attention from many scientists and researchers, and it has introduced many issues, including the wave equation. This type of nonlinearity appears naturally in supersymmetric field theory and inflation cosmology and has numerous applications in many branches of physics, such as nuclear physics, optics and geophysics [1,2,3]. In the past decades, many authors have studied the well-posedness, regularity and blow-up of the solution for wave equations in a bounded domain of ${\mathbb{R}}^n$. For example, Sattinger in [4] treated the following semilinear wave equation with polynomial nonlinearity

$$\ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})=\varrho \left(\varkappa \right),\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,$$

(1)

and showed, by introducing the concept of the potential well, the existence of the local as well as the global solutions for Equation (1). Messaoudi, in [5], proved that the obtained solution of the problem

$$\ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})+{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\zeta )\Delta \varkappa (\mathrm{y},\zeta )\mathrm{d}\zeta +a\varkappa (\mathrm{y},\mathfrak{s})|\dot{\varkappa }{|}^{m-2}=b\varkappa (\mathrm{y},\mathfrak{s}){|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2},$$

for $\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0$, where p is a real number, in a bounded domain $\mathrm{\Omega }$ with initial and boundary conditions of the Dirichlet type, blow-up in a finite time if $p>m(m\in \mathbb{N})$ and the initial energy is sufficiently negative. Filippo Gazzola and Marco Squassina, in [6], established a blow-up result with an arbitrarily high initial energy for the semilinear Cauchy problem

$$\ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})-w\Delta \dot{\varkappa }+\mu \dot{\varkappa }=b\varkappa (\mathrm{y},\mathfrak{s}){|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2},\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,$$

where $p\in \mathbb{R}$, in an open bounded Lipschitz subset $\mathrm{\Omega }$ of ${\mathbb{R}}^n$, provided that $w=0$ and $\mu \ge 0$. This result was later extended by Wang in [7] to the whole space ${\mathbb{R}}^n$ for the nonlinear Klein–Gordon equation with polynomial nonlinearity of the form

$$\ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})+m^2\varkappa (\mathrm{y},\mathfrak{s})=\varrho \left(\varkappa \right),\mathrm{y}\in {\mathbb{R}}^n,\mathfrak{s}>0,$$

where $m\in \mathbb{N}$. On the other hand, for the p-Laplacian wave equations, the authors in [8] gave, by the multiplier method, the energy decay of the solution of the following problem

$$\ddot{\varkappa }-{\Delta }_p\varkappa (\mathrm{y},\mathfrak{s})-\Delta \dot{\varkappa }+\dot{\varkappa }|\dot{\varkappa }{|}^{q-2}=\varkappa (\mathrm{y},\mathfrak{s}){|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2},\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,$$

(2)

where $p,q\in \mathbb{R}$. Later, in [9], the authors proved an exponential and polynomial decay rate of the solutions by using the inequality of Nakao for the Problem (2). In the case of logarithmic nonlinearity, Ma et al. [10] studied the following problem

$$\ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})-\Delta \dot{\varkappa }=\varkappa (\mathrm{y},\mathfrak{s})ln{|\varkappa (\mathrm{y},\mathfrak{s})|}^2,\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,$$

and proved that the blow-up of the solution occurs in infinite time. In addition, the existence of global solutions was shown by the use of a family of potential wells which includes the single potential well W as a particular case together with the perturbation energy technique. Di et al. [11] considered the strongly damped nonlinear wave equation

$$\ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})-\Delta \dot{\varkappa }={\varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|,\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,$$

(3)

where $p\in \mathbb{R}$. They discussed the uniqueness, global existence, energy decay estimates and finite time blow-up phenomena to Problem (3) by modifying the potential well method. Tae Gab Ha et al. [12] introduced the following equation

$$\begin{array}{cc}\hfill \ddot{\varkappa }-\Delta \varkappa (\mathrm{y},\mathfrak{s})& +{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\zeta )\Delta \varkappa (\mathrm{y},\zeta )\mathrm{d}\zeta -\Delta \dot{\varkappa }={\varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|,\hfill \end{array}$$

(4)

for $\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0$ where $p\in \mathbb{R}$. The existence, uniqueness and regularities of the weak solution to the Problem (4) are proved for all $\varkappa (0,\mathfrak{s})\in H_0^1\left(\mathrm{\Omega }\right)$ and $\dot{\varkappa }{|}_{(0,\mathfrak{s})}\in L^2\left(\mathrm{\Omega }\right)$ by applying the Faedo–Galerkin method and the contraction mapping principle. A finite time blow-up property of the solutions was also derived at three different energy levels, $E\left(0\right)=0$, $E\left(0\right)<0$ and $0<E\left(0\right)<d$. This result was later pursued by Liao [13] for certain solutions with a high initial energy. Meanwhile, explicit upper and lower bound estimates to the blow-up time have been proved. Inspired by the above studies, in this work, we investigate the global behaviour of solutions for a delayed viscoelastic-type Petrovesky wave equation with a p-Laplacian operator and logarithmic source under some appropriate conditions.

We consider the initial-boundary value problem of the following nonlinear wave equation with strong damping and logarithmic source terms

$$\left\{\begin{array}{cc}{\displaystyle |\dot{\varkappa }(\mathrm{y},\mathfrak{s}){|}^l\ddot{\varkappa }(\mathrm{y},\mathfrak{s})-{\Delta }_p\varkappa (\mathrm{y},\mathfrak{s})}\hfill & \\ {\displaystyle +{\Delta }^2\left(\varkappa \left(\mathfrak{s}\right)-{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\varkappa \left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)}\hfill & \\ {\displaystyle -{\mu }_1\Delta \dot{\varkappa }(\mathrm{y},\mathfrak{s})-{\mu }_2\Delta \dot{\varkappa }(\mathrm{y},\mathfrak{s}-\mathsf{\zeta })-\Delta \ddot{\varkappa }(\mathrm{y},\mathfrak{s})}\hfill & \\ {\displaystyle ={\varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|,}\hfill & \mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ \varkappa =\Delta \varkappa =0,\hfill & \mathrm{y}\in \partial \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ \varkappa (\mathrm{y},0)={\varkappa }_0\left(\mathrm{y}\right),\dot{\varkappa }{|}_{(\mathrm{y},0)}={\varkappa }_1\left(\mathrm{y}\right),\hfill & \mathrm{y}\in \mathrm{\Omega },\hfill \\ \dot{\varkappa }{|}_{(\mathrm{y},\mathfrak{s}-\mathsf{\tau })}=h_0(\mathrm{y},\mathfrak{s}-\mathsf{\tau })\hfill & \mathrm{y}\in \mathrm{\Omega },0<\mathfrak{s}<\mathsf{\tau }\hfill \end{array}\right.$$

(5)

where $\dot{\varkappa }={\varkappa }_{\mathfrak{s}}(\mathrm{y},\mathfrak{s})$, $\ddot{\varkappa }={\varkappa }_{\mathfrak{s}\mathfrak{s}}(\mathrm{y},\mathfrak{s})$, $\mathrm{\Omega }$ is a bounded domain of ${\mathbb{R}}^n$, $n\in \mathbb{N}$ and $p\in \mathbb{R}$, with smooth boundary $\partial \mathrm{\Omega }$, ${\varkappa }_0\left(\mathrm{y}\right)$ and ${\varkappa }_1\left(\mathrm{y}\right)$ are given initial data. Problem (5) describes an evolution problem with an interior logarithmic source and the investigation of this problem answers the question what will happen if one replaces the power source term by other source terms, for example, the logarithmic source term? This paper provides an affirmative reply to such a situation.

The rest of this paper can be sketched out concisely as follows: In Section 2, we introduce some basic concepts and state the important and necessary results. In Section 3.1, we shall use the Galerkin approximation technique combined with the potential well method to prove the global existence of weak solutions. Meanwhile, we will derive the decay rate of the energy functional using Nakao’s inequality and some techniques on logarithmic nonlinearity in Section 3.2. The numerical examples and simulation are provided in Section 4. Finally, a conclusion is drawn in Section 5.

2. Preliminaries

In this section, we present some material and assumptions needed for the proof of our results. For a Banach space X, ${\parallel .\parallel }_X$ denotes the norm of X. For simplicity, we denote ${\parallel .\parallel }_{L^q\left(\mathrm{\Omega }\right)}$ by ${\parallel .\parallel }_q$ and ${\parallel .\parallel }_{L^2\left(\mathrm{\Omega }\right)}$ by ${\parallel .\parallel }_2$. Here, ${\Delta }_{p}u$ is the standard p-Laplace operator defined by

$${\Delta }_p\varkappa =div\left({|\nabla \varkappa |}^{p-2}\nabla \varkappa \right),p>max\left\{1,{\displaystyle \frac{2n}{n+2}}\right\},$$

for $p\in \mathbb{R}$ and $n\in \mathbb{N}$ where $\nabla =\left(\frac{\partial }{\partial \mathrm{y}},\frac{\partial }{\partial \mathfrak{s}}\right)$.

Lemma 1.

Theorem 4.4 in [14]. Let Ω be a bounded domain with Lipschitz boundary. In the space $X=H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$, the norm ${\parallel ·\parallel }_X$ and ${\parallel ·\parallel }_2$ are equivalent norms.

Lemma 2.

Theorem 5.4 in [15]. Let Ω be a domain in ${\mathbb{R}}^n$ that has the cone property; then, for $n>2$ and $2\le q\le \frac{2n}{n-2}$, there exist the following imbeddings

$$H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)\hookrightarrow W^{1,q}\left(\mathrm{\Omega }\right)\hookrightarrow L^q\left(\mathrm{\Omega }\right).$$

There exists constants $c_1,c_{*},c_2>0$ depending on Ω and q such that

$${\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_q\le c_1{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2{,\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_q\le c_{*}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_q{,\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_q\le c_2{\parallel \Delta u\left(t\right)\parallel }_2.$$

(6)

Lemma 3.

(Logarithmic Sobolev Inequality) [16]. Let $\varkappa \in W_0^{1,p}\left(\mathrm{\Omega }\right)\setminus \left\{0\right\}$. Then, for any $p>1$ and $\mu >0$, we can write

$$p{\int }_{\mathrm{\Omega }}{\left(\varkappa (\zeta ,\mathfrak{s})\right)}^{p}ln\left({\displaystyle \frac{|\varkappa (\zeta ,\mathfrak{s})|}{{\parallel \varkappa (\zeta ,\mathfrak{s})\parallel }_p}}\right)\mathrm{d}\zeta \le {\mu \parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p-{\displaystyle \frac{n}{p}}ln\left({\displaystyle \frac{p\mu e}{n{\mathcal{L}}_p}}\right){\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p,$$

where

$${\mathcal{L}}_p={\displaystyle \frac{p}{n}}{\left({\displaystyle \frac{p-1}{e}}\right)}^{p-1}{\pi }^{-p/2}{\left({\displaystyle \frac{\mathsf{\Gamma }\left(\left(\frac{n}{2}\right)+1\right)}{\mathsf{\Gamma }\left(\frac{n(p-1)}{p}+1\right)}}\right)}^{p/2}.$$

Lemma 4.

(Generalised Young’s Inequality) Suppose that $X,Y$ and σ are positive constants and $\zeta \ge 1$. Then, Young’s inequality reads

$$XY\le {\displaystyle \frac{{\sigma }^{\zeta }}{\zeta }}{X}^{\zeta }+{\displaystyle \frac{\zeta -1}{\zeta }}{\sigma }^{-\zeta /\left(\zeta -1\right)}{Y}^{\zeta /\left(\zeta -1\right)}.$$

We prove the global existence and the blow-up property for solutions of Problem (5) under the following suitable assumptions.

(H1)

The relaxation function $g:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is a twice-differentiable and bounded function satisfying $g\left(\mathfrak{s}\right)\ge 0,$ and

$$1-{\int }_0^{\infty }g\left(\varrho \right)\mathrm{d}\varrho =:\vartheta >0.$$

There exist constants ${\xi }_1,{\xi }_2,{\xi }_3>0$ depending on $\mathrm{\Omega }$ such that

$$-{\xi }_1\le g^{\prime }\left(\mathfrak{s}\right)\le -{\xi }_{3}g\left(\mathfrak{s}\right),0\le g^{″}\left(\mathfrak{s}\right)\le {\xi }_{2}g\left(\mathfrak{s}\right),$$

whenever $\mathfrak{s}\ge 0$.

(H2)

The exponent p satisfies $2<p<\infty$ for $n\le 2$ and $2<p<\frac{n}{n-2}$ for $n>2$.

(H3)

Assume that l satisfies $0<l<\frac{2}{n-2}$ whenever $n\ge 3$ and $l>0$ whenever $n=1,2$.

To obtain the main result, we have the lemmas as follows.

Lemma 5.

[17] Suppose that $\varphi \left(\mathfrak{s}\right)$ is a bounded nonnegative function nonincreasing on $[0,\mathsf{\delta }]$ where $\mathsf{\delta }>0$ and satisfying

$${\varphi }^{1+\mathsf{\alpha }}\left(\mathfrak{s}\right)\le \sigma (\varphi \left(\mathfrak{s}\right)-\varphi (\mathfrak{s}+1)),\forall \mathfrak{s}\in [0,\mathsf{\delta }],$$

for some positive constants $\mathsf{\alpha }$ and σ. Then, we have

$$\varphi \left(\mathfrak{s}\right)\le \left\{\begin{array}{cc}\varphi \left(0\right)exp\left(-{[\mathfrak{s}-1]}^{+}ln\left(\frac{\sigma }{\sigma -1}\right)\right),\hfill & \mathsf{\alpha }=0,\hfill \\ {\left(\varphi {\left(0\right)}^{-\mathsf{\alpha }}+{\sigma }^{-1}\mathsf{\alpha }{[\mathfrak{s}-1]}^{+}\right)}^{\frac{-1}{\mathsf{\alpha }}},\hfill & \mathsf{\alpha }>0,\hfill \end{array}\right.$$

where ${[\mathfrak{s}-1]}^{+}=max\{\mathfrak{s}-1,0\}$.

To deal with the time delay term, we introduce the following new variable $\top (\mathrm{y},\eta ,\mathfrak{s})$ to represent the delay term as in [18]

$$\top (\mathrm{y},\eta ,\mathfrak{s})=\dot{\varkappa }{|}_{(\mathrm{y},\mathfrak{s}-\eta \mathsf{\tau })}.$$

(7)

Therefore, $\top (\mathrm{y},\eta ,\mathfrak{s})$ satisfies

$$\mathsf{\tau }\dot{\top }{|}_{(\mathrm{y},\eta ,\mathfrak{s})}+{\top }_{\eta }(\mathrm{y},\eta ,\mathfrak{s})=0,(\mathrm{y},\eta ,\mathfrak{s})\in \mathrm{\Omega }\times (0,1)\times (0,\infty ).$$

(8)

Using the above transformation (7), system (5) can be rewritten as equivalent form

$$\left\{\begin{array}{cc}{\displaystyle |\dot{\varkappa }{(\mathrm{y},\mathfrak{s})|}^l\ddot{\varkappa }(\mathrm{y},\mathfrak{s})-{\Delta }_p\varkappa (\mathrm{y},\mathfrak{s})}\hfill & \\ {\displaystyle +{\Delta }^2\left(\varkappa -{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\varkappa \left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)}\hfill & \\ {\displaystyle -{\mu }_1\Delta \dot{\varkappa }(\mathrm{y},\mathfrak{s})-{\mu }_2\Delta \top (\mathrm{y},1,\mathfrak{s})-\Delta \ddot{\varkappa }(\mathrm{y},\mathfrak{s})}\hfill & \\ {\displaystyle ={\varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|,}\hfill & \mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ {\displaystyle \mathsf{\tau }\dot{\top }{|}_{(\mathrm{y},\eta ,\mathfrak{s})}+{\top }_{\eta }(\mathrm{y},\eta ,\mathfrak{s})=0,}\hfill & \mathrm{y}\in \mathrm{\Omega },\eta \in (0,1),\mathfrak{s}>0,\hfill \\ \varkappa =0,\hfill & \mathrm{y}\in \partial \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ \top (\mathrm{y},0,\mathfrak{s})=\dot{\varkappa },\hfill & \mathrm{y}\in \partial \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ \varkappa (\mathrm{y},0)={\varkappa }_0\left(\mathrm{y}\right),\dot{\varkappa }{|}_{(\mathrm{y},0)}={\varkappa }_1\left(\mathrm{y}\right),\hfill & \mathrm{y}\in \mathrm{\Omega }.\hfill \end{array}\right.$$

(9)

Let $\xi$ be a positive constant satisfying

$$\mathsf{\tau }{\displaystyle \frac{|{\mu }_2|}{2}}\le \xi \le \mathsf{\tau }\left({\mu }_1-{\displaystyle \frac{|{\mu }_2|}{2}}\right)$$

(10)

The energy functional associated to Problem (9) is defined as

$$\begin{array}{cc}E\left(\mathfrak{s}\right)\hfill & {\displaystyle :={\displaystyle \frac{1}{l+2}}\parallel \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}+\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2}\hfill \\ \hfill & {\displaystyle +{\displaystyle \frac{1}{p}}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta \varkappa \right)\left(\mathfrak{s}\right)}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\zeta +{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p}\hfill \\ \hfill & {\displaystyle +\xi {\int }_{\mathrm{\Omega }}{\int }_0^1{|\nabla \top (\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\eta \mathrm{d}\mathrm{y},}\hfill \end{array}$$

(11)

where

$$(g\circ \varphi )\left(\mathfrak{s}\right):={\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\parallel \varphi \left(\mathfrak{s}\right)-\varphi \left(\mathsf{\zeta }\right)\parallel }_2^2\mathrm{d}\mathsf{\zeta }.$$

Multiplying the first equation in (9) by $\dot{\varkappa }(\mathrm{y},\mathfrak{s})$ and integrating over $\mathrm{\Omega }$, using integration by part, we see that

$$\begin{array}{cc}{\displaystyle {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\{{\displaystyle \frac{1}{l+2}}{\parallel \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}}\hfill & {\displaystyle +\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2}\hfill \\ \hfill & {\displaystyle +{\displaystyle \frac{1}{p}}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta \varkappa \right)\left(\mathfrak{s}\right)}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\}}\hfill \\ \hfill & {\displaystyle +{\mu }_1{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2+{\mu }_2{\int }_{\mathrm{\Omega }}\nabla \top (\mathrm{y},1,\mathfrak{s})\nabla \dot{\varkappa }(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}}\hfill \\ \hfill & {\displaystyle ={\displaystyle \frac{1}{2}}(g^{\prime }\circ \Delta \varkappa )\left(\mathfrak{s}\right)-{\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2.}\hfill \end{array}$$

(12)

We multiply the second equation in (9) by $-\xi \Delta \top (\mathrm{y},\eta ,\mathfrak{s})$ and integrate the result over $\mathrm{\Omega }\times (0,1)$ to obtain

$$\begin{array}{cc}\hfill -\xi {\int }_{\mathrm{\Omega }}{\int }_0^1\dot{\top }(\mathrm{y},\eta ,\mathfrak{s})\Delta \top (\mathrm{y},\eta ,\mathfrak{s})\mathrm{d}\eta \mathrm{d}\mathrm{y}& ={\displaystyle \frac{\xi }{\mathsf{\tau }}}{\int }_{\mathrm{\Omega }}{\int }_0^1{\top }_{\eta }(\mathrm{y},\eta ,\mathfrak{s})\Delta \top (\mathrm{y},\eta ,\mathfrak{s})\mathrm{d}\eta \mathrm{d}\mathrm{y}\hfill \\ \hfill & =-{\displaystyle \frac{\xi }{2\mathsf{\tau }}}{\int }_{\mathrm{\Omega }}{\int }_0^1{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\eta }}{|\nabla \top (\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\eta \mathrm{d}\mathrm{y}\hfill \\ \hfill & =-{\displaystyle \frac{\xi }{2\mathsf{\tau }}}{\int }_{\mathrm{\Omega }}\left({|\nabla \top (\mathrm{y},1,\mathfrak{s})|}^2-{|\nabla \top (\mathrm{y},0,\mathfrak{s})|}^2\right)\mathrm{d}\mathrm{y},\hfill \end{array}$$

which gives

$$\begin{array}{cc}{\displaystyle \xi {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_{\mathrm{\Omega }}{\int }_0^1{|\nabla \top (\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\eta \mathrm{d}\mathrm{y}}\hfill & {\displaystyle =-{\displaystyle \frac{\xi }{\mathsf{\tau }}}{\int }_{\mathrm{\Omega }}\left({|\nabla \top (\mathrm{y},1,\mathfrak{s})|}^2-{|\nabla \top (\mathrm{y},0,\mathfrak{s})|}^2\right)\mathrm{d}\mathrm{y}}\hfill \\ \hfill & {\displaystyle =-{\displaystyle \frac{\xi }{\mathsf{\tau }}}{\int }_{\mathrm{\Omega }}\left({|\nabla \top (\mathrm{y},1,\mathfrak{s})|}^2-{|\nabla \dot{\varkappa }(\mathrm{y},\mathfrak{s})|}^2\right)\mathrm{d}\mathrm{y}.}\hfill \end{array}$$

(13)

Using Young’s inequality, we have

$${\mu }_2{\int }_{\mathrm{\Omega }}\nabla \top (\mathrm{y},1,\mathfrak{s})\nabla \dot{\varkappa }(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\le {\displaystyle \frac{|{\mu }_2|}{2}}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2+{\displaystyle \frac{|{\mu }_2|}{2}}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2.$$

(14)

Combining (12)–(14), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}E\left(\mathfrak{s}\right)& \le \frac{1}{2}(g^{\prime }\circ \Delta \varkappa )\left(\mathfrak{s}\right)-\frac{1}{2}g\left(\mathfrak{s}\right)\parallel \Delta \varkappa \left(\mathfrak{s}\right){\parallel }_2^2-\left({\mu }_1-\frac{\xi }{\mathsf{\tau }}-\frac{|{\mu }_2|}{2}\right){\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & -\left(\frac{\xi }{\mathsf{\tau }}-\frac{|{\mu }_2|}{2}\right){\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2.\hfill \end{array}$$

(15)

By using condition (10), we obtain $k_0={\mu }_1-{\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}>0$, $k_1={\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}>0$, which implies

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}E\left(\mathfrak{s}\right)& \le {\displaystyle \frac{1}{2}}(g^{\prime }\circ \Delta \varkappa )\left(\mathfrak{s}\right)-{\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right)\parallel \nabla \varkappa \left(\mathfrak{s}\right){\parallel }_2^2-k_0\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right){\parallel }_2^2-k_1{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2<0,\hfill \end{array}$$

(16)

for almost $\mathfrak{s}\in [0,\mathsf{\delta })$ and hence

$$E\left(\mathfrak{s}\right)+k_0{\int }_0^{\mathfrak{s}}\parallel \nabla \dot{\varkappa }{\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho +k_1{\int }_0^{\mathfrak{s}}{\parallel \nabla \top (\mathrm{y},1,\varrho )\parallel }_2^2\mathrm{d}\varrho \le E\left(0\right).$$

(17)

Next, we introduce two potential energy functionals on $H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$ as follows:

$$\begin{array}{cc}\hfill J\left(\varkappa \right)& ={\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{p}}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p,\hfill \\ \hfill I\left(\varkappa \right)& =\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & -{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(19)

By a direct computation,

$$J\left(\varkappa \right)=\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right)\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)d\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(s\right)\parallel }_2^2+{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(s\right)\parallel }_p^p+{\displaystyle \frac{1}{p}}I\left(\varkappa \right).$$

(20)

Clearly,

$$\begin{array}{cc}{\displaystyle E\left(\mathfrak{s}\right)}\hfill & {\displaystyle ={\displaystyle \frac{1}{l+2}}\parallel \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}+{\displaystyle \frac{1}{2}}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}(g\circ \Delta \varkappa )\left(\mathfrak{s}\right)}\hfill \\ \hfill & {\displaystyle +\xi {\int }_{\mathrm{\Omega }}{\int }_0^1{|\nabla \top (\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\eta \mathrm{d}\mathrm{y}+J\left(\varkappa \right).}\hfill \end{array}$$

(21)

Define the Nehari’s manifold

$$\mathcal{N}=\left\{\varkappa \in H^3\left(\mathrm{\Omega }\right)\cap H_0^1{\left(\mathrm{\Omega }\right)|I\left(\varkappa \right)=0,\parallel \Delta \varkappa \parallel }_2\ne 0\right\}.$$

Next, let us define the stable set W and the unstable set V as follows:

$$\begin{array}{cc}\hfill W& =\left\{\varkappa \in H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)|I\left(\varkappa \right)>0,J\left(\varkappa \right)<d\right\}\cup \left\{0\right\},\hfill \\ \hfill V& =\left\{\varkappa \in H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)|I\left(\varkappa \right)<0,J\left(\varkappa \right)<d\right\}.\hfill \end{array}$$

The mountain pass level d, also known as potential well depth, is characterized by

$$d=\underset{0\ne \varkappa \in H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)}{inf}\underset{\lambda \ge 0}{sup}J\left(\lambda \varkappa \right)=\underset{\varkappa \in \mathcal{N}}{inf}J\left(\varkappa \right).$$

(22)

3. Global Existence and Energy Decay

First, we state and prove a few lemmas.

Lemma 6.

The depth d of the potential well d is positive.

Proof. 

Fix $u\in \mathcal{N}$, and using the fact ${\varkappa }^{p}ln|\varkappa |\le {|\varkappa |}^{p+\mathsf{\alpha }}$ for $|\varkappa |>1$ and for all $\mathsf{\alpha }>0$, we arrive at

$$\begin{array}{cc}\hfill {\displaystyle \left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)}& {\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \\ \hfill & {\displaystyle ={\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}}\hfill \\ \hfill & {\displaystyle \le {\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_{p+\mathsf{\alpha }}^{p+\mathsf{\alpha }}\le c_1^{p+\mathsf{\alpha }}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^{p+\mathsf{\alpha }}.}\hfill \end{array}$$

(23)

Taking $\mathsf{\alpha }$ such that $p+\mathsf{\alpha }\le 2^{*}={\displaystyle \frac{2n}{n-2}}$, we deduce

$${\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2\ge {\left({\displaystyle \frac{\vartheta }{c_1^{p+\mathsf{\alpha }}}}\right)}^{1/p+\mathsf{\alpha }-2},$$

which implies

$$\begin{array}{cc}\hfill J\left(\varkappa \right)& =\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right)\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \\ \hfill & \ge \vartheta \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right){\left({\displaystyle \frac{\vartheta }{c_1^{p+\mathsf{\alpha }}}}\right)}^{2/p+\mathsf{\alpha }-2}.\hfill \end{array}$$

Therefore,

$$d\ge \vartheta \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right){\left({\displaystyle \frac{\vartheta }{c_1^{p+\mathsf{\alpha }}}}\right)}^{2/p+\mathsf{\alpha }-2}.$$

The proof is complete. □

Lemma 7.

For any $\varkappa \in H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$, ${\parallel \Delta \varkappa \left(s\right)\parallel }_2\ne 0$ there exists a unique ${\lambda }_0={\lambda }_0\left(\varkappa \right)>0$ such that the following assertions hold:

(i)

${lim}_{\lambda \to o^{+}}J\left(\lambda \varkappa \right)=0$, ${lim}_{\lambda \to +\infty }J\left(\lambda u\right)=-\infty$;

(ii)

$J\left(\lambda \varkappa \right)$ is increasing in the interval $0<\lambda \le {\lambda }_0$, decreasing in the interval ${\lambda }_0\le \lambda <+\infty$ and takes its maximum at $\lambda ={\lambda }_0$ where ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}\lambda }}{J\left(\lambda \varkappa \right)|}_{\lambda ={\lambda }_0}=0$;

(iii)

$I\left(\lambda \varkappa \right)>0$ for $0<\lambda <{\lambda }_0$, $I\left(\lambda \varkappa \right)<0$ for ${\lambda }_0<\lambda <+\infty$ and $I\left({\lambda }_0\varkappa \right)=0$.

Proof. 

For $\lambda >0$, we know that

$$\begin{array}{cc}\hfill J\left(\lambda \varkappa \right)& :={\displaystyle \frac{1}{2}}{\lambda }^2\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{{\lambda }^p}{p}}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \\ \hfill & -{\displaystyle \frac{{\lambda }^p}{p}}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}-{\displaystyle \frac{{\lambda }^p}{p}}ln|\lambda |{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^p\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\displaystyle \frac{{\lambda }^p}{p}}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^p\mathrm{d}\mathrm{y}.\hfill \end{array}$$

Taking the derivative of $J\left(\lambda \varkappa \right)$, we obtain

$$\begin{array}{cc}\hfill {\displaystyle {\displaystyle \frac{\partial }{\partial \lambda }}J\left(\lambda \varkappa \right)}& {\displaystyle =\lambda \left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\lambda }^{p-1}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p}\hfill \\ \hfill & {\displaystyle -{\lambda }^{p-1}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}-{\lambda }^{p-1}ln|\lambda |{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^p\mathrm{d}\mathrm{y}.}\hfill \end{array}$$

(24)

Making (24) equal zero is equivalent to

$$\begin{array}{cc}\hfill {\displaystyle {\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p}& {\displaystyle ={\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}+ln|\lambda |{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^p\mathrm{d}\mathrm{y}}\hfill \\ \hfill & {\displaystyle -{\lambda }^{2-p}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2.}\hfill \end{array}$$

(25)

We define

$$\begin{array}{cc}\hfill {\varphi }_{\varkappa }\left(\lambda \right)& :={\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}+ln|\lambda |{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^p\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\lambda }^{2-p}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2.\hfill \end{array}$$

The function ${\varphi }_{\varkappa }\left(\lambda \right)$ is increasing on $0<\lambda <\infty$, and we remark that

$$\underset{\lambda \to o^{+}}{lim}{\varphi }_{\varkappa }\left(\lambda \right)=-\infty ,\underset{\lambda \to +\infty }{lim}{\varphi }_{\varkappa }\left(\lambda \right)=+\infty .$$

Therefore, there exists a unique ${\lambda }^{*}$ such that ${\varphi }_{\varkappa }\left({\lambda }^{☆}\right)=0$, ${\varphi }_{\varkappa }\left(\lambda \right)<0$ on $0<\lambda <{\lambda }^{☆}$ and ${\varphi }_{\varkappa }\left(\lambda \right)>0$ on ${\lambda }^{☆}<\lambda <\infty$. We can clearly perceive that there exists a unique ${\lambda }_0>{\lambda }^{☆}$ such that ${\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p={\varphi }_{\varkappa }\left(\lambda \right).$ Again, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial \lambda }}J\left(\lambda \varkappa \right)={\lambda }^{p-1}\left({\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p-{\varphi }_{\varkappa }\left(\lambda \right)\right)& :=K_{\varkappa }\left(\lambda \right).\hfill \end{array}$$

We also obtain ${\varphi }_{\varkappa }\left(\lambda \right)\le 0$ for $0<\lambda <{\lambda }^{☆}$, $0<{\varphi }_{\varkappa }\left(\lambda \right)\le {\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p$ for ${\lambda }^{☆}<\lambda <{\lambda }_0$ and ${\varphi }_{\varkappa }\left(\lambda \right)>{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p$ for ${\lambda }_0<\lambda <\infty$, and we have (ii). Because $I\left(\lambda \varkappa \right)=\lambda \frac{\partial J\left(\lambda \varkappa \right)}{\partial \lambda }$ which is verified by a direct computation, then one has (iii). □

Lemma 8.

(Invariant Set W when $E\left(0\right)<d$). Let (H1)–(H4) hold. Assume that ϰ is a weak solution of Problem (5) with $I\left({\varkappa }_0\right)>0$ and $E\left(0\right)<d$, then the solution of the Problem (5) satisfies $\varkappa (\mathrm{y},\mathfrak{s})\in W$, $0\le \mathfrak{s}\le \mathsf{\delta }$, where $\mathsf{\delta }$ is the maximal existence time of the solutions.

Proof. 

Arguing by contradiction, we suppose that there exists ${\mathfrak{s}}_1\in (0,\mathsf{\delta })$ such that $\varkappa \left({\mathsf{\delta }}_1\right)\in \partial W$, and then we obtain $I\left(\varkappa \left({\mathfrak{s}}_1\right)\right)=0$ or $J\left(\varkappa \left({\mathfrak{s}}_1\right)\right)=d$. Going back to (21), we have $E\left(\mathfrak{s}\right)\ge J\left(\varkappa \right)$. Then, $J\left(\varkappa \left({\mathfrak{s}}_1\right)\right)=d$ gives $E\left({\mathfrak{s}}_1\right)\ge d$ and (17) implies $E\left(\mathfrak{s}\right)<d$. This leads to a contradiction. Assuming that ${\mathfrak{s}}_1$ is the first time such that $I\left(\varkappa \left({\mathfrak{s}}_1\right)\right)=0$ and ${\parallel \Delta \varkappa \parallel }_2\ne 0$, then $I\left(\varkappa \right)>0$ in the interval $(0,{\mathfrak{s}}_1)$ and $\varkappa \left({\mathfrak{s}}_1\right)\in \mathcal{N}$ which implies $d\le J\left(\varkappa \left({\mathfrak{s}}_1\right)\right)$. Using (21), we have $E\left({\mathfrak{s}}_1\right)\ge d$ which contradicts the nonincreasing property of $E\left(\mathfrak{s}\right)$. Thus, the proof of Lemma (8) is completed. □

Now, under the hypotheses (H1)–(H4), we shall use the Galerkin approximation technique combined with the potential well method to prove the global existence of weak solutions for Problem (9) as long as ${\varkappa }_0\in W$. Meanwhile, we shall obtain the asymptotic stability of the global solutions.

3.1. Global Existence for Low Initial Energy $J\left({\varkappa }_0\right)<d$

Theorem 1.

Assume that assumptions (H1)–(H3) are in place and $h_0\in H_0^1(\mathrm{\Omega },H^1(0,1))$ satisfying the compatibility condition $h(.,0)={\varkappa }_1$. Then, for given initial data ${\varkappa }_0\in H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$, ${\varkappa }_1\in H_0^1\left(\mathrm{\Omega }\right)$, the Cauchy problem (9) possesses a unique global weak solution

$$\begin{array}{cc}\hfill \varkappa & \in L^{\infty }([0,\infty ),H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)),\hfill \\ \hfill \dot{\varkappa }& \in L^{\infty }([0,\infty ),H_0^1\left(\mathrm{\Omega }\right)),\hfill \\ \hfill \ddot{\varkappa }& \in L^2([0,\infty ),H_0^1\left(\mathrm{\Omega }\right)).\hfill \end{array}$$

In addition, said solution satisfies the energy inequality

$$\begin{array}{cc}\hfill E\left(\mathfrak{s}\right)& -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta \varkappa )\left(\varrho \right)\mathrm{d}\varrho +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\varrho \right){\parallel \Delta \varkappa \left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla \dot{\varkappa }\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla \top (\mathrm{y},1,\varrho )\parallel }_2^2\mathrm{d}\varrho \le E\left(0\right).\hfill \end{array}$$

(26)

Proof. 

The main idea is to use the Galerkin method. Let $\mathsf{\delta }>0$ be fixed, and for each $n\in \mathbb{N}$, define $V_n=Span\{w_1,w_2,\dots ,w_n\}$ the linear space dense in $H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$, where $\{w_1,w_2,\dots ,w_n,\dots \}$ is an orthonormal basis of $L^2\left(\mathrm{\Omega }\right)$ generated by the eigenvectors of ${\Delta }^2{w}_i={\lambda }_i{w}_i\in \mathrm{\Omega }$, $w_i=\Delta w_i=0$ on $\partial \mathrm{\Omega }$, where $0<{\lambda }_1\le {\lambda }_2\le \dots$ are the corresponding eigenvalues. Now, we define the sequence ${\left\{{\varphi }_i(\mathrm{y},\eta )\right\}}_{i=1}^n$ satisfying ${\varphi }_i(\mathrm{y},0)=w_i$. Then, we may extend ${\varphi }_i(\mathrm{y},0)$ by ${\varphi }_i(\mathrm{y},\eta )$ over $L^2(\mathrm{\Omega }\times [0,1])$ such that ${\left\{{\varphi }_i\right\}}_{i=1}^n$ forms a basis of $L^2(\mathrm{\Omega },H^2(0,1))$ and denote ${\mathfrak{Y}}_k$ the space generated by $\left\{{\varphi }^n\right\}$. We define

$${\varkappa }^n\left(\mathfrak{s}\right)=\sum _{i=1}^n{\mathsf{\alpha }}_{in}\left(\mathfrak{s}\right)w_i\left(\mathrm{y}\right),{\top }^n\left(\mathfrak{s}\right)=\sum _{i=1}^n{\beta }_{in}\left(\mathfrak{s}\right){\varphi }_i(\mathrm{y},\eta ),n=1,2,3,\dots ,$$

as the approximated solutions which satisfy the nonlinear ordinary differential equations for $1\le i\le n$,

$$\left\{\begin{array}{cc}{\displaystyle {\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}}\hfill & \\ {\displaystyle +{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}}\hfill & \\ {\displaystyle +{\int }_{\mathrm{\Omega }}\Delta \left({\varkappa }^n(\mathrm{y},\mathfrak{s})-{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\varkappa }^n\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)\Delta w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}}\hfill & \\ {\displaystyle +{\mu }_1{\int }_{\mathrm{\Omega }}\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}}\hfill & \\ {\displaystyle +{\mu }_2{\int }_{\mathrm{\Omega }}\nabla {\top }^n(\mathrm{y},1,\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}}\hfill & \\ {\displaystyle +{\int }_{\mathrm{\Omega }}\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}}\hfill & \\ {\displaystyle ={\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y},}\hfill & \mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ {\top }^n(\mathrm{y},0,\mathfrak{s})={\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}),\hfill & \mathrm{y}\in \partial \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ {\varkappa }^n(\mathrm{y},0)={\varkappa }_{0n}\left(\mathrm{y}\right),{\dot{\varkappa }}^n(\mathrm{y},0)={\varkappa }_{1n}\left(\mathrm{y}\right),\hfill & \mathrm{y}\in \mathrm{\Omega },\hfill \end{array}\right.$$

(27)

and

$$\left\{\begin{array}{c}{\displaystyle \mathsf{\tau }{\int }_0^1{\int }_{\mathrm{\Omega }}{\dot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s}){\varphi }_i(\mathrm{y},\eta )\mathrm{d}\mathrm{y}\mathrm{d}\eta }\hfill \\ {\displaystyle +{\int }_0^1{\int }_{\mathrm{\Omega }}{\top }_{\eta }(\mathrm{y},\eta ,\mathfrak{s}){\varphi }_i(\mathrm{y},\eta )\mathrm{d}\mathrm{y}\mathrm{d}\eta =0,}\hfill \\ {\displaystyle {\top }^n(\mathrm{y},\eta ,0)={\top }_{0n},}\hfill \end{array}\right.$$

(28)

where ${\varkappa }_{0n},{\varkappa }_{1n}$ are chosen in $V_n$ so that

$$\begin{array}{c}{\varkappa }_{0n}\to {\varkappa }_0\mathrm{strongly}\mathrm{in}{H}^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right),\hfill \\ u_{1n}\to u_1\mathrm{strongly}\mathrm{in}{H}^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right),\hfill \end{array}$$

(29)

and ${\top }_{0n}\in V_n$ such that

$${\top }_{0n}\to h_0(\mathrm{y},-\eta \mathsf{\tau })\mathrm{strongly}\mathrm{in}{H}_0^2(\mathrm{\Omega }\times [0,1]).$$

(30)

As $n\to \infty$. Thanks to the Sobolev embeddings $H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)\hookrightarrow L^{2(l+1)}\left(\mathrm{\Omega }\right)$ and using the generalised Hölder inequality with exponents $l/2(l+1),1/2(l+1)$ and $1/2$, the nonlinear term $(|{\dot{\varkappa }}^n\left(\mathfrak{s}\right){{|}^l{\ddot{\varkappa }}^n\left(\mathfrak{s}\right),w_i)}_{L^2\left(\mathrm{\Omega }\right)}$ makes sense

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}& \le \parallel {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_{2(l+1)}^l\parallel {\ddot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2{\parallel w_i\parallel }_{2(l+1)}\hfill \\ \hfill & \le c_1^{l+1}\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^l\parallel {\ddot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2{\parallel \Delta w_i\parallel }_2\hfill \\ \hfill & \le C\left\{\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^{l+1}+{\parallel {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^{l+1}\right\},\hfill \end{array}$$

and using the fact ${\varkappa }^{p}ln|\varkappa |\le {|\varkappa |}^{p+\mathsf{\alpha }}$ for $|\varkappa |>1$ and for all $\mathsf{\alpha }>0$, we can estimate

$${\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y},$$

as follows by choosing $\mathsf{\alpha }=1$,

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s}){|{\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}& ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\int }_{{\mathrm{\Omega }}_1}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{{\mathrm{\Omega }}_2}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|w_i\left(\mathrm{y}\right)\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \parallel w_i{\parallel }_2{\int }_{{\mathrm{\Omega }}_2}|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{2p}\mathrm{d}\mathrm{y},\le C{\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^p,\hfill \end{array}$$

where

$${\mathrm{\Omega }}_1=\left\{\mathrm{y}\in \mathrm{\Omega }:|{\varkappa }^n(\mathrm{y},\mathfrak{s})|\le 1\right\},{\mathrm{\Omega }}_2=\left\{\mathrm{y}\in \mathrm{\Omega }:|{\varkappa }^n(\mathrm{y},\mathfrak{s})|>1\right\}.$$

We may show by the standard theory of ordinary differential equation that the initial value Problems (27) and (28) is uniquely solvable. More precisely, we obtain a local solution ${\varkappa }^n\left(\mathfrak{s}\right)\in {\left(H^3[0,{\mathsf{\delta }}_n)\right)}^2$ extended to a maximal interval $0\le \mathfrak{s}\le {\mathsf{\delta }}_n$ with $0<{\mathsf{\delta }}_n$, owing to Zorn lemma because the unknown functions ${\mathsf{\alpha }}_{in},{\mathsf{\beta }}_{in}$ and their time derivatives are continuous, and by using the embedding $H^3[0,{\mathsf{\delta }}_n]\hookrightarrow C^2[0,{\mathsf{\delta }}_n]$, we deduce the solution ${\varkappa }^n\left(\mathfrak{s}\right)\in C^2[0,{\mathsf{\delta }}_n)$. Next, using a standard compactness argument, we shall obtain a priori estimates for the solution of systems (27) and (28), so that it can be extended to a global solution defined for all $\mathfrak{s}>0$. Multiplying (27) by ${\mathsf{\alpha }}_{in}^{\prime }\left(\mathfrak{s}\right)$, summing with respect to i and integrating by parts over the time variable from 0 to $\mathfrak{s}$, we shall obtain from (21) the following estimate

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\{{\displaystyle \frac{1}{l+2}}{\parallel {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}& +\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{p}}{\parallel \nabla {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }^n\right)\left(\mathfrak{s}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{p^2}}{\parallel {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_p^p\}\hfill \\ \hfill & +{\mu }_1{\parallel \nabla {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2+{\mu }_2{\int }_{\mathrm{\Omega }}\nabla {\top }^n(\mathrm{y},1,\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\mathfrak{s}\right)-{\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right){\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2.\hfill \end{array}$$

(31)

Replacing $\mathfrak{s}$ with $\varrho$ in (31) and integrating over $\varrho \in [0,\mathfrak{s}]$ to arrive at

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{l+2}}{\parallel {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}& +\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+J\left({\varkappa }^n\right)+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }^n\right)\left(\mathfrak{s}\right)+{\mu }_1{\int }_0^{\mathfrak{s}}{\parallel \nabla {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +{\mu }_2{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\nabla \top (\mathrm{y},1,\varrho )\nabla {\dot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\varrho \right){\parallel \Delta {\varkappa }^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & =J\left({\varkappa }_{0n}\right)+{\displaystyle \frac{1}{l+2}}\parallel {\varkappa }_{1n}{\parallel }_{l+2}^{l+2}+{\parallel \nabla {\varkappa }_{1n}\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\parallel \Delta {\varkappa }_{0n}{\parallel }_2^2+{\displaystyle \frac{1}{p}}{\parallel \nabla {\varkappa }_{0n}\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }_{0n}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^{p}ln|{\varkappa }_{0n}|\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{p^2}}{\parallel {\varkappa }_{0n}\parallel }_p^p.\hfill \end{array}$$

(32)

Replacing ${\varphi }_i(\mathrm{y},\eta )$ in (28) with $-\Delta {\varphi }_i(\mathrm{y},\eta )$, multiplying by ${\beta }_{in}\left(\mathfrak{s}\right)/\mathsf{\tau }$ and adding those equations with respect to i from 1 to n, we obtain

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}|\nabla {\top }^n{(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\displaystyle \frac{1}{2\mathsf{\tau }}}{\int }_{\mathrm{\Omega }}|\nabla {\top }^n{(\mathrm{y},1,\mathfrak{s})|}^2-{|\nabla {\top }^n(\mathrm{y},0,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}=0.$$

Integrating in terms of $\mathfrak{s}$, we obtain that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\top }^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta & +{\displaystyle \frac{1}{2\mathsf{\tau }}}{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}|\nabla {\top }^n{(\mathrm{y},1,\varrho )|}^2-{|\nabla {\top }^n(\mathrm{y},0,\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}|\nabla {\top }_{0n}{|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta ={\displaystyle \frac{1}{2}}{\parallel {\top }_{0n}\parallel }_{H_0^1(\mathrm{\Omega }\times (0,1))}^2.\hfill \end{array}$$

(33)

Multiplying (33) by $\xi$ and summing up with (32), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{l+2}}{\parallel {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}& +\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+J\left({\varkappa }^n\right)+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }^n\right)\left(\mathfrak{s}\right)\hfill \\ \hfill & +{\displaystyle \frac{\xi }{2}}{\int }_0^1{\parallel \nabla {\top }^n(\mathrm{y},\eta ,\mathfrak{s})\parallel }_2^2\mathrm{d}\eta \hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\top }^n(\mathrm{y},1,\varrho )\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\varrho \right){\parallel \Delta {\varkappa }^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & \le J\left({\varkappa }_{0n}\right)+{\displaystyle \frac{1}{l+2}}\parallel {\varkappa }_{1n}{\parallel }_{l+2}^{l+2}+{\parallel \nabla {\varkappa }_{1n}\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\parallel \Delta {\varkappa }_{0n}{\parallel }_2^2+{\displaystyle \frac{1}{p}}{\parallel \nabla {\varkappa }_{0n}\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }_{0n}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^{p}ln|{\varkappa }_{0n}|\mathrm{d}\zeta +{\displaystyle \frac{1}{p^2}}\parallel {\varkappa }_{0n}{\parallel }_p^p+{\displaystyle \frac{\xi }{2}}{\parallel {\top }_{0n}\parallel }_{H_0^1(\mathrm{\Omega }\times (0,1))}^2.\hfill \end{array}$$

(34)

On one hand, from the mean value theorem, we assert that

$$\left|{\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^{p}ln|{\varkappa }_{0n}|\mathrm{d}\mathrm{y}-|{\varkappa }_0{|}^{p}ln|{\varkappa }_0|\mathrm{d}\mathrm{y}\right|\le \parallel {\varphi }^{\prime }({\varkappa }_0(1-\epsilon )+\epsilon {\varkappa }_{0n}){\parallel }_2·{\parallel {\varkappa }_{0n}-{\varkappa }_0\parallel }_2,$$

where $\varphi \left(v\right)={|v|}^{p}ln|v|$, ${\varphi }^{\prime }\left(v\right)={p|v|}^{p-1}ln|v|+{|v|}^{p-1}$ and $0<\epsilon <1$. Moreover, by the Minkowski inequality and the fact [19]

$${\varkappa }^{\mathsf{\alpha }}ln|u|\le \left\{\begin{array}{cc}{|\varkappa |}^{\mathsf{\alpha }+\mathsf{\beta }},\hfill & |\varkappa |>1,\hfill \\ {\displaystyle \frac{1}{e\mathsf{\alpha }}},\hfill & |\varkappa |\le 1,\hfill \end{array}\right.$$

(35)

for any $\mathsf{\beta },\mathsf{\alpha }>0$. We obtain by applying Hölder’s inequality with $\frac{p}{p-1}$ and p

$$\begin{array}{cc}\hfill \parallel {\varphi }^{\prime }{\left(v\right)\parallel }_2& \le p{\left({\int }_{{\mathrm{\Omega }}_1}{||v|}^{p-1}{|ln|v||}^2\mathrm{d}\mathrm{y}+{\int }_{{\mathrm{\Omega }}_2}{|v|}^{p-1}|ln|v|{|}^2\mathrm{d}\mathrm{y}\right)}^{\frac{1}{2}}+{\left({\int }_{\mathrm{\Omega }}{|v|}^{2(p-1)}\mathrm{d}\mathrm{y}\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le p{\displaystyle \frac{\sqrt{|{\mathrm{\Omega }}_1|}}{e(p-1)}}+(p+1){\left({\int }_{\mathrm{\Omega }}{|v|}^{2(p-1)}\mathrm{d}\mathrm{y}\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le p{\displaystyle \frac{\sqrt{|{\mathrm{\Omega }}_1|}}{e(p-1)}}+{(p+1)|\mathrm{\Omega }|}^{\frac{1}{2p}}{\parallel v\parallel }_{2p}^{p-1}\hfill \\ \hfill & \le A+(p+1)c_1^{p-1}{|\mathrm{\Omega }|}^{\frac{1}{2p}}{\parallel \Delta v\parallel }_2^{p-1}.\hfill \end{array}$$

Therefore, as $p<\frac{n}{n-2}$, we obtain $2p<\frac{2n}{n-2}=2^{*}$ and

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^{p}ln|{\varkappa }_{0n}|\mathrm{d}\mathrm{y}& -|{\varkappa }_0{|}^{p}ln|{\varkappa }_0|\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le c_1\{A+(p+1)c_1^{p-1}{|\mathrm{\Omega }|}^{\frac{1}{2p}}(\parallel \Delta u_0{\parallel }_2^{p-1}\hfill \\ \hfill & +\parallel \Delta {\varkappa }_{0n}{\parallel }_2^{p-1}\left)\right\}·\parallel \Delta {\varkappa }_{0n}-\Delta {\varkappa }_0{\parallel }_2.\hfill \end{array}$$

So, by (29) and hypothesis (H3), we obtain for sufficiently large n

$$\left|{\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^{p}ln|{\varkappa }_{0n}|\mathrm{d}\mathrm{y}-|{\varkappa }_0{|}^{p}ln|{\varkappa }_0|\mathrm{d}\mathrm{y}\right|\le A_p\parallel \Delta {\varkappa }_0{\parallel }_2^{p-1}·{\parallel \Delta {\varkappa }_{0n}-\Delta {\varkappa }_0\parallel }_2.$$

Together with ${\varkappa }_{0n}\to {\varkappa }_0$ strongly in $H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$ as $n\to \infty$, we derive

$${\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^{p}ln|{\varkappa }_{0n}|\mathrm{d}\mathrm{y}\to {\int }_{\mathrm{\Omega }}|{\varkappa }_0{|}^{p}ln|{\varkappa }_0|\mathrm{d}\mathrm{y},\mathit{as}n\to \infty .$$

(36)

By taking $\varphi \left(v\right)={|v|}^p$, we obtain for sufficiently large n

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }_{0n}|}^p\mathrm{d}\mathrm{y}& -{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }_0|}^p\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le p{\int }_{\mathrm{\Omega }}|\nabla {\varkappa }_0(1-\epsilon )+\epsilon \nabla {\varkappa }_{0n}{|}^{p-1}|\nabla {\varkappa }_{0n}-\nabla {\varkappa }_0|\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le c_2{2}^{p-1}p\left\{\parallel \Delta {\varkappa }_{0n}{\parallel }_{2(p-1)}^{p-1}+{\parallel \Delta {\varkappa }_0\parallel }_{2(p-1)}^{p-1}\right\}.{\parallel \Delta {\varkappa }_{0n}-\Delta {\varkappa }_0\parallel }_2\hfill \\ \hfill & \le A_p\parallel \Delta {\varkappa }_0{\parallel }_2^{p-1}·{\parallel \Delta {\varkappa }_{0n}-\Delta {\varkappa }_0\parallel }_2.\hfill \end{array}$$

(37)

Together with ${\varkappa }_{0n}\to {\varkappa }_0$ strongly in $H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)$ as $n\to \infty$, we deduce that

$${\int }_{\mathrm{\Omega }}|\nabla {\varkappa }_{0n}{|}^p\mathrm{d}\zeta \to {\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }_0|}^p\mathrm{d}\zeta ,\mathit{as}n\to \infty ,$$

(38)

By (29), we achieve ${\varkappa }_{0n}\to {\varkappa }_0$ almost everywhere in $\mathrm{\Omega }\times (0,\mathsf{\delta })$, which implies by the continuity of the function $v\mapsto {|v|}^{p}v$ that

$$|{\varkappa }_{0n}{|}^p{\varkappa }_{0n}\to {|{\varkappa }_0|}^p{\varkappa }_0,\mathrm{almost}\mathrm{everywhere}\mathrm{in}\mathrm{\Omega }\times (0,\mathsf{\delta }).$$

(39)

Using (29)–(39) and from Aubin–Lions Lemma, we derive

$$|{\varkappa }_{0n}{|}^p{\varkappa }_{0n}\to {|{\varkappa }_0|}^p{\varkappa }_0\mathrm{weakly}\mathrm{in}{L}^2(0,\mathsf{\delta },L^2\left(\mathrm{\Omega }\right)).$$

(40)

So, by (40), we obtain as $n\to \infty$ that

$${\int }_{\mathrm{\Omega }}v(|{\varkappa }_{0n}{|}^p{\varkappa }_{0n}-|{\varkappa }_0{|}^p{\varkappa }_0)\mathrm{d}\mathrm{y}\to 0\mathrm{for}\mathrm{any}v\in L^2\left(\mathrm{\Omega }\right).$$

By taking $v={\varkappa }_0$ and Hölder’s inequality, we deduce for sufficiently large n that

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}{|{\varkappa }_{0n}|}^p\mathrm{d}\zeta & -{\int }_{\mathrm{\Omega }}{|{\varkappa }_0|}^p\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le \left|{\int }_{\mathrm{\Omega }}({\varkappa }_{0n}-{\varkappa }_0){\varkappa }_{0n}{|{\varkappa }_{0n}|}^{p-2}\mathrm{d}\mathrm{y}\right|\hfill \\ \hfill & +\left|{\int }_{\mathrm{\Omega }}{\varkappa }_0({\varkappa }_{0n}|{\varkappa }_{0n}{|}^{p-2}-{\varkappa }_0|{\varkappa }_0{|}^{p-2})\mathrm{d}\mathrm{y}\right|\hfill \\ \hfill & \le \parallel {\varkappa }_{0n}{\parallel }_p^{p-1}{\parallel {\varkappa }_{0n}-{\varkappa }_0\parallel }_p\hfill \\ \hfill & +\left|{\int }_{\mathrm{\Omega }}{\varkappa }_0({\varkappa }_{0n}|{\varkappa }_{0n}{|}^{p-2}-{\varkappa }_0|{\varkappa }_0{|}^{p-2})\mathrm{d}\mathrm{y}\right|\hfill \\ \hfill & \le c_1\parallel {\varkappa }_0{\parallel }_p^{p-1}{\parallel \Delta {\varkappa }_{0n}-\Delta {\varkappa }_0\parallel }_2\hfill \\ \hfill & +\left|{\int }_{\mathrm{\Omega }}{\varkappa }_0({\varkappa }_{0n}|{\varkappa }_{0n}{|}^{p-2}-{\varkappa }_0|{\varkappa }_0{|}^{p-2})\mathrm{d}\mathrm{y}\right|\to 0,\hfill \end{array}$$

and consequently, for almost everywhere $\mathfrak{s}$ in $(0,\infty )$,

$${\int }_{\mathrm{\Omega }}|{\varkappa }_{0n}{|}^p\mathrm{d}\mathrm{y}\to {\int }_{\mathrm{\Omega }}{|{\varkappa }_0|}^p\mathrm{d}\mathrm{y},\mathit{as}n\to \infty .$$

(41)

According to (36), (38) and (41), we assert that $J\left({\varkappa }_{0n}\right)\to J\left({\varkappa }_0\right)$ an $n\to \infty$, which together with (34) implies for sufficiently large n that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{l+2}}{\parallel {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}& +\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+J\left({\varkappa }^n\right)+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }^n\right)\left(\mathfrak{s}\right)\hfill \\ \hfill & +{\displaystyle \frac{\xi }{2}}{\int }_0^1{\parallel \nabla {\top }^n(\mathrm{y},\eta ,\mathfrak{s})\parallel }_2^2\mathrm{d}\eta \hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\top }^n(\mathrm{y},1,\varrho )\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\varrho \right){\parallel \Delta {\varkappa }^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & \le J\left({\varkappa }_0\right)+M(\parallel \Delta {\varkappa }_0{\parallel }_2,\parallel \Delta {\varkappa }_1{\parallel }_2)+{\displaystyle \frac{\xi }{2}}{\parallel h_0\parallel }_{H_0^2(\mathrm{\Omega }\times (0,1))}^2\hfill \\ \hfill & \le d+M(\parallel \Delta {\varkappa }_0{\parallel }_2,\parallel \Delta {\varkappa }_1{\parallel }_2)+{\displaystyle \frac{\xi }{2}}{\parallel h_0(\mathrm{y},-\eta \mathsf{\tau })\parallel }_{H_0^2(\mathrm{\Omega }\times (0,1))}^2.\hfill \end{array}$$

(42)

Taking into account (20) in (42), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{l+2}}{\parallel {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}& +\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right)\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{p^2}}{\parallel {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_p^p+{\displaystyle \frac{1}{p}}I\left({\varkappa }^n\right)+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }^n\right)\left(\mathfrak{s}\right)\hfill \\ \hfill & +{\displaystyle \frac{\xi }{2}}{\int }_0^1{\parallel \nabla {\top }^n(\mathrm{y},\eta ,\mathfrak{s})\parallel }_2^2\mathrm{d}\eta \hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\varkappa }_{\mathfrak{s}}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\top }^n(\mathrm{y},1,\varrho )\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\varrho \right){\parallel \Delta {\varkappa }^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & \le d+M(\parallel \Delta {\varkappa }_0{\parallel }_2,\parallel \Delta {\varkappa }_1{\parallel }_2)+{\displaystyle \frac{\xi }{2}}{\parallel h_0(\mathrm{y},-\eta \mathsf{\tau })\parallel }_{H_0^2(\mathrm{\Omega }\times (0,1))}^2.\hfill \end{array}$$

(43)

Noting that ${\varkappa }_{0n}\to u_0$ as $n\to \infty$, we see that ${\varkappa }_0\in W$ implies ${\varkappa }_{0n}\in W$ for sufficiently large n, and using Lemma (8), we prove that ${\varkappa }^n\left(\mathfrak{s}\right)\in W$ for sufficiently large n. Therefore, we conclude that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{l+2}}{\parallel {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}& +\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right)\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{p^2}}\parallel {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta {\varkappa }^n\right)\left(\mathfrak{s}\right)+{\displaystyle \frac{\xi }{2}}{\int }_0^1{\parallel \nabla {\top }^n(\mathrm{y},\eta ,\mathfrak{s})\parallel }_2^2\mathrm{d}\eta \hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{2\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\top }^n(\mathrm{y},1,\varrho )\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\varrho \right){\parallel \Delta {\varkappa }^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & \le d+M(\parallel \Delta {\varkappa }_0{\parallel }_2,\parallel \Delta {\varkappa }_1{\parallel }_2)+{\displaystyle \frac{\xi }{2}}{\parallel h_0(\mathrm{y},-\eta \mathsf{\tau })\parallel }_{H_0^2(\mathrm{\Omega }\times (0,1))}^2.\hfill \end{array}$$

(44)

Setting

$$\mathring{d}:=d+M(\parallel \Delta {\varkappa }_0{\parallel }_2,\parallel \Delta {\varkappa }_1{\parallel }_2)+{\displaystyle \frac{\xi }{2}}{\parallel h_0(\mathrm{y},-\eta \mathsf{\tau })\parallel }_{H_0^2(\mathrm{\Omega }\times (0,1))}^2.$$

By (44), we know that ${\mathsf{\delta }}_n$ can be extended to $\mathsf{\delta }$, and we obtain

$$\begin{array}{cc}\hfill {\left\{{\varkappa }^n\right\}}_{n=1}^{\infty }& \mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right))\cap L^{\infty }(0,\mathsf{\delta };L^p\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\left\{{\dot{\varkappa }}^n\right\}}_{n=1}^{\infty }& \mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right))\cap L^2(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\left\{{\top }^n\right\}}_{n=1}^{\infty }& \mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1(\mathrm{\Omega }\times [0,1]))\cap L^2(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right)).\hfill \end{array}$$

(47)

On the other hand, for ${\varkappa }_0\in W$ and applying Lemma 3, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{p}}& \parallel \nabla {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_p^p=J\left({\varkappa }^n\right)-{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}-{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \\ \hfill & \le d+{\displaystyle \frac{1}{p^2}}\left\{p{\int }_{\mathrm{\Omega }}|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p}ln\left({\displaystyle \frac{|{\varkappa }^n(\mathrm{y},\mathfrak{s})|}{\parallel {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_p}}\right)\mathrm{d}\mathrm{y}+{p\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^{p}ln{\parallel {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_p\right\}\hfill \\ \hfill & \le d+{\displaystyle \frac{1}{p^2}}\left\{\mu \parallel \nabla {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_p^p-{\displaystyle \frac{n}{p}}ln\left({\displaystyle \frac{p\mu e}{n{\mathcal{L}}_p}}\right)\parallel {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_p^p+{p\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^{p}ln{\parallel {\varkappa }^n\parallel }_p\right\}.\hfill \end{array}$$

Choosing $\mu <p$ and using (45), we deduce that $\parallel \nabla {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_p^p\le c_d$ which implies that $(\nabla {\varkappa }^n)$ is bounded in $L^p(\mathrm{\Omega }\times (0,\delta ))$ and hence $(\nabla {\varkappa }^n{|}^{p-2}\nabla {\varkappa }^n)$ is bounded in $L^{p/p-1}(\mathrm{\Omega }\times (0,\mathsf{\delta }))$. Applying Dunford–Pettis’ Theorem, we observe from (45)–(47) that there exist subsequences $\left({\dot{\varkappa }}^n\right)$ and $\left({\dot{\top }}^n\right)$ such that

$$\begin{array}{cc}\hfill & {\varkappa }^n\rightharpoonup \varkappa \mathrm{weakly}\mathrm{star}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right))\cap L^{\infty }(0,\mathsf{\delta };L^p\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill & {\dot{\varkappa }}^n\rightharpoonup \dot{\varkappa }\mathrm{weakly}\mathrm{star}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right))\cap L^2(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(49)

$$\begin{array}{c}\hfill {\top }^n\to \top \mathrm{weakly}\mathrm{star}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1(\mathrm{\Omega }\times [0,1]))\cap L^2(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right)),\end{array}$$

(50)

$$\begin{array}{cc}\hfill & |\nabla {\varkappa }^n{|}^{p-2}\nabla {\varkappa }^n\to \psi \mathrm{weakly}\mathrm{in}{L}^{\frac{p}{p-1}}(\mathrm{\Omega }\times (0,\mathsf{\delta })).\hfill \end{array}$$

(51)

Using (48), (49) and [20], we deduce that

$${\varkappa }^n\to \varkappa \mathrm{in}C([0,\mathsf{\delta }],L^2\left(\mathrm{\Omega }\right)),\forall \mathrm{y}\in \overline{\mathrm{\Omega }},$$

(52)

and ${\varkappa }^n\to \varkappa$ a.e $\mathrm{y}\in \mathrm{\Omega }$, for all $\mathfrak{s}\ge 0$. Clearly, (52) implies

$${\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln{\varkappa }^n(\mathrm{y},\mathfrak{s})\to \varkappa (\mathrm{y},\mathfrak{s}){|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln\varkappa (\mathrm{y},\mathfrak{s}),$$

(53)

a.e $\mathrm{y}\in \mathrm{\Omega },\mathfrak{s}\in (0,\mathsf{\delta })$. On the other hand, a direct calculation using (35), (45) and Lemma 2 with $\mathsf{\beta }=1$ gives

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}|{\varkappa }^n(\mathrm{y},\mathfrak{s})& |{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|{|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\int }_{{\mathrm{\Omega }}_1}|{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|{|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{{\mathrm{\Omega }}_2}|{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|{|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{|\mathrm{\Omega }|}{e^2{(p-1)}^2}}+{\int }_{\mathrm{\Omega }}{|{\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{2p}\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{|\mathrm{\Omega }|}{e^2{(p-1)}^2}}+c_1^{2p}{\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^{2p}\le C_p\left(\mathrm{\Omega }\right).\hfill \end{array}$$

(54)

Recalling Lion’s ([21], Lemma 1.3), we arrive at

$${\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|\rightharpoonup \varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|,$$

weakly star in $L^{\infty }(0,\mathsf{\delta };L^2\left(\mathrm{\Omega }\right))$. Differentiating (27) with respect to $\mathfrak{s}$ and after multiplying by ${\mathsf{\alpha }}_{in}^{″}\left(\mathfrak{s}\right)$ and summing over i from 1 to n, we have

$$\begin{array}{cc}\hfill l{\int }_{\mathrm{\Omega }}& |{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}){|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\stackrel{⃛}{\varkappa }}^n(\mathrm{y},\mathfrak{s}){\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +(p-2){\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-4}(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\Delta {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}-g\left(0\right){\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{g}^{\prime }(\mathfrak{s}-\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\mu }_1{\parallel \nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{∥\nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)∥}_2^2+{\mu }_2{\int }_{\mathrm{\Omega }}\nabla {\top }_{\mathfrak{s}}^n(\mathrm{y},1,\mathfrak{s})\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & =(p-1){\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\mathfrak{s}){|{\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(55)

On one hand, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\right\}& ={\int }_{\mathrm{\Omega }}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l\right\}{|{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2\right\}\mathrm{d}\mathrm{y},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l\right\}\mathrm{d}\mathrm{y}& =l{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}){|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s}).\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\right\}& =l{\int }_{\mathrm{\Omega }}|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}){|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +2{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\stackrel{⃛}{\varkappa }}^n(\mathrm{y},\mathfrak{s}){\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\stackrel{⃛}{\varkappa }}^n(\mathrm{y},\mathfrak{s}){\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}& ={\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & -{\displaystyle \frac{l}{2}}{\int }_{\mathrm{\Omega }}|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}){|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

On the other hand, it is convenient to observe that

$$\begin{array}{cc}\hfill -g\left(0\right){\int }_{\mathrm{\Omega }}{|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}& +g\left(0\right){\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{g}^{\prime }(\mathfrak{s}-\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\hfill \\ \hfill & -g^{\prime }\left(0\right){\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{g}^{″}(\mathfrak{s}-\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\hfill \\ \hfill & =g\left(0\right){\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{g}^{\prime }(\mathfrak{s}-\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }.\hfill \end{array}$$

(56)

Taking into account (56) and integrating (55) over $(0,\mathfrak{s})$ yields

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}& |{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{2}}\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\mu }_1{\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\parallel \nabla {\ddot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+g\left(0\right){\int }_0^{\mathfrak{s}}{\parallel \Delta {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & =-{\displaystyle \frac{l}{2}}{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}|{\ddot{\varkappa }}^n{(\mathrm{y},\varrho )|}^2{\dot{\varkappa }}^n(\mathrm{y},\varrho ){|{\dot{\varkappa }}^n(\mathrm{y},\varrho )|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}|{\varkappa }_{1n}{\left(\mathrm{y}\right)|}^l|{\ddot{\varkappa }}^n{(\mathrm{y},0)|}^2\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{2}}\parallel \Delta {\varkappa }_{1n}{\parallel }_2^2+{\displaystyle \frac{1}{2}}{\parallel \nabla {\ddot{\varkappa }}^n\left(0\right)\parallel }_2^2\hfill \\ \hfill & -(p-2){\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-4}(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\varrho )|}^{p-2}\nabla {\dot{\varkappa }}_{\mathfrak{s}}^n(\mathrm{y},\varrho )\nabla {\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +g\left(0\right)\left\{{\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}-{\int }_{\mathrm{\Omega }}\Delta {\varkappa }_{0n}\Delta {\varkappa }_{1n}\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & +{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{g}^{\prime }(\mathfrak{s}-\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\hfill \\ \hfill & -g^{\prime }\left(0\right){\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\varrho )\Delta {\dot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & -{\int }_0^{\mathfrak{s}}{\int }_0^{\varrho }{\int }_{\mathrm{\Omega }}{g}^{\prime \prime }(\varrho -\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\varrho \right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\varrho \hfill \\ \hfill & -{\mu }_2{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\nabla {\dot{\top }}^n(\mathrm{y},1,\varrho )\nabla {\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +(p-1){\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\varrho )|{\varkappa }^n{(\mathrm{y},\varrho )|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\varrho )|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\varrho ){|{\varkappa }^n(\mathrm{y},\varrho )|}^{p-2}{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho .\hfill \end{array}$$

(57)

Differentiating (8) with respect to $\mathfrak{s}$ gives

$${\int }_0^1{\int }_{\mathrm{\Omega }}(\mathsf{\tau }{\ddot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s})+{\dot{\top }}_{\eta }^n(\mathrm{y},\eta ,\mathfrak{s})){\varphi }_i(\mathrm{y},\eta )\mathrm{d}\mathrm{y}\mathrm{d}\eta =0.$$

(58)

Replacing ${\varphi }_i(\mathrm{y},\eta )$ with $-\Delta {\varphi }_i(\mathrm{y},\eta )$, multiplying by ${\beta }_{in}^{\prime }\left(\mathfrak{s}\right)$ and summing over i from 1 to n, we obtain

$${\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}|\nabla {\dot{\top }}^n{(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\eta }}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta =0.$$

(59)

Therefore, we obtain

$${\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}\left(|\nabla {\dot{\top }}^n{(\mathrm{y},1,\mathfrak{s})|}^2-{|\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\right)\mathrm{d}\mathrm{y}=0.$$

(60)

Integrating (60) with respect to $\mathfrak{s}$, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathsf{\tau }}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta & +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},1,\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & ={\displaystyle \frac{\mathsf{\tau }}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},\eta ,0)|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta \hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho .\hfill \end{array}$$

(61)

Summing (57) and (61), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}& |{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{2}}\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+\left({\mu }_1-{\displaystyle \frac{1}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\parallel \nabla {\ddot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+g\left(0\right){\int }_0^{\mathfrak{s}}{\parallel \Delta {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\tau }}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}|\nabla {\dot{\top }}^n{(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},1,\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & =-{\displaystyle \frac{l}{2}}{\int }_{\mathrm{\Omega }}|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}){|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}|{\varkappa }_{1n}{\left(\mathrm{y}\right)|}^l|{\ddot{\varkappa }}^n{(\mathrm{y},0)|}^2\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{2}}{\parallel \Delta {\varkappa }_{1n}\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\parallel \nabla {\ddot{\varkappa }}^n{\left(0\right)\parallel }_2^2+{\displaystyle \frac{\mathsf{\tau }}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},\eta ,0)|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta \hfill \\ \hfill & -(p-2){\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-4}(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}|\nabla {\varkappa }^n{(\mathrm{y},\varrho |}^{p-2}\nabla {\dot{\varkappa }}^n(\mathrm{y},\varrho )\nabla {\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +g\left(0\right)\{{\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}\Delta {\varkappa }_{0n}\Delta {\varkappa }_{1n}\mathrm{d}\mathrm{y}\}+{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{g}^{\prime }(\mathfrak{s}-\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\hfill \\ \hfill & -g^{\prime }\left(0\right){\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\varrho )\Delta {\dot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & -{\int }_0^{\mathfrak{s}}{\int }_0^{\varrho }{\int }_{\mathrm{\Omega }}{g}^{\prime \prime }(\varrho -\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\varrho \right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\varrho \hfill \\ \hfill & -{\mu }_2{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\nabla {\dot{\top }}^n(\mathrm{y},1,\varrho )\nabla {\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +(p-1){\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\varrho )|{\varkappa }^n{(\mathrm{y},\varrho )|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\varrho )|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\varrho ){|{\varkappa }^n(\mathrm{y},\varrho )|}^{p-2}{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho .\hfill \end{array}$$

(62)

Now, we estimate each term on the right-hand side of (62). Taking into account the Cauchy–Schwarz and Hölder inequalities, we have for any $\sigma >0$

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-4}& (\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le {\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\varrho )|}^{p-2}\nabla {\dot{\varkappa }}^n(\mathrm{y},\varrho )\nabla {\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \parallel \nabla {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_{2(p-1)}^{p-2}\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_{2(p-1)}{\parallel \nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2\hfill \\ \hfill & \le c_2^{p-2}{\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^{p-2}\left\{{\displaystyle \frac{c_2^2{\kappa }_1^2}{4\sigma }}+\sigma {\parallel \nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\right\}\hfill \\ \hfill & \le c_2^{p-2}{\kappa }_0^{p-2}\left\{{\displaystyle \frac{c_2^2{\kappa }_1^2}{4\sigma }}+\sigma {\parallel \nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\right\},\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill \left|{\int }_{\mathrm{\Omega }}\Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\right|& \le {\displaystyle \frac{1}{4\sigma }}\parallel \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+\sigma {\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & \le {\displaystyle \frac{{\kappa }_0^2}{4\sigma }}+\sigma {\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2,\hfill \end{array}$$

(64)

and

$$\left|{\int }_{\mathrm{\Omega }}\Delta {\varkappa }_{0n}\Delta {\varkappa }_{1n}\mathrm{d}\mathrm{y}\right|\le {\displaystyle \frac{1}{2}}\parallel \Delta {\varkappa }_{0n}{\parallel }_2^2+{\displaystyle \frac{1}{2}}{\parallel \Delta {\varkappa }_{1n}\parallel }_2^2,$$

(65)

Moreover,

$$\begin{array}{cc}\hfill |{\int }_0^{\mathfrak{s}}& {\int }_{\mathrm{\Omega }}{g}^{\prime }(\mathfrak{s}-\zeta )\Delta {\varkappa }^n\left(\zeta \right)\Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\zeta |\hfill \\ \hfill & \le \sigma {\int }_{\mathrm{\Omega }}{|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{4\sigma }}{\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )\Delta {\varkappa }^n\left(\zeta \right)\mathrm{d}\zeta \right)}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \sigma {\int }_{\mathrm{\Omega }}{|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\displaystyle \frac{1}{4\sigma }}{\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )\left(|\Delta {\varkappa }^n\left(\zeta \right)-\Delta {\varkappa }^n\left(\mathfrak{s}\right)|+|\Delta {\varkappa }^n\left(\mathfrak{s}\right)|\right)\mathrm{d}\zeta \right)}^2\mathrm{d}\mathrm{y}.\hfill \end{array}$$

Using Hypothesis (H1), we obtain

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}& {\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )(|\Delta {\varkappa }^n\left(\zeta \right)-\Delta {\varkappa }^n\left(\mathfrak{s}\right)|+|\Delta {\varkappa }^n\left(\mathfrak{s}\right)|)\mathrm{d}\zeta \right)}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le {\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )(|\Delta {\varkappa }^n\left(\zeta \right)-\Delta {\varkappa }^n\left(\mathfrak{s}\right)|)\mathrm{d}\zeta \right)}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )|\Delta {\varkappa }^n\left(\mathfrak{s}\right)|\mathrm{d}\zeta \right)}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +2{\int }_{\mathrm{\Omega }}\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )\left(|\Delta {\varkappa }^n\left(\zeta \right)-\Delta {\varkappa }^n\left(\mathfrak{s}\right)|\right)\mathrm{d}\zeta \right)\hfill \\ \hfill & \times {\int }_{\mathrm{\Omega }}\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )|\Delta {\varkappa }^n\left(\mathfrak{s}\right)|\mathrm{d}\zeta \right)\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \left(1+{\displaystyle \frac{1}{\sigma }}\right){\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )\left(|\Delta {\varkappa }^n\left(\zeta \right)-\Delta {\varkappa }^n\left(\mathfrak{s}\right)|\right)\mathrm{d}\zeta \right)}^2\mathrm{d}\zeta +(1+\sigma )\hfill \\ \hfill & \times {\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta )|\Delta {\varkappa }^n\left(\mathfrak{s}\right)|\mathrm{d}\zeta \right)}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \left(1+{\displaystyle \frac{1}{\sigma }}\right){\int }_{\mathrm{\Omega }}\left({\int }_0^{\mathfrak{s}}{g}^{\prime }\left(\zeta \right)\mathrm{d}\zeta \right){\int }_0^{\mathfrak{s}}{g}^{\prime }(\mathfrak{s}-\zeta ){|\Delta {\varkappa }^n\left(\zeta \right)-\Delta {\varkappa }^n\left(\mathfrak{s}\right)|}^2\mathrm{d}\zeta \mathrm{d}\mathrm{y}\hfill \\ \hfill & +(1+\sigma ){\int }_{\mathrm{\Omega }}{\left({\int }_0^{\mathfrak{s}}{g}^{\prime }\left(\zeta \right)\mathrm{d}\zeta \right)}^2{|\Delta {\varkappa }^n\left(\mathfrak{s}\right)|}^2\mathrm{d}\zeta \mathrm{d}\mathrm{y}\hfill \\ \hfill & \le g\left(0\right)\left(1+{\displaystyle \frac{1}{\sigma }}\right)(g^{\prime }\circ \Delta {\varkappa }^n)\left(\mathfrak{s}\right)+g^2\left(0\right)(1+\sigma ){\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill |{\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}& g^{\prime }(\mathfrak{s}-\zeta )\Delta {\varkappa }^n\left(\zeta \right)\Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\zeta |\hfill \\ \hfill & \le \sigma \parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+g^2\left(0\right){\displaystyle \frac{1+\sigma }{4\sigma }}{\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & \le \sigma \parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+g^2\left(0\right){\displaystyle \frac{1+\sigma }{4\sigma }}{\kappa }_0^2.\hfill \end{array}$$

(66)

By (H2) and using the similar arguments as the estimate (66), we obtain

$$\begin{array}{cc}\hfill |{\int }_0^{\mathfrak{s}}{\int }_0^{\varrho }{\int }_{\mathrm{\Omega }}& g^{\prime \prime }(\varrho -\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\varrho \right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\varrho |\hfill \\ \hfill & \le {\xi }_2\left|{\int }_0^{\mathfrak{s}}{\int }_0^{\mathsf{\eta }}{\int }_{\mathrm{\Omega }}g(\varrho -\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\varrho \right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\varrho \right|\hfill \\ \hfill & \le {\xi }_2\{\sigma {\int }_0^{\mathfrak{s}}{\parallel \Delta {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho +(1-\vartheta )\left(1+{\displaystyle \frac{1}{\sigma }}\right){\int }_0^{\mathfrak{s}}(g\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho \hfill \\ \hfill & +(1+\sigma ){(1-\vartheta )}^2{\int }_0^{\mathfrak{s}}{\parallel \Delta {\varkappa }^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \}\hfill \\ \hfill & \le {\xi }_2\{\sigma {\int }_0^{\mathfrak{s}}{\parallel \Delta {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +(1-\vartheta )\left(1+{\displaystyle \frac{1}{\sigma }}\right){\int }_0^{\mathfrak{s}}(g\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho +{\kappa }_0^2(1+\sigma ){(1-\vartheta )}^2\mathsf{\delta }\},\hfill \end{array}$$

(67)

On one hand, using hypothesis (H2) with (44), we obtain

$${\xi }_3{\int }_0^{\mathfrak{s}}(g\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho \le -{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta {\varkappa }^n)\left(\varrho \right)\mathrm{d}\varrho \le 2\mathring{d}.$$

(68)

Substituting (68) in (67), we conclude

$$\begin{array}{cc}\hfill |{\int }_0^{\mathfrak{s}}{\int }_0^{\varrho }{\int }_{\mathrm{\Omega }}& g^{\prime \prime }(\varrho -\mathsf{\zeta })\Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\Delta {\dot{\varkappa }}^n\left(\varrho \right)\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\varrho |\hfill \\ \hfill & \le \sigma {\xi }_2{\int }_0^{\mathfrak{s}}{\parallel \Delta {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +2{\displaystyle \frac{{\xi }_2}{{\xi }_3}}(1-\vartheta )\left(1+{\displaystyle \frac{1}{\sigma }}\right)\mathring{d}+{\xi }_2{\kappa }_0^2(1+\sigma ){(1-\vartheta )}^2\mathsf{\delta }.\hfill \end{array}$$

(69)

Choosing $\mathsf{\beta }=1$ in (35) and after using generalised Young’s inequality with exponents $1/2p$, $p-1/2p$ and $1/2$, we will establish the following estimate for

$${\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{\dot{\varkappa }}^n(\mathrm{y},\varrho )|{\varkappa }^n{(\mathrm{y},\varrho )|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\varrho )|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho ,$$

indeed,

$$\begin{array}{cc}\hfill {\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}& {\dot{\varkappa }}^n(\mathrm{y},\varrho )|{\varkappa }^n{(\mathrm{y},\varrho )|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\varrho )|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & \le {\displaystyle \frac{1}{e(p-2)}}{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_1}|{\dot{\varkappa }}^n(\mathrm{y},\varrho )||{\ddot{\varkappa }}^n(\mathrm{y},\varrho )|\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_2}|{\dot{\varkappa }}^n(\mathrm{y},\varrho )||{\varkappa }^n{(\mathrm{y},\varrho )|}^{p-1}|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )|\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & \le {\displaystyle \frac{1}{4e(p-2)\sigma }}{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_1}{|{\dot{\varkappa }}^n(\mathrm{y},\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{\sigma }{e(p-2)}}{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_1}{|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_2}|{\ddot{\varkappa }}^n{(\mathrm{y},\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho +{\displaystyle \frac{1}{2p}}{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_2}{|{\dot{\varkappa }}^n(\mathrm{y},\varrho )|}^{2p}\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & +{\displaystyle \frac{p-1}{2p}}{\int }_0^{\mathfrak{s}}{\int }_{{\mathrm{\Omega }}_2}{|{\varkappa }^n(\mathrm{y},\varrho )|}^{2p}\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & \le c_{*}^2{\displaystyle \frac{\mathsf{\delta }}{4e(p-2)\sigma }}{\kappa }_1^2+c_{*}^2\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sigma }{e(p-2)}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +c_{*}^{2p}{\displaystyle \frac{\mathsf{\delta }}{2p}}{\kappa }_1^{2p}+c_1^{2p}{\displaystyle \frac{p-1}{2p}}{\kappa }_0^{2p}.\hfill \end{array}$$

(70)

On one hand, as estimate (63), we obtain

$$\begin{array}{cc}\hfill {\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}\dot{\varkappa }(\mathrm{y},\varrho )& |{\varkappa }^n{(\mathrm{y},\varrho )|}^{p-2}{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & \le c_1^{p-2}{\kappa }_0^{p-2}\left\{\sigma c_1^2{\int }_0^{\mathfrak{s}}\parallel \Delta {\dot{\varkappa }}^n{\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho +{\displaystyle \frac{1}{4\sigma }}{c}_{*}^2{\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \right\},\hfill \end{array}$$

On the other hand, we have

$$\begin{array}{cc}\hfill {\displaystyle {\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}}& \nabla {\dot{\top }}^n(\mathrm{y},1,\varrho )\nabla {\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & {\displaystyle \le \sigma {\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}|\nabla {\dot{\top }}^n{(\mathrm{y},1,\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho +{\displaystyle \frac{1}{4\sigma }}{\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho .}\hfill \end{array}$$

(71)

Using Hölder’s inequality with exponents $1/2$, $1/l+1$ and $l-1/2(l+1)$, we obtain

$$\begin{array}{cc}\hfill {\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}& |{\ddot{\varkappa }}^n{(\mathrm{y},\varrho )|}^2{\dot{\varkappa }}^n(\mathrm{y},\varrho ){|{\dot{\varkappa }}^n(\mathrm{y},\varrho )|}^{l-2}{\ddot{\varkappa }}^n(\mathrm{y},\varrho )\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & \le {\int }_0^{\mathfrak{s}}{\left({\int }_{\mathrm{\Omega }}{|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )|}^{2(l+1)}\mathrm{d}\mathrm{y}\right)}^{\frac{1}{l+1}}{\left({\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\varrho )|}^{2(l+1)}\mathrm{d}\mathrm{y}\right)}^{\frac{l-1}{2(l+1)}}\hfill \\ \hfill & \times {\left({\int }_{\mathrm{\Omega }}{|{\ddot{\varkappa }}^n(\mathrm{y},\varrho )|}^2\mathrm{d}\mathrm{y}\right)}^{\frac{1}{2}}\mathrm{d}\varrho \hfill \\ \hfill & \le c_{*}^{l+1}{\kappa }_1^{l-1}{\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^3\mathrm{d}\varrho .\hfill \end{array}$$

Testing (27) by ${\mathsf{\alpha }}_{in}^{\prime \prime }\left(\mathfrak{s}\right)$ and choosing $\mathfrak{s}=0$, we obtain

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}{|\nabla {\ddot{\varkappa }}^n(\mathrm{y},0)|}^2& ={\int }_{\mathrm{\Omega }}{\varkappa }_{0n}\left(\mathrm{y}\right)|{\varkappa }_{0n}{\left(\mathrm{y}\right)|}^{p-2}ln|{\varkappa }_{0n}\left(\mathrm{y}\right)|{\ddot{\varkappa }}^n(\mathrm{y},0)\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}|{\varkappa }_{1n}{\left(\mathrm{y}\right)|}^l{|{\ddot{\varkappa }}^n(\mathrm{y},0)|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }_{0n}\left(\mathrm{y}\right)|}^{p-2}\nabla {\varkappa }_{0n}\left(\mathrm{y}\right)\nabla {\ddot{\varkappa }}^n(\mathrm{y},0)\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{\Delta }^2{\varkappa }_{0n}\left(\mathrm{y}\right){\ddot{\varkappa }}^n(\mathrm{y},0)\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\Delta }^2{\varkappa }_{0n}\left(\mathsf{\zeta }\right){\ddot{\varkappa }}^n(\mathrm{y},0)\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\mu }_1{\int }_{\mathrm{\Omega }}\nabla {\varkappa }_{1n}\left(\mathrm{y}\right)\nabla {\ddot{\varkappa }}^n(\mathrm{y},0)\mathrm{d}\mathrm{y}-{\mu }_2{\int }_{\mathrm{\Omega }}\nabla {\top }_{0n}\nabla {\ddot{\varkappa }}^n(\mathrm{y},0)\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(72)

Taking (29) and (30) into account with a large n equality (72) yields

$$\parallel \nabla {\ddot{\varkappa }}^n{(\mathrm{y},0)\parallel }_2^2\le c_3.$$

(73)

We insert (63)–(65), (66), (69)–(71) and (73) in (62) to obtain

$$\begin{array}{cc}{\displaystyle \frac{1}{2}}\hfill & {\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l|{\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s}|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +\left({\displaystyle \frac{1}{2}}-g\left(0\right)\sigma -\sigma \right)\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+\left({\displaystyle \frac{1}{2}}-c_2^{p-2}{\kappa }_0^{p-2}\sigma \right){\parallel \nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +\left({\mu }_1-c_{*}^2(p-1)\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sigma }{e(p-2)}}\right)-{\displaystyle \frac{{\mu }_2}{4\sigma }}-{\displaystyle \frac{c_1^{p-2}{\kappa }_0^{p-2}{c}_{*}^2}{4\sigma }}\right)\hfill \\ \hfill & \times {\int }_0^{\mathfrak{s}}\parallel \nabla {\ddot{\varkappa }}^n{\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho +{\displaystyle \frac{\mathsf{\tau }}{2}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta \hfill \\ \hfill & +\left(g\left(0\right)-{\displaystyle \frac{g^{\prime }\left(0\right)}{4\sigma }}-\sigma {\xi }_2-c_1^{p-2}{\kappa }_0^{p-2}{c}_1^2\sigma \right){\int }_0^{\mathfrak{s}}{\parallel \Delta {\dot{\varkappa }}^n\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \hfill \\ \hfill & +\left({\displaystyle \frac{1}{2}}-{\mu }_2\sigma \right){\int }_0^{\mathfrak{s}}{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\top }}^n(\mathrm{y},1,\varrho )|}^2\mathrm{d}\mathrm{y}\mathrm{d}\varrho \hfill \\ \hfill & \le A\left(\mathsf{\delta }\right)+{\displaystyle \frac{l}{2}}{c}_{*}^{l+1}{\kappa }_1^{l-1}{\int }_0^{\mathfrak{s}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\varrho \right)\parallel }_2^3\mathrm{d}\varrho .\hfill \end{array}$$

(74)

Now, we choose $\sigma$ small enough so that

$$\frac{1}{2}-g\left(0\right)\sigma -\sigma >0,g\left(0\right)-\frac{g^{\prime }\left(0\right)}{4\sigma }-\sigma {\xi }_2-c_1^{p-2}{\kappa }_0^{p-2}{c}_1^2\sigma >0,\frac{1}{2}-{\mu }_2\sigma >0.$$

(75)

After that, according to (10), we may choose ${\mu }_1$ large enough such that

$${\mu }_1-c_{*}^2(p-1)\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sigma }{e(p-2)}}\right)-{\displaystyle \frac{{\mu }_2}{4\sigma }}-{\displaystyle \frac{c_1^{p-2}{\kappa }_0^{p-2}{c}_{*}^2}{4\sigma }}>0.$$

(76)

Putting $z\left(\mathfrak{s}\right)=\parallel {\ddot{\varkappa }}^n{\left(\varrho \right)\parallel }_2^2$, Inequality (74) becomes

$$z\left(\mathfrak{s}\right)\le C_1+C_2{\int }_0^{\mathfrak{s}}{z}^{\frac{3}{2}}\left(\varrho \right)d\varrho .$$

(77)

Differentiating both sides of the equation $w\left(\mathfrak{s}\right)=C_1+C_2{\int }_0^{\mathfrak{s}}{w}^{\frac{3}{2}}\left(\varrho \right)d\varrho$, we obtain

$$w^{\prime }\left(\mathfrak{s}\right)=C_2{w}^{\frac{3}{2}}\left(\mathfrak{s}\right),w\left(0\right)=C_1.$$

(78)

A simple integration of (78) gives

$$w\left(\mathfrak{s}\right)={\left[C_1^{\frac{-1}{2}}-{\displaystyle \frac{1}{2}}{C}_2\mathfrak{s}\right]}^{-2}.$$

(79)

So, by a standard comparison theorem, we obtain $z\left(\mathfrak{s}\right)\le w\left(\mathfrak{s}\right)$. Although $w\left(\mathfrak{s}\right)$ blows up in finite time, there exists a time $0<\delta <{\delta }_n$ such that $z\left(\mathfrak{s}\right)\le w\left(\mathfrak{s}\right)\le \kappa +1$, where $\mathfrak{s}\in [0,\delta ]$ and $\kappa >1$ is independent of n. Therefore, (74) and conditions (75) and (76) ensure that

$$\begin{array}{cc}\hfill {\left\{{\dot{\varkappa }}^n\right\}}_{n=1}^{\infty }& \mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,T;H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(80)

$$\begin{array}{cc}\hfill {\left\{{\ddot{\varkappa }}^n\right\}}_{n=1}^{\infty }& \mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill {\left\{{\dot{\top }}^n\right\}}_{n=1}^{\infty }& \mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1(\mathrm{\Omega }\times [0,1])).\hfill \end{array}$$

(82)

Applying Dunford–Pettis’ Theorem, we observe from (81) and (82) that there exist subsequences $\left({\dot{\varkappa }}^n\right)$ and ${(}_{\mathfrak{s}}^n)$ such that

$$\begin{array}{cc}\hfill {\dot{\varkappa }}^n& \rightharpoonup \dot{\varkappa }\mathrm{weakly}\mathrm{star}\mathrm{in}{L}^{\infty }(0,T;H^2\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill {\ddot{\varkappa }}^n& \rightharpoonup \ddot{\varkappa }\mathrm{weakly}\mathrm{star}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1\left(\mathrm{\Omega }\right)),\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill {\dot{\top }}^n& \rightharpoonup \dot{\top }\mathrm{weakly}\mathrm{star}\mathrm{in}{L}^{\infty }(0,\mathsf{\delta };H_0^1(\mathrm{\Omega }\times [0,1])).\hfill \end{array}$$

(85)

Using (83) and (84) and [20], we deduce that ${\dot{\varkappa }}^n\to \dot{\varkappa }$ in $C([0,\mathsf{\delta }],L^2\left(\mathrm{\Omega }\right)),$ for all $\mathrm{y}\in \overline{\mathrm{\Omega }}$, and ${\dot{\varkappa }}^n\to \dot{\varkappa }$ a.e $\mathrm{y}\in \mathrm{\Omega }$, $\forall \mathfrak{s}\ge 0$. Replacing $w_i\left(\mathrm{y}\right)$ in (27) with $-\Delta w_i\left(\mathrm{y}\right)$, multiplying by ${\mathsf{\alpha }}_{in}^{\prime }\left(\mathfrak{s}\right)$ and summing over i from 1 to n, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\{{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2& +\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2\}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\nabla \Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\nabla \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\mu }_1{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2+{\mu }_2{\int }_{\mathrm{\Omega }}\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & =-{\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(86)

Integrating by parts and noting that ${\dot{\varkappa }}^n=0$ on $\partial \mathrm{\Omega }$, we have

$$\begin{array}{cc}\hfill -{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l& {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & =l{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^{l-1}{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y},\hfill \end{array}$$

(87)

and

$$\begin{array}{cc}\hfill l{\int }_{\mathrm{\Omega }}{\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})& |{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^{l-1}{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & -2{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}){|}^l|\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(88)

Inserting (88) in (87), we deduce

$$\begin{array}{cc}\hfill -{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l& {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(89)

On the other hand,

$$\begin{array}{cc}\hfill -{\int }_{\mathrm{\Omega }}{\int }_0^{\mathfrak{s}}& g(\mathfrak{s}-\mathsf{\zeta })\nabla \Delta {\varkappa }^n\left(\mathsf{\zeta }\right)\nabla \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right){\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2-{\displaystyle \frac{1}{2}}(g^{\prime }\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)-\left({\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\right\}.\hfill \end{array}$$

(90)

Replacing ${\varphi }_i(\mathrm{y},\eta )$ with ${\Delta }^2{\varphi }_i(\mathrm{y},\eta )$, multiplying by ${\beta }_{in}\left(\mathfrak{s}\right)$ and summing over i from 1 to n, we obtain

$${\displaystyle \frac{\mathsf{\tau }}{2}}{\int }_0^1{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_{\mathrm{\Omega }}|\Delta {\top }^n{(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\displaystyle \frac{1}{2}}{\int }_0^1{\displaystyle \frac{d}{\mathrm{d}\eta }}{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta =0.$$

(91)

Therefore, we obtain

$${\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}|\Delta {\top }^n{(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}|\Delta {\top }^n{(\mathrm{y},1,\mathfrak{s})|}^2-{|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}=0.$$

(92)

Inserting (89) and (90) in (86) and after summing the result with (92), we deduce

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\{& \parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+2{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)-\left({\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\}\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}|\Delta {\top }^n{(\mathfrak{s},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta +{\mu }_1{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right)\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}-{\displaystyle \frac{1}{2}}(g^{\prime }\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\parallel \Delta \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2^2-{\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\mu }_2{\int }_{\mathrm{\Omega }}\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(93)

On the other hand, it is convenient to observe that

$$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}& |\nabla {\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & -(p-2){\int }_{\mathrm{\Omega }}|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s}){|}^{p-4}(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})))\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

Therefore, (93) is rewritten as

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}& \{\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+2{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)-\left({\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\}\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta \hfill \\ \hfill & +{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}(g^{\prime }\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)+{\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right){\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\mu }_1\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\parallel \Delta \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2^2-{\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & -{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\dot{\varkappa }}^n(\mathrm{y},t\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & +(p-2){\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-4}(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s}))\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}-{\mu }_2{\int }_{\mathrm{\Omega }}\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(94)

Applying Young’s inequality and using (80) and (81), we obtain

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l& \nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le {\displaystyle \frac{l}{2(l+1)}}{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{2(l+1)}\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}|\nabla {\ddot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{2(l+1)}}{\int }_{\mathrm{\Omega }}{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^{2(l+1)}\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{l}{2(l+1)}}{c}_1^{2(l+1)}\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^{2(l+1)}+{\displaystyle \frac{1}{2}}{\parallel \nabla {\ddot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{c_2^{2(l+1)}}{2(l+1)}}{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^{2(l+1)}\hfill \\ \hfill & \le {\displaystyle \frac{{\kappa }_2^2}{2(l+1)}}(l{c}_1^{2(l+1)}+c_2^{2(l+1)})+{\displaystyle \frac{{\kappa }_3^2}{2}},\hfill \end{array}$$

(95)

and from (45), we obtain

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}& \nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le {\displaystyle \frac{p-2}{2(p-1)}}{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{2(p-1)}\mathrm{d}\mathrm{y}\hfill \\ \hfill & +{\displaystyle \frac{1}{2(p-1)}}{\int }_{\mathrm{\Omega }}|\nabla {\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^{2(p-1)}\mathrm{d}\mathrm{y}+{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}{|\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{p-2}{2(p-1)}}{c}_2^{2(p-1)}{\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^{2(p-1)}\hfill \\ \hfill & +{\displaystyle \frac{c_2^{2(p-1)}}{2(p-1)}}\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^{2(p-1)}+{\displaystyle \frac{1}{2}}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & \le {\displaystyle \frac{p-2}{2(p-1)}}{c}_2^{2(p-1)}{\kappa }_0^{2(p-1)}+{\displaystyle \frac{c_2^{2(p-1)}}{2(p-1)}}{\kappa }_2^{2(p-1)}+{\displaystyle \frac{1}{2}}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2.\hfill \end{array}$$

(96)

Moreover, we obtain

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})& |{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le {\int }_{\mathrm{\Omega }}{|{\varkappa }^n(\mathrm{y},\mathfrak{s},\mathfrak{s})|}^p\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s},\mathfrak{s})\mathrm{d}\mathrm{y},\mathfrak{s}+{\displaystyle \frac{1}{e(p-1)}}{\int }_{\mathrm{\Omega }}\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \parallel {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_{2p}^p\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2+{\displaystyle \frac{\sqrt{|\mathrm{\Omega }|}}{e(p-1)}}{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2\hfill \\ \hfill & \le c_1^p\parallel \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^p\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2+{\displaystyle \frac{\sqrt{|\mathrm{\Omega }|}}{e(p-1)}}{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2\hfill \\ \hfill & \le {\kappa }_2\left(c_1^p{\kappa }_0^p+{\displaystyle \frac{\sqrt{|\mathrm{\Omega }|}}{e(p-1)}}\right),\hfill \end{array}$$

(97)

and using (45) and (80), we obtain

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-4}& \nabla {\varkappa }^n((\mathrm{y},\mathfrak{s})\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s}))(\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s}))\mathrm{d}\mathrm{y}|\hfill \\ \hfill & \le \parallel \nabla {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_{2(p-1)}^{p-2}.\parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_{2(p-1)}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2\hfill \\ \hfill & \le c_2^{p-2}{\parallel \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^{p-2}\left(\sigma \parallel \nabla {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_{2(p-1)}^2+{\displaystyle \frac{1}{4\sigma }}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\right)\hfill \\ \hfill & \le c_2^{p-2}{\kappa }_0^{p-2}\left(c_2^2\sigma \parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{4\sigma }}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\right)\hfill \\ \hfill & \le c_2^{p-2}{\kappa }_0^{p-2}\left(c_2^2{\kappa }_2^2\sigma +{\displaystyle \frac{1}{4\sigma }}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\right),\hfill \end{array}$$

(98)

and

$$\begin{array}{cc}\hfill |{\int }_{\mathrm{\Omega }}\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})\Delta {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}|& \le {\displaystyle \frac{1}{4\sigma }}{\int }_{\mathrm{\Omega }}|\Delta {\top }^n{(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+\sigma {\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & \le {\displaystyle \frac{1}{4\sigma }}{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+\sigma {\kappa }_2^2.\hfill \end{array}$$

(99)

Substituting (95)–(99) in (94), we conclude

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}& \{\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +2{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)\}\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta \hfill \\ \hfill & +{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}(g^{\prime }\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)+{\displaystyle \frac{1}{2}}g\left(\mathfrak{s}\right){\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\mu }_1\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le A_2+\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{4\sigma }}\right)\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{{\mu }_2}{4\sigma }}{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y},\hfill \end{array}$$

(100)

for some constant $A_2>0$. On the other hand, we observe that

$$\begin{array}{cc}\hfill -{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}& \nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le \parallel \nabla {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_{2(p-1)}^{p-1}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2\hfill \\ \hfill & \le {\displaystyle \frac{c_1^{2(p-1)}}{2}}\parallel \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^{2(p-1)}+{\displaystyle \frac{1}{2}}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & \le {\displaystyle \frac{c_1^{2(p-1)}{\kappa }_0^{2(p-1)}}{2}}+{\displaystyle \frac{1}{2}}{\parallel \nabla \Delta {\varkappa }^n\left(\mathfrak{s}\right)\parallel }_2^2.\hfill \end{array}$$

Therefore,

$$c_1^{2(p-1)}{\kappa }_0^{2(p-1)}+\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\ge 0.$$

(101)

Recalling (H1), using (100) and (101), we arrive at

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}& \{\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +2{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}+(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)\}\hfill \\ \hfill & +{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}\left\{{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\right\}\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\tau }}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}}{\int }_0^1{\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\eta \hfill \\ \hfill & +{\displaystyle \frac{{\xi }_3}{2}}(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)+{\mu }_1{\parallel \Delta {\dot{\varkappa }}^n\left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +\left({\displaystyle \frac{1}{2}}-{\mu }_2{\displaystyle \frac{c_{*}^2}{4\sigma }}\right){\int }_{\mathrm{\Omega }}{|\Delta {\top }^n(\mathrm{y},1,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & \le A+\parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla \Delta {\varkappa }^n(\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}.\hfill \end{array}$$

(102)

Choosing $\sigma$ large enough such that $\frac{1}{2}-{\mu }_2\frac{c_{*}^2}{4\sigma }>0$, and after applying Gronwall’s inequality, we obtain

$$\begin{array}{cc}\hfill \parallel \nabla \Delta {\varkappa }^n{\left(\mathfrak{s}\right)\parallel }_2^2& +\parallel \Delta {\dot{\varkappa }}^n{\left(\mathfrak{s}\right)\parallel }_2^2+{\int }_{\mathrm{\Omega }}|{\dot{\varkappa }}^n{(\mathrm{y},\mathfrak{s})|}^l{|\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\hfill \\ \hfill & +(g\circ \nabla \Delta {\varkappa }^n)\left(\mathfrak{s}\right)+{\int }_0^{\mathfrak{s}}{\parallel \nabla \ddot{\varkappa }\left(\varrho \right)\parallel }_2^2\mathrm{d}\varrho \le A\left(\mathsf{\delta }\right).\hfill \end{array}$$

At this step, similar as in [22], we have $\psi ={|\nabla \varkappa |}^{p-2}\nabla \varkappa$. Taking $\theta \left(\mathfrak{s}\right)\in \mathcal{D}(0,\mathsf{\delta })$ a nonnegative function, where $\mathcal{D}(0,\mathsf{\delta })$ is the space of $C^{\infty }$-function with compact support in $(0,\delta )$, and multiplying (27) by $\theta \left(\mathfrak{s}\right)$. Integrating the obtained result over $(0,\delta )$, we conclude

$$\begin{array}{cc}\hfill -{\displaystyle \frac{1}{l+1}}& {\int }_0^{\delta }{\int }_{\mathrm{\Omega }}{|{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})|}^l{\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}{|\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})|}^{p-2}\nabla {\varkappa }^n(\mathrm{y},\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\Delta \left({\varkappa }^n(\mathrm{y},\mathfrak{s})-{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\varkappa }^n\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)\Delta w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\mu }_1{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\nabla {\dot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\mu }_2{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\nabla {\top }^n(\mathrm{y},1,\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\nabla {\ddot{\varkappa }}^n(\mathrm{y},\mathfrak{s})\nabla w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & ={\int }_0^{\delta }{\int }_{\mathrm{\Omega }}{\varkappa }^n(\mathrm{y},\mathfrak{s})|{\varkappa }^n{(\mathrm{y},\mathfrak{s})|}^{p-2}ln|{\varkappa }^n(\mathrm{y},\mathfrak{s})|w_i\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

(103)

Multiplying (28) by $\theta \left(\mathfrak{s}\right)$ and integrating the result over $(0,\delta )$, we obtain

$$\begin{array}{cc}\hfill \mathsf{\tau }{\int }_0^{\delta }{\int }_0^1{\int }_{\mathrm{\Omega }}& {\dot{\top }}^n(\mathrm{y},\eta ,\mathfrak{s}){\varphi }_i(\mathrm{y},\eta )\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\eta \mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_0^1{\int }_{\mathrm{\Omega }}{\top }_{\eta }(\mathrm{y},\eta ,\mathfrak{s}){\varphi }_i(\mathrm{y},\eta )\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\eta \mathrm{d}\mathfrak{s}=0.\hfill \end{array}$$

(104)

Recalling convergences (48)–(51), (53) and (83), we can pass to the limit as n goes to ∞ in (103) and (104) to obtain

$$\begin{array}{cc}\hfill -{\displaystyle \frac{1}{l+1}}& {\int }_0^{\delta }{\int }_{\mathrm{\Omega }}{|\dot{\varkappa }(\mathrm{y},\mathfrak{s})|}^l\dot{\varkappa }(\mathrm{y},\mathfrak{s})w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}{|\nabla \varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}\nabla \varkappa (\mathrm{y},\mathfrak{s})\nabla w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\Delta \left(\varkappa (\mathrm{y},\mathfrak{s})-{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\varkappa \left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)\Delta w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\mu }_1{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\nabla \dot{\varkappa }(\mathrm{y},\mathfrak{s})\nabla w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\mu }_2{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\nabla \top (\mathrm{y},1,\mathfrak{s})\nabla w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_0^{\delta }{\int }_{\mathrm{\Omega }}\nabla \ddot{\varkappa }(\mathrm{y},\mathfrak{s})\nabla w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & ={\int }_0^{\delta }{\int }_{\mathrm{\Omega }}{\varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|w\left(\mathrm{y}\right)\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathsf{\tau }{\int }_0^{\delta }{\int }_0^1{\int }_{\mathrm{\Omega }}& \dot{\top }(\mathrm{y},\eta ,\mathfrak{s})\varphi (\mathrm{y},\eta )\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\eta \mathrm{d}\mathfrak{s}\hfill \\ \hfill & {\displaystyle +{\int }_0^{\delta }{\int }_0^1{\int }_{\mathrm{\Omega }}{\top }_{\eta }(\mathrm{y},\eta ,\mathfrak{s}){\varphi }_i(\mathrm{y},\eta )\theta \left(\mathfrak{s}\right)\mathrm{d}\mathrm{y}\mathrm{d}\eta \mathrm{d}\mathfrak{s}=0.}\hfill \end{array}$$

Then, the local existence of weak solutions is established. □

3.2. General Decay of Global Solution

We will derive the decay rate of the energy functional for Cauchy problem (9) by Nakao’s method, as in [23].

Theorem 2.

Assume that the assumptions (H1)–(H3) hold. Let ${\varkappa }_0\in W$ be given. The energy associated to Problem (9) satisfies for a positive constant $\sigma >0$,

$$E\left(\mathfrak{s}\right)\le \left\{\begin{array}{cc}E\left(0\right)e^{-{[\mathfrak{s}-1]}^{+}ln\left({\displaystyle \frac{\sigma }{\sigma -1}}\right)},\hfill & l=2,\hfill \\ {\left(E{\left(0\right)}^{-\frac{l}{2}}+{\sigma }^{-1}\frac{l}{2}{[\mathfrak{s}-1]}^{+}\right)}^{\frac{-2}{l}},\hfill & l>2,\hfill \end{array}\right.$$

(105)

Proof. 

By integrating (15) over $[\mathfrak{s},\mathfrak{s}+1]$, we obtain

$$\begin{array}{cc}\hfill B^2\left(\mathfrak{s}\right)& :=-{\displaystyle \frac{1}{2}}{\int }_{\mathfrak{s}}^{\mathfrak{s}+1}(g^{\prime }\circ \Delta u)\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+{\displaystyle \frac{1}{2}}{\int }_{\mathfrak{s}}^{\mathfrak{s}+1}g\left(\mathfrak{s}\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2\mathrm{d}\mathfrak{s},\hfill \end{array}$$

(106)

where $B^2\left(\mathfrak{s}\right)=E\left(\mathfrak{s}\right)-E(\mathfrak{s}+1)$. By (106), we observe that

$$\begin{array}{cc}\hfill {\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\int }_{\mathrm{\Omega }}{|\dot{\varkappa }(\mathrm{y},\mathfrak{s})|}^{l+2}\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}& +\left({\mu }_1-{\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le c_{*}^{l+2}{\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_{\mathfrak{s}}^{\mathfrak{s}+1}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le \sigma \left(\mathrm{\Omega }\right)B^2\left(\mathfrak{s}\right).\hfill \end{array}$$

By mean value theorem, there exists ${\mathfrak{s}}_1\in \left[\mathfrak{s},\mathfrak{s}+\frac{1}{4}\right]$ and ${\mathfrak{s}}_2\in \left[\mathfrak{s}+\frac{3}{4},\mathfrak{s}+1\right]$ such that

$$\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_{l+2}^{l+2}+\parallel \nabla \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_2^2+{\parallel \nabla \top (\mathrm{y},1,{\mathfrak{s}}_i)\parallel }_2^2\le 4\sigma \left(\mathrm{\Omega }\right)B^2\left(\mathfrak{s}\right),i=1,2.$$

(107)

Multiplying the first equation of (9) by $\varkappa \left(\mathfrak{s}\right)$ and integrating by parts the result over $\mathrm{\Omega }\times \left[{\mathfrak{s}}_1,{\mathfrak{s}}_2\right]$, we obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}& |\dot{\varkappa }{(\mathrm{y},\mathfrak{s})|}^l\ddot{\varkappa }(\mathrm{y},\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}+{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}{\Delta }^2\left(\varkappa (\mathrm{y},\mathfrak{s})-{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\varkappa \left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right)\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\mu }_1{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \dot{\varkappa }(\mathrm{y},\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\mu }_2{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \top (\mathrm{y},1,\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \ddot{\varkappa }(\mathrm{y},\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & ={\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

(108)

By integrating by parts and using Cauchy–Schwarz inequality, we deduce

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}{|\dot{\varkappa }(\mathrm{y},\mathfrak{s})|}^l\ddot{\varkappa }(\mathrm{y},\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}& \le {\displaystyle \frac{1}{1+l}}\sum _{i=1}^2\parallel \varkappa \left({\mathfrak{s}}_i\right){\parallel }_{2+l}{\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right)\parallel }_{2+l}^{1+l}\hfill \\ \hfill & +{\displaystyle \frac{1}{1+l}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}\mathrm{d}\mathfrak{s},\hfill \\ \hfill -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \ddot{\varkappa }(\mathrm{y},\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}& \le \sum _{i=1}^2\parallel \nabla \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_2\parallel \nabla \varkappa \left({\mathfrak{s}}_i\right){\parallel }_2+{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s},\hfill \\ \hfill & -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \dot{\varkappa }(\mathrm{y},\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2{\parallel \nabla u\left(\mathfrak{s}\right)\parallel }_2\hfill \\ \hfill -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \top (\zeta ,1,\mathfrak{s})\varkappa (\mathrm{y},\mathfrak{s})\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}& \le {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

(109)

We notice that

$$\begin{array}{cc}\hfill -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}& {\Delta }^2\varkappa (\mathrm{y},\mathfrak{s}){\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\varkappa (\mathrm{y},\mathsf{\zeta })\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & ={\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}\Delta \varkappa (\mathrm{y},\mathfrak{s}){\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })(\Delta \varkappa (\mathrm{y},\mathfrak{s})-\Delta \varkappa (\mathrm{y},\mathsf{\zeta }))\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s},\hfill \end{array}$$

(110)

and

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}& \Delta \varkappa (\mathrm{y},\mathfrak{s}){\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })(\Delta \varkappa (\mathrm{y},\mathfrak{s})-\Delta \varkappa (\mathrm{y},\mathsf{\zeta }))\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\{{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\left({\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\left({\parallel \Delta \varkappa \left(\mathfrak{s}\right)-\Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\}\hfill \\ \hfill & +{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

(111)

Combining (110) and (111), we obtain

$$\begin{array}{cc}\hfill -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}& {\int }_{\mathrm{\Omega }}{\Delta }^2\varkappa (\mathrm{y},\mathfrak{s}){\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\varkappa (\mathrm{y},\mathsf{\zeta })\mathrm{d}\mathrm{y}\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\{{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\left({\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\left({\parallel \Delta \varkappa \left(\mathfrak{s}\right)-\Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\right)\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}+{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}(g\circ \Delta \varkappa )\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

(112)

Substituting (109) and (112) in (108), adding and subtracting the term

$${\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s},$$

we conclude

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}I\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}& ={\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\mathrm{d}\mathfrak{s}-{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le {\displaystyle \frac{1}{1+l}}\sum _{i=1}^2\parallel \varkappa \left({\mathfrak{s}}_i\right){\parallel }_{2+l}\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_{2+l}^{1+l}+{\displaystyle \frac{1}{1+l}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\sum _{i=1}^2\parallel \nabla \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_2\parallel \nabla \varkappa \left({\mathfrak{s}}_i\right){\parallel }_2+{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_{{\varkappa }_1}^{{\varkappa }_2}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\tau }){\parallel \Delta \varkappa \left(\mathsf{\tau }\right)\parallel }_2^2\mathrm{d}\mathsf{\tau }\mathrm{d}\eta +{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}(g\circ \Delta \varkappa )\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

(113)

Moreover, by (21), we have

$$\begin{array}{cc}\hfill E\left(\mathfrak{s}\right)& ={\displaystyle \frac{1}{l+2}}\parallel \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}+{\displaystyle \frac{1}{2}}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}(g\circ \Delta \varkappa )\left(\mathfrak{s}\right)\hfill \\ \hfill & +\xi {\int }_{\mathrm{\Omega }}{\int }_0^1{|\nabla \top (\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\mathrm{y}\mathrm{d}\zeta \hfill \\ \hfill & +\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right)\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \parallel }_p^p+{\displaystyle \frac{1}{p}}I\left(\varkappa \right).\hfill \end{array}$$

(114)

Now, we will estimate the right-hand side of (113). Using (107), (114) and Lemma 2, we obtain

$$\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_{l+2}^{l+1}=\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_{l+2}^{l-1}\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_{l+2}^2\le c_{*}^{l-1}{(l+2)}^{\frac{2}{l+2}}{E}^{\frac{2}{l+2}}\left(0\right){\parallel \nabla \dot{\varkappa }\left({\mathfrak{s}}_i\right)\parallel }_2^{l-1},$$

and

$$\parallel \varkappa \left({\mathfrak{s}}_i\right){\parallel }_{l+2}\le c_1{\parallel \Delta \varkappa \left({\mathfrak{s}}_i\right)\parallel }_2\le c_1\sqrt{{\displaystyle \frac{2p}{\vartheta (p-2)}}}\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right).$$

Therefore,

$$\begin{array}{cc}\parallel \varkappa \left({\mathfrak{s}}_i\right){\parallel }_{l+2}{\parallel \dot{\varkappa }\left({\mathfrak{s}}_i\right)\parallel }_{l+2}^{l+1}\hfill & \le 4^{\frac{l-1}{2}}{c}_1\sqrt{{\displaystyle \frac{2p}{\vartheta (p-2)}}}{c}_{*}^{l-1}{\sigma }^{\frac{l-1}{2}}\left(\mathrm{\Omega }\right)\hfill \\ \hfill & \times {\left((l+2)E\left(0\right)\right)}^{\frac{2}{l+2}}{B}^{l-1}\left(\mathfrak{s}\right)\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right),\hfill \end{array}$$

(115)

and

$$\begin{array}{c}\hfill \parallel \nabla \dot{\varkappa }\left({\mathfrak{s}}_i\right){\parallel }_2{\parallel \nabla \varkappa \left({\mathfrak{s}}_i\right)\parallel }_2\le 4c_2\sqrt{{\displaystyle \frac{\sigma \left(\mathrm{\Omega }\right)p}{\vartheta (p-2)}}}B\left(\mathfrak{s}\right)\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right).\end{array}$$

(116)

Moreover, we have

$$\begin{array}{cc}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill & \le {\displaystyle \frac{\sigma \left(\mathrm{\Omega }\right)}{\left({\mu }_1-\frac{\xi }{\mathsf{\tau }}-\frac{|{\mu }_2|}{2}\right)}}{B}^2\left(\mathfrak{s}\right)\hfill \\ {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}\mathrm{d}\eta \hfill & \le \sigma \left(\mathrm{\Omega }\right)B^2\left(\mathfrak{s}\right).\hfill \end{array}$$

(117)

By using Hölder’s inequality, we observe that

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2\mathrm{d}\mathfrak{s}& \le {\left({\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\right)}^{\frac{1}{2}}{\left({\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le c_2\sqrt{2{\displaystyle \frac{p\sigma \left(\mathrm{\Omega }\right)}{\vartheta \left({\mu }_1-\frac{\xi }{\mathsf{\tau }}-\frac{|{\mu }_2|}{2}\right)(p-2)}}}B\left(\mathfrak{s}\right)\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right).\hfill \end{array}$$

(118)

Similarly, we obtain

$${\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2\mathrm{d}\mathfrak{s}\le c_2\sqrt{2{\displaystyle \frac{p\sigma \left(\mathrm{\Omega }\right)}{\vartheta \left(\frac{\xi }{\mathsf{\tau }}-\frac{|{\mu }_2|}{2}\right)(p-2)}}}B\left(\mathfrak{s}\right)\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right).$$

(119)

Applying Young’s inequality for convolution ${\parallel \varphi \ast \psi \parallel }_q\le {\parallel \varphi \parallel }_r{\parallel \psi \parallel }_s$,

$${\displaystyle \frac{1}{q}}={\displaystyle \frac{1}{r}}+{\displaystyle \frac{1}{s}}-1,1\le q,r,s\le \infty ,$$

and recalling (19), (23) and (114), we obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}& {g(\mathfrak{s}-\mathsf{\zeta })\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\le {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}g\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le {\displaystyle \frac{1-\vartheta }{\vartheta }}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\left(I\left(\mathfrak{s}\right)+{\int }_{\mathrm{\Omega }}{|\varkappa (\mathrm{y},\mathfrak{s})|}^{p}ln|\varkappa (\mathrm{y},\mathfrak{s})|\mathrm{d}\mathrm{y}\right)\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le {\displaystyle \frac{1-\vartheta }{\vartheta }}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\left(I\left(\mathfrak{s}\right)+c_1^{p+\mathsf{\beta }}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^{p+\mathsf{\beta }}\right)\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le {\displaystyle \frac{1-\vartheta }{\vartheta }}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}I\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+c_1^{p+\mathsf{\beta }}{\displaystyle \frac{1-\vartheta }{\vartheta }}{\left({\displaystyle \frac{2p}{\vartheta (p-2)}}\right)}^{\frac{p+\mathsf{\beta }}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{E}^{\frac{p+\mathsf{\beta }}{2}}\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}.\hfill \end{array}$$

Taking $\mathsf{\beta }=2$ and noting that ${\mathfrak{s}}_2-{\mathfrak{s}}_1\le 1$, we have

$$\begin{array}{cc}{\displaystyle {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}}\hfill & {\displaystyle {g(\mathfrak{s}-\mathsf{\zeta })\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}}\hfill \\ \hfill & {\displaystyle \le {\displaystyle \frac{1-\vartheta }{\vartheta }}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}I\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+c_1^{p+2}{\displaystyle \frac{1-\vartheta }{\vartheta }}{\left({\displaystyle \frac{2p}{\vartheta (p-2)}}\right)}^{\frac{p+2}{2}}{E}^{\frac{p}{2}}\left(0\right)\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}E\left(\mathfrak{s}\right).}\hfill \end{array}$$

(120)

On the other hand,

$$\begin{array}{cc}{\displaystyle {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}}\hfill & {\displaystyle \le {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\displaystyle \frac{2p}{\vartheta (p-2)}}E\left(\mathfrak{s}\right){\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}}\hfill \\ \hfill & {\displaystyle \le {\displaystyle \frac{2p}{\vartheta (p-2)}}(1-\vartheta )\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}E\left(\mathfrak{s}\right).}\hfill \end{array}$$

(121)

Exploiting (120), (121) and the fact ${(x-y)}^2\le 2(x^2+y^2)$ for any $x,y\in \mathbb{R}$, we arrive at

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}& \left(g\circ \Delta \varkappa \right)\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}={\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)-\Delta \varkappa \left(\eta \right)\parallel }_2^2\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le 2\{{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta }){\parallel \Delta \varkappa \left(\mathsf{\zeta }\right)\parallel }_2^2\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2{\int }_0^{\mathfrak{s}}g(\mathfrak{s}-\mathsf{\zeta })\mathrm{d}\mathsf{\zeta }\mathrm{d}\mathfrak{s}\}\hfill \\ \hfill & \le 2{\displaystyle \frac{1-\vartheta }{\vartheta }}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}I\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+{\displaystyle \frac{2(1-\vartheta )}{\vartheta }}\{c_1^{p+2}{\left({\displaystyle \frac{2p}{\vartheta (p-2)}}\right)}^{\frac{p+2}{2}}{E}^{\frac{p}{2}}\left(0\right)\hfill \\ \hfill & +{\displaystyle \frac{2p}{p-2}}\}\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}E\left(\mathfrak{s}\right).\hfill \end{array}$$

(122)

Replacing (115)–(119), (120)–(122) in (113), we can infer

$$\begin{array}{cc}\hfill {\displaystyle \frac{2\vartheta -1}{\vartheta }}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}I\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}& \le {\sigma }_0\{\left(B^{l-1}\left(\mathfrak{s}\right)+B\left(\mathfrak{s}\right)\right)\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right)\hfill \\ \hfill & +B^2\left(\mathfrak{s}\right)+\underset{{\mathfrak{s}}_1\le \eta \le {\mathfrak{s}}_2}{sup}E\left(\mathfrak{s}\right)\}.\hfill \end{array}$$

(123)

On the other hand, by integrating (114) over $({\mathfrak{s}}_1,{\mathfrak{s}}_2)$ and using (123), we obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}E\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}& ={\displaystyle \frac{1}{l+2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\parallel \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}\mathrm{d}\mathfrak{s}+{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \nabla \dot{\varkappa }\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}(g\circ \Delta \varkappa )\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+\xi {\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\int }_{\mathrm{\Omega }}{\int }_0^1{|\nabla \top (\mathrm{y},\eta ,\mathfrak{s})|}^2\mathrm{d}\eta \mathrm{d}\mathrm{y}\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}}\right){\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}\left(1-{\int }_0^{\mathfrak{s}}g\left(\mathsf{\zeta }\right)\mathrm{d}\mathsf{\zeta }\right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}\hfill \\ \hfill & +{\displaystyle \frac{1}{p^2}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\mathrm{d}\mathfrak{s}+{\displaystyle \frac{1}{p}}{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}I\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}\hfill \\ \hfill & \le {\sigma }_0^{\prime }\left\{\left(B^{l-1}\left(\mathfrak{s}\right)+B\left(\mathfrak{s}\right)\right)\underset{\mathfrak{s}\le \eta \le \mathfrak{s}+1}{sup}{E}^{\frac{1}{2}}\left(\mathfrak{s}\right)+B^2\left(\mathfrak{s}\right)+\underset{\mathfrak{s}\le \eta \le \mathfrak{s}+1}{sup}E\left(\mathfrak{s}\right)\right\}.\hfill \end{array}$$

(124)

Because ${\mathfrak{s}}_2-{\mathfrak{s}}_1\ge 1/2$, we conclude by applying the mean theorem that

$$E\left(\mathfrak{s}\right)\le 2({\mathfrak{s}}_2-{\mathfrak{s}}_1)E\left({\mathfrak{s}}_2\right)\le 2{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}E\left(\mathfrak{s}\right)d\mathfrak{s}.$$

(125)

Morever, by integrating (16) over $(\mathfrak{s},{\mathfrak{s}}_2)$, recalling (106) and using (125), we have

$$\begin{array}{cc}\hfill E\left(\mathfrak{s}\right)& {\displaystyle \le E\left({\mathfrak{s}}_2\right)-{\displaystyle \frac{1}{2}}{\int }_{\mathfrak{s}}^{{\mathfrak{s}}_2}(g^{\prime }\circ \Delta \varkappa )\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+{\displaystyle \frac{1}{2}}{\int }_{\mathfrak{s}}^{{\mathfrak{s}}_2}g\left(\mathfrak{s}\right){\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}}\hfill \\ \hfill & {\displaystyle +k_0{\int }_{\mathfrak{s}}^{{\mathfrak{s}}_2}\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2^2\mathrm{d}\mathfrak{s}+k_1{\int }_{\mathfrak{s}}^{{\mathfrak{s}}_2}{\parallel \nabla \top (\mathrm{y},1,\mathfrak{s})\parallel }_2^2\mathrm{d}\mathfrak{s}}\hfill \\ \hfill & {\displaystyle \le 2{\int }_{{\mathfrak{s}}_1}^{{\mathfrak{s}}_2}E\left(\mathfrak{s}\right)\mathrm{d}\mathfrak{s}+B^2\left(\mathfrak{s}\right).}\hfill \end{array}$$

(126)

Combining (124) with (126) and using the nonincreasing property of $E\left(\mathfrak{s}\right)$, we obtain

$$\begin{array}{cc}\hfill E\left(\mathfrak{s}\right)& \le {\sigma }_1^{\prime }\left\{\left(B^{l-1}\left(\mathfrak{s}\right)+B\left(\mathfrak{s}\right)\right)E^{\frac{1}{2}}\left(\mathfrak{s}\right)+B^2\left(\mathfrak{s}\right)+E\left(\mathfrak{s}\right)\right\}.\hfill \end{array}$$

After utilizing Young’s inequality, we have

$$E\left(\mathfrak{s}\right)\le \sigma \left\{B^{2(l-1)}\left(\mathfrak{s}\right)+B^2\left(\mathfrak{s}\right)\right\}.$$

(127)

By taking $l=2$, we have $E\left(\mathfrak{s}\right)\le \sigma B^2\left(\mathfrak{s}\right)=\sigma (E\left(\mathfrak{s}\right)-E(\mathfrak{s}+1))$. Utilising Lemma 5, we conclude that

$$E\left(\mathfrak{s}\right)\le E\left(0\right)e^{-{[\mathfrak{s}-1]}^{+}ln\left({\displaystyle \frac{\sigma }{\sigma -1}}\right)}.$$

By taking $l>2$, using (127) and because $B^2\left(\mathfrak{s}\right)\le E\left(\mathfrak{s}\right)\le E\left(0\right)$, we have

$$\begin{array}{cc}\hfill E^{\frac{l+2}{2}}\left(\mathfrak{s}\right)& \le {\sigma }^{\prime }{B}^{l+2}\left(\mathfrak{s}\right)\left\{B^{(l-2)(l+2)}\left(\mathfrak{s}\right)+1\right\}\hfill \\ \hfill & \le {\sigma }^{\prime }{E}^{\frac{l}{2}}\left(0\right)B^2\left(\mathfrak{s}\right)\left\{E^{\frac{(l-2)(l+2)}{2}}\left(0\right)+1\right\}\hfill \\ \hfill & \le \sigma \left(E\right(\mathfrak{s})-E(\mathfrak{s}+1\left)\right).\hfill \end{array}$$

Utilizing Lemma 5 with $\mathsf{\alpha }={\displaystyle \frac{l}{2}}$, we conclude that

$$E\left(\mathfrak{s}\right)\le {\left(E{\left(0\right)}^{-\frac{l}{2}}+{\sigma }^{-1}\frac{l}{2}{[\mathfrak{s}-1]}^{+}\right)}^{\frac{-2}{l}}.$$

Therefore, we completed the proof of Theorem (105). □

4. An Example and Numerical Study

In this section, we present an illustrative example which guarantees our main results. Furthermore, we provide nice algorithms which help us to calculate all the numerical results.

Example 1.

Consider the initial-boundary value problem of nonlinear wave equation with strong damping and logarithmic source terms.

$$\left\{\begin{array}{cc}{\displaystyle |\dot{\varkappa }{|}^l\ddot{\varkappa }-{\Delta }_p\varkappa (\mathrm{y},\mathfrak{s})+{\Delta }^2\left(\varkappa \left(\mathfrak{s}\right)-{\int }_0^{\mathfrak{s}}\frac{\varkappa \left(\mathsf{\zeta }\right)}{exp(\mathfrak{s}-\mathsf{\zeta })+2}\mathrm{d}\mathsf{\zeta }\right)}\hfill & \\ {\displaystyle -{\mu }_1\Delta \dot{\varkappa }-{\mu }_2\Delta \dot{\varkappa }(\mathrm{y},\mathfrak{s}-\mathsf{\zeta })-\Delta \ddot{\varkappa }}\hfill & \\ {\displaystyle ={\varkappa (\mathrm{y},\mathfrak{s})|\varkappa (\mathrm{y},\mathfrak{s})|}^{p-2}ln|\varkappa (\mathrm{y},\mathfrak{s})|,}\hfill & \mathrm{y}\in \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ \varkappa =\Delta \varkappa =0,\hfill & \mathrm{y}\in \partial \mathrm{\Omega },\mathfrak{s}>0,\hfill \\ \varkappa (\mathrm{y},0)=0,\dot{\varkappa }{|}_{(\mathrm{y},0)}=\sqrt[3]{{\mathrm{y}}^2},\hfill & \mathrm{y}\in \mathrm{\Omega },\hfill \\ \dot{\varkappa }{|}_{(\mathrm{y},\mathfrak{s}-\mathsf{\zeta })}=\frac{\mathfrak{s}-\mathsf{\zeta }+2}{\mathrm{y}+5},\hfill & \mathrm{y}\in \mathrm{\Omega },0<\mathfrak{s}<\mathsf{\zeta },\hfill \end{array}\right.$$

(128)

for $\mathfrak{s}>0$, $p=2$ and $l=0.4$. Clearly, $g\left(\mathfrak{s}\right)=\frac{1}{exp\left(\mathfrak{s}\right)+2}$, ${\varkappa }_0\left(\mathrm{y}\right)=0$, ${\varkappa }_1\left(\mathrm{y}\right)=\sqrt[3]{{\mathrm{y}}^2}$, $h_0(\mathrm{y},\mathfrak{s})=\frac{\mathfrak{s}+2}{\mathrm{y}+5}$ and

$$\vartheta =1-{\int }_0^{\infty }g\left(\zeta \right)\mathrm{d}\zeta \simeq 0.45069>0.$$

Consider positive constants ${\xi }_1=0.2,{\xi }_2=1.9,{\xi }_3=0.25$; then, we have

$$-{\xi }_1\le g^{\prime }\left(\mathfrak{s}\right)\le -{\xi }_{3}g\left(\mathfrak{s}\right),0\le g^{\prime \prime }\left(\mathfrak{s}\right)\le {\xi }_{2}g\left(\mathfrak{s}\right),$$

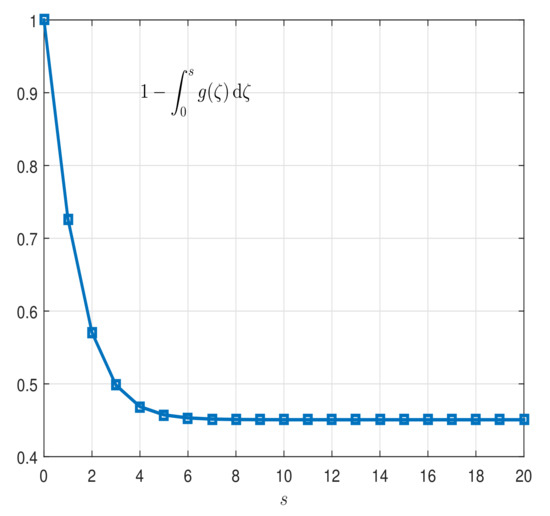
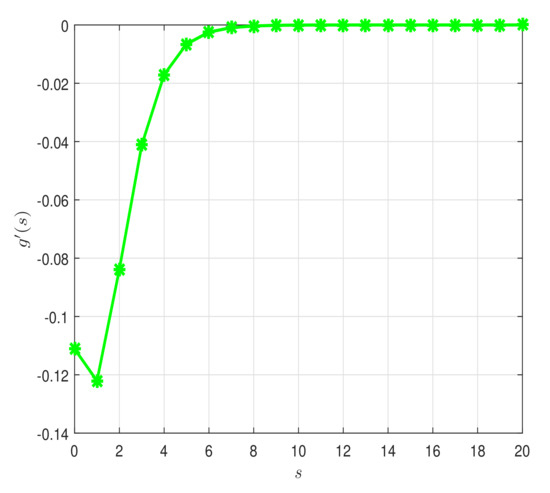
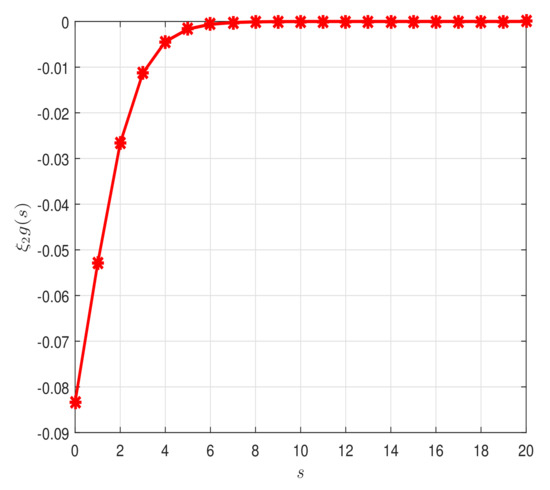
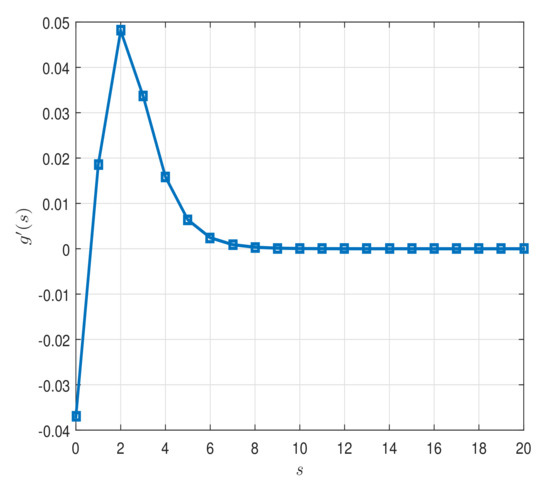
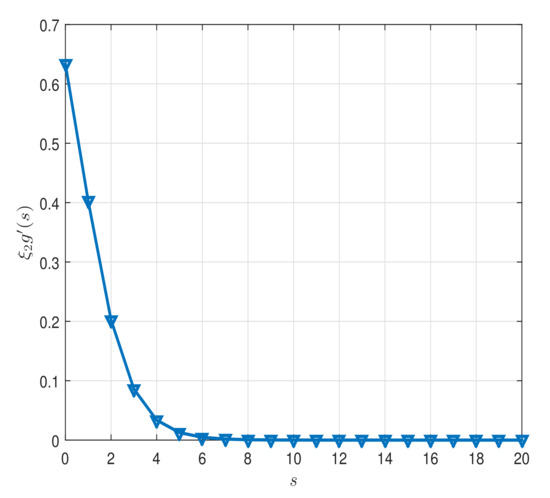
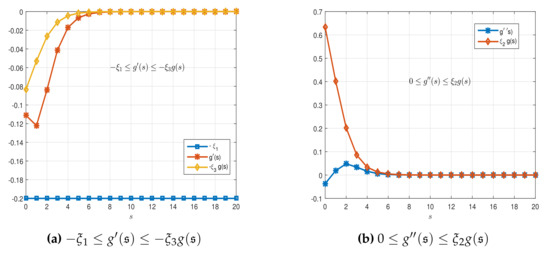
whenever $\mathfrak{s}\ge 0$. Table 1 shows the numerical results. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show graphical representation of the variables. Therefore, assumptions (H1)–(H3) hold and so the Cauchy problem (128) possesses a unique global weak solution $\varkappa \in L^{\infty }([0,\infty ),H^3\left(\mathrm{\Omega }\right)\cap H_0^1\left(\mathrm{\Omega }\right)).$ See Figure 6a,b.

Table 1. Numerical values of $1-{\int }_0^{\mathfrak{s}}g\left(\zeta \right)\mathrm{d}\zeta ,g^{\prime }\left(\mathfrak{s}\right),-{\xi }_{3}g\left(\mathfrak{s}\right),g^{\prime \prime }\left(\mathfrak{s}\right),{\xi }_{2}g\left(\mathfrak{s}\right)$ in Example 1 for $\mathfrak{s}>0$.

$\mathfrak{s}$	$1-{\int }_0^{\mathfrak{s}}\mathit{g}\left(\mathit{\zeta }\right)\mathbf{d}\mathit{\zeta }$	${\mathit{g}}^{\prime }\left(\mathfrak{s}\right)$	$-{\mathit{\xi }}_3\mathit{g}\left(\mathfrak{s}\right)$	${\mathit{g}}^{\prime \prime }\left(\mathfrak{s}\right)$	${\mathit{\xi }}_2\mathit{g}\left(\mathfrak{s}\right)$
$0.00$	$0.633333$	$1.000000$	$-0.111111$	$-0.037037$	$-0.083333$
$1.00$	$0.402689$	$0.726416$	$-0.122103$	$0.018588$	$-0.052985$
$2.00$	$0.202363$	$0.570466$	$-0.083820$	$0.048110$	$-0.026627$
$3.00$	$0.086029$	$0.498155$	$-0.041178$	$0.033720$	$-0.011320$
$4.00$	$0.033570$	$0.468682$	$-0.017044$	$0.015840$	$-0.004417$
$5.00$	$0.012632$	$0.457387$	$-0.006560$	$0.006386$	$-0.001662$
$6.00$	$0.004686$	$0.453166$	$-0.002454$	$0.002430$	$-0.000617$
$7.00$	$0.001729$	$0.451605$	$-0.000909$	$0.000905$	$-0.000228$
$8.00$	$0.000637$	$0.451029$	$-0.000335$	$0.000335$	$-0.000084$
$9.00$	$0.000234$	$0.450817$	$-0.000123$	$0.000123$	$-0.000031$
$10.00$	$0.000086$	$0.450739$	$-0.000045$	$0.000045$	$-0.000011$
$11.00$	$0.000032$	$0.450711$	$-0.000017$	$0.000017$	$-0.000004$
$12.00$	$0.000012$	$0.450700$	$-0.000006$	$0.000006$	$-0.000002$
$13.00$	$0.000004$	$0.450696$	$-0.000002$	$0.000002$	$-0.000001$
$14.00$	$0.000002$	$0.450695$	$-0.000001$	$0.000001$	$0.000000$
$15.00$	$0.000001$	$0.450694$	$0.000000$	$0.000000$	$0.000000$
$16.00$	$0.000000$	$0.450694$	$0.000000$	$0.000000$	$0.000000$
$17.00$	$0.000000$	$0.450694$	$0.000000$	$0.000000$	$0.000000$
$18.00$	$0.000000$	$0.450694$	$0.000000$	$0.000000$	$0.000000$
$19.00$	$0.000000$	$0.450694$	$0.000000$	$0.000000$	$0.000000$
$20.00$	$0.000000$	$0.450694$	$0.000000$	$0.000000$	$0.000000$

Figure 1. Two-dimensional graph of $1-{\int }_0^{\mathfrak{s}}g\left(\zeta \right)\mathrm{d}\zeta$ for $\mathfrak{s}>0$ in Example 1.

Figure 2. Two-dimensional graph of $g^{\prime }\left(\mathfrak{s}\right)$ for $\mathfrak{s}>0$ in Example 1.

Figure 3. Two-dimensional graph of $-{\xi }_{3}g\left(\mathfrak{s}\right)$ for $\mathfrak{s}>0$ in Example 1.

Figure 4. Two-dimensional graph of $g^{\prime \prime }\left(\mathfrak{s}\right)$ for $\mathfrak{s}>0$ in Example 1.

Figure 5. Two-dimensional graph of ${\xi }_{2}g\left(\mathfrak{s}\right)$ for $\mathfrak{s}>0$ in Example 1.

Figure 6. Graphical representation of (H1) and (H2) for $\mathfrak{s}\ge 0$ in Example 1.

In addition, by using Equation (11), the energy functional associated to Problem (128) is obtained as

$$\begin{array}{cc}\hfill E\left(\mathfrak{s}\right)& ={\displaystyle \frac{1}{l+2}}\parallel \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_{l+2}^{l+2}+\parallel \nabla \dot{\varkappa }{\left(\mathfrak{s}\right)\parallel }_2^2+{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\mathfrak{s}}g\left(\zeta \right)\mathrm{d}\zeta \right){\parallel \Delta \varkappa \left(\mathfrak{s}\right)\parallel }_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{p}}{\parallel \nabla \varkappa \left(\mathfrak{s}\right)\parallel }_p^p+{\displaystyle \frac{1}{2}}\left(g\circ \Delta \varkappa \right)\left(\mathfrak{s}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{p}}{\int }_{\mathrm{\Omega }}{|\varkappa (\zeta ,\mathfrak{s})|}^{p}ln|\varkappa (\zeta ,\mathfrak{s})|\mathrm{d}\zeta +{\displaystyle \frac{1}{p^2}}{\parallel \varkappa \left(\mathfrak{s}\right)\parallel }_p^p\hfill \\ \hfill & +\xi {\int }_{\mathrm{\Omega }}{\int }_0^1{|\nabla \top (\zeta ,\eta ,\mathfrak{s})|}^2\mathrm{d}\eta \mathrm{d}\zeta ,\hfill \end{array}$$

where $\left(g\circ \varphi \left)\right(\mathfrak{s}\right)={\int }_0^{\mathfrak{s}}\frac{1}{exp(\mathfrak{s}-\zeta )+2}{\parallel \varphi \left(\mathfrak{s}\right)-\varphi \left(\zeta \right)\parallel }_2^2\mathrm{d}\zeta .$

In addition, the solution satisfies the energy inequality

$$\begin{array}{cc}\hfill E\left(\mathfrak{s}\right)& -{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}(g^{\prime }\circ \Delta \varkappa )\left(\zeta \right)\mathrm{d}\zeta +{\displaystyle \frac{1}{2}}{\int }_0^{\mathfrak{s}}g\left(\zeta \right){\parallel \Delta \varkappa \left(\zeta \right)\parallel }_2^2\mathrm{d}\zeta \hfill \\ \hfill & +\left({\mu }_1-{\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla \dot{\varkappa }\left(\zeta \right)\parallel }_2^2\mathrm{d}\zeta \hfill \\ \hfill & +\left({\displaystyle \frac{\xi }{\mathsf{\tau }}}-{\displaystyle \frac{|{\mu }_2|}{2}}\right){\int }_0^{\mathfrak{s}}{\parallel \nabla \top (\mathrm{y},1,\zeta )\parallel }_2^2\mathrm{d}\zeta \le E\left(0\right).\hfill \end{array}$$

5. Conclusions

Evolution problems with an interior logarithmic source have a wide range of applications in physics, such as nuclear physics, optics and geophysics. In recent years, there have been many works concerning the global existence and stabilisation of the wave equation, including a constant delay or time-varying delay. However, to the best of our knowledge, there is no decay result for the nonlinear p-Laplacian viscoelastic Petrovesky equation with a delay term and logarithmic nonlinearity. In this paper, we study the global existence of solutions for a delayed viscoelastic-type Petrovesky wave equation with a p-Laplacian operator and logarithmic source under some appropriate conditions. By making some essential assumptions on the memory kernel function and exponents $p,l$, we proved that the rate of decay of the total energy is exponential or polynomial, depending on the exponent l. The illustrative examples are designed to validate the theoretical findings. The equation under the equation studies and evolution problems with an interior logarithmic source answer the question as to what will happen if one replaces the power source term by other source terms, for example, the logarithmic source term. This paper provides an affirmative reply to such a situation.