Backstepping Control Strategy of an Autonomous Underwater Vehicle Based on Probability Gain

Abstract

In this paper, an underwater robot system with nonlinear characteristics is studied by a backstepping method. Based on the state preservation problem of an Autonomous Underwater Vehicle (AUV), this paper applies the backstepping probabilistic gain controller to the nonlinear system of the AUV for the first time. Under the comprehensive influence of underwater resistance, turbulence, and driving force, the motion of the AUV has strong coupling, strong nonlinearity, and an unpredictable state. At this time, the system’s output feedback can solve the problem of an unmeasurable state. In order to achieve a good control effect and extend the cruising range of the AUV, first, this paper will select the state error to make it a new control objective. The system’s control is transformed into the selection of system parameters, which greatly simplifies the degree of calculation. Second, this paper introduces the concept of a stochastic backstepping control strategy, in which the robot’s actuators work discontinuously. The actuator works only when there is a random disturbance, and the control effect is not diminished. Finally, the backstepping probabilistic gain controller is designed according to the nonlinear system applied to the simulation model for verification, and the final result confirms the effect of the controller design.

1. Introduction

With the development of science and technology, ocean exploration technology has reached an unprecedented new level. With the help of science and technology, AUVs have been developed [1,2]. It is now possible to conduct scientific investigations on the seabed at a depth of 10,000 m. However, AUV development is inseparable from control technology development and progress, especially control technology progress in the nonlinear field. Their limitations and deficiencies are known based on previously known control techniques such as PID, robust control, and homogeneous controllers [3,4,5,6]. PID can only control simple systems [3,4] and has little effect when handling coupled nonlinear systems. In particular, the model and system structure are required to be exactly known. A robust control method provides more flexibility, Taking an autonomous vehicle as an example [5,6], the weight change of the passengers or cargo in the vehicle will cause the controlled system to change. Such common problems pose challenges to the design of the controller, so the designed controller must have sufficient robustness to continuously control the vehicle over the course of these changes [7,8,9,10].

It is well-known that nonlinearities exist in all systems. For example [11,12,13,14,15], control problems exist in industry, in relationships in social systems, and in biological relationships in nature; we cannot express them with specific mathematical formulas. However, some researchers [16,17] have simplified and approximated these systems by studying salient relationships in the system and ignoring others considered less important. With the advancement of science and technology, researchers [18,19] found that the influence of the neglected nonlinearity on the whole system cannot be omitted. Therefore, it is necessary to reconsider these characteristics, such as nonlinearity, uncertainty, and randomness. Especially a system’s nonlinear problem, which is the basis of modern control theory research, needs to be addressed. The control problem of the AUV studied in this paper [20,21,22] has a very typical nonlinear characteristic. The system’s various elements are coupled with each other and accompanied by uncertain disturbances in the external environment. This makes the design of the AUV control system very challenging, such as Figure 1. Existing control theory research results contain no solutions to this problem. Some researchers [23,24] study the robot’s motion control problem by restricting the motion of the underwater robot-like vehicle, assuming that the AUV’s trajectory is in a plane and does not involve space motion [25,26]. Such assumptions can simplify the motion problem from the AUV’s six degrees of freedom to the three degrees of freedom. However, it ignores the random interference phenomena.

Figure 1. (a) Typical autonomous underwater vehicle model; (b) an autonomous underwater vehicle underwater experiment.

On the one hand, the environment can cause a variety of nonlinear systems. Such nonlinear disturbances are called randomly nonlinear systems. According to a recent research paper [27,28], external random disturbances satisfy a time-invariant Bernoulli distribution. The scope of this paper was to find a solution for the stochastic nonlinear system. In [29], a time-invariant probability stochastic nonlinear AUV system was used to control an AUV’s hovering. A particularly hot research topic is the design of a high-gain observer and feedback controller in which unmeasurable states can be observed by the high-gain observer. In this paper, we will introduce a coordinate transformation for the output feedback controller [30] and compare the system’s real value and the observed value. This method simplifies the computational complexity of a control system and improves the control effectiveness. According to the calculation method, the parameter selection can be obtained, and the design problem of the controller is transformed into a parameter selection problem.

The objective of this paper is to consider the output of a high-gain observer in developing a stochastic control system. The main contributions of this paper include the following:

• The high-gain method is used to observe the system’s unmeasurable states, and the complex nonlinear system control problem is transformed into a parameter selection problem by introducing coordinate transformation, which simplifies the calculation process and complexity.
• The literature assumes that the external disturbance is randomly occurring and the concept of a probability gain controller is introduced. With the control effect unchanged, we convert continuous control to intermittent control. The endurance problem of the AUV is solved under intermittent control, saving significant energy and extending the cruising range.
• Based on the backstepping control method, the complex nonlinear system control problems is decomposed into a calculation method that can perform iterative recursion. The final controller can be calculated through the designed virtual controller.
• An easy-to-implement probabilistic control algorithm is designed, and a Bernoulli probability gain controller is designed. This is more lenient than traditional control methods. In the case of simultaneous external interference, system uncertainty, and time delay, the closed-loop system can ensure that all indices are stable. Finally, a simulation example is used to demonstrate the effectiveness of the proposed method.

2. Description of Dynamic Modelling of a Deepwater Robot

This section mainly introduces the principle and components of the AUV. It can be seen from Figure 2 that the AUV model is a front-drive model, which is mainly powered by a vectored thruster at the tail. The four rudder pages at the robot’s tail are used to change the AUV’s directions. With the right amount of propulsion, the rotation angle of the propeller is controlled by three connecting rods to provide 360° of power.

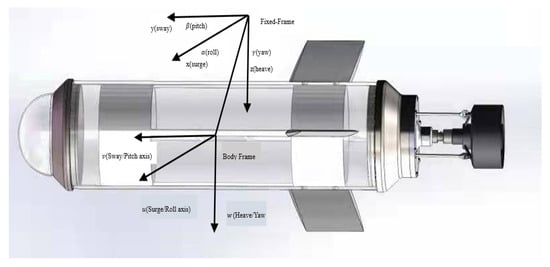
Figure 2. Body-fixed frame and earth-fixed reference frame for underwater robot.

An underactuated underwater robot dynamics model can be expressed as the following formula:

$$\begin{array}{c}\hfill M\dot{\nu }+C\left(\nu \right)\nu +D\left(\nu \right)\nu +g\left(ϵ\right)=F\end{array}$$

(1)

where M and $C\left(\nu \right)$ are the inertia, additional quality matrix, and Coriolis centripetal force, respectively. $D\left(\nu \right)$ and $g\left(ϵ\right)$ are the fluid damping and operation and the restoring force of the gravity according to the buoyancy. $F={\left[F_X{F}_Y{F}_Z{F}_K{F}_M{F}_N\right]}^T$ are a series of moments and forces; $\dot{\nu }={\left[\dot{u}\dot{\nu }\dot{\omega }\dot{p}\dot{q}\dot{r}\right]}^T$ are the accelerations in the body frame; $\nu ={\left[u\nu \omega pqr\right]}^T$ are velocity in roll, pitch, and yaw direction, respectively, in the moving frame; $ϵ={\left[xyz\alpha \beta \gamma \right]}^T$ are surge position, sway position and heave position, and roll angle, pitch angle, and yaw angle in the fixed frame, respectively. In the moving frame, the accelerations of the AUV model can be decomposed into two different parts, linear velocity ${\nu }_1={\left[u\nu \omega \right]}^T$ and angular velocity ${\nu }_2={\left[pqr\right]}^T$. In the fixed-frame, the velocity of the AUV model can be decomposed into position ${ϵ}_1={\left[xyz\right]}^T$ and orientation ${ϵ}_2={\left[\alpha \beta \gamma \right]}^T$. In this paper, we research the AUV’s linear velocity ${\nu }_1={\left[u\nu \omega \right]}^T$ and linear position ${ϵ}_1={\left[xyz\right]}^T$.

Here, $M=M_{RB}+M_A$.

$M_{RB}$ can be expressed such as $M_{RB}$=$\left(\begin{array}{cccccc}m& 0& 0& 0& m{z}_G& -m{y}_G\\ 0& m& 0& -m{z}_G& 0& m{x}_G\\ 0& 0& m& m{y}_G& -m{x}_G& 0\\ 0& -m{z}_G& m{y}_G& I_x& -I_{xy}& -I_{xz}\\ m{z}_G& 0& -m{x}_G& -Iyx& I_y& -I_{yz}\\ -m{y}_G& m{x}_G& 0& -Izx& -Izy& I_z\end{array}\right)$

additional quality matrix $M_A$ can be expressed: $M_A$=$\left(\begin{array}{cccccc}{X}_{\dot{u}}& X_{\dot{v}}& X_{\dot{w}}& X_{\dot{p}}& X_{\dot{q}}& X_{\dot{r}}\\ Y_{\dot{u}}& Y_{\dot{v}}& Y_{\dot{w}}& Y_{\dot{p}}& Y_{\dot{q}}& Y_{\dot{r}}\\ Z_{\dot{u}}& Z_{\dot{v}}& Z_{\dot{w}}& Z_{\dot{p}}& Z_{\dot{q}}& Z_{\dot{r}}\\ K_{\dot{u}}& K_{\dot{v}}& K_{\dot{w}}& K_{\dot{p}}& K_{\dot{q}}& K_{\dot{r}}\\ M_{\dot{u}}& M_{\dot{v}}& M_{\dot{w}}& M_{\dot{p}}& M_{\dot{q}}& M_{\dot{r}}\\ N_{\dot{u}}& N_{\dot{v}}& N_{\dot{w}}& N_{\dot{p}}& N_{\dot{q}}& N_{\dot{r}}\end{array}\right)$

Here, $C\left(v\right)=C_{RB}\left(v\right)+C_A\left(v\right)$. $C_A\left(v\right)$ is fluid damping and operation matrix.

$C_A\left(v\right)$ can be expressed: $C_A\left(v\right)$=$\left(\begin{array}{cccccc}0& 0& 0& 0& -a_3& a_2\\ 0& 0& 0& a_3& 0& -a_1\\ 0& 0& 0& -a_2& a_1& 0\\ 0& -a_3& a_2& 0& -b_3& b_2\\ a_3& 0& -a_1& b_3& 0& -b_1\\ -a_2& a_1& 0& -b_2& b_1& 0\end{array}\right)$

where

$a_1=X_{\dot{u}}u+X_{\dot{v}}v+X_{\dot{w}}w+X_{\dot{p}}p+X_{\dot{q}}q+X_{\dot{r}}r$

$a_2=X_{\dot{v}}u+Y_{\dot{v}}v+Y_{\dot{w}}w+Y_{\dot{p}}p+Y_{\dot{q}}q+Y_{\dot{r}}r$

$a_3=X_{\dot{w}}u+Y_{\dot{w}}v+Z_{\dot{w}}w+Z_{\dot{p}}p+Z_{\dot{q}}q+Z_{\dot{r}}r$

$b_1=X_{\dot{p}}u+Y_{\dot{p}}v+Z_{\dot{p}}w+K_{\dot{p}}p+K_{\dot{q}}q+K_{\dot{r}}r$

$b_2=X_{\dot{q}}u+Y_{\dot{q}}v+Z_{\dot{q}}w+K_{\dot{q}}p+M_{\dot{q}}q+M_{\dot{q}}r$

$b_3=X_{\dot{r}}u+Y_{\dot{r}}v+Z_{\dot{r}}w+K_{\dot{r}}p+M_{\dot{r}}q+N_{\dot{r}}r$

Next, Formula (2) is introduced to explain the connection between the body frame and the fixed frame:

$$\begin{array}{c}\hfill {\dot{ϵ}}_1=J\left(ϵ\right){\nu }_1\end{array}$$

(2)

Well-known, $J\left(ϵ\right)$ is a particular matrix, which is a kinematic transformation and is in the following form:

$J\left(ϵ\right)$=$\left(\begin{array}{ccc}c\gamma c\beta & -s\gamma c\alpha +c\gamma s\beta s\alpha & s\gamma s\alpha +c\gamma c\beta s\alpha \\ s\gamma c\beta & c\gamma c\alpha +s\gamma s\beta s\alpha & -c\gamma s\alpha +s\gamma s\beta c\alpha \\ -s\beta & c\beta s\alpha & c\beta c\alpha \end{array}\right)$

Well-known, s is the $sin$ function, and c is the $cos$ function. Another, ${ϵ}_2={\left[\alpha \beta \gamma \right]}^T$ is the orientation variable, which is underfined for $\beta =\pm$${90}^{\circ }$ and is below ±${90}^{\circ }$. For this, the coordinate transformation $({ϵ}_1,{\nu }_1)\stackrel{\mu }{⟶}({ϵ}_1,{\dot{ϵ}}_1)$ is performed using (2), which yields:

$\left(\begin{array}{c}{ϵ}_1\\ {\dot{ϵ}}_1\end{array}\right)$=$\left[\begin{array}{cc}I& 0\\ 0& J\left(ϵ\right)\end{array}\right]$$\left(\begin{array}{c}{ϵ}_1\\ {\nu }_1\end{array}\right)$$\mu$ is the coordinate transformation. According to $\mu$, the dynamic model of the underwater robot can become as the following form:

$$\begin{array}{c}\hfill M_{{ϵ}_1}{\ddot{ϵ}}_1+C_{{ϵ}_1}{\dot{ϵ}}_1+D_{{ϵ}_1}{\dot{ϵ}}_1+g_{{ϵ}_1}=F_{{ϵ}_1}\end{array}$$

(3)

where

$$\begin{array}{cc}\hfill M_{{ϵ}_1}& =J{\left(ϵ\right)}^{-T}MJ{\left(ϵ\right)}^{-1}\hfill \\ \hfill C_{{ϵ}_1}& =J{\left(ϵ\right)}^{-T}\left(C\left(\nu \right)-MJ{\left(ϵ\right)}^{-1}\dot{J}\left(ϵ\right)\right)J{\left(ϵ\right)}^{-1}\hfill \\ \hfill D_{{ϵ}_1}& =J{\left(ϵ\right)}^{-T}D\left(\nu \right)J{\left(ϵ\right)}^{-1}\hfill \\ \hfill g_{{ϵ}_1}& =J{\left(ϵ\right)}^{-T}g\left(ϵ\right)\hfill \\ \hfill F_{{ϵ}_1}& =J{\left(ϵ\right)}^{-T}F\hfill \end{array}$$

(4)

Next, a series of assumptions are introduced.

Assumption 1. 

The literature researches the AUV’s velocity, which is $\dot{l}={({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)}^{\frac{1}{2}}$. Considering the system origin stations, ${ϵ}_1\left(0\right)=\left[000\right]$ and ${\dot{ϵ}}_1\left(0\right)=\left[000\right]$.

Assumption 2. 

In the literature. the velocity ${ϵ}_1=\left[xyz\right]$ and the angle ${ϵ}_2=\left[\alpha \beta \gamma \right]$ is known by using different sensors(such as speed and angle sensors).

According to the features of the AUV system, we can use the dynamic model to obtain a broad mathematical model as follows.

$$\begin{array}{cc}\hfill d{l}_1& =l_{2}dt+f_1(t,l\left(t\right),u)dt+g_1\left(l\right)d\omega \hfill \\ \hfill d{l}_2& =udt+f_2(t,l\left(t\right),u)dt+g_2\left(l\right)d\omega \hfill \\ \hfill y& =l_1\hfill \end{array}$$

(5)

where $l={(l_1,l_2)}^T\in R^2$ are the states, $u\in R$ is the input, and $y\in R$ is the output. Here, we will lead into a stochastic process: $\omega$ is an m - dimensional standard Wiener process defined on the complete probability space $(\Omega ,\Gamma ,P)$ with $\Omega$, $\Gamma$, and P being a sample space, filtration, and probability measure, respectively. $l_2$ is a state value and unmeasurable. ${\mathit{f}}_i:{\mathbb{R}}^n\to \mathbb{R}$ and $g_i:{\mathbb{R}}^n\to {\mathbb{R}}^r,i=1,2$ is a linear growth (11) and is local Lipschitz. Meanwhile, $f_i\left(0\right)=0,g_i\left(0\right)=0$.

Definition 1. 

For a given function $V\in C^2({\mathbb{R}}^2;\mathbb{R})$ associated (2), the differential operator £ is defined as

$$\begin{array}{c}\hfill \pounds V\left(l\right)=\frac{\partial V\left(l\right)}{\partial l}f(l,t)+\frac{1}{2}Tr\left\{g^T(l,t)\frac{{\partial }^{2}V\left(l\right)}{\partial l^2}g(l,t)\right\}\end{array}$$

(6)

Definition 2. 

Assume γ and ${\gamma }^{{}^{\prime }}$ is the ${\mathcal{K}}_{\infty }$ function, ${\gamma }^{{}^{\prime }}$ is the derivative of γ and exists, $R_2\left(l\right)$ meets $R_2\left(l\right)=R_2^T\left(l\right)>0$ for all l and is a matrix-valued function. $u={\alpha }_1$ is a continuous feedback control function except for the origin $\alpha \left(0\right)=0$, which can make the equilibrium point $l=0$ be probability stable, the cost function $J\left(u\right)=E\left({\int }_0^{\infty }\left[s\left(x\right)+\gamma (|R_2{\left(l\right)}^{1/2}u|)\right]d\tau \right)$ can take the optimal value, which expresses the probability of the system (5) control problem is to be accomplished.

Next, an inverse optimal control scheme based on probability will be given:

Lemma 1. 

According to the following control method:

$$\begin{array}{c}\hfill u=\alpha \left(l\right)=-R_2^{-1}{\left(L_{g2}V\right)}^T\frac{\ell \gamma (|L_{g2}V{R}_2^{-1/2}|)}{|L_{g2}V{R}_2^{-1/2}{|}^2}\end{array}$$

(7)

Well-known, $V\left(l\right)$ is the Lyapunov function, which is preselected. ${\gamma }^{{}^{\prime }}$ is the derivative of $\gamma (·)$, which is ${\mathcal{K}}_{\infty }$ function, and $R_2\left(l\right)$ meet $R_2\left(l\right)=R_2^T\left(l\right)>0$, which is a matrix function.

$$\begin{array}{c}\hfill u^{*}={\alpha }^{*}\left(l\right)=-\frac{\beta }{2}{R}_2^{-1}{\left(L_{g2}V\right)}^T\frac{{\left({\gamma }^{{}^{\prime }}\right)}^{-1}(|L_{g2}V{R}_2^{-1/2}|)}{|L_{g2}V{R}_2^{-1/2}|},\beta \ge 2\end{array}$$

(8)

is able to make the cost function

$$\begin{array}{c}\hfill J\left(u\right)=E\left({\int }_0^{\infty }\left[s\left(l\right)+{\beta }^2\gamma \left(\frac{2}{\beta }|R_2{\left(l\right)}^{1/2}u|\right)\right]d\tau \right)\end{array}$$

(9)

According to the system, (5) can be solved by minimizing the $s\left(x\right)$ function, satisfying

$$\begin{array}{cc}\hfill s\left(l\right)=& 2\beta \left[\ell \gamma (|L_{g2}V{R}_2^{-1/2}|)-L_{f}V-\frac{1}{2}Tr\left(g_1^T\frac{{\partial }^{2}V}{\partial l^2}{g}_1\right)\right]\hfill \\ \hfill & +\beta (\beta -2)\ell \gamma (|L_{g2}V{R}_2^{-1/2}|)\hfill \end{array}$$

(10)

Assumption 3. 

$C_f,C_g\ge 0$ is a known positive constant, which satisfies the following inequality

$$\begin{array}{cc}\hfill |f_i\left(l\right)|& \le C_f\left(|l_1|+\cdots +|l_i|\right),\hfill \\ \hfill |g_i\left(l\right)|& \le C_g\left(|l_1|+\cdots +|l_i|\right)\hfill \end{array}$$

(11)

Young inequality: For any two vectors l and y, which have the same dimension. $l^{T}y\le \frac{{\lambda }^p}{p}{|l|}^p+\frac{1}{q{\lambda }^q}{|y|}^q$, here $\lambda >0,p>1,q>1$, and $p^{-1}+q^{-1}=1.$

Based on the assumptions, the inverse optimization problem is solvable by designing a smooth output feedback controller for system (5) so that the closed-loop system at the origin is globally asymptotically stable.

3. State Keeping Probability-Dependent Gain-Scheduled Control Design

In the third section, we mainly introduce the design of the state-preserving probability gain controller, which includes three parts. The first part is the introduction of a high-gain observer; the second part is the introduction of backstepping control; the third part is the gain coefficient design of a Bernoulli probability distribution controller.

3.1. High-Gain Observer Design

The system’s state measurement has been a thorny problem in the control field. Some systems or states are unmeasurable due to the sensor’s complexity, the system’s design, and the observer’s design. Neither can measure the data very well. This increases difficulty for the system control. Some researchers have designed an observer to obtain all the system states value. In this paper, a high-gain observer is introduced, which is different from the general Lomborg observer in that the gain coefficient of the observer is a powder form, which significantly improves the observer’s accuracy.

The state $l_1$ is measurable; the state $l_2$ is unmeasurable. Next, we construct an observer, which has high gain:

$$\begin{array}{cc}\hfill {\dot{\widehat{l}}}_1& ={\widehat{l}}_2+H^1{K}_1\left(l_1-{\widehat{l}}_1\right),\hfill \\ \hfill {\dot{\widehat{l}}}_2& =u+H^2{K}_2\left(l_1-{\widehat{l}}_1\right),\hfill \end{array}$$

(12)

In the above observers, the $H>0$ and $K_i>0$ are an unknown parameter and known constants. The following matrix A=$\left(\begin{array}{cc}-K_1& 1\\ -K_2& 0\end{array}\right)$ is stable; P is a matrix, which is positive definite and meets $A^{T}P+PA=-I$. According to the system (5), we can obtain the error equation, which can be defined as the following form:

$$\begin{array}{cc}\hfill \tilde{l}& ={\left({\tilde{l}}_1,{\tilde{l}}_2\right)}^T,{\tilde{l}}_i=\frac{l_i-{\widehat{l}}_i}{H^{i-1}},i=1,2\hfill \end{array}$$

(13)

In line with (5) and (12), we can obtain the system error model as follows

$$\begin{array}{cc}\hfill d\tilde{l}& =HA\tilde{l}dt+F\left(l\right)dt+G\left(l\right)d\omega \hfill \end{array}$$

(14)

where

$$\begin{array}{ccc}\hfill F\left(l\right)& ={\left(f_1\left(l\right),\frac{1}{H}{f}_2\left(l\right)\right)}^T,G\left(l\right)\hfill & \hfill ={\left(g_1^T\left(l\right),\frac{1}{H}{g}_2^T\left(l\right)\right)}^T\end{array}$$

(15)

Choosing $V_0\left(\tilde{l}\right)=3{\tilde{l}}^{T}P\tilde{l}$ , applying $|\frac{1}{H^{i-1}}{l}_i|\le |\frac{1}{H^{i-1}}{\widehat{l}}_i|+|{\tilde{l}}_i|$ , ${\left({\sum }_{i=1}^2{a}_i\right)}^2\le 2{\sum }_{i=1}^2{a}_i^2,$$H>0$, Definition 1 and Assumption 3, we can obtion

$$\begin{array}{cc}\hfill \pounds V_0& =3H{\tilde{l}}^T\left(A^{T}P+PA\right)\tilde{l}+6{\tilde{l}}^{T}PF\left(l\right)+3Tr\left\{G^T\left(l\right)PG\left(l\right)\right\}\hfill \\ \hfill & \le -3H{|\tilde{l}|}^2+3{|{\tilde{l}}^{T}P|}^2+3\left(\sum _{i=1}^2{|\frac{f_i\left(l\right)}{H^{i-1}}|}^2+{\lambda }_{max}\left(P\right)\sum _{i=1}^2{|\frac{g_i\left(l\right)}{H^{i-1}}|}^2\right)\hfill \\ \hfill & \le -3H{|\tilde{l}|}^2+3{\parallel P\parallel }^2{|\tilde{l}|}^2+3C_f^2{\left(\sum _{i=1}^2\frac{1}{H^{i-1}}\right)}^2{\left(|l_1|+\frac{|l_2|}{H}+\cdots +\frac{|l_2|}{H^1}\right)}^2\hfill \\ \hfill & +3{\lambda }_{max}\left(P\right)C_f^2{\left(\sum _{i=1}^2\frac{1}{H^{i-1}}\right)}^2{\left(|l_1|+\frac{|l_2|}{H}+\cdots +\frac{|l_2|}{H^1}\right)}^2\hfill \\ \hfill & =-3H{|\tilde{l}|}^2+3{\parallel P\parallel }^2{|\tilde{l}|}^2+c_1{\left(|l_1|+\frac{|l_2|}{H}+\cdots +\frac{|l_2|}{H^1}\right)}^2\hfill \\ \hfill & \le -3H{|\tilde{l}|}^2+3{\parallel P\parallel }^2{|\tilde{l}|}^2+c_1{\left(\sum _{i=1}^2|\frac{1}{H^{i-1}}{\widehat{l}}_i|+\sum _{i=1}^2|{\tilde{l}}_i|\right)}^2\hfill \\ \hfill & =-\left(3H-3{\parallel P\parallel }^2-4c_1\right){|\tilde{l}|}^2+4c_1\left({\widehat{l}}_1^2+\frac{{\widehat{l}}_2^2}{H^2}\right)\hfill \end{array}$$

(16)

where

$$\begin{array}{cc}\hfill c_1& =3(C_f^2+{\lambda }_{max}\left(P\right)C_g^2){\left(\sum _{i=1}^2\frac{1}{H^{i-1}}\right)}^2\hfill \\ \hfill & =\frac{3(C_f^2+{\lambda }_{max}\left(P\right)C_g^2)}{H^2}\left(\sum _{i=0}^1(i+1)H^i+(3-i)H^2\right)\hfill \end{array}$$

(17)

3.2. Output-Feedback Controller Design

The second part is the design of the output feedback controller. In the control system of the AUV, the states are not entirely measurable. At this time, it is necessary to use the system’s output state to design the output feedback controller. However, due to the system’s complexity, the system’s states are firstly transformed to reduce the difficulty and complexity of controller design. On the other hand, according to the backstepping controller’s design characteristics, the nonlinear system’s complexity can be well considered, and the controller can be designed even when the state is not entirely measurable. However, at the last iteration of the derivation, the dummy controller is offset, and only the final controller is obtained.

$$\begin{array}{c}\hfill z_1={\tilde{l}}_1,z_2={\tilde{l}}_2-{\alpha }_1\left({\widehat{l}}_{\left[1\right]}\right)\end{array}$$

(18)

Well-known ${\alpha }_1\left({\widehat{l}}_{\left[1\right]}\right)$ is a series of controller, which is virtual and step designed.

Step 1: defining

$$\begin{array}{c}\hfill V_1(\tilde{l},z_1)=V_0\left(\tilde{l}\right)+\frac{1}{2}{z}_1^2\end{array}$$

(19)

According to Definition 1, Young’s inequality, and Equations (12) and (16)–(19)

$$\begin{array}{cc}\hfill \pounds V_1& \le -\left(3H-3{\parallel P\parallel }^2-4c_1\right){|\tilde{l}|}^2+4c_1\left({\widehat{l}}_1^2+\frac{{\widehat{l}}_2^2}{H^2}\right)+z_1({\widehat{l}}_2+H{l}_1{\tilde{l}}_1)\hfill \\ \hfill & \le -\left(3H-3{\parallel P\parallel }^2-4c_1\right){|\tilde{l}|}^2+4c_1{z}_1^2+4c_1\frac{{\widehat{l}}_2^2}{H^2}+z_1{\alpha }_1+z_1{z}_2+H{\tilde{l}}_1^2+\frac{H}{4}{l}_1^2{z}_1^2\hfill \end{array}$$

(20)

Using (18) and ${(a+b)}^2\le 2a^2+2b^2$, choosing $H\ge 8c_1$, we can obtion

$$\begin{array}{c}\hfill 4c_1{z}_1^2\le \frac{H}{2}{z}_1^2,4c_1\frac{1}{H^2}{\widehat{l}}_2^2\le 8c_1\frac{1}{H^2}{z}_2^2+8c_1\frac{1}{H^2}{\alpha }_1^2\end{array}$$

(21)

In line with Equations (20) and (21), the first virtual controller has the form as follows

$$\begin{array}{cc}\hfill {\alpha }_1\left({\widehat{l}}_1\right)& =-H{b}_1{z}_1,b_1=\frac{1}{2}+\frac{l_1^2}{4}+2\hfill \end{array}$$

(22)

renders

$$\begin{array}{cc}\hfill \pounds V_1& \le -\left(3H-3{\parallel P\parallel }^2-4c_1\right){|\tilde{l}|}^2+H\left(\frac{1}{2}+\frac{l_1^2}{4}\right)z_1+8c_1\frac{1}{H^2}{z}_2^2+8c_1\frac{1}{H^2}+z_1{\alpha }_1+z_1{z}_2+H{\tilde{l}}_1^2\hfill \\ \hfill & \le -\left(2H-3{\parallel P\parallel }^2-4c_1\right){|\tilde{l}|}^2-(2H-8c_1{b}_1^2)z_1^2+8c_1\frac{1}{H^2}{z}_2^2+z_1{z}_2\hfill \end{array}$$

(23)

In the last step, through backstepping theory, we select the controller.

$$\begin{array}{cc}\hfill z_2& ={\widehat{l}}_2+H{b}_1{\widehat{l}}_1\hfill \\ \hfill d{z}_2& =\left(u+H^2{d}_{20}{\tilde{l}}_1+H^2{d}_{21}{z}_1+H^2{\overline{d}}_{2,1}{z}_1+H^2{d}_{22}{z}_2\right)dt\hfill \end{array}$$

(24)

where

$$\begin{array}{cc}\hfill d_{i0}& =l_i+b_{i-1}{l}_{i-1}+b_{i-1}{b}_{i-2}{l}_{i-2}+\cdots +b_{i-1}{b}_{i-2}\cdots b_1{l}_1\hfill \\ \hfill d_{ij}& =\prod _{k=j-1}^{i-1}b-k-b_j\prod _{k=j}^{i-1}{b}_k,j=1,\cdots ,i-2,b_0=0\hfill \\ \hfill {\overline{d}}_{i,i-1}& =b_{i-1}{b}_{i-2}-b_{i-1}^2,d_{ii}=b_{i-1}\hfill \end{array}$$

(25)

By (24), choosing the control law

$$\begin{array}{c}\hfill u\left({\widehat{l}}_{\left[2\right]}\right)=-H{b}_2{z}_2=-M\left(\widehat{l}\right)z_2=-\sum _{i=1}^2{H}^i\left(\prod _{j=2-(i-1)}^2{b}_j\right){\widehat{l}}_{2-(i-1)}\end{array}$$

(26)

renders

$$\begin{array}{cc}\hfill \pounds V_2& \le -\left(H-3{\parallel P\parallel }^2-4c_1\right){|\tilde{l}|}^2-\sum _{j=1}^i\frac{1}{H^{2j-2}}\left(H-8c_1{b}_j^2\right)z_j^2-\frac{1}{H^2}H{z}_2^2\hfill \\ \hfill \end{array}$$

(27)

where

$$\begin{array}{c}\hfill V_2(\tilde{l},z_{\left[2\right]})=3{\tilde{l}}^{T}P\tilde{l}+\sum _{j=1}^2\frac{1}{2H^{2(j-1)}}{z}_j^2\end{array}$$

(28)

$M(\widehat{l})=H{b}_2,b_2>0$ is a real number that satisfies (22) and does not depend on H.

The third part introduces the controller coefficients based on the Bernoulli probability distribution. In previous research few people combined Bernoulli probability distribution with the controller. In this paper, the author uses the Bernoulli probability distribution to transform a continuous controller into a discrete intermittent controller. In this case, it not only saves the energy consumption of the controller to extend the cruising range but also reduces the calculator computing power.

Theorem 1. 

The random probability distribution $\xi \left(t\right)$ will be introduced here, which is the control probability of the random variable distribution for the AUV and satisfies the Bernoulli distribution as follows:

$$\begin{array}{cc}\hfill Prob\left\{\xi \right(t)=1\}& =E\left\{\xi \right(t\left)\right\}=P\left(t\right),\hfill \\ \hfill Prob\left\{\xi \right(t)=0\}& =1-E\left\{\xi \right(t\left)\right\}=1-P\left(t\right),\hfill \end{array}$$

(29)

In the above Formula (29), when $\xi \left(l\right)$ is a constant proportional distribution, its value range is the interval $[P_1,P_2]$, where $P_1$ and $P_2$ are the minimum and maximum values of $\xi \left(l\right)$, respectively. For the convenience of calculation in this article, we assume that parameter $\xi \left(t\right)$ is irrelevant.

In this paper, we are interested in designing a probability gain controller as follows:

$$\begin{array}{c}\hfill u\left(l\right)=K\left(P\right)l\left(t\right),\end{array}$$

(30)

For Formula (30), the parameter $K\left(P\right)$ is the controller gain, which can be designed as follows:

$$\begin{array}{c}\hfill K\left(P\right)=K_0+P\left(t\right)K_u,\end{array}$$

(31)

Remark 1. 

The controller’s gain includes $K_0,K_u$, and the time-invariant parameter $P\left(t\right)$. In this paper, the controller will be regarded as a fixed value. It is less conservative than the other controller. The gain filtering problem has attracted many researchers’ attention. Due to the special structure of the controller gain, this gain controller deserves special attention. The constant gains of the controllers $K_0$ and $K_u$ are obtained using this paper’s main results. The Bernoulli probability gain is introduced into the backstepping controller as a stochastic gain, which solves the stochastic problem and the complexity of controller design.

3.3. Stability Analysis of Stochastic Nonlinear System

Theorem 2. 

Where $H_1^{*}\ge 0$, and $H>H_1^{*}$ are constants, system (5) satisfies Assumption 3. Finally, (8) and (26) are as follows:

Conclusion:

(1)

The system has initial stations $(l_0,{\widehat{l}}_0)$; system (5), (8), and (26) is unique.

(2)

Initially, the system is stable based on probability.

(3)

Control law

$$\begin{array}{c}\hfill u^{*}={\alpha }^{*}\left(\widehat{l}\right)=-\beta H{b}_2{z}_2,\beta \ge 2\end{array}$$

(32)

makes the system stable. The cost function as follows

$$\begin{array}{c}\hfill J\left(u\right)=E\left({\int }_0^{\infty }\left[s(\tilde{l},\widehat{l})+\frac{1}{H^2}{M}^{-1}\left(\widehat{l}\right)u^2\right]d\tau \right)\end{array}$$

(33)

is minimum. The well-known function $s(\tilde{l},\widehat{l})$ and Equation (10) have the same circumscription, and $\widehat{l}={({\widehat{l}}_1,{\widehat{l}}_2)}^T,\overline{f}(\tilde{l},\widehat{l})={({\left(HA\tilde{l}\right)}^T+F^T\left(l\right),H{s}_1{\tilde{l}}_1+{\widehat{l}}_2,H^2{s}_2\tilde{l})}^T,{\tilde{g}}_1(\tilde{l},\widehat{l})=(G^T\left(l\right),0),{\overline{g}}_2(\tilde{l},\widehat{l})={(0,1)}^T,V=V_2$

Proof. 

According to $d_{ii}=b_{i-1}$ and Equations (22) and (25), we can obtion $b_i>b_{i-1},b_0=0,b_i>1(i=1,2)$. According to $max\{4c_1,8c_1,8c_1{b}_1^2\}=8c_1{b}_1^2$. If

$$\begin{array}{c}\hfill H>8c_1{b}_1^2+3{\parallel P\parallel }^2\end{array}$$

(34)

is found. In line with Theorem 1, Equation (27), and Equation (28), the above conclusions (1) and (2) are found.

When $i=1$, by researching Equations (34), (17), and (22) and the literature, we can obtain $c_1$ which relies on H and $b_1$ which does not rely on H. It is well-known that $H>\frac{24(C_f^2+{\lambda }_{max}\left(P\right)C_g^2)}{H^2}\left({\sum }_{i=0}^1(i+1)H^i+(3-i)H^2\right)b_1^2+3{\parallel P\parallel }^2$ is equivalent to the following.

$$\begin{array}{cc}\hfill H^3>& 24(C_f^2+{\lambda }_{max}\left(P\right)C_g^2)b_1^2\left(\sum _{i=0}^i(i+1)H^i+(3-i)H^2\right)+3{\parallel P\parallel }^2{H}^2\hfill \end{array}$$

(35)

renders

$$\begin{array}{c}\hfill H^3+\sum _{i=0}^2{a}_i{H}^i>0\end{array}$$

(36)

When $a_0=-\Delta ,a_1=-2\Delta ,a_2=-\Delta -3{\parallel P\parallel }^2,\Delta =24(C_f^2+{\lambda }_{max}\left(P\right)C_g^2)b_1^2$. Now, we discuss selecting the $H_1^{*}$ in two cases:

(i)

If there is at least one positive real number in $H_1,H_2,H_3$, choose $H_1^{*}=ma{x}_{1\le i\le 3}\left\{H_i\right\}$ to be the largest real root.

$$\begin{array}{cc}\hfill H& =8c_1{b}_1^2+{3\parallel P\parallel }^2=24(C_f^2+{\lambda }_{max}\left(P\right)C_g^2)b_1^2{(1+\frac{1}{H})}^2+3{\parallel P\parallel }^2\hfill \end{array}$$

(37)

(ii)

Otherwise, select $H_1^{*}=0$, where $H_1^{*}\ge 0$ must be held, so (31) isfound for any $H>H_1^{*}$. The next step is to certify conclusion (3). Equations (12) and (14) can be expressed

$$\begin{array}{c}\hfill \left(\begin{array}{c}d\tilde{l}\\ d\widehat{l}\end{array}\right)=\overline{f}(\tilde{l},\widehat{l})dt+{\overline{g}}_1(\tilde{l},\widehat{l})d\omega +{\overline{g}}_2(\tilde{l},\widehat{l})udt\end{array}$$

(38)

By choosing $\gamma \left(r\right)=\frac{1}{2H^2}{r}^2$, we can obtain ${\left({\gamma }^{{}^{\prime }}\right)}^{-1}\left(r\right)=H^{2}r$ and $\ell \gamma \left(r\right)=\frac{1}{2}{H}^2{r}^2$, according to (7), (37), and $V=V_2$ and can obtain

$$\begin{array}{cc}\hfill u=\alpha \left(\widehat{l}\right)& =-R_2^{-1}\left(\widehat{l}\right)\frac{1}{H^2}{z}_2\frac{1}{2}{H}^2=-\frac{1}{2}{R}_2^{-1}\left(\widehat{l}\right)z_2\hfill \end{array}$$

(39)

choosing $R_2\left(\widehat{l}\right)={\left(2M\left(\widehat{l}\right)\right)}^{-1}=\frac{1}{2H{b}_2}$, which can obtain $u=-M\left(\widehat{l}\right)z_2$. It and Equation (26) have the same shape. In line with conclusion (2) and Lemma 1, the controller can be expressed as follows

$$\begin{array}{cc}\hfill u^{*}={\alpha }^{*}\left(\widehat{l}\right)& =-\frac{\beta }{2}{R}_2^{-1}\left(\widehat{l}\right)\frac{1}{H^2}{z}_2\frac{1}{2}{H}^2=-\frac{\beta }{2}{R}_2^{-1}\left(\widehat{l}\right)z_2=\beta \alpha \left(\widehat{l}\right),\beta \ge 2\hfill \end{array}$$

(40)

minimizes the cost function. □

Remark 2. 

In [8,31,32], the author studied the robust controller and the observer design for uncertain time-delay systems. In this part of the stability analysis, we can obtain the optimal solution controller form. According to the nonlinear system (5) satisfying the assumptions and theorems, the optimal value of the brother parameters can be obtained by introducing the cost function. Moreover, H is the optimal value we obtained through stability analysis, where the value of H can be further reduced so that the constraints of the entire controller become smaller. Finally, through proof, the optimal value can be obtained under the guidance of theory. Under the theory with the most controllers, the designed probability gain controller can be more relaxed, and it can adapt to many more nonlinear systems and expand the application range of the controller.

4. Underwater Robot Transportation Model Example

Remark 3. 

In this section, this paper calculates the numerical simulations in which stochastic noise is used instead of the AUV’s external stochastic disturbances [33]. However, in a realistic environment, such noise disturbances do not exist, and such an approach is idealized.

Consider the following stochastic nonlinear system:

$$\begin{array}{cc}\hfill {\dot{l}}_1& =l_2+\frac{1}{10}{l}_1{l}_2+\frac{1}{10}{l}_1{l}_2\dot{\omega }\hfill \\ \hfill {\dot{l}}_2& =u+\frac{1}{10}{l}_{2}sin{l}_1+\frac{1}{10}{l}_{2}sin{l}_1\dot{\omega }\hfill \\ \hfill y& =l_1\hfill \end{array}$$

(41)

Assumption 3 was found. Here, we choose $C_f=\frac{1}{10}$ and $C_g=\frac{1}{10}$ and the high-gain observer as follows

$$\begin{array}{cc}\hfill {\dot{\widehat{l}}}_1& ={\widehat{l}}_2+H(l_1-{\widehat{l}}_1)\hfill \\ \hfill {\dot{\widehat{l}}}_2& =u+H^2(l_1-{\widehat{l}}_1)\hfill \end{array}$$

(42)

Selected parameters are $K_1=K_2=1$; the $H>0$ is the unknown and real number gain, which can be obtained. By circumscription of ${\tilde{l}}_1=l_1-{\widehat{l}}_1$ and ${\tilde{l}}_2=\frac{l_2-{\widehat{l}}_2}{H}$, the following is obtained:

$$\begin{array}{cc}\hfill \mathrm{d}\tilde{l}& =HA\tilde{l}\mathrm{d}t+F\left(l\right)dt+G\left(l\right)\mathrm{d}\omega ,\tilde{l}={({\tilde{l}}_1,{\tilde{l}}_2)}^T\hfill \\ \hfill F\left(l\right)& ={\left(\frac{1}{10}{l}_{2}sin{l}_1,\frac{1}{10}{\left(l_1{l}_2\right)}^{\frac{1}{2}}\right)}^T\hfill \\ \hfill G\left(l\right)& ={\left(\frac{1}{10}{l}_{2}sin{l}_1,\frac{1}{10}{\left(l_1{l}_2\right)}^{\frac{1}{2}}\right)}^T\hfill \end{array}$$

(43)

Introduction,

$$\begin{array}{cc}\hfill z_1& ={\widehat{l}}_1\hfill \\ \hfill z_2& ={\widehat{l}}_2-{\alpha }_1\left({\widehat{l}}_1\right)\hfill \end{array}$$

(44)

According to the theorem and controller law proposed, we can obtain the probability controller.

$$\begin{array}{c}\hfill {\alpha }_1\left({\widehat{l}}_1\right)=-H{b}_1{z}_1,b_1=\frac{1}{2}+\frac{1}{4}+2=2.75,H\ge 8c_1\end{array}$$

(45)

$$\begin{array}{cc}\hfill u& =-H{b}_2{z}_2,b_2=\frac{d_{20}^2}{4}+\frac{d_{21}^2}{4}+d_{22}+2=19.03\hfill \end{array}$$

(46)

Meanwhile,

$$\begin{array}{c}\hfill c_1=\frac{3}{100}\left(1+{\lambda }_{max}\left(P\right)\right){\left(1+\frac{1}{H}\right)}^2\end{array}$$

(47)

P = $\left(\begin{array}{cc}0& -\frac{1}{2}\\ -\frac{1}{2}& 1\end{array}\right)$, $\parallel P\parallel =\frac{\sqrt{6}}{2}$, ${\lambda }_{max}\left(P\right)=\frac{1+\sqrt{2}}{2}$, $d_{20}=1+b_1=3.75,d_{21}=1-b_1^2=-6.56,d_{22}=b_1=2.75$. In this part, by using Theorem 1 for a specific AUV control system described in Figure 2, we can lay out a Bernoulli probability controller as follows: $u=-K\left(P\right)H{b}_2{z}_2$. We selected the unknown parameters as $H>H_1^{*}=9.9609$.

4.1. Simple State Keeping Results in the Presence of Underwater Stochastic Disturbances

In line with the above analysis, according to the proposed strategy, we conduct a simulation to prove the effectiveness. Figure 3, Figure 4 and Figure 5 are the simulation results. ${[l_1\left(0\right),l_2\left(0\right),{\widehat{l}}_1\left(0\right),{\widehat{l}}_2\left(0\right)]}^T={[5,0,0,0]}^T$ are the chosen initial conditions.

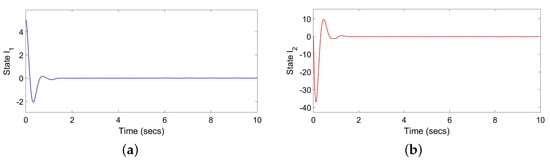
Figure 3. (a) State $l_1$ under probabilistic gain controller; (b) state $l_2$ under probabilistic gain controller.

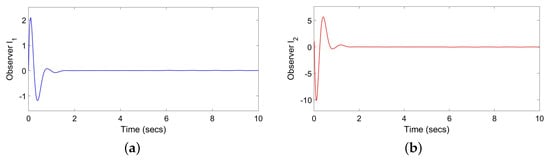
Figure 4. (a) Observer $l_1$ under probabilistic gain controller; (b) observer $l_2$ under probabilistic gain controller.

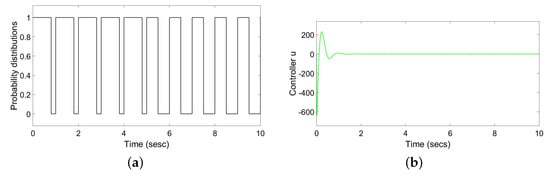
Figure 5. (a) Time-varying probability distribution; (b) controller u under probabilistic gain controller.

4.2. Without the Probability Gain Simulation Results in the Presence of Underwater Stochastic Disturbances

In this section, we will compare the probability gain simulation results with the ordinary nonlinear backstepping control. From Figure 6, Figure 7 and Figure 8, it can be seen that there are random disturbances in the state and observed values of the system, and the probability distribution observer can eliminate and suppress the disturbance very well.

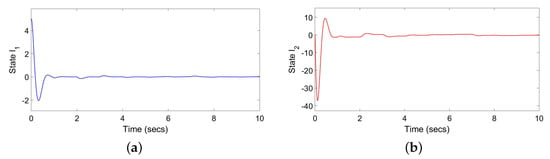
Figure 6. (a) State $l_1$ without probabilistic gain controller; (b) state $l_2$ without probabilistic gain controller.

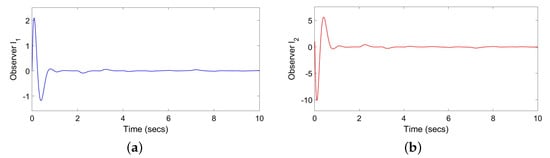
Figure 7. (a) Observer $l_1$ without probabilistic gain controller; (b) observer $l_2$ without probabilistic gain controller.

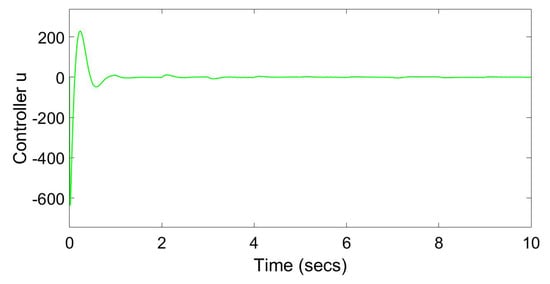
Figure 8. Controller u without probabilistic gain controller.

By comparing Figure 3, Figure 4 and Figure 5 and Figure 6, Figure 7 and Figure 8, we can see that in the absence of the Bernoulli probability controller, the system’s state will be affected by external interference, and there will still be fluctuations in the state under the action of the controller. After the addition of the Bernoulli probability controller, the simulation results from Figure 3, Figure 4 and Figure 5 strongly prove that the probability gain controller can achieve the effect of eliminating external interference, and the time and efficiency of the controller are not affected under the action of the probability controller. Finally, by comparing with the PID control effect Figure 9 and Figure 10, we can reduce the control time from 10 s to 2 s. However, due to the enhanced control effect, the peak consumption of this controller increases from 4 to 200, and the increase of the controller consumption is within our tolerance range. Nevertheless, the controller’s action time was reduced from 15 s to less than 1 s.

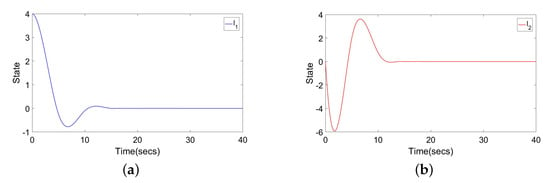
Figure 9. (a) State $l_1$ under PID controller; (b) state $l_2$ under PID controller.

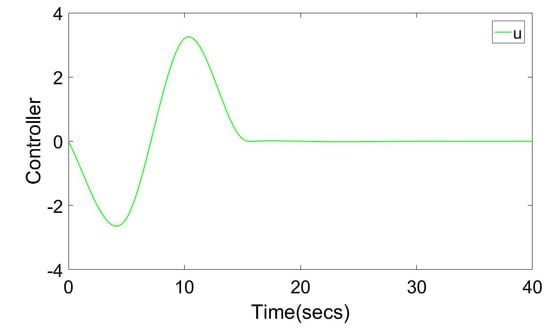
Figure 10. Controller u under PID controller.

5. Concluding and Future Prospects

According to the simulation results, the system’s unmeasurable states can be observed using a high-gain observer, and the complex nonlinear control problem is transformed into a parameter selection problem by introducing coordinate transformation, which simplifies the calculation process and complexity. The paper assumes that the external disturbance randomly occurs, and the concept of a probability controller is introduced. With the control effect unchanged, it can convert continuous control to intermittent control. The endurance problem of the AUV is solved under intermittent control. The control method significantly saves energy and extends the cruising range. Based on the backstepping control method, the complex nonlinear controller is decomposed into a computational method that can perform iterative recursion. The final controller can be calculated through the designed virtual controller. An easy-to-implement probabilistic control algorithm is designed, and a Bernoulli probability gain controller with constant parameters and time invariance is designed. This is more lenient than traditional control methods. In the case of simultaneous external interference, system uncertainty, and time delay, the closed-loop system can ensure that all states are stable. Finally, a simulation example is used to demonstrate the effectiveness of the proposed design method.

In this research, the continuous system is mainly studied, which limits the application scope of the probability gain controller because the information obtained in the actual project and the execution of the command are discrete information. The next step in our research is to discretize continuous systems so that the probability gain control method can be applied to discrete systems; on the other hand, it is aimed at the simplified AUV system. This article mainly considers three degrees of freedom, which is different from actual engineering. Another direction is to satisfy the six-degree-of-freedom controller when the controller realizes practical engineering applications.