A Method for Predicting the Academic Performances of College Students Based on Education System Data

Abstract

With the development of university campus informatization, effective information mined from fragmented data can greatly improve the management levels of universities and the quality of student training. Academic performances are important in campus life and learning and are important indicators reflecting school administration, teaching level, and learning abilities. As the number of college students increases each year, the quality of teaching in colleges and universities is receiving widespread attention. Academic performances measure the learning ‘effects’ of college students and evaluate the educational levels of colleges and universities. Existing studies related to academic performance prediction often only use a single data source, and their prediction accuracies are often not ideal. In this research, the academic performances of students will be predicted using a feedforward spike neural network trained on data collected from an educational administration system and an online learning platform. Finally, the performance of the proposed prediction model was validated by predicting student achievements on a real dataset (involving a university in Shenyang). The experimental results show that the proposed model can effectively improve the prediction accuracies of student achievements, and its prediction accuracy could reach 70.8%. Using artificial intelligence technology to deeply analyze the behavioral patterns of students and clarify the deep-level impact mechanisms of the academic performances of students can help college educators manage students in a timely and targeted manner, and formulate effective learning supervision plans.

1. Introduction

Due to the widespread use of educational information management systems in colleges and universities, the amount of data in databases has grown, and the data held by colleges and universities have become more abundant [1]. Unfortunately, the use of this part of the data has not been further studied, it is still only for the purpose of providing simple inquiries and statistical reports. It is impossible to obtain implicit value information from a large amount of data, such as the relationship between students’ grades and daily behavior, where students go after graduation, etc. [2]. How to effectively use these data could effectively guide college administrators, improve the teaching management levels at colleges and universities, and further improve the quality of running schools; these will be key issues that college and university administrators will consider in the future.

In college and university educational affairs activities, student achievements are important for evaluating knowledge; they are also key factors for evaluating teaching quality [3]. With the current open teaching management model in colleges and universities, and the rapid development of online education, coupled with the outbreak of COVID-19 (coronavirus disease 2019), there are more data on online learning behaviors. This allows students to have a higher degree of learning freedom; students are free to set their plans and goals, which also leads to more factors that affect academic performance [4]. The changing laws of academic performances are discovered from the information and associations behind data, such as in-depth research, factor analyses that affect student performances, and artificial intelligence algorithms used to find the key factors affecting academic performances [5]. Thus, it is practical to analyze students’ grades and predict future grades. Changes in grades can provide suggestions for teaching, improve education and management, and improve learning efficiencies. Therefore, this is of great significance in theory and practical applications.

Academic achievement prediction refers to predicting a student’s future academic performance based on existing behavioral data. Academic achievement prediction is one of the most primitive and popular applications in the field of educational data mining [6]. Specifically, academic performance prediction generally predicts the development trend of academic performance by collecting the behavioral data of students and analyzing behavioral patterns using statistical or data mining methods. The role of academic performance prediction is to predict the development trend of academic performance in advance and find out the possible problems of students in time. This allows students and teachers to react in a timely manner and prevent the risk of failing the course. As the educational environment continues to change, so does research in this field [5]. Academic achievement prediction is an important research problem in the field of educational data mining, which has been intensively studied by many researchers [7]. However, many challenges remain in terms of prediction accuracy and interpretability due to the lack of richness and diversity of data sources and related features. Some representative works are summarized as follows. Qu et al. [8] proposed a student achievement predicting framework, which includes data processing and student achievement predicting. The proposed method has a better performance in comparison to support vector machines, naïve Bayes, logistic regression, and multi-layer perception. Kostopoulos [9] presented a novel semi-supervised regression algorithm for predicting the final grade of undergraduate students in a distance online course. Yang et al. [10] predicted course achievements in Moodle through the procrastination behaviours of students using their homework submission data. A Moodle course from the University of Tartu in Estonia was used, which included 242 students to assess the efficacy of the proposed approach. Tomasevic et al. [7] provided a comprehensive analysis and comparison of the state-of-the-art supervised machine learning techniques used to solve exam performance predictions. Nieto-Reyes et al. [11] proposed a methodology that automates the prediction of academic performances at the end of the course using data recorded during the first tasks of the academic year. This methodology allows teachers and evaluators to define the variables that they consider most appropriate to measure those aspects related to the academic performances of students. Miao et al. [12] improved the neural network algorithm, and combined support vector machines to build a student grade-prediction model; they used the principle component analysis to reduce the dimensionality of the sample data. Ali et al. [13] predicted the achievement of 82 undergraduates enrolled in a hybrid English for Business Communication course using clustering techniques. Classification results revealed that log data and engagement activities successfully predicted academic performances with more than 88% accuracy. Baashar et al. [14] examined and surveyed the current literature regarding the ANN methods used in predicting academic performances; they attempted to capture a pattern of the most used artificial neural network techniques and algorithms. Li et al. [15] proposed an end-to-end deep learning model that automatically extracts features from students’ multi-source heterogeneous behavior data to predict academic performances. Liu et al. [16] proposed a student achievement prediction model based on the evolutionary spiking neural network. The experimental results show that the proposed method can effectively improve the prediction accuracies of student achievements.

Although the above models have been successfully applied to student achievement predictions and these experiences are very helpful for improving the accuracy of student achievement predictions, these prediction models still have some room for improvement in the design stage and implementation of actual teaching data prediction, such as limited data sources, prediction low precision, poor efficiency, etc. Therefore, this paper mainly explores a student achievement prediction model based on the feedforward spiking neural network. The learning prediction model was deeply studied to improve the generalization performance and prediction accuracy of the feedforward spiking neural network, and a real dataset was analyzed from student information and course information data (from the 19th-grade IoT at a university in Shenyang, China). Finally, the proposed model was applied to student grade prediction on the dataset and compared with state-of-the-art algorithms to verify its effectiveness. The experimental results show that the proposed algorithm is better than similar learning algorithms in the accuracy of student achievement prediction.

The main contributions of this paper are as follows.

• This paper processed real student and course data from a university in Shenyang and used it for the training and testing of the predicted model.
• A feedforward spiking neural network model is proposed to predict students’ grades; the simulation results show the advantages of the proposed model using student grade data and course information data in predicting real students’ grades.
• It is helpful for teachers to implement timely intervention and for students to adjust their learning statuses, which is of great significance to the harmonious development of teaching and learning.

The remainder of this paper is summarized below. Section 2 describes the concept of student achievement prediction, pattern classification, and spiking neural network. Section 3 describes the content related to the real dataset from a university in Shenyang. Section 4 describes how to design the proposed model in detail, including encoding and algorithm designs. Section 5 presents the results of the experimental evaluation. The proposed model is compared with the state-of-the-art models, and the simulation results are evaluated and discussed. Finally, Section 6 presents the conclusions and outlines future research lines.

2. Related Works

2.1. Student Achievement Prediction

With the rapid development of educational big data technology, the learning data recorded in the college education system have become more abundant, and grade prediction has become more accurate [17]. Student achievements can be seen as the sum of the results of cognition, behavior, skills, and emotional attitudes produced by students after completing a series of teaching activities [18]. Under the guidance of theories, such as teaching evaluation, one may look at how to determine the key factors of academic performances or identify variables that have significant impacts on academic performances [19]. They play great roles in establishing data models for predicting student achievements and in improving the accuracy of student achievement prediction [20], specifically as the first student/course data are collected, such as corresponding questionnaires, educational administration systems, or online teaching platforms. Secondly, the prediction model is used to predict academic performance, and to determine the predicted grades of the students. Finally, students with different degrees of learning crises are screened out to help teachers and students adjust their teaching and learning statuses in time.

At present, the research on learning performance prediction in an educational environment is often based on the educational administration system or the online learning platforms of colleges and universities [21]. The selected predictors of student achievements include interactive information (such as student–platform interactions, student collaborations, and teacher–student communications), population data (such as age and gender), psychological emotions (such as motivation, and attitude), etc. [22]. The prediction techniques for student achievements include classification, regression, clustering, association rule mining, exploratory analysis, etc. [1]. The prediction results of the models are mainly measured by the sum of squared errors, root mean square error, accuracy, precision, F1-measure, etc. [7].

2.2. Pattern Classification

Pattern classification is the mapping of a dataset to a given category by constructing a classification function or classification model [23]. It is the core research content of pattern recognition, which is related to the overall efficiency of its recognition and is widely used in various research fields. Pattern classification methods mainly include support vector machine, BP neural network, K-nearest neighbor, naïve Bayes, linear discriminant analysis, quadratic discriminant analysis, etc. The high efficiency of support vector machines and the applicability of BP neural networks to deal with complex problems make these two methods the most widely used classification methods [24]. The K-nearest neighbor method is a weight-based clustering method, which can obtain better classification effects in classification. Naïve Bayes is a probability-based classification method that is easy to understand and implement. Linear discriminant analysis and quadratic discriminant analysis are discriminant analysis methods using different discriminant functions and are the most commonly used classification methods.

According to the classification algorithm of supervision, classification learning problems can be divided into three categories, supervised classification, semi-supervised classification, and unsupervised classification [25]. Supervised classification means that all samples used to train the classifier have been labeled manually or in other ways. Many well-known classifier algorithms belong to supervised learning methods, such as AdaBoost, support vector machine (SVM), neural network algorithm, and perceptron algorithm. Unsupervised classification means that all samples are not labeled, and the classification algorithm needs to use the information from the samples to complete the classification learning task. This method is usually called clustering. Commonly used clustering algorithms include the expectation maximization algorithm, fuzzy C-means clustering algorithm, etc. Semi-supervised classification means that only a part of the training samples (very few) have class labels. The classification algorithm needs to use both labeled and unlabeled samples to learn classification. The results of training with two kinds of samples are more effective than those with only labeled samples. These algorithms are usually improved by supervised learning algorithms, such as manifold regularization, semi-supervised SVM, etc. The student achievement prediction problem studied in this paper is a supervised classification problem.

2.3. Spiking Neural Network

In biological research, studying neurons in the biological brain is important. From a biological point of view, the brain is composed of hundreds of millions of neurons, which are interconnected according to different types and functions. The structure of the neuron is shown in Figure 1. These neurons are combined to form a layered structure, which constitutes various organs in the biological brain, and a complex neural network system is also formed in the biological brain. This complex nervous system will receive external stimuli. This function allows neurons to receive stimuli and transmit signals to the next neuron. One neuron will process and judge the received stimulus signal, and finally, the neuron will respond to external stimuli [26].

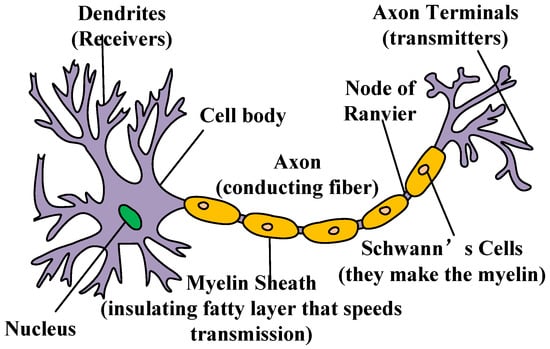
Figure 1. Neuron structure diagram.

Although the neurons in the biological brain will evolve into different organs according to different functions, the neuron structure that constitutes each organ is similar, and general neurons can be divided according to the morphological and functional characteristics of their respective components. Neurons are divided into neuronal axons, neuronal dendrites, and neuronal cell bodies according to their components, as shown in Figure 1. The dendrites in a neuron are connected to other neurons, and their role is to collect the information transmitted by other neurons in the form of neurotransmitters, and then pass the information to the cell body. When the membrane potential reaches a certain threshold, a nerve spike is generated, which is then passed back through the axon to the synapse, which also transmits information to the next neuron by firing neurotransmitters [27].

The spiking neural network is considered to be a third-generation neural network, which provides a high-speed real-time implementation of solving complex problems in an energy-efficient manner, inspired by biological neurons. Through the process of stimulating information transmission in brain neurons, we can know that the synapse plays a very important role in the process of information transmission. It is responsible for the transmission of stimulation information between two neurons. Regarding internal and external stimulation, the neurons will generate spikes, the spikes are transmitted to the synaptic position on the neuron and then act on the postsynaptic neuron, affecting the membrane potential of the postsynaptic neuron; the postsynaptic membrane potential will respond differently to different types of spike signals. Different spike signals are caused by different types of synapses. There are two types of synapses, excitatory and inhibitory. The decisive factor for the type of synapse is the neurotransmitter released by the previous neuron synapse and the current neuron. These receptors are linked together to form either inhibitory or excitatory synapses.

Compared with other first-generation and second-generation artificial neural networks, the third-generation spiking neural network can simulate almost all functions more efficiently by using fewer neuron models and structures, and its computing power and efficiency are significantly improved. Although the spiking neural network model has not been developed for a long time, it has shown good learning ability in many fields, including biological signal processing [28], robot control [29], image recognition [30], etc. All of these applications show that the spiking neural network has great practical significance and is worthy of in-depth study. Therefore, the research on the spiking neural network in this paper, especially the student achievement prediction algorithm, is meaningful and valuable.

3. Real Datasets in Education Systems

In this section, we will use the dataset in the educational administration system of all students in the 19th-grade of the Internet of Things major from a university in Shenyang, and course learning data from the Chaoxing Xuexitong system to analyze and study the factors that have the greatest impacts on the final grades of students. Based on this dataset, a suitable feedforward spiking neural network prediction model is established to predict student achievements.

With the popularization of information technology, more data in the school’s education information system can be used for research, and the data can be deeply excavated to discover the inherent laws of the data itself, to help decision-makers better manage schools [31]. Early research on student achievement prediction focused on education and psychology, using data mostly from questionnaires or student self-reports. Different from previous studies, we obtained datasets for predicting student performances through the school’s educational administration system, the online learning platform of the Chaoxing Xuexitong system, and the enrollment information statistics table. From a macro perspective, the mining of these data is very valuable. If the data can be correlated, many research questions can be generated. After removing the private data of the student’s identity, we can match the data with the student’s identity one-to-one, to better manage and supervise the students’ studies effectively.

Throughout the student achievement prediction modeling, the first thing to do is preprocess the data from different sources in the information systems [32]. Data preprocessing takes about 40% of the time, and the quality of data processing directly affects the accuracy of the model. The preprocessed data not only save a lot of space and time, but they also obtain the prediction results that have a better role in decision-making and prediction. Secondly, due to the different sources of educational data, the dimensions of attributes and features are inconsistent, and there is a lack of data features. In order to obtain better-quality modeling data, certain data integration, cleaning, regularization, and transformation must be performed [33]. More specifically, data integration is a technique that involves combining data from multiple data sources (databases, data cubes, or generic files) into a consistent data store (such as a data warehouse). Since the data integration of different disciplines involves different theoretical foundations and rules, data integration can be said to be a difficult point in data preprocessing. Naming rules and requirements for each data source may be inconsistent. To extract data from multiple data sources into a data warehouse, in order to ensure the accuracy of the experimental results, all data formats must be unified. There are two broad categories of methods for implementing a unified format. One is to modify each data source first, and then extract it uniformly into the data warehouse. Data cleaning is the most time-consuming and tedious, but also the most important step in the data preparation process. This step can effectively reduce the problem of conflicting situations that may arise during the learning process. Data transformation is the use of linear or nonlinear mathematical transformation methods to compress multi-dimensional data into data with fewer dimensions and eliminate their differences in characteristics, such as space, attributes, time, and precision. Although such methods are usually lossy to the original data, the results tend to have greater utility.

4. Proposed Method

If the examination is one of the most important means to evaluate the quality of college training, then the course’s score is the most direct factor to evaluate the quality of students. If students can predict their grades in advance based on their previous academic performances, and this reminds them to study hard to avoid failing, this is of great significance in education and teaching research [34]. Figure 2 shows the overall experimental process scheme for the construction of the experimental model of student achievement predictions based on the spiking neural network. The proposed feedforward spiking neural network mainly consists of three parts: encoding the input data, training and learning the spiking neural network, and decoding and outputting the learning results, as shown in Figure 2. The model mainly realizes the classifications of students’ grades, i.e., predicts the course grades of students in three grades.

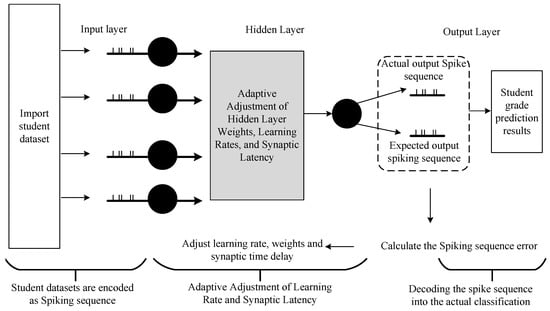
Figure 2. Structure topology of spiking neural network based on student achievement prediction.

According to Figure 2, the implementation process of the proposed feedforward spiking neural network is shown in Figure 3. The first spiking coding is used to encode the student data and course data into the input spiking sequence and the expected spiking sequence; the spiking sequence is passed to the hidden layer, where the learning rate and the synaptic time delay are adaptively adjusted and the information is transmitted to the output layer. The output layer outputs the actual spiking sequence and compares it with the expected output spiking sequence to generate an error rate, and then back-propagates to adjust the learning according to the value of the error rate and synaptic time delay, thereby reducing the error value until the error is less than a certain limit or the iteration number reaches the required number of iterations to stop learning, and decode the output spike sequence into classification categories.

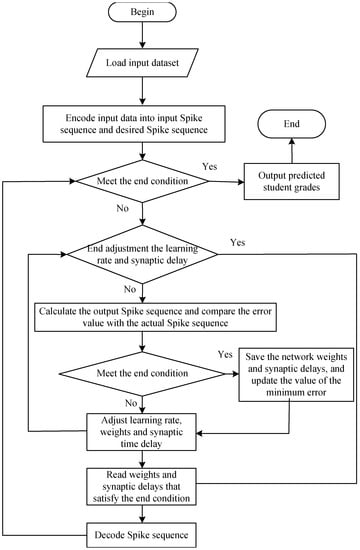
Figure 3. The architecture of student achievement prediction model.

To simplify the operation of spiking neural networks, the weight-learning rules in this paper were learned based on gradient descent, which can speed up network training while the spiking neural network is running. Gradient descent learning rules are the most commonly used and relatively classic and mature algorithms in neural network learning. The idea is to construct the loss function of the spiking neural network, and use the principle of gradient descent to obtain the optimal value of the loss function, and the rules of the gradient descent learning algorithm of the spiking neural network are similar to the principle of the artificial neural network. The difference between the target output and the actual output is used to construct a loss function, and then the error is backpropagated to change the weights in the network. The adjustment of network weights can be expressed as Equation (1).

$$\Delta w=-\eta \nabla E=-\eta \frac{\partial E}{\partial w}$$

(1)

where $\eta$ represents the learning rate of the spiking neural network. $\nabla E$ represents the partial derivative of the loss function E to the weight w in the spiking neural network, and the gradient value of the loss function is adjusted to the weight.

The specific expression of the error loss function E is shown in Equation (2).

$$E=\frac{1}{2}\sum _{f=1}^N{(t^f-⌃t^f)}^2$$

(2)

where $t^f$ represents the actual excitation time of the f-th spike in the spiking neural network; $⌃t^f$ is the expected output time of the f-th spike in the spiking neural network; N is the number of spikes fired by a neuron in a spiking neural network.

Gradient descent learning algorithms should budget based on the neuron’s internal state variables. This paper uses spike response mode (SRM) 0, which is a simplified model of the SRM model [35], and its specific internal state variables are shown in Equation (3).

$$\begin{array}{cc}\hfill u_j\left(t\right)& =\sum _i\sum _k{w}_{ij}^k\epsilon (t-t_i-d_{ij}^k)\hfill \\ \hfill & =\sum _i\sum _k{w}_{ij}^k{y}_{ij}^k\hfill \end{array}$$

(3)

where i is the number of spikes in the pre-synaptic neuron and $y_{ij}^k$ is the symbolic representation of the activation function.

The training rule is shown in Equation (4).

$$\begin{array}{cc}\hfill ▵d_i& =-\frac{\alpha }{2}\sum _{f=1}^N\frac{\partial \left({(t^f-⌃t^f)}^2\right)}{\partial d_i}\hfill \\ \hfill & =-\frac{\alpha }{2}\sum _{f=1}^N\frac{\partial \left({(t^f-⌃t^f)}^2\right)}{\partial t_f}\frac{\partial t_f}{\partial d_i}\hfill \\ \hfill & =-\alpha \sum _{f=1}^N(t^f-⌃t^f)\frac{\partial t_f}{\partial d_i}\hfill \end{array}$$

where $▵d_i$ represents the adjustment amount of the i-th synaptic time delay of a neuron in the spiking neural network. $\alpha$ is similar to the learning rate in weight adjustment, indicating the magnitude of each time delay adjustment. Only the $\frac{\partial t_f}{\partial d_i}$ item needs to be calculated separately, and the rest are obtained in the intermediate calculation process of the weights.

The calculation method of $\frac{\partial t_f}{\partial d_i}$ is also similar to the weight adjustment. It adopts the recursive theory based on the gradient descent method. The adjustment result of the synaptic time delay in the next iteration has an important relationship with the spike time of the previous iteration process. The formula is shown in Equation (4).

$$\begin{array}{cc}\hfill & \frac{\partial t_f}{\partial d_i}=\frac{\partial t_f}{\partial u\left(t^f\right)}(\frac{\partial u\left(t_f\right)}{\partial d_i}+\frac{\partial u\left(t_f\right)}{\partial t(f-1)}\frac{\partial t(f-1)}{\partial d_i})\hfill \\ \hfill & \frac{\partial t(f-1)}{\partial d_i}=\frac{\partial t(f-1)}{\partial u\left(t\right(f-1\left)\right)}(\frac{\partial u\left(t\right(f-1\left)\right)}{\partial d_i}+\frac{\partial u\left(t\right(f-1\left)\right)}{\partial t(f-2)}\frac{\partial t(f-2)}{\partial d_i})\hfill \\ \hfill & ⋮\hfill \\ \hfill & \frac{\partial t_1}{\partial d_i}=\frac{\partial t_1}{\partial u\left(t_1\right)}\frac{\partial u\left(t_1\right)}{\partial d_i}\hfill \end{array}$$

(4)

In Formula (4), only the $\frac{\partial u\left(t_f\right)}{\partial d_i}$ item needs to be calculated separately; the rest of the calculation results are involved in the weight calculation process, and they need to be called directly. This operation both facilitates computations and adjusts synaptic time delays with minimal effort. $\frac{\partial u\left(t_f\right)}{\partial d_i}$ can be calculated according to Equation (5).

$$\begin{array}{cc}\hfill \frac{\partial u\left(t_f\right)}{\partial d_i}& =\frac{\partial \left({\sum }_{i=1}^N{w}_i\epsilon (t-d_i)\right)}{\partial d_i}\hfill \\ \hfill & =w_i\frac{\partial \left({\sum }_{i=1}^N{w}_i\epsilon (t^f-t_i^g-d_i)\right)}{\partial d_i}\hfill \\ \hfill & =w_i\sum _{i=1}^N\frac{t^f-t_i^g-d_i}{\partial {\tau }_2}{e}^{1-\frac{t^f-t_i^g-d_i}{\tau }}-\frac{e^{1-\frac{t^f-t_i^g-d_i}{\tau }}}{\tau }\hfill \\ \hfill & =w_i\sum _{i=1}^N\tau (t^f-t_i^g-d_i)(\frac{1}{\tau }-\frac{1}{t^f-t_i^g-d_i})\hfill \end{array}$$

(5)

In order to ensure the accuracy of the training and testing of the proposed feedforward spiking neural network and its authenticity, this paper divides the student data set into two parts, one for training and one for testing. In order to better explain the proposed model, the pseudo-code of its specific algorithm is shown in Algorithm 1.

Algorithm 1 The pseudo-code of the proposed algorithm for student achievement prediction.

Require: Student dataset and course dataset.  Ensure: Predicted results.   1: Load the student dataset and course dataset, and initialize the weights and synaptic delays of the spiking neural network.   2: Set the parameters of the spiking neural network, including the initial learning rate $L_0$, time step t, different time constants $\tau$, threshold $\vartheta$, the number of neurons in the output layer $o\_n$, the number of neurons in the input layer and hidden layer $h\_n$, and the connections between neurons number $c\_n$ and the number of synaptic time delays d in each connection.   3: Randomly generate initial weights and synaptic time delays, and normalize these parameters.   4: Start training the spiking neural network and forward the spiking information to the next neuron. Computation of the internal state variables requires a comparison of the postsynaptic membrane potential with the thresholds of the spiking neural network. If the value of the internal state variable is greater than the threshold, a spike signal is generated and the time of the spiking emission is recorded.   5: Use the actual spike time and the expected spike time to construct an error function, and judge the updated range of the learning rate according to the error value.   6: According to the obtained new learning rate L, back-propagation is performed, and the gradient descent principle is used to change the weight of the output layer and the hidden layer of the spiking neural network, so that the error gradually becomes smaller.   7: Repeat the above process until the error is less than the minimum error of the original algorithm or meet a certain number of iterations.   8: Decode the network output.

5. Experimental Studies

In order to verify the effect of the student achievement prediction model proposed in this paper, an experiment was designed to compare the proposed model with other similar models, and the final exam results of students were predicted. The prediction task is to predict the grades based on both the student and some of the courses, and the prediction results are accurate concerning whether the student can pass a course or the possible test levels of a certain course. The data and comparison methods used in the experiments are described below. First, we describe the real education datasets and the evaluation indicator used in the experiment. All experiments are based on the real education dataset of a university in Shenyang city, Liaoning Province, China. Second, we give a brief comparison of the five experimental models and provide the experimental setup used in this study. These models include the decision tree, random forest, neural network, XGBoost, and SVM. Finally, the comparison results of these experimental models under the real education datasets are discussed.

5.1. Experimental Datasets and Experimental Conditions

5.1.1. Datasets

In order to verify the validity of the proposed model, we collected and sorted out two datasets, corresponding to the student datasets and course datasets of the 19th-grade Internet of Things major at a university in Shenyang city, Liaoning Province, China. The features used in the experiments include basic attribute information of students and courses. We deciphered the student data and course data; there were a total of 3976 pieces of processed data. Table 1 gives the basic information about the above two datasets, respectively. There are 55 students in the dataset, and it covers student performance data for 62 courses in 6 semesters. The dataset contains 26 variables related to student grades. The size of the dataset is 3976 entries, which includes the results from normal exams (3410) and make-up exams (566).

Table 1. Student Personal Information.

Number of Students	Boys/Girls	Number of Semesters	Number of Courses
55	32/23	6	62

The dataset contains 55 student records from different genders for 6 semesters, consisting of 26 information properties, including student ID, grade point average (GPA), entrance grades, semester, course attributes, performance in class, etc. About 70 percent of students came from the province where the university was located. This paper analyzed these datasets and we built a model to predict student grades. Through the modeling results, it was discovered that there were imbalanced data in the dataset. The imbalance of data makes the sample size of some rare attribute values obtained in the training set more sparse, which further exacerbates the sparsity of sample features. To address the problem of data imbalance, we divide the predicted grades into three levels [‘L’, ‘M’, ‘H’], which will be used as the standard for judging students’ grades. Among them, ‘L’ (0–64) means a failing score, ‘M’ (65–84) means a medium score, and ‘H’ (85–100) means a high score. The datasets were modeled under three-level classification tasks in Table 2. The original value in Table 2 is the real value in the dataset. The classification in Table 2 refers to the three values of the three-level classification system on a 100-point scale. The encoding in Table 2 represents the three-category numerical value for the convenience of the programming.

Table 2. The three-level classification system.

Category	Excellent	Satisfactory	Fail
Original value	85–100	65–84	0–64
Classification	H	M	L
Encoding	1	2	3

Figure 4 shows the proportion of students by gender in the real educational datasets, of which 32 are boys and 23 are girls.

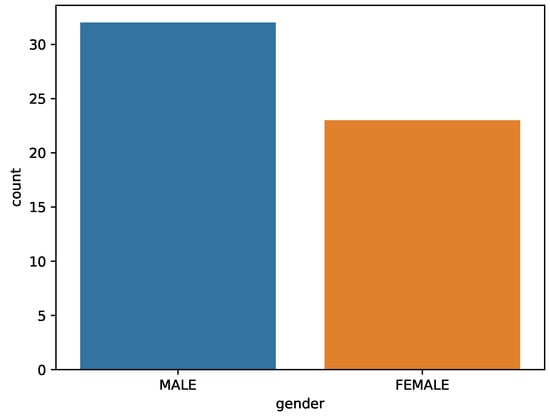
Figure 4. Statistics of Student Gender.

The student enrollment data table includes information, such as college entrance examination scores, class, major, grade, no. (student ID), gender, place of origin, political status, graduate high school, date of birth, etc. It was found through the experiments that college entrance examination scores, gender, political affiliation, grades, and other information greatly influence the results of the scores. The experimental data in Figure 5 shows that most student scores are distributed between 500 points, some of the scores were between 500 and 520, and the number of students below 500 points is very small.

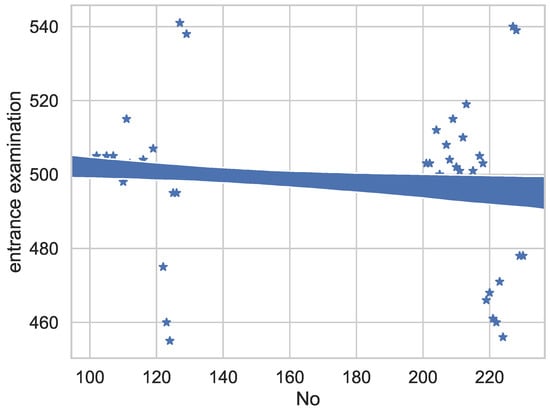
Figure 5. Student performance analysis entrance examination.

As can be seen from Figure 6, most students can obtain good grades in most courses. Among them, the number of courses with good grades was 52.82% of the total number of courses, the number of courses with middle grades was 39.89% of the total number of courses, and the courses with poor grades accounted for 7.29% of the total number of courses. This result shows that most students could master the knowledge points of the course and achieve ideal grades.

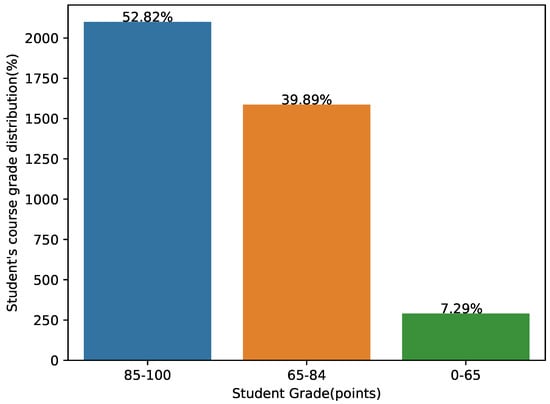
Figure 6. Proportional distribution of course grades.

In order to further analyze the behaviors of these students, a questionnaire for statistical work and postgraduate entrance examination was set up. The results of the questionnaire are shown in Figure 7. Observing Figure 7, it is not difficult to find that the number of boys who chose to work; graduate school was the same, while the number of girls who chose to work was more.

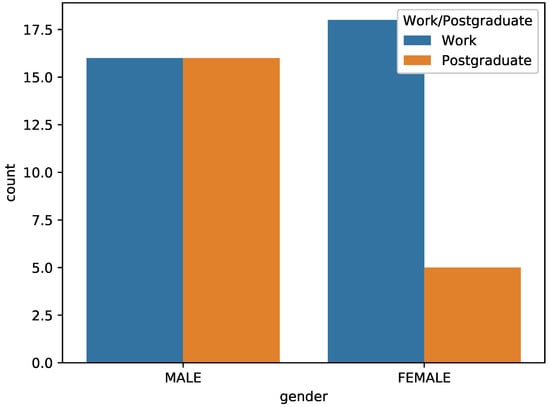
Figure 7. The relationship between gender and the proportion of graduate career choices.

Figure 8 shows the proportion of students’ political affiliations. It can be seen from Figure 8 that most of the students were members of the Communist Youth League, and the number of male party members was higher than the number of female party members.

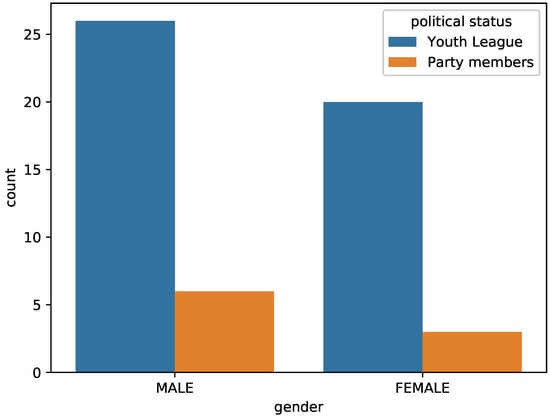
Figure 8. The relationship between gender and the proportion of party members.

The overall ranking of the 55 students is shown in Figure 9. The comparative relationship between the overall grades of college courses and the college entrance examination scores of 55 students. The purple dotted line in the middle of Figure 9 represents the results of the college entrance examination. It can be seen from the figure that the scores of the students in the college entrance examination are relatively similar. However, the blue star line indicates the ranking of all university courses. From the results in Figure 9, it can be seen that after entering the university, the grades among students gradually opened up. This has a lot to do with the degree of effort and the major interest of the students after admission.

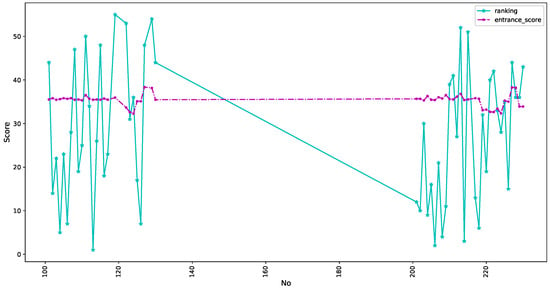
Figure 9. Overall ranking of 55 students.

5.1.2. Experimental Conditions

In order to verify the advantages of the proposed model in predicting student achievement, this paper selects five machine learning models for comparison. These models include the decision tree, random forest, neural network, XGBoost, and SVM. They were employed to evaluate the performance of the proposed model.

These experimental models were carried out on a 64-bit platform with a Windows 10 operating system, which consists of memory 12GB, the processor with Intel i7-4710MQ (the main frequency of 2.50 GHz), and the software used in the PyCharm community with Python 3.10. In addition, due to the different dimensions in the dataset, there is a certain degree of a sample annihilation problem. Before executing these experimental models, this paper adopted the normalization technique to process the datasets.

Since the student achievement data obtained in this paper contained a certain amount of noise, the generalization error could not be directly used as a signal to understand the generalization ability of the prediction model. It is very expensive to reciprocate between the deployment environment and the training model, and the model cannot be used for the training dataset. The degree of fit is used as a signal to understand the generalization ability of the model. Therefore, a better way is to split the student achievement dataset into two parts, the training dataset, and the test dataset. We can use the training dataset to train the model, and then use the error on the test dataset as the generalization error of the final model in response to real-world scenarios. With the test dataset, we want to verify the final effect of the model. We only need to calculate the error of the trained model on the test dataset, and we can consider this error to be an approximation of the generalization error. We only need to let our trained model on the test dataset be the smallest error. The distributions of the training dataset and test dataset of the student achievement dataset in this paper are shown in Table 3.

Table 3. The distribution of the training dataset and test dataset of the student achievement dataset.

Datasets	Number
Training dataset	3578
Test dataset	398

5.2. Comparing the Results of All Experimental Algorithms

The normalized dataset was selected to evaluate the predictive ability of the proposed model for student achievement and compare it with these experimental models. Note that we converted student grades to ‘H’, ‘M’, and ‘L’ according to the rules in Table 2.

5.2.1. Comparing Results with All Experimental Models on the Real Educational Datasets

Table 4 shows the prediction results of all experimental models on the real educational dataset. Observing the experimental results in Table 4, it was concluded that the results of the proposed model were significantly better than those of other models. From the experimental results in Table 4, it can be seen that random forest had the worst results. The proposed model outperformed the comparison models in the experiments in four metrics precision, including recall, f1-score, and accuracy. It is particularly worth noting that the proposed model achieved good results in that the prediction ability on ‘L’ was significantly better than other models. This led to an overall improvement in the performance of the proposed model. This result is related to the fact that ‘L’ belongs to small samples, which illustrates the predictive ability of the proposed model on small sample data.

Table 4. Comparing the results with all experimental algorithms on the ‘xAPI-Edu-data’ dataset.

Algorithm	Classification	Precision	Recall	F1-Score	Support	Accuracy
Decision Tree	H	0.70	0.74	0.72	224	0.625628
	M	0.54	0.53	0.53	148
	L	0.28	0.19	0.23	26
Random Forest	H	0.70	0.73	0.71	224	0.610553
	M	0.51	0.51	0.51	148
	L	0.27	0.15	0.20	26
Neural Network	H	0.72	0.79	0.75	224	0.655779
	M	0.56	0.57	0.57	148
	L	0.00	0.00	0.00	26
XGBoost	H	0.77	0.77	0.77	224	0.670854
	M	0.58	0.61	0.59	148
	L	0.24	0.15	0.19	26
SVM	H	0.72	0.79	0.75	224	0.663317
	M	0.58	0.59	0.58	148
	L	0.00	0.00	0.00	26
Proposed Algorithm	H	0.79	0.78	0.79	224	0.708543
	M	0.61	0.70	0.65	148
	L	0.50	0.15	0.24	26

To further analyze the predictive ability of the proposed algorithm, Figure 10 presents the prediction results of each model. Figure 10 shows the performance prediction results of each model on the test dataset. It is easy to find that most models show poor results in the 100-point prediction. The experimental results show that this is related to factors, such as data imbalance and incomplete student data attributes.

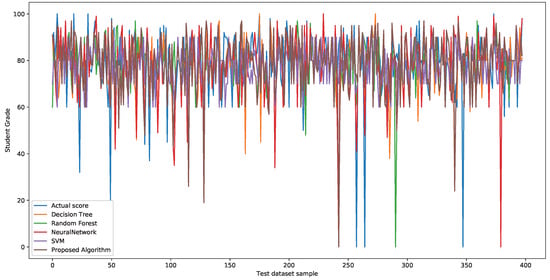
Figure 10. Predicted results of percentile grades.

5.2.2. Discussions

From the results in Table 4, we can see that the proposed model achieves good results in most of the experimental results. The feedforward spiking neural network model designed in this paper further improves the prediction performance, indicating that the model is effective and can better predict students’ final grades. Based on the above experimental results, we can conclude that the proposed model is effective to predict student achievement.

Through the development of the above experiments and the implementation of the practical research on the prediction of academic performance based on the feedforward spiking neural network, some theoretical and practical research results have been achieved. However, due to the limitations of some factors, this study has the following three shortcomings.

• We carried out a study on the prediction of academic performances on the basis of the feedforward spike neural network but did not try more new intelligent analysis techniques; the selected case samples are expected to be further expanded and judged through more evaluation index comparisons, the accuracy, and validity of the learning performance prediction model, and the practical value of teaching.
• The deep relationship between portrait application and academic performance prediction is expected to be further explored. Since this study focused on building a learning performance prediction model, the dimensions of the learner portrait construction and the corresponding data indicators were very rich (which affect the accuracy of learning achievement prediction). On the one hand, it still needed to be further verified and revised to improve the support efficiency of learner portraits for teaching and learning; on the other hand, the prediction effect of academic performance can be improved by optimizing the spiking neural network model, and the key factors of academic performance prediction can be further explored to help teachers and students. It can provide more accurate and personalized learning services.
• Experimental data samples were limited since the learner samples selected in this study were from two classes in one grade; for six-semester courses, the acquisition of learning data was also limited by the online learning platform and educational administration system. These data were still shallow and single, and the data amounts were limited. They were also relatively sparse, so the prediction accuracy of student grades still needed to be further improved. In the follow-up, on the one hand, we will combine the latest research results of behavioral science and brain science to collect more data on the learning processes of learners.

6. Conclusions

In a digital campus environment, the multi-source heterogeneous data of college students is integrated to break data barriers between different online and offline learning spaces and provide theoretical and technical bases for the research on the trend prediction of college students’ academic performances [36]. It is very important to mine effective information from scattered information data to promote the development of campus activities. Student performance is the most important factor to measure a student’s personal ability and a teacher’s teaching level [37]. Predicting a student’s course performance in advance can provide early warnings and timely correction roles for students and teachers. Student performance prediction is also the most important direction in educational data mining.

This paper mainly studied the relationship between the content of the courses that students study and the test scores. Based on the analysis results, knowledge features are used to predict academic performances, and a new model for predicting student performances based on the feedforward spiking neural network was designed. This paper studied the prediction of follow-up grades through the relevant data information and course information of students. In order to verify the accuracy of the performance prediction model proposed in this paper, this paper mainly completed the following work. First of all, regarding data preprocessing, due to the selection of real college student achievement data, it is necessary to perform operations, such as data normalization and default value processing. Secondly, the influence of a single feature on academic performance was analyzed, and the features that had greater impacts on the academic performances were screened. Third, the academic performance was predicted based on the feedforward spiking neural network prediction model. At the same time, the optimal academic achievement model was constructed through parameter tuning. Finally, the advantages of the proposed feedforward spiking neural network in predicting academic performances were demonstrated through simulation experiments. The research data came from the personal statistics and student transcripts of 19th-grade IoT students at the School of Information Engineering (at a university in Shenyang). Based on these data, this paper proposes a model to predict student performances. The experiments in this paper were based on real educational datasets. Through a large number of experiments and result analyses, the effectiveness of the curriculum knowledge characteristics and prediction model obtained by the feedforward spiking neural network proposed in this paper were verified in predicting the learning performances.

This paper systematically summarizes the predictors of academic performance, which could help improve the efficiency and quality of academic performance predictions. However, the inductive perspectives of the academic achievement predictors used in this paper are relatively simple, and there is a lack of standardized data selection methods. The perspective of academic achievement prediction is course-centered and student-centered and lacks the behavioral characteristics of some students. Furthermore, the research focuses on evaluating the performances of forecasting algorithms, and it is easy to overlook the importance of rationally choosing data metrics. The relationship between student portraits and academic performance prediction needs to be further explored. Student portraits can describe the characteristics of students at different learning stages, and learning outcomes can standardize and quantify learning outcomes. Combined with keywords such as “learning/academic performance prediction”, there are few detailed studies in this field, indicating that the relationship between student portraits and academic performance prediction research is not close, and the advantages of student portraits in future research will depend on the performance improvements in prediction [38].