Abstract
This paper presents the first review of noise models in classification covering both label and attribute noise. Their study reveals the lack of a unified nomenclature in this field. In order to address this problem, a tripartite nomenclature based on the structural analysis of existing noise models is proposed. Additionally, a revision of their current taxonomies is carried out, which are combined and updated to better reflect the nature of any model. Finally, a categorization of noise models is proposed from a practical point of view depending on the characteristics of noise and the study purpose. These contributions provide a variety of models to introduce noise, their characteristics according to the proposed taxonomy and a unified way of naming them, which will facilitate their identification and study, as well as the reproducibility of future research.
MSC:
62R07
1. Introduction
Human nature and limitations of measurement tools mean that the data that real-world applications rely on often contain, to a greater or lesser extent, errors or noise [1,2,3]. In classification [4,5], it can affect both output class labels [6,7] and input attributes [8,9] in the form of corruptions in the corresponding values. Learning from noisy data implies that classifiers are less accurate and more complex, since errors may be modeled [10,11]. These facts have caused the study of noisy data to have an important rise in current data science research [12,13,14]. In this context, since noise in real-world data is normally not quantifiable and its characteristics are unknown, noise models [15,16] have been proposed to introduce errors into them in a controlled way. They allow conclusions to be drawn from experimentation based on the type of noise, its frequency and characteristics [17].
In the current literature on noisy data in classification, there are no reviews on noise introduction models dealing with both label and attribute noise. On the other hand, there are two main proposals of taxonomies for noise models [18,19]. The first one, proposed by Frénay and Verleysen [18], can be used to categorize label noise models depending on whether they use class or attribute information to decide which samples are mislabeled. The second one, proposed by Nettleton et al. [19], divided noise models considering the affected variables, the distribution of the errors and their magnitude. Note that, despite the introduction of these taxonomies, these works mainly focused on different aspects of noisy data, such as noise preprocessing or robustness of algorithms.
This paper provides a review of relevant noise models for classification data, paying special attention to recent works found in the specialized literature [15,20,21]. A total of 72 noise models will be presented, considering schemes to introduce label noise [22,23] but also attribute noise [24,25] and both in combination [26,27], which tend to receive less attention in research works. The revision of the literature on noisy data shows some ambiguity in the terminology related to noise models and that there is no unified criteria for naming them [28,29,30]. In this regard, one might ask: is it possible to characterize the operation of noise models in such a way that it allows to define an approach to name and categorize them? For this, as a consequence of the study of existing noise models, their structure will be analyzed, reaching conclusions about the components that allow their characterization. Then, a tripartite nomenclature will be proposed to name both existing and future models in a descriptive way, referring to their main components. This nomenclature will ease their identification, avoiding terminological differences among works and the need to provide complete descriptions each time they are used; this will also help simplify the reproducibility of the experiments carried out. Additionally, the current taxonomies [18,19] will be revised and adapted according to relevant characteristics of existing noise models. This will result in a single expanded taxonomy to better reflect the nature of each noise model and its different components, allowing them to be categorized regardless of the type of noise they introduce. Finally, noise models will also be classified into different groups according to the characteristics of the noise to be studied and the available knowledge of the problem domain. All these aspects add practical value to this paper since it offers a wide range of alternatives as a basis for research, describing and suggesting noise models based on the needs and objective of the study. In summary, the main contributions of this work are the following:
- 1.
- Presentation of the first review of noise models for classification, including label noise, attribute noise and both in combination.
- 2.
- Analysis of the structure of noise models, which is usually overlooked in the literature, identifying the fundamental components that allow their characterization.
- 3.
- Detection of the absence and lack of uniformity in the nomenclature of noise models in the literature.
- 4.
- Proposal of nomenclature to name noise models in a descriptive way, referring to their main structural components.
- 5.
- Unification of existing taxonomies in the literature and updates to better reflect the types of noise models and their characteristics.
- 6.
- Categorization of noise models from a practical point of view, depending on the characteristics of noise and the available knowledge of the problem domain.
The rest of this paper is organized as follows. Section 2 provides the background on the current terminology and taxonomies of noise models. Section 3 and Section 4 present the proposed nomenclature and taxonomy, respectively. Then, Section 5 and Section 6 introduce the label and attribute noise models, organizing them from a practical point of view. Finally, Section 7 concludes this work and offers ideas about future research.
2. Background
This section focuses on the current state of terminology and taxonomies of noise models in classification. Section 2.1 highlights the difficulties and discrepancies in the nomenclature of noise models. Then, Section 2.2 describes the taxonomies to categorize them.
2.1. Need for a Unified Nomenclature
Nomenclature can be defined as the set of principles and rules that are applied for the unequivocal and distinctive naming of a series of related elements. In any discipline, it is of crucial importance for scientific advancement and to allow researchers to communicate unambiguously about them. Nevertheless, an in-depth study of the literature on noisy data reflects that there is no unified criterion for naming noise models due to two main causes [28,29,31]:
- 1.
- Many models are not assigned an identifying name,
- 2.
- There are discrepancies when naming known models.
The first and very frequent cause of a lack of nomenclature is that, in fact, most of the noise models used in the literature are only described, and a name is not usually associated with them [32,33]. This situation occurs both with models traditionally used [31,32,34] and recent proposals [33,35], among other examples [36,37].
The second cause involves discrepancies in the name of the noise models, as well as in the terminology related to them [28,29]. In order to delve into this aspect, the notation compiled in Table 1 is used, which is also employed in the remainder of this work. Let D be a classification dataset composed by n samples (), m input attributes () and one output class taking one among c possible labels in . The value of the variable , either input or output, in the sample is denoted as .

Table 1.
Notation used.
As an example of ambiguous nomenclature, consider one of the most widely used noise models [38], in which the label of each sample can be corrupted to a different label , with being the probability of choice of each class label and being known as the noise level [6] in the dataset. This simple noise model is referred to in different ways in the literature, such as symmetric [28,39,40], uniform [29,41,42] or random [30,43]. Some of these terms, such as symmetric and uniform, are also used to designate other different models, such as that in which the label of each sample can be corrupted to any class label , being the probability of each alternative [44,45,46].
Other commonly used terms with discrepancies are asymmetric and class-conditional, which sometimes are used to mention a different noise level for each class [43,47,48]. Both terms, along with other ones such as flip-random, are also used to refer to different probabilities among classes when choosing the noisy label for a sample [45,49,50]. They are also used to indicate different noise models [51,52]. For example, asymmetric or pair noise [51,53,54], along with other names [29,45], are used to designate the model in which each class label can be corrupted to any other prefixed label . Simultaneously, these terms are also used to refer to the noise model consisting of corrupting the label to the next label , , when an order between class labels is assumed [52,55,56]. Finally, note that the term asymmetric has also been used in binary classification to indicate that one class can change to the other but not vice versa [22,57] and even to designate the fact that noise levels in the training and field data are different [58].
The concept non-uniform is also presented in several contexts [59,60]. It is used to identify models in which the probability of noise of each sample depends on its attributes () [59,61,62] but also to mention different probabilities of noise for each class [60,63]. This terminological ambiguity is a consequence, among other aspects, of the existence of a dichotomy between those studies that use terms such as symmetric/uniform and asymmetric/class-conditional referring to the probability that each class contains noise [43,47,48] and those referring to, when noise for a certain class occurs, the probability of choosing each label [52,64,65]. The aforementioned facts make the terminology related to noise models not unique throughout the literature: different models are known by the same name, whereas different names design the same model depending on the research work, which can lead to confusing scenarios.
2.2. Current Taxonomies
There exist two main proposals of taxonomies for noise models [18,19]. The most recent one [18], although originally proposed to categorize label noise from a statistical point of view, can be translated into models that introduce this type of noise. Thus, it considers a single dimension to classify label noise models, which are divided into three types depending on the information used to determine if a sample is mislabeled:
- 1.
- Noisy completely at random (NCAR). These are the simplest models to introduce noise. In NCAR models, the probability of mislabeling a sample does not depend on the information in classes or attributes [38].
- 2.
- Noisy at random (NAR). In NAR models, the mislabeling probability of a sample depends on its class label . This type of model allows considering a different noise level for each of the classes in the dataset. NAR is usually modeled by means of the transition matrix [56] (Equation (1)), where () is the probability of a sample with label to be mislabeled as :
- 3.
- Noisy not at random (NNAR). These use both the information in class labels and attribute values () to determine mislabeled samples. They constitute a more realistic scenario consisting of mislabeling samples in specific areas, such as decision boundaries, where classes share similar characteristics [22].
Note that these categories were also used to show the dependency of the sample’s noisy label on the original label (in NCAR and NAR) or on the label and attribute values (in NNAR). In contrast to the previous taxonomy for label noise models, the work in [19] proposed another one for any type of noise (label and attributes) based on three dimensions:
- 1.
- Affected variables. This divides the noise models according to whether they introduce label noise, attribute noise or their combination.
- 2.
- Error distribution. This classifies the models by considering whether the introduced errors follow some known probability distribution, such as Gaussian.
- 3.
- Magnitude of errors. This divides the models according to whether the magnitude of the generated errors is relative to the values of each sample or to the minimum, maximum or standard deviation of each variable.
3. A New Unified Nomenclature for Noise Models
Due to the lack of a unified terminology for noise models, this section presents a procedure for naming them with a twofold objective: (i) assigning an unequivocal name to each noise model and (ii) being as descriptive as possible, providing information on the noise introduction process.
The analysis of existing noise models, as well as the dichotomy in research works when naming noise models discussed in Section 2.1, reveal that they have three main components that allow them to be described (see Figure 1):
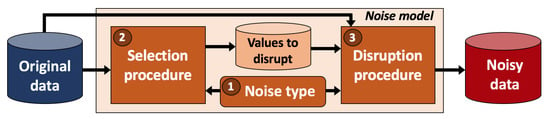
Figure 1.
Structure and components of noise models.
- 1.
- Noise type. It is a characteristic that indicates the variables affected by the noise model. Thus, any noise model introduces noise into class labels [15,23,66], attribute values [25,67,68] or both in combination [26,27].
- 2.
- Selection procedure. Let be the set of indices of samples and be the set of indices of variables (output class label and input attributes) in a dataset D to be corrupted. The selection procedure creates a set of pairs with the values to be altered. An element indicates that the variable in the sample (that is, the value ) must be corrupted. Note that for label noise models, for attribute noise models and for combined noise models.The set can be seen as the indices of the samples to corrupt for each variable () in which noise is introduced. There are multiple ways to select such samples [20,69,70]. For example, all samples can have the same probability of being chosen [38,71], a different probability can be defined for the samples according to their class label [20,72], the probability of choosing a sample can depend on its proximity to the decision boundaries [69,70,73], the samples in a certain area of the domain can be altered [16,74] or even all the samples in the dataset can be selected to be corrupted [67].
- 3.
- Disruption procedure. Given the set indicating the samples to be corrupted for each noisy variable (), this procedure allows altering their original values by changing them to new noisy ones . As in the case of the selection procedure, there are different alternatives to modify the original values by the disruption procedure [24,71,75]. For example, a new value within the domain can be chosen including the original value [26,76] or excluding it [38,77], a default value can be chosen dependently from the original value [75,78,79] or independently [71,72], additive noise following a Gaussian distribution can be considered [17,67], among others [80,81].
Based on these three components, a tripartite nomenclature for noise models is proposed. Each part is formed by an identifier that evokes a characteristic of each of the previous components. Table 2 shows examples of identifiers defined for each component, together with their description and a research work using it. In those terms traditionally used in the literature where there are discrepancies (such as symmetric [28,39], asymmetric [51,53] or uniform [41,42]), one of their most used meanings has been adopted.

Table 2.
Examples of identifiers defined for the nomenclature of noise models.
Once the identifier of each part is determined, the name of the model is formed from the type of noise it introduces, concatenating each part as follows:
In order to facilitate recognition of the name of the noise model, it should be written in italics and with its first letter capitalized. Evoking the characteristics of each noise model makes the proposed nomenclature easier to remember. At the same time, the existence of noise models with the same selection, disruption or type names indicates that they are closely related to each other. The proposal for applying this nomenclature to the noise models considered in this work, together with their corresponding references, is found in Table 3. Note that, in some specific cases, there may be slight differences between the nomenclature and the exact noise model applied in the corresponding paper. This is mainly due to the fact that some works use noise models with specific configurations to achieve particular objectives and, in these cases, a name representing the model in a more general way is proposed. For example, in [78], some specific attributes of interest to the dataset used are chosen to corrupt. However, to provide a general name to this noise model, the identifier symmetric has been used for its selection procedure, referring to the fact that all attributes can be corrupted to the same degree. Other examples are the models used in [82], which introduce errors in binary attributes. In this case, even though the identifier bidirectional in Table 2 could be used for the disruption process, the identifier uniform has been chosen considering that these models can also be applied to attributes with more than two values. Thus, the above approach can be employed to increase consistency when naming new models so that the specific application can be separated from the noise model used.

Table 3.
List of noise models and references.
As an example of the naming process, consider the noise model in which each sample has the same probability of noise and can be mislabeled with any class label other than the original [38]. Since the model introduces noise into class labels, its type identifier is label. The selection of samples to modify considers the same probability for all of them, so this identifier takes the value symmetric. Finally, since the disruption process chooses the noisy label following a uniform distribution excluding the original value, its identifier takes the value uniform. Therefore, the name of this noise introduction model is Symmetric uniform label noise.
As discussed above, it should be noted that although many of the noise models originally lacked a distinctive name, others were specifically named [46,71,82]. Some examples among label noise models are Symmetric default label noise (originally called background flip noise [71]), Symmetric unit-simplex label noise (called random label flip noise [46]), Symmetric double-random label noise (called flip2 noise [80]) or Symmetric hierarchical label noise (called hierarchical corruption [23]). Among attribute noise models, Asymmetric uniform attribute noise (originally called asymmetric independent attribute noise [82]) or Symmetric Gaussian attribute noise (called Gaussian attribute noise [17]) can be mentioned.
4. Proposal for an Extended Taxonomy of Noise Models
Even though the current taxonomies of noise models [18,19] fulfill the purpose for which they were designed, the analysis of existing models shows the need not only to consider them as a whole but also to modify them appropriately to better reflect the nature of any model. The taxonomy proposed by Frénay and Verleysen [18] allows classifying label noise models based on the information source (class and attributes) used to determine which samples are mislabeled. It is interesting to extend this idea to attribute noise models, as well as simultaneously consider other dimensions proposed by Nettleton et al. [19]. This joint taxonomy can be expanded to include other dimensions derived from the structure of noise models shown in Figure 1, which allow the development of a more detailed and descriptive categorization. Thus, the following dimensions are proposed to form part of the final taxonomy, each one described in a separate section:
- Noise type (Section 4.1). This classifies the models based on the introduction of label noise, attribute noise or both.
- Selection source (Section 4.2). This categorizes the models according to the information sources (class and/or attributes) used by the selection procedure.
- Disruption source (Section 4.3). This is similar to the selection source but aimed at the disruption procedure.
- Selection distribution (Section 4.4). The main probability distribution, if any, underlying the selection procedure.
- Disruption distribution (Section 4.5). The main probability distribution related to the disruption procedure.
Since the taxonomy defined by the dimensions above is based on previous approaches [18,19], these provide similar categorization results in those cases where they are comparable. For example, the taxonomy in [18], which is designed for label noise, could be compared to the selection source dimension if label noise models were considered. Similarly, this occurs with the noise type dimension, which was previously used in [19]. This fact, along with the appropriate extensions that are detailed throughout this section, make the proposed taxonomy adapt to previous versions and incorporate features to better reflect the variability of noise models and their characteristics.
4.1. Noise Type
This dimension is essential to divide the models between those introducing label noise [15,22], attribute noise [8,78] or their combination [26,27]. The most representative models within each noise type (label, attributes and combined) are Symmetric uniform label noise [38], Symmetric uniform attribute noise [77] and Symmetric completely-uniform combined noise [26], respectively. These models allow noise to be studied in a generic way since they introduce random errors and do not require knowing the domain of the problem addressed or making assumptions about the data. Both the selection of samples to be corrupted and their noisy values (in class labels or attributes) are carried out considering that the alternatives have the same probability of being chosen [31,98]. In addition, they allow the percentage of errors in the dataset to be controlled by means of a noise level, facilitating the analysis of the consequences of noise as the number of errors in the data increases [77]. These characteristics make them some of the most widely used models [15,24,44].
The analysis of the 72 models in Table 3 with respect to the noise type shows that a high percentage () is focused on label noise. Attribute noise models represent , whereas combined noise models are . These frequencies are consistent with the limited number of works involving attribute noise [78,82]. This fact is due to the greater complexity that is usually associated with the identification and treatment of errors in attribute values compared to those in class labels [8].
4.2. Selection Source
This dimension will allow the models to be divided according to the information sources (classes and/or attributes) used by the selection procedure. It is inspired by the taxonomy proposed in [18], properly adapted to categorize all the models and types of noise. Thus, the analysis of existing noise models shows that the categorization in [18] should be expanded because there are label noise models [62,86] whose selection procedure uses only attribute information (and not class information), which had not been previously contemplated. For example, Quadrant-based uniform label noise [62] allows determining the probability of mislabeling samples in four different regions of the domain based on the values of two attributes. Following the naming style in [18], the selection source of this new type of noise models is denoted as noisy partially at random (NPAR). On the other hand, it is necessary to update this dimension to cover attribute noise [58,78], making it valid for any model regardless of the type of noise addressed. Thus, the selection source finally divides the noise models, either label or attribute noise, into the following categories:
- 1.
- Noisy completely at random (NCAR). These are models that do not consider the information of labels or attributes to select the noisy samples. For example, Symmetric uniform label noise [38] corrupts the class labels in the dataset assigning to each sample the same probability of being altered, whereas Unconditional vp-Gaussian attribute noise [67] corrupts all the samples.
- 2.
- Noisy at random (NAR). These are models whose selection procedure uses the same information source as the noise type they introduce. Therefore, NAR label [33,35] and attribute [58,82] noise models, respectively, use class information () and attribute information ( or with ) to determine the samples to corrupt. For example, Asymmetric uniform label noise [20] and Asymmetric uniform attribute noise [82] consider a different noise probability for each class label and attribute , respectively.
- 3.
- Noisy partially at random (NPAR). These are models whose selection procedure uses the opposite information source to the noise type they introduce. Examples of this type of selection source are found in Attribute-mean uniform label noise [86], which gives a higher probability of corrupting the samples whose attributes are closer to the mean values, or in the aforementioned Quadrant-based uniform label noise [62].
- 4.
- Noisy not at random (NNAR). The selection procedure of these models uses class and attribute information to determine the noisy samples. For example, Neighborwise borderline label noise [15] determines the samples to corrupt by computing a noise score for each sample as a function of its distances to its nearest neighbors (using the information from attributes) of the same and different class (using the information from class labels).
Note that, in contrast to [18], the categories in this dimension do not indicate, for example, the dependency of a specific noisy label on the original label or attributes. These relations have been reflected through a new dimension (see Section 4.3) since the selection procedure (which selects the values in the dataset to corrupt) and disruption procedure (which chooses the noisy values for the selected data) do not necessarily use the same information sources for their purpose.
4.3. Disruption Source
Since the disruption process is different from the selection process, models can also be classified according to the information sources used to choose the noisy values. Thus, analogously to the selection source, models can be divided into the following categories according to the information sources used by the disruption procedure:
- 1.
- Disruption completely at random (DCAR). These are models whose disruption procedure does not use information from class labels or attribute values. For example, Symmetric default label noise [71] always chooses the same class label as the noisy value regardless of the class and attribute values of each sample, whereas Symmetric completely-uniform label noise [44] chooses the value of the noisy label uniformly among all the possibilities in the domain.
- 2.
- Disruption at random (DAR). These are models whose disruption procedure uses only the same information source as the noise type they introduce. For example, Symmetric adjacent label noise [89] chooses one of the classes adjacent to that of the sample to corrupt, whereas Symmetric Gaussian attribute noise [17] adds another one to the value of the original attribute that follows a zero-mean Gaussian distribution.
- 3.
- Disruption partially at random (DPAR). These are models whose disruption procedure uses the opposite information source to the noise type they introduce. Even though this characteristic is not usually considered in the literature, it is interesting to define it for potential noise models.
- 4.
- Disruption not at random (DNAR). These are models whose disruption procedure uses class and attribute information. For example, in Symmetric nearest-neighbor label noise [41], the noisy label for each sample is taken from its closest sample of a different class. Therefore, it uses class and attribute information to determine the new noisy labels.
4.4. Selection Distribution
This dimension refers to the categorization of noise models based on the main probability distribution on which the selection procedure is based. In this context, a great variety of probability distributions can be distinguished, such as multivariate Bernoulli (in Symmetric uniform label noise [38]), Gaussian (in Gaussian-level uniform label noise [61]), exponential (in Exponential/smudge completely-uniform label noise [76]), Laplace (in Laplace borderline label noise [73]) or gamma (in Gamma borderline label noise [70]). Other models introduce noise in all samples of the dataset unconditionally [67]. Among them, the most used is the multivariate Bernoulli distribution, from which it is interesting to distinguish the following subcategories for the selection distribution:
- Symmetric [44,71]. Each sample follows a Bernoulli distribution of parameter to be corrupted. Thus, a multivariate Bernoulli distribution of parameter on is followed by the n samples of all the classes/attributes (according to the type of noise introduced), which therefore have the same probability of being selected.
- Asymmetric [20,82]. A total of k different multivariate Bernoulli distributions of parameters are applied separately to the samples of each class () or attribute () depending on the type of noise introduced. Therefore, samples of each class/attribute have a different probability of being corrupted.
4.5. Disruption Distribution
This dimension refers to the main probability distribution associated with the disruption process. As in the case of the selection distribution, there are multiple alternatives for the disruption distribution [38,71,72]. For example, the new noisy value can be chosen following a uniform distribution, including the original value [44] or excluding it [38], following the natural distribution of values in the original data [72], using an additive zero-mean Gaussian distribution [17], choosing the new value uniformly within a given interval [58] or choosing a default value [71], among others [41,80]. Note that this dimension can also consider models with a deterministic choice of noisy values [33,95].
5. Label Noise Models
Label noise [99,100,101] occurs when the samples in the dataset are labeled with wrong classes. In real-world data, label noise can proceed from several sources [43,69,102]. Thus, human mistakes due to weariness, routine or quick examination of each case, as well as the imprecise information or subjectivity during the labeling process can produce this type of noise [102]. Additionally, automated approaches to collect labeled data, such as data mining on social media and search engines, inevitably involve label noise [43]. Label noise models [70,87,92] are designed to simulate these real-world labeling errors. Depending on the characteristics of the noise and the application to be studied, the following main groups of label noise models are considered:
(1) Unrestricted label noise [38,44]. The objective of these models is to introduce label noise that affects all classes equally so that they allow the noise problem to be studied in a generalized way. The most widely used models in this group are Symmetric uniform label noise [38] and Symmetric completely-uniform label noise [44], which belong to the DAR and DCAR disruption procedures, respectively. Another option to consider is Symmetric unit-simplex label noise [46], in which the probability of choosing each of the class labels as noisy by the disruption procedure is based on a k-dimensional unit-simplex ().
(2) Borderline label noise [15,69]. These models represent common scenarios in real-world applications, where mislabeled samples are more likely to occur near the decision boundaries [22,70]. Garcia et al. [15] proposed two borderline label noise models: Non-linearwise borderline label noise, in which a noise metric for each sample is based on its distance to the decision limit induced by SVM [103], and Neighborwise borderline label noise, which calculates a noise measure for each sample based on the distances to its closest samples:
with NN being the nearest neighbor of and the Euclidean distance between the samples and . Similarly, Small-margin borderline label noise [87] trains a logistic regression classifier [104] and selects to corrupt a percentage of the correctly classified samples closest to the decision boundary.
Other models are also based on the distances of the samples to the decision boundaries, which are then used to estimate the probability that each sample is mislabeled, employing different probability density functions (PDF) [69,73]. For example, once the distance of a sample to the decision boundary is computed, Gaussian borderline label noise [22] uses the PDF of a Gaussian distribution to assign its noise probability , which could also be adapted for samples of different classes:
Other PDFs that have been used are that of the exponential distribution (in Exponential borderline label noise [69]), the gamma distribution (in Gamma borderline label noise [70]) or the Laplace distribution (in Laplace borderline label noise [73]). In some of these models, such as Uneven-Laplace borderline label noise and Uneven-Gaussian borderline label noise [73], noise probability affects samples unequally depending on which side of the decision boundary they are on.
There are also noise models that are not based on distances to the decision boundaries but on predictions of some classifier to determine borderline samples [81,85]. For example, Misclassification prediction label noise [81] selects incorrectly classified samples by a multi-layer preceptron to be corrupted using their predicted labels. Score-based confidence label noise [85] calculates a noise score for each sample based on the outputs () of a Deep Neural Network (DNN) [105] at Q different epochs:
Finally, of samples with the highest noise scores are chosen to be corrupted with the more reliable different labels offered by DNN. Note that some of the previous models [69,70,73] were proposed for binary datasets and, therefore, the identifier bidirectional in Table 2 could be used for their disruption process. However, they have been assigned the identifier borderline considering their potential use in multi-class problems, where the disruption procedure could follow a strategy coherent with this type of noise and choose any label as noisy, such as the majority label among the closest samples with a label different from that of the sample to be modified.
(3) Label noise in other domain areas [16,62]. In addition to noise in class boundaries, models have been proposed to introduce label noise in other regions of the dataset [16,74,86]. Thus, One-dimensional uniform label noise [74] and Quadrant-based uniform label noise [62] allow the practitioner to focus on specific areas of the domain based on the values of one and two variables of interest, respectively. Other examples in this group are Attribute-mean uniform label noise [86], which makes samples closer to attribute mean values more likely to be mislabeled, and Large-margin uniform label noise [87], which mislabels a percentage of the correctly classified samples that are farthest from the decision boundaries. Hubness-proportional uniform label noise [16] gives samples closer to hubs in the dataset a higher chance of being corrupted. Thus, samples are chosen to be mislabeled, with each sample having a probability of being selected:
with being the hubness of , that is, the number of times that is among the k nearest-neighbors of any other sample.
(4) Label noise based on synthetic attributes [76,88]. Other models may consider additional attributes in the dataset to make noise dependent on them. For example, Exponential/smudge completely-uniform label noise [76] uses a new attribute with values uniformly distributed in to determine the error probability of each sample employing an exponential function of parameter :
with s being a user parameter to scale the attribute . On the other hand, Smudge-based completely-uniform label noise [88] uses a specific feature in the data to indicate the presence of label noise. This can be achieved, for example, by assigning a certain value to existing or new attributes of mislabeled samples.
(5) Label noise using default values [71,91]. This type of label noise typically occurs when the true class cannot be determined for certain samples and a default value is assigned to them (for example, the value other). Thus, whenever noise in a sample occurs, its label is incorrectly assigned to a previously established class. In order to introduce it, Symmetric default label noise [71] and Asymmetric default label noise [72] can be used. Instead of a single default class, Symmetric double-default label noise [91] randomly chooses one of two possible default classes.
(6) Label noise assuming order among classes [75,89]. In some data science applications, classes have a natural order relation [89]. For example, a reader can use the labels {bad, good, excellent} for a book review. There are several label noise models considering this peculiarity [75,89]. Symmetric next-class label noise [75] mislabels a sample of class to the next label (with ), whereas Symmetric adjacent label noise [89] randomly picks one of the classes adjacent to as noisy. Prati et al. [72] proposed several label noise models in this scenario. For example, Symmetric diametrical label noise makes distant classes more likely to be chosen as noisy. An alternative to defining the probabilities of a sample with label to be mislabeled as is:
Other models are Symmetric optimistic label noise (in which labels higher than that of the noisy sample are more likely to be chosen by the disruption procedure) or Symmetric pessimistic label noise (which gives a higher probability of choice to labels lower than that of the sample).
(7) Label noise in out-of-distribution classes [41]. Sometimes the set of labels used in a classification problem is not complete and some of them are not considered. This fact implies that the samples of the classes that are ignored (out-of-distribution, OOD) are mislabeled with the labels that were finally preserved (in-distribution, ID). The simplest model in this group is Open-set ID/uniform label noise [41], which chooses a random label among ID classes for samples of OOD classes. Another example of this type of model is Open-set ID/nearest-neighbor label noise [41], which is similar to the previous one, but it chooses the label from the closest sample of the ID classes.
(8) Label noise in binary classification [33,92]. Binary classification, in which , is common in certain applications, such as medical datasets [106] (where healthy and unhealthy patients are commonly distinguished) or fraud detection [35]. Even though other label noise models can be applied to this type of data, there are some that are specifically designed for them. One of the most studied problems in binary classification is that of class imbalance [107], in which one of the classes has fewer samples than the other. In order to introduce label noise in these problems while keeping the number of samples in both classes, IR-stable bidirectional label noise [33] has been proposed. Minority-driven bidirectional label noise [92] allows controlling both the total number of corrupted samples by means of the noise level , as well as the number of those samples in the minority class () and the majority class () by means of the parameter :
with being the number of samples in the minority class. Finally, in the context of fraud detection, Fraud bidirectional label noise [35] has been used, which introduces noise mainly in the minority class and, to a much lesser extent, in the majority class. Specifically, when the number of majority samples is high enough, it introduces noisy samples in the dataset:
with being a parameter to control the number of majority of noisy samples, the amount of minority samples corrupted and the relatively small amount of majority samples corrupted.
(9) Label noise between pairs of classes [21,95]. It is common for each of the classes to be more prone to being confused with another [81]. These models simulate this scenario, but they usually require some knowledge or assumptions about the problem since the practitioner commonly decides which classes are confused with each other. They all tend to work in a similar way [21,84]. Let and be two classes. Then, of the samples of are randomly selected and labeled as .
In Majority-class unidirectional label noise, which can be applied to both binary [21] and multi-class [24] data, is the majority class and is usually the second majority class. Multiple-class unidirectional label noise [81] is similar but allows defining multiple pairs of classes for the valid transitions in the dataset. Finally, Pairwise bidirectional label noise [95] considers that noise can occur in both directions (from to and from to ), whereas Asymmetric sparse label noise [84] requires determining a different noise level for each of the classes.
(10) Label noise with class hierarchy [23,79]. In certain applications, the set of labels can be grouped into different superclasses [79]. For example, when classifying the following animals in a certain region {wolf, goat, snake, lizard}, the first two belong to the superclass mammal, whereas the last two belong to the superclass reptile. In this type of problem, mislabeling between labels of the same superclass is the most natural scenario, and noise between labels of different superclasses usually does not occur [91]. In this context, in Symmetric hierarchical label noise [23], the samples can be randomly mislabeled as belonging to any class within the corresponding superclass. Similarly, when classes are ordered, Symmetric hierarchical/next-class label noise [79] chooses the next class within its superclass as the new noisy label.
(11) Choosing noisy labels in the disruption procedure [90,94]. In addition to class labels being chosen uniformly within the domain (as in those models with identifiers uniform [16,38] and completely-uniform [44,76] for the disruption procedure), there are other noise models that allow more alternatives to select the new noisy labels [72,94]. For example, Symmetric non-uniform label noise [94] considers different probabilities in the disruption procedure to choose each noisy label according to the original class. On the other hand, in Symmetric natural-distribution label noise [72], when noise for a certain class occurs, another class with a probability proportional to the original class distribution replaces it:
with being the class proportion of . In Symmetric nearest-neighbor label noise [41], the noisy label for each sample is taken from its closest sample of a different class. Symmetric confusion label noise [63] considers that the probability of choosing each noisy label given the original one is based on a normalized confusion matrix obtained from the dataset. Finally, in Symmetric center-based label noise [90], closer classes , with , are more likely to be confused:
with being the distance between the centers of classes and .
(12) Different noise levels in different classes [20,93]. These models are suitable in those applications where certain classes are more prone to errors than others. Some of these models adopt the asymmetric version (with NAR selection procedure and different noise levels in each class) of the models mentioned above, such as Asymmetric uniform label noise [20] or Asymmetric default label noise [72]. Another example is Minority-proportional uniform label noise [93], which considers a noise level in each class based on the number of samples it has relative to the minority class:
with being the proportion of samples in the minority class, the proportion of samples in the class and . Note that the expression accompanying in Equation (12) is in the interval , so the final noise is also in . Similarly, this situation occurs in Equations (10)–(11), where the factor accompanying is in .
6. Attribute Noise Models
Attribute noise [68,78] involves errors in the attribute values of the samples in a dataset. Even though it may have a human cause, its origin is usually related to instrumental measurement errors (for example, in sensor devices), limitations in the transmission media and so on [8]. In order to represent the variety of scenarios in which errors in attributes can occur, different models for their introduction have been used [25,67,96]. Thus, depending on the type of noise and the application to be studied, attribute noise models in the literature can be grouped into the following main types:
(1) Unrestricted attribute noise [24,77]. These models are appropriate if restrictions in the noise introduction process are not relevant. They allow studying attribute noise in a generic way, introducing errors affecting any part of the domain [24]. Under these premises, the most recommended models are Symmetric uniform attribute noise [77] and Symmetric completely-uniform attribute noise (note that the latter comes from considering only the attribute noise introduction process of the model proposed in [26]). Considering a noise level , both independently introduce the same amount of errors in each attribute and randomly select noisy values following a uniform distribution within the attribute domain. The main difference is that the former excludes the original value as noisy. Thus, for a numeric attribute , a noisy value satisfies the following expression:
whereas the completely-uniform alternative can choose the original value as noisy.
(2) Attribute noise in specific domain areas [68,78]. These models are suitable for applications where attribute noise is known to affect certain parts of the domain. For example, Symmetric end-directed attribute noise [78] can be used to introduce extreme noise affecting the limits of the domain. For each attribute value to be corrupted, the following procedure is applied to determine its noisy value :
- if , ;
- if , ;
- if , one of the above options is chosen;
with and . Another example is Boundary/dependent Gaussian attribute noise [68], which was originally proposed to simulate an outlier effect in the data. It corrupts a percentage of the samples close to the decision boundary in a classification problem by introducing additive noise into the original values using a zero-mean Gaussian distribution.
(3) Attribute noise simulating small errors [17,58]. In these cases, errors are desired to be introduced in attribute values with a controlled variation, generally small, with respect to the original value. These models are useful in applications where measurement tools can generate minor inaccuracies in their operation. Thus, Symmetric Gaussian attribute noise [17] makes smaller errors more likely to be introduced. It corrupts each attribute () by adding random errors that follow a Gaussian distribution:
with . Another way to introduce this type of error is by choosing the noisy values following a uniform distribution within a bounded area close to the original value [58,97]. For example, Symmetric interval-based attribute noise [58] selects the noisy value from one of the intervals adjacent to that of the original value after dividing the attribute using an equal-height histogram. Based on a model originally used in the context of active learning [97], Unconditional fixed-width attribute noise sets a margin E around the original value to uniformly select the erroneous value:
In contrast to attribute noise using a zero-mean Gaussian distribution, which gives more probability to errors close to the original value, these models [58,97] give the same probability to all errors within the stated intervals.
(4) Attribute noise affecting all samples [67]. In certain applications, for example, when attribute values are obtained by a faulty automatic procedure, all samples may experience errors. Therefore, the probability of error for each sample is . In these cases, models such as Unconditional vp-Gaussian attribute noise [67] (which considers an additive zero-mean Gaussian noise with variance proportional to the variance of the attribute to corrupt) or the aforementioned Unconditional fixed-width attribute noise, among others, can be used. For a given attribute , these models satisfy:
with being the set of pairs with the values to be altered created by the selection procedure.
(5) Dependent attribute noise [68,82]. The selection process in attribute noise models is commonly applied for each attribute independently [77] so the samples that are corrupted in each attribute are usually different. In certain situations, when noise in a sample occurs, it affects all its attribute values simultaneously [82]. This type of noise is introduced by models such as Symmetric/dependent uniform attribute noise [82] (which randomly chooses noisy values within the domain) or Boundary/dependent Gaussian attribute noise [68] (which uses an additive Gaussian noise in samples close to decision boundaries).
(6) Attribute noise in image classification [96,108]. Even though other attribute noise models can be used in dealing with image classification [109], there are some schemes designed for this application considering that these problems have their attributes in the same domain (the value of the pixels). For example, in Symmetric/dependent Gaussian-image attribute noise [96], each image is replaced with random values following a Gaussian distribution with the same mean and variance as the original image distribution. Another example is Symmetric/dependent random-pixel attribute noise [96], in which the pixels of each image are shuffled using independent random permutations.
(7) Different noise levels in different attributes [58,82]. These models may require knowledge of the domain of the problem addressed since they usually need to specify a different noise level for each of the attributes. Once the noise levels have been determined, the disruption process can randomly choose values within the domain, as in Asymmetric uniform attribute noise [82], or restricted to an area close to the original attribute value, as in Asymmetric interval-based attribute noise [58]. A special case of this type of model is Importance interval-based attribute noise [58], in which different noise levels are assigned to attributes based on their information gain.
7. Conclusions and Future Directions
In this work, a review of noise models in classification has been presented. The analysis of the literature has shown the lack of a unified terminology in this field, for which a tripartite nomenclature has been proposed to name noise models. Additionally, the current taxonomies for noise models [18,19] have been revised, combined and expanded, resulting in a single taxonomy that encompasses both label and attribute noise models. Finally, the noise models have been grouped from a pragmatic point of view, according to the possible application and the type of noise to be studied.
The proposed taxonomy helps to deepen the knowledge of noise models and their characteristics. It is easy to interpret as it uses concepts from the field of noisy data in classification. The categorization is mainly based on the information sources of all classification problems (class labels and attributes), as well as on the fundamental components of noise models. From these main aspects, the different dimensions are coherently defined. Thus, noise models can be classified in each of such dimensions. The dimensions of noise type, selection source and disruption source can be easily identified according to the information sources involved. This fact also occurs with the selection distribution and the disruption distribution, even though for those models using several distributions simultaneously, it may be useful to define a category considering them together. Finally, note that the dimensions defined in the proposed taxonomy can also be applied to future models. Three of them (noise type, selection source and disruption source) are based on the aforementioned information sources in the classification. Since such sources are present in all classification datasets, these dimensions and their categories can be used in the future. New noise models can also use the rest of the dimensions (selection distribution and disruption distribution), although considering distributions not used until now will imply the appearance of new categories in them.
It is important to note that most of the existing models have been developed to introduce label noise [21,22,38]. The number of attribute noise models [77,78] is more limited, and the number of models combining label and attribute noise [26,27] is even smaller. This fact clearly shows that label noise is being widely studied in the literature, whereas attribute noise receives less recognition [8]. Therefore, it is necessary to pay more attention to this type of noise and develop new models for its introduction in a controlled way since it is frequent but often overlooked in classification problems [58,78].
Furthermore, in relation to attribute noise, other models closer to the noise produced in real-world datasets can be studied. Thus, even though there are different models introducing realistic label noise (for example, those focusing on borderline label noise [69,73]), these types of models are scarcer in attribute noise. On the other hand, most attribute noise models consider the same noise level in each attribute [17,77]. The exception could be asymmetric models [58,82], which allow defining a noise level in each attribute. Nevertheless, they may require knowledge of the problem to determine the noise level of each attribute and which of them are more or less altered. In order to overcome this problem, models based on the scheme employed in [110] (which was used for unsupervised problems) could be designed. It defines a single noise level, avoiding the difficulty of having multiple noise levels, and this is applied to all attributes using a salt-and-pepper procedure [110].
The separation of the selection and disruption procedures in each noise model also allows the creation of new models that combine the selection of a given model and the disruption of another. Finally, despite the large number of noise models proposed in the literature, there is a line for model design that has not yet been sufficiently explored, consisting of the imitation of real-world datasets with noisy values. This requires further study of datasets in which errors can be identified [111,112]. The design of new models could be based on the similarity they achieve by imitating the errors in these data. In this way, it will be possible to approximate the errors that usually occur in real-world datasets, which can be an important aspect in the design of noise models.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Yu, Z.; Wang, D.; Zhao, Z.; Chen, C.L.P.; You, J.; Wong, H.; Zhang, J. Hybrid incremental ensemble learning for noisy real-world data classification. IEEE Trans. Cybern. 2019, 49, 403–416. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Gupta, A. Dealing with noise problem in machine learning data-sets: A systematic review. Procedia Comput. Sci. 2019, 161, 466–474. [Google Scholar] [CrossRef]
- Martín, J.; Sáez, J.A.; Corchado, E. On the regressand noise problem: Model robustness and synergy with regression-adapted noise filters. IEEE Access 2021, 9, 145800–145816. [Google Scholar] [CrossRef]
- Liu, T.; Tao, D. Classification with noisy labels by importance reweighting. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 447–461. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Liu, Y.; Ding, X.; Wang, G.; Yu, H.; Luo, Y. Granular ball computing classifiers for efficient, scalable and robust learning. Inf. Sci. 2019, 483, 136–152. [Google Scholar] [CrossRef]
- Nematzadeh, Z.; Ibrahim, R.; Selamat, A. Improving class noise detection and classification performance: A new two-filter CNDC model. Appl. Soft Comput. 2020, 94, 106428. [Google Scholar] [CrossRef]
- Zeng, S.; Duan, X.; Li, H.; Xiao, Z.; Wang, Z.; Feng, D. Regularized fuzzy discriminant analysis for hyperspectral image classification with noisy labels. IEEE Access 2019, 7, 108125–108136. [Google Scholar] [CrossRef]
- Sáez, J.A.; Corchado, E. ANCES: A novel method to repair attribute noise in classification problems. Pattern Recognit. 2022, 121, 108198. [Google Scholar] [CrossRef]
- Adeli, E.; Thung, K.; An, L.; Wu, G.; Shi, F.; Wang, T.; Shen, D. Semi-supervised discriminative classification robust to sample-outliers and feature-noises. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 515–522. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, M.; Deng, Z.; Luo, J.; Li, Y. A new fuzzy set and nonkernel SVM approach for mislabeled binary classification with applications. IEEE Trans. Fuzzy Syst. 2017, 25, 1536–1545. [Google Scholar] [CrossRef]
- Yu, Z.; Lan, K.; Liu, Z.; Han, G. Progressive ensemble kernel-based broad learning system for noisy data classification. IEEE Trans. Cybern. 2022, 52, 9656–9669. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Zheng, S.; Wang, G.; Gao, X.; Wang, B. Granular ball sampling for noisy label classification or imbalanced classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, in press. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Zheng, Y.; Wang, G.; He, P.; Li, H.; Chen, Z. Random space division sampling for label-noisy classification or imbalanced classification. IEEE Trans. Cybern. 2021, in press. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Shao, Y.; Zhang, J.; Zhao, Y.; Teng, J. Robust rescaled hinge loss twin support vector machine for imbalanced noisy classification. IEEE Access 2019, 7, 65390–65404. [Google Scholar] [CrossRef]
- Garcia, L.P.F.; Lehmann, J.; de Carvalho, A.C.P.L.F.; Lorena, A.C. New label noise injection methods for the evaluation of noise filters. Knowl.-Based Syst. 2019, 163, 693–704. [Google Scholar] [CrossRef]
- Tomasev, N.; Buza, K. Hubness-aware kNN classification of high-dimensional data in presence of label noise. Neurocomputing 2015, 160, 157–172. [Google Scholar] [CrossRef]
- Sáez, J.A.; Galar, M.; Luengo, J.; Herrera, F. Analyzing the presence of noise in multi-class problems: Alleviating its influence with the One-vs-One decomposition. Knowl. Inf. Syst. 2014, 38, 179–206. [Google Scholar] [CrossRef]
- Frénay, B.; Verleysen, M. Classification in the presence of label noise: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 845–869. [Google Scholar] [CrossRef]
- Nettleton, D.; Orriols-Puig, A.; Fornells, A. A study of the effect of different types of noise on the precision of supervised learning techniques. Artif. Intell. Rev. 2010, 33, 275–306. [Google Scholar] [CrossRef]
- Zhao, Z.; Chu, L.; Tao, D.; Pei, J. Classification with label noise: A Markov chain sampling framework. Data Min. Knowl. Discov. 2019, 33, 1468–1504. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Q.; Wu, Q.; Zhang, Z.; Gong, Y.; He, Z.; Zhu, F. SMOTE-NaN-DE: Addressing the noisy and borderline examples problem in imbalanced classification by natural neighbors and differential evolution. Knowl.-Based Syst. 2021, 223, 107056. [Google Scholar] [CrossRef]
- Bootkrajang, J.; Chaijaruwanich, J. Towards instance-dependent label noise-tolerant classification: A probabilistic approach. Pattern Anal. Appl. 2020, 23, 95–111. [Google Scholar] [CrossRef]
- Hendrycks, D.; Mazeika, M.; Wilson, D.; Gimpel, K. Using trusted data to train deep networks on labels corrupted by severe noise. Adv. Neural Inf. Process. Syst. 2018, 31, 10477–10486. [Google Scholar]
- Shanthini, A.; Vinodhini, G.; Chandrasekaran, R.M.; Supraja, P. A taxonomy on impact of label noise and feature noise using machine learning techniques. Soft Comput. 2019, 23, 8597–8607. [Google Scholar] [CrossRef]
- Koziarski, M.; Krawczyk, B.; Wozniak, M. Radial-based oversampling for noisy imbalanced data classification. Neurocomputing 2019, 343, 19–33. [Google Scholar] [CrossRef]
- Teng, C. Polishing blemishes: Issues in data correction. IEEE Intell. Syst. 2004, 19, 34–39. [Google Scholar] [CrossRef]
- Kazmierczak, S.; Mandziuk, J. A committee of convolutional neural networks for image classification in the concurrent presence of feature and label noise. In Proceedings of the 16th International Conference on Parallel Problem Solving from Nature, Leiden, The Netherlands, 5–9 September 2020; Volume 12269; LNCS, pp. 498–511. [Google Scholar]
- Mirzasoleiman, B.; Cao, K.; Leskovec, J. Coresets for robust training of deep neural networks against noisy labels. Adv. Neural Inf. Process. Syst. 2020, 33, 11465–11477. [Google Scholar]
- Kang, J.; Fernandez-Beltran, R.; Kang, X.; Ni, J.; Plaza, A. Noise-tolerant deep neighborhood embedding for remotely sensed images with label noise. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2551–2562. [Google Scholar] [CrossRef]
- Koziarski, M.; Wozniak, M.; Krawczyk, B. Combined cleaning and resampling algorithm for multi-class imbalanced data with label noise. Knowl.-Based Syst. 2020, 204, 106223. [Google Scholar] [CrossRef]
- Xia, S.; Wang, G.; Chen, Z.; Duan, Y.; Liu, Q. Complete random forest based class noise filtering learning for improving the generalizability of classifiers. IEEE Trans. Knowl. Data Eng. 2019, 31, 2063–2078. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, D.; Tan, X. Robust class-specific autoencoder for data cleaning and classification in the presence of label noise. Neural Process. Lett. 2019, 50, 1845–1860. [Google Scholar] [CrossRef]
- Chen, B.; Xia, S.; Chen, Z.; Wang, B.; Wang, G. RSMOTE: A self-adaptive robust SMOTE for imbalanced problems with label noise. Inf. Sci. 2021, 553, 397–428. [Google Scholar] [CrossRef]
- Pakrashi, A.; Namee, B.M. KalmanTune: A Kalman filter based tuning method to make boosted ensembles robust to class-label noise. IEEE Access 2020, 8, 145887–145897. [Google Scholar] [CrossRef]
- Salekshahrezaee, Z.; Leevy, J.L.; Khoshgoftaar, T.M. A reconstruction error-based framework for label noise detection. J. Big Data 2021, 8, 1–16. [Google Scholar] [CrossRef]
- Abellán, J.; Mantas, C.J.; Castellano, J.G. AdaptativeCC4.5: Credal C4.5 with a rough class noise estimator. Expert Syst. Appl. 2018, 92, 363–379. [Google Scholar] [CrossRef]
- Wang, C.; Shi, J.; Zhou, Y.; Li, L.; Yang, X.; Zhang, T.; Wei, S.; Zhang, X.; Tao, C. Label noise modeling and correction via loss curve fitting for SAR ATR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Wei, Y.; Gong, C.; Chen, S.; Liu, T.; Yang, J.; Tao, D. Harnessing side information for classification under label noise. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3178–3192. [Google Scholar] [CrossRef]
- Chen, P.; Liao, B.; Chen, G.; Zhang, S. Understanding and utilizing deep neural networks trained with noisy labels. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97; PMLR, pp. 1062–1070. [Google Scholar]
- Song, H.; Kim, M.; Lee, J.G. SELFIE: Refurbishing unclean samples for robust deep learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97; PMLR, pp. 5907–5915. [Google Scholar]
- Seo, P.H.; Kim, G.; Han, B. Combinatorial inference against label noise. Adv. Neural Inf. Process. Syst. 2019, 32, 1171–1181. [Google Scholar]
- Wu, P.; Zheng, S.; Goswami, M.; Metaxas, D.N.; Chen, C. A topological filter for learning with label noise. Adv. Neural Inf. Process. Syst. 2020, 33, 21382–21393. [Google Scholar]
- Cheng, J.; Liu, T.; Ramamohanarao, K.; Tao, D. Learning with bounded instance and label-dependent label noise. In Proceedings of the 37th International Conference on Machine Learning, virtual, 3–18 July 2020; Volume 119; PMLR, pp. 1789–1799. [Google Scholar]
- Ghosh, A.; Lan, A.S. Contrastive learning improves model robustness under label noise. In Proceedings of the 2021 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Virtual, 19–25 July 2021; pp. 2703–2708. [Google Scholar]
- Wang, Z.; Hu, G.; Hu, Q. Training noise-robust deep neural networks via meta-learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, virtual, 14–19 June 2020; pp. 4523–4532. [Google Scholar]
- Jindal, I.; Pressel, D.; Lester, B.; Nokleby, M.S. An effective label noise model for DNN text classification. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MA, USA, 9–14 June 2019; pp. 3246–3256. [Google Scholar]
- Scott, C.; Blanchard, G.; Handy, G. Classification with asymmetric label noise: Consistency and maximal denoising. In Proceedings of the 26th Annual Conference on Learning Theory, Princeton, NJ, USA, 12–14 June 2013; Volume 30; JMLR, pp. 489–511. [Google Scholar]
- Yang, P.; Ormerod, J.; Liu, W.; Ma, C.; Zomaya, A.; Yang, J. AdaSampling for positive-unlabeled and label noise learning with bioinformatics applications. IEEE Trans. Cybern. 2019, 49, 1932–1943. [Google Scholar] [CrossRef]
- Feng, L.; Shu, S.; Lin, Z.; Lv, F.; Li, L.; An, B. Can cross entropy loss be robust to label noise? In Proceedings of the 29th International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020; pp. 2206–2212. [Google Scholar]
- Ghosh, A.; Kumar, H.; Sastry, P. Robust loss functions under label noise for deep neural networks. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1919–1925. [Google Scholar]
- Tanaka, D.; Ikami, D.; Yamasaki, T.; Aizawa, K. Joint optimization framework for learning with noisy labels. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5552–5560. [Google Scholar]
- Sun, Z.; Liu, H.; Wang, Q.; Zhou, T.; Wu, Q.; Tang, Z. Co-LDL: A co-training-based label distribution learning method for tackling label noise. IEEE Trans. Multimed. 2022, 24, 1093–1104. [Google Scholar] [CrossRef]
- Li, J.; Wong, Y.; Zhao, Q.; Kankanhalli, M.S. Learning to learn from noisy labeled data. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5051–5059. [Google Scholar]
- Harutyunyan, H.; Reing, K.; Steeg, G.V.; Galstyan, A. Improving generalization by controlling label-noise information in neural network weights. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; Volume 119; PMLR, pp. 4071–4081. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.W.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31, 8536–8546. [Google Scholar]
- Nikolaidis, K.; Plagemann, T.; Kristiansen, S.; Goebel, V.; Kankanhalli, M. Using under-trained deep ensembles to learn under extreme label noise: A case study for sleep apnea detection. IEEE Access 2021, 9, 45919–45934. [Google Scholar] [CrossRef]
- Bootkrajang, J.; Kabán, A. Learning kernel logistic regression in the presence of class label noise. Pattern Recognit. 2014, 47, 3641–3655. [Google Scholar] [CrossRef]
- Mannino, M.V.; Yang, Y.; Ryu, Y. Classification algorithm sensitivity to training data with non representative attribute noise. Decis. Support Syst. 2009, 46, 743–751. [Google Scholar] [CrossRef]
- Ghosh, A.; Manwani, N.; Sastry, P.S. On the robustness of decision tree learning under label noise. In Proceedings of the 21th Conference on Advances in Knowledge Discovery and Data Mining, Jeju, Korea, 23–26 May 2017; Volume 10234; LNCS, pp. 685–697. [Google Scholar]
- Arazo, E.; Ortego, D.; Albert, P.; O’Connor, N.E.; McGuinness, K. Unsupervised label noise modeling and loss correction. In Proceedings of the 36th International Conference on Machine Learning, Beach, CA, USA, 9–15 June 2019; Volume 97; PMLR, pp. 312–321. [Google Scholar]
- Liu, D.; Yang, G.; Wu, J.; Zhao, J.; Lv, F. Robust binary loss for multi-category classification with label noise. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, ON, Canada, 6–11 June 2021; pp. 1700–1704. [Google Scholar]
- Ghosh, A.; Manwani, N.; Sastry, P.S. Making risk minimization tolerant to label noise. Neurocomputing 2015, 160, 93–107. [Google Scholar] [CrossRef]
- Ortego, D.; Arazo, E.; Albert, P.; O’Connor, N.E.; McGuinness, K. Towards robust learning with different label noise distributions. In Proceedings of the 25th International Conference on Pattern Recognition, Milan, Italy, 10–15 January 2020; pp. 7020–7027. [Google Scholar]
- Fatras, K.; Damodaran, B.; Lobry, S.; Flamary, R.; Tuia, D.; Courty, N. Wasserstein adversarial regularization for learning with label noise. IEEE Trans. Pattern Anal. Mach. Intell. 2021, in press. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, Z.; Li, Y.; Guo, J. Making deep neural networks robust to label noise: Cross-training with a novel loss function. IEEE Access 2019, 7, 130893–130902. [Google Scholar] [CrossRef]
- Schneider, J.; Handali, J.P.; vom Brocke, J. Increasing trust in (big) data analytics. In Proceedings of the 2018 Advanced Information Systems Engineering Workshops, Tallinn, Estonia, 11–15 June 2018; Volume 316; LNBIP, pp. 70–84. [Google Scholar]
- Huang, X.; Shi, L.; Suykens, J.A.K. Support vector machine classifier with pinball loss. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 984–997. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, T. Support vector classification with input data uncertainty. Adv. Neural Inf. Process. Syst. 2004, 17, 161–168. [Google Scholar]
- Bootkrajang, J. A generalised label noise model for classification in the presence of annotation errors. Neurocomputing 2016, 192, 61–71. [Google Scholar] [CrossRef]
- Bootkrajang, J. A generalised label noise model for classification. In Proceedings of the 23rd European Symposium on Artificial Neural Networks, Bruges, Belgium, 22–23 April 2015; pp. 349–354. [Google Scholar]
- Ren, M.; Zeng, W.; Yang, B.; Urtasun, R. Learning to reweight examples for robust deep learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm Sweden, 10–15 July 2018; Volume 80; PMLR, pp. 4331–4340. [Google Scholar]
- Prati, R.C.; Luengo, J.; Herrera, F. Emerging topics and challenges of learning from noisy data in nonstandard classification: A survey beyond binary class noise. Knowl. Inf. Syst. 2019, 60, 63–97. [Google Scholar] [CrossRef]
- Du, J.; Cai, Z. Modelling class noise with symmetric and asymmetric distributions. In Proceedings of the 29th AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2589–2595. [Google Scholar]
- Görnitz, N.; Porbadnigk, A.; Binder, A.; Sannelli, C.; Braun, M.L.; Müller, K.; Kloft, M. Learning and evaluation in presence of non-i. In i.d. label noise. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; Volume 33; PMLR, pp. 293–302. [Google Scholar]
- Gehlot, S.; Gupta, A.; Gupta, R. A CNN-based unified framework utilizing projection loss in unison with label noise handling for multiple Myeloma cancer diagnosis. Med Image Anal. 2021, 72, 102099. [Google Scholar] [CrossRef] [PubMed]
- Denham, B.; Pears, R.; Naeem, M.A. Null-labelling: A generic approach for learning in the presence of class noise. In Proceedings of the 20th IEEE International Conference on Data Mining, Sorrento, Italy, 17–20 November 2020; pp. 990–995. [Google Scholar]
- Sáez, J.A.; Galar, M.; Luengo, J.; Herrera, F. Tackling the problem of classification with noisy data using multiple classifier systems: Analysis of the performance and robustness. Inf. Sci. 2013, 247, 1–20. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Hulse, J.V. Empirical case studies in attribute noise detection. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 379–388. [Google Scholar] [CrossRef]
- Kaneko, T.; Ushiku, Y.; Harada, T. Label-noise robust generative adversarial networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 2462–2471. [Google Scholar]
- Ghosh, A.; Lan, A.S. Do we really need gold samples for sample weighting under label noise? In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 3921–3930. [Google Scholar]
- Wang, Q.; Han, B.; Liu, T.; Niu, G.; Yang, J.; Gong, C. Tackling instance-dependent label noise via a universal probabilistic model. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; pp. 10183–10191. [Google Scholar]
- Petety, A.; Tripathi, S.; Hemachandra, N. Attribute noise robust binary classification. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 13897–13898. [Google Scholar]
- Zhang, Y.; Zheng, S.; Wu, P.; Goswami, M.; Chen, C. Learning with feature-dependent label noise: A progressive approach. In Proceedings of the 9th International Conference on Learning Representations, Online, 3–7 May 2021; pp. 1–13. [Google Scholar]
- Wei, J.; Liu, Y. When optimizing f-divergence is robust with label noise. In Proceedings of the 9th International Conference on Learning Representations, Online, 3–7 May 2021; pp. 1–11. [Google Scholar]
- Chen, P.; Ye, J.; Chen, G.; Zhao, J.; Heng, P. Beyond class-conditional assumption: A primary attempt to combat instance-dependent label noise. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; pp. 11442–11450. [Google Scholar]
- Nicholson, B.; Sheng, V.S.; Zhang, J. Label noise correction and application in crowdsourcing. Expert Syst. Appl. 2016, 66, 149–162. [Google Scholar] [CrossRef]
- Amid, E.; Warmuth, M.K.; Srinivasan, S. Two-temperature logistic regression based on the Tsallis divergence. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Japan, 16 April 2019; Volume 89; PMLR, pp. 2388–2396. [Google Scholar]
- Thulasidasan, S.; Bhattacharya, T.; Bilmes, J.A.; Chennupati, G.; Mohd-Yusof, J. Combating label noise in deep learning using abstention. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97; PMLR, pp. 6234–6243. [Google Scholar]
- Cano, J.R.; Luengo, J.; García, S. Label noise filtering techniques to improve monotonic classification. Neurocomputing 2019, 353, 83–95. [Google Scholar] [CrossRef]
- Pu, X.; Li, C. Probabilistic information-theoretic discriminant analysis for industrial label-noise fault diagnosis. IEEE Trans. Ind. Inform. 2021, 17, 2664–2674. [Google Scholar] [CrossRef]
- Han, B.; Yao, J.; Niu, G.; Zhou, M.; Tsang, I.W.; Zhang, Y.; Sugiyama, M. Masking: A new perspective of noisy supervision. Adv. Neural Inf. Process. Syst. 2018, 31, 5841–5851. [Google Scholar]
- Folleco, A.; Khoshgoftaar, T.M.; Hulse, J.V.; Bullard, L.A. Software quality modeling: The impact of class noise on the random forest classifier. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation, Hong Kong, 1–6 June 2008; pp. 3853–3859. [Google Scholar]
- Zhu, X.; Wu, X. Cost-guided class noise handling for effective cost-sensitive learning. In Proceedings of the 4th IEEE International Conference on Data Mining, Brighton, UK, 1–4 November 2004; pp. 297–304. [Google Scholar]
- Kang, J.; Fernández-Beltran, R.; Duan, P.; Kang, X.; Plaza, A.J. Robust normalized softmax loss for deep metric learning-based characterization of remote sensing images with label noise. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8798–8811. [Google Scholar] [CrossRef]
- Fefilatyev, S.; Shreve, M.; Kramer, K.; Hall, L.O.; Goldgof, D.B.; Kasturi, R.; Daly, K.; Remsen, A.; Bunke, H. Label-noise reduction with support vector machines. In Proceedings of the 21st International Conference on Pattern Recognition, Munich, Germany, 30 July–2 August 2012; pp. 3504–3508. [Google Scholar]
- Huang, L.; Zhang, C.; Zhang, H. Self-adaptive training: Beyond empirical risk minimization. Adv. Neural Inf. Process. Syst. 2020, 33, 19365–19376. [Google Scholar]
- Ramdas, A.; Póczos, B.; Singh, A.; Wasserman, L.A. An analysis of active learning with uniform feature noise. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; Volume 33; JMLR, pp. 805–813. [Google Scholar]
- Yuan, W.; Guan, D.; Ma, T.; Khattak, A. Classification with class noises through probabilistic sampling. Inf. Fusion 2018, 41, 57–67. [Google Scholar] [CrossRef]
- Ekambaram, R.; Fefilatyev, S.; Shreve, M.; Kramer, K.; Hall, L.; Goldgof, D.; Kasturi, R. Active cleaning of label noise. Pattern Recognit. 2016, 51, 463–480. [Google Scholar] [CrossRef]
- Zhang, T.; Deng, Z.; Ishibuchi, H.; Pang, L. Robust TSK fuzzy system based on semisupervised learning for label noise data. IEEE Trans. Fuzzy Syst. 2021, 29, 2145–2157. [Google Scholar] [CrossRef]
- Berthon, A.; Han, B.; Niu, G.; Liu, T.; Sugiyama, M. Confidence scores make instance-dependent label-noise learning possible. In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; Volume 139; PMLR, pp. 825–836. [Google Scholar]
- Sáez, J.A.; Krawczyk, B.; Woźniak, M. On the influence of class noise in medical data classification: Treatment using noise filtering methods. Appl. Artif. Intell. 2016, 30, 590–609. [Google Scholar] [CrossRef]
- Baldomero-Naranjo, M.; Martínez-Merino, L.; Rodríguez-Chía, A. A robust SVM-based approach with feature selection and outliers detection for classification problems. Expert Syst. Appl. 2021, 178, 115017. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley and Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Dombrowski, A.K.; Anders, C.J.; Müller, K.R.; Kessel, P. Towards robust explanations for deep neural networks. Pattern Recognit. 2022, 121, 108194. [Google Scholar] [CrossRef]
- Belarouci, S.; Chikh, M. Medical imbalanced data classification. Adv. Sci. Technol. Eng. Syst. J. 2017, 2, 116–124. [Google Scholar] [CrossRef]
- Bao, F.; Deng, Y.; Kong, Y.; Ren, Z.; Suo, J.; Dai, Q. Learning deep landmarks for imbalanced classification. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2691–2704. [Google Scholar] [CrossRef]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
- Pradhan, A.; Mishra, D.; Das, K.; Panda, G.; Kumar, S.; Zymbler, M. On the classification of MR images using “ELM-SSA” coated hybrid model. Mathematics 2021, 9, 2095. [Google Scholar] [CrossRef]
- Iam-On, N. Clustering data with the presence of attribute noise: A study of noise completely at random and ensemble of multiple k-means clusterings. Int. J. Mach. Learn. Cybern. 2020, 11, 491–509. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Arik, S.Ö.; Lee, H.; Pfister, T. Distilling effective supervision from severe label noise. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 9291–9300. [Google Scholar]
- Lee, K.; He, X.; Zhang, L.; Yang, L. CleanNet: Transfer learning for scalable image classifier training with label noise. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018 2018; pp. 5447–5456. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).