Single Image Super-Resolution with Arbitrary Magnification Based on High-Frequency Attention Network

Abstract

Among various developments in the field of computer vision, single image super-resolution of images is one of the most essential tasks. However, compared to the integer magnification model for super-resolution, research on arbitrary magnification has been overlooked. In addition, the importance of single image super-resolution at arbitrary magnification is emphasized for tasks such as object recognition and satellite image magnification. In this study, we propose a model that performs arbitrary magnification while retaining the advantages of integer magnification. The proposed model extends the integer magnification image to the target magnification in the discrete cosine transform (DCT) spectral domain. The broadening of the DCT spectral domain results in a lack of high-frequency components. To solve this problem, we propose a high-frequency attention network for arbitrary magnification so that high-frequency information can be restored. In addition, only high-frequency components are extracted from the image with a mask generated by a hyperparameter in the DCT domain. Therefore, the high-frequency components that have a substantial impact on image quality are recovered by this procedure. The proposed framework achieves the performance of an integer magnification and correctly retrieves the high-frequency components lost between the arbitrary magnifications. We experimentally validated our model’s superiority over state-of-the-art models.

1. Introduction

Owing to convolutional neural networks (CNNs), image super-resolution shows excellent high-resolution reconstruction from low-resolution images. In addition, research is being conducted to improve the performance of various computer vision applications by converting low-resolution images into high-resolution images using super-resolution.

For example, in object detection, regions of interest are detected in an image through an object detection neural network. Subsequently, it is essential to adjust the detection region to the size of the object attribute recognition neural network. However, real-world images taken using CCTV cameras, black boxes, drones, etc., have small object areas, and when the image is resized by general interpolation, it causes blur and lowers the performance of object recognition. To solve this problem, Lee et al. [1] applied the super-resolution approach to an image that has a small object area. By applying this approach, object recognition accuracy was improved compared to the existing interpolation method. However, small object areas of various sizes cannot be converted into target sizes utilizing existing super-resolution methods. Conventional super-resolution methods restore only integer magnifications (×2, ×4). Alternatively, the input image is enlarged or reduced by a decimal (floating-point) magnification using the interpolation method, and then, an arbitrary magnification is performed through a super-resolution neural network. This method causes a loss of restoration capability and an increase in computing cost due to the deformation of the input image. Therefore, a super-resolution neural network capable of arbitrary magnification is required for the task at hand. Figure 1 is an example application of arbitrary magnification super-resolution in object recognition tasks. Object detection results taken by CCTV cameras can have arbitrary resolutions. There is a problem when using detection results for object recognition because most recognition models have a fixed input size. To resolve this problem, bicubic interpolation can be considered. However, it causes blur then lowers the performance of object recognition. Therefore, an arbitrary magnification super-resolution is required to upscale the image with an arbitrary resolution while preserving image quality, as shown in Figure 1. When applying our method to the application in Figure 1, it can perform the arbitrary magnification super-resolution with a single weight of an integer magnification model and small capacity weights for each decimal magnification model. To this end, weights for the decimal magnification candidates should be stored in the memory in advance.

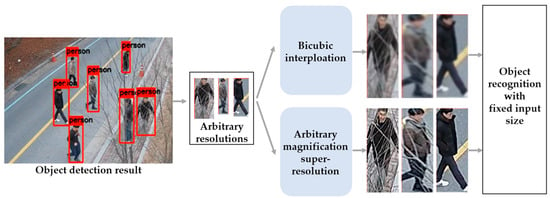
Figure 1. Example application of arbitrary magnification super-resolution in object recognition task.

In addition, the necessity of arbitrary magnification super-resolution for other tasks is described in the related works section. When constructing an arbitrary magnification super-resolution, it should be magnified to the target size through the decimal magnification by interpolation. In this case, various interpolation methods can be applied, but existing interpolation methods expand to a state in which many low-frequency components are not preserved. Applying this to a super-resolution model causes a decrease in image restoration capability. Therefore, for arbitrary super-resolution, a method capable of expanding to a target magnification while preserving the preservation of low-frequency components is essential. We propose a method using DCT to solve this problem. We utilized the principle that in the DCT spectrum domain, low-frequency components are concentrated in the upper-left direction, and high-frequency components are concentrated in the lower-right direction. In this case, while preserving a low-frequency component that greatly affects performance, it expands in the lower-right direction, which is a high-frequency component. Using this, we can preserve the low-frequency components and obtain an image magnified at an arbitrary magnification in which only the high-frequency component is insufficient. From the acquired image, we use DCT to more delicately extract high-frequency components through the mask generated using hyperparameters. The extracted high-frequency component is amplified through a high-frequency attention network. The amplified high-frequency component is added to the input image, and the arbitrary magnification is completed. The proposed high-frequency attention network gives the network a definite purpose of high-frequency restoration by receiving high-frequency components as input. This leads to good performance as the network is more focused on purpose.

In this study, a super-resolution network capable of arbitrary magnification is proposed as follows: Integer scaling is performed through a super-resolution neural network, and the space for residual scaling is expanded in the DCT spectral domain. In this case, the expanded DCT spaces were part of the high-frequency region. Therefore, arbitrary magnification is performed by filling in the insufficient high-frequency space in the spatial domain through the high-frequency attention network. The arbitrary magnification model proposed in this study has better restoration performance than other arbitrary magnification methods by retaining the advantages of the integer magnification model and proceeding with additional arbitrary magnification.

The highlights of this study are summarized as follows:

• The image is enlarged to target resolution in the DCT spectral domain.
• The high frequency, which is insufficient owing to the DCT spectral domain spatial expansion, is restored through the spatial domain high-frequency concentration network.
• The proposed model preserves the superiority of the existing integer super-resolution model. By simply adding the hybrid-domain high-frequency model without modifying and additionally training on the existing integer super-resolution model, our model’s arbitrary magnification restoration performance is better than that of state-of-the-art models.

2. Related Works

2.1. Conventional Single Image Super-Resolution

The purpose of super-resolution is to use a low-resolution image as input and predict a corresponding high-resolution image. However, this is an ill-posed problem to solve because various degradations occur while reducing the image quality from high resolution to low resolution. Various studies have been conducted to address this problem. Super-resolution convolutional neural network (SRCNN) [2] showed innovative restoration performance using a super-resolution CNN for the first time. Based on this, studies on better super-resolution performance were conducted. A very deep convolutional network (VDSR) [3] designed the model more deeply through a residual learning strategy. An efficient sub-pixel convolutional neural network (ESPCNN) [4] overcomes the limitation of inputting an image with a target magnification as input by implementing a pixel-shuffling layer that can be learned with an upsampling module. Computing overhead is reduced because the input images do not need to be enlarged by interpolation, and a deeper network can be built using small-sized filters. Deep back-projection networks (DBPN) [5] created a structure that repeatedly stacks the image upscaling and downscaling layers. It showed better performance by repeatedly reducing and enlarging the size of the input image. Residual channel attention network (RCAN) [6] introduced a channel attention mechanism to create a deep model. Dual regression networks (DRN) [7] improved the restoration ability by constructing a closed circuit inside the model and adding a low-resolution domain loss function that calculates the difference from the input image by downscaling the super-resolution result image, in addition to the existing high-resolution domain loss function. Residual dense network (RDN) [8] learned the hierarchical representation of all feature maps through the residual density structure. Second-order attention network (SAN) [9] showed good performance by strongly improving the representation of image feature maps and learning the interdependencies between feature maps. SRGAN [10] used adversarial learning to improve super-resolution performance. This model consists of a generator and a discriminator network, and the generator aims to create a super-resolution output that the discriminator cannot differentiate from a sample input. Recently, SRFlow [11], which uses a normalizing flow to predict a complex probability distribution from a normal distribution, has been attracting attention. SRFlow transforms a high-resolution image into a complex probability distribution and gradually differentiates the probability distribution into a normal distribution of a low-resolution image by using the Jacobian matrix. In addition, there is an affine coupling layer in SRFlow, which divides the dimension of the input value into two, leaving one dimension unchanged and performing shift and affine transformations on the other dimension. This transform makes it easy to compute the inverse transform and the Jacobian determinant. This differentiation process is learned, and when a normal distribution of a low-resolution image is processed, it can be transformed into a complex probability distribution. Complex probability distributions generate images from probability distributions using a flow-based generative model. The advantage of SRFlow is that it has enhanced diversity to create high-resolution images from fewer low-resolution images than a generative adversarial network (GAN). In addition, the log-likelihood loss is used to prevent divergence during learning to ensure stability, and it is easier to learn than the generator and discriminator of the GAN separately. SRFlow-DA [12] showed improved performance by adding six more convolution layers to extend the receptive field of the SRFlow model and removing the normalization layer that does not fit the super-resolution structure. Noise conditional SRFlow (NCSR) [13] inserts noise into low-resolution and high-resolution images during training and removes artifacts caused by noise. SwinIR [14] proposed a strong baseline model for image restoration based on the swin transformer [15]. SwinIR is composed of several residual swin transformer blocks, each of which has several swin transformer layers together with a residual connection. Through this, SwinIR showed excellent image restoration ability. A cross-scale non-local network (CSNLN) [16] proposed the first cross-scale non-local (CS-NL) attention module with integration into a recurrent neural network. Additionally, they combine the new CS-NL prior with local and non-local priors. These methods present good quality image results and have a lot of advantages, as shown in Table 1. However, due to the various resolutions of taken images in the real world, the need for arbitrary magnification is emerging. Despite the development of the latest super-resolution as above, these methods have shortcomings, as shown in Table 1. To perform the arbitrary magnification super-resolution, existing methods should utilize interpolation methods such as bicubic, bilinear, etc. Due to this limitation, the interpolation results show poor image quality. Therefore, to deal with this problem, we propose a super-resolution network capable of arbitrary magnification.

Table 1. Conventional single image super-resolution methods’ advantages and shortcomings.

Method	Advantages (Characteristics)	Shortcomings
SRCNN	Uses only three convolutional layers and enhances the performance of super-resolution.	Perform integer super-resolution only and should utilize interpolation methods to perform the arbitrary magnification super-resolution.
VDSR	Cascades small filters many times; information over an image is exploited in an efficient way.
ESPCNN	Effectively replacing the bicubic filter, computing cost is reduced.
DBPN	Concatenates the features of the repeated upsampling and downsampling, super-solution performance improved.
RCAN	Bypasses multiple skip connections and focuses on learning high-frequency information.
DRN	Estimates kernel and utilizes it to restore low-resolution images.
RDN	Learns hierarchical representation and stabilizes the training process.
SAN	Rescales the features adaptively and learns feature expressions and feature correlation.
SRGAN	Uses adversarial learning and recovers heavily downsampled images.
SRFlow-DA	Enlarges the receptive field and takes more expressive power.
NCSR	Adds the noise conditional layer and extends diversity.
SwinIR	Applies a Swin transformer and utilizes interactions between image content and attention weights.
CSNLN	Finds and utilizes more cross-scale feature correlations.

2.2. Arbitrary Magnification Single Image Super-Resolution

Most of the super-resolution rely on non-learning-based interpolation when scaling low-resolution images to decimal magnifications. ESPCNN proposed a magnification method capable of learning by proposing a pixel-shuffling layer. Using this, VDSR can magnify a low-resolution image to a target resolution and put it into a super-resolution model for arbitrary magnification. However, if the image is enlarged and passed through a neural network, it requires significant computing resources, and it has to have a large model weight for each magnification; thereby, its performance is more specialized for integer magnification. Meta-SR [17] can perform arbitrary magnification with only one model by replacing the enlarged part of the existing super-resolution model with an upscale module. Meta-SR has a weight prediction layer that can be trained to predict weights expanded by an integer magnification. This weight is applied to the upscale module and magnifies the image by an integer magnification. In the image enlarged by an integer multiple, a pixel value is selected according to the size suitable for arbitrary magnification by using a suitable pixel mask. This overcomes the limitations of existing algorithms by applying the k-neighborhood algorithm to deep learning. SRWarp [18] receives images warped by enlargement, reduction, distortion, etc., as input values. For the input image, the backbone extracts a feature map for each magnification (×1, ×2, ×4), and the adaptive warping layer predicts a transform function that can restore the feature map image to its original shape. Thereafter, multiscale blending combines the feature maps for each magnification, which are restored to a non-warping form, using the rich information possessed by each magnification (×1, ×2, ×4). Thus, SRWarp proposed a neural network that allows arbitrary magnification through the multiscale blending of an image. Wang et al. [19] proposed a plug-in module for existing super-resolution networks to perform arbitrary magnification, which consists of multiple scale-aware feature adaption blocks and a scale-aware upsampling layer. These methods have a lot of advantages, as shown in Table 2. However, these arbitrary magnification methods have shortcomings that cannot preserve the integer super-resolution performance. It is because these arbitrary magnification models replaced the upscale module of the existing integer magnification super-resolution models with the proposed arbitrary upscale module. Due to the replacement of the upscale module, the restoration capability of the integer magnification super-resolution model is not maintained, resulting in poor performance. There is a need for a method that preserves the performance of the integer magnification model as much as possible in the arbitrary magnification model and enables arbitrary magnification. Therefore, in order to maintain the performance of the model, this paper proposes a high-frequency attention network capable of arbitrary magnification without modifying the structure of the integer magnification model.

Table 2. Arbitrary magnification single image super-resolution methods’ advantages and shortcomings.

Method	Advantages (Characteristics)	Shortcomings
Meta-SR	Upscales images with arbitrary scale factors through a single model.	Cannot preserve the integer super-resolution performance due to the replacement of the upscale module.
SRWarp	Uses a multiscale blending and handles numerous possible deformations.	Focuses on the warp of the image and is similar to Meta-SR performance.
Wang et al.’s	Uses multiple scale-aware feature adaption blocks and a scale-aware upsampling layer.	Needs additional training of integer super-resolution model due to the replacement of the existing module.

2.3. Frequency Domain Super-Resolution

Images can be transformed into various frequency domains, and studies have been conducted to predict various frequency information that can express high-resolution images through CNNs. Kumar et al. [20] proposed convolutional neural networks for wavelet domain super-resolution (CNNWSR) to predict wavelet coefficients of high-resolution images. The predicted wavelet coefficients are used to reconstruct a high-resolution image using a two-dimensional inverse discrete wavelet transform (DWT). Frequency domain neural network for fast image super-resolution (FNNSR) [21] and improved frequency domain neural networks super-resolution (IFNNSR) [22] solve the super-resolution problem in the Fourier domain. FNNSR formulated a neural network that parameterizes with point-wise multiplication in the spectral domain using a single convolutional layer to approximate the Rectified Linear Unit (ReLU) activation function. IFNNSR uses Hartley transform instead of Fourier transform and multiple convolutional layers to approximate the ReLU activation function well. It also emphasizes the error of high-frequency components by proposing a new weighted Euclidean loss. Aydin et al. [23] predict DCT coefficients that can reconstruct a high-resolution image through a fully connected (FC) layer in the DCT spectral domain after extending the input image to a target magnification through interpolation. The loss is defined as the mean square error with the DCT coefficient for the corresponding high-resolution image, which showed the possibility of CNN learning in the DCT spectral domain. These methods have a lot of advantages, as shown in Table 3. Although it is a super-resolution model that uses the frequency domain, it shows lower performance than other spatial domain super-resolution models despite the fast speed. It is because these frequency domain-based models do not properly consider spatial domain information. In this paper, frequency and spatial domain are used as a hybrid to utilize the advantages of each domain. In the frequency domain, a high-frequency component is extracted using the principle of the DCT spectral domain. In the spatial domain, an amplified high-frequency component can be obtained by using the extracted high-frequency component through a high-frequency attention network. These advantages can lead to excellent performance when performing arbitrary magnification.

Table 3. Frequency domain super-resolution methods’ advantages and shortcomings.

Method	Advantages (Characteristics)	Shortcomings
CNNW SR	Predicts the wavelet coefficients of three images that can be used for image restoration.	Provide lower performance than other spatial domain super-resolution models despite the fast speed.
FNNSR	Applies Fourier transform to super-resolution and is faster than the alternatives.
IFNNSR	Learns the basic features in transformed images.
Aydin et al.’s	Predicts DCT coefficients and reconstruct an image in the DCT spectral domain.

2.4. State-of-the-Art Task-Driven Arbitrary Magnification Super-Resolution

Previous studies on single image super-resolution cannot deal with arbitrary magnification super-resolution. To perform the arbitrary magnification super-resolution, it should be resized by interpolation after passing through the integer super-resolution network. However, these results do not show acceptable performance for each task. To deal with this, recent studies were conducted in each task by adapting arbitrary magnification super-resolution.

According to Zhu et al. [24], high-quality medical images with various resolutions are important in the current clinical process. To acquire magnetic resonance (MR) images for each magnification, they should scan each scale, as shown in Figure 2a. However, scanning all medical images with arbitrary magnifying factors requires enormous acquisition time and equipment constraints. On the other hand, as shown in Figure 2b, an arbitrary super-resolution model can upscale to various target resolutions while preserving the high image quality without multiple scans. Consequently, they devised an approach for medical image arbitrary-scale super-resolution (MIASSR), in which they combined a meta-learning method with GAN to super-resolve medical images at any scale of magnification.

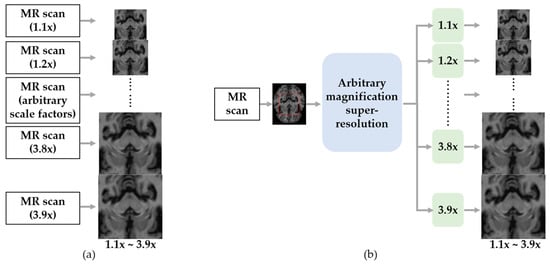
Figure 2. Example application of arbitrary magnification super-resolution in medical image processing task. (a) Conventional approach to obtain arbitrary magnification MR images. (b) Arbitrary magnification super-resolution approach to obtain arbitrary magnification MR images.

According to Zhi et al. [25], it is a common requirement to zoom the image arbitrarily by rolling the mouse wheel, as shown in Figure 3. It can be used for identifying the object detail in the satellite image. To meet the requirement, they proposed arbitrary scale super-resolution (ASSR) that consists of a feature learning module and an arbitrary upscale module.

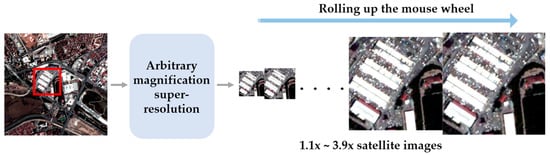
Figure 3. Example application of arbitrary magnification super-resolution in satellite image processing task.

According to Truong et al. [26], a depth map allows for structural information to be utilized in various applications, such as view synthesis or 3D reconstruction. However, the resolution of depth maps is often much lower than the resolution of RGB images due to the limitations of depth sensors. To solve this problem, the low-resolution depth image can be upscaled to target resolution through the depth image super-resolution with arbitrary scale factors, as shown in Figure 4.

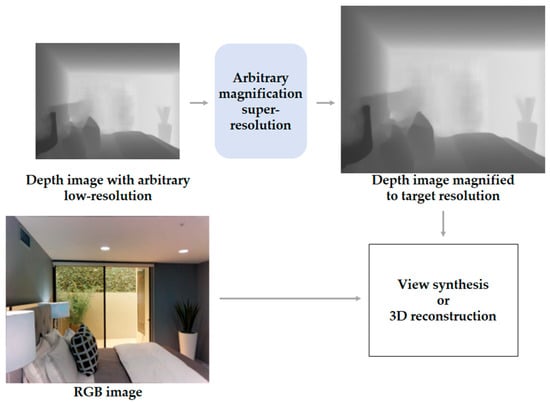
Figure 4. Example application of arbitrary magnification super-resolution in camera sensor depth image processing task.

Lee et al. [1] presented a high character recognition accuracy via integer magnification super-resolution in low-resolution conditions. However, in the real world, detected object areas may have arbitrary resolutions depending on the distance between the camera and the subject, as shown in Figure 5. It is mentioned that applying an arbitrary magnification in low-resolution conditions would provide a higher character recognition performance than applying bicubic interpolation.

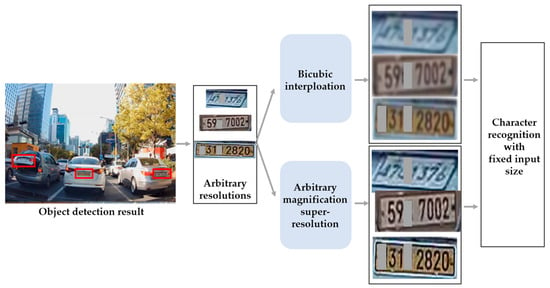
Figure 5. Example application of arbitrary magnification super-resolution in license plate character recognition task. One or two characters were masked due to privacy policies.

The above studies proposed arbitrary magnification super-resolution models to solve the limit of integer magnification and suggested the application of arbitrary magnification super-resolution. These studies also indicate that the arbitrary magnification super-resolution works well for the object recognition task, medical image processing, satellite image processing, depth image processing, and character recognition task. In conclusion, we note that arbitrary magnification super-resolution is required for various real-world tasks.

3. Proposed Method

This section describes the method proposed in this study for an arbitrary magnification super-resolution. In Section 3.1, the DCT overview is first described, the proposed hybrid-domain high-frequency attention network is described in Section 3.2, and the loss function defined in this network is described in Section 3.3.

3.1. Discrete Cosine Transform (DCT)

A spatial domain signal can be transformed into a spectral domain signal, and the converse also holds through. The most commonly used transform for this procedure is the discrete Fourier transform (DFT). In DFT, even if the input signal is a real number, the conversion result includes a complex number. A complex number can be calculated, but computational overhead is an issue. Therefore, DCT, which decomposes a signal into a cosine function and produces only real values from its spectral representation, is widely used in low-cost devices. A two-dimensional spatial domain discrete signal input of size N × M can be expressed in the frequency domain through DCT as given below.

$$F(u,v)=\alpha (u)\beta (v){\displaystyle \sum _{x=0}^N{\displaystyle \sum _{y=0}^{M}f(x,y)\gamma (x,y,u,v)}}$$

(1)

$$\gamma (x,y,u,v)=\cos (\frac{\mathsf{\pi }(2x+1)u}{2N})\cos (\frac{\mathsf{\pi }(2y+1)v}{2M})$$

(2)

$$\alpha (u)=\{\begin{array}{l}\sqrt{\frac{1}{N}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u=\hspace{0.17em}0\\ \sqrt{\frac{2}{N}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u\hspace{0.17em}\ne \hspace{0.17em}0\end{array}$$

(3)

$$\beta (v)=\{\begin{array}{l}\sqrt{\frac{1}{M}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}v=\hspace{0.17em}0\\ \sqrt{\frac{2}{M}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}v\hspace{0.17em}\ne \hspace{0.17em}0\end{array}$$

(4)

$$f(x,y)={\displaystyle \sum _{u=0}^N{\displaystyle \sum _{v=0}^M\alpha (u)\beta (v)F(u,v)\gamma (x,y,u,v)}}$$

(5)

In Equation (1), $f$$\left(x,y\right)$ is the pixel value of the $\left(x,y\right)$ position of the input image, and $F$$\left(u,v\right)$ is the DCT coefficient value at the $\left(u,v\right)$ position. Equations (2)–(4) show the definitions of the cosine basis function and regularization constant, respectively. In contrast, the signal transformed into the frequency domain can be transformed into the spatial domain using a two-dimensional inverse DCT (IDCT), as shown in Equation (5). Figure 6a shows a sample image and the results of the two-dimensional DCT on the image. It is easy to observe the frequency information of various components, although not intuitively because of the deformation of the spatial structure. Figure 6b shows the 64 8 × 8 cosine basis functions. After expanding the image space in the DCT spectrum domain, IDCT can be performed to generate the resulting image with the target size. In this case, when expanding the DCT spectrum, the image may be extended in the upper-left or lower-right direction. Because many low-frequency components are concentrated in the upper-left direction and high-frequency components are concentrated in the lower-right direction, depending on the area to be enlarged, the image has insufficient frequency information. The goal of image super-resolution is to improve a blurry image into a sharp image, which can be seen as restoring the high-frequency components that make the image sharp. In this study, we propose a hybrid-domain high-frequency attention network for arbitrary magnification super-resolution (H²A²-SR). First, we expand the image in the DCT spectrum domain to the target magnification. Second, frequency bands are divided according to hyperparameters to extract the high-frequency components. Finally, the high-frequency attention network restores the lost high-frequency.

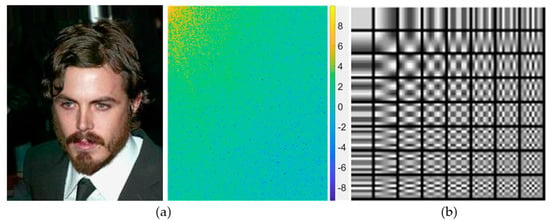
Figure 6. (a) 2D DCT example; (b) 8 × 8 cosine basis functions.

3.2. Hybrid-Domain High-Frequency Attention Network

In this section, the H²A²-SR framework is described. The architecture of the proposed model is shown in Figure 7. The low-resolution image received as input is magnified by an integer magnification close to the target magnification through the integer super-resolution network. For example, when the target magnification is ×2.5, the integer magnification network performs ×2 magnification, and when the target magnification is ×3.5, ×3 magnification is performed. The image magnified by an integer magnification was converted from the spatial domain to the spectral domain through DCT. We use the characteristics of DCT, in which the low-frequency in the upper left and the high frequency in the lower-right direction are concentrated and expand the spatial area by the residual decimal magnification in the lower-right direction. According to the principle that the spatial domain extended in the DCT spectrum has the same spatial size in the spatial domain, the resultant image adjusted to the target magnification can be obtained when it is re-converted to the spatial domain through IDCT. Because the high-frequency region is arbitrarily expanded, the image acquired through this process lacks high-frequency components. DCT follows the principle of energy conservation. When the image is expanded or reduced in the DCT domain, the brightness of the image is restored by multiplying it by the corresponding coefficient value. However, there is still a lack of high-frequency components. To overcome this problem, we designed a model that focuses on the accurate reconstruction of high-frequency components. The high-frequency attention network uses a channel attention layer that can learn the correlation between RGB channels to create high-frequency information and deepens the model through the residual learning structure. As shown in Figure 8, a block unit channel attention called the residual channel attention block (RCAB) [6] is configured. The proposed model is constructed by stacking five RCABs in layers, and residual learning is applied to each block to determine the correlation between each block.

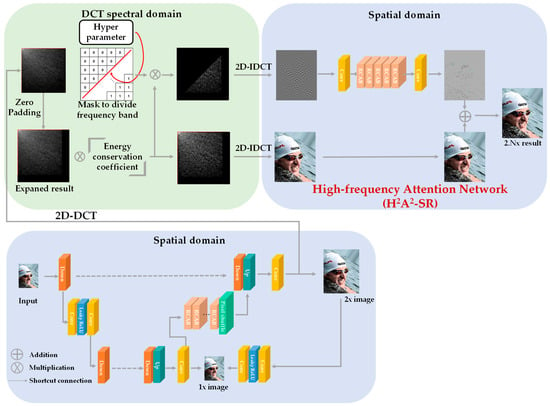
Figure 7. Overall organization of the proposed H²A²-SR model.

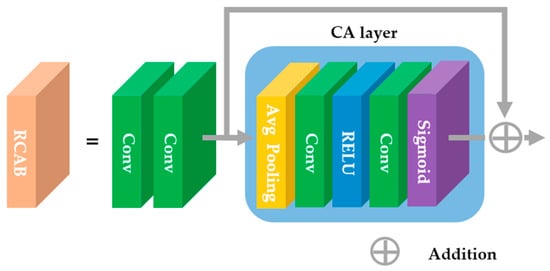
Figure 8. Configuration of RCAB [6] structure.

To focus the network on high-frequency reconstruction, we extract high frequencies by dividing the frequency domain according to the hyperparameters in the DCT domain. As shown in Figure 9a, $D$ denotes the index of the zig-zag scan for 10 × 10 pixels. If the hyperparameter $\lambda$ is set to 15, it is possible to extract high-frequency components except for components up to 15, as shown in Figure 9b. To this end, we determine a mask $\mathcal{M}$ by using $\lambda$ as

$$\mathcal{M}\left(x,y\right)=\{\begin{array}{c}0, D\left(x,y\right) \le \lambda \\ 1, \mathrm{otherwise}\end{array}$$

(6)

where $x$ and $y$ denote horizontal and vertical coordinates, respectively.

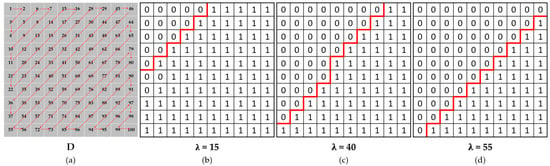
Figure 9. (a) Index of zig-zag scan for 10 × 10 pixels. (b) A mask obtained from the hyperparameter $\lambda$ of 15. (c) A mask obtained from the hyperparameter $\lambda$ of 40. (d) A mask obtained from the hyperparameter $\lambda$ of 55.

Then, an image constructed with the extracted high-frequency components is passed through the network. In addition, to focus the network on high-frequency reconstructions, an expanded image with many low-frequency components is added to the result. The overall procedure of the proposed algorithm is also given in Algorithm 1. We note that the main contribution of our proposed method is not using RCAB but using high-frequency images obtained in the DCT domain as inputs to pass through the high-frequency attention network. In the existing arbitrary magnification method, the computation cost and the capacity of the model increase by passing the super-resolution neural network after magnification to the target magnification through the bicubic interpolation method. In addition, in actual use cases, all super-resolution networks must be trained at each arbitrary magnification and, therefore, require a large capacity of memory. In contrast, our model preserves the integer magnification performance by preserving its weight as it is and can achieve high-performance arbitrary magnification by adding a relatively small capacity network. In addition, unlike conventional methods of restoring the entire frequency band of an image at once, better performance can be achieved by intensively restoring a target high-frequency component.

Algorithm 1 H2A2-SR model

INPUT: low-resolution image (L), target magnification factor (s). OUTPUT: arbitrary magnification image result (O). Step 1: Obtain integer magnification image (I) from L by using the baseline SR model. Step 2: Transform I into the DCT domain. Step 3: Expand to residual decimal magnification (r = s/(s – floor(s))) in the DCT domain. Step 4: Multiply the energy conservation factor (r2) to the expanded image (E). Step 5: Generate a mask (M) according to Equation (6). Step 6: Multiply E and M for high-frequency (H) extraction. Step 7: Convert E and H into the spatial domain through IDCT. Step 8: Make H into 64 channels through the conv layer. Step 9: Recover high-frequency (Hr) through 64 channels and 5 RCAB layers. Step 10: Make Hr into 3 channels through the conv layer. Step 11: Obtain O by adding E and the attention network’s result.

3.3. Loss Function for High-Frequency Attention Network

In the proposed model, a loss function is $L$ defined as in Equation (7) to restore the high-frequency component in the region extended by the DCT.

$$L=\frac{1}{N}{\Vert F_{H^2{A}^2-SR}(F_{SR}(x^{lr}))-x^{hr}\Vert }^2$$

(7)

where $N$ denotes the image batch size, $F_{sr}(x^{lr})$ denotes a model that enlarges a low-resolution image by an integer magnification through a super-resolution network, and $F_{H^2{A}^2-SR}$ denotes a residual decimal magnification model. A loss function for network learning is calculated using the mean square error between the arbitrary magnification super-resolution model results and the corresponding high-resolution image.

4. Experimental Results

4.1. Network Training

In traditional super-resolution learning, each patch unit is obtained from a low-resolution image, i.e., an input image, and a high-resolution image, i.e., a target image, and it is learned through comparison. For example, with respect to a 60 × 60 high-resolution patch, in the ×2 magnification model, a low-resolution input patch of 30 × 30 size was used, and network training was performed. However, performing an arbitrary magnification is an issue. If a pixel value is a decimal when performing an arbitrary magnification, a pixel shift phenomenon occurs as the decimal value is discarded from the image. Therefore, we have to cut the high-resolution image according to the arbitrary magnification and construct the low-resolution image individually. Because this is very time-consuming, we used the torch.nnf.interpolate function from Pytorch 1.8.0, an open-source machine learning library in Python, to create low-resolution images inside the code. We used PyTorch 1.8.0 to implement our model and use python 3.8.8, CUDA 11.2, and cuDNN 8.2.0. In addition, 2D-DCT and 2D-IDCT were implemented using the built-in functions of torch.fft.rfft and torch.fft.irfft, respectively. Our experiment was performed with AMD Ryzen 5 5600X 6-Core Processor CPU, 32GB memory, and NVIDIA RTX 3070 GPU. Our model was trained by Adam optimizer with ${\beta }_1=0.9$, ${\beta }_2=0.999$. ${\beta }_1$, ${\beta }_2$ denote exponential decay rates of the estimated moments, as the previous value is successively multiplied by the value less than 1 in each iteration. We set the training batch size to 16, the number of epochs to 200, and the learning rate to 10⁻⁴. Note that the optimized values were determined experimentally.

4.2. Performance Comparison of Meta-SR and the Proposed Method

In this section, we compare the performance of the proposed H²A²-SR with Meta-SR, a model that can arbitrarily magnify images. Since Meta-SR can perform arbitrary magnification with a single weight, Meta-SR does not require training for each magnification factor. However, Meta-SR has limitations in image restoration performance because this method does not use a specialized weighting model according to the magnification factor. We note that there is a trade-off between weight capacity and image restoration performance. By focusing on improving image restoration performance, individual training for each magnification factor can be considered so that arbitrary magnification super-resolution models provide the optimized image restoration performance. Therefore, we trained the Meta-SR network and H²A²-SR for each magnification factor. We denote the Meta-SR network trained for each magnification factor as Meta-SR*. In addition, the results of the original Meta-SR that have a single weight are presented in Table 4 to compare it with H²A²-SR. Since a model that proceeds with integer magnification is required for an arbitrary magnification model, in this study, DRN is learned for ×2 and ×3 magnifications and used as an integer magnification model. The peak signal-to-noise ratio (PSNR) of the DRN ×2 model was 35.87 dB, and the PSNR of the DRN ×3 model was 32.22 dB. CelebA [27] was used as the dataset, with 40,920 and 5060 samples for training and validation, respectively. While Meta-SR selects pixel values according to the appropriate size for an arbitrary magnification from an image enlarged by an integer multiple, H²A²-SR concentrates the purpose of high-frequency restoration on the network to further enhance the edges and textures related to high-frequency components. It can be seen from the images in Figure 10 that the proposed model performs well on the dataset. We additionally present the expanded results in DCT to provide step-wise results of our method, as shown in Figure 10. It can be seen that H²A²-SR has less image noise than any other arbitrary magnification model. As shown in the enlarged image in Figure 10, the proposed model is restoring the eye area such as the eyelid, iris, and pupil more clearly. In addition, in the quantitative evaluation, H²A²-SR showed a higher PSNR value and a higher SSIM value than the existing method, as shown in Table 4. The inference time of our model was measured from ×2 to 19 ms and ×3 to 23 ms. The size of the image passed through the model is 178 × 218, and the input is an image reduced according to the corresponding magnification. At this time, the high-resolution image was cropped by 1 to 2 pixels depending on the scale.

Table 4. Comparison of the quantitative quality arbitrary super-resolution models in terms of PSNR (dB) and SSIM.

	PSNR (dB)/SSIM on CelebA with Arbitrary Scale Factors
Method	Metric	×2.2	×2.5	×2.8	×3.2	×3.5	×3.8
DRN + Meta-SR	PSNR SSIM	29.02 0.7268	31.37 0.7665	31.33 0.7696	27.51 0.6494	28.14 0.6533	28.00 0.6437
DRN + Meta-SR*	PSNR SSIM	33.80 0.8462	32.91 0.8142	31.80 0.7787	31.94 0.7618	31.41 0.7487	30.20 0.7024
DRN + H2A2-SR (ours)	PSNR SSIM	35.23 0.8766	33.98 0.8476	32.98 0.8201	32.22 0.7978	31.52 0.7788	30.77 0.7543

Meta-SR* denotes the Meta-SR network trained for each magnification factor. The bold represents the best scores.

Figure 10. Comparison between our H²A²-SR results and Meta-SR results: (a) bicubic results; (b) DRN + Meta-SR results; (c) DRN + Meta-SR* results; (d) DRN + expanded results in DCT; (e) DRN + H²A²-SR results; (f) high-resolution image.

4.3. Performance Comparison of the Existing Arbitrary Magnification Method and the Proposed Method

For additional performance comparison with the existing arbitrary magnification methods, the experiment was conducted using the training dataset and the test dataset used in the existing arbitrary magnification method [17], as in the proposed method. The proposed network was trained using the DIV2K [28] dataset, and B100 [29] was used as the dataset for testing the trained model. To generate arbitrary magnification input images, it was reduced using bicubic interpolation n of torch.nnf for each arbitrary magnification. To compare with the existing state-of-the-art network capable of integer magnification, the input image was expanded to bicubic for decimal magnification, and the image for each arbitrary magnification was passed through our model without any modifications. For the arbitrary magnification model, the RDN model was set as the base model for an equal comparison. The PSNR of the RDN ×2 model is 31.22 dB, and the PSNR of the RDN ×3 model is 27.49 dB. The base model freezes training when learning arbitrary magnification weights. For reference, SRWarp could not be tested because the source code for the arbitrary magnification test is not currently available. Because there is no other arbitrary magnification model, we magnified the low-resolution image as an input to the state-of-the-art model in a bicubic format to match the magnification and used it as an input value. The PSNR of the HAN [30] ×2 model is 31.39 dB, and the PSNR of the HAN ×3 model is 27.70 dB. The PSNR of the SwinIR [14] ×2 model is 32.45 dB, and the PSNR of the SwinIR ×3 model is 29.39 dB. The PSNR of the CSNLN [16] ×2 model is 32.40 dB, and the PSNR of the CSNLN ×3 model is 29.34 dB. As can be seen in Table 5, even a small range in the image, such as ×2.2 and ×3.2 magnifications, is expanded, but the PSNR value is greatly lost. However, our proposed model is robust against scaling for decimal magnification, so it shows an advantage of approximately 1.5 dB in terms of average PSNR and 0.1013 in terms of average SSIM. Figure 11 also shows the comparison of the subjective visual quality on B100 for different scale factors. In Figure 11, red arrows were used to emphasize the improved part. We note in the figure that the proposed model outperforms the existing algorithms in many edge regions such as the whiskers, the window, the tree, and the statue.

Table 5. Quantitative comparison of the state-of-the-art SR methods.

	PSNR (dB)/SSIM on B100 with Arbitrary Scale Factors
Method	Metric	×2.2	×2.5	x2.8	×3.2	×3.5	×3.8
RDN + bicubic	PSNR SSIM	27.34 0.8087	26.87 0.7849	26.25 0.7586	25.88 0.7086	25.33 0.6906	24.86 0.6728
HAN + bicubic	PSNR SSIM	28.39 0.8180	27.42 0.7852	26.51 0.7563	25.88 0.7102	25.26 0.6914	24.77 0.6731
CSNLN + bicubic	PSNR SSIM	29.52 0.8471	28.21 0.8072	26.28 0.7221	24.89 0.6739	24.377 0.6639	24.28 0.6543
SwinIR + bicubic	PSNR SSIM	28.50 0.8162	27.28 0.7954	26.75 0.7866	25.86 0.6973	25.40 0.6961	24.47 0.6639
RDN + Meta-SR*	PSNR SSIM	28.51 0.8262	28.19 0.8063	27.41 0.7801	27.01 0.7530	26.50 0.7315	25.95 0.7075
RDN + H2A2-SR	PSNR SSIM	29.52 0.8473	28.31 0.8097	27.63 0.7819	27.34 0.7638	26.81 0.7433	26.32 0.7237

Meta-SR* denotes the Meta-SR network trained for each magnification factor. The bold represents the best scores.

Figure 11. Super-resolution reconstruction results: (a) bicubic results; (b) RDN results; (c) HAN results; (d) SwinIR results; (e) CSNLN results; (f) RDN + META-SR results; (g) RDN + H²A²-SR results; (h) high-resolution images.

4.4. Ablation Study

For the ablation study, we compare the network with H²A²-SR and without H²A²-SR. In Table 6, it can be seen H²A²-SR is effective as much as 4.5 dB and as low as 0.6 dB. In Figure 12, the results are numbered step-by-step inside the model for a better understanding. Figure 13 shows the results of the step-by-step images. Step 1 refers to an image using the base SR model for integer magnification. Step 2 is the result of multiplying the integer magnification image by the energy conservation factor after extending it to the target magnification in the DCT spectral domain. In the Step 2 image of Figure 13, it can be seen that the image is well expanded to the target magnification by multiplying the energy conservation coefficient. However, it can also be seen that the expression of textures or lines, which are high-frequency components, is insufficient owing to excessive expansion. Step 3 extracts high-frequency components from the result of step 2 with a mask generated through a hyperparameter. Step 4 is the result of the high-frequency components extracted in Step 3 through the high-frequency attention network. As shown in the Step 4 image of Figure 13, it can be seen that our network effectively reconstructs the high-frequency components of lines and textures well. In Step 5, by adding the results of Steps 4 and 2, the model is used to reconstruct the high-frequency component well. It can be seen that the jagged between the swimming cap and the face is eliminated, and the arbitrary magnification is clear by effectively removing the noise around the logo of the swimming cap. It can be seen that our H²A²-SR is effective not only at arbitrary magnification but also in making the image clearer by restoring high-frequency components well.

Table 6. Quantitative comparison between our H²A²-SR with and without high-frequency attention model.

PSNR (dB) on CelebA with Arbitrary Scale Factors
Method	Metric	×2.2	×2.5	×2.8	×3.2	×3.5	×3.8
Without high-frequency attention model	PSNR	30.89	29.62	28.48	31.73	30.90	30.15
DRN + H2A2-SR (ours)	PSNR	35.23	33.98	32.98	32.22	31.52	30.77

The bold represents the best scores.

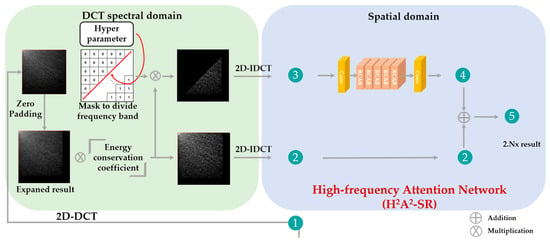
Figure 12. Flowchart of H²A²-SR’s steps. Each number represents a step in H²A²-SR.

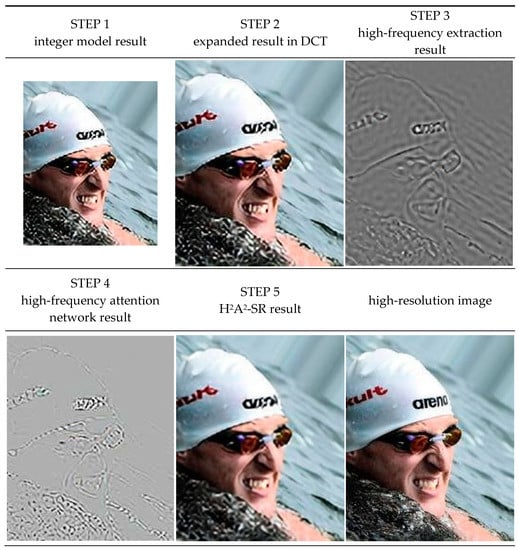
Figure 13. Result examples of H²A²-SR’s steps.

Meanwhile, our method may have limitations. First, since our model is an add-on algorithm, it depends on the performance of the adopted integer super-resolution model. Therefore, it is important to adopt the appropriate integer super-resolution model. Second, our H²A²-SR model requires the training process for each magnification to obtain better image restoration performance. Therefore, our model needs memory capacity for storing weights for each decimal magnification factor in practical applications. We note that there is a trade-off between weight capacity and image restoration performance. To address this trade-off issue, optimization techniques such as network weight compression or weight sharing can be further applied.

5. Conclusions

In this paper, we propose an arbitrary magnification super-resolution method to reconstruct high-frequency components using spatial and spectral hybrid domains. Through spatial expansion in the DCT spectral domain, an image can be flexibly expanded to a target resolution, and it is restored through a high-frequency attention network that supplements the insufficient high-frequency components of the expanded image. Thus, the accuracy of the existing integer magnification super-resolution model is preserved even at arbitrary magnification, and high-performance decimal magnification results can be obtained by adding the proposed arbitrary magnification model without modifying or re-learning the existing model. Experimental results show that the proposed method has excellent restoration performance, both quantitatively and qualitatively, compared to the existing arbitrary magnification super-resolution methods. As a future study, it will be possible to lighten the network by appropriately combining the weight sharing method between integer multipliers and the knowledge distillation technique. In addition, research to improve the object recognition rate for low-resolution images by integrating an arbitrary magnification super-resolution network and an object recognition network can be conducted.