Image Reconstruction with Multiscale Interest Points Based on a Conditional Generative Adversarial Network

Abstract

A new image reconstruction (IR) algorithm from multiscale interest points in the discrete wavelet transform (DWT) domain was proposed based on a modified conditional generative adversarial network (CGAN). The proposed IR-DWT-CGAN model generally integrated a DWT module, an interest point extraction module, an inverse DWT module, and a CGAN. First, the image was transformed using the DWT to provide multi-resolution wavelet analysis. Then, the multiscale maxima points were treated as interest points and extracted in the DWT domain. The generator was a U-net structure to reconstruct the original image from a very coarse version of the image obtained from the inverse DWT of the interest points. The discriminator network was a fully convolutional network, which was used to distinguish the restored image from the real one. The experimental results on three public datasets showed that the proposed IR-DWT-CGAN model had an average increase of 2.9% in the mean structural similarity, an average decrease of 39.6% in the relative dimensionless global error in synthesis, and an average decrease of 48% in the root-mean-square error compared with several other state-of-the-art methods. Therefore, the proposed IR-DWT-CGAN model is feasible and effective for image reconstruction with multiscale interest points.

1. Introduction

Image reconstruction (IR) has always been a research focus in image processing. Specifically, the IR from singular points or interest points, such as maxima, zero crossing, contour, or edge points in a multiscale transform domain, is of paramount importance. Early in 1992, Mallat et al. stated that singularities and irregular structures often carry the most important information in one- and two-dimensional signals [1]. As an application, Mallat developed an alternating projection algorithm to reconstruct an image from the local modulus maxima of its wavelet transform. In 2013, Maji et al. found that major information in an image is encoded in its edge points, which is also supported by neurophysics [2]. Maji concluded that an image can be accurately reconstructed from the compact representation of its edge pixels. In 2018, Soulard and Carré designed a new color IR algorithm based on monogenic features that appeared to be extremely good at preserving contours and color information [3]. It is likely to reconstruct a color image only with the monogenic maxima features. Several image reconstruction experiments were conducted to recover a close approximation of the original image. Recently, in our previous work in 2021, Liu et al. proposed an IR algorithm from multiscale interest points in the dual-tree complex wavelet transform (DT-CWT) domain [4]. The accurate multiscale interest points were detected in the DT-CWT domain due to the shift invariance and directional selectivity properties of the DT-CWT coefficients. The images were then reconstructed from the phases and the magnitudes of the multiscale interest points by alternating orthogonal projections between the CT-DWT space and its affine space.

The traditional IR methods mentioned above are effective and achieved good results; however, they also have some shortcomings. For example, a large number of iterations and a long execution time are involved in the IR algorithms. To overcome the shortcomings of the traditional IR methods while ensuring high performance, a neural network was introduced for the IR [5]. Inspired by the outstanding performance of a convolutional neural network (CNN) in extracting signal features, Xiao et al. proposed an excellent CNN approach for brightness temperature IR mirrored aperture synthesis (MAS) [6], where a deep CNN for learning the MAS IR mapping and system errors was employed to improve the brightness temperature IR. In 2020, Jeyaraj et al. proposed a deep learning model from the AlexNet architecture for the estimation and reconstruction of highly complex features from medical images [7]. To alleviate the computational complexity, Antholzer et al. developed an efficient and direct IR framework based on deep learning, where the conventional iterative IR algorithms were replaced by a CNN [8]. Gan et al. proposed an unsupervised deep registration-augmented reconstruction method (U-Dream) to train a DNN framework to reconstruct high-quality images by directly mapping pairs of unregistered and artifact-corrupted images [9]. U-Dream was widely applicable to many biomedical IR tasks due to it not requiring registered data.

There are many recent works concerning IR problems [10,11], such as positron microscopy [12], lensless imaging [13], MR imaging [14,15], low-dose CT [16], photoacoustic [17,18] and ultrasound [19], and compressed sensing [20].

Although there has been much progress in traditional IR algorithms regarding particular interest points, the previous studies mainly focused on IR based on both high- and low-frequency information of the original image, such as detail coefficients and low-frequency band coefficients in the DWT domain, leading to either non-desirable performance for lossy IR or computationally expensive iterative processes.

Therefore, a new IR method [21] for an image’s multiscale interest points extracted in the DWT domain was proposed with a conditional generative adversarial network (CGAN). Specifically the maxima points in the DWT domain were treated as the interest points. The proposed IR model is called the IR-DWT-CGAN. First, the image is transformed by DWT to provide a multi-resolution image representation in the DCT domain. Then, the multiscale maxima points are extracted in the DWT domain. With a U-net structured generator [22], the original image is restored from a very coarse version of the image (also referred to as the multiscale points feature map) obtained from the inverse DWT of the interest points. The restored image is distinguished from the real image with a fully convolutional network, i.e., a discriminator network.

The main contributions of our proposed algorithm are as follows.

(1)

Based on the corresponding magnitudes of the wavelet coefficients, multiscale interest points were obtained with the proposed interest points (i.e., maxima) extraction module. A new dataset was built by compositing natural images and their interest point maps.

(2)

Based on the CGAN, a new and efficient IR model using multiscale interest points, i.e., IR-DWT-CGAN, was proposed. The generative network (generator) has a U-net-like structure, while the discriminator focuses on discriminating the reconstructed image from the corresponding real counterpart. The IR-DWT-CGAN was conditioned on a very coarse version of the reconstructed image based on the inverse DWT of the corresponding wavelet maxima map.

(3)

The proposed IR-DWT-CGAN outperformed some traditional IR algorithms in terms of both the reconstruction image quality and time consumption.

The rest of this paper is organized as follows. In Section 2, the relevant work and some fundamentals are reviewed, and some quantitative metrics are given. In Section 3, the proposed IR-DWT-CGAN framework is detailed. In Section 4, simulation results and analysis are provided. Finally, a brief conclusion is reached in Section 5.

2. Related Work

2.1. Discrete Wavelet Transform

Wavelet transform (WT) is based on small waves, i.e., wavelets, of varying frequencies and limited durations. This makes the WT suitable for analyzing irregular data patterns, such as impulses occurring at various instances. The WT maps a function of continuous variables into a sequence of coefficients. If a function itself is a discrete signal, the resulting coefficients are called the discrete wavelet transform (DWT) of the function. The DWT has received considerable attention in various signal processing applications. Each wavelet transform has a wavelet function, which we call the mother wavelet, and a scaling function, which is the father wavelet. The basis functions of the wavelet are actually formed via scaling and translation of the mother wavelet and the father wavelet. The DWT has advantages such as the similarity of data structure in terms of the resolution and available decomposition at any level. It can be implemented as a multiscale transform. At any level in the DWT domain, an image is decomposed into four sub-bands denoted as LL, LH, HL, and HH, where LH, HL, and HH are called the detail components, representing the finest scale wavelet coefficients, and LL is called the approximate component, standing for the coarse-level coefficients.

In this study, a three-level DWT was implemented in Matlab 2016b (Jack L.; Cleve M. Natick, MA, USA), with the mother wavelet used in [1], which was equal to the first-order derivative of a smoothing function.

2.2. Generative Adversarial Networks

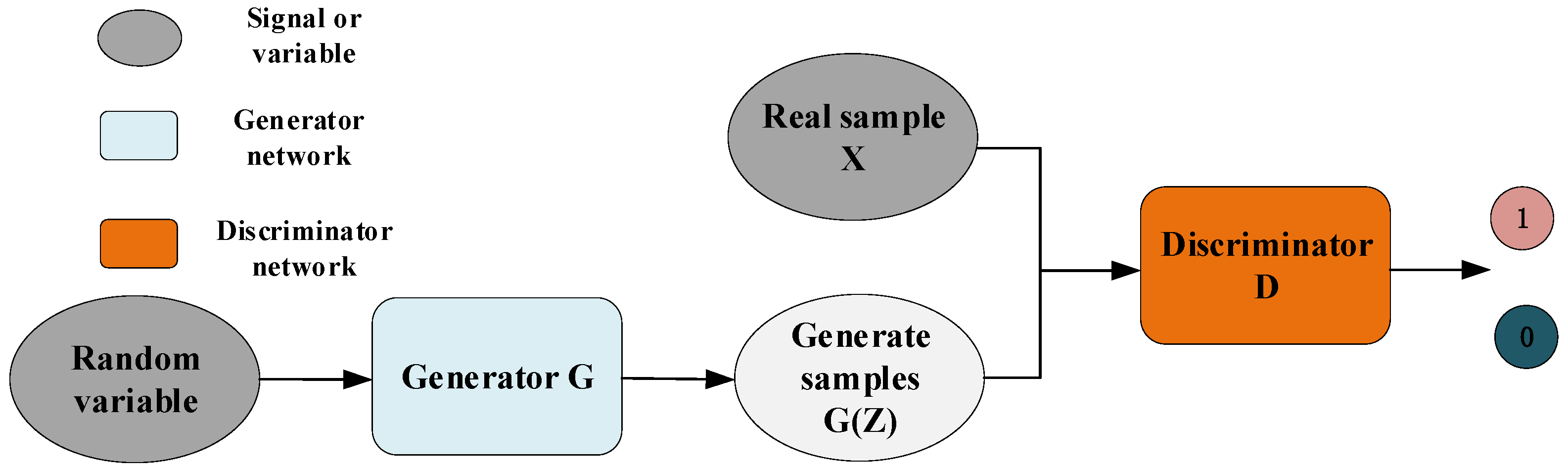
The generative adversarial network was proposed by Goodfellow et al. [23] in 2014. Based on the idea of game theory, the GAN realizes the learning and fitting of the network to the target sample data distribution through the countermeasure process. At present, the GAN has been successfully applied to many fields, such as handwritten font generation [24], image preprocessing [25], data enhancement [26], and IR [27]. Generally, a GAN consists of a generator unit G and a discriminator unit D. The GAN structure is shown in Figure 1.

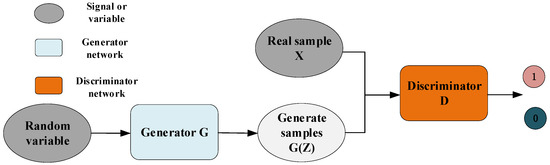
Figure 1. GAN structure.

The goal of generator G is to learn the data distribution of the target threshold samples to better generate sample data similar to the target threshold samples; the goal of the discriminator D is to distinguish the source of the input sample accurately, that is, whether the input sample is from the real sample data or the sample data generated by the generator G. The GAN is usually constructed using a multi-layer perceptron or deep neural network to achieve better feature learning and sample fitting ability. The specific implementation process of the whole network is as follows: the generator G receives the random variable Z and generates a sample G(Z) with this random variable, while the discriminator D receives both the real sample X and the generated sample G(Z). After the discrimination, it outputs the probability that the sample is a true sample. Under ideal conditions, the generator can accurately learn the data distribution of target threshold samples and generate the sample data, which can confuse the false data with the true data. In the end, the discriminator D is unable to distinguish the real samples from the generated ones correctly, and the whole network reaches the state of a Nash equilibrium.

2.3. Image Reconstruction Based on Multiscale Interest Points

The IR with multiscale local maxima in the DWT domain and the dual-tree complex wavelet transform (DT-CWT) domain were studied in [1,4]. Mallat studied the properties of multiscale edge points in the DWT domain and proposed an algorithm to reconstruct a close approximation of images from their multiscale edge points [1]. The image reconstruction errors were below human visual sensitivity and could thus be neglected in many image processing or computer vision tasks. Liu proposed a novel IR algorithm from singular (local maxima) points in the DT-CWT domain by taking advantage of the shift invariance and directional selectivity of the DT-CWT coefficients [4]. Liu’s IR algorithm outperforms some typical IR algorithms in terms of several performance metrics, such as the peak signal-to-noise ratio and structural similarity.

2.4. Image Reconstruction Based on Deep Learning

In recent years, deep learning has been playing an important role in IR. In 2022, Xiao [6] proposed a deep-learning-based method for the mirrored aperture synthesis IR in which the mirrored aperture synthesis IR mapping and system errors were learned by a deep CNN framework. In 2020, by consolidating the needed high-level features from a deep CNN system, an effective deformable IR algorithm was designed to achieve a better mean square error, structural similarity index, and high-frequency error norm [7].

3. The Proposed IR-DWT-CGAN Model

3.1. IR-DWT-CGAN Architecture

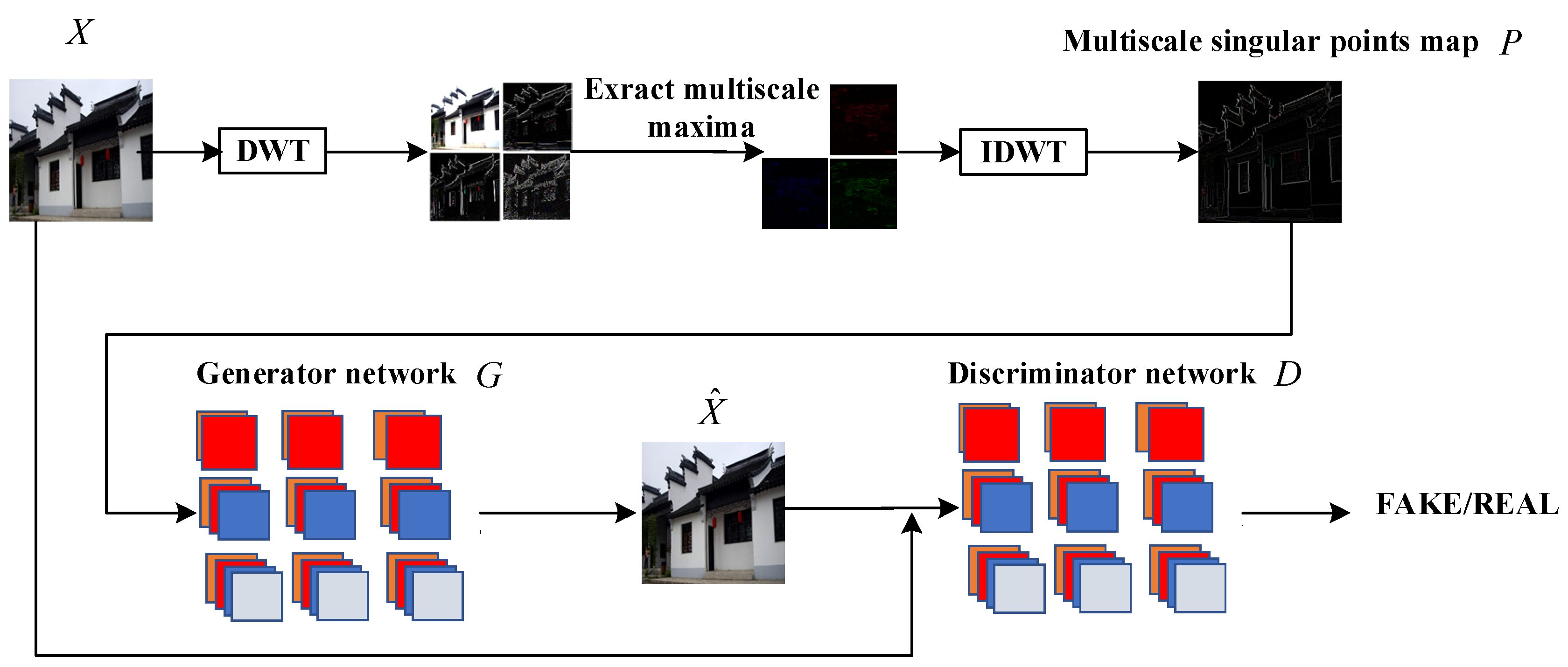
Based on the GAN, the overall architecture of the proposed IR-DWT-CGAN model was designed, as shown in Figure 2. An image was transformed into the DWT domain using a discrete wavelet transform, and the maximal points in the DWT domain were chosen as interest points for performing an inverse DWT to obtain a very coarse version of the image, which is called the multiscale points feature map. The multiscale points feature map, whose dimension is the same as the original image, is the input of the generator network. Based on the multiscale points feature map, the generator reconstructs the original image in such a way that the reconstructed image is as close as possible to the original image. The goal of the discriminator is to correctly distinguish the reconstructed image recovered with the generator from the real image. At the end of the network training, the generator was well trained enough to make it almost impossible for the discriminator to distinguish the restored image from the real one.

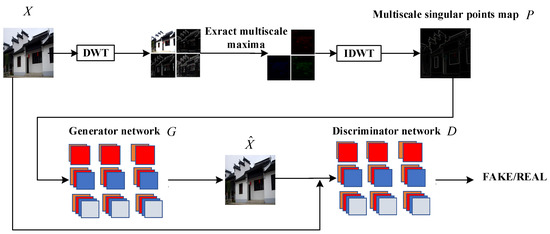
Figure 2. MSCGAN architecture.

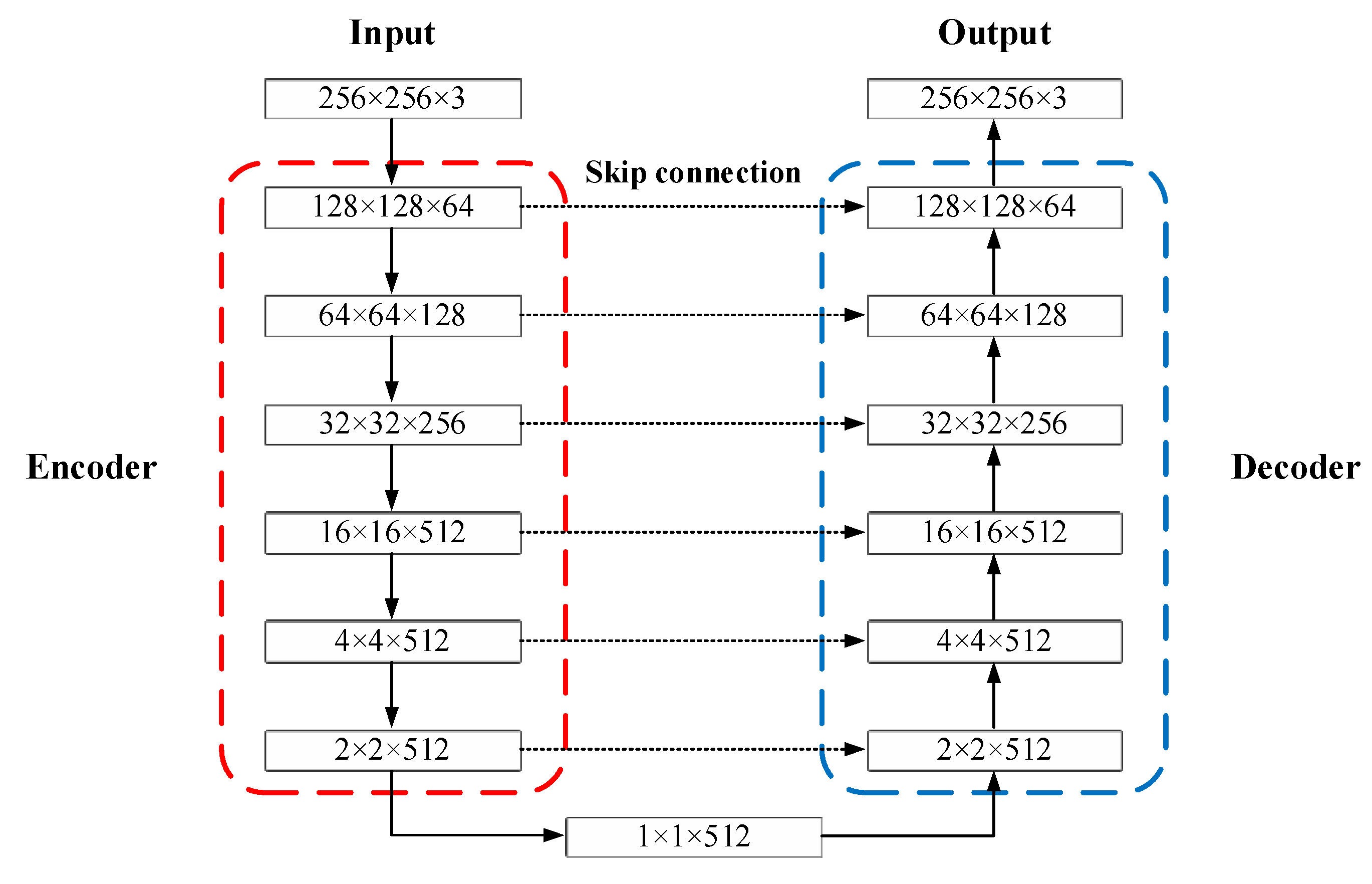
3.2. Proposed Generator Network

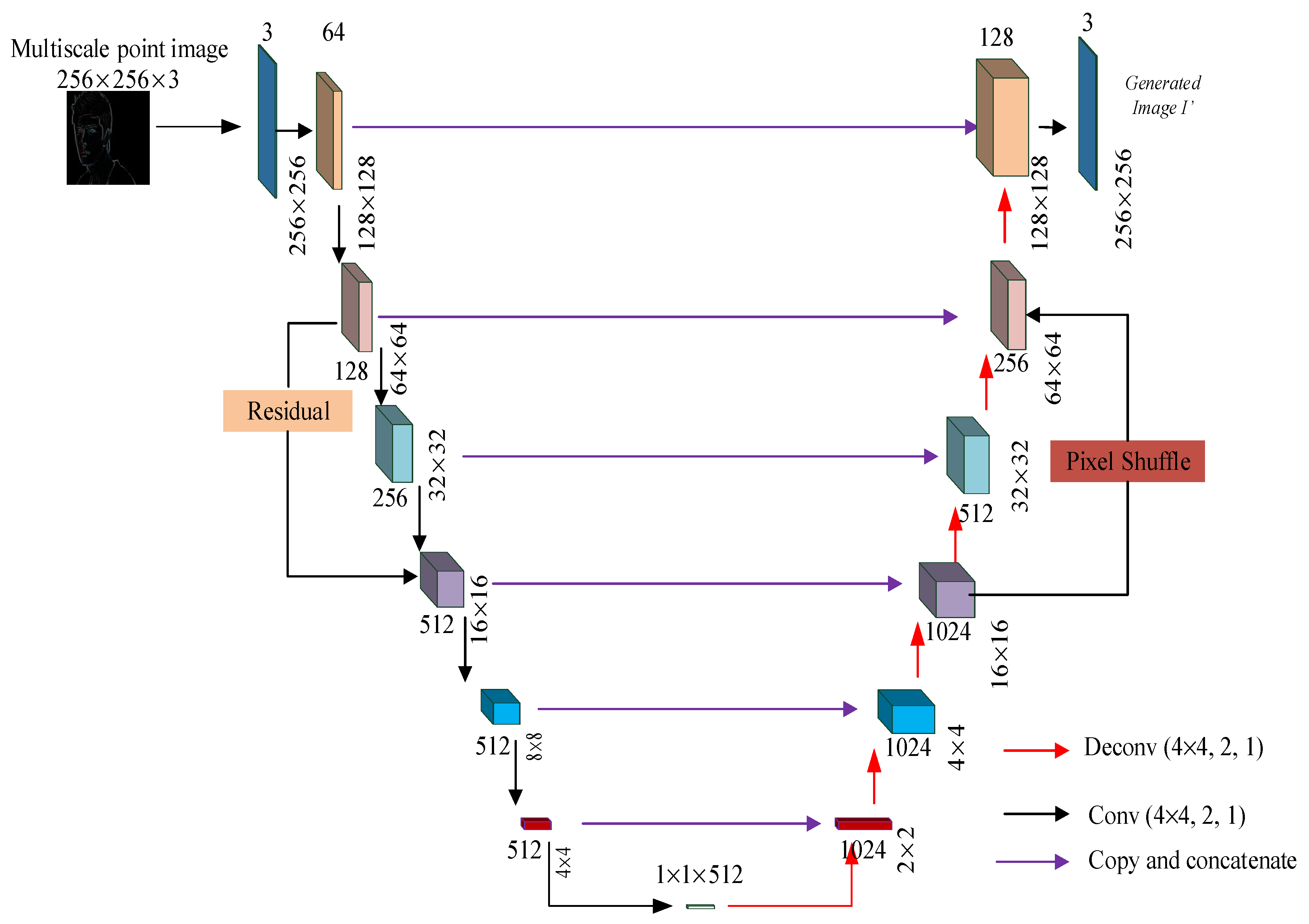
The goal of the generator is to reconstruct a high-quality image directly from the multiscale points feature map. Therefore, the details of the original image should be restored to the multiscale local maxima. The generator should be able to connect the features of different feature layers in the generator network effectively, maximize the information flow transmission from the shallow network to the deep network, and enhance the repeatability of the features. The structure of the proposed generator network is shown in Figure 3.

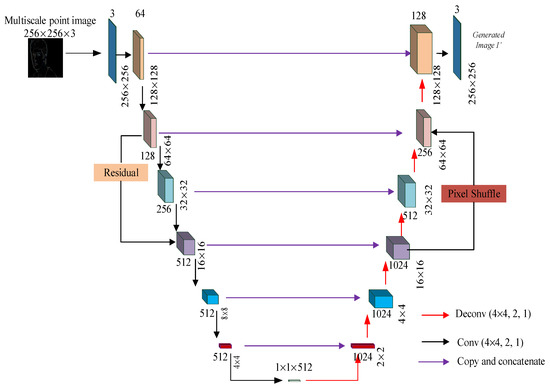
Figure 3. Proposed generator network.

The proposed IR-DWT-CGAN generator part consists of two parts: the left encoder part and the right decoder part. Assuming that the three wavelet transform coefficient bands HL, LH, and HH of the input image (X) are extracted from the multiscale maxima combined into an overall feature array and denoted as H, then the multiscale feature map P of interest points is obtained using an inverse wavelet transform. The feature maps image P is input into the left encoder part of the generator network; after three CNN blocks, the output feature maps are fetched and sent to ResBlocks, and at the same time, the feature maps are also fetched and sent to an adder in the lower part. All the ResBlocks have the same structure and are used to retain more information about the container, as shown in Figure 4. In a residual block, we set up a three-layer CNN and a residual branch. The output of the two structures is passed to the PReLU activation layer after an adder operation, resulting in a complete output. The output feature maps ($1\times 1\times 512$ $1\times 1\times 512$) are fed to the decoder part on the right side, involving three CNN layers, each with a convolutional layer, a batchnorm layer, and an activation layer. The output from the third layer of the CNN is transmitted to the pixel shuffle module. The adder adds the pixel shuffle module and the output of the fifth CNN layer to form another residual network for the reconstruction effect. Finally, the above output is passed into the two layers of the CNN to obtain the generated $I^{\prime }$.

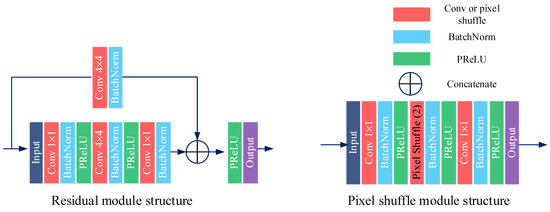
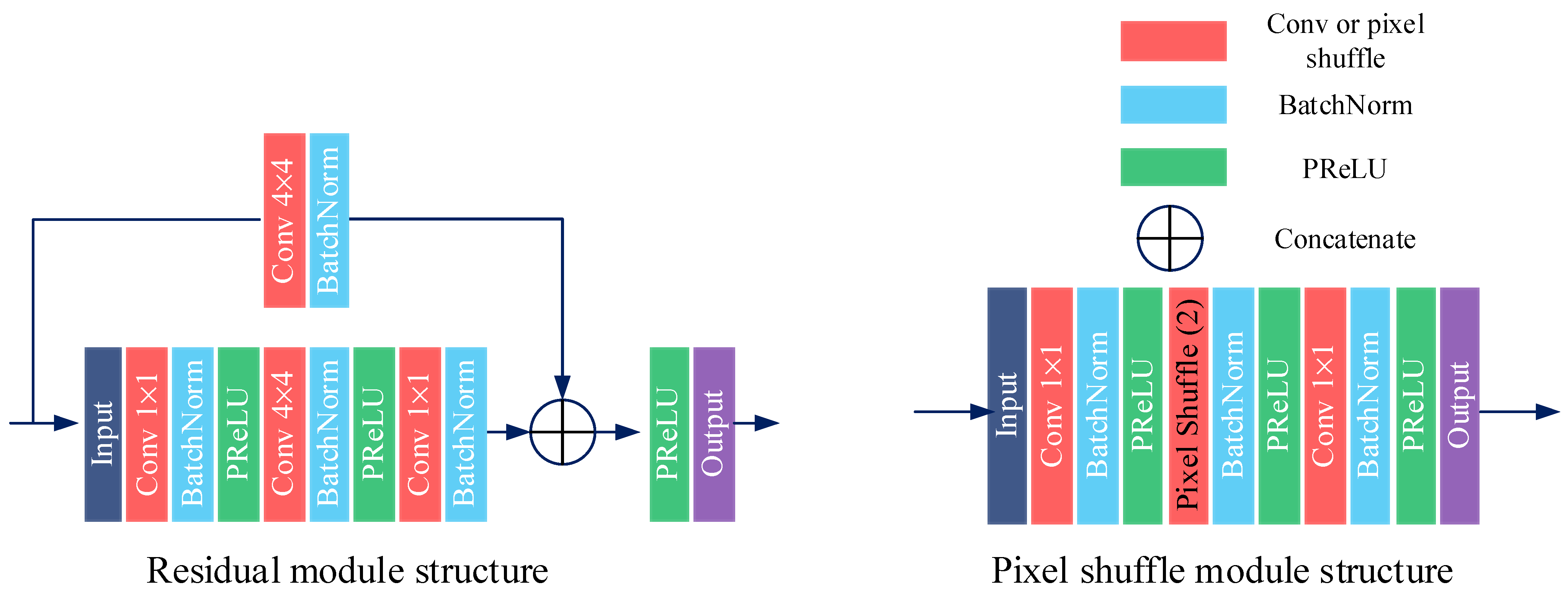
Figure 4. Proposed residual block and pixel shuffle block.

To improve the reconstruction performance, a residual block was placed between each convolutional layer and the deconvolutional layer, which was inspired by the skip connection in ResNet [26]. The residual block could deepen the generator network and help to achieve fast convergence. As shown in Figure 4, the proposed residual block can speed up the convergence during training and also help to prevent overfitting. The pixel shuffle module plays an up-sampling role in the image reconstruction process. It is a hierarchical structure and is capable of extracting different levels of feature details of the input data. The lower convolutional layers tend to capture the edge details of the input data and compress them into lower-dimensional vectors, while the higher deconvolutional layers tend to decode the compressed features into a denser matrix without losing any important information.

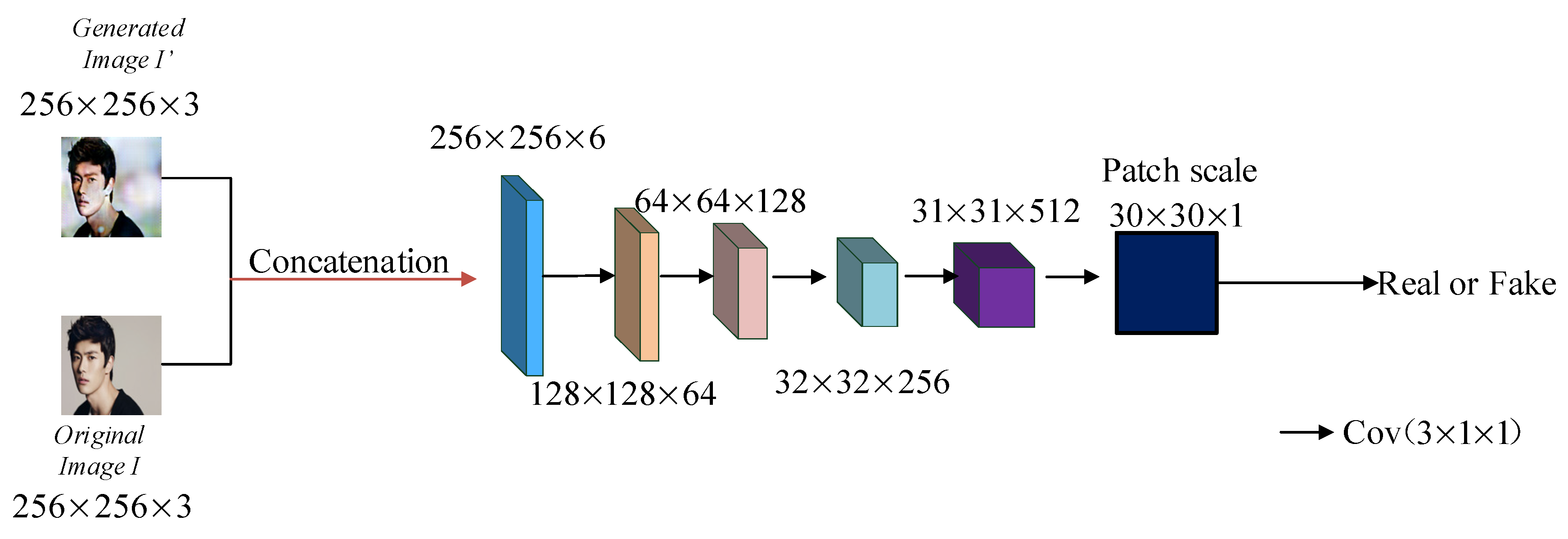
3.3. Proposed Discriminator Network

The goal of the discriminator is to accurately distinguish between the reconstructed image restored by the generator and the real image. The structure of the discriminator network is shown in Figure 5. A fully convolutional neural network architecture was adopted, and the network outputs a discrimination matrix in which the convolution kernel size for the convolution operation is 3 × 3, the step size is 2 × 2, and the edge zero filling is 1 × 1. The complete module consists of five CNN layers, and each pixel in the matrix represents the probability that an image block in the input is from either a restored sample or a real sample. Therefore, the impact of different regions in the image on the discrimination results can be fully considered so that the generator can pay more attention to the details, textures, and other information of the restored image during the training process, which helps to reduce the artifacts of the restored image. Finally, the average value of all elements in the matrix is calculated for the output. The discriminator adopts a fully convolutional neural network structure and applies different weight values to different feature maps to accelerate the convergence of the network. The generator and the discriminator play games in the process of the alternative training of samples. The generator continuously learns to approximate the data distribution of the real samples, which eventually makes the discriminator unable to accurately distinguish between the restored image samples and the real image samples to make the network reach a state of Nash equilibrium. A $30\times 30\times 1$ probability vector is obtained from the output, and the index of the maximal value in the vector is real or fake.

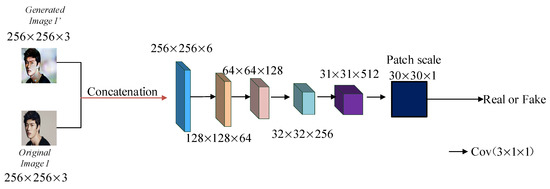
Figure 5. Proposed discriminator module.

3.4. Parameter Settings of the Model

3.4.1. Generator Network Parameters Setting

We augmented two fully connected layers between the convolution and the deconvolution modules to enhance the feature mapping ability. The detailed parameters of the encoder and the decoder parts of the generator are described in Table 1 and Table 2, respectively. In addition, in the proposed IR-DWT-CGAN, the rectified linear units (ReLUs) were replaced by the parametric rectified linear units (PReLUs), which can achieve faster convergence than the ReLUs [22]. Table 1 illustrates the complete structure of the generator network, while Table 2 illustrates the complete structure of the discriminator.

Table 1. Encoder parameters of the proposed generator network.

Layer	Filters	Feature Map	Kernel	Strides	Paddings
Image input layer		256 × 256 × 6
1st convolutional layer	64	128 × 128 × 64	4 × 4 × 3	2 × 2	1 × 1
Leaky ReLUs		128 × 128 × 64
1st residual block layer		128 × 128 × 64
2nd convolutional layer	128	64 × 64 × 128	4 × 4 × 64	2 × 2	1 × 1
Batch normalization
Leaky ReLUs
2nd residual block layer
3rd convolutional layer	256	32 × 32 × 256	4 × 4 × 128	2 × 2	1 × 1
Batch normalization		64 × 64 × 128
Leaky ReLUs		64 × 64 × 128
3rd residual block layer		128 × 128 × 64
4th convolutional layer	512	16 × 16 × 512	4 × 4 × 256	2 × 2	1 × 1
Batch normalization
Leaky ReLUs
4th residual block layer
5th convolutional layer	512	4 × 4 × 512	4 × 4 × 512	2 × 2	1 × 1
Batch normalization
Leaky ReLUs
5th residual block layer
6th convolutional layer	512	2 × 2 × 512	4 × 4 × 512	2 × 2	1 × 1
Batch normalization
Leaky ReLUs
6th residual block layer
7th convolutional layer	512	1 × 1 × 512	4 × 4 × 512	2 × 2	1 × 1
Batch normalization
ReLUs

Table 2. Decoder architecture parameters for the proposed generator network.

Layer	Filters	Feature Map	Kernel	Strides	Paddings
1st deconvolutional layer	512	2 × 2 × 512	4 × 4 × 512	2 × 2	1 × 1
Batch normalization		2 × 2 × 512
Concatenation (+7th conv)		2 × 2 × 1024
ReLU		2 × 2 × 1024
7th residual block layer		2 × 2 × 1024
2nd deconvolutional layer	512	4 × 4 × 512	4 × 4 × 1024	2 × 2	1 × 1
Batch normalization		4 × 4 × 512
Concatenation (+6th conv)		4 × 4 × 1024
ReLU		4 × 4 × 1024
8th residual block layer		4 × 4 × 1024
3rd deconvolutional layer	512	16 × 16 × 512	4 × 4 × 1024	2 × 2	1 × 1
Batch normalization		16 × 16 × 512
Concatenation (+5th conv)		16 × 16 × 1024
ReLU		16 × 16 × 1024
9th residual block layer		16 × 16 × 1024
4th deconvolutional layer	256	32 × 32 × 256	4 × 4 × 1024	2 × 2	1 × 1
Batch normalization		32 × 32 × 256
Concatenation (+4th conv)		32 × 32 × 1024
ReLU		32 × 32 × 1024
10th residual block layer		32 × 32 × 1024
5th deconvolutional layer	128	64 × 64 × 128	4 × 4 × 512	2 × 2	1 × 1
Batch normalization		64 × 64 × 128
Concatenation (+4th conv)		64 × 64 × 256
ReLU		64 × 64 × 256
11th residual block layer		64 × 64 × 256
6th deconvolutional layer	64	128 × 128 × 64	4 × 4 × 256	2 × 2	1 × 1
Batch normalization		128 × 128 × 64
Concatenation (+2nd conv)		128 × 128 × 128
ReLU		128 × 128 × 128
12th residual block layer		128 × 128 × 128
7th deconvolutional layer	3	256 × 256 × 3	4 × 4 × 128	2 × 2	1 × 1
Tanh (output layer)		256 × 256 × 3

3.4.2. Discriminator Network Parameter Setting

As shown in Figure 5, the fully convolutional neural network architecture is also used in the discriminator network. The network outputs a discrimination matrix, where the convolution kernel size for the convolution operation is 3 × 3, the step size is 2 × 2, and the edge zero padding is 1 × 1. The detailed parameters are collected in Table 3.

Table 3. The architecture of the proposed discriminator network.

Layer	Filters	Feature Map	Kernel	Strides	Paddings
Image input layer (input + target or output)		256 × 256 × 6 (concatenation)
1st convolutional layer	64	128 × 128 × 64	4 × 4 × 6	2 × 2	1 × 1
Leaky ReLU		128 × 128 × 64
2nd convolutional layer	128	64 × 64 × 128	4 × 4 × 64	2 × 2	1 × 1
Batch normalization		64 × 64 × 128
Leaky ReLU		64 × 64 × 128
3rd convolutional layer	256	32 × 32 × 256	4 × 4 × 128	2 × 2	1 × 1
Batch normalization		32 × 32 × 256
Leaky ReLU		32 × 32 × 256
4th convolutional layer	512	31 × 31 × 512	4 × 4 × 256	1 × 1	1 × 1
Batch normalization		31 × 31 × 512
Leaky ReLU		31 × 31 × 512
5th convolutional layer	1	30 × 30 × 1	4 × 4 × 512	1 × 1	1 × 1
Sigmoid layer		30 × 30 × 1

3.4.3. Image Size and Feature Maps Transformation Process

The size of the multiscale points feature map that is input to the generator is initially 256 × 256 × 3. The detailed feature map dimensions and image size variations during the image reconstruction process (both training and testing processes) are shown in Figure 6 and Figure 7.

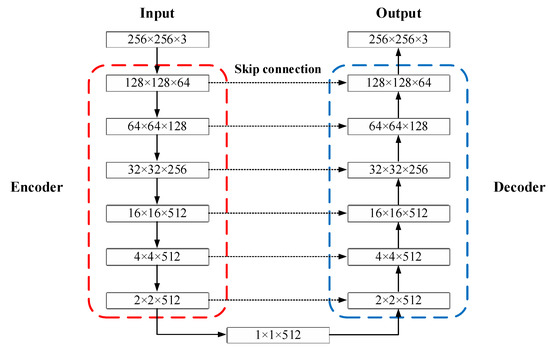
Figure 6. Feature map size changes in the generator network.

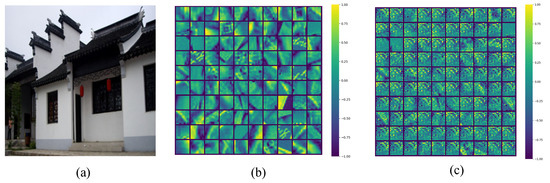
Figure 7. Feature map transformation process: (a) an original image; (b) feature maps presented consecutively in the output of the generator network; (c) feature maps presented consecutively in the discriminator.

3.5. Objective Function and Modified Conditional GAN

The first step in this study was to train the generating function $G$, which estimates the corresponding original image $F^{\mathrm{original}}$ from the given multiscale points feature map $F^{\mathrm{maxima}}$. The objective function of the proposed model was related to the adversarial competitive loss and the reconstruction loss, which are respectively expressed as

$$\begin{array}{cc}{ℒ}_{cGAN}(G,D)=& {\mathbb{E}}_{F^{\mathrm{maxima}},}{}_{F^{\mathrm{original}}}\left[\lg D(F^{\mathrm{maxima}},F^{\mathrm{original}})\right]\\ & +{\mathbb{E}}_{F^{\mathrm{maxima}}}\left[\lg (1-D(F^{\mathrm{maxima}},G(F^{\mathrm{maxima}}))\right]\end{array},$$

(1)

$${ℒ}_{L1}(G)={\mathbb{E}}_{F^{\mathrm{maxima}},}{}_{F^{\mathrm{original}}}\left[{\Vert F^{\mathrm{original}}-G(F^{\mathrm{maxima}})\Vert }_1\right].$$

(2)

Thus, the total loss is the weighted sum of the above two loss functions. The final optimization problem was as follows:

$$G^{*}=\arg \underset{G}{\min }\underset{D}{\max }\left[{ℒ}_{cGAN}(G,D)+\lambda {ℒ}_{L1}(G)\right],$$

(3)

where the balance factor $\lambda =0.5$. Generally, a conditional GAN applies the multiscale points feature maps to the generator in the form of dropout to prevent a deterministic output. However, the various outputs generated due to dropout can transform the vein patterns of the image to be recovered, which can lead to degradation in the recognition performance.

For the original GAN, the input into the generator is noise. For a conditional GAN (CGAN), such as the one used in our work, the input into the generator is an image, namely, $F^{\mathrm{maxima}}$. This image (or condition) we used was the coarse version of the reconstructed image obtained from the inverse DWT of the interest points feature map to speed up the training process compared with considering the noise as the conditional input.

Therefore, a modified conditional GAN without dropout was proposed in this study since the deterministic output is required rather than the various outputs. Finally, the reconstructed image $F^{\mathrm{recostruction}}$ from $F^{\mathrm{maxima}}$ is generated based on Equation (3).

The reconstruction loss contains a squared error term and an ${\ell }_2$ regularization:

$$C_r={\displaystyle {\sum }_i^N{\left[y^i-{\widehat{y}}^i\right]}^2}+\frac{\lambda }{2N}{\displaystyle {\sum }_j{W}_j{W}_j^T},$$

(4)

where $y^i$ and ${\widehat{y}}^i$ represent the $i^{th}$ real image and the corresponding reconstructed one, respectively; $W_j$ is the $j^{th}$ weight matrix; and $W_j^T$ is the transpose of $W_j$.

$${\omega }_t={\omega }_{t-1}-\alpha \cdot m_t^{\prime }/\left(\sqrt{n_t^{\prime }}+\epsilon \right),$$

(5)

where ${\omega }_t$ and ${\omega }_{t-1}$ are the weights after and before the update, respectively; $\alpha$ is the initial learning rate; $m_t^{\prime }$ is the first bias-corrected moment estimate; $n_t^{\prime }$ is the second bias-corrected moment estimate; and $\epsilon$ is a constant.

4. Simulation Results and Analysis

4.1. Development Environment

The model in this study ran in a hardware environment with an Intel(R) Core (TM) i7-8700 CPU@ 3.2GHz, 32 GB RAM, and two GeForce RTX 2080Ti graphics adapters, with Windows 10 as the workstation operating system. The integrated development environment and deep learning symbolic library were PyCharm-Python 3.7 (V. 2020.2.3. JetBrains S.R.O. Prague, Czech Republic) and Pytorch (V.1.1.0 Adam P.; Sam G.; Soumith C. Silicon Valley, CA, USA), respectively.

The proposed IR-DWT-CGAN was trained on a subset of ImageNet [28] that contained 49,100 color images in RGB color space and their multiscale points feature maps. Each image in the training dataset was reshaped to a size of 256 × 256 to save on storage space. All test images were taken from the Waterloo dataset of the test dataset [29]. All images in the ImageNet dataset and the Waterloo dataset were reshaped to a size of 256 × 256 for training and testing.

4.2. Quantitative Metrics

Four quantitative image reconstruction quality indices were utilized for the performance evaluation, namely, the mean square error (MSE), mean structural similarity (MSSIM), relative dimensionless global error in synthesis (ERGAS, abbreviation in French), and average absolute pixel error (APE).

The MSE is a measure of the quality difference between the reconstructed image and the original one. The MSE is commonly used to quantify the difference between two images by computing the variation in pixel values. The reconstructed image is close to the reference one if the MSE value is near zero. If the pixel value of the image to be evaluated, i.e., X, is $X(i,j),0\le i\le M-1,0\le j\le N-1$ and the pixel value of its reference image, i.e., $\widehat{X}$, is $\widehat{X}(i,j),0\le i\le M-1,0\le j\le N-1$, then the MSE between $X$ and $\widehat{X}$ is defined as

$$\mathrm{MSE}(X,\widehat{X})=\frac{1}{MN}{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}{\left[X\left(i,j\right)-\widehat{X}\left(i,j\right)\right]}^2}}.$$

The SSIM, which measures the similarity between images $X$ and $\widehat{X}$, is

$$\mathrm{SSIM}(X,\widehat{X})=\frac{\left(2{\mu }_X{\mu }_{\widehat{X}}+C_1\right)\left(2{\sigma }_{X\widehat{X}}+C_2\right)}{\left({\mu }_X^2+{\mu }_{\widehat{X}}^2+C_1\right)\left({\sigma }_X^2+{\sigma }_{\widehat{X}}^2+C_2\right)},$$

where ${\mu }_X$ and ${\mu }_{\widehat{X}}$ are the mean intensities of the original image and the reconstructed one, respectively; ${\sigma }_X$ and ${\sigma }_{\widehat{X}}$ are the standard deviation of the original image and the reconstructed one, respectively, $C_1$ and $C_2$ are the constants used to maintain stability, where $C_1={(K_{1}L)}^2$ and $C_2={(K_{2}L)}^2$, with L being the dynamic range of the pixel values, the default $K_1$ = 0.01, and $K_2$ = 0.03. SSIM is used to compare the local patterns of the pixel intensities between the two compared images with values between 0 and 1. An SSIM value 1 indicates that the reference image and the reconstructed one are identical. The MSSIM is defined as the mean SSIM over non-overlapped image blocks.

The PSNR is defined as

$$\mathrm{PSNR}=10\lg \frac{M\times N\times {255}^2}{{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left[X\left(i,j\right)-\widehat{X}\left(i,j\right)\right]}^2}}},$$

where $M\times N$ is the size of the original image.

The ERGAS is used to determine the quality of the image in terms of the normalized average error for each band. The smaller the ERGAS, the more similar the reconstructed image is to the reference image. The ERGAS is defined as

$$\mathrm{ERGAS}(X,\widehat{X})=\frac{100}{d}\sqrt{\frac{1}{S}{\displaystyle \sum _{i=1}^S\frac{\mathrm{MSE}(X^i,{\widehat{X}}^i)}{{\mu }_{{\widehat{X}}^i}^2}}},$$

where ${\mu }_{{\widehat{X}}^i}$ is the mean of ${\widehat{X}}^i$ for the i^th sub-block, $\mathrm{MSE}(X^i,{\widehat{X}}^i)$ is the mean squared error between $X^i$ and ${\widehat{X}}^i$, d is a spatial down-sampling factor, and S is the number of partitioned non-overlapped sub-blocks.

The APE is often used to represent the absolute pixel values of the errors between images $X$ and $\widehat{X}$, and is defined as

$$\mathrm{APE}(X,\widehat{X})=\frac{1}{MN}{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}\left|X(i,j)-\widehat{X}(i,j)\right|}}.$$

4.3. Proposed Database MAX

In this study, the proposed database MAX was built from 49,100 color images and their corresponding multiscale points feature maps, which were sufficient to train a large number of weights in the deep CNN structure. The MAX database contained pairs of reshaped natural images and their multiscale point feature maps, as shown in Figure 8. The detailed procedure used to establish the database is presented below.

Figure 8. Processing of multiscale singular points map.

• Step 1: For a three-channel RGB image, a two-scale wavelet transform was performed individually on each of the three components.
• Step 2: The low-frequency band was discarded while retaining the other three high-frequency bands. The maxima of the three bands were obtained as image features. It makes sense to choose an appropriate model to calculate the DWT coefficients. The applied model can select the fewest local maxima to reconstruct an approximate image. These local maxima were selected with the modulus of the coefficients in the DWT domain with respect to the neighborhood.
• Step 3: The maxima obtained in step 2 were regarded as interest points to which an inverse DWT was applied, along with the zero low-frequency band, to obtain a very coarse version of the desired restored image.

4.4. Training Process

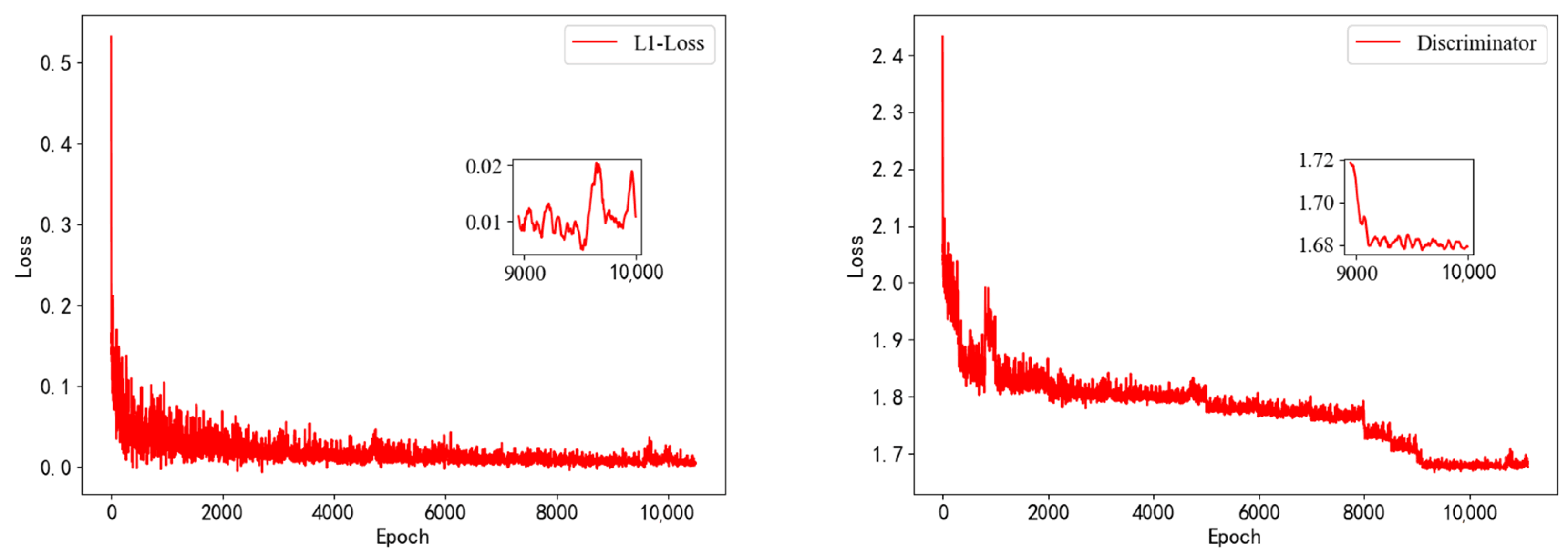
The maximum number of epochs, mini-batch size, and learning rate used in IR-DWT-CGAN were set to 12,000, 25, and 0.002, respectively. During the training period, random jitter was applied to the scale [30]. Moreover, adaptive moment (Adam) optimization [31] was used to train the IR-DWT-CGAN model. During the training process, the generator network and the discriminator network were trained simultaneously. To effectively suppress overfitting and accelerate the network convergence, an Adam optimizer with a batch size of 8 was used to minimize the backpropagation-based loss function.

The network training lasted more than 100 days and converged after 8000 epochs. As can be seen in Figure 9, the loss function ${ℒ}_{L1}(G)$ and the discriminator loss function $G^{*}$ decreased rapidly in the initial few thousand iterations, approaching a very small value after 8000 epochs.

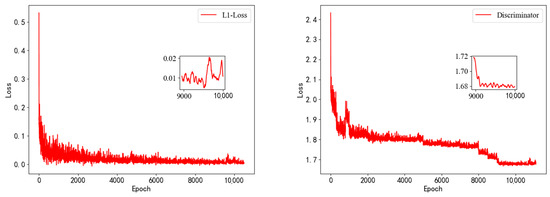
Figure 9. Loss function curves for the generator loss ${ℒ}_{L1}(G)$ and discriminator loss $G^{*}$.

4.5. Results

The images reconstructed from their multiscale feature maps at different scales are shown in Figure 10. As can be seen in Figure 10, based on images (b), (c), and (d), a clear texture of the original image can be perceived. However, the number of interest points with high magnitude values was decreasing. As shown in Table 4, the images reconstructed based on the multiscale interest point map with scale = 1 produced better quality in terms of the PSNR, MSE, MSSIM, and ERGAS values while using fewer interest points. In summary, the DWT-based multiscale points feature maps with scale = 1 exhibited better performance than those with scale = 2 and scale = 3.

Figure 10. Images reconstructed based on different multiscale interest points feature maps at different scales. (a) Original image, (b) and (e) are the multiscale points feature maps and the corresponding reconstructed images when scale = 1; (c) and (f) are the multiscale singular maps and the corresponding reconstructed images when scale = 2; (d) and (g) are the multiscale singular maps and the corresponding reconstructed images when scale = 3.

Table 4. Average number of interest points of the reconstructed images at different scales and their corresponding image PSNR, MSE, MSSIM, and ERGAS values.

Scale	Number of Singular Points	PSNR (dB)	MSE	MSSIM	ERGAS
1	5878	33.11	47.98	0.98	0.656
2	3739	26.56	541.07	0.88	3.982
3	2314	24.49	693.67	0.85	4.187

4.6. Analysis of the Image Reconstruction Schemes

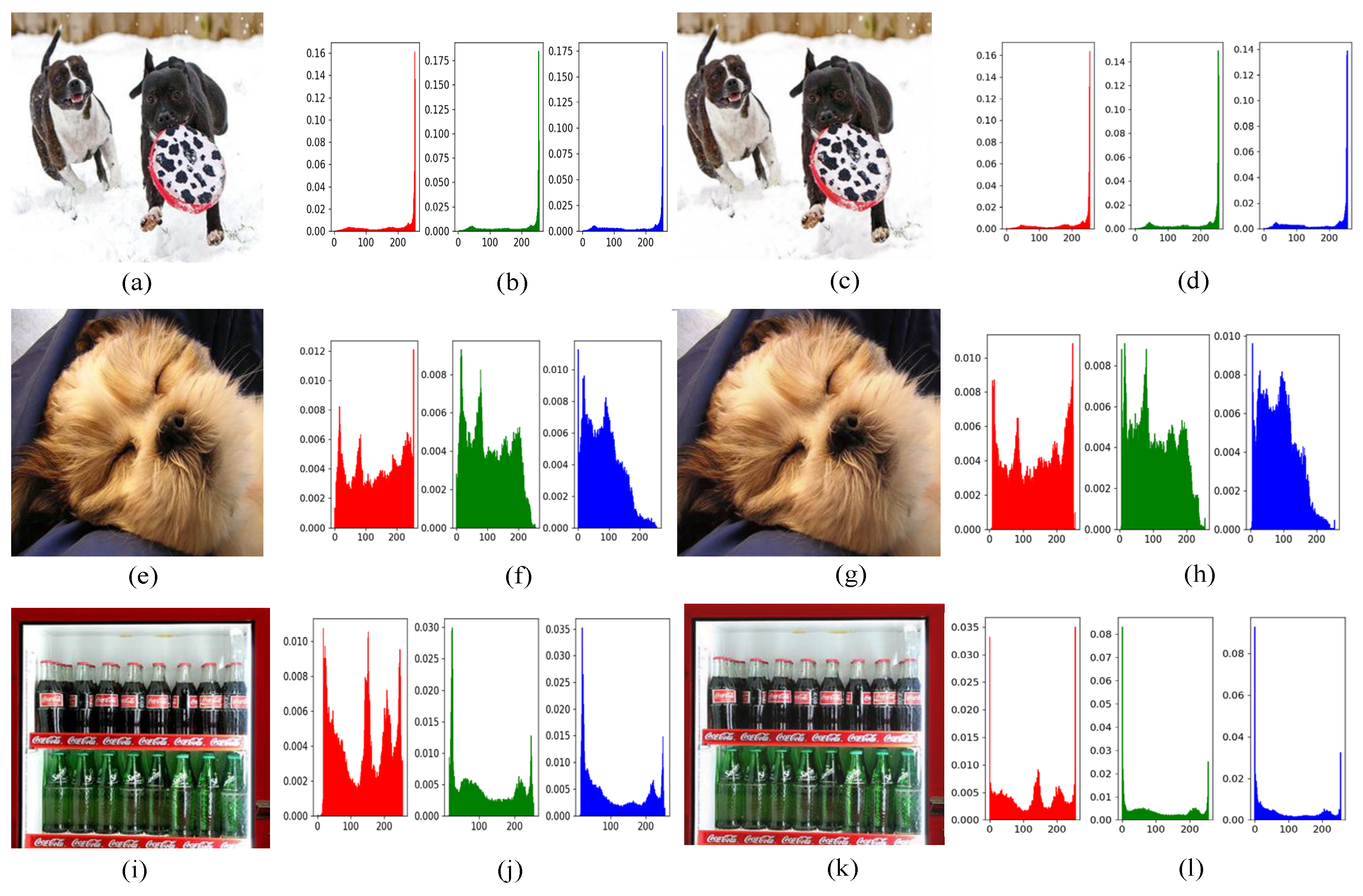
Figure 11 shows the histograms of the original and reconstructed images. When the scale was chosen as 1, the image histograms did not change significantly in shape for all three channels, indicating the desired IR performance from another point of view.

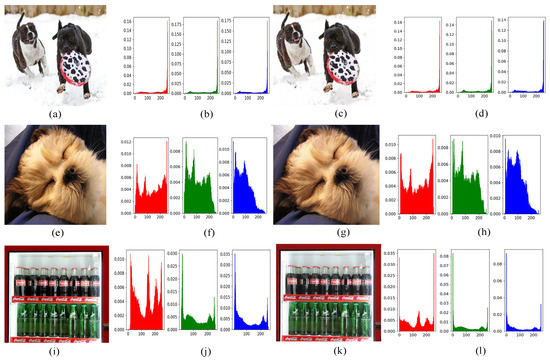
Figure 11. Image histograms for the three test images: (a), (e), and (i): original images; (b), (f), and (j): histograms of (a), (e), and (i) for the three (RGB) channels, respectively; (c), (g), and (k): reconstructed images; (d), (h), and (l): histograms of (c), (g), and (k) for the three (RGB) channels, respectively, when scale = 1.

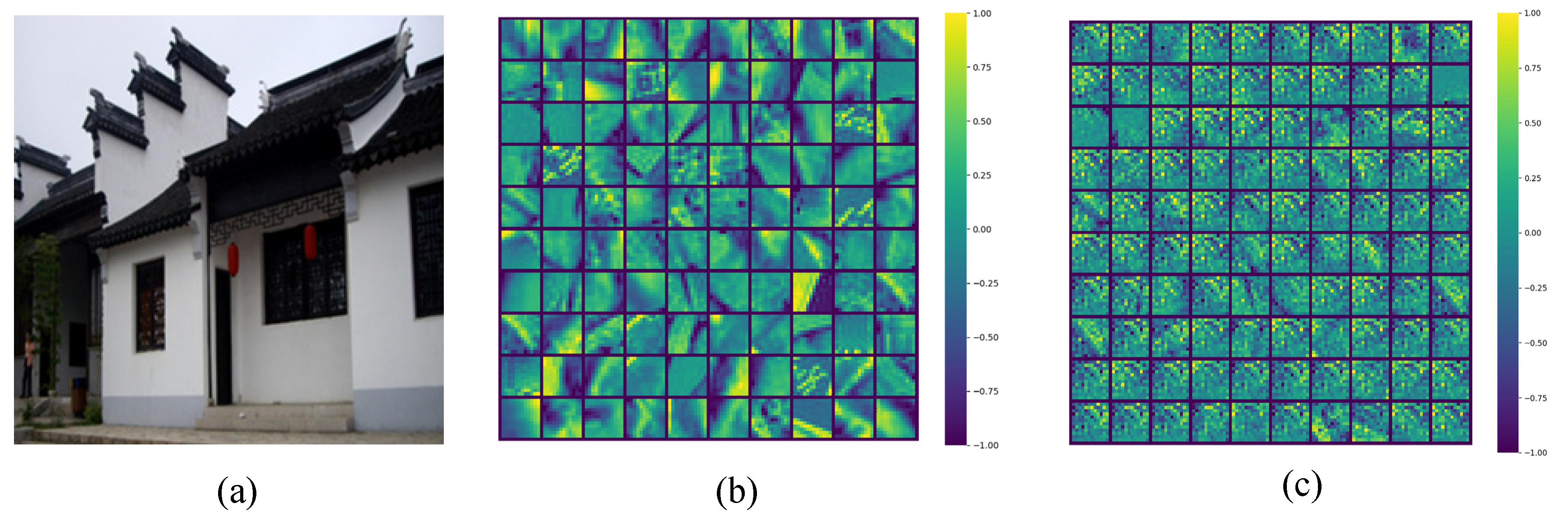
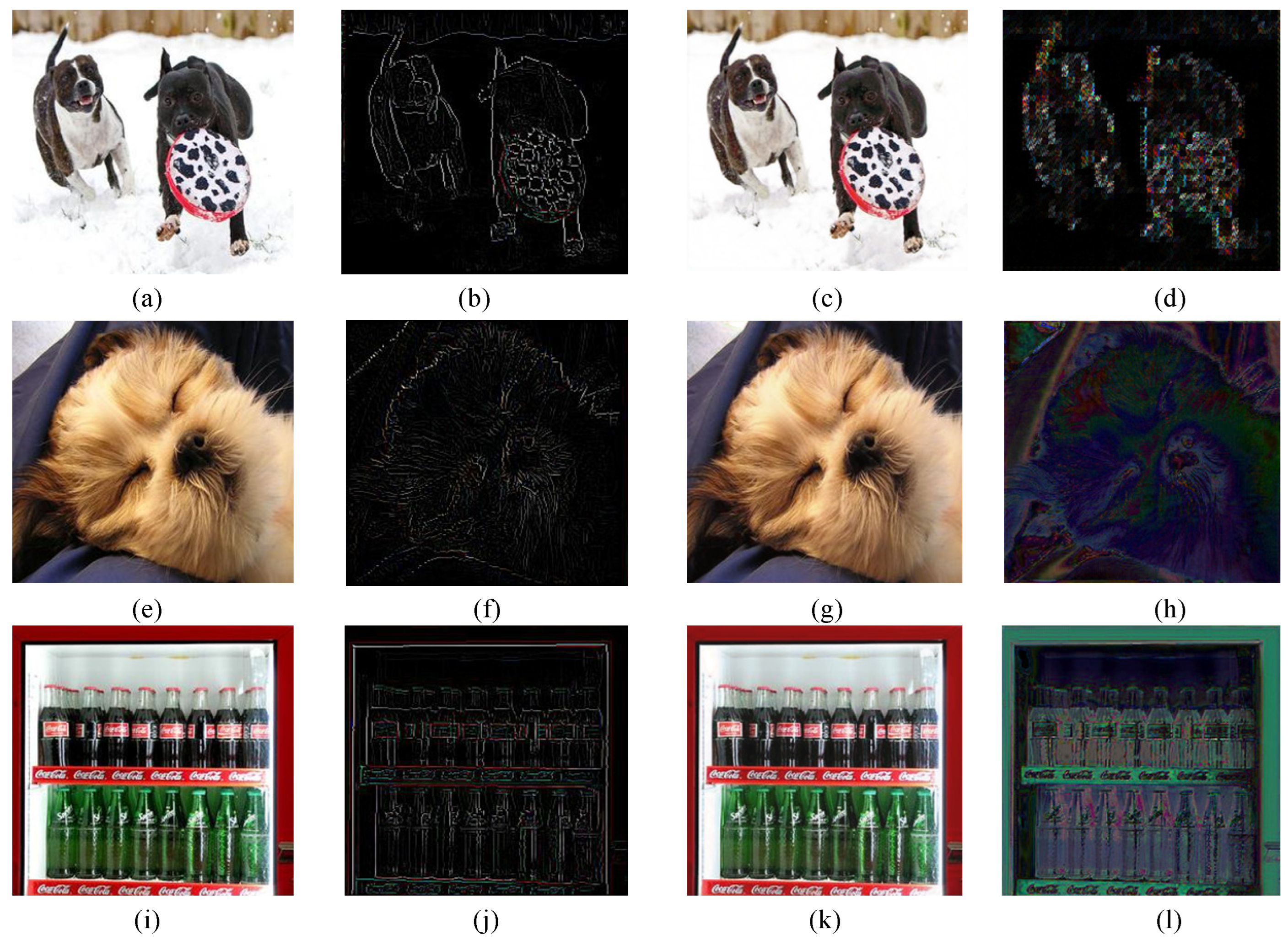
Furthermore, the difference image between the original and the reconstructed images is often used to observe the error between these two images. The difference images between the original images and the corresponding reconstructed ones are shown in the fourth column in Figure 12, where (d), (h), and (l) are the difference images |(a)–(c)|, |(e)–(g)|, and |(i)–(k)|, respectively. Obviously, some slight differences near the edges can be perceived visually.

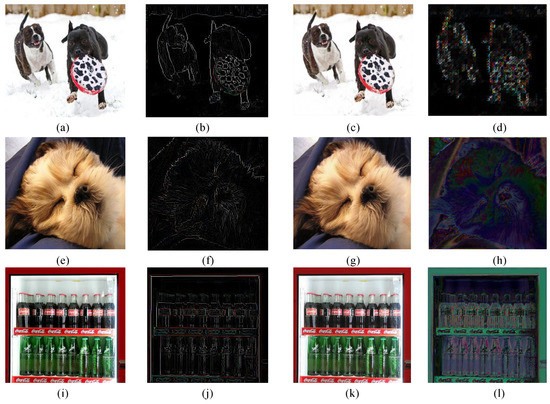
Figure 12. Difference images between the test image and the reconstructed one. (a), (e), and (i) are the original test images; (b), (f), and (j) are the multiscale interest points feature maps of (a), (b), and (i), respectively; (c), (g), and (k) are the reconstructed images of (a), (e), and (i), respectively; (d), (h), and (l) are the difference images of |(a)–(c)|, |(e)–(g)|, and |(i)–(k)|, respectively, when scale = 1.

The evaluation metrics PSNR, MSE, and MSSIM, as well as APE for the RGB channels, are presented in Table 5. As shown in Table 5, for the image in the first row of Figure 12, the PSNR values of the reconstructed image were sufficiently high. The structural similarities between the original images and their corresponding reconstructed ones were acceptable. The MSEs between the original images and the reconstructed ones were quite obvious. Similar results were obtained for the other two images and their corresponding reconstructed images, as shown in the second and third rows in Figure 12.

Table 5. PSNR and image MSSIM, MSE, and APE values for the reconstructed images.

Image Group	PSNR (dB)	MSE	MSSIM	Original vs. Reconstructed Image APE (R, G, B)
First row	33.11	47.98	0.98	23.12, 21.51, 19.02
Second row	32.66	105.74	0.97	32.78, 23.12, 21.08
Third row	30.12	238.38	0.88	45.13, 39.12, 40.98

4.7. Data Requirements for the Reconstruction Scheme

Data requirements are an important consideration in IR. As shown in Table 6, the percentage of interest points used from the original image in the three (RGB) channels shows that the proposed image reconstruction algorithm was very efficient. For the proposed scheme, the time consumption was almost negligible. Each group had five images of size 256 × 256. More interest points can be seen in Table 6.

Table 6. MSSIM, MSE, and PSNR values of the proposed IR-DWT-CGAN.

Image Group	Channel	No. of SPs	Ratio of SPs over Original Channel (%)	MSSIM	MSE	PSNR (dB)
1	R	2346	3.57	0.881	517.63	26.13
	G	2273	3.46
	B	2120	3.23
2	R	2092	3.19	0.857	651.15	24.67
	G	1991	3.03
	B	1809	2.76
3	R	2190	3.34	0.873	542.75	25.31
	G	2177	3.32
	B	2130	3.25

4.8. Comparison of the Image Quality and Time Consumption with Other Algorithms

The proposed algorithm was compared with the algorithms in Refs [1,3,4,32]. Figure 13 presents the reconstructed images using five different algorithms. One can conclude from Figure 13 that the model performance was improved prominently with the help of the generative network, and the proposed algorithm gave the best results.

Figure 13. Comparison of the IR results for different algorithms: (a) original image; (b) proposed algorithm; (c) Ref [4]; (d) Ref [1]; (e) Ref [3]; (f) Ref [32]; (g) multiscale interest points feature maps of (a); (h), (i), (j), (k), and (l) are the difference images of |(a)–(b)| $\times$5, |(a)–(c)| $\times$ 5, |(a)–(d)| $\times$ 5, |(a)–(e)| $\times$ 5, and |(a)–(f)| $\times$ 5, respectively.

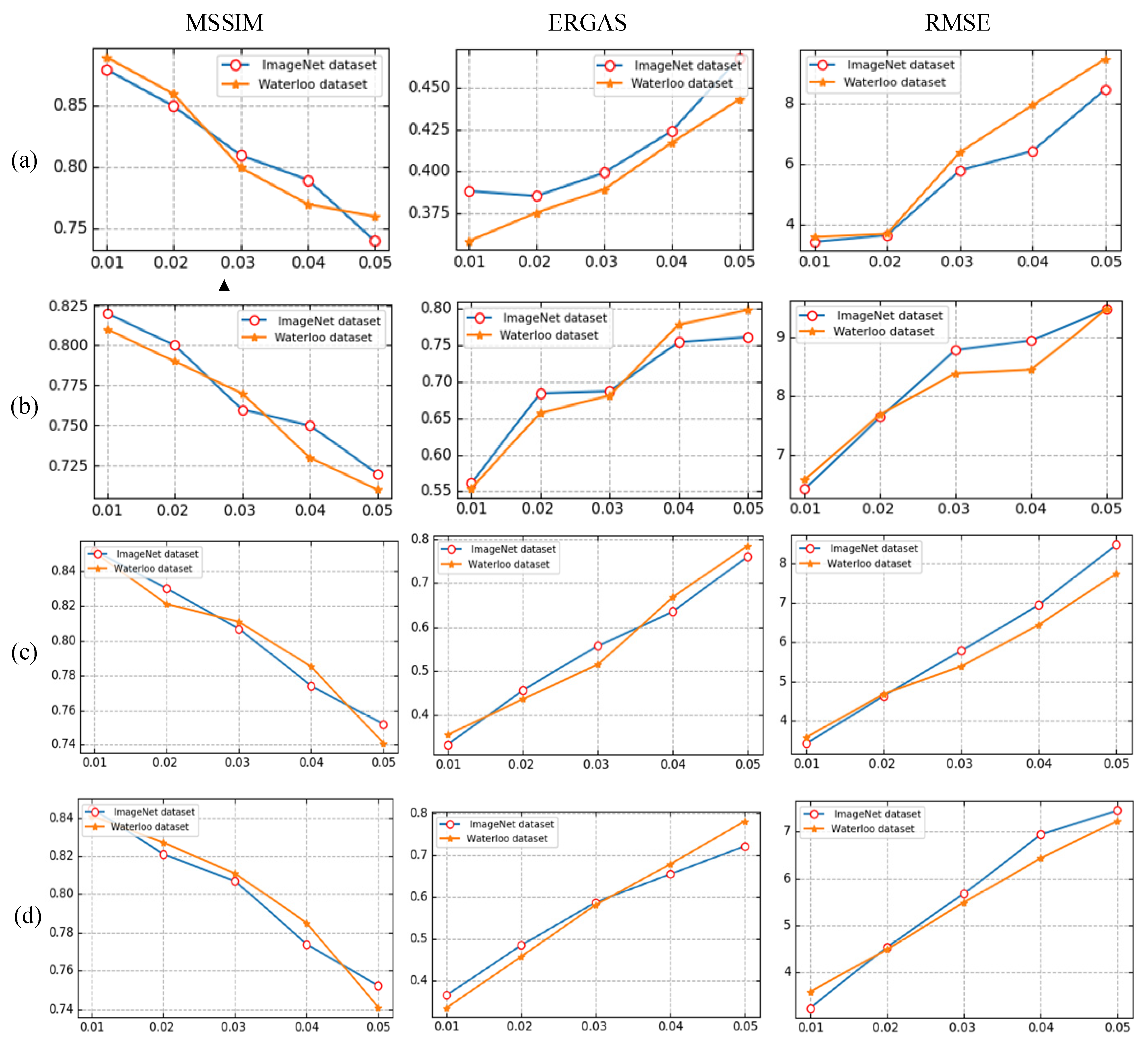
In addition, we conducted experiments to test the resistance of the proposed model to the different levels of noise contamination added to the original images. The results are shown in Figure 14. As can be seen in Figure 14, the MSSIM decreased as the noise intensity increased but it was still within an acceptable range. Compared with the methods in Ref [1], Ref [3], and Ref [32], the proposed method provided a significant improvement in terms of the MSSIM, ERGAS, and RMSE. As shown in Table 7, the time consumption was 6.862 s, 5.628 s, and 5.651 s lower on average compared with [1], [3], and [32], respectively. It can be concluded that the proposed IR-DWT-CGAN algorithm was more efficient than other IR algorithms based on the alternating projection method.

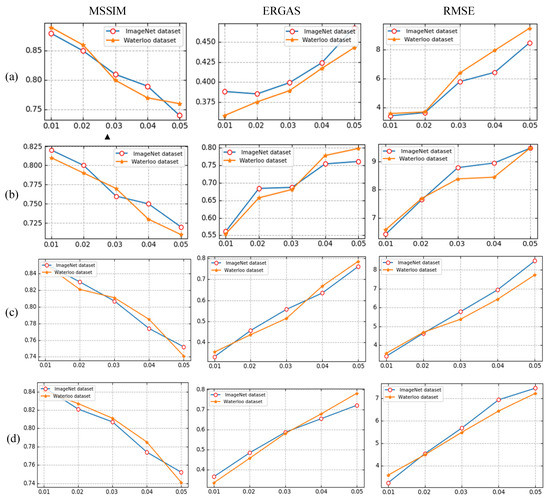
Figure 14. Comparison of the results of the RMSE, ERGAS, and MSSIM relative to the noise levels for different algorithms: (a) proposed algorithm, (b) Ref [32], (c) Ref [1], and (d) Ref [3].

Table 7. Time consumption compared with other methods.

Scheme	Time (s)
	Group 1	Group 2	Group 3
Proposed algorithm	0.314	0.434	0.365
Ref. [1]	7.232	7.314	7.154
Ref. [3]	5.857	6.207	5.933
Ref. [32]	5.932	6.112	6.024

5. Conclusions

A new dataset based on multiscale interest points and a new image reconstruction model IR-DWT-CGAN based on CGAN were proposed for the first time. A new database named MAX was built from natural images and their multiscale interest point feature maps. The proposed image reconstruction model, namely, IR-DWT-CGAN, treats wavelet maxima as interest points, from which a coarse version of the desired reconstruction images is obtained using inverse DWT. The new database was constructed from pairs of original images and their corresponding multiscale interest point feature maps. The generator network reconstructs the image from the multiscale interest point feature maps, while the discriminator network distinguishes the restored images from their corresponding ground truths during the training process and is no longer used for the testing process. It was demonstrated that the feasibility of the proposed IR-DWT-CGAN and the high compression ratio validated the effectiveness of the proposed IR-DWT-CGAN-based image reconstruction algorithm. Furthermore, the comparison results of different IR algorithms showed that the IR-DWT-CGAN model outperformed other typical classical IR algorithms.