Identifying the Exact Value of the Metric Dimension and Edge Dimension of Unicyclic Graphs

Abstract

Given a simple connected graph G, the metric dimension dim$(G)$ (and edge metric dimension edim$(G)$) is defined as the cardinality of a smallest vertex subset $S\subseteq V(G)$ for which every two distinct vertices (and edges) in G have distinct distances to a vertex of S. It is an interesting topic to discuss the relation between these two dimensions for some class of graphs. This paper settles two open problems on this topic for unicyclic graphs. We recently learned that Sedlar and Škrekovski settled these problems, but our work presents the results in a completely different way. By introducing four classes of subgraphs, we characterize the structure of a unicyclic graph G such that dim$(G)$ and edim$(G)$ are equal to the cardinality of any minimum branch-resolving set for unicyclic graphs. This generates an approach to determine the exact value of the metric dimension (and edge metric dimension) for a unicyclic graph.

1. Introduction

This paper focuses on the unicyclic graphs [1]. In what follows, we first describe some notations and definitions that are used in the following sections, and then give a brief review on the history of (edge) metric dimension.

Throughout the paper, we only consider graphs that are finite, simple, and undirected. We use $V(G)$ and $E(G)$ to denote the vertex set and edge set of a graph G, respectively. The degree of a vertex $v\in V(G)$ in G, denoted by $d_G(v)$, is the number of vertices adjacent to v. If a vertex has degree k (respectively, at least k) in G, then we call it a k-vertex (respectively, $k^{+}$-vertex) of G. The distance $d_G(u_1,u_2)$ between two vertices $u_1,u_2\in V(G)$ of a connected graph G is the length of a shortest path from $u_1$ to $u_2$, and the distance $d_G(v,e)$ between a vertex $v\in V(G)$ and an edge $e\in E(G)$ is defined as $d_G(v,e)=min\{d_G(v,v_1),d_G(v,v_2)\}$, where $e=v_1{v}_2$. A path from a vertex v to an edge e refers to a path from v to an arbitrary endpoint of e. Throughout this paper, the notation $P_{u,v}$ (respectively, $P_{u,e}$) is used to denote a shortest path from vertex u to vertex v (respectively, vertex u to edge e). Let G be a connected graph and $S\subseteq V(G)$. For any $u,u^{\prime }\in V(G)$ (respectively, $e,e^{\prime }\in E(G)$), we say that S distinguishes u and $u^{\prime }$ (respectively, e and $e^{\prime }$) if there exists a vertex $v\in S$ such that $d_G(v,u)\ne d_G(v,u^{\prime })$ (respectively, $d_G(v,e)\ne d_G(v,e^{\prime })$); it is also said that v distinguishes $u,u^{\prime }$ (respectively, $e,e^{\prime }$). Then, S is referred to as a metric generator if S distinguishes any two vertices of G. Similarly, we call S an edge metric generator of G if S distinguishes any two edges of G. The minimum k for which G has a metric (respectively, edge metric) generator of cardinality k is called the metric (respectively, edge metric) dimension of G, denoted by dim(G) (respectively, edim(G)).

One of the first people to define metric dimension was Slater [2], who used the term ‘location number’ originally in connection with a location problem of uniquely determining the position of an intruder in a network. This concept was independently discovered by Harary and Melter [3], who were the first to use the term ‘metric dimension’. Metric dimension is an important concept in graph theory, and has many applications in diverse areas, such as image processing and pattern recognition [4,5], and robot navigation [6], to name a few. The problem of determining the metric dimension of a graph is NP-complete. Recently, motivated by an observation that there exist graphs where any metric generator does not distinguish all pairs of edges, Kelenc et al. [7] proposed the concept of the edge metric generator, which aims to distinguish edges instead of vertices, and made a comparison between these two dimensions. They also proved that determining the edge metric dimension is NP-hard, and proposed some open problems, most of which have been settled subsequently [8,9]. Since then, researchers have shown an increased interest in determining edge metric dimension for special classes of graphs, for example, generalized Petersen graphs [10,11], convex polytopes [12,13], graph operations [14], hollow coronoid [15], windmill graphs [16], möbius networks [17], etc. For more information on edge metric dimension, please refer to recent papers [18,19].

By the similarity of the metric dimension and the edge metric dimension, it is interesting to study the relation between them. In [7], it was found that there exist graphs whose metric dimension is less than, equal to, or greater than their edge metric dimension. In [8], it was proved that $\frac{\dim (G)}{\mathrm{edim}(G)}$ is not bounded from above. More recently, Knor et al. [20] further studied the ratio $\frac{\dim (G)}{\mathrm{edim}(G)}$, and by constructing graphs based on a family of special unicyclic graphs they proved that there are graphs G for which both $\dim (G)-\mathrm{edim}(G)$ and $\mathrm{edim}(G)-\dim (G)$ can be arbitrarily large. They also posed two problems on how to characterize a unicyclic graph G with $\dim (G)>\mathrm{edim}(G)$ or $\dim (G)=\mathrm{edim}(G)+1$.

Problem 1

([20]). Determine unicyclic graphs G with $\dim (G)>\mathrm{edim}(G)$ or $\dim (G)=\mathrm{edim}(G)+1$.

For a unicyclic graphs G, Sedlar and Škrekovski [21] obtained the bounds on metric and edge metric dimensions, and proved that $|\dim (G)-\mathrm{edim}(G)|\le 1$. Furthermore, they proposed a similar problem to Problem 1.

Problem 2

([21]). Determine unicyclic graphs G when the difference $\mathrm{edim}(G)-\dim (G)=-1$, $\mathrm{edim}(G)-\dim (G)=0$, and $\mathrm{edim}(G)-\dim (G)=1$.

In this paper, for a unicyclic graph G, by introducing four classes of subgraphs, we obtain the exact values of edim$(G)$ and dim$(G)$. Our results settle the above two problems. Although these problems were addressed in a recent published paper [1], our work presents the results in a completely different way. It is a pity that we did not find the work in [1] until recently. We still want to make it clear that we did not copy anything from [1] and the configurations of unicyclic graphs characterized in our paper are different from those in [1]. More specifically, the approach in [1] was to characterize indistinguishable configurations of vertices (respectively, edges) in a unicyclic graph and then determine the vertex metric generator (respectively, edge metric generator). Our approach is to construct a configuration in which all vertices or edges can be distinguished in a unicyclic graph, and then characterize the odd graphs and even graphs with respect to the cardinality of a smallest vertex metric generator (respectively, edge metric generator).

The section below describes terminologies and notation we adopt in our proofs and some (known and new) conclusions.

2. Preliminaries

We follow the same notations in [21] with a slight change. Given a graph G, we use $G-V^{\prime }$ and $G-E^{\prime }$ to denote the resulting graph obtained from G by deleting all vertices in $V^{\prime }$ (and all of their incident edges) and all edges in $E^{\prime }$, respectively, where $V^{\prime }\subseteq V(G)$ and $E^{\prime }\subseteq E(G)$. Especially, when $V^{\prime }=\left\{v\right\}$ and $E^{\prime }=\left\{e\right\}$, we replace them with $G-v$ and $G-e$, respectively. For two integers $i,j$ such that $0\le i<j$, we use $[i,j]$ to denote the set $\{i,i+1,\dots ,j\}$. The focus of this paper is on unicyclic graphs, which are graphs containing exactly one cycle. Let G be a unicyclic graph. For the sake of convenience, we use $\mathcal{C}(G)$ and $\ell (G)$ (or simply $\mathcal{C}$ and ℓ when G is clear from the context) to denote the unique cycle of G and the length of $\mathcal{C}$, respectively, and denote by $\mathcal{O}(\ell )$ and $\mathcal{E}(\ell )$ the sets of unicyclic graphs with $\ell \equiv 1$ (mod 2) and $\ell \equiv 0$ (mod 2), respectively. Clearly, $\ell \ge 3$.

In what follows, for any unicyclic graph G, we always let $\mathcal{C}=a_0{a}_1\dots a_{\ell -1}{a}_0$. Note that $G-E(\mathcal{C})$ is a forest. For each $i\in [0,\ell -1]$, we denote by $T_{a_i}$ the component of $G-E(\mathcal{C})$ containing $a_i$, and call $a_i$ the master of every vertex of $T_{a_i}$ (it is necessary here to clarify that $a_i$ is also its own master). For any $S\subseteq V(G)$, we say that $a_i\in V(\mathcal{C}),i\in [0,\ell -1]$ is S-active if $T_{a_i}$ contains a vertex of S, and use $\mathcal{A}(S)$ to denote the set of all S-active vertices on $\mathcal{C}(G)$. For a vertex $u\in V(G)$, if $u\notin V(\mathcal{C})$ is a $3^{+}$-vertex or $u\in V(\mathcal{C})$ is a $4^{+}$-vertex, then we call u a branching vertex of G. Clearly, if $T_{a_i}$ contains no branching vertex, then $T_{a_i}$ is a path. For every vertex u with $d_G(u)\ge 3$, a thread attached to u is a path $u_1\dots u_k$ such that $u_i$ is a 2-vertex for $i\in [1,k-1]$, $u_k$ is an 1-vertex, and $u_{1}u\in E(G)$, where $k\ge 1$. By $\mathcal{S}(u)$ we denote the set of threads that are attached to u. A $4^{+}$-vertex $u\in V(\mathcal{C})$ is called a bad vertex of G if there is a thread attached to u. A branch-resolving set of G is a set $S\subseteq V(G)$ such that for every $3^{+}$-vertex v, at least $|\mathcal{S}(v)|-1$ threads in $\mathcal{S}(v)$ contain a vertex of S. Indeed, we are interested in the branch-resolving set containing the minimum number of vertices. Obviously, the cardinality of any minimum branch-resolving set, denoted by $L(G)$, is determined by

$$L(G)=\sum _{v\in V(G),|\mathcal{S}(v)|>1}(|\mathcal{S}(v)|-1).$$

Observe that each thread has exactly one 1-vertex; therefore, we can choose a minimum branch-resolving set which consists of only 1-vertices. We use $\mathcal{B}(G)$ to denote the set of all such minimum branch-resolving sets of G. When $S(\in \mathcal{B}(G))\ne \varnothing$, we can label vertices on $\mathcal{C}$ in a specific way: $a_0\in \mathcal{A}(S)$ and the maximum i such that $a_i$ is an S-active vertex and should be as small as possible. Such labeling is called normal labeling with respect to S of $\mathcal{C}$ (or simply normal labeling of $\mathcal{C}$).

Let G be a unicyclic graph and $a_i,a_j,a_k$ be three vertices on $\mathcal{C}$. If $d_G(a_i,a_j)+d_G(a_j,a_k)+d_G(a_k,a_i)=\ell$, then $a_i,a_j,a_k$ are said to form a geodesic triple. Let $S\in \mathcal{B}(G)$ and $r=max\left\{i\right|a_i$ is S-active}. Notice that when $\mathcal{C}$ is labeled normally, if $r>\lfloor \frac{\ell }{2}\rfloor$, then $a_0$, $a_p$, and $a_q$ form a geodesic triple for $p=max\{i|i\in [1,\lfloor \frac{\ell }{2}\rfloor ]$ and $a_i\in \mathcal{A}(S)\}$ and $q=min\{i|i\in [\lfloor \frac{\ell }{2}\rfloor +1,\ell -1]$ and $a_i\in \mathcal{A}(S)\}$. In addition, if $\ell \equiv 0$ (mod 2) and $r=\lfloor \frac{\ell }{2}\rfloor$, then either $\mathcal{A}(S)=\{a_0,a_r\}$ or $\mathcal{A}(S)$ contains three vertices that form a geodesic triple.

The following part of this section moves on to describe some basic conclusions. We first present three known results given by Sedlar and Škrekovski [21].

Lemma 1

([21]). Let G be a unicyclic graph. If S is a metric generator (respectively, edge metric generator), then $|\mathcal{A}(S)|\ge 2$ and S is a branch-resolving set.

Lemma 2

([21]). Let G be a unicyclic graph and $S\subseteq V(G)$ a branch-resolving set of G. If $\mathcal{A}(S)$ contains three vertices that form a geodesic triple, then S is a metric generator (and also an edge metric generator) of G.

Lemma 3

([21]). Let G be a unicyclic graph. If $S\subseteq V(G)$ is a branch-resolving set of G such that $|\mathcal{A}(S)|\ge 2$, then any two vertices (also any two edges) from each $T_{a_i}$, $i\in [0,\ell -1]$, can be distinguished by S.

What follows are three useful lemmas by which we derive our main results in the subsequent sections.

Lemma 4.

Suppose that G is a unicyclic graph with $|\mathcal{A}(S)|\ge 2$, where $S\in \mathcal{B}(G)$. Let $a_i,a_j$ be two S-active vertices such that $0<|j-i|\le \lfloor \frac{\ell -1}{2}\rfloor$ ( $\mathcal{C}$ is labeled normally). If neither $a_i$ nor $a_j$ is a bad vertex, then any two vertices $v_1,v_2$ (respectively, any two edges $e_1,e_2$) such that $\{v_1,v_2\}\cap (V(T_{a_i}\cup V(T_{a_j}))\ne \varnothing$ (respectively, $\{e_1,e_2\}\cap (E(T_{a_i}\cup E(T_{a_j}))\ne \varnothing$) can be distinguished by S.

Proof. 

Let $i=0$ and $i<j\le \lfloor \frac{\ell -1}{2}\rfloor$. It suffices to deal with $\{v_1,v_2\}\cap V(T_{a_0})\ne \varnothing$ (respectively, $\{e_1,e_2\}\cap E(T_{a_0})\ne \varnothing$), since the case that $\{v_1,v_2\}\cap V(T_{a_j})\ne \varnothing$ (respectively, $\{e_1,e_2\}\cap E(T_{a_j})\ne \varnothing$) can be addressed in a similar way. Without loss of generality, assume that $v_1\in V(T_{a_0})$ (respectively, $e_1\in E(T_{a_0})$) and let $v_2\in V(T_{a_{j^{\prime }}})$ (respectively, $e_2\in E(T_{a_{j^{\prime }}})$ or $e_2=a_{j^{\prime }}{a}_{j^{\prime }+1}\in E(\mathcal{C})$), where $j^{\prime }\in [0,\ell -1]$ and $a_{\ell }=a_0$. By Lemma 3, we only consider the case $v_2\notin V(T_{a_0})$ (respectively, $e_2\notin E(T_{a_0})$). Let $u\in (V_{T_{a_0}}\cap S)$ and $v\in (V_{T_{a_j}}\cap S)$. In the remainder of the proof, we suppose that $d_G(u,v_1)=d_G(u,v_2)$ (respectively, $d_G(u,e_1)=d_G(u,e_2)$). Clearly, $v_1\notin V(P_{u,a_0})$ (respectively, $e_1\notin E(P_{u,a_0})$, otherwise $d_G(u,v_1)<d_G(u,v_2)$ (respectively, $d_G(u,e_1)<d_G(u,e_2)$). Moreover, since $d_G(u)=1$, $u\notin V(P_{a_0,v_1})$ (respectively, $u\notin E(P_{a_0,e_1}$). We denote by $x\in V(P_{u,v_1})\cap V(P_{u,a_0})$ (respectively, $x\in V(P_{u,e_1})\cap V(P_{u,a_0})$) the vertex that has the minimum distance with $a_0$ ($x=a_0$ is possible).

$\left\{\begin{array}{c}{d}_G(u,v_1)=d_G(u,x)+d_G(x,v_1)\hfill \\ d_G(u,v_2)=d_G(u,x)+d_G(x,a_0)+d_G(a_0,v_2)\hfill \\ d_G(v,v_1)=d_G(v,a_j)+j+d_G(x,a_0)+d_G(x,v_1)\hfill \\ d_G(v,v_2)=d_G(v,a_j)+d_G(a_j,a_{j^{\prime }})+d_G(a_{j^{\prime }},v_2)\hfill \end{array}\right.$

(respectively, $\left\{\begin{array}{c}{d}_G(u,e_1)=d_G(u,x)+d_G(x,e_1)\hfill \\ d_G(u,e_2)=d_G(u,x)+d_G(x,a_0)+d_G(a_0,e_2)\hfill \\ d_G(v,e_1)=d_G(v,a_j)+j+d_G(a_0,x)+d_G(x,e_1)\hfill \\ d_G(v,e_2)=d_G(v,a_j)+d_G(a_j,e_2)\hfill \end{array}\right.$)

Beginning with the premise $d_G(u,v_1)=d_G(u,v_2)$ (respectively, $d_G(u,e_1)=d_G(u,e_2)$), we have $d_G(x,v_1)=d_G(x,a_0)+d_G(a_0,a_{j^{\prime }})+d_G(a_{j^{\prime }},v_2)$ (respectively, $d_G(x,e_1)=d_G(x,a_0)+d_G(a_0,e_2)$). Now, suppose that $d_G(v,v_1)=d_G(v,v_2)$ (respectively, $d_G(v,e_1)=d_G(v,e_2)$). Then,

$$d_G(a_j,a_{j^{\prime }})=j+2d_G(x,a_0)+d_G(a_0,a_{j^{\prime }})(respectively,d_G(a_j,e_2)=j+2d_G(x,a_0)+d_G(a_0,e_2))$$

(1)

Case 1. $x\ne a_0$. Then, $d_G(x,a_0)>0$. By Equation (1), $j^{\prime }>\lfloor \frac{\ell }{2}\rfloor$. Thus, $d_G(a_0,a_{j^{\prime }})=\ell -j^{\prime }$ (respectively, $d_G(a_0,e_2)=\ell -j^{\prime }+d_G(a_{j^{\prime }},e_2)$ when $e_2\notin E(\mathcal{C})$ and $d_G(a_0,e_2)=\ell -j^{\prime }-1$ when $e_2\in E(\mathcal{C})$). If $j^{\prime }-j\le \lfloor \frac{\ell -1}{2}\rfloor$, then $d_G(a_j,a_{j^{\prime }})=j^{\prime }-j$ (respectively, $d_G(a_j,e_2)=j^{\prime }-j+d_G(a_{j^{\prime }},e_2)$ when $e_2\notin E(\mathcal{C})$ and $d_G(a_j,e_2)=j^{\prime }-j$ when $e_2\in E(\mathcal{C})$), which implies (by Equation (1)) that $2d_G(x,a_0)=2j^{\prime }-2j-\ell \le 0$ (or $2d_G(x,a_0)=2j^{\prime }-2j-\ell +1\le 0$ when $e_2\in E(\mathcal{C})$, since $\ell \equiv 1$ (mod 2) in this case), a contradiction. If $j^{\prime }-j>\lfloor \frac{\ell -1}{2}\rfloor$, then $d_G(a_j,a_{j^{\prime }})=\ell -j^{\prime }+j$ (respectively, $d_G(a_j,e_2)=\ell -j^{\prime }+j+d_G(a_{j^{\prime }},e_2)$ when $e_2\notin E(\mathcal{C})$ and $d_G(a_j,e_2)=\ell -j^{\prime }-1+j$ when $e_2\in E(\mathcal{C})$), which implies (by Equation (1)) that $d_G(x,a_0)=0$, a contradiction.

Case 2. $x=a_0$. Then, $d_G(u,v_1)=d_G(u,v_2)$ (respectively, $d_G(u,e_1)=d_G(u,e_2)$) implies that $d_G(a_0,v_1)=d_G(a_0,v_2)$ (respectively, $d_G(a_0,e_1)=d_G(a_0,e_2)$). Notice that $v_1\ne a_0$ (respectively, $e_1\notin E(P_{u,a_0})$). We have that $T_{a_0}-a_0$ is disconnected. Let $T^{\prime }$ be the component of $T_{a_0}-a_0$ that contains $v_1$ (respectively, $e_1$ or one endpoint of $e_1$ when $a_0\in V(e_1)$). Clearly, $u\notin V(T^{\prime })$. Since $a_0$ is not a bad vertex, $V(T^{\prime })\cap S\ne \varnothing$. Let $w\in (V(T^{\prime })\cap S)$ and let $w^{\prime }\in (V(P_{w,v_1})\cap V(P_{a_0,v_1}))$ (respectively, $w^{\prime }\in (V(P_{w,e_1})\cap V(P_{a_0,v_1}))$) be the vertex that has the minimum distance with $a_0$. Clearly, $w^{\prime }\ne a_0$. Observe that $d_G(w)=1$. Thus, $w\notin V(P_{a_0,v_1})$ (except for the case that $w=v_1$, for which $d_G(w,v_1)=0<d_G(w,v_2)$) and $w\notin V(P_{a_0,e_1})$. We also assume that $v_1$ (respectively, $e_1$) is not on $P_{a_0,w}$; otherwise $d_G(w,v_1)<d_G(w,v_2)$ (respectively, $d_G(w,e_1)<d_G(w,e_2)$). Thus, $d_G(w,v_1)=d_G(w,w^{\prime })+d_G(w^{\prime },v_1)$ and $d_G(a_0,v_1)=d_G(a_0,w^{\prime })+d_G(w^{\prime },v_1)$ (respectively, $d_G(w,e_1)=d_G(w,w^{\prime })+d_G(w^{\prime },e_1)$ and $d_G(a_0,e_1)=d_G(a_0,w^{\prime })+d_G(w^{\prime },e_1)$). As a result, $d_G(w,v_2)=d_G(w,w^{\prime })+d_G(w^{\prime },a_0)+d(a_0,v_2)=d_G(w,w^{\prime })+d_G(w^{\prime },a_0)+d_G(a_0,v_1)$ (respectively, $d_G(w,e_2)=d_G(w,w^{\prime })+d_G(w^{\prime },a_0)+d_G(a_0,e_1)$). If $d_G(w,v_1)=d_G(w,v_2)$ (respectively, $d_G(w,e_1)=d_G(w,e_2)$), then $d_G(a_0,w^{\prime })=0$, i.e., $a_0=w^{\prime }$, a contradiction. □

Lemma 5.

Let $G\in \mathcal{E}(\ell )$ and $S\in \mathcal{B}(G)$. Suppose that $\mathcal{A}(S)$ contains two vertices, say $a_0,a_j$, such that $1\le j\le \frac{\ell -2}{2}$. Then, each vertex $w\in (V(T_{a_k})\cap S)$ for $k\in [1,j-1]$ can distinguish two vertices $v_1\in V(T_{a_{i^{\prime }}})$ and $v_2\in V(T_{a_{j^{\prime }}})$ (respectively, two edges $e_1\in E(T_{a_{i^{\prime }}})$ and $e_2\in V(T_{a_{j^{\prime }}})$) for $i^{\prime }\in [1,j-1]$ and $j^{\prime }\in [\frac{\ell }{2}+1,\frac{\ell }{2}+j]$ such that $d_G(a_0,v_1)=d_G(a_0,v_2)$ and $d_G(a_j,v_1)=d_G(a_j,v_2)$ (respectively, $d_G(a_0,e_1)=d_G(a_0,e_2)$ and $d_G(a_j,e_1)=d_G(a_j,e_2)$).

Proof. 

For convenience, we use $x_i$ to denote $v_i$ or $e_i$ for $i\in [1,2]$, and let $d_G(a_{i^{\prime }},v_i)=m_i$ (respectively, $d_G(a_{i^{\prime }},e_i)=m_i$). Then, for any $x_i\in \{v_i,e_i\}$ ($i\in [1,2]$), $d_G(a_0,x_1)=i^{\prime }+m_1,d_G(a_0,x_2)=\ell -j^{\prime }+m_2,d_G(a_j,x_1)=j-i^{\prime }+m_1,$ and $d_G(a_j,x_2)=j^{\prime }-j+m_2$. By $d_G(a_0,v_1)=d_G(a_0,v_2)$ and $d_G(a_j,v_1)=d_G(a_j,v_2)$ (respectively, $d_G(a_0,e_1)=d_G(a_0,e_2)$ and $d_G(a_j,e_1)=d_G(a_j,e_2)$), we deduce that $m_1-m_2=\ell -(i^{\prime }+j^{\prime })$ and $\ell =2(i^{\prime }+j^{\prime }-j)$. Let $d_G(w,a_k)=m$, where $a_k$ is the master of vertices of $T_{a_k}$, $k\in (1,j-1)$.

Case 1. $k\ne i^{\prime }$. In this case, $d_G(w,x_1)=m+|k-i^{\prime }|+m_1$. When $j^{\prime }-k\le \frac{\ell }{2}$, $d_G(w,x_2)=m+j^{\prime }-k+m_2$. If $d_G(w,x_1)=d_G(w,x_2)$, then either $\ell =2(i^{\prime }+j^{\prime }-k)$ (when $k>i^{\prime }$) which implies that $k=j$, or $j^{\prime }=\frac{\ell }{2}$ (when $k<i^{\prime }$). When $j^{\prime }-k>\frac{\ell }{2}$, $d_G(w,x_2)=m+k+\ell -j^{\prime }+m_2$. If $d_G(w,x_1)=d_G(w,x_2)$, then either $i^{\prime }=0$ (when $k>i^{\prime }$), or $k=0$ (when $k<i^{\prime }$). Clearly, each of these cases yields a contradiction.

Case 2. $k=i^{\prime }$. If $x_1$ is on $P_{w,a_{i^{\prime }}}$, it is clear that $d_G(w,v_1)<d_G(w,v_2)$ (respectively, $d_G(w,e_1)<d_G(w,e_2)$). Thus, suppose that $x_1$ is not on $P_{w,a_{i^{\prime }}}$. Let $w^{\prime }$ be the common vertex shared by $P_{w,a_{i^{\prime }}}$ and $P_{w,x_1}$ that has the minimum distance with $a_{i^{\prime }}$. Then, $d_G(w,x_1)=d_G(w,w^{\prime })+d_G(w^{\prime },x_1)$ and $m_1=d_G(a_{i^{\prime }},w^{\prime })+d_G(w^{\prime },x_1)$. Note that $j^{\prime }\ge \frac{\ell }{2}+1$, $m_2=m_1-\ell +(i^{\prime }+j^{\prime })$, and $d_G(w^{\prime },x_1)\le m_1$. When $j^{\prime }-i^{\prime }\le \frac{\ell }{2}$, we have that $d_G(w,x_2)=d_G(w,w^{\prime })+d_G(w^{\prime },a_{i^{\prime }})+j^{\prime }-i^{\prime }+m_2=d_G(w,w^{\prime })+d_G(w^{\prime },a_{i^{\prime }})+(2j^{\prime }-\ell )+m_1>d_G(w,x_1)$. When $j^{\prime }-i^{\prime }>\frac{\ell }{2}$, we have that $d_G(w,x_2)=d_G(w,w^{\prime })+d_G(w^{\prime },a_{i^{\prime }})+\ell -j^{\prime }+i^{\prime }+m_2=d_G(w,w^{\prime })+d_G(w^{\prime },a_{i^{\prime }})+2i^{\prime }+m_1>d_G(w,x_1)$. □

Lemma 6.

Suppose that G is a unicyclic graph. Then, for any $0<j\le \lfloor \frac{\ell -1}{2}\rfloor$, two vertices $v_1\in V(T_{a_{i^{\prime }}})$ and $v_2\in V(T_{a_{j^{\prime }}})$ (respectively, two edges $e_1\in E(T_{a_{i^{\prime }}})$ and $e_2\in E(T_{a_{j^{\prime }}}$)) such that $i^{\prime },j^{\prime }\in [0,\ell -1]\setminus \{i,j\}$, say $i=0$ and $i^{\prime }<j^{\prime }$ cannot be distinguished by $\{a_0,a_j\}$ if and only if one of the following conditions holds, where $m_1=d_G(a_{i^{\prime }},v_1)$ and $m_2=d_G(a_{i^{\prime }},v_2)$ (respectively, $m_1=d_G(a_{i^{\prime }},e_1)$ and $m_2=d_G(a_{i^{\prime }},e_2)$).

(i) 

$j^{\prime }\in [j+1,\lfloor \frac{\ell }{2}\rfloor ]$, $i^{\prime }>j$, and $m_1-m_2=j^{\prime }-i^{\prime }$;

(ii) 

$j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +1,\lfloor \frac{\ell }{2}\rfloor +j]$, $i^{\prime }<j$, $\ell =2i^{\prime }+2j^{\prime }-2j$, and $m_1-m_2=\ell -j^{\prime }-i^{\prime }$;

(iii) 

$j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +j+1,\ell -1]$, $\ell =2(i^{\prime }-j)$, and $m_1-m_2=i^{\prime }-j^{\prime }$; or $i^{\prime }>\lfloor \frac{\ell }{2}\rfloor +j$ and $m_1-m_2=i^{\prime }-j^{\prime }$.

Proof. 

Notice that when (i) holds, $d_G(a_0,v_1)=i^{\prime }+m_1,d_G(a_0,v_2)=j^{\prime }+m_2,d_G(a_j,v_1)=i^{\prime }-j+m_1$, and $d_G(a_j,v_2)=j^{\prime }-j+m_2$; when (ii) holds, $d_G(a_0,v_1)=i^{\prime }+m_1,d_G(a_0,v_2)=\ell -j^{\prime }+m_2,d_G(a_j,v_1)=j-i^{\prime }+m_1$, and $d_G(a_j,v_2)=j^{\prime }-j+m_2$; when (iii) holds, $d_G(a_0,v_1)=\ell -i^{\prime }+m_1,d_G(a_0,v_2)=\ell -j^{\prime }+m_2,d_G(a_j,v_1)=\frac{\ell }{2}+m_1$, and $d_G(a_j,v_2)=\ell +j-j^{\prime }+m_2$; or $d_G(a_0,v_1)=\ell -i^{\prime }+m_1,d_G(a_0,v_2)=\ell -j^{\prime }+m_2,d_G(a_j,v_1)=\ell -i^{\prime }+j+m_1$, and $d_G(a_j,v_2)=\ell +j-j^{\prime }+m_2$. One can readily check that $d_G(a_0,v_1)=d_G(a_0,v_2)$ and $d_G(a_j,v_1)=d_G(a_j,v_2)$ when one of the above three conditions holds.

Now, suppose that $v_1,v_2$ (respectively, $e_1,e_2$) cannot be distinguished by S, i.e., $d_G(a_0,a_{i^{\prime }})+m_1=d_G(a_0,a_{j^{\prime }})+m_2$ and $d_G(a_j,a_{i^{\prime }})+m_1=d_G(a_j,a_{j^{\prime }})+m_2$. Then,

$$d_G(a_0,a_{i^{\prime }})-d_G(a_0,a_{j^{\prime }})=d_G(a_j,a_{i^{\prime }})-d_G(a_j,a_{j^{\prime }}),\mathrm{and}{m}_1-m_2=d_G(a_0,a_{j^{\prime }})-d_G(a_0,a_{i^{\prime }})$$

(2)

Clearly, $j^{\prime }>j$ (otherwise, $d_G(a_0,a_{i^{\prime }})-d_G(a_0,a_{j^{\prime }})<0$ but $d_G(a_j,a_{i^{\prime }})-d_G(a_j,a_{j^{\prime }})>0$, a contradiction).

Case 1. $j^{\prime }\in [j+1,\lfloor \frac{\ell }{2}\rfloor ]$. Then, $d_G(a_0,a_{i^{\prime }})=i^{\prime },d_G(a_0,a_{j^{\prime }})=j^{\prime },d_G(a_j,a_{i^{\prime }})=|j-i^{\prime }|$, and $d_G(a_j,a_{j^{\prime }})=j^{\prime }-j.$ By Equation (2), if $i^{\prime }<j$, then we derive $i^{\prime }=j$, a contradiction. Therefore, $i^{\prime }>j$, and hence $m_1-m_2=j^{\prime }-i^{\prime }$.

Case 2. $j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +1,\lfloor \frac{\ell }{2}\rfloor +j]$. When $i^{\prime }>\lfloor \frac{\ell }{2}\rfloor$, $d_G(a_0,a_{i^{\prime }})=\ell -i^{\prime },d_G(a_0,a_{j^{\prime }})=\ell -j^{\prime },d_G(a_j,a_{i^{\prime }})=i^{\prime }-j$, and $d_G(a_j,a_{j^{\prime }})=j^{\prime }-j.$ By Equation (2), we derive $i^{\prime }=j^{\prime }$, a contradiction. When $i^{\prime }\le \lfloor \frac{\ell }{2}\rfloor$, $d_G(a_0,a_{i^{\prime }})=i^{\prime },d_G(a_0,a_{j^{\prime }})=\ell -j^{\prime },d_G(a_j,a_{i^{\prime }})=|j-i^{\prime }|$, and $d_G(a_j,a_{j^{\prime }})=j^{\prime }-j.$ By Equation (2), if $i^{\prime }>j$, then $\ell =2j^{\prime }$, a contradiction. Therefore, it holds that $i^{\prime }<j$, by which we derive $\ell =2i^{\prime }+2j^{\prime }-2j$ and $m_1-m_2=\ell -j^{\prime }-i^{\prime }$.

Case 3. $j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +j+1,\ell -1]$. When $i^{\prime }\le \lfloor \frac{\ell }{2}\rfloor$, $d_G(a_0,a_{i^{\prime }})=i^{\prime },d_G(a_0,a_{j^{\prime }})=\ell -j^{\prime },d_G(a_j,a_{i^{\prime }})=|j-i^{\prime }|$, and $d_G(a_j,a_{j^{\prime }})=\ell -j^{\prime }+j.$ By Equation (2), we deduce that either $i^{\prime }=0$ (when $i^{\prime }<j$) or $j=0$ (when $i^{\prime }>j$), a contradiction. Therefore, $i^{\prime }>\lfloor \frac{\ell }{2}\rfloor$. Moreover, when $\lfloor \frac{\ell }{2}\rfloor <i^{\prime }\le \lfloor \frac{\ell }{2}\rfloor +j$, $d_G(a_0,a_{i^{\prime }})=\ell -i^{\prime },d_G(a_0,a_{j^{\prime }})=\ell -j^{\prime },d_G(a_j,a_{i^{\prime }})=i^{\prime }-j$, and $d_G(a_j,a_{j^{\prime }})=\ell -j^{\prime }+j.$ By Equation (2), we deduce that $\ell =2i^{\prime }-2j$ and $m_1-m_2=i^{\prime }-j^{\prime }$. When $i^{\prime }>\lfloor \frac{\ell }{2}\rfloor +j$, then $d_G(a_0,a_{i^{\prime }})=\ell -i^{\prime }$ and $d_G(a_0,a_{j^{\prime }})=\ell -j^{\prime }$, which implies that $m_1-m_2=i^{\prime }-j^{\prime }$. □

3. Metric Dimension

This section is devoted to the argument of our main results for metric dimension. Similar conclusions for edge metric dimension are presented in the next section. To achieve our purpose, we need to construct four families of graphs G for which dim(G) = $L(G)$ or edim(G) = $L(G)$. The first two families of graphs (for metric dimension) are described here (Definition 1), while the other two families of graphs (for edge metric dimension) are introduced in the following section (Definition 2).

Definition 1.

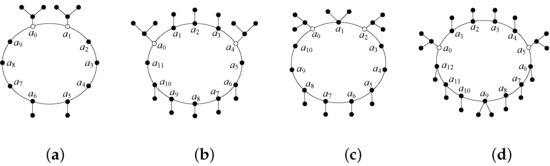
Suppose that G is a unicyclic graph of length $\ell (\ge 3)$ and $j\in [1,\lfloor \frac{\ell -1}{2}\rfloor ]$. If $G\in \mathcal{O}(\ell )$ satisfies either $j=\lfloor \frac{\ell -1}{2}\rfloor$ or the following two conditions (i) and (ii) hold, then we call G an odd-$(\ell ,j)$graph; if $G\in \mathcal{E}(\ell )$ satisfies the following three conditions, (i), (ii), and (iii), then we call G an even-$(\ell ,j)$graph.

(i) 

Neither $a_0$ nor $a_j$ is a bad vertex.

(ii) 

If $j<\lfloor \frac{\ell -2}{2}\rfloor$, $V(T_{a_k})=\left\{a_k\right\}$ for every $k\in \{\ell -1,\dots ,\ell -(\lfloor \frac{\ell -2}{2}\rfloor -j)\}\cup \{j+1,\dots ,j+(\lfloor \frac{\ell -2}{2}\rfloor -j)\}$.

(iii) 

If $j>1$ and $T_{a_k}$ contains no branching vertex for every $k\in [1,j-1]$, then the length of $T_{a_k}$ is at most $\frac{\ell -2}{2}-j$.

We use $\mathcal{O}(\ell ,j)$ and $\mathcal{E}(\ell ,j)$ to denote the set of all odd-$(\ell ,j)$ graphs and even-$(\ell ,j)$ graphs, respectively. See Figure 1 for some examples of odd-$(\ell ,j)$ graphs and even-$(\ell ,j)$ graphs.

Figure 1. (a) Even-(10,1); (b) even-(12,4); (c) odd-(11,2); (d) odd-(13,5).

We observe that when $G\in \mathcal{O}(\ell )$, $\{a_0,a_{\frac{\ell -1}{2}}\}$ is enough to distinguish two vertices not in the same $T_{a_i}$ for $i\in [0,\ell -1]$, by which we obtain the following conclusion, but this result does not hold for $G\in \mathcal{E}(\ell )$.

Lemma 7.

Let $G\in \mathcal{O}(\ell )$. Then, $S\in \mathcal{B}(G)$ is a metric generator if there are two S-active vertices with distance $\frac{\ell -1}{2}$.

Proof. 

By symmetry, let $a_0\in \mathcal{A}(S)$ and $a_{\gamma }\in \mathcal{A}(S)$, where $\gamma =\frac{\ell -1}{2}$. Let $x,y\in V(G)$ be two distinct vertices, and $a_i$ and $a_j$ ($i,j\in [0,\ell -1]$) be the masters of x and y, respectively. By Lemma 3, let $i\ne j$. Moreover, if $\{i,j\}\cap \{0,\gamma \}\ne \varnothing$, say $i=0$ (the other cases can be discussed in the same way), then under the condition of $d_G(a_0,x)=d_G(a_0,y)$ we deduce that $d_G(a_{\gamma },x)=d(a_0,x)+\gamma =d(a_0,y)+\gamma =d_G(a_0,a_j)+d_G(a_j,y)+\gamma >d_G(a_j,y)+d_G(a_j,a_{\gamma })=d_G(a_{\gamma },y)$ (since $d_G(a_0,a_j)>0$ and $d_G(a_j,a_{\gamma })<\gamma$). Therefore, we assume $i<j$ and $i,j\in [0,\ell -1]\setminus \{0,\gamma \}$. Then, by Lemma 6, x and y can be distinguished by $\{a_0,a_{\gamma }\}$, i.e., $d_G(x,a_0)\ne$$d_G(y,a_0)$ and $d_G(x,a_{\gamma })\ne$$d_G(y,a_{\gamma })$. Moreover, since $a_0$ and $a_{\gamma }$ are S-active vertices, we let $s_1=V(T_{a_0}\cap S$), $s_2=V(T_{a_{\gamma }}\cap S$), $m_1$=$d_G(s_1,a_0)$, and $m_2$ = $d_G(s_2,a_{\gamma })$. Then, $d_G(x,a_0)+m_1\ne$$d_G(y,a_0)+m_1$ and $d_G(x,a_{\gamma })+m_2\ne$$d_G(y,a_{\gamma })+m_2$. This implies that x and y can be distinguished by S. □

Let us now turn to a more general sufficient condition for a unicyclic graph G satisfying $\dim (G)$ = $L(G)$.

Lemma 8.

Suppose that G is a unicyclic graph such that $|\mathcal{A}(S)|\ge 2$, where $S\in \mathcal{B}(G)$. Label $\mathcal{C}(G)$ normally. If there exists an integer $j\in [1,\lfloor \frac{\ell -1}{2}\rfloor ]$ such that $a_j\in \mathcal{A}(S)$ and $G\in \mathcal{O}(\ell ,j)\cup \mathcal{E}(\ell ,j)$, then $\dim (G)$ = $L(G)$.

Proof. 

By Lemma 1, it suffices to prove that S is a metric generator. If $\ell \equiv 1$ (mod 2) and $j=\frac{\ell -1}{2}$, then the conclusion follows from Lemma 7. Thus, assume that $1\le j\le \lfloor \frac{\ell -2}{2}\rfloor$. Let $x,y$ be two distinct vertices in G, whose masters are $a_{i^{\prime }}$ and $a_{j^{\prime }}$ ($i^{\prime },j^{\prime }\in [0,\ell -1]$), respectively. By Lemmas 3 and 4, assume that $i^{\prime }\ne j^{\prime }$ (say $i^{\prime }<j^{\prime }$) and $\{i^{\prime },j^{\prime }\}\cap \{0,j\}=\varnothing$. Let $u\in V(T_{a_0})\cap S$, $v\in V(T_{a_j})\cap S$, $m_1=d_G(x,a_{i^{\prime }})$, and $m_2=d_G(y,a_{j^{\prime }})$. In the below, we suppose that

$$d_G(a_0,x)=d_G(a_0,y)and{d}_G(a_j,x)=d_G(a_j,y)$$

(3)

By Lemma 6, one of the following conditions holds: (i) $j^{\prime }\in [j+1,\lfloor \frac{\ell }{2}\rfloor ]$, $i^{\prime }>j$, and $m_1-m_2=j^{\prime }-i^{\prime }$; (ii) $j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +1,\lfloor \frac{\ell }{2}\rfloor +j]$, $i^{\prime }<j$, $\ell =2i^{\prime }+2j^{\prime }-2j$, and $m_1-m_2=\ell -j^{\prime }-i^{\prime }$; (iii) $j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +j+1,\ell -1]$, $\ell =2(i^{\prime }-j)$, and $m_1-m_2=i^{\prime }-j^{\prime }$; or $i^{\prime }>\lfloor \frac{\ell }{2}\rfloor +j$ and $m_1-m_2=i^{\prime }-j^{\prime }$.

For (i), by $G\in \mathcal{O}(\ell ,j)\cup \mathcal{E}(\ell ,j)$ (Definition 1 (ii)), we deduce that $m_1=0$ and $m_2=i^{\prime }-j^{\prime }<0$, a contradiction. For (ii), we have that $\ell \equiv 0$ (mod 2) and $m_1=\frac{\ell }{2}-j+m_2\ge \frac{\ell }{2}-j$. Therefore, by $G\in \mathcal{E}(\ell ,j)$ (Definition 1 (iii)), there exists a vertex $k\in [1,j-1]$ such that $T_{a_k}$ contains a branching vertex. Thus, $S\cap V(T_{a_k})\ne \varnothing$, say $w\in S\cap V(T_{a_k})$. By Lemma 5, x and y can be distinguished by w. For (iii), we have that $j^{\prime }\ge \lceil \frac{\ell +2}{2}\rceil +j$ and $m_2=j^{\prime }-i^{\prime }+m_1>0$ (which implies that $|V(T_{a_{j^{\prime }}})|>1$), a contradiction to $G\in \mathcal{E}(\ell ,j)$ (Definition 1 (ii)). □

Based on Lemma 8, we can obtain one of our main results (for metric dimension) as follows.

Theorem 1.

Suppose that G is a unicyclic graph with $|\mathcal{A}(S)|\ge 2$, where $S\in \mathcal{B}(G)$. Label $\mathcal{C}(G)$ normally and let $j=max\{i:a_i\in \mathcal{A}(S)\}$. S is a metric generator if and only if $G\in \mathcal{O}(\ell ,j)\cup \mathcal{E}(\ell ,j)$ or $\mathcal{A}(S)$ contains three vertices that form a geodesic triple.

Proof. 

By Lemmas 2 and 8, it suffices to consider the necessity. Let S be a metric generator. Suppose that $\mathcal{A}(S)$ does not contain three vertices that form a geodesic triple, which implies $j\le \lfloor \frac{\ell }{2}\rfloor$. In particular, when $j=\lfloor \frac{\ell }{2}\rfloor$ and $G\in \mathcal{E}(\ell )$, it has that $\mathcal{A}(S)=\{a_0,a_j\}$ and $d_G(s,a_i)=d_G(s,a_{\ell -i})$ for every $i\in [1,\frac{\ell -2}{2}]$ and every $s\in S$, a contradiction. In the below, we assume that $j\le \lfloor \frac{\ell -1}{2}\rfloor$ and we prove that $G\in \mathcal{O}(\ell ,j)\cup \mathcal{E}(\ell ,j)$.

Suppose, to the contrary, that $G\notin \mathcal{O}(\ell ,j)$ (respectively, $G\notin \mathcal{E}(\ell ,j)$). Then, at least one of the following conditions (i) and (ii) (respectively, (i), (ii), and (iii)) holds.

(i)

$a_0$ or $a_j$ is a bad vertex.

(ii)

When $j<\lfloor \frac{\ell -2}{2}\rfloor$, there exists a $k\in (\{\ell -1,\dots ,\ell -(\lfloor \frac{\ell -2}{2}\rfloor -j)\}\cup \{j+1,\dots ,j+(\lfloor \frac{\ell -2}{2}\rfloor -j)$ such that $|V(T_{a_k})|>1$.

(iii)

When $j>1$ and $T_{a_{k^{\prime }}}$ contains no branching vertex for every $k^{\prime }\in [1,j-1]$, there exists some $k\in [1,j-1]$ such that the length of $T_{a_k}$ is at least $\frac{\ell }{2}-j$.

For (i), suppose that $a_0$ is a bad vertex (the case for $a_j$ can be discussed similarly). By the selection of S, there is a thread $T^{\prime }$ attached to $a_0$ which contains no vertex of S. Let $u\in V(T^{\prime })$ be the vertex adjacent to $a_0$, $0\le j^{\prime }\le j$. Then, $d_G(u,s)=1+j^{\prime }+d_G(a_{j^{\prime }},s)=d_G(a_{\ell -1},s)$ for any $s\in S\cap ({\cup }_{0\le j^{\prime }\le j}V(T_{a_{j^{\prime }}}))$. Thus, S cannot distinguish u and $a_{\ell -1}$, a contradiction.

For (ii), consider the vertex $u\in V(T_{a_k})$ that is adjacent to $a_k$. If $k\in \{\ell -1,\dots ,\ell -(\lfloor \frac{\ell -2}{2}\rfloor -j)\}$, then $k-1\ge \lceil \frac{\ell }{2}\rceil +j$, and hence $d_G(u,s)=1+(\ell -k)+j^{\prime }+d_G(a_{j^{\prime }},s)=d_G(a_{k-1},s)$ for any $s\in S\cap ({\cup }_{0\le j^{\prime }\le j}V(T_{a_{j^{\prime }}}))$. Thus, S cannot distinguish u and $a_{\ell -1}$, a contradiction. If $k\in \{j+1,\dots ,j+(\lfloor \frac{\ell -2}{2}\rfloor -j)$, then $k+1\le \lfloor \frac{\ell }{2}\rfloor$, and hence $d_G(u,s)=1+(k-j^{\prime })+d_G(a_{j^{\prime }},s)=d_G(a_{k+1},s)$ for any $s\in S\cap ({\cup }_{0\le j^{\prime }\le j}V(T_{a_{j^{\prime }}}))$. Thus, S cannot distinguish u and $a_{\ell -1}$, a contradiction.

For (iii), S contains only vertices in $V(T_{a_0})\cup V(T_{a_j})$. Let $u\in V(T_{a_k})$ be the vertex that has distance $\frac{\ell }{2}-j$ with $a_k$. Consider the vertex $a_{\frac{\ell }{2}+j-k}$. Since $\frac{\ell }{2}+j-k>\frac{\ell }{2}$ and $\frac{\ell }{2}+j-k-j=\frac{\ell }{2}-k<\frac{\ell }{2}$, we have that $d_G(a_{\frac{\ell }{2}+j-k},s)=\frac{\ell }{2}-j+k+d(a_0,s)=d_G(u,a_0)$ for any $s\in S\cap V(T_{a_0})$ and $d_G(a_{\frac{\ell }{2}+j-k},s^{\prime })=(\frac{\ell }{2}-j)+(j-k)+d_G(a_j,s^{\prime })=d_G(u,a_j)$ for any $s^{\prime }\in S\cap V(T_{a_j})$. Thus, S cannot distinguish u and $a_{\frac{\ell }{2}+j-k}$, a contradiction. □

Notice that for every two distinct vertices $a_p,a_q\in V(\mathcal{C})$ we can always find a vertex $a_r\in V(\mathcal{C})\setminus \{a_p,a_q\}$ such that $a_p,a_q,a_r$ form a geodesic triple. Thus, by Lemmas 1 and 2, we have that 2 ≤ dim(G) $\le 3$ when $L(G)=0$, $L(G)+1\le$ dim(G) $\le L(G)+2$ when $L(G)=1$, and $L(G)\le$ dim(G) $\le L(G)+1$ when $L(G)\ge 2$. Then, the following result holds by Theorem 1.

Corollary 1.

Given a unicyclic graph G and $S\in \mathcal{B}(G)$, we label $\mathcal{C}(G)$ normally and let $j=max\{i:a_i\in \mathcal{A}(S)\}$ when $|\mathcal{A}(S)|\ge 2$. If $G\in \mathcal{O}(\ell )$, it holds that

(1) 

When $\mathcal{A}(S)=\varnothing$, $\dim (G)=2$.

(2) 

When $|\mathcal{A}(S)|=1$, $\dim (G)=L(G)+1$.

(3) 

When $|\mathcal{A}(S)|\ge 2$, if $G\in \mathcal{O}(\ell ,j)$ or $\mathcal{A}(S)$ contains three vertices that form a geodesic triple, then $\dim (G)=L(G)$; otherwise, $\dim (G)=L(G)+1$.

Moreover, if $G\in \mathcal{E}(\ell )$, it holds that

(1) 

When $\mathcal{A}(S)=\varnothing$, if there are two vertices on $\mathcal{C}$ (say $a_0$ and $a_k$) such that $G\in \mathcal{E}(\ell ,k)$, then dim(G) = 2; otherwise dim(G) = 3.

(2) 

When $|\mathcal{A}(S)|=1$, let $\mathcal{A}(S)=\left\{a_k\right\}$. If there exists a vertex $a_{k^{\prime }}\in V(\mathcal{C})\setminus \left\{a_k\right\}$ such that $G\in \mathcal{E}(\ell ,k^{\prime })$ (let $k=0$) or $G\in \mathcal{E}(\ell ,k)$ (let $k^{\prime }=0$), then dim(G)=$L(G)+1$; otherwise, dim(G) = $L(G)$ + 2.

(3) 

When $|\mathcal{A}(S)|\ge 2$, if $G\in \mathcal{E}(\ell ,j)$ or $\mathcal{A}(S)$ contains three vertices that form a geodesic triple, then dim(G) = $L(G)$; otherwise, dim(G) = $L(G)+1$.

4. Edge Metric Dimension

The previous section showed that the metric dimension of unicyclic graphs can be exactly determined by the aid of odd- and even-$(\ell ,j)$ graphs. This section moves on to consider the edge metric dimension of unicyclic graphs. Before proceeding further, it is important to introduce the other two families of graphs.

Definition 2.

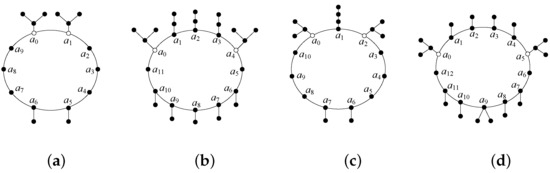
Suppose that G is a unicyclic graph of length $\ell (\ge 3)$ and $j\in [1,\lfloor \frac{\ell -1}{2}\rfloor ]$. If $G\in \mathcal{O}(\ell )$ satisfies the following condition (i), (ii), and (iii), then we call G an edge-odd-$(\ell ,j)$graph; if $G\in \mathcal{E}(\ell )$ satisfies the following conditions (i), (ii), and (iv), then we call G an edge-even-$(\ell ,j)$graph.

(i) 

Neither $a_0$ nor $a_j$ is a bad vertex.

(ii) 

When $j<\lfloor \frac{\ell -1}{2}\rfloor$, $V(T_{a_k})=\left\{a_k\right\}$ for every $k\in \{\ell -1,\dots ,\ell -(\lfloor \frac{\ell -1}{2}\rfloor -j)\}\cup \{j+1,\dots ,j+(\lfloor \frac{\ell -1}{2}\rfloor -j)\}$.

(iii) 

When $j>1$ and $T_{a_k}$ contains no branching vertex for every $k\in [1,j-1]$, then the length of $T_{a_k}$ is at most $\frac{\ell -1}{2}-j$.

(iv) 

When $j>1$ and both $T_{a_k}$ and $T_{a_{k^{\prime }}}$ contain no branching vertex for every $k\in [1,j-1]$ and $k^{\prime }=\frac{\ell }{2}+j-k$, if $|V(T_{a_{k^{\prime }}})|>1$, then the length of $T_{a_k}$ is at most $\frac{\ell }{2}-j$.

We use ${\mathcal{O}}_e(\ell ,j)$ and ${\mathcal{E}}_e(\ell ,j)$ to denote the set of all edge-odd-$(\ell ,j)$ graphs and edge-even-$(\ell ,j)$ graphs, respectively. See Figure 2 for some examples of edge-odd-$(\ell ,j)$ graphs and edge-even-$(\ell ,j)$ graphs.

Figure 2. (a) Edge-even-(10,1); (b) edge-even-(12,4); (c) edge-odd-(11,2); (d) edge-odd-(13,5).

Let us now turn to the discussion of the edge metric dimension of unicyclic graphs based on edge-odd and edge-even graphs. Although the conclusions (and their proofs) in this section are analogous to those in Section 3, there are still a number of important differences between them. Thus, we fully describe them as well.

Lemma 9.

Let G be a unicyclic graph with $|\mathcal{A}(S)|\ge 2$, where $S\in \mathcal{B}(G)$. Label $\mathcal{C}(G)$ normally. If there exists a $j\in [1,\lfloor \frac{\ell -1}{2}\rfloor ]$ such that $a_j\in \mathcal{A}(S)$ and $G\in {\mathcal{O}}_e(\ell ,j)\cup {\mathcal{E}}_e(\ell ,j)$, then $\mathrm{edim}(G)$ = $L(G)$.

Proof. 

By Lemma 1, it suffices to show that S is an edge metric generator. Note that $\mathcal{C}$ is labeled normally. If there exists some $r>\lfloor \frac{\ell }{2}\rfloor$ for which $a_r\in \mathcal{A}(S)$, then $\mathcal{A}(S)$ contains three vertices that form a geodesic triple, and S is an edge metric generator of G by Lemma 2. Thus, we assume that $T_{a_r}$ contains no branching vertex for every $\lfloor \frac{\ell }{2}\rfloor <r\le \ell -1$.

Let $e_1,e_2$ be an arbitrary pair of edges in G. Clearly, if both $e_1\in E(\mathcal{C})$ and $e_2\in E(\mathcal{C})$, then $e_1$ and $e_2$ can be distinguished by $\{a_0,a_j\}$, and also by S. By Lemmas 3 and 4, $e_1$ and $e_2$ can be distinguished by S if $e_1\in E(T_{a_i})$ and $e_2\in E(T_{a_i})$ for some $i\in [0,\ell -1]$ or $\{e_1,e_2\}\cap (E(T_{a_0})\cup E(T_{a_j}))\ne \varnothing$. In the below, we assume that $e_2\in E(T_{a_{j^{\prime }}})$ for some $j^{\prime }\in [0,\ell -1]$, $\{e_1,e_2\}\cap (E(T_{a_0})\cup E(T_{a_j}))=\varnothing$, and there does not exist any $i\in [0,\ell -1]$ such that $\{e_1,e_2\}\subseteq E(T_{a_i})$. Let $e_2=w_1{w}_2$ and $d_G(a_{j^{\prime }},e_2)=d_G(a_{j^{\prime }},w_1)=m_2$. This also implies that $d_G(a_0,e_2)=d_G(a_0,w_1)$ and $d_G(a_j,e_2)=d_G(a_j,w_1)$. Now, suppose that

$$d_G(a_0,e_1)=d_G(a_0,e_2)\mathrm{and}{d}_G(a_j,e_1)=d_G(a_j.e_2)$$

(4)

We derive a contradiction or show that $e_1$ and $e_2$ can be distinguished by a vertex in $S\setminus (V(T_{a_0})\cup V(T_{a_j}))$.

Case 1. $e_1\in E(\mathcal{C})$. Let $e_1=a_{i^{\prime }}{a}_{i^{\prime }+1}$, where $i^{\prime }\in [0,\ell -1]$ and $a_{\ell }=a_0$. By $G\in {\mathcal{O}}_e(\ell ,j)\cup {\mathcal{E}}_e(\ell ,j)$ (Definition 2 (ii)), we have that $j^{\prime }\in [1,j-1]$ or $\lfloor \frac{\ell -1}{2}\rfloor <j^{\prime }<\ell -\lfloor \frac{\ell -1}{2}\rfloor +j$ (note that $j^{\prime }\notin \{0,j\}$). Moreover, when $j^{\prime }>\lfloor \frac{\ell -1}{2}\rfloor$, it follows that $i^{\prime }<j^{\prime }$; otherwise, $d_G(a_0,e_1)=d_G(a_0,a_{i^{\prime }+1})<d_G(a_0,a_{j^{\prime }})\le d_G(a_0,e_2)$, a contradiction to Equation (4).

Case 1.1. $j^{\prime }\in [1,j-1]$. Then, $d_G(a_0,e_2)=j^{\prime }+m_2$ and $d_G(a_j,e_2)=j-j^{\prime }+m_2$. If $i^{\prime }\le j$, then either $d_G(a_0,e_1)<d_G(a_0,e_2)$ (when $i^{\prime }<j^{\prime }$) or $d_G(a_j,e_1)<d_G(a_j,e_2)$ (when $i^{\prime }\ge j^{\prime }$), a contradiction to Equation (4). If $j<i^{\prime }\le \lfloor \frac{\ell -1}{2}\rfloor$, then $d_G(a_0,e_1)=i^{\prime }$ and $d_G(a_j,e_1)=i^{\prime }-j$. By Equation (4), we deduce that $j=j^{\prime }$, a contradiction. If $\lfloor \frac{\ell -1}{2}\rfloor +j<i^{\prime }\le \ell -1$, then $d_G(a_0,e_1)=\ell -(i^{\prime }+1)$ and $d_G(a_j,e_1)=\ell -(i^{\prime }+1)$ +j (notice that in this case $i^{\prime }$ does not exist when $\ell \equiv 1$ (mod 2) and $j=\frac{\ell -1}{2}$). By Equation (4), we deduce that $j^{\prime }=0$, a contradiction.

Moving on now to consider $\lfloor \frac{\ell -1}{2}\rfloor <i^{\prime }\le \lfloor \frac{\ell -1}{2}\rfloor +j$, it follows that $d_G(a_0,e_1)=\ell -i^{\prime }-1$ and $d_G(a_j,e_1)=i^{\prime }-j$. Then, by Equation (4), we derive $\ell =2i^{\prime }+2j^{\prime }-2j+1$ and $m_2=i^{\prime }+j^{\prime }-2j=\frac{\ell -1}{2}-j$. This shows that there does exist a $j^{″}\in [1,j-1]$ for which $S\cap V(T_{a_{j^{″}}})\ne \varnothing$, since if not, $T_{a_i}$ contains no branching vertex for every $i\in [1,j-1]$ while $T_{a_{j^{\prime }}}$ has length of at least $m_2+1=\frac{\ell -1}{2}-j+1$, a contradiction to $G\in {\mathcal{O}}_e(\ell ,j)$ (Definition 2 (iii)). Let $w\in S\cap V(T_{a_{j^{″}}})\ne \varnothing$ and we will prove that $e_1$ and $e_2$ can be distinguished by w.

For this, we construct a new graph $G^{\prime }$ that is obtained from G by subdividing edge $e_1$ (i.e., delete $e_1$, add a new vertex, say $a^{\prime }$, and join $a^{\prime }$ to $a_{i^{\prime }}$ and $a_{i^{\prime }+1}$). Let ${\ell }^{\prime }=\ell +1$ and consider $G^{\prime }$. Clearly, $G^{\prime }\in \mathcal{E}({\ell }^{\prime })$, $j\in [1,\frac{{\ell }^{\prime }-2}{2}]$, and $S\in \mathcal{B}(G^{\prime })$. With regard to $\mathcal{C}(G^{\prime })$, a normal labeling can be obtained based on $\mathcal{C}(G)$ by relabeling $a^{\prime }$ with $a_{i^{\prime }+1}$ and $a_i$ with $a_{i+1}$ for every $i\in \{i^{\prime }+1,\dots ,\ell -1\}$. Notice that $j^{\prime },j^{″}\in [1,j-1]$, $\frac{{\ell }^{\prime }}{2}+1\le i^{\prime }+1\le \frac{{\ell }^{\prime }}{2}+j$, $d_G(a_0,w_2)=d_G(a_0,e_2)+1$, and $d_G(a_j,w_2)=d_G(a_j,e_2)+1$. Thus, $d_{G^{\prime }}(a_0,a_{i^{\prime }+1})=d_G(a_0,a_{i^{\prime }})=d_G(a_0,e_1)+1=d_G(a_0,e_2)+1=d_G(a_0,w_2)$ and $d_{G^{\prime }}(a_j,a_{i^{\prime }+1})=d_G(a_j,a_{i^{\prime }})+1=d_G(a_j,e_1)+1=d_G(a_j,e_2)+1=d_G(a_j,w_2)$. Then, by Lemma 5, $d_{G^{\prime }}(w,a_{i^{\prime }+1})\ne d_{G^{\prime }}(w,w_2)$. For graph G (and also for $G^{\prime }$), if $e_2$ is on $P_{w,a_{j^{\prime }}}$, then clearly $d_G(w,e_2)<d_G(w,e_1)$. We therefore assume that $e_2$ is not on $P_{w,a_{j^{\prime }}}$, which implies that $d_G(w,e_2)=d_G(w,w_1)=d_G(w,w_2)-1=d_{G^{\prime }}(w,w_2)-1$. Additionally, when (in $G^{\prime }$) $i^{\prime }+1-j^{″}\le \frac{{\ell }^{\prime }}{2}$, it holds that (in G) $i^{\prime }-j^{″}\le \frac{\ell -1}{2}$ and hence $d_G(w,e_1)=d_G(w,a_{i^{\prime }})=d_{G^{\prime }}(w,a_{i^{\prime }+1})-1$; when (in $G^{\prime }$) $i^{\prime }+1-j^{″}>\frac{{\ell }^{\prime }}{2}$, it holds that (in G) $i^{\prime }-j^{″}>\frac{\ell -1}{2}$ and hence $d_G(w,e_1)=d_G(w,a_{i^{\prime }+1})=d_{G^{\prime }}(w,a_{i^{\prime }+2})=d_{G^{\prime }}(w,a_{i^{\prime }+1})-1$. As a conclusion, $d_G(w,e_1)=d_{G^{\prime }}(w,a_{i^{\prime }+1})-1\ne d_{G^{\prime }}(w,w_2)-1=d_G(w,e_2)$.

Case 1.2. $\lfloor \frac{\ell -1}{2}\rfloor <j^{\prime }<\ell -\lfloor \frac{\ell -1}{2}\rfloor +j$. Then, $i^{\prime }<j^{\prime }\le \ell -\lfloor \frac{\ell -1}{2}\rfloor +j-1$, and $d_G(a_0,e_2)=\ell -j^{\prime }+m_2$ and $d_G(a_j,e_2)=j^{\prime }-j+m_2$. Furthermore, if $0\le i^{\prime }\le \lfloor \frac{\ell -1}{2}\rfloor$, then $d_G(a_0,e_1)=i^{\prime }$, and $d_G(a_j,e_1)=i^{\prime }-j$ (when $i^{\prime }\ge j$) or $d_G(a_j,e_1)=j-(i^{\prime }+1)$ (when $i^{\prime }<j$). By Equation (4), we derive $m_2=i^{\prime }-j^{\prime }<0$ (when $i^{\prime }\ge j$) or $m_2=j-\frac{\ell +1}{2}<0$ (when $i^{\prime }<j$), a contradiction. If $\lfloor \frac{\ell -1}{2}\rfloor +1\le i^{\prime }<\ell -\lfloor \frac{\ell -1}{2}\rfloor +j-1$, then $i^{\prime }-j<\lfloor \frac{\ell }{2}\rfloor$, and $d_G(a_0,e_1)=\ell -(i^{\prime }+1)$ and $d_G(a_j,e_1)=i^{\prime }-j$. By Equation (4), we have $2i^{\prime }=2j^{\prime }-1$, a contradiction.

Case 2. $e_1\notin E(\mathcal{C})$. Let $e_1\in T_{a_{i^{\prime }}}$ for some $i^{\prime }\in [0,\ell -1]\setminus \{0,j,j^{\prime }\}$ and $d_G(a_{i^{\prime }},e_1)=m_1$. Without loss of generality, we assume that $i^{\prime }<j^{\prime }$. Then, by Equation (4) and Lemma 6, one of the following conditions holds: (i) $j^{\prime }\in [j+1,\lfloor \frac{\ell }{2}\rfloor ]$, $i^{\prime }>j$, and $m_1-m_2=j^{\prime }-i^{\prime }$; (ii) $j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +1,\lfloor \frac{\ell }{2}\rfloor +j]$, $i^{\prime }<j$, $\ell =2i^{\prime }+2j^{\prime }-2j$, and $m_1-m_2=\ell -j^{\prime }-i^{\prime }$; (iii) $j^{\prime }\in [\lfloor \frac{\ell }{2}\rfloor +j+1,\ell -1]$, $\ell =2(i^{\prime }-j)$, and $m_1-m_2=i^{\prime }-j^{\prime }$; or $i^{\prime }>\lfloor \frac{\ell }{2}\rfloor +j$ and $m_1-m_2=i^{\prime }-j^{\prime }$.

For (i), by $G\in {\mathcal{O}}_e(\ell ,j)\cup {\mathcal{E}}_e(\ell ,j)$ (Definition 2 (ii)), we deduce that $m_1=0$ and $m_2=i^{\prime }-j^{\prime }<0$, a contradiction. For (ii), we have that $\ell \equiv 0$ (mod 2), $j^{\prime }=\frac{\ell }{2}+j-i^{\prime }$, and $m_1=\frac{\ell }{2}-j+m_2\ge \frac{\ell }{2}-j$ (which implies that the length of $T_{a_{i^{\prime }}}$ is at least $m_1+1\ge \frac{\ell }{2}-j+1$). Therefore, by $G\in {\mathcal{E}}_e(\ell ,j)$ (Definition 2 (iv)), there exists a vertex $k\in [1,j-1]$ such that $T_{a_k}$ contains a branching vertex. Thus, $S\cap V(T_{a_k})\ne \varnothing$, say $w\in S\cap V(T_{a_k})$. By Lemma 5, x and y can be distinguished by w. For (iii), we have that $j^{\prime }\ge \lceil \frac{\ell +2}{2}\rceil +j$ and $|V(T_{a_{j^{\prime }}})|>1$, a contradiction to $G\in \mathcal{E}(\ell ,j)$ (Definition 2 (ii)). □

Theorem 2.

Suppose that G is a unicyclic graph such that $|\mathcal{A}(S)|\ge 2$, where $S\in \mathcal{B}(G)$. Label $\mathcal{C}(G)$ normally and let $j=max\{i:a_i\in \mathcal{A}(S)\}$. S is an edge metric generator if and only if $G\in {\mathcal{O}}_e(\ell ,j)\cup {\mathcal{E}}_e(\ell ,j)$ or $\mathcal{A}(S)$ contains three vertices that form a geodesic triple.

Proof. 

The sufficiency follows from Lemmas 2 and 9. Suppose that S is an edge metric generator, and there are not three S-active vertices forming a geodesic triple. This shows that $j\le \lfloor \frac{\ell }{2}\rfloor$, and $\mathcal{A}(S)=\{a_0,a_j\}$ when $j=\lfloor \frac{\ell }{2}\rfloor$ and $G\in \mathcal{E}(\ell )$ (however, in this case $d_G(s,a_i{a}_{i+1})=d_G(s,a_{\ell -i-1}{a}_{\ell -i})$ for every $i\in [0,\frac{\ell -2}{2}]$ and every $s\in S$, where $a_{\ell }=a_0$, a contradiction). In the below, we assume that $j\le \lfloor \frac{\ell -1}{2}\rfloor$ and we will prove that $G\in \mathcal{O}(\ell ,j)\cup \mathcal{E}(\ell ,j)$. To the contrary, if $G\notin {\mathcal{O}}_e(0,j)$ (respectively, $G\notin {\mathcal{E}}_e(0,j)$), then at least one of the following conditions (i), (ii), and (iii) (respectively, (i), (ii), and (iv)) holds.

(i)

$a_0$ or $a_j$ is a bad vertex.

(ii)

When $j<\lfloor \frac{\ell -1}{2}\rfloor$, there exists a $k\in (\{\ell -1,\dots ,\ell -(\lfloor \frac{\ell -1}{2}\rfloor -j)\}\cup \{j+1,\dots ,j+(\lfloor \frac{\ell -1}{2}\rfloor -j)$ such that $|V(T_{a_k})|>1$.

(iii)

When $j>1$ and $T_{a_{k^{\prime }}}$ contains no branching vertex for every $k^{\prime }\in [1,j-1]$, there exists a $k\in [1,j-1]$ such that $T_{a_k}$ is a path of length at least $\frac{\ell +1}{2}-j$.

(iv)

When $j>1$ and both $T_{a_i}$ and $T_{a_{i^{\prime }}}$ contain no branching vertex for every $i\in [1,j-1]$ and $i^{\prime }=\frac{\ell }{2}+j-i$, there exists a $k\in [1,j-1]$ and a $k^{\prime }=\frac{\ell }{2}+j-k$ such that $|V(T_{a_{k^{\prime }}})|>1$ and $T_{a_k}$ has length at least $\frac{\ell }{2}-j+1$.

For (i), suppose that $a_0$ is a bad vertex. By the selection of S, there is a thread $T^{\prime }$ attached to $a_0$ such that $V(T^{\prime })\cap S=\varnothing$. Let $u\in V(T^{\prime })$ such that $u{a}_0\in E(G)$. Then, $d_G(s,u{a}_0)=j^{\prime }+d_G(s,a_{j^{\prime }})=d_G(s,a_{\ell -1}{a}_0)$ for any $s\in S\cap ({\cup }_{0\le j^{\prime }\le j}V(T_{a_{j^{\prime }}}))$. Therefore, S cannot distinguish $u{a}_0$ and $a_{\ell -1}{a}_0$.

For (ii), consider the vertex $u\in V(T_{a_k})$ that is adjacent to $a_k$. If $k\in \{\ell -1,\dots ,\ell -(\lfloor \frac{\ell -1}{2}\rfloor -j)\}$, then $k-1\ge \lceil \frac{\ell -1}{2}\rceil +j$, and hence $d(s,u{a}_k)=(\ell -k)+j^{\prime }+d_G(s,a_0)=d(s,a_{k-1}{a}_k)$ for any $s\in S\cap ({\cup }_{0\le j^{\prime }\le j}V(T_{a_{j^{\prime }}}))$. Therefore, S cannot distinguish $u{a}_k$ and $a_{k-1}{a}_k$. If $k\in \{j+1,\dots ,j+(\lfloor \frac{\ell -1}{2}\rfloor -j)$, then $d_G(s,u{a}_k)=d_G(s,a_k)=d_{(}s,a_k{a}_{k+1})$ for any $s\in S\cap ({\cup }_{0\le j^{\prime }\le j}V(T_{a_{j^{\prime }}}))$. Therefore, S cannot distinguish $u{a}_k$ and $a_k{a}_{k+1}$.

For (iii), $\ell \equiv 1$ (mod 2) and S contains only vertices in $V(T_{a_0})\cup V(T_{a_j})$. Let $u{u}^{\prime }\in E(T_{a_k})$ be the edge that has distance $\frac{\ell -1}{2}-j$ with $a_k$. Consider edge $a_{k^{\prime }}{a}_{k^{\prime }+1}$ where $k^{\prime }=\frac{\ell -1}{2}+j-k$. Observe that $k\in [1,j-1]$; we have $k^{\prime }=\frac{\ell -1}{2}-k+j>\frac{\ell -1}{2}$ and $k^{\prime }-j<\frac{\ell -1}{2}$. Therefore, $d_G(s,a_{k^{\prime }}{a}_{k^{\prime }+1})=\ell -(k^{\prime }+1)+d_G(a_0,s)=\frac{\ell -1}{2}-j+k+d_G(a_0,s)=d_G(s,u{u}^{\prime })$ for any $s\in S\cap V(T_{a_0})$ and $d_G(s^{\prime },a_{k^{\prime }}{a}_{k^{\prime }+1})=k^{\prime }-j+d_G(a_j,s^{\prime })=(\frac{\ell -1}{2}-j)+(j-k)+d_G(a_j,s^{\prime })=d_G(s^{\prime },u{u}^{\prime })$ for any $s^{\prime }\in S\cap V(T_{a_j})$. Therefore, S cannot distinguish $u{u}^{\prime }$ and $a_{k^{\prime }}{a}_{k^{\prime }+1}$.

For (iv), $\ell \equiv 0$ (mod 2) and S contains only vertices in $V(T_{a_0})\cup V(T_{a_j})$. Let $u{u}^{\prime }\in E(T_{a_k})$ be the edge that has distance exactly $\frac{\ell }{2}-j$ with $a_k$, and $v{a}_{k^{\prime }}\in E(T_{a_{k^{\prime }}})$, where $k^{\prime }=\frac{\ell }{2}+j-k$. Observe that $k\in [1,j-1]$. We have that $k^{\prime }>\frac{\ell }{2}$ and $k^{\prime }-j<\frac{\ell }{2}$. Therefore, $d_G(s,v{a}_{k^{\prime }})=\ell -k^{\prime }+d_G(a_0,s)=(\frac{\ell }{2}-j)+k+d_G(a_0,s)=d_G(s,u{u}^{\prime })$ for any $s\in S\cap V(T_{a_0})$ and $d_G(s^{\prime },v{a}_{k^{\prime }})=k^{\prime }-j+d_G(a_j,s^{\prime })=(\frac{\ell }{2}-j)+(j-k)+d_G(a_j,s^{\prime })=d_G(s^{\prime },u{u}^{\prime })$ for any $s^{\prime }\in S\cap V(T_{a_j})$. Therefore, S cannot distinguish $u{u}^{\prime }$ and $v{a}_{k^{\prime }}$. □

Again, since for every two distinct vertices $a_p,a_q\in V(\mathcal{C})$ we can always find a vertex $a_r\in V(\mathcal{C})\setminus \{a_p,a_q\}$ such that $a_p,a_q,a_r$ form a geodesic triple, it follows by Lemmas 1 and 2 that 2 ≤ edim(G)$\le 3$ when $L(G)=0$, $L(G)+1\le$ edim(G)$\le L(G)+2$ when $L(G)=1$, and $L(G)\le$ edim(G)$\le L(G)+1$ when $L(G)\ge 2$. Thus, the following result holds by Theorem 2.

Corollary 2.

Given a unicyclic graph G and $S\in \mathcal{B}(G)$, we label $\mathcal{C}(G)$ normally and let $j=max\{i:a_i\in \mathcal{A}(S)\}$ when $|\mathcal{A}(S)|\ge 2$. Then,

(1) 

When $\mathcal{A}(S)=\varnothing$, if there are two vertices on $\mathcal{C}$, say $a_0$ and $a_j$, such that $G\in {\mathcal{O}}_e(\ell ,j)\cup {\mathcal{E}}_e(\ell ,j)$, then edim(G) = 2; otherwise edim(G) = 3.

(2) 

When $|\mathcal{A}(S)|=1$, let $\mathcal{A}(S)=\left\{a_k\right\}$. If there exists a vertex $a_{k^{\prime }}\in V(\mathcal{C})\setminus \left\{a_k\right\}$ such that $G\in {\mathcal{O}}_e(\ell ,k^{\prime })\cup {\mathcal{E}}_e(\ell ,k^{\prime })$ (let $k=0$) or $G\in {\mathcal{O}}_e(\ell ,k)\cup {\mathcal{E}}_e(\ell ,k)$ (let $k^{\prime }=0$), then edim(G)=$L(G)+1$; otherwise, edim(G) = $L(G)$ + 2.

(3) 

When $|\mathcal{A}(S)|\ge 2$, if $G\in {\mathcal{O}}_e(0,j)\cup {\mathcal{E}}_e(0,j)$ or $\mathcal{A}(S)$ contains three vertices that form a geodesic triple, then edim(G)=$L(G)$; otherwise, edim(G) = $L(G)+1$.

5. Remarks and Conclusions

According to Definitions 1 and 2, we see that ${\mathcal{O}}_e(\ell ,j)\subset \mathcal{O}(\ell ,j)$ and $\mathcal{E}(\ell ,j)\subset {\mathcal{E}}_e(\ell ,j)$. Therefore, by Corollaries 1 and 2, we can determine the relation between metric dimension and edge metric dimension for unicyclic graphs, as shown in Table 1, and give an answer to Problems 1 and 2. Indeed, by Table 1, we can generate an efficient algorithm to compute the value of $\dim (G)$, $\mathrm{edim}(G)$, and $\dim (G)-\mathrm{edim}(G)$.

Table 1. Metric dimension and edge metric dimension of unicyclic graphs, and their relation. When $\mathcal{A}(S)$ does not contain three vertices that form a geodesic triple, we make the following assumptions: if $|\mathcal{A}(S)|\ge 2$, $\mathcal{C}$ is labeled normally (which means that $a_0\in \mathcal{A}(S)$) and let $j=max\left\{i\right|a_i$ is S-active}; if $|\mathcal{A}(S)|=1$, let $\mathcal{A}(S)=\left\{a_k\right\},k\in [0,\ell -1]$. In addition, we denote by $R_1:$$\mathcal{C}$ contains two vertices, say $a_0$ and $a_k$, such that $G\in {\mathcal{O}}_e(\ell ,k)$; $R_2:$ there is a $a_{k^{\prime }}\in V(\mathcal{C})\setminus \left\{a_k\right\}$ such that $G\in {\mathcal{O}}_e(\ell ,k^{\prime })$ (when let $k=0$) or $G\in {\mathcal{O}}_e(\ell ,k)$ (when let $k^{\prime }=0$); $R_3:$$G\in {\mathcal{O}}_e(\ell ,j)$ or $G\notin \mathcal{O}(\ell ,j)$; $R_4:$ there are two vertices on $\mathcal{C}$ (say $a_0$ and $a_k$) such that $G\in \mathcal{E}(\ell ,k)$, or for every two vertices (also say $a_0$ and $a_k$) on $\mathcal{C}$, $G\notin {\mathcal{E}}_e(\ell ,k)$; $R_5:$ there exists a $a_{k^{\prime }}\in V(\mathcal{C})\setminus \left\{a_k\right\}$ such that $G\in \mathcal{E}(\ell ,k)$ when let $k^{\prime }=0$ (or $G\in \mathcal{E}(\ell ,k^{\prime })$ when let $k=0$), or for every $a_{k^{\prime }}\in V(\mathcal{C})\setminus \left\{a_k\right\}$) $G\notin {\mathcal{E}}_e(\ell ,k)$ (when let $k^{\prime }=0$) and $G\notin {\mathcal{E}}_e(\ell ,k^{\prime })$ (when let $k=0$); $R_6:$$G\in \mathcal{E}(\ell ,j)$ or $G\notin {\mathcal{E}}_e(\ell ,j)$; and $\neg R_i$ denotes the negative of $R_i$ for $i\in [1,6]$.

A Unicyclic Graph G and $\mathit{S}\in \mathcal{B}(\mathit{G})$				$\mathbf{dim}(\mathit{G})$	$\mathbf{edim}(\mathit{G})$	$\mathbf{dim}(\mathit{G})$-$\mathbf{edim}(\mathit{G})$
$\mathcal{A}(S)$ contains three vertices forming a geodesic triple				$L(G)$	$L(G)$	0
$\mathcal{A}(S)$ contains no three vertices forming a geodesic triple	$\ell \equiv 1$ (mod 2)	$|\mathcal{A}(S)|=0$	$R_1$	2	2	0
			$\neg R_1$	2	3	−1
		$|\mathcal{A}(S)|=1$	$R_2$	$L(G)+1$	$L(G)+1$	0
			$\neg R_2$	$L(G)+1$	$L(G)+2$	−1
		$|\mathcal{A}(S)|\ge 2$	$R_3$	$L(G)$ (or L(G) + 1)	$L(G)$ (or $L(G)$ + 1)	0
			$\neg R_3$	$L(G)$	$L(G)$ + 1	−1
	$\ell \equiv 0$ (mod 2)	$|\mathcal{A}(S)|=0$	$R_4$	2 (or 3)	2 (or 3)	0
			$\neg R_4$	3	2	1
		$|\mathcal{A}(S)|=1$	$R_5$	$L(G)+1$ (or $L(G)$ + 2)	$L(G)+1$ (or $L(G)$ + 2)	0
			$\neg R_5$	$L(G)+2$	$L(G)+1$	1
		$|\mathcal{A}(S)|\ge 2$	$R_6$	$L(G)$ (or L(G) + 1)	$L(G)$ (or $L(G)$ + 1)	0
			$\neg R_6$	$L(G)+1$	$L(G)$	1

It is worth re-emphasizing here that although Sedlar and Škrekovski in [1] described a method to determine the (edge) metric dimension of unicyclic graphs, our work differs from theirs in a number of respects. First, our motivation to construct the four families of graphs was to characterize the structures of graphs G with $\dim (G)$ = $L(G)$ and $\mathrm{edim}(G)=L(G)$, respectively, which is different from that in [1] (indeed, our approach is completely opposite to that in [1]). Second, in the case of $|\mathcal{A}(S)|\ge 2$, based on the four families of graphs that we constructed, we obtained a necessary and sufficient condition for a set of vertices to be a metric (respectively, edge metric) generator of a unicyclic graph (Theorems 1 and 2). Third, in the case of $|\mathcal{A}(S)|<2$, we used a straightforward way to determine (edge) metric dimension, while in [1], the authors introduced an indirect definition based on their configurations to accomplish this, namely, $ABC$-positivity and $ABC$-negativity (a similar definition for edge metric dimension).

Our approach is more intuitive than the method in [1] and our discussions give a more thorough analysis on (edge) metric generator of a unicyclic graph (we characterize necessary and sufficient conditions for a vertex subset to be a (edge) metric generator). Moreover, our result can also be used to analyze dimensions for cactus graphs, which is left as future work. What follows is a direct application to a class of double-cyclic graphs.

A double-cyclic graph is a graph that contains exactly two edge disjoint cycles. Similarly, for a double-cyclic graph G, a branch-resolving set of G is a set $S\subseteq V(G)$ such that for every $3^{+}$-vertex v, at least $|\mathcal{S}(v)|-1$ threads in $\mathcal{S}(v)$ contain a vertex of S, where $\mathcal{S}(v)$ is the set of threads that are attached to v, and

$$L(G)=\sum _{v\in V(G),|\mathcal{S}(v)|>1}(|\mathcal{S}(v)|-1).$$

Clearly, dim$(G)\ge L(G)$. Here, we consider a special class of double-cyclic graphs, which are defined as follows.

Definition 3.

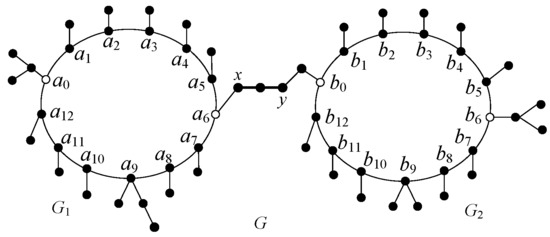
Let $G_1$ and $G_2$ be two unicyclic graphs such that for $i=1,2$, $G_i\in \mathcal{O}(\ell ,j)\cup \mathcal{E}({\ell }^{\prime },j^{\prime })$ and $|\mathcal{A}(S_i)|\ge 2$ for $S_i\in \mathcal{B}(G_i)$. Now, we construct a class of double-cyclic graph, denoted by $\mathcal{D}$, by connecting two vertices (say x and y respectively, where $x\in V(G_1)$ and $y\in V(G_2$) by an path $P_{x,y}$ with ends x and y such that the resulting graph G satisfies $L(G)=L(G_1)+L(G_2)$. See Figure 3 for an example.

Figure 3. A double-cyclic graph, where $G_1$ and $G_2$ are odd-$(13,6)$ graphs.

Lemma 10.

Let $G\in \mathcal{D}$ and $G_i$, $i=1,2$, is the unicyclic graph defined in Definition 3. Let $S_i\in \mathcal{B}(G_i)$ for $i=1,2$. If $|\mathcal{A}(S_i)|\ge 2$, then any two vertexes u and v such that $u\in V(G_1)$ and $v\in V(G_2)$ can be distinguished by $S_1\cup S_2$.

Proof. 

Denote by $u^{\prime }$ and $v^{\prime }$ the masters of u and v, respectively. Let $s\in S_1$ and $s^{\prime }$ is the master of s. Then, $d_G(s,u)=d_G(s,s^{\prime })+d_G(s^{\prime },u^{\prime })+d_G(u^{\prime },u)$ and $d_G(s,v)=d_G(s,s^{\prime })+d_G(s^{\prime },x)+d_G(x,y)+d_G(y,v^{\prime })+d_G(v^{\prime },v)$. Let $t\in S_2$ and $t^{\prime }$ is the master of t.

Notice that $d_G(s^{\prime },u^{\prime })\le d_G(s^{\prime },x)+d_G(x,u^{\prime })$. If $d_G(s,u)=d_G(s,v)$, then $d_G(x,u^{\prime })+d_G(u^{\prime },u)\ge d_G(x,y)+d_G(y,v^{\prime })+d_G(v^{\prime },v)$. On the other hand, $d_G(t,v)=d_G(t,t^{\prime })+d_G(t^{\prime },v^{\prime })+d_G(v^{\prime },v)$ and $d_G(t,u)=d_G(t,t^{\prime })+d_G(t^{\prime },y)+d_G(y,x)+d_G(x,u^{\prime })+d_G(u^{\prime },u)$ $\ge d_G(t,t^{\prime })+d_G(t^{\prime },y)+d_G(y,x)+d_G(x,y)+d_G(y,v^{\prime })+d_G(v^{\prime },v)=d_G(t,t^{\prime })+d_G(t^{\prime },y)+2d_G(x,y)+d_G(y,v^{\prime })+d_G(v^{\prime },v)$. Now, suppose that $d_G(t,v)=d_G(t,u)$. We have that $d_G(t^{\prime },v^{\prime })\ge d_G(t^{\prime },y)+2d_G(x,y)+d_G(y,v^{\prime })$. Observe that $d_G(x,y)>0$. It follows that y is not on the path $P_{t^{\prime },v^{\prime }}$. Then, $d_G(t^{\prime },v^{\prime })\le d_G(t^{\prime },y)+d_G(y,v^{\prime })$, which indicates that $d_G(t^{\prime },v^{\prime })<d_G(t^{\prime },y)+2d_G(x,y)+d_G(y,v^{\prime })$, a contradiction. Thus, $d_G(t,v)\ne d_G(t,u)$. □

Theorem 3.

Let $G\in \mathcal{D}$, and $G_i$, $i=1,2$, is the unicyclic graph defined in Definition 3. Let $S_i\in \mathcal{B}(G_i)$ for $i=1,2$. If $|\mathcal{A}(S_i)|\ge 2$, then, dim(G) = dim($G_1$) + dim($G_2$) = L($G_1$) + L($G_2$).

Proof. 

Since $G_i\in \mathcal{O}(\ell ,j)\cup \mathcal{E}({\ell }^{\prime },j^{\prime })$ and $|\mathcal{A}(S_i)|\ge 2$ for $i=1,2$, it follows by Lemma 8 that $S_i$ is a metric generator of $G_i$ and $|S_i|$ = dim($G_i$) = L($G_i$). Let u and v be any two vertices in G. If u and v belong to the same $G_i$ for some $i\in \{1,2\}$, then they can be distinguished by $S_i$. If one of u and v belongs to $P_{x,y}$, say u, then they can be distinguished by $S_1$ (when $v\in V(G_2)$) or $S_2$ (when $v\in V(G_1)$). If u and v belong to $G_1$ and $G_2$, respectively, then by Lemma 10 they can be distinguished by $S_1\cup S_2$. This implies that dim(G) ≤ dim($G_1$) + dim($G_2$) = L($G_1$) + L($G_2$). On the other hand, since $L(G)=L(G_1)+L(G_2)$, we have that dim(G) ≥ L($G_1$) + L($G_2$) = dim($G_1$) + dim($G_2$). Therefore, the conclusion holds. □