Abstract
Meta-analysis techniques allow researchers to jointly analyse different studies to determine common effects. In the field of transcriptomics, these methods have gained popularity in recent years due to the increasing number of datasets that are available in public repositories. Despite this, there is a limited number of statistical software packages that implement proper meta-analysis functionalities for this type of data. This article describes DExMA, an R package that provides a set of functions for performing gene expression meta-analyses, from data downloading to results visualization. Additionally, we implemented functions to control the number of missing genes, which can be a major issue when comparing studies generated with different analytical platforms. DExMA is freely available in the Bioconductor repository.
MSC:
62P10
1. Introduction
In recent years, due to the widespread use of high-throughput gene expression technologies, the amount of gene expression data stored in public databases such as GEO [1] has grown drastically [2]. Gene expression is the process by which a product (usually a protein) is generated from the information encoded in genes. Gene expression studies usually measure the expression levels of thousands of genes simultaneously and generate a gene expression matrix with thousands of variables (genes) and tens or hundreds of samples. Each element of the matrix represents the amount of mRNA of a gene in a sample. One of the main types of analyses carried out in these studies is finding genes that are differentially expressed among groups of samples by means of hypothesis testing of mean differences (case–control studies). Therefore, these databases are invaluable resources to help researchers perform new analyses and gain new scientific insights.
A meta-analysis is a statistical technique that has achieved considerable popularity during the last few years for the integration of gene expression studies and making inferences about a population of interest. Gene expression meta-analyses have been widely applied for different purposes such as increasing statistical power for the identification of biomarkers [3,4], the discovery of common gene expression patterns between different diseases [5,6], or the search for inverse gene expression patterns between different conditions [7].
An important step of a meta-analysis is to carry out prior quality control to reduce bias, check the homogeneity of data, detect unmeasured values, etc. This also helps to select the most appropriate method to be applied and avoid inaccurate results. The publication of inconsistent results and misinterpretations has been severely criticized in recent years [8,9]. Therefore, it is necessary to implement dedicated software that allows users to apply the different meta-analysis methods properly.
R packages have been previously developed for gene expression meta-analyses such as MetaIntegrator [10] or MetaVolcanoR [11]. Surprisingly, most of the available packages discard the genes not available in all the datasets included in the meta-analysis. Nevertheless, these missing genes may lead to the omission of relevant information, losing relevant patterns, and this can cause different results to be obtained between studies [12]. In other contexts, a typical solution to deal with missing values is to impute the missing values from the samples with available data within the same study. However, this approach is not applicable to gene expression meta-analyses, since expression values are absent for all the samples. The use of models to impute these missing genes from the correlation with other non-missing genes has been proposed [12]. Furthermore, methods that perform imputation from the samples of other studies have also been proposed, obtaining fewer errors when comparing the imputed and real values [13]. Nevertheless, none of these methods have been previously implemented in gene expression meta-analysis packages.
The DExMA package has been implemented to perform all the steps of gene expression meta-analyses, providing two functions to treat missing genes across datasets. The first approach is based on imputing missing genes from the samples of other studies using the k-nearest neighbours (sampkeKNN method) [13]. The second approach consists of considering those genes with available values in a minimum proportion of datasets selected by the user in the meta-analysis.
Moreover, DExMA allows users to download data from the GEO database simply by using the corresponding codes. In addition, it includes quality control steps and heterogeneity testing. This package is available in the Bioconductor repository (http://bioconductor.org/packages/release/bioc/html/DExMA.html, accessed on 31 August 2022).
In this article, we describe the main functions and functionalities of the DExMA package. In the first section, the different implemented meta-analysis methods are described. Next, we present the workflow through a use case with simulated data, and in the last section, we present results from the analysis of real expression datasets.
2. Materials and Methods
2.1. Meta-Analysis Methods
A gene expression meta-analysis encompasses a set of statistical methods that allow us to combine results from different gene expression studies to obtain a single result with greater statistical power and sample size. The most suitable method depends on the nature and characteristics of the analysed datasets [14]. The DExMA package includes most of the methods from the two main meta-analysis approaches: effect size combination and p-value combination.
2.1.1. Effect Size Combination Methods
A meta-analysis based on effect size combination aims to explain the strength of a measure (effect) between different groups (e.g., experimental and control groups). In the specific case of gene expression studies, the effect to be calculated is the difference in standardized means between the expression level of the experimental group and the control group. This model has the following assumptions [15]:
- There is independence between the experimental and the control group.
- Both the experimental and control groups are distributed according to a normal distribution with means μE and μC, respectively, and with the same σ2 variance.
Therefore, the effect size of a gene in the i-th dataset (Ti) is described as:
The DExMA package internally calculates Hedges’ g as an estimator of the effect size, which is obtained [15]:
where:
- , is a factor that corrects the positive bias. nE and nC are the sample sizes of the experimental and control groups, respectively.
- and are the gene expression means of the experimental and control group, respectively.
- is the standard deviation between studies. and are the variances in the experimental and control groups, respectively.
Moreover, the within-study variance of this estimator is calculated:
Once effect sizes and their variances have been calculated for each gene in the different studies, the combined effect size must be calculated to determine if a gene is differentially expressed.
To obtain the combined effect size and its corresponding p-value, DExMA provides the application of two models: the Fixed Effects Model (FEM) and the Random Effects Model (REM).
The FEM assumes that all studies share a true common effect size, that is to say, studies with more information have greater weight in the combined effect size. Therefore, the combined effect size ( and its variance (V) for k studies are calculated [15]:
where:
- Ti is the effect size of the i-th study.
- ωi is the weight assigned to the i-th study. In the case of a meta-analysis, the inverse of the variance is used as weights, .
Since the FEM model assumes the existence of normality, the z-value (z) of the combined effect size for a standard normal:
This z-value is used to calculate the p-value. Furthermore, in the specific case of a gene expression meta-analysis, this z-value is used to determine if the gene is over-expressed (z > 0) or under-expressed (z < 0).
The REM model considers that the true effect size varies from one study to another, that is, there is a distribution of the true effect sizes. The combined effect size () and its variance (V*) are calculated:
In this case, the calculation of the weights differs from the FEM, since it influences both the within-study variance (Vi) and between-study variance (τ2) [15]. The between-study variance is obtained:
where:
- represents the total variance, where:
- ωi is the calculated weight for the Fixed Effects Model.
- T. is the combined effect size for the Fixed Effects Model (Equation (2)).
- is a scaling-related factor related to the fact that Q is a weighted sum of squares.
- df = k − 1 are the degrees of freedom for the meta-analysis.
Therefore, the weights for the REM are calculated:
As in the FEM, the z-value of the combined effect size for a standard normal is calculated:
As for the FEM, this z-value is used to determine if the gene is over-expressed (z > 0) or under-expressed (z < 0).
2.1.2. p-Values Combination Methods
A meta-analysis based on p-values combination methods aims to merge all the p-values from different hypothesis tests into a single p-value. p-value combination methods have the following assumptions [16]:
- p1, …, pk are the p-values from the k independent studies.
- The t1, …, tk test statistics have absolute continuous probability distributions under their corresponding null hypotheses.
In the specific case of a gene expression meta-analysis, it seeks to obtain a combined p-value for each of the genes. The p-values are obtained from performing a differential expression analysis for each of the datasets. The DExMA package internally uses the limma Bioconductor package [17] in order to obtain the individual p-values. Afterward, to merge the individual p-values, DExMA implements five different p-value combination methods: Fisher’s method, Stouffer’s method, Tippett’s method, Wilkinson’s method, and the Aggregated Cauchy Association Test method (ACAT).
Fisher’s method calculates a statistic (SF) as the sum of the logarithm of the p-values, [18]. Under the null hypothesis, SF is distributed as x2 with 2 × k degrees of freedom [16].
Stouffer’s method assumes that [16], where is the standard normal cumulative distribution function. Then, for k independent studies, the statistic is calculated as the sum of the Zi values divided by the square root of the number of studies, . Under the null hypothesis, SS is distributed as a standard normal distribution [16]. Moreover, Stouffer’s method allows the inclusion of each of the datasets, . The DExMA package implements the square roots of sample sizes as weights [19].
Tippett’s method (also called the minimum of p-values method) and Wilkinson’s method (also called the maximum of p-values method) use the minimum of p-values and the maximum of p-values, respectively, as statistics, that is to say, and ). Under the null hypothesis, ST is distributed as a Beta(1,K), while SW is distributed as a Beta(K,1).
Finally, the ACAT method uses a weighted sum of the Cauchy transformation of individual p-values, , as a statistic, where the weights ωi are non-negative and . Under the null hypothesis, is distributed as a standard Cauchy distribution [20,21].
2.2. Control of Missing Genes
DExMA contains two different approaches to control the possible existence of missing genes: (i) the selection of the minimum number of datasets in which a gene must appear and (ii) missing genes imputation.
The first approach consists of performing a meta-analysis by only considering those genes contained in a minimum number (or proportion) of datasets. For example, if a gene is in 2 of 4 datasets and the user-defined threshold is that the gene should be contained in 75% of the studies, this gene will be discarded. In the final results, a variable is shown with the proportion of studies in which the gene is contained to help users to correctly interpret the results obtained.
The second approach applies the sampleKNN method described by Mancuso et al. [13]. This method imputes the gene expression of a gene by applying the KNN imputation in the space of samples. Firstly, to impute the expression value of missing genes, the k samples of datasets without missing genes and with the most similar expression are chosen. Then, the gene expression of these missing genes is imputed by calculating the weighted average of the expression in the k selected samples.
3. Results
3.1. The DExMA Package
The DExMA package includes the main methods for gene expression meta-analyses described previously. The DExMA workflow consists of five main steps (Figure 1): meta-analysis object creation, gene annotation, quality control, gene expression meta-analysis, and visualization. The DExMA package provides a set of functions that provide additional information. Table 1 contains a summary of all available functions.
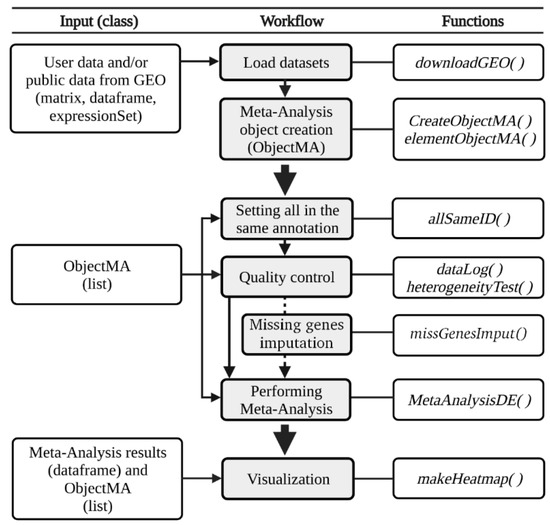
Figure 1.
DExMA workflow. The figure shows the main steps of the DExMA package workflow: (1) data load and meta-analysis object creation, (2) gene annotation, (3) quality control, (4) missing gene imputation (optional), (5) gene expression meta-analysis, and (6) visualization.

Table 1.
Functions implemented in DExMA. Brief description of the functions developed in DExMA.
In this section, the main steps to perform the gene expression meta-analysis are described. For this purpose, simulated gene expression data contained in the package itself, called DExMAExampleData, were analysed. The data DExMAExampleData contain six different objects:
- “listMatrixEX”: a list of four expression matrices.
- “listPhenodatas”: a list of the four phenodata dataframes corresponding to four expression matrices.
- “listExpressionSets”: a list of four ExpressionSet objects. It contains the same information as listMatrixEX and listPhenodatas.
- “ExpressionSetStudy5”: an ExpressionSet object similar to the ExpressionSets objects of listExpressionSets.
- “maObjectDif”: the meta-analysis object (objectMA) created from the listMatrixEx and listPhenodatas objects.
- “maObject”: the meta-analysis object (objectMA) after setting all the studies in Official Gene Symbol annotation.
Specifically, the listMatrixEX and listPhenodatas objects are used in the examples.
3.1.1. Meta-Analysis Object Creation
The first step in the analysis is the data entry. To this end, DExMA uses an objectMA object which is a list of nested lists where each one contains two elements: a gene expression matrix (with genes in rows and samples in columns) and a vector of 0 and 1 that indicates the group to which each sample belongs (0 represents the control group and 1 represents the experimental group).
DExMA provides the function createObjectMA() to facilitate the objectMA creation (details are provided in the package documentation).
When datasets with different gene names are used, it is necessary to convert them to a common gene identifier (ID). DExMA provides the allSameID() function, which allows us to translate genes to a common ID. Supported Gene IDs are official Gen Symbol or standard IDs from Entrez or Ensembl databases.
3.1.2. Quality Control
Quality control is a crucial step to conduct a proper meta-analysis and avoid misinterpretation. DExMA implements standard pre-processing steps in gene expression data analysis, such as data normalization and the analysis of heterogeneity [14].
Specifically, the datalog() function can be used to check if the data are in log scale or to perform log transformation, which is important when p-value combination methods are applied. To analyse data heterogeneity, DExMA provides the heterogeneityTest() function that implements two ways of measuring heterogeneity.
On the one hand, it returns a QQ-plot of Cochran’s heterogeneity test (Figure 2) [22]. In the case of homogeneity, it is expected that the majority of the values will be close to the expected distribution (the central line of the graph).
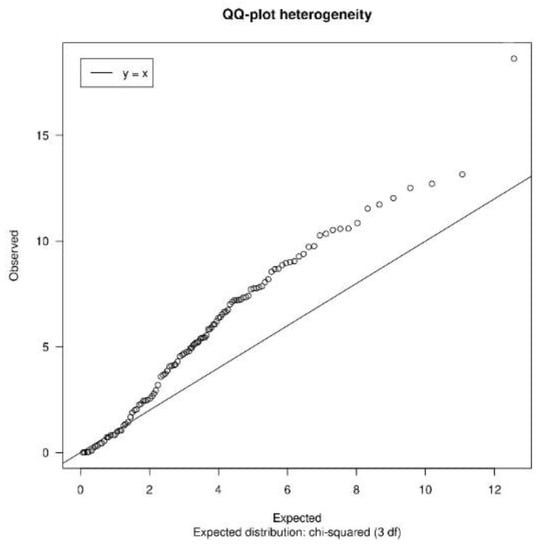
Figure 2.
Heterogeneity QQ-plot. QQ-plot of Cochran’s heterogeneity test values. The further the values are from the reference distribution (central line), the more heterogeneity there is.
In the case of homogeneity, it is expected that the majority of the values will be close to the expected distribution (the central line of the graph). On the contrary, if these points are distant from the central line, this is an indicator of heterogeneity.
On the other hand, the heterogeneityTest() function returns the quantiles of the I2 statistic. The I2 statistic measures the inconsistency, that is, the percentage of variation across studies due to heterogeneity [23]. When interpreting the I2 results, it is considered that there is low heterogeneity when the I2 value is less than 0.25 [23]. Therefore, to consider homogeneity, most of the I2 values must be less than 0.25.
3.1.3. Missing Gene Imputation
DExMA allows users to impute the expression of missing genes with the missGenesImput() function, which imputes the unmeasured expression using the k-nearest neighbours (KNN) in the space of samples (sampleKNN method). The function returns the objectMA with all the imputed studies.
Moreover, the missGenesImput() function returns an object (imputIndicators) with different indicators of the imputation. This item contains:
- imputValuesSample: the number of missing values imputed per sample.
- imputPercentageSample: the percentage of missing values imputed per sample.
- imputValuesGene: the number of missing values imputed per gene.
- imputPercentageGene: the percentage of missing values imputed per gene.
3.1.4. Performing Gene Expression Meta-Analysis
As it has been explained before, the main objective of the DExMA package is to perform the gene expression meta-analysis of several studies. For this purpose, DExMA includes the metaAnalysisDE() function. This function allows users to apply seven different techniques of meta-analysis described in the methods sections: the Fixed Effect Model (FEM); the Random Effects Model (REM); Fisher’s p-value combination method (Fisher); Stouffer’s p-value combination method (Stouffer); Wilkinson’s p-value combination method (maxP); Tippett’s p-value combination method (minP); and the Aggregated Cauchy Association Test method (ACAT).
If data imputation has not been previously applied, this function provides the option of considering genes that are in a minimum number of datasets. For example, if we have four datasets and we select that a gene must be in 75% of the datasets, those genes that are present in three or four datasets will be included in the meta-analysis. This allows users to control missing genes that are only present in a low number of datasets. Once the meta-analysis is complete, the function returns a table with the obtained results for both effect sizes and p-values based on the meta-analysis (see the package documentation for more details).
The results are also provided as heatmaps of the significant differentially expressed genes (see Figure 3). DExMA provides the makeHeatmap() function for that purpose, which implements four types of scaling options:

Figure 3.
Synthetic data heatmap. Heatmap of the meta-analysis results for the 40 most significant genes. The red colour indicates that a gene is overexpressed in that sample, blue that it is under-expressed, and grey that is not present.
- “rscales”: this applies rescale function of the scales package [24]. Therefore, values will be between −1 and 1.
- “zscor”: this calculates a z-score value for each gene and sample.
- “swr”: this scales relative to a reference dataset approach [25].
- “none”: no scaling approach is performed.
3.1.5. Other Useful Functions
DExMA provides some functions that allow users to speed up the analysis, correct the batch effect, or complete the results. With regard to accelerating the meta-analysis process, the function downloadGEOData() allows users to download multiple ExpressionSets objects from the GEO database [1]. In addition, the function elementObjectMA() can be used to create an element which can be added directly to a previously created objectMA, which avoids the user having to re-create the object from scratch. Regarding the batch effect correction, DExMA contains the function batchremove. The batchRemove function eliminates the effects of different covariates in the data variability. Finally, the functions calculateES() and pvalueIndAnalysis() return the effect sizes or the individual p-values of each study, respectively. This can help the user to better understand the results obtained.
3.2. Applying DExMA to Real Data
To illustrate the benefits of the DexMA package, it was applied to three real datasets. These data belong to systemic lupus erythematosus (SLE) gene expression studies, and they were extracted from the ADEX database [26]. Specifically, the identifiers of the selected studies were: GSE24706 [27], GSE50772 [28], and GSE82221_GPL10558 [29]. These studies were chosen because of their samples were generated from the same cell tissue, peripheral blood mononuclear cells (PBMCs). In this way, a greater homogeneity between datasets was ensured than if they were extracted from different cell types. The code used for the data preparation for the use case is available in Appendix A.
In this case, it was not necessary to apply the allSameID() function, since all the datasets are annotated in the Official Gene Symbol. In the study of heterogeneity, a QQ-plot (Figure 4) was obtained in which most of the points were quite far from the reference line. In addition, 25% of the genes had an I2 greater than 0.71, so it was concluded that there was heterogeneity between the different datasets. Therefore, as all the studies belonged to the same tissue, and there was heterogeneity between them, we decided to apply a Random Effects Model (REM).
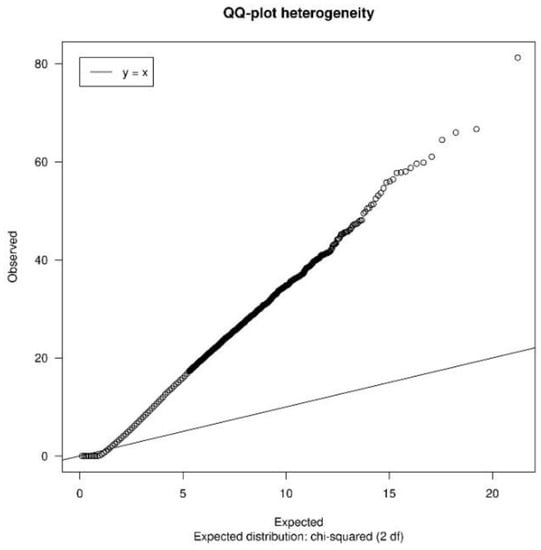
Figure 4.
Heterogeneity QQ-plot of SLE data. QQ-plot of Cochran’s heterogeneity test values for the SLE case study data.
To demonstrate the usefulness of the package, the meta-analysis was applied from three different approaches:
- Using only common genes (common genes approach).
- Considering the genes that are present in at least two of the studies (66%) (minimum proportion approach).
- Performing a previous imputation of missing genes before accomplishing the meta-analysis (called the imputing missing genes approach).
The meta-analysis of only common genes took into account 11,298 genes, which only represented 49.5% of the total available genes, of which 1896 were found to be significant (16.8% of genes considered) (adjusted p-value (FDR) < 0.05). The minimum proportion approach worked with 14,548 genes, which represented 63.8% of the total available genes, of which 2444 were found to be significant (16.8% of genes considered). Finally, the meta-analysis of imputed missing genes considered all available genes, 22,807 genes (22,807), of which 4830 were found to be significant (21.1% of genes considered).
These results suggest that if only common genes were considered, an important part of the information would be lost (in this use case, more than 50% of the available genes would not influence the final result). Moreover, to verify this loss of information, the heatmap of the 50 most significant genes obtained by the minimum proportion approach was generated (Figure 5). This heatmap revealed that several of the most significant genes would have disappeared from the final result if the common genes approach was applied (missing values are marked in grey).
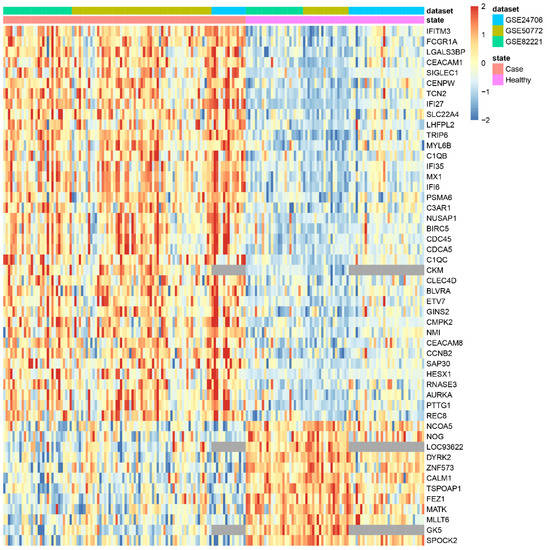
Figure 5.
Heatmap of the 50 most significant genes in SLE data without imputation.
Finally, a functional enrichment analysis of the over-expressed genes was performed using GeneCodis4 [30,31] to validate the biological significance of the obtained results. The systemic lupus erythematosus pathway did not appear among the 10 most enriched pathways using the Bioplanet 2019 database [32] when the common genes approach and the minimum proportion approach were applied (Figure 6). Nevertheless, when the missing genes imputation was applied, the systemic lupus erythematosus biological pathway became the most significant pathway. Moreover, genes belonging to this pathway were recovered if the imputation of the missing genes was applied before the common genes approach and the minimum proportion approach.
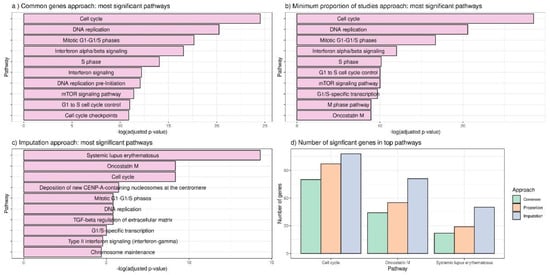
Figure 6.
Graphical representations of the most significant pathways for each of the meta-analysis approaches. (a) Ten most significant pathways in common genes approach. (b) Ten most significant pathways considering genes that are contained in at least two studies. (c) Ten most significant pathways in the missing genes imputation approach. (d) Number of significant genes in top pathways in each approach.
These results highlight the impact of discarding missing genes in a gene expression meta-analysis, which can bias the final results.
3.3. Comparison to Other Available R Packages
Currently, apart from DExMA, there are eight R packages available in CRAN or Bioconductor repositories that allow one to perform gene expression meta-analyses: metahdep [33], GeneMeta [34], metaRNASeq [35], metaSeq [36], metaMA [37], crossmeta [38], MetaIntegrator [10], and MetaVolcanoR [11]. Table 2 shows a summary of the main features of the packages currently available for performing gene expression meta-analyses.

Table 2.
Comparison of the main features of gene expression meta-analysis packages. Input: “User data” means that the user can enter their own data, while “GEO data” means that the user can include GEO database codes. QC (quality control): “Yes” if the package has implemented functions for performing quality controls. ES: “Yes” if the package performs effect sizes combination methods. PV: “Yes” if the package performs p-value combination methods. Considers Missing Genes: “Yes” if the package somehow considers the unmeasured genes. Imputes Missing genes: “Yes” if the package somehow imputes the unmeasured genes. Visualization: “Yes” if the package has implemented a function to visualize the results.
Most implemented packages usually use previously curated data by the user as input, while crossmeta allows the use of data downloaded from the GEO database. DExMA has the advantage that it admits users to work with both user data as well as with GEO-downloaded datasets. Furthermore, it provides a function that facilitates the creation of the object needed to perform the meta-analysis from the information entered by the user.
Regarding the different steps of a gene expression meta-analysis, DExMA, unlike the rest of the packages, contains functions to perform quality control before the meta-analysis and help in the decision of which meta-analysis method to apply. Several packages mention the importance of these previous steps; only the MetaIntegrator package implements a function related to quality control, but it does not include anything about the heterogeneity of the studies.
Moreover, as previously referenced, most of these packages only perform the analyses with the genes common to all datasets. Only crossmeta, MetaVolcvanoR, and MetaInetgrator consider the possible existence of missing genes but do not make any imputation of them, nor do they show their possible effect on the final result.
4. Discussion
The accumulation and availability of experimental data in public repositories has fuelled the development of meta-analysis techniques as important tools to integrate heterogeneous datasets. In the field of transcriptomics, these techniques have been applied to jointly analyse gene expression for biomarker discovery or drug-repurposing applications, among others. The number of scientific publications with meta-analysis studies is growing exponentially, and as have been reported [8,9], a high proportion of these published analyses are misleading meta-analyses or have serious methodological flaws. In this context, it is important for the scientific community that software packages that implement proper statistical methods and dedicated workflows are available.
This article introduces DExMA, an R package that implements the main steps and methods for gene expression meta-analyses. Moreover, to avoid the loss of information due to the use of only common genes, DExMA allows users to deal with missing genes with two approaches: selecting the proportion of datasets that must contain a gene or imputing the missing genes by using the KNN imputation method in the space of samples (sampleKNN). To the best of our knowledge, DExMA is the first gene expression meta-analysis package that controls missing genes. Although there are other packages that also consider the possible existence of unmeasured genes (crossmeta, MetaIntegrator, and MetaVolcanoR), none of them perform the imputation of these missing genes, nor do they show the possible effect of this lack of information in the results.
DExMA also offers the possibility of using both GEO codes and one’s own data as well as performing the different steps of a gene expression meta-analysis (homogenizing gene annotation, quality control, and results visualization), which contributes to making appropriate use of these methods.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math10183376/s1.
Author Contributions
Conceptualization, J.A.V.-G., J.M.-M. and P.C.-S.; methodology, J.A.V.-G. and D.T.-D.; software, J.A.V.-G., J.M.-M. and D.T.-D.; validation, J.A.V.-G. and J.M.-M.; formal analysis, J.A.V.-G.; investigation, J.A.V.-G.; resources, Y.R.-M. and P.F.; data curation, J.A.V.-G. and J.M.-M.; writing—original draft preparation, J.A.V.-G.; writing—review and editing, J.A.V.-G., J.M.-M., D.T.-D., Y.R.-M., P.F. and P.C.-S.; visualization, J.A.V.-G. and D.T.-D.; supervision, P.C.-S.; project administration, P.C.-S.; funding acquisition, P.C.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the Teaching Staff Programme, implemented by the Ministerio de Universidades (grant number FPU19/01999). This work is funded by grants PID2020-119032RB-I00, MCIN/AEI/10.13039/501100011033, and FEDER/Junta de Andalucía-Consejería de Transformación Económica, Industria, Conocimiento y Universidades (Grants P20_00335 and B-CTS-40-UGR20). Toro-Domínguez. is supported through the aid granted of the ‘Consejería de Transformación Económica, Industria, Conocimiento y Universidades’ (CTEICU), in the 2020 call, being co-financed by the European Union through the European Social Fund (ESF) named ‘Andalucía se mueve con Europa”, within the framework of the Andalusian ESF Operational Program 2014–2020. Martorell-Marugán is funded by European Union—NextGenerationEU, Ministerio de Universidades (Spain’s Government) and Recovery, Transformation and Resilience Plan, through a call from the University of Granada.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the “SLE_Data.RData” supplementary file.
Acknowledgments
This work is part of Juan Antonio Villatoro-García’s Ph.D. results. Juan Antonio Villatoro-García is enrolled in the Mathematical and Applied Statistics Ph.D. program.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KNN K | nearest neighbours |
| FEM | Fixed Effects Model |
| REM | Random Effects Model |
| ID | Identifier |
| SLE | systemic lupus erythematosus |
Appendix A
Loading and Preparing the Case Study Data Directly from the ADEX Database
The data used in the case study are available in the ADEx database [26] (https://adex.genyo.es/, accessed on 15 August 2022). Specifically, we downloaded the following datasets: GSE24706, GSE50772, and GSE82221_GLP10558. Once the studies were downloaded, four files were obtained:
- GSE24706.tsv: gene expression matrix of the study GSE24706.
- GSE50772.tsv: gene expression matrix of the study GSE50772.
- GSE82221_GPL10558.tsv: gene expression matrix of the study GSE82221.
- metadata.tsv: dataframe with the information from the different samples of the studies (phenodata).
We loaded these files and prepared them for the use case:
R> #Loading gene expression matrix
R> GSE24706Ex <- as.matrix(read.delim(“GSE24706.tsv”, header = TRUE,
+ row.names = 1))
R> GSE50772Ex <- as.matrix(read.delim(“GSE50772.tsv”, header = TRUE,
+ row.names = 1))
R> GSE82221Ex <- as.matrix(read.delim(“GSE82221_GPL10558.tsv”,
+ header = TRUE, row.names = 1))
R> #Preparing studies phenodatas
R> Pheno <- read.delim(“metadata.tsv”, header = T, row.names = 1)
R> GSE24706Pheno <- Pheno[colnames(GSE24706Ex),]
R> GSE50772Pheno <- Pheno[colnames(GSE50772Ex),]
R> GSE82221Pheno <- Pheno[colnames(GSE82221Ex),]
Once the expression matrices were loaded and the phenodata were obtained for each of the studies, the data were ready for the case study.
References
- Barrett, T.; Wilhite, S.E.; Ledoux, P.; Evangelista, C.; Kim, I.F.; Tomashevsky, M.; Marshall, K.A.; Phillippy, K.H.; Sherman, P.M.; Holko, M.; et al. NCBI GEO: Archive for Functional Genomics Data Sets—Update. Nucleic Acids Res. 2013, 41, D991–D995. [Google Scholar] [CrossRef] [PubMed]
- Perez-Riverol, Y.; Zorin, A.; Dass, G.; Vu, M.-T.; Xu, P.; Glont, M.; Vizcaíno, J.A.; Jarnuczak, A.F.; Petryszak, R.; Ping, P.; et al. Quantifying the Impact of Public Omics Data. Nat. Commun. 2019, 10, 3512. [Google Scholar] [CrossRef] [PubMed]
- Song, G.G.; Kim, J.-H.; Seo, Y.H.; Choi, S.J.; Ji, J.D.; Lee, Y.H. Meta-Analysis of Differentially Expressed Genes in Primary Sjogren’s Syndrome by Using Microarray. Hum. Immunol. 2014, 75, 98–104. [Google Scholar] [CrossRef] [PubMed]
- Afroz, S.; Giddaluru, J.; Vishwakarma, S.; Naz, S.; Khan, A.A.; Khan, N. A Comprehensive Gene Expression Meta-Analysis Identifies Novel Immune Signatures in Rheumatoid Arthritis Patients. Front. Immunol. 2017, 8, 74. [Google Scholar] [CrossRef]
- Badr, M.T.; Häcker, G. Gene Expression Profiling Meta-Analysis Reveals Novel Gene Signatures and Pathways Shared between Tuberculosis and Rheumatoid Arthritis. PLoS ONE 2019, 14, e0213470. [Google Scholar] [CrossRef]
- Kelly, J.; Moyeed, R.; Carroll, C.; Albani, D.; Li, X. Gene Expression Meta-Analysis of Parkinson’s Disease and Its Relationship with Alzheimer’s Disease. Mol. Brain 2019, 12, 16. [Google Scholar] [CrossRef]
- Ibáñez, K.; Boullosa, C.; Tabarés-Seisdedos, R.; Baudot, A.; Valencia, A. Molecular Evidence for the Inverse Comorbidity between Central Nervous System Disorders and Cancers Detected by Transcriptomic Meta-Analyses. PLoS Genet. 2014, 10, e1004173. [Google Scholar] [CrossRef]
- Ioannidis, J.P.A. The Mass Production of Redundant, Misleading, and Conflicted Systematic Reviews and Meta-Analyses. Milbank Q. 2016, 94, 485–514. [Google Scholar] [CrossRef]
- Park, J.H.; Eisenhut, M.; van der Vliet, H.J.; Shin, J.I. Statistical Controversies in Clinical Research: Overlap and Errors in the Meta-Analyses of MicroRNA Genetic Association Studies in Cancers. Ann. Oncol. 2017, 28, 1169–1182. [Google Scholar] [CrossRef]
- Haynes, W.A.; Vallania, F.; Liu, C.; Bongen, E.; Tomczak, A.; Andres-Terrè, M.; Lofgren, S.; Tam, A.; Deisseroth, C.A.; Li, M.D.; et al. Empowering Multi-Cohort Gene Expression Analysis to Increase Reproducibility. Pac. Symp. Biocomput. 2016, 22, 144–153. [Google Scholar]
- Prada, C.; Lima, D.; Nakaya, H. MetaVolcanoR: Gene Expression Meta-Analysis Visualization Tool. 2022. Available online: https://www.bioconductor.org/packages/release/bioc/html/MetaVolcanoR.html (accessed on 1 July 2022).
- Bobak, C.A.; McDonnell, L.; Nemesure, M.D.; Lin, J.; Hill, J.E. Assessment of Imputation Methods for Missing Gene Expression Data in Meta-Analysis of Distinct Cohorts of Tuberculosis Patients. Pac. Symp. Biocomput. 2020, 25, 307–318. [Google Scholar] [PubMed]
- Mancuso, C.A.; Canfield, J.L.; Singla, D.; Krishnan, A. A Flexible, Interpretable, and Accurate Approach for Imputing the Expression of Unmeasured Genes. Nucleic Acids Res. 2020, 48, e125. [Google Scholar] [CrossRef] [PubMed]
- Toro-Domínguez, D.; Villatoro-García, J.A.; Martorell-Marugán, J.; Román-Montoya, Y.; Alarcón-Riquelme, M.E.; Carmona-Sáez, P. A Survey of Gene Expression Meta-Analysis: Methods and Applications. Brief. Bioinform. 2021, 22, 1694–1705. [Google Scholar] [CrossRef] [PubMed]
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.T.; Rothstein, H.R. Introduction to Meta-Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021; ISBN 978-1-119-55838-5. [Google Scholar]
- Heard, N.A.; Rubin-Delanchy, P. Choosing between Methods of Combining p-Values. Biometrika 2018, 105, 239–246. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Phipson, B.; Wu, D.; Hu, Y.; Law, C.W.; Shi, W.; Smyth, G.K. Limma Powers Differential Expression Analyses for RNA-Sequencing and Microarray Studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Tseng, G.C. An Adaptively Weighted Statistic for Detecting Differential Gene Expression When Combining Multiple Transcriptomic Studies. Ann. Appl. Stat. 2011, 5, 994–1019. [Google Scholar] [CrossRef]
- Zaykin, D.V. Optimally Weighted Z-Test Is a Powerful Method for Combining Probabilities in Meta-Analysis. J. Evol. Biol. 2011, 24, 1836–1841. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Li, Z.; Morrison, A.C.; Boerwinkle, E.; Lin, X. ACAT: A Fast and Powerful p Value Combination Method for Rare-Variant Analysis in Sequencing Studies. Am. J. Hum. Genet. 2019, 104, 410–421. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, J. Cauchy Combination Test: A Powerful Test with Analytic p-Value Calculation under Arbitrary Dependency Structures. J. Am. Stat. Assoc. 2020, 115, 393–402. [Google Scholar] [CrossRef]
- Higgins, J.P.T.; Thompson, S.G. Quantifying Heterogeneity in a Meta-Analysis. Stat. Med. 2002, 21, 1539–1558. [Google Scholar] [CrossRef]
- Higgins, J.P.T.; Thompson, S.G.; Deeks, J.J.; Altman, D.G. Measuring Inconsistency in Meta-Analyses. BMJ 2003, 327, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Wickham, H.; Seidel, D. Scales: Scale Functions for Visualization. 2020. Available online: https://cran.r-project.org/web/packages/scales/index.html (accessed on 30 June 2022).
- Lazar, C.; Meganck, S.; Taminau, J.; Steenhoff, D.; Coletta, A.; Molter, C.; Weiss-Solís, D.Y.; Duque, R.; Bersini, H.; Nowé, A. Batch Effect Removal Methods for Microarray Gene Expression Data Integration: A Survey. Brief. Bioinform. 2013, 14, 469–490. [Google Scholar] [CrossRef] [PubMed]
- Martorell-Marugán, J.; López-Domínguez, R.; García-Moreno, A.; Toro-Domínguez, D.; Villatoro-García, J.A.; Barturen, G.; Martín-Gómez, A.; Troule, K.; Gómez-López, G.; Al-Shahrour, F.; et al. A Comprehensive Database for Integrated Analysis of Omics Data in Autoimmune Diseases. BMC Bioinform. 2021, 22, 343. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.-Z.; Karp, D.R.; Quan, J.; Branch, V.K.; Zhou, J.; Lian, Y.; Chong, B.F.; Wakeland, E.K.; Olsen, N.J. Risk Factors for ANA Positivity in Healthy Persons. Arthritis Res. Ther. 2011, 13, R38. [Google Scholar] [CrossRef]
- Kennedy, W.P.; Maciuca, R.; Wolslegel, K.; Tew, W.; Abbas, A.R.; Chaivorapol, C.; Morimoto, A.; McBride, J.M.; Brunetta, P.; Richardson, B.C.; et al. Association of the Interferon Signature Metric with Serological Disease Manifestations but Not Global Activity Scores in Multiple Cohorts of Patients with SLE. Lupus Sci. Med. 2015, 2, e000080. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Mi, W.; Luo, H.; Chen, T.; Liu, S.; Raman, I.; Zuo, X.; Li, Q.-Z. Whole-Genome Transcription and DNA Methylation Analysis of Peripheral Blood Mononuclear Cells Identified Aberrant Gene Regulation Pathways in Systemic Lupus Erythematosus. Arthritis Res. Ther. 2016, 18, 162. [Google Scholar] [CrossRef]
- Carmona-Saez, P.; Chagoyen, M.; Tirado, F.; Carazo, J.M.; Pascual-Montano, A. GENECODIS: A Web-Based Tool for Finding Significant Concurrent Annotations in Gene Lists. Genome Biol. 2007, 8, R3. [Google Scholar] [CrossRef]
- Garcia-Moreno, A.; López-Domínguez, R.; Villatoro-García, J.A.; Ramirez-Mena, A.; Aparicio-Puerta, E.; Hackenberg, M.; Pascual-Montano, A.; Carmona-Saez, P. Functional Enrichment Analysis of Regulatory Elements. Biomedicines 2022, 10, 590. [Google Scholar] [CrossRef]
- Huang, R.; Grishagin, I.; Wang, Y.; Zhao, T.; Greene, J.; Obenauer, J.C.; Ngan, D.; Nguyen, D.-T.; Guha, R.; Jadhav, A.; et al. The NCATS BioPlanet—An Integrated Platform for Exploring the Universe of Cellular Signaling Pathways for Toxicology, Systems Biology, and Chemical Genomics. Front. Pharmacol. 2019, 10, 445. [Google Scholar] [CrossRef]
- Stevens, J.R.; Nicholas, G. Metahdep: Hierarchical Dependence in Meta-Analysis. 2022. Available online: https://www.bioconductor.org/packages/release/bioc/html/metahdep.html (accessed on 25 June 2022).
- Lusa, L.; Gentleman, R.; Ruschhaupt, M. GeneMeta: MetaAnalysis for High Throughput Experiments 2021. Available online: https://www.bioconductor.org/packages/release/bioc/html/GeneMeta.html (accessed on 25 June 2022).
- Marot, G.; Rau, A.; Jaffrezic, F.; Blanck, S. MetaRNASeq: Meta-Analysis of RNA-Seq Data 2021. Available online: https://cran.r-project.org/web/packages/metaRNASeq/index.html (accessed on 27 June 2022).
- Tsuyuzaki, K.; Nikaido, I. MetaSeq: Meta-Analysis of RNA-Seq Count Data in Multiple Studies 2022. Available online: https://www.bioconductor.org/packages/release/bioc/html/metaSeq.html (accessed on 27 June 2022).
- Marot, G. MetaMA: Meta-Analysis for MicroArrays 2022. Available online: https://cran.r-project.org/web/packages/metaMA/index.html (accessed on 27 June 2022).
- Pickering, A. Crossmeta: Cross Platform Meta-Analysis of Microarray Data 2022. Available online: https://www.bioconductor.org/packages/release/bioc/html/crossmeta.html (accessed on 27 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).