The Improved Stability Analysis of Numerical Method for Stochastic Delay Differential Equations

Abstract

In this paper, the improved split-step $\theta$ method, named the split-step composite $\theta$ method, is proposed to study the mean-square stability for stochastic differential equations with a fixed time delay. Under the global Lipschitz and linear growth conditions, it is proved that the split-step composite $\theta$ method with $\theta \ge 0.5$ shows mean-square stability. An approach to improving numerical stability is illustrated by choices of parameters of this method. Some numerical examples are presented to show the accordance between the theoretical and numerical results.

1. Introduction

Stochastic delay differential equations have been widely applied in many applications such as signal processing, biological systems, and financial engineering [1,2,3]. As one of central problems in numerical analysis of stochastic systems, the stability theory has attracted a great deal of attention [4,5]. Due to the characteristics of stochastic delay differential equations themselves, it is not easy to obtain an analytical solution of equations; therefore, numerical solution analysis has certain theoretical value and practical significance.

Stability analysis of numerical methods for stochastic delay differential equations has made some achievements [6,7]. The split-step $\theta$ method, as an important numerical method, has been applied to various stochastic systems. Rathinasamy [8] investigated mean-square stability of the split-step $\theta$ method for stochastic delay Hopfield neural networks under suitable conditions. Cao et al. [9] studied the exponential mean-square stability of the split-step $\theta$ method for stochastic differential equations with a fixed time delay. Huang [10] proved that the split-step $\theta$ method with $\theta \ge 0.5$ still unconditionally preserves the exponential mean-square stability of the underlying systems under a coupled condition on the drift and diffusion coefficients. Rathinasamy and Balachandran [11] analyzed the T-stability of the split-step $\theta$ method for linear stochastic delay integro-differential equations. The mean-square stability of the split-step composite $\theta$ method for stochastic differential equation has been introduced by Guo et al. [12].

In the paper, we construct the split-step composite $\theta$ method for stochastic delay differential equations and improve stability by changing the values of parameters $\theta$ and $\lambda$. It is proved that the mean-square stability of the split-step composite $\theta$ method is superior to that of the split-step $\theta$ method. In Section 2, we introduce the split-step composite $\theta$ method. The stability of this method for linear stochastic delay differential equations is analyzed in Section 3. In Section 4, corresponding numerical examples further illustrate the obtained theoretical results. The conclusions will be expressed in the last section.

2. Preliminaries and the Split-Step Composite $\mathit{\theta }$ Method

Throughout this paper, unless otherwise specified, let $(\mathsf{\Omega },\mathcal{F},P)$ be a complete probability space with a filtration ${\left({\mathcal{F}}_t\right)}_{t\ge 0}$, which increases and is right-continuous, and ${\mathcal{F}}_0$ contains all P-null sets. $\mathsf{\Omega }$ and P are the sample space and probability, respectively. Let $|·|$ be the Euclidean norm. The Wiener process $W\left(t\right)$ is defined on $(\mathsf{\Omega },\mathcal{F},P)$ [13].

Consider the following stochastic delay differential equation [13]

$$\left\{\begin{array}{c}dx\left(t\right)=f(t,x(t),x(t-\tau \left)\right)dt+g(t,x(t),x(t-\tau \left)\right)dW\left(t\right)\hfill \\ x\left(t\right)=\phi \left(t\right)\hfill \end{array}\right.$$

(1)

where $t\in [-\tau ,0]$, $\tau >0$ is a constant. Let the $C\left(\right[-\tau ,0];\mathbb{R})$-valued initial segment $\phi \left(t\right)$ be an ${\mathcal{F}}_0$-measurable one-dimensional random variable such that ${\mathbb{E}\left|\right|\phi \left|\right|}^2<\infty$, where $\left|\right|\phi \left|\right|={\sup }_{-\tau \le t\le 0}\left|\phi \left(t\right)\right|$. $W\left(t\right)$ is one-dimensional Wiener process.

We impose some assumptions for Equation (1).

Assumption 1.

$f:[0,T]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ and $g:[0,T]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ satisfy the global Lipschitz condition and the linear growth condition.

(1). Global Lipschitz condition: there is positive constant K, such that for all $x_1,x_2,y_1,y_2\in \mathbb{R}$, and $t\in [0,T]$

$$\begin{array}{cc}\hfill & \max \left\{\right|f(t,x_1,y_1)-f(t,x_2,y_2){|}^2,|g(t,x_1,y_1)-g(t,x_2,y_2){|}^2\}\hfill \\ \hfill & \le K\left(\right|x_1-x_2{|}^2+|y_1-y_2{|}^2);\hfill \end{array}$$

(2). Linear growth condition: there is positive constant $L>0$, such that

$$\begin{array}{c}\hfill {\max \left\{\right|f(t,x,y)|}^2{,\left|g(t,x,y)\right|}^2{\}\le L(1+\left|x\right|}^2+{\left|y\right|}^2)\end{array}$$

holds for every $x_1,y_1\in \mathbb{R}$ and $t\in [0,T]$.

The split-step composite $\theta$ method is an improved numerical method, parameter $\lambda$ is introduced on the basis of the split-step $\theta$ method. Now, we present the split-step composite $\theta$ method [12]

$$\left\{\begin{array}{c}{x}_n^{\star }=x_n+(\theta f(t_n,x_n^{\star },x_{n-m}^{\star })+(1-\theta )f(t_n,x_n,x_{n-m}))h\hfill \\ x_{n+1}=x_n^{\star }+(\lambda g(t_n,x_n^{\star },x_{n-m}^{\star })+(1-\lambda )g(t_n,x_n,x_{n-m}))\Delta W_n\hfill \end{array}\right.$$

(2)

where parameters $\theta$ and $\lambda \in [0,1]$, $x_n$ is an approximation to analytical solution $x\left(t_n\right)$, $h=\frac{T}{N}$ is the given step-size with $\tau =mh$ for a positive integer m, N is a given positive integer, $t_n=nh,\Delta W_n=W\left(t_{n+1}\right)-W\left(t_n\right)$ are independent $N(0,h)$ distributed stochastic variables, $x_p^{\star }=x_p=\phi \left(ph\right)$, and $-m\le p\le 0$. When the parameter $\lambda =1$, it is the split-step $\theta$ method [14,15]. When the parameters $\theta =1$ and $\lambda =1$, it is the split-step back-Euler method [16,17]. When the parameters $\theta =0$ and $\lambda =1$, it is the split-step forward-Euler method [18]. The split-step $\theta$ method, split-step back-Euler method, and split-step forward-Euler method are different numerical methods. The split-step $\theta$ method achieves stability by changing the value of $\theta$, while the other two methods are ysed to adjust the stability by changing the step size or equation coefficients [19,20].

Definition 1

([13]). If there is a constant $\rho >0$ and $\parallel \phi \parallel <\rho$, such that

$$\underset{t\to \infty }{\lim }E{\left|x\left(t\right)\right|}^p=0$$

(3)

then the solution of Equation (1) is said to be pth-moment exponentially stable, E is expectation. When $p=2$, it is said to show mean-square stability.

3. Stability of the Split-Step Composite $\mathit{\theta }$ Method

In this section, we will discuss the stability of the split-step composite $\theta$ method for linear stochastic delay differential equations

$$\left\{\begin{array}{c}dx\left(t\right)=ax\left(t\right)dt+\left(bx\right(t)+cx(t-\tau \left)\right)dW\left(t\right),t\ge 0\hfill \\ x\left(t\right)=\phi \left(t\right),t\in [-\tau ,0]\hfill \end{array}\right.$$

(4)

where $a,b,c\in \mathbb{R}$.

Definition 2

([13]). The numerical method applied to Equation (1) is said to present mean-square stability if for every step size h, the numerical approximation $\left\{x_n\right\}$ produced by the split-step composite θ method satisfies

$$\underset{n\to \infty }{\lim }E{\left|X_n\right|}^2=0$$

(5)

Theorem 1.

Let $a,b,c$ be the coefficients of Equation (4), θ and λ be parameters, and h be the step size. If $a,b,c$ satisfy

$$a+\frac{1}{2}\left(\right|b|+{\left|c\right|)}^2<0$$

(6)

and the parameter $\theta \ge \max \{\frac{1}{2},\lambda -\frac{2}{\left|a\right|h}\}$, then the split-step composite θ method shows mean-square stability.

Proof. 

The split-step composite $\theta$ method is applied to Equation (4). The numerical scheme is constructed as follows:

$$\left\{\begin{array}{c}{x}_n^{\star }=x_n+[\theta a{x}_n^{\star }+(1-\theta )a{x}_n]h\hfill \\ x_{n+1}=x_n^{\star }+[\lambda (b{x}_n^{\star }+c{x}_{n-m}^{\star })+(1-\lambda )(b{x}_n+c{x}_{n-m}])\Delta W_n\hfill \end{array}\right.$$

(7)

namely

$$\begin{array}{c}\hfill (1-\theta ah)x_n^{\star }=(1+(1-\theta )ah)x_n,\end{array}$$

$$x_n^{\star }=\frac{1+(1-\theta )ah}{1-\theta ah}{x}_n,$$

(8)

$$\begin{array}{c}\hfill x_{n-m}^{\star }=\frac{1+(1-\theta )ah}{1-\theta ah}{x}_{n-m},\end{array}$$

substituting (8) into the second equation of (7), we have

$$\begin{array}{cc}\hfill x_{n+1}& =(1+\lambda b\Delta W_n)x_n^{\star }+\lambda c\Delta W_n{x}_{n-m}^{\star }+[(1-\lambda )(b{x}_n+c{x}_{n-m})]\Delta W_n\hfill \\ \hfill & =[\frac{(1+\lambda b\Delta W_n)(1+(1-\theta )ah)}{1-\theta ah}+(1-\lambda )b\Delta W_n]x_n\hfill \\ \hfill & +[\frac{(\lambda c\Delta W_n)(1+(1-\theta )ah)}{1-\theta ah}+(1-\lambda )c\Delta W_n]x_{n-m}.\hfill \end{array}$$

Squaring both the above equation, we obtain

$$\begin{array}{cc}\hfill {(1-\theta ah)}^2{x}_{n+1}^2& ={[1+(1-\theta )ah+b\Delta W_n+(\lambda -\theta )abh\Delta W_n]}^2{x}_n^2\hfill \\ \hfill & + {[c\Delta W_n+(\lambda -\theta )ach\Delta W_n]}^2{x}_{n-m}^2+2[1+(1-\theta )ah\hfill \\ \hfill & + b\Delta W_n+(\lambda -\theta )abh\Delta W_n\left]\right[c\Delta W_n\hfill \\ \hfill & +(\lambda -\theta )ach\Delta W_n]x_n{x}_{n-m}.\hfill \end{array}$$

(9)

Using the inequality $2\alpha \beta \le {\alpha }^2+{\beta }^2$ and taking mathematical expectation on (9), we obtain

$$\begin{array}{cc}\hfill {(1-\theta ah)}^{2}E{\left|x_{n+1}\right|}^2& \le [{(1+(1-\theta )ah)}^2+b^{2}h+{(\lambda -\theta )}^2{a}^2{b}^2{h}^3\hfill \\ \hfill & + 2(\lambda -\theta )a{b}^2{h}^2]E{x}_n^2+[c^{2}h+{(\lambda -\theta )}^2{a}^2{c}^2{h}^3\hfill \\ \hfill & + 2(\lambda -\theta )a{c}^2{h}^2]E{x}_{n-m}^2+[|bc|h+2(\lambda -\theta )\left|abc\right|h^2\hfill \\ \hfill & + {(\lambda -\theta )}^2{a}^2\left|bc\right|h^3](E{x}_n^2+E{x}_{n-m}^2).\hfill \end{array}$$

(10)

that is

$$\begin{array}{c}\hfill {(1-\theta ah)}^{2}E{\left|x_{n+1}\right|}^2\le A(a,b,c,h,\theta ,\lambda )E{x}_n^2+B(a,b,c,h,\theta ,\lambda )E{x}_{n-m}^2,\end{array}$$

(11)

where

$$\begin{array}{cc}\hfill A(a,b,c,h,\theta ,\lambda )& ={(1+(1-\theta )ah)}^2+b^{2}h+{(\lambda -\theta )}^2{a}^2{b}^2{h}^3+2(\lambda -\theta )a{b}^2{h}^2\hfill \\ \hfill & + \left|bc\right|h+2(\lambda -\theta )\left|abc\right|h^2+{(\lambda -\theta )}^2{a}^2\left|bc\right|h^3\hfill \end{array}$$

$$\begin{array}{cc}\hfill B(a,b,c,h,\theta ,\lambda )& =c^{2}h+{(\lambda -\theta )}^2{a}^2{c}^2{h}^3+2(\lambda -\theta )a{c}^2{h}^2+\left|bc\right|h\hfill \\ \hfill & + 2(\lambda -\theta )\left|abc\right|h^2+{(\lambda -\theta )}^2{a}^2\left|bc\right|h^3,\hfill \end{array}$$

$1-\theta ah>0$ and the condition (6) holds. It is obvious that if

$$\begin{array}{c}\hfill A(a,b,c,h,\theta ,\lambda )+B(a,b,c,h,\theta ,\lambda )<{(1-\theta ah)}^2,\end{array}$$

the above inequality is equivalent to

$$\begin{array}{c}\hfill (1-2\theta )a^{2}h+2a+{(1+(\lambda -\theta )ah)}^2\left(\right|b|+{\left|c\right|)}^2<0,\end{array}$$

(12)

If $|1+(\lambda -\theta \left)ah\right|\le 1$, then from condition (6) we have $a<0$ and

$$\begin{array}{c}\hfill 2a+{(1+(\lambda -\theta )ah)}^2\left(\right|b|+{\left|c\right|)}^2<0,\end{array}$$

Thus, when $\theta \ge 0.5$, the inequality (12) holds. We obtain the relationship of $h,\theta ,\lambda$ from $|1+(\lambda -\theta \left)ah\right|\le 1$, that is

$$\begin{array}{c}\hfill \theta \ge \lambda -\frac{2}{\left(\right|a\left|h\right)},\end{array}$$

The theorem is proven. □

4. Numerical Example

Taking coefficients of Equation (4) as $a=-20,b=4,c=2$. The coefficients satisfy the condition (6). We use Matlab to randomly generate 2000 discrete trajectories, that is

$$\begin{array}{c}\hfill Y_j=\frac{1}{2000}\sum _{i=1}^{2000}{\left|y_j^i\right|}^2\end{array}$$

where $y_j^i$ is the numerical solution of i trajectories at the time $t_j$.

Parameter $\lambda =0.8$ can be fixed with step-size $h=1$. Figure 1 shows that the split-step composite $\theta$ method does not show mean-square stability when $\theta =0.5$, while for $\theta =0.8$, the split-step composite $\theta$ method is stable. When the parameter $\theta$ is closer to 1, the split-step composite $\theta$ method is more stable.

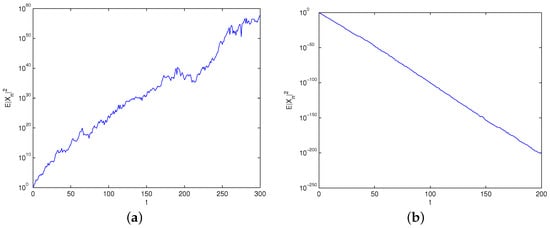
Figure 1. The split-step composite $\theta$ method with (a) $\theta =0.5$; (b) $\theta =0.8$.

Parameter $\theta =0.5$ can be fixed with step-size $h=0.25$. We change the value of parameter $\lambda =1$ to $\lambda =0.8$, as shown in Figure 2. From Figure 2, the second-order moment of numerical solution blows up when $\lambda =1$ and tends to be zero for $\lambda =0.8$, as observed. Appropriately adjusting the parameter value $\lambda$ can improve stability.

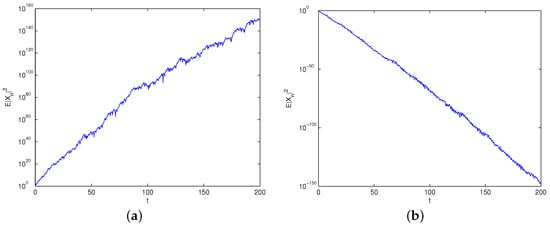
Figure 2. The split-step composite $\theta$ method with (a) $\lambda =1$; (b) $\lambda =0.8$.

Fix parameters $\theta =0.5$ when $\lambda =0.8$. We choose the step-size $h=0.5$, $h=0.25$, and the computer simulation result is shown in Figure 3. It is shown that the split-step composite $\theta$ method can maintain stability when $h=0.25$.

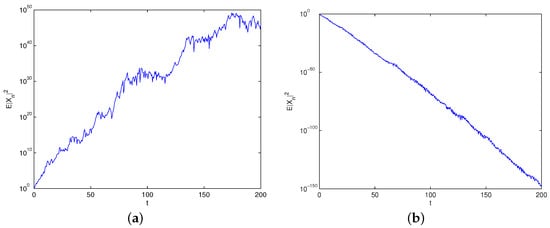
Figure 3. The split-step composite $\theta$ method with (a) $h=0.5$; (b) $h=0.25$.

5. Conclusions

We discuss the stability of the split-step composite $\theta$ method for stochastic delay differential equations in the paper. It is proven that the split-step composite $\theta$ method with $\theta \ge 0.5$ shows mean-square stability. We can maintain and improve the stability of the split-step composite $\theta$ method for stochastic systems by adjusting the values of parameters $\theta$ and $\lambda$. Meanwhile, it is proven that the split-step composite $\theta$ method is superior to that of the split-step $\theta$ method.