Abstract
Intercity railway is an important system for the development of urban agglomeration, and the site selection of the Line Management Department of Intercity Railway (LMDIR) is a significant task for the railway department when constructing intercity railways. Owing to the complexity and uncertainty during the selection process, we constructed a multiple expert multi-criteria decision making (MEMCDM) method to provide a rational decision support model for a railway management department in the Fermatean cubic fuzzy set context. In this regard, an innovative extension called Fermatean cubic fuzzy sets (FCFSs) that integrates Fermatean fuzzy sets (FFSs) and cubic sets; several basic theories of FCFSs, including the score and accuracy functions; and distance measures are also given. Then, a series of Fermatean cubic fuzzy Hamacher operators are put forward to flexibly fuse Fermatean cubic fuzzy information, and the corresponding valuable characteristics of these operators are also investigated. Thirdly, the Fermatean cubic fuzzy logarithmic percentage-change-driven objective weighting (LOPCOW) approach is recommended based on the score function to recognize the importance of criteria, and the similarity-based method is deployed to identify the expert weight information. Fourthly, a hybrid MEMCDM methodology integrating the proposed Fermatean cubic fuzzy Hamacher operators, the LOPCOW method, whose evaluation is based on distance from average solution (EDAS) method based on regret theory, is designed to ascertain the prioritization of the schemes. Consequently, an empirical test concerning the site selection of LMDIR is shown to validate the feasibility and usefulness of the designed MEMCDM approach. The analysis involving the sensibility test and comparison study with prior methods is displayed to emphasize the effectuality and advantages of the propounded method. The outcomes demonstrate that the hybrid method recommended in this research possesses superior robustness and feasibility to cope with complicated decision issues. The findings of this research show that the presented method can recommend more credible site selection of LMDIR when encountering uncertainties and abundant impact factors.
Keywords:
Fermatean cubic fuzzy set; multiple expert multi-criteria decision making; LOPCOW approach; EDAS approach; regret theory MSC:
90B50; 94D05; 03E72
1. Introduction
With the increasing complexity and uncertainty of the decision environment, group decision making improves the comprehensiveness and scientificity of decision making by integrating the wisdom of experts in different fields and making full use of their professional knowledge, experience and background [1]. In light of its merits in decision analysis, it is widely used in various fields in society and organizations to unfold complex decision analysis and further the rationality of the final decisions’ consequences. Owing to the cognitive limitations and professional differences of evaluators, various uncertainties will appear in subjective evaluations, and classical evaluation methods based on accurate preference information struggle to fit complicated developments. In order to work out the above-mentioned problem, fuzzy sets (FSs) [2] originated by Zadeh employing the fuzzy information expressions, such as fuzzy numbers, instead of crisp numbers to describe the initial evaluation values given by experts, which provides a quantitative analysis method for solving the uncertainty problems in complex systems. Subsequently, considering that the complexity and uncertainty of different practical applications and the fuzziness and hesitation of experts’ cognitive abilities are widespread across diverse domains, a series of extensions based on FSs, such as intuitionistic FSs [3], Pythagorean FSs [4,5], hesitant FSs [6], 2-type FSs [7] and fuzzy multi-sets [8], have been proposed to represent experts’ complex cognitive preferences. As an innovative extension of FSs, Fermatean fuzzy sets [9] extend the evaluation information contained in intuitionistic FSs and Pythagorean FSs with the aid of weakening the requirements for membership and nonmembership to provide more freedom for experts to express their preferences. Since then, the investigations on FFSs have been deeply researched and discussed and further attained a multitude of achievements [10,11,12]. Furthermore, some extensions on the basis of FFSs have also been propounded as new information representation tools, such as the Fermatean fuzzy linguistic set [13], interval-valued FFSs [14] and interval-valued hesitant FFSs [15]. The mentioned extensions have been applied to decision models and applications successfully.
From the extant literature of FFSs, we can find that the prior studies mainly concern decision approach construction by some extensions based on hesitant FSs and interval-valued FSs and their applications, rather than failing to portray two-dimensional information under a Fermatean fuzzy setting. For this, Jun et al. [16] introduced a new concept called cubic sets (CSs) by combining the use of interval-valued fuzzy numbers and fuzzy numbers. Since its introduction, research on CSs has successively been put forward to establish uncertain decision algorithms [17,18,19]. At present, we have failed to find that any research on the combination of FFSs and CSs exists which has constructed a new uncertain information representation model.
Decision methodology plays an important role in experts unfolding multiple criteria decision analysis. Currently, a series of decision methods, such as TOPSIS [20], VIKOR [21], ARAS [22] and WASPAS [23] methods, have been presented to provide decision support for practical decision analysis. However, these approaches also have several shortcomings which will can cause reasonable and incomplete decision outcomes. Recently, a novel method called EDAS was proposed by Keshavarz Ghorabaee et al. [24] to achieve more robust results. The EDAS method can effectively avoid the distortion of the original evaluation information and has stability, effectiveness and simplicity in the calculation process by calculating the forward distance and reverse distance between the scheme and the average solution to characterize the gap and advantages and disadvantages of each alternative. In light of the advantageous in the field of decision analysis, the EDAS method has been extended to dissimilar fuzzy and uncertain environments to construct decision models and recommender algorithms, such as the intuitionistic fuzzy set [25,26], neutrosophic soft set [27], q-rung orthopair fuzzy set [28,29], interval type-2 fuzzy set [30] and linguistic neutrosophic set [31]. Nevertheless, there is no research combining the EDAS method and regret theory under a Fermatean cubic fuzzy setting to build a decision methodology. Furthermore, as a novel, objectively weighted determination method, the LOPCOW approach originated by Ecer and Pamucar [32] can validly compute the criteria’s weights objectively after computing the standard deviation and percentage values of each criterion. However, to the best of our knowledge, there has been no investigation presenting an improved LOPCOW method for FCFSs to determine criteria’s weights. Accordingly, based on the mentioned analysis, the goal of this study was to build a MEMCDM decision maker by merging the FCFSs and the EDAS method based on regret theory and the LOPCOW method for ranking the site selection of LMDIR.
In view of the above discussion, the research motivations of this research are outlined as follows:
- ♠
- The current extension of the Fermatean fuzzy set considers the situations of hesitant degree, interval uncertainty and linguistic variable, which fails to represent the membership and nonmembership grades by two-dimensional information. Based on this, inspired by the academic though of cubic fuzzy set, the new combination of Fermatean cubic fuzzy set should be defined as a stronger indeterminacy information expression tool.
- ♠
- The existing weight determination approaches, such as the entropy weight method and CRITIC algorithm, will cause wide differences between the weight information attained by those methods. Considering that the logarithmic percentage change-driven objective weighting (LOPCOW) approach can validly eliminate the differences among the decision data, the Fermatean cubic fuzzy LOPCOW algorithm should be presented to ascertain the importance of the decision criteria.
- ♠
- As a classical and widely used decision method, the EDAS method has been generalized to diverse uncertain environments and practical applications to provide decision support for decision experts. Nevertheless, the extant extensions ignore the psychological preferences of decision makers by considering the sudden and urgent of actual situations. Hence, it is necessary to build up an innovative extension of the EDAS method by using regret theory under the Fermatean cubic fuzzy setting.
- ♠
- Based on the advanced Fermatean cubic fuzzy set, the group decision framework is important and significant for the application of complex uncertain decision analysis. As a consequence, an integrated MEMCDM model should be constructed for decision makers to flexibly and effectively settle complicated decision problems.
Based upon the motivations of this research, the objective of this study was to develop a novel extension of the Fermatean fuzzy set named the Fermatean cubic fuzzy set, which allows the membership and nonmembership grades of Fermatean fuzzy set to be signified by a cubic set. Further, the fundamental theories of the Fermatean cubic fuzzy set are introduced, and a group decision approach is also built up through pondering the unknown weight information and psychological features. In order to achieve the above-mentioned goal, the contributions of this research are listed below:
- 🗸
- An innovative uncertain information representation model called the Fermatean cubic fuzzy set is introduced that combines the Fermatean fuzzy set and cubic set. Meanwhile, several basic conceptions of Fermatean cubic fuzzy set, including score and accuracy functions, comparison laws and the distance measure, are defined as the foundations of a decision algorithm’s construction.
- 🗸
- Based upon the Hamacher T-norm and S-norm, the Fermatean cubic fuzzy Hamacher operations are defined and some operators are propounded to aggregate Fermatean cubic fuzzy information correspondingly, and a series of valuable characteristics of these operators are discussed at length.
- 🗸
- The Fermatean cubic fuzzy LOPCOW method is proposed on the basis of the score function to generate more rational weight information of criteria.
- 🗸
- The Fermatean cubic fuzzy EDAS approach based on regret theory is brought forward to determine the prioritization of decision schemes.
- 🗸
- A hybrid MEMCDM algorithm was constructed by integrating the LOPCOW, EDAS and regret theory to develop group decision analysis under the Fermatean cubic fuzzy context.
The organization of the manuscript is as follows. Section 2 presents the related work. Section 3 succinctly recalls some essential preliminaries for this research. Section 4 propounds the definition of the Fermatean cubic fuzzy set and corresponding basic notions. Section 5 puts forward several Fermatean cubic fuzzy Hamacher operators and studies some properties of the operators. Section 6 builds up a hybrid Fermatean cubic fuzzy MEMCDM decision algorithm based on the LOPCOW, EDAS and regret theory and the proposed operators. An empirical case about site selection of LMDIR is settled through employing the constructed Fermatean cubic fuzzy MEMCDM decision approach in Section 7. In addition, the sensitivity analysis and contrast analysis are also implemented with the previous approaches to analyze its superiorities. Some concludingremarks are given in Section 8.
2. Literature Review
In this section, we propound the related work.
2.1. Fermatean Fuzzy Sets
In order to overcome the cognitive uncertainty and fuzziness of decision makers due to time pressure and insufficient knowledge, the FSs [2] were created to model the fuzziness of objective assessments provided by decision makers. Subsequently, some extensions based on FSs were propounded to express the vague cognition of experts by considering the different practical situations [3,5,6,16]. After that, a novel generalization of intuitionistic FSs called FFSs was introduced to express stronger uncertainty and provided more widespread space to express assessments than intuitionistic FSs and Pythagorean FSs. Based on FFSs, many theories and applications were propounded to develop uncertain decision analysis. For instance, Gül [33] presented three approaches within the Fermatean fuzzy context to choosing a suitable COVID-19 testing laboratory, SAW, ARAS and VIKOR. Tan et al. [34] suggested a hybrid group decision framework by combining the extended MABAC method based on prospect theory, the proposed Fermatean fuzzy Frank aggregation operators and a novel distance measure to resolve the risk investment problem. Wei et al. [35] constructed a group green supplier decision model by merging the combination weight model and CoCoSo approach based on a novel entropy measure and Schweizer–Sklar operators within Fermatean fuzzy environments. Gonzales et al. [36] studied the Fermatean fuzzy DEMATEL and MMDE algorithm to analyze the barriers of implementing Education 4.0. In order to model complex assessment information, Lai et al. [37] proposed a hesitant Fermatean fuzzy CoCoSo group decision algorithm to evaluate the blockchain platforms. After that, to cope with the two-dimensional uncertain decision problems, Akram et al. [38] brought forward the VIKOR group decision model with complex Fermatean fuzzy information. Simić et al. [39] propounded an integrated group decision approach based on the MEREC method and CoCoSo approach to manage urban transport planning. Yang et al. [40] provided a MCDM framework based upon a novel weighted distance and TOPSIS method to assess the green low-carbon port. Rani et al. [41] built up a comprehensive group decision framework based on the MEREC method and ARAS decision algorithm to select the optimal food waste treatment technology, where the fusion process also takes into account the correlation between the considered criteria. Chen et al. [42] put forward a novel group decision model based upon the Fermatean fuzzy linguistic sets and CoCoSo approach to evaluate the occupational health and safety risk, wherein the weights of risk factors are determined by the extended block-wise ratings of the attribute weighting method. In addition, to express the inherent uncertainty of experts, Rani et al. [43] advanced an interval-valued Fermatean fuzzy group decision framework based on the COPRAS method and the presented Einstein aggregation operators and improved score function.
2.2. Cubic Set
The cubic set proposed by Jun et al. [16] is a novel uncertain information expression model that uses the integration of interval-valued fuzzy numbers and fuzzy numbers to depict vague information. The merits of CSs are that the CSs can validly settle the possible disagreements of the agreed interval values and vice versa. Since its introduction, CSs have achieved lots of attention in the construction of decision models [44,45]. In addition, Abdullah [46] defined the intuitionistic cubic fuzzy set and further proposed an aggregation-based decision model to select the optimal supplier. Liu et al. [47] suggested a novel group decision model based on linguistic intuitionistic cubic fuzzy copula operators for assessing online education live platforms. Fahmi et al. [48] propounded several cubic Pythagorean linguistic Maclaurin symmetric mean operators to establish decision algorithms. Riaz et al. [49] defined some cubic bipolar fuzzy correlation coefficients and used them for clustering analysis and pattern recognition. Garg et al. [50] constructed the MCDM method to consider the correlations among multiple criteria on the basis of the proposed cubic q-Rung orthopair fuzzy linguistic Muirhead mean operators. In order to take into account the behavioral of decision makers, Wang and Zhao [51] introduced a Pythagorean cubic fuzzy MCDM approach based on an innovative geometric distance measure and prospect theory. Yu et al. [52] propounded several q-rung orthopair cubic fuzzy maclaurin symmetric mean operators and have a MCDM algorithm based on the defined operators to ponder the interrelationship among diverse data. Jamil and Riaz [53] put forward the cubic bipolar fuzzy information using TOPSIS and ELECTRE-I approaches to cope with the problem of bipolar disorder diagnosis. Seker and Kahraman [54] introduced two decision methods with incomplete weight information under a Pythagorean cubic fuzzy setting to choose the best software package. However, we found that there is no study combining the FFSs and CSs to build a decision model.
2.3. EDAS Approach
The EDAS method proposed by Keshavarz Ghorabaee et al. [24] is a famous decision method to identify the order relation of schemes based on the distance value between each scheme and the average scheme. The EDAS method can not only effectively evade the distortion of the original evaluation information, but also makes the computational process more reliable, straightforward and rational. Accordingly, it has been applied to diverse fields, such as healthcare [55], bank efficiency evaluation [56] and online hotel reviews [57]. Further, Mi and Liao [58] developed a hybrid MCDM approach based on the BWM method, a novel normalization technique and the EDAS method to select commercial endowment insurance products under a hesitant fuzzy setting. To manage the decision problems with quantitative and qualitative information, Zhang et al. [59] presented a comprehensive multi-criteria evaluation framework with the aid of a social network analysis method, AHP entropy and an EDAS approach with 2-dimension uncertain linguistic information to assess the multiple choices of loaders. Krishankumar et al. [60] introduced an integrated decision framework by combining the EDAS method and an evidence-based Bayesian approach to prioritize zero-carbon measures in a double hierarchy hesitant linguistic fuzzy environment. Hou et al. [61] suggested an integrated assessment framework with the help of credal networks and the EDAS method to evaluate the safety risk of metro construction under a complex uncertain context. Lei et al. [62] proposed the probabilistic, double hierarchy, linguistic MEMCDM decision approach by combining the EDAS method and CRITIC algorithm to choose the optimal 3D printer. In addition, compared with the single decision model, the combination decision approach, incorporating other decision methods and weight models, has strong robustness and validity decision outcomes. Thereafter, several compound decision methods have been propounded on the basis of the EDAS method to achieve more credible assessments and decision consequences [63,64,65,66]. The above extensions of the EDAS method in various fuzzy contexts have been successfully applied to diverse domains for promoting decision analysis. Subsequently, to consider the psychological behavioral of experts in the decision process, Su et al. [67] proposed a new generalization of EDAS method based on prospect theory with probabilistic uncertain linguistic information for green finance assessment. Further, Huang et al. [68] built up the improved EDAS method on the basis of cumulative prospect theory to analyze the loss and gain of experts in the process of decision making.
3. Preliminaries
This part succinctly presents some foundational notion for the study.
Definition 1
([9]). Let H be a nonempty set. Then, a Fermatean fuzzy set (FFS) G on H is expressed as
wherein : and : , respectively, stand for the functions of membership and non-membership for every element , and meet the condition that . The pair is expressed as a Fermatean fuzzy number (FFN) and simplified as . The hesitancy grade is indicated as .
Definition 2
([12]). For two arbitrary FFNs, and , the basic operational laws are defined as below:
3.1. Cubic Set
Definition 3
([16]). A cubic set on H is defined as below:
wherein the first part is an interval-valued number and the second part is a real number. and stand for the membership and non-membership grades, respectively.
3.2. Hamacher Operations
Definition 4
([69]). Let be two nonnegative real numbers. Then, the Hamacher t-norm and t-conorm are defined as:
4. Fermatean Cubic Fuzzy Set
This section defines the Fermatean cubic fuzzy set via combining the FFS and cubic set, and gives the definitions of score and accuracy functions, comparison laws and distance measures.
Definition 5.
Suppose that H is a nonempty set. Then, the Fermatean cubic fuzzy set (FCFS) Ψ in H can be stated as follows:
in which and denote the exact grade of membership and exact grade of non-membership, respectively, of Ψ, and meet the condition that , . For simplicity, is called as a Fermatean cubic fuzzy number (FCFN). Furthermore, if we set , then the FCFN can also be indicated as . The hesitancy grade is indicated as: .
Based on the definition of FCFSs, the score and accuracy functions of FCFNs are defined to compare FCFNs.
Definition 6.
Assume that is an FCFN. Then, the score function of Ψ is expressed as follows:
As the score function cannot compare two FCFNs when their score values are equal, the accuracy function of FCFN is defined as below.
Definition 7.
Assume that be a FCFN. Then, the accuracy function of Ψ is expressed as follows:
On the basis of the score function and accuracy function , the comparison laws of two FCFNs are given as:
Definition 8.
For two arbitrary FCFNs, are two FCFNs. Then, the comparison algorithm of and is as below:
- (1)
- If , then is smaller than , signified as ;
- (2)
- If , then we need to compare their accuracy values:
- If , then is bigger than , signified as ;
- If , then has no difference from , signified as .
Definition 9.
Suppose that are two FCFNs. Then, the generalized Fermatean cubic fuzzy distance between and is defined as below:
Remark 1.(1) The generalized Fermatean cubic fuzzy distance can be degenerated into Fermatean cubic fuzzy Hamming distance when , which can be expressed as
(2) The generalized Fermatean cubic fuzzy distance can be degenerated into Fermatean cubic fuzzy Euclid distance when :
5. Fermatean Fuzzy Cubic Hamacher Aggregation Operators
This section first propounds the Fermatean fuzzy cubic Hamacher operations based upon the Hamacher t-norm and t-conorm. Then, we put forward several Fermatean fuzzy cubic Hamacher aggregation operators and discuss the associated properties.
Definition 10.
are two FCFNs. Then, the Fermatean fuzzy cubic Hamacher operations are defined as follows:
It is obvious that the above-mentioned operational laws have the following characteristics.
Theorem 1.
For two arbitrary FCFNs, are two FCFNs. Then
Proof.
The proof of Theorem is omitted because it is straightforward. □
In what follows, several Fermatean cubic fuzzy Hamacher aggregation operators are introduced to integrate the Fermatean fuzzy cubic information. At the same time, several worthwhile properties and especial instances of the proffered operators are dissected at length.
5.1. Fermatean Cubic Fuzzy Hamacher Weighted Averaging Operators
The FCFHWA and FCFHOWA operators are defined, and the corresponding properties are also investigated.
Definition 11.
Assume that is a family of FCFNs. Then, the FCFHWA operator is a mapping from to Γ. If
then FCFHWA is called a Fermatean cubic fuzzy, Hamacher weighted averaging operator. Γ signifies the collection of FCFNs. is the importance of with with . Furthermore, the FCFHWA operator can be considered an FCFHA operator when .
The following theorem can be attained on the basis of Definition 11.
Theorem 2.
Assume that is a family of FCFNs. Then, the fusion value of "β" FCFNs via utilizing FCFHWA operator is still a FCFN and can be portrayed as
Proof.
The mathematical induction method is utilized to finish the proof.
It is obvious that Equation (16) holds when . Further, if we suppose that Equation (16) holds for , one has
Next, if , one has
In the next part, several innovative properties of the FCFHWA operator are shown.
Property 1
(Idempotency). Suppose that is a family of FCFNs. If for each , then
Proof.
□
Property 2
(Monotonicity). Suppose that and are two sets of FCFNs. If for all l, then
Property 3
(Boundedness). Suppose that is a family of FFNs. If and , then
Definition 12.
Assume that is a family of FCFNs. Then, the FCFHOWA operator is a mapping from to Γ. If
then FCFHOWA is called a Fermatean cubic fuzzy, Hamacher ordered weighted averaging operator. Γ signifies the collection of FCFNs, wherein is a permutation of within for . be the importance of with with .
A series of interesting properties of FCFHOWA operator are talked about below.
Theorem 3.
Assume that is a family of FCFNs. Then, the integration consequence of "l" FCFNs via utilizing FCFHOWA operator is still an FFN and portrayed as
Property 4
(Idempotency). Suppose that is a family of FCFNs. If for each , then
Property 5
(Monotonicity). Suppose that and are two sets of FCFN. If for all l, then
Property 6
(Boundedness). Suppose that be a family of FFNs. If and , then
The proof of Properties 4–6 is equivalent to the Properties 1–3; thus, we omit it here.
5.2. Fermatean Cubic Fuzzy Hamacher Weighted Geometric Operators
This subsection propounds FCFHWG and FCFHOWG operators, and the corresponding properties are also investigated.
Definition 13.
Assume that is a family of FCFNs. Then, the FCFHWG operator is a mapping from to Γ. If
then FCFHWG is called a Fermatean cubic fuzzy, Hamacher weighted geometric operator. Γ signifies the collection of FCFNs. is the importance of with with . Furthermore, the FCFHWG operator can be an FCFHG operator when .
Theorem 4.
Assume that is a family of FCFNs. Then, the fusion value of "l" FCFNs via utilizing FCFHWG operator is still a FCFN and portrayed as
Definition 14.
Assume that is a family of FCFNs. Then, FCFHOWG operator is a mapping from to Γ. If
then FCFHOWG is called a Fermatean cubic fuzzy, Hamacher ordered weighted geometric operator. Γ signifies the collection of FCFNs, wherein is a permutation of within for . is the importance of with with .
Theorem 5.
Assume that is a family of FCFNs. Then, the integration consequence of "l" FCFNs via utilizing FCFHOWG operator is still an FCFN:
Homoplastically, the FCFHWG and FCFHOWG operators possess the same properties as FCFHWA and FCFHOWA.
6. A Hybrid Fermatean Cubic Fuzzy MEMCDM Decision Approach
This section puts forward a MEMCDM decision approach through combining the FCFS and LOPCOW approaches, the EDAS algorithm and regret theory. The detailed decision procedure of the proffered approach was built on the basis of a distance measure, the FCFHWA operator and the score function in the Fermatean cubic fuzzy setting. We also provide a visual flowchart of the proposed method for evaluators to apply it conveniently.
6.1. Decision Problem Depiction
Aiming at a general MEMCDM decision problem, several pre-defined notations of are defined below. Assume that the decision problem comes down to schemes denoted as and criteria denoted as . The expert group possesses members to take part in the decision activity. The importance of the experts and criteria are, respectively, indicated as and , and . Assume that these schemes are assessed by experts under the pondered criteria within the Fermatean cubic fuzzy context. The assessment preference are collected as a decision matrix , listed as follows.
wherein denotes the assessment of scheme given by expert under dissimilar criteria . The is denoted as an FCFN. The solution of the this decision problem is to attain the prioritization order of schemes. In what follows, we build a hybrid MEMCDM decision approach to cope with this problem validly.
6.2. The Propounded Hybrid MEMCDM Decision Algorithm
We design a novel MEMCDM decision approach by integrating the LOPCOW approach, the EDAS algorithm and regret theory with Fermatean cubic fuzzy information for the emergence decision. First of all, the similarity-based method is constructed on the basis of a generalized Fermatean cubic fuzzy distance measure to compute the weights of experts. Next, the Fermatean cubic fuzzy LOPCOW approach is proposed in view of the score function to confirm the objective weights of criteria. Further, the EDAS approach based on regret theory is propounded for the Fermatean cubic fuzzy setting to ascertain the prioritization order of the scheme.
Step 1: Acquire the original decision matrices by experts.
Step 2: Calculate the weight information of experts.
In this step, we utilize the similarity-based method to calculate the weight vector of experts.
(1) Compute the ideal matrix based on the experts’ decision matrices by the FCFHWA operator.
(2) Determine the similarity degree between the ideal assessment value and the expert assessment information .
where is the Fermatean fuzzy cubic generalized distance measure.
(3) Compute the expert weight vector based on the similarity degree between the ideal matrix and expert matrix,
where .
Step 3: Compute the normalized expert decision matrices .
Step 4: Attaining the fused assessment decision opinion.
In this step, we employ the FCFHWA operator to fuse the matrices of decision experts and obtain the comprehensive assessment opinions of alternatives according to different experts. Hence, we create the aggregated Fermatean cubic fuzzy decision matrix as below.
Step 5: Identify the criteria’s weights via LOPCOW approach.
The LOPCOW approach was proposed by Ecer and Pamucar [32] to objectively criterion weight through computing the standard deviation and percentage value of each criterion. The merit of the LOPCOW approach is that it can eliminate the differences of entropy weight methods and attain more credible and acceptable criterion weight information. In these steps, the Fermatean cubic fuzzy LOPCOW approach is presented based on score function to evaluate the criteria’s weights.
(1) Attain the score matrix of the group assessment matrix with the help of the Fermatean cubic fuzzy score function in Definition 6.
(2) Calculate the standard deviation of every criterion with the aid of Equation (34).
(3) Compute the percentage values (PV) of each criterion via Equation (35).
(4) Based on the percentage values of each criterion, the criterion’s weight is calculated via Equation (36).
Step 6: Deduce the utility group assessment matrix of the scheme.
Based upon the score matrix obtained from step 4, the utility group assessment matrix of scheme can be worked out by Equation (37):
in which is the utility value of each scheme with the respect to criteria, and is the risk preference index. is the score value of group assessment information.
Step 7: Determine the ideal assessment value of each criterion.
Step 8: Determine the regret assessment matrix of each scheme.
in which is the utility value of the ideal assessment value and signifies the risk aversion index of experts.
Step 9: Identify the overall utility matrix of the scheme.
Step 10: Ascertain the averaging solution of each criterion.
Step 11: Confirm the positive and negative distance matrices from the averaging solution.
Step 12: Compute the appraisal score value of each scheme.
Step 13: Attain the prioritization relation of each scheme on the basis of the appraisal score values .
The mentioned decision procedures show the concrete decision steps of the proposed approach. Moreover, a visual flowchart displayed in Figure 1 is provided in the following to summarize those steps.
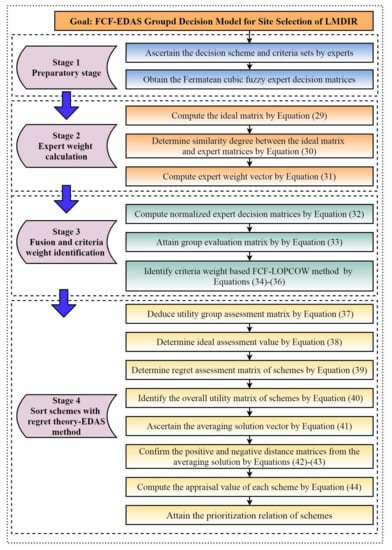
Figure 1.
The propounded FCF-EDAS group decision framework.
7. Illustrate Example
This section discusses the practicality and rationality of the propounded hybrid MEMCDM decision approach. First, an example about site selection of LMDIR is utilized to demonstrate the feasibility of the proffered approach. Then, the sensibility analysis of the designed method is conducted through discussing the influences of different parameter values on the final assessment outcomes. Furthermore, a comparison is presented on the effectuality and superiority of the advanced method.
7.1. Background Introduction
The rapid development of urban agglomeration makes the travel demand between adjacent cities in the urban agglomeration increasingly prominent. This kind of travel mode is generally 25–200 km for medium and short distances, and has the characteristics of high passenger flow intensity, high proportions of public and business uses and high transfer requirements. Therefore, the construction and development of intercity railway systems with less land occupation, low energy consumption, large capacities and high efficiency have become inevitable for cities. The construction of intercity railway can not only enhance rapid movement between cities in the urban agglomeration, but also effectively promote the cooperation between cities in economy, finance, trade, information and so on. After a comprehensive investigation, field research and expert consultation, some alternative station sites of LMDIR were determined by the government management department and intercity railway engineers to select most satisfying sites for stations of LMDIR. An expert group composed of three experts considered four criteria, coordination (), sustainability (), functionality () and effectiveness (), to comprehensively evaluate the five alternative station sites of LMDIR , and have the corresponding priority relationship to provide decision support for experts. Herein, the type of all criteria was regarded as benefit criteria by the expert discussion and investigation. As the weights of experts for criteria were all completely known, the proposed hybrid MEMCDM decision approach was applied to handle this sit selection problem.
7.2. Decision Analysis
In light of the introduction of the background, the proposed FCF-EDAS method based on regret theory was employed to handle the station sites of LMDIR problem. The detailed decision analysis steps are depicted below.
Step 1: Acquire the original decision matrices from experts.
Based on the expert assessment committee denoted as and criteria set , the experts provided their assessments in the form of Fermatean cubic fuzzy numbers, and we collected their assessments to construct the expert decision matrices , displayed in Table 1.

Table 1.
Fermatean cubic fuzzy assessment matrices provided by experts.
Step 2: Calculate the weight information of experts.
Based on the distance measure between two FCFNs, we further obtained the distance measure between two Fermatean cubic fuzzy decision matrices. Then, with the help of Equations (29)–(31), the expert weights were computed as:
Step 3: Attain the normalized expert decision matrices .
In light of Equation (32), The normalized expert decision matrices were acquired by Equation (32). Owing to all criteria being benefit criteria, .
Step 4: Obtain the fused assessment matrix .
In this step, the FCFHWA operator displayed in Equation (33) was employed to aggregate the experts’ assessment information and form the the integration group decision matrix , displayed in Table 2.

Table 2.
Fermatean cubic fuzzy group decision matrix .
Step 5: Compute the importance of the considered criteria.
As an innovative objective weight identification approach, the LOPCOW method can reduce the differences among diverse criteria and obtain more rational weight information. Hence, in view of the introduced Fermatean cubic fuzzy LOPCOW approach displayed in Equations (34) and (35), the criteria’s weights were worked out with the aid of Equations (34)–(36), displayed as:
Step 6: Derive the group utility assessment matrix.
The group utility assessment matrix was calculated utilizing Equation (37), as displayed in Table 3.

Table 3.
Utility group assessment matrix .
Step 7: Determine the ideal assessment value.
On the basis of Equation (38), the ideal assessment value of each criterion can be attained as follows:
Step 8: Identify the regret assessment matrix.

Table 4.
Regret assessment matrix .
Step 9: Determine the overall utility matrix.

Table 5.
Overall utility matrix .
Step 10: Determine the averaging solution of criteria.
The averaging solution of each criterion was ascertained via Equation (41), displayed as: .
Step 11: Determine the positive and negative distance matrices.
The positive and negative distance matrices from the averaging solution were confirmed via Equations (42) and (43), as displayed in Table 6 and Table 7.

Table 6.
Positive distance matrix.

Table 7.
Negative distance matrix.
Step 12: Obtain the appraisal score values of station sites.
The appraisal score values of each scheme were computed by Equation (44) and are listed as below.
Step 13: Deduce the order of the alternative station sites.
The prioritization relation of station sites of LMDIR were attained by the appraisal score values , namely, . The bigger the appraisal value, the better the station sites of LMDIR is. Henceforth, the optimal station sites of LMDIR are .
7.3. Sensitivity Analysis
In this subsection, the parameter analysis is shown, which analyzes the sensitivity degree of final ranking outcome to each parameter. In our proposed method, the parameter ℵ in FCFHWA operator and in the generalized Fermatean fuzzy cubic distance measure may influence the final results. Therefore, we took different values of ℵ and and attained the appraisal score values and ranks of station sites of LMDIR. The corresponding outcomes are exhibited in Table 8 and Table 9.

Table 8.
Decision results regarding different parameter values in the FCFHWA operator.

Table 9.
Decision results regarding different parameter values for the distance measure.
First, we analyzed the change in decision result by assigning different values of the parameter ℵ to the FCFHWA operator. From Table 8 and Figure 2, we can see that the sorting value of the station sites of LMDIR is regardless of the value of the parameter ℵ, which implies that the ranking of station sites of LMDIR is relatively stable for the parameter ℵ.

Figure 2.
Decision results regarding different parameter ℵ for the FCFHWA operator.
Next, we discuss the impact of parameter on the ultimate ranking results. From Table 9 and Figure 3, we can see that the appraisal scores of the station sites of LMDIR increase with the increase in parameter . According to the appraisal scores of the scheme through taking different values of parameter , the order relation of station sites of LMDIR is always —namely, the best option is . The outcomes show that the proposed MEMCDM decision approach is robust regarding the parameter .
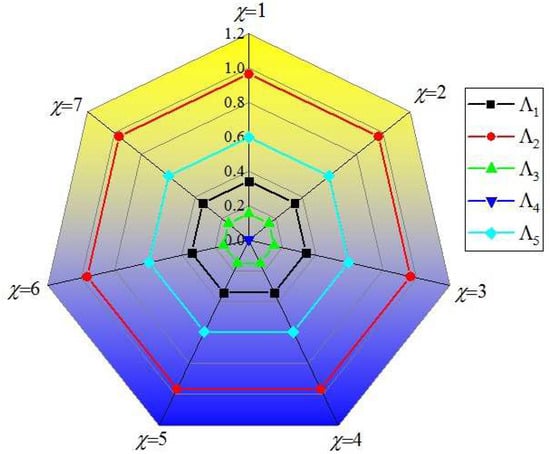
Figure 3.
Decision results under different parameters for the distance measure.
7.4. Comparison Study
The current subsection presents the comparison analysis to verify the effectiveness and significant superiority of the proposed hybrid group decision methodology. The FCFS is first propounded to represent the uncertain information and construct group decision making approach. Thus, we first show the results of some existing approaches, including the method based on the ICFWA operator [46], the method based on the ICFWG operator [46], the method based on the PCFWA operator [44] and the PCF-TOPSIS method [54], in resolve the above case, and further validate the effectiveness and advantages of the proposed method. Then, we present the Fermatean cubic fuzzy WPM and WASPAS methods and compare their decision results with those of the presented MEMCDM approach. The comparison results of various methods are displayed in Table 10.

Table 10.
Decision results attained by different approaches.
Based on the comparison results listed in Table 10, we can see that the methods based on ICFWA and ICFWG operators failed to cope with this case, because the assessment information provided by experts does not meet the initial condition of the sum of membership and nonmembership grade being less than one. Hence, the ICFWA and ICFWG operators fail to deal with this kind of problem. Next, we utilized the method based on the PCFWA operator [44], the PCF-TOPSIS method [54] and the FCF-WPM and FCF-WASPAS methods to rank the site station of LMDIR. The outcomes show that their optimal option is consistent with the results of the method proposed in this paper, which illustrates the validity of our approach. Nevertheless, the ranks of schemes obtained by above methods possess slight differences from our results.
In light of the above difference, the propounded approach is compared with other methods as follows:
Compared with the methods based on ICFWA and ICFWG operators. The ICFWA and ICFWG operators are special cases of the Fermatean cubic Hamacher operators, which only utilize the simple aggregation ideal to obtain comprehensive values of a scheme but ignore the internal influence and behavioral characteristics of experts. In addition, the ICFSs make experts have strong restrictions when providing preferences for schemes. Therefore, the proposed Fermatean cubic fuzzy EDAS method based on regret theory possesses a more widespread range of applications than ICFWA and ICFWG operators.
Compared with the PCF-TOPSIS method. The PCF-TOPSIS method [54] solves the problem by determining the distance from the positive ideal solution and the negative ideal solution to the scheme, and then determining the ranking for the scheme by relative closeness. We can see that the PCF-TOPSIS method has some deficiencies: (1) it fails to consider the psychological conditions of experts in the process of making decisions; (2) it cannot process the preference that the sum of squares of membership and nonmembership degrees is less than or equal to one. However, the proposed Fermatean cubic fuzzy EDAS method based on regret theory can validly settle the mentioned defects and attain more robust and rational ranking outcomes.
Compared with the FCF-WASPAS method. The FCF-WASPAS method ascertains the ranking outcomes based on the weight sum and weight product models utilizing utility theory. However, it not only lacks the flexibility but also ignores the psychological preferences of experts in the course of decision making. On the contrary, the proposed approach provides an effective decision framework through considering the behavioral decisions and unknown weights of experts and criteria. Accordingly, the proposed hybrid Fermatean cubic fuzzy EDAS method is more generalized and flexible than the FCF-WASPAS method.
From the above-mentioned discussion and analysis, the propounded approach is a universal and robust group decision framework for experts that considers complex uncertainty information and behavioral features to perform decision analysis. Furthermore, the significant features of the proposed method compared with thsoe of the extant approaches are summarized in Table 11.

Table 11.
Characteristic comparison between the propounded methods and extant approaches.
7.5. Managerial Implications
Based upon the analysis mentioned, the propounded Fermatean cubic fuzzy EDAS method based on regret theory possesses some managerial implications for selecting the station sites of LMDIR, and provides a more rational and viable decision support model for actual applications. Firstly, the propounded approach implements the proposed Fermatean cubic fuzzy set, which can allow experts to express their indeterminacy by FFSs and IVFFSs. In this way, the proposed method can successfully overcome the vagueness and uncertainty of experts’ sophisticated cognition in the course of site selection for LMDIR stations. Secondly, the established approach confirms the importance of criteria by utilizing the Fermatean cubic fuzzy LOPCOW method objectively. In this way, the criteria’s weights are worked out rationally based on the assessment information on station sites of the LMDIR, which further strengthens the practicability of the proposed method. Thirdly, based on the merging of FCFSs, the EDAS method and regret theory, the propounded approach models the psychological behavior of decision makers, letting it provide a more reasonable and practicable ranking of station sites of the LMDIR. Accordingly, the developed Fermatean cubic fuzzy EDAS approach provides an efficient and viable group decision model for the selection of station sites of the LMDIR, which can further provide reasonable decision references for the railway administration department.
8. Conclusions
The objective of this investigation was to build up a hybrid MEMCDM approach to select the most satisfied service center under a Fermatean cubic fuzzy environment. The presented approach was developed based upon the FCFHWA operator, and LOPCOW and EDAS methods with FCFSs. To begin with, the definition and related basic theories, including comparison rules and distance measure of FCFSs, were defined. Secondly, several Fermatean cubic fuzzy Hamacher operators were propounded to attain the fused Fermatean cubic fuzzy information. Thirdly, the LOPCOW method was extended based on the Fermatean cubic fuzzy score function for evaluating the importance of criteria. Fourthly, a hybrid MEMCDM methodology with the aid of the similarity-based method, LOPCOW method and EDAS method based on regret theory, was brought forward to attain the rank of schemes. The case of station sites of LMDIR, selection was employed to verify the feasibility of the introduced method. The assessment outcome illustrated that the second site station of LMDIR would be the optimal option according to experts with the help of the proposed FCF-EDAS approach. In addition, the sensibility analysis also verified that the best site station of LMDIR is , which guarantees the stability of the proposed method for the station sites of LMDIR’s selection. Comparisons with previous methodologies were executed to verify the advantages of the recommended hybrid decision model. The contrast study exhibits that the propounded FCF-EDAD group decision approach can validly and rationally cope with the problem of station sites of LMDIR’s selection. Based on these discussions, it was proved that the established method provides a simple and practical group decision model to manage the complex MCDM issues by pondering the unknown weight information and psychological features of experts.
In what follows, we discuss some limitations of the presented MEMCDM approach in this paper. (1) During the process of expert information fusion, the interrelationship of the Fermatean cubic fuzzy numbers is not considered and further causes the deviation for the group assessment information. (2) In the stage of criterion weight determination, the subjective weight information is ignored because of the different knowledge and cognition of experts. (3) The assessment system of the service center selection should take into consideration the green and sustainability criterion.
In the future, we shall try to make up for the deficiencies of the proposed approach and develop other investigations to enrich the theory and applications of the FCFSs. Further, some new aggregation operators based on other operations and functional operators, such as the Muirhead mean [70], Maclaurin symmetric mean [71] and copula-based operator [72], will be developed to consider the interrelationship during the process of Fermatean cubic fuzzy information aggregation. Then, some classical decision approaches, such as the taxonomy method [73], WASPAS method [74] and MACONT approach [75], can be extended to Fermatean cubic fuzzy environment for constructing diverse decision frameworks dealing with different characteristic decision problems [76,77,78]. In addition, the information measures theories, such as distance measure, similarity measure and coefficient measures, should be researched to lay a foundation for building more decision algorithms.
Author Contributions
Conceptualization, W.N., Y.R., L.Y. and L.H.; Formal analysis, W.N., Y.R., L.Y. and L.H.; Investigation, L.Y.; Methodology, W.N., Y.R. and L.H.; Project administration, L.Y.; Writing—original draft, W.N.; Writing—review & editing, W.N., Y.R., L.Y. and L.H. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the General Program of National Natural Science Foundation of China (No: 12071280).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LMDIR | Line Management Department of Intercity Railway |
| MEMCDM | Multiple expert Multi-Criteria Group Decision-Making |
| FCFSs | Fermatean Cubic Fuzzy Sets |
| FFSs | Fermatean Fuzzy Sets |
| LOPCOW | LOgarithmic Percentage Change-driven Objective Weighting |
| EDAS | Evaluation based on Distance from Average Solution |
| FSs | Fuzzy Sets |
| CSs | Cubic Sets |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| VIKOR | VIse KriterijumsaOptimiz acija I KOmpromisno Resenje |
| WASPAS | Weighted Aggregated Sum Product ASsessment |
| MCDM | Multi-Criteria Group Decision-Making |
| ARAS | Additive Ratio ASsessment |
| CRITIC | CRiteria Importance Through Intercriteria Correlation |
| CoCoSo | Combined Compromise Solution |
| MEREC | Method Based on the Removal Effects of Criteria |
| DEMATEL | Decision Making Trial and Evaluation Laboratory |
| COPRAS | Complex Proportional Assessment |
| SAW | Simple Additive Weighting |
| FCFHWA | Fermatean Cubic fuzzy Hamacher weighted averaging operator |
| FCFHWG | Fermatean Cubic fuzzy Hamacher weighted geometric operator |
| FCFHOWA | Fermatean Cubic fuzzy Hamacher ordered weighted averaging operator |
| FCFHOWG | Fermatean Cubic fuzzy Hamacher ordered weighted geometric operator |
| ICFWA | Intuitionistic Cubic Fuzzy Weighted Averaging operator |
| ICFWG | Intuitionistic Cubic Fuzzy Weighted Geometric operator |
| PCFWA | Pythagorean Cubic fuzzy weighted averaging operator |
| WPM | Weighted Product Model |
| MACONT | Mixed Aggregation by COmprehensive Normalization Technique |
References
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Mizumoto, M.; Tanaka, K. Some properties of fuzzy sets of type 2. Inf. Control 1976, 31, 312–340. [Google Scholar] [CrossRef]
- Miyamoto, S. Remarks on basics of fuzzy sets and fuzzy multisets. Fuzzy Sets Syst. 2005, 156, 427–431. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy sets. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 663–674. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Some new operations over Fermatean fuzzy numbers and application of Fermatean fuzzy WPM in multiple criteria decision making. Informatica 2019, 30, 391–412. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Garg, H.; Li, X. Differential calculus of Fermatean fuzzy functions: Continuities, derivatives, and differentials. Int. J. Comput. Intell. Syst. 2021, 14, 282–294. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Fermatean fuzzy Einstein aggregation operators-based MULTIMOORA method for electric vehicle charging station selection. Expert Syst. Appl. 2021, 182, 115267. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Y.; Chen, X. Fermatean fuzzy linguistic set and its application in multicriteria decision making. Int. J. Intell. Syst. 2019, 34, 878–894. [Google Scholar] [CrossRef]
- Jeevaraj, S. Ordering of interval-valued Fermatean fuzzy sets and its applications. Expert Syst. Appl. 2021, 185, 115613. [Google Scholar]
- Mishra, A.R.; Liu, P.; Rani, P. COPRAS method based on interval-valued hesitant Fermatean fuzzy sets and its application in selecting desalination technology. Appl. Soft Comput. 2022, 119, 108570. [Google Scholar] [CrossRef]
- Jun, Y.B.; Kim, C.S.; Yang, K.O. Cubic sets. Ann. Fuzzy Math. Inform. 2012, 4, 83–98. [Google Scholar]
- Fahmi, A.; Abdullah, S.; Amin, F.; Siddiqui, N.; Ali, A. Aggregation operators on triangular cubic fuzzy numbers and its application to multi-criteria decision making problems. J. Intell. Fuzzy Syst. 2017, 33, 3323–3337. [Google Scholar] [CrossRef]
- Fahmi, A.; Amin, F.; Abdullah, S.; Ali, A. Cubic fuzzy Einstein aggregation operators and its application to decision-making. Int. J. Syst. Sci. 2018, 49, 2385–2397. [Google Scholar] [CrossRef]
- Riaz, M.; Tehrim, S.T. Cubic bipolar fuzzy ordered weighted geometric aggregation operators and their application using internal and external cubic bipolar fuzzy data. Comput. Appl. Math. 2019, 38, 87. [Google Scholar] [CrossRef]
- Lai, Y.J.; Liu, T.Y.; Hwang, C.L. Topsis for MODM. Eur. J. Oper. Res. 1994, 76, 486–500. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Chakraborty, S.; Zavadskas, E.K. Applications of WASPAS method in manufacturing decision making. Informatica 2014, 25, 1–20. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Kahraman, C.; Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Cevik Onar, S.; Yazdani, M.; Oztaysi, B. Intuitionistic fuzzy EDAS method: An application to solid waste disposal site selection. J. Environ. Eng. Landsc. Manag. 2017, 25, 1–12. [Google Scholar] [CrossRef]
- Mishra, A.R.; Mardani, A.; Rani, P.; Zavadskas, E.K. A novel EDAS approach on intuitionistic fuzzy set for assessment of health-care waste disposal technology using new parametric divergence measures. J. Clean. Prod. 2020, 272, 122807. [Google Scholar] [CrossRef]
- Peng, X.; Liu, C. Algorithms for neutrosophic soft decision making based on EDAS, new similarity measure and level soft set. J. Intell. Fuzzy Syst. 2017, 32, 955–968. [Google Scholar] [CrossRef]
- Li, Z.; Wei, G.; Wang, R.; Wu, J.; Wei, C.; Wei, Y. EDAS method for multiple attribute group decision making under q-rung orthopair fuzzy environment. Technol. Econ. Dev. Econ. 2020, 26, 86–102. [Google Scholar] [CrossRef]
- Darko, A.P.; Liang, D. Some q-rung orthopair fuzzy Hamacher aggregation operators and their application to multiple attribute group decision making with modified EDAS method. Eng. Appl. Artif. Intell. 2020, 87, 103259. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new multi-criteria model based on interval type-2 fuzzy sets and EDAS method for supplier evaluation and order allocation with environmental considerations. Comput. Ind. Eng. 2017, 112, 156–174. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, J.Q.; Wang, T.L. A linguistic neutrosophic multi-criteria group decision-making approach with EDAS method. Arab. J. Sci. Eng. 2019, 44, 2737–2749. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. A novel LOPCOW-DOBI multi-criteria sustainability performance assessment methodology: An application in developing country banking sector. Omega 2022, 112, 102690. [Google Scholar] [CrossRef]
- Gül, S. Fermatean fuzzy set extensions of SAW, ARAS, and VIKOR with applications in COVID-19 testing laboratory selection problem. Expert Syst. 2021, 38, e12769. [Google Scholar] [CrossRef]
- Tan, J.; Liu, Y.; Senapati, T.; Garg, H.; Rong, Y. An extended MABAC method based on prospect theory with unknown weight information under Fermatean fuzzy environment for risk investment assessment in B&R. J. Ambient. Intell. Humaniz. Comput. 2022, 1–30. [Google Scholar] [CrossRef]
- Wei, D.; Meng, D.; Rong, Y.; Liu, Y.; Garg, H.; Pamucar, D. Fermatean Fuzzy Schweizer–Sklar Operators and BWM-Entropy-Based Combined Compromise Solution Approach: An Application to Green Supplier Selection. Entropy 2022, 24, 776. [Google Scholar] [CrossRef]
- Gonzales, G.; Costan, F.; Suladay, D.; Gonzales, R.; Enriquez, L.; Costan, E.; Ocampo, L. Fermatean fuzzy DEMATEL and MMDE algorithm for modelling the barriers of implementing education 4.0: Insights from the Philippines. Appl. Sci. 2022, 12, 689. [Google Scholar] [CrossRef]
- Lai, H.; Liao, H.; Long, Y.; Zavadskas, E.K. A Hesitant Fermatean Fuzzy CoCoSo Method for Group Decision-Making and an Application to Blockchain Platform Evaluation. Int. J. Fuzzy Syst. 2022, 1–19. [Google Scholar] [CrossRef]
- Akram, M.; Muhiuddin, G.; Santos-Garcıa, G. An enhanced VIKOR method for multi-criteria group decision-making with complex Fermatean fuzzy sets. Math. Biosci. Eng. 2022, 19, 7201–7231. [Google Scholar] [CrossRef]
- Simić, V.; Ivanović, I.; Dorić, V.; Torkayesh, A.E. Adapting urban transport planning to the COVID-19 pandemic: An integrated fermatean fuzzy model. Sustain. Cities Soc. 2022, 79, 103669. [Google Scholar] [CrossRef]
- Yang, S.; Pan, Y.; Zeng, S. Decision making framework based Fermatean fuzzy integrated weighted distance and TOPSIS for green low-carbon port evaluation. Eng. Appl. Artif. Intell. 2022, 114, 105048. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Saha, A.; Hezam, I.M.; Pamucar, D. Fermatean fuzzy Heronian mean operators and MEREC-based additive ratio assessment method: An application to food waste treatment technology selection. Int. J. Intell. Syst. 2022, 37, 2612–2647. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Liu, H.C.; Wang, J.H.; Shi, H. New model for occupational health and safety risk assessment based on Fermatean fuzzy linguistic sets and CoCoSo approach. Appl. Soft Comput. 2022, 126, 109262. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Deveci, M.; Antucheviciene, J. New complex proportional assessment approach using Einstein aggregation operators and improved score function for interval-valued Fermatean fuzzy sets. Comput. Ind. Eng. 2022, 169, 108165. [Google Scholar] [CrossRef]
- Khan, F.; Khan, M.S.A.; Shahzad, M.; Abdullah, S. Pythagorean cubic fuzzy aggregation operators and their application to multi-criteria decision making problems. J. Intell. Fuzzy Syst. 2019, 36, 595–607. [Google Scholar] [CrossRef]
- Ayub, S.; Abdullah, S.; Ghani, F.; Qiyas, M.; Yaqub Khan, M. Cubic fuzzy Heronian mean Dombi aggregation operators and their application on multi-attribute decision-making problem. Soft Comput. 2021, 25, 4175–4189. [Google Scholar] [CrossRef]
- Abdullah, S. Multicriteria group decision-making for supplier selection based on intuitionistic cubic fuzzy aggregation operators. Int. J. Fuzzy Syst. 2020, 22, 810–823. [Google Scholar]
- Liu, H.B.; Liu, Y.; Xu, L.; Abdullah, S. Multi-attribute group decision-making for online education live platform selection based on linguistic intuitionistic cubic fuzzy aggregation operators. Comput. Appl. Math. 2021, 40, 16. [Google Scholar] [CrossRef]
- Fahmi, A.; Yaqoob, N.; Chammam, W. Maclaurin symmetric mean aggregation operators based on cubic Pythagorean linguistic fuzzy number. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 1925–1942. [Google Scholar] [CrossRef]
- Riaz, M.; Habib, A.; Khan, M.J.; Kumam, P. Correlation coefficients for cubic bipolar fuzzy sets with applications to pattern recognition and clustering analysis. IEEE Access 2021, 9, 109053–109066. [Google Scholar] [CrossRef]
- Garg, H.; Mahmood, T.; Ahmmad, J.; Khan, Q.; Ali, Z. Cubic q-Rung Orthopair Fuzzy Linguistic Set and Their Application to Multiattribute Decision-making with Muirhead Mean Operator. J. Artif. Intell. Technol. 2021, 1, 37–50. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, X. Prospect-theory and geometric distance measure-based Pythagorean cubic fuzzy multicriteria decision-making. Int. J. Intell. Syst. 2021, 36, 4117–4142. [Google Scholar] [CrossRef]
- Yu, Q.; Cao, J.; Tan, L.; Liao, Y.; Liu, J. Multiple attribute decision-making based on maclaurin symmetric mean operators on q-rung orthopair cubic fuzzy sets. Soft Comput. 2022, 1–25. [Google Scholar] [CrossRef]
- Jamil, N.; Riaz, M. Bipolar disorder diagnosis with cubic bipolar fuzzy information using TOPSIS and ELECTRE-I. Int. J. Biomath. 2022, 15, 2250030. [Google Scholar] [CrossRef]
- Seker, S.; Kahraman, C. A Pythagorean cubic fuzzy methodology based on TOPSIS and TODIM methods and its application to software selection problem. Soft Comput. 2022, 26, 2437–2450. [Google Scholar] [CrossRef]
- Özçelik, G.; Nalkıran, M. An extension of EDAS method equipped with trapezoidal bipolar fuzzy information: An application from healthcare system. Int. J. Fuzzy Syst. 2021, 23, 2348–2366. [Google Scholar] [CrossRef]
- Lukić, R. Application of the EDAS Method in the Evaluation of Bank Efficiency in Serbia. Bankarstvo 2021, 50, 64–75. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z.; Gou, X. The Interval probabilistic double hierarchy linguistic EDAS method based on natural language processing basic techniques and its application to hotel online reviews. Int. J. Mach. Learn. Cybern. 2022, 13, 1517–1534. [Google Scholar] [CrossRef]
- Mi, X.; Liao, H. An integrated approach to multiple criteria decision making based on the average solution and normalized weights of criteria deduced by the hesitant fuzzy best worst method. Comput. Ind. Eng. 2019, 133, 83–94. [Google Scholar] [CrossRef]
- Zhang, F.; Ju, Y.; Gonzalez, E.D.S.; Wang, A. SNA-based multi-criteria evaluation of multiple construction equipment: A case study of loaders selection. Adv. Eng. Inform. 2020, 44, 101056. [Google Scholar] [CrossRef]
- Krishankumar, R.; Pamucar, D.; Deveci, M.; Ravichandran, K.S. Prioritization of zero-carbon measures for sustainable urban mobility using integrated double hierarchy decision framework and EDAS approach. Sci. Total Environ. 2021, 797, 149068. [Google Scholar] [CrossRef]
- Hou, W.H.; Wang, X.K.; Zhang, H.Y.; Wang, J.Q.; Li, L. Safety risk assessment of metro construction under epistemic uncertainty: An integrated framework using credal networks and the EDAS method. Appl. Soft Comput. 2021, 108, 107436. [Google Scholar] [CrossRef]
- Lei, F.; Wei, G.; Shen, W.; Guo, Y. PDHL-EDAS method for multiple attribute group decision making and its application to 3D printer selection. Technol. Econ. Dev. Econ. 2022, 28, 179–200. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Luo, S.Z. An integrated EDAS-ELECTRE method with picture fuzzy information for cleaner production evaluation in gold mines. IEEE Access 2018, 6, 65747–65759. [Google Scholar] [CrossRef]
- Zhan, J.; Jiang, H.; Yao, Y. Covering-based variable precision fuzzy rough sets with PROMETHEE-EDAS methods. Inf. Sci. 2020, 538, 314–336. [Google Scholar] [CrossRef]
- Asante, D.; He, Z.; Adjei, N.O.; Asante, B. Exploring the barriers to renewable energy adoption utilising MULTIMOORA-EDAS method. Energy Policy 2020, 142, 111479. [Google Scholar] [CrossRef]
- Karatop, B.; Taşkan, B.; Adar, E.; Kubat, C. Decision analysis related to the renewable energy investments in Turkey based on a Fuzzy AHP-EDAS-Fuzzy FMEA approach. Comput. Ind. Eng. 2021, 151, 106958. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, M.; Wei, G.; Wei, C.; Chen, X. Probabilistic uncertain linguistic EDAS method based on prospect theory for multiple attribute group decision-making and its application to green finance. Int. J. Fuzzy Syst. 2022, 24, 1318–1331. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, R.; Chen, X. An enhancement EDAS method based on prospect theory. Technol. Econ. Dev. Econ. 2021, 27, 1019–1038. [Google Scholar] [CrossRef]
- Hamacher, H. Uber logische verknupfungen unscharfer aussagen und deren zugehÃurige bewertungsfunktionen. Prog. Cybern. Syst. Res. 1978, 3, 267–287. [Google Scholar]
- Rong, Y.; Liu, Y.; Pei, Z. Novel multiple attribute group decision-making methods based on linguistic intuitionistic fuzzy information. Mathematics 2020, 8, 322. [Google Scholar] [CrossRef]
- Rong, Y.; Liu, Y.; Pei, Z. Complex q-rung orthopair fuzzy 2-tuple linguistic Maclaurin symmetric mean operators and its application to emergency program selection. Int. J. Intell. Syst. 2021, 35, 1749–1790. [Google Scholar] [CrossRef]
- Rong, Y.; Liu, Y.; Pei, Z. A novel multiple attribute decision-making approach for evaluation of emergency management schemes under picture fuzzy environment. Int. J. Mach. Learn. Cybern. 2021, 13, 633–661. [Google Scholar] [CrossRef]
- Liu, P.; Wang, D. An extended taxonomy method based on normal T-spherical fuzzy numbers for multiple-attribute decision-making. Int. J. Fuzzy Syst. 2022, 24, 73–90. [Google Scholar] [CrossRef]
- Wei, D.; Rong, Y.; Garg, H. An extended WASPAS approach for teaching quality evaluation based on pythagorean fuzzy reducible weighted Maclaurin symmetric mean. J. Intell. Fuzzy Syst. 2022, 42, 3121–3152. [Google Scholar] [CrossRef]
- Wen, Z.; Liao, H.; Zavadskas, E.K. MACONT: Mixed aggregation by comprehensive normalization technique for multi-criteria analysis. Informatica 2020, 31, 857–880. [Google Scholar] [CrossRef]
- Lin, S.S.; Zhang, N.; Zhou, A.; Shen, S.L. Risk evaluation of excavation based on fuzzy decision-making model. Autom. Constr. 2022, 136, 104143. [Google Scholar] [CrossRef]
- Reda, H.; Dvivedi, A. Decision-making on the selection of lean tools using fuzzy QFD and FMEA approach in the manufacturing industry. Expert Syst. Appl. 2022, 192, 116416. [Google Scholar] [CrossRef]
- Liu, H.C.; Shi, H.; Li, Z.; Duan, C.Y. An integrated behavior decision-making approach for large group quality function deployment. Inf. Sci. 2022, 582, 334–348. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).