Soliton-like Solutions of General Variable Coefficient Cylindrical/Spherical KdV Equation

Abstract

The general variable coefficient cylindrical/spherical KdV equation has been investigated by using the simplified homogeneous balance method. It has been proven that if its coefficients satisfy certain constraint conditions, then the cylindrical/spherical KdV equation has a nonlinear transformation that converts the solution of the quadratic form equation into the solution of the cylindrical/spherical KdV equation. The quadratic form equation admits a series of solutions expressed by the exponential functions, therefore one soliton-like solution and multi soliton-like solutions of the cylindrical/spherical KdV equation can be obtained exactly.

1. Introduction

In the present paper we investigate general variable coefficient cylindrical/spherical KdV equation [1,2,3] in the form

$$u_t+\alpha (t)u{u}_x+\beta (t)u_{xxx}+\frac{m}{2t}u=0,$$

(1)

where $\alpha (t)$ is the nonlinear coefficient and $\beta (t)$ is the dispersion coefficient. The last term containing an arbitrary and positive integer “m” represents the geometry effects: when $m=1$, it represents the cylindrical geometry effect, and Equation (1) is called the cylindrical KdV equation; when $m=2$, it represents the spherical geometry effect, and Equation (1) is called the spherical KdV equation.

In Ref. [4], by using the conventional reductive perturbation method, the authors derived the cylindrical (spherical) KdV and mKdV equations and obtained the progressive wave solutions. Through the use of the reductive perturbation method, an approximate analytical method for the progressive wave solution is presented for the cylindrical (spherical) KdV and the modified KdV equations in the sense of the weighted residual method in Ref. [5]. Although several researchers derived these evolution equations for various type of plasma structures, there is no analytical progressive soliton-like solution available, especially for the general variable coefficient cylindrical/spherical KdV equation.

The question considered in the paper is to find out what constraint condition exists for $\alpha (t)$ and $\beta (t)$, such that Equation (1) admits an exact soliton-like solution, as well as exact multi soliton-like solutions. We shall apply the simplified homogeneous balance method (SHB) [6,7,8,9,10], different from the homogeneous balance method (HB) [11,12,13], to investigate Equation (1), thereby to answer this question. By this method, a nonlinear transformation from the solution for a quadratic form equation to the solution for the general variable coefficient cylindrical/spherical KdV equation is derived, and one soliton-like solution and multi soliton-like solutions are obtained via the nonlinear transformation successfully. It is worth noting that these solutions have not been mentioned in the previous literature. The geometric shapes of some soliton-like solutions are studied by numerical simulation. The constraint condition of a solution for a variable coefficient is discussed and the comparison of the influence of parameters on its shape is investigated.

2. Derivation of Constraint Condition and Nonlinear Transformation

Considering the homogeneous balance between $u{u}_x$ and $u_{xxx}$ in Equation (1) ($2m+1=m+3\Rightarrow m=2$) according to the simplified homogeneous balance method, we can suppose that the solution of Equation (1) is of the form

$$u(x,t)=A(t){(\ln \phi )}_{xx},$$

(2)

where we use $A(t)\ln \phi$ instead of the undetermined functions $f(\phi )$ appearing in the homogeneous balance method to simplify the original HB; functions $A(t)$ and $\phi =\phi (x,t)$ are to be determined later. The aim of the simplified HB is to find the variable coefficient $A(t)$ and the function $\phi =\phi (x,t)$, such that the expressions (2) exactly satisfy Equation (1).

From (2) it is easy to obtain that

$$u_t=A^{\prime }(t){\left(\ln \phi \right)}_{xx}+A(t)\left(\frac{{\phi }_{xt}}{\phi }-\frac{{\phi }_x{\phi }_t}{{\phi }^2}\right),$$

(3)

$$u{u}_x=A\frac{\partial }{\partial x}\left[\frac{A}{2}\left(\frac{{\phi }_{xx}^2}{{\phi }^2}-\frac{2{\phi }_x^2{\phi }_{xx}}{{\phi }^3}+\frac{{\phi }_x^4}{{\phi }^4}\right)\right],$$

(4)

$$u_{xxx}=A\frac{\partial }{\partial x}\left(\frac{{\phi }_{xxxx}}{\phi }-\frac{3{\phi }_{xx}^2+4{\phi }_x{\phi }_{xxx}}{{\phi }^2}+\frac{12{\phi }_x^2{\phi }_{xx}}{{\phi }^3}-\frac{6{\phi }_x^4}{{\phi }^4}\right).$$

(5)

Substituting (2)–(5) into the left hand side of Equation (1) and collecting all terms with ${\phi }^{-i}\left(i=1,2,3,4\right)$ together, yields

$$\begin{array}{c}{u}_t+\alpha (t)u{u}_x+\beta (t)u_{xxx}+\frac{m}{2t}u=(A^{\prime }+\frac{m}{2t}A){(\ln \varphi )}_{xx}\hfill \\ +A\frac{\partial }{\partial x}[\frac{{\phi }_{xt}+\beta {\phi }_{xxxx}}{\phi }+\frac{-{\phi }_x{\phi }_t+(\frac{A\alpha }{2}-3\beta ){\phi }_{xx}^2-4\beta {\phi }_x{\phi }_{xxx}}{{\phi }^2}\hfill \\ +\frac{(-A\alpha +12\beta ){\phi }_x^2{\phi }_{xx}}{{\phi }^3}+(\frac{A\alpha }{2}-6\beta )\frac{{\phi }_x^4}{{\phi }^4}].\hfill \end{array}$$

(6)

In (6), setting the coefficient of $\frac{{\varphi }_x^4}{{\varphi }^4}$ and the coefficient of ${(\ln \varphi )}_{xx}$ to zero, yields

$$\frac{A\alpha }{2}-6\beta =0,A^{\prime }+\frac{m}{2t}A=0.$$

(7)

Solving the first equation in (7) yields

$$A(t)=\frac{12\beta }{\alpha }.$$

(8)

Substituting (8) into the second equation in (7), we obtain

$$\frac{\mathrm{d}}{\mathrm{d}t}[\ln (\frac{\alpha }{\beta })]=\frac{m}{2t},$$

(9)

which is the constraint condition for $\alpha (t)$ and $\beta (t)$.

Substituting (8) into (2) yields

$$u(x,t)=\frac{12\beta }{\alpha }{(\ln \phi )}_{xx}.$$

(10)

Using (7) and (8), the expression (6) can be simplified as

$$\begin{array}{l}{u}_t+\alpha u{u}_x+\beta u_{xxx}+\frac{m}{2t}u\\ =\frac{12\beta }{\alpha }\frac{\partial }{\partial x}\left[\frac{\phi {({\phi }_t+\beta {\phi }_{xxx})}_x-{\phi }_x({\phi }_t+\beta {\phi }_{xxx})+3\beta ({\phi }_{xx}^2-{\phi }_x{\phi }_{xxx})}{{\phi }^2}\right]=0,\end{array}$$

(11)

provided that $\phi =\phi (x,t)$ satisfies the quadratic form equation

$$\phi {({\phi }_t+\beta {\phi }_{xxx})}_x-{\phi }_x({\phi }_t+\beta {\phi }_{xxx})+3\beta ({\phi }_{xx}^2-{\phi }_x{\phi }_{xxx})=0.$$

(12)

Using (9)–(12), we come to the conclusion that is the theorem in the following.

Theorem 1.

If$\alpha (t)$and$\beta (t)$in Equation (1) satisfy the constraint condition (9),$\phi =\phi (x,t)$is the solution of the quadratic form Equation (12), then the expression (10) satisfies Equation (1) exactly.

Theorem 1 shows that the expression (10) and the quadratic form Equation (12) together have comprised the nonlinear transformation for Equation (1)

$$u(x,t)=\frac{12\beta }{\alpha }((\ln \phi {)}_{xx},$$

(13)

$$\phi {({\phi }_t+\beta {\phi }_{xxx})}_x-{\phi }_x({\phi }_t+\beta {\phi }_{xxx})+3\beta ({\phi }_{xx}^2-{\phi }_x{\phi }_{xxx})=0,$$

(14)

provided that $\alpha (t)$ and $\beta (t)$ satisfy the constraint condition (9).

By the nonlinear transformation, the problem to solve Equation (1) becomes the one to solve the quadratic form Equation (14). In the next section, a series of solutions of Equation (14) will be given, then a soliton-like solution and multi soliton-like solutions of Equation (1) can be obtained.

3. Soliton-Like Solutions of Equation (1)

Using the $\epsilon$-expansion method [14], or Hirota’s method [15], a series of solutions of Equation (14) can be obtained as follows:

$${\phi }_1=1+{\mathrm{e}}^{\xi },\xi =kx-k^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau }$$

$${\phi }_2=1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}},{\mathrm{e}}^{A_{12}}=\frac{{(k_1-k_2)}^2}{{(k_1+k_2)}^2},{\xi }_i=k_{i}x-k^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau },i=1,2,$$

$${\phi }_3=1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_3}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}}+{\mathrm{e}}^{{\xi }_1+{\xi }_3+A_{13}}+{\mathrm{e}}^{{\xi }_2+{\xi }_3+A_{23}}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+{\xi }_3+A_{12}+A_{13}+A_{23}},$$

……

$${\mathrm{e}}^{A_{ij}}=\frac{{(k_i-k_j)}^2}{{(k_i+k_j)}^2},i<j,{\xi }_i=k_{i}x-k_i^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau },i=1,2,3,$$

$${\phi }_N={\displaystyle \sum _{\mu =0,1}\exp \left({\displaystyle \sum _{i=1}^N{\mu }_i{\xi }_i}+{\displaystyle \sum _{1\le i<j\le N}{\mu }_i{\mu }_j}{A}_{ij}\right)},$$

where ${\displaystyle \sum _{\mu =0,1}}$ indicates the summation over all possible combinations of ${\mu }_1=0,1, {\mu }_2=0,1,$ $\dots ,{\mu }_N=0,1.$, while ${\displaystyle \sum _{1\le i<j\le N}}$ indicates the summation over all possible combinations of $i$ and $j$ from $1$ to $N$ subject to $i<j$.

Substituting the solution ${\phi }_1$ of Equation (14) into the expression (13), we have one soliton-like solution of Equation (1) as follows:

$$u_1(x,t)=\frac{3k^2\beta (t)}{\alpha (t)}\sec h^2(\frac{1}{2}\xi ),\xi =kx-k^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau }.$$

The amplitude of $u_1(x,t)$ is $\frac{3k^2\beta (t)}{\alpha (t)},$ and the velocity of $u_1(x,t)$ is $\frac{\mathrm{d}x}{\mathrm{d}t}=k^2\beta (t).$ Both amplitude and velocity are all changed with the variable $t$.

Substituting the solution ${\phi }_2$ of Equation (14) into the expression (13), we have two soliton-like solutions of Equation (1) as follows:

$$u_2(x,t)=\frac{12\beta (t)}{\alpha (t)}\frac{k_1^2{\mathrm{e}}^{{\xi }_1}+k_2^2{\mathrm{e}}^{{\xi }_2}+2{(k_1+k_2)}^2{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}}+(k_2^2{\mathrm{e}}^{2{\xi }_1+{\xi }_2+A_{12}}+k_1^2{\mathrm{e}}^{{\xi }_1+2{\xi }_2+A_{12}})}{{(1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}})}^2}.$$

.....

Substituting ${\phi }_N$ into (13), we have $N$ soliton-like solutions as:

$$u_N(x,t)=\frac{12\beta (t)}{\alpha (t)}{(\ln {\phi }_N)}_{xx},$$

where $\alpha (t)$ and $\beta (t)$ satisfy expression (9), which is the following relationship:

$$\frac{\alpha (t)}{\beta (t)}=t^{\frac{m}{2}}.$$

4. An Example

Consider the cylindrical/spherical KdV equation in the form [16]:

$$u_t+t^{\frac{m}{2}}f(t)u{u}_x+f(t)u_{xxx}+\frac{m}{2t}u=0,$$

(15)

where $f(t)$ is an arbitrary analytical function, in view of

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\ln \left(\frac{t^{\frac{m}{2}}f(t)}{f(t)}\right)\right]=\frac{m}{2t}$$

Thus, based on the theorem in Section 2, Equation (15) has a nonlinear transformation expressed as (16) and (17):

$$u(x,t)=\frac{12}{t^{\frac{m}{2}}}{(\ln \phi )}_{xx},$$

(16)

$$\phi {({\phi }_t+f(t){\phi }_{xxx})}_x-{\phi }_x({\phi }_t+f(t){\phi }_{xxx})+3f(t)({\phi }_{xx}^2-{\phi }_x{\phi }_{xxx})=0.$$

(17)

Equation (17) admits a series of solutions as follows:

$${\phi }_1=1+{\mathrm{e}}^{\xi },\xi =kx-k^3{\displaystyle {\int }_{}^{t}f(\tau )\mathrm{d}\tau },$$

$${\phi }_2=1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}},{\mathrm{e}}^{A_{12}}=\frac{{(k_1-k_2)}^2}{{(k_1+k_2)}^2},{\xi }_i=k_{i}x-k^3{\displaystyle {\int }_{}^{t}f(\tau )\mathrm{d}\tau },i=1,2,$$

$${\phi }_3=1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_3}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}}+{\mathrm{e}}^{{\xi }_1+{\xi }_3+A_{13}}+{\mathrm{e}}^{{\xi }_2+{\xi }_3+A_{23}}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+{\xi }_3+A_{12}+A_{13}+A_{23}},$$

$${\mathrm{e}}^{A_{ij}}=\frac{{(k_i-k_j)}^2}{{(k_i+k_j)}^2},i<j,{\xi }_i=k_{i}x-k_i^3{\displaystyle {\int }_{}^{t}f(\tau )\mathrm{d}\tau },i=1,2,3.$$

……

Substituting ${\phi }_1,{\phi }_2,{\phi }_3,\dots$ into expression (16), respectively, then one soliton-like solution (Figure 1), two soliton-like solutions (Figure 2 and Figure 3), and three soliton-like solutions (Figure 4 and Figure 5) can be obtained, respectively, as follows:

$$u_1(x,t)=\frac{3k^2}{t^{\frac{m}{2}}}\mathrm{sech}(\frac{1}{2}\xi ),\xi =kx-k^3{\displaystyle {\int }_{}^{t}f(\tau )\mathrm{d}\tau },$$

$$u_2(x,t)=\frac{12}{t^{\frac{m}{2}}}\frac{k_1^2{\mathrm{e}}^{{\xi }_1}+k_2^2{\mathrm{e}}^{{\xi }_2}+2{(k_1+k_2)}^2{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}}+(k_2^2{\mathrm{e}}^{2{\xi }_1+{\xi }_2+A_{12}}+k_1^2{\mathrm{e}}^{{\xi }_1+2{\xi }_2+A_{12}})}{{(1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}})}^2},$$

$$u_3(x,t)=\frac{12}{t^{\frac{m}{2}}}{(\ln {\phi }_3)}_{xx}$$

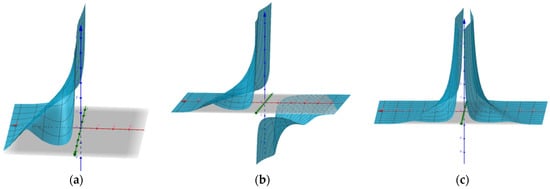
Figure 1. For the one soliton-like solution $u_1(x,t)$, when $f(t)=t,k=1$, the corresponding graphs of $m=1,m=2$ and $m=4$ are given as above. $(\mathbf{a}) f(t)=t,k=1,m=1$; $(\mathbf{b}) f(t)=t,k=1,m=2$; $(\mathbf{c}) f(t)=t,k=1,m=4$.

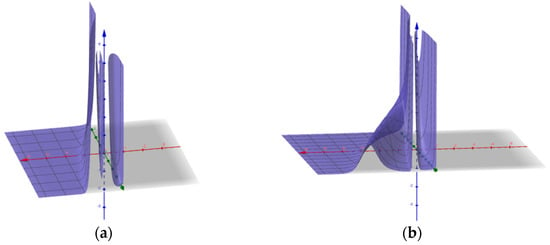
Figure 2. For the two soliton-like solution $u_2(x,t)$, when $f(t)=t,m=1$, the corresponding figures of $k_1=2,k_2=3$ and $k_1=3,k_2=1$ are given as above. $(\mathbf{a}) f(t)=t,m=1,k_1=2,k_2=3$; $(\mathbf{b}) f(t)=t,m=1,k_1=3,k_2=1$.

Figure 3. For the two soliton-like solution $u_2(x,t)$, when $f(t)=t,m=2$, the corresponding figures of $k_1=2,k_2=3$ and $k_1=3,k_2=1$ are given as above. $(\mathbf{a}) f(t)=t,m=2,k_1=2,k_2=3$; $(\mathbf{b}) f(t)=t,m=2,k_1=3,k_2=1$.

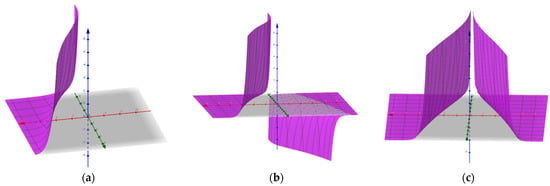
Figure 4. For the three soliton-like solution $u_3(x,t)$, when $f(t)=t,k_1=1,k_2=3,k_3=2$, the corresponding graphs of $m=1,m=2$ and $m=4$ are given as above. $(\mathbf{a}) f(t)=t,k_1=1, k_2=3,k_3=2,m=1$; $(\mathbf{b}) f(t)=t,k_1=1,k_2=3,k_3=2,m=2$; $(\mathbf{c}) f(t)=t,k_1=1,k_2=3,k_3=2,m=4$.

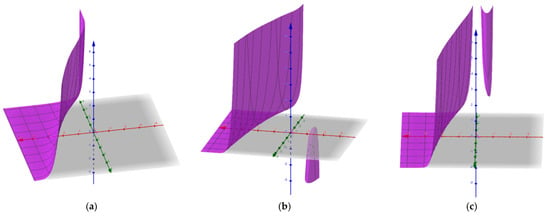
Figure 5. For the three soliton-like solution $u_3(x,t)$, when $f(t)=t^2,k_1=1,k_2=3,k_3=2$, the corresponding graphs of $m=1,m=2$ and $m=4$ are given as above. $(\mathbf{a}) f(t)=t^2,k_1=1,k_2=3,k_3=2,m=1$; $(\mathbf{b}) f(t)=t^2,k_1=1,k_2=3,k_3=2,m=2$; $(\mathbf{c}) f(t)=t^2,k_1=1,k_2=3,k_3=2,m=4$.

The comparison of different geometric structures of solitons clearly shows that for $u_1$ and $u_2$, fixed $f(t)=t$ and $f(t)=t^2$, and different parameters $k,k_1,k_2,k_3$ are selected, the soliton solution morphology changes little. However, for $u_3$, when $f(t)$ is different, the soliton solution will fluctuate greatly.

5. Conclusions

The general variable coefficient cylindrical/spherical KdV equation in the form

$$u_t+\alpha (t)u{u}_x+\beta (t)u_{xxx}+\frac{m}{2t}u=0,$$

(18)

has been investigated by using the simplified homogeneous balance method. The results obtained in this paper are that if $\alpha (t)$ and $\beta (t)$ satisfy the constraint condition

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\ln \left(\frac{\alpha (t)}{\beta (t)}\right)\right]=\frac{m}{2t}$$

(19)

i.e., $\frac{\alpha (t)}{\beta (t)}=t^{\frac{m}{2}},$ then Equation (18) has a nonlinear transformation, as follows

$$u(x,t)=\frac{12\beta }{\alpha }(\ln \phi {)}_{xx},$$

(20)

$$\phi {({\phi }_t+\beta {\phi }_{xxx})}_x-{\phi }_x({\phi }_t+\beta {\phi }_{xxx})+3\beta ({\phi }_{xx}^2-{\phi }_x{\phi }_{xxx})=0.$$

(21)

The quadratic form Equation (21) admits a series of solutions, as follows

$${\phi }_1=1+{\mathrm{e}}^{\xi },\xi =kx-k^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau },$$

$${\phi }_2=1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}},{\mathrm{e}}^{A_{12}}=\frac{{(k_1-k_2)}^2}{{(k_1+k_2)}^2},{\xi }_i=k_{i}x-k^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau },i=1,2,$$

$${\phi }_3=1+{\mathrm{e}}^{{\xi }_1}+{\mathrm{e}}^{{\xi }_2}+{\mathrm{e}}^{{\xi }_3}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+A_{12}}+{\mathrm{e}}^{{\xi }_1+{\xi }_3+A_{13}}+{\mathrm{e}}^{{\xi }_2+{\xi }_3+A_{23}}+{\mathrm{e}}^{{\xi }_1+{\xi }_2+{\xi }_3+A_{12}+A_{13}+A_{23}},$$

$${\mathrm{e}}^{A_{ij}}=\frac{{(k_i-k_j)}^2}{{(k_i+k_j)}^2},i<j,{\xi }_i=k_{i}x-k_i^3{\displaystyle {\int }_{}^t\beta (\tau )\mathrm{d}\tau },i=1,2,3.$$

……

Thus, substituting ${\phi }_i$ (i = 1,2,3,…) into expression (20), respectively, one soliton-like solution and multi soliton-like solutions of Equation (18) can be obtained.

In particular, when m = 1 and m = 2, soliton-like solutions of the general variable coefficient cylindrical/spherical KdV equation, that is the particular case of Equation (18), are also successfully obtained. The results obtained in this paper are different from those reported earlier. The simplified homogeneous balance method is also applicable to other nonlinear differential equations.