Adaptive State-Feedback Stabilization for Stochastic Nonlinear Systems with Time-Varying Powers and Unknown Covariance

Abstract

This paper investigates the adaptive state-feedback stabilization problem for stochastic nonlinear systems. Compared with the existing results, we consider more general and more practical systems, i.e., systems with time-varying powers and unknown covariance simultaneously. We propose a new adaptive state-feedback control method, which ensures that the closed-loop system is globally stable in probability and the states are regulated to the origin almost surely. Finally, the feasibility of the design method is verified by two examples.

1. Introduction

In many industrial applications, due to the ubiquity of stochastic noise and nonlinearity, real systems are often modeled by stochastic differential equations [1,2], which attract researchers to pay more and more attention to the control of stochastic systems. The prior work is reported in [3,4,5,6,7], which was further developed by [8,9,10,11,12,13]. Recently, there have been many reports on designs for stochastic high-order nonlinear systems [14,15,16,17,18,19]. The authors of [15] proposed a new stochastic homogeneous domination method to relax the power restrictions in [14]. The authors of [18] focused on the cooperative control problem of multiple nonlinear systems perturbed by second-order moment processes in a directed topology. The authors of [19] developed a state-feedback controller by using a combination of backstepping method and type-3 fuzzy neural network. All the results reported in [14,15,16,17,18,19] require that the order should be constant. For stochastic systems with time-varying powers, Ref. [20] is the first paper to work out the state-feedback stabilization problem. The authors of [21] solved the decentralized stabilization problem of large-scale stochastic systems with time-varying powers. However, in [20,21], it is required that their covariances are known identity matrices.

The designs above are for systems without unknown parameters. Nevertheless, parameter uncertainties are common and inevitable in many systems [22,23]. For systems with unknown parameters, adaptive control is an effective approach, with a strong ability to compensate for unknown parameters and fast convergence speed. Thus, stochastic adaptive control is a useful method to process unknown covariance. The authors of [24] considered stochastic nonlinear systems with a non-vanishing noise vector field and unknown covariance, and constructed an adaptive controller for strict-feedback systems. The authors of [25] extended the results in [24] to output-feedback stabilization. The authors of [26] proposed a novel least-squares algorithm to estimate the unknown covariance and designed adaptive control to guarantee that the states are regulated to zero almost surely. Although the authors of [24,25,26] considered stochastic systems with unknown covariance, it should be highlighted that the powers of their systems are constant, and they did not consider time-varying powers. However, many real applications require the order to be time-varying. For instance, the powers of boiler-turbine units [27] and underactuated mechanical systems [28] are time-varying.

On the basis of the above observations, we study the adaptive state-feedback stabilization problem for stochastic nonlinear systems with time-varying powers and unknown covariance. The main contributions include:

(1) The system model we take into account is more applicable than the existing results [14,15,16,17,18,19,20,21,24,25,26]. Unlike the systems studied in [14,15,16,17,18,19,20,21] with known identity matrix, this paper studies the systems with unknown covariance, whose characteristics are that the systems are affected by the noise of unknown intensity. Different from the systems with constant powers [24,25,26], this paper considers the time-varying power model, which makes the results more general. In fact, the inherent time-varying characteristics and unknown factors of the system make the design and stability analysis full of challenges.

(2) We propose a new adaptive control scheme. Since the powers are time-varying and the covariance is unknown, the control schemes in [14,15,16,17,18,19,20,21,24,25,26] are invalid here. We use the time-varying power’s bounds to design a new time-invariant controller to ensure that the closed-loop system is globally stable in probability and the states are regulated to the origin almost surely.

The rest of this paper is listed as follows. Section 2 is the problem formulation. Section 3 describes the controller design and stability analysis. Section 4 gives two simulations. The conclusions are collected in Section 5.

2. Problem Formulation

Consider the following system

$$\begin{array}{cc}\hfill d{\zeta }_1=& \left({\left[{\zeta }_2\right]}^{m\left(t\right)}+f_1(t,{\zeta }_1)\right)dt+g_1^T(t,{\zeta }_1)\mathrm{\Sigma }\left(t\right)d\omega \left(t\right),\hfill \\ \hfill d{\zeta }_2=& \left({\left[{\zeta }_3\right]}^{m\left(t\right)}+f_2(t,{\overline{\zeta }}_2)\right)dt+g_2^T(t,{\overline{\zeta }}_2)\mathrm{\Sigma }\left(t\right)d\omega \left(t\right),\hfill \\ \hfill ⋮& \hfill \\ \hfill d{\zeta }_n=& \left({\left[u\right]}^{m\left(t\right)}+f_n(t,{\overline{\zeta }}_n)\right)dt+g_n^T(t,{\overline{\zeta }}_n)\mathrm{\Sigma }\left(t\right)d\omega \left(t\right),\hfill \end{array}$$

(1)

where ${\overline{\zeta }}_i={({\zeta }_1,...,{\zeta }_i)}^T\in {\mathrm{R}}^i$ and $u\in \mathrm{R}$ are the system state and control input, respectively. The functions $f_i:{\mathrm{R}}^{+}\times {\mathrm{R}}^i\to \mathrm{R}$ and $g_i:{\mathrm{R}}^{+}\times {\mathrm{R}}^i\to {\mathrm{R}}^r$ are assumed to be smooth, and $f_i(t,0)=0,g_i(t,0)=0,i=1,...,n$. $\omega$ is an $r-$dimensional standard Wiener process, which is defined on the complete probability space $(\mathrm{\Omega },\mathcal{F},{\mathcal{F}}_t,P)$ with the filtration ${\mathcal{F}}_t$ satisfying the general conditions, and $\mathrm{\Sigma }:{\mathrm{R}}^{+}\to {\mathrm{R}}^{r\times r}$ is Borel measurable and bounded, and the matrix $\mathrm{\Sigma }\left(t\right)$ is nonnegative-definite for each $t\ge 0$. $m\left(t\right):{\mathrm{R}}^{+}\to {\mathrm{R}}^{+}$ is a continuously bounded function, which satisfies $1\le \underline{m}\le m\left(t\right)\le \overline{m}$ with $\underline{m}$ and $\overline{m}$ being constants. The power sign function ${[·]}^{\alpha }$ is defined as ${[·]}^{\alpha }:=\mathrm{sign}(·){|·|}^{\alpha }$ with $\alpha \in (0,+\infty )$.

To realize this control objective, we need the following assumption.

Assumption 1.

There are two nonnegative smooth functions ${\tilde{f}}_i\left({\overline{\zeta }}_i\right)$ and ${\tilde{g}}_i\left({\overline{\zeta }}_i\right),i=1,...,n$, such that

$$\begin{array}{cc}\hfill |f_i(t,{\overline{\zeta }}_i)|\le & {\tilde{f}}_i\left({\overline{\zeta }}_i\right)\left(|{\zeta }_1{|}^{m\left(t\right)}+|{\zeta }_2{|}^{m\left(t\right)}+...+{\left|{\zeta }_i\right|}^{m\left(t\right)}\right),\hfill \\ \hfill |g_i(t,{\overline{\zeta }}_i)|\le & {\tilde{g}}_i\left({\overline{\zeta }}_i\right)\left(|{\zeta }_1{|}^{m\left(t\right)}+|{\zeta }_2{|}^{m\left(t\right)}+...+{\left|{\zeta }_i\right|}^{m\left(t\right)}\right).\hfill \end{array}$$

Remark 1.

It should be noted that $\mathrm{\Sigma }\left(t\right)$ is unknown because the system (1) is affected by arbitrary bounded intensity noise. One of the difficulties of this paper is to deal with this item. When the power is constant, Assumption 1 is the same as the assumed condition in [14,15,16,17,18,19,20,21]. How to deal with the unknown $\mathrm{\Sigma }\left(t\right)$ and the time-varying power $m\left(t\right)$ is nontrivial.

For a bounded function $X:{\mathrm{R}}^{+}\to {\mathrm{R}}^{n\times m}$

$$\begin{array}{c}\hfill {\left|\right|X\left|\right|}_{\infty }\equiv \underset{t\in {\mathrm{R}}^{+}}{sup}\left|X\left(t\right)\right|.\end{array}$$

The space of $n\times m$ matrices with real entries will be denoted by ${\mathrm{R}}^{n\times m}$, $\left|X\right|$ denotes the Frobenius norm of $\left|X\right|\in {\mathrm{R}}^{n\times m}:\left|X\right|={\left({\sum }_{i=1}^n{\sum }_{j=1}^m{X}_{ij}^2\right)}^{1/2}$. A detailed explanation is given in [24].

3. Controller Design

In this section, for the system (1) under Assumption 1, we first construct an adaptive state-feedback controller and then analyze the stability of the closed-loop system.

3.1. Controller Design

In this part, our control objective is controller design. Before that, we need to deal with the unknown parameters. Since $\mathrm{\Sigma }$ is unknown, it is not necessary to estimate the entire matrix $\mathrm{\Sigma }$. Instead, by using an estimate $\widehat{\rho }$, we only need to estimate the unknown parameter $\rho =\left|\right|\mathrm{\Sigma }{\mathrm{\Sigma }}^T{\left|\right|}_{\infty }$.

Proof. 

Firstly, introduce the coordinate transformation

$$\begin{array}{c}\hfill {\xi }_i={\zeta }_i-{\zeta }_i^{*},i=1,2,...,n,\end{array}$$

(2)

where ${\zeta }_i^{*}$ is the virtual controller and ${\zeta }_1^{*}=0$. By using Itô’s differentiation rule, we have

$$\begin{array}{cc}\hfill d{\xi }_i=& {\left[{\zeta }_{i+1}\right]}^{m\left(t\right)}dt+\left(f_i\left({\overline{\zeta }}_i\right)-\sum _{k=1}^{i-1}\frac{\partial {\zeta }_i^{*}}{\partial {\zeta }_k}\left({\left[{\zeta }_{k+1}\right]}^{m\left(t\right)}+f_k\left({\zeta }_k\right)\right)\right)dt\hfill \\ \hfill & -\left(\frac{1}{2}\sum _{j,k=1}^{i-1}\frac{{\partial }^2{\zeta }_i^{*}}{\partial {\zeta }_j\partial {\zeta }_k}{g}_j^T\left({\overline{\zeta }}_j\right)\mathrm{\Sigma }{\mathrm{\Sigma }}^T{g}_k\left({\overline{\zeta }}_k\right)+\frac{\partial {\zeta }_i^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)dt+{\widehat{g}}_i^T\mathrm{\Sigma }\left(t\right)d\omega ,\hfill \end{array}$$

(3)

where ${\widehat{g}}_i=g_i\left({\overline{\zeta }}_i\right)-{\sum }_{k=1}^{i-1}\frac{\partial {\zeta }_i^{*}}{\partial {\zeta }_k}{g}_k\left({\overline{\zeta }}_k\right),i=2,...,n,$ with ${\zeta }_{n+1}=u$.

Next, the following is a detailed derivation of the controller.

Step 1. From (3), we obtain

$$\begin{array}{c}\hfill d{\xi }_1={\left[{\zeta }_2\right]}^{m\left(t\right)}dt+f_1\left({\zeta }_1\right)dt+{\widehat{g}}_1^T\mathrm{\Sigma }\left(t\right)d\omega .\end{array}$$

(4)

Choose $V_1=\frac{1}{4}{\xi }_1^4+\frac{1}{2\sigma }{\tilde{\rho }}^2$ with $\sigma >0$ being any constant and $\tilde{\rho }=\left|\right|\mathrm{\Sigma }{\mathrm{\Sigma }}^T{\left|\right|}_{\infty }-\widehat{\rho }$. From (4) and Assumption 1, we get

$$\begin{array}{cc}\hfill \mathcal{L}{V}_1=& {\xi }_1^3{\left[{\zeta }_2\right]}^{m\left(t\right)}+{\xi }_1^3{f}_1+\frac{3}{2}\mathrm{Tr}\left\{\mathrm{\Sigma }{\left(t\right)}^T{\widehat{g}}_1{\xi }_1^2{\widehat{g}}_1^T\mathrm{\Sigma }\left(t\right)\right\}-\frac{\tilde{\rho }\dot{\widehat{\rho }}}{\sigma }\hfill \\ \hfill \le & {\xi }_1^3{\left[{\zeta }_2\right]}^{m\left(t\right)}+{\tilde{f}}_1\left({\zeta }_1\right)|{\xi }_1{|}^{m\left(t\right)+3}+\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right)|{\zeta }_1{|}^{2m\left(t\right)+2}||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }-\frac{\tilde{\rho }\dot{\widehat{\rho }}}{\sigma }\hfill \\ \hfill \le & {\xi }_1^3{\left[{\zeta }_2\right]}^{m\left(t\right)}+{\tilde{f}}_1\left({\zeta }_1\right)|{\xi }_1{|}^{m\left(t\right)+3}+\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right)|{\zeta }_1{|}^{m\left(t\right)-1}{|{\xi }_1|}^{m\left(t\right)+3}\left(\tilde{\rho }+\widehat{\rho }\right)-\frac{\tilde{\rho }\dot{\widehat{\rho }}}{\sigma }\hfill \\ \hfill \le & {\xi }_1^3{\left[{\zeta }_2\right]}^{m\left(t\right)}+{\tilde{f}}_1\left({\zeta }_1\right)|{\xi }_1{|}^{m\left(t\right)+3}+\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right){\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}-1}{2}}\widehat{\rho }{|{\xi }_1|}^{m\left(t\right)+3}\hfill \\ \hfill & -\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right){\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}-1}{2}}{|{\xi }_1|}^{m\left(t\right)+3}\right)\hfill \\ \hfill \le & {\xi }_1^3\left({\left[{\zeta }_2\right]}^{m\left(t\right)}-{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}\right)+{\xi }_1^3{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}+{\beta }_1({\zeta }_1,\widehat{\rho }){|{\xi }_1|}^{m\left(t\right)+3}\hfill \\ \hfill & -\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right){\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}-1}{2}}{|{\xi }_1|}^{\overline{m}+3}\right),\hfill \end{array}$$

(5)

where ${\beta }_1({\zeta }_1,\widehat{\rho })={\tilde{f}}_1\left({\zeta }_1\right)+\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right){\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}-1}{2}}\widehat{\rho }$ is irrelevant to $m\left(t\right)$.

Let

$$\begin{array}{c}\hfill {\tau }_1\left({\zeta }_1\right)=\frac{3}{2}{\tilde{g}}_1^2\left({\zeta }_1\right){\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}-1}{2}}{|{\xi }_1|}^{\overline{m}+3}.\end{array}$$

(6)

Thus, if we choose ${\zeta }_2^{*}$ as

$$\begin{array}{c}\hfill {\zeta }_2^{*}=-{\left(c_1+{\beta }_1({\zeta }_1,\widehat{\rho })+(n-1)\widehat{\rho }\right)}^{\frac{1}{\underline{m}}}{\zeta }_1:=-{\alpha }_1({\zeta }_1,\widehat{\rho }){\xi }_1,\end{array}$$

(7)

we can get

$$\begin{array}{c}\hfill {\xi }_1^3{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}=-{\alpha }_1^{m\left(t\right)}({\zeta }_1,\widehat{\rho })|{\xi }_1{|}^{m\left(t\right)+3}\le -\left(c_1+{\beta }_1({\zeta }_1,\widehat{\rho })+(n-1)\widehat{\rho }\right){|{\xi }_1|}^{m\left(t\right)+3},\end{array}$$

(8)

where $c_1\ge 1$ and ${\alpha }_1({\zeta }_1,\widehat{\rho })={\left(c_1+{\beta }_1({\zeta }_1,\widehat{\rho })+(n-1)\widehat{\rho }\right)}^{\frac{1}{\underline{m}}}\ge 1$ are irrelevant to $m\left(t\right)$.

Substituting (6) and (8) into (5) yields

$$\begin{array}{cc}\hfill \mathcal{L}{V}_1\le & -c_1|{\xi }_1{|}^{m\left(t\right)+3}-(n-1)\widehat{\rho }{|{\xi }_1|}^{m\left(t\right)+3}\hfill \\ \hfill & +{\xi }_1^3\left({\left[{\zeta }_2\right]}^{m\left(t\right)}-{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}\right)-\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_1\left({\zeta }_1\right)\right).\hfill \end{array}$$

(9)

Step 2. By (3), we have

$$\begin{array}{cc}\hfill d{\xi }_2=& {\left[{\zeta }_3\right]}^{m\left(t\right)}dt+\left(f_2\left({\overline{\zeta }}_2\right)-\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}\left({\left[{\zeta }_2\right]}^{m\left(t\right)}+f_1\left({\zeta }_1\right)\right)\right)dt\hfill \\ \hfill & -\left(\frac{1}{2}\frac{{\partial }^2{\zeta }_2^{*}}{\partial {\zeta }_1^2}{g}_1^T\left({\zeta }_1\right)\mathrm{\Sigma }{\mathrm{\Sigma }}^T{g}_1\left({\zeta }_1\right)+\frac{\partial {\zeta }_2^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)dt+{\widehat{g}}_2^T\mathrm{\Sigma }\left(t\right)d\omega .\hfill \end{array}$$

(10)

Choosing $V_2=V_1+\frac{1}{4}{\xi }_2^4$, by (9) and (10), we obtain

$$\begin{array}{cc}\hfill \mathcal{L}{V}_2\le & -c_1|{\xi }_1{|}^{m\left(t\right)+3}-(n-1)\widehat{\rho }{|{\xi }_1|}^{m\left(t\right)+3}+{\xi }_1^3\left({\left[{\zeta }_2\right]}^{m\left(t\right)}-{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}\right)+{\xi }_2^3{\left[{\zeta }_3^{*}\right]}^{m\left(t\right)}\hfill \\ \hfill & +{\xi }_2^3\left(f_2\left({\overline{\zeta }}_2\right)-\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}\left({\left[{\zeta }_2\right]}^{m\left(t\right)}+f_1\left({\zeta }_1\right)\right)-\frac{1}{2}\frac{{\partial }^2{\zeta }_2^{*}}{\partial {\zeta }_1^2}{g}_1^T\left({\zeta }_1\right)\mathrm{\Sigma }{\mathrm{\Sigma }}^T{g}_1\left({\zeta }_1\right)-\frac{\partial {\zeta }_2^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)\hfill \\ \hfill & +{\xi }_2^3\left({\left[{\zeta }_3\right]}^{m\left(t\right)}-{\left[{\zeta }_3^{*}\right]}^{m\left(t\right)}\right)+\frac{3}{2}\mathrm{Tr}\left\{{\mathrm{\Sigma }}^T{\widehat{g}}_2{\xi }_2^2{\widehat{g}}_2^T\mathrm{\Sigma }\right\}-\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_1\left({\zeta }_1\right)\right).\hfill \end{array}$$

(11)

By (2), (7) and using Lemma 1 in [29], we get

$$\begin{array}{c}\hfill {\xi }_1^3\left({\left[{\zeta }_2\right]}^{m\left(t\right)}-{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}\right)\le \overline{m}\left(2^{\overline{m}-2}+2\right)\left(|{\xi }_1{|}^3|{\xi }_2{|}^{m\left(t\right)}+{\alpha }_1^{\overline{m}-1}({\zeta }_1,\widehat{\rho })|{\xi }_1{|}^{m\left(t\right)+2}|{\xi }_2|\right).\end{array}$$

(12)

By using Lemma 2.1 in [30], we obtain

$$\begin{array}{c}\hfill \overline{m}\left(2^{\overline{m}-2}+2\right)|{\xi }_1{|}^3|{\xi }_2{|}^{m\left(t\right)}\le \frac{1}{4}|{\xi }_1{|}^{m\left(t\right)+3}+{\beta }_{211}{|{\xi }_2|}^{m\left(t\right)+3},\\ \hfill \overline{m}\left(2^{\overline{m}-2}+2\right){\alpha }_1^{\overline{m}-1}({\zeta }_1,\widehat{\rho })|{\xi }_1{|}^{m\left(t\right)+2}|{\xi }_2|\le \frac{1}{4}|{\xi }_1{|}^{m\left(t\right)+3}+{\beta }_{212}{|{\xi }_2|}^{m\left(t\right)+3},\end{array}$$

(13)

where

$$\begin{array}{cc}\hfill {\beta }_{211}=& \frac{\overline{m}}{\underline{m}+3}{\left(\overline{m}\left(2^{\overline{m}-2}+2\right)\right)}^{\frac{\overline{m}+3}{\underline{m}}}{\left(\frac{\underline{m}+3}{12}\right)}^{-\frac{3}{\overline{m}}},\hfill \\ \hfill {\beta }_{212}=& \frac{1}{\underline{m}+3}{\left(\overline{m}\left(2^{\overline{m}-2}+2\right){\alpha }_1^{\overline{m}-1}\right)}^{\overline{m}+3}{\left(\frac{\underline{m}+3}{4(\overline{m}+2)}\right)}^{-(\overline{m}+2)}.\hfill \end{array}$$

Substituting (13) into (12) yields

$$\begin{array}{c}\hfill {\xi }_1^3\left({\left[{\zeta }_2\right]}^{m\left(t\right)}-{\left[{\zeta }_2^{*}\right]}^{m\left(t\right)}\right)\le \frac{1}{2}|{\xi }_1{|}^{m\left(t\right)+3}+{\beta }_{21}({\zeta }_1,\widehat{\rho }){|{\xi }_2|}^{m\left(t\right)+3},\end{array}$$

(14)

where ${\beta }_{21}({\zeta }_1,\widehat{\rho })={\beta }_{211}+{\beta }_{212}({\zeta }_1,\widehat{\rho })\ge 0$ is irrelevant to $m\left(t\right)$.

By (2), (7) and using Lemma 5 in [31], we have

$$\begin{array}{cc}\hfill |{\zeta }_2{|}^{m\left(t\right)}=& |{\xi }_2+{\zeta }_2^{*}{|}^{m\left(t\right)}\hfill \\ \hfill \le & {\left(|{\xi }_2|+{\alpha }_1({\zeta }_1,\widehat{\rho }){\xi }_1\right)}^{m\left(t\right)}\hfill \\ \hfill \le & 2^{\overline{m}-1}\left(|{\xi }_2{|}^{m\left(t\right)}+{|{\alpha }_1({\zeta }_1,\widehat{\rho }){\xi }_1|}^{m\left(t\right)}\right)\hfill \\ \hfill \le & 2^{\overline{m}-1}{\alpha }_1^{\overline{m}}({\zeta }_1,\widehat{\rho })\left(|{\xi }_2{|}^{m\left(t\right)}+{|{\xi }_1|}^{m\left(t\right)}\right),\hfill \end{array}$$

(15)

which means that

$$\begin{array}{c}\hfill |{\zeta }_1{|}^{m\left(t\right)}+{|{\zeta }_2|}^{m\left(t\right)}\le {\phi }_2({\zeta }_1,\widehat{\rho })\left(|{\xi }_2{|}^{m\left(t\right)}+{|{\xi }_1|}^{m\left(t\right)}\right),\end{array}$$

(16)

where ${\phi }_2({\zeta }_1,\widehat{\rho })=2^{\overline{m}-1}{\alpha }_1^{\overline{m}}({\zeta }_1,\widehat{\rho })+1$ is irrelevant to $m\left(t\right)$.

By (16), using Assumption 1 and Lemma 2.1 in [30], we get

$$\begin{array}{cc}\hfill & {\xi }_2^3\left(f_2\left({\overline{\zeta }}_2\right)-\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}\left({\left[{\zeta }_2\right]}^{m\left(t\right)}+f_1\left({\zeta }_1\right)\right)\right)\hfill \\ \hfill & \le |{\xi }_2{|}^3\left(|{\zeta }_1{|}^{m\left(t\right)}+{|{\zeta }_2|}^{m\left(t\right)}\right)\left({\tilde{f}}_2\left({\overline{\zeta }}_2\right)+\left|\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}\right|\left(1+{\tilde{f}}_1\left({\zeta }_1\right)\right)\right)\hfill \\ \hfill & \le |{\xi }_2{|}^3\left(|{\xi }_1{|}^{m\left(t\right)}+{|{\xi }_2|}^{m\left(t\right)}\right){\phi }_2({\zeta }_1,\widehat{\rho })\left({\tilde{f}}_2\left({\overline{\zeta }}_2\right)+\left|\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}\right|\left(1+{\tilde{f}}_1\left({\zeta }_1\right)\right)\right)\hfill \\ \hfill & \le |{\xi }_2{|}^3\left(|{\xi }_1{|}^{m\left(t\right)}+{|{\xi }_2|}^{m\left(t\right)}\right){\tilde{\phi }}_2({\overline{\zeta }}_2,\widehat{\rho })\hfill \\ \hfill & \le \frac{1}{2}|{\xi }_1{|}^{m\left(t\right)+3}+{\beta }_{22}({\overline{\zeta }}_2,\widehat{\rho }){|{\xi }_2|}^{m\left(t\right)+3},\hfill \end{array}$$

(17)

where ${\tilde{\phi }}_2({\overline{\zeta }}_2,\widehat{\rho })\ge 1$ and ${\beta }_{22}({\overline{\zeta }}_2,\widehat{\rho })\ge 0$ are irrelevant to $m\left(t\right)$.

From (7), (16) and Assumption 1, we obtain

$$\begin{array}{c}\hfill |{\widehat{g}}_2^T|=\left|g_2^T\left({\overline{\zeta }}_2\right)-\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1}{g}_1^T\left({\zeta }_1\right)\right|\le {\tilde{\sigma }}_2({\overline{\zeta }}_2,\widehat{\rho })\left(|{\xi }_1{|}^{m\left(t\right)}+{|{\xi }_2|}^{m\left(t\right)}\right),\end{array}$$

(18)

where ${\tilde{\sigma }}_2\left({\overline{\zeta }}_2\right)\ge 0$ is irrelevant to $m\left(t\right)$.

From (2), (18) and Lemma 2.1 in [30], we get

$$\begin{array}{cc}\hfill & \frac{3}{2}\mathrm{Tr}\left\{\mathrm{\Sigma }{\left(t\right)}^T{\widehat{g}}_2{\xi }_2^2{\widehat{g}}_2^T\mathrm{\Sigma }\left(t\right)\right\}\hfill \\ \hfill & \le \frac{3}{2}{\tilde{\sigma }}_2^2({\overline{\zeta }}_2,\widehat{\rho }){\xi }_2^2{\left(|{\xi }_1{|}^{m\left(t\right)}+{|{\xi }_2|}^{m\left(t\right)}\right)}^2||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill & \le 3{\tilde{\sigma }}_2^2({\overline{\zeta }}_2,\widehat{\rho })\left(|{\xi }_1{|}^{m\left(t\right)-1}|{\xi }_1{|}^{m\left(t\right)+1}|{\xi }_2{|}^2+|{\xi }_2{|}^{m\left(t\right)-1}{|{\xi }_2|}^{m\left(t\right)+3}\right)||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill & \le 3{\tilde{\sigma }}_2^2({\overline{\zeta }}_2,\widehat{\rho })\left({\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}-1}{2}}|{\xi }_1{|}^{m\left(t\right)+1}|{\xi }_2{|}^2+{\left({\left({\zeta }_2+{\alpha }_1{\zeta }_1\right)}^2+1\right)}^{\frac{\overline{m}-1}{2}}{|{\xi }_2|}^{m\left(t\right)+3}\right)\left(\widehat{\rho }+\tilde{\rho }\right)\hfill \\ \hfill & \le \frac{1}{2}\widehat{\rho }|{\xi }_1{|}^{m\left(t\right)+3}+\frac{1}{2}\tilde{\rho }|{\xi }_1{|}^{m\left(t\right)+3}+{\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })\widehat{\rho }|{\xi }_2{|}^{m\left(t\right)+3}+{\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })\tilde{\rho }{|{\xi }_2|}^{m\left(t\right)+3},\hfill \end{array}$$

(19)

where ${\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })\ge 0$ is irrelevant to $m\left(t\right)$, and

$$\begin{array}{c}\hfill {\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })=\frac{2}{\underline{m}+3}{\left(3{\tilde{\sigma }}_2^2{({\zeta }_1^2+1)}^{\frac{\overline{m}-1}{2}}\right)}^{\frac{\overline{m}+3}{2}}{\left(\frac{\underline{m}+3}{2(\overline{m}+1)}\right)}^{-\frac{\overline{m}+1}{2}}+3{\tilde{\sigma }}_2^2{({({\zeta }_2+{\alpha }_1{\zeta }_1)}^2+1)}^{\frac{\overline{m}-1}{2}}.\end{array}$$

By using Lemma 2.1 in [30] and Assumption 1, we have

$$\begin{array}{cc}\hfill -& \frac{1}{2}{\xi }_2^3\frac{\partial {\zeta }_2^{*}}{\partial {\zeta }_1^2}{g}_1^T\left({\zeta }_1\right)\mathrm{\Sigma }{\mathrm{\Sigma }}^T{g}_1\left({\zeta }_1\right)\hfill \\ \hfill \le & \frac{1}{2}\left|\frac{{\partial }^2{\zeta }_2^{*}}{\partial {\zeta }_1^2}\right|{\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}}{2}}{\tilde{g}}_1^2\left({\zeta }_1\right)|{\xi }_1{|}^{m\left(t\right)}|{\xi }_2{|}^3||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill \le & \frac{1}{2}\widehat{\rho }|{\xi }_1{|}^{m\left(t\right)+3}+\frac{1}{2}\tilde{\rho }|{\xi }_1{|}^{m\left(t\right)+3}+{\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })\widehat{\rho }|{\xi }_2{|}^{m\left(t\right)+3}+{\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })\tilde{\rho }{|{\xi }_2|}^{m\left(t\right)+3},\hfill \end{array}$$

(20)

where ${\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })\ge 0$ is irrelevant to $m\left(t\right)$, and

$$\begin{array}{c}\hfill {\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })=\frac{3}{(\underline{m}+3)}{\left(\frac{1}{2}\left|\frac{{\partial }^2{\zeta }_2^{*}}{\partial {\zeta }_1^2}\right|{\left({\zeta }_1^2+1\right)}^{\frac{\overline{m}}{2}}{\tilde{g}}_1^2\left({\zeta }_1\right)\right)}^{\frac{\overline{m}+3}{3}}{\left(\frac{\underline{m}+3}{2\overline{m}}\right)}^{-\frac{\overline{m}}{3}}.\end{array}$$

Substituting (14), (17), (19) and (20) into (11) yields

$$\begin{array}{cc}\hfill \mathcal{L}{V}_2\le & -(c_1-1)|{\xi }_1{|}^{m\left(t\right)+3}-(n-2)\widehat{\rho }{|{\xi }_1|}^{m\left(t\right)+3}+{\xi }_2^3\left({\left[{\zeta }_3\right]}^{m\left(t\right)}-{\left[{\zeta }_3^{*}\right]}^{m\left(t\right)}\right)\hfill \\ \hfill & +{\xi }_2^3\left({\left[{\zeta }_3^{*}\right]}^{m\left(t\right)}-\frac{\partial {\zeta }_2^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)+{\beta }_2({\overline{\zeta }}_2,\widehat{\rho }){|{\xi }_2|}^{m\left(t\right)+3}-\tilde{\rho }(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_1\left({\zeta }_1\right)\hfill \\ \hfill & -\left({\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })+{\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })\right)|{\xi }_2{|}^{\overline{m}+3}-{|{\xi }_1|}^{\overline{m}+3}),\hfill \end{array}$$

(21)

where ${\beta }_2({\overline{\zeta }}_2,\widehat{\rho })={\beta }_{21}({\zeta }_1,\widehat{\rho })+{\beta }_{22}({\overline{\zeta }}_2,\widehat{\rho })+{\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })\widehat{\rho }+{\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })\widehat{\rho }\ge 0$ is irrelevant to $m\left(t\right)$.

Let

$$\begin{array}{c}\hfill {\tau }_2({\overline{\zeta }}_2,\widehat{\rho })={\tau }_1\left({\zeta }_1\right)+\left({\beta }_{23}({\overline{\zeta }}_2,\widehat{\rho })+{\beta }_{24}({\overline{\zeta }}_2,\widehat{\rho })\right)|{\xi }_2{|}^{\overline{m}+3}+{|{\xi }_1|}^{\overline{m}+3}.\end{array}$$

(22)

Choosing the virtual controller ${\zeta }_3^{*}$ as

$$\begin{array}{cc}\hfill {\zeta }_3^{*}& =-{\left(\left(c_2+{\beta }_2({\overline{\zeta }}_2,\widehat{\rho })+(n-2)\widehat{\rho }\right){|{\xi }_2|}^{\overline{m}}-\frac{\partial {\zeta }_2^{*}}{\partial \widehat{\rho }}\sigma {\tau }_2({\overline{\zeta }}_2,\widehat{\rho })\right)}^{\frac{1}{\underline{m}}}\hfill \\ \hfill & :=-{({\alpha }_{21}({\overline{\zeta }}_1,\widehat{\rho }){\xi }_1^{\overline{m}}+{\alpha }_{22}({\overline{\zeta }}_2,\widehat{\rho }){\xi }_2^{\overline{m}})}^{\frac{1}{\underline{m}}},\hfill \end{array}$$

(23)

we have

$$\begin{array}{cc}\hfill {\xi }_2^3{\left[{\zeta }_3^{*}\right]}^{m\left(t\right)}\le & -({\alpha }_{21}({\overline{\zeta }}_1,\widehat{\rho }){\xi }_1^{\overline{m}}+{\alpha }_{22}({\overline{\zeta }}_2,\widehat{\rho }){\xi }_2^{\overline{m}}){|{\xi }_2|}^3\hfill \\ \hfill \le & -\left(c_2+{\beta }_2({\overline{\zeta }}_2,\widehat{\rho })+(n-2)\widehat{\rho }\right)|{\xi }_2{|}^{m\left(t\right)+3}+\frac{\partial {\zeta }_2^{*}}{\partial \widehat{\rho }}\sigma {\tau }_2({\overline{\zeta }}_2,\widehat{\rho }){|{\xi }_2|}^3,\hfill \end{array}$$

(24)

where $c_2\ge 1$, ${\alpha }_{21}({\overline{\zeta }}_1,\widehat{\rho })\ge 1$ and ${\alpha }_{22}({\overline{\zeta }}_2,\widehat{\rho })\ge 1$ are irrelevant to $m\left(t\right)$.

By using (21), (22) and (24), we obtain

$$\begin{array}{cc}\hfill \mathcal{L}{V}_2\le & -(c_1-1)|{\xi }_1{|}^{m\left(t\right)+3}-(n-2)\widehat{\rho }\left(|{\xi }_1{|}^{m\left(t\right)+3}+{|{\xi }_2|}^{m\left(t\right)+3}\right)-c_2{|{\xi }_2|}^{m\left(t\right)+3}\hfill \\ \hfill & +{\xi }_2^3\left({\left[{\zeta }_3\right]}^{m\left(t\right)}-{\left[{\zeta }_3^{*}\right]}^{m\left(t\right)}\right)-\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_2({\overline{\zeta }}_2,\widehat{\rho })\right).\hfill \end{array}$$

(25)

Deductive Step. Suppose that steps $1,...,i-1$ have been completed, there exists a virtual controller ${\zeta }_i^{*}$ as

$$\begin{array}{c}\hfill {\zeta }_i^{*}:=-{\left(\sum _{k=1}^{i-1}{\alpha }_{i-1k}({\overline{\zeta }}_k,\widehat{\rho }){\xi }_k^{\overline{m}}\right)}^{\frac{1}{\underline{m}}},\end{array}$$

(26)

such that the positive definite Lyapunov function $V_{i-1}$ satisfies

$$\begin{array}{cc}\hfill \mathcal{L}{V}_{i-1}\le & -\sum _{k=1}^{i-1}(c_k+k-i+1)|{\xi }_k{|}^{m\left(t\right)+3}+\sum _{k=1}^{i-3}(n-k-2){\lambda }_k{|{\xi }_k|}^{m\left(t\right)+3}\hfill \\ \hfill & -(n-i+1)\widehat{\rho }\sum _{k=1}^{i-1}{|{\xi }_k|}^{m\left(t\right)+3}+{\xi }_{i-1}^3\left({\left[{\zeta }_i\right]}^{m\left(t\right)}-{\left[{\zeta }_i^{*}\right]}^{m\left(t\right)}\right)\hfill \\ \hfill & -\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_{i-1}({\overline{\zeta }}_{i-1},\widehat{\rho })\right),\hfill \end{array}$$

(27)

where ${\lambda }_k>0$ is any constant, and ${\alpha }_{i-1k}({\overline{\zeta }}_k,\widehat{\rho })\ge 1,k=1,...,i-3$ are irrelevant to $m\left(t\right)$.

For completing the induction, we choose the following Lyapunov function at the ith step.

$$\begin{array}{c}\hfill V_i=V_{i-1}+\frac{1}{4}{\xi }_i^4.\end{array}$$

(28)

From (2), (3), (27), and (28), we get

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i\le & -\sum _{k=1}^{i-1}(c_k+k-i+1)|{\xi }_k{|}^{m\left(t\right)+3}+\sum _{k=1}^{i-3}(n-k-2){\lambda }_k{|{\xi }_k|}^{m\left(t\right)+3}\hfill \\ \hfill & -(n-i+1)\widehat{\rho }\sum _{k=1}^{i-1}{|{\xi }_k|}^{m\left(t\right)+3}+{\xi }_{i-1}^3\left({\left[{\zeta }_i\right]}^{m\left(t\right)}-{\left[{\zeta }_i^{*}\right]}^{m\left(t\right)}\right)\hfill \\ \hfill & +{\xi }_i^3\left(f_i\left({\overline{\zeta }}_i\right)-\sum _{k=1}^{i-1}\frac{\partial {\zeta }_i^{*}}{\partial {\zeta }_k}\left({\left[{\zeta }_{k+1}\right]}^{m\left(t\right)}+f_k\left({\overline{\zeta }}_k\right)\right)-\frac{\partial {\zeta }_i^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)\hfill \\ \hfill & +{\xi }_i^3\left({\left[{\zeta }_{i+1}\right]}^{m\left(t\right)}-{\left[{\zeta }_{i+1}^{*}\right]}^{m\left(t\right)}\right)+{\xi }_i^3{\left[{\zeta }_{i+1}^{*}\right]}^{m\left(t\right)}+\frac{3}{2}\mathrm{Tr}\left\{\mathrm{\Sigma }{\left(t\right)}^T{\widehat{g}}_i{\xi }_i^2{\widehat{g}}_i^T\mathrm{\Sigma }\left(t\right)\right\}\hfill \\ \hfill & -\frac{1}{2}{\xi }_i^3\sum _{j,k=1}^{i-1}\frac{{\partial }^2{\zeta }_i^{*}}{\partial {\zeta }_j\partial {\zeta }_k}{g}_j^T\left({\overline{\zeta }}_j\right)\mathrm{\Sigma }{\mathrm{\Sigma }}^T{g}_k\left({\overline{\zeta }}_k\right)-\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_{i-1}({\overline{\zeta }}_{i-1},\widehat{\rho })\right).\hfill \end{array}$$

(29)

By (2), (26), Lemma 1 in [29] and using the Minkowski inequality, we have

$$\begin{array}{cc}\hfill & {\xi }_{i-1}^3\left({\left[{\zeta }_i\right]}^{m\left(t\right)}-{\left[{\zeta }_i^{*}\right]}^{m\left(t\right)}\right)\hfill \\ \hfill & \le \overline{m}\left(2^{\overline{m}-2}+2\right)\left(|{\xi }_{i-1}{|}^3|{\xi }_i{|}^{m\left(t\right)}+\sum _{k=1}^{i-1}{\alpha }_{i-1k}({\overline{\zeta }}_k,\widehat{\rho })|{\xi }_k{|}^{m\left(t\right)-1}|{\xi }_{i-1}^3||{\xi }_i|\right).\hfill \end{array}$$

(30)

By using Lemma 2.1 in [30], we get

$$\begin{array}{cc}\hfill \overline{m}\left(2^{\overline{m}-2}+2\right)|{\xi }_{i-1}{|}^3{|{\xi }_i|}^{m\left(t\right)}\le & \frac{1}{4}|{\xi }_{i-1}{|}^{m\left(t\right)+3}+{\beta }_{i11}{|{\xi }_i|}^{m\left(t\right)+3},\hfill \\ \hfill \sum _{k=1}^{i-1}{\alpha }_{i-1k}|{\xi }_k{|}^{m\left(t\right)-1}|{\xi }_{i-1}^3||{\xi }_i|\le & \frac{1}{4}|{\xi }_{i-1}{|}^{m\left(t\right)+3}+\sum _{k=1}^{i-2}{\lambda }_k|{\xi }_k{|}^{m\left(t\right)+3}+{\beta }_{i12}{|{\xi }_i|}^{m\left(t\right)+3},\hfill \end{array}$$

(31)

where ${\beta }_{i11}\ge 0$ and ${\beta }_{i12}({\overline{\zeta }}_{i-1},\widehat{\rho })\ge 0$ are irrelevant to $m\left(t\right)$.

Substituting (31) into (30), yields

$$\begin{array}{c}\hfill {\xi }_{i-1}^3\left({\left[{\zeta }_i\right]}^{m\left(t\right)}-{\left[{\zeta }_i^{*}\right]}^{m\left(t\right)}\right)\le \frac{1}{2}|{\xi }_{i-1}{|}^{m\left(t\right)+3}+\sum _{k=1}^{i-2}{\lambda }_k|{\xi }_k{|}^{m\left(t\right)+3}+{\beta }_{i1}({\overline{\zeta }}_{i-1},\widehat{\rho }){|{\xi }_i|}^{m\left(t\right)+3},\end{array}$$

(32)

where ${\beta }_{i1}({\overline{\zeta }}_{i-1},\widehat{\rho })={\beta }_{i11}+{\beta }_{i12}({\overline{\zeta }}_{i-1},\widehat{\rho })\ge 0$ is irrelevant to $m\left(t\right)$.

From (2), (26), Assumption 1 and Lemma 2.1 in [30], we get

$$\begin{array}{cc}\hfill & {\xi }_i^3\left(f_i\left({\overline{\zeta }}_i\right)-\sum _{k=1}^{i-1}\frac{\partial {\zeta }_i^{*}}{\partial {\zeta }_k}\left({\left[{\zeta }_{k+1}\right]}^{m\left(t\right)}+f_k\left({\overline{\zeta }}_k\right)\right)\right)\hfill \\ \hfill & \le |{\xi }_i{|}^3\left(\sum _{k=1}^i{|{\zeta }_k|}^{m\left(t\right)}\right)\left({\tilde{f}}_i\left({\overline{\zeta }}_i\right)+\sum _{k=1}^{i-1}\left|\frac{\partial {\zeta }_i^{*}}{\partial {\zeta }_k}\right|\left(1+{\tilde{f}}_k\left({\zeta }_k\right)\right)\right)\hfill \\ \hfill & \le |{\xi }_i{|}^3\left(\sum _{k=1}^i{|{\xi }_k|}^{m\left(t\right)}\right){\phi }_i({\overline{\zeta }}_{i-1},\widehat{\rho })\left({\tilde{f}}_i\left({\overline{\zeta }}_i\right)+\sum _{k=1}^{i-1}\left|\frac{\partial {\zeta }_i^{*}}{\partial {\zeta }_k}\right|\left(1+{\tilde{f}}_k\left({\zeta }_k\right)\right)\right)\hfill \\ \hfill & \le |{\xi }_i{|}^3\left(\sum _{k=1}^i{|{\xi }_k|}^{m\left(t\right)}\right){\tilde{\phi }}_i({\overline{\zeta }}_i,\widehat{\rho })\hfill \\ \hfill & \le \frac{1}{2}\sum _{k=1}^{i-1}|{\xi }_k{|}^{m\left(t\right)+3}+{\beta }_{i2}({\overline{\zeta }}_i,\widehat{\rho }){|{\xi }_i|}^{m\left(t\right)+3},\hfill \end{array}$$

(33)

where ${\tilde{\phi }}_i({\overline{\zeta }}_i,\widehat{\rho })\ge 1$ and ${\beta }_{i2}({\overline{\zeta }}_i,\widehat{\rho })\ge 0$ are irrelevant to $m\left(t\right)$.

By (3), (26), using Assumption 1 and Lemma 2.1 in [30], we get

$$\begin{array}{cc}\hfill & \frac{3}{2}\mathrm{Tr}\left\{\mathrm{\Sigma }{\left(t\right)}^T{\widehat{g}}_i{\xi }_i^2{\widehat{g}}_i^T\mathrm{\Sigma }\left(t\right)\right\}\hfill \\ \hfill & \le \frac{3}{2}{\tilde{\sigma }}_i^2({\overline{\zeta }}_i,\widehat{\rho })|{\xi }_i{|}^2{\left(|{\xi }_1{|}^{m\left(t\right)}+|{\xi }_2{|}^{m\left(t\right)}+...+{|{\xi }_i|}^{m\left(t\right)}\right)}^2||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill & \le \frac{3i}{2}{\tilde{\sigma }}_i^2({\overline{\zeta }}_i,\widehat{\rho })\left(|{\xi }_i{|}^2\sum _{k=1}^{i-1}|{\xi }_k{|}^{m\left(t\right)+1}|{\xi }_k{|}^{m\left(t\right)-1}+|{\xi }_i{|}^{m\left(t\right)-1}{|{\xi }_i|}^{m\left(t\right)+3}\right)||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill & \le \frac{3i}{2}{\tilde{\sigma }}_i^2({\overline{\zeta }}_i,\widehat{\rho })\left(|{\xi }_i{|}^2\sum _{k=1}^{i-1}|{\xi }_k{|}^{m\left(t\right)+1}{\left({\xi }_k^2+1\right)}^{\frac{\overline{m}-1}{2}}+{\left({\xi }_i^2+1\right)}^{\frac{\overline{m}-1}{2}}{|{\xi }_i|}^{m\left(t\right)+3}\right)\left(\widehat{\rho }+\tilde{\rho }\right)\hfill \\ \hfill & \le \left(\frac{1}{2}\sum _{k=1}^{i-1}|{\xi }_k{|}^{m\left(t\right)+3}+{\beta }_{i3}({\overline{\zeta }}_i,\widehat{\rho }){|{\xi }_i|}^{m\left(t\right)+3}\right)\left(\widehat{\rho }+\tilde{\rho }\right),\hfill \end{array}$$

(34)

where ${\tilde{\sigma }}_i^2({\overline{\zeta }}_i,\widehat{\rho })\ge 0$ and ${\beta }_{i3}({\overline{\zeta }}_i,\widehat{\rho })\ge 0$ are irrelevant to $m\left(t\right)$.

By Assumption 1 and using Lemma 2.1 in [30], we have

$$\begin{array}{cc}\hfill -& \frac{1}{2}{\xi }_i^3\sum _{j,k=1}^{i-1}\frac{{\partial }^2{\zeta }_i^{*}}{\partial {\zeta }_j\partial {\zeta }_k}{g}_j^T\left({\overline{\zeta }}_j\right)\mathrm{\Sigma }{\mathrm{\Sigma }}^T{g}_k\left({\overline{\zeta }}_k\right)\hfill \\ \hfill \le & |{\xi }_i{|}^3{\left(|{\zeta }_1{|}^{m\left(t\right)}+|{\zeta }_2{|}^{m\left(t\right)}+...+{|{\zeta }_{i-1}|}^{m\left(t\right)}\right)}^2{\beta }_{i41}({\overline{\zeta }}_i,\widehat{\rho })||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill \le & |{\xi }_i{|}^3{\left(|{\xi }_1{|}^{m\left(t\right)}+|{\xi }_2{|}^{m\left(t\right)}+...+{|{\xi }_{i-1}|}^{m\left(t\right)}\right)}^2{\beta }_{i42}({\overline{\zeta }}_i,\widehat{\rho })||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }\hfill \\ \hfill \le & |{\xi }_i{|}^3\left(|{\xi }_1{|}^{m\left(t\right)}+|{\xi }_2{|}^{m\left(t\right)}+...+{|{\xi }_{i-1}|}^{m\left(t\right)}\right){\beta }_{i43}({\overline{\zeta }}_i,\widehat{\rho })\left(\widehat{\rho }+\tilde{\rho }\right)\hfill \\ \hfill \le & \left(\frac{1}{2}\sum _{k=1}^{i-1}|{\xi }_k{|}^{m\left(t\right)+3}+{\beta }_{i4}({\overline{\zeta }}_i,\widehat{\rho }){|{\xi }_i|}^{m\left(t\right)+3}\right)\left(\widehat{\rho }+\tilde{\rho }\right),\hfill \end{array}$$

(35)

where ${\beta }_{i41}({\overline{\zeta }}_i,\widehat{\rho }),{\beta }_{i42}({\overline{\zeta }}_i,\widehat{\rho }),{\beta }_{i43}({\overline{\zeta }}_i,\widehat{\rho })$ and ${\beta }_{i4}({\overline{\zeta }}_i,\widehat{\rho })$ are irrelevant to $m\left(t\right)$.

Substituting (32)–(35) into (29), we get

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i\le & -\sum _{k=1}^{i-1}(c_k+k-i)|{\xi }_k{|}^{m\left(t\right)+3}+\sum _{k=1}^{i-2}(n-k-1){\lambda }_k|{\xi }_k{|}^{m\left(t\right)+3}-(n-i)\widehat{\rho }\sum _{k=1}^{i-1}{|{\xi }_k|}^{m\left(t\right)+3}\hfill \\ \hfill & +{\xi }_i^3\left({\left[{\zeta }_{i+1}\right]}^{m\left(t\right)}-{\left[{\zeta }_{i+1}^{*}\right]}^{m\left(t\right)}\right)+{\xi }_i^3\left({\left[{\zeta }_{i+1}^{*}\right]}^{m\left(t\right)}-\frac{\partial {\zeta }_i^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)+{\beta }_i({\overline{\zeta }}_i,\widehat{\rho }){|{\xi }_i|}^{m\left(t\right)+3}\hfill \\ \hfill & -\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_{i-1}({\overline{\zeta }}_{i-1},\widehat{\rho })-\left({\beta }_{i3}({\overline{\zeta }}_i,\widehat{\rho })+{\beta }_{i4}({\overline{\zeta }}_i,\widehat{\rho })\right)|{\xi }_i{|}^{\overline{m}+3}-\sum _{k=1}^{i-1}{|{\xi }_k|}^{\overline{m}+3}\right),\hfill \end{array}$$

(36)

where ${\beta }_i({\overline{\zeta }}_i,\widehat{\rho })={\beta }_{i1}({\overline{\zeta }}_{i-1},\widehat{\rho })+{\beta }_{i2}({\overline{\zeta }}_i,\widehat{\rho })+{\beta }_{i3}({\overline{\zeta }}_i,\widehat{\rho })\widehat{\rho }+{\beta }_{i4}({\overline{\zeta }}_i,\widehat{\rho })\widehat{\rho }\ge 0$ is irrelevant to $m\left(t\right)$.

Let

$$\begin{array}{c}\hfill {\tau }_i({\overline{\zeta }}_i,\widehat{\rho })={\tau }_1\left({\zeta }_1\right)+\sum _{k=2}^i\left({\beta }_{k3}({\overline{\zeta }}_k,\widehat{\rho })+{\beta }_{k4}({\overline{\zeta }}_k,\widehat{\rho })\right)|{\xi }_k{|}^{\overline{m}+3}+\sum _{k=1}^i(i-k){|{\xi }_k|}^{\overline{m}+3}.\end{array}$$

(37)

Clearly, setting the virtual controller ${\zeta }_{i+1}^{*}$ as

$$\begin{array}{cc}\hfill {\zeta }_{i+1}^{*}& =-{\left(\left(c_i+{\beta }_i({\overline{\zeta }}_i,\widehat{\rho })+(n-i)\widehat{\rho }\right){|{\xi }_i|}^{\overline{m}}-\frac{\partial {\zeta }_i^{*}}{\partial \widehat{\rho }}\sigma {\tau }_i({\overline{\zeta }}_i,\widehat{\rho })\right)}^{\frac{1}{\underline{m}}}\hfill \\ \hfill & :=-{\left(\sum _{k=1}^i{\alpha }_{ik}({\overline{\zeta }}_k,\widehat{\rho }){\xi }_k^{\overline{m}}\right)}^{\frac{1}{\underline{m}}},\hfill \end{array}$$

(38)

we get

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i\le & -\sum _{k=1}^i(c_k+k-i)|{\xi }_k{|}^{m\left(t\right)+3}+\sum _{k=1}^{i-2}(n-k-1){\lambda }_k{|{\xi }_k|}^{m\left(t\right)+3}\hfill \\ \hfill & -(n-i)\widehat{\rho }\sum _{k=1}^i{|{\xi }_k|}^{m\left(t\right)+3}+{\xi }_i^3\left({\left[{\zeta }_{i+1}\right]}^{m\left(t\right)}-{\left[{\zeta }_{i+1}^{*}\right]}^{m\left(t\right)}\right)\hfill \\ \hfill & -\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_i({\overline{\zeta }}_i,\widehat{\rho })\right),\hfill \end{array}$$

(39)

where $c_i\ge 1$ and ${\alpha }_{ik}({\overline{\zeta }}_k,\widehat{\rho })\ge 1$ are irrelevant to $m\left(t\right)$.

Step n. Choose

$$\begin{array}{c}\hfill V_n=\sum _{k=1}^n\frac{1}{4}{\xi }_k^4+\frac{1}{2\sigma }{\tilde{\rho }}^2,\end{array}$$

(40)

where $\sigma >0$ is a constant.

By using (40), in the same way with (36), we have

$$\begin{array}{cc}\hfill \mathcal{L}{V}_n\le & -\sum _{k=1}^{n-1}(c_k+k-n)|{\xi }_k{|}^{m\left(t\right)+3}+\sum _{k=1}^{n-2}(n-k-1){\lambda }_k{|{\xi }_k|}^{m\left(t\right)+3}\hfill \\ \hfill & +{\xi }_n^3\left({\left[u\right]}^{m\left(t\right)}-\frac{\partial {\zeta }_n^{*}}{\partial \widehat{\rho }}\dot{\widehat{\rho }}\right)+{\beta }_n({\overline{\zeta }}_n,\widehat{\rho }){|{\xi }_n|}^{m\left(t\right)+3}\hfill \\ \hfill & -\tilde{\rho }\left(\frac{\dot{\widehat{\rho }}}{\sigma }-{\tau }_{n-1}({\overline{\zeta }}_{n-1},\widehat{\rho })-\left({\beta }_{n3}({\overline{\zeta }}_n,\widehat{\rho })+{\beta }_{n4}({\overline{\zeta }}_n,\widehat{\rho })\right)|{\xi }_n{|}^{\overline{m}+3}-\sum _{k=1}^{n-1}{|{\xi }_k|}^{\overline{m}+3}\right),\hfill \end{array}$$

(41)

where ${\beta }_n({\overline{\zeta }}_n,\widehat{\rho })={\beta }_{n1}({\overline{\zeta }}_{n-1},\widehat{\rho })+{\beta }_{n2}({\overline{\zeta }}_n,\widehat{\rho })+{\beta }_{n3}({\overline{\zeta }}_n,\widehat{\rho })\widehat{\rho }+{\beta }_{n4}({\overline{\zeta }}_n,\widehat{\rho })\widehat{\rho }\ge 0$ is irrelevant to $m\left(t\right)$.

Design the adaptive law as

$$\begin{array}{cc}\hfill \dot{\widehat{\rho }}=& \sigma {\tau }_n({\overline{\zeta }}_n,\widehat{\rho }),\hfill \\ \hfill {\tau }_n({\overline{\zeta }}_n,\widehat{\rho })=& {\tau }_1\left({\zeta }_1\right)+\sum _{k=2}^n\left({\beta }_{k3}({\overline{\zeta }}_k,\widehat{\rho })+{\beta }_{k4}({\overline{\zeta }}_k,\widehat{\rho })\right)|{\xi }_k{|}^{\overline{m}+3}+\sum _{k=1}^n(n-k){|{\xi }_k|}^{\overline{m}+3},\hfill \end{array}$$

(42)

and the controller as

$$\begin{array}{cc}\hfill u=& -{\left(\left(c_n+{\beta }_n({\overline{\zeta }}_n,\widehat{\rho })\right){|{\xi }_n|}^{\overline{m}}-\frac{\partial {\zeta }_n^{*}}{\partial \widehat{\rho }}\sigma {\tau }_n({\overline{\zeta }}_n,\widehat{\rho })\right)}^{\frac{1}{\underline{m}}}\hfill \\ \hfill :=& -{\left(\sum _{k=1}^n{\alpha }_{nk}({\overline{\zeta }}_k,\widehat{\rho }){\xi }_k^{\overline{m}}\right)}^{\frac{1}{\underline{m}}}.\hfill \end{array}$$

(43)

Choosing appropriate ${\lambda }_k$ such that $(n-k-1){\lambda }_k=1,k=1,...,n-2$, we have

$$\begin{array}{c}\hfill \mathcal{L}{V}_n\le -\sum _{k=1}^{n-2}(c_k+k-n-1)|{\xi }_k{|}^{m\left(t\right)+3}-(c_{n-1}-1)|{\xi }_{n-1}{|}^{m\left(t\right)+3}-c_n{|{\xi }_n|}^{m\left(t\right)+3},\end{array}$$

(44)

where $c_n\ge 1$ is a constant to be designed, and ${\alpha }_{nk}({\overline{\zeta }}_n,\widehat{\rho })\ge 1$ is a smooth function irrelevant to $m\left(t\right)$. □

Remark 2.

Although [24,25,26] solve the adaptive control problems for stochastic nonlinear systems with unknown covariance, their powers are $m\left(t\right)=1$. In this paper, the power $m\left(t\right)\ge 1$ is time-varying and non-differentiable, which makes the deduction of the controller much more difficult. To solve this problem, we introduce two constants $\overline{m}$ and $\underline{m}$, which are reasonably used in the design process, see (7) and (12). In this way, the controller (43) can be designed independently of $m\left(t\right)$, which is crucial to guarantee stability.

Remark 3.

In the derivation process, there is a complex term $\frac{1}{2}\mathrm{Tr}\left\{{\mathrm{\Sigma }}^{T}g\left(\zeta \right)\frac{{\partial }^{2}V}{\partial {\zeta }^2}{g}^T\left(\zeta \right)\mathrm{\Sigma }\right\}$, which is produced inevitably (see (5) and (11)). Because $\mathrm{\Sigma }\left(t\right)$ is unknown, it is difficult to deal with this term directly. To solve this problem, we first estimate $\rho =||\mathrm{\Sigma }{\mathrm{\Sigma }}^T{||}_{\infty }$ with $\widehat{\rho }$ and replace the resulting ρ with $\widehat{\rho }+\tilde{\rho }$ (see (19) and (34)). Then, we combine the terms with $\tilde{\rho }$ to design ${\tau }_1,{\tau }_2,...,{\tau }_n$, which can be found in (6), (22) and (42). Finally, the adaptive law (42) is derived. This is one of the main innovations of this paper.

3.2. Stability Analysis

Firstly, we prove a lemma, which is crucial in proving that the system (1) has a unique solution.

Lemma 1.

For $\zeta \in \mathrm{R}$, the function $h\left(\zeta \right)={\left[\zeta \right]}^{m\left(t\right)}$ satisfies the local Lipschitz condition.

Proof. 

If $\zeta =0$, we get

$$\begin{array}{cc}\hfill h_{+}^{{}^{\prime }}\left(0\right)=& \underset{\zeta \to 0^{+}}{lim}\frac{h\left(\zeta \right)-h\left(0\right)}{\zeta }=0,\hfill \\ \hfill h_{-}^{{}^{\prime }}\left(0\right)=& \underset{\zeta \to 0^{-}}{lim}\frac{h\left(\zeta \right)-h\left(0\right)}{\zeta }=0.\hfill \end{array}$$

Then, we have

$$\begin{array}{c}\hfill \frac{dh}{d\zeta }{|}_{\zeta =0}=h_{+}^{{}^{\prime }}\left(0\right)=h_{-}^{{}^{\prime }}\left(0\right)=0,\end{array}$$

thus, $h\left(\zeta \right)$ is a differentiable function in $\zeta =0$ and so meets the local Lipschitz condition in $\zeta =0$.

As $\zeta >0$, we get

$$\begin{array}{c}\hfill h\left(\zeta \right)={\left[\zeta \right]}^{m\left(t\right)}={\zeta }^{m\left(t\right)}.\end{array}$$

For $m\left(t\right)\ge 1$, $h\left(\zeta \right)$ is a differentiable function in $\zeta >0$, so meets the local Lipschitz condition in $\zeta >0$. Similarly, as $\zeta <0$, the conclusion is valid.

Therefore, the conclusion holds for $\zeta \in \mathrm{R}$. □

Next, we present the stability results.

Theorem 1.

For the system (1), we use the adaptive state-feedback controller (42) and (43) with

$$\begin{array}{cc}\hfill c_k& \ge n+2-k,1\le k\le n-2,\hfill \\ \hfill c_{n-1}& \ge 2,\hfill \\ \hfill c_n& \ge 1.\hfill \end{array}$$

(45)

If Assumption 1 holds, we obtain that

(1) For each $({\zeta }_0,{\widehat{\rho }}_0)$, the closed-loop system has an almost surely unique solution on $[0,\infty )$;

(2) The equilibrium $(\zeta ,\tilde{\rho })=(0,0)$ of the closed-loop system is globally stable in probability;

(3) For each $({\zeta }_0,{\widehat{\rho }}_0),\mathrm{P}\{{lim}_{t\to \infty }(|{\zeta }_1|+\cdots +|{\zeta }_n|)=0\}=1,\mathrm{P}\{{lim}_{t\to \infty }\widehat{\rho }\left(t\right)$ exists and is finite$\}=1$.

Proof. 

By (1), (43) and using Lemma 1, we conclude that the system (1) fulfills the local Lipschitz condition. By using (44) and (45), we get

$$\begin{array}{c}\hfill \mathcal{L}{V}_n\le -\sum _{k=1}^n{|{\xi }_k|}^{m\left(t\right)+3}.\end{array}$$

(46)

By using Lemma 5 in [31] and Lemma 5 in [29], we get

$$\begin{array}{c}\hfill \mathcal{L}{V}_n\le -\frac{1}{n^{\overline{m}+2}}{\left(\sum _{k=1}^n|{\xi }_k|\right)}^{m\left(t\right)+3}\le -\frac{1}{n^{\overline{m}+2}}\left(\frac{{\left({\sum }_{k=1}^n|{\xi }_k|\right)}^{\overline{m}+3}}{1+{\left({\sum }_{k=1}^n|{\xi }_k|\right)}^{2\overline{m}-\underline{m}+3}}\right).\end{array}$$

(47)

$\mathcal{L}{V}_n$ in (44) takes the same form as (3.19) in [24]. By (40) and using Lemma 1 in [32], we can follow the same procedure as in the proof of Theorem 3.1 in [24] to prove Theorem 1. □

Remark 4.

In the stability analysis process, we use two constants $\overline{m}$ and $\underline{m}$ to overcome the difficulties caused by $m\left(t\right)$, see (47), which is one of our major contributions.

Remark 5.

The control design parameters $c_1,c_2,\cdots ,c_n$ should satisfy (45). From (43), the larger these parameters are, the larger the regulator (43) is and the faster the converge rates of the states ${\zeta }_1,...,{\zeta }_n$ are. In other words, larger control effort yields larger convergence speed.

4. Two Simulation Examples

In this part, we give two examples to illustrate the design methods.

Example 1.

Consider the global stabilization for the following system

$$\begin{array}{cc}\hfill d{\zeta }_1=& \left({\left[{\zeta }_2\right]}^{\frac{3}{2}+\frac{1}{2}sint}+{\zeta }_1^3\right)dt+{\zeta }_1{sin}^2{\zeta }_1\mathrm{\Sigma }\left(t\right)d\omega ,\hfill \\ \hfill d{\zeta }_2=& \left({\left[u\right]}^{\frac{3}{2}+\frac{1}{2}sint}+{\zeta }_2^{2}sin{\zeta }_1\right)dt+{\zeta }_2{sin}^2{\zeta }_1\mathrm{\Sigma }\left(t\right)d\omega ,\hfill \end{array}$$

(48)

where $m\left(t\right)=\frac{3}{2}+\frac{1}{2}sint$, $\underline{m}=1$, $\overline{m}=2$. Clearly, system (48) satisfies Assumption 1.

According to our design process, the control u is

$$\begin{array}{c}\hfill u=-\left(c_2+{\beta }_2({\overline{\zeta }}_2,\widehat{\rho })\right){\left({\zeta }_2+\frac{8}{3}{\zeta }_1+\frac{2}{3}\widehat{\rho }{\zeta }_1\left({\zeta }_1^2+1\right)\right)}^2+\frac{2}{3}\left({\zeta }_1^2+1\right)\sigma {\tau }_2,\end{array}$$

(49)

and the adaptive law is

$$\begin{array}{c}\hfill \dot{\widehat{\rho }}=\sigma {\tau }_2,\end{array}$$

(50)

where

$$\begin{array}{c}\hfill {\tau }_2=\left(\frac{2}{3}{\left({\zeta }_1^2+1\right)}^{\frac{1}{2}}+1\right){\zeta }_1^5+{\left({\zeta }_2+\frac{8}{3}{\zeta }_1+\frac{2}{3}\widehat{\rho }{\zeta }_1\left({\zeta }_1^2+1\right)\right)}^5.\end{array}$$

(51)

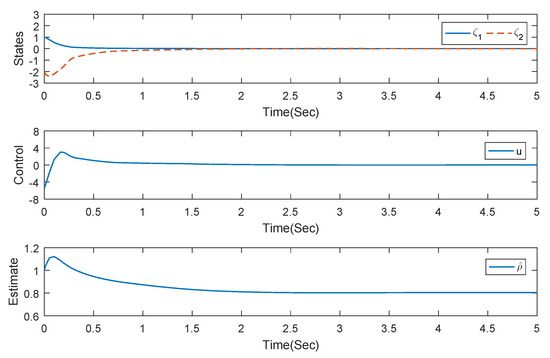
In the simulation, we set parameters as $c_1=2,c_2=3,\sigma =1$, and the initial conditions as ${\zeta }_1\left(0\right)=1,{\zeta }_2\left(0\right)=-2,\widehat{\rho }\left(0\right)=1$. Finally, we obtain Figure 1, which illustrates that the responses of $({\zeta }_1,{\zeta }_2,\widehat{\rho },u)$ are bounded, and $({\zeta }_1,{\zeta }_2,u)$ converge to zero. Thus, the example presents the merit of the control scheme proposed in Section 3.

Figure 1. The response of the closed-loop system (48)–(51).

Example 2.

Consider the one-link manipulator which contains motor dynamics and stochastic disturbances [33].

The system is described as

$$\begin{array}{cc}\hfill & D\ddot{q}+B\dot{q}+Nsin\left(q\right)={\tau }_r+{\tau }_d,\hfill \\ \hfill & M{\dot{\tau }}_r+H{\tau }_r=u-K_m\dot{q},\hfill \end{array}$$

(52)

where $q,\dot{q},\ddot{q}$ denote the link position, velocity, and acceleration, respectively. ${\tau }_r$ is the torque produced by the electrical subsystem, and ${\tau }_d=a_{1}sin\left(q\right)\dot{\omega }$ is the torque disturbance with constant $a_1$ and the torque stochastic disturbance ω defined in system (1). $\mathrm{\Sigma }\left(t\right)$ is an unknown nonnegative-definite matrix for each $t\ge 0$. u is the control input used to represent the electromechanical torque. In addition, $D,B,N,M,H$ and $K_m$ are defined in [33].

To obtain a state model for the one-link manipulator system, we introduce ${\zeta }_1=MDq$, ${\zeta }_2=MD\dot{q},{\zeta }_3=M{\tau }_r$. Then, from (52), we get the state-space form as

$$\begin{array}{cc}\hfill d{\zeta }_1=& {\zeta }_{2}dt,\hfill \\ \hfill d{\zeta }_2=& {\zeta }_{3}dt-\left(\frac{B}{D}{\zeta }_2+MNsin\left(\frac{{\zeta }_1}{MD}\right)\right)dt+a_{1}Msin\left(\frac{{\zeta }_1}{MD}\right)\mathrm{\Sigma }\left(t\right)d\omega ,\hfill \\ \hfill d{\zeta }_3=& udt-\left(\frac{K_m}{MD}{\zeta }_2+\frac{H}{M}{\zeta }_3\right)dt.\hfill \end{array}$$

(53)

We choose $D=2,B=2,N=1,M=0.5,H=0.1,K_m=0.2,a_1=0.1$. Obviously, (53) is a special form of the stochastic nonlinear system (1) and system (53) satisfies Assumption 1.

By following the design procedure developed in Section 3, the control u is

$$\begin{array}{cc}\hfill u=& -\left(c_3-\frac{1}{2}\widehat{\rho }\right)\left({\zeta }_3+\left(c_2-\frac{9}{2}\widehat{\rho }\right)\left({\zeta }_2+c_1{\zeta }_1-2\widehat{\rho }{\zeta }_1\right)+\frac{3}{2}{\zeta }_1\sigma {\tau }_2\right)\hfill \\ \hfill & +\frac{9}{2}({\zeta }_2+c_1{\zeta }_1-2\widehat{\rho }{\zeta }_1)\sigma {\tau }_3,\hfill \end{array}$$

(54)

where

$$\begin{array}{cc}\hfill {\tau }_2=& \frac{3}{2}{\zeta }_1^4+\frac{9}{2}{\left({\zeta }_2+c_1{\zeta }_1-2\widehat{\rho }{\zeta }_1\right)}^4,\hfill \\ \hfill {\tau }_3=& {\tau }_2+\frac{1}{2}{\left({\zeta }_3+\left(c_2-\frac{9}{2}\widehat{\rho }\right)({\zeta }_2+c_1{\zeta }_1-2\widehat{\rho }{\zeta }_1)+\frac{3}{2}{\zeta }_1\sigma {\tau }_2\right)}^4,\hfill \end{array}$$

(55)

and the adaptive law is

$$\begin{array}{c}\hfill \dot{\rho }=\sigma {\tau }_3.\end{array}$$

(56)

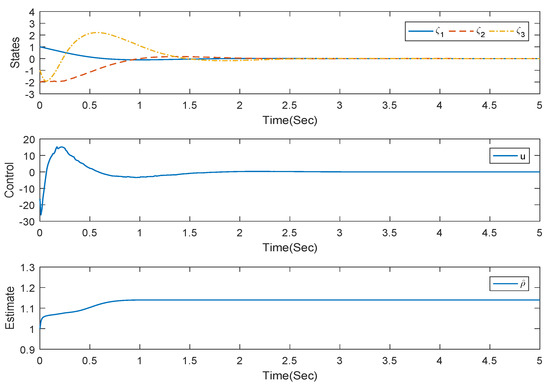
We select the parameters $c_1=5,c_2=8,c_3=15,\sigma =0.1$, and the initial values of the system states of (53) are ${\zeta }_1\left(0\right)=1,{\zeta }_2\left(0\right)=-2,{\zeta }_3\left(0\right)=-1,\widehat{\rho }\left(0\right)=1$. In the simulation, we use the Matlab module “Band-Limited White Noise” to describe the Wiener process. The parameters of “Band-Limited White Noise” are Noise power [20], Sample time 0.01 s, and Seed value [23341]. We obtain Figure 2, which shows that the states in the system (53) are regulated to zero. Therefore, the effectiveness of the adaptive law and the controller design developed in Section 3 is demonstrated. We show the response of the Wiener process in Figure 3.

Figure 2. The response of the closed-loop system (53)–(56).

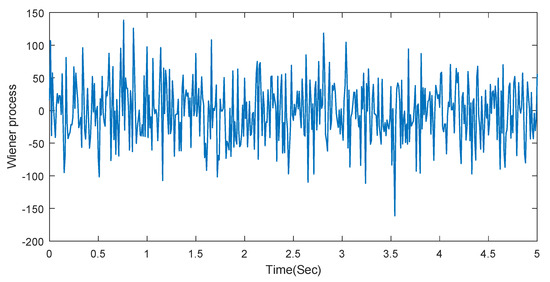
Figure 3. The response of the Wiener process.

5. Concluding Remarks

This paper has solved the adaptive stabilization problem for stochastic nonlinear systems with time-varying powers and unknown covariance. The constructed controller ensures that the closed-loop system is globally stable in probability and the states are regulated to the origin almost surely.

There are some related problems to be studied, such as how to extend the result to more general systems [34,35,36,37,38,39]. Specifically, we require that the system structure is fixed in this paper, but the structure of the actual system is likely to change [36,38]. Our next work is to extend the results in this paper to systems with Markovian switching [34]. In addition, in this paper, we require all the states of the systems are measurable, without considering the case of unmeasurable states [35,37,39]. Thus, how to design the output-feedback controller with unmeasurable states is an interesting problem. Moreover, as we discussed earlier, in practical applications, both systems reported in [27,28] are systems with time-varying power. How to apply the results of this paper to these practical systems is an important future work.