Feature Selection Using Artificial Gorilla Troop Optimization for Biomedical Data: A Case Analysis with COVID-19 Data

Abstract

Feature selection (FS) is commonly thought of as a pre-processing strategy for determining the best subset of characteristics from a given collection of features. Here, a novel discrete artificial gorilla troop optimization (DAGTO) technique is introduced for the first time to handle FS tasks in the healthcare sector. Depending on the number and type of objective functions, four variants of the proposed method are implemented in this article, namely: (1) single-objective (SO-DAGTO), (2) bi-objective (wrapper) (MO-DAGTO1), (3) bi-objective (filter wrapper hybrid) (MO-DAGTO2), and (4) tri-objective (filter wrapper hybrid) (MO-DAGTO3) for identifying relevant features in diagnosing a particular disease. We provide an outstanding gorilla initialization strategy based on the label mutual information (MI) with the aim of increasing population variety and accelerate convergence. To verify the performance of the presented methods, ten medical datasets are taken into consideration, which are of variable dimensions. A comparison is also implemented between the best of the four suggested approaches (MO-DAGTO2) and four established multi-objective FS strategies, and it is statistically proven to be the superior one. Finally, a case study with COVID-19 samples is performed to extract the critical factors related to it and to demonstrate how this method is fruitful in real-world applications.

1. Introduction

Good health is the hallmark of life. But the story of disease is one that has affected humanity in various forms, forcing humans to struggle and compelling researchers to reveal the secrets of disease. Machine learning (ML) has established a method of feature selection where the features consist the cause of creating a disease in humans. A medical diagnosis constitutes a difficult procedure that necessitates clinical expertise. The demand for precise judgments, on the other hand, must be tempered with an understanding of the uncertainty that exists in many clinical circumstances. Rather than assuming diagnostic certainty, complicated presentations sometimes necessitate probabilistic assumptions. People can produce and store data at an unbelievable rate in the digital realm. This explosion of accessible data for additional analysis may be seen in medicine just as much as it can be seen in other fields. Various artificial intelligence technologies have been used to solve a variety of medical challenges with the goal of automating time-consuming and frequently subjective manual procedures carried out by physicians in a variety of disciplines. However, it is difficult to translate AI research into clinically verified and adequately regulated systems that can benefit everyone in a safe and timely manner. Clinical assessment is critical, with measurements that are understandable to physicians and ideally go beyond technical correctness to encompass quality of treatment and patient outcomes.

A vast number of illness indicators are frequently found in medical databases. Concretely, some illness indicators are not helpful in clinical data processing and they can even be harmful. As a result, feature selection is crucial since it can exclude illness signs that are not significant. It also improves the efficacy of the medical decision support systems by reducing their learning time and improving data understanding. FS has been particularly successful in clinical uses, as it may not only shrink dimensions but also aid in the understanding of illness aetiology.

FS techniques are mainly distinguished into three groups, namely wrapper, filter, and embedding procedures [1]. Wrappers look at the quasi-optimal sub-strings of attributes and a classifier for the wrapper process. More to the point, wrappers offer better consequences than filtering methods owing to the employment of a prediction system, but these tactics take longer to implement because of the classification system’s constant learning [2]. An alternative approach is to use statistical concepts and information theories to identify a subset of features that have the highest connection with a certain outcome while simultaneously minimising any internal correlations [1]. Embedded approaches also seek to incorporate the FS process into the classification training phase [3].

Evolutionary techniques have been presented as a response to the challenges outlined above. Due to population-based and global search potentiality, these designs are able to find better optimal results in contrast to greedy techniques [4,5,6,7,8,9]. Few studies have attempted to integrate filter and wrapper models by using evolutionary computing (EC) techniques, as the most extant EC algorithms follow one of these two models: filter or wrapper. The majority also treats FS as a one-objective task.

The artificial gorilla troop optimization (AGTO) is an advanced metaheuristic approach presented for the resolution of optimisation issues [10]. In previous studies, this method was found to achieve minimal feature evaluation, high speed, and great global and local finding capabilities [11,12]. The full potential of this strategy for addressing the FS job has yet to be discovered to our knowledge.

In this particular paper, our effort is to find the relevant aspects related to a particular disease by employing a novel discrete artificial gorilla troop optimization algorithm with various combinations of objective functions. Four different types of the proposed method are implemented here based on the number and type of objective function. These are: (1) single-objective (SO-DAGTO), (2) bi-objective (wrapper) (MO-DAGTO1), (3) bi-objective (filter wrapper hybrid) (MO-DAGTO2), and (4) tri-objective (filter wrapper hybrid) (MO-DAGTO3) in terms of feature selection in the medical era.

In this study, we have looked into the following objectives in particular:

• To learn about the latest metaheuristic FS assignments as well as their benefits and drawbacks;
• To propose a discrete version of the AGTO, entitled DAGTO, for handling FS work in the biomedical era;
• To introduce a DAGTO with various combinations of objective functions to discover Pareto fronts for the FS work by simultaneously optimizing filter and wrapper conditions for the first time;
• To boost the diversity of the population and speed up its convergence, we present an efficient and effective gorilla initialization technique based on label mutual information (MI);
• To offer a comprehensive assessment report on the achievement of DAGTO in FS task using clinical information by executing four distinct variations of DAGTO according to the objective functions used;
• To compare the introduced SO-DAGTO strategy to three standard single-objective mechanisms and MO-DAGTO approaches to four popular multi-criteria frameworks, and to prove if the offered strategies outcompete benchmarking approaches in minimizing feature subset width and rising accuracy rate;
• To use the “knee point” concept for selecting the best one from the external repository, in the case of MO-DAGTOs; and
• To validate the efficiency of the provided technique by testing with a real-world COVID-19 dataset.

The following is the paper’s structure. The background material is introduced in Section 2. The proposed approach is presented in Section 3, and the experimental setups and findings are discussed in Section 4 and Section 5 respectively. The strong points of the proposed approaches are listed in Section 6, whereas an application of the proposed method in real-world COVID-19 data is presented in the Section 7. Finally, Section 8 brings the paper to a close.

2. Background

2.1. Artificial Gorilla Troop Optimizer (AGTO)

AGTO is a novel metaheuristic approach based on the group behaviours of gorillas. Five distinct operators illustrated in Figure 1 are employed in the AGTO method regarding exploitation and exploration operations.

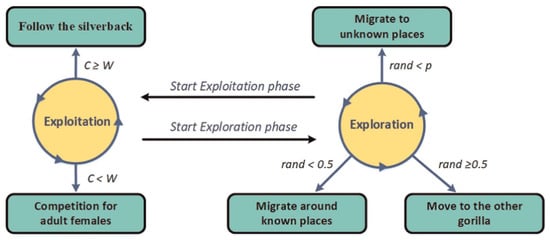
Figure 1. Phases of AGTO [10].

The optimization arena of the AGTO method has three types of solutions; P represents the location of the gorilla and G represents the location of the candidate gorilla formed in every step and operating if it outperforms the existing one. Finally, in each repetition, the “silverback” is the best alternative.

2.1.1. Exploration Phase

Regarding the exploration process, three separate strategies are used: migrating to an unseen site, migrating towards a recognised position, and movement to other gorillas. The technique of migration to an unknown place is chosen by using a parameter called p. When $rand<p$ is used, the first mechanism is chosen. If rand is greater than or equal to $0.5$, the gorilla-to-gorilla moving method is chosen. On the other hand, if rand is less than $0.5$, the migration strategy to a known site is chosen.

Mathematically, these can be written as following:

$$G(It+1)=\left\{\begin{array}{c}(ub-lb)·rnd1+lb, rand<p\hfill \\ (rnd2-C)·P_r\left(It\right)+L·H,rand\ge 0.5\\ P\left(It\right)-L·(L·(P\left(It\right)-G_r\left(It\right))+rnd3·(P\left(It\right)-G_r\left(It\right))),rand<0.5\end{array}\right.,$$

(1)

where

• $P\left(It\right)$ is the the gorilla’s present location;
• $P(It+1)$ is the candidate gorilla location in the following $It$ iteration;
• $rnd1$, $rnd2$, $rnd3$ and $rand$ are random numbers between 0 and 1;
• p is a parameter with range in [0–1] that must be set prior to the optimization procedure;
• $ub$ and $lb$ are the minimum and maximum values of the variables, respectively;
• $P_r$ is a randomly chosen gorilla; and
• $G_r$ is a randomly chosen candidate gorilla:

$$C=F·\left(1-\frac{It}{maxIt}\right)$$

(2)

$$F=cos(2·rnd4)+1$$

(3)

$$L=C·l$$

(4)

where $It$ is the current iteration, $maxIt$ is the maximum number of iterations to conduct, and l is a random number in the range $[-1,1]$. The factor H in the Equation (1) is calculated as follows:

$$H=Z·P\left(It\right)$$

(5)

$$Z=[-C,C].$$

(6)

A group development activity is performed after the exploration activity by evaluating all G solutions and using the $G\left(It\right)$ solution as the $P\left(It\right)$ solution if the cost is $G\left(It\right)<P\left(It\right)$. As a result, the best solution found during this phase is referred to as a “silverback”.

2.1.2. Exploitation Phase

In this phase, the C value in Equation (2) is used to choose between two mechanisms; either by following the silverback (if $C\ge W$) or with a competition for adult females (if $C<W$), where W is a pre-specified parameter.

• Follow the Silverback: The silverback is a young and fit gorilla, and the other males in the troop are likewise young and sharply observe him. They also obey all of silverback’s commands to travel to diverse locations in search of food supplies and to stay with him. This behaviour is simulated by using the following Equation (7):

  $$G(It+1)=L·M·\left(P\left(It\right)-P_{Silverback}\right)+P\left(It\right)$$

  (7)

  $$M={\left({\left|\frac{1}{N}\sum _{j=1}^N{G}_j\left(It\right)\right|}^g\right)}^{1/g}$$

  (8)

  where

  $$g=2^L.$$

  (9)
• Competition for Adult Females: When juvenile gorillas enter adolescence, they engage in risky competition with other males in order to pick grown-up females and to expand their troop. These brawls can extend for days and include several individuals. This process is simulated using Equation (10).

$$G(It+1)=P_{Silverback}-(P_{Silverback}·Q-P\left(It\right)·Q)·A$$

(10)

$$Q=2·rnd5-1$$

(11)

$$A=\beta ·E$$

(12)

$$E=\left\{\begin{array}{cc}N1,& rnd\ge 0.5\\ N2,& rnd<0.5\end{array}\right.$$

(13)

where Q simulates the impact force, A is the coefficient vector to assess the level of violence in a dispute, $\beta$ is a preset parameter, and E replicates the impact of violence on solution dimensions.

A group development activity is performed after the exploration activity by evaluating all G solutions and using the $G\left(It\right)$ solution as the $P\left(It\right)$ solution if the cost is $G\left(It\right)<P\left(It\right)$. As a result, the optimal one found during this step is referred to as a “silverback”.

2.2. Single-Objective vs. Multi-Objective Optimization

The main purpose of single-objective optimization (SOP) is to identify the optimal solution, which refers to the lowest or maximum value of a single objective function that combines all multiple objectives into one. This type of optimization is useful as a tool for providing planners with information about the problem at hand, but it rarely provides a set of potential solutions that trade-off distinct objectives.

On the other hand, in a multi-objective optimization (MOP) with competing objectives, there is no single best solution. The interplay of several objectives results in a collection of compromised solutions, which are sometimes referred to as trade-offs, non-dominated, non-inferior, or Pareto-optimal options. A fitness comparison is used to establish a candidate’s superiority over other alternatives in an SOP. Despite this, the idea of dominance is used in MOP to assess the merit of a potential solution. If the following two requirements are true, a solution $A1$ in the feasible region of a C-objective problem dominates another solution, $A2$.

• For all C: A1 is not inferior than A2
• There is a c: A1c is surely superior than A2c

2.3. Related Work

FS techniques can be divided into three categories: embedded, filter, and wrapper. Here, for the first time, we have explored AGTO in the domain of feature selection for medical data, and we have also considered both filter and wrapper characteristics during optimization. Therefore, the following subsections briefly describe the existing work on both filter-based and wrapper-based FS techniques.

2.3.1. Filter-Based FS Techniques

Focus [13] and Relief [14] are two non-metaheuristic-based filter approaches for the FS task. The Relief approach assigns a weight to each characteristic based on how important it is. The fundamental disadvantage of this strategy is that it does not take into account feature redundancy. On the other hand, one of the most well-known filter methods is the Focus algorithm, which does a comprehensive search to analyze the whole subset of potential characteristics, which is computationally intensive and often impossible. Furthermore, employing information theory ideas, filter approaches such as mRmR [15] and MIFS [16] attempt to improve the efficiency of the FS algorithm.

Starting with metaheuristic-based filter techniques for FS problems, in [17], NSGAII looked at developing two filter techniques—NSGAIIMI and NSGAIIE—by using MI and entropy as the assessment criteria, respectively. Recently, a text feature selection technique based on a filter-based multi-objective algorithm was proposed in [18]. A text feature’s significance is determined by using the relative discriminative criterion (RDC), whereas redundancy is determined by using the correlation measure. In [19], the authors employed rough set theory and MOBPSO to implement filter-based FS. There were two multi-objective filter FS methods proposed in [20], both of which employed BPSO, modified MI, and entropy to perform superior classification. Three multi-objective ABC techniques (MOABC) were developed in [21], focusing on information theory and incorporating three filter objectives.

The authors of [22] have provided two new filter FS approaches for classification issues based on binary PSO and information theory. The first approach utilizes BPSO and the MI between each pair of attributes to assess the subset’s significance and duplication, whereas the second approach examines the relevance and duplication of the chosen feature subset by using BPSO and the entropy of each feature group. To control duplicate and undesired aspects in a dataset, the work in [23] introduced a filter technique employing an elitism-based MODE for FS, entitled FAEMODE. The uniqueness lies in this algorithm’s objective preparation, which takes into account linear as well as non-linear interdependence among feature sets. Two alternative multi-objective filter-based FS architectures built on the boolean cuckoo optimization technique, utilising the concept of non-dominated sorting GAs, NSGAIII (BCNSG3), and NSGAII (BCNSG2), have been proposed in [24]. To this end, four different multi-objective filter-based FS techniques were developed, each using MI and gain ratio-based entropy as filter assessment measurements.

2.3.2. Wrapper-Based FS Techniques

Wrapper approaches look at the quasi-optimal sub-strings of attributes and a classification model for the wrapper process. According to the searching process, these can be divided into two types: metaheuristic-based and non-metaheuristic-based. Branch & Bound [25], SFS [26], and SBS [27] are some of the most well-known non-metaheuristic-based FS methods. Despite their simplicity of design, these strategies have issues such as convergence to a local optimal and considerable computation complexity in big datasets. Both the SFS and SBS approaches contain a structural flaw, which means that the already appended (or discarded) characteristics cannot be eliminated (or inserted) in subsequent phases [1]. SFFS and SBFS have been presented as solutions to this problem [28]. However, these algorithms advancements have not been able to overcome the local optima convergence issue [13].

Researchers have applied metaheuristic algorithms to tackle the challenges outlined above and utilize improved discovery procedure. These techniques develop and rate several alternatives at the same time and provide a more comprehensive global search than conventional techniques because they are population-based. Furthermore, single-objective wrapper approaches often follow the goals of lowering feature subset size by maximising classification efficiency, or a combination of these goals. Some of the most popular evolutionary methods used for single-objective FS are: GA [29], PSO [30], WOA [31], GWO [32], FPA [33], ABC [34], ACO [35], GP [36], and FOA [37].

Due to the concurrent examination of numerous, frequently competing demands and the delivery of a sequence of non-dominated (ND) options, multi-objective FS strategies seem to be the subject of major research in recent years. An innovative technique, called MOGWO, was presented in [38], wherein a reservoir is used in this strategy to keep the ND options. Currently, in another work, a MOQBHHO method for identifying needed aspects affecting different diseases, has been introduced [39]. Authors additionally demonstrated the efficacy of the suggested strategy by matching its findings to those of deep-based AE and TSFS. In [40], a bi-objective FOA was proposed for handling the FS challenge. Several of the latest published articles [41,42,43] have focused on fixing the FS problem and improving the classifier’s variables at the same time. For more on multi-objective FS approaches, one can refer to [20,44,45,46,47,48,49,50].

To tackle the FS challenge, many variants of genetic algorithms (GA) have been suggested. Chromosomes are binary in primitive form; when a feature is chosen, the associated gene value is 1; otherwise, it is 0 [1]. In addition, a hybrid wrapper-embedded strategy to handle the FS problem is proposed in [29], wherein the proposed algorithm aims to carry out feature selection and create the prediction model by using the novel chromosomal expression technique at the same time. A hybrid technique combining the PSO algorithm and local search is presented in [51]. Local search is used in this research to choose the fewest and most differentiating criteria while also directing the PSO search. Finally, the authors of [52] developed a new strategy for particle initialization and updating to improve the performance of PSO in FS.

2.3.3. Hybrid Filter-Wrapper FS Techniques

Studies in the last few years have shown that merging the filter with the wrapper technique can produce outstanding results, as in [53], where two filter and one wrapper criteria are handled by multi-objective GA. With mutual information as filter fitness, a new multi-objective GWO for FS is proposed in [54], and the generated solutions are enhanced toward higher classification results by the use of wrapper fitness. In another similar work [55], a hybrid bat algorithm (BA) based on MI and naive Bayes, called BAMI, is introduced. A strategy based on filter-GA for FS, known as the GAFFS technique, has been presented in [56]. Information gain, gain ratio, ReliefF, chi-square, and correlation feature selector were chosen for selecting the most promising attributes from real-world datasets. To pick the most relevant features, GA is then applied with chromosomal fitness measured by using the KNN classifier’s classification accuracy. By using the whale optimization technique (WOA), a new hybrid filter-wrapper FS solution is suggested in [57]. This technique is a multi-objective one that optimizes both filter and wrapper fitness in a concurrent way. The effectiveness of this approach is proved on twelve standard datasets by a thorough evaluation with seven popular algorithms.

Though many researchers have assumed their approach to be multi-objective, this implies that the optimization procedure is simultaneously taking place, but the FS is still limited to one objective task as they optimize the objective functions sequentially during the filter and wrapper stages, respectively.

3. Proposed Techniques

As per the study in the previous part, the discrete form of AGTO to fix Boolean optimization jobs like FS has not been entrenched so far. Moreover, there has been no proposal to use AGTO as a SOP or MOP to address FS. There is an initiatory distinct AGTO in this section, which tried to address the FS challenge in medical data quarry by taking into account both the SOP and MOP aspects of the problem. Specifically, the four proposed variants of DAGTO differ in the number and types of objective functions used. Therefore, for clear understanding, we have divided the proposed techniques into two main categories, which are single-objective DAGTO (SO-DAGTO) and multi-objective DAGTOs (MO-DAGTO1, MO-DAGTO2, and MO-DAGTO3). The original AGTO was employed for solving continuous optimization tasks [10]. However, FS is treated as a discrete optimization problem and therefore, the following modifications to the various steps are required. The details of all the proposed variants are given in the following subsections.

3.1. Single-Objective DAGTO (SO-DAGTO)

• Steps of Single-objective DAGTO: The step-by-step procedure for single-objective DAGTO is given below:

  (a)

  Step 1: Gorilla initialization based on MI: The goal of FS is to get rid of features that are not needed. During initialization of the gorilla, the insignificant features should have fewer chances to participate in the optimization process and reducing the gorilla’s search space. The MI, which is more sensitive to non-linear dependency, is used in this paper to quantify the amount of information shared between two variables (e.g., feature and class attribute). It is expressed as

  $$MI(f_i,class)=H\left(f_i\right)-H\left(f_i\right|class),$$

  (14)

  where $H\left(f_i\right)$ is the entropy for $f_i$ and $H\left(f_i\right|class)$ is the conditional entropy for $f_i$ given $class$. The greater the MI value of a feature $f_i$, the more important it is, and the more likely it is to be picked up as an initial selection. Based on this concept, we define a probability to determine the likelihood of a feature being picked up by an initial gorilla. It is defined as

  $$pro{b}_i=\frac{MI(f_i,class)}{max\left(MI(f_k,class)\right)},wherek=1,2,\dots ,L.$$

  (15)

  Furthermore, the greater the MI value of a feature, the higher the feature’s likelihood. A gorilla is created based on the likelihood of $pro{b}_i$ by selecting its elements one by one from the entire feature set. As an example, the components of the ith gorilla, i.e., $P_i=(p_{i1},p_{i2},\dots ,p_{iL})$, are chosen in the following manner. Specifically, a feature will be selected for the gorilla,

  $$p_{ik}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}rnd<pro{b}_k\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

  (16)

  where $rnd$ is a random number between 0 and 1, and $pro{b}_k$ is the probability of the kth feature. We have used this initialization technique for $70\%$ of the gorilla population. The positions of the rest of the gorillas are randomly initialized to enhance the diversity of the population.

  (b)

  Step 2: Fitness Assessment: To assess the individual solution in wrapper FS, a fitness/objective function is necessary. Feature selection’s main purpose is to improve prediction accuracy while reducing the number of characteristics. More to the point, the objective function (OF), which includes both criteria, is used in this variant of the proposed work and is described as [58],

  $$OF\left(P\right)=\alpha ·classification\_error+(1-\alpha )·\frac{LS}{L},$$

  (17)

  where $classification\_error$ is the error rate of the learning algorithm, $LS$ is the size of the feature substring, L is the original dimension, and $\alpha$ (here $\alpha =0.99$) is a control parameter for the effect of classification performance and feature size.

  (c)

  Step 3: Gorilla Location Update: Each gorilla position is initially updated by using Equation (1) and it is denoted as $\Delta {p_i}^L(It+1)$. As FS is a discrete optimization issue, a sigmoid transfer function is applied here to transmute the original AGTO to DAGTO, i.e., to compute the probability value by using the following Equation (18),

  $$T(\Delta {p_i}^L(It+1))=sigmoid(\Delta {p_i}^L(It+1))=\frac{1}{1+e^{-2\Delta {p_i}^L(It+1)}}.$$

  (18)

  Then, each candidate gorilla location is calculated in the discrete domain by using the following Equation (19),

  $${p_i}^L(It+1)=\left\{\begin{array}{cc}1,\hfill & rnd<T(\Delta {p_i}^L(It+1))\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

  (19)

  where i is the ith bit of the gorilla’s position, L is the true dimension and $rnd$ is a random number in the range $[0,1]$. In following, each candidate gorilla is evaluated by using the fitness function given in Equation (17) and if new locations are found to be better than the older ones, then the corresponding replacement occurs. As a next step, a “silverback” solution is chosen, which is the best option for the updated population to continue the exploitation phase. In this stage, depending on the value of C and W described in Section 2.1.2, Equations (7) and (10) are used to alter the location of individual gorillas in the population. More to the point, the continuous location space is converted to a discrete one by employing the above Equation (19). If an updated gorilla position is found to be fitter than the existing one, it will be replaced.

  (d)

  Step 4: Finding Silverback: At the completion of every repetition, the fittest alternative (the one having a minimum $OF$ value) is treated as a temporary silverback solution. As a result, it is compared with the older silverback and if it is found to be better, it replaces the existing one, otherwise not.

• Algorithm for Single-objective DAGTO for FS: The detailed algorithm for the proposed single-objective DAGTO is given in Algorithm 1. There, in line 8, the exploration phase starts, while in line 14, the group is created. Furthermore, in line 18 the exploitation phase is taking place, whereas the corresponding group is created in line 26.

  Algorithm 1 Single-objective DAGTO for FS

  1: input Population size N, maximum number of iterations $maxIt$ and parameters $\beta$ and p 2: output The $silverback$ and its $OF$ value 3: Set the initial gorilla location $P_i(i=1,2,\dots ,N)$ as given in Section 3.1 4: Compute the $OF$ of each gorilla $P_i$ 5: for$COUNT\leftarrow 1$ to $maxIt$ do 6:    Alter the C using Equation (2) 7:    Alter the L using Equation (4) 8:    for all Gorilla $P_i$ do 9:       Alter the gorilla location by Equation (1) 10:     Apply sigmoid to convert the gorilla location into probability figure 11:     Compute candidate gorilla position in discrete domain using Equation (19) 12:   end for 13:   for $i\leftarrow 1$ to N do 14:      Compute $OF$ of each candidate gorilla ($G_i$) 15:      If $G_i$ is fitter than $P_i$, replace it, where G is the candidate Gorilla location 16:   end for 17:   Set best location as the Silverback 18:   for all Gorilla $P_i$ do 19:       if $C\ge W$ then 20:           Alter the Gorilla location employing Equations (7) and (19) 21:       else 22:           Alter the Gorilla position applying Equations (10) and (19) 23:      end if 24:   end for 25:   for $i\leftarrow 1$ to N do 26:      Compute $OF$ of each candidate gorilla ($G_i$) 27:      If $G_i$ is fitter than $P_i$, replace it, where G is the candidate Gorilla location 28:   end for 29:   Set best location as the Silverback 30: end for

• Complexity Analysis: The computational complexity of single-objective DAGTO for FS depends on three important steps: initialization, $OF$ evaluation, and update of the gorilla location. The initialization of gorilla, as explained in Section 3.1, requires $O(N·L)$ basic operations, and the evaluation of all gorillas needs the calculation of $OF$ and N. The complexity of the position update procedure depends on both exploration and exploitation stages. In each case, an update operation is executed on all the gorilla solutions, and the fittest one is selected, requiring
  $O(maxIt·N)+O(maxIt·N·L)·2$.
  Thus, the total computational complexity of single-objective DAGTO is
  $O(N·L)+N·\left[O\right(L)+O(Q·L\left)\right]+O(maxIt·N)+O(maxIt·N·L)·2$, where Q is the number of samples in the training dataset and the computational complexity of KNN model on Q samples is $O(Q·L)$.

3.2. Multi-Objective DAGTOs (MO-DAGTO1, MO-DAGTO2, and MO-DAGTO3)

• Steps of Multi-objective DAGTOs: The step-by-step procedure of the proposed MO-DAGTOs is illustrated in Figure 2 and the three different cases are elaborated upon below.
  

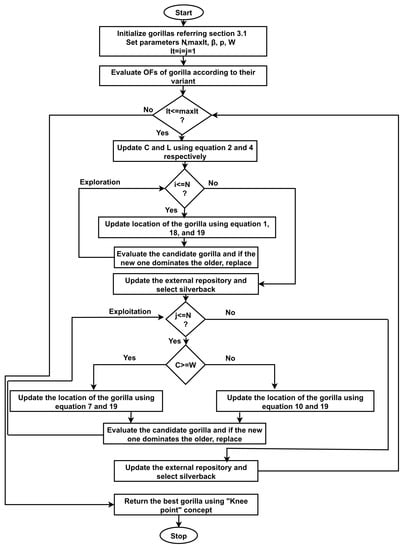  Figure 2. Steps of MO-DAGTOs.

  (a)

  Step 1: Gorilla Initialization based on MI: For all these three variants of the proposed multi-objective DAGTO, the exact same population initialization strategy, based on MI, is followed as described in Section 3.1.

  (b)

  Step 2: Fitness Assessment:

  • MO-DAGTO1: This first variant treats FS as a two-objective discrete optimization task whose intention is to reduce the feature dimension and simultaneously improve the classification efficiency. Therefore, each gorilla in the population is assessed by employing the following two $OF$s [48],

    $$OF1\left(P\right)=\sum _{j=1}^L{p}_j,if{p}_j=1,$$

    (20)

    where P is the location string of a gorilla with length L.

    $$OF2\left(P\right)=ClassificationAccuracy$$

    (21)
  • MO-DAGTO2: This second variant considers FS as a two-criteria hybrid filter wrapper optimization challenge. The sole aim of FS is to shrink the number of attributes along with the classification error. Thus, the first objective function is formulated by using Equation (22) [58],

    $$OF1\left(P\right)=\alpha ·classification\_error+\left(1-\alpha \right)·\frac{LS}{L},$$

    (22)

    where

    $$classification\_error=\frac{\#\mathrm{Wrongly}\mathrm{Predicted}\mathrm{Samples}}{\#\mathrm{Total}\mathrm{Samples}}$$

    (23)

    and $LS$ is the length of the feature substring, L is the total feature_count, and $\alpha$ is a controlling parameter, as already mentioned.
    In order to select the appropriate characteristics, one must look for a group of features that collectively have the most relevance to the target and the least redundancy among themselves. Therefore, the maximum of the correlation among the attribute substring, the target attribute and the reduction of the dependency between the characteristics in an attribute substring are normally emphasised for FS purposes. MI as well as the Pearson correlation coefficient (PCC) are typical characteristics of relevance or interdependency. This motivated us to formulate the second objective function by using Equation (24) [23], which we aim to maximize,

    $$OF2\left(P\right)=\frac{1}{LS}\sum MI\left(f_i,class\right)·\frac{1}{LS}\sum PCC\left(f_i,class\right),$$

    (24)

    where $f_i$ are the discrete characteristics present in the feature subgroup and $class$ is a class attribute.
  • MO-DAGTO3: When two characteristics are highly linked, removing one does not have a significant impact on the prediction strength of the other. As a result, unnecessary characteristics can be removed by reducing their interdependence. Therefore, this variant treats FS as a tri-objective hybrid filter-wrapper optimization task, wherein the first two $OF$s are the same as in MO-DAGTO2, and the third $OF$ is calculated as

    $$OF3\left(P\right)=\frac{1}{{\left|LS\right|}^2}\sum MI(f_i,f_j)·\frac{1}{{\left|LS\right|}^2}\sum \left|PCC(f_i,f_j)\right|.$$

    (25)
    $OF3$ measures both linear and non-linear dependence between variables in a feature space in this case. As a result, reducing $OF3$ may result in a redundancy reduction.

  (c)

  Step 3: Repository Maintenance: After the exploration and exploitation phases of the proposed variants, an external storehouse is needed to keep all the non-dominated (ND) solutions so far because any multi-objective approach outputs a set of Pareto solutions rather than one. When inserting a new ND solution $N{A}_{new}$ into the external repository, the following situations may arise and the following actions should be taken.

  • If the $N{A}_{new}$ is dominated by any member of the external repository, then it is discarded.
  • If any existing member of the repository is dominated by the new one, then $N{A}_{new}$ will replace that solution.
  • Insert $N{A}_{new}$ into the external repository if $N{A}_{new}$ and the archive members are not dominating each other, i.e., they are all non-dominated solutions, and the repository capacity is greater than the current repository size.
  • If neither $N{A}_{new}$ nor the current repository solutions are dominated, but the repository overflows, throw any solution from the most gathered region and then push $N{A}_{new}$ to the archive [48].

  The pictorial representation of repository update is illustrated in Figure 3.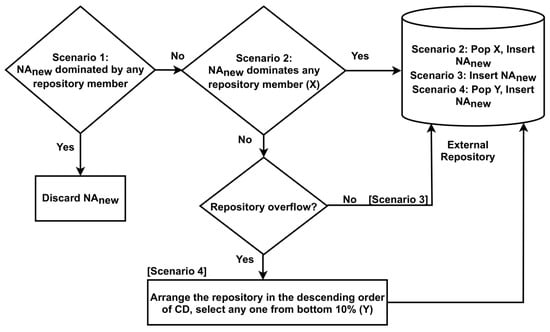

  

  Figure 3. Repository update for MO-DAGTOs.

  (d)

  Step 4: Gorilla Location Update: Each gorilla position is first updated by using Equation (1), and it can be denoted as $\Delta {p_i}^L(It+1)$. As FS is a discrete optimization issue, a sigmoid transfer function is applied here to convert the original AGTO to DAGTO, i.e., to compute the probability value by using Equation (18). Then each candidate gorilla location is calculated in the discrete domain by using Equation (19). After that, each candidate gorilla is evaluated by using the objective functions according to their variants, and if the older gorilla location is dominated by the new location, then the corresponding replacement occurs. As the MO-DAGTO1, MO-DAGTO2, and MO-DAGTO3 are all under the category of multi-objective optimization problems, a solution $A1$ is considered better than another solution $A2$ if $A1$ is not dominated by $A2$ as explained in Section 2.2. Then, a silverback solution is chosen, which is the best solution for the updated population to continue the exploitation phase. A silverback is picked from the top $10\%$ of the reservoir, which is arranged in decreasing order of $CD$, during the exploration and exploitation process. As a result, selecting a solution from the front of the repository implies the selection of the best option from the unique solution existing in the less populated region. In the exploitation phase, depending on the value of C and W described in Section 2.1.2, Equations (7) and (10) are used to twist the location of individual gorillas in the population. As a result, the continuous location space is converted to a discrete one by employing Equation (19). If an updated gorilla position dominates the existing one, it will be replaced.

  (e)

  Step 5: Returning the Best Solution by using the Concept of Knee: The external repository contains all the solutions that are not mutually dominated after the given number of iterations maxIt. As a screening method, the “knee point” concept is utilized here to pick an optimum combination of features from a group of non-dominated ones [59,60].

• Complexity Analysis: The initialization and fitness computation of gorillas, as explained in Section 3.1 for single-objective DAGTO, requires $O(N·L)+N·\left[O\right(L)+O(Q·L\left)\right]$. During each iteration, the position update, the fitness calculation, the finding of non-dominated solutions, and the selection of silverback operations are performed twice, one for exploration and another for exploitation phase. Mathematically, this can be calculated as:

  $$\begin{array}{c}O\left(positionupdate\right)+O\left(fitnesscalculation\right)+O\left(findingNDsolutions\right)+O\left(selectingsilverback\right)=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} maxIt·[2·[O(N·L)+N·\left[O\right(L)+O(Q·L)+O(C·N·logN)+O(C·N·logN\left)\right]\left]\right].\hfill \end{array}$$

  (26)
  Here, we have used the idea of a dominance tree for extracting the Pareto solutions, which reduces the number of comparisons, causing a complexity of $O(C·N·logN)$. To find the silverback, the repository needs to be arranged on the basis of decreasing $CD$ values, which requires $O(C·N·logN)$. The final output of multi-objective DAGTO is the best of the repository and it is chosen as the knee point in the Pareto front. The complexity of calculating the knee point (assuming the case when all N solutions are in the repository) is $O\left(N\right)$. Finally, the time complexity of the proposed multi-objective techniques can be expressed as

  $$\begin{array}{c}O(Multi-objectiveDAGTOsforFS)=O(N·L)+N·\left[O\right(L)+O(Q·L\left)\right]+\hfill \\ maxIt·[2·[O(N·L)+N·\left[O\right(L)+O(Q·L)+O(C·N·logN)+O(C·N·logN\left)\right]\left]\right]+O\left(N\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \simeq O\left(NlogN\right).\hfill \end{array}$$

  (27)

4. Setup for the Experiments

4.1. Datasets

The evaluation of all the DAGTO variants is tested by taking seven standard medical datasets of varied width from UCI and three microarray cancer datasets [61]. The details of each dataset are depicted in Table 1. In this study, a KNN classifier with a k value equal to 5 is used to determine the classification accuracy on normalized data.

Table 1. Datasets.

SID	Name	#Samples	#Characteristics	#Target Labels
D1	Lymphography	148	18	3
D2	Diabetic	1151	19	2
D3	Cardiotocography	2126	21	3
D4	Cervical Cancer	858	35	2
D5	Lung Cancer	32	56	3
D6	Arrhythmia	452	279	16
D7	Parkinson	756	754	2
D8	Colon Tumor	62	2000	2
D9	SRBCT	83	2308	4
D10	Leukemia	72	7129	2

4.2. Benchmark Methods and Performance Criteria for Comparison

The performance of the proposed single-objective DAGTO is compared with three standard methods; these are HLBDA [62], BSHO [63], and QBHHO [58]. In this study, the mean fitness value, the average accuracy, the average feature size [58], and the average execution time are used as evaluation criteria. Similarly, the performance of the best multi-objective DAGTO is checked with four other benchmark multi-objective FS techniques, namely NSGA-II [64], BMOFOA [40], FW-GPAWOA [57], and BMOChOA [65]. The four very popular multi-objective performance indicators, which are IGD, HV, Spread, and SCC [65], are used to compare the efficiency of the multi-objective FS techniques to solve feature selection jobs in healthcare data. A population size of 20 and 100 iterations are set in all algorithms to have a fair assessment. Each dataset was subjected to a total of 20 separate runs of each method, and they were implemented in Python $3.7$ on an Intel Core i3-7020U CPU @ $2.30$ GHz and a $4.00$ GB RAM machine. This setup concerns the evaluation of both experiments presented in Section 5 and Section 7.

4.3. Parameter Settings

The user-defined parameter values for implementing all the above-mentioned single-objective and multi-objective approaches are listed in Table 2. The KNN method with $k=5$ and 10-fold cross validation is used to grade the subset of identified factors. The KNN approach has a lower algorithmic expense, resulting thus in a lower overall overhead of the wrapper technique.

Table 2. Parameter values.

Approaches	Parameters	Values
Single objective (Population Size = 20, Maximum Number of Iterations = 100)
HLBDA	pl	0.4
	dl	0.7
BSHO	$\overrightarrow{h}$	[5, 0]
	M	[0.5, 1]
	$\lambda$	0.99
	$\omega$	0.01
QBHHO	$\alpha$	0.99
Single-objective DAGTO	$\beta$	3
	W	0.8
	p	0.03
Multi objective (Population Size = 20, Maximum Number of Iterations = 100, Repository Size = 50)
NSGA-II	Crossover rate (CR)	0.8
	Mutation rate (MR)	0.01
BMOFOA	Transfer rate	10%
	Lifetime	20
	LSC	2
	GSC	7
BMOChOA	Chaotic map	Tent
Multi-objective DAGTOs	$\beta$	3
	W	0.8
	p	0.03

4.4. Design of Experiments

In this section, a list of nine experiments utilized in this research is discussed. All the experiments are conducted for each of the ten aforementioned datasets.

• Single-objective DAGTO
  • Experiment 1: Performance comparison of the proposed single-objective DAGTO with other benchmark methods, like HLBDA, BSHO, and QBHHO.
  • Experiment 2: Convergence analysis of all the four single-objective FS approaches.
  • Experiment 3: Implementation of a Wilcoxon signed rank test to prove the superiority of the proposed approach.
• Multi-objective DAGTOs
  • Experiment 4: Performance comparison between all the proposed multi-objective DAGTO variants using the multi-objective performance indicators discussed in Section 4.2.
  • Experiment 5: Conduct of a Wilcoxon signed rank test on hyper volume (HV) to verify the efficiency of the best variant out of three.
  • Experiment 6: Performance comparison between best variants of multi-objective DAGTO and four well-known multi-objective FS techniques using average feature size and average classification accuracy for equitable and fair comparison.
  • Experiment 7: Conduct of a Wilcoxon signed rank test on HV to verify the significance of the proposed approach with respect to the others (NSGA-II, BMOFOA, BMOChOA, and FW-GPAWOA).
  • Experiment 8: Execution time comparison.
  • Experiment 9: Comparison between the proposed SO-DAGTO and the best of the MO-DAGTOs, which is proven to be MO-DAGTO2.

5. Experimental Results and Discussion

5.1. Single-Objective DAGTO

5.1.1. Experiment 1

This section compares the proposed single-objective DAGTO to three well-known algorithms, namely HLBDA [62], BSHO [63], and QBHHO [58]. Three performance assessment metrics are computed to assess the efficiency of single-objective DAGTO. These measures are the mean fitness value, the average classification accuracy, and the average feature substring length. Each approach is executed 20 times due to the stochastic nature of the optimization procedure. Concretely, after 20 separate runs, the averages of the findings are gathered and reposed in Table 3. Table 3 shows that the proposed SO-DAGTO correctly predicted the optimal mean fitness values on eight out of ten datasets. SO-DAGTO consistently outperformed other methods both in finding the optimal feature subset in four datasets and in finding the optimal feature subset because they gave slightly higher average accuracy in the remaining six datasets with a large difference in the number of selected features. For example, the BSHO produces $0.3\%$ better accuracy at the cost of 7 extra features in the Lymphography dataset. Similarly, for datasets such as Cervical Cancer, Arrhythmia, SRBCT, and Leukemia, the presented single-objective DAGTO is able to choose fewer but more significant components causing the diseases.

Table 3. Performance comparison of single-objective FS methods.

Datasets	Criteria	SO-DAGTO	HLBDA	BSHO	QBHHO
Lymphography	Mean_fitness	0.184	0.197	0.2	0.201
	Avg_accuracy	0.813	0.804	0.816	0.816
	Avg_feature_size	6.66	7	13	13.33
	Avg_execution time (min)	5.01	4.78	5.02	4.56
Diabetic	Mean_fitness	0.307	0.33	0.324	0.318
	Avg_accuracy	0.689	0.686	0.7	0.649
	Avg_feature_size	7	7	9.6	6
	Avg_execution time (min)	8.02	8.13	7.86	7.73
Cardiotocography	Mean_fitness	0.091	0.104	0.097	0.101
	Avg_accuracy	0.924	0.908	0.915	0.91
	Avg_feature_size	8	8	7	11
	Avg_execution time (min)	11.01	10.97	11.06	10.96
Cervical Cancer	Mean_fitness	0.048	0.058	0.058	0.059
	Avg_accuracy	0.956	0.968	0.945	0.953
	Avg_feature_size	6	12	13.6	12
	Avg_execution time (min)	5.12	4.89	5.05	5.02
Lung Cancer	Mean_fitness	0.36	0.384	0.397	0.354
	Avg_accuracy	0.65	0.63	0.618	0.643
	Avg_feature_size	22	42.1	28	13
	Avg_execution time (min)	2.00	2.02	3.19	2.00
Arrhythmia	Mean_fitness	0.344	0.366	0.38	0.377
	Avg_accuracy	0.629	0.624	0.606	0.611
	Avg_feature_size	61	131	108	105
	Avg_execution time (min)	5.79	5.43	5.87	5.38
Parkinson	Mean_fitness	0.12	0.132	0.132	0.123
	Avg_accuracy	0.89	0.878	0.88	0.887
	Avg_feature_size	255.23	251.3	248	271.34
	Avg_execution time (min)	10.32	11.01	10.87	10.12
Colon Tumor	Mean_fitness	0.159	0.161	0.176	0.17
	Avg_accuracy	0.84	0.855	0.838	0.838
	Avg_feature_size	962	1000.3	1129	850.4
	Avg_execution time (min)	9.53	9.68	9.46	9.48
SRBCT	Mean_fitness	0.117	0.124	0.146	0.137
	Avg_accuracy	0.878	0.883	0.864	0.867
	Avg_feature_size	654	754	804	976
	Avg_execution time (min)	13.22	13.75	12.89	12.38
Leukemia	Mean_fitness	0.139	0.1424	0.125	0.135
	Avg_accuracy	0.862	0.86	0.887	0.87
	Avg_feature_size	1811	3201	2003.87	1991.13
	Avg_execution time (min)	28.04	26.87	27.09	26.49

5.1.2. Experiment 2

Figure 4 illustrates the convergence curves for each of the four single-objective FS methods on 10 different datasets. When it comes to determining the best feature subset, the suggested DAGTO outperformed other approaches because of its superior convergence behaviour due to the excellent gorilla initialization technique based on label MI. For example, DAGTO is capable of converging more quickly and deeper to identify the global optimum by using the datasets of Lymphography, Diabetic, Cardiotocography, Cervical Cancer, Arrhythmia, Parkinson, and Colon Tumor because GTO’s capacity to discover and utilize the search space is quite excellent and exceptional. The results clearly depict the advantages of the suggested DAGTO in all dimensions of the FS challenges.

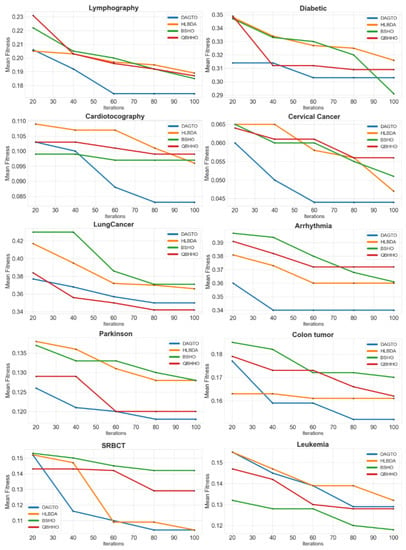
Figure 4. Convergence curves of single-objective FS methods.

5.1.3. Experiment 3

The Wilcoxon signed rank test [58] is used in this study to do pairwise comparisons of data. In this statistical test, if the p-value is greater than $0.05$, then the performance of the two approaches is determined to be comparable, i.e., =; otherwise, the two methods are substantially different in the comparison, i.e., + in positive significance and − in negative significance). The Wilcoxon test findings on the mean fitness values of SO-DAGTO with other approaches are given in Table 4. The suggested SO-DAGTO achieved much lower mean fitness value than its rivals in the majority of circumstances.

Table 4. Wilcoxon signed rank test results of SO-DAGTO vs. others.

Datasets	SO-DAGTO vs. HLBDA	SO-DAGTO vs. BSHO	SO-DAGTO vs. QBHHO
Lymphography	=	+	+
Diabetic	=	+	+
Cardiotocography	+	=	+
Cervical Cancer	+	+	+
Lung Cancer	+	+	−
Arrhythmia	+	+	+
Parkinson	+	+	=
Colon Tumor	=	+	+
SRBCT	+	+	+
Leukemia	+	−	−

5.2. Multi-Objective DAGTOs

In each of the 20 separate runs, all the multi-objective FS techniques yield distinct subsets of non-dominated traits for each dataset. For comparison, the feature subsets offered by each technique are unified into one set. The non-dominated solutions are chosen as the best Pareto fronts from this group and in following, they are compared. To present an equitable comparison between the best results of all the four multi-objective approaches, we have taken the number of features and the corresponding classification accuracy values irrespective of the objective functions taken by them.

5.2.1. Experiment 4

In this experiment, the performance of the three proposed MO-DAGTOs are compared and verified in terms of the average accuracy, and the average feature size; to assess the quality of the Pareto front, the HV along with the number of Pareto solutions are used. The goal of HV is to find the portion of the objective plane that is bordered by the Pareto front and a reference point r [66]. Because it can measure both convergence and diversity of the solutions, this indicator is commonly used to compare multi-objective optimization techniques. Table 5 enlists the value of average accuracy, average feature size, average HV, and average number of Pareto solutions produced by each of the three MO-DAGTOs from 20 runs for each dataset. For the Lymphography, Diabetic, Cervical Cancer, SRBCT, and Leukemia datasets, the MO-DAGTO2 achieves the highest average classification accuracy with a satisfactory number of features as compared to the other two. On the other hand, the MO-DAGTO1 performs well in predicting the most relevant features in the cases of Cardiotocography, Lung Cancer and Colon Tumor datasets. Regarding Arrhythmia and Parkinson datasets, MO-DAGTO3 proved its efficiency in the FS task. From Table 5, it can be derived that the HV of the obtained Pareto fronts by MO-DGATO2 is more than the corresponding of MO-DAGTO1 and MO-DAGTO3 for nine out of ten datasets indicating the higher convergence speed and diverged solutions. For most of the datasets, the MO-DAGTO3 contains more number of solutions in its Pareto front because it optimizes three criteria at a time and the amount of alternatives increases with the increase of number of objective functions.

Table 5. Performance comparison among MO-DAGTOs.

Datasets	Methods	Avg_Accuracy	Avg_Feature_Size	HV	#Pareto Solutions
Lymphography	MO-DAGTO1	0.824	3	0.204	2
	MO-DAGTO2	0.825	4	0.384	5
	MO-DAGTO3	0.81	5.5	0.178	6
Diabetic	MO-DAGTO1	0.673	2	0.1	1
	MO-DAGTO2	0.7	3.5	0.241	4
	MO-DAGTO3	0.69	4.25	0.245	4
Cardiotocography	MO-DAGTO1	0.904	5.14	0.15	7
	MO-DAGTO2	0.902	3.5	0.242	4
	MO-DAGTO3	0.846	6.77	0.121	9
Cervical Cancer	MO-DAGTO1	0.962	3	0.292	3
	MO-DAGTO2	0.963	9	0.493	2
	MO-DAGTO3	0.96	4.66	0.318	3
Lung Cancer	MO-DAGTO1	0.675	2	0.1	1
	MO-DAGTO2	0.592	2.5	0.368	2
	MO-DAGTO3	0.575	2.25	0.226	4
Arrhythmia	MO-DAGTO1	0.62	3	0.297	3
	MO-DAGTO2	0.623	3	0.314	3
	MO-DAGTO3	0.64	4.88	0.117	9
Parkinson	MO-DAGTO1	0.84	5	0.15	7
	MO-DAGTO2	0.846	62	0.363	18
	MO-DAGTO3	0.86	6.33	0.122	9
Colon Tumor	MO-DAGTO1	0.85	123	0.1	1
	MO-DAGTO2	0.8	236.2	0.393	4
	MO-DAGTO3	0.81	956.85	0.144	7
SRBCT	MO-DAGTO1	0.69	151.14	0.177	7
	MO-DAGTO2	0.903	92.33	0.305	3
	MO-DAGTO3	0.67	1026.22	0.122	9
Leukemia	MO-DAGTO1	0.81	174.25	0.275	4
	MO-DAGTO2	0.872	964	0.305	3
	MO-DAGTO3	0.83	941.28	0.163	7

5.2.2. Experiment 5

Previous experiment 4 reveals that the overall performance of the MO-DAGTO2 is better than that of the MO-DAGTO1 and MO-DAGTO3. Therefore, in this experiment, we have applied the Wilcoxon signed rank test to statistically prove the excellency of MO-DAGTO2 over others. Based on the acquired testing Pareto fronts, 20 HVs are computed for each of the three variations across the 20 separate runs, and in following the Wilcoxon test ($\alpha =0.05$) is used to check if there is a substantial difference between the approaches by examining the hypotheses listed below.

• Null hypothesis (p-value > $\alpha$): performance of MO-DAGTO2 is similar “=” to that of MO-DAGTO1 and MO-DAGTO3.
• Alternative hypothesis (p-value < $\alpha$): performance of MO-DAGTO2 is significantly superior “+” (or inferior “−”) to that of MO-DAGTO1 and MO-DAGTO3.

Table 6 depicts that the HV metrics produced by MO-DAGTO2 are substantially better than those generated by MO-DAGTO3 for nine datasets and markedly worse for one dataset, whereas the improved efficiency of the introduced MO-DAGTO2 method is more clear when compared to MO-DAGTO1. MO-DAGTO2 produces similar or considerably better outcomes than its competitors in 19 of the 20 p-values (2 methods, 10 datasets), and it obtains significantly poorer performance in just one of the 20 p-values.

Table 6. Wilcoxon test results for MO-DAGTO1, MO-DAGTO2, and MO-DAGTO3.

MO-DAGTO2 vs.	MO-DAGTO1		MO-DAGTO3
	$\mathit{p}$-Value	Significance	$\mathit{p}$-Value	Significance
Lymphography	3.870 × 10${}^{-3}$	+	2.671 × 10${}^{-2}$	+
Diabetic	2.432 × 10${}^{-4}$	+	4.270 × 10${}^{-2}$	−
Cardiotocography	1.520 × 10${}^{-2}$	+	1.113 × 10${}^{-2}$	+
Cervical Cancer	4.890 × 10${}^{-4}$	+	7.564 × 10${}^{-5}$	+
Lung Cancer	2.980 × 10${}^{-2}$	+	4.867 × 10${}^{-3}$	+
Arrhythmia	0.071	=	3.560 × 10${}^{-3}$	+
Parkinson	4.983 × 10${}^{-5}$	+	6.480 × 10${}^{-5}$	+
Colon Tumor	3.591 × 10${}^{-2}$	+	4.238 × 10${}^{-3}$	+
SRBCT	5.390 × 10${}^{-5}$	+	6.123 × 10${}^{-5}$	+
Leukemia	0.068	=	4.219 × 10${}^{-3}$	+

5.2.3. Experiment 6

In experiment 5, we found that MO-DAGTO2 is superior as compared to MO-DAGTO1 and MO-DAGTO3 in producing better Pareto fronts in the majority of the datasets. Therefore, in this experiment, we have compared the performance results of MO-DAGTO2 with those of four other benchmark multi-objective FS strategies, namely NSGA-II, BMOFOA, BMOChOA, and FW-GPAWOA. For each dataset, Table 7 enlists the value of average classification accuracy, average feature size, and four multi-objective performance indicators (IGD, HV, Spread, and SCC) as described in Section 4.2, for all the five multi-objective FS approaches. The entries of Table 7 indicate that the HV values of the Pareto fronts generated by MO-DAGTO2 for eight (Lymphography, Cardiotocography, Cervical Cancer, Lung Cancer, Arrhythmia, Parkinson, Colon Tumor, and Leukemia) out of ten datasets are high as compared to others. Moreover, the IGD and Spread values are quite satisfactory in case of MO-DAGTO2, proving its efficiency in producing a Pareto front that is closer to the actual Pareto front and that covers a larger area in the objective plane. This excellence may be due to the efficient gorilla initialization strategy proposed in this research. The high SCC value entries by MO-DAGTO2 for most of the datasets reveals that the number of common elements between actual Pareto fronts and the calculated Pareto fronts by MO-DAGTO2 is greater than that of the other four techniques.

Table 7. Performance comparison among MO-DAGTO2 with benchmark methods.

Datasets	Methods	Avg_Acc	Avg_Feature_Size	IGD	HV	Spread	SCC
Lymphography	NSGA-II	0.823	7.16	0.088	0.178	0.695	0
	BMOFOA	0.795	3.75	0.028	0.245	0.658	0
	BMOChOA	0.812	6.66	0.102	0.334	0.961	0
	FW-GPAWOA	0.789	3	0.091	0.301	0.724	1
	MO-DAGTO2	0.825	4	0.264	0.384	0.845	3
Diabetic	NSGA-II	0.658	3.75	0.073	0.254	0.786	0
	BMOFOA	0.629	4.66	0.148	0.312	0.845	0
	BMOChOA	0.688	2	1.179	0.1	0	1
	FW-GPAWOA	0.689	3.33	0.177	0.3	0.78	0
	MO-DAGTO2	0.7	3.5	0.084	0.241	0.667	3
Cardiotocography	NSGA-II	0.864	7.6	0.022	0.201	0.62	0
	BMOFOA	0.875	5.8	0.024	0.199	0.592	0
	BMOChOA	0.868	4.6	0.015	0.204	0.734	0
	FW-GPAWOA	0.89	6.25	0.091	0.134	0.58	0
	MO-DAGTO2	0.902	3.5	0.055	0.242	0.677	2
Cervical Cancer	NSGA-II	0.952	10.42	0.269	0.152	0.581	0
	BMOFOA	0.951	4	0.189	0.201	0.642	0
	BMOChOA	0.961	4.33	0.073	0.315	0.786	0
	FW-GPAWOA	0.962	2	0.159	0.255	0	1
	MO-DAGTO2	0.963	9	0.257	0.493	1.248	1
Lung Cancer	NSGA-II	0.473	19.5	1.114	0.199	0.569	0
	BMOFOA	0.464	18.6	1.039	0.238	0.639	0
	BMOChOA	0.597	10	0.895	0.29	0.548	0
	FW-GPAWOA	0.545	2.5	0.631	0.353	0.668	0
	MO-DAGTO2	0.592	2.5	0.592	0.368	0.808	0
Arrhythmia	NSGA-II	0.63	126.5	0.118	0.222	0.375	0
	BMOFOA	0.664	84	0.121	0.219	0.329	0
	BMOChOA	0.619	122.33	0.227	0.162	0.316	0
	FW-GPAWOA	0.664	5.125	0.255	0.135	0.578	0
	MO-DAGTO2	0.623	3	0.015	0.314	0.756	1
Parkinson	NSGA-II	0.811	346.4	0.036	0.111	0.195	0
	BMOFOA	0.835	300.33	0.308	0.26	0.199	0
	BMOChOA	0.802	109.875	0.046	0.139	0.834	0
	FW-GPAWOA	0.83	25.4	0.023	0.114	0.869	0
	MO-DAGTO2	0.85	62.55	0.055	0.363	0.585	0
Colon Tumor	NSGA-II	0.835	966	0.307	0.22	0.26	0
	BMOFOA	0.784	438.5	0.472	0.167	0.769	0
	BMOChOA	0.839	896.33	0.396	0.265	0.212	1
	FW-GPAWOA	0.822	633.2	0.136	0.215	0.761	0
	MO-DAGTO2	0.8	236.2	0.06	0.393	1.427	4
SRBCT	NSGA-II	0.722	1111.286	0.121	0.145	0.237	0
	BMOFOA	0.745	209	0.093	0.227	1.081	2
	BMOChOA	0.864	299.5	0.451	0.408	0.947	0
	FW-GPAWOA	0.776	142.83	0.049	0.205	0.949	1
	MO-DAGTO2	0.903	92.33	0.27	0.305	0.904	3
Leukemia	NSGA-II	0.817	1371.714	0.048	0.162	0.893	2
	BMOFOA	0.855	1316.5	0.168	0.258	0.788	0
	BMOChOA	0.849	1454.2	0.116	0.213	0.941	0
	FW-GPAWOA	0.83	475.5	0.171	0.275	1.055	2
	MO-DAGTO2	0.872	964	0.28	0.305	0.832	2

The Pareto solutions of NSGA-II, BMOFOA, BMOChOA, FW-GPAWOA, and MO-DAGTO2 are illustrated in Figure 5. The average number of chosen characteristics is shown in the x direction of each plot, and the average classification accuracy is shown on the y axis. The actual dimension of each dataset along with its corresponding classification accuracy is depicted at the top of each plot. According to Figure 5, in nine out of ten datasets, we notice that the Pareto fronts obtained by MO-DAGTO2 dominate others. According to the graphical findings of Cervical Cancer dataset, the Pareto front of MO-DAGTO2 is marginally dominated by the fronts of NSGA-II, BMOFOA, and BMOChOA. We can also observe that the optimum Pareto front created by MO-DAGTO2 in nine datasets has solutions that pick fewer than half of the entire number of features and improves classification accuracy above that offered by using all attributes. For example, in the case of Lymphography, by selecting only $22\%$ of the original features on average, our approach was able to boost the accuracy from $79\%$ to $82.5\%$. Similarly, regarding the Cardiotocography dataset, by taking into consideration a reduced dataset with only $14\%$ of the actual dimension, the MO-DAGTO2 produces $5.2\%$ more accuracy. In the high dimensional datasets, MO-DAGTO2 enhances the classification accuracy from $64\%$ to $90.3\%$ considering only $4\%$ of the actual width in SRBCT and from $77.9\%$ to $87.2\%$ in the Leukemia dataset by taking only $13\%$ relevant features. In the case of the Lymphography, Diabetic, Cervical Cancer, Arrhythmia, Parkinson, SRBCT, and Leukemia datasets, the Pareto fronts of MO-DAGTO2 and FW-GPAWOA are very close to each other as they both are hybridization of wrapper and filter approaches, and they exhibit rapid convergence as compared to others. For Parkinson samples, when the number of features is between 2 and 94, the optimal front of FW-GPAWOA is present above the front of MO-DAGTO2. However, when the number of selected features increased above 94, the MO-DAGTO2 started performing well in the FS task. The performance of the BMOChOA is also quite satisfactory in executing the FS task in the Cervical Cancer and Leukemia datasets.

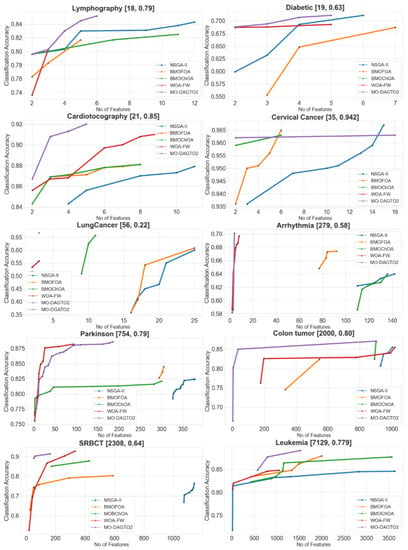
Figure 5. Number of features vs. classification accuracy of multi-objective FS methods.

5.2.4. Experiment 7

Table 8 presents the p-values of the Wilcoxon signed rank test on HV metrics for MO-DAGTO2 against NSGA-II, BMOFOA, BMOChOA, and FW-GPAWOA. For nine datasets, the HV metrics for MO-DAGTO2 are substantially better than those produced by NSGA-II, BMOFOA, and BMOChOA. They are similar for one dataset with NSGA-II (Diabetic) and BMOChOA (Lymphography), equivalent for three datasets with FW-GPAWOA (Diabetic, Lung Cancer, and Leukemia), and significantly worse for one dataset with BMOFOA (Diabetic), and BMOChOA (SRBCT). In general, for the 40 p-values (4 methods and 10 datasets), our proposed algorithm MO-DAGTO2 produced equivalent or considerably better findings in 38 instances, and significantly worse results in just two situations.

Table 8. Results of Wilcoxon rank test for MO-DAGTO2 vs. others.

MO-DAGTO2 vs.	NSGA-II		BMOFOA		BMOChOA		FW-GPAWOA
	$\mathit{p}$-Value	Signf	$\mathit{p}$-Value	Signf	$\mathit{p}$-Value	Signf	$\mathit{p}$-Value	Signf
Lymphography	2.387 × 10${}^{-2}$	+	3.114 × 10${}^{-2}$	+	0.069	=	8.393 × 10${}^{-2}$	+
Diabetic	1.000	=	3.762 × 10${}^{-3}$	−	2.918 × 10${}^{-3}$	+	0.0761	=
Cardiotocography	9.113 × 10${}^{-2}$	+	7.391 × 10${}^{-2}$	+	9.778 × 10${}^{-2}$	+	5.213 × 10${}^{-2}$	+
Cervical Cancer	2.125 × 10${}^{-3}$	+	3.613 × 10${}^{-3}$	+	9.210 × 10${}^{-2}$	+	7.120 × 10${}^{-2}$	+
Lung Cancer	5.912 × 10${}^{-3}$	+	7.112 × 10${}^{-3}$	+	6.452 × 10${}^{-2}$	+	1.000	=
Arrhythmia	2.987 × 10${}^{-2}$	+	2.135 × 10${}^{-2}$	+	6.432 × 10${}^{-3}$	+	3.762 × 10${}^{-3}$	+
Parkinson	3.127 × 10${}^{-3}$	+	9.923 × 10${}^{-2}$	+	8.312 × 10${}^{-3}$	+	5.328 × 10${}^{-3}$	+
Colon Tumor	7.560 × 10${}^{-4}$	+	3.190 × 10${}^{-5}$	+	9.569 × 10${}^{-3}$	+	4.238 × 10${}^{-5}$	+
SRBCT	2.013 × 10${}^{-3}$	+	4.612 × 10${}^{-3}$	+	2.678 × 10${}^{-3}$	−	3.780 × 10${}^{-3}$	+
Leukemia	3.456 × 10${}^{-4}$	+	1.784 × 10${}^{-2}$	+	1.001 × 10${}^{-2}$	+	0.0827	=

5.2.5. Experiment 8

Over the 20 separate runs, Table 9 displays the average execution duration (in minutes) of NSGA-II, BMOFOA, BMOChOA, FW-GPAWOA, and MO-DAGTO2. It is important to notice that all methods have the same population size as well as the same number of repetitions, and were executed on the same machine. Table 9 reports that for the majority of datasets (Lymphography, Diabetic, Cervical Cancer, Lung Cancer, Arrhythmia, Parkinson, Colon Tumor, SRBCT, and Leukemia), our strategy takes longer to execute than the other alternatives. Although the suggested technique picks smaller feature subsets, which should result in fewer wrapper assessments, it thus requires less computing time. Consequently, the reason why the proposed technique takes longer may be explained by the fact that it explores and exploits all of the options available to the population. As a result, each time transfer function must convert continuous to discrete values, which is a rather time-consuming procedure. In addition, when the external archive is full, it employs the crowding distance in the archiving strategy and the deletion process; this distance needs a significant computational cost. It computes the knee point once more in the ending to discover the best of the repository. Because two populations are mixed in NSGA-II and separate fronts are determined at each iteration, the average execution time of NSGA-II and MO-DAGTO2 is quite close in most circumstances. However, in BMOChOA, each gorilla is assigned to either exploration or exploitation phase, depending on the parameter $\mu$. This might be one of the reasons for its faster execution. Although both FW-GPAWOA and the proposed MO-DAGTO2 constitute hybridization of filter and wrapper techniques, the running time of the latter is longer than the former because FW-GPAWOA calculates only MI in its filter evaluation, whereas MO-DAGTO computes both MI and PCC to find its second fitness criteria.

Table 9. Execution time (in minutes) of multi-objective FS methods.

Datasets	NSGA-II	BMOFOA	BMOChOA	FW-GPAWOA	MO-DAGTO2
Lymphography	5.67	5.18	4.39	4.18	6.09
Diabetic	8.12	7.04	7.23	7.02	8.13
Cardiotocography	18.21	10.67	8.98	7.89	13.78
Cervical Cancer	4.12	4.89	2.23	2.03	5.81
Lung Cancer	4.37	5.03	3.12	3.04	6.03
Arrhythmia	9.01	8.03	7.61	7.01	10.35
Parkinson	14.78	13.67	14.11	14.56	17.04
Colon Tumor	5.89	7.02	5.19	5.17	5.96
SRBCT	12.90	10.34	12.34	12.89	14.04
Leukemia	17.21	15.45	16.78	17.45	19.14

5.2.6. Experiment 9

This experiment pertains to the comparison of the efficiency of the proposed SO-DAGTO and MO-DAGTO2 toward the FS task in predicting a particular disease. Regarding the classification performance introduced in Table 10, in six out of ten datasets (Lymphography, Diabetic, Cervical Cancer, Arrhythmia, SRBCT, and Leukemia), MO-DAGTO2 outputs a higher accuracy value by considering relatively fewer features. Specifically, in the case of Cardiotocography and Lung Cancer datasets, SO-DAGTO is able to achieve $2\%$ and $5\%$ more accuracy at the cost of 5 and 20 additional features, respectively. The performance of SO-DAGTO for Parkinson and Colon Tumor datasets is very attractive in terms of classification accuracy at the expense of a larger number of features as compared to MO-DAGTO2. In the end, we have employed the knee point concept [59,60] to filter the best of the optimum solutions present in the external repository. However, for datasets having flat extrema, we have selected the same by using the CD measure. According to the entries in the last column of the Table 10, for the Cervical Cancer, Lung Cancer, Parkinson, Colon Tumor, SRBCT, and Leukemia datasets, MO-DAGTO2 is capable of extracting the best optimum solution in terms of both the number of features and the classification accuracy. In particular, for high-dimensional datasets like Colon Tumor, SRBCT, and Leukemia, the efficiency of MO-DAGTO2 is quite satisfactory in solving the FS job. Overall, we can state that both SO-DAGTO and MO-DAGTO2 have proven to be the best in solving the FS task in medical datasets of variable dimensions. However, researchers are nowadays concentrating more on multi-objective FS approaches because they help practitioners take their vital decisions on the basis of multiple alternatives at hand.

Table 10. Comparison between SO-DAGTO and MO-DAGTO2.

Dataset	Method	Avg_acc	Avg_Feature_Size	Optimum Solution
Lymphography	SO-DAGTO	0.813	6.66	[5,0.831]
	MO-DAGTO2	0.825	4	[2,0.796]
Diabetic	SO-DAGTO	0.689	7	[7,0.7]
	MO-DAGTO2	0.7	3.5	[2,0.688]
Cardiotocography	SO-DAGTO	0.924	8	[7,0.93]
	MO-DAGTO2	0.902	3.5	[3,0.908]
Cervical Cancer	SO-DAGTO	0.956	6	[3,0.958]
	MO-DAGTO2	0.963	9	[2,0.962]
Lung Cancer	SO-DAGTO	0.65	22	[36,0.658]
	MO-DAGTO2	0.592	2.5	[3,0.667]
Arrhythmia	SO-DAGTO	0.629	61	[61,0.644]
	MO-DAGTO2	0.623	3	[4,0.701]
Parkinson	SO-DAGTO	0.89	255.23	[264,0.872]
	MO-DAGTO2	0.85	62.55	[162,0.882]
Colon Tumor	SO-DAGTO	0.84	962	[970,0.857]
	MO-DAGTO2	0.8	236.2	[903,0.871]
SRBCT	SO-DAGTO	0.878	654	[556,0.89]
	MO-DAGTO2	0.903	92.33	[164,0.914]
Leukemia	SO-DAGTO	0.862	1811	[1674,0.877]
	MO-DAGTO2	0.872	964	[794,0.877]

6. Advantages (Pros) of the Suggested Fs Methods

After a careful review of the results of the preceding subsections, it can be inferred that the presented MO-DAGTO2 approach might be an effective candidate for removing extraneous elements from health data. The power of the introduced MO-DAGTO2 method can be summarized as follows.

• This is the first attempt to apply MO-DAGTO for solving discrete optimization tasks such as feature selection.
• MO-DAGTO2 is a multi-objective approach and thus can help medical professionals to make better decisions due to the availability of a large number of optimal solutions.
• It can simultaneously optimize filter and wrapper criteria, resulting in a stronger set of features that really affect the disease and by using which, one can easily and correctly predict a particular issue.
• When comparing MO-DAGTO2 against the other standard multi-objective FS techniques, it is proven to be superior at providing the best Pareto fronts respecting the lower number of traits and higher accuracy it offers.
• The most distinctive feature of this suggested method is its ability to build a reservoir of Pareto optimal solutions, each of which is extremely unique due to the crowding distance.
• In our wrapper evaluation, we choose KNN as a classification algorithm because it is a superior supervised classifier with low computational complexity.
• The suggested MO-DAGTO2 algorithm, with a fusion of both filter and wrapper approaches, achieves better classification accuracy by incorporating short length feature substrings, according to the experimental observations of all nine FS algorithms.
• Because of the great gorilla initialization methodology based on mutual information, the rate of convergence of all four suggested DAGTO algorithms is high when compared to others.
• Because of the greater HV and spread values, the MO-DAGTO2 approach generates Pareto fronts that can control a huge volume in the objective plane.
• Among all the above discussed multi-objective FS strategies, MO-DAGTO2 has the greatest contribution toward discovering the true Pareto front as the SCC values are very impressive in most of the datasets. This indicates its rapid convergence toward the optimal solution set.

7. Case Study with COVID-19 Dataset

The World Health Organization (WHO) stated in 2020 that the Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) had begun to target China and had spread quickly around the globe. Since August 2020, the SARS-CoV-2 virus, called COVID-19, has killed more than 600,000 people all over the world [67]. Machine learning (ML) has recently emerged as a technical revolution that can be used to battle COVID-19 through diagnosing, treatment and identification [68]. Classification and clustering have been both shown to benefit from ML-based techniques. When it comes to constructing scalable ML models, we focus on the features that are most relevant to each dataset. However, it is difficult to build feature vectors that preserve as much information as possible because ML models require a feature string as input. Because of this, even scalability becomes a problem when the datasets are so enormous [69]. Moreover, genomic data from COVID-19 patients has been extensively studied [70,71]. An important issue in this scenario is the convertion of genomic sequences into a fixed-length feature space so that they may be used as inputs for ML classifiers when making predictions. Here, we provide a method for accurately predicting patient death based on a wide range of variables. Doctors can use this problem to prescribe drugs and devise tactics in advance that will assist in saving the majority of the corresponding lives. MO-DAGTO2, the suggested and proven best FS method, is used to predict COVID-19 patient health in this study by using the COVID-19 dataset presented in Table 11 along with five well-known classification models [69], namely KNN, Logistic Regression (LR), Support Vector Machine (SVM), Random Forest (RF), and Decision Tree (DT).

Table 11. Details of COVID-19 Dataset.

SNO	Name	Details	Values
1	case_month	Date received by CDC	March 2020, April 2020, ... , August 2021
2	res_state	State name of USA	AK, CO, FL, ... , UT, VT
3	state_fips_code	Federal Information Processing Standards (FIPS) code for states
4	res_county	Country name
5	county_fips_code	FIPS code foe countries
6	age_group	Patients’s age group	0–17, 18–49, 50–64, and 65+ years
7	Sex	Gender of patient	M, F, other, unknown
8	Race	Race of patient	American Indian/Alaska Native, Asian, Black, Multiple/Other, Native Hawaiian/Other Pacific Islander, White, Unknown
9	Ethnicity		Hispanic, Non-Hispanic, Unknown
10	case_positive_specimen_interval	Weeks between the initial positive specimen collection and the earliest date of collection
11	case_onset_interval	Weeks between earliest date and date of symptom onset
12	Process	Under what process was the case first recognised	Clinical evaluation, routine surveillance, multiple,...
13	exposure_yn	Any of the following known exposures, such as local or international travel, incarceration, a community event, or contact with a previously reported case of COVID-19, did the patient have in the 14 days before becoming ill?	Yes, unknown
14	current_status	Current status of the patient	Laboratory-confirmed case, Probable case.
15	symptom_status	Symptom status of the patient	Asymptomatic, Symptomatic, Unknown
16	hosp_yn	Was the patient hospitalized?	Yes, no, unknown
17	icu_yn	Was the patient admitted to an ICU?	Yes, no, unknown
18	underlying_conditions_yn	Whether the patient is having diabetes, hypertension, cardiovascular disease, etc.	Yes, no
19	death_yn	Whether the patient die as a result of this illness	Yes, no, unknown

The dataset used in this work for case study is known as the COVID-19 Case Surveillance dataset, and it may be found on the website of the Centers for Disease Control and Prevention in the United States (https://data.cdc.gov/Case-Surveillance/COVID-19-Case-Surveillance-Public-Use-Data-with-Ge/n8mc-b4w4/data, accessed on 8 July 2022). There are a total of 32,806,678 records. However, the used dataset consists of only 101,017 patient records after deleting the missing and blank entries. The attributes are listed in Table 11.

Figure 6 illustrates the accuracy and feature size of the suggested MO-DAGTO2 and the other four multi-objective techniques. It can be shown that MO-DAGTO2 attained an excellent classification accuracy of $94\%$ by using only seven factors, which are sex, number of weeks between earliest date and date of symptom onset, known exposures, country, process, underlying conditions, and patient’s age group. The classification results of before and after FS with the utilization of MO-DAGTO2 method are listed in Table 12. Here, the RF classifier outperforms the other classifiers by achieving classification accuracy equal to $95\%$, while considering only seven out of 18 features.

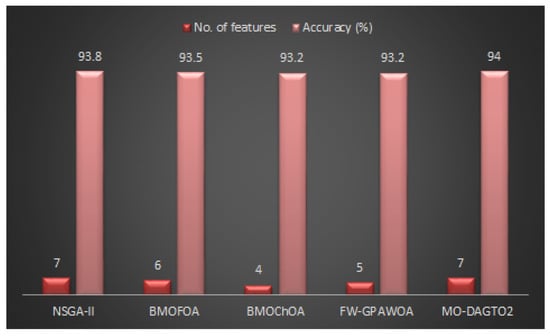
Figure 6. Number of features vs. classification accuracy on COVID-19 data.

Table 12. Classification results of COVID-19 dataset.

Methods		Accuracy	Sensitivity	Specificity	Precision	FPR	Error
KNN	BFS	0.93	0.978	0.385	0.967	0.615	0.051
	AFS	0.94	0.977	0.482	0.973	0.518	0.046
LR	BFS	0.934	1	0.004	0.947	0.996	0.053
	AFS	0.934	1	0	0.947	1	0.053
SVM	BFS	0.934	1	0	0.947	0.5	0.041
	AFS	0.934	1	0	0.947	1	0.053
RF	BFS	0.946	0.982	0.5	0.974	0.5	0.041
	AFS	0.95	0.981	0.459	0.972	0.541	0.041
DT	BFS	0.935	0.976	0.472	0.972	0.528	0.048
	AFS	0.942	0.982	0.442	0.971	0.558	0.044

Our strategy enables doctors to allocate limited medical resources to the most vulnerable groups, especially during situations of medical scarcity, as well as to deliver urgent care. Clinicians may use the risk prediction method to determine which of their patients is most at risk of death, and they can then implement a tailored preventative strategy. A generic clinical decision support system based on our findings might benefit not just COVID-19 but also other possible pandemics in the future. What is more, biologists may be able to use the patterns extracted by this data to develop more effective vaccines and vaccination tactics.

8. Conclusions and Future Research

This study is the first to present a discrete gorilla troop optimization (DAGTO) algorithm to handle the FS task in the biomedical area. We have introduced four DAGTO versions depending on the number and type of fitness criteria to establish the approaches as top candidates for the FS mission. Moreover, an excellent gorilla initialization technique based on mutual information is attempted for faster convergence. The findings of all four DAGTO variants are evaluated and studied, and the MO-DAGTO2 version, which integrates both filter and wrapper approaches, is precisely confirmed as the supreme one at recognizing the ND solutions that is closest to the real Pareto frontiers. The best proven FS technique, MO-DAGTO2, is compared to four well-known multi-objective FS techniques, namely NSGA-II, BMOFOA, BMOChOA, and FW-GPAWOA, to ensure its consistency. When compared to the other four prominent approaches, MO-DAGTO2 has proven to be the most effective in terms of obtaining smaller feature dimensions and better recognition accuracy. In most datasets, the proposed MO-DAGTO2 technique yields the highest standard Pareto fronts, which are confirmed by using different multi-objective performance assessment criteria. By running a Wilcoxon rank test on the HV metric of the estimated fronts from the five techniques, the validity of the recommended MO-DAGTO2 is statistically confirmed once more. The suggested approach was also tested on a dataset regarding patients related to COVID-19.

Furthermore, we have noticed that MO-DAGTO2 takes longer to execute in most circumstances due to the application of the transfer function in both exploration and exploitation of all the members of the repository. In addition, the fitness evaluation involved the calculation of MI, PCC, and classification error rate. As a result, it is our keen interest to examine additional fitness functions in the future to achieve higher efficiency without increasing the running duration. We are also enthusiastic about combining various evolutionary algorithms [72] with other classification algorithms like random forest and ANN. Also, various advanced initialization procedures can also be applied to MO-DAGTO2 to boost its efficiency. Only healthcare data is used here to verify the efficacy of the suggested DAGTOs. However, the proposed approaches may be used to address different optimization challenges in the real world.